A structured additive modeling of diabetes and hypertension in Northeast India

Strong P Marbaniang; Holendro Singh Chungkham; Hemkhothang Lhungdim

doi:10.1371/journal.pone.0262560

. 2022 Jan 13;17(1):e0262560. doi: 10.1371/journal.pone.0262560

A structured additive modeling of diabetes and hypertension in Northeast India

Strong P Marbaniang ^1,^2,^*,^#, Holendro Singh Chungkham ^3,^4,^#, Hemkhothang Lhungdim ¹

Editor: Mohammad Asghari Jafarabadi⁵

PMCID: PMC8758063 PMID: 35025967

Abstract

Background

Multiple factors are associated with the risk of diabetes and hypertension. In India, they vary widely even from one district to another. Therefore, strategies for controlling diabetes and hypertension should appropriately address local risk factors and take into account the specific causes of the prevalence of diabetes and hypertension at sub-population levels and in specific settings. This paper examines the demographic and socioeconomic risk factors as well as the spatial disparity of diabetes and hypertension among adults aged 15–49 years in Northeast India.

Methods

The study used data from the Indian Demographic Health Survey, which was conducted across the country between 2015 and 2016. All men and women between the ages of 15 and 49 years were tested for diabetes and hypertension as part of the survey. A Bayesian geo-additive model was used to determine the risk factors of diabetes and hypertension.

Results

The prevalence rates of diabetes and hypertension in Northeast India were, respectively, 6.38% and 16.21%. The prevalence was higher among males, urban residents, and those who were widowed/divorced/separated. The functional relationship between household wealth index and diabetes and hypertension was found to be an inverted U-shape. As the household wealth status increased, its effect on diabetes also increased. However, interestingly, the inverse was observed in the case of hypertension, that is, as the household wealth status increased, its effect on hypertension decreased. The unstructured spatial variation in diabetes was mainly due to the unobserved risk factors present within a district that were not related to the nearby districts, while for hypertension, the structured spatial variation was due to the unobserved factors that were related to the nearby districts.

Conclusion

Diabetes and hypertension control measures should consider both local and non-local factors that contribute to the spatial heterogeneity. More importance should be given to efforts aimed at evaluating district-specific factors in the prevalence of diabetes within a region.

Introduction

Diabetes and hypertension are major global health concerns. They impose a heavy burden on the public healthcare sector and affect socioeconomic development [1,2]. Statistics from the International Diabetes Federation (IDF) and the World Health Organization (WHO) show that about 463 million adults were living with diabetes in 2019 [3] and 1.13 billion with hypertension in 2015 [4]. According to estimates from 2019, India had the second-highest number (77 million) of diabetic people in the world, and the number is expected to increase to 134 million by 2045 [3]. Evidence from a study based on the Demographic Health Survey shows that 11.3% of Indians aged 15–54 years have diabetes, with the prevalence being higher among men (13.8%) than women (8.8%) [5].

Northeast India, which is located in the Northeastern part of India, is composed of eight small states, namely Assam, Arunachal Pradesh, Manipur, Meghalaya, Mizoram, Nagaland, Sikkim, and Tripura. The region is mostly inhabited by tribal communities belonging to different ethnic groups [6]. Geographically, the region is mostly hilly, which acts as a major hurdle to transportation and communication, affecting the access to and the proper functioning of healthcare facilities in the rainy season [7]. Despite low per capita income, the prevalence of hypertension in the region is much higher than in states that are more socioeconomically developed and have much higher per capita incomes [8]. According to the Indian Demographic Health Survey (2019–20) report, the prevalence of diabetes and hypertension in Northeast India is higher among men than women. As per the survey report, 15.6 percent of men have diabetes as compared to 12.7 percent of women, and 27.6 percent of men have hypertension as compared to 22.3 percent of women [9].

The epidemiology of diabetes and hypertension reveals multiple risk factors. Previous studies have shown that socioeconomic factors–such as low levels of education, high household economic status, and demographic factors like age and sex–increase the risk of diabetes and hypertension [10,11]. Lifestyle behaviours like smoking, alcohol consumption [11–13], low physical activity [14], and dietary habits [15,16] also significantly influence the risk of diabetes and hypertension. Individuals in the same geographical area usually have common beliefs and culture, which may lead to similar levels of exposure to diseases, including diabetes and hypertension [17–19]. Hence, countries with a diverse culture and wide differences in dietary habits are likely to have large variations in the prevalence of diabetes and hypertension based on their geographical location [20,21].

Despite the diversity in dietary habits and cultural practices, studies on diabetes and hypertension in Northeast India have not, to our knowledge, investigated the geographical heterogeneity in the causes of diabetes and hypertension [22,23]. According to Koissi et al., overlooking the effects of heterogeneity in the statistical model may lead to biased parameter estimates [24]. It is important to note here that geographical heterogeneity can be an effect of unobserved factors that may be mostly contextual. Geographical differences in the causes of diabetes and hypertension can be explained by large-scale variability in environmental factors like availability of green spaces in a catchment area of 1 km radius around the residential location [25], level of urbanization and westernization [26], differences in dietary patterns [20,21], level of poverty, and access to medical facilities [27]. Studies have shown that obesity, which leads to diabetes and hypertension, is associated with the availability of green spaces or parks [25,28]. A study by Haynes-Maslow et al. showed that an increase in the number of fast-food restaurants in a county is associated with increasing prevalence of diabetes in that particular county [29]. Several studies from India and abroad [18,20,21] have considered geographical heterogeneity while modeling diabetes and hypertension; however they have overlooked the non-linear effects of continuous variables (that is, using the bivariate spline approach) while modeling the geographical heterogeneity.

This paper contributes to the understanding of spatial variations in diabetes and hypertension in Northeast India by using the Bayesian spatial mixed model approach, which is based on the Markov Chain Monte Carlo (MCMC) simulation technique. To the best of the authors’ knowledge, this study is the first to map diabetes and hypertension in Northeast India in terms of the spatial effect. The map is likely to have significant implications for our understanding of how diabetes and hypertension are spatially distributed and will help health promotion programmes allocate the resources equitably and efficiently.

Material and methods

Study area and data

The focus of the study was Northeast India. Data used in the analysis was drawn from the nationally representative Indian Demographic Health Survey (IDHS), also known as the National Family Health Survey (NFHS-4) which was conducted across the country between 2015 and 2016. The Indian Demographic Health Survey (IDHS) was conducted by the International Institute for Population Sciences (IIPS), Mumbai, a nodal agency appointed by the Ministry of Health and Family Welfare, Government of India [30]. After completing the registration for getting the approval to download the dataset, the data can be downloaded from the DHS website [31]. Since this study used publicly available secondary data and de-identified the respondents, the institutional review board (IRB) exempted it from seeking approval.

The survey employed a two-stage stratified sampling design. In the first stage, primary sampling units (PSUs) were selected based on probability proportional to population size. In rural areas, villages were the PSUs, while in urban areas, census enumeration blocks formed the PSUs. In every selected rural and urban PSU, a complete household mapping and listing was conducted prior to the main survey. Among the selected PSUs, those having at least 300 households were divided into segments of 100–150 households. In NFHS-4, a cluster is either a PSU or a segment of a PSU. In the second stage, 22 households were selected from every selected urban and rural cluster using the systematic random sampling method. From each selected household, information was sought from women aged 15–49 years and men aged 15–54 years [30]. The study excluded Sikkim because its boundary is not connected to the map of Northeast India and including it would have made estimating the spatial effects difficult (Fig 1). The shapefile map used in this study was downloaded from the website of GADM and can be used under the Creative Commons Attribution License (CCAL), CC BY 4.0 [32].

Sampling

The sample for this study comprised 112,062 respondents (98,702 females and 13,360 males) aged 15–49 years. Males comprised only 12 percent of the total sample size because the survey had collected information from males from only 15 percent of the sampled households. A total of 6,878 respondents had diabetes, while 17,677 respondents had hypertension. The study covered 82 districts, whose breakup by states is given in the supporting file S1 Table.

Operational definitions

Diabetes

A FreeStyle Optium H Glucometer device was used to measure the blood glucose. The device uses a small drop of blood drawn from the fingertips to measure the blood glucose level. The blood sample was drawn only once at a random time during the day irrespective of when the respondent last ate. Usually, the presence or absence of diabetes in an individual is determined on the basis of fasting blood glucose level. However, NFHS-4 measured the random blood glucose level. A respondent is considered to have diabetes if the random blood glucose level is >140mg/dl.

Hypertension

Blood pressure was measured with an Omron Hem 7203 blood pressure monitor. Three blood pressure readings were taken in all, with an interval of 5 minutes between the readings. The first reading was discarded and the average of the last two readings was calculated. A respondent was classified as hypertensive if the average systolic blood pressure was ≥ 140 mmHg, or if the average diastolic blood pressure ≥ 90 mmHg, or if the person was taking antihypertensive medication to lower blood pressure at the time of the survey [30].

Dependent variables

The outcome variables were diabetes and hypertension status of a respondent. The values were binary, with 1 implying “Yes” (meaning presence of diabetes or hypertension) and 0 implying “No” (meaning absence).

Explanatory variables

The choice of the explanatory variables was guided by the existing literature. The demographic variables considered in the study were age and sex of the respondents. The socioeconomic variables included the respondents’ caste, marital status, level of education, place of residence, and household wealth. The variables for lifestyle behaviors included cigarette smoking and tobacco and alcohol consumption. To capture the effects of dietary habits on chronic diseases, we included foods consumed by the respondents and categorized them as milk, pulses, vegetables, fish, fruits, eggs, chicken, aerated drinks, and fried food. The fixed effects are compared according to the effect-coding given in Table 1.

Table 1. Prevalence of diabetes and hypertension among adults aged 15–49 years by fixed covariates with effect coding used in the model).

Variables	Diabetes		Hypertension		Effect Coding
Variables	(%)	P^*	(%)	P^*	Effect Coding
Sex
Female	6.16	0.000	15.59	0.000	-1^@
Male	8.03		20.84		1
Residence
Rural	5.88	0.000	15.98	0.000	-1^@
Urban	7.73		16.85		1
Current marital status
Never married	4.00	0.000	8.43	0.000	-1^@
Married	7.18		19.15		1
Widowed/Divorced/Separated	9.41		22.24		2
Caste
Scheduled tribe	6.40	0.639	15.74	0.000	-1^@
Scheduled caste	6.16		16.89		1
Others	6.45		16.63		2
Level of education
Illiterate	7.06	0.000	22.27	0.000	-1^@
Primary	7.21		17.55		1
Secondary	5.84		14.20		2
Higher secondary	7.13		15.50		3
Consume milk
No	7.01	0.000	16.38	0.529	-1^@
Yes	6.27		16.18		1
Consume pulses
No	5.71	0.400	20.87	0.000	-1^@
Yes	6.38		16.17		1
Consume vegetables
No	4.21	0.152	18.42	0.328	-1^@
Yes	6.38		16.21		1
Eat fruits
No	7.15	0.189	20.52	0.000	-1^@
Yes	6.36		16.14		1
Consume egg
No	8.16	0.000	20.13	0.000	-1^@
Yes	6.32		16.10		1
Eat fish
No	7.26	0.069	15.74	0.518	-1^@
Yes	6.36		16.22		1
Eat chicken
No	8.26	0.000	19.35	0.000	-1^@
Yes	6.33		16.13		1
Eat fried food
No	6.73	0.349	21.23	0.000	-1^@
Yes	6.36		16.01		1
Take aerated drinks
No	6.88	0.000	17.31	0.000	-1^@
Yes	6.23		15.90		1
Consume alcohol
No	6.20	0.000	15.16	0.000	-1^@
Yes	7.42		22.51		1
Currently smoke cigarettes
No	6.24	0.000	16.11	0.000	-1^@
Yes	8.56		17.91		1
Consume tobacco
No	6.28	0.000	16.24	0.194	-1^@
Yes	9.27		15.43		1

Open in a new tab

@: Reference category

*: p-value of chi-square test of independence.

The continuous explanatory variables for the study were age of the respondents (in years), body mass index (kg/m²), and wealth index score.

Statistical analysis

A multiple logistic regression was applied to select the potential covariates of diabetes and hypertension prior to the spatial analysis. To allow for more potential covariates for the spatial analysis, a significance level of 20% was set for the selection of the potential covariates. They are listed in Table 1.

The traditional linear regression model has the limitation of not being able to incorporate spatial and non-linear effects more flexibly in the model. For a study like ours, where the primary objective was to explore unobserved heterogeneity in the structured and unstructured spatial effects, geo-additive models were better suited than the linear regression models. Therefore, the data were fitted using geo-additive logistic regression models to understand the fixed as well as the spatial effects for diabetes and hypertension (the term chronic disease was used in place of diabetes and hypertension). The respondents’ status of chronic disease was a binary outcome; it was distributed as Bernoulli (p_ij) where p_ij was the probability that respondent j in district i had a chronic disease. The district of the respondent was labelled as s_iϵ (1, 2, 3….,82), where the label matched the labels on the map. The spatial effect of district s_i, in which the respondent resided, was given by f_spatial(s_i). The spatial effect comprised two parts: a spatially correlated (or structured) effect and an uncorrelated (or unstructured) effect. Thus,

f_{s p a t i a l} (s_{i}) = f_{s t r u c t u r e d} (s_{i}) + f_{u n s t r u c t u r e d} (s_{i})

The following models were fitted to estimate the fixed and spatial effects.

M0: logit ${(p}_{i j}) = z_{i}^{T} β$
M1: logit ${(p}_{i j}) = z_{i}^{T} β + f_{1} (u_{i 1}) + f_{2} (u_{i 2}) + f_{3} (u_{i 3}) + \dots \dots + f_{p} (u_{i p})$
M2: logit ${(p}_{i j}) = z_{i}^{T} β + f_{s t r u c t u r e d} (s_{i}) + f_{u n s t r u c t u r e d} (s_{i})$
M3: logit ${(p}_{i j}) = z_{i}^{T} β + f_{1} (u_{i 1}) + f_{2} (u_{i 2}) + f_{3} (u_{i 3}) + \dots \dots + f_{p} (u_{i p}) + f_{s t r u c t u r e d} (s_{i})$
M4: logit ${(p}_{i j}) = z_{i}^{T} β + f_{1} (u_{i 1}) + f_{2} (u_{i 2}) + f_{3} (u_{i 3}) + \dots \dots + f_{p} (u_{i p}) + f_{u n s t r u c t u r e d} (s_{i})$
M5: logit ${(p}_{i j}) = z_{i}^{T} β + f_{1} (u_{i 1}) + f_{2} (u_{i 2}) + f_{3} (u_{i 3}) + \dots \dots + f_{p} (u_{i p}) + f_{s t r u c t u r e d} (s_{i}) + f_{u n s t r u c t u r e d} (s_{i})$

In model M0, all the categorical and continuous variables were considered as fixed effects, and β was the parameter in the vector form. In model M1, categorical variables were treated as fixed effects, while continuous variables were modelled as a non-parametric smooth function f_js. In model M2, all the covariates were modelled as fixed covariates, and the district of the respondent was modelled as a spatial effect. Model M3 was a combination of M1 and M2 in which the smooth function f_js was assigned with Bayesian P-spline priors and the spatial effect f_structured(s_i) with Markov random field priors [33,34]. We considered a fourth model, M4, which was again a combination of M1 and M2, where the smooth function f_js was assigned with Bayesian P-spline priors and the spatial effect as f_unstructured(s_i). We considered a fifth and the final model, M5, which was a combination of M3 and M4, where both structured and unstructured spatial effects were included. The spatial effects represented the effects of the unobserved covariates that were not incorporated in the model and accounted for spatial autocorrelation.

The structured spatial effect f_structured(s_i) accounted for the spatial variation due to the unobserved influences that arose due to the assumption that the nearby districts were likely to be correlated with respect to their outcomes. However, in the case of the unstructured spatial effect, f_unstructured(s_i), the spatial variation was due to the unobserved influences that were present locally, that is, within a district. Markov random field (MRF) priors were specified for the structured spatial effect. Two districts were defined as neighbors if they shared a common boundary. The conditional mean of f_structured(s_i) was an average of the evaluations of f_structured(s_i) of other neighboring districts. In the same way, i.i.d Gaussian priors were assigned for the unstructured spatial effects f_unstructured(s_i).

A fully Bayesian integrated approach, based on the Markov Chain Monte Carlo (MCMC) simulation, was used to estimate the model parameters. The estimated prior odds ratio (OR) could be interpreted as the odds ratio from the logistic regression. The model was fitted in R using the freely available package bamlss [35]. For the analysis, we used a total of 40,000 MCMC iterations and 10,000 burns in the sample. Convergence checks of the models were based on autocorrelation and the sampling paths. Finally, all the models used in the analysis were compared using the Deviance Information Criterion (DIC) values [36]; the model with the smallest DIC values was preferred for estimating the parameters. DIC is defined as $D I C = \bar{D} + p_{D}$ , where $\bar{D}$ is the posterior mean of the model deviance, which is a measure of goodness of fit, and p_D is the effective number of parameters, which indicates the complexity of the model and penalizes over-fitting.

Results

Descriptive statistics

Table 1 shows the prevalence of diabetes and hypertension across the categorical covariates. It is evident from the results that males, urban residents, and widowed, divorced or separated individuals had a higher prevalence of diabetes and hypertension. There was a significant gender difference in the prevalence of diabetes and hypertension. This difference was also seen for place of residence, marital status, and educational level of the respondents.

The prevalence of diabetes and hypertension was the highest among respondents who were widowed, divorced or separated. The results also show that the prevalence of diabetes was lower among respondents who consumed milk than those who did not. However, this association was not significant for the prevalence of hypertension. Consuming fruits and fried foods showed a positive impact in reducing the prevalence of hypertension. Unhealthy lifestyle behaviors, such as cigarette smoking and drinking alcohol, were significantly associated with a high prevalence of diabetes and hypertension. Since all the categorical variables listed in Table 1 showed a significant association with diabetes and hypertension at 20% level of significance in the preliminary analysis, they were all included in the spatial logistic regression model (Tables 3 and 4).

Table 3. Posterior estimates of the fixed effects parameters for diabetes in Northeast India.

Variables	Mean	SD	2.5% Quantile	Median	97.5% Quantile
Sex
Female^@
Male	0.138^*	0.025	0.088	0.137	0.187
Residence
Rural^@
Urban	0.028	0.017	-0.006	0.028	0.064
Current marital status
Never married^@
Married	-0.104^*	0.025	-0.151	-0.105	-0.056
Widowed/Divorced/Separated	-0.030	0.040	-0.110	-0.030	0.044
Caste
Scheduled tribe^@
Scheduled caste	-0.030	0.034	-0.095	-0.028	0.033
Others	-0.028	0.036	-0.099	-0.028	0.044
Level of education
Illiterate^@
Primary	0.032	0.031	-0.029	0.031	0.096
Secondary	-0.031	0.024	-0.077	-0.030	0.015
Higher secondary	-0.062^*	0.032	-0.121	-0.062	-0.001
Consume milk
No^@
Yes	-0.025	0.020	-0.062	-0.026	0.016
Consume pulses
No^@
Yes	0.075	0.080	-0.069	0.076	0.235
Consume vegetables
No^@
Yes	0.054	0.171	-0.269	0.050	0.392
Eat fruits
No^@
Yes	-0.076	0.050	-0.175	-0.075	0.025
Consume egg
No^@
Yes	-0.043	0.045	-0.137	-0.044	0.044
Eat fish
No^@
Yes	-0.078	0.054	-0.181	-0.077	0.024
Eat chicken
No^@
Yes	-0.007	0.050	-0.108	-0.008	0.088
Eat fried food
No^@
Yes	0.005	0.038	-0.069	0.005	0.082
Take aerated drinks
No^@
Yes	-0.012	0.018	-0.047	-0.012	0.023
Consume alcohol
No^@
Yes	-0.023	0.023	-0.066	-0.023	0.019
Smoke cigarettes
No^@
Yes	0.003	0.027	-0.049	0.002	0.059
Consume tobacco
No^@
Yes	-0.038^*	0.016	-0.069	-0.038	-0.006

Open in a new tab

@: Reference category

*: Statistical significance at 5%.

Table 4. Posterior estimates of the fixed effects parameters for hypertension in Northeast India.

Variables	Mean	SD	2.5% Quantile	Median	97.5% Quantile
Sex
Female^@
Male	0.159^*	0.017	0.125	0.160	0.192
Residence
Rural^@
Urban	0.05^*	0.013	0.026	0.050	0.074
Current marital status
Never married^@
Married	-0.053^*	0.021	-0.085	-0.053	-0.019
Widowed/Divorced/Separated	0.006	0.024	-0.051	0.007	0.063
Caste
Scheduled tribe^@
Scheduled caste	-0.034	0.021	-0.076	-0.034	0.008
Others	0.034	0.024	-0.013	0.035	0.079
Level of education
Illiterate^@
Primary	0.009	0.021	-0.032	0.008	0.051
Secondary	0.004	0.015	-0.025	0.004	0.034
Higher secondary	-0.096^*	0.021	-0.136	-0.096	-0.054
Consume milk
No^@
Yes	-0.036^*	0.015	-0.065	-0.036	-0.007
Consume pulses
No^@
Yes	-0.074	0.048	-0.065	-0.076	0.023
Consume vegetables
No^@
Yes	-0.139	0.091	-0.307	-0.141	0.044
Eat fruits
No^@
Yes	-0.025	0.034	-0.091	-0.025	0.043
Consume egg
No^@
Yes	-0.071^*	0.032	-0.132	-0.072	-0.010
Eat fish
No^@
Yes	0.081^*	0.041	0.001	0.083	0.162
Eat chicken
No^@
Yes	-0.018	0.035	-0.086	-0.018	0.052
Eat fried food
No^@
Yes	-0.035	0.023	-0.081	-0.036	0.011
Take aerated drinks
No^@
Yes	-0.002	0.012	-0.026	-0.003	0.021
Consume alcohol
No^@
Yes	-0.12^*	0.015	-0.147	-0.120	-0.091
Smoke cigarettes
No^@
Yes	0.086^*	0.021	0.042	0.086	0.126
Consume tobacco
No^@
Yes	0.012	0.011	-0.010	0.013	0.033

Open in a new tab

@: Reference category

*: Statistical significance at 5%.

Empirical bayesian results

Model selection

The selection of a better model is based on DIC and deviance values. A model with the smallest DIC and deviance values is considered the best model. It can be seen from Table 2 that model M5 had the smallest DIC and deviance values for both diabetes and hypertension. Models with differences in DIC values less than 3 cannot be differentiated, while those with values between 3 and 7 can be weakly differentiated [37]. Taking all of these criteria into account, this study based the interpretation of the results of the analysis on model M5, the geo-additive model with both structured and unstructured spatial effects.

Table 2. Comparison of models based on deviance information criterion (DIC).

Diabetes	Model Fit	Deviance ( $\bar{D}$ )	p _D	*DIC*	Δ ^§ *DIC*
	M0	42763.22	9.9387	42773.17	2941.24
	M1	46648.94	73.9609	46722.91	6890.98
	M2	40199.76	101.2486	40301.01	469.08
	M3	39725.00	111.2923	39836.30	4.37
	M4	39722.80	112.4136	39835.28	3.35
	M5	3971844	113.4988	39831.93	Reference
Hypertension	Model Fit	Deviance ( $\bar{D}$ )	p _D	*DIC*	Δ ^§ *DIC*
	M0	79703.78	9.8346	79713.62	7402.04
	M1	88477.04	77.5036	88554.55	16242.97
	M2	73197.80	105.1395	73302.95	991.37
	M3	72204.20	112.3875	72316.50	4.92
	M4	72200.80	113.9219	72314.78	3.20
	M5	72327.87	115.5265	72311.58	Reference

Open in a new tab

M0:Categorical and continuous covariates were treated as fixed effect; M1:Categorical were treated as fixed and continuous as non-linear effect; M2: All covariates were treated as fixed effect, and districts as spatial effect; M3: Combination of M1 and M2 with only structured spatial effect; M4: Combination of M1 and M2 with only unstructured spatial effect; M5: Combination of M3 and M4; ^§: Difference of M5 against M0, M1, M2, M3 and M4.

Fixed effects

In model M5, the effects of the categorical covariates were assumed to be fixed and were estimated jointly with the continuous and spatial covariates. The posterior means and the corresponding 97.5% credible intervals of the fixed effects parameters are shown in Table 3. The fixed effects covariates which were significant to diabetes were sex, current marital status, level of education, and consumption of tobacco. The fixed effect coefficient for males was positive, which indicates that being male increased the risk of diabetes as compared to being female. The coefficient for marital status ‘married’ was negative, which means that married individuals were at a reduced risk of diabetes as compared to never married individuals. Individuals who consumed tobacco were also seen as being at a reduced risk of diabetes.

For hypertension, the posterior means and the corresponding 97.5% credible intervals of the fixed effects parameters are given in Table 4. Urban residence had a positive effect on hypertension, meaning that individuals who lived in urban areas were at an increased risk of hypertension. Individuals who were educated up to the higher secondary (high school) level were found to be less likely to suffer from hypertension than individuals without an education. Consumption of milk showed a negative coefficient, meaning that having milk reduced the risk of hypertension. An interesting finding of our analysis was that individuals who consumed alcohol were at a lower risk of hypertension as compared to those who did not.

Non-linear effects

Another important advantage of using the geo-additive model is its ability to incorporate non-linear effects due to continuous covariates. In this study, we incorporated the non-linear effects of body mass index (BMI), wealth index score, and age of the respondents.

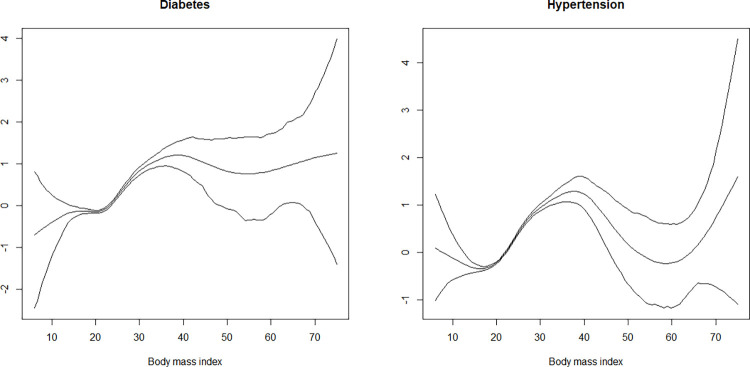
Body mass index of individuals had a non-linear effect on diabetes and hypertension (Fig 2). It is evident from Fig 1 that as the BMI increased, its effect on diabetes and hypertension also increased. The risk of diabetes and hypertension was lower at BMI values of 20 to 25; however, the risk increased for BMI values of 50 and more.

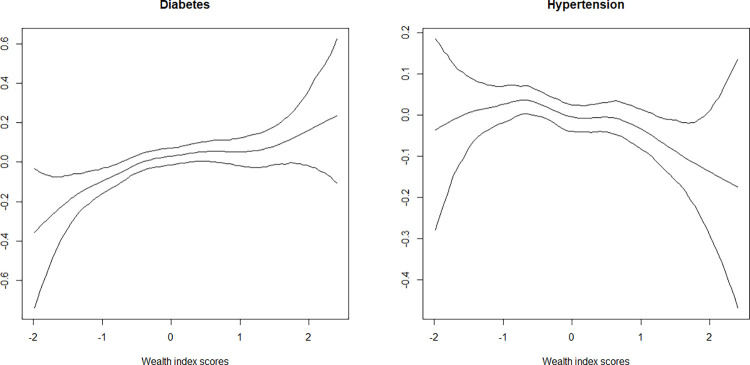
Household wealth index scores had a non-linear effect on diabetes and hypertension (Fig 3). The functional relationship between household wealth index and diabetes and hypertension was almost inverted U-shaped. With increasing household wealth status, the effect on diabetes also increased. Interestingly, the reverse was observed in the case of hypertension, that is, as the household wealth status increased, its effect on hypertension decreased.

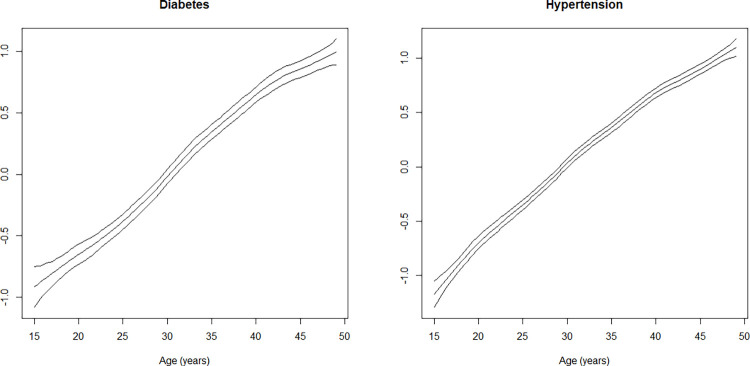
Age of respondents showed an almost linear relationship with diabetes and hypertension (Fig 4). The effect of age on diabetes and hypertension was the lowest at age 15 years and the maximum at age 49 years.

Spatial effects

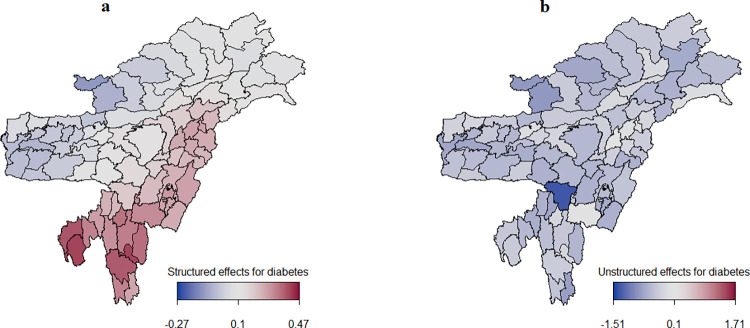
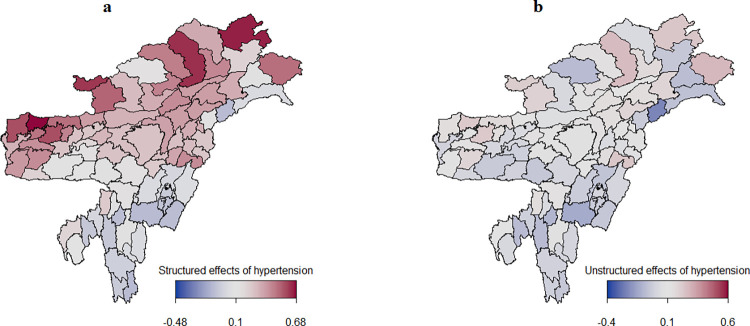
Figs 5 and 6 present the estimated spatial effects of diabetes and hypertension, with color ranges from blue to maroon indicating low to high risk of diabetes and hypertension. Districts marked in blue had a negative spatial effect and were, therefore, associated with lower odds of diabetes and hypertension. Districts shown in maroon had a positive spatial effect and were, therefore, associated with higher odds of diabetes and hypertension. Spatial effects are surrogates for unknown influences like environmental factors, climate, availability of proper transport, and access to good healthcare facilities.

Fig 5A clearly shows a significant clustering of diabetes in Northeast India, with the risk of diabetes being higher in the districts of Nagaland, Manipur, Mizoram, and Tripura. Districts with low risk of diabetes are in the states of Assam, Arunachal Pradesh, and Meghalaya. However, overall, the whole of Northeast India appears to be less affected by the unstructured spatial effects of diabetes (Fig 5B). The structured spatial effects of diabetes, which ranged from -0.27 to 0.47, were weak in comparison to the unstructured spatial effects, which ranged from -1.51 to 1.71

Fig 6 shows spatial clustering of hypertension. It can be seen that the risk of hypertension was higher in the districts of Assam, Arunachal Pradesh, Nagaland, and Meghalaya and lower in the districts of Manipur, Mizoram, Tripura, and Hills and Barak valley of Assam. In Fig 6B, the unstructured spatial effects of hypertension can be observed in some districts of Arunachal Pradesh (Anjaw, Dibang valley, and West Siang), suggesting that the spatial variation was due to the effect of unmeasured local influences. For hypertension, the structured spatial effects ranged from -0.48 to 0.68, which dominated the unstructured spatial effects (-0.4 to 0.6).

Discussion

This study attempted to explore the linear, non-linear, and spatial determinants of diabetes and hypertension among adults 15–49 years of age in Northeast India. The findings of this study reveal that the linear or fixed effect variables, namely sex of respondents, place of residence, marital status, and level of education, were significantly associated with the risk of diabetes and hypertension. Furthermore, the study noticed that the continuous variables, namely age of the respondents, body mass index, and household wealth index score, had a non-linear effect on the risk of diabetes and hypertension. This study adopted the geo-additive logistic approach to examine the relationship between diabetes and hypertension and their risk factors. The geo-additive model had the advantage of allowing mapping of the residual spatial effects to diabetes and hypertension while considering the effect of the non-linear covariates on the assumption of additivity.

In a geo-additive model, the spatial effect is the sum of the structured and unstructured spatial effects. This method has the advantage that it allows to account for possible unmeasurable factors and heterogeneity. In addition, the model allows for the exploration of the subtle influence of the non-linear relationship of the continuous covariates that is not possible in a linear model.

Spatial effects for diabetes

The findings of the study reveal that the structured spatial effects for diabetes were relatively weaker in comparison with the unstructured spatial effects (Fig 5), meaning that the role of a district on the risk of diabetes was not similar to that of the neighbouring districts. This is an indication that geographical and environmental factors which surpass the boundaries of districts likely do not play any significant role in diabetes. With unstructured spatial effects for diabetes being dominant in this study, it can be concluded that there are unobserved district-specific influences that are not structured spatial effects (that is, not interrelated with those of neighboring districts) contributing to diabetes [38]. Such district-specific factors contributing to diabetes may include availability of healthcare facilities, cost and quality of healthcare, and cost of living. These factors may vary significantly between and within the states.

A study in Northeast India by Ngangbam & Roy found that people living in districts with many medical institutions and better road connectivity were more likely to seek formal healthcare services because of the easy accessibility [39]. Their study also revealed that high treatment cost and poor quality of healthcare services reduced the probability of utilizing the healthcare services in a given place [39].

Spatial effects for hypertension

The results indicate the clustering of hypertension in the districts of Arunachal Pradesh, Assam, and Nagaland (Fig 6). A high prevalence of hypertension in these three states has been reported in a previous study as well [40]. The present study revealed that structured spatial effects for hypertension dominated the unstructured spatial effects, meaning that the risk of hypertension in a particular district was similar to that in districts that were in close proximity. This is an indication that geographical and environmental factors surpassing district boundaries may have a significant role in hypertension. This clear structured spatial pattern for hypertension begs an explanation. The geographical or environmental factors contributing to hypertension may include lifestyle differences and urbanization [27]. One possible reason for the high prevalence of hypertension in Arunachal Pradesh may be that the region is located at a high altitude. A study in Tibet showed a strong correlation between the prevalence of hypertension and altitude, with every 100 m increase in altitude corresponding to a 2% increase in the prevalence of hypertension [41]. However, the relationship between hypertension and altitude is not clear and needs further investigation. Another possible explanation may lie in the intake of large amounts of sodium by way of salt that is added to yak butter tea. The consumption of yak butter tea helps to keep the body warm in the cold environment of the Himalayan mountains [42,43].

Studies suggest that consuming five cups or more of yak butter tea daily exposes an individual to a higher risk of hypertension as compared to those whose consumption is less [44]. Frequent consumption of salty butter tea may elevate the daily salt intake by four to five times, which is above the limits recommended by the World Health Organization [41]. But it is also well-known that even though people living at high altitudes are used to consuming large amounts of salt, they are less obese and fitter than those living at lower altitudes [45].

The high prevalence of hypertension in Arunachal Pradesh may also be attributed to the high alcohol consumption [46]. In Assam, it may be attributed to the high salt intake, higher body mass index, consumption of locally prepared alcohol, and central obesity [47]. In Nagaland, the high prevalence of hypertension may be attributed to lifestyle changes and changes in diet, which are direct outcomes of socioeconomic development and food consumption pattern [48].

Fixed and non-linear effects

The fixed effect factors for diabetes and hypertension, which were significant in this study, were sex of the respondent, place of residence, marital status, and highest level of education (Tables 3 and 4). The influence of these factors on the risk of diabetes and hypertension is in agreement with the findings of previous studies [8,16]. The finding that men are more likely to suffer from diabetes and hypertension has also been reported in previous studies [49,50]. Men are associated with more smoking and a higher consumption of alcohol, both of which are common risk factors of diabetes and hypertension [5]. The results also demonstrate that the consumption of milk and eggs significantly reduces the risk of hypertension. An interesting finding was that the consumption of alcohol was associated with a lower risk of hypertension. One possible reason for this finding is that the current drinkers may have cut down on their alcohol intake to moderate levels, resulting in their blood pressure coming back to normal levels [51].

Body mass index (BMI) was found to have a non-linear relationship with diabetes and hypertension. The results of the non-linear effect of BMI reveal that the risk of diabetes and hypertension was low among individuals having a normal BMI. It increased among those having BMI ranging from 30 to 40, then decreased among those with BMI ranging from 40 to 60, and then again increased among those having BMI above 60 (Fig 2). The non-linear effect of BMI on the risk of cardiovascular diseases and mortality has been reported in many studies [52,53]. Individuals with a higher BMI may not necessarily have high fat mass composition, but a high muscle or lean mass composition [54]. A higher amount of lean mass in an individual may act as a protective factor against cardiovascular disease and the individual may be considered healthy or having a good health [54,55]. By contrast, an individual may have a low BMI but a high body fat mass composition, increasing their likelihood of having cardiovascular disease [53].

Household wealth index score was found to have a non-linear relationship with diabetes and hypertension (Fig 3). The risk of diabetes was the highest among individuals with the richest wealth index score as compared to their counterparts having a poorer wealth index score. However, the risk of hypertension was the highest among individuals having the poorest wealth index score as compared to their counterparts having the richest wealth index score. Consistent with the previous studies, this study revealed that economic status is inversely related with the risk of hypertension [56–59]. Individuals with a higher income can afford to pay for a healthier lifestyle, including regular physical exercise and a healthier diet and benefit from accessibility to advanced and quality healthcare services. All such efforts likely reduce the risk of hypertension.

Our study is not without limitations. Firstly, it was cross-sectional in nature and, therefore, no causal inferences could be made from the results and findings. Secondly, since the study was based on secondary data sets, we were constrained to use only the variables found in the IDHS. Thirdly, the unavailability of district-level information on such factors as cost of living, cost of treatment for diabetes and hypertension, medical institutions, level of urbanization, availability of green space, and altitude meant that we were unable to ascertain the influence of these factors on the spatial variability of diabetes and hypertension. Despite the limitations, the strength of the study lies in the application of the Bayesian geo-additive model, which allowed for a joint estimation of fixed effect covariates, non-linear covariates, spatially structured variation, and spatially unstructured heterogeneity.

Conclusion

In conclusion, it is evident that there are spatial effects for diabetes and hypertension in Northeast India. The results suggest that district-specific factors (that is, factors not related to neighboring districts) are most likely to increase the prevalence of diabetes. However, in the case of hypertension, factors found in districts in proximity to one another are most likely to increase its prevalence. Gender, place of residence, level of education, household wealth status, BMI, and consumption of egg and milk are significant to the risk of diabetes and hypertension. Besides considering the factors that are already known, diabetes and hypertension control measures for Northeast India should take into account the risk factors present within the districts and those related to the proximate districts as they possibly play a role in driving the spatial variability of diabetes and hypertension in the region. Evaluation of district-specific factors of diabetes within the region should be give importance.

Supporting information

S1 Table. Breakup of 82 districts by states in Northeast India.

(PDF)

Click here for additional data file.^{(43.5KB, pdf)}

Acknowledgments

The authors are grateful to the Demographic Health Survey (DHS) Program for providing the data for this study. Authors would like to thank the editor and two anonymous reviewers for their valuable comments and suggestions towards improvement of the paper. Also, the authors would like to thank Shailja Thakur for copyediting the manuscript.

Data Availability

The data can be found from the following link: https://dhsprogram.com/data/dataset/India_Standard-DHS_2015.cfm?flag=1.

Funding Statement

The author(s) received no specific funding for this work.

References

1.Constant AF, Geladari E V., Geladari C V. “The Economic Burden of Hypertension.” In: Andreadis EA, editor. Hypertension and Cardiovascular Disease [Internet]. Cham: Springer International Publishing; 2016. p. 351–9. Available from: http://link.springer.com/10.1007/978-3-319-39599-9. [Google Scholar]
2.Lin X, Xu Y, Pan X, Xu J, Ding Y, Sun X, et al. Global, regional, and national burden and trend of diabetes in 195 countries and territories: an analysis from 1990 to 2025. Sci Rep [Internet]. 2020. Dec 8;10(1):14790. Available from: doi: 10.1038/s41598-020-71908-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
3.International Diabetes Federation. Advocacy guide to the IDF Diabetes Atlas Ninth edition 2019 [Internet]. Brussels, Belgium:International Diabetes Federation; 2019 [cited 2019 Nov 14]. Available from: http://www.diabetesatlas.org/.
4.World Health Organization. Hypertension [Internet]. WHO. 2019. [cited 2021 Feb 3]. Available from: https://www.who.int/news-room/fact-sheets/detail/hypertension. [Google Scholar]
5.Gupta R, Gaur K, S. Ram CV. Emerging trends in hypertension epidemiology in India. J Hum Hypertens [Internet]. 2019. Aug 25 [cited 2019 Nov 16];33(8):575–87. Available from: doi: 10.1038/s41371-018-0117-3 [DOI] [PubMed] [Google Scholar]
6.Marbaniang SP. Women Care and Practices in the Management of Childhood Diarrhea in Northeast India. Child Care Pract [Internet]. 2020. Sep 17;1–13. Available from: https://www.tandfonline.com/doi/full/10.1080/13575279.2020.1812534. [Google Scholar]
7.Hossain F. Levels of Health Care and Health Outcomes in Northeast India. Indian J Hum Dev. 2019;13(2):221–32. [Google Scholar]
8.Ghosh S, Kumar M. Prevalence and associated risk factors of hypertension among persons aged 15–49 in India: a cross-sectional study. BMJ Open [Internet]. 2019. Dec 16;9(12):e029714. Available from: doi: 10.1136/bmjopen-2019-029714 [DOI] [PMC free article] [PubMed] [Google Scholar]
9.IIPS and ICF. National Family Health Survey (NFHS-5): Fact Sheet Key Indicators 22 States/UTs from Phase-1 [Internet]. 2020. Available from: http://rchiips.org/nfhs/factsheet_NFHS-5.shtml. [Google Scholar]
10.Akhtar S, Dhillon P. Prevalence of diagnosed diabetes and associated risk factors: Evidence from the large-scale surveys in India. J Soc Heal Diabetes [Internet]. 2017. Jun 23;05(01):028–36. Available from: http://www.thieme-connect.de/DOI/DOI?10.4103/2321-0656.194001. [Google Scholar]
11.Nam K Do Van NB, Hoang LV Duc TP, Thi Ha TT Tuan VT, et al. Hypertension in a mountainous province of Vietnam: prevalence and risk factors. Heliyon [Internet]. 2020. Feb;6(2):e03383. Available from: doi: 10.1016/j.heliyon.2020.e03383 [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Li G, Wang H, Wang K, Wang W, Dong F, Qian Y, et al. The association between smoking and blood pressure in men: a cross-sectional study. BMC Public Health [Internet]. 2017. Dec 10;17(1):797. Available from: http://bmcpublichealth.biomedcentral.com/articles/10.1186/s12889-017-4802-x. doi: 10.1186/s12889-017-4802-x [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Marbaniang SP, Lhungdim H, Chauhan S, Srivastava S. Interaction of multiple risk factors and population attributable fraction for type 2 diabetes and hypertension among adults aged 15–49 years in Northeast India. Diabetes Metab Syndr Clin Res Rev [Internet]. 2021. Sep;15(5):102227. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1871402121002472. doi: 10.1016/j.dsx.2021.102227 [DOI] [PubMed] [Google Scholar]
14.Sobngwi E, Mbanya J-CN, Unwin N, Kengne A, Fezeu L, Minkoulou E, et al. Physical activity and its relationship with obesity, hypertension and diabetes in urban and rural Cameroon. Int J Obes [Internet]. 2002. Jul 25;26(7):1009–16. Available from: http://www.nature.com/articles/0802008. doi: 10.1038/sj.ijo.0802008 [DOI] [PubMed] [Google Scholar]
15.Campbell AP. DASH Eating Plan: An Eating Pattern for Diabetes Management. Diabetes Spectr [Internet]. 2017. May 15;30(2):76–81. Available from: http://spectrum.diabetesjournals.org/lookup/doi/10.2337/ds16-0084. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Marbaniang SP, Lhungdim H, Yadav B, Yajurvedi VK. Overweight/obesity risks and prevalence of diabetes and hypertension in North Eastern India: An analysis using seemingly unrelated probit model. Clin Epidemiol Glob Heal [Internet]. 2021. Jul;11:100764. Available from: https://linkinghub.elsevier.com/retrieve/pii/S2213398421000683. [Google Scholar]
17.Adebayo SB, Gayawan E, Fagbamigbe AF, Bello FW. Bayesian geo-additive spatial modelling of HIV prevalence using data from population-based surveys. HIV AIDS Rev [Internet]. 2019;18(4):247–60. Available from: https://www.termedia.pl/doi/ doi: 10.5114/hivar.2019.83852 [DOI] [Google Scholar]
18.van der Sande M, Milligan P, Walraven G, Dolmans W, Newport M, Nyan O, et al. Geographical variation in prevalence of hypertension within The Gambia. J Hum Hypertens [Internet]. 2001. Oct 12;15(10):733–9. Available from: http://www.nature.com/articles/1001259. doi: 10.1038/sj.jhh.1001259 [DOI] [PubMed] [Google Scholar]
19.Hernandez AM, Jia P, Kim H-Y, Cuadros DF. Geographic Variation and Associated Covariates of Diabetes Prevalence in India. JAMA Netw Open [Internet]. 2020. May 1;3(5):e203865. Available from: https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2765281. doi: 10.1001/jamanetworkopen.2020.3865 [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Singh S, Puri P, Subramanian S V. Identifying spatial variation in the burden of diabetes among women across 640 districts in India: a cross-sectional study. J Diabetes Metab Disord [Internet]. 2020. Jun 27;19(1):523–33. Available from: http://link.springer.com/10.1007/s40200-020-00545-w. doi: 10.1007/s40200-020-00545-w [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Ghosh K, Dhillon P, Agrawal G. Prevalence and detecting spatial clustering of diabetes at the district level in India. J Public Health (Bangkok) [Internet]. 2020. Oct 24 [cited 2020 Feb 20];28(5):535–45. Available from: http://link.springer.com/10.1007/s10389-019-01072-6. [Google Scholar]
22.Zaman FA, Borang A. Prevalence of diabetes mellitus amongst rural hilly population of North Eastern India and its relationship with associated risk factors and related co-morbidities. J Nat Sci Biol Med [Internet]. 2014. Jul;5(2):383–8. Available from: https://pubmed.ncbi.nlm.nih.gov/25097420. doi: 10.4103/0976-9668.136195 [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Borah PK, Mahanta J, Kalita HC, Bhattacharjee CK. Distribution of hypertension subtypes in a hill tribe of Mizoram, Northeast India. Indian Heart J [Internet]. 2020;72(5):398–402. Available from: doi: 10.1016/j.ihj.2020.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Koissi M-C, Högnäs G. Using WinBUGS to Study Family Frailty in Child Mortality, with an Application to Child Survival in Ivory Coast. African Popul Stud [Internet]. 2013. Nov 1;20(1):1–17. Available from: http://aps.journals.ac.za/pub/article/view/384. [Google Scholar]
25.Astell-Burt T, Feng X, Kolt GS. Is Neighborhood Green Space Associated With a Lower Risk of Type 2 Diabetes? Evidence From 267,072 Australians. Diabetes Care [Internet]. 2014. Jan;37(1):197–201. Available from: http://care.diabetesjournals.org/lookup/doi/10.2337/dc13-1325. [DOI] [PubMed] [Google Scholar]
26.Kandala N-B, Stranges S. Geographic Variation of Overweight and Obesity among Women in Nigeria: A Case for Nutritional Transition in Sub-Saharan Africa. Kazembe L, editor. PLoS One [Internet]. 2014. Jun 30;9(6):e101103. Available from: doi: 10.1371/journal.pone.0101103 [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Kandala NB, Tigbe W, Manda SO, Stranges S. Geographic Variation of Hypertension in Sub-Saharan Africa: A Case Study of South Africa. Am J Hypertens [Internet]. 2013. Mar 1;26(3):382–91. Available from: https://academic.oup.com/ajh/article-lookup/doi/10.1093/ajh/hps063. [DOI] [PubMed] [Google Scholar]
28.Astell-Burt T, Feng X, Kolt GS. Greener neighborhoods, slimmer people? Evidence from 246 920 Australians. Int J Obes [Internet]. 2014. Jan 3;38(1):156–9. Available from: http://www.nature.com/articles/ijo201364. doi: 10.1038/ijo.2013.64 [DOI] [PubMed] [Google Scholar]
29.Haynes-Maslow L, Leone LA. Examining the relationship between the food environment and adult diabetes prevalence by county economic and racial composition: an ecological study. BMC Public Health [Internet]. 2017. Dec 9;17(1):648. Available from: http://bmcpublichealth.biomedcentral.com/articles/10.1186/s12889-017-4658-0. doi: 10.1186/s12889-017-4658-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
30.International Institute for Population Sciences (IIPS) and ICF. National Family Health Survey (NFHS-4), 2015–16: India [Internet]. Mumbai:IIPS; 2017. Available from: http://rchiips.org/nfhs/NFHS-4Reports/India.pdf.
31.DHS. The DHS Program-India: Standard DHS, 2015–16 Dataset, [Internet]. Demographic Health Survey. 2017. Available from: https://dhsprogram.com/data/dataset/India_Standard-DHS_2015.cfm?flag=1, Accessed on 12 March 2018.
32.GADM [Internet]. 2021. Available from: https://gadm.org/download_country.html Accessed on 26 November 2021.
33.Lang S, Brezger A. Bayesian P-Splines. J Comput Graph Stat [Internet]. 2004. Mar;13(1):183–212. Available from: http://www.tandfonline.com/doi/abs/10.1198/1061860043010. [Google Scholar]
34.Besag J, York J, Mollié A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math [Internet]. 1991. Mar;43(1):1–20. Available from: http://link.springer.com/10.1007/BF00116466. [Google Scholar]
35.Umlauf N, Klein N, Simon T, Zeileis A. bamlss: A Lego Toolbox for Flexible Bayesian Regression (and Beyond). 2019. Sep 25; Available from: http://arxiv.org/abs/1909.11784. [Google Scholar]
36.Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. J R Stat Soc Ser B (Statistical Methodol [Internet]. 2002. Oct;64(4):583–639. Available from: http://doi.wiley.com/10.1111/1467-9868.00353. [Google Scholar]
37.Besag J, Kooperberg C. On Conditional and Intrinsic Autoregression. Biometrika [Internet]. 1995. Dec;82(4):733. Available from: https://www.jstor.org/stable/2337341?origin=crossref. [Google Scholar]
38.Ngianga-Bakwin K, Madise N. The Spatial Epidemiology of Childhood Diseases in Malawi and Zambia. African Popul Stud [Internet]. 2004;19 Supplem:199–226. Available from: https://tspace.library.utoronto.ca/handle/1807/5833. [Google Scholar]
39.Ngangbam S, Roy AK. Determinants of Health-seeking Behaviour in Northeast India. J Health Manag [Internet]. 2019. Jun 22;21(2):234–57. Available from: http://journals.sagepub.com/doi/10.1177/0972063419835118. [Google Scholar]
40.Ghosh S, Kumar M. Prevalence and associated risk factors of hypertension among persons aged 15–49 in India: a cross-sectional study. BMJ Open [Internet]. 2019. Dec 16;9(12):e029714. Available from: https://bmjopen.bmj.com/lookup/doi/10.1136/bmjopen-2019-029714. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Mingji C, Onakpoya IJ, Perera R, Ward AM, Heneghan CJ. Relationship between altitude and the prevalence of hypertension in Tibet: a systematic review. Heart [Internet]. 2015. Jul 1;101(13):1054–60. Available from: https://heart.bmj.com/lookup/doi/10.1136/heartjnl-2014-307158 [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Mayilvaganan M, Khatoon N, Bej S. Tawang, Monpas and Tibetan Buddhism in Transition [Internet]. Mayilvaganan M, Khatoon N, Bej S, editors. Tawang, Monpas and Tibetan Buddhism in Transition. Singapore: Springer Singapore; 2020. Available from: http://link.springer.com/10.1007/978-981-15-4346-3. [Google Scholar]
43.Wei C. Yak Butter Tea Is a Traditional Tibetan Drink With a Practical Purpose [Internet]. Eater. 2016. [cited 2021 Feb 25]. Available from: https://www.eater.com/2016/8/25/12624068/butter-coffee-tea-tibet-yak. [Google Scholar]
44.Zhiwen T. Correlation Analysis between Hypertension Prevalence and Diet Habits among Tibetan Residents in Lhasa Community. J Chengdu Med Coll. 2018;13(5). [Google Scholar]
45.Hanna JM. Climate, Altitude, and Blood Pressure. Hum Biol [Internet]. 1999;71(4):553–82. Available from: https://www.jstor.org/stable/41465763?origin=JSTOR-pdf&seq=1. [PubMed] [Google Scholar]
46.Bansal SK, Goel D, Saxena V, Kandpal SD, Gray WK, Walker RW. The prevalence of hypertension and hypertension risk factors in a rural Indian community: A prospective door-to-door study. J Cardiovasc Dis Res [Internet]. 2012. Apr;3(2):117–23. Available from: http://linkinghub.elsevier.com/retrieve/pii/S0975358312320111. doi: 10.4103/0975-3583.95365 [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Hazarika NC, Biswas D, Mahanta J. Hypertension in the elderly population of Assam. J Assoc Physicians India. 2003. Jun;51:567–73. [PubMed] [Google Scholar]
48.Mungreiphy NK, Kapoor S, Sinha R. Association between BMI, Blood Pressure, and Age: Study among Tangkhul Naga Tribal Males of Northeast India. J Anthropol [Internet]. 2011. Dec 25;2011:1–6. Available from: https://www.hindawi.com/archive/2011/748147/. [Google Scholar]
49.Anjana RM, Deepa M, Pradeepa R, Mahanta J, Narain K, Das HK, et al. Prevalence of diabetes and prediabetes in 15 states of India: results from the ICMR–INDIAB population-based cross-sectional study. Lancet Diabetes Endocrinol [Internet]. 2017. Aug 1 [cited 2019 Dec 9];5(8):585–96. Available from: https://linkinghub.elsevier.com/retrieve/pii/S2213858717301742. doi: 10.1016/S2213-8587(17)30174-2 [DOI] [PubMed] [Google Scholar]
50.Ghosh S, Mukhopadhyay S, Barik A. Sex differences in the risk profile of hypertension: a cross-sectional study. BMJ Open [Internet]. 2016. Jul 27;6(7):e010085. Available from: http://bmjopen.bmj.com/lookup/doi/10.1136/bmjopen-2015-010085. [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Husain K, Ansari RA, Ferder L. Alcohol-induced hypertension: Mechanism and prevention. World J Cardiol [Internet]. 2014;6(5):245. Available from: http://www.wjgnet.com/1949-8462/full/v6/i5/245.htm. doi: 10.4330/wjc.v6.i5.245 [DOI] [PMC free article] [PubMed] [Google Scholar]
52.Carbone S, Canada JM, Billingsley HE, Siddiqui MS, Elagizi A, Lavie CJ. Obesity paradox in cardiovascular disease: Where do we stand? Vasc Health Risk Manag. 2019;15:89–100. doi: 10.2147/VHRM.S168946 [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Zaccardi F, Dhalwani NN, Papamargaritis D, Webb DR, Murphy GJ, Davies MJ, et al. Nonlinear association of BMI with all-cause and cardiovascular mortality in type 2 diabetes mellitus: a systematic review and meta-analysis of 414,587 participants in prospective studies. Diabetologia [Internet]. 2017;60(2):240–8. Available from: doi: 10.1007/s00125-016-4162-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Carbone S, Lavie CJ, Arena R. Obesity and Heart Failure: Focus on the Obesity Paradox. Mayo Clin Proc [Internet]. 2017. Feb;92(2):266–79. Available from: doi: 10.1016/j.mayocp.2016.11.001 [DOI] [PubMed] [Google Scholar]
55.Kraemer WJ, Torine JC, Silvestre R, French DN, Ratamess NA, Spiering BA, et al. Body Size and Composition of National Football League Players. J Strength Cond Res [Internet]. 2005;19(3):485. Available from: http://nsca.allenpress.com/nscaonline/?request=get-abstract&doi=10.1519%2F18175.1. [DOI] [PubMed] [Google Scholar]
56.Rasiah R, Yusoff K, Mohammadreza A, Manikam R, Tumin M, Chandrasekaran SK, et al. Cardiovascular disease risk factors and socioeconomic variables in a nation undergoing epidemiologic transition. BMC Public Health [Internet]. 2013. Dec 25;13(1):886. Available from: http://bmcpublichealth.biomedcentral.com/articles/10.1186/1471-2458-13-886 [DOI] [PMC free article] [PubMed] [Google Scholar]
57.Sear AM, Weinrich M, Hersh JE, Lam JJ. The relationship between income, education and hypertension. J Biosoc Sci [Internet]. 1982. Apr;14(2):213–21. Available from: https://www.cambridge.org/core/product/identifier/S0021932000014036/type/journal_article. doi: 10.1017/s0021932000014036 [DOI] [PubMed] [Google Scholar]
58.Sabri S, Bener A, Eapen V, Azhar AA, Abdishakure A, Singh J. Correlation between hypertension and income distribution among United Arab Emirates population. Med J Malaysia. 2005;60(4):416–25. [PubMed] [Google Scholar]
59.Baek T-H, Lee H-Y, Lim N-K, Park H-Y. Gender differences in the association between socioeconomic status and hypertension incidence: the Korean Genome and Epidemiology Study (KoGES). BMC Public Health [Internet]. 2015. Dec 3;15(1):852. Available from: doi: 10.1186/s12889-015-2175-6 [DOI] [PMC free article] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0262560.r001

Decision Letter 0

Mohammad Asghari Jafarabadi

27 Sep 2021

PONE-D-21-09955A Structured-additive modeling of Diabetes and Hypertension in Northeast IndiaPLOS ONE

Dear Dr. Marbaniang,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Please submit your revised manuscript by Nov 11 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: https://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.

We look forward to receiving your revised manuscript.

Kind regards,

Mohammad Asghari Jafarabadi

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf.

2. We suggest you thoroughly copyedit your manuscript for language usage, spelling, and grammar. If you do not know anyone who can help you do this, you may wish to consider employing a professional scientific editing service.

Whilst you may use any professional scientific editing service of your choice, PLOS has partnered with both American Journal Experts (AJE) and Editage to provide discounted services to PLOS authors. Both organizations have experience helping authors meet PLOS guidelines and can provide language editing, translation, manuscript formatting, and figure formatting to ensure your manuscript meets our submission guidelines. To take advantage of our partnership with AJE, visit the AJE website (http://learn.aje.com/plos/) for a 15% discount off AJE services. To take advantage of our partnership with Editage, visit the Editage website (www.editage.com) and enter referral code PLOSEDIT for a 15% discount off Editage services. If the PLOS editorial team finds any language issues in text that either AJE or Editage has edited, the service provider will re-edit the text for free.

Upon resubmission, please provide the following:

The name of the colleague or the details of the professional service that edited your manuscript

A copy of your manuscript showing your changes by either highlighting them or using track changes (uploaded as a *supporting information* file)

A clean copy of the edited manuscript (uploaded as the new *manuscript* file).

3. We note that Figures 1, 5 and 6 in your submission contain map images which may be copyrighted. All PLOS content is published under the Creative Commons Attribution License (CC BY 4.0), which means that the manuscript, images, and Supporting Information files will be freely available online, and any third party is permitted to access, download, copy, distribute, and use these materials in any way, even commercially, with proper attribution. For these reasons, we cannot publish previously copyrighted maps or satellite images created using proprietary data, such as Google software (Google Maps, Street View, and Earth). For more information, see our copyright guidelines: http://journals.plos.org/plosone/s/licenses-and-copyright.

We require you to either (1) present written permission from the copyright holder to publish these figures specifically under the CC BY 4.0 license, or (2) remove the figures from your submission:

a. You may seek permission from the original copyright holder of Figures 1, 5 and 6 to publish the content specifically under the CC BY 4.0 license.

We recommend that you contact the original copyright holder with the Content Permission Form (http://journals.plos.org/plosone/s/file?id=7c09/content-permission-form.pdf) and the following text:

“I request permission for the open-access journal PLOS ONE to publish XXX under the Creative Commons Attribution License (CCAL) CC BY 4.0 (http://creativecommons.org/licenses/by/4.0/). Please be aware that this license allows unrestricted use and distribution, even commercially, by third parties. Please reply and provide explicit written permission to publish XXX under a CC BY license and complete the attached form.”

Please upload the completed Content Permission Form or other proof of granted permissions as an "Other" file with your submission.

In the figure caption of the copyrighted figure, please include the following text: “Reprinted from [ref] under a CC BY license, with permission from [name of publisher], original copyright [original copyright year].”

b. If you are unable to obtain permission from the original copyright holder to publish these figures under the CC BY 4.0 license or if the copyright holder’s requirements are incompatible with the CC BY 4.0 license, please either i) remove the figure or ii) supply a replacement figure that complies with the CC BY 4.0 license. Please check copyright information on all replacement figures and update the figure caption with source information. If applicable, please specify in the figure caption text when a figure is similar but not identical to the original image and is therefore for illustrative purposes only.

The following resources for replacing copyrighted map figures may be helpful:

USGS National Map Viewer (public domain): http://viewer.nationalmap.gov/viewer/

The Gateway to Astronaut Photography of Earth (public domain): http://eol.jsc.nasa.gov/sseop/clickmap/

Maps at the CIA (public domain): https://www.cia.gov/library/publications/the-world-factbook/index.html and https://www.cia.gov/library/publications/cia-maps-publications/index.html

NASA Earth Observatory (public domain): http://earthobservatory.nasa.gov/

Landsat: http://landsat.visibleearth.nasa.gov/

USGS EROS (Earth Resources Observatory and Science (EROS) Center) (public domain): http://eros.usgs.gov/#

Natural Earth (public domain): http://www.naturalearthdata.com/

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: I would like to mention the following comments:

1- In title and abstract, there is no refer to simulation.

2- The total number of database is not clear. Was sampling census (all people) or sampled? How?

3- Diabetes: The criteria for DM is not clear. Twice sampling with threshold of 126?

4- In addition to types of foods, the amount of consumption is also necessary.

5- There is no explanation about "Effect coding" in method section.

6- Table 1: It is not clear if this able is the results of real data or simulation data?

7- Table 2: M0, M1, M2 and M3 must be defined at the bottom of the table.

8- Why not random effects? Was non-linear effect fixed?

9- The interpretation of estimated compared to observed data is mising.

10- "Conclusions" subtitle might be better to change into "Conclusion".

Good Luck

Reviewer #2: The manuscript titled “A structured-additive modeling of diabetes and hypertension in Northeast India” addresses very important issue of diabetes and hypertension in India. The manuscript utilized the IDHS survey data and applied geo-additive logistic regression model to understand the influence of fixed effects and spatial heterogeneity. It also addresses the issue of non-linearity in spatial context. Overall, the work is important and study is conducted systematically to conclude about the findings.

There are some concerns which can be addressed before the manuscript can be accepted for publication

Abstract

L28: Rewrite the sentence as it is not clear.

L38: It can also be mentioned that why traditional linear regression models may fail to capture the spatial effects and why you choose Bayesian Geo-additive model. Very briefly, it can also be highlighted about the importance of accounting for spatial autocorrelation and how it can lead to bias in estimates.

L45, L46 and L47: The sentence can be re-written to make to clear about importance of unstructured effect for diabetes and structured effect for hypertension.

L49: It is not clear what you mean here by local and non-local factors.

L51: You mean to say here should “be” given more importance?

Introduction

L54 and L55: Reference can be added for these statements

L65-67: The statement can be re-written to make it clear

L67-69: Cite reference for this statement

L74: Sentence can be re-written a it appears you are mentioning about your findings in introduction.

L92: The reference cited (Ref No. 20) explores the availability of green spaces in neighborhood of individual households and it is not clear from your statement. It will be better to mention about the spatial scale here.

Materials and Methods

L112: Sentence is starting with abbreviation, kindly change it

L112: It can be mentioned in the reference when it was accessed/downloaded (Ref. No. 25)

L113: What necessary permissions were obtained? Please elaborate

L116: It can be made clear before this sentence that the survey done by IDHS and not done in this study to avoid confusion to readers

L122: There is some space in the total respondents which can be deleted – 112,062 and for 13,360

L127: The breakup of 82 districts sampled for each state can be mentioned.

L129: Rewrite the sentence to make it clear

L134: OMRON is trade name so can be named appropriately

L146: The explanatory variables were selected from the IDHS survey? If so, mention how many variables were there in the IDHS database and how many were selected in this study? In addition, there is no mention about the continuous variables (BMI, wealth index and age) in your methods, but you present the results.

L155: It is not justified why you choose to use multiple regression model for narrowing down to the number of variables. As mentioned in comment for L146, you need to mention the total number of variables. You have left to readers to count the variables. There are many variable selection methods to reduce the number of variables before applying your Bayesian Geo-additive model. You need to justify your method or you have to perform variable selection method before narrowing down to the number of variables

L158: Again, mention about the number of variables which were used for fitting the Geo-additive logistic regression model

L164: You need to mention how you are defining your neighbor here? Did you use adjacency matric or any other method to define neighborhood, then you need to mention about it and may write the equation/formula for the same.

L169: It is advisable to use two more models here to understand the influence of spatially structure and spatially unstructured heterogeneity. The two models can be combination of M1 and M2 with spatial structured heterogeneity in one model and spatial unstructured heterogeneity in the other model. In this way it can be known about the drop/increase in DIC.

L189: How it was arrived to use 40,000 iterations? The convergence of different parameters should be tested using Gelman-Rubin statistics and mentioned that how these values were. You have not performed any cross validation statistics using CPO and PIT which is required to know the model performance.

L196: It should also be mentioned how you are deciding significance of variables based on 97.5% credible interval and values which do not bridge zero were not considered significant

Results

L199: The overall prevalence can also be shown on a map so that it can be compared with the spatial structured and unstructured heterogeneity maps for diabetes and hypertension

L237, Table 3: If this is the result of your M3 model which you say is combination of M1 and M2 then why the co-efficient of your continuous variables are not shown in this table? You have separately shown the non-linear effect of continuous variable in figures but this should also be reflected in your table or justify why it was not done so. It is not clear from your methods that whether your non-linear model using continuous variables also included categorical variables. It should be mentioned clearly to avoid confusion to readers. Your final model has all the variables which is my concern as mentioned in comment for L155 you need to reduce the total number of variables for your final model so that significant variables can be rightly identified.

L249, Table 4: same comments as for L237

Discussion

L300: You can start your discussion by saying about significant variables in your final model and then about the capturing non-linear effect using Geo-additive model

L327: You can refer your figures in discussion.

L350: This point contradicts your findings as mentioned on L246, that individuals who consume alcohol are at lower risk of hypertension. If this is the case only for Arunachal Pradesh or other states?

L358: Refer table number of your results

L359: It can be re-written with proper citation

L375 & 376: You mention previous studies, but cite only one reference.

L376: Need to add reference for this statement

L381-L383: It can be justified why you were constrained to use only IDHS data and why other variables were not included. You mentioned in several places about other variables like medical institutions, health care facilities, cost of living, urbanization and altitude may be playing a role in driving your spatial variability. It will be important to mention why you did not include other variables as this would have helped in even planning interventions and resource allocation in high risk areas for diabetes and hypertension

Conclusion

L395: As pointed out previously you need to mention clearly what you mean by local and non-local factors and preferable use other words to describe this pattern.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: Yes: Masoud Amiri

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

Attachment

Submitted filename: Comments to authors_PONE-D-21-09955.docx

Click here for additional data file.^{(16.5KB, docx)}

PLoS One. 2022 Jan 13;17(1):e0262560. doi: 10.1371/journal.pone.0262560.r002

Author response to Decision Letter 0

1 Dec 2021

Reviewer #1: I would like to mention the following comments:

Comment 1- In title and abstract, there is no refer to simulation.

Response: Thank you for the comment. The present study uses the individual level data for the whole North-Eastern states of India from the latest round of Indian National Family Health Survey (INFHS). The model we applied is not on the simulated data. We hope this clarifies the point.

Comment 2- The total number of database is not clear. Was sampling census (all people) or sampled? How?

Response: Thank you for the comment. The survey is not a census survey but it is a random sampling. We have incorporated a detailed explanation about the sampling procedure of the survey in the revised manuscript along with the reference.

Comment 3- Diabetes: The criteria for DM is not clear. Twice sampling with threshold of 126?

Response: Thank you for the comment. The measuring of random blood glucose level was performed only once. The blood sample was collected at a random time during the day. Detailed explanation was incorporated in the revised manuscript.

Comment 4- In addition to types of foods, the amount of consumption is also necessary.

Response: Thank you for this important suggestion. We do agree with the reviewer that the quantity of food consumption is also an important covariate, however we could not incorporate this information in the analysis as this information is not available in the dataset.

Comment 5- There is no explanation about "Effect coding" in method section.

Response: Thank you to the reviewer for giving an opportunity to clarify. The effect coding, we adopted is the zero-sum coding. The definition is mentioned in the heading of Table 1. As suggested we have included a short explanation in the manuscript about effect coding adopted on Page 8, L177. We adopted this coding just to compare the effects of categories in a particular covariate. The corresponding interpretations are in the Results section of the manuscript.

Comment 6- Table 1: It is not clear if this table is the results of real data or simulation data?

Response: Thank you for the comment. As mentioned earlier, figures provided in Table 1 are authors calculation from the real data that was used in the whole analysis (IDHS).

Comment 7- Table 2: M0, M1, M2 and M3 must be defined at the bottom of the table.

Response: Thank you for highlighting this important point. We have incorporated the suggestion.

Comment 8- Why not random effects? Was non-linear effect fixed?

Response: Thank you for the comment. The non-linear effect represents the influence of the continuous independent variables (e.g., age, BMI, wealth index score) on the dependent variable and the effect is not fixed but rather it allows for possible non-linear patterns in the model.

Comment 9- The interpretation of estimated compared to observed data is missing.

Response: Thank you for the comment. The estimated values in Table 3 and Table 4 represent the posterior mean effect of the fixed covariates on the outcome variables. These values were estimated from the observed data using Model M3. Their interpretation has also been reported under the Fixed effect section.

Comment 10- "Conclusions" subtitle might be better to change into "Conclusion".

Response: Thank you for the comment. Now we have made the correction as suggested

Reviewer#2:

The manuscript titled “A structured-additive modeling of diabetes and hypertension in Northeast India” addresses very important issue of diabetes and hypertension in India. The manuscript utilized the IDHS survey data and applied geo-additive logistic regression model to understand the influence of fixed effects and spatial heterogeneity. It also addresses the issue of non-linearity in spatial context. Overall, the work is important and study is conducted systematically to conclude about the findings.

Response: Thank you for appreciating our work.

There are some concerns which can be addressed before the manuscript can be accepted for publication

Abstract

L28: Rewrite the sentence as it is not clear.

Response: Thank you for the suggestion. We now have rephrased the sentences.

Response: Thanks a lot to the reviewer for pointing out the issue. In order to make the readers more understandable regarding the model adopted we have added a short explanation of the advantage of geo-additive over traditional linear regression in the manuscript on Page 8, L186-189. We hope we clarify to the doubt and the reviewer is pleased.

L45, L46 and L47: The sentence can be re-written to make to clear about importance of unstructured effect for diabetes and structured effect for hypertension.

Response: Thank you for the comment. We now have rephrased the sentences.

L49: It is not clear what you mean here by local and non-local factors.

Response: Thank you for the comment. By local factors we mean the unobserved risk factors present within the districts where the respondents reside. However, by non-local factors we mean the unobserved risk factors that are related to the nearby districts i.e., nearby districts may have similar risk factors

L51: You mean to say here should “be” given more importance?

Response: Thank you for point out this issue. We mean to say the same thing as per your suggestion and hence we have incorporated the suggestion.

Introduction

L54 and L55: Reference can be added for these statements

Response: Comment incorporated.

L65-67: The statement can be re-written to make it clear

Response: Comment incorporated

L67-69: Cite reference for this statement

Response: Thank you for the suggestion. We now have incorporated the reference

L74: Sentence can be re-written a it appears you are mentioning about your findings in introduction.

Response: Comment incorporated.

Response: Thank you for the suggestion. We now have incorporated the suggestion.

Materials and Methods

L112: Sentence is starting with abbreviation, kindly change it

Response: We now have made the necessary changes

L112: It can be mentioned in the reference when it was accessed/downloaded (Ref. No. 25)

Response: Accessed date is now incorporated in the reference.

L113: What necessary permissions were obtained? Please elaborate

Response: Before getting access to download the DHS dataset, it is compulsory for the data user to register on the website https://dhsprogram.com/data/new-user-registration.cfm. After the registration is complete the user will receive an email notification in the registered email id which will give the permission to download the data.

L116: It can be made clear before this sentence that the survey done by IDHS and not done in this study to avoid confusion to readers

Response: Thank you for the suggestion. We now have elaborated in the revised manuscript that IDHS was conducted by the International Institute for Population Sciences (IIPS), Mumbai a nodal agency appointed by the Ministry of Health and Family Welfare, Government of India.

L122: There is some space in the total respondents which can be deleted – 112,062 and for 13,360

Response: Thank you for highlighting this error. We now have made the correction.

L127: The breakup of 82 districts sampled for each state can be mentioned.

Response: Table of breakup of 82 districts by States was attached as supplementary information in the revised manuscript.

L129: We now have rewritten the sentence to make it clear

Response: Thank you for the comment. Now the sentences were rephrased.

L134: OMRON is trade name so can be named appropriately

Response: Thank you for the suggestion. We now have renamed appropriately.

Response: The IDHS questionnaire obtained information on Household characteristics, Women and Child characteristics, Men, and Biomarker.

Household dataset have 5183 variables.

Women and Child dataset have 4797 variables

Men dataset have 747 variables

Biomarker dataset have 270 variables

As guided by the literature review, we have selected 21 explanatory variables for this study namely Age, Gender, Place of residence, Marital status, Level of education, Wealth Index Score, Body Mass Index, Caste, Consumption of milk, pulses, vegetables, fruits, egg, fish, chicken, fried food, aerated drinks, alcohol, cigarette, tobacco.

We now have included the explanatory variables BMI, Age, and wealth Index score in the methods section.

Response: Thanks a lot to the reviewer. Actually, the selection of variables are guided by review of literature and available data in the context of India. First, we included more plausible variables and apply the usual linear regression model to select variables with a significance level of 20% in order to keep more plausible variables before applying the complex and time consuming geo-additive models. We do agree that the selection can be done in the geo-additive models itself. But because of time consumed in running one model for geo-additive, we did not adopt this approach. We hope the reviewer is satisfied with the response.

L158: Again, mention about the number of variables which were used for fitting the Geo-additive logistic regression model

Response: Thanks a lot. We have mentioned the variables retained for the geo-additive model on Page 8, L185.

Response: Thanks a lot to the reviewer for the suggestion. Instead of writing a complex equation, we have included few lines about the construction of neighbours on Page 10, L216-221.

Response: Thanks a lot for the comment. We would like to clarify that in the old manuscript we have mistakenly written the AIC value instead of the Deviance value in Table 2. Now, in the revised manuscript we have correctly written the Deviance value (Table 2). We hope the reviewer accept our mistake.

As suggested we have included two more models i.e. M3 and M4. Then M3 is re-named as M5 as the best model. We considered the change in DIC and used the difference of less than 3 as negligible (Besag J, Kooperberg C: On conditional and intrinsic autoregressions. Biometrika 1995, 82:733–746). We found the differnces in DIC as: M0-M5=2941.24, M1-M5=6890.98, M2-M5=469.08, M3-M5=7.62, M4-M5=3.35 for Diabetes, which are all greater than 3. Similarly, for hypertension the differences are 7402.04, 16242.97, 991.37, 4.76, 4.20 respectively. We hope the reviewer is satisfied.

L189: How it was arrived to use 40,000 iterations? The convergence of different parameters should be tested using Gelman-Rubin statistics and mentioned that how these values were. You have not performed any cross-validation statistics using CPO and PIT which is required to know the model performance.

Response: Thanks a lot for pointing out this issue. In order to check we set enough number of iterations while running the model. In this way we set the iterations as 40,000. We do understand it is also important to check the predictive power of the fitted model. We however would like to emphasize that we have checked the convergence through trace plots for all the estimated parameters. We found no autocorrelations in the trace plots. We are very sorry to say that the package we used “bamlss” does not support to calculate/plot the PIT additional out of sample measures. We, however checked whether any of the cpo values are non-zero. We found none of them are non-zero for both the outcomes i.e. hypertension and diabetes. As suggested by literatures we checked the negative of the mean of logarithm of cpo values for the final fitted model i.e. M5. We found the values as: 0.4012 for hypertension and 0.2189. We hope these are some of the measures that can be provided in addition to the measures DIC, pD which are popular measures in Bayesian analysis. Regarding the Gelman-Rubin statistics, we need to run the final model for at least 2 chains which takes a lot of time and need to present many figures for that many variables. Just to make a clarification to the reviewer we provide some figures along with gelman plot. We would like to emphasize that the command we used for Gelman-Rubin diagnostics provided by the package “coda” is that it might mis-diagnose convergence if the shrink factor happens to be close to 1 by chance. Looking at the values provided by the Gelman-Rubin statistics, none of them are extremely well above the value 1, this confirms the convergence as we found in the trace plots.

Diabetes model:

Potential scale reduction factors:

Point est. Upper C.I.

pi.s.s(age).b1 1.02 1.09

pi.s.s(age).b2 1.03 1.12

pi.s.s(age).b3 1.01 1.06

pi.s.s(age).b4 1.01 1.04

pi.s.s(age).b5 1.00 1.00

pi.s.s(age).b6 1.01 1.03

pi.s.s(age).b7 1.01 1.05

pi.s.s(age).b8 1.01 1.04

pi.s.s(age).b9 1.00 1.02

pi.s.s(age).b10 1.01 1.03

pi.s.s(age).b11 1.02 1.08

pi.s.s(age).b12 1.02 1.10

pi.s.s(age).b13 1.02 1.10

pi.s.s(age).b14 1.01 1.05

pi.s.s(age).b15 1.01 1.04

pi.s.s(age).b16 1.02 1.10

pi.s.s(age).b17 1.03 1.15

pi.s.s(age).b18 1.01 1.05

pi.s.s(age).b19 1.00 1.00

pi.s.s(age).tau21 1.01 1.04

Multivariate psrf

1.05

Hypertension model:

Potential scale reduction factors:

Point est. Upper C.I.

pi.s.s(age).b1 1.004 1.017

pi.s.s(age).b2 0.999 1.000

pi.s.s(age).b3 1.001 1.007

pi.s.s(age).b4 1.000 1.003

pi.s.s(age).b5 1.003 1.007

pi.s.s(age).b6 1.000 1.002

pi.s.s(age).b7 1.000 1.000

pi.s.s(age).b8 1.000 1.001

pi.s.s(age).b9 1.003 1.012

pi.s.s(age).b10 0.999 1.000

pi.s.s(age).b11 0.999 0.999

pi.s.s(age).b12 1.000 1.001

pi.s.s(age).b13 1.001 1.002

pi.s.s(age).b14 1.003 1.005

pi.s.s(age).b15 1.002 1.014

pi.s.s(age).b16 1.006 1.020

pi.s.s(age).b17 1.003 1.017

pi.s.s(age).b18 1.001 1.003

pi.s.s(age).b19 1.000 1.001

pi.s.s(age).tau21 1.062 1.088

Multivariate psrf

1.02

In the same way we can check for other terms like “bmi” and “wealth index”. We hope these clarify to the points raised by the reviewer to some extend.

L196: It should also be mentioned how you are deciding significance of variables based on 97.5% credible interval and values which do not bridge zero were not considered significant

Response: Thanks a lot for giving us to make a clarification. Actually, there is no as such theoretical reason behind using 97.5%. We also adopted the generally adopted significance level. Just would like to mention that these are actually the 95% credible intervals.

Results

L199: The overall prevalence can also be shown on a map so that it can be compared with the spatial structured and unstructured heterogeneity maps for diabetes and hypertension

Response: Thanks a lot for the comment. Yes, we do agree the reviewer’s view. But because of small numbers of districts in the map, it will be very messy to show all the prevalences on the map. Therefore, we dropped the idea to show on the map.

Response: Thanks a lot for the comment. Basically, we wanted to see the whether there are non-linear effects of age, bmi and wealth index in the model and did not intend to understand the effects as such. We therefore thought that it is better to show as a figure as done in most of studies. Yes, the combined model includes both fixed and non-linear effects of the variables age, BMI and wealth index. To make it clearer to the readers we have elaborated

L249, Table 4: same comments as for L237

Response: Thanks a lot for the comments. Now we have changed completely on Pages 9 and 10, L198-225.

Discussion

L300: You can start your discussion by saying about significant variables in your final model and then about the capturing non-linear effect using Geo-additive model

Response: Thank you for the suggestion. We now have incorporated the suggestion.

L327: You can refer your figures in discussion.

Response: Thank you for the suggestion. Now figure reference have been incorporated in the discussion.

Response: Thank you for the comment. The statement in L350 we mean to explain for Arunachal Pradesh only, as it is well known that Arunachal Pradesh had the highest consumption of alcohol in India and high prevalence of hypertension. However, the statement in line L246 explains for the whole of Northeast India.

L358: Refer table number of your results

Response: Comment Incorporated

L359: It can be re-written with proper citation

Response: Thank you for the comment. Now the sentences have been re-written with proper citation.

L375 & 376: You mention previous studies, but cite only one reference.

Response: Thank you for the comment. We now have added some reference from the related articles.

L376: Need to add reference for this statement

Response: This sentence has been rephrased with proper references.

Response: Thank you for the important suggestion. I do agree with you that medical institutions and healthcare facilities, cost of living index, urbanization, and altitude may play a role in driving the spatial clustering of diabetes and hypertension. Since these information’s was not available in the IDHS data, hence we cannot study their influence on the spatial variability of diabetes and hypertension.

Considering your suggestion, we have included this as one of the limitations in our study.

Conclusion

L395: As pointed out previously you need to mention clearly what you mean by local and non-local factors and preferable use other words to describe this pattern.

Response: Thank you for the suggestion. By local factors we mean the risk factors present within the districts and non-local factors mean the risk factors which are related to proximate districts. We have renamed and rephrased the sentences.

Attachment

Submitted filename: Response to Reviewer.docx

Click here for additional data file.^{(56.2KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0262560.r003

Decision Letter 1

Mohammad Asghari Jafarabadi

30 Dec 2021

A Structured Additive Modeling of Diabetes and Hypertension in Northeast India

PONE-D-21-09955R1

Dear Dr. Marbaniang,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Mohammad Asghari Jafarabadi

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: In answer to reviewers and revised main text, all comments have been considered and appropriately addressed.

Reviewer #2: Thank you for addressing all the issues raised. Overall the manuscript is important contribution towards understanding the spatial variability in diabetes and hypertension in the region by using robust Bayesian Geo-additive model. Overall good piece of work.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: Yes: Masoud Amiri

Reviewer #2: No

PLoS One. doi: 10.1371/journal.pone.0262560.r004

Acceptance letter

Mohammad Asghari Jafarabadi

5 Jan 2022

PONE-D-21-09955R1

A Structured Additive Modeling of Diabetes and Hypertension in Northeast India

Dear Dr. Marbaniang:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Professor Mohammad Asghari Jafarabadi

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Table. Breakup of 82 districts by states in Northeast India.

(PDF)

Click here for additional data file.^{(43.5KB, pdf)}

Attachment

Submitted filename: Comments to authors_PONE-D-21-09955.docx

Click here for additional data file.^{(16.5KB, docx)}

Attachment

Submitted filename: Response to Reviewer.docx

Click here for additional data file.^{(56.2KB, docx)}

Data Availability Statement

The data can be found from the following link: https://dhsprogram.com/data/dataset/India_Standard-DHS_2015.cfm?flag=1.

[pone.0262560.ref001] 1.Constant AF, Geladari E V., Geladari C V. “The Economic Burden of Hypertension.” In: Andreadis EA, editor. Hypertension and Cardiovascular Disease [Internet]. Cham: Springer International Publishing; 2016. p. 351–9. Available from: http://link.springer.com/10.1007/978-3-319-39599-9. [Google Scholar]

[pone.0262560.ref002] 2.Lin X, Xu Y, Pan X, Xu J, Ding Y, Sun X, et al. Global, regional, and national burden and trend of diabetes in 195 countries and territories: an analysis from 1990 to 2025. Sci Rep [Internet]. 2020. Dec 8;10(1):14790. Available from: doi: 10.1038/s41598-020-71908-9 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref003] 3.International Diabetes Federation. Advocacy guide to the IDF Diabetes Atlas Ninth edition 2019 [Internet]. Brussels, Belgium:International Diabetes Federation; 2019 [cited 2019 Nov 14]. Available from: http://www.diabetesatlas.org/.

[pone.0262560.ref004] 4.World Health Organization. Hypertension [Internet]. WHO. 2019. [cited 2021 Feb 3]. Available from: https://www.who.int/news-room/fact-sheets/detail/hypertension. [Google Scholar]

[pone.0262560.ref005] 5.Gupta R, Gaur K, S. Ram CV. Emerging trends in hypertension epidemiology in India. J Hum Hypertens [Internet]. 2019. Aug 25 [cited 2019 Nov 16];33(8):575–87. Available from: doi: 10.1038/s41371-018-0117-3 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref006] 6.Marbaniang SP. Women Care and Practices in the Management of Childhood Diarrhea in Northeast India. Child Care Pract [Internet]. 2020. Sep 17;1–13. Available from: https://www.tandfonline.com/doi/full/10.1080/13575279.2020.1812534. [Google Scholar]

[pone.0262560.ref007] 7.Hossain F. Levels of Health Care and Health Outcomes in Northeast India. Indian J Hum Dev. 2019;13(2):221–32. [Google Scholar]

[pone.0262560.ref008] 8.Ghosh S, Kumar M. Prevalence and associated risk factors of hypertension among persons aged 15–49 in India: a cross-sectional study. BMJ Open [Internet]. 2019. Dec 16;9(12):e029714. Available from: doi: 10.1136/bmjopen-2019-029714 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref009] 9.IIPS and ICF. National Family Health Survey (NFHS-5): Fact Sheet Key Indicators 22 States/UTs from Phase-1 [Internet]. 2020. Available from: http://rchiips.org/nfhs/factsheet_NFHS-5.shtml. [Google Scholar]

[pone.0262560.ref010] 10.Akhtar S, Dhillon P. Prevalence of diagnosed diabetes and associated risk factors: Evidence from the large-scale surveys in India. J Soc Heal Diabetes [Internet]. 2017. Jun 23;05(01):028–36. Available from: http://www.thieme-connect.de/DOI/DOI?10.4103/2321-0656.194001. [Google Scholar]

[pone.0262560.ref011] 11.Nam K Do Van NB, Hoang LV Duc TP, Thi Ha TT Tuan VT, et al. Hypertension in a mountainous province of Vietnam: prevalence and risk factors. Heliyon [Internet]. 2020. Feb;6(2):e03383. Available from: doi: 10.1016/j.heliyon.2020.e03383 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref012] 12.Li G, Wang H, Wang K, Wang W, Dong F, Qian Y, et al. The association between smoking and blood pressure in men: a cross-sectional study. BMC Public Health [Internet]. 2017. Dec 10;17(1):797. Available from: http://bmcpublichealth.biomedcentral.com/articles/10.1186/s12889-017-4802-x. doi: 10.1186/s12889-017-4802-x [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref013] 13.Marbaniang SP, Lhungdim H, Chauhan S, Srivastava S. Interaction of multiple risk factors and population attributable fraction for type 2 diabetes and hypertension among adults aged 15–49 years in Northeast India. Diabetes Metab Syndr Clin Res Rev [Internet]. 2021. Sep;15(5):102227. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1871402121002472. doi: 10.1016/j.dsx.2021.102227 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref014] 14.Sobngwi E, Mbanya J-CN, Unwin N, Kengne A, Fezeu L, Minkoulou E, et al. Physical activity and its relationship with obesity, hypertension and diabetes in urban and rural Cameroon. Int J Obes [Internet]. 2002. Jul 25;26(7):1009–16. Available from: http://www.nature.com/articles/0802008. doi: 10.1038/sj.ijo.0802008 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref015] 15.Campbell AP. DASH Eating Plan: An Eating Pattern for Diabetes Management. Diabetes Spectr [Internet]. 2017. May 15;30(2):76–81. Available from: http://spectrum.diabetesjournals.org/lookup/doi/10.2337/ds16-0084. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref016] 16.Marbaniang SP, Lhungdim H, Yadav B, Yajurvedi VK. Overweight/obesity risks and prevalence of diabetes and hypertension in North Eastern India: An analysis using seemingly unrelated probit model. Clin Epidemiol Glob Heal [Internet]. 2021. Jul;11:100764. Available from: https://linkinghub.elsevier.com/retrieve/pii/S2213398421000683. [Google Scholar]

[pone.0262560.ref017] 17.Adebayo SB, Gayawan E, Fagbamigbe AF, Bello FW. Bayesian geo-additive spatial modelling of HIV prevalence using data from population-based surveys. HIV AIDS Rev [Internet]. 2019;18(4):247–60. Available from: https://www.termedia.pl/doi/ doi: 10.5114/hivar.2019.83852 [DOI] [Google Scholar]

[pone.0262560.ref018] 18.van der Sande M, Milligan P, Walraven G, Dolmans W, Newport M, Nyan O, et al. Geographical variation in prevalence of hypertension within The Gambia. J Hum Hypertens [Internet]. 2001. Oct 12;15(10):733–9. Available from: http://www.nature.com/articles/1001259. doi: 10.1038/sj.jhh.1001259 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref019] 19.Hernandez AM, Jia P, Kim H-Y, Cuadros DF. Geographic Variation and Associated Covariates of Diabetes Prevalence in India. JAMA Netw Open [Internet]. 2020. May 1;3(5):e203865. Available from: https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2765281. doi: 10.1001/jamanetworkopen.2020.3865 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref020] 20.Singh S, Puri P, Subramanian S V. Identifying spatial variation in the burden of diabetes among women across 640 districts in India: a cross-sectional study. J Diabetes Metab Disord [Internet]. 2020. Jun 27;19(1):523–33. Available from: http://link.springer.com/10.1007/s40200-020-00545-w. doi: 10.1007/s40200-020-00545-w [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref021] 21.Ghosh K, Dhillon P, Agrawal G. Prevalence and detecting spatial clustering of diabetes at the district level in India. J Public Health (Bangkok) [Internet]. 2020. Oct 24 [cited 2020 Feb 20];28(5):535–45. Available from: http://link.springer.com/10.1007/s10389-019-01072-6. [Google Scholar]

[pone.0262560.ref022] 22.Zaman FA, Borang A. Prevalence of diabetes mellitus amongst rural hilly population of North Eastern India and its relationship with associated risk factors and related co-morbidities. J Nat Sci Biol Med [Internet]. 2014. Jul;5(2):383–8. Available from: https://pubmed.ncbi.nlm.nih.gov/25097420. doi: 10.4103/0976-9668.136195 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref023] 23.Borah PK, Mahanta J, Kalita HC, Bhattacharjee CK. Distribution of hypertension subtypes in a hill tribe of Mizoram, Northeast India. Indian Heart J [Internet]. 2020;72(5):398–402. Available from: doi: 10.1016/j.ihj.2020.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref024] 24.Koissi M-C, Högnäs G. Using WinBUGS to Study Family Frailty in Child Mortality, with an Application to Child Survival in Ivory Coast. African Popul Stud [Internet]. 2013. Nov 1;20(1):1–17. Available from: http://aps.journals.ac.za/pub/article/view/384. [Google Scholar]

[pone.0262560.ref025] 25.Astell-Burt T, Feng X, Kolt GS. Is Neighborhood Green Space Associated With a Lower Risk of Type 2 Diabetes? Evidence From 267,072 Australians. Diabetes Care [Internet]. 2014. Jan;37(1):197–201. Available from: http://care.diabetesjournals.org/lookup/doi/10.2337/dc13-1325. [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref026] 26.Kandala N-B, Stranges S. Geographic Variation of Overweight and Obesity among Women in Nigeria: A Case for Nutritional Transition in Sub-Saharan Africa. Kazembe L, editor. PLoS One [Internet]. 2014. Jun 30;9(6):e101103. Available from: doi: 10.1371/journal.pone.0101103 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref027] 27.Kandala NB, Tigbe W, Manda SO, Stranges S. Geographic Variation of Hypertension in Sub-Saharan Africa: A Case Study of South Africa. Am J Hypertens [Internet]. 2013. Mar 1;26(3):382–91. Available from: https://academic.oup.com/ajh/article-lookup/doi/10.1093/ajh/hps063. [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref028] 28.Astell-Burt T, Feng X, Kolt GS. Greener neighborhoods, slimmer people? Evidence from 246 920 Australians. Int J Obes [Internet]. 2014. Jan 3;38(1):156–9. Available from: http://www.nature.com/articles/ijo201364. doi: 10.1038/ijo.2013.64 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref029] 29.Haynes-Maslow L, Leone LA. Examining the relationship between the food environment and adult diabetes prevalence by county economic and racial composition: an ecological study. BMC Public Health [Internet]. 2017. Dec 9;17(1):648. Available from: http://bmcpublichealth.biomedcentral.com/articles/10.1186/s12889-017-4658-0. doi: 10.1186/s12889-017-4658-0 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref030] 30.International Institute for Population Sciences (IIPS) and ICF. National Family Health Survey (NFHS-4), 2015–16: India [Internet]. Mumbai:IIPS; 2017. Available from: http://rchiips.org/nfhs/NFHS-4Reports/India.pdf.

[pone.0262560.ref031] 31.DHS. The DHS Program-India: Standard DHS, 2015–16 Dataset, [Internet]. Demographic Health Survey. 2017. Available from: https://dhsprogram.com/data/dataset/India_Standard-DHS_2015.cfm?flag=1, Accessed on 12 March 2018.

[pone.0262560.ref032] 32.GADM [Internet]. 2021. Available from: https://gadm.org/download_country.html Accessed on 26 November 2021.

[pone.0262560.ref033] 33.Lang S, Brezger A. Bayesian P-Splines. J Comput Graph Stat [Internet]. 2004. Mar;13(1):183–212. Available from: http://www.tandfonline.com/doi/abs/10.1198/1061860043010. [Google Scholar]

[pone.0262560.ref034] 34.Besag J, York J, Mollié A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math [Internet]. 1991. Mar;43(1):1–20. Available from: http://link.springer.com/10.1007/BF00116466. [Google Scholar]

[pone.0262560.ref035] 35.Umlauf N, Klein N, Simon T, Zeileis A. bamlss: A Lego Toolbox for Flexible Bayesian Regression (and Beyond). 2019. Sep 25; Available from: http://arxiv.org/abs/1909.11784. [Google Scholar]

[pone.0262560.ref036] 36.Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. J R Stat Soc Ser B (Statistical Methodol [Internet]. 2002. Oct;64(4):583–639. Available from: http://doi.wiley.com/10.1111/1467-9868.00353. [Google Scholar]

[pone.0262560.ref037] 37.Besag J, Kooperberg C. On Conditional and Intrinsic Autoregression. Biometrika [Internet]. 1995. Dec;82(4):733. Available from: https://www.jstor.org/stable/2337341?origin=crossref. [Google Scholar]

[pone.0262560.ref038] 38.Ngianga-Bakwin K, Madise N. The Spatial Epidemiology of Childhood Diseases in Malawi and Zambia. African Popul Stud [Internet]. 2004;19 Supplem:199–226. Available from: https://tspace.library.utoronto.ca/handle/1807/5833. [Google Scholar]

[pone.0262560.ref039] 39.Ngangbam S, Roy AK. Determinants of Health-seeking Behaviour in Northeast India. J Health Manag [Internet]. 2019. Jun 22;21(2):234–57. Available from: http://journals.sagepub.com/doi/10.1177/0972063419835118. [Google Scholar]

[pone.0262560.ref040] 40.Ghosh S, Kumar M. Prevalence and associated risk factors of hypertension among persons aged 15–49 in India: a cross-sectional study. BMJ Open [Internet]. 2019. Dec 16;9(12):e029714. Available from: https://bmjopen.bmj.com/lookup/doi/10.1136/bmjopen-2019-029714. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref041] 41.Mingji C, Onakpoya IJ, Perera R, Ward AM, Heneghan CJ. Relationship between altitude and the prevalence of hypertension in Tibet: a systematic review. Heart [Internet]. 2015. Jul 1;101(13):1054–60. Available from: https://heart.bmj.com/lookup/doi/10.1136/heartjnl-2014-307158 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref042] 42.Mayilvaganan M, Khatoon N, Bej S. Tawang, Monpas and Tibetan Buddhism in Transition [Internet]. Mayilvaganan M, Khatoon N, Bej S, editors. Tawang, Monpas and Tibetan Buddhism in Transition. Singapore: Springer Singapore; 2020. Available from: http://link.springer.com/10.1007/978-981-15-4346-3. [Google Scholar]

[pone.0262560.ref043] 43.Wei C. Yak Butter Tea Is a Traditional Tibetan Drink With a Practical Purpose [Internet]. Eater. 2016. [cited 2021 Feb 25]. Available from: https://www.eater.com/2016/8/25/12624068/butter-coffee-tea-tibet-yak. [Google Scholar]

[pone.0262560.ref044] 44.Zhiwen T. Correlation Analysis between Hypertension Prevalence and Diet Habits among Tibetan Residents in Lhasa Community. J Chengdu Med Coll. 2018;13(5). [Google Scholar]

[pone.0262560.ref045] 45.Hanna JM. Climate, Altitude, and Blood Pressure. Hum Biol [Internet]. 1999;71(4):553–82. Available from: https://www.jstor.org/stable/41465763?origin=JSTOR-pdf&seq=1. [PubMed] [Google Scholar]

[pone.0262560.ref046] 46.Bansal SK, Goel D, Saxena V, Kandpal SD, Gray WK, Walker RW. The prevalence of hypertension and hypertension risk factors in a rural Indian community: A prospective door-to-door study. J Cardiovasc Dis Res [Internet]. 2012. Apr;3(2):117–23. Available from: http://linkinghub.elsevier.com/retrieve/pii/S0975358312320111. doi: 10.4103/0975-3583.95365 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref047] 47.Hazarika NC, Biswas D, Mahanta J. Hypertension in the elderly population of Assam. J Assoc Physicians India. 2003. Jun;51:567–73. [PubMed] [Google Scholar]

[pone.0262560.ref048] 48.Mungreiphy NK, Kapoor S, Sinha R. Association between BMI, Blood Pressure, and Age: Study among Tangkhul Naga Tribal Males of Northeast India. J Anthropol [Internet]. 2011. Dec 25;2011:1–6. Available from: https://www.hindawi.com/archive/2011/748147/. [Google Scholar]

[pone.0262560.ref049] 49.Anjana RM, Deepa M, Pradeepa R, Mahanta J, Narain K, Das HK, et al. Prevalence of diabetes and prediabetes in 15 states of India: results from the ICMR–INDIAB population-based cross-sectional study. Lancet Diabetes Endocrinol [Internet]. 2017. Aug 1 [cited 2019 Dec 9];5(8):585–96. Available from: https://linkinghub.elsevier.com/retrieve/pii/S2213858717301742. doi: 10.1016/S2213-8587(17)30174-2 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref050] 50.Ghosh S, Mukhopadhyay S, Barik A. Sex differences in the risk profile of hypertension: a cross-sectional study. BMJ Open [Internet]. 2016. Jul 27;6(7):e010085. Available from: http://bmjopen.bmj.com/lookup/doi/10.1136/bmjopen-2015-010085. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref051] 51.Husain K, Ansari RA, Ferder L. Alcohol-induced hypertension: Mechanism and prevention. World J Cardiol [Internet]. 2014;6(5):245. Available from: http://www.wjgnet.com/1949-8462/full/v6/i5/245.htm. doi: 10.4330/wjc.v6.i5.245 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref052] 52.Carbone S, Canada JM, Billingsley HE, Siddiqui MS, Elagizi A, Lavie CJ. Obesity paradox in cardiovascular disease: Where do we stand? Vasc Health Risk Manag. 2019;15:89–100. doi: 10.2147/VHRM.S168946 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref053] 53.Zaccardi F, Dhalwani NN, Papamargaritis D, Webb DR, Murphy GJ, Davies MJ, et al. Nonlinear association of BMI with all-cause and cardiovascular mortality in type 2 diabetes mellitus: a systematic review and meta-analysis of 414,587 participants in prospective studies. Diabetologia [Internet]. 2017;60(2):240–8. Available from: doi: 10.1007/s00125-016-4162-6 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref054] 54.Carbone S, Lavie CJ, Arena R. Obesity and Heart Failure: Focus on the Obesity Paradox. Mayo Clin Proc [Internet]. 2017. Feb;92(2):266–79. Available from: doi: 10.1016/j.mayocp.2016.11.001 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref055] 55.Kraemer WJ, Torine JC, Silvestre R, French DN, Ratamess NA, Spiering BA, et al. Body Size and Composition of National Football League Players. J Strength Cond Res [Internet]. 2005;19(3):485. Available from: http://nsca.allenpress.com/nscaonline/?request=get-abstract&doi=10.1519%2F18175.1. [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref056] 56.Rasiah R, Yusoff K, Mohammadreza A, Manikam R, Tumin M, Chandrasekaran SK, et al. Cardiovascular disease risk factors and socioeconomic variables in a nation undergoing epidemiologic transition. BMC Public Health [Internet]. 2013. Dec 25;13(1):886. Available from: http://bmcpublichealth.biomedcentral.com/articles/10.1186/1471-2458-13-886 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0262560.ref057] 57.Sear AM, Weinrich M, Hersh JE, Lam JJ. The relationship between income, education and hypertension. J Biosoc Sci [Internet]. 1982. Apr;14(2):213–21. Available from: https://www.cambridge.org/core/product/identifier/S0021932000014036/type/journal_article. doi: 10.1017/s0021932000014036 [DOI] [PubMed] [Google Scholar]

[pone.0262560.ref058] 58.Sabri S, Bener A, Eapen V, Azhar AA, Abdishakure A, Singh J. Correlation between hypertension and income distribution among United Arab Emirates population. Med J Malaysia. 2005;60(4):416–25. [PubMed] [Google Scholar]

[pone.0262560.ref059] 59.Baek T-H, Lee H-Y, Lim N-K, Park H-Y. Gender differences in the association between socioeconomic status and hypertension incidence: the Korean Genome and Epidemiology Study (KoGES). BMC Public Health [Internet]. 2015. Dec 3;15(1):852. Available from: doi: 10.1186/s12889-015-2175-6 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

A structured additive modeling of diabetes and hypertension in Northeast India

Strong P Marbaniang

Holendro Singh Chungkham

Hemkhothang Lhungdim

Roles

Abstract

Background

Methods

Results

Conclusion

Introduction

Material and methods

Study area and data

Fig 1. Map showing the location of the study area.

Sampling

Operational definitions

Diabetes

Hypertension

Dependent variables

Explanatory variables

Table 1. Prevalence of diabetes and hypertension among adults aged 15–49 years by fixed covariates with effect coding used in the model).

Statistical analysis

Results

Descriptive statistics

Table 3. Posterior estimates of the fixed effects parameters for diabetes in Northeast India.

Table 4. Posterior estimates of the fixed effects parameters for hypertension in Northeast India.

Empirical bayesian results

Model selection

Table 2. Comparison of models based on deviance information criterion (DIC).

Fixed effects

Non-linear effects

Fig 2. Non-linear effects of body mass index on the log-odds of diabetes and hypertension (the figure shows posterior means along with the 97.5% credible intervals).

Fig 3. Non-linear effects of wealth index score on the log-odds of diabetes and hypertension (posterior means with the 97.5% credible interval are shown).

Fig 4. Non-linear effects of age on the log-odds of diabetes and hypertension (posterior means along with the 97.5% credible interval are shown).

Spatial effects

Fig 5.

Fig 6.

Discussion

Spatial effects for diabetes

Spatial effects for hypertension

Fixed and non-linear effects

Conclusion

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Mohammad Asghari Jafarabadi

Roles

Author response to Decision Letter 0

Decision Letter 1

Mohammad Asghari Jafarabadi

Roles

Acceptance letter

Mohammad Asghari Jafarabadi

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases