Abstract
The assembly of functional biomolecular condensates often involves liquid-liquid phase separation (LLPS) of proteins with multiple modular domains, which can be folded or conformationally disordered to various degrees. To understand the LLPS-driving domain-domain interactions, a fundamental question is how readily the interactions in the condensed phase can be inferred from interdomain interactions in dilute solutions. In particular, are the interactions leading to LLPS exclusively those underlying the formation of discrete interdomain complexes in homogeneous solutions? We address this question by developing a mean-field LLPS theory of two stoichiometrically constrained solute species. The theory is applied to the neuronal proteins SynGAP and PSD-95, whose complex coacervate serves as a rudimentary model for neuronal postsynaptic densities (PSDs). The predicted phase behaviors are compared with experiments. Previously, a three SynGAP/two PSD-95 ratio was determined for SynGAP/PSD-95 complexes in dilute solutions. However, when this 3:2 stoichiometry is uniformly imposed in our theory encompassing both dilute and condensed phases, the tie-line pattern of the predicted SynGAP/PSD-95 phase diagram differs drastically from that obtained experimentally. In contrast, theories embodying alternate scenarios postulating auxiliary SynGAP-PSD-95 as well as SynGAP-SynGAP and PSD-95-PSD-95 interactions, in addition to those responsible for stoichiometric SynGAP/PSD-95 complexes, produce tie-line patterns consistent with experiment. Hence, our combined theoretical-experimental analysis indicates that weaker interactions or higher-order complexes beyond the 3:2 stoichiometry, but not yet documented, are involved in the formation of SynGAP/PSD-95 condensates, imploring future efforts to ascertain the nature of these auxiliary interactions in PSD-like LLPS and underscoring a likely general synergy between stoichiometric, structurally specific binding and stochastic, multivalent “fuzzy” interactions in the assembly of functional biomolecular condensates.
Significance
It has become increasingly clear that functional biomolecular condensates underpinned by liquid-liquid phase separation (LLPS) are stabilized by dynamic multivalent interactions as well as by structurally specific interactions. To gain insights into the role of stoichiometric binding in biomolecular LLPS, we develop theories for LLPS driven solely by interactions that stabilize stoichiometric protein complexes in dilute solution and for alternate scenarios in which auxiliary interactions also contribute. Application of our formulations to experimental measurements of dilute- and condensed-phase protein concentrations of the SynGAP/PSD-95 condensate model of postsynaptic densities reveals that its assembly involves interactions auxiliary to those stabilizing the 3:2 SynGAP/PSD-95 complex in dilute solution, exemplifying a synergy between specific and stochastic interactions in the assembly of biomolecular condensates.
Introduction
Biomolecular condensates composing of various proteins, nucleic acids, and small molecules are important for biological functions (1). Examples include intracellular compartments, often referred to as “membraneless organelles,” e.g., P-granules, nuclear speckles, and Cajal bodies (2,3), and extracellular materials such as the precursory tropolelastin coacervates of elastic connective tissues (4). Some membraneless organelles, such as nucleoli and stress granules, are organized further into subcompartments (5,6). Biomolecular condensates serve diverse functions, including but not limited to gene regulation, cell growth, and synaptic activities (1,7, 8, 9). Membraneless organelles reduce biomolecular noise in the cell (10) and provide regulated local environments that facilitate specific biochemical processes, yet they can also assemble or disassemble rapidly in response to environmental changes (11). Biophysically, liquid-liquid phase separation (LLPS) is recognized as a major—albeit not the only (12)—mechanism in the assembly, including subcompartmentalization (5), of many of these condensates (13).
Main ingredients of biomolecular condensates can be intrinsically disordered proteins (IDPs), folded globular proteins, RNA, and/or proteins with folded domains and intrinsically disordered regions (IDRs) (5,14, 15, 16). When only parts of the proteins (e.g., folded domains (17)) engage in significant favorable interchain interactions while other parts (e.g., parts of or entire IDRs) do not, LLPS energetics may be conceptualized using a “stickers and linkers” picture (18, 19, 20). The sticker or linker distinction is not always clear-cut, however, because every part of a protein chain may contribute to LLPS-driving interactions. For folded domains, the interactions can be, though not always, structurally specific or entail “folding upon binding” when IDR-interacting partners are involved (21,22). In contrast, for interactions among IDPs and IDRs, the molecular recognition mechanisms underlying their sequence-dependent LLPS (14,23, 24, 25, 26) are stochastic or “fuzzy” (27) in that they involve diverse, dynamic conformations and transient interactions (28, 29, 30, 31). However, some of the transient interactions may entail fluctuations between disordered chain configurations with labile, but nonetheless specific, fibril-like structures (32,33).
It has been known for some time that proteins participating in signaling pathways are often organized structurally and sequentially in a modular fashion, with folded domains such as SH2 and SH3 acting as modules playing key regulatory roles (34). Recently, multivalent interactions involving some of these domains are found to be important for the assembly of biomolecular condensates. Thus, LLPS can be a key physicochemical mechanism exploited by nature for physiological regulation, as LLPS’s essentially all-or-none features entail sharp transitions among conformationally and hence functionally distinct states of these proteins (17).
In view of the central role of multivalency in biomolecular condensates (17,18,35), network concepts such as percolation transition (18, 19, 20,36) and graph theory (37,38) have been applied to provide rationalizations and theoretical formulations of LLPS and gelation (39). In this perspective, the nodes or “stickers” are folded or labile IDR-interacting domains, and the LLPS or gelation transition is determined in large measure by the number of connections (valence of attractive interactions) that can be effectuated between the nodes. Recent applications of this approach include elucidating the role of RNA-binding valence in creating sufficient connectivity of a ribonucleoprotein network (37) in the assembly of stress granules (40,41), and in the competition between gelation and LLPS of the cancer-related protein SPOP with its substrate (38).
Postsynaptic densities
With these general considerations in mind, this work aims to gain insight into the LLPS-driving interactions of two modular proteins, synaptic Ras GTPase-activating protein (SynGAP) and postsynaptic density protein 95 (PSD-95), which are major constituents of postsynaptic densities (PSDs) (42). Recent advances indicate that biomolecular condensates play critical roles in neural function, probably because of their ability to respond rapidly to stimuli; thus, misregulated LLPS can lead to neurological diseases (43, 44, 45, 46). In particular, phase separation is important for proper communication between neurons because LLPS is involved in the assembly of synaptic vesicles attached on presynaptic plasma membranes (47,48) as well as the PSDs beneath postsynaptic membranes (8,42,49,50).
Each PSD is a disk-shaped membraneless protein-rich compartment, an assembly made up of nucleic acids and thousands of different types of proteins (43,51). These include RNA-binding proteins (52); transmembrane layer proteins such as N-methyl D-aspartate receptor (NMDAR) (53); actins in the cytoskeleton layer; scaffold proteins such as PDZ-domain-containing PSD-95s, which are membrane-associated guanylate kinases (MAGUKs) (54); guanylate kinase (GK)-associated protein (GKAP) (55); SH3 and multiple ankyrin repeat domain proteins (Shanks) (56); and the Homer family of adaptor proteins (57), as well as the SynGAP protein known to be highly enriched in PSDs (8,58). Situated adjacent to postsynaptic membranes, PSDs can exchange materials with the cytoplasm in synaptic spines and accordingly serve to provide spatial and temporal organization of the neurotransmitter receptors at the synapse (43). The functional importance of PSDs is highlighted by intriguing recent observations that PSDs are downsized during sleep (59,60), which suggest that synaptic strength is renormalized during sleep and that a SynGAP/PSD-95 condensate model of PSD (42) can be disassembled by moderate hydrostatic pressure (16,61), which points to a possible biophysical origin of the high-pressure neurological syndrome experienced by divers (62).
A minimal experimental model of PSD constructed using SynGAP and PSD-95, both of which are very abundant in PSDs, has been observed to self-organize into highly condensed, PSD-like droplets in vitro, offering the first indication that LLPS is a significant biophysical underpinning of PSD assembly (42). Subsequently, more realistic in vitro models of PSD—encompassing SynGAP and three scaffold proteins GKAP, Shank3, and Homer3 (in addition to PSD-95), as well as NR2B as another glutamate receptor—have also been constructed as a versatile research platform (8). Here, as a first step toward elucidating the statistical mechanics of PSD assembly, we focus on the simpler two-component SynGAP/PSD-95 construct, the same system we have utilized recently for studying the effect of hydrostatic pressure on PSD stability (61). SynGAP and PSD-95 undergo LLPS together when mixed, but each of the individual components, SynGAP or PSD-95 (up to 100 μM concentration each), does not phase separate by itself (42). It follows that the SynGAP/PSD-95 condensate is a complex coacervate, the formation of which must involve favorable interactions between SynGAP and PSD-95 molecules.
LLPS of stoichiometric SynGAP/PSD-95 complexes as a possible mechanism of PSD assembly
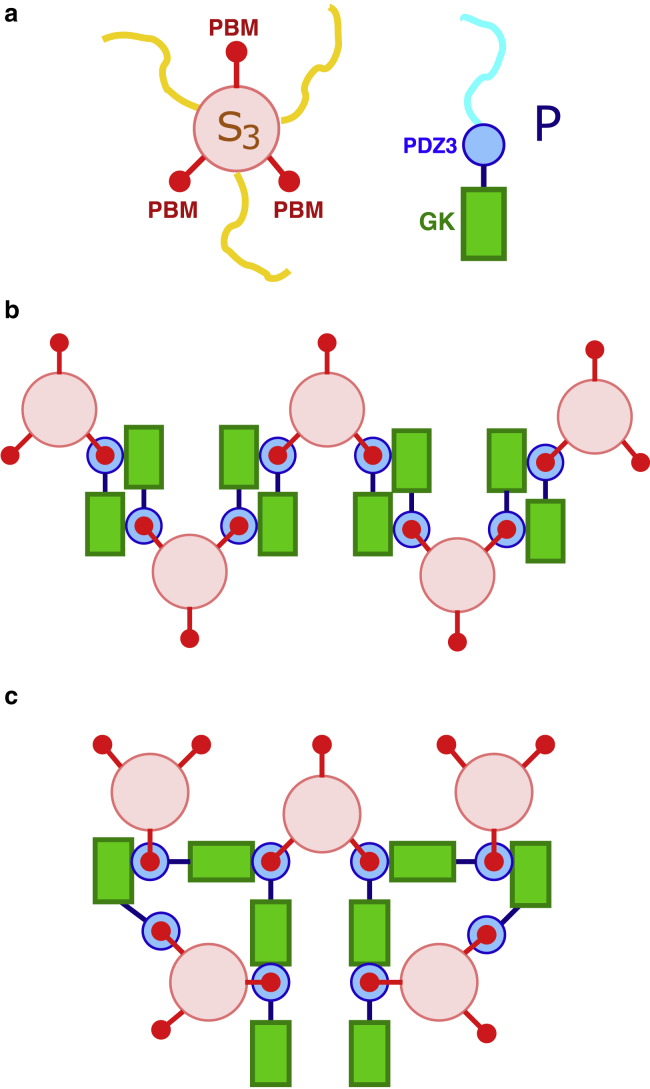
Wild-type SynGAP has a long coiled-coil (CC) domain that can dock onto two other such domains in an intertwining manner, resulting in a highly stable SynGAP trimer, which we term S3 hereafter. The SynGAP trimer can, in turn, form a complex with two PSD-95 molecues (42). We refer to this SynGAP/PSD-95 complex with a 3:2 stoichiometry, which is observed in dilute solution of SynGAP and PSD-95, as S3P2. Experimental studies indicate that formation of the trimer S3 is necessary for PSD-like complex coacervation because a SynGAP mutant that abolishes SynGAP’s ability to trimerize does not undergo LLPS in the presence of PSD-95 (42). Taken together, these observations raise the tantalizing possibility that units of the S3P2 complex act as the only nodes of favorable interactions in a SynGAP/PSD-95 condensate. In other words, the condensate is stabilized solely by interactions among the S3P2 complexes. Examples of how inter-S3P2 favorable interactions may arise from known interactions among SynGAP and PSD-95 domains that stabilize individual S3P2 complexes (42,50) are provided in Fig. 1. Recent experiments indicate that the GK domain of a P molecule interacts favorably with one of the PDZ domains of another P molecule when that PDZ domain is bound to one of the PDZ binding domains (PBMs) of an S3 (50). These GK-PDZ-PBM interactions can lead to a network of favorably interacting S3P2s (Fig. 1, b and c). Although such interactions may lead merely to a linear array of favorably interacting S3P2 complexes (Fig. 1 b) as previously envisioned (50), they may also result in a three-dimensional network of favorably interacting S3P2s (Fig. 1 c) and may therefore stabilize a condensed phase of S3P2 complexes. The hypothetical scenario that SynGAP/PSD-95 condensate is stabilized entirely by favorable interactions among units of S3P2 complexes represents a strong coupling between the S3 + 2P S3P2 binding equilibrium and LLPS-driving interactions. As such, it is instructive to ascertain, theoretically, the implications of this assumed scenario on the predicted LLPS properties. This knowledge would be useful, in general, for studying not only the SynGAP/PSD-95 systems but also other coacervate systems that involve a similar binding equilibrium or a chemical equilibrium of reversible reactions that takes an equivalent mathematical form as a binding equilibrium. The theoretically predicted mesoscopic phase properties, such as coexistence curves and phase diagrams, may then be compared against corresponding experimental observations to assess whether the assumed microscopic stoichiometric pattern of network interactions is indeed the case or, alternatively, whether auxiliary nodes of favorable interactions in addition to S3P2 complexes are involved in stabilizing the condensed coacervate phase.
Figure 1.
Schematics of hypothetical multiple SynGAP/PSD-95 configurations that are based upon interactions among stoichiometric S3P2 complexes. (a) Caricatures of the SynGAP trimer (S3, left) and PSD-95 (P, right). For S3, the pink circle represents the SynGAP CC trimer, the three red circles represent the PDZ binding domains (PBMs) at the C termini of the three S chains, and the three yellow chains represent the rest of each of the three S sequences N-terminal to the CC domain. For P, the blue circle represents the three PDZ domains, and the green rectangle represents the C-terminal guanylate kinase (GK) domain. The SH3 domain sequentially situated between these two domains is not depicted explicitly. The blue curve represents the part of P N-terminal to the PDZ domains. Domain organizations of SynGAP and PSD-95 are described in more detail in Figs. 1 and 2 of (42). (b) S3P2 multimerization by connecting each S3P2 to two other S3P2s results in a linear chain of S3P2 complexes. This scenario corresponds to that in Fig. 7 of (50). As described in this reference, the binding between an S3 with two Ps is mediated by PDZ-PBM contacts (shown by concentric red and blue circles); favorable interaction between two S3P2s is then effectuated by binding of a PDZ-PBM of one S3P2 to the GK (and SH3) of another S3P2 (indicated by a contact between a green rectangle with a set of concentric red and blue circles). (c) S3P2 multimerization by connecting each S3P2 to three other S3P2s results in a network of S3P2 complexes. The notation for binding interactions is the same as that in (b).
Probing interaction networks in SynGAP/PSD-95 condensates by theory and LLPS experiment
To this end, we endeavor to develop a theoretical formulation for protein complex coacervation with an emphasis on the interactions among the folded protein domains under constraints similar to those imposed by the modular organization, multivalency, and stoichiometry of the SynGAP/PSD-95 system. In contrast, most of the recent attention of theoretical and computational developments on biomolecular condensates has been on IDPs and IDRs. Although insights have been gained into multiple-component LLPS by several recent theoretical and modeling studies (e.g., (5,19,29,31,39,63)) and some folded domains such as the helicase domain in LAF-1 have been considered in explicit-chain simulations (64), the preponderance of the efforts thus far are on systems with a single IDP or IDR species. For instance, sequence-dependent IDP LLPS has been studied using analytical theory (23,65), coarse-grained explicit-chain lattice (20,66,67), and continuum (24,26,64,68) as well as field-theoretic (31,69) simulations. These efforts have focused on how the LLPS propensity of heteropolymeric chain molecules depends on the sequence of charged monomers (23,70,71) in general (as characterized, e.g., by quantitative charge pattern parameters (72,73)); the effects of sequence patterns of hydrophobic (74), aromatic (25), and other amino acid residues (26,64) on IDP phase behaviors; and the impact of sequence patterns on the phase properties of synthetic polymers (75,76).
The microscopic complexity of the SynGAP/PSD-95 system makes modeling its LLPS in atomic details with quantitative precision infeasible. To gain insight into the essential biophysics of the system, we construct a highly simplified model that treats each S3 or P molecule as a single particle that can engage in certain interactions suggested by experimental observations. The model is for LLPS driven largely by folded domain association. As such, it is substantially different from the aforementioned theories for IDP LLPS that take into account the conformational diversity of IDP chains. In this respect, the conceptual underpinnings of this model are akin to those of patchy-particle models of colloids (77, 78, 79), which have been applied recently to study phase behaviors of folded proteins such as lens crystallins (80), ribonucleoprotein droplets in which both the proteins and RNA are modeled as patchy articles (81), and the relationship between patchy-particle and coarse-grained explicit-chain models of biomolecular LLPSs including assembly of multicomponent condensates (82). The model developed herein is structurally and energetically more simplified than patchy-particle formulations in that the valencies of S3 and P are now treated in a mean-field manner without considering the interactions’ anisotropic directionality. This simplicity notwithstanding, our tractable model provides a critical assessment of SynGAP/PSD-95 coacervation scenarios because the model features a possible coupling between the formation of the 3:2 S3P2 complex and phase separation. We find that the constraints imposed by an exclusively complex-driven phase separation entail drastically different S3 and P compositions of coexisting phases from those predicted by classical Flory-Huggins theories (83,84) in the absence of such coupling. Therefore, whether SynGAP/PSD-95 coacervation is driven solely by interactions among S3P2 complexes can be assessed by comparing our theoretical predictions against experiment. With this recognition, we have now conducted extensive experimental measurements of S3/P compositions of coexisting phases. The results are consistent with classical Flory-Huggins theory, but not the exclusively complex-driven LLPS theory, indicating a hitherto unknown prevalence of auxiliary interactions beside those among the S3P2 complexes in the SynGAP/PSD-95 condensed phase. Details of these findings and their ramifications are provided below.
Materials and methods
A general mean-field theoretical framework for stoichiometric complex-driven LLPS
Before delving into the particulars of the SynGAP/PSD-95 system, it is useful and instructive to first construct a general LLPS theory for a solution containing two species of solutes A and B that are capable of forming a stoichiometric complex AxBy (where x, y are two fixed positive integers) and whose complex coacervation is contingent upon, i.e., coupled to, the formation of such complexes. The formation and dissociation of the complex may be expressed as a reversible binding or chemical reaction:
| (1) |
Now let the total solution volume be V, and the number of solutes A and B in the solution be, respectively, nA and nB. Proceeding with a Flory-Huggins (FH)-type lattice argument (83,85), we assume for simplicity that individual A and B solute molecules occupy equal volume, denoted by vs, and discretize the solution volume conceptually to a total of M = V/vs lattice sites. Accordingly, a lattice site in the system can be occupied by an A or B solute molecule in its entirety, part of an AxBy complex, or an entire solvent molecule. In other words, each A, B, or solvent molecule takes up one lattice site, whereas each AxBy complex occupies a contiguous chunk of x + y sites.
Consider a situation in which m complexes are formed in the solution. The binding reaction and the configurational freedom of such a state is described by the partition function
| (2) |
where −ϵb < 0 is the free energy associated with the favorable complex-forming binding (forward) reaction in Eq. 1, kB is Boltzmann constant, and T is absolute temperature. The free energy ϵb does not account for the part of translational entropy described by the combinatoric factors in Eq. 2. Nonetheless, in general ϵb can contain enthalpic as well as entropic components with entropic contributions from, e.g., change in the solvent orientational entropy associated with the binding reaction. It should also be noted that for notational simplicity, a standard FH factor, [(z − 1)/M]m(x + y − 1), to account for the spatial contiguity of each of the AxBy complexes (where z is the coordination number of the lattice for a flexible, polymer-like complex and z − 1 → 1 for a rigid complex (85)) is omitted in Eq. 2 because the factor may be formally absorbed into the entropic component of ϵb by redefining ϵb → ϵb + kBT(x + y − 1)ln[z − 1)/M].
We further assume that LLPS of our model system is driven by short spatial range contact-like interactions between individual bound solute A or B molecules from different AxBy complexes. For each m-complex state, the energetic contribution for these interactions is given by the following free energy
| (3) |
where ZLLPS(m) is the pertinent partition function and ϵps is the contact free energy of an A-A, B-B, or A-B interaction (which are assumed to carry the same ϵps for simplicity). In situations in which these interactions are relatively weak, as is apparently the case for the SynGAP/PSD-95 system according to a recent analysis of experimental data on the system’s sensitivity to hydrostatic pressure (61), one may consider only the pairwise O(m2) contribution in Eq. 3, which corresponds to the lowest-order interaction term in coordinate-space polymer lattice cluster theory (86).
It should be emphasized that the ϵps for A-A, B-B, and A-B contacts in this formulation is only for intercomplex interactions between different AxBy units. The parameter ϵps is not involved in the assembly of an individual AxBy complex, which is stipulated separately by a chemical equilibrium (Eq. 1) as will be described further below. In our mean-field formulation, each unit of AxBy interacts as a whole in an isotropic manner. In this context, assigning different energies to intercomplex A-A, B-B, and A-B contacts would only amount, mathematically, to a redefinition of ϵps, which is effectively a weighted average intercomplex energy over different types of contacts between the complexes’ A and B constituents. Going forward, it would be interesting in future investigations to extend our approach to structurally and energetically more realistic models that allow for anisotropic interactions, such as patchy-particle models (82). Under those extended frameworks, it would then be useful to study the effects of different intercomplex energies for A-A, B-B, and A-B contacts.
Here, with Zbind and ZLLPS in place, the total partition function for our model solution system that takes into account all possible m-complex states is given by
| (4) |
where mmax, the integer part of min{nA/x, nB/y}, is the maximal number of AxBy complexes possible for a given solution system and f(m) is the m-state free energy per lattice site in units of kBT. Application of Stirling’s approximation for the factorials to Eqs. 2 and 3 leads to the following approximate expression for Mf(m):
| (5) |
where χ = zϵps/(2kBT) is an effective FH parameter (86,87). In arriving at Eq. 5, we have neglected O(1/M) and O([lnM]/M) contributions to f(m) because these terms vanish in the M → ∞ thermodynamic limit. Accordingly, the χm(x + y)2 term from Eq. 3 and terms from the (2πn)1/2 part of the Stirling approximation n !≈ (2πn)1/2nne−n are not included in Eq. 5.
Following common notation in FH phase-separation theory, we define φA nA/M and φB nB/M as overall volume fractions for A and B, respectively; ψ m(x + y)/M as the volume fraction for AxBy; and ψA φA − xψ/(x + y) and ψB φB − yψ/(x + y) as volume fractions, respectively, of unbound A and B (i.e., that do not form AxBy). Using this notation, Eq. 5 may be rewritten as
| (6) |
where
| (7) |
is a reduced (dimensionless) dissociation constant of AxBy in dilute solution (the “0” superscript symbolizes dilute solution), the unit of which will be clarified below.
We are now ready to derive an approximate expression for the system described by by replacing the summation in Eq. 4 with a single term at the saddle point of f(ψ). In other words, the free energy of the system
| (8) |
where is obtained by solving
| (9) |
Multiplying every term on the right-hand side of Eq. 9 by x + y and taking the exponential of all terms result in the equivalent condition
| (10) |
which can be further rewritten as
| (11) |
where [A], [B], and [AxBy] are the equilibrium concentrations, respectively, of A, B, and AxBy and is the dissociation constant of AxBy in dilute solution. These quantities are given by
| (12a) |
| (12b) |
| (12c) |
and
| (12d) |
where [AT] and [BT] are total concentrations of A and B, irrespective of whether they are unbound or part of an AxBy complex. As expected, when χ = 0, Eq. 11 reduces to the equilibrium equation for the binding reaction in Eq. 1 for dilute solution. In contrast, when χ 0, i.e., in the presence of the LLPS-driving interactions, the dissociation constant of AxBy defined by [A]x[B]y/[AxBy] in Eq. 11 decreases exponentially as χ increases. This is because the individual A and B solutes in an AxBy complex cannot dissociate from one another as long as the AxBy complex is interacting with another AxBy complex via the LLPS-driving FH interaction. This constraint results in an enhanced binding affinity between A and B relative to that in a dilute solution in which the LLPS-driving intercomplex interactions are absent.
Experimental materials and methods
Protein expression and purification
The PSD-95 construct containing PDZ, SH3, and GK tandem (amino acids R306–L721 of the protein, referred to as PSD-95 in this work) was polymerase chain reaction (PCR) amplified from human complementary DNA (cDNA) library (NCBI: NP_001122299). The SynGAP construct containing a trimeric CC domain and a PSD-95 PDZ binding domain (PBM) (encoding amino acids A1147–V1308, lacking 1192V–1193K and 1293E–1295G of the protein; referred to as SynGAP in this work) was PCR amplified from mouse cDNA library (UniProt: J3QQ18) (42). The genes encoding PSD-95 and SynGAP were individually cloned into vectors containing an N-terminal His6-affinity tag. Recombinant proteins were expressed in Escherichia coli BL21 (DE3) cells in Luria Broth (LB) medium at 16°C overnight and purified using a nickel-nitrilotriacetic acid (Ni-NTA) agarose affinity column followed by size-exclusion chromatography (Superdex 200, GE Healthcare Life Sciences, Piscataway, NJ) with a column buffer containing 50 mM Tris (pH 8.2), 100 mM NaCl, 1 mM EDTA, 1 mM dithiothreitol (DTT). The fusion tag of each protein was cleaved by human rhinovirus (HRV) 3C protease and separated by another step of size-exclusion chromatography.
Sedimentation-based assay of phase separation and phase diagram
All proteins were precleared through high-speed centrifugation (16,873 × g 10 min) at 25°C before sedimentation assay. Proteins were mixed at each designed concentration in 50 μL total volume. After 10 min equilibration at room temperature, the mixture was centrifuged at 16,873 × g at 25°C for 10 min. The supernatant was collected, and pellet was thoroughly resuspended in 50 μL buffer. Proteins from supernatant and pellet fractions were analyzed through sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE) with Coomassie blue R250 staining.
The phase diagram was constructed from the sedimentation-based phase-separation assay. Phase separation of a SynGAP/PSD-95 mixture was considered to occur if the concentrations of SynGAP and PSD-95 recovered from the pellet of the mixture were higher than the pellet fraction of the individual protein alone in each sedimentation assay.
Quantification of protein concentration in the condensed phase
Concentrations of PSD-95 in the condensed phase were measured according to the previous reported protocol (8). Briefly, Cy3-labeled PSD-95 was diluted into the final concentration of 1% by mixing with unlabeled protein. 1% Cy3-labeled PSD-95 was further mixed with SynGAP to form condensates. The mixture was injected into a 96-well glass-bottomed plate (Thermo Fisher Scientific, Waltham, MA). Confocal fluorescence images were captured using a Zeiss LSM880 confocal microscope with a 63× objective lens (Carl Zeiss, Oberkochen, Germany). The confocal slice images spanning the middle of each droplet were used to quantify the concentration of PSD-95.
To calculate concentration of PSD-95 in each droplet, a standard calibration curve was generated. Cy3-labeled PSD-95 alone in dilute solutions at different concentrations were added into a glass-bottomed plate. The fluorescence intensity of each confocal slice image was measured using the same settings as that for the droplet quantifications. According to the standard curve, the fluorescence intensity of PSD-95 in each condensate can be converted into absolute molar concentration.
Results and discussion
A mean-field theory of stoichiometric complex-driven SynGAP/PSD-95 LLPS
We are now in a position to apply the general theory developed above to the SynGAP/PSD-95 system, with the amino acid sequence information of the SynGAP and PSD-95 constructs (157 and 416 residues, respectively) specified above in Experimental materials and methods. For wild-type SynGAP, because of the extremely strong propensity to trimerize (42), we consider, as a very good approximation, that all SynGAP molecules exist as part of S3 trimers in solution. Accordingly, we set A = S3, B = P, x = 1, and y = 2 (Fig. 2 a) in the formalism of the last section to obtain from Eq. 6 the free energy for the SynGAP/PSD-95 system:
| (13) |
where
| (14a) |
| (14b) |
and
| (14c) |
follow from Eq. 11. The LLPS-driving interaction network envisioned by this formulation is schematically illustrated in Fig. 2 b.
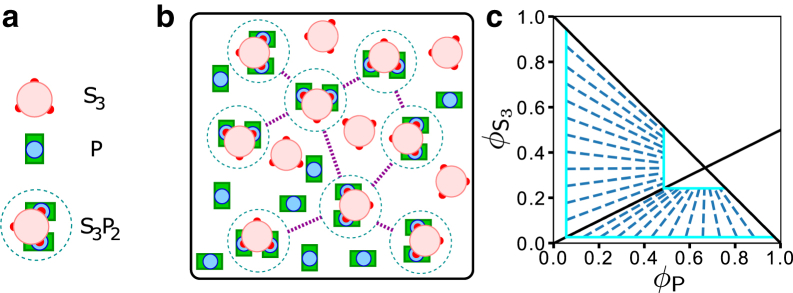
Figure 2.
Prediction of a mean-field theory that assumes SynGAP/PSD-95 complex coacervation is driven solely by favorable interactions among stoichiometric S3P2 complexes (Eq. 13). (a) Simplified schematic representation of S3, P, and S3P2. The three S3 PBMs and their connecting chain segments to the CC trimer (large pink circle, see Fig. 1a) are now shown as small red circles, the PDZ3-SH3-GK domains of P are now shown as a blue circle encased in a green rectangle, and the yellow and blue N-terminal chain segments in Fig. 1a are not depicted explicitly. Each S3P2 is enclosed by a dashed circle to underscore its role as a unit of phase-separation-driving interaction in the mean-field theory. (b) Schematic picture of a hypothetical SynGAP/PSD-95 condensed phase. The formulation in Eq. 13 stipulates that although unbound S3 and P may be present in the condensed phase, phase separation is only driven by interactions between units of S3P2 (magenta dashed lines). These interunit favorable interactions may include binding of a PDZ/PBM of one S3P2 to the SH3-GK of another S3P2 as envisioned in Fig. 1, b and c. (c) Predicted phase diagram for this hypothetical scenario based upon Eq. 13, using = 10−10 and χ = 1.5 as illustration. The boundary of binodal phase separation is shown by the light blue lines. Each of the dashed dark blue lines is a tie line indicating a pair of coexisting phases on the boundary of the phase-separated region. The overall volume constraint of + φP ≤ 1 is marked by the solid black line with slope = −1 for + φP = 1, whereas the /φP = 1/2 stoichiometric ratio of the S3P2 complex is indicated by the black solid line with slope = 1/2.
The corresponding phase-coexistence behaviors are solved by the numerical method described in (29). In general, for a solution with overall average protein volume fractions , the free energy without phase separation is given by
| (15) |
Whether the system phase separates is determined by the difference between fbulk and the free energy fsep of a phase-separated system with two coexisting phases labeled by α and β, viz.,
| (16) |
where v is the fraction of the total system volume in phase α. By definition, v satisfies 0 < v < 1 and the volume conservation conditions
| (17a) |
and
| (17b) |
which, in turn, can be used to relate volume fractions in the β phase to those in the α phase, allowing fsep for overall volume fractions , to be rewritten as a function of v, , and :
| (18) |
The system will phase separate if there exists at least a set of values for which fsep < fbulk. In that case, the final protein volume fractions—i.e., the binary coexistence phase boundary—are the volume fractions that minimize fsep. This minimization is achieved numerically by implementing a three-variable sequential least-squares programming algorithm (88) using the scipy.optimize.minimize function in SciPy, a Python-based numerical package for scientific computation (89). To ensure that there are no numerical errors in our calculation, we check the optimized sequential least-squares programming solutions against the following equations for chemical potential balance of coexisting phases to confirm that these conditions are indeed satisfied:
| (19a) |
| (19b) |
and
| (19c) |
where
| (20a) |
| (20b) |
and
| (20c) |
with x ∈ {S3, P} and y ∈ {α, β}.
The trend of phase behaviors predicted by the free energy given by Eq. 13 for this model of stoichiometric complex-driven LLPS is illustrated by the phase diagram in Fig. 2 c, which features an L-shape phase-separated regime (bound by the light blue solid lines and the diagonal black solid line with slope = −1). Apparently, a hallmark of stoichiometric complex-driven LLPS is a trend of converging tie lines (dark blue dashed lines in Fig. 2 c) from the dilute, protein-depleted phase boundary (large light blue L in Fig. 2 c) to the condensed, protein-rich phase boundary (small light blue L). When the overall concentrations (volume fractions) of S3 and P are in the dilute-solution stoichiometric ratio of 1:2 ( = 1/2), the tie line has slope = 1/2, coinciding exactly with the black solid line in Fig. 2 c with the same slope, indicating that this 1:2 stoichiometric ratio is maintained in both the dilute and condensed phases. When 1/2, the molecular species (S3 or P) that is in excess of the 1/2 ratio has no effect on phase separation because they do not generate more S3P2 complexes, and, by model construction, only interactions among S3P2 complexes are capable of driving LLPS. Consequently, the tie lines connecting coexisting dilute and condensed phases are converging toward the /φP = 1/2 line, meaning that the condensed phase is always closer than the dilute phase to the /φP = 1/2 stoichiometric ratio if 1/2 because of the larger number of favorable interactions among S3P2 complexes in the condensed phase. With this ramification of a hypothetical stoichiometric complex-driven LLPS elucidated, we now proceed to test experimentally whether the real SynGAP/PSD-95 system indeed undergoes such a complex coacervation process.
Experimental measurements of the PSD-95 concentrations in the condensed phase of SynGAP/PSD-95 mixtures
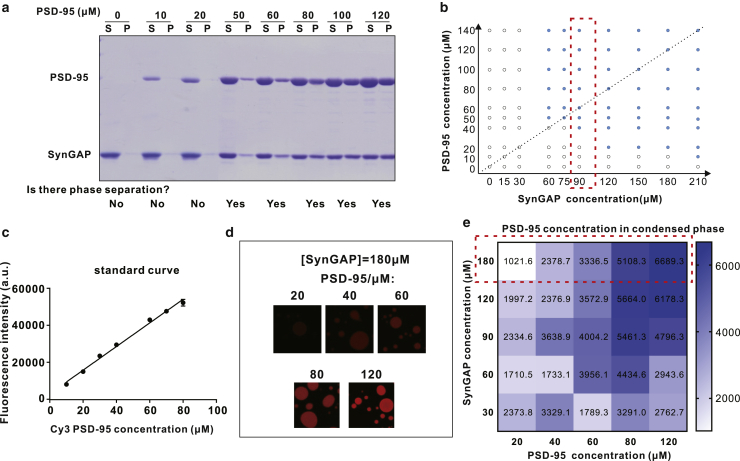
Our previous study showed that SynGAP and PSD-95 could undergo phase separation together. In the dilute phase, the two proteins form a homogenous 3:2 complex (42). However, the binding mode of SynGAP and PSD-95 in the condensed phase is unknown. To explore whether the two proteins also form a stoichiometric 3:2 complex in the condensed phase, we measured concentrations of the two proteins in the dilute phase and in the condensed phase (labeled in Fig. 3 a as “S” for supernatant and “P” for pellet, respectively, as in Fig. 4 of (42), not to be confused with the notation S for SynGAP and P for PSD-95). SynGAP and PSD-95 were mixed at different molar ratios. Sedimentation-based assay was used to assess their distributions in the dilute and condensed phases by SDS-PAGE with Coomassie blue staining (Fig. 3 a). The percentages of SynGAP and PSD-95 recovered in the pellet were analyzed. A phase diagram of the SynGAP/PSD-95 system was then constructed according to the data obtained from the sedimentation-based assay. Here, the phase diagram in Fig. 3 b shows that complex coacervation of SynGAP and PSD-95 is highly sensitive to the concentrations of the two proteins. When concentrations of the two components were higher than certain threshold values, phase separation of the mixtures occurred persistently. Interestingly, when fixing the concentration of one component at a value below a certain threshold, increasing the concentration of the other component could also induce phase separation. For instance, there was no phase separation when SynGAP was at 30 μM and PSD-95 was at 20 μM. However, when the concentration of SynGAP was increased to 120 μM with [PSD-95] unchanged at 20 μM, phase separation of the mixture was observed (Fig. 3 b). This observation suggests that SynGAP and PSD-95 not only interacted with each other through the PDZ domain of PSD-95 and the PBM of SynGAP, but that the interactions might also involve other sites of the two proteins. To quantitatively measure the absolute concentration of PSD-95 in the condensed phase so as to enable the theoretical analysis below that provides a clearer answer to this basic question, we used a confocal fluorescence image-based method developed in our earlier study (8) (Fig. 3, c and d). The fluorescence intensity of PSD-95 in the condensed droplets under each condition was converted into the absolute concentration of the protein based on the standard curve of Cy3-labeled PSD-95 obtained in dilute solutions (Fig. 3 c). The derived absolute concentrations of PSD-95 under the conditions shown in the phase diagram of the PSD-95 and SynGAP mixtures (Fig. 3 b) are shown by the heat map in Fig. 3 e.
Figure 3.
Experimental measurements of SynGAP/PSD-95 phase separation. (a) Sedimentation assay showing the dilute phase (marked by “S” at the top of the columns) and the condensed phase (marked by “P” at the top of the columns) distribution of PSD-95 and SynGAP mixed at different concentrations of PSD-95 and a fixed concentration of SynGAP at 90 μM. (b) Phase diagram of PSD-95 and SynGAP condensates. The open circles in phase diagram indicate no phase separation, and solid circles represent condensed-phase formation. The results enclosed in the dashed red box correspond to those from (a). The inclined dashed line indicate the dilute-solution 3:2 ratio for [SynGAP]/[PSD-95]. (c) Standard curve of Cy3-labeled PSD-95 obtained from dilute solutions. (d) Confocal images showing an indicative confocal slice of condensed droplets of each concentration of Cy3-labeled PSD-95 mixed with unlabeled SynGAP at a fixed concentration at 180 μM. (e) Heat map plot showing the PSD-95 concentrations in condensed phase at different combinations of PSD-95 and SynGAP concentrations. Each number represents the PSD-95 concentration (μM) in the condensed phase. The data enclosed in the dashed red box correspond to those from (d). a.u., arbitrary unit.
Experimental concentrations of SynGAP and PSD-95 in coexisting condensed and dilute phases
The next step in our investigation is to analyze the experimental data to determine whether they are consistent with the predicted behaviors in Fig. 2 c for the hypothetical scenario in which LLPS is driven solely by favorable interactions among stoichiometric S3P2 complexes. Consider an aqueous solution of S and P with initial concentrations [S0] and [P0]. Using a notation similar to that in Eqs. 16, (17a), (17b), and 18 for this system when it has undergone phase separation, we define v as the fraction of total volume in the dilute phase, and thus 1 − v is the fraction of total volume in the condensed phase. It follows from the conservation of S and P that
| (21a) |
and
| (21b) |
where quantities in the dilute and condensed phases are labeled, respectively, by the superscripts “dil” and “cond.” Note that we have defined the concentrations in Eqs. 21a and 21b purposely to correspond to those measured in the experiments (Fig. 3) in that they refer to the total concentrations of S and P molecules or their concentrations in the dilute and condensed phases irrespective of their binding status. Nonetheless, based on prior experiments (42) as noted in the introductory discussion above, we recognize that virtually all S molecules are in the form of S3 under these experimental conditions such that [S0] ≈ 3[], [Sdil] ≈ 3, and [Scond] ≈ 3 for the concentrations, whereas the volume fraction φS ≈ .
To construct a binary phase diagram, our goal here is to determine [Sdil], [Scond], [Pdil], and [Pcond] from two sets of experiments: 1) the 121 centrifugation-based assays providing the fractional numbers of protein molecules in the condensed phase, denoted here as
| (22a) |
and
| (22b) |
and 2) the 25 confocal microscopy measurements affording the condensed-phase concentration, [Pcond], of PSD-95 (P), which may be identified, aside from a proportionality constant, to the volume fraction of P:
| (23) |
Because the γS and γP in Eqs. 22a and 22b determined from centrifugation measurements (two experimental data points per condition) are by themselves insufficient to determine both [Sdil] and [Pdil] as well as v (three variables) in Eqs. 21a and 21b, we can only make the full determination of dilute- and condensed-phase protein concentrations for the 25 conditions for which confocal microscopy data are also available, with
For each of these given conditions, we may first use Eq. 22b to obtain
| (24) |
by using γP from centrifugation measurements and [Pcond] from confocal microscopy. Once v is determined, [Pdil] follows from Eq. 21b as
| (25) |
and the SynGAP concentrations in the dilute and condensed phases follow, respectively, from Eqs. 21a and 22a as
| (26a) |
and
| (26b) |
by using the solved value of v and γS from centrifugation measurements.
The general trend of binary SynGAP/PSD-95 phase behaviors inferred from experimental data is not consistent with the stoichiometric complex-driven LLPS scenario
The above-described analysis of experimental data yields the ([Pdil], [Sdil]) and ([Pcond], [Scond]) data points in Fig. 4 (orange and blue dots) as well as the tie lines connecting their coexisting values (dashed lines in Fig. 4). Because the protein concentrations of the initial states in the experiments are very close to those of the dilute phases and the dilute-phase concentrations are not measured directly, there is appreciable scatter in the ([Pdil], [Sdil]) and ([Pcond], [Scond]) data points. This is because when initial concentrations of S and P are low, the droplets formed through phase separation are very small. The thickness of individual droplet is often smaller than the confocal optical section thickness (∼0.9 μm). In such situations, the fluorescence intensity measured by confocal microscope is not only affected by fluorescence signal in the droplet but also interfered with by the glass of the coverslip and labeled proteins in solution. This basic limitation precludes an accurate quantification of the uncertainties in measured condensed-phase concentrations when overall protein concentrations are low, making it impractical to construct a smooth phase boundary from the plotted data. In future investigations, this difficulty can possibly be overcome by using solutions that lead to larger droplets, in which case the quality of the data may be evaluated by comparing signal intensities for different Z stacks obtained by confocal microscopy. For instance, if the thickness of droplet is larger than the confocal optical section thickness, the fluorescence intensities of several layers spanning the middle of each droplet should be comparable (see, e.g., Fig. 3 of (8)).
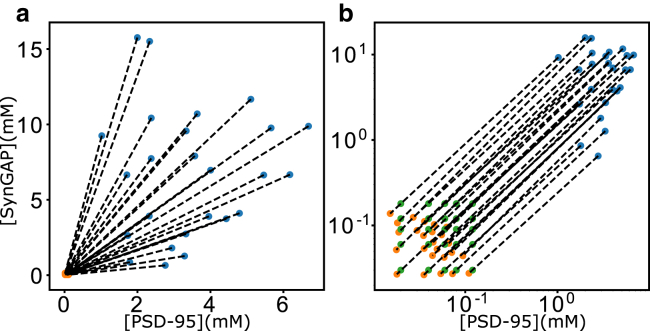
Figure 4.
Experimental trend of SynGAP/PSD-95 coexisting phases. Shown data are inferred from confocal microscopy and centrifugation measurements as described in the text. Initial (overall) concentrations ([P0], [S0]) are plotted as green data points. The phase-separated dilute phase ([Pdil], [Sdil]) are plotted as orange data points, and the condensed phase ([Pcond], [Scond]) are plotted as blue data points. Dashed lines are tie lines connecting coexisting phases. Results are shown in linear (a) as well as log-log (b) scales for clarity, as the green data points are not visible in the linear plot in (a) because they are very close to the orange data points. Note that because the dilute-phase ([Pdil], [Sdil]) concentrations (orange data points) are all very close to the origin, the slopes of tie lines in the log-log plot in (b) are all approximately equal to 1. The diversity of the actual tie-line slopes as seen in (a) is manifested by the offsets of the log-log tie lines (different intercepts) in (b).
Experimental limitations notwithstanding, one unmistakably clear message from Fig. 4 a is that the tie lines diverge from the protein-depleted phases (orange data points in Fig. 4 a) to the protein-rich phases (blue data points in Fig. 4 a), a trend that is opposite to the converging tie lines from the dilute, protein-depleted phase boundary to the condensed, protein-rich phase boundary in Fig. 2 c. This information is of critical importance, despite noted experimental uncertainties in measuring concentrations, because if the stabilizing interactions in the SynGAP/PSD-95 coacervate are only those between S3P2 complexes, the relative concentrations of S and P in the condensed phase should not change or should not vary much even when experimental uncertainties are taken into account. As discussed above, the converging tie lines and the L-shaped phase boundary in Fig. 2 c are direct consequences of the premise, based on the scenario illustrated in Fig. 2 b, that the only LLPS-driving favorable interactions are those among stoichiometric S3P2 complexes. In that hypothetical scenario, tie lines would have negative as well as positive slopes (positive slopes when overall S and P concentrations are relatively low, negative slopes when either S or P concentration is high; see Fig. 2 c). In contrast, the slopes of the experimental tie lines in Fig. 4 a are all positive, spanning an approximate range from 0.24 to 9.1. It stands to reason, therefore, based on the fact that the trend inferred from experimental data in Fig. 4 a is drastically different from that in Fig. 2 c, that the data imply that favorable interactions among stoichiometric S3P2 complexes are not the only (or not at all) the LLPS-driving interactions in the assembly of the SynGAP/PSD-95 coacervate.
Theoretical analysis of experimental data suggests that nonstoichiometric auxiliary interactions are involved in the assembly of SynGAP/PSD-95 coacervates
To rationalize the SynGAP/PSD-95 phase properties in Fig. 4, it is useful to note that the trend of diverging tie lines in Fig. 4 a is similar to that predicted by the simple FH model for certain interaction strengths, such as that reported in Fig. 6 a of (29). Accordingly, we now apply FH approaches to assess alternate scenarios of SynGAP/PSD-95 coacervation (Fig. 5). Because SynGAP/PSD-95 LLPS must involve interaction between S and P (S or P does not individually phase separate), one may first consider a simple FH model with free energy in units of kBTM given by
| (27) |
where χSP is the favorable energetic (FH χ) parameter characterizing S-P contacts as the only LLPS-driving interactions in this scenario (Fig. 5 a). An example of the binary phase diagrams predicted by this model is provided in Fig. 5 c. In contrast to the converging tie lines in Fig. 2 c, the tie lines in Fig. 5 c exhibit some degree of divergence from the protein-depleted to the protein-rich phase boundary, but the divergence is not as prominent as that in Fig. 4 a. Recognizing that the simple free energy function f1(, φP) in Eq. 27 does not provide any bias toward formation of S3P2 complexes, although such complexes are observed experimentally in dilute solution (42), it is reasonable to test whether incorporating favorability toward formation of S3P2 complexes in the model would result in predicted phase diagrams that conform better with the experimental trend. We do so by making the following modifications to the free energy f(, φP) in Eq. 13 (which already contains favorable energy for S3P2 formation):
| (28a) |
and
| (28b) |
wherein Eq. 28a stipulates that individual S3 trimers (not complexed with P in the manner of the S3P2 complex) and individual P molecules may participate in LLPS-driving interactions and/or that higher-order SynGAP/PSD-95 complexes in addition to S3P2 are present when protein concentrations are high, and these higher-order complexes also participate in LLPS-driving interactions because the two scenarios are accounted for by the same highly coarse-grained, mean-field formulation in Eq. 28a (Fig. 5 b). Moreover, unlike the stoichiometric complex-driven LLPS model free energy in Eq. 13, by dropping the exp(6χ) factor in Eq. 14c, Eq. 28b signifies that S3P2 formation is not coupled to the LLPS-driving interactions provided by the FH χ parameters (right-hand side of Eq. 28a) in the modified formulation described by (28a), (28b). The modified formulation describes a system in which S3P2 complexes are formed at low protein concentrations, whereas phase separation at higher protein concentrations is underpinned by a multitude of different S3 and P interactions.
Figure 5.
Alternate scenarios of SynGAP/PSD-95 phase separation with auxiliary interactions beyond those underpinning the assembly of stoichiometric S3P2 in dilute solution. The schematic representations of S3 and P here are the same as those in Fig. 2a. (a) Favorable LLPS-driving interactions are envisioned to be restricted to those between S3 and P (red dashed lines) as modeled by the χSP term in Eq. 27 for a simple FH model. (b) LLPS is envisioned to be driven also by favorable interactions among S3 (blue dashed lines) and among P (green dashed lines) as modeled by the χSS and χPP terms in Eq. 28a. The bias afforded by this model toward formation of S3P2 complexes in the dilute phase is not exhibited in this schematic depiction of the condensed phase. (c–e) Mean-field FH theory predictions for SynGAP/PSD-95 phase behaviors in the alternate scenario in (a) (c and d) and the alternate scenario in (b) (e). The black solid lines with slopes = 1/2 and −1, the dashed tie lines, and the light blue phase boundaries in the three phase diagrams carry the same meanings as those in Fig. 2c. The FH parameters are (c) χSP = 10.0 in Eq. 27; (d) = 10−10, χSP = 10.0, and χSS = χPP = 0 in (28a), (28b); and (e) = 10−10, χSP = 4.0, and χSS = χPP = 3.5 in (28a), (28b).
As exemplified by the two example phase diagrams in Fig. 5, d and e, the trend of tie-line divergence predicted by this modified formulation is more akin to the experimental results in Fig. 4 a than that predicted by the simple FH model in Fig. 5 c, although the differences between the predicted tie-line patterns among Fig. 5, c–e are not dramatic. Between the two models in Fig. 5, d and e with the same strongly favorable S-P interactions, it is instructive to note that the model in Fig. 5 e with favorable S-S and P-P interactions (consistent with experiment, these interactions are chosen to be insufficiently strong by themselves for S or P to phase separate individually) exhibits more tie-line divergence and thus captures slightly better the tie-line trend in Fig. 4 a than the model in Fig. 5 d with only favorable S-P interactions. In particular, the range of tie-line slopes, ([Scond] − [Sdil])/([Pcond] − [Pdil]), for the experimental results in Fig. 4 a (slope ∼0.24–9.1, as mentioned above) are quite similar to that for the theoretical results in Fig. 5 e (slope ∼0.28–12.0, calculated by multiplying each volume-fraction slope by a factor of 3). This model feature suggests that auxiliary S-S, P-P, and S-P interactions in addition to those associated with S3P2 assembly, rather than auxiliary S-P interactions alone, are likely in play in the phase separation of the experimental SynGAP/PSD-95 system as well. Nonetheless, the similarity of the tie lines in Fig. 5, c–e and the robustness of their overall pattern of divergence indicate that the experimentally observed phase properties are largely underpinned by auxiliary favorable S-P interactions.
Conclusions
It has become increasing apparent that the assembly and disassembly of biomolecular condensates are driven by stochastic, “fuzzy” interactions involving intrinsically disordered protein regions (see, e.g., (2,9,14,90)) as well as structurally specific interactions, including stoichiometric binding of folded domains in some instances (see, e.g., (8,33,37,91,92)). Deciphering how these interactions impart molecular recognition and how they may act in concert to achieve function is of fundamental importance to molecular biology (93,94), as has been emphasized in a recent study of the critical role of specific binding of the GIT1 and β-Pix GTPase regulatory enzymes in their complex coacervation (92). At a smaller length scale, a similar synergy between structurally specific interactions and stochastic, dynamic multivalent interactions has previously been indicated in the functional binding of IDPs in discrete, binary fuzzy complexes (95,96). In this context, the formation of the stoichiometric SynGAP/PSD-95 complex S3P2 in dilute solution (42) raises interesting questions regarding the role of these stoichiometric complexes in SynGAP/PSD-95 LLPS. Intuitively, a possible scenario would be that LLPS is driven solely by favorable interactions among S3P2 complexes. Theoretical considerations reveal that this scenario implies a peculiar form of binary phase diagrams with an L-shaped phase boundary and converging tie lines. However, subsequent experiments indicate that the LLPS properties of SynGAP/PSD-95 do not conform to this hypothetical scenario. Instead, our combined theoretical/experimental approach suggests strongly that auxiliary interactions beside those responsible for the formation of S3P2 are also involved in stabilizing the SynGAP/PSD-95 condensate. Our analysis has thus paved the way for investigating the nature of these auxiliary interactions. It appears that such LLPS-driving auxiliary interactions are readily available for certain folded proteins, as in the cases of lysozyme and crystallin (16). It would be instructive to compare SynGAP/PSD-95 with these simpler systems and also explore a possible involvement of disordered regions (97) in the formation of SynGAP/PSD-95 condensates. For instance, based on the interface between the third PDZ and SH3-GK domains in PSD-95 (98), the contacts leading to higher-order structures among PSD-95 molecules likely involve both hydrophobic and ionic interactions. Moreover, bioinformatics considerations (99) suggest that a stretch of chain sequence enriched in arginines, lysines, and glutamic acids between the coiled-coil and PBM domains of SynGAP is likely disordered. Such IDRs are potential participants in LLPS-driving interactions as well. In this regard, recently employed techniques for characterizing the roles of electrostatic and nonionic interactions in biomolecular condensates (100,101) would be useful. In any event, having demonstrated the capability of the relatively simple formulation developed here to gain fundamental insights into the mechanism of complex coacervation of SynGAP and PSD-95, we hope that our methodology will be useful for analyzing the role of stoichiometric complexes in the assembly of other biomolecular condensates as well.
Author contributions
Y.-H.L., M.Z., and H.S.C. designed research. Y.-H.L., H.W., and B.J. performed research. Y.-H.L. and H.W. analyzed data. Y.-H.L., H.W., M.Z., and H.S.C. wrote the article.
Acknowledgments
We thank Julie Forman-Kay for helpful discussions. We also thank three anonymous referees, whose constructive comments have helped improve the clarity of our presentation.
This work was supported by Canadian Institutes of Health Research grant NJT-155930 and Natural Sciences and Engineering Research Council of Canada Discovery grant RGPIN-2018-04351 to H.S.C. and National Key R & D Program of China grant 2019YFA0508402 and Research Grants Council of Hong Kong grant AoE-M09-12 to M.Z., as well as computational resources provided generously by Compute/Calcul Canada.
Editor: Robert Best.
Footnotes
Yi-Hsuan Lin and Haowei Wu contributed equally to this work.
Y.-H. Lin's present address: HTuO BioSciences Inc., Vancouver, British Columbia, Canada.
Contributor Information
Mingjie Zhang, Email: zhangmj@sustech.edu.cn.
Hue Sun Chan, Email: huesun.chan@utoronto.ca.
References
- 1.Banani S.F., Lee H.O., et al. Rosen M.K. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017;18:285–298. doi: 10.1038/nrm.2017.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brangwynne C.P., Eckmann C.R., et al. Hyman A.A. Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science. 2009;324:1729–1732. doi: 10.1126/science.1172046. [DOI] [PubMed] [Google Scholar]
- 3.Mao Y.S., Zhang B., Spector D.L. Biogenesis and function of nuclear bodies. Trends Genet. 2011;27:295–306. doi: 10.1016/j.tig.2011.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Muiznieks L.D., Sharpe S., et al. Keeley F.W. Role of liquid-liquid phase separation in assembly of elastin and other extracellular matrix proteins. J. Mol. Biol. 2018;430:4741–4753. doi: 10.1016/j.jmb.2018.06.010. [DOI] [PubMed] [Google Scholar]
- 5.Feric M., Vaidya N., et al. Brangwynne C.P. Coexisting liquid phases underlie nucleolar subcompartments. Cell. 2016;165:1686–1697. doi: 10.1016/j.cell.2016.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Riback J.A., Zhu L., et al. Brangwynne C.P. Composition-dependent thermodynamics of intracellular phase separation. Nature. 2020;581:209–214. doi: 10.1038/s41586-020-2256-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chong P.A., Forman-Kay J.D. Liquid-liquid phase separation in cellular signaling systems. Curr. Opin. Struct. Biol. 2016;41:180–186. doi: 10.1016/j.sbi.2016.08.001. [DOI] [PubMed] [Google Scholar]
- 8.Zeng M., Chen X., et al. Zhang M. Reconstituted postsynaptic density as a molecular platform for understanding synapse formation and plasticity. Cell. 2018;174:1172–1187.e16. doi: 10.1016/j.cell.2018.06.047. [DOI] [PubMed] [Google Scholar]
- 9.Kim T.H., Tsang B., et al. Forman-Kay J.D. Phospho-dependent phase separation of FMRP and CAPRIN1 recapitulates regulation of translation and deadenylation. Science. 2019;365:825–829. doi: 10.1126/science.aax4240. [DOI] [PubMed] [Google Scholar]
- 10.Klosin A., Oltsch F., et al. Zechner C. Phase separation provides a mechanism to reduce noise in cells. Science. 2020;367:464–468. doi: 10.1126/science.aav6691. [DOI] [PubMed] [Google Scholar]
- 11.Mitrea D.M., Kriwacki R.W. Phase separation in biology; functional organization of a higher order. Cell Commun. Signal. 2016;14:1. doi: 10.1186/s12964-015-0125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McSwiggen D.T., Mir M., et al. Tjian R. Evaluating phase separation in live cells: diagnosis, caveats, and functional consequences. Genes Dev. 2019;33:1619–1634. doi: 10.1101/gad.331520.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Alberti S., Gladfelter A., Mittag T. Considerations and challenges in studying liquid-liquid phase separation and biomolecular condensates. Cell. 2019;176:419–434. doi: 10.1016/j.cell.2018.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nott T.J., Petsalaki E., et al. Baldwin A.J. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell. 2015;57:936–947. doi: 10.1016/j.molcel.2015.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Banerjee P.R., Milin A.N., et al. Deniz A.A. Reentrant phase transition drives dynamic substructure formation in ribonucleoprotein droplets. Angew. Chem. Int. Ed. Engl. 2017;56:11354–11359. doi: 10.1002/anie.201703191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cinar H., Fetahaj Z., et al. Winter R.H.A. Temperature, hydrostatic pressure, and osmolyte effects on liquid-liquid phase separation in protein condensates: physical chemistry and biological implications. Chemistry. 2019;25:13049–13069. doi: 10.1002/chem.201902210. [DOI] [PubMed] [Google Scholar]
- 17.Li P., Banjade S., et al. Rosen M.K. Phase transitions in the assembly of multivalent signalling proteins. Nature. 2012;483:336–340. doi: 10.1038/nature10879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Harmon T.S., Holehouse A.S., et al. Pappu R.V. Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. eLife. 2017;6:e30294. doi: 10.7554/eLife.30294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Harmon T.S., Holehouse A.S., Pappu R.V. Differential solvation of intrinsically disordered linkers drives the formation of spatially organized droplets in ternary systems of linear multivalent proteins. New J. Phys. 2018;20:045002. [Google Scholar]
- 20.Choi J.-M., Dar F., Pappu R.V. LASSI: a lattice model for simulating phase transitions of multivalent proteins. PLoS Comput. Biol. 2019;15:e1007028. doi: 10.1371/journal.pcbi.1007028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Uversky V.N. Natively unfolded proteins: a point where biology waits for physics. Protein Sci. 2002;11:739–756. doi: 10.1110/ps.4210102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen T., Song J., Chan H.S. Theoretical perspectives on nonnative interactions and intrinsic disorder in protein folding and binding. Curr. Opin. Struct. Biol. 2015;30:32–42. doi: 10.1016/j.sbi.2014.12.002. [DOI] [PubMed] [Google Scholar]
- 23.Lin Y.-H., Forman-Kay J.D., Chan H.S. Sequence-specific polyampholyte phase separation in membraneless organelles. Phys. Rev. Lett. 2016;117:178101. doi: 10.1103/PhysRevLett.117.178101. [DOI] [PubMed] [Google Scholar]
- 24.Schuster B.S., Dignon G.L., et al. Mittal J. Identifying sequence perturbations to an intrinsically disordered protein that determine its phase-separation behavior. Proc. Natl. Acad. Sci. USA. 2020;117:11421–11431. doi: 10.1073/pnas.2000223117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Martin E.W., Holehouse A.S., et al. Mittag T. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science. 2020;367:694–699. doi: 10.1126/science.aaw8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Das S., Lin Y.-H., et al. Chan H.S. Comparative roles of charge, π, and hydrophobic interactions in sequence-dependent phase separation of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA. 2020;117:28795–28805. doi: 10.1073/pnas.2008122117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sharma R., Raduly Z., et al. Fuxreiter M. Fuzzy complexes: specific binding without complete folding. FEBS Lett. 2015;589:2533–2542. doi: 10.1016/j.febslet.2015.07.022. [DOI] [PubMed] [Google Scholar]
- 28.Brady J.P., Farber P.J., et al. Kay L.E. Structural and hydrodynamic properties of an intrinsically disordered region of a germ cell-specific protein on phase separation. Proc. Natl. Acad. Sci. USA. 2017;114:E8194–E8203. doi: 10.1073/pnas.1706197114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lin Y.-H., Brady J.P., et al. Chan H.S. Charge pattern matching as a ‘fuzzy’ mode of molecular recognition for the functional phase separations of intrinsically disordered proteins. New J. Phys. 2017;19:115003. [Google Scholar]
- 30.Amin A.N., Lin Y.-H., et al. Chan H.S. Analytical theory for sequence-specific binary fuzzy complexes of charged intrinsically disordered proteins. J. Phys. Chem. B. 2020;124:6709–6720. doi: 10.1021/acs.jpcb.0c04575. [DOI] [PubMed] [Google Scholar]
- 31.Pal T., Wessén J., et al. Chan H.S. Subcompartmentalization of polyampholyte species in organelle-like condensates is promoted by charge-pattern mismatch and strong excluded-volume interaction. Phys. Rev. E. 2021;103:042406. doi: 10.1103/PhysRevE.103.042406. [DOI] [PubMed] [Google Scholar]
- 32.Murray D.T., Kato M., et al. Tycko R. Structure of FUS protein fibrils and its relevance to self-assembly and phase separation of low-complexity domains. Cell. 2017;171:615–627.e16. doi: 10.1016/j.cell.2017.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kato M., McKnight S.L. A solid-state conceptualization of information transfer from gene to message to protein. Annu. Rev. Biochem. 2018;87:351–390. doi: 10.1146/annurev-biochem-061516-044700. [DOI] [PubMed] [Google Scholar]
- 34.Pawson T. Protein modules and signalling networks. Nature. 1995;373:573–580. doi: 10.1038/373573a0. [DOI] [PubMed] [Google Scholar]
- 35.Banani S.F., Rice A.M., et al. Rosen M.K. Compositional control of phase-separated cellular bodies. Cell. 2016;166:651–663. doi: 10.1016/j.cell.2016.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shillcock J.C., Brochut M., et al. Ipsen J.H. Phase behaviour and structure of a model biomolecular condensate. Soft Matter. 2020;16:6413–6423. doi: 10.1039/d0sm00813c. [DOI] [PubMed] [Google Scholar]
- 37.Sanders D.W., Kedersha N., et al. Brangwynne C.P. Competing protein-RNA interaction networks control multiphase intracellular organization. Cell. 2020;181:306–324.e28. doi: 10.1016/j.cell.2020.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Schmit J.D., Bouchard J.J., et al. Mittag T. Protein network structure enables switching between liquid and gel states. J. Am. Chem. Soc. 2020;142:874–883. doi: 10.1021/jacs.9b10066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lin Y.-H., Forman-Kay J.D., Chan H.S. Theories for sequence-dependent phase behaviors of biomolecular condensates. Biochemistry. 2018;57:2499–2508. doi: 10.1021/acs.biochem.8b00058. [DOI] [PubMed] [Google Scholar]
- 40.Yang P., Mathieu C., et al. Taylor J.P. G3BP1 is a tunable switch that triggers phase separation to assemble stress granules. Cell. 2020;181:325–345.e28. doi: 10.1016/j.cell.2020.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Guillén-Boixet J., Kopach A., et al. Franzmann T.M. RNA-induced conformational switching and clustering of G3BP drive stress granule assembly by condensation. Cell. 2020;181:346–361.e17. doi: 10.1016/j.cell.2020.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zeng M., Shang Y., et al. Zhang M. Phase transition in postsynaptic densities underlies formation of synaptic complexes and synaptic plasticity. Cell. 2016;166:1163–1175.e12. doi: 10.1016/j.cell.2016.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kaizuka T., Takumi T. Postsynaptic density proteins and their involvement in neurodevelopmental disorders. J. Biochem. 2018;163:447–455. doi: 10.1093/jb/mvy022. [DOI] [PubMed] [Google Scholar]
- 44.Ryan V.H., Fawzi N.L. Physiological, pathological, and targetable membraneless organelles in neurons. Trends Neurosci. 2019;42:693–708. doi: 10.1016/j.tins.2019.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chen X., Wu X., et al. Zhang M. Phase separation at the synapse. Nat. Neurosci. 2020;23:301–310. doi: 10.1038/s41593-019-0579-9. [DOI] [PubMed] [Google Scholar]
- 46.Wu X., Cai Q., et al. Zhang M. Liquid-liquid phase separation in neuronal development and synaptic signaling. Dev. Cell. 2020;55:18–29. doi: 10.1016/j.devcel.2020.06.012. [DOI] [PubMed] [Google Scholar]
- 47.Milovanovic D., De Camilli P. Synaptic vesicle clusters at synapses: a distinct liquid phase? Neuron. 2017;93:995–1002. doi: 10.1016/j.neuron.2017.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Milovanovic D., Wu Y., et al. De Camilli P. A liquid phase of synapsin and lipid vesicles. Science. 2018;361:604–607. doi: 10.1126/science.aat5671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Feng Z., Chen X., et al. Zhang M. Phase separation as a mechanism for assembling dynamic postsynaptic density signalling complexes. Curr. Opin. Neurobiol. 2019;57:1–8. doi: 10.1016/j.conb.2018.12.001. [DOI] [PubMed] [Google Scholar]
- 50.Zeng M., Ye F., et al. Zhang M. PDZ ligand binding-induced conformational coupling of the PDZ-SH3-GK tandems in PSD-95 family MAGUKs. J. Mol. Biol. 2018;430:69–86. doi: 10.1016/j.jmb.2017.11.003. [DOI] [PubMed] [Google Scholar]
- 51.Zhu J., Shang Y., Zhang M. Mechanistic basis of MAGUK-organized complexes in synaptic development and signalling. Nat. Rev. Neurosci. 2016;17:209–223. doi: 10.1038/nrn.2016.18. [DOI] [PubMed] [Google Scholar]
- 52.Zhang G., Neubert T.A., Jordan B.A. RNA binding proteins accumulate at the postsynaptic density with synaptic activity. J. Neurosci. 2012;32:599–609. doi: 10.1523/JNEUROSCI.2463-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Iacobucci G.J., Popescu G.K. NMDA receptors: linking physiological output to biophysical operation. Nat. Rev. Neurosci. 2017;18:236–249. doi: 10.1038/nrn.2017.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Won S., Levy J.M., et al. Roche K.W. MAGUKs: multifaceted synaptic organizers. Curr. Opin. Neurobiol. 2017;43:94–101. doi: 10.1016/j.conb.2017.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kim E., Naisbitt S., et al. Sheng M. GKAP, a novel synaptic protein that interacts with the guanylate kinase-like domain of the PSD-95/SAP90 family of channel clustering molecules. J. Cell Biol. 1997;136:669–678. doi: 10.1083/jcb.136.3.669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Monteiro P., Feng G. SHANK proteins: roles at the synapse and in autism spectrum disorder. Nat. Rev. Neurosci. 2017;18:147–157. doi: 10.1038/nrn.2016.183. [DOI] [PubMed] [Google Scholar]
- 57.Brakeman P.R., Lanahan A.A., et al. Worley P.F. Homer: a protein that selectively binds metabotropic glutamate receptors. Nature. 1997;386:284–288. doi: 10.1038/386284a0. [DOI] [PubMed] [Google Scholar]
- 58.Cheng D., Hoogenraad C.C., et al. Peng J. Relative and absolute quantification of postsynaptic density proteome isolated from rat forebrain and cerebellum. Mol. Cell. Proteomics. 2006;5:1158–1170. doi: 10.1074/mcp.D500009-MCP200. [DOI] [PubMed] [Google Scholar]
- 59.de Vivo L., Bellesi M., et al. Cirelli C. Ultrastructural evidence for synaptic scaling across the wake/sleep cycle. Science. 2017;355:507–510. doi: 10.1126/science.aah5982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Diering G.H., Nirujogi R.S., et al. Huganir R.L. Homer1a drives homeostatic scaling-down of excitatory synapses during sleep. Science. 2017;355:511–515. doi: 10.1126/science.aai8355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Cinar H., Oliva R., et al. Winter R. Pressure sensitivity of SynGAP/PSD-95 condensates as a model for postsynaptic densities and its biophysical and neurological ramifications. Chemistry. 2020;26:11024–11031. doi: 10.1002/chem.201905269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Talpalar A.E. High pressure neurological syndrome. Rev. Neurol. 2007;45:631–636. [PubMed] [Google Scholar]
- 63.Jacobs W.M., Frenkel D. Phase transitions in biological systems with many components. Biophys. J. 2017;112:683–691. doi: 10.1016/j.bpj.2016.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Dignon G.L., Zheng W., et al. Mittal J. Sequence determinants of protein phase behavior from a coarse-grained model. PLoS Comput. Biol. 2018;14:e1005941. doi: 10.1371/journal.pcbi.1005941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lin Y.-H., Brady J.P., et al. Ghosh K. A unified analytical theory of heteropolymers for sequence-specific phase behaviors of polyelectrolytes and polyampholytes. J. Chem. Phys. 2020;152:045102. doi: 10.1063/1.5139661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Das S., Eisen A., et al. Chan H.S. A lattice model of charge-pattern-dependent polyampholyte phase separation. J. Phys. Chem. B. 2018;122:5418–5431. doi: 10.1021/acs.jpcb.7b11723. [DOI] [PubMed] [Google Scholar]
- 67.Robichaud N.A.S., Saika-Voivod I., Wallin S. Phase behavior of blocky charge lattice polymers: crystals, liquids, sheets, filaments, and clusters. Phys. Rev. E. 2019;100:052404. doi: 10.1103/PhysRevE.100.052404. [DOI] [PubMed] [Google Scholar]
- 68.Nilsson D., Irbäck A. Finite-size scaling analysis of protein droplet formation. Phys. Rev. E. 2020;101:022413. doi: 10.1103/PhysRevE.101.022413. [DOI] [PubMed] [Google Scholar]
- 69.McCarty J., Delaney K.T., et al. Shea J.-E. Complete phase diagram for liquid–liquid phase separation of intrinsically disordered proteins. J. Phys. Chem. Lett. 2019;10:1644–1652. doi: 10.1021/acs.jpclett.9b00099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Das S., Amin A.N., et al. Chan H.S. Coarse-grained residue-based models of disordered protein condensates: utility and limitations of simple charge pattern parameters. Phys. Chem. Chem. Phys. 2018;20:28558–28574. doi: 10.1039/c8cp05095c. [DOI] [PubMed] [Google Scholar]
- 71.Wessén J., Pal T., et al. Chan H.S. A simple explicit-solvent model of polyampholyte phase behaviors and its ramifications for dielectric effects in biomolecular condensates. J. Phys. Chem. B. 2021;125:4337–4358. doi: 10.1021/acs.jpcb.1c00954. [DOI] [PubMed] [Google Scholar]
- 72.Das R.K., Pappu R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA. 2013;110:13392–13397. doi: 10.1073/pnas.1304749110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Sawle L., Ghosh K. A theoretical method to compute sequence dependent configurational properties in charged polymers and proteins. J. Chem. Phys. 2015;143:085101. doi: 10.1063/1.4929391. [DOI] [PubMed] [Google Scholar]
- 74.Statt A., Casademunt H., et al. Panagiotopoulos A.Z. Model for disordered proteins with strongly sequence-dependent liquid phase behavior. J. Chem. Phys. 2020;152:075101. doi: 10.1063/1.5141095. [DOI] [PubMed] [Google Scholar]
- 75.Perry S.L., Sing C.E. 100th anniversary of macromolecular science viewpoint: opportunities in the physics of sequence-defined polymers. ACS Macro Lett. 2020;9:216–225. doi: 10.1021/acsmacrolett.0c00002. [DOI] [PubMed] [Google Scholar]
- 76.Sing C.E., Perry S.L. Recent progress in the science of complex coacervation. Soft Matter. 2020;16:2885–2914. doi: 10.1039/d0sm00001a. [DOI] [PubMed] [Google Scholar]
- 77.Wertheim M.S. Fluids with highly directional attractive forces. IV. Equilibrium polymerization. J. Stat. Phys. 1986;42:477–492. [Google Scholar]
- 78.Teixeira P.I.C., Tavares J.M. Phase behaviour of pure and mixed patchy colloids — Theory and simulation. Curr. Opin. Colloid Interface Sci. 2017;30:16–24. [Google Scholar]
- 79.Kamp M., de Nijs B., et al. van Blaaderen A. Multivalent patchy colloids for quantitative 3D self-assembly studies. Langmuir. 2020;36:2403–2418. doi: 10.1021/acs.langmuir.9b03863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Kastelic M., Kalyuzhnyi Y.V., Vlachy V. Modeling phase transitions in mixtures of β-γ lens crystallins. Soft Matter. 2016;12:7289–7298. doi: 10.1039/c6sm01513a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Nguemaha V., Zhou H.-X. Liquid-liquid phase separation of patchy particles illuminates diverse effects of regulatory components on protein droplet formation. Sci. Rep. 2018;8:6728. doi: 10.1038/s41598-018-25132-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Espinosa J.R., Joseph J.A., et al. Collepardo-Guevara R. Liquid network connectivity regulates the stability and composition of biomolecular condensates with many components. Proc. Natl. Acad. Sci. USA. 2020;117:13238–13247. doi: 10.1073/pnas.1917569117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Flory P.J. Cornell University Press; Ithaca, NY: 1953. Principles of Polymer Chemistry. [Google Scholar]
- 84.de Gennes P.-G. Cornell University Press; Ithaca, NY: 1979. Scaling Concepts in Polymer Physics. [Google Scholar]
- 85.Chan H.S., Dill K.A. Solvation: effects of molecular size and shape. J. Chem. Phys. 1994;101:7007–7026. [Google Scholar]
- 86.Baker D., Chan H.S., Dill K.A. Coordinate-space formulation of polymer lattice cluster theory. J. Chem. Phys. 1993;98:9951–9962. [Google Scholar]
- 87.Bawendi M.G., Freed K.F., Mohanty U. A lattice field theory for polymer systems with nearest-neighbor interaction energies. J. Chem. Phys. 1987;87:5534–5540. [Google Scholar]
- 88.Kraft D. Deutsche Forschungs- und Versuchsanstalt für Luft- und Raumfahrt; Köln: 1988. A Software Package for Sequential Quadratic Programming. [Google Scholar]
- 89.Jones E., Oliphant T., Peterson P. 2001. SciPy: Open source scientific tools for Python.http://www.scipy.org/ [Google Scholar]
- 90.Brangwynne C., Tompa P., Pappu R. Polymer physics of intracellular phase transitions. Nat. Phys. 2015;11:899–904. [Google Scholar]
- 91.Guo L., Kim H.J., et al. Shorter J. Nuclear-import receptors reverse aberrant phase transitions of RNA-binding proteins with prion-like domains. Cell. 2018;173:677–692.e20. doi: 10.1016/j.cell.2018.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Zhu J., Zhou Q., et al. Zhang M. GIT/PIX condensates are modular and ideal for distinct compartmentalized cell signaling. Mol. Cell. 2020;79:782–796.e6. doi: 10.1016/j.molcel.2020.07.004. [DOI] [PubMed] [Google Scholar]
- 93.Fare C.M., Villani A., et al. Shorter J. Higher-order organization of biomolecular condensates. Open Biol. 2021;11:210137. doi: 10.1098/rsob.210137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Schmit J.D., Feric M., Dundr M. How hierarchical interactions make membraneless organelles tick like clockwork. Trends Biochem. Sci. 2021;46:525–534. doi: 10.1016/j.tibs.2020.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Borg M., Mittag T., et al. Chan H.S. Polyelectrostatic interactions of disordered ligands suggest a physical basis for ultrasensitivity. Proc. Natl. Acad. Sci. USA. 2007;104:9650–9655. doi: 10.1073/pnas.0702580104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Mittag T., Marsh J., et al. Forman-Kay J.D. Structure/function implications in a dynamic complex of the intrinsically disordered Sic1 with the Cdc4 subunit of an SCF ubiquitin ligase. Structure. 2010;18:494–506. doi: 10.1016/j.str.2010.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Rana U., Brangwynne C.P., Panagiotopoulos A.Z. Phase separation vs aggregation behavior for model disordered proteins. J. Chem. Phys. 2021;155:125101. doi: 10.1063/5.0060046. [DOI] [PubMed] [Google Scholar]
- 98.Zhang J., Lewis S.M., et al. Lee A.L. Supertertiary structure of the MAGUK core from PSD-95. Structure. 2013;21:402–413. doi: 10.1016/j.str.2012.12.014. [DOI] [PubMed] [Google Scholar]
- 99.Erdős G., Pajkos M., Dosztányi Z. IUPred3: prediction of protein disorder enhanced with unambiguous experimental annotation and visualization of evolutionary conservation. Nucleic Acids Res. 2021;49:W297–W303. doi: 10.1093/nar/gkab408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Krainer G., Welsh T.J., et al. Knowles T.P.J. Reentrant liquid condensate phase of proteins is stabilized by hydrophobic and non-ionic interactions. Nat. Commun. 2021;12:1085. doi: 10.1038/s41467-021-21181-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Kim T.H., Payliss B.J., et al. Kay L.E. Interaction hot spots for phase separation revealed by NMR studies of a CAPRIN1 condensed phase. Proc. Natl. Acad. Sci. USA. 2021;118 doi: 10.1073/pnas.2104897118. e2104897118. [DOI] [PMC free article] [PubMed] [Google Scholar]