Application of machine learning classifiers to X-ray diffraction imaging with medically relevant phantoms

Abstract

Purpose:

Recent studies have demonstrated the ability to rapidly produce large field of view X-ray diffraction images, which provide rich new data relevant to the understanding and analysis of disease. However, work has only just begun on developing algorithms that maximize the performance towards decision-making and diagnostic tasks. In this study, we present the implementation of and comparison between rules-based and machine learning classifiers on X-ray diffraction images of medically relevant phantoms to explore the potential for increased classification performance.

Methods:

Medically relevant phantoms were utilized to provide well-characterized ground-truths for comparing classifier performance. Water and polylactic acid (PLA) plastic were used as surrogates for cancerous and healthy tissue, respectively, and phantoms were created with varying levels of spatial complexity and biologically relevant features for quantitative testing of classifier performance. Our previously developed X-ray scanner was used to acquire co-registered X-ray transmission and diffraction images of the phantoms. For classification algorithms, we explored and compared two rules-based classifiers (cross-correlation, or matched-filter, and linear least-squares unmixing) and two machine learning classifiers (support vector machines and shallow neural networks). Reference X-ray diffraction spectra (measured by a commercial diffractometer) were provided to the rules-based algorithms, while 60% of the measured X-ray diffraction pixels were used for training of the machine learning algorithms. The area under the receiver operating characteristic curve (AUC) was used as a comparative metric between the classification algorithms, along with the accuracy performance at the midpoint threshold for each classifier.

Results:

The AUC values for material classification were 0.994 (cross-correlation, CC), 0.994 (least-squares, LS), 0.995 (support vector machine, SVM), and 0.999 (shallow neural network, SNN). Setting the classification threshold to the midpoint for each classifier resulted in accuracy values of CC=96.48%, LS=96.48%, SVM=97.36%, and SNN=98.94%. If only considering pixels ± 3 mm from water-PLA boundaries (where partial volume effects could occur due to imaging resolution limits), the classification accuracies were CC=89.32%, LS=89.32%, SVM=92.03%, and SNN=96.79%, demonstrating an even larger improvement produced by the machine-learned algorithms in spatial regions critical for imaging tasks. Classification by transmission data alone produced an AUC of 0.773 and accuracy of 85.45%, well below the performance levels of any of the classifiers applied to X-ray diffraction image data.

Conclusions:

We demonstrated that machine learning-based classifiers outperformed rules-based approaches in terms of overall classification accuracy and improved the spatially resolved classification performance on X-ray diffraction images of medical phantoms. In particular, the machine learning algorithms demonstrated considerably improved performance whenever multiple materials existed in a single voxel. The quantitative performance gains demonstrate an avenue to extract and harness X-ray diffraction imaging data to improve material analysis for research, industrial, and clinical applications.

Introduction

During the onset of various types of cancers, changes occur at the cellular level, which impact structures including collagen, extracellular matrices, and bone-mineral compositions^1,2. X-ray diffraction (XRD) is a technology capable of detecting these changes through measuring the interference patterns of X-rays scattering off the molecular-scale structures^3–6. While prior XRD measurement and analysis methods have proven useful for studying diseases^7–10, they have typically been limited to analyzing only a few discrete locations at the surface of a prepared sample or specimen.

XRD imaging approaches have been developed that seek to circumvent sample preparation, which is often destructive to samples and their spatial correlations, while enabling faster measurements with larger fields of view^11–15. These imaging methods, including energy-dispersive and angular-dispersive raster scanning measurements, coherent scattering computed tomography, and coded aperture systems, seek to measure the XRD signatures of materials throughout a large field of view within reasonable scan times while maintaining adequate spatial resolutions for imaging applications. While simulation studies are often conducted for the design and optimization of these novel imaging architectures^16–19, experimental validations on biologically-relevant phantoms^20–23 and real biospecimens^{3,6,8,13,15,24} have also occurred. These results have shown that tissues can be differentiated by spatially resolved XRD measurements; however, the resulting rich spatio-spectral datasets necessitate automatic data processing and classification techniques to parse the large data volume.

Conventional XRD classifiers depend on matching scatter peak locations or correlating measured spectra with databases, but more advanced algorithms offer the potential to outperform these simpler methods²⁵. Studies have implemented multivariate analysis (e.g., principal component analysis) for tissue classification²⁶, while more advanced algorithms (particularly convolution neural networks (CNNs) and their variants) have been applied extensively to crystalline XRD data^27–31. Beyond algorithm development focused on XRD spectra, there have been developments to classify materials based on their 2D raw scatter measurements^32–36. In contrast, our development of coded aperture XRD imaging systems has generated large amounts of data in the form of XRD images that contain full XRD spectra within each voxel of an object. Our previous success at developing CNN-based classification algorithms³⁷ combined with the multitude of other approaches discussed above show that machine learning (ML) classifiers offer advantages relative to rules-based classifiers when applied to XRD data.

In this study, we perform a comparison of classifier performances using medical XRD phantoms with different geometries that are intended to model cancerous and adipose breast tissue. These phantoms provide well-characterized ground-truths that allow us to investigate the performance of multiple classification algorithms operating on data-rich XRD images. Our previously developed X-ray fan beam coded aperture imaging system^15,19 is used to obtain XRD images that are fed into the classification algorithms for analysis. For all phantoms, 4 classification algorithms are compared: cross-correlation (CC), least-squares (LS) unmixing, support vector machines (SVM), and shallow neural networks (SNN).

Materials & Methods

Although the medical phantoms and material discrimination approaches discussed in this study are agnostic to XRD imaging architecture, we briefly describe the operation of our imaging system for the sake of completeness. After presenting the imaging system, we discuss our designed medical phantoms for XRD imaging and their purposes. Lastly, we outline the classification algorithms explored in this study for comparing rules-based and ML-based algorithms.

X-ray Fan Beam Coded Aperture Imaging System Data Acquisition

Our previously developed X-ray fan beam coded aperture imaging system^15,19 allows for reduced measurement time by making multiplexed measurements of an object’s XRD data. The fan beam measures a 150x1 mm² region through a single step-and-shoot exposure, while the coded aperture and a physics-based forward model of the system enable us to determine the origin of scattered X-rays along the fan beam extent^38–40.

This X-ray imaging system was used to record the co-registered X-ray transmission and diffraction images used for training and testing in this study. As shown in Fig. 1 and discussed in depth in prior work^15,19, the system consists of a spectrally-filtered X-ray tube (XRB Monoblock, Spellman HV, NY) that is spatially collimated to produce a fan beam at the sample plane. The sample is illuminated by the primary fan beam, and both the transmitted and XRD signals are measured at the detector (Xineos-2329, Teledyne Dalsa, CA). The system (Fig. 1B) is capable of transmission and XRD imaging of a 15x15 cm² field of view within minutes. This rapid imaging makes it possible to generate large datasets that can be used in ML algorithm development.

Fig 1.

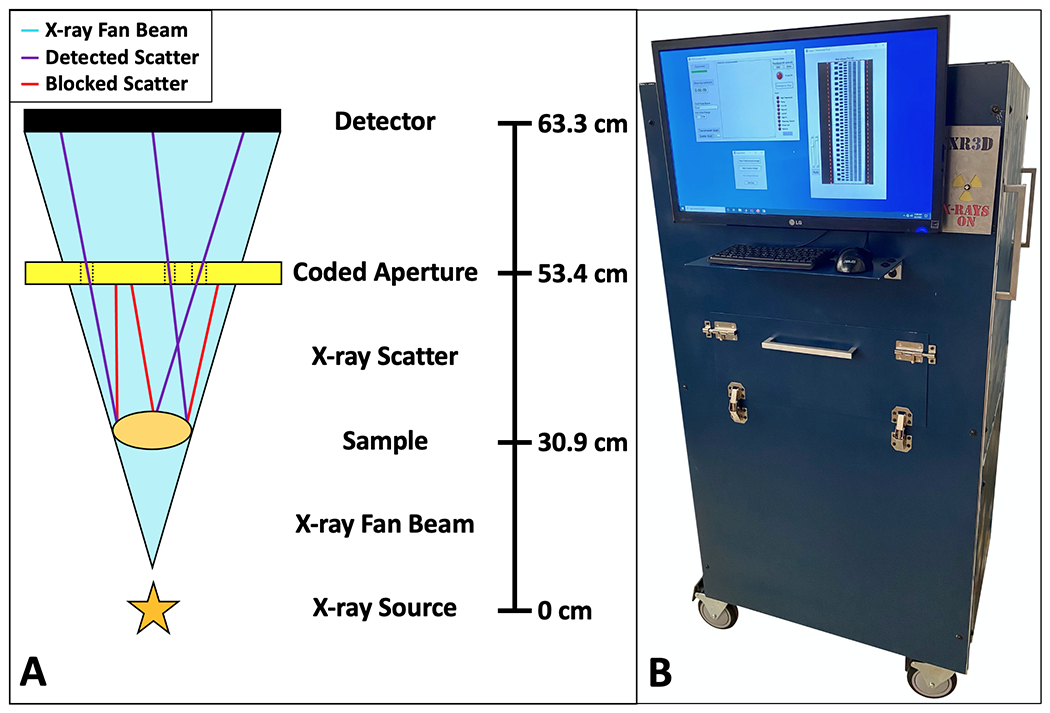
The X-ray fan beam coded aperture transmission and diffraction imaging system schematic and prototype. A) Schematic of the X-ray fan beam coded aperture transmission and diffraction system, where a collimated X-ray source produces a fan beam that illuminates a sample while signal is acquired at the detector. Scatter produced by the sample passes through the 2D coded aperture and is encoded prior to its measurement at the detector (purple = encoded scatter making it to detector, red = scatter blocked by coded aperture, teal = primary fan beam) (online version only). Scatter data is acquired sequentially after transmission scans. Denoted distances are from X-ray source focal spot to X-ray entrance of each object B) Photo of the constructed X-ray fan beam coded aperture imaging system, including a built-in monitor, computer, and lead shielding for operation, along with GUI apps for data acquisition and display.

During transmission image measurements, the system operates with the X-ray generator at 80 kVp/6 mA/100 ms fan slice-exposures. When the system has acquired fan beam data for the full extent of the scanned object, all slices are stitched together (with 50 μm overlap of adjacent fan acquisitions that is corrected in post-processing), with outer air scans used to display the scan in a logarithmic display of transmitted intensity that is standard for radiographs. The system has a transmission spatial resolution of ≈0.6 mm², which is limited primarily by the X-ray source focal spot size. After acquiring the X-ray transmission data for each phantom, we acquire XRD data by a similar approach. The X-ray generator is operated at 160 kVp/3 mA/15 s fan slice-exposures. The XRD spectrum at each pixel in the object is determined from the raw scatter data using a post-acquisition reconstruction algorithm^38,40,41. Using this approach, the current system’s XRD spatial resolution is ≈1.4 mm² with a 0.01 1/Å momentum transfer resolution (q)¹⁵. For this study, we consider only geometrically thin (i.e., 5–10 mm) samples and focus on phantoms relevant to imaging biospecimens. Additionally, in this study q is defined as

$$q=\frac{hc}{E}*\sin \left(\frac{\theta }{2}\right)$$

where h is Planck’s constant, c is the speed of light, E is the energy of the X-rays, and θ is the angles the X-rays scatter at.

Designed Phantoms for Quantifying Material Classification Performance

To test the performance of classification algorithms on XRD image data, it is important to know the correct ground truth/labels of materials within each measured pixel. However, human tissues can have complex variations in their XRD spectra due to differences in patient genetics and mixing of tissue types within measured pixels. In addition, there are currently no standard methods for performing large field of view (≥10x10 cm²) XRD imaging. It is, therefore, prudent for empirical investigations of classification algorithms to start with manufactured phantoms that have known materials in all locations. Such phantoms allow for a direct, quantitative comparison between the perfectly known ground truth and recovered XRD spectra at each location within the phantom.

It is important to design phantoms that are consistent with intended application. Here we focus on the ability for XRD imaging to correctly classify cancer and benign tissues based on their XRD spectra; therefore, for the design of the phantom objects, water and polylactic acid (PLA) plastic were identified as viable simulants for cancer⁴² and adipose (fat)^43,44,45(p3) tissue, respectively. Shown in Fig. 2A are the XRD spectra of breast cancer and adipose tissue¹, along with XRD spectra of water and PLA that we measured within a commercial diffractometer (D2 Phaser, Bruker, MA). Observing the average XRD spectra for adipose (which is typically the most prevalent breast tissue by volume) and breast cancer as measured in literature¹, it can be noted that adipose and PLA have narrower and higher intensity peaks at lower q values, while breast cancer and water have broader and lower intensity peaks spread out at higher q values. It is for this reason that water and PLA were selected as simulants—within the XRD domain, water’s relation to PLA is comparable to breast cancer’s relation with adipose. This phantom material choice is in agreement with previous XRD studies^46,47. Additionally, water and PLA have similar densities to cancer and adipose (≈1 g/cm³), producing sufficiently similar scatter intensities.

Fig 2.

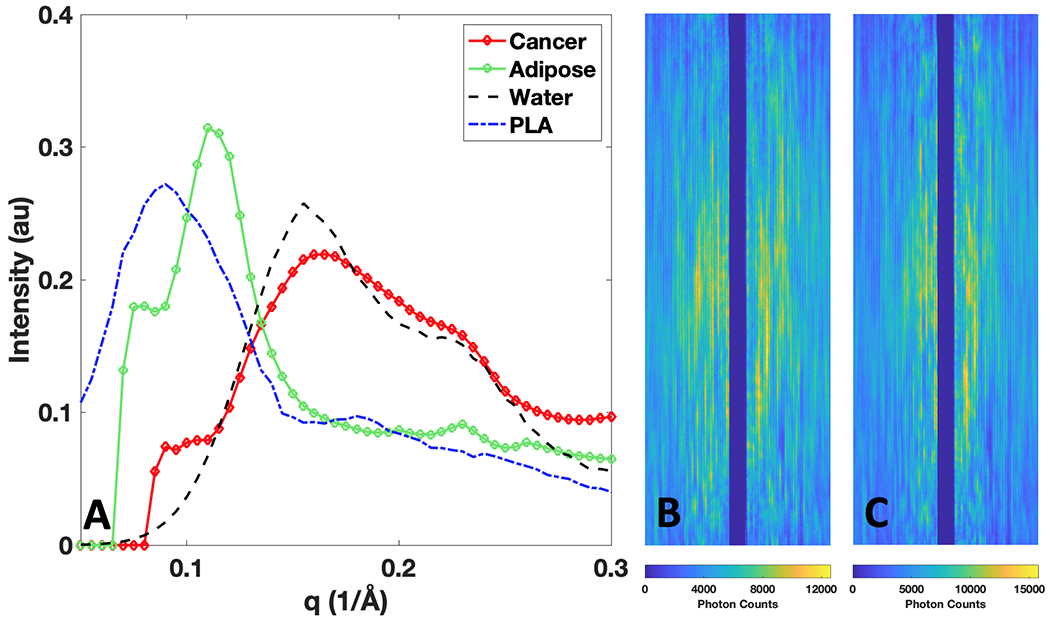
X-ray diffraction (XRD) spectra (in intensity vs momentum transfer (q) units) of breast tissues and simulant materials, along with raw 2D scatter measurements taken by the X-ray fan beam coded aperture system for water and PLA. A) XRD spectra of breast cancer and adipose¹, along with their simulants of water and PLA B) Raw X-ray fan beam coded aperture measurement of water’s scattered X-rays along whole fan extent C) Raw X-ray fan beam coded aperture measurement of PLA’s scattered X-rays along whole fan extent.

It is worth noting that, while we focused on water and PLA in this study, this approach can be generalized to other materials (e.g. using other 3D printed materials and/or soft materials^2,22 to fill the empty space). In addition, one can use more than two materials while still maintaining perfect spatial and material labeling at each pixel of the object.

For visualization of the raw scatter measurements taken on these simulants, Fig. 2B and 2C show the encoded scatter X-ray measurements of water and PLA acquired when water and PLA occupied the full extent of the fan beam (i.e., for the phantom shown in Fig. 3A). Water’s higher mean q value leads to a wider distribution of coherently scattered X-rays along the horizonal axis in Fig. 2B, while PLA’s lower mean q value generates a narrower distribution perpendicular to the fan beam extent. The higher peak intensity of PLA is shown in the maximum photon counts detected within a pixel being ≈15,000 counts, while water’s maximum intensity is lower at ≈12,000 counts—this is expected given PLA’s density of 1.24 g/cm³ relative to water’s density of 1 g/cm³.

Fig 3.

Phantoms composed of water and PLA plastic (6 mm thick) for testing material classification of the X-ray fan beam coded aperture imaging system. A) A trough phantom containing rectangular regions of water and PLA B) A wedge phantom with three triangle water wells C) A ramp phantom that transitions from 6 mm PLA (left side) to 5.5 mm water (right side) by a ramp that changes the ratio of the materials through the axial dimension D) Tissue phantoms modeled after real lumpectomy tissue slices, with water wells placed at the locations of the tumors within the real samples. For imaging, the fan extends along the vertical axis of these images, while the scan direction occurs on the horizontal axis (together creating the transverse plane). The axis through the thickness of the phantoms represents the axial dimension.

With the simulant materials selected, we next designed phantoms (6 mm thick) with specific spatial-material configurations to test different aspects of the system’s material classification performance (see Fig. 3). A trough phantom was designed with a 150x10x5.5 mm³ well for placing water on the left side of a 154x24x6 mm³ block of PLA (see Fig. 3A). This object allows for testing the measurement and classification performance of materials while there is primarily a single material within the full extent of the X-ray fan beam during a measurement. This object can also be used to check the quality and uniformity of the measured XRD spectra over fan beam locations and time. The wedge phantom shown in Fig. 3B was designed as a more complex test, with the width of water along the X-ray fan beam extent going from a point to 20 mm wide across an 80 mm extent, with wells uniformly 5.5 mm deep. With a continuum of water widths, this object can show the resolution for detecting the water material embedded within PLA. Three wells were created within the wedge phantom (total phantom volume of 102x82x6 mm³) as an additional quality check of water detection resolution on the top, middle, and bottom region of the X-ray fan beam extent. The ramp phantom shown in Fig. 3C allows for testing material classification performance as the amount of each material varies through the thickness of the object (analogous to how tissue composition can vary within a 6 mm thick region), with the overall phantom volume being 17x33x6 mm³. On the left side of the ramp phantom is a 3 mm wide ledge of 6 mm thick PLA, which slowly ramps downward across 25 mm width leaving a 3 mm wide ledge of 0.5 mm thick PLA—water covers this ramp to create regions that vary from containing majority PLA to majority water throughout the phantom thickness. The final designed phantoms shown in Fig. 3D are tissue phantoms modeled after real malignant breast lumpectomy slices (based on digital slides provided for modeling by Duke Hospital Surgical Pathology, as shown in supplemental Fig. S1). These phantoms represent a biologically relevant test, as the spatial distribution of PLA represents healthy tissue while the location of water wells (all 5.5 mm deep) represents locations of malignant tumors. Unlike the previous phantoms, the tissue phantoms are not composed of rectangles/triangles and instead have curved boundaries between air, PLA, and water, providing more biologically realistic spatial distribution of simulant materials. This final set of phantoms seeks to characterize the potential performance as it relates to the specific task of classifying cancer and healthy tissue in excised breast lumpectomy specimens. These phantoms are a simplification of the real biological scenario, given that tissue heterogeneity through a 6 mm slice of tissue would in fact cause mixtures along the thickness of the material being scanned (with the presence of fibroglandular and other tissue types); however, the phantoms are taken as a reasonable approximation as it relates to the task of identifying primary tumors that are a few millimeters in diameter. Scans of the trough, wedge, ramp, and tissue phantoms were conducted over planar areas of 150x33 mm², 150x89 mm², 150x41 mm², and 150x66 mm², with the total scan times taking 8.25, 22.25, 10.25, and 16.5 minutes, respectively. Having presented these phantoms for conducting the material classification algorithm study, we next outline the classification algorithms under consideration.

Material Classification Algorithms

We considered both rule-based and ML-based approaches for performing classification on the measured XRD spectra. While rule-based approaches can take advantage of previously known differences (in the form of a database of XRD spectra that can be used for matched filtering⁴⁸ or simple unmixing approaches⁴⁹), ML approaches have the capability to learn additional relevant features^50–52. Each XRD spectrum in this study is composed of 43 intensity values sampled from a q range of 0.09 to 0.3 Å⁻¹, providing a sufficient number of features for the ML training process. This study seeks to evaluate the performance of both approaches—rule-based methods have well-established performance bounds and are straightforward in interpretation given their non-learned nature, whereas ML approaches have the potential for higher performance by overcoming noise and non-linearities at the cost of requiring larger training data and their behavior being less well understood.

For rule-based approaches, the first method considered is CC of each measured XRD spectrum with the commercial diffractometer measurements of water and PLA. To remove slight variations in material densities as an impacting factor, all database and measured spectra are normalized so their sum of squares equals 1 for all classifiers (for spectra $s$ the normalization is: $s=s/\sqrt{\Sigma s^2}$. We note that, for CC, this allows for using the inner product to compute the match ranging from 0 (effectively orthogonal) to 1 (perfectly identical). Pixels are classified as the material from the database with which they show the greatest match, while a threshold for cutting out measurements not belonging to any member of the database is implemented, such that any pixel with <80% CC with a database measurement is marked as a null class. We note that this choice of null threshold is well above water’s 60% match with PLA. While this null class was added to the algorithm to prevent poor matches being classified as a database material, in this study no measurements belonged to the null class due to the quality of measurements and fact that the phantoms only contained the two known materials. Another rule-based approach explored in this study is linear unmixing by LS, which aims to estimate the abundance of materials within a pixel by estimating the spectral mixture of database measurements that produces the best match with the data. We use MATLAB’s “lsqnonneg()” function to conduct non-negative linear LS unmixing by a previously developed algorithm⁵³. As with the CC approach, the reference database and measured spectra are normalized by sum of squares. With each pixel’s predicted abundance of database materials generated, individual pixels are classified as their highest abundance material (for comparison to other binary classification methods considered) with the algorithm set to sort any perfect 50:50 mixture to be classified as the cancer simulant, water.

In consideration of ML approaches, SVMs and SNNs were identified as potential candidates for working with moderate amounts of training data⁵². When developing machine learning models, it is standard practice to divide all available data into a “training” dataset for training the model, a “validation” dataset for preventing overfitting, and a test dataset for quantifying performance. In this study we use the common splitting ratios of 60:20:20 for division of data into the training, validation, and test groups⁵⁴ (for the SVM and SNN). Thus, we begin training of the SVM and SNN models by first randomly selecting 80% of the pixels along with their ground truth labeling to be used as a training/validation dataset pool (with the remaining 20% held out as an independent test set). For identification of the ML models that generalized best for classifying water and PLA, 60% of the pixels (3/4 of the training/validation pool) were randomly used for training, while the remaining 20% (1/4 of the training/validation pool) was used for validation to identify the ML models that generalized best. This training + validation process was repeated for 200 SVM and SNN models on the same pool of data (80%), allowing pixels to randomly shuffle between the training/validation groups in order to identify the sensitivity to this splitting and best observed generalization. The SVM and SNN models that performed best on the validation group (in terms of the receiver operating characteristic (ROC) area under the curve (AUC) value), were saved for comparison between classifiers. Lastly, the best SVM and SNN models were run on the test data (i.e., the final 20% of pixels that had been held out from the training/validation process) to quantify performance on an separate dataset. The schematic shown in Fig. 4 illustrates the classification approaches taken by the explored algorithms.

Fig 4.

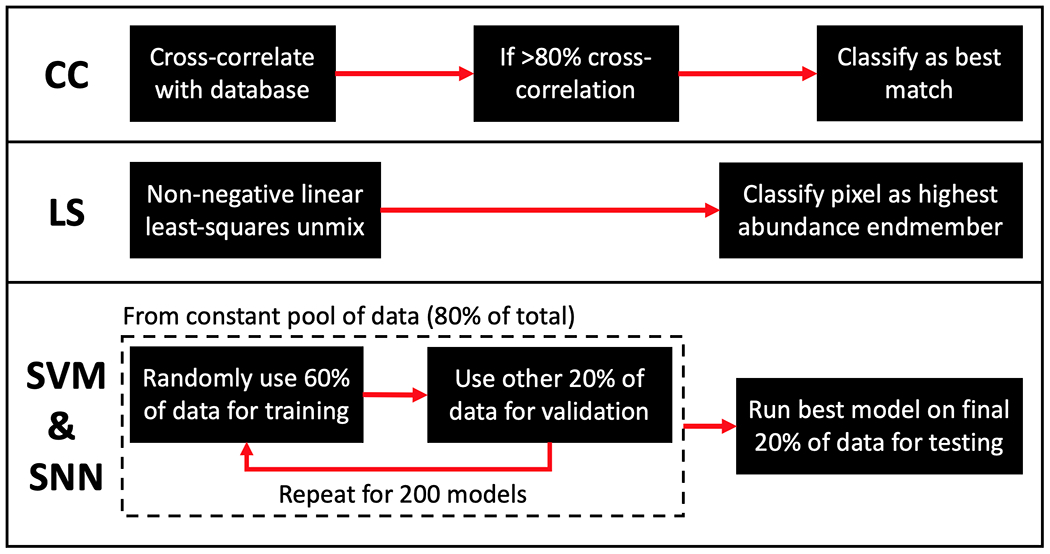
Schematic of algorithmic flow for 4 classification methods explored. CC) Shows the deterministic matched-filter approach taken by the cross-correlation method LS) Shows the classification method of the non-negative linear least-squares approach utilizing known endmember XRD spectra SVM & SNN) Shows the training approach for the support vector machine and shallow neural network classifiers.

When training the SVM models, MATLAB’s “fitcsvm()” function (which uses a sequential minimal optimization⁵⁵) was used for training, with a radial basis function kernel identified as optimal due to allowing for non-linearity in the classification boundary⁵⁶. When training the SNN models, while the amount of data is not large enough to feasibly train a generalizable deep neural network, a SNN with 1-hidden layer containing 10 neurons was identified as optimal (by training/validating with varying numbers of hidden layers and neurons) for our XRD image dataset. A MATLAB “patternnet()” model was created which used Bayesian regularization backpropagation^57,58 for training the SNN.

It should be noted that, for the current study, X-ray transmission data is obtained by the imaging system and is being utilized to identify locations in which no object is present (i.e., to mask out regions consisting of only air). For this study with 6 mm thick objects, pixels are marked as air if their attenuation is less than that of 0.5 mm of water. The air-material boundary is obtained with higher resolution by the transmission data (i.e., ≈0.6 mm² transmission resolution vs ≈1.4 mm² XRD resolution). Beyond removing air pixels, X-ray transmission data is used for visualization of XRD data by combining transmission data with mean q values of each pixel, producing a visualization of attenuation and average coherent scatter angle within a single 2D image¹⁵. An example of this colorized image is shown later in Fig. 6. This visualization is used for display purposes only and does not affect the classifier training data or results.

Fig 6.

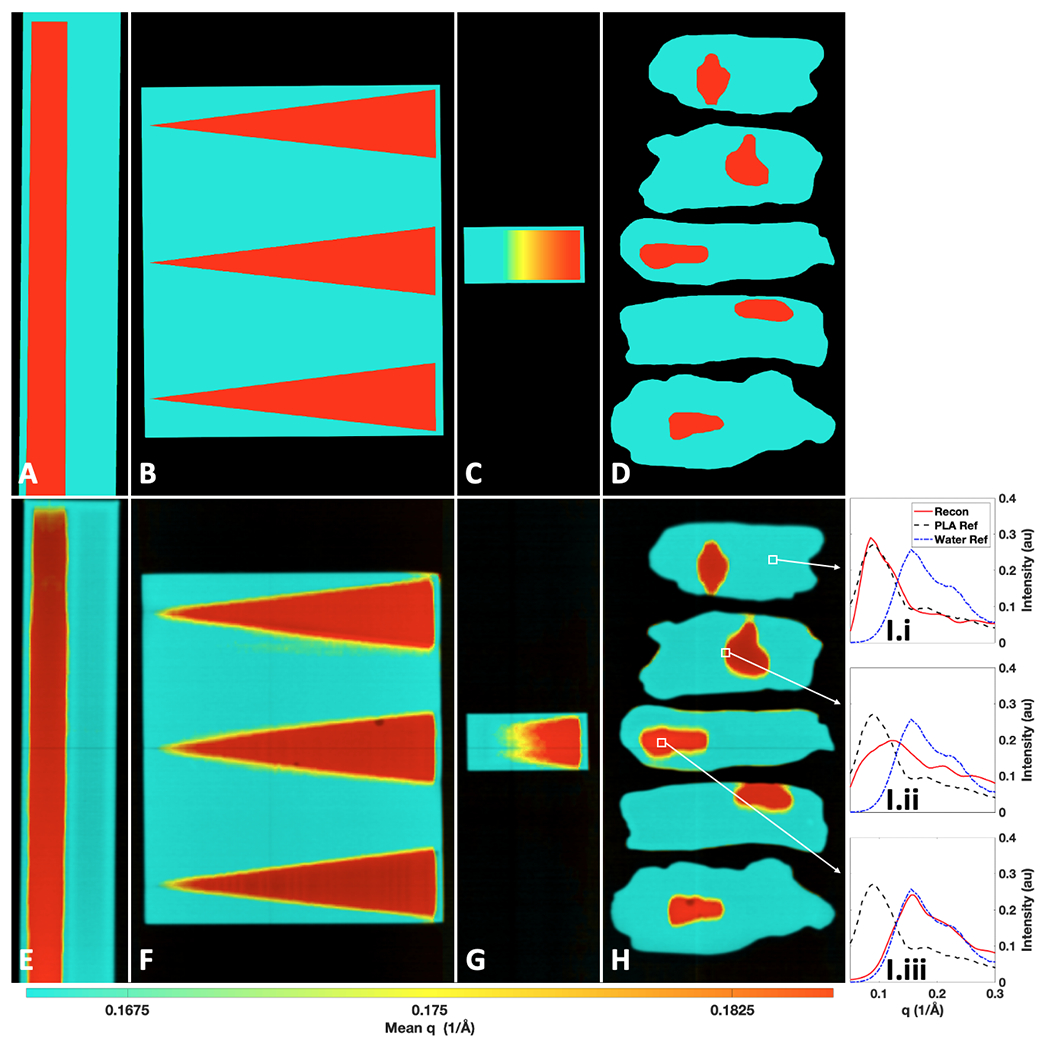
Ground truth and measured X-ray transmission + momentum transfer (q) colorization (TQC) images of the water-PLA phantoms. Ground truth TQC images of the: trough (A), wedge (B), ramp (C), and tissue (D) phantoms. Measured TQC images of the: trough (E), wedge (F), ramp (G), and tissue (H) phantoms. Water and PLA correspond to red and teal coloring, respectively, on a continuum (online version only). I) The full reconstructed XRD spectra from marked regions in H containing PLA (I.i), a mixture of PLA and water (I.ii), and water (I.iii) compared against XRD spectra of water and PLA measured in a commercial diffractometer.

To obtain a robust comparison between the material classification algorithms, ROC curves were generated to view the trade-off between true positives and false positives at decision thresholds beyond the initially explored midpoint thresholds. Water is treated as the positive class since it is the simulant for cancer. For the CC algorithm, non-binary labels were generated by using a CC metric¹⁹ that ranged from 0 (PLA) to 1 (water) based on the material’s match. For LS, the abundance was taken as the non-binary label. For SVM and SNN, the naturally generated non-binary predicted labels were used. The ROC AUC value was computed for each curve for quantitative comparison of their overall performance. To quantify the global and material boundary performances, the accuracy, ROC curves, and AUC values are generated for the entire area of all phantoms as well as just for the regions surrounding the water-PLA boundaries. A region of ±3 mm around a boundary was selected for the latter analysis as it is slightly larger than the spatial resolution of the XRD system and, as such, will naturally include partial volume effects at the boundaries between different materials.

Results

X-ray Transmission and Diffraction Images of the Water-PLA Phantoms

X-ray transmission images were acquired by the X-ray fan beam coded aperture system for all four sets of water-PLA phantoms, as shown in Fig. 5. It is worth noting that, while the differences in attenuation typically aid in highlighting the regions of PLA vs wells filled with another material (water in this study), this data alone does not uniquely identify the materials as water and PLA. This can be seen clearly in Fig. 5A and Fig. 5B, where a tilt relative to gravity or the presence of bubbles causes an apparent difference in attenuation that is attributable to thickness rather than material composition. Similarly, in Fig. 5C, the transmitted intensity looks almost perfectly uniform across the phantom, even though the ratio of water to PLA varies greatly across the phantom. Lastly, an effect similar to the trough phantom can be observed in Fig. 5D: water tension and variable thickness of water in wells create a range of attenuation intensities that all still belong to pixels containing water (with some being more and others less attenuating than the surrounding PLA). Beyond this qualitative assessment, supplemental Fig. S2 demonstrates a quantitative classification based on the log of the transmission intensities, where a ROC AUC of 0.773 and accuracy of 85.45% are achieved. Despite the transmission scans’ deficiencies in differentiating water from PLA, the ≈0.6 mm² spatial resolution for this system’s transmission images¹⁵ provide a fine resolution for masking out air pixels within XRD images that do not contain materials before performing material classification.

Fig 5.

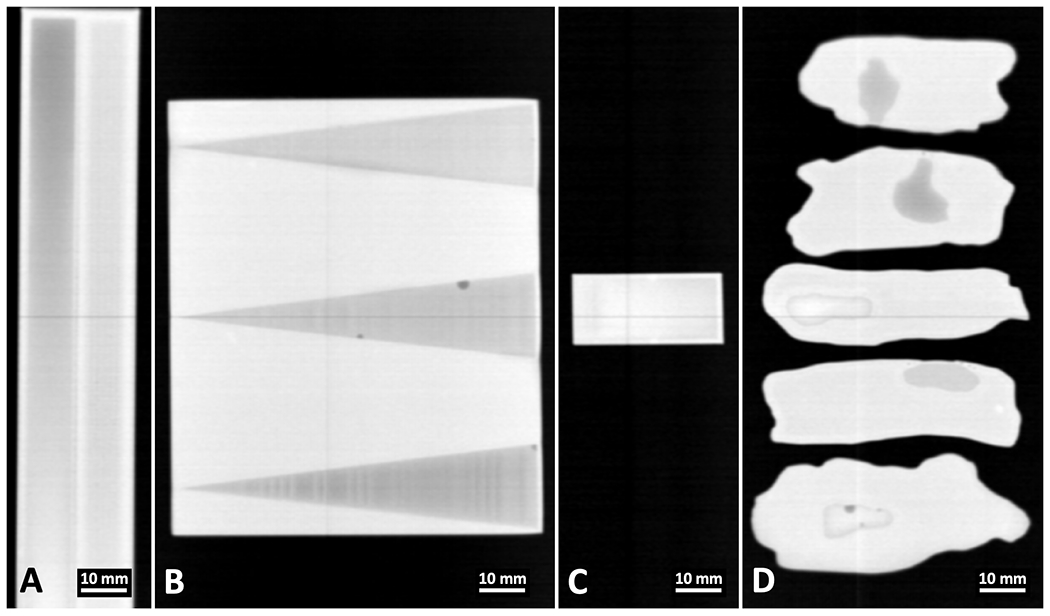
X-ray transmission scans of the water-PLA phantoms taken by the X-ray fan beam coded aperture imaging system. Transmission scan for the A) Trough phantom B) Wedge phantom C) Ramp phantom and D) Tissue phantoms.

Shown in Fig. 6 are the ground truth and measured X-ray transmission + q colorization (TQC) images created by combining XRD data with the transmission images. While each pixel does contain a full XRD spectrum (as an example, XRD spectra from Fig. 6H are shown within Fig. 6I.i–iii), colorizing the transmission scan by an intensity-weighted mean q value from the XRD spectra allows for visual separation of materials that have differences in their mean q values. Here red pixels contain water and teal pixels contain PLA, with a continuum of colors providing information about the mean q value (i.e., mean atomic spacing of the material present at a given location)¹⁵.

It should be emphasized that the ground truth images in Fig. 6A–D do not fully identify PLA from water, since for all wells there is a 0.5 mm thickness of PLA below the water for holding the liquid (though this signal relative to 5.5 mm of water is believed to have a negligible impact/be below the sensitivity of the system as observed in the average water spectrum measured in supplemental Fig. S3). Further, Fig. 6C is the most complex phantom given the mixing of water and PLA through the thickness. The visible gradient demonstrates the expected change in mean q colorization based on the abundance of each material along the ramp. Beyond this visualization of the ground truths’ mean q colorization, the classification labels for the ground truth pixels are treated as binary, where pixels are labeled as the most abundant material present within a 1/3 mm² measurement sampling. For this study’s focus of classifying pixels that contain a majority of water or PLA, this simplification is acceptable.

As shown in Fig. 6E–H, PLA has a lower intensity-weighted mean q value compared to that of water (also observable in Fig. 3), allowing for the TQC images to provide better visual differentiation of water and PLA compared to transmission data alone (especially when compared to the range of attenuation values observed in Fig. 5 that all correspond to water). An appropriate windowing of mean q mapping to teal and red was selected for these two materials, but a color map with a wider range of colors and or colorization based on different spectral properties (e.g., median q, peak location, spectrum shape) could be used for various materials of interest. Within Fig. 6E–H, yellow pixels appear at the boundary of water and PLA. This spectral shift is due to the spectrally mixed XRD measurements that occur due to the ≈1.4 mm² XRD spatial resolution of the utilized imaging system. This mixing of XRD spectra is shown in Fig. 6I.ii, where the XRD spectrum associated with an object pixel at a boundary of water and PLA has intensities that appear as a weighted combination of the two materials. The matching of X-ray fan beam coded aperture measurements from regions predominantly containing PLA and water in Fig. 6I.i and 6I.iii with commercial diffractometer measurements of water and PLA is encouraging, suggesting that the main challenge for accurate material classification will arise at pixels containing mixtures of materials. While for most of the phantoms these mixtures only occur in the transverse dimension (defined by the fan extent and scan direction plane in Fig. 3), within Fig. 6G we can observe how mean q colorization slowly shifts from teal to red down the ramp due to abundance of both materials changing throughout the phantom thickness (along the axial dimension) and our measurements’ integration along depth. See supplemental Fig. S4 for a comparison between the ramp phantom’s ground truth abundance vs the LS estimated abundance of water.

Performance of Material Classification Algorithms on the Water-PLA Phantoms

With the X-ray transmission and XRD data collected by the X-ray fan beam coded aperture imaging system (with 159,808 material pixels measured), we next conducted our study of the four material classification algorithms under consideration. The ML models were trained as previously described, with supplemental Fig. S5 showing the distribution of validation set AUC values along with the training, validation, and test dataset ROC curves for the best SVM and SNN models. A visual representation of the performance of each classifier across all phantoms (when operated at their midpoint classification thresholds) is shown in Fig. 7. Looking at the relative performances of the explored classifiers, the CC and LS method underperform in comparison to the ML approaches of SVMs and SNNs. While many pixels are classified correctly in the CC & LS approaches, there are more incorrectly classified pixels at the boundaries between water and PLA and as a function of water depth (in the ramp phantom) as compared to SNN. The SVM classifier reduces the misclassified pixels in regions where the ≈1.4 mm² XRD spatial resolution appears to have impacted the CC & LS approaches. For the SNN classifier, the misclassified pixels at water-PLA boundaries have been reduced beyond that of the SVM approach; however, a few misclassifications occur in some homogenous material regions (see supplemental Fig. S6 for additional insight on the XRD spectra of these pixels classified by the SNN).

Fig 7.

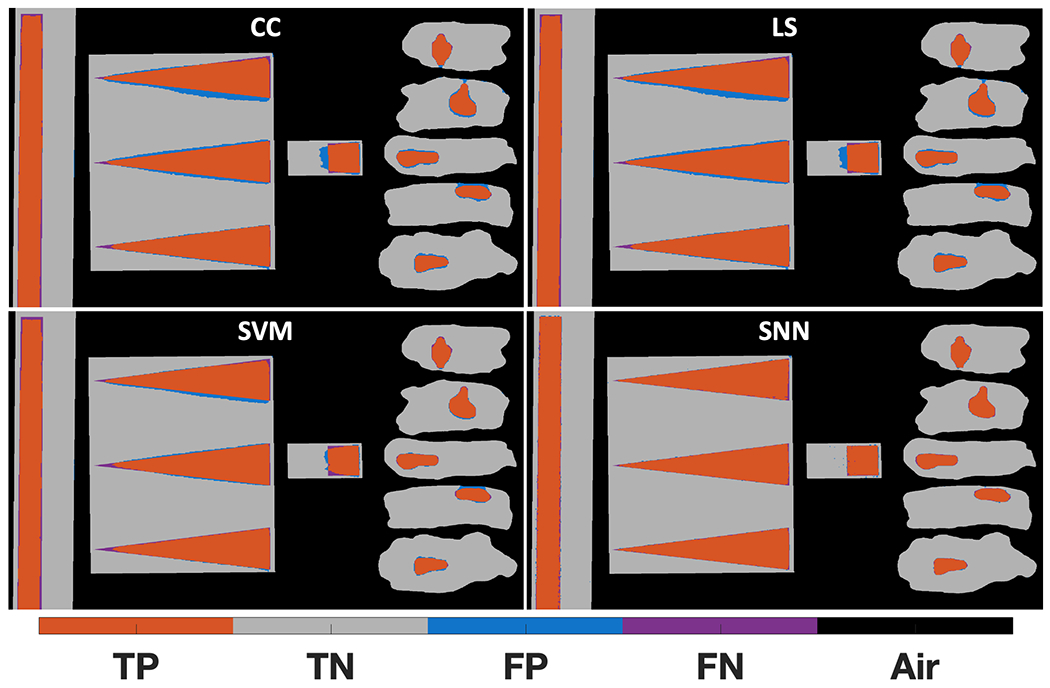
Material classifier performance on the XRD data of the water-PLA phantoms. Sub-plots are shown for the cross-correlation (CC), linear least-squares (LS), support vector machine (SVM), and shallow neural network (SNN) classifiers. With water as the cancerous simulant, correctly identified water pixels are orange true positives, correctly identified PLA pixels are grey true negatives, and blue false positives and purple false negatives represent misclassified PLA and water pixels, respectively (online version only).

While the results shown in Fig. 7 represent binary classification of each pixel with its best match, the classification approaches provide predictions that exist on a continuum between 0 (PLA) and 1 (water). To complement these spatial representations of classification performance, we also quantitatively analyze the overall classification performance for all pixels across a range of different thresholds and show the resulting ROC curves in Fig. 8.

Fig 8.

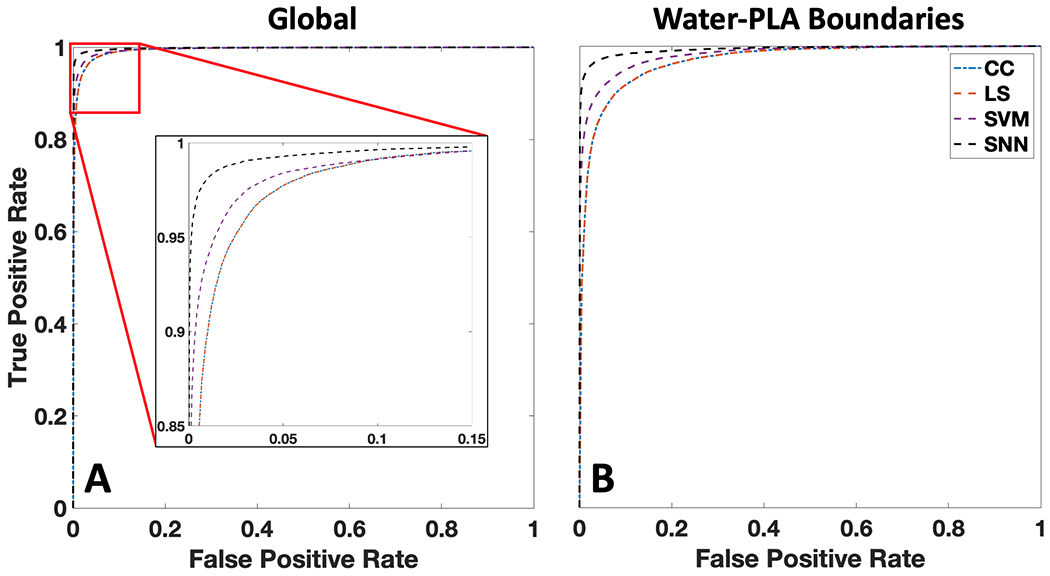
Receiver operating characteristic (ROC) curves for the explored material classification algorithms for global and material boundary pixels within the water-PLA phantoms. A) ROC curves for all pixels within the 4 phantoms (global). Cross-correlation (CC) and least-squares unmixing (LS) have near identical performance, while support vector machine (SVM) and shallow neural network (SNN) improve performance. B) ROC curves generated from pixels within 3 mm of water-PLA boundaries for all four phantoms.

From Fig. 8, it can be observed that the ML approaches of SVM and SNN out-perform the rules-based CC and LS algorithms for all detection thresholds and across all pixels. This improvement is further accentuated when one considers only the regions surrounding material boundaries, which is particularly important for clinically relevant tasks such as margin assessment and identifying the extent of disease surrounded by healthy tissue. To provide quantification of the data shown in Figs. 7–8, Table 1 provides the percentage of correctly classified material pixels (when using a predicted classification of 0.5 as the threshold for positive as in Fig. 7) along with the AUC values for each classifier’s ROC curve. These metrics are provided for all pixels (‘global’) as well as the water-PLA boundary pixels (‘boundary’).

Table 1.

Comparison of material pixel classification accuracy and ROC AUC values for all algorithms applied to the XRD images of the water-PLA phantoms. Accuracy was computed as (% material pixels identified correctly) / (total number of material pixels), excluding air pixels from the metric. Accuracy and AUC values are reported for all phantom pixels (global) as well as those that are 3 mm from water-PLA boundaries (boundary). The commercial diffractometer measurements of water and PLA represent the 2 “database cases” provided to the cross-correlation and least squares algorithms, while the 95,885 cases represent the 60% of all material pixels that the SVM and SNN were trained on.

Classifier	# Database or Training Spectra	Global Accuracy	Global AUC	Boundary Accuracy	Boundary AUC
Cross-Correlation	2	96.48%	0.9941	89.32%	0.9683
Least Squares	2	96.48%	0.9941	89.32%	0.9682
Support Vector Machine	95,885	97.36%	0.9952	92.03%	0.9760
Shallow Neural Network	95,885	98.94%	0.9989	96.79%	0.9938

Table 1 shows that both CC measurements with a known database and predicting materials by largest abundance of database member (after LS unmixing) result in similar global accuracy levels (96.48%). While minor differences in their classification results on a per-pixel basis can be observed in Fig. 7, neither classifier appears to offer a distinct advantage over the other for this binary classification task. The SVM approach was the second-best performer with a global accuracy of 97.36%, while the SNN approach was shown to be the best for classifying materials, with a global accuracy of 98.94%. This ranking of performance is consistent across metrics (accuracy/AUC for global/boundary regions), suggesting that for any selected positive class threshold the ML approaches improve material classification performance. While the percentage point increase in global performance from worst to best algorithm is small (2.46%), within the material boundaries the percentage point increase is greater (7.47%), demonstrating that improvement of primary material classification within regions containing mixtures was achieved.

The ML model performance demonstrated in Table 1, particularly the ROC AUC value that agrees with the test set’s AUC value shown in supplemental Fig. S5, is suggestive that ML approaches are superior to rules-based classification. As an additional demonstration of the generalizability of the SNN, Fig. 9 shows that the SNN maintains a substantial (>2.04%) accuracy percentage point improvement relative to CC for a spatially complex, varying-thickness phantom that was not part of the internal training, validation, and test datasets.

Fig 9.

A target phantom made of circular PLA wells of different heights containing water to study the impact of variable thickness while running CC and SNN classifiers on a new external test object. A) A sideview photograph of the target phantom with water in each of the PLA wells. B) A top view photograph of the target phantom, showing the uniform water within each PLA ring C) X-ray transmission scan of the target phantom. D) A transmission + q colorization (TQC) image of the target phantom. E) The target phantom confusion matrix image for the CC classifier previously shown in Fig. 7. F) Same as E, but for the SNN classifier with fewer blue false positive and purple false negative pixels (online version only).

The target phantom material heights from outer diameter to center are 5, 7.5, and 10 mm, with PLA walls and inner wells each 5 mm wide for an overall phantom diameter of 55 mm (Fig. 9A). All water regions have 0.5 mm of PLA at the bottom of the well, leading to water thicknesses of 4.5, 7, and 9.5 mm. As shown in Fig. 9C, slightly higher attenuation of PLA compared to water for each thickness is visible, while both materials’ attenuation values (intensity within this image) increase as thickness increases towards the center of the target phantom. Similar to Fig. 6E–H, the TQC image of the target phantom adds visual contrast between the PLA and water regions (Fig. 9D). Applying the same CC classifier used in Fig. 7 to the target phantom creates the confusion matrix image shown in Fig. 9E, achieving a 94.93% accuracy where PLA-water boundary pixels cause the most false positive and false negative pixels, with a few false positive pixels observable at the PLA-air boundary. Utilizing the SNN classifier developed on the previous phantoms achieves an accuracy of 96.97% (Fig. 9F), which is a 2.04% percentage point increase compared to the CC rules-based classifier. The SNN applied to the target phantom demonstrated generalizability to objects with variable thickness (5-10 mm compared to the 6 mm thick phantoms it was trained on) while eliminating misclassifications at the PLA-air boundary and reducing misclassifications at the PLA-water boundaries. The accuracies of the CC and SNN on this phantom are ≈2% lower than each classifiers’ respective performance on the phantoms used for training —this was anticipated given that the target phantom was designed with many more PLA-water boundaries (the most difficult to classify regions) compared to all other phantoms. The results of Fig. 9 suggest variable object thickness from 5 – 10 mm does not adversely impact XRD-based classifier performance for this study’s combination of imaging system and classifier algorithms. Additionally, the performance predicted by the SNN test set in supplemental Fig. S5 is realized using a new phantom that was not used as part of the SNN model’s initial training, validation, and testing process.

Discussion

This research has demonstrated the first application of ML based classification on X-ray diffraction imaging data of non-crystalline, biologically relevant phantoms. In particular, we found that ML algorithms outperformed conventional, rules-based approaches, especially in situations in which spectral mixing occurred. It was shown that classification algorithms based on CC, LS, SVM, and SNN could identify water and PLA with 96.48%, 96.48%, 97.36%, and 98.94% global accuracy when operated at the middle classification threshold value, respectively. Additionally, the ROC curves for the classification algorithms had AUC values of 0.994, 0.994, 0.995, and 0.999, respectively. In addition, we showed that co-registered, high-resolution X-ray transmission projection data, while only achieving a classification accuracy of 85.45% and ROC AUC of 0.773 by itself, is helpful for identifying regions containing only air. The material combination of water and PLA is of interest given that the XRD spectra and scatter intensity of water and PLA are similar to that of breast cancer and adipose tissue, suggesting this approach and level of performance could translate to medically focused imaging tasks and improve diagnostic and decision-based procedures if shown to be capable of identifying cancer surrounded by any type of real tissues (see supplemental Fig. S7 for how simulants of additional tissue types could be created).

The ability for ML algorithms to outperform a matched filter, which is the optimal linear classifier in the presence of additive noise, suggests a variety of opportunities for future improvement. For example, it suggests that such nonlinear classifiers can assist with overcoming issues that are typically inherent in computational imaging systems, such as non-gaussian and object-dependent noise in the XRD imaging measurement system, error within the physics models used for multiplexed measurement reconstruction, and mismatches between the spectral library and measured spectra. In addition, we find that the ML classification process, which nonlinearly maps the XRD spectra into the material subspace, results in a classification spatial resolution that is superior to the imaging spatial resolution. This result is analogous to nonlinear optical super-resolution techniques⁵⁹, except that in this case the improved resolution is purely realized as a data processing step with task-specific applicability. Another example of the potential benefits of improved classifiers is better performance at a fixed SNR or comparable performance at reduced SNR, thus allowing for faster scan times. In the future, information theory methods will be explored to evaluate whether classifiers are reaching their optimal performance for various signal-to-noise levels that are affected by different XRD imaging systems⁶⁰ and scan durations.

While the phantoms in this study consisted of two materials, future studies should consider phantoms with multiple materials and material mixtures. This situation arises in nearly all biological and medical imaging applications, where a variety of different materials are present in various concentrations and with a morphology that might vary at spatial scales smaller than the imaging system resolution. Future studies will explore how the classification methods shown here, combined with improved transverse and axial resolution, perform in the presence of more complex material distributions. In addition, studies involving the classification of mixed materials or thicker objects with variable X-ray attenuation will likely benefit from using our co-registered X-ray transmission information to further inform and constrain the reconstruction and classification process. Finally, the construction of new XRD imaging systems that take advantage of photon-counting detectors⁶⁰ or more advanced filtration methods⁶¹ could further improve upon the performances demonstrated.

There are a variety of imaging tasks towards which the approaches demonstrated within this study can be adapted. For example, this imaging capability could be implemented in surgical pathology for identifying key tissue slices to turn into H&E slides for pathology assessment, while allowing for a reduction in the total number of tissue slices analyzed by this time-consuming process. Beyond medical applications, one could imagine applying this technology and classification approach to material composition analysis of raw materials and quality assurance of foods and pills—all via classification by rapidly acquired XRD images. To adapt this study’s presented ML classification of XRD images for more complex applications, it will be important to account for materials with higher variability in XRD signatures that still belong to the same class. This need could be addressed by conducting model training on simulated data that accurately accounts for the potential mixtures, scatter texturing, and measurement system noise that will be present in real measurements. Additionally, for tasks including tissue classification with known variation throughout the volume of the samples, it will be important to understand the composition throughout the sample thickness.

Conclusion

Medically relevant phantoms were created, imaged by an X-ray fan beam coded aperture system to obtain XRD images, and improved classification demonstrated by ML algorithms. Combining XRD images with ML classification algorithms demonstrated improved material classification accuracy and spatial resolution beyond what rules-based algorithms have previously achieved. Future work will seek to apply these methods to more complex tasks involving objects with higher degrees of mixing and spectral variations. The presented phantom structures and classification approaches can be implemented in a variety of XRD imaging systems and applications, leading to improved capabilities in research, industrial analysis, and medical tasks.

Supplementary Material

fS1

Fig S1 Example breast tissue lumpectomy slice and pathologist annotation that were used for creating water-PLA tissue phantoms. A) Photograph of a breast lumpectomy sample that is 5 mm thick containing cancer, adipose, and fibroglandular that are not immediately differentiable by the photograph B) A hematoxylin and eosin (H&E) stained slide from 10 μm of cells that were sliced and plated from the surface of the tissue in A after paraffin embedding, where a senior pathologist marked in red the region containing invasive ductal carcinoma (while the white regions are typically adipose tissue and pink regions are primarily fibroglandular tissue) C) The water-PLA phantom used in this study that was based on the pathologist annotation in B, where the approximate shape of the sample was traced and made of PLA, while the approximate shape of the cancerous region was turned into a 5.5 mm thick well for filling with the cancer simulant of water.

fS2

Fig S2 Classification of water-PLA phantoms based on X-ray transmission intensity. A) Histograms of transmission intensity in units of linear attenuation coefficient (μ) coupled with X-ray length (L) traveled along phantom thicknesses B) Receiver operating characteristic curve (ROC) generated by varying the μL classification threshold for identifying the positive class of water (cancer simulant), with an area under the curve (AUC) of 0.773 C) Confusion matrix image generated when operating at a μL classification threshold of 0.1281 (location marked by red vertical line in A and by red circle in B), with an overall accuracy of 85.45% for correctly classifying water and PLA. The wider distribution of water μL values can be attributed to some wells containing less water (underfilled) or more water (water tension allowing for bubbling above PLA height), and while volumetric measurements (e.g., CT scans) could potentially aid in overcoming this impact of variable thickness, it should be noted that for the ramp phantom that has water level with the top of PLA walls, the water μL values are inseparable from PLA (as shown by the primarily FN square in C, as well as uniform intensity shown in Fig. 5). These results demonstrate that transmission intensity alone can fail to robustly separate materials of interest (compared to Fig. 7), motivating this study’s exploration of X-ray diffraction data along with advanced machine learning classifiers.

fS3

Fig S3 Bruker D2 Phaser measured X-ray diffraction (XRD) spectra of water and PLA compared against the mean ± standard deviation of all water and PLA pixels measured by the X-ray fan beam coded aperture imaging system, where the deviation is based on pixel-to-pixel variations. A) The water XRD spectrum measured by the D2 Phaser (red) compared against the mean ± standard deviation spectrum (blue) of the reconstructed/imaged spectra of all pixels containing a majority of water from the studies four medical phantoms. The cross-correlation (CC) between the commercial diffractometer measurement (used by the rules-based algorithms) and measured mean spectrum of water are 99.99974% B) Same as A but for the PLA spectrum measured by the D2 Phaser (red) and mean ± standard deviation spectrum (blue) measured in this study for pixels containing a majority of PLA, with a CC of 99.99989%. These matches demonstrate that a commercial diffractometer and X-ray fan beam coded aperture imaging system used in this study achieve near-identical spectral imaging results for water and PLA, suggesting there is no innate difference/skewing of measurements obtained by our prototype imaging system that would necessitate using the prototype to generate the database/reference spectra for the rules-based approaches.

fS5

Fig S5 The distribution of the 200 created models’ validation group ROC AUC values and the ROC curves for the training, validation, and test dataset groups of the best SVM and SNN models (zoomed into TPR of 0.9 – 1 and FPR of 0 – 0.1). A) Histogram of ROC AUC values for all 200 created SVM models, where the model with the best validation group AUC value is saved as the best model for the final test against the 20% of data held out from the training process for measuring performance on new independent measurements. This process of creating 200 models and randomly shuffling the training/validation examples allows for identifying a model that generalizes best due to better random sorting of the data (while also allowing for quantification of variability in model performance over random instantiations), and then after this process comparing the best model’s performance to the 20% test data it has never seen. This process of training multiple of the same model while varying the training/validation sorting has been done previously for identifying feature/model stability and best generalization^62,63 B) Same as A, but for the 200 SNN models C) All dataset group’s ROC curves for the best SVM model, showing AUC values all within a range of 0.9949 – 0.9963 (varying by third decimal place or less), suggesting the model did not overtrain, and that the representation of XRD cases in each dataset (split 60:20:20) was sufficient for creating a generalizable model D) same as C, but for the best SNN model. Unlike the SVM, a slightly better performance for the training dataset ROC can be observed in the top left, showing how for these pixels the SNN learned from, the model performs slightly better compared to the validation and testing group. The SNN AUC values are all within the range of 0.9987 – 0.9989, showing an even more consistent performance between datasets compared to the SVM. Due to all dataset groups for both the SVM and SNN having near identical AUC values (within individual models), in the main text Fig. 8 the ROC curves presented are for all pixels (not just test group) when comparing against the CC and LS classifiers.

fS4

Fig S4 Water abundance estimation in the ramp phantom for the least squares (LS) classification algorithm compared against ground truth water abundance. A) Side-profile photograph of the ramp phantom from main text Fig. 3C, shown again to highlight the phantom’s composition (through thickness) transitioning from PLA plastic (left) to water (right) B) LS estimated water abundance values from X-ray diffraction (XRD) spectra within each pixel, for the central region of the ramp phantom (not including outer PLA-only walls) C) Comparison of mean LS estimated water abundance (per column in B) vs ground truth abundances for each column as a red scatter plot, showing a trend in general agreement with the dashed black line that represents perfect agreement. Ledges on the left and right of the scatter plot suggest the LS water abundance estimate is not sensitive to 10-20% of water or PLA when the remaining abundance is the other material. Additionally, the LS estimated water abundance reaches 50% when ground truth abundance is 45% – this overestimation is observed in main text Fig. 7 LS, where there are blue false positive pixels to the left of the column where water becomes the majority abundance, when the correct binary label is PLA.

fS6

Fig S6 Mean XRD spectra with standard deviation bars for all phantom pixels sorted by the confusion matrix groups of the SNN used in the main text. This XRD data is from all pixels of the four types of phantoms from Fig. 7 subpanel “SNN”, with the confusion matrix classification based on the agreement/disagreement of ground truth and SNN predicted class. Unlike supplemental Fig. S3 that reports the average PLA and water spectra measured by the system based solely on ground truth classification, these results further subdivide the measurements based on which ones are correctly (TP, TN) or incorrectly (FP, FN) classified by the top performing SNN classifier. From these results, one can obtain insights into what XRD spectra shapes the SNN has learned from the normalized (by sum of squares) XRD spectra data, highlighting that the average TP and TN spectra are a great match with the XRD spectra of water and PLA as in Fig. S3, while showing that FP and FN present as a spectral mix of these two materials pure XRD spectra. The average FP measurements have higher intensities around 0.2 Å⁻¹ in q space (closer to the spectral shape of water), while average FN measurements have higher intensities around 0.12 Å⁻¹ (closer to the spectral shape of PLA). These mistakes present as reasonable for the SNN to make, suggesting both that the model has learned reasonable definitions for each material and that these few misclassified cases are the result of spectral mixing at the boundary of these materials on a spatial scale that is below the X-ray fan beam coded aperture imaging system’s ≈1.4 mm XRD spatial resolution. While the SNN has improved this spatial resolution from a classification task standpoint, there are still cases (FP, FN) at this boundary where the binary ground truth may be unreasonable given that the XRD spectra are around a 50:50 mixture of PLA-water.

fS7

Fig S7 A phantom made of PLA plastic wells containing mixtures of water and ethanol to study the impact of homogenous mixtures on X-ray fan beam coded aperture measured X-ray diffraction (XRD) spectra. A) Photograph of the phantom with wells filled (from top to bottom) with 100:0, 73.3:26,7, 46.7:53.3, and 20:80 water:ethanol mixtures. B) X-ray transmission scan of the water-ethanol phantom, where it can be observed that the attenuation of ethanol is lower than water. While this change in attenuation is observable, the identification of materials in each well is not immediately clear. C) A transmission + q colorization (TQC) image coloring each pixel by its average scattering angle, highlighting a greater difference between each well, while still not demonstrating the full amount of information present for all pixels containing full XRD spectra. D.i-iv) Example XRD measurements with matching colors for the wells they originated from, along with reference spectra from a commercial diffractometer (D2 Phaser, Bruker) for the mixtures of water and ethanol used in each well. This data demonstrates that for homogenous mixtures, it is possible to detect shifts in XRD spectra caused by variations in the concentration of each material within a given XRD image pixel. The combination of imaging system resolution (both spatial and momentum transfer) and classification algorithm sensitivity will dictate the smallest amount of a given material within a pixel mixture that can be detected. The approach of mixing homogenous materials together to obtain a desired XRD spectra could be used in future studies to simulate fibroglandular tissue that has a spectrum between that of adipose and cancer¹ (shown here to be a close XRD spectral match to ≈50:50 water:ethanol in D.iii), testing the performance of classification algorithms in more complex cases.

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.