Machine-Assisted Interpolation Algorithm for Semi-Automated Segmentation of Highly Deformable Organs

Abstract

Purpose:

Accurate and robust auto-segmentation of highly deformable organs (HDOs), e.g., stomach or bowel, remains an outstanding problem due to these organs’ frequent and large anatomical variations. Yet, time-consuming manual segmentation of these organs presents a particular challenge to time-limited modern radiotherapy techniques such as on-line adaptive radiotherapy and high-dose-rate brachytherapy. We propose a machine-assisted interpolation (MAI) that uses prior information in the form of sparse manual delineations to facilitate rapid, accurate segmentation of the stomach from low field magnetic resonance images (MRI) and the bowel from computed tomography (CT) images.

Methods:

Stomach MR images from 116 patients undergoing 0.35T MRI-guided abdominal radiotherapy and bowel CT images from 120 patients undergoing high dose rate pelvic brachytherapy treatment were collected. For each patient volume, the manual delineation of the HDO was extracted from every 8th slice. These manually drawn contours were first interpolated to obtain an initial estimate of the HDO contour. A 2-channel 64×64 pixel patch-based convolutional neural network (CNN) was trained to localize the position of the organ’s boundary on each slice within a 5-pixel wide road using the image and interpolated contour estimate. This boundary prediction was then input, in conjunction with the image, to an organ closing CNN which output the final organ segmentation. A Dense-UNet architecture was used for both networks. The MAI algorithm was separately trained for the stomach segmentation and the bowel segmentation. Algorithm performance was compared against linear interpolation (LI) alone and against fully automated segmentation (FAS) using a Dense-UNet trained on the same datasets. The Dice Similarity Coefficient (DSC) and mean surface distance (MSD) metrics were used to compare the predictions from the three methods. Statistically significance was tested using Student’s t test.

Results:

For the stomach segmentation, the mean DSC from MAI (0.91 ± 0.02) was 5.0% and 10.0% higher as compared to LI and FAS respectively. The average MSD from MAI (0.77 ± 0.25 mm) was 0.54 and 3.19 mm lower compared to the two other methods. Only 7% of MAI stomach predictions resulted in a DSC<0.8, as compared to 30% and 28% for LI and FAS, respectively. For the bowel segmentation, the mean DSC of MAI (0.90 ± 0.04) was 6% and 18% higher, and the average MSD of MAI (0.93 ± 0.48 mm) was 0.42 and 4.9 mm lower as compared to LI and FAS. 16% of the predicted contour from MAI resulted in a DSC<0.8, as compared to 46% and 60% for FAS and LI, respectively. All comparisons between MAI and the baseline methods were found to be statistically significant (p-value<0.001).

Conclusions:

The proposed machine-assisted interpolation algorithm significantly outperformed linear interpolation in terms of accuracy and robustness for both stomach segmentation from low-field MRIs and bowel segmentation from CT images. At this time, fully automated segmentation methods for HDOs still require significant manual editing. Therefore, we believe that the MAI algorithm has the potential to expedite the process of HDO delineation within the radiation therapy workflow.

I. INTRODUCTION

Organs that show large variations in shape, size, position, and texture on a day-to-day or an hourly basis are often referred as Highly Deformable Organs (HDOs). Such examples are the stomach and the bowel which not only show large anatomical variations between patients, but also manifest intra-day variations due to their dependence on food intake and metabolism.[1]

In external beam radiation therapy and brachytherapy, it is essential to accurately delineate the target and organs at risk to create an optimal treatment with minimal side- effects. To date, clinical contouring of HDOs remains a time-consuming manual process that is subject to substantial inter-observer variation effects.[2, 3] Lamb et al have shown that the complete process of abdominal and pelvic intra-fraction contour adjustment takes up to 22 minutes for the MRIdian system (ViewRay Inc. Oakwood Village, OH, USA).[2] They also highlighted that the segmentation of the stomach is done exclusively from scratch due to the inability of the built-in auto-contouring algorithm to capture large changes in organ size. This time-consuming aspect of manual delineation not only limits the number of treatments performed every day but may also lead to less efficient treatment plans due to patient discomfort and an increased risk of patient motion.[2]

Over the years, several concepts have proven to be successful in segmenting structures in the head and neck, abdominal, and pelvic regions. Atlas-based methods [4, 5], for example, are historically among the most established in the clinic. However, these methods generally fail for HDOs due to their propensity to be shape-conserving. Statistical shape models [6] and pixel-wise classification methods [7–9] have been proposed to solve this issue, but these methods were found to be laborious due to the requirement of feature definitions, which can be subjective. Hence, segmenting HDOs remains a challenging problem for the current era.

With the recent rise in computing power, deep learning shows huge potential in the field of medical imaging. [10, 11] Today, the use of fully convolutional neural networks [12] (CNNs) is the focus of a great deal of research effort and is rapidly becoming the state of the art for medical segmentation. [13] The U-Net [14] is an example of a CNN which is extensively used in biomedical image segmentation. Several studies have shown that the U-Net [15–18], and its extensions [19–21] can be used to accurately segment various organs and tumors in the abdomen, pelvic, and head & neck regions. However, the learning process in many of these proposed concepts is facilitated by regularly shaped organs [22], which generally leads to an increase in mislabeling and loss in accuracy in the context of HDOs. Hence, while these algorithms produce acceptable results on stable anatomical organs, they generally fail when it comes to the more deformable organs.

To address this learning problem, Tong et al proposed a task-wise, self-paced learning strategy to avoid over-fitting their network with respect to the stable organs. [23] While this method has been shown to improve the segmentation of HDOs on CT images, there is still a considerable performance gap between the segmentation of stable organs and HDOs which require further investigation. Some other groups have tried to improve the segmentation of these more difficult cases by connecting the CNN with a post-processing layer. One such example has been shown by Christ et al where they applied densely connected conditional random field (CRF) layers to refine the segmentation result of their CNN. [24] However, its implementation was found to be impractical due to the extensive memory it requires, particularly for large 3D datasets. Fu et al have shown a more feasible approach by proposing a correction network that can be implemented into the CNN, without requiring a post-processing step. [25] The network presented was composed of three sub-CNNs, where the second and third CNNs were used to improve the segmentation results from the first CNN through iterative feedback; the result from one CNN was concatenated with the original image and fed to the next CNN, which used its own loss function to refine the initial segmentation. While this method imposed some type of anatomical constraints and was found to have great potential in contouring both relatively stable organs and HDOs in the abdomen region, the first CNN allowed the possibility of erroneous labeling which was not always corrected by the subsequent CNNs. Their results have shown a 10% decrease in Dice Similarity Coefficient [26] (DSC) when comparing the stomach segmentation results to that of the liver (a relatively more stable organ) and a 8.7% decrease from bowel segmentation to liver segmentation. Hence, in regards to these highly deformable organs, we believe that the overall performance has room for further improvement.

The goal of this work is to propose a practical and alternative solution to a task that has been proven to be challenging for the current auto-segmentation methods, while still helping to expedite the process of contouring HDOs. The proposed technique was inspired by an interpolation-based contouring strategy that is commonly used in manual organ contouring by radiation therapy planners. In this strategy the organ of interest is contoured on sparse slices, while slices in between are skipped. Subsequently, linear interpolation is performed to fill in the missing slices. The planner then corrects the interpolated contours.

Based on this manual delineation technique, we propose a Machine-Assisted Interpolation (MAI) algorithm that uses a CNN to correct linearly interpolated contours, reducing the amount of time needed for manual correction, thus reducing overall contouring time. This technique is evaluated using stomach segmentation from 0.35T MRI-guided radiotherapy, and bowel segmentation from CT-guided high-dose rate brachytherapy. The specific implementation is as follows. Manual contours were extracted from every 8th slice within a patient volume and linearly interpolated on the skipped slices. Subsequently, a patch-based CNN, named the Boundary Detection Network (BDN), is used to predict the approximate position of the boundaries of the HDO on the target images. The input to the BDN is the interpolated contour, and the corresponding target images (i.e., image on which the contour is interpolated). The output of the BDN, an estimated boundary, is then input together with the target image to a second CNN, called the Organ Closing Network (OCN), which produces the final organ segmentation.

II. METHODS

A. Dataset

The MAI algorithm was separately trained and tested on two datasets; a low-field MR dataset for stomach segmentation and a CT dataset for bowel segmentation. Our first dataset consisted of 116 planning MRIs that were collected from patients undergoing treatment on the MRIdian system at the UCLA Medical Center. All of the 116 patients received treatment in the abdomen region, including the liver, pancreas, and stomach. The images were acquired during treatment planning using a built-in 0.35T MR imaging system with a balanced steady state free precession sequence (bSSFP). The second dataset was composed of 120 planning CT scans obtained from patients undergoing High-Dose Rate (HDR) Brachytherapy treatment in the pelvic region at the UCLA Medical Center. The CT scans were acquired using a SOMATOM Sensation Open CT scanner (Siemens, Munich, Germany). Both datasets were collected under the auspices of IRB-approved retrospective analysis protocols. Clinical stomach and bowel contouring was performed by experienced dosimetrists and medical physicists. Prior to algorithm training, contours were inspected and corrected as needed for optimal accuracy.

The 116 MR volumes had a pixel spacing of either 1.5 × 1.5 mm² or 1.63 × 1.63 mm², and slice thickness of 3 mm. The image sizes varied between 276 ×276 pixels and 334 × 300 pixels. The CT images had pixel spacing ranging from 0.27 × 0.27 mm² to 0.66 × 0.66 mm², and slice thickness of 2 mm. To ensure uniformity over the whole dataset, the MR and CT volumes were resampled through linear interpolation to have voxel sizes of 1.5 × 1.5 × 3 mm³ and 1 × 1 × 2 mm³, respectively. For the CT dataset, a threshold of [−1000, 2000] Hounsfield units was imposed on the images in order to minimize the effects of artifacts due to procedure implants and air in the urinary and gastro-intestinal regions. The manually delineated HDO contours were saved as binary masks and received the same resampling and cropping process as the MR and CT volumes. This resampling and cropping process was performed in the MATLAB programming environment (Mathworks Inc, Natick, MA, USA).

B. Data Pre-processing

For each patient volume, the HDO was present in a discrete range of 2D slices indexed by S ∈ [1, c], where 0 is the index of the first slice containing the HDO, and c is the index of the last slice containing the HDO. The slices containing the organ of interest, or target images, can then be denoted as t_S and the binary masks as b_S. Binary masks from b_S were extracted every 8th slices starting from the slice index S = i, where i is a randomly chosen integer between 1 and 4. The extracted binary masks’ indices can then be denoted as K ∈ [i, i+8, …, i+p], where p is the largest integer between i and s-i which is divisible by 8.

The extracted binary masks b_K were resampled using a linear interpolation method to produce a set of interpolated masks b_v, where v ∈ [i, i+1, i+2, …, i+p]. At this point, every target image in tv had its corresponding interpolated mask in B_v. Each target image, T_v, was then concatenated with its corresponding interpolated mask B_v to obtain I^(v): a 2-channel image, where the first channel contained the target image, and the second channel, the interpolated contour.

$$I_{;;1}^{(v)}=T_v$$ #(1)

$$I_{;;2}^{(v)}=B_v$$ #(2)

C. Boundary Detection Network (BDN)

For each image I^(v), 64 × 64 × 2 patches were extracted. These patches were centered about the boundary points of B_v and the number of patches extracted for each slice was directly proportional to the length of the contour obtained from B_v. The patch size was chosen to allow focusing on target organ boundary, while avoiding over-focusing such a given patch always or almost always contained the target boundary.

The exact boundary of the targeted organ is not necessarily known at the precision of one pixel. Hence, a 5-pixel wide contour line around the true contour of the HDO was used as ground truth during this phase of our algorithm as shown in Figure 1. This width was found to produce less spurious labeling compared to smaller and larger widths.

Figure 1:

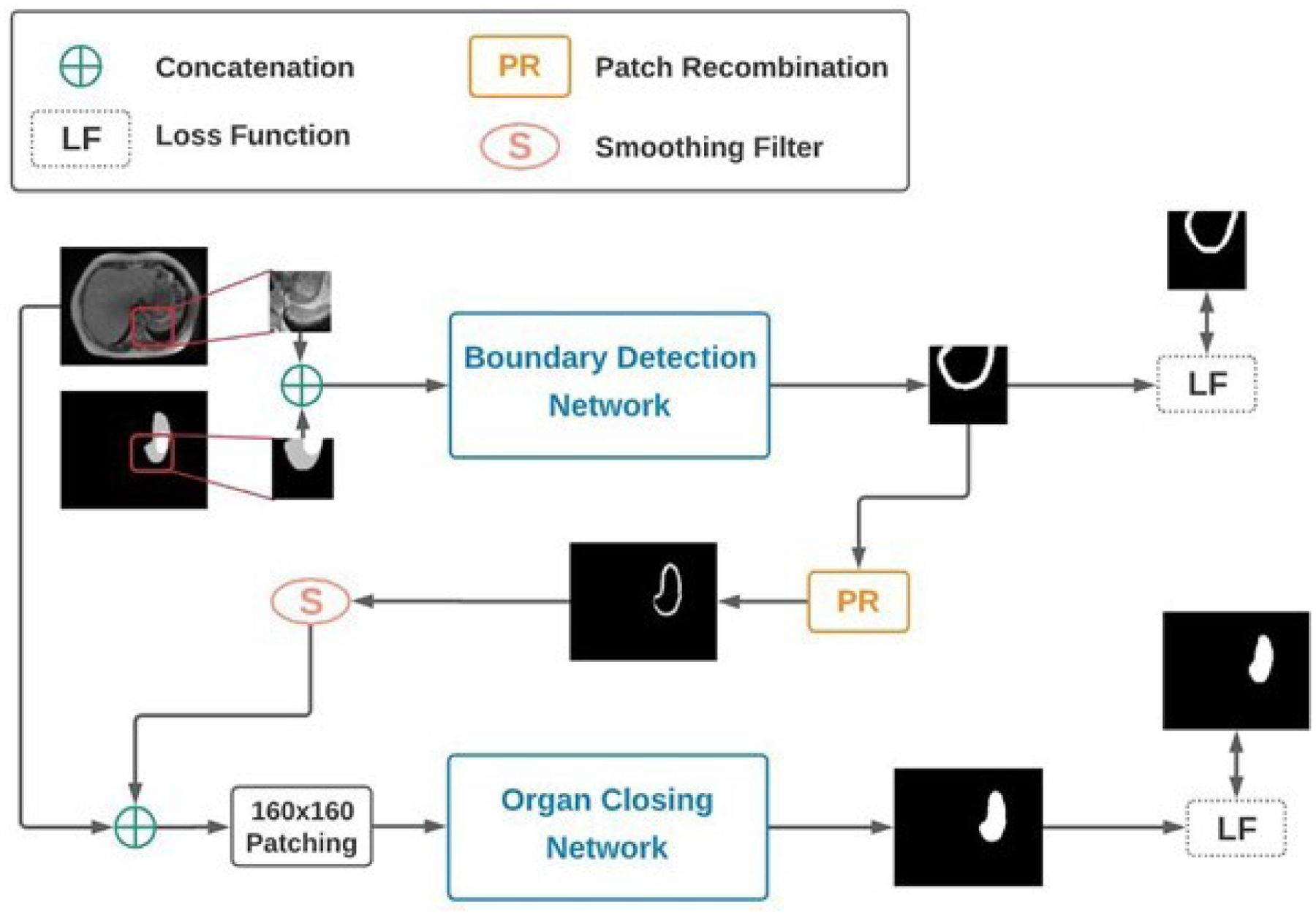
Schematic of the proposed MAI algorithm. The Boundary Detection Network is used to identify the boundary of the organ while the Organ Closing Network uses this boundary information to give the final segmentation of the desired organ.

The Dense-UNet [27] architecture was used for BDN as shown in Figure 2a. This architecture was composed of a dense contracting path (left side) that captures contextual features from the input, followed by a dense expanding path (right side) that extract these local features. The Dense Block constituted of four densely connected layers, each comprising seven layers as shown in Figure 2b. All four densely connected layers in the Dense Block were connected to each other in a feed-forward mode. This method was used to maximize feature reuse and had been shown to be computationally efficient, thereby allowing a deeper network.

Figure 2:

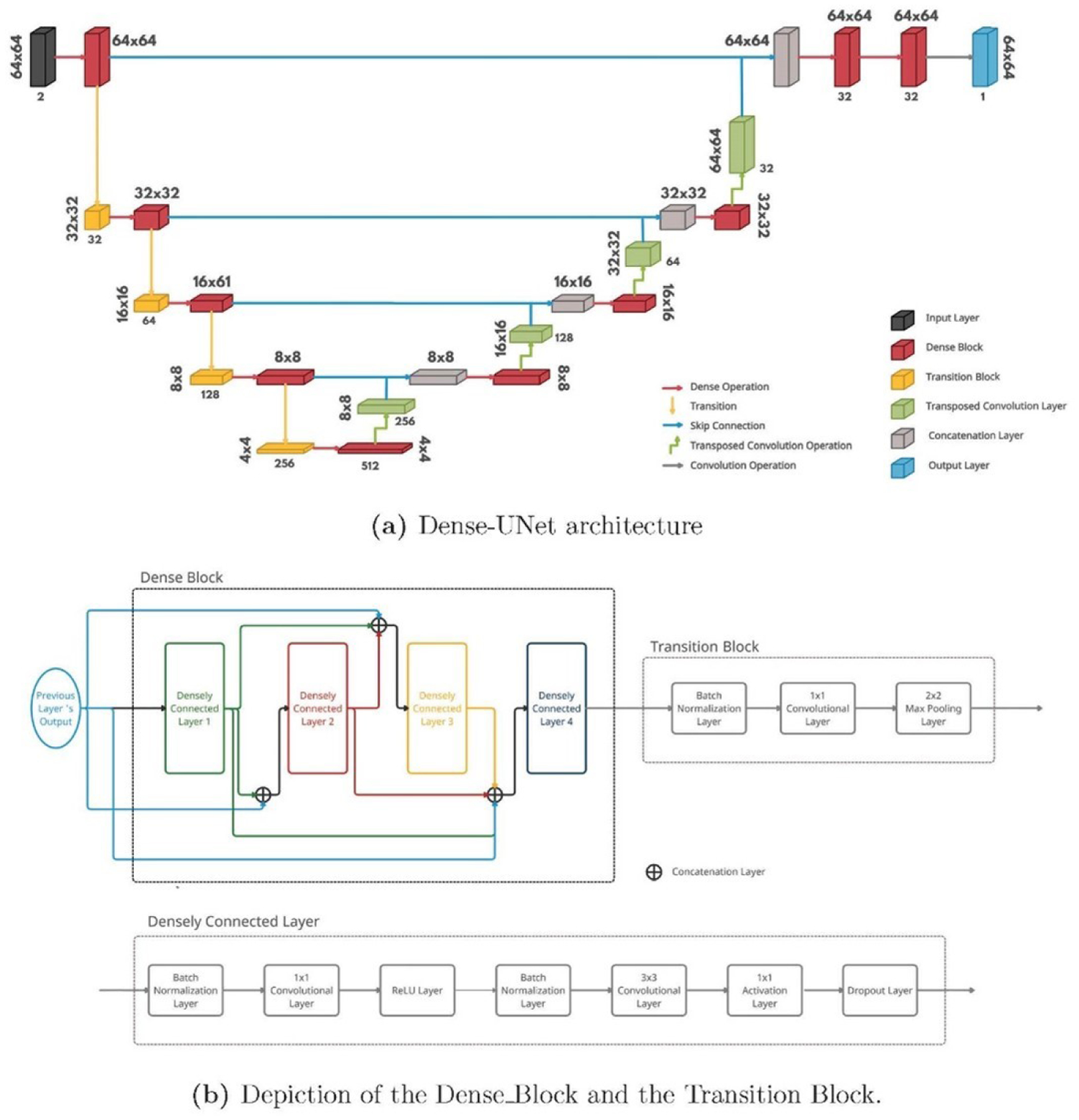
Illustration of the Dense-UNet architecture used for the Boundary Detection phase of our algorithm. This architecture was composed of a dense contracting path (left side) that captures contextual features from the input, followed by a dense expanding path (right side) that extract these local features. The densely connected layers in the Dense Block were connected in a feed-forward mode to maximize feature reuse.

D. Organ Closing Network

For each image I^(v), the patch-wise predictions from the BDN were re-assembled to regain the original size of the target image. As the 64 × 64 patches frequently overlapped with each other, re-assembling them resulted in a weighted boundary where a higher pixel value meant a higher probability of a boundary at that position. The weighted boundary was then smoothed using a 3×3 averaging filter to minimize the effect of spurious labeling. The smoothed boundary B_v2, considered a better approximation to the desired contour, was subsequently used to replace the linearly interpolated contour in I^(v). Hence, the second channel in I^(v) can be denoted as follows:

$$I_{;;2}^{(v)}=B_{v2}$$ #(3)

The new prior information, B_v2, was used to extract a 160 × 160 × 2 patches centered about the centroid of each contour in B_v2. The 160 × 160 patches were found to provide enough global positional and spatial context to the OCN while also providing positional constraints such that spurious labeling outside of the region of interest is avoided. During this phase of our algorithm, the binary masks from the manually delineated HDO contours were used as ground truth, as seen in Figure 1.

The OCN used the same Dense-UNet architecture as the BDN. However, due to the larger patch size, this network required a larger set of parameters and hence, more memory. To avoid GPU memory overflow, each dense block in the OCN was composed of 3 densely connected layers, and the number of filters at each level was reduced to half as compared to the BDN shown in Figure 2a.

E. Loss Function

Both networks used a combination of a Dice loss function [28] and a boundary loss function [29] as shown in equation 4.

$$L=\alpha D_L+(1-\alpha )B_L$$ #(4)

Where α is a variable between 0 and 1, D_L is the Dice loss function, and B_L is the boundary loss function.

The Dice loss function was used to maximize the area of overlap between the prediction mask and the ground truth mask. The boundary loss function works by converting the ground truth’s boundary to a distance-to-boundary array, which is then multiplied to the model’s prediction to give a measure of the distance between the two contours.

During training, α was decreased from 1 to 0.8 by 0.02 increments for the first 10 epochs, after which it was kept constant at 0.8. This loss functions schedule was chosen because it maximized overall accuracy.

F. Training Configuration

Separate experiments were performed on the low-field MR images (stomach segmentation) and on the CT images (bowel segmentation). Each dataset was shuffled and randomly split into a training, validation, and test set. For the stomach segmentation, the training set was composed of 79 MR patients, the validation set of 7 patients, and the test set of 30 patients. In the case of bowel segmentation, the training set constituted of 84 CT patients, the validation set of 6 patients, and the test set of 30 patients. The proposed networks were implemented using Tensorflow 2.2 with Keras backend. The networks were trained using Adam Optimizer [30] with a starting learning rate of 10⁻⁴. The models were evaluated after each epoch using the validation set and the learning rate was reduced by a factor of 0.8 if the validation loss did not improve for 20 consecutive epochs. The BDN and OCN were trained until the training loss did not improve for 25 consecutive epochs, and for each network, the model with the minimum validation loss was saved. For the stomach segmentation, the BDN and OCN models converged after 59 and 154 epochs, respectively. In the case of the bowel segmentation, the BDN and OCN models converged after 49 and 200 epochs, respectively.

G. Evaluation Metrics

The Dice Similarity Coefficient and the mean surface distance [31] (MSD) were used to compare the predicted contours against the ground truth contours on a slice-by-slice basis and in terms of their volume. MSD was obtained by calculating the average of the minimum distances from each point on one surface to the other surface as shown below:

$$MSD=\frac{\left(\frac{G\to P}{G}\right)+\left(\frac{P\to G}{P}\right)}{2}$$ #(5)

Where G → P is the sum of minimum distances from the ground truth surface to the predicted surface, G is the number of points on the surface of the ground truth volume, P → G is the sum of distances from the prediction surface to the ground truth surface, and P is the number of points on the surface of the prediction volume.

To demonstrate the usefulness of the neural networks in our algorithm, we compared our predicted contours to the linearly interpolated contours mentioned in Section II B. We also trained a single-channel Dense-UNet for fully-automatic segmentation (FAS) without using any prior information. This comparison was performed to validate the use of the prior information. Student t-test was used to assess statistical significance of differences between groups, with a p value <0.05 being considered statistically significant.

III. RESULTS AND ANALYSIS

A. Quantitative Analysis

The validation metrics were calculated for 30 MR patients (623 slices) and 30 CT patients (511 slices) present in our test sets. To make the method comparisons fair, slices where the prior information were extracted from were excluded from our analysis.

Table II shows a brief summary of the results obtained from MAI, LI, and FAS by comparing their prediction volume to the ground truth volume. For each method, we also reported the number of slices below a threshold DSC of 0.8, and the number of slices with MSD >3 mm in Table III. Figure 3 and Figure S-1 summarize the DSC of the three methods on a slice-by-slice basis for each of the 30 test cases. We believe that these metrics can provide enough information to compare the performance of the three methods in each of the segmentation tasks.

TABLE II:

Average 3D Dice coefficient (DSC) and mean 3D surface distance (MSD) between the predicted volumes of LI, FAS and MAI, and the ground truth volumes, including their standard deviations. The best results are in bold.

	Stomach		Bowel
	DSC	MSD (mm)	DSC	MSD (mm)
Linear Interpolation (LI)	0.86 ± 0.03	1.31 ± 0.26	0.84 ± 0.06	1.35 ± 0.54
Automatic Segmentation (FAS)	0.81 ± 0.11	3.96 ± 3.12	0.72 ± 0.11	5.81 ± 5.37
MAI Algorithm	0.91 ± 0.02	0.77 ± 0.25	0.90 ± 0.04	0.93 ± 0.48

TABLE III:

Results of the slice-by-slice analysis of each method to compare the robustness of each method. The number of slices, along with the percentage of slices, falling within the given thresholds are shown. The best results are highlighted in bold

		Linear Interpolation (LI)	Automatic Segmentation (FAS)	MAI Algorithm
Stomach	# DSC <0.8	184 (30%)	175 (28%)	44 (7%)
	# MSD >3 mm	377 (61%)	312 (50%)	159 (26%)
Bowel	# DSC <0.8	236 (46%)	305 (60%)	80 (16%)
	# MSD >3 mm	231 (45%)	361 (71%)	105 (21%)

Figure 3:

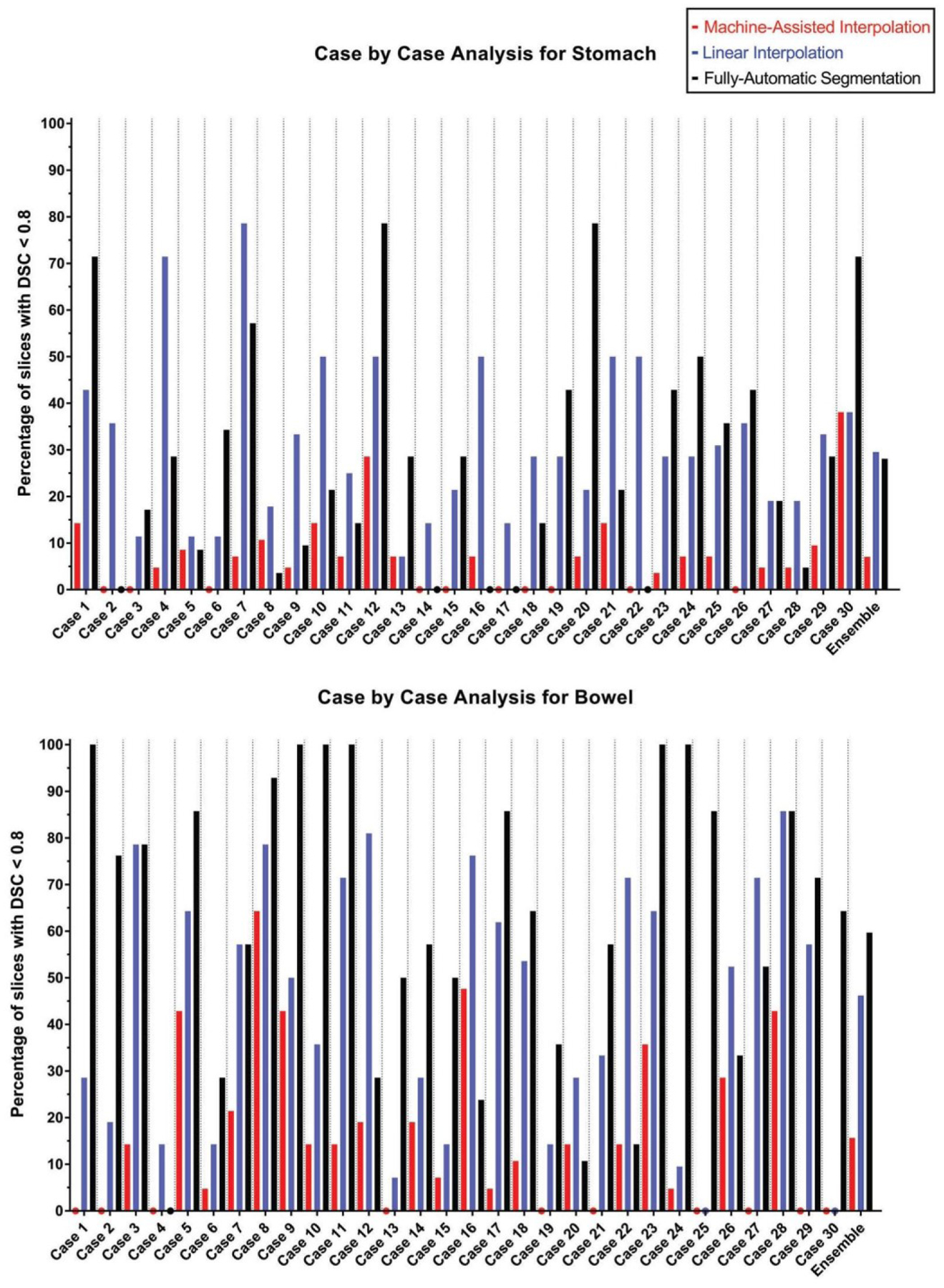
The bar graphs show the percentage of slices with a DSC of less than 0.8 for each test case using MAI, LI, and FAS. The colored dots denote a value of 0% and the bar graphs to the far right show combined results over all test cases. MAI: Machine-Assisted Interpolation; LI: Linear Interpolation; FAS: Fully-Automatic Segmentation.

From Tables II and III, it can be observed that the Machine-Assisted Interpolation outperformed the two other methods both in terms of accuracy and robustness. Furthermore, Figure 3 and Figure S-1 show that MAI obtained superior results in the majority of test cases as compared to LI and FAS. All of our comparisons in our analysis were found to be statistically significant with a p-value <0.001.

IV. DISCUSSION

We proposed a Machine-Assisted Interpolation algorithm which used a few manually contoured slices to automatically segment a highly deformable organ for the rest of the patient volume. The first part of the algorithm consisted of a Boundary Detection Network that utilized global anatomical and positional context to find the boundaries of the HDO. The predicted boundary was then used in our Organ Closing Network to segment the HDO from the target image. The proposed method was employed for two segmentation tasks; stomach segmentation from low-field MR images and bowel segmentation from brachytherapy planning CT images. Our results have shown that MAI outperforms the LI in terms of accuracy and robustness in the given segmentation tasks. For the stomach segmentation, the DSC of MAI was on average 5% higher compared to LI, and the average MSD was 0.54 mm lower (both p-values <0.001). For the bowel segmentation, MAI yielded a DSC 6% higher compared to LI, and the average MSD was 0.42 mm lower (both p-values <0.001). Figure 3 demonstrates the ability of MAI to produce a significantly smaller number of sub-optimal segmentation of the stomach and the bowel in most test cases when compared to LI. From Figure S-1, it can also be observed that MAI outperformed LI in terms of the median and inter-quartile range in every single test case for the stomach and for 29 out of 30 cases for the bowel.

To qualitatively analyze our results, Figure 4 below shows direct comparisons of the prediction from MAI to the prediction of the LI and FAS on three selected slices. Figures 4(a)–(c) and Figures S-2 (a)–(h) show that the predictions from MAI are closer to the gold standard as compared to FAS, which demonstrates the ability of our algorithm to acquire useful information from the prior information to output a better segmentation of the stomach. The importance of positional and spatial constraint used during different the phases of our method can be particularly observed in Figure 4(c) and Figures S-2 (a), (d), (f), (g), and (h). The constraints provided from our prior information forced our networks to stay within a particular region of interest and avoid spurious labeling in the wrong regions as seen with FAS.

Figure 4:

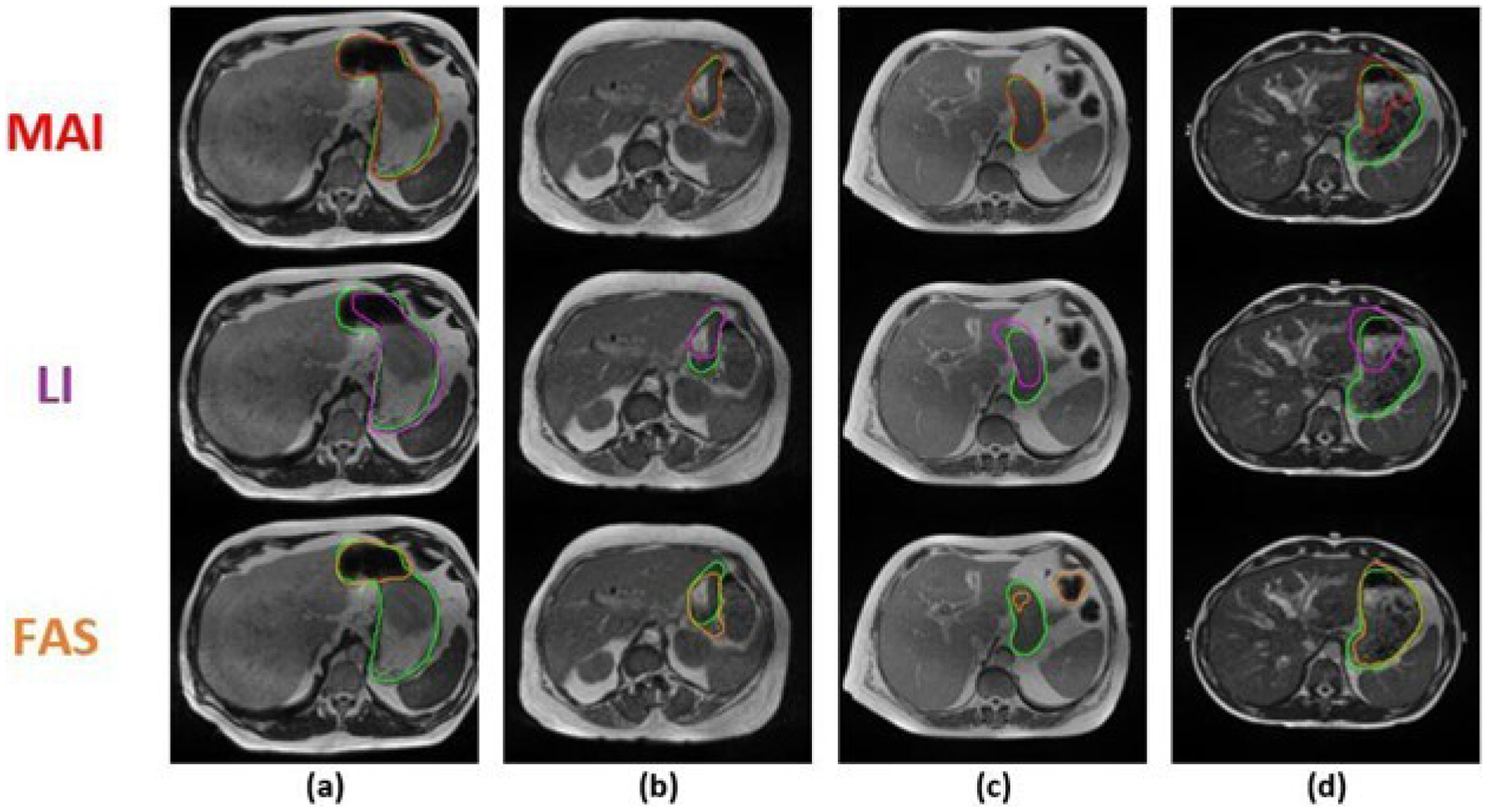
Comparison between the stomach segmentation results of the Machine-Assisted Interpolation (MAI), Linear Interpolation (LI), and Fully-Automatic Segmentation (FAS) on 4 selected MR slices (a-d) across 4 unique patients (cases 4, 8, 20, and 30, respectively). The top row shows the predicted stomach contour from MAI (red contour), the second row, the result from LI (purple contour), and the third row, the results from FAS (orange contour). On all slices, the ground truth contour is shown in green.

Similarly, we can see from Figures 5(a)–(c) and Figures S-3(a)–(h) that MAI has proven to yield more accurate bowel contours as compared to the FAS. Again, it can be observed that the use of prior information provides practical information that allows for a more accurate and robust delineation of the bowel. Furthermore, in the case of brachytherapy treatment, the sigmoid is usually identified separately from the bowel. We have observed that MAI has been efficient in avoiding the mis-identification of the sigmoid as the bowel. On the other hand, FAS frequently misrepresented the sigmoid as the bowel as pointed out in cases (a)-(c) in Figure 5 (FAS contours). We believe that MAI has more potential in avoiding confusion during the delineation of the bowel and the sigmoid, and can thereby expedite the contouring process as compared to FAS or LI.

Figure 5:

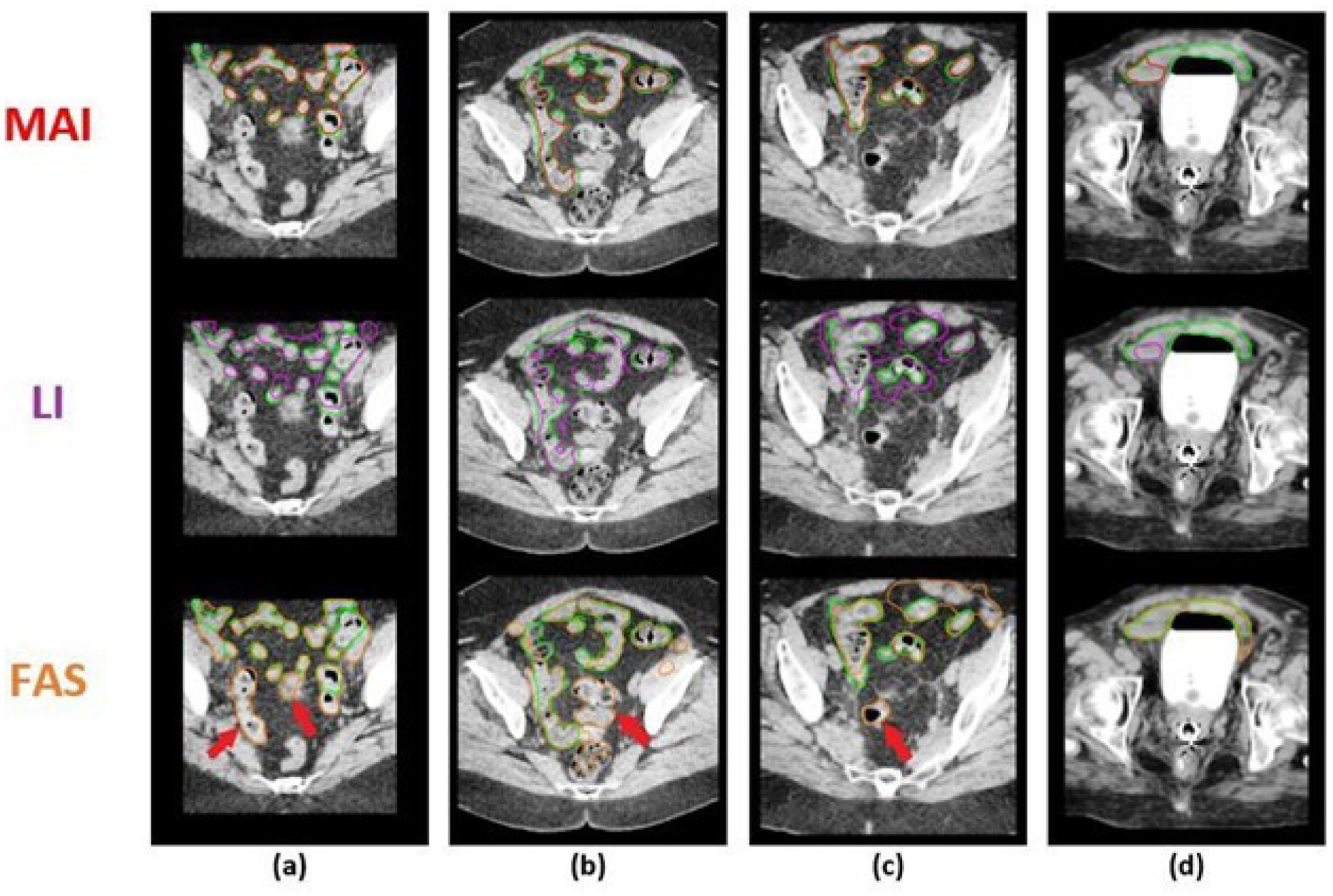
Comparison between the bowel segmentation results of the Machine-Assisted Interpolation (MAI), Linear Interpolation (LI), and Fully-Automatic Segmentation (FAS) on 4 selected CT slices (a-d) across 4 unique patients (cases 3, 7, 17, and 29, respectively). The top row shows the predicted stomach contour from MAI (red contour), the second row, the result from LI (purple contour), and the third row, the results from FAS (orange contour). On all slices, the ground truth contour is shown in green. The red arrows point to contours that were clinically identified as the sigmoid.

However, due to the variations in texture within the organ, the BDN can sporadically perceive an abrupt change in texture within the HDO as a boundary. These erroneous boundary labels may sometime propagate through the OCN and give rise to sub-optimal contours. Furthermore, too much reliance on the prior information may lead the network to segmenting only a sub-section of the targeted organ in cases where the boundary of the organ is far from that of the prior information. In this case, the positional and spatial constraint provided by the prior information can be found to be misleading as seen in Figures 4(d) and 5(d). However, as seen in Figure 3, Figure S-1, and Table III, these occurrences are very rare and do not considerably impact the superiority of MAI when compared to LI and FAS.

Compared to the state-of-the-art automatic segmentation methods involving the stomach [23, 25, 32–36] (reported DSC 0.81–0.90) and bowel [25, 37–41] (reported DSC 0.78–0.89), MAI shows higher segmentation accuracy. Because auto-segmentation results are sensitive to the composition of training and evaluation datasets, we also compared MAI to a fully-automated Dense- UNet segmentation that was trained and evaluated on our own dataset. For the stomach segmentation, the DSC of MAI was on average 10% higher compared to FAS, and the average MSD was 3.19 mm lower (both p-values <0.001). For the bowel segmentation, MAI yielded a DSC 18% higher compared to FAS, and the average MSD was 4.9 mm lower (both p-values <0.001). Furthermore, it can be observed from Figure 6 that MAI outperformed FAS in terms of the median and inter-quartile range in 28 out of 30 stomach test cases, and 27 out of 30 bowel test cases. Yet, the most important aspect to note from Figure 3 and Figure S-1 is the ability of MAI to produce more consistent results throughout the test cases as compared to FAS where the method occasionally fails to produce good results (e.g., Cases 6, 7, 12, 20, and 30 for the stomach, and Cases 1, 10, 11, 23, and 24 for the bowel).

However, the prior information used in our algorithm gives our method an obvious advantage in segmenting the stomach and the bowel accurately as opposed to the fully-automatic segmentation methods. Hence, comparing our results to these automatic segmentation methods is not the primary aim of this study. The main goal of this work is to instead provide a practical solution that can exploit the information obtained from the expert user to contour HDOs with high accuracy, which MAI has shown its efficacy in during our testing phase. Furthermore, inspired by a commonly used manual interpolation-based contouring strategy, MAI can potentially be implemented in the radiation therapy workflow without disrupting the user’s current practice and habits during the contouring process. This aspect of MAI, together with the results obtained from our experiments, make us believe that our algorithm can speed up the contouring process within the external beam radiation therapy and brachytherapy workflow where the automatic segmentation tool is not always the preferred choice.

Leger et al. also demonstrated the concept of prior information usage in the context of bladder segmentation. [42] Their results showed that the use of prior information outperformed both the standard UNet and a registration-based contour propagation method when the prior information is extracted within 5 slices from the target image. However, the bladder is an organ that is amenable to highly accurate auto-segmentation. In contrast, in this work we focused on stomach and the bowel which are generally believed to be more difficult tasks due to their larger variations in shape, size, and position.

This work is subject to certain limitations. First, HDOs often show significant patient- to-patient variation. Our evaluation dataset size of 30 patients per organ site may not completely capture the range of performance that might be observed on a much larger dataset. Secondly, while we demonstrated increased accuracy of MAI versus linear interpolation, in a clinical workflow, some edits would likely still be needed. We were unable to assess whether the corresponding time differences for correction would be practically significant. These additional tests will be pursued in future studies. Nevertheless, the differences in DSC and MSD reported in this work are consistent with differences that are regarded as significant in the literature. [23, 25, 42]

From our observations, our algorithm takes an average of 12.4 seconds/case (0.6 seconds/slice) and 22.1 seconds/case (1.3 seconds/slice) to segment the stomach and the bowel, respectively, using an Nvidia Quadro P1000 4GB GPU (Nvidia Corporation, Santa Clara, CA, USA) system with 16GB RAM. As our algorithm has not been optimized for fast execution time, a run time optimization could further reduce the inference time. However, we believe that MAI is sufficiently fast to be clinically implemented as-is. Future works also include applying this algorithm to segment multiple organs in the abdominal and pelvic regions, which has the potential of further expediting the contouring process within the radiation therapy workflow.

V. CONCLUSION

The stomach and the bowel can be characterized as highly deformable organs due to their large and frequent changes in shape, size, and texture. Hence, it is a time-consuming task to manually locate and delineate these organs, even for the experienced professionals in the clinic. Automatic segmentation tools have thus far proven to be inefficient in solving this issue for HDOs due to their lack in accuracy and robustness.

We proposed herein a robust MAI algorithm which can accurately segment both the stomach from low-field MR images and the bowel from brachytherapy planning CT images using a few manually contoured slices as prior information. This algorithm has the potential of facilitating the localization and delineation of the stomach and the bowel in the external beam radiation therapy and brachytherapy workflow.

TABLE I:

Definitions of relevant acronyms used in this paper

Acronym	Definition
HDO	Highly Deformable Organ
CNN	Convolutional Neural Network
BDN	Boundary Detection Network
OCN	Organ Closing Network
MAI	Machine-Assisted Interpolation
LI	Linear Interpolation
FAS	Fully-Automatic Segmentation

VII. Data Availability

Aggregate data available upon request to the corresponding author. The data are not publicly available due to privacy or ethical restrictions.