Forecasting Covid-19 Transmission with ARIMA and LSTM Techniques in Morocco

Abstract

In this paper, we are interested to forecast and predict the time evolution of the Covid-19 in Morocco based on two different time series forecasting models. We used Auto-Regressive Integrated Moving Average (ARIMA) and Long short-term memory (LSTM) models to predict the outbreak of Covid-19 in the upcoming 2 months in Morocco. In this work, we measured the effective reproduction number using the real data and also the fitted forecasted data produced by the two used approaches, to reveal how effective the measures taken by the Moroccan government have been controlling the Covid-19 outbreak. The prediction results for the next 2 months show a strong evolution in the number of confirmed and death cases in Morocco. According to the measures of the effective reproduction number, the transmissibility of the disease will continue to expand in the next 2 months, but fortunately, the higher value of the effective reproduction number is not considered to be dramatic and, therefore, may give hope for controlling the disease.

Introduction

In late December 2019, an outbreak of Coronavirus disease 2019 (Covid-19) started in Wuhan city of China and quickly spread in China and in the whole world [1]. The World Health Organization (WHO) declared the epidemic of Covid-19 as a pandemic on March 12 2020 [2]. Until the day of (22/11/2020), 59,525,364 cases of Covid-19 have been confirmed worldwide. Sadly, 1,401,571 of them have been deceased and fortunately 41,147,262 of them have been healed [3]. Looking into these numbers of confirmed and death cases, we know the extremely serious danger of this pandemic situation. In Morocco, Covid-19 pandemic was confirmed start to propagate in Morocco on 2 March 2020, when the first confirmed Covid-19 case was found in Casablanca [4]). Few weeks later, many activities and shops were closed by the Moroccan authorities to contain the spread of this new virus. Unfortunately, 327,528 confirmed and 5,396 death cases were reported in Morocco until now [5]. Compared to other countries over the world, which suffer more from the outbreak of Covid-19, we can say that the Moroccan population has managed to control this danger situation avoiding a big disaster.

To reduce the Covid-19 spreading rate, many countries began increasing restrictions such as lockdown, quarantine and social distance protocols, travel restrictions, close borders and schools, mandatory use of face masks and so on. At the start of the Covid-19 crisis, Moroccan authorities reacted decisively to the threat of the pandemic by declaring a month-long state of emergency across the country until 20 April 2020. The government had decided to give a great importance to the Covid-19 crisis, by considering national security and public health as top priorities. Taking into consideration the evolution of the epidemiological situation in Morocco, the government has decided to extend the state of emergency until May 20, 2020, and re-extended it with an ease of restrictions until 21 June 2020.

Almost all countries announced that they entered at the stage of easing the quarantine and releasing of restrictions. In Morocco, the government starts to release and ease the restrictions from the mid of June 2020. This phase of easing the restrictions will include further measures, giving the green light to the opening of additional economic, social and cultural activities. The approach adopted foresees prevention and control measures for the contamination sphere not based on human but on the geographical contours of environments and living areas. The deconfinement zone constitutes the base of a beginning of general deconfinement of the whole Moroccan national territory. Furthermore, deconfinement by zone is not an irreversible process and must not lead to confusion: a local authority declared healthy can move from zone 1 “safe” to zone 2 “precarious” if the preventive measures are not respected. In addition, deconfinement by area can be effective and efficient and can induce a gradual and safe deconfinement provided that the population agrees favorably to the restrictions of protection and the rigorous respect of prevention measures such as social distancing, the wearing of a mask. Any relaxation of these measures can generate a new wave of contamination whose consequences will be unpredictable [6, 7]. Thus, the risk of another Covid-19 waves remains even with the presence of an antidote or an effective vaccine that protects susceptible people from infection. Unfortunately, this is mainly due to the emergence of several variants of Covid-19 virus in different part of the world [8].

At the height of this crisis, many researches over the world tried their best to predict or to forecast the evolution of Covid-19 in their countries using various Mathematical, Statistical, Computing, and Deep Learning approaches and models. To understand and, more especially, to predict the spread of Covid-19, several studies have been done since the appearance of this new virus, using various mathematical models. These mathematical models, which are based on differential equations, have the major drawback of failing to produce realistic and useful results, particularly for complex disease systems like Covid-19. In contrast, time series forecasting outbreaks like Covid-19 using statistical models and deep learning are of critical importance, especially in these unprecedented times. It not only provides a short or long-term overview of the situations of Covid-19 in a particular country, but also helps the “decision makers” to take the right actions wisely. Using a Covid-19 dataset, we can forecast the transmission of the virus, which allows us to make the decisions to follow to reduce or limit its severity. On the other hand, the value of the effective reproduction number $R_t$ can be considered as a useful aid to the governments over the world to control the quarantine measures based on the epidemiological situation in their countries. $R_t$ is a dynamic method specifically used to estimate the epidemiological trend in a population over time. It referred as the effective reproduction number, which is the number of people that can get the infection from an infected person over time [9].

In this paper, we propose two different approaches that could be useful for predicting the spread of Covid-19 in Morocco. Basically, we used the ARIMA model and LSTMs Networks to predict the epidemiological trend of the confirmed and death cases of Covid-19. Therefore, we developed a time series forecasting models, based on the extracted data provided by the John Hopkins university [10] and the Moroccan Ministry of Health website [5] to predict Covid-19 daily confirmed and death cases for next 60 days. We also estimated the value of $R_t$ using the extracted daily new confirmed cases data and the forecasted data generated by our proposed approaches, to investigate the change in the effective reproduction number for the upcoming 2 months. In this work, we make new key contributions: First, we propose new configurations of ARIMA and LSTMs models to predict Covid-19 outbreaks in Morocco. Then, propose the use of the effective reproduction number $R_t$ on predicted data to get a better overview on the Covid-19 situation. Finally, we compare results provided by these models using evaluation metrics.

The paper is organized as follows. In the next section, we discuss the different proposed works related to our paper. In the third section, we present the dataset and the forecasting models used in this paper to study and predict the outbreak of Covid-19 in Morocco. In the fourth section, we present our results and we discuss the actual and the predicted epidemic situation for the next 2 months. Finally, the last section concludes this paper.

Related Works

In this part, we discuss almost all relevant scientific reports related to our work. In detail, we give a literature review on studies and reports that propose mathematical, statistical, computing, and deep learning approaches or models to forecast Covid-19 pandemic trends. Starting with models based on mathematical approaches, Yang et al. [11], proposed a modified SEIR epidemiological model integrated with an LSTM model to predict the trend of Covid-19 in China. The proposed LSTM model is used to predict the SEIR model rates and fit model results with the Covid-19 dataset. Peng et al. [12], proposed a generalized SEIR model that includes the self-protection and quarantine compartments to estimate the Covid-19 trends in different states of China. Another work proposed by Prem et al. in [13], where they simulated the ongoing trajectory of the Covid-19 outbreak using an age-structured SEIR model for several physical distances. To describe the dynamics of Covid-19 and clearly parameterize the intervention effects of control measures, Hou et al. proposed a Susceptible, Un-quarantined infected, Quarantined infected, and Confirmed infected (SUQC) model, in [14].

On the other hand, many other authors used time series forecasting based on statistical models, especially the ARIMA model. Benvenuto et al. used the ARIMA model to predict the Covid-19 trend of the confirmed and death cases in [15]. Similarly, Yousaf et al. in [16] and Zeynep in [17] used ARIMA models to predict the Covid-19 trends in their countries and regions. In [18], Chakraborty and Ghosh proposed a novel hybrid ARIMA-WBF model to forecast the trends of Covid-19 cases. The model is tested on different datasets from different countries to measure the impact of social distancing procedures implemented by these countries. Chintalapudi et al. used the ARIMA model to forecast the trends of Covid-19 in Italy to demonstrate the importance of lockdown, self-isolation, and social distancing in the control of pandemic transmission in [19].

Time series forecasting cannot only be done using statistical models, many other research has implemented Artificial Intelligence (AI) and Deep Learning techniques in their models. Chimmula et al. proposed a forecasting model using LSTM networks to predict the Covid-19 trends in Canada and other countries, in [20]. Tomar et al., in [21], use the same LSTM network technique with different configurations to forecast Covid-19 trends in India. In the early stages of the Covid-19 outbreak, Wu et al. used a generalized logistic growth model to predict the trends of Covid-19 in 29 states in China and in the rest of the world in [22]. Roosa et al. generated short-term forecasts of Covid-19 trends in China using three different machine-learning models from February 5th to February 24th, 2020 in [23]. Pourhomayoun et al. used different machine-learning models to forecast the Covid-19 mortality rate in [24]. Recently, Santosh in [25], presented an overview of forecasting modeling based on the use of AI-driven tools for Covid-19. He also mentioned the uses of deep learning algorithms in screening and decision-making.

Since the beginning of the Covid-19 outbreak, many proposed models and techniques have been used to forecast and predict Covid-19 trends all over the world. This demonstrates the significance of forecasting in understanding current reality and planning future steps in the best possible scenario. However, mathematical approaches based on epidemiological models and curve fitting cannot predict as effectively as other models based on statistical and AI approaches [25]. For this reason, the current study uses statistical and AI approaches to forecast short-term confirmed and death cases of Covid-19 in Morocco.

Forecasting Models

Data Description

The daily prevalence data were obtained from the John Hopkins university [10] and the official website of the Moroccan Health Ministry that reports latest information of Covid-19 pandemic in Morocco [5]. The dataset is available in the time series format with date, month and year, so that the temporal components are not neglected. The data model development was done based on the update of 22 November 2020. The daily prevalence data consisted of three groups, namely confirmed cases, recovered cases and death cases. In this study, we excluded the recovered cases information and to focus on forecasting the number of confirmed and death cases for the next 2 months. A descriptive statistics of the Covid-19 data of the confirmed and death cases in Morocco between 22/01/2020–22/11/2020 are given in Table 1. In Moroccan’s population of 36.03 million, the prevalence is on average equal to 53727.032 and the deaths is on average equal to 932.705. These values are very low if compared the ones of many countries. This proves that the policy adopted by the Moroccan government through proactive measures was indeed effective in combating the spread of Covid-19.

Table 1.

Descriptive statistics on the prevalence and incidence of Covid-19 in Morocco

Case	Mean	SE mean	St. Dev	Minimum	Maximum	Skewness	Kurtosis
Confirmed cases	53727.032	4670.176	81694.720	0	324941	1.72755	1.990845
Death cases	932.705	77.618	1357.764	0	5316	1.652762	1.663929

Non-seasonal ARIMA Model

The general ARIMA model introduced by Box and Jenkins [26] is used when one can predict future behavior based on past behavior. It is used for forecasting when there is some correlation between values in a time series. An ARIMA model can be understood simply by outlining each of its components as the following [27]:

• Autoregression (AR) refers to a model where a value from a time series is regressed on previous values from that same time series, i.e., a model that uses the dependent relationship between an observation and some number of lagged observations.

• Integrated (I) represents the differencing of raw observations (i.e., subtracting an observation from an observation at the previous time step) to make the time series stationary.

• Moving average (MA) incorporates the dependency between an observation and a residual error from a moving average model applied to lagged observations.

For ARIMA models, a standard notation is summarized as ARIMA(p,d,q), where integer values substitute for the parameters to indicate the type of ARIMA model used. The parameters can be defined as:

• p: the number of lag observations in the model; also known as the lag order.

• d: the number of times that the raw observations are differentiated; also known as the degree of differencing.

• q: the size of the moving average window; also known as the order of the moving average.

By summing above parameters with non-seasonal ARIMA model, the general forecasting equation (1) can be written as follows:

$$\begin{array}{c}\hfill \widehat{y_t}=\mu +{\phi }_1{y}_{t-1}+...+{\phi }_p{y}_{t-p}-{\theta }_1{e}_{t-1}-...-{\theta }_q{e}_{t-q},\end{array}$$ 1

where $\widehat{y_t}$ is the predicted value of the time series $y_t$ at period t, based on the observed data up to the period $t-1$. The parameter $\mu$ is the constant of the model and ${\phi }_k$ (resp. ${\theta }_k$) is the AR (resp MA) coefficient at lag k. The term $e_{t-k}=y_{t-k}-{\widehat{y}}_{t-k}$ is the forecast error that was made at period $t-k$. In this work, the model equation is specified by the set of parameter (p, d, q).

The (seasonal and non-seasonal) ARIMA models have higher fitting and forecasting accuracy than exponential smoothing models [17, 28]. In this work, by examining the confirmed and death cases in Morocco, we see no seasonal pattern, and hence, we will focus on non-seasonal ARIMA models to forecast the number of confirmed and death cases in Morocco for the upcoming 2 months. To check the seasonality, stationarity and differencing, we shall the time series plot, the Autocorrelation function (ACF) and Partial Autocorrelation function (PACF). The prediction intervals until the end of September is produced from the fitted model and evaluated using the Akaike Information Criteria, to determine the best ARIMA model. All statistical results were produced using Python library ‘statsmodels and sklearn’ [29, 30] developed for generating ARIMA models.

LSTM Networks for Modeling Time Series

The Long Short-Term Memory, or LSTM, network is a type of Recurrent Neural Network (RNN) that is highly recommended for sequence problems [31]. The recurrent connections add memory to the network to allow learning the ordered nature of observations within input sequences. However, because of the vanishing gradient problem, it would be difficult to train standard RNNs to solve problems that require learning long-term temporal dependencies. LSTM networks are RNN with memory and forgotten capacities, which allow them to learn longer-term dependencies, and thus are very well suited to classifying, processing and making predictions based on long sequences of data. There are many types of LSTM models that can be used for each specific type of time series forecasting problem. Recently, LSTM networks got lot of attention by the machine-learning researchers. It has been successfully applied to many sequence learning tasks such as speech recognition [32], machine translation [33] and natural language generation [34].

In our case, we need to predict the Covid-19 confirmed and death cases for the upcoming 2 months. This is considered as a time series forecasting problem that requires a prediction of multiple time steps into the future [31]. Specifically, these are problems where the forecast horizon or interval is more than one time step. One of the major LSTM models that can be used to solve the multi-step time series forecasting problem is the Encoder-Decoder Model [35]. We start first by explaining the internal architecture of LSTM networks, then we present our proposed model design.

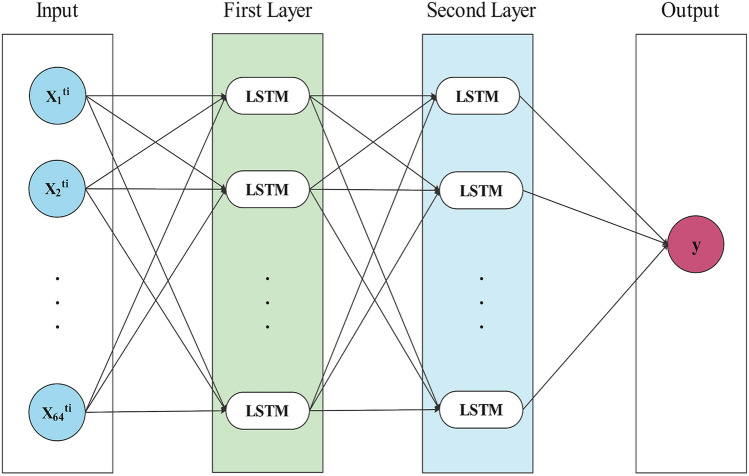
The key to LSTM networks is the cell state. The cell state is kind of like a connector between LSTM blocks. It is the main cell of the data flow, which runs straight down the entire RNNs chain, with only some minor linear interactions. Each block of LSTM Networks contain 3 gates: input gate, forget gate and output gate. The forget gate removes information from the cell state if it is no longer required for the LSTM learning. The input gate discovers which useful information can be added to the cell state. The output gate has a function to decide which part of the current cell makes it to the output. For a description of the internal architecture of LSTM in more details, we refer to reference Ref. [36]. The model architecture used in this paper is shown in Fig. 1. Here, we used two LSTM Layers, the first one contains 64 LSTM blocks and the second one contains 32 LSTM blocks. The forecasting results of this approach were produced using Python library Keras [37] and TensorFlow [38].

Fig. 1.

LSTM architecture used in this paper

Estimating Covid-19’s $R_t$ in Real Time

In every outbreak of a new virus, the epidemiologists are interested in the basic reproduction number ($R_0$), to determine if an emerging infectious disease can propagate in a population. Consequently, it helps to determine what decision makers must be taken as measures to eradicate an epidemic outbreak. However, it is rare for all people in the world to be completely susceptible to a pandemic. Some of the population could be isolate, as an example, the current situation of Covid-19, where almost all countries in the world went into lockdown. Therefore, the population cannot be all become infected, as a result, the basic reproduction number could be greater than the average number of secondary cases per infectious cases. In fact, $R_0$ is a static measure that does not fit with changes in the population behavior and the countries restrictions during a pandemic. On the other hand, the effective reproduction number ($R_t$) could be more effective, since it can be updated as a function of time.

Currently, the organizations and governments of countries over the world take into consideration the value of $R_t$, to evaluate the epidemiological situation in their countries. It also gives them vital information that could help them to make decisions. $R_t$ changes over time according to the measures to control the pandemic that have been applied differently in each country [39]. It is very important to know the current value of $R_t$, the lower value of $R_t$ means the epidemiological situation is under control. As in commonly used infection models, when $R_t>1$, the pandemic will propagate widely over the country. However, if $R_t<1$, the pandemic will slow down significantly before it reaches many people.

In this study, we estimate the real time of $R_t$ using both the real Covid-19 data from “Data Description” and also the predicted data produced by ARIMA and LSTMs approaches. Here, we used a modified version of the solution created by Bettencourt and Ribeiro [40] to estimate real-time $R_t$ using a Bayesian approach [41] and incorporating a process model with Gaussian noise to estimate a time-varying $R_t$ [42].

Results and Discussion

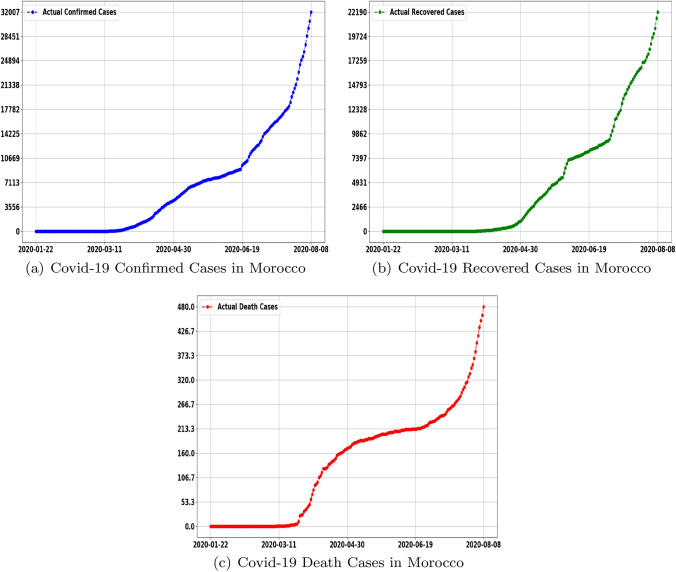
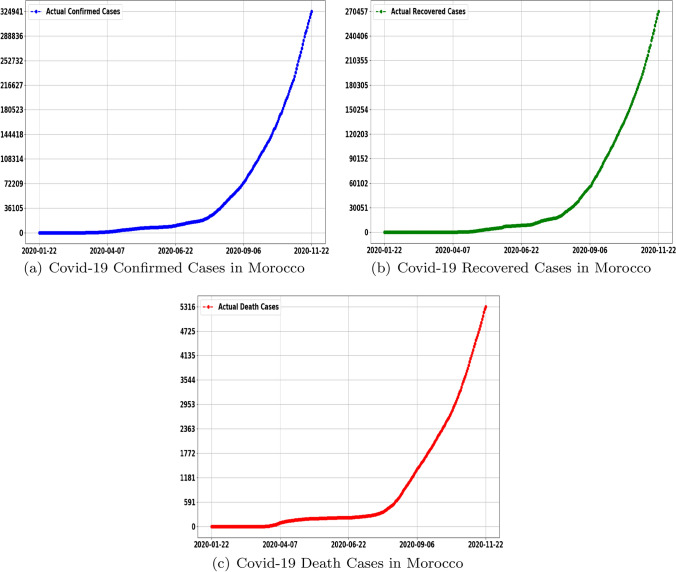
First, we start with analyzing the current data of Covid-19 in Morocco. In Figs. 2 and 3, we show the time evolution of number confirmed, recovered and death cases. From Fig. 2a, it is clearly seen that, thanks to the containment strategy adopted by the Moroccan authorities, the slope of the confirmed cases curve decreases with time. The growth of infection begins to flatten out at nearly 20 June 2020, tending towards blunting the peak infection rate. However, on this date, which corresponds to the beginning of deconfinement by zone adopted by the Moroccan authorities, the slope of the confirmed curve increases sharply, showing the start of a new wave of Covid-19. In addition, an alarming situation was observed at the end of June, when there was a sudden increase in the death rate (Fig. 3c). Fortunately, the number of recovered cases is also increasing (Fig. 3b) thanks to the creation of several military field hospitals, to alleviate the pressure on existing health establishments, by providing additional health care capacities.

Fig. 2.

Daily confirmed cases, recoveries and deaths of Covid-19 in Morocco in the period (22.01.2020–08.08.2020)

Fig. 3.

Daily confirmed cases, recoveries and deaths of Covid-19 in Morocco in the period (22.01.2020–22.11.2020)

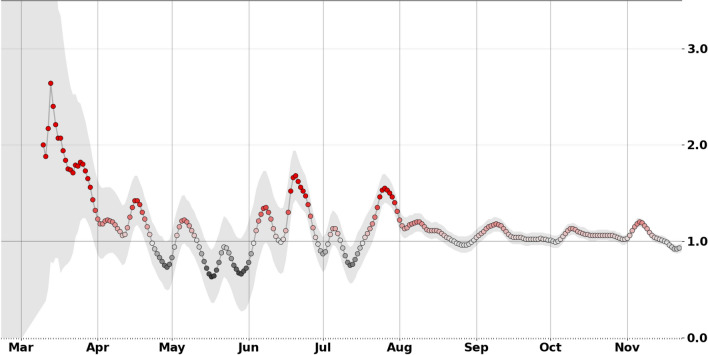
The effects of Moroccan’s strategy to contain the pandemic can be clearly seen from Fig. 4. At the first observation, we see that $R_t$ exhibits a decreasing oscillation from March to August, followed by an almost stationary value. This decrease of $R_t$ is essentially due to the containment strategy adopted during the 3 months March, April and May. During the month of Jun, $R_t$ is increased again to reach higher peak value of about 1.7. This behavior is essentially due to the strategy of deconfinement by zone where the individuals of zone 1 tend to not respect the conditions of protection. Since August, Moroccan population begin to live normally without worrying about the danger of Covid-19, despite the health restrictions adopted by the Moroccan state.

Fig. 4.

Real-time $R_t$ using actual Covid-19 data in Morocco in the period (22.01.2020–22.11.2020)

In this paper, we consider two different forecasting approaches, to forecast the future number of confirmed and death cases in Morocco in the next 2 months from 22 November to 21 January 2021. Now, we shall explain the steps we used to calibrate the forecasting models using the obtained Covid-19 data described in “Data Description”. First, we started with choosing features that we need for the forecasting. We converted the selected features raw data from the original data in a time series from 22 February 2020 to 22 November 2020 using Python Pandas Package. We prepared the selected data for training and validation of the model. The training partition, typically the largest partition (80%), contains the data used to build the two forecasting models. The validation partition (20%) is used to assess the performance of each model so that we can compare models and pick the best one.

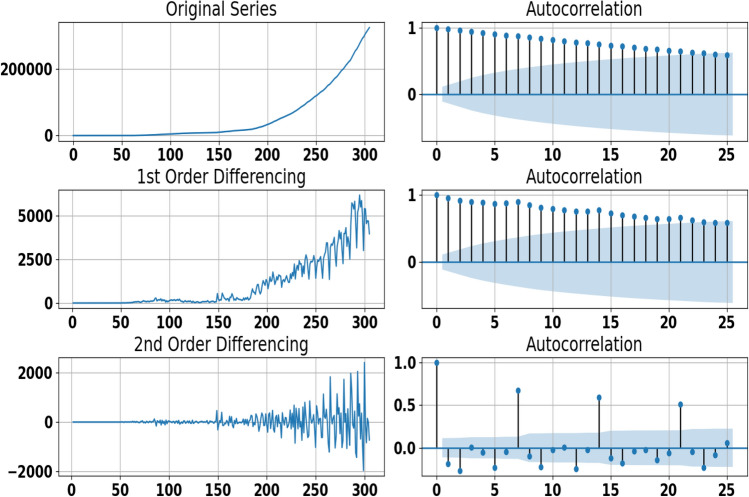
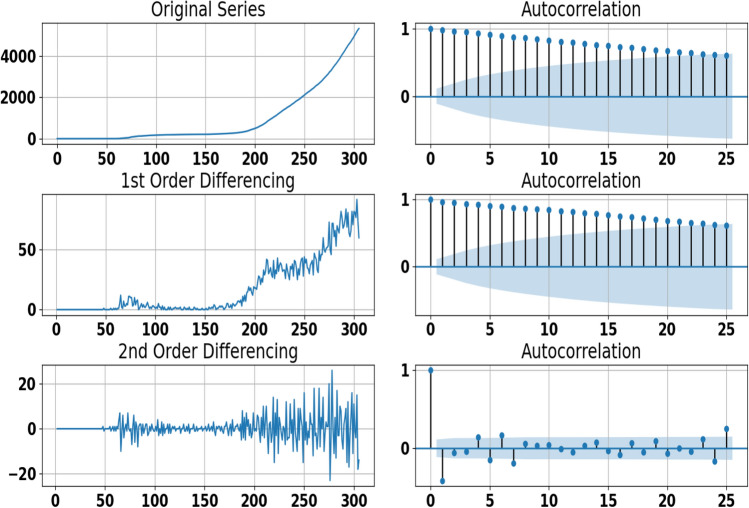
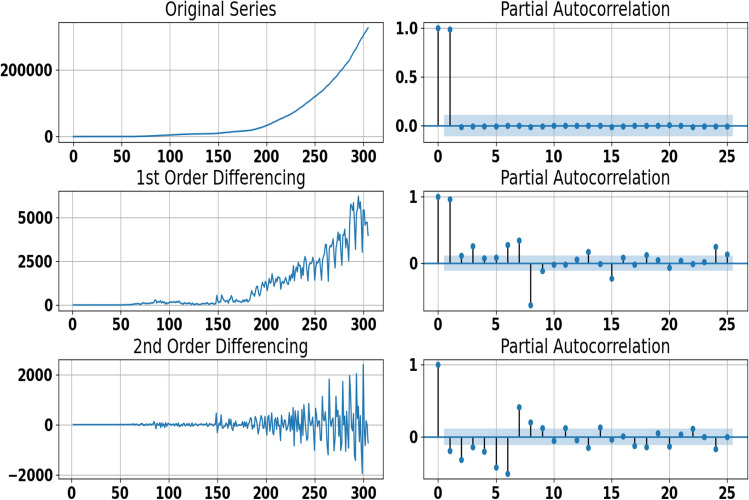
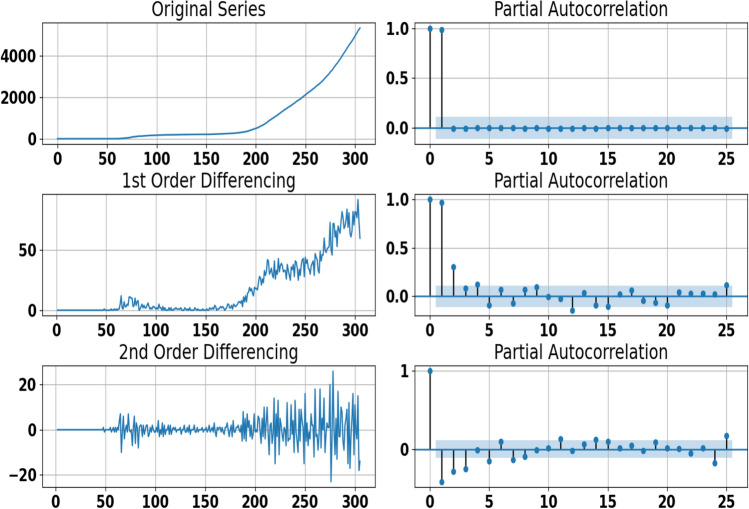
Since the dataset used in this paper is considered as a time series, it is very important to analyze the time original series plots, Autocorrelation Function (ACF), and Partial Autocorrelation Function (PACF) graphs to check the seasonality, stationarity and differencing. The time original series plots, as shown by Fig. 3 confirm that the overall prevalence and incidence of Covid-19 used in this paper show non-seasonal patterns. In Figs. 5 and 6, we show the estimated autocorrelations at the first difference for the time series of Covid-19 confirmed and death cases in Morocco. The autocorrelation plot indicates that the process is non-stationary and suggests an ARIMA model. The results show that the first-order difference of the Covid-19 confirmed and death cases time series is not stationary because autocorrelations are reduced very slightly. Therefore, a second-order difference is needed to eliminate the trends of all time series. In Figs. 5, 6, 7, and 8, we show the ACF and PACF plots for both the confirmed and death time series in the second-order difference. We can see that trend signals are removed in the second-order differentiated series. Moreover, we confirm the stationarity of these differentiated series because ACF and PACF are reduced very fast to reach 0 after the first lag. This proves that the number of times that the series are differentiated to find out stationarity is $d=2$.

Fig. 5.

Time series plot for adjusted confirmed cases data (left) and estimated autocorrelations (right) for Morocco before and after first and second differencing

Fig. 6.

Time series plot for adjusted death cases data (left) and estimated autocorrelations (right) for Morocco before and after first and second differencing

Fig. 7.

Time series plot for adjusted confirmed cases data (left) and estimated partial autocorrelations (right) for Morocco before and after first and second differencing

Fig. 8.

Time series plot for adjusted death cases data (left) and estimated partial autocorrelations (right) for Morocco before and after first and second differencing

Now, we need to find out which ARIMA models can effectively forecast Covid-19 confirmed and death cases in Morocco. For that reason, we evaluate the parameters of the ARIMA models for different integer values of p and q. In Table 2, we show all of our tested ARIMA models for both confirmed and death cases data in Morocco. Based on the Akaike Information Criteria (AIC), we found that ARIMA(1, 2, 1) and ARIMA(3, 2, 1) were selected as the best ARIMA models to determine the prevalence of Covid-2019 confirmed and death cases, respectively, with a minimum $AI{C}_{\text{ConfirmedCases}}=3177.777$ and $AI{C}_{\text{DeathCases}}=1221.613$. Table 3 shows the parameter estimates for the best chosen ARIMA models. As we can see, the p-values associated with the parameters are $<0.05$, which means that we could reject the null hypothesis and that this effect reflects the characteristics of the whole population.

Table 2.

Comparison of tested ARIMA models

Dataset	Model	AIC	BIC
Confirmed cases	ARIMA(0,2,0)	3226.022	3229.511
	ARIMA(0,2,1)	3183.315	3193.782
	ARIMA(0,2,2)	3178.066	3192.021
	ARIMA(1,2,0)	3204.709	3215.176
	ARIMA(1,2,1)	3177.777	3191.733
	ARIMA(1,2,2)	3183.668	3201.113
	ARIMA(2,2,0)	3203.077	3217.033
	ARIMA(2,2,1)	3179.100	3196.545
	ARIMA(2,2,2)	3179.392	3200.326
Death cases	ARIMA(0,2,0)	1314.725	1321.703
	ARIMA(0,2,1)	1232.299	1242.766
	ARIMA(0,2,2)	1233.902	1247.858
	ARIMA(0,2,3)	1235.464	1252.909
	ARIMA(1,2,0)	1259.549	1270.016
	ARIMA(1,2,1)	1233.953	1247.908
	ARIMA(1,2,2)	1232.230	1249.674
	ARIMA(1,2,3)	1232.758	1253.692
	ARIMA(2,2,0)	1247.208	1261.164
	ARIMA(2,2,1)	1261.134	1278.579
	ARIMA(2,2,2)	1233.602	1254.535
	ARIMA(2,2,3)	1225.629	1250.052
	ARIMA(3,2,0)	1224.804	1242.249
	ARIMA(3,2,1)	1221.613	1242.546
	ARIMA(3,2,2)	1223.601	1248.023
	ARIMA(3,2,3)	1223.758	1251.669

Table 3.

Parameters of ARIMA models

Dataset	Best model	Parameters	Coef.	Std error	t statistic	p value
Confirmed cases	ARIMA(1, 2, 1)	MA(1)	− 0.7573	0.060	− 12.723	0.000
Death cases	ARIMA(3, 2, 1)	MA(1)	0.131	0.050	3.414	0.001

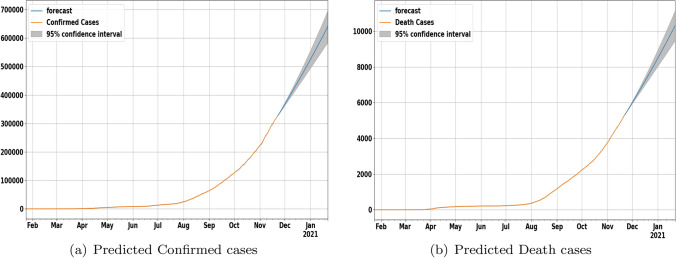
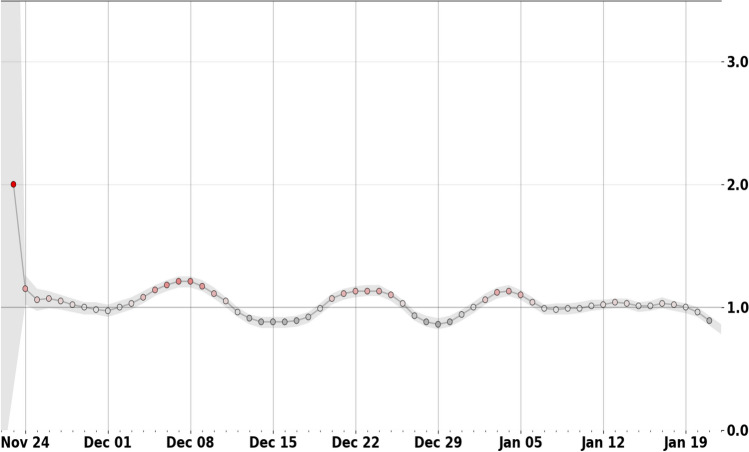
We generate the forecasted results of confirmed and death cases in Morocco for next 60 days starting from 22 November 2020, based on available data using ARIMA(1, 2, 1) model for forecasting confirmed cases and ARIMA(3, 2, 1) model for forecasting death cases. Figure 9a and b shows the 2 months forecasting of confirmed and death cases that fall between the ranges of 570,000–700,000 and 9,300–15,000, respectively, with confidence intervals (CI) of 95%, by 21 January 2021. On the other hand, in Fig. 10, we show the value of $R_t$ for the next 2 months using the predicted data generated by ARIMA(1, 2, 1) model. We can see that the spread of Covid-19 will continue to increase in the next 60 days. The observed values of $R_t$ are fluctuated between 0.9 and 1.3 with a mean value around 1, 2. This indicates that, during this period, the transmission of Covid-19 in Morocco will continue to expand in the next 2 months. Fortunately, the higher value of $R_t$ of 1.3 is not considered to be dramatic and therefore may give hope for controlling the disease.

Fig. 9.

Predicted cases in Morocco using ARIMA model up to 21 January 2021

Fig. 10.

Real-time $R_t$ using Moroccan predicted data produced by ARIMA approach

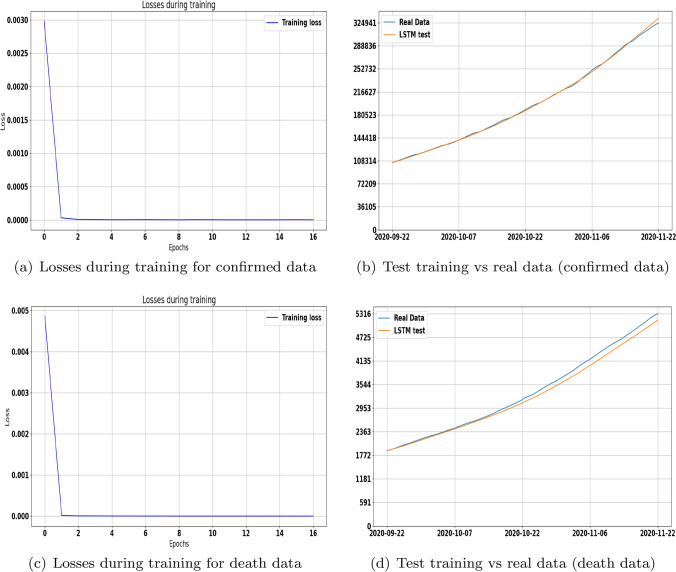
Now, it is time to analyze our second approach, which is the LSTM Networks model. We examined our forecasting model using mean square error (MSE) and optimized using the adaptive Gradient Algorithm. A line plot is created showing the mean squared error loss over the training epochs for both confirmed and death cases (Fig. 11a, c). We can see that the model converged very quickly to understand that mean squared error is a good match for LSTM learning this problem. In Fig. 11b, we show the results of test of training of our model versus real data from 22 September 2020 to 22 November 2020. We can observe that the test values mimic the actual values at the beginning of the period considered and deviate more and more as the period increases. Often, it will be difficult to be able to fit a good statistical model if the size of training data is not large enough. In this approach, we trained and tested our LSTM network on Moroccan Confirmed and death cases dataset.

Fig. 11.

Test and validation of LSTM model for confirmed and death cases using 20% of data

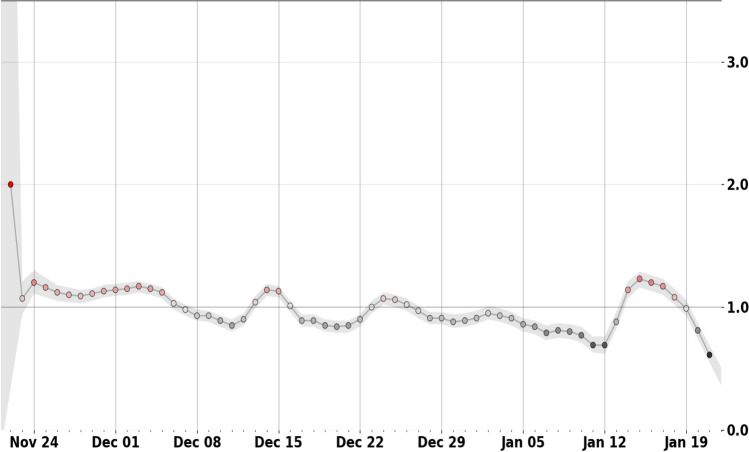
In Fig. 12, we show the number of confirmed and death cases using LSTM model approach up to 21 January 2021. From the figure, we can observe that the number of confirmed cases will continue to increase in the next 2 months. The LSTM model predicts an increase in confirmed and death cases, falling between the ranges of 450,000–715,000 and 5960–10,000, respectively, with confidence intervals (CI) of 95%, by 21 January 2021. Figure 13 shows the values of $R_t$ using the predicted output of LSTM network. Here we have observed that $R_t$ will follow a very slight decrease, reaching value around 0.7 at the end of December, with an increase at the mid of January 2021. This means that during this period, transmission of Covid-19 will continue to spread in Morocco, with a slight decrease in new confirmed cases at the end of December and an increase at the mid of January 2021.

Fig. 12.

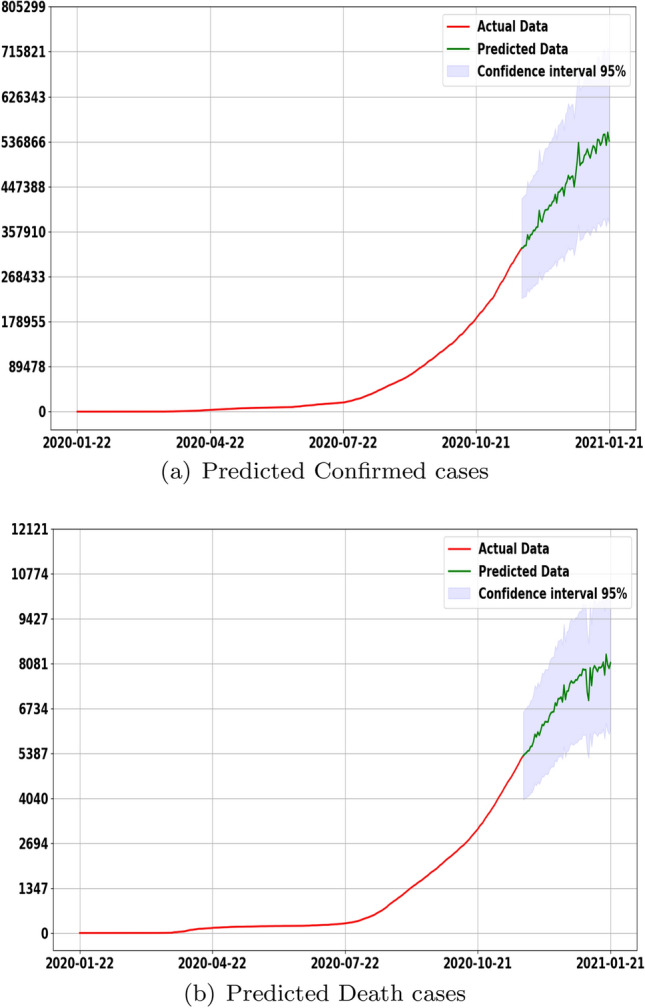
Forecast cases using LSTM model approach up to 21 January 2021

Fig. 13.

Real-time $R_t$ using Moroccan predicted data produced by LSTM model approach

By comparing the two prediction models, we see that both predict an increase in confirmed and death cases, with a clear difference in terms of predicted values. By comparing the prediction errors of the two models (Table 4), we tend to choose LSTM for the prediction. The LSTM models used in this paper are the most efficient to forecast the Covid-19 evolution in Morocco based on RMSE, MSLE, RMSLE, MAE and MAPE evaluation metrics. We think that LSTM have provided a better performance in predicting Covid-19 transmission and this is mainly due to the existence of a bigger dataset.

Table 4.

Evaluation metrics results

	RMSE	MSLE	RMSLE	MAE	MAPE
Confirmed cases
ARIMA(1, 2, 1) model	1862.10979	0.00006	0.00752	1287.30570	41.18312
LSTM model	795.29370	0.00002	0.00394	653.64891	40.98831
Death cases
ARIMA(3, 2, 1) model	108.95183	0.00069	0.02633	86.90287	37.46442
LSTM model	106.45369	0.00001	0.00274	7.20269	35.94537

Conclusion

The patterns from the current data reveals that prompt and effective measures taken by Moroccan authorities to contain the pandemic is showing a positive impact when compared with other countries. Based on the obtained data from the John Hopkins university and the Moroccan Health Ministry, we predicted the evolution of Covid-19 using the ARIMA and LSTM Models. Although the results generated by these models are quantitatively different, both models have predicted an important increase in confirmed cases and deaths in Morocco in the next 2 months. The forecasted results were assisted by estimating the value of effective reproduction number $R_t$. The finding indicates that the transmission of Covid-19 in Morocco will continue to expand in the next 2 months. Fortunately, both models predict that the situation will not considered to be dramatic and therefore may give hope for controlling the disease. Finally, we hope that these results will help the Moroccan government to better control and prevent the outbreak of Covid-19 in the future.

Funding

The Department of Higher Education and Scientific Research, the National Center for Scientific and Technical Research and Chouaib Doukkali University.

Declarations

Conflict of Interest

The authors have declared that no conflict of interest exists.