Abstract
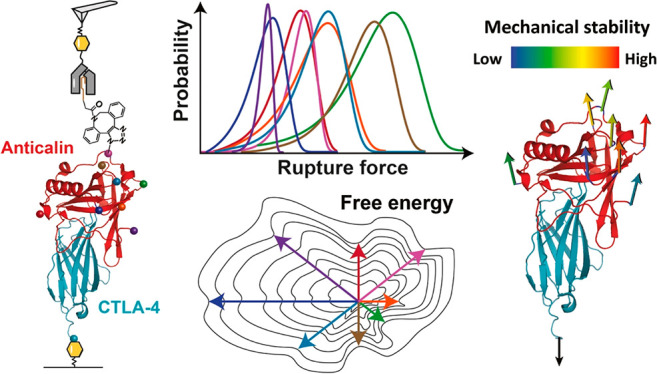
We used single-molecule AFM force spectroscopy (AFM-SMFS) in combination with click chemistry to mechanically dissociate anticalin, a non-antibody protein binding scaffold, from its target (CTLA-4), by pulling from eight different anchor residues. We found that pulling on the anticalin from residue 60 or 87 resulted in significantly higher rupture forces and a decrease in koff by 2–3 orders of magnitude over a force range of 50–200 pN. Five of the six internal anchor points gave rise to complexes significantly more stable than N- or C-terminal anchor points, rupturing at up to 250 pN at loading rates of 0.1–10 nN s–1. Anisotropic network modeling and molecular dynamics simulations helped to explain the geometric dependency of mechanostability. These results demonstrate that optimization of attachment residue position on therapeutic binding scaffolds can provide large improvements in binding strength, allowing for mechanical affinity maturation under shear stress without mutation of binding interface residues.
Keywords: atomic force microscopy, protein engineering, single-molecule force spectroscopy, mechanical anisotropy, click chemistry, Go̅-Martini model, PCA
Introduction
Mechanical anisotropy refers to the various mechanical responses that manifest when force is applied to macromolecules from different directions. For example, double stranded DNA/RNA double helices and hairpins1−4 can be mechanically unzipped at low forces (∼10–20 pN) where the base paired hydrogen bonds are broken in series or sheared apart at high forces (>50 pN) where the hydrogen bonds are broken in parallel. Folded protein domains also exhibit different mechanical responses depending on the pulling geometry, as was shown for globular domains including GFP,5 ubiquitin,6 E2lip3,7 and GB1.8 Structure-based heuristics based on α-helix vs β-strand content are available for predicting the mechanical stability of folded domains stretched between their N- and C-termini,9−12 and conserved structural motifs referred to as mechanical clamps are known to impart mechanostability to folded domains.13−15 A recent study also reported application of force from an internal sequence position to transmembrane bacteriorhodopsin to dislodge transmembrane helices in a defined order from the membrane and quantify intermediate folding states.16
For receptor–ligand binding interfaces, unbinding mechanics is known to depend on whether a receptor is anchored from the N- or C-terminus, as was shown for cohesin–dockerin and streptavidin–biotin systems.17−19 Differences in shear vs zip geometry have also been reported for protein-based coiled coils.20 However, for protein–protein interactions, no general heuristics are available. It remains unclear how anchor point geometry modulates the binding strength of protein–protein complexes. Single-molecule AFM force spectroscopy (AFM-SMFS) provides a powerful tool to study the response of protein–protein interaction to forces, and state-of-the-art bioconjugate methods can control for anchor point geometry of receptor–ligand systems and measure a wide range of forces.21−23
For applications in targeted drug delivery using nanoparticles, liposomes, or engineered viruses, the shear force that a receptor can withstand while remaining bound to its target is a potentially valuable optimization parameter. One current trend in biotherapeutics is to move beyond full length IgG antibodies toward development of non-antibody scaffolds that are smaller in size and easier to manufacture.24,25 Anticalins are a class of non-antibody scaffolds sharing homologous backbone structures (Figure S1). Their ligand binding loops can be engineered to specifically bind diverse molecular targets, including proteins, peptides, and small molecules.26−28 One target, cytotoxic T-lymphocyte antigen 4 (CTLA-4), is involved in negative regulation of T-cell immune function and maintenance of immune homeostasis29,30 and represents an important target for cancer immunotherapy.
Here, we used AFM-SMFS to study the response of an engineered anticalin bound to its target (CTLA-4) and mechanically dissociated under a variety of pulling geometries. Our new experimental methodology was combined with molecular dynamics (MD) simulations, which provided mechanistic insight into the unbinding pathways of the complex under different loading geometries. We found that pulling from central positions results in highly stable cooperative interactions that require high forces to dissociate, while pulling from the termini results in more plastic molecular deformation and unbinding at low forces. These observations establish a mechanical analogue to conventional affinity maturation. Instead of requiring mutagenesis and screening, our mechanical affinity maturation paradigm relies on informed selection of anchor points for attachment to surfaces or molecular cargo. We show that leveraging molecular level mechanical properties can provide significant improvements in binding strength of non-antibody scaffolds under exposure to shear forces.
Results
Selection of Anchor Points, Protein Expression, and AFM Measurement Setup
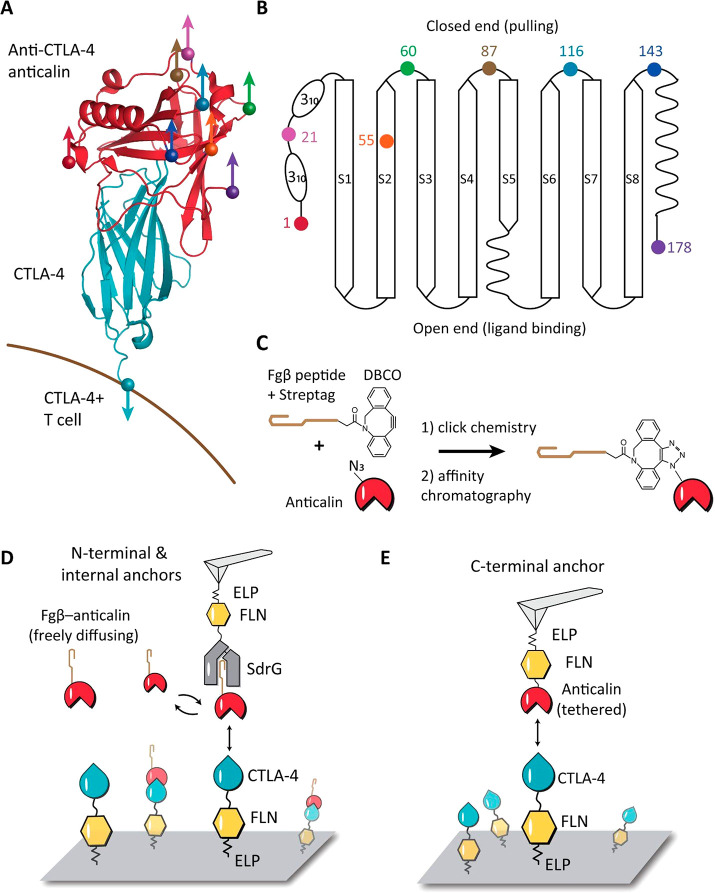
The anticalin targeting CTLA-4 was derived from human neutrophil gelatinase-associated lipocalin (NGAL). The structure of anticalin in complex with the extracellular domain of CTLA-4 is shown in Figure 1A (PDB code 3BX7).26 CTLA-4 is a human T cell receptor with the C-terminus of the extracellular domain anchored to the cell surface. As shown in Figure S1, the structure of anticalin is highly homologous to other previously reported lipocalin folds,31−35 comprising a β-barrel formed by eight antiparallel β-strands, flanked by helical regions at the N- and C-termini.36,37 The core β-barrel fold has a ligand-binding open end and a more compacted closed end. We selected eight anchor points on anticalin that spanned the entire protein sequence length. These anchor points were the N- and C- termini (residues 1 and 178), five residues located along flexible linkers connecting the β-strands (residues 21, 60, 87, 116, and 143), and one located within β-strand S2 (residues 55). All internal anchor points were located at the closed end of the barrel (Figure 1A and B), while N- and C- terminal anchor points were located toward the open end closer to the binding interface.
Figure 1.
Anchor point selection and AFM-SMFS measurement setups. (A) Structure of CTLA-4 in complex with anticalin (PDB code 3BX7). Anchor points on the anticalin are shown as colored spheres. The anchor point on CTLA-4 is fixed at the C-terminus, mimicking the natural tethering geometry on the cell surface. (B) Anticalin has a central β-barrel, consisting of eight antiparallel β-strands (S1–S8) connected by short flexible linkers. The anchor points shown as colored dots were chosen at the closed end of the β-barrel to avoid interference with the binding interface. (C) Bioorthogonal conjugation of a fibrinogen β (Fgβ) peptide to the anticalin. The residue at the selected anchor point was replaced by p-azido-phenylalanine using amber suppression to introduce an azide group. The azide was covalently linked with a synthetic peptide comprising Fgβ-StrepTag and a C-terminal DBCO group using click chemistry. (D) AFM measurement setup for testing N-terminal and internal anchor points with freely diffusing Fgβ-anticalin. Anticalin conjugated with Fgβ was added to the measurement buffer to a final concentration of 1 μM. SdrG-FLN-ELP-ybbr was immobilized on the AFM tip, and the ligand (CTLA-4-FLN-ELP-ybbr) was immobilized on the glass surface covalently via a ybbr tag. (E) AFM measurement setup with tethered anticalin for probing the C-terminal anticalin anchor point. Anticalin-FLN-ELP-ybbr was immobilized on the cantilever, and CTLA4-FLN-ELP-ybbr was immobilized on the glass surface.
Each anchor point on the anticalin molecule corresponds to a precisely defined pulling geometry in the AFM measurements. In order to attach the AFM tip to anticalin through a given internal anchor point (residues 21, 55, 60, 87, 116, and 143), we combined non-canonical amino acid (NCAA) incorporation, click chemistry, and an AFM-SMFS measurement setup with freely diffusing receptor molecules.18,23 As shown in Figure 1C, the residue at the selected anchor point was replaced by a p-azido-l-phenylalanine using amber suppression to introduce an azide group.38 A synthetic peptide comprising the N-terminal fibrinogen β (Fgβ) peptide, Strep-tag, and C-terminus dibenzocyclooctyne (DBCO) group was subsequently conjugated to the azide group on anticalin using copper-free click chemistry.39 The reaction product was purified with size-exclusion and Strep-trap columns to remove excess peptide and unreacted anticalin. Successful conjugation of the peptide increased the molecular weight of anticalin by 3 kDa, as confirmed by SDS-PAGE and mass spectrometry (Figure S2). Each anticalin with Fgβ clicked onto a given residue was expressed and purified and measured in separate AFM experiments.
The AFM experimental setup with freely diffusing or immobilized anticalin is shown in Figure 1D,E. SD-repeat protein G (SdrG) from S. epidermidis which binds Fgβ was cloned into the polyprotein SdrG-FLN-ELP-ybbr and immobilized on the AFM tip. For the C-terminal anchor point, CTLA-4 was cloned to the N-terminus of a polyprotein, followed by an FLN unfolding fingerprint domain,40 an elastin-like peptide (ELP) elastic linker, and a ybbr tag at the C-terminus. The ybbr tag enabled site-specific covalent surface immobilization of the polyprotein41 to the glass surface.
For N-terminal and internal anchor points, we adapted a previously reported freely diffusing ligand system for AFM measurements.18 The anticalin with Fgβ peptide conjugated to the selected anchor point was added to the measurement buffer to a final concentration of ∼1 μM, which saturated immobilized CTLA-4 on the surface. SdrG on the cantilever was brought to the surface, forming a three-member complex consisting of cantilever-immobilized SdrG bound to Fgβ-anticalin, which was itself bound to CTLA-4.
The SdrG:Fgβ complexes can withstand forces as high as 2 nN,42 and the significantly weaker anticalin:CTLA-4 complex was the first to break when the cantilever was retracted, leaving the Fgβ conjugated anticalin on the cantilever. The moderate equilibrium affinity of SdrG bound to Fgβ (KD ∼ 400 nM)43 enabled rapid exchange of anticalin molecules on the cantilever, preventing the AFM tip from clogging. In addition, the DBCO conjugated Fgβ peptide is more convenient to synthesize compared to other high-force handles such as cohesin–dockerin systems. Tens of thousands of approach–retract cycles were performed in this format over a range of pulling speeds from 100 to 800 nm s–1 to build up large statistics. In this format, the cantilever and surface molecules are always freshly probed, so the refoldability of the cantilever-borne molecules does not play a role.
Different Pulling Geometries Gave Rise to Diverse Unbinding Energy Profiles
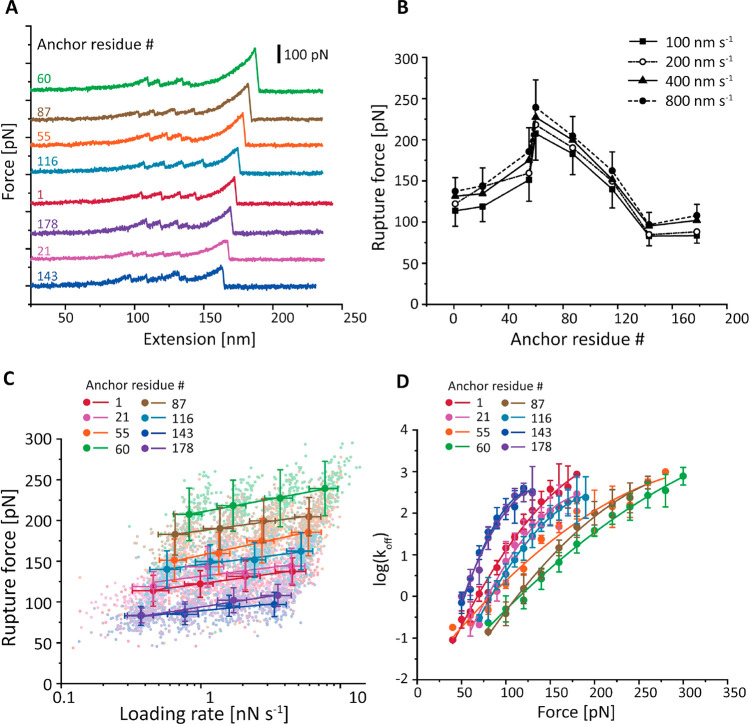
In a typical AFM measurement of 12 h, ∼10,000 force–extension curves were recorded and transformed into contour length space using a freely rotating chain (FRC) elasticity model.44 Curves were filtered for the two-step unfolding pattern and 32 nm contour length increment of two FLN fingerprint domains.40 Example force–extension curves of different pulling geometries are shown in Figures 2A and S3. Intermediate unfolding events were observed in ∼9% of selected force curves, including all eight pulling geometries (Figure S3). We aligned the contour length histograms of all of the selected curves using cross-correlation analysis. The resulting superposition histogram (Figure S4)45,46 showed contour length increments corresponding to the two FLN domains (32 nm each).
Figure 2.
Dependency of anticalin:CTLA-4 complex stability on anticalin anchor position. (A) Example AFM force–extension traces measured with eight different pulling geometries. Each trace shows unfolding of two FLN fingerprint domains and rupture of the anticalin:CTLA-4 complex for a given anchor residue on anticalin. (B) Most probable rupture forces of the anticalin:CTLA-4 complex at various pulling speeds were plotted against the anchor residue number on anticalin. Error bars represent the standard deviation of rupture forces measured at 100 nm s–1 (minus) and 800 nm s–1 (plus) pulling speeds. (C) Most probable rupture forces measured at different pulling speeds were plotted against the logarithm of average loading rate and fitted linearly to extract the zero-force off rate k0 and distance to the transition state Δx⧧. Error bars represent the standard deviation of rupture forces and loading rates. (D) The force-dependent off rate of the anticalin:CTLA-4 complex was plotted against force and fitted using eq 6 (see the Supporting Information) to extract k0, Δx⧧, and ΔG⧧. Error bars represent the standard deviation of off rates measured at four different pulling speeds.
Rupture forces of the anticalin:CTLA-4 complex for each Fgβ anchoring residue number were measured in separate AFM experiments at four pulling speeds from 100 to 800 nm s–1. The forces required to dissociate anticalin from CTLA-4 were plotted as histograms, as shown in Figure S5. The histograms were fitted to extract the most probable rupture forces, which were plotted against the anchor residue number on anticalin (Figure 2B). It is clear from the plot that the mechanical stability of the anticalin:CTLA-4 complex is highly dependent on the anticalin anchor residue number. N- and C-terminal pulling points were among the lowest in stability, rupturing at 100–125 pN, and the stability significantly rose for anchor points located near the middle of the protein sequence. Peak stability (∼225 pN) was achieved when anticalin was anchored at residue 60, between β-strands S2 and S3.
We used the Bell–Evans (BE)47,48 and Dudko–Hummer–Szabo (DHS)49,50 models to estimate energy landscape parameters for each pulling geometry. As shown in Figure 2C, the most probable rupture forces were linearly fitted against the logarithm of average loading rate at a given pulling speed to extract the zero force off rate (k0) and the distance to the energy barrier (Δx⧧) using the BE model. We next used the DHS model (Figure 2D) to transform the rupture force histograms into force-dependent off rates (eq 4, see the Supporting Information) and fitted the resulting plot using eq 6 to obtain the k0, Δx⧧, and energy barrier height (ΔG⧧). The parameters estimated from both models are listed in Table 1.
Table 1. Unbinding Energy Landscape Parameters of the Anticalin:CTLA-4 Complex under Different Pulling Geometries.
| anchor point on anticalin | log(k0) (DHS) | log(k0) (BE) | Δx⧧ [nm] (DHS) | Δx⧧ [nm] (BE) | ΔG⧧ [kBT] (DHS) |
|---|---|---|---|---|---|
| 1 | –3.0 ± 0.2 | –3.1 ± 0.3 | 0.50 ± 0.05 | 0.40 ± 0.03 | 16.8 ± 0.6 |
| 21 | –4.2 ± 0.5 | –4 ± 3 | 0.63 ± 0.09 | 0.4 ± 0.2 | 18 ± 1 |
| 55 | –2.0 ± 0.3 | –2.4 ± 0.3 | 0.27 ± 0.04 | 0.26 ± 0.02 | 13.9 ± 0.9 |
| 60 | –2.7 ± 0.2 | –4.7 ± 0.2 | 0.25 ± 0.02 | 0.30 ± 0.01 | 17 ± 1 |
| 87 | –3.7 ± 0.3 | –6.0 ± 0.6 | 0.38 ± 0.03 | 0.41 ± 0.03 | 17.8 ± 0.4 |
| 116 | –4.0 ± 0.1 | –5 ± 1 | 0.57 ± 0.02 | 0.44 ± 0.07 | 17.2 ± 0.2 |
| 143 | –4.4 ± 0.6 | –3 ± 1 | 1.0 ± 0.1 | 0.6 ± 0.1 | 18 ± 1 |
| 178 | –3.8 ± 0.6 | –1.6 ± 0.4 | 0.8 ± 0.1 | 0.36 ± 0.04 | 17 ± 1 |
Based on Figure 2 and Table 1, it is clear that the complex crossed unbinding energy barriers with significantly different heights and shapes when pulled from different anchor points. Depending on the anchor residue number, the kinetic off rate koff at a given force can vary by 2–3 orders of magnitude (Figure 2D, 100 pN). Both DHS and BE models extracted short Δx⧧ values for anchor residue 60 (DHS, 0.25 ± 0.02 nm; BE, 0.30 ± 0.01 nm), indicating a short steep energy barrier when tension was applied through the middle of the β-barrel on anticalin. In addition, we applied an anisotropic network model (ANM) to calculate the effective spring constants between different pairs of residues51,52 in the protein complex and studied the relationship between the spring constants and energy profile parameters (see Figures S6 and S7, Table S1, and Supplementary Note 2).
To test equilibrium behavior, we measured the dissociation constant between CTLA-4 and three anticalin mutants using microscale thermophoresis (MST). As shown in Table S2, although the anticalin E60AzF and E143AzF mutants have distinct responses to force, they have a similar affinity toward CTLA-4 at equilibrium. The exception was the I55AzF mutant, which has a slightly lower affinity for CTLA-4. Residue 55 is on a β-strand S2 of the anticalin β-barrel structure. Mutation at that site to pAzF and conjugation to peptide or fluorescent dye slightly destabilized the anticalin:CTLA-4 complex, resulting in a lower energy barrier in SMFS measurement (see Table 1) as well as a lower equilibrium affinity in bulk experiments compared to other anticalin constructs.
Go̅-Martini Model Provides Insights into Deformation Pathways
Next, we analyzed the anticalin:CTLA-4 system using a coarse grained model that combined the Martini force field53,54 with a structure-based approach, the so-called Go̅-like description that takes into account all native contacts in order to maintain secondary and tertiary structures in the protein. This model has been used in previous studies on the mechanical stability of single protein domains55−57 and protein aggregates.58−61 The combined Go̅-Martini model now allows analysis of large conformational changes in proteins, protein assembly in membranes,62 and the characterization of protein mechanical properties.63,64
Here we applied Go̅-Martini simulations to the description of the anticalin:CTLA-4 dissociation under different pulling geometries. The initial energetic parametrization by the Martini force field using the PDB structural information on the complex system failed to reproduce the pulling-geometry-dependent rupture force profile as obtained by SMFS (Figure S8). This indicates an incomplete representation of the energetics at the interface of complexes, a known issue in the Martini force field.65 We therefore utilized the experimental data to calibrate the Martini model description of protein binding interfaces (see Supplementary Note 4). We then analyzed the trajectories from the calibrated model to help explain the observed differences in binding strength as a function of anchor point.
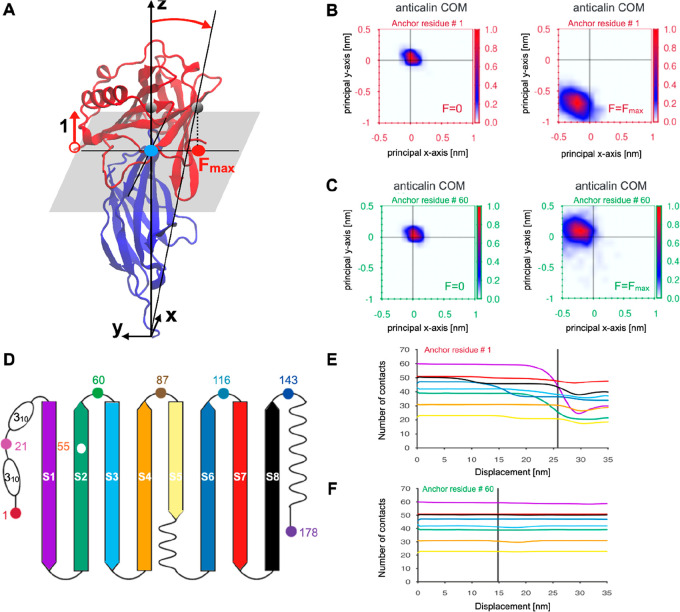
The first computational analysis was to monitor the center-of-mass (COM) of anticalin during the pulling simulations (see Figure 3A). Panels B and C of Figure 3 compare the COM position of anticalin at zero force and at the maximal force observed in the simulation (Fmax) for anticalin anchor residues 1 (low stability) and 60 (high stability). For anchor residue 1, at Fmax, the COM of anticalin was clearly shifted in the negative y direction by ∼0.75 nm and in the negative x direction by ∼0.2 nm. However, when pulling anticalin from residue 60, the anticalin COM stayed close to its original position, translating slightly in the positive y (∼0.1 nm) and negative x directions (∼0.2 nm). These differences suggest a scenario where pulling from the N-terminus results in a peeling behavior of anticalin while pulling from position 60 results in a well-aligned system that cooperatively breaks without xy translation. Analysis of the xy translation of the anticalin COM was carried out for each anchor residue under pulling simulations (Figure S10). These plots show that the COM translation behavior is distinct for each anchor point. The lowest stability anchor point tested experimentally (residue no. 143) shows a broad distribution of translation values for anticalin COMs at Fmax, suggesting significant deformation of the complex and rearrangement under tension for that anchor residue.
Figure 3.
Molecular characterization of the Go̅-Martini trajectory for the anticalin:CTLA-4 complex at different pulling geometries. (A) The translation of the anticalin COM for anchor residue 1 under a force applied along the z direction. The CTLA-4 was used as a reference system to define the normal plane. The blue circle denotes the starting anticalin COM position and the red one its translation along the −y direction at Fmax. (B and C) The relative translation of the anticalin COM with respect to the CTLA-4 molecule for two anticalin anchor residues 1 (B) and 60 (C) at F = 0 and F = Fmax. Color bars indicate the probability of finding the COM in a given position along the X–Y plane which is perpendicular to the z direction of symmetry of the complex. (D) The β-sheet structure of the anticalin and its color representation. (E and F) The intrachain native contact (NC) evolution for anticalin computed for each β-sheet during the pulling process. Severe loss of contacts affects the anticalin for pulling residue 1 (E), whereas almost no loss of NC is reported for anchor residue 60 (F). The color line is in agreement with panel D.
The second computational analysis was to analyze the loss of native contacts (NCs) in different regions of anticalin. When pulling from residue 1, NCs were steadily lost in N-terminal β-strands S1, S2, S3, as well as S6 prior to rupture (Figure 3E). However, when pulling from residue 60, few to no intramolecular NCs were lost in anticalin (Figure 3F). The anticalin COM shift is more pronounced when several anticalin β-sheets lose some of the stabilizing NCs (Figure S11). Our analysis of the intrachain NCs suggests that breaking NCs in the β-strands makes the anticalin more flexible and its COM samples new positions through different pathways. Furthermore, pathways involving partial unfolding processes and severe loss of NCs were observed for anchor residues 1 and 21 (Figure S11). The NCs on the binding interface also behave differently depending on the pulling geometry (Table S4 and Figure S12). The interface NCs were lost at different rates with different pulling geometries, and the number of remaining interface NCs at Fmax (immediately prior to rupture) varies across the simulations and shows positive correlation (p < 0.05) with the rupture force measured both in vitro and in silico (Figure S13). In addition, a few non-native contacts (about five, see Figure S12) are established after the rupture. However, the new protein–protein interactions established during the dissociation trajectory were not strong enough to maintain the bound complex. Based on the simulation analyses, we conclude that the persistence of the original set of interface NCs, the translation of the anticalin COM, and the loss of β-strand structure explain the geometric dependency of the mechanical properties of the complex.
Discussion
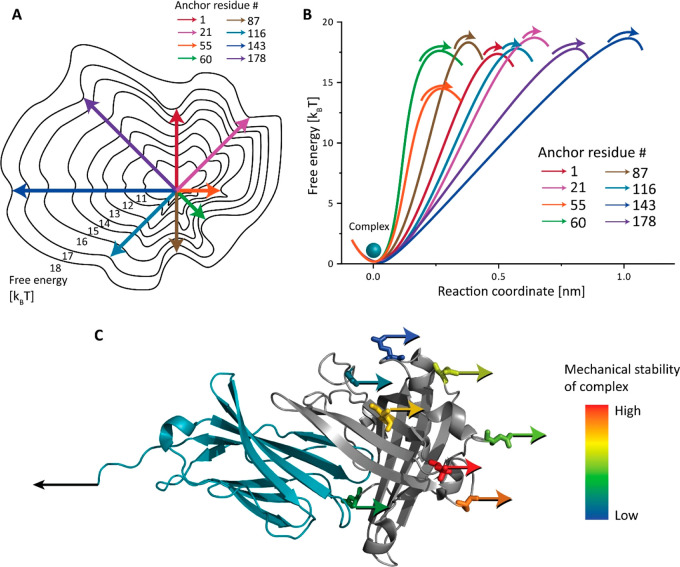
We reported an AFM-SMFS study where we covalently clicked a peptide handle onto internal residue positions of the non-antibody scaffold anticalin/lipocalin and measured the rupture forces of anticalin:CTLA-4 complexes using an AFM setup with freely diffusing molecules. We observed how the anticalin:CTLA-4 complex responds to external forces applied from different directions and found a clear trend in stability. When pulling anticalin from residue positions near the middle of the sequence (e.g., residues 60 and 87), the complex withstood high forces up to 200 pN which were ∼2× higher than the least mechanically stable anchor points located toward the termini (residues 1, 143, and 178). Panels A and B of Figure 4 illustrate the complex dissociation energy landscape. The unbinding pathways have energy barriers with different shapes and heights. It is worth noting that the energy barrier of the most mechanostable pulling geometry (anchor residue 60) is not the highest, but the short Δx⧧ contributed to the high resistance to external force. On the contrary, although the pulling geometry with anchor residue 143 has the highest energy barrier, the long Δx⧧ made it the least mechanostable geometry. Residue 55 has a unique energy landscape with the lowest energy barrier and a short Δx⧧, giving rise to a moderate rupture force. Therefore, the mechanical stability of the complex is determined by an interplay between the height and the shape of unbinding energy barriers which is dependent on the pulling point.
Figure 4.
Depictions of the anticalin:CTLA-4 complex unbinding energy landscape as a function of molecular pulling geometry. (A) Energy landscape depiction where anchor point residues are represented as compass directions. Under a constrained pulling geometry, the complex is forced to traverse different unbinding pathways across the energy landscape. These different paths give rise to energy barriers with diverse heights and shapes. (B) 1D depiction of unbinding energy barrier heights and positions calculated using the DHS model for each pulling geometry (see Table 1). (C) Anchor points on the anticalin colored based on mechanical stability of the complex pulled through that position. The most and least mechanostable anchor points on the anticalin are residues 60 (red) and 143 (dark blue), respectively.
The computational approach for investigating the mechanical stability of the anticalin:CTLA-4 complex under different pulling directions was parametrized by tuning the interface energy through an additional contact, which was not present in our initial Go̅ contact map obtained from the PDB structure. This rendered the Go̅-Martini approach a very predictable model for the study of large conformational changes of protein complexes at much cheaper computational cost than in regular SMD simulation and allowed larger sampling of pathways. Our computational study explained the observed trends in stability in terms of translations of anticalin COM and loss of NCs in anticalin.
Our measurements and simulations demonstrate that the mechanical stability of protein–protein interactions can be tuned over a wide dynamic range of stabilities by precisely controlling the loading geometry, and these changes do not alter the equilibrium binding properties. This suggests a new paradigm for mechanical affinity maturation of non-antibody scaffolds by correctly choosing the anchor points. Such an approach could be particularly beneficial for targeting nano- and microparticles or imaging probes which can exert shear forces onto binding interfaces.
Acknowledgments
This work was supported by the University of Basel, ETH Zurich, an ERC Starting Grant (MMA-715207), the NCCR in Molecular Systems Engineering, and the Swiss National Science Foundation (Project 200021_175478). The authors thank Peter Schultz for providing the pEVOL-pAzF plasmid and Lloyd Ruddock for providing the pMJS205 plasmid. The authors thank Timothy Sharpe and the Biophysics Facility of Biozentrum, University of Basel, for the help with affinity measurements using MST. A.B.P. acknowledges financial support from the National Science Centre, Poland, under Grant No. 2017/26/D/NZ1/00466 and the grant MAB PLUS/11/2019 from the Foundation for Polish Science. Computational resources were supported by the PL-GRID infrastructure, the Jülich Supercomputing Centre on the supercomputer JURECA at Forschungszentrum Jülich, and the TUL Computing & Information Services Center infrastructure.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c03584.
Materials and Methods, Figures S1−S13 including additional experimental and computational data analysis, Tables S2−S4, Supplementary Notes 1−4 including amino acid sequence information and AddGene accession codes (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Krautbauer R.; Rief M.; Gaub H. E. Unzipping DNA Oligomers. Nano Lett. 2003, 3 (4), 493–496. 10.1021/nl034049p. [DOI] [Google Scholar]
- Rief M.; Clausen-Schaumann H.; Gaub H. E. Sequence-Dependent Mechanics of Single DNA Molecules. Nat. Struct. Biol. 1999, 6 (4), 346–349. 10.1038/7582. [DOI] [PubMed] [Google Scholar]
- Woodside M. T.; Behnke-Parks W. M.; Larizadeh K.; Travers K.; Herschlag D.; Block S. M. Nanomechanical Measurements of the Sequence-Dependent Folding Landscapes of Single Nucleic Acid Hairpins. Proc. Natl. Acad. Sci. U. S. A. 2006, 103 (16), 6190–6195. 10.1073/pnas.0511048103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bockelmann U.; Essevaz-Roulet B.; Heslot F. Molecular Stick-Slip Motion Revealed by Opening DNA with Piconewton Forces. Phys. Rev. Lett. 1997, 79 (22), 4489–4492. 10.1103/PhysRevLett.79.4489. [DOI] [Google Scholar]
- Dietz H.; Berkemeier F.; Bertz M.; Rief M. Anisotropic Deformation Response of Single Protein Molecules. Proc. Natl. Acad. Sci. U. S. A. 2006, 103 (34), 12724–12728. 10.1073/pnas.0602995103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrion-Vazquez M.; Li H.; Lu H.; Marszalek P. E.; Oberhauser A. F.; Fernandez J. M. The Mechanical Stability of Ubiquitin Is Linkage Dependent. Nat. Struct. Mol. Biol. 2003, 10 (9), 738–743. 10.1038/nsb965. [DOI] [PubMed] [Google Scholar]
- Brockwell D. J.; Paci E.; Zinober R. C.; Beddard G. S.; Olmsted P. D.; Smith D. A.; Perham R. N.; Radford S. E. Pulling Geometry Defines the Mechanical Resistance of a β-Sheet Protein. Nat. Struct. Mol. Biol. 2003, 10 (9), 731–737. 10.1038/nsb968. [DOI] [PubMed] [Google Scholar]
- Li Y. D.; Lamour G.; Gsponer J.; Zheng P.; Li H. The Molecular Mechanism Underlying Mechanical Anisotropy of the Protein GB1. Biophys. J. 2012, 103 (11), 2361–2368. 10.1016/j.bpj.2012.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes M. L.; Dougan L. The Physics of Pulling Polyproteins: A Review of Single Molecule Force Spectroscopy Using the AFM to Study Protein Unfolding. Rep. Prog. Phys. 2016, 79 (7), 076601. 10.1088/0034-4885/79/7/076601. [DOI] [PubMed] [Google Scholar]
- Hoffmann T.; Dougan L. Single Molecule Force Spectroscopy Using Polyproteins. Chem. Soc. Rev. 2012, 41 (14), 4781–4796. 10.1039/c2cs35033e. [DOI] [PubMed] [Google Scholar]
- Hoffmann T.; Tych K. M.; Hughes M. L.; Brockwell D. J.; Dougan L. Towards Design Principles for Determining the Mechanical Stability of Proteins. Phys. Chem. Chem. Phys. 2013, 15 (38), 15767–15780. 10.1039/c3cp52142g. [DOI] [PubMed] [Google Scholar]
- Crampton N.; Brockwell D. J. Unravelling the Design Principles for Single Protein Mechanical Strength. Curr. Opin. Struct. Biol. 2010, 20 (4), 508–517. 10.1016/j.sbi.2010.05.005. [DOI] [PubMed] [Google Scholar]
- Valbuena A.; Oroz J.; Hervás R.; Vera A. M.; Rodríguez D.; Menéndez M.; Sulkowska J. I.; Cieplak M.; Carrión-Vázquez M. On the Remarkable Mechanostability of Scaffoldins and the Mechanical Clamp Motif. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (33), 13791–13796. 10.1073/pnas.0813093106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdorfer T.; Bernardi R.; Meinhold A.; Ott W.; Luthey-Schulten Z.; Nash M. A.; Gaub H. E. Combining in Vitro and in Silico Single Molecule Force Spectroscopy to Characterize and Tune Cellulosomal Scaffoldin Mechanics. J. Am. Chem. Soc. 2017, 139 (49), 17841–17852. 10.1021/jacs.7b07574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sikora M.; Sułkowska J. I.; Cieplak M. Mechanical Strength of 17,134 Model Proteins and Cysteine Slipknots. PLoS Comput. Biol. 2009, 5 (10), e1000547. 10.1371/journal.pcbi.1000547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson D. R.; Uyetake L.; Perkins T. T. Membrane-Protein Unfolding Intermediates Detected with Enhanced Precision Using a Zigzag Force Ramp. Biophys. J. 2020, 118 (3), 667–675. 10.1016/j.bpj.2019.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoeler C.; Bernardi R. C.; Malinowska K. H.; Durner E.; Ott W.; Bayer E. A.; Schulten K.; Nash M. A.; Gaub H. E. Mapping Mechanical Force Propagation through Biomolecular Complexes. Nano Lett. 2015, 15 (11), 7370–7376. 10.1021/acs.nanolett.5b02727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sedlak S. M.; Schendel L. C.; Melo M. C. R.; Pippig D. A.; Luthey-Schulten Z.; Gaub H. E.; Bernardi R. C. Direction Matters: Monovalent Streptavidin/Biotin Complex under Load. Nano Lett. 2019, 19 (6), 3415–3421. 10.1021/acs.nanolett.8b04045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sedlak S. M.; Schendel L. C.; Gaub H. E.; Bernardi R. C. Streptavidin/biotin: Tethering Geometry Defines Unbinding Mechanics. Sci. Adv. 2020, 6 (13), eaay5999. 10.1126/sciadv.aay5999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goktas M.; Luo C.; Sullan R. M. A.; Bergues-Pupo A. E.; Lipowsky R.; Vila Verde A.; Blank K. G. Molecular Mechanics of Coiled Coils Loaded in the Shear Geometry. Chem. Sci. 2018, 9 (20), 4610–4621. 10.1039/C8SC01037D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ott W.; Jobst M. A.; Schoeler C.; Gaub H. E.; Nash M. A. Single-Molecule Force Spectroscopy on Polyproteins and Receptor–ligand Complexes: The Current Toolbox. J. Struct. Biol. 2017, 197 (1), 3–12. 10.1016/j.jsb.2016.02.011. [DOI] [PubMed] [Google Scholar]
- Sedlak S. M.; Bauer M. S.; Kluger C.; Schendel L. C.; Milles L. F.; Pippig D. A.; Gaub H. E. Monodisperse Measurement of the Biotin-Streptavidin Interaction Strength in a Well-Defined Pulling Geometry. PLoS One 2017, 12 (12), e0188722. 10.1371/journal.pone.0188722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang B.; Liu Z.; Liu H.; Nash M. A. Next Generation Methods for Single-Molecule Force Spectroscopy on Polyproteins and Receptor-Ligand Complexes. Front Mol. Biosci 2020, 7, 85. 10.3389/fmolb.2020.00085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bedford R.; Tiede C.; Hughes R.; Curd A.; McPherson M. J.; Peckham M.; Tomlinson D. C. Alternative Reagents to Antibodies in Imaging Applications. Biophys. Rev. 2017, 9 (4), 299–308. 10.1007/s12551-017-0278-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards D. A. Exploring Alternative Antibody Scaffolds: Antibody Fragments and Antibody Mimics for Targeted Drug Delivery. Drug Discovery Today: Technol. 2018, 30, 35–46. 10.1016/j.ddtec.2018.10.005. [DOI] [PubMed] [Google Scholar]
- Schönfeld D.; Matschiner G.; Chatwell L.; Trentmann S.; Gille H.; Hülsmeyer M.; Brown N.; Kaye P. M.; Schlehuber S.; Hohlbaum A. M.; Skerra A. An Engineered Lipocalin Specific for CTLA-4 Reveals a Combining Site with Structural and Conformational Features Similar to Antibodies. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (20), 8198–8203. 10.1073/pnas.0813399106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggenstein E.; Eichinger A.; Kim H.-J.; Skerra A. Structure-Guided Engineering of Anticalins with Improved Binding Behavior and Biochemical Characteristics for Application in Radio-Immuno Imaging And/or Therapy. J. Struct. Biol. 2014, 185 (2), 203–214. 10.1016/j.jsb.2013.03.009. [DOI] [PubMed] [Google Scholar]
- Renders L.; Budde K.; Rosenberger C.; van Swelm R.; Swinkels D.; Dellanna F.; Feuerer W.; Wen M.; Erley C.; Bader B.; et al. First-in-Human Phase I Studies of PRS-080# 22, a Hepcidin Antagonist, in Healthy Volunteers and Patients with Chronic Kidney Disease Undergoing Hemodialysis. PLoS One 2019, 14 (3), e0212023. 10.1371/journal.pone.0212023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K. M.; Chuang E.; Griffin M.; Khattri R.; Hong D. K.; Zhang W.; Straus D.; Samelson L. E.; Thompson C. B.; Bluestone J. A. Molecular Basis of T Cell Inactivation by CTLA-4. Science 1998, 282 (5397), 2263–2266. 10.1126/science.282.5397.2263. [DOI] [PubMed] [Google Scholar]
- Walker L. S. K.; Sansom D. M. The Emerging Role of CTLA4 as a Cell-Extrinsic Regulator of T Cell Responses. Nat. Rev. Immunol. 2011, 11 (12), 852–863. 10.1038/nri3108. [DOI] [PubMed] [Google Scholar]
- Goetz D. H.; Holmes M. A.; Borregaard N.; Bluhm M. E.; Raymond K. N.; Strong R. K. The Neutrophil Lipocalin NGAL Is a Bacteriostatic Agent That Interferes with Siderophore-Mediated Iron Acquisition. Mol. Cell 2002, 10 (5), 1033–1043. 10.1016/S1097-2765(02)00708-6. [DOI] [PubMed] [Google Scholar]
- Deuschle F.-C.; Morath V.; Schiefner A.; Brandt C.; Ballke S.; Reder S.; Steiger K.; Schwaiger M.; Weber W.; Skerra A. Development of a High Affinity Anticalin® Directed against Human CD98hc for Theranostic Applications. Theranostics 2020, 10 (5), 2172–2187. 10.7150/thno.38968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebauer M.; Schiefner A.; Matschiner G.; Skerra A. Combinatorial Design of an Anticalin Directed against the Extra-Domain B for the Specific Targeting of Oncofetal Fibronectin. J. Mol. Biol. 2013, 425 (4), 780–802. 10.1016/j.jmb.2012.12.004. [DOI] [PubMed] [Google Scholar]
- Korndörfer I. P.; Beste G.; Skerra A. Crystallographic Analysis of an “Anticalin” with Tailored Specificity for Fluorescein Reveals High Structural Plasticity of the Lipocalin Loop Region. Proteins: Struct., Funct., Genet. 2003, 53 (1), 121–129. 10.1002/prot.10497. [DOI] [PubMed] [Google Scholar]
- Breustedt D. A.; Chatwell L.; Skerra A. A New Crystal Form of Human Tear Lipocalin Reveals High Flexibility in the Loop Region and Induced Fit in the Ligand Cavity. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2009, 65 (10), 1118–1125. 10.1107/S0907444909031011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flower D. R. The Lipocalin Protein Family: Structure and Function. Biochem. J. 1996, 318 (1), 1–14. 10.1042/bj3180001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coles M.; Diercks T.; Muehlenweg B.; Bartsch S.; Zölzer V.; Tschesche H.; Kessler H. The Solution Structure and Dynamics of Human Neutrophil Gelatinase-Associated Lipocalin. J. Mol. Biol. 1999, 289 (1), 139–157. 10.1006/jmbi.1999.2755. [DOI] [PubMed] [Google Scholar]
- Chin J. W.; Santoro S. W.; Martin A. B.; King D. S.; Wang L.; Schultz P. G. Addition of P-Azido-L-Phenylalanine to the Genetic Code of Escherichia Coli. J. Am. Chem. Soc. 2002, 124 (31), 9026–9027. 10.1021/ja027007w. [DOI] [PubMed] [Google Scholar]
- Debets M. F.; van Berkel S. S.; Schoffelen S.; Rutjes F. P. J. T.; van Hest J. C. M.; van Delft F. L. Aza-Dibenzocyclooctynes for Fast and Efficient Enzyme PEGylation via Copper-Free (3 + 2) Cycloaddition. Chem. Commun. 2010, 46 (1), 97–99. 10.1039/B917797C. [DOI] [PubMed] [Google Scholar]
- Schwaiger I.; Kardinal A.; Schleicher M.; Noegel A. A.; Rief M. A Mechanical Unfolding Intermediate in an Actin-Crosslinking Protein. Nat. Struct. Mol. Biol. 2004, 11 (1), 81–85. 10.1038/nsmb705. [DOI] [PubMed] [Google Scholar]
- Yin J.; Straight P. D.; McLoughlin S. M.; Zhou Z.; Lin A. J.; Golan D. E.; Kelleher N. L.; Kolter R.; Walsh C. T. Genetically Encoded Short Peptide Tag for Versatile Protein Labeling by Sfp Phosphopantetheinyl Transferase. Proc. Natl. Acad. Sci. U. S. A. 2005, 102 (44), 15815–15820. 10.1073/pnas.0507705102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milles L. F.; Schulten K.; Gaub H. E.; Bernardi R. C. Molecular Mechanism of Extreme Mechanostability in a Pathogen Adhesin. Science 2018, 359 (6383), 1527–1533. 10.1126/science.aar2094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponnuraj K.; Bowden M. G.; Davis S.; Gurusiddappa S.; Moore D.; Choe D.; Xu Y.; Hook M.; Narayana S. V. L. A “dock, Lock, and Latch” Structural Model for a Staphylococcal Adhesin Binding to Fibrinogen. Cell 2003, 115 (2), 217–228. 10.1016/S0092-8674(03)00809-2. [DOI] [PubMed] [Google Scholar]
- Livadaru L.; Netz R. R.; Kreuzer H. J. Stretching Response of Discrete Semiflexible Polymers. Macromolecules 2003, 36 (10), 3732–3744. 10.1021/ma020751g. [DOI] [Google Scholar]
- Puchner E. M.; Franzen G.; Gautel M.; Gaub H. E. Comparing Proteins by Their Unfolding Pattern. Biophys. J. 2008, 95 (1), 426–434. 10.1529/biophysj.108.129999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jobst M. A.; Schoeler C.; Malinowska K.; Nash M. A. Investigating Receptor-Ligand Systems of the Cellulosome with AFM-Based Single-Molecule Force Spectroscopy. J. Visualized Exp. 2013, (82), e50950. 10.3791/50950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell G. I. Models for the Specific Adhesion of Cells to Cells. Science 1978, 200 (4342), 618–627. 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- Evans E.; Ritchie K. Dynamic Strength of Molecular Adhesion Bonds. Biophys. J. 1997, 72 (4), 1541–1555. 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudko O. K.; Hummer G.; Szabo A. Intrinsic Rates and Activation Free Energies from Single-Molecule Pulling Experiments. Phys. Rev. Lett. 2006, 96 (10), 108101. 10.1103/PhysRevLett.96.108101. [DOI] [PubMed] [Google Scholar]
- Dudko O. K.; Hummer G.; Szabo A. Theory, Analysis, and Interpretation of Single-Molecule Force Spectroscopy Experiments. Proc. Natl. Acad. Sci. U. S. A. 2008, 105 (41), 15755–15760. 10.1073/pnas.0806085105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atilgan A. R.; Durell S. R.; Jernigan R. L.; Demirel M. C.; Keskin O.; Bahar I. Anisotropy of Fluctuation Dynamics of Proteins with an Elastic Network Model. Biophys. J. 2001, 80 (1), 505–515. 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyal E.; Lum G.; Bahar I. The Anisotropic Network Model Web Server at 2015 (ANM 2.0). Bioinformatics 2015, 31 (9), 1487–1489. 10.1093/bioinformatics/btu847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Souza P. C. T.; Thallmair S.; Conflitti P.; Ramírez-Palacios C.; Alessandri R.; Raniolo S.; Limongelli V.; Marrink S. J. Protein-Ligand Binding with the Coarse-Grained Martini Model. Nat. Commun. 2020, 11 (1), 3714. 10.1038/s41467-020-17437-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Souza P. C. T.; Alessandri R.; Barnoud J.; Thallmair S.; Faustino I.; Grunewald F.; Patmanidis I.; Abdizadeh H.; Bruininks B. M. H.; Wassenaar T. A.; Kroon P. C.; Melcr J.; Nieto V.; Corradi V.; Khan H. M.; Domanski J.; Javanainen M.; Martinez-Seara H.; Reuter N.; Best R. B.; Vattulainen I.; Monticelli L.; Periole X.; Tieleman D. P.; de Vries A. H.; Marrink S. J. Martini 3: A General Purpose Force Field for Coarse-Grain Molecular Dynamics. Nat. Methods 2021, 18, 382. 10.1038/s41592-021-01098-3. [DOI] [PubMed] [Google Scholar]
- Poma A. B.; Li M. S.; Theodorakis P. E. Generalization of the Elastic Network Model for the Study of Large Conformational Changes in Biomolecules. Phys. Chem. Chem. Phys. 2018, 20, 17020–17028. 10.1039/C8CP03086C. [DOI] [PubMed] [Google Scholar]
- Chwastyk M.; Bernaola A. P.; Cieplak M. Statistical Radii Associated with Amino Acids to Determine the Contact Map: Fixing the Structure of a Type I Cohesin Domain in the Clostridium Thermocellum Cellulosome. Phys. Biol. 2015, 12 (4), 046002. 10.1088/1478-3975/12/4/046002. [DOI] [PubMed] [Google Scholar]
- Senapati S.; Poma A. B.; Cieplak M.; Filipek S.; Park P. S. H. Differentiating between Inactive and Active States of Rhodopsin by Atomic Force Microscopy in Native Membranes. Anal. Chem. 2019, 91 (11), 7226–7235. 10.1021/acs.analchem.9b00546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poma A. B.; Chwastyk M.; Cieplak M. Elastic Moduli of Biological Fibers in a Coarse-Grained Model: Crystalline Cellulose and β-Amyloids. Phys. Chem. Chem. Phys. 2017, 19 (41), 28195–28206. 10.1039/C7CP05269C. [DOI] [PubMed] [Google Scholar]
- Moreira R. A.; Chwastyk M.; Baker J. L.; Guzman H. V.; Poma A. B. Quantitative Determination of Mechanical Stability in the Novel Coronavirus Spike Protein. Nanoscale 2020, 12 (31), 16409–16413. 10.1039/D0NR03969A. [DOI] [PubMed] [Google Scholar]
- Poma A. B.; Guzman H. V.; Li M. S.; Theodorakis P. E. Mechanical and Thermodynamic Properties of Aβ42, Aβ40, and α-Synuclein Fibrils: A Coarse-Grained Method to Complement Experimental Studies. Beilstein J. Nanotechnol. 2019, 10, 500–513. 10.3762/bjnano.10.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poma A. B.; Thu T. T. M.; Tri L. T. M.; Nguyen H. L.; Li M. S. Nanomechanical Stability of Aβ Tetramers and Fibril-like Structures: Molecular Dynamics Simulations. J. Phys. Chem. B 2021, 125 (28), 7628–7637. 10.1021/acs.jpcb.1c02322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmood M. I.; Poma A. B.; Okazaki K.-I. Optimizing Go̅-MARTINI Coarse-Grained Model for F-BAR Protein on Lipid Membrane. Front. Mol. Biosci. 2021, 8, 619381. 10.3389/fmolb.2021.619381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poma A. B.; Cieplak M.; Theodorakis P. E. Combining the MARTINI and Structure-Based Coarse-Grained Approaches for the Molecular Dynamics Studies of Conformational Transitions in Proteins. J. Chem. Theory Comput. 2017, 13 (3), 1366–1374. 10.1021/acs.jctc.6b00986. [DOI] [PubMed] [Google Scholar]
- Fontana F.; Gelain F. Probing Mechanical Properties and Failure Mechanisms of Fibrils of Self-Assembling Peptides. Nanoscale Advances 2020, 2 (1), 190–198. 10.1039/C9NA00621D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alessandri R.; Souza P. C. T.; Thallmair S.; Melo M. N.; de Vries A. H.; Marrink S. J. Pitfalls of the Martini Model. J. Chem. Theory Comput. 2019, 15 (10), 5448–5460. 10.1021/acs.jctc.9b00473. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.