Matching anticancer compounds and tumor cell lines by neural networks with ranking loss

ABSTRACT

Computational drug sensitivity models have the potential to improve therapeutic outcomes by identifying targeted drug components that are likely to achieve the highest efficacy for a cancer cell line at hand at a therapeutic dose. State of the art drug sensitivity models use regression techniques to predict the inhibitory concentration of a drug for a tumor cell line. This regression objective is not directly aligned with either of these principal goals of drug sensitivity models: We argue that drug sensitivity modeling should be seen as a ranking problem with an optimization criterion that quantifies a drug’s inhibitory capacity for the cancer cell line at hand relative to its toxicity for healthy cells. We derive an extension to the well-established drug sensitivity regression model PaccMann that employs a ranking loss and focuses on the ratio of inhibitory concentration and therapeutic dosage range. We find that the ranking extension significantly enhances the model’s capability to identify the most effective anticancer drugs for unseen tumor cell profiles based in on in-vitro data.

INTRODUCTION

Cancer is a leading cause of death worldwide and case numbers are expected to rise in an aging population (1). Traditional one-size-fits-all cancer therapies fail to address the diverse nature of the disease: being caused by a combination of genetic mutations, no two cancers are the same, which explains the vast range of therapeutic outcomes for seemingly similar clinical presentations. Driven by advances in genomic testing, personalized oncology aims at providing the best therapy, given all available information—including the entire genetic tumor profile. Genomic alterations and the transcriptome of cancer cells, in combination with information about the employed drugs, are among the factors that determine the diverse outcomes of cancer therapies (2). Increasingly, data-driven machine learning approaches are used to facilitate precision oncology (3).

In vitro compound sensitivity is known to be a predictor for clinical therapy success (4). Many machine learning approaches to precision oncology therefore rely on large-scale drug sensitivity screening data. The data are created by exposing cultivated tumor cell lines to a variety of anti-cancer compounds in vitro, and measuring the survival rate of the cancer cells as a function of the drug concentration. The inhibitory concentration IC50 is derived from each experiment and often serves as a measure of drug efficacy (5–10).

Each combination of a cell line, an anticancer drug compound that the cell line has been exposed to, and the observed inhibitory concentration IC50 constitutes a data point. The resulting databases, most prominently GDSC (11,12), are then used to train models that can potentially predict the IC50 of unknown pairs of candidate drugs and cell lines (13). This approach carries the potential to revert the trend of declining drug-discovery productivity (14).

Drug sensitivity models usually rely on cell and drug features. Genomic cell features that have been studied include mutation, gene copy number variation, and microsatellite instability data. However, the most predictive cell feature is believed to be the transcriptome (15), as measured by cellular RNA levels. For anticancer compounds, features encode information about the chemical structure. For instance, MACCS fingerprints—binary vectors indicating the presence of structural features in a molecule—can be used to this effect (16).

Many different machine learning architectures have been employed to model IC50 values (17). Menden et al. (6) have used a simple feed-forward neural network on genomic and fingerprint features. Ammad-ud-din et al. (8) have been rethinking drug sensitivity prediction as a recommendation problem and were able to incorporate the high-dimensional RNA expression data by applying a kernelized matrix factorization approach. They also employed a strict cross-validation strategy and differentiated between cell cold-start and drug cold-start evaluation. This facilitates the analysis of the model’s essential ability to predict the IC50 values for cells and drugs that are not present in the training data, respectively. Gupta et al. (9) used a kernelized support vector machine and decision tree-based ensemble models were, amongst others, employed by Su et al. (10). Baptista et al. (18) provide a comprehensive overview on deep-learning approaches to drug-sensitivity prediction.

PaccMann, a well-established multi-modal attention-based neural-network model (15), forms the basis for this work. PaccMan is trained to minimize the squared loss for its estimates of the IC50 values of pairs of drug components and cell lines. This approach is misaligned with the underlying goals in two significant ways. First, the cytotoxicity of anticancer drugs and, as a result, the dosage ranges vary greatly across drug compounds. The inhibitory concentration IC50 of highly toxic compounds is always lower than the inhibitory dose of compounds on the less toxic end of the spectrum. For resistant cell lines, the inhibitory dose of highly cytotoxic compounds can still be a low absolute value, even though that value may exceed the therapeutic range or even the lethal concentration. Therefore, it is not the inhibitory concentration itself that indicates therapeutic usefulness, but rather the inhibitory concentration normalized to the therapeutic dosage range. In this paper, we will develop this approach into an optimization criterion.

Secondly, the squared loss as optimization criterion puts equally large weights on the model’s ability to estimate the inhibitory concentration of the most effective and the least effective pairs of drugs and cell lines. This aligns poorly with the practical goal of precision oncology. To serve its purpose as a therapeutic tool, the model has to identify the therapeutically most effective drug candidates for a given cell line whereas a differentiation between the inhibitory concentrations of ineffective drugs is not relevant. Ranking loss functions such as the normalized discounted cumulative gain (NDCG) (19) specifically quantify a model’s ability to identify highly-rated candidates from a base set. Ranking loss functions have previously been employed in the context of targeted cancer therapy within a kernelized ranking SVM (20). In this paper, we will explore ranking loss functions for targeted cancer therapy using for deep neural networks.

The paper is structured as follows. After introducing the PaccMan model for regressing the inhibitory concentration, the paper will lay out the problem setting and discuss adequate performance metrics. We will proceed to develop a neural network that directly minimizes the chosen ranking loss function. We will then present and discuss our experimental results before concluding.

MATERIALS AND METHODS

PaccMan: Regressing IC50 with neural networks

PaccMann uses RNA expression levels of the cell lines and the tokenized SMILES strings of the drug molecules as inputs for the network. A SMILES string is a one-dimensional representation of a molecule, based on the atom-bond network structure. The SMILES code of a compound is not unique because it depends on the starting point of a walk across the molecule. In order to address this issue, training data is often augmented by adding multiple SMILES representations of the same molecule.

Additionally, PaccMan incorporates prior knowledge about drug-target information and protein-protein interactions to reduce the dimensionality of the gene expression data by using network propagation. Weights are initialized to 1 for reported target genes and to a small, positive value for other genes. Propagation of these values through the protein-protein interaction network results in activation values that roughly correspond to the functional relatedness of genes (21). Using only the RNA expression level data of the 20 highest-scoring genes for each compound reduces the number of cell features from 17 737 to 2089.

PaccMann uses attention-based network modules to encode both the tokenized SMILES string and gene expression subsets. Attention-based encoders are trained to assign high weights to the most informative input features. The network parameters are trained to minimize the mean squared error. Figure 1 gives an overview of the PaccMan architecture.

Figure 1.

PaccMann (15) multi-modal architecture. Cell RNA expression data dimension is reduced from 17 737 genes to 2089 genes using network propagation and encoded with a 4-head self-attention encoder. Tokenized SMILES string of the compound is padded to a length of 155 and embedded by an embedding layer with 16 dimensions. The compound embedding is encoded with 3 parallel convolutional channels (kernel sizes: 3, 5 and 11) and a residual skip connection. Each channel is further encoded with a multihead of four contextual attention layers, that use the encoded gene expression as context. The results are concatenated and fed to a set of dense layers (number of units: 512, 128, 64, 16 and 1) with dropout and batch normalization.

Problem setting and performance metrics

The goal of precision medicine is to identify the most promising candidate compounds for a cell line at hand. For ineffective drugs, it is sufficient for the model not to rate them among the most likely candidates. Since a medical practitioner will only consider a limited number of treatment options, the model does not need to be able to estimate the inhibitory concentration of ineffective drugs with high accuracy. The optimization criterion should therefore not trade a model’s ability to identify the most effective drugs against its precision in estimating the inhibitory concentration of ineffective drugs.

This application scenario corresponds best to the abstract problem setting of learning a ranking function. A ranking is an ordering of items according to a ranking model that approximates the ordering given by an underlying definition of relevance.

Ranking loss functions quantify a ranking model’s ability to bring the most relevant items of a list into the correct order, while putting a lower weight on the correct order of items on the far end of the list. In our application of precision medicine, items are drugs d for a given cell line c; the ranking is over a set of drugs {d₁, …, d_n} for a fixed cancer cell line c.

In drug development, the ratio of efficacy to toxicity is generally referred to as the therapeutic index (22). Efficacy is usually measured in terms of the effective dose and toxicity can be measured in terms of the lethal dose. Since neither of these doses are available in our in vitro data, we use the inhibitory concentration IC50 as proxy of efficacy and the maximum therapeutic dosage range as proxy of the toxicity for healthy cells. We therefore construct the relevance of a drug d for a given cell line c as the ratio

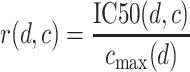of the inhibitory concentration of the drug for the cell line to the maximum therapeutic concentration c_max for the drug compound. Intuitively, if a small fraction of the possible therapeutic dose inhibits cell growth, the cell is sensitive to the drug, whereas an inhibitory dose in excess of the therapeutic dose indicates a resistant cell line. This definition ensures that the most relevant drug-cell line combinations achieve the strongest inhibitory response in the available dosage range.

We write the ranking of items given by a ranking model as π, where π(d|c) is the position in the ordering assigned by the ranking model to drug d for given cell line c. Using neural networks, ranking models are implemented by means of a ranking function f_π(d|c) that assigns relevance scores to items by which these items are then sorted.

Several ranking performance measures quantify the usefulness of rankings. The discounted cumulative gain at k (DCG@k) sums the ground-truth relevance scores r(d, c) of the k most relevant items, where the relevance of each item is divided by the logarithm of the item’s position π(x) in the ranking:

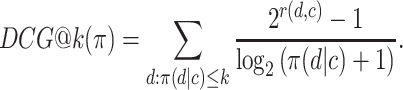In order to maximize the DCG, the most relevant items have to occupy the first ranks, because the relevance of each item is discounted by its position in the ranking. Constant k has to be chosen as the number of candidate drugs that a medical practitioner would typically take into consideration before making a therapeutic decision. The relevance of items beyond position k does not impact the DCG metric, because these items would be ignored in any case by the medical practitioner.

The DCG depends on the absolute relevance of ranked items, and so the DCG values for rankings of different item sets cannot be compared. The NDCG therefore normalizes the DCG by the DCG of the ideal ranking, in which items are ranked strictly by ground-truth relevance:

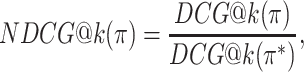where

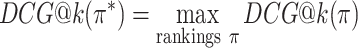is the DCG of an ideal ranking. The NDCG quantifies the merit of a ranking on a scale from 0 to 1 where 1 is the perfect ranking according to the ground-truth relevance function.

We will also refer to the precision at k as an additional ranking performance metric that has an intuitive and easy-to-understand meaning. The precision at k is the fraction of the k most relevant items that which are part of the top-k predictions of the model. For precision medicine, this is the proportion of the most effective drug compounds that are present in the k highest-rated compounds. For example, a precision at 10 of 90% means that 9 out of the 10 most effective drugs are included in the 10 drugs that a model rates highest. Unlike the NDCG, the precision at k does not measure how well the top k items are sorted by their relevance.

We investigate the cell cold-start problem. Training data contains observations of the inhibitory concentration IC50 for pairs of drug compounds and cell lines. These data can be used to optimize parameters of a model In the cell cold-start situation, at application time one is faced with new cell lines that do not occur in the training data. By contrast, the drug compounds that are available at application time also occur in the training data.

Optimizing the ranking loss

Being based on a discrete ordering, NDCG@k and precision@k are non-convex and non-differentiable functions; as such, they do not lend themselves well to direct maximization with gradient methods. In order to still be able to approximately maximize the NDCG with a deep neural network, Qin et al. (23) approximate the position by a smooth function of the relevance, and the truncation function by a smooth function of positions of items. Thus, the NDCG can be approximated as

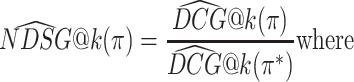(1)

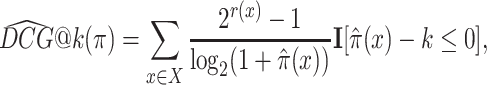(2)

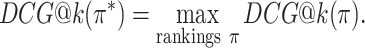(3)

Here, I[·] is a smooth approximation of an indicator function that can be implemented as a logistic function

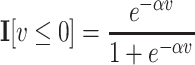with scaling constant α, and 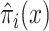is a smooth approximation of the index function that can be implemented as a sum, over all other items y, of the indicator function indicating that y receives a higher score than x from the ranking function f_π:

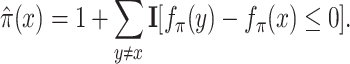The appxoximate NDCG of Equation (1) is differentiable; a neural-network model that implements ranking function f_π can directly be optimized for this criterion. We optimize the PaccMan neural network using the TensorFlow implementation of PaccMann (available at https://github.com/drugilsberg/paccmann) and the TensorFlow-ranking library (available at https://github.com/tensorflow/ranking). In contrast to the original PaccMan model, the instances of the ranking model are no longer drug-cell pairs. Each training input is a list of drugs and relevance scores for a given cell profile. We refer to the method as PaccMan with NDCG loss.

Experimental setting

We employ 5-fold cross validation to evaluate the models. We investigate the setting of Cell cold-start, meaning that we split cell lines into training and test portions with no overlap. For each cross-validation fold, we train PaccMan with NDCG loss (Figure 2) and each of the reference models; for the neural network models, we execute 1 000 000 training steps with a batch size of 390. We average the resulting ranking performance measures over the 5-fold.

Figure 2.

Feed-forward neural network baseline architecture. Cell RNA expression data dimension is reduced from 17 737 genes to subset of 2089 genes using network propagation. SMILES strings are tokenized, encoded with a 16-dimensional embedding layer. The embedded SMILES and reduced gene expression tensors are concatenated and fed to a set of dense layers (number of units: 64, 32, 16 and 1) with dropout and batch normalization.

We judge the statistical significance of differences in the performance of models with two-sided paired t- and Wilcoxon tests and for equal means.

Reference models

The first, natural reference method that we include in our experiments is the original PaccMan method with squared loss. We train the PaccMan network in each cross-validation fold using the hyperparameters from the original paper (15).

The next reference method is a simple feed-forward neural network, as shown in Figure 2. This network concatenates one-hot encoded SMILES codes and gene-expression features into an input layer that is followed by three fully-connected hidden layers and a linear output unit to predict a relevance score. Dropout, batch normalization and ReLu activation are applied after each hidden layer. The network is trained with mean squared error (referred to as simple NN) and approximate NDCG loss (simple NN with NDCG-loss), respectively. The network is illustrated in Figure 2.

The final reference method is kernelized rank learning (KRL) (20). Kernalized rank learning directly optimizes a convex upper bound of the NDCG at k using a kernelized linear model. Hyperparameters are tuned on the training portion of each cross-validation fold using the code from the original paper (20).

Data

We obtain IC50 and RNA expression data from the Genomics of Drug Sensitivity in Cancer (GDSC) database (11) that contains screening data for 957 cell lines against 220 drugs. The tokenized, canonical SMILES codes, acquired with the chemical software RDKit (available at https://www.rdkit.org/), are available for 208 of the compounds.

RESULTS

Prediction performances

Figures 3 and 4 and Table 1 compare precision at k and NDCG at k of the 5-fold cross-validation for different values of k. Here, each ranking is an ordering of drug compounds for a given cell line; precision and NDCG values are averaged over the drug rankings for all cell lines. Table 1 also shows the P values of paired two-sided t-tests and Wilcoxon tests with the null hypothesis that the NDCG of PaccMan with NDCG-loss is equal to the NDCG of each of the reference methods. PaccMan with NDCG-loss outperforms all reference methods both in terms of precision at k and NDCG at k, for every value of k under investigation. The difference in NDCG k is statistically significant for every reference method and every value for k with P < 0.01.

Figure 3.

Precision at k for different values of k of PaccMan with NDCG loss and reference methods for drug rankings. Error bars depict the standard error.

Figure 4.

NDCG at k for different values of k of PaccMan with NDCG loss and reference methods for drug rankings. Error bars depict the standard error.

Table 1.

Precision at k and NDCG at k for different values of k of PaccMann with NDCG loss and reference methods for rankings over drug compounds

k	Precision	NDCG	Model	P (t-test)	P (Wilcoxon)
1	0.364 ± 0.018	0.525 ± 0.012	KRL	0.0	0.021
	0.491 ± 0.022	0.885 ± 0.006	simple NN with NDCG-loss	0.141	0.602
	0.211 ± 0.055	0.726 ± 0.043	simple NN	0.02	0.009
	0.494 ± 0.021	0.889 ± 0.007	PaccMann with NDCG-loss	-	-
	0.245 ± 0.046	0.78 ± 0.02	PaccMann	0.002	0.009
3	0.307 ± 0.008	0.517 ± 0.014	KRL	0.0	0.021
	0.397 ± 0.011	0.849 ± 0.003	simple NN with NDCG-loss	0.003	0.009
	0.244 ± 0.037	0.734 ± 0.042	simple NN	0.038	0.009
	0.397 ± 0.008	0.869 ± 0.004	PaccMann with NDCG-loss	-	-
	0.279 ± 0.014	0.795 ± 0.01	PaccMann	0.001	0.009
5	0.325 ± 0.006	0.534 ± 0.013	KRL	0.0	0.021
	0.414 ± 0.008	0.848 ± 0.003	simple NN with NDCG-loss	0.018	0.047
	0.274 ± 0.036	0.74 ± 0.041	simple NN	0.043	0.009
	0.422 ± 0.008	0.862 ± 0.005	PaccMann with NDCG-loss	-	-
	0.299 ± 0.011	0.803 ± 0.008	PaccMann	0.001	0.009
30	0.543 ± 0.001	0.645 ± 0.01	KRL	0.0	0.021
	0.562 ± 0.005	0.867 ± 0.003	simple NN with NDCG-loss	0.001	0.009
	0.447 ± 0.045	0.776 ± 0.036	simple NN	0.04	0.009
	0.629 ± 0.004	0.891 ± 0.003	PaccMann with NDCG-loss	-	-
	0.538 ± 0.004	0.845 ± 0.004	PaccMann	0.0	0.009

Naturally, the performance difference is higher for lower values of cutoff values k. For low values of k, the models are evaluated in terms of their ability to pick the few, most promising drug compounds. By contrast, regression models are optimized to estimate the inhibitory concentration for every single effective or ineffective drug.

Figure 5 shows how the ranking performance varies across different cell lines. For the vast majority of cell lines, the quality of the ranking differs between 60% (for ‘hard’ cell lines) and 100% (for ‘easy’ cell lines) of the DCG of an ideal ranking. There are 5 out of around 957 cell lines which the NDCG @ 5 is less than or equal to 0.5; there is no cell line for which the NDCG @ 30 is below 0.5. An NDCG of 0.5 corresponds to a random ordering of drug compounds.

Figure 5.

Distribution of NDCG at k values for cell lines using the PaccMan model with NDCG loss.

Attention weight analysis

We were interested in the attention weights generated by the learning procedure, and whether the biological processes induced by the respective genes reflect prior knowledge. Thus, for each gene we average the attention weights across all cell lines and discarded genes with average attention weight 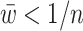, where n is the number of genes used. This results in 939 highly attended  genes. Enrichment analysis with the ConsensusPathDB resource (24) reveals numerous cancer-relevant processes that are indicative of anti-cancer drug action either inhibiting the growth or cell division of tumor cells (cytostatic) or increasing their mortality (cytotoxic) through DNA damage and the induction of apoptosis (Table 2). Consequently, programmed cell death (apoptosis) is among the most-enriched pathway (Q = 3.21E-03) which points to the fact that many of the cancer drugs indeed kill tumor cells, which is then reflected by the attention weights (25).

Table 2.

Top thirty KEGG pathways enriched by the 939 highly attended genes

P-value	q-value	Pathway	Pathway size	Overlap genes
3.74e-08	3.72e-06	FoxO signaling pathway	132	24
4.340e-08	3.72e-06	Pathways in cancer	526	57
1.14e-07	5.02e-06	MAPK signaling pathway	295	38
1.19e-07	5.02e-06	Human cytomegalovirus infection	225	32
2.30e-07	7.78e-06	PI3K-Akt signaling pathway	354	42
3.53e-06	9.95e-05	Proteoglycans in cancer	201	27
6.80e-06	0.000146	Prostate cancer	97	17
8.20e-06	0.000146	Neurotrophin signaling pathway	119	19
8.89e-06	0.000146	Focal adhesion	199	26
9.03e-06	0.000146	Progesterone-mediated oocyte maturation	99	17
9.68e-06	0.000146	Human immunodeficiency virus 1 infection	212	27
1.04e-05	0.000146	HIF-1 signaling pathway	100	17
1.19e-05	0.000155	Hepatitis B	144	21
1.90e-05	0.000229	Central carbon metabolism in cancer	65	13
2.15e-05	0.000243	ErbB signaling pathway	85	15
3.15e-05	0.000332	Epithelial cell signaling in Helicobacter pylori infection	68	13
4.63e-05	0.000460	T cell receptor signaling pathway	101	16
5.26e-05	0.000494	Cell cycle	124	18
6.94e-05	0.000618	Kaposi sarcoma-associated herpesvirus infection	186	23
0.000113	0.000953	Hepatitis C	155	20
0.000127	0.001021	Ras signaling pathway	232	26
0.000209	0.001608	Epstein-Barr virus infection	201	23
0.000234	0.001680	C-type lectin receptor signaling pathway	104	15
0.000240	0.001680	Chemokine signaling pathway	189	22
0.000248	0.001680	p53 signaling pathway	72	12
0.000274	0.001783	Tuberculosis	179	21
0.000524	0.003214	Apoptosis	136	17
0.000551	0.003214	Gastric cancer	149	18
0.000551	0.003214	Non-alcoholic fatty liver disease (NAFLD)	149	18
0.000581	0.003259	Toxoplasmosis	113	15

The most enriched pathway relates to FoxO signaling (Q = 3.72E-06). Forkhead box O proteins (FoxOs) are transcriptional regulators important for cell differentiation, development and stem cell maintenance. They are associated with many disease processes and are considered as tumor suppressors that prolongate cancer progression by promoting apoptosis, DNA repair and cell cycle arrest (26). Carbon metabolism in cancer (Q = 2.29E-04) is the most enriched metabolic pathway. Cancer cells adapt their metabolism in order to support enhanced proliferation and survival and, thus, one route of cytotoxic anti-cancer therapy has been the design of anti-metabolites that interfere with the division of cancer cells such as the anti-folate 5-fluorouracil among others which is reflected by the attention weights of the respective genes (27).

The highest average attention weight across all cell lines has the gene RAI2. Retinoic acid plays a critical role in development, cellular growth, and differentiation. The specific function of Retinoic Acid-Induced Protein 2 is largely unknown and has only recently been associated with cancer and cancer therapy. Reduced expression of RAI2 was found in breast cancer and in colorectal cancer RAI2 acts as a tumor suppressor by inhibiting AKT signaling. Moreover, methylation of the RAI2 promoter is a mark for poor prognosis in colorectal cancer (28).

For each cell line i we interrogated the attention weights gained by the procedure for outliers (w_i > μ_i + 5σ_i) where μ_i and σ_i are the mean and standard deviation across all attention weights for that cell line. We found that the number of outliers varies with increasing mutation load of the cell lines with respect to important driver mutations. For example, many cell lines that are of colon cancer origin (COREAD) have mutations in the APC (37 out of 46), KRAS (28) and TP53 (34) genes which account for the major driver mutations in colon cancer. The number of outliers identified by the attention weights assigned to the colon cancer cell lines varies between 2 and 13 genes and this variation is greater in the cell lines with higher mutation loads than in the cell lines with lower mutation load (R² = 0.994). This reflects the fact that mutations lead to expression variations (29,30) and may indicate further cell line differentiation and dysregulation during cancer progression which is captured by different genes that are important for cell line characterization during the learning process.

Example Use case: drugs against colon cancer

We investigate the predictions for the subset of colon cancer cell lines (TCGA classification COREAD (31)) for those drugs that are approved or in clinical studies for colon cancer. In total, 46 different cell lines are available. As suggested by a recent review (32), targeted therapies for colon cancer can be classified into inhibitors of the EGF/EGFR-related pathways that target proliferation of the tumor cells, inhibitors of the VEGF/VEGFR-related pathways that target angiogenesis, and inhibitors of other growth factors such as HGF/c-MET pathway.

Ranking predictions across the COREAD cell lines vary greatly (Figure 6), while EGF/EGFR-related therapies show on average lower ranks compared to VEGF/VEGFR-related therapies. The lowest ranking-position is held by trametinib, an inhibitor of the ERK/MAPK signaling pathway. The putative targets of trametinib are MEK1 and MEK2, two members of the RAS-RAF–MEK–ERK signaling pathway that transmits signals from growth factor receptors to the nucleus and other organelles to regulate cell proliferation, differentiation, survival and invasion. The compound is currently investigated in combination with other compounds for the treatment of patients with BRAFV600E metastatic colon cancer (33).

Figure 6.

Box plots of predicted rankings of the drugs across 46 colon-cancer cell lines. Drugs are selected among approved drugs or drugs that are in clinical trials according to a recent review (32) and are color coded: yellow and brown panel refer to EGF/EGFR-related therapies, green panel refers to VEGF/VEGFR-related therapies and grey panel to other growth-factor inhibitors.

The second best performing compound, according to the ranking model, that is currently approved or in clinical trials for colon cancer is the RTK signaling inhibitor foretinib that targets a couple of kinases, such as MET. Foretinib has been shown to inhibit colon tumor growth in vitro and in xenograft models (34).

It is also visible in Figure 6 that the group of approved or clinically investigated therapies targeting the EGF/EGFR pathway improves over other targeted therapies, however, the ranking results for the group of cytotoxic drugs are better. Thus, recommendations should distinguish both groups, since the targeted drugs are supposed to have less severe side-effects and thus induce less severe viability effects to the cellular system under study.

Conclusions

We have studied a variant of the deep neural network PaccMan (15) that directly maximizes a smooth approximation of the NDCG at k. From our experiments, we can conclude that PaccMan with NDCG loss significantly outperforms the original version of PaccMan, kernelized rank learning, and a simple neural-network baseline with respect to both NDCG at k and precision at k for all values of k under investigation.

We observe that in example ranking of drugs for colorectal cancer, the top ranks are held by plausible drug compounds that are currently in clinical trials. We also note that he maximum dosage range of a drug is an imperfect proxy of toxicity, because the severity of side-effects at that dose can varies across drugs. Therefore, the rankings of targeted therapies and cytotoxic drugs for a given cell line should be viewed separately.

DISCUSSION

We argue that drug sensitivity models for precision oncology should be evaluated in terms of their ability to select a small set of candidate drug compounds that achieve the most favorable trade-off between their inhibitory concentration for cancer cells and their toxic concentration for healthy cells for a given cell line at hand. The squared loss of the inhibitory concentration IC50 is a poor proxy of either of these overarching objectives. Therefore, we have developed a ranking model that maximizes the ranking criterion NDCG at k, where the relevance criterion is the IC50, normalized to the maximum therapeutic concentration.

From our experiments, we can conclude that rethinking drug sensitivity modeling as a learning-to-rank learning problem significantly improves the efficacy of the drug compounds on top ranks. PaccMann with NDCG-loss outperforms PaccMann not only in terms of the NDCG @ k for unseen cell lines—which it has been specifically trained for—but also in terms of precision @ k. In contrast to drug sensitivity regression, ranking models are closer to the envisioned application in precision oncology. Regression metrics such as Pearson correlation or the mean squared error are not directly interpretable in the context of drug recommendation. Precision @ k however, is a metric which might prove useful for the intercommunication between oncologist and machine learning engineers.

In this study, we have quantified the therapeutic potential of drug compounds as the ratio of inhibitory concentration IC50 to maximum dosage range, the rationale being that the dosage range is a proxy of the drug’s cytotoxicity for healthy cells. The dosage range is readily available for all drug compounds that have undergone clinical studies. Since, however, the dosage may be constrained by factors other than cytotoxicity, it may not be a perfect proxy. Toxicity indicators such as the LD50 for mice may potentially be a better gauge of toxicity for human patients, but they are not reported in GDSC or other databases for all drug compounds.

Our ranking model is trained on in vitro data while therapeutic recommendations are ultimately made for human patients. Being trained on in vitro data, the model cannot account for factors such as the the drug’s bioavailability in the affected tissue, or interaction between cancer cells, drugs, and the immune system. Clinical data will likely always be a rare commodity. In many application areas, transfer learning of neural networks is achieved by pre-training the model on auxiliary data, and fine-tuning it on a smaller set of data from the target domain. Applied to precision oncology, this would mean to train the model on in vitro data first, and fine-tuning its parameters on clinical data. As an additional intermediate step, it appears promising to additionally incorporate measurements of inhibitory concentrations on ex vivo and organoid tissues into the training process (35).

Alternative approaches to learning-to-rank have been studied, such as the boosted-tree model LambdaMart (36). Boosted trees have proven to be most useful in applications in which limited volumes of training data are available. As the trove of globally available drug-sensitivity data grows, we expect the relevance of boosted-tree models to diminish in this application area.

Apart from algorithmic improvements, utilizing additional data sources might enhance drug sensitivity models. As an example, encoding drug molecules structures as a one-dimensional SMILES code is a considerable simplification. Strong molecule encoders that use the readily available 3D-structure of molecules might provide additional information for drug-ranking models and advance drug cold-start capabilities.

We showed evidence for the ranking predictions among the drugs for colon cancer (cf. Figure 6). Additionally, we investigated the potential of the ranking model to predict cancer subtype-specific drug differences in the context of breast cancer. The available 49 breast cancer cell lines can be classified into five different subtypes according to estrogen receptor (ER), progesterone receptor (PR), and human epithelial receptor 2 (HER2) status, namely luminal A (7 cell lines), luminal B (6), HER2-positive (7), triple-negative A (12) and triple-negative B (10) (37); 7 cell lines remained unclassified. We then derived the predicted ranking of drugs for the subtypes by computing the median predicted rank across all cell lines within the respective subtype. Although, we found that both the rankings according to ground-truth IC50 and the predicted ranks overall are very similar, we can identify selected examples of subtype-specific drug responses that show literature evidence either by existing clinical trials or previously identified molecular targets.

For example, entinostat, an HDAC inhibitor, has lower median rank (43) in the HER2-positive cell lines compared to luminal (76.5) and triple-negative (62.5) cell lines indicating a benefit for the HER2-positive subtype. This finding is supported by literature evidence of a recent phase Ib study where entinostat in combination with other therapies had positive effects on HER2+ metastatic breast cancer patients (38). Another drug that has different predicted subgroup effects is the PI3K and mTOR inhibitor dactolisib. It has a median rank of 9 among the HER2-positive cell lines and rank 15 for the luminal A cell lines. This is supported by literature where it has been found that dactolisib selectively induced cell death in breast cancer cell lines with HER2 amplification (39).

Triple-negative breast cancers are very heterogeneous and thus deriving potential targeted therapies is particularly difficult. It has been proposed that specific subgroups of triple-negative breast cancer patients can take advantage from mTOR inhibitors (40,41). In our predicted rankings, we observe the drug WYE-125132, an mTOR inhibitor, as selective for triple-negative type B cell lines (median rank 13) rather than HER2-positive cell lines (median rank 16). The same is true for the mTOR inhibitors omipalisib and PI-103 which have lower predicted ranks in the triple-negative cell lines (10 and 40) compared to the HER2-positive cell lines (11 and 46). Most breast cancers (80%) are of luminal type, either luminal A (ER+ and/or PR+/HER2−) or the more aggressive luminal B type (ER+ and/or PR+/HER2+). Our predictions suggest different effects among these subtypes for example for the PI3K/mTOR inhibitor dactolisib, that has a median rank of 9 for the luminal B cell lines and 15 for the luminal A cell lines, and for the MEK1/2 inhibitor PD0325901, that has rank 19 in luminal B cell lines and rank 25 in luminal A cell lines. The corresponding markers have been identified previously as promising targets for luminal B breast cancer therapies (42).

Comparing drug predictions across different drugs and cell lines is a difficult task regarding the different ranges of drug sensitivities and the evolution of cell lines across time due to mutations and other factors (43). We observed that ranking robustifies drug sensitivity predictions and improves overall prediction performance on the one hand. On the other hand, the ranking is influenced by differences in sensitivity ranges in the actual measurements. For example, cells are typically more sensitive to cytotoxic drugs yielding a lower dose range, even after normalization, compared to targeted drugs (cf. Figure 6). Thus, ranking predictions should be applied in practice in a semi-supervised way including biomedical knowledge and comparing subsets of drugs with similar mechanisms (e.g. EGFR inhibitors).

Besides variations of drug sensitivity measurements across different drugs, this strategy has also to cope with factors due to the cell line differences. In our screens, we used gene expression data as the main source of molecular data to characterize cell line differences. However, attempts have been made to characterize cancer cell lines with different types of molecular data including methylation, splicing and protein expression as well as CRISPR-Cas9 knockout data with respect to critical mutations which may lead to a better biological subtyping and thus to a better transferability to the in vivo situation (44). Other factors that affect cell line variability have been identified, for example technical assay effects, drug concentration ranges and even image-processing algorithms for cell counting after treatment as well as biological factors such as media composition, karyotypes, variable growth rates and drug exposure times and reproducibility studies across different centers may help in identifying and reducing the main influence factors (45).

DATA AVAILABILITY

The source code used in this work is available at https://github.com/prassepaul/mlmed_ranking.

All experiments reported in this paper are based on the GDSC database (11,12).

FUNDING

German Federal Ministry of Research and Education [01IS18044].

Conflict of interest statement. Chris Bauer is employee of MicroDiscovery GmbH Berlin. None declared by all other authors.