First measurements of low-energy cosmic rays on the surface of the lunar farside from Chang’E-4 mission

The intensity of low-energy cosmic rays on the lunar farside is consistent with that observed in the near-earth space.

Abstract

Human activities on the lunar surface are severely constrained by the space radiation dominated by cosmic rays (CRs). Here, we report the first measurements of the low-energy (about 10 to 100 MeV/nuc) CR spectra on the lunar surface from China’s Chang’E-4 (CE-4) mission around the solar minimum 24/25. The results show that for the proton, helium, CNO, and heavy-ion groups, the ratios (ratio errors) of the CE-4 fluxes to those from the near-earth spacecraft are 1.05 (0.15), 1.30 (0.18), 1.08 (0.16), and 1.24 (0.21), respectively, and to those predicted by the models [CRÈME96 and CRÈME2009] are instead [1.69 (0.17), 2.25 (0.23)], [1.66 (0.17), 1.76 (0.18)], [1.08 (0.11), 1.07 (0.11)], and [1.33 (0.18), 1.17 (0.15)]. Moreover, a notable enhancement of ³He/⁴He ratio is observed at ~12 MeV/nuc, and the CR dawn-dusk symmetry is confirmed. These results provide valuable insights into the CRs on the lunar farside surface and will benefit future lunar exploration.

INTRODUCTION

The Moon is a barren dusty body with an atmosphere about 13 orders of magnitude thinner than on Earth and without a shielding global magnetic field: the result in a drastically different radiation environment from our planet. In general, the radiations mainly associated with cosmic rays (CRs) can easily reach the lunar surface, especially for the high linear energy transfer charged particles from the CR hadronic components with energies at a few megaelectron volts and above. CRs typically consist of solar energetic particles (SEPs), galactic CRs (GCRs), and anomalous CRs (ACRs). SEPs, originating from the Sun, are frequently associated with intense solar activities like solar flares and coronal mass ejections (CMEs), and they are believed to be accelerated to the energies at megaelectron volt or above (and perhaps up to gigaelectron volt) via CME-driven shock waves (1, 2). GCRs are deemed to come from the explosions of supernovae within our own Milky Way Galaxy (3), but an extra-galactic origin for ultrahigh-energy particles cannot be ruled out (4). The supernova remnants are considered to be powerful accelerators of CR particles up to the energies ∼10¹⁷ eV, as reported in the literature (5–7). The ACR component was first discovered by Garcia-Munoz et al. (8) when an anomalous enhancement was observed in the low-energy end of the He spectrum during solar quiet times in 1972. To explain the origin of ACRs, a favored interpretation was soon proposed by Fisk et al. (9). Specifically, neutral atoms of the local interstellar medium drift into the inner heliosphere, where they are singly ionized by solar ultraviolet radiation and/or charge-exchanged with solar wind ions, and then are picked up by the solar wind and transported to the outer heliosphere where they are accelerated to hundreds of megaelectron volts, presumably at the solar wind termination shock (10, 11). ACR components have been confirmed in several species of elements with high first ionization potentials (FIPs) like H, He, N, O, Ne, and Ar in the outer heliosphere, while in the inner heliosphere all of them except H have been observed (12–14). Most elements with FIPs lower than that of H have been deflected by the interplanetary magnetic field as they approach the heliosphere because they have been ionized in the local interstellar medium (11, 14). GCRs mainly consist of protons (~87%), helium (~12%), and heavier nuclei (~1%) (15), dominating the radiation environment in deep space during solar quiet periods (16). GCRs are continuous, while SEPs are sporadic and can occur at any point of a solar cycle, although most likely at the solar maximum (17). Further details about GCRs and ACRs can be found in our recent work (18).

Gamma rays and low-energy alpha particles make a predominantly contribution to the Earth’s radiation dose, while ions of high atomic number and energy are the major contributors of deep space radiation, such as on the lunar surface (19). Astronauts and precision instruments on deep-space missions are exposed to substantial amounts of radiation, arising from high linear energy transfer ions and secondary particles (proton, neutron, gamma ray, electron, positron, heavy ions, and many other elementary particles) produced by interactions with the elements in the lunar regolith (20, 21). Arguably, one of the most serious challenges in extraterrestrial travel derive from safety concerns relating to exposure to space radiation, which effective protection measures could escalate costs beyond reach (19). Studies show that long-term exposure to high-energy radiation may carry a heavy health risk, for instance, increasing the risk of developing cataracts (22), cancer (23, 24), and degeneration of the central nervous system (25). Furthermore, the charged high-energy particles may cause the dielectric breakdown of the materials with sufficiently low conductivity within an instrument (26). Therefore, it is essential to produce an accurate estimation of the space radiation environment in consideration of the safety of both astronauts and instruments as well as the cost control. Overestimation will lead to a notable increase in manufacturing costs due to severe mass constraints in spaceflight, whereas underestimation will pose a serious threat to the safety of both astronauts and instruments.

An accurate evaluation of the radiation environment on the lunar surface, such as the determination of radiation dose rate along with the type and fluxes of radiation particles, is an important prerequisite for planning an extended human presence on the lunar surface. Before the launch of the Chang’E-4 (CE-4) mission, the assessment of the lunar radiation environment was mainly based on the data obtained by the Radiation Monitor (RADOM) and the Cosmic Ray Telescope for the Effects of Radiation Experiment (CRaTER) onboard the Chandrayaan-1 and the Lunar Reconnaissance Orbiter (LRO) spacecraft, respectively. The Chandrayaan-1/RADOM, a miniature dosimeter-spectrometer, was aimed at monitoring the local radiation environment both en route and in lunar orbit, including measurements of the total absorbed dose rate, the flux of surrounding energetic particles, and the spectrum of the deposited energy from high-energy particles (27). The LRO/CRaTER is designed to characterize the radiation environment to serve NASA’s future lunar return missions. The LRO/CRaTER linear energy transfer measurements are used to constrain the models of the biological effects of ionizing radiation combined with the models of radiation transport through materials in the lunar environment, and they also provide valuable information about the radiation effects on electronic systems (28).

The lunar radiation environment is far more complex than previously thought, with many factors likely to affect it, such as the lunar exosphere, dust grains, and lunar magnetic anomalies. The lunar exosphere is rather tenuous at around 10⁻⁹ mbar: This was first detected by in situ measurements of the Apollo missions and found to consist of atoms and light molecular species, such as Ar, He, Ne, Na, K, and H (29). Dust grains above the surface are regarded to come from ejecta produced by the continual bombardment of the Moon by interplanetary micrometeoroids and small grains lifted by plasma-induced near-surface electric fields (30). The existence of lunar magnetic anomalies, i.e., regions of local magnetization, has been confirmed (31–33). Some magnetic anomalies have surface fields of up to hundreds of nanoteslas. The landing site of the CE-4 (177.6°E, 45.4°S) (34) is located near the edge of the largest lunar magnetic anomaly and called the Imbrium antipode, centered at (162°E, 33°S) with a radius larger than 600 km (32); however, the influence of the major antipodal impact on the charged particles downstream remains unclear. Furthermore, the radiation environment near the lunar surface may also be affected by many other factors, such as the solar wind reflected particles, the local terrain obscuring, and the secondary particles produced by the interactions between CRs and the nuclei of lunar regolith.

As reported by Mazur et al. (35), a clear altitude dependence of the dose rate was found by the LRO/CRaTER. The Chandrayaan-1/RADOM also observed the variation of the particle flux at lunar altitudes in the range between 92 and 118 km (27). On 3 January 2019, China successfully sent a lander (CE-4) and a rover (Yutu-2) to the Von Kármán crater in the South Pole Aitken basin, the largest known impact crater on the Moon and one of the largest in the solar system (36). They are both still active at the time of writing. One of the payloads onboard the lander is the Lunar Lander Neutrons and Dosimetry (LND) experiment. To have an insight into the radiation environment, Zhang et al. (37) investigated the radiation dose rate and the linear energy transfer spectrum on the surface of the lunar farside based on the data collected by the CE-4/LND during the first two lunar days. It was found that the average absorbed dose rate from charged particles is consistent with the LRO/CRaTER measurements when the LRO flew over the location of the CE-4. They also propose that the contribution of neutral particles (neutrons and gamma rays, mainly produced by the interactions between CRs and the lunar regolith) to the absorbed dose rate is nonnegligible with a fraction up to (23 ± 17) % around solar minimum. To evaluate the influence of the abovementioned factors (the lunar exosphere, the dust grains, and the lunar magnetic anomalies, etc.) on the CRs, an effective method is to compare the CR spectral difference between the CE-4 measurements and those made from space.

In addition, chemistry modifications and space weathering of physical matter by the radiation interactions of energetic particles at megaelectron volt are ubiquitous on the Moon due to the strong penetration ability of these particles (26). As an almost airless body, the radiation interactions of the Moon can deepen our understanding of radiation-induced chemistry and space weathering. For example, the radiation interactions at the Moon can be applied to detect the near-surface deposits of water ice via the absorption of low-energy neutrons produced by CR interactions [see (38) and references therein]. CRs are an important source of chemical modification and space weathering, and thus, the CR spectrum on the lunar surface plays a key role in the studies of the evolution of the lunar surface. However, our data of the CR spectrum on the lunar surface are limited and those derived from CR particle flux models are generally taken as an approximate substitution. Therefore, the CR spectrum on the lunar surface can provide these CR-related studies with actual measurements and tools to refine related models (39–43). Moreover, the differential flux ratio of ³He to ⁴He, which is a powerful tool to constrain the CR propagation models, was measured in various experiments as reported by Wu and Chen (44) and the literature therein. These experimental results were in the energy range between ~100 MeV/nuc and several GeV/nuc, with fewer below ~100 MeV/nuc.

Benefiting from the CE-4/LND CR measurements, we aim to (i) report the low-energy CR spectrum on the surface of the lunar farside during the solar quiet period (January 2019 to February 2020), (ii) inspect the influence of lunar surroundings on the CR spectrum on the lunar surface, (iii) calculate the differential flux ratio of ³He to ⁴He at low energies (about 10 to 100 MeV/nuc), and (iv) verify the CR dawn-dusk symmetry.

RESULTS

CR energy spectrum

The low-energy CR spectra measured by the CE-4/LND during the weakest solar minimum 24/25 (18, 45, 46) are shown in Fig. 1. These ions are separated into four groups according to their respective atomic number (Z): protons (Z = 1), He (Z = 2), CNO group (Z = 6 to 8), and heavy-ion (HI) group (Z ≥ 10, including Ne, Na, Mg, Al, Si, S, Ar, Ca, Fe, and Ni). Besides the CE-4/LND measurements, the CR spectra both observed by the near-earth spacecraft [Advanced Composition Explorer (ACE), Solar and Heliospheric Observatory (SOHO), and Solar Terrestrial Relations Observatory Ahead (STEREO-A)] and modeled by the Cosmic Ray Effects on Micro-Electronics (CRÈME) models (39, 40) are also plotted in the same period. In Table 1, we list the time interval of the CE-4/LND that is studied here. Of note here is that the Moon was outside of the Earth’s magnetotail during the CE-4/LND working periods. To make a more intuitive and quantitative comparison, the differential flux ratios of the CE-4/LND measurements to the spacecraft observations and the numerical modeling results are calculated and displayed in Fig. 2, and the weighted average flux ratios of each particle group over different kinetic energies are shown in Fig. 3. From Fig. 3, we can see that the CE-4/LND data are comparable to those observations from the near-earth spacecraft within 1.7 SD (1.7σ) for all particle groups, while the flux ratios of the CE-4/LND measurements to the CRÈME predictions reach up to a level of 1.7 with more than 4.0σ for the proton. A notable discrepancy in the predictions between the CRÈME96 (39) and CRÈME2009 (40) models at energies below ~20 MeV/nuc for the proton and He and below ~5 MeV/nuc for the CNO and HI groups, respectively, is also worth noting, ascribing to the differences in their respective embedded dependency models (Fig. 1). To be specific, the CRÈME96 model may suffer partial contamination from the SEPs at low energies because of its use of the Nymmik model (47), while the revised Nymmik model (48) is applied in the CRÈME2009 code and the influence from SEPs is fully removed.

Fig. 1. Comparisons of the CR fluxes between the CE-4/LND measurements and the in situ measurements made at 1 AU and the predictions of the CRÈME models.

(A) For proton, (B) for He, (C) for CNO group, and (D) for HI group (Ne, Na, Mg, Al, Si, S, Ar, Ca, Fe, and Ni). Note that EPHIN, SIS and EPAM, and LET are the four instruments aboard the SOHO, ACE, and STEREO-A spacecraft, respectively. See the text for details.

Table 1. Time interval used in this study from the CE-4/LND.

No.	Start time	End time
1	2019-01-03 06:00:00	2019-01-12 11:00:00
2	2019-01-30 17:00:00	2019-02-10 07:00:00
3	2019-03-30 12:00:00	2019-04-10 08:00:00
4	2019-07-27 02:00:00	2019-08-06 09:00:00
5	2019-08-25 03:00:00	2019-09-05 09:00:00
6	2019-09-24 02:00:00	2019-10-03 04:00:00
7	2019-10-23 02:00:00	2019-11-03 09:00:00
8	2019-11-22 04:00:00	2019-12-03 07:00:00
9	2019-12-21 02:00:00	2020-01-01 10:00:00
10	2020-01-20 02:00:00	2020-01-31 07:00:00
11	2020-02-18 02:00:00	2020-03-01 05:00:00

Fig. 2. CR flux ratios of the CE-4/LND measurements to the in situ measurements made at 1 AU and to the CRÈME modeling results.

(A) For proton, (B) for He, (C) for CNO group, and (D) for HI group (Ne, Na, Mg, Al, Si, S, Ar, Ca, Fe, and Ni). The ratio of 1.0 is indicated by a red dotted line for reference.

Fig. 3. Similar to Fig. 2, but are averaged over the energies of each group.

See the text for details.

From the proton spectrum shown in Fig. 1A, it is found that the observations from the CE-4/LND (red upward triangles) are comparable with those from the SOHO/EPHIN (Electron Proton Helium Instrument; blue squares) and the STEREO-A/LET (Low-Energy Telescope; violet diamonds) with an average flux ratio of (1.05 ± 0.15) (violet bar in the first column of Fig. 3), but the comparisons of these observed results with those predicted by the models (aquamarine solid and lime dashed lines for the CRÈME96 and CRÈME2009 models, respectively) exhibit obvious deviations. Specifically, the observed fluxes are smaller than the predictions from the CRÈME96 model at energies below ~10 MeV/nuc, while for energies above ~10 MeV/nuc the opposite is true by a respective factor of (0.69 ± 0.17) and (1.25 ± 0.23) (green and orange bars in the first column of Fig. 3 for the CRÈME96 and CRÈME2009 models, respectively). There is also an obvious difference in the predictions between the CRÈME96 and CRÈME2009 models in the energy range between ~20 and 50 MeV/nuc, where the CRÈME2009 model gives a relatively larger prediction than the CRÈME96 model. The proton flux ratios of the CE-4/LND measurements to the near-earth spacecraft observations are shown in Fig. 2A, along with are those of the CE-4/LND measurements to the CRÈME modeling results. For the flux ratios of the CE-4/LND measurements to the spacecraft observations, the values of these data points (filled violet circles) are comparable to 1.0 within 1.6σ with slight fluctuations. As for the flux ratios of the CE-4/LND measurements to the CRÈME modeling results (green diamonds and orange squares for the CRÈME96 and CRÈME2009 models, respectively), they vary in the ranges of (1.20 ± 0.15 to 2.54 ± 0.51) and (1.88 ± 0.22 to 3.38 ± 0.42) for CRÈME96 and CRÈME2009 at energies ranging in (9.77 and 24.88) MeV/nuc, respectively. In addition, a prominent enhancement centered at ~20 MeV/nuc, which corresponds to the contribution of the ACR component, was observed in the CR proton spectrum by the Voyager spacecraft around the solar minimum spanning from the years 1993 to 1999 [at 63.7 and 49.6 astronomical units (AU) for Voyager 1 and Voyager 2, respectively] (14), but no such enhancement is observed in our measurements, which confirms that these low-energy (~10 to ~50 MeV) protons are of galactic origin during solar quiet times in the inner heliosphere.

The energy spectrum of He is shown in Fig. 1B. It is evident that the agreement of energy spectrum above ~5 MeV/nuc between the CE-4/LND (red downward and red upward triangles for ⁴He and ³He + ⁴He, respectively) and the spacecraft [orange hexagons, blue squares, and violet diamonds for ⁴He, ³He + ⁴He, and ³He + ⁴He from the ACE/SIS (Solar Isotope Spectrometer), the SOHO/EPHIN, and the STEREO-A/LET, respectively] is relatively good, while the comparisons of the ³He + ⁴He predictions from the CRÈME models (aquamarine solid and lime dashed lines for the CRÈME96 and CRÈME2009 models, respectively) with those observations from the CE-4/LND and the spacecraft exhibit obvious deviations in general. We find that the ³He + ⁴He observations from the CE-4/LND are consistent with those from the spacecraft (SOHO/EPHIN, blue squares in Fig. 1B) within 1.7σ, as shown by the violet bar in the second column of Fig. 3, and are larger than those predictions made by the CRÈME models as well by a respective average factor of (0.66 ± 0.17) and (0.76 ± 0.18) (green and orange bars in the second column of Fig. 3 for the CRÈME96 and CRÈME2009 models, respectively). The predictions from the CRÈME96 and CRÈME2009 models above ~20 MeV overlap almost completely. It seems that the predicted curve from the CRÈME96 model can reflect the variation trend of the combined data collected by the ACE/EPAM (Electron, Proton, and Alpha Particle Monitor; green thin-cross symbols for ³He + ⁴He) and the STEREO-A/LET (violet thick-cross symbols for ⁴He) at energies below ~5 MeV/nuc with limited accuracy. Also, we can see an enhancement centered at ~20 MeV/nuc (see lime dashed line) in the energy range between ~10 and ~50 MeV/nuc, which can be ascribed to the contribution of the ACR component (49). In addition, the ³He + ⁴He flux ratios of the CE-4/LND measurements to the spacecraft observations and the CRÈME modeling results are shown in Fig. 2B. For the flux ratio of the CE-4/LND measurement to the spacecraft observation (SOHO/EPHIN, blue squares in Fig. 1B), the values of these data points (filled violet circles), varying in the range of (1.17 ± 0.22 to 1.42 ± 0.27) at energies from 14.18 to 24.81 MeV/nuc, are consistent with 1.0 within 1.6σ. Concerning the flux ratios of the CE-4/LND measurements to the CRÈME modeling results (green diamonds and orange squares for the CRÈME96 and CRÈME2009 models, respectively), they vary in the ranges of (1.57 ± 0.25 to 1.82 ± 0.29) and (1.66 ± 0.33 to 1.94 ± 0.31) for CRÈME96 and CRÈME2009, respectively. Also, the CE-4/LND can distinguish He isotopic components, ³He and ⁴He, which conduces to the extraction of the flux ratio of ³He to ⁴He, as will be shown in the next subsection.

Figure 1C presents the energy spectrum for the CNO group. The predictions from the CRÈME models (aquamarine solid and lime dashed lines for the CRÈME96 and CRÈME2009 models, respectively) match the observations from the ACE/SIS (orange hexagons) relatively closely, but are slightly lower than the STEREO-A/LET (violet diamonds) measurements. Meanwhile, the observations from the CE-4/LND (red upward triangles) are consistent with those from the ACE/SIS and comparable to those predictions made by the CRÈME models as well as with fluctuations. More specifically, the CNO observations from the CE-4/LND are consistent with those predictions from the CRÈME96 and CRÈME2009 models within 1.0σ with a respective ratio of (1.08 ± 0.11) and (1.07 ± 0.11) (green and orange bars in the third column of Fig. 3 for the CRÈME96 and CRÈME2009 models, respectively) and are also comparable to those from the ACE/SIS with a ratio of (1.08 ± 0.16) within 1.0σ (violet bar in the third column of Fig. 3). Furthermore, the CNO flux ratios of the CE-4/LND measurement to the ACE/SIS observations are shown in Fig. 2C, together with those of the CE-4/LND measurements to the predictions made by the CRÈME models. As for the flux ratios of the CE-4/LND measurements to the ACE/SIS observations, these data points (filled violet circles) fluctuate slightly around the line with a value of 1.0. For the flux ratios of the CE-4/LND measurements to the CRÈME modeling results (green diamonds and orange squares for the CRÈME96 and CRÈME2009 models, respectively), they overlap almost completely and vary in the ranges of (0.77 ± 0.28 to 5.82 ± 2.25) and (0.78 ± 0.29 to 5.49 ± 2.13) for CRÈME96 and CRÈME2009 in the energy range between 18.45 and 66.75 MeV/nuc, respectively. For some energy points beyond the ACE/SIS measurements, the differential flux values for ratio calculations are taken from those predictions made by the CRÈME2009 model as substitutions because CRÈME2009 can reproduce the ACE/SIS observations comparatively well at the energies nearby. Besides, we can see a bump centered at ~10 MeV/nuc due to the ACR component as well (49), as shown by the CRÈME2009 model (lime dashed line). It is also essential to point out that the CNO spectra of the ACE/SIS and the STEREO-A/LET are separately extracted from their respective spectra for elements C, N, and O. Here, the spectrum with data points detected directly by the ACE/SIS [STEREO-A/LET] is specified as the original spectrum. For each component element, the data points detected directly by the ACE/SIS [STEREO-A/LET] in the original spectrum are relatively sparse. To obtain an extensive spectrum with denser data points, the interpolation with the Bezier Curves method (50) is applied to the original spectrum of each component element. However, only the nominal values of differential fluxes for these interpolated data points can be acquired based on this method. To further estimate the absolute error of the differential flux for a specific interpolated data point in the extensive spectrum, the average relative error of differential fluxes of its two nearest data points on both sides in the original spectrum is taken as its relative error, and then its corresponding absolute error can be obtained simply. As for the spectrum of the CNO group, the kinetic energy value is adopted directly from those of the energy channels of its component elements, and the nominal value of differential flux for the corresponding energy is calculated by summing up that of each component element. Concerning the absolute error of the differential flux, it is the summation of those from its component elements in quadrature. On the basis of the strategy mentioned above, data points of the CNO group from the ACE/SIS [STEREO-A/LET] can be acquired, as shown in Fig. 1C, marked as CNO(SIS) [CNO(LET)] in the legend.

The energy spectrum for the HI group is presented in Fig. 1D, which is obtained by following the same methodology applied to the CNO group. The observations from the ACE/SIS are in comparatively good agreement with the predictions from the CRÈME models at energies above ~40 MeV/nuc, while divergency is seen between the predictions and those from the ACE/SIS and the STEREO-A/LET at energies below ~40 MeV/nuc. Moreover, the data points measured by the CE-4/LND fluctuate around those made by the near-earth spacecraft due to the relatively low statistics and complex constituents of the HI group. The HI observations made by the CE-4/LND are consistent with those from the ACE/SIS within 1.2σ with a ratio of (1.24 ± 0.21) (violet bar in the fourth column of Fig. 3) and are also comparable to the predictions from the CRÈME96 and CRÈME2009 models within 1.9σ with a respective ratio of (1.33 ± 0.18) and (1.17 ± 0.15) (orange and green bars in the fourth column of Fig. 3). Besides, the HI flux ratios of the CE-4/LND measurements to the ACE/SIS observations as well as those of the CE-4/LND measurements to the CRÈME modeling results are shown in Fig. 2D. Concerning the flux ratios of the CE-4/LND measurements to the ACE/SIS observations, these data points (filled violet circles) fluctuate intensely around the line with a value of 1.0 at energies between 30.45 and 116.03 MeV/nuc. The predictions of CRÈME96 are larger than those made by CRÈME2009 by a factor of (0.15 ± 0.23) for the flux ratios of the CE-4/LND measurements to the CRÈME modeling results (green diamonds and orange squares for the CRÈME96 and CRÈME2009 models, respectively).

We can conclude that the CR fluxes on the lunar surface measured by the CE-4/LND instrument at energies ~10 to ~100 MeV/nuc are consistent with those observed near the Earth. Specifically, the CE-4/LND measurements are comparable to the spacecraft observations within 1.0σ for the proton and the CNO group. The ratios for He and the HI group are (1.30 ± 0.18) and (1.24 ± 0.21), consistent with 1 within 1.7σ and 1.2σ, respectively. Because the higher-energy particles are less sensitive to the lunar physical environment, we can infer that the higher-energy CRs on the lunar surface are likely to be comparable to those near the Earth. As mentioned earlier, the largest magnetic anomaly Imbrium antipode is located northwest of the CE-4/LND. Therefore, the influence of lunar magnetic anomalies, as well as other lunar environment factors on the CR spectrum (>~10 MeV/nuc), is negligible. Of note here is that systematic errors for the CE-4/LND and the near-earth spacecraft have been considered in this paper. Specifically, a relative systematic error of 10% is separately conservatively assigned to the CE-4/LND and the ACE/SIS, SOHO/EPHIN, and STEREO-A/LET spacecraft, which mainly arises from various factors when determining the geometric factor, such as the geometry configuration and the detection efficiency.

In addition, it is essential to point out that the weighted averages of the flux ratios over different energies for each particle group shown in Fig. 3 are derived from the data of Fig. 2 with a standard weighted least-square procedure method, of which the detailed description can be found in the literature [(51), pp. 15–18].

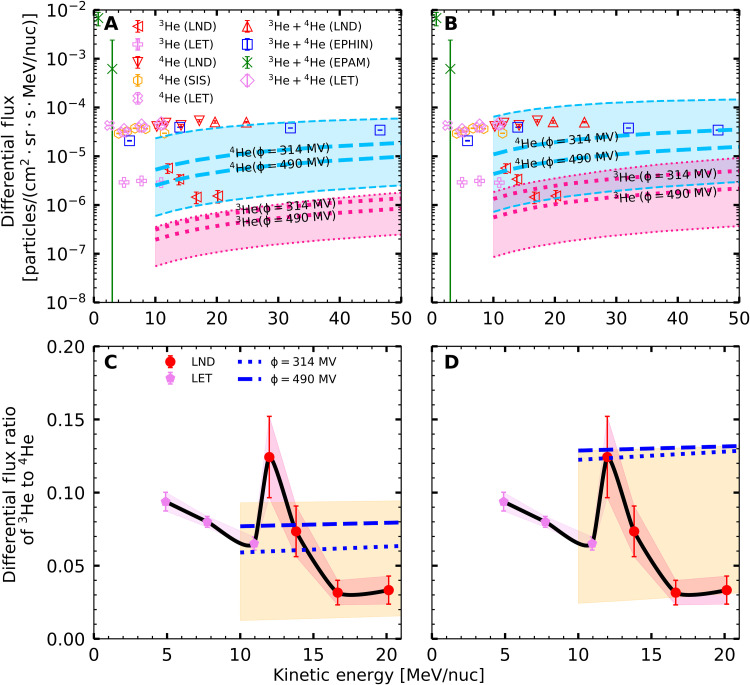
Differential flux ratio of ³He to ⁴He

The differential flux ratios of ³He to ⁴He above ~100 MeV/nuc have been reported in previous experiments, such as the balloon-borne experiments [IMAX92 (52, 53), BESS (54), and BESS-Polar II (55)] and the space instruments [AMS-01 (56) and PAMELA (57)]. Here, we show the results based on the combined data collected by the CE-4/LND and the STEREO-A/LET along with the predictions from the Galactic Propagation (GALPROP) model (41) within the energy range between ~5 and ~20 MeV/nuc. The predictions from the GALPROP model in the left column (Fig. 4, A and C) and the right column (Fig. 4, B and D) are based on a conventional reacceleration model (58, 59) and a plain diffusion model (59), respectively, of which the isotopic abundances have been tuned to reproduce those from the ACE observations (60). The subfigures in the upper row (Fig. 4, A and B) show the comparisons of differential fluxes between the spacecraft observations and the GALPROP model’s predictions for ³He and ⁴He with solar modulation potentials (Φ) ranging from 100 to 1000 MV; the corresponding value ranges of differential fluxes for ³He and ⁴He are indicated by shaded pink and shaded sky-blue areas limited by two thin dotted and two thin dashed lines, respectively. The predicted differential fluxes of ³He and ⁴He with two different modulation potentials, Φ = 314 and 490 MV, are indicated by thick dotted pink and thick dashed sky-blue lines, respectively. In the GALPROP model, Φ is an important parameter in determining CR fluxes, and we have chosen two values (314 and 490 MV) to represent the modulation level during the period 2019–2020. Φ = 314 MV is directly obtained from http://cosmicrays.oulu.fi/phi/Phi_mon.txt, and Φ = 490 MV is calculated with the method from Usoskin et al. (61) using the average Oulu neutron monitor count rates during the working periods of the CE-4/LND. The comparisons of flux ratios of ³He to ⁴He between the observations from the CE-4/LND and those from the STEREO-A/LET and the predictions from the GALPROP model are shown in Fig. 4 (C and D). The filled red circles [filled violet pentagons] with error bars denote the observation from the CE-4/LND [STEREO-A/LET] and the shaded red [shaded violet] areas correspond to the 1 SD band, while the dotted and dashed blue lines denote the predictions from the GALPROP model with Φ = 314 and 490 MV, respectively. The shaded orange areas show the predicted value range of flux ratio of ³He to ⁴He with modulation potentials Φ in the range between 100 and 1000 MV from the GALPROP model. It is worth noting that the lower limit of kinetic energy for the GALPROP model is 10 MeV/nuc; thus, there is no prediction at energies below 10 MeV/nuc.

Fig. 4. The CR energy spectra of ³He and ⁴He and the ratios of ³He to ⁴He.

(A and B) The thick dashed sky-blue [dotted pink] lines denote the predictions from the GALPROP model with the specified modulation potentials for ⁴He [³He], and the shaded sky-blue [pink] areas limited by two thin dashed sky-blue [dotted pink] lines correspond to the value range of the GALPROP modeling results with modulation potentials Φ = 100 to 1000 MV for ⁴He [³He]. (C and D) The filled red circles with error bars denote the observation from the CE-4/LND and the shaded red areas show the 1 SD band, while the filled violet pentagon with error bars and the shaded violet areas denote the observation from the STEREO-A/LET. The dashed and dotted blue lines denote the GALPROP modeling results with Φ = 490 and 314 MV, respectively, and the shaded orange areas denote the value range of the predictions from the GALPROP model with Φ = 100 to 1000 MV. Note that the predictions in (A) and (C) are from the GALPROP conventional reacceleration model, and in (B) and (D) are from the GALPROP plain diffusion model.

The observed flux ratios of ³He to ⁴He in the energy range between ~5 and ~20 MeV/nuc are within (12.43 ± 2.78) %. Also, we can see a prominent enhancement at ~12 MeV/nuc. The values of the observations first decrease gradually from (9.38 ± 0.64) % to (6.52 ± 0.45) %, with increasing kinetic energy in the range between 4.90 and 10.95 MeV/nuc, and then increase sharply to reach a peak (12.43 ± 2.78) % at 11.99 MeV/nuc. With the continuous increase in the kinetic energy, the values of the observations decrease gradually again to the minimum value of (3.16 ± 0.84) % at 16.66 MeV/nuc and then remain relatively stable. The GALPROP model cannot give a good prediction to the observation from the CE-4/LND and the third data point from the STEREO-A/LET. The values of the observations vary dramatically, while those of the GALPROP modeling results remain stable with the increase of kinetic energy. The anomaly may ascribe to the contribution of the ACR component, which can be further confirmed by the poor consistency of differential fluxes between the observations and the predictions in the energy range between ~10 and ~50 MeV/nuc for He shown in Fig. 4 (A and B). As mentioned earlier, there is an enhancement in the energy spectrum due to the ACR component in the energy range between ~10 and ~50 MeV/nuc for He shown in Fig. 1B. The predicted differential fluxes of ³He and ⁴He based on the conventional reacceleration model with Φ = 314 and 490 MV shown in Fig. 4A are both lower than the observations, while those based on the plain diffusion model perform a little better shown in Fig. 4B. However, the difference between the observations and the predictions in the flux ratio of ³He to ⁴He is still large. Of note is that the weighted average (51) of the differential fluxes of ⁴He from the CE-4/LND has been used to calculate the flux ratios of ³He to ⁴He in consideration of its relatively uniform distribution in the energy range of ³He.

Dawn-dusk symmetry of the CR spectrum

The differential flux ratios between the dawn and dusk sides of these particle groups are shown in Fig. 5. The flux ratios from the spacecraft lie on the line with a value of 1.0 within the error bar for all particle groups, which indicates that the CR flux in deep space is isotropic as expected. The flux ratios from the CE-4/LND have similar distributions, although fluctuations in the flux ratios for the CNO and HI groups are observed, which could be attributed to the relative low statistics of these two particle groups. Thus, both the low-energy CR spectra in the lunar local morning and the lunar local afternoon are consistent. The dawn-dusk symmetry in the low-energy CR spectrum during solar quiet times around the solar minimum is confirmed, which could also be extended to the higher energy range of the CR spectrum since the solar modulation weakens with the increase of the energies of particles.

Fig. 5. The ratios of the observed CR fluxes in the lunar local morning to those in the lunar local afternoon.

(A) For proton, (B) for He, (C) for CNO group, and (D) for HI group (Ne, Na, Mg, Al, Si, S, Ar, Ca, Fe, and Ni). The ratio of 1.0 is indicated by a red dotted line for reference.

DISCUSSION

Crewed missions to the Moon are essential for both scientific and commercial endeavors. The safety of astronauts and the reliability of sensitive instruments are severely compromised by the harsh radiation environment at the lunar surface: However, our understanding of its nature is far from complete.

In this study, on the basis of the CE-4/LND measurement around the extraordinarily quiet solar cycle 24/25 minimum, the low-energy CR spectrum on the surface of the lunar farside is reported and it is further compared with measurements from several spacecraft near the Earth, such as the ACE, the SOHO, and the STERE-A. The differential flux ratio of ³He to ⁴He is extracted, and the dawn-dusk symmetry of the CR spectrum on the lunar surface is considered too.

Our analysis shows that the CR spectra on the lunar surface are comparable to the observations from the spacecraft within 1.7σ. Specifically, the measurements made by the CE-4/LND are consistent with the spacecraft observations within the error bar for the proton and the CNO group. As for He and the HI group, the observations made by the spacecraft are comparable with those made by the CE-4/LND within 1.7σ. Thus, the CR spectra observed by the CE-4/LND ranging at energies ~10 to ~100 MeV/nuc are consistent with those detected by the spacecraft near the Earth: Accordingly, we can conclude that the influence of the physical environment near the lunar surface is negligible for these low-energy CRs. In addition, the CR spectra, in particular, the CR proton spectrum measured by the CE-4/LND, can provide in situ precise input data for CR-related studies like the interactions between CRs and the lunar surface, which can enhance our understanding on the proton, neutron, and gamma emission spectroscopy from the lunar surface. Further, they can also be used to test theoretical models such as CRÈME, which diverge the CE-4/LND measurements remarkably for the proton. Meanwhile, the flux ratios of ³He to ⁴He from the CE-4/LND diverge considerably from the predictions of the GALPROP model: This can be used to improve the model and other related theoretical models. We confirm the dawn-dusk symmetry of the CR spectrum on the lunar surface, which will guide the selections of landing times for future crewed lunar missions and extravehicular activities on the lunar surface.

Although these findings can deepen our understanding of the radiation environment on the lunar surface, they are still far from exhaustive: The energy range of the CR spectrum measured by the CE-4/LND is limited, and the precisions of some measurements need to be improved. At present, the CE-4/LND is still in operation on the lunar farside and continuing harvesting data. This will lead to the production of more precise spectra of the various elements of interest.

MATERIALS AND METHODS

CR observations

In this work, we have used CR measurements from two sources: One is from the LND instrument aboard the CE-4 mission, and the other is from three near-earth spacecraft in space (ACE, SOHO, and STEREO-A). The ACE and SOHO spacecraft orbit the Sun-Earth first Lagrangian (L1) point in a halo orbit, as illustrated in Fig. 6. The STEREO-A is a space-based observatory orbiting the Sun just inside 1 AU. These data were collected from 3 January 2019 to 1 March 2020 (see Table 1 for details) during the solar minimum 24/25. Note that the working periods of these instruments are not identical due to the different cadences of their data products used in this work. However, the influence of these differences is essentially negligible considering the relatively long total working times. The 5-min level-2, 256-s level-2, 10-min level-1, and 1-min level-3 average flux data [in units of particles/(cm² · sr · s · MeV/nuc)] of the ACE/EPAM, the ACE/SIS, the STEREO-A/LET, and the SOHO/EPHIN are applied, respectively. A brief introduction to these instruments is as follows.

Fig. 6. Illustration of the relative positions of the ACE, SOHO, and ARTEMIS-P1 spacecraft in the X-Y GSE plane during the working periods of the CE-4/LND.

The ARTEMIS mission consists of two identical probes, P1 and P2, in orbit around the Moon (74), whose trajectories can approximate the position of the Moon. The bow shock model and the magnetopause model are obtained from Fairfield (75). R_E is the radius of the Earth.

The CE-4 mission, which is the first mission to the surface of the lunar farside, is composed of a lander (CE-4), a rover (Yutu-2), and a relay satellite [Queqiao relay satellite, which was successfully launched on 21 May 2018 and is currently orbiting the Earth-Moon second Lagrangian (L2) point]. Four scientific payloads are aboard the lander and the rover, respectively. More details of the CE-4 mission can be found in the literature (62). The LND instrument aboard the lander is developed to determine the dose rate and the linear energy transfer spectrum as well as the particle flux on the surface of the lunar farside, which contributes to the studies related to the lunar surface environment and heliospheric science (36). The results of the time series–based dose rate and the linear energy transfer spectrum have been reported on the basis of the data collected by the LND during the first two lunar days (37), and on 6 May 2019, the LND instrument measured its first SEP event on the lunar farside (63). The LND instrument, mounted in the payload compartment of the lander, is composed of an electron box (EB) and a sensor head (SH). The EB is connected with the instrument control unit as the electrical and data interface of the LND with the lander. The SH is mounted close to the upper deck of the lander with a resealable door to ensure an unobstructed field of view into the sky. The door keeps open during working hours in the lunar daytime but closed during the cold lunar night to protect the payloads inside. The SH has a telescope configuration, a stack of ten 500-μm-thick dual-segment Si solid-state detectors labeled A through J as shown in figure 4 of (36), to ensure the detection of charged-particle radiations and the identification of its composition. The differential flux of a specific type of charged particles in a certain kinetic energy range can be obtained on the basis of the information of their count rate, geometric factor, and kinetic energy range interval. More details about the LND instrument can be found in the literature (36, 64).

The ACE spacecraft was launched on 25 August 1997 and has been continuously monitoring the solar wind plasmas, interplanetary magnetic fields, and energetic particles (both SEPs and CRs) at the Sun-Earth L1 point over two consecutive solar cycles. The SIS and the EPAM are the two main instruments aboard the ACE spacecraft. The SIS instrument is designed to measure the isotopic compositions of some energetic nuclei from He to Ni (Z = 2 to 28) with energies ranging from ∼10 to ∼100 MeV/nuc (65). The EPAM instrument consists of five telescopes of three types: two Low Energy Foil Spectrometers (LEFS) designed for the measurement of the fluxes and directions of electrons above 30 keV, two Low Energy Magnetic Spectrometers (LEMS) for the fluxes and directions of ions, and one Composition Aperture (CA) for the compositions of ions (66). For more information about the ACE mission, the reader can refer to the literature (67).

The SOHO spacecraft aims to study the Sun from its deep core to the outer corona and the solar wind (68). There are 12 payloads in total aboard the SOHO spacecraft, including the Comprehensive Suprathermal and Energetic Particle Analyzer (COSTEP). The COSTEP is designed to measure the energetic particles emitted by the Sun, and it consists of two instruments: the EPHIN and the Low Energy Ion and Electron Instrument (LION). Resembling the ACE/SIS, the SOHO/EPHIN measures the fluxes of energetic particles (electron, proton, and helium) from the solar corona during large solar events, while particles from GCRs and ACRs are measured during the solar quiet times. Further details of the SOHO mission can be found in the literature (68).

The STEREO mission, consisting of two nearly identical spacecraft, STEREO-A and STEREO Behind (STEREO-B), is in orbit around the Sun at ~1 AU (69, 70). The STEREO-A is moving ahead of the Earth, and the STEREO-B is moving behind. The STEREO, carrying four instrument packages, was launched on 25 October 2006. The LET is one of four sensors making up the SEP instrument of the In situ Measurements of Particles and CME Transients (IMPACT) investigation. The LET can measure the elemental compositions, energy spectra, angular distributions, and arrival times of ions (Z = 1 to 28) over the energy range between ~3 and ~30 MeV/nuc and identify the rare isotope ³He and trans-iron nuclei with Z = 30 to 83 (70). Of note here is that communications with the STEREO-B have been lost since 1 October 2014 due to multiple hardware anomalies affecting control of the spacecraft orientation. More details about the STEREO and the LET can be found in (69, 70), respectively.

CR models

For comparison with spacecraft measurements, two widely used CR numerical models are used here: the CRÈME (39, 40, 71, 72) and the GALPROP (41).

The CRÈME model (https://creme.isde.vanderbilt.edu/), first proposed by the Naval Research Laboratory, is a widely used semi-empirical model that can provide a numerical evaluation of the radiation effects on the electronic systems in spacecraft orbiting near the Earth (39, 40). CRÈME96 is an upgraded version released in 1996, which can offer a more accurate description of the solar cycle variation in the GCR flux by relating the solar cycle variation to the historical sunspot number (39). The contribution to the CR spectrum from the ACR component is also included in this version. In addition, an announcement stating that the CRÈME96 model is valid only for the years between 1950 and 1997 was made on the CRÈME website in 2010. Concurrently, CRÈME2009, a revised version, was released. However, CRÈME96 has been extensively used after 1997 (73). In this work, both results from the CRÈME96 and CRÈME2009 models were adopted. CRÈME2009 is the latest improved version, of which the method to calculate the Wolf number has been optimized compared to that of CRÈME96 (73). CRÈME2009 is more advantageous for the prediction of the modulation level up to 1 year beforehand by using the sunspot number as a representation of solar modulation compared with other models (40).

The GALPROP model (https://galprop.stanford.edu/webrun/), a numerical code for the calculations of the propagation of relativistic charged particles and the diffuse emissions produced during their propagation, is widely used in high-energy astrophysics and its related areas. The GALPROP code has been a sophisticated, efficient, and configurable tool for high-energy astrophysics through the evolution of several decades since the 1990s. The code is devoted to incorporating as many realistic astrophysical inputs as possible, together with the latest theoretical developments, which aims to calculate the propagation of CR nuclei, antiprotons, electrons, and positrons, as well as the diffuse gamma rays and synchrotron emission in the same framework (41). In this work, the GALPROP webRun v54, the latest stable version, was used.

Calculation method

For a specified kind of particles detected in the channel at energies between E_i and E_f, its differential flux F, in units of particles/(cm² · sr · s · MeV/nuc), can be calculated by

$$\mathit{F}=\mathit{C}(\text{GF}·\mathrm{\Delta }\mathit{t}·\mathrm{\Delta }\mathit{E})$$ (1)

where GF is the geometric factor for the detection of these particles in units of cm² · sr; Δt is the measurement live time of a good data record, which can be substituted by the cadence of data product approximately under conditions of low and moderate count rates; ΔE, in units of MeV/nuc, is the interval of the energy channel E_f – E_i; and C is the total number of signal counts accumulated in Δt. The corresponding error of F, δF, can be given as

$$\mathrm{\delta }\mathit{F}=\mathit{F}·\sqrt{{(\mathrm{\delta }\mathit{C}/\mathit{C})}^2+{(\mathrm{\delta }\mathit{G}\mathit{F}/\mathit{G}\mathit{F})}^2}$$ (2)

where δC and δGF are the errors of C and GF, respectively.

The average value of differential flux in a specified period can be obtained by

$$\overline{\mathit{F}}={\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}({\mathit{F}}_{\mathit{i}}·\mathrm{\Delta }{\mathit{t}}_{\mathit{i}})/{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}\mathrm{\Delta }{\mathit{t}}_{\mathit{i}}$$ (3)

where N is the total number of good data records in this specified period, and F_i and Δt_i are the differential flux and the measurement live time of the ith good data record, respectively. The corresponding error can be written as

$$\mathrm{\delta }\overline{\mathit{F}}=\sqrt{{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}{(\mathrm{\delta }{\mathit{F}}_{\mathit{i}}·\mathrm{\Delta }{\mathit{t}}_{\mathit{i}})}^2}/{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}\mathrm{\Delta }{\mathit{t}}_{\mathit{i}}$$ (4)

Using these equations, the average values of differential flux in this specified period can be calculated on the basis of the flux data collected by the spacecraft and the CE4/LND. Of note here is that the GF of the CE-4/LND has been updated (see the Supplementary Materials for details).

In addition, the daily average differential flux ${\overline{\mathit{F}}}_{\text{pre}}$ predicted by the CRÈME models can be obtained by

$${\overline{\mathit{F}}}_{\text{pre}}=\left({\displaystyle \sum _{\mathit{j}=1}^{\mathit{M}}}{\mathit{F}}_{\mathit{j}}\right)/\mathit{M}$$ (5)

where M is the total number of days in this specified period and F_j is the average differential flux of the jth day. No error is provided in the predicted results from the CRÈME models.

Supplementary Materials

This PDF file includes:

Determination of geometric factor of CE-4/LND

Table S1

Legends for data files S1 to S5

References

Other Supplementary Material for this manuscript includes the following:

Data files S1 to S5