A reflective millimeter-wave photonic limiter

Wide-aperture free-space limiter with enhanced damage threshold provides protection from high-power millimeter-wave radiation.

Abstract

Millimeter-wave (mm-wave) communications and radar receivers must be protected from high-power signals, which can damage their sensitive components. Many of these systems arguably can be protected by using photonic limiting techniques, in addition to electronic limiting circuits in receiver front-ends. Here we demonstrate, experimentally and numerically, a free-space, reflective mm-wave limiter based on a multilayer structure involving a nanolayer of vanadium dioxide VO₂, which experiences a heat-related insulator-to-metal phase transition. The multilayer acts as a variable reflector, controlled by the incident wave intensity. At low intensities VO₂ remains dielectric, and the multilayer exhibits strong resonant transmittance. When the incident intensity exceeds a threshold level, the emerging metallic phase renders the multilayer highly reflective while safely dissipating a small portion of the input power, without damage to the limiter. In the case of a Gaussian beam, the limiter has a nearly constant output above the limiting threshold input.

INTRODUCTION

Millimeter-wave (mm-wave) is a valuable network and sensing technology that uses frequency bands in between 30 and 300 GHz (1–3). Operating in this spectral range has important advantages over lower-frequency bands. Not only do mm-waves allow larger bandwidths to transmit data at multigigabit speeds (4), but they also provide higher spatial resolution due to shorter wavelengths, which can be exploited for a variety of accurate sensing applications (5). At the same time, mm-waves are more readily scattered by small, millimeter-sized particles and stronger absorbed by moisture and oxygen present in the atmosphere. Thus, mm-wave signals work best with line-of-sight propagation and at frequencies falling within atmospheric electromagnetic transparency windows (at about 35, 94, 140, and 220 GHz).

In recent decades, there has been growing attention to the threat of high-power microwaves (HPM) to electronic systems, including radio communications and radar receivers (6–8). HPM sources nowadays can reach peak powers of 1 GW in short pulses of ~0.1 μs at repetition rates of several 100 Hz or average powers of 100 kW at frequencies from 1 to more than 100 GHz (9, 10). At sufficiently high power densities, the effects of HPM on electronics may result in failure or even permanent damage of the circuits, because of thermal effects (7). In this regard, the receiver is particularly vulnerable, because it contains highly sensitive electronics such as low-noise amplifier (LNA), while the attached antenna provides a front door for HPM to couple into the system. PIN-diode power limiters (11), introduced between the antenna and LNA, cannot protect the receiver from the front-door coupling. Moreover, they are best suited for lower frequencies (≤15 GHz) (12) and are prone to overheating, which can be particularly damaging in highly integrated systems enabled by short wavelength of mm-waves. On the bright side though, the size of system components required to receive and process mm-wave signals is small enough to allow using mature optical techniques (13–19), such as optical limiting.

Optical limiting is a technique to protect photosensitive devices from damage caused by intense optical radiation (20, 21). Optical limiters are therefore designed to block high-intensity laser radiation while transmitting low-intensity light. Most passive optical limiters use materials with nonlinear absorption, which are transparent to low-intensity light but turn opaque if the light intensity exceeds a certain (limiting) threshold level (22–24). A typical passive limiter, however, absorbs a substantial portion of high-level radiation, which can cause overheating and damage to the limiter itself (21, 25).

To overcome this problem, the concept of a reflective photonic limiter, which reflects rather than absorbs high-intensity radiation, has been introduced (26–28). A passive reflective photonic limiter involves a photonic bandgap structure, such as a multilayer cavity, incorporating a nonlinear (28, 29) or a phase-change material (PCM) (30, 31). At low intensities, the photonic structure displays a strong resonant transmittance. High-intensity radiation, however, forces nonlinearity to kick in or phase transition to be induced, producing an impedance mismatch resulting in a strong broadband reflectivity. The high reflectivity prevents the limiter from overheating, thereby greatly increasing the limiter damage threshold. Other important advantages of the photonic design include orders-of-magnitude larger extinction ratio (the ratio of transmittances below and above the limiting threshold) and the possibility to substantially lower the limiting threshold by adjusting the photonic structure hosting the nonlinear material or a PCM. The aforementioned approach thus provides advanced broadband protection from high-level radiation, although low-intensity transmission is essentially narrowband because of its resonant nature. Arguably, free-space mm-wave limiters can be designed in much the same way to protect system receivers from high-power signals and to allow the receivers to function normally when these high-power signals are not present.

Here, we report a free-space, reflective photonic limiter for the W band (75 to 110 GHz), inspired by recent optical designs. Our mm-wave limiter is based on a resonant multilayer structure incorporating a nanolayer of vanadium dioxide (VO₂), undergoing an insulator-to-metal phase transition when heated above the critical temperature of θ_c ≈ 69 ° C. Thus, we first discuss the design and fabrication of the multilayer structure and then investigate the mm-wave limiting properties of the multilayer by low-power spectral measurements at successively increasing temperatures and by time-resolved continuous-wave (CW) measurements at high input powers. Our experimental results are then corroborated by three-dimensional (3D) MULTIPHYSICS simulations, which allow us to gain deeper insight into the limiting process by exploring the dynamics of the limiter driven by the VO₂ phase transition.

The approach based on the use of insulator-to-metal transition materials is highly scalable and can be replicated in any spectral range, from microwave (MW) to optical [see, for example, (32–35) and references therein]. At MW frequencies, however, the insulator-to-metal transition is accompanied by much greater change in the complex permittivity of the PCM—orders of magnitude in our case. This provides an unprecedented flexibility in control of the MW radiation flow, unattainable in optics.

RESULTS

Mm-wave limiter design and low-power measurements at varying temperature

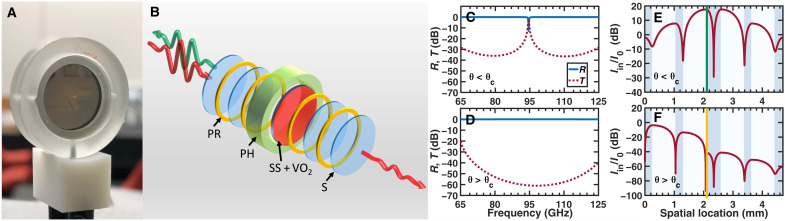
The reflective mm-wave limiter studied in this work is illustrated in Fig. 1 (A and B). The limiter design involves a photonic bandgap structure constructed of 76.2-mm-diameter C-cut sapphire (Al₂O₃) wafers, with a 525-μm-thick wafer in the middle and four 256-μm-thick wafers on the sides, separated by air gaps of a uniform thickness of about 792 μm. The middle sapphire wafer is coated on one side with a polycrystalline VO₂ to a thickness of approximately 150 nm (see Materials and Methods and fig. S1). Measurements of sheet resistance of the VO₂ coating reveal an abrupt insulator-to-metal transition at ~67° C, with a four-orders-of-magnitude change in the sheet resistance over a temperature range of ~5° C (fig. S2). According to literature (36–38), in the transition region, the electrical and optical properties of thin-film VO₂ are determined by the volume fraction of the thin film transformed into the metallic phase.

Fig. 1. Reflective mm-wave photonic limiter.

A picture (A) and schematic (B) of the mm-wave photonic limiter consisting of 256-μm-thick (S) and 525-μm-thick (SS) sapphire wafers separated by 792-μm air-gap spacers (PR) and a 150-nm VO₂ layer deposited on the SS sapphire. The layer stack is retained in a plastic holder (PH). (C and D) Simulated transmittance T and reflectance R of the photonic structure at normal incidence, at θ > θ_c (C) and θ < θ_c (D). (E and F) Simulated internal intensity profiles in the direction of wave propagation of the incident intensity I₀ at the resonance frequency 95 GHz, at θ > θ_c (E) and θ < θ_c (F). Sapphire and air-gap layers are shown in dark and light blue, and the VO₂ layer in green and yellow at the lower and higher temperatures, respectively. Photo credit: Rodion Kononchuk, The University of Texas at San Antonio.

The resonant setting of Fig. 1 (A and B) allows to enhance the limiter extinction ratio by orders of magnitude while markedly lowering the limiting threshold, as compared to that provided by a VO₂ layer on a substrate. Below θ_c, the multilayer structure exhibits resonant transmittance (with a resonance Q factor of 260) of the incident intensity I₀ at a frequency of the localized (defect) mode of f₀ ≈ 95 GHz (see Fig. 1C). The spatial distribution of the electric field intensity within the multilayer at the resonance frequency is plotted with a solid red line in Fig. 1E. The position of the VO₂ layer (shown in green) coincides with an antinodal plane of the resonant electric field. The resonance conditions facilitate the initial mm-wave heating of the VO₂ nanolayer and the adjacent sapphire layer, resulting in a substantial lowering of the limiting threshold. When the VO₂ temperature exceeds θ_c, the multilayer turns highly reflective over the entire W band, as seen in Fig. 1D. Moreover, the metallic VO₂ layer (shown in orange in Fig. 1F) is now shielded from incident radiation by the multilayer front end. The latter substantially increases the limiter damage threshold. Note that the resonance Q factor defines both (i) the operational frequency range below θ_c, which is given by the full width at half maximum (FWHM) of the transmittance peak, $\text{FWHM}=\frac{f_0}{Q}$, and (ii) the resonant absorptance, which determines the limiting threshold. A reduction in the limiting threshold thus comes at a cost of narrower-band operation of the limiter. Away from the resonant frequency, the multilayer is highly reflective regardless of θ, leaving the VO₂ in dielectric state even at high incident intensity levels.

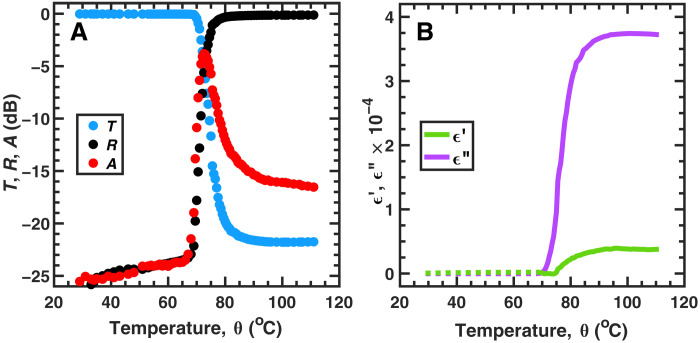
Since design and modeling of the photonic limiter requires accurate values of the dielectric properties of the constitutive materials, we perform mm-wave measurements of the sapphire and VO₂-on-sapphire wafers at low power (≤10 mW) and successively increased temperatures from 27° to 110° C (see Materials and Methods). The (ordinary) effective relative permittivity of sapphire in the W band, ϵ_s = 9.32 + i0.009, is determined from measurements of insertion loss and phase of the sapphire wafer and remains unchanged on heating over the whole temperature range. Figure 2A shows the transmittance T (blue circles), reflectance R (black circles), and absorptance A = 1−T−R (red circles) of the VO₂-on-sapphire wafer at 95 GHz (in the vicinity of the Fabry-Perot resonance of the substrate) as a function of increasing temperature. The phase transition in the VO₂ layer manifests itself as an abrupt drop in the transmittance accompanied by a steep increase in the reflectance and a sharp peak in the absorptance, because of marked change in the permittivity of VO₂ during the transition (see Fig. 2B). The effective relative permittivity, ϵ_VO2 = ϵ′_VO2 + iϵ ′′_VO2, is found by fitting the observed insertion loss and phase of the VO₂-on-sapphire wafer to those obtained from numerical simulations using 2 × 2 transfer-matrix formalism (39). The real and imaginary parts, ϵ′_VO2 and ϵ ′′_VO2, obtained from the fit at θ ≥ 69 ° C are plotted with the increasing temperature by solid lines (in green and magenta, respectively) in Fig. 2B. Below 69° C, the VO₂ contribution to the insertion loss and phase is too small to be observed; it is observed, though, in mm-wave measurements of the photonic limiter that follow. The corresponding ϵ′_VO2 and ϵ′′ _VO2 are shown by the dashed lines in Fig. 2B.

Fig. 2. Mm-wave dielectric properties of the VO₂ nanolayer at low input power and increasing temperature.

(A) Mm-wave transmittance T, reflectance R, and absorptance A of the VO₂-on-sapphire wafer at 95-GHz input power of ≤10 mW and successively increasing temperature θ. (B) Temperature-dependent real (ϵ′_VO2) and imaginary (ϵ ′′_VO2) parts of the relative permittivity of the VO₂ layer at 95 GHz, determined from the measurements of the insertion loss and phase of the VO₂-on-sapphire wafer (solid lines) and transmittance measurements of the photonic limiter (dashed lines).

According to Fig. 2A, the VO₂-on-sapphire wafer can act as a temperature-controlled mm-wave limiter with an extinction ratio of 20 dB. As for self-induced mm-wave limiting, the threshold level of such a limiter is too high because of very low absorptance and thus weak heating effect at low temperatures. By using the highest (in this study) mm-wave input power (55 W) and by starting at room temperature, we could not heat the wafer up to θ_c.

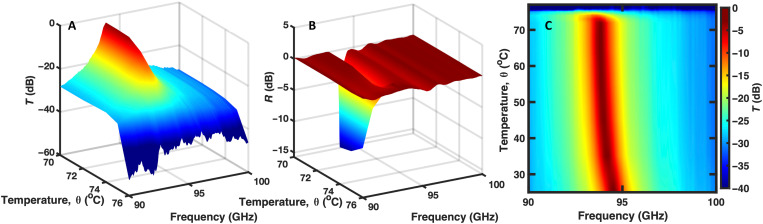
In Fig. 3, the mm-wave measurements of the photonic limiter at low power and successively increased temperatures agree well with the transfer-matrix calculations of Fig. 1. The resonance transmittance peak is seen to drop by 40 dB within the 70° to 75° C temperature range, and to completely disappear by the end of the transition (Fig. 3A). When this takes place, the limiter becomes totally reflective (Fig. 3B). Below the transition temperature, the transmittance peak is seen gradually shifting to lower frequencies (Fig. 3C), indicating an increase in the refractive index of VO₂ with the increasing temperature, while its peak value remains unchanged, implying negligible VO₂ absorption below θ_c. The extracted ϵ′_VO2 and ϵ′_VO2 ≈ 0 are plotted by dashed lines in Fig. 2B. Note that no noticeable change was observed in transmittance spectra of the multilayer without VO₂ coating in the same temperature range.

Fig. 3. Mm-wave measurements of the photonic limiter at low input power and increasing temperature.

(A and B) Spectra of transmittance T (A) and reflectance R (B) of the photonic limiter at input power of ≤10 mW over the resonance spectral range and phase-transition temperature interval. (C) Transmittance spectra over the wider temperature range from 27° to 76° C.

High-power measurements of the mm-wave limiter

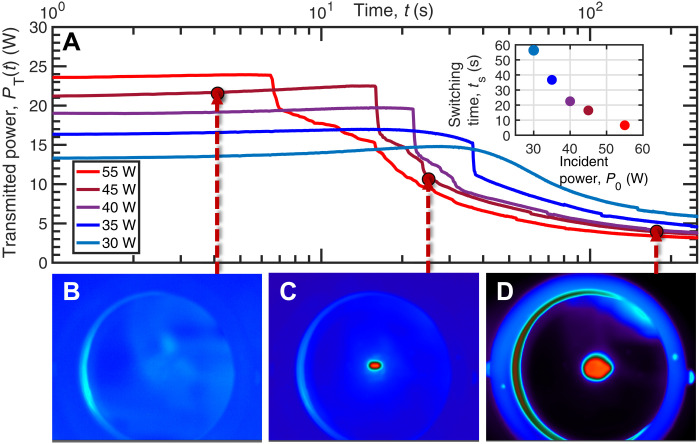
To investigate self-induced mm-wave limiting, time-resolved transmission measurements of the limiter have been carried out with the use of a high-power CW source centered on 95 GHz with an FWHM of 300 MHz (see Materials and Methods). To prevent adverse effects of back-reflected radiation on the mm-wave source, the reflective limiter was tilted by an angle of 6° from the normal incidence direction, thus shifting the transmission resonance to a higher frequency than 95 GHz. Figure 4A shows linear-log plots of the transmitted power P_T(t) for incident Gaussian beams of a waist radius of 16.5 mm and input powers P₀ = 30, 35, 40, 45, and 55 W. For each input power, P_T(t) is seen to initially increase and then decrease with time. This is due to the fact that the transmission resonance shifts to lower frequencies with increasing temperature, in accordance with Fig. 3C, crossing the source frequency of 95 GHz at a time of maximum transmission. In addition, at input powers P₀ > 30 W, P_T(t) exhibits a sharp drop associated with the insulator-to-metal transition in the VO₂ layer. The corresponding transition or switching time, t_s, is plotted versus P₀ in the inset; notice that at 30 W input power, the transition is not manifested in P_T(t). The shortest switching time observed in these proof-of-concept measurements was about 7 s at the highest available input power of 55 W. It can be substantially reduced by increasing the input power or ambient temperature or by modifying the limiter design, as discussed in the following sections.

Fig. 4. High-power mm-wave measurements of the photonic limiter.

(A) Time-varying transmitted power P_T(t) of the photonic limiter following excitation by a CW 95-GHz Gaussian beam with the waist radius r₀ = 16.5 mm and input powers P₀ = 30, 35, 40, 45, and 55 W. Inset: Switching time t_s, corresponding to the onset of the metallic phase in the VO₂ layer, versus the input power P₀. (B to D) Thermal images of the limiter front end at the elapsed times indicated by the respective dashed arrows in (A), for P₀ = 45 W.

The transition in the VO₂ layer was observed with an forward-looking infrared (FLIR) thermal camera that could distinguish between the dielectric and metallic phases of VO₂ because of their different emissivities in the infrared. Figure 4 (B to D) displays thermal images of the limiter front end at elapsed times indicated by red dashed arrows in Fig. 4A for the incident power of 45 W. The first occurrence of the metallic phase in the center of the VO₂ layer (red spot in Fig. 4C) coincides with the sharp drop in P_T(t). Then, the metallic domain grows in size (Fig. 4D), accompanied by further decrease in P_T(t), until thermal equilibrium is reached. When high input power is no longer present, the VO₂ reverts from the metallic to the dielectric phase after a brief delay (movie S1).

The equilibrium size of the metallic domain and thus the extinction ratio of the limiter increase with the incident power P₀. In contrast, the transmitted power P_T(t) in the steady-state regime (i.e., at longer times) is nearly independent of P₀, as seen in Fig. 4A. This practically important feature is, in fact, due to the Gaussian spatial intensity distribution of the incident beam, $I(r)=(2P_0/\mathrm{\pi }{r}_0^2)\text{exp}(-2r^2/r_0^2)$, where r is the radial distance from the center axis of the beam, and r₀ is the beam waist radius, at which the field amplitude falls to 1/e of its axial value. Indeed, if the beam is centered on and blocked by an opaque disk of radius a, then the transmitted power is $P_{\mathrm{T}}\approx P_0\text{exp}(-2a^2/r_0^2)$ provided the limiter aperture is considerably larger than the disk. Assuming that the value of a is determined from I(r = a) = I_t, where I_t is the intensity threshold value, the transmitted power is virtually independent of the input power P₀, $P_{\mathrm{T}}\approx \frac{\mathrm{\pi }{r}_0^2{I}_{\mathrm{t}}}{2}.$ By contrast, in the case of a top-hat incident beam with a near-uniform intensity I ≥ I_t within a circular disk, the transmitted power would be suppressed by orders of magnitude shortly after switching of the VO₂ from the dielectric to the metallic state (in accordance with Fig. 1D). Alternatively, substantial suppression of the transmitted intensity can be achieved by using a circular aperture of r ≤ a positioned just behind the multilayer, as shown in fig. S3.

Electromagnetic and heat transfer modeling of the mm-wave limiter

To gain deeper insight into the mm-wave limiting process in the photonic limiter, we perform time-domain 3D MULTIPHYSICS simulations of a Gaussian beam propagating through the multilayer of Fig. 1. The electric field component E of the incident Gaussian beam (assuming polarization in the radial direction $\widehat{\mathit{r}}$ and propagation in the +z direction) is given by

$$\mathit{E}(z,r)=E_0\widehat{\mathit{r}}\text{exp}(-\frac{r^2}{r_0^2})\text{exp}(-\mathit{ikz})$$ (1)

where E₀ is the on-axis (r = 0) electric field amplitude, $E_0=\sqrt{4{\mathrm{\eta }}_0{P}_0/\mathrm{\pi }{r}_0^2}$, η₀ = 377 Ω is the wave impedance of free space, r₀ = 16.5 mm, and k = 2π/λ is the wave number for a free-space wavelength λ.

The mm-wave propagation in the case of temperature-dependent permittivity of the VO₂ layer is described by the following set of coupled electromagnetic and thermal equations

$$\mathbf{\nabla }\times \mathit{H}=\mathit{j}+\mathrm{\epsilon }\frac{\mathrm{\partial }\mathit{E}}{\mathrm{\partial }t},\mathbf{\nabla }\times \mathit{E}=-\mathrm{\mu }\frac{\mathrm{\partial }\mathit{H}}{\mathrm{\partial }t}$$ (2)

$$\mathrm{\rho }c\frac{\mathrm{\partial }\mathrm{\theta }}{\mathrm{\partial }t}=\mathbf{\nabla }\bullet (\mathrm{\kappa }\mathbf{\nabla }\mathrm{\theta })+\stackrel{·}{Q}$$

where H is the magnetic field component, j = σE is the current density, σ(z, θ) is the electrical conductivity, ε(z, θ) = ε′(z, θ) + iε′′ (z, θ) is the permittivity, and μ is the permeability. In the second line of equations (2), $\stackrel{·}{Q}=\frac{1}{2}(\mathit{\text{Re}}(\mathit{j}\bullet \mathit{E})+\mathrm{\omega }\mathrm{\epsilon }\prime \prime {\mid \mathit{E}\mid }^2)$ is the volumetric heat production rate, which can be recast as $\stackrel{·}{Q}=\frac{1}{2}\mathrm{\omega }{\mathrm{\epsilon }}_0\mathrm{ϵ}\prime \prime {\mid \mathit{E}\mid }^2$, where ω is the angular frequency, ε₀ is the vacuum permittivity, and ϵ′′ is the imaginary part of the effective relative permittivity, which can be directly obtained from our measurements. The other parameters in Eq. 2 include the specific heat capacity c(z), the mass density ρ(z), and the thermal conductivity κ(z). In the modeling, we assume that the multilayer is thermally insulated on the cylindrical surface (due to the plastic holder) and that the heat flux q across the limiter front and rear ends dissipates by convection, i.e., q = h(θ − θ₀), where h = 100 W/(m²K) is the convection heat transfer coefficient (40), and θ₀ = 296 K is the ambient temperature. Furthermore, we use the experimentally determined effective relative permittivities of sapphire (ϵ_s) and VO₂ (ϵ_VO2) and assume μ to be the magnetic permeability of free space, μ = μ₀. Last, the thermal properties of the constitutive materials used in the simulations are listed in table S1.

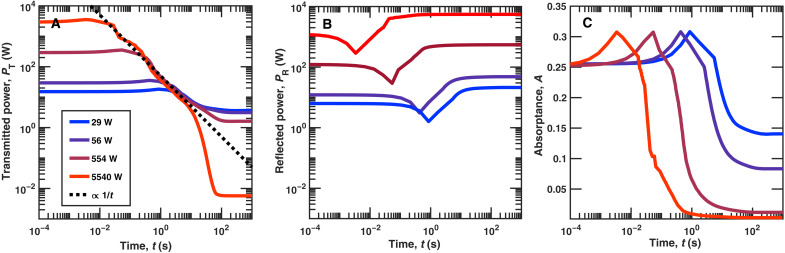
There are two equations in (2) which are solved simultaneously using the coupled Microwave and Heat Transfer modules of COMSOL MULTIPHYSICS software (41). Figure 5 shows the computed time-dependent transmitted power P_T(t), reflected power P_R(t), and absorptance A(t) = (P₀ − P_T(t) − P_R(t))/P₀ of the limiter following excitation by a 95-GHz Gaussian beam of input powers P₀= 29, 56, 554, and 5540 W. A good agreement between the numerical simulations and the experimental data of Fig. 4 is evident. Specifically, P_T(t) exhibits abrupt, steep decrease once VO₂ has reached θ_c (Fig. 5A). Also, in the steady limiting regime (flat portion of the curves at later times), the input power is reflected to a greater extent than is absorbed (Fig. 5, B and C). We further note in Fig. 5A that the switching time is inversely proportional to the input power, t_s ∝ 1/P₀, and that at t > t_s, the transmitted power decreases inversely with time, P_T(t) ∝ 1/t (shown by a dotted black line).

Fig. 5. Simulated temporal response of the photonic limiter under monochromatic excitation.

(A to C) Time evolution of the transmitted power P_T(t) (A), reflected power P_R(t) (B), and absorptance A(t) (C) of the limiter following excitation by a 95-GHz Gaussian beam with the waist radius r₀ = 16.5 mm and input powers P₀ = 29, 56, 554, and 5540 W. The black dashed line in (A) indicates a slope of P_T(t) ∝ 1/t.

The dependence of t_s on P₀ can be understood from the solution of a heat balance equation (42) for the VO₂ layer in the beam center. Assuming for the time being that the temperature distribution in the VO₂-on-sapphire wafer is uniform in the +z direction and neglecting transverse thermal conduction away from the beam center, the heat balance equation is

$$C\frac{d\mathrm{\theta }}{\mathit{dt}}=A{I}_{\text{in}}+h\prime ({\mathrm{\theta }}_0-\mathrm{\theta })$$ (3)

where C is the heat capacity per unit surface area, h′ is the thermal exchange coefficient, A is the absorptance, and I_in ~ I₀ exp (L/2ξ) is the internal intensity in the middle of the multilayer length L, wherein ξ is the decay length associated with the spatial distribution of the resonant defect mode (Fig. 1E). Assuming that the initial temperature of the VO₂ layer is equal to the ambient temperature, θ(t = 0) = θ₀, and that C, A, and h′ are temperature-independent below θ_c, the solution of Eq. 3 is

$$\mathrm{\theta }(t)={\mathrm{\theta }}_0+\frac{A{I}_{\text{in}}}{h^{\prime }}(1-\text{exp}(-\frac{h^{\prime }}{C}t))$$ (4)

for θ₀ ≤ θ < θ_c. At intensities I_in > h′ (θ_c − θ₀)/A, the temperature θ(t) grows until it reaches the phase transition value θ_c at time

$$t_{\mathrm{s}}=-\frac{C}{h^{\prime }}\text{ln}(1-\frac{h^{\prime }}{A{I}_{\text{in}}}({\mathrm{\theta }}_{\mathrm{c}}-{\mathrm{\theta }}_0))\approx \frac{C({\mathrm{\theta }}_{\mathrm{c}}-{\mathrm{\theta }}_0)}{A{I}_{\text{in}}}\propto \frac{1}{P_0}$$ (5)

Note that in the case of the Gaussian beam of Eq. 1, the larger the radial distance r is, the longer it takes to reach θ_c. As a result, the radius r_m of the metallic domain grows with time according to $t=C({\mathrm{\theta }}_{\mathrm{c}}-{\mathrm{\theta }}_0)/A{I}_{\text{in}}\text{exp}(-2r_{\mathrm{m}}^2/r_0^2)$, for t ≥ t_s (movie S2). Since the transmitted power is $P_{\mathrm{T}}\approx \left(\frac{\mathrm{\pi }{r}_0^2{I}_0}{2}\right)\text{exp}(-2r_{\mathrm{m}}^2/r_0^2)$, it decreases with time as $P_{\mathrm{T}}(t)\approx \mathrm{\pi }{r}_0^{2}C({\mathrm{\theta }}_{\mathrm{c}}-{\mathrm{\theta }}_0)/2\mathit{At}\text{exp}(L/2\mathrm{\xi })\propto 1/t$, in agreement with Fig. 5A.

According to Fig. 5, it takes ~100 s for P_T(t) to reach the steady state. By then, P_T(t) has already dropped substantially compared to its initial level. At the input powers P₀ < 60 W, the steady-state P_T(t) is independent of P₀ in agreement with the experiment (Fig. 4A). At P₀ > 60 W, however, P_T(t) falls further down as the metallic domain becomes comparable to the limiter aperture in size (Fig. 6B). At P₀ = 5540 W, P_T(t) falls by 60 dB, much like in the measurements of transmittance at successively increasing spatially uniform temperatures (Fig. 3A) and of transmitted power through the aperture (fig. S3).

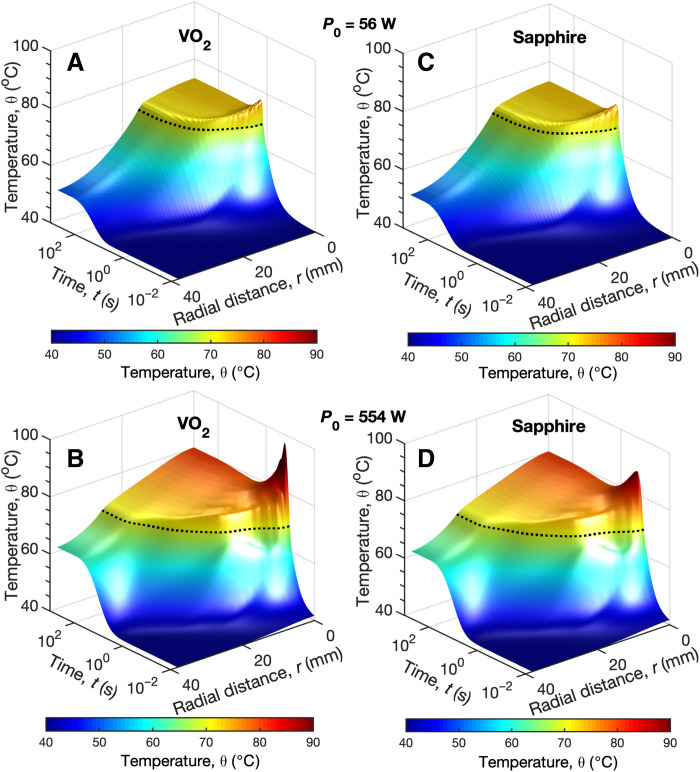
Fig. 6. Simulated temperature evolution of the VO₂-on-sapphire wafer inside the photonic limiter under monochromatic excitation.

(A and B) Radial temperature distribution of the VO₂ layer as a function of elapsed time t following excitation by a 95-GHz Gaussian beam with the waist radius r₀ = 16.5 mm and input powers of 56 W (A) and 554 W (B). (C and D) the same for the opposite (uncoated) side of the sapphire wafer. The black dashed lines correspond to θ_c = 69° C.

As seen from Fig. 5C, the resonant setting of the multilayer enhances the initial (low-temperature) absorptance by two orders of magnitude compared to the stand-alone VO₂-on-sapphire wafer. In the presence of continuous input power P₀, A(t) rises up to a peak of ~0.32 regardless of P₀ and then falls down to a constant level depending on P₀. This absorptance behavior, which is characteristic of the entire multilayer rather than the stand-alone VO₂-on-sapphire wafer (for comparison, see Fig. 2A), is essential to understanding the mm-wave limiting process in the photonic limiter. The increase in absorptance resulting from the heating effect triggers thermal runaway, in which the VO₂ temperature quickly runs up to θ_c and higher (Fig. 6, A and B), carrying VO₂ through the phase transition. However, because of rapidly increasing reflectivity with the fraction of VO₂ transformed into the metallic phase, the absorptance changes instantly from rising to falling, and the VO₂ layer from heating to cooling, until equilibrium is reached. The equilibrium sets in at a particular metallic fraction of VO₂, at which the limiter is capable of fully dissipating the absorbed power while reflecting most of the input power. If the input power further increases or decreases, then so does the metallic fraction of VO₂ to reset the equilibrium. In contrast, the stand-alone VO₂-on-sapphire wafer exhibits only thermal runaway and lacks equilibrium at θ > 69° C, because its absorbance at θ ≥ θ_c is higher than that at θ < θ_c (Fig. 2A).

The picture of the self-regulating limiting process in the photonic limiter is further supported by computed temperature time evolution of the VO₂-on-sapphire wafer inside the photonic limiter at input powers of 56 and 554 W shown in Fig. 6. Because of the limiter’s axial symmetry, we plot the time-varying radial temperature distributions at the two z-positions: in the VO₂ layer (Fig. 6, A and B) and on the opposite side of the sapphire wafer (Fig. 6, C and D). Below 69° C (shown by a black dashed line), the temperature distributions at these two positions are nearly the same, indicating that the VO₂ layer (assumed to be lossless) is efficiently heated by the absorbing sapphire wafer. At θ > 69° C, the VO₂ temperature rises faster and higher than in sapphire, particularly at the beam center (r = 0) and the higher power of 554 W. The two temperatures peak and fall at the same time despite a temperature gradient across the sapphire wafer, indicating that sapphire is shielded by VO₂ from the incident beam as the VO₂ is being transformed into the metallic phase. Next, the two temperatures quickly level off, eventually reaching equilibrium temperatures of 75° and 80° C for input powers of 56 and 554 W, respectively, in accordance with Fig. 5 and the subsequent discussion.

DISCUSSION

We have designed and demonstrated a free-space, reflective photonic limiter for the W band as an alternative or a complement to electronic limiting circuits used in mm-wave receivers. The proposed photonic limiter is a resonant air/sapphire multilayer structure, incorporating a 150-nm VO₂ layer undergoing an insulator-to-metal transition when heated above the critical temperature, θ_c ≈ 69° C. The multilayer structure is so thin (a few millimeters) that it can be used to cover a wide area, such as a phase antenna array. The limiter acts as a variable reflector, controlled by the incident wave intensity I₀. If I₀ is below a certain threshold level I_t, the VO₂ layer remains in the dielectric state, and the multilayer exhibits high transmittance in a finite frequency band, despite the fact that a small portion of I₀ is absorbed by the multilayer, leading to the initial heating of VO₂. When I₀ exceeds I_t, a fraction of the VO₂ layer transitions into the metallic phase with sharply increased electrical conductivity, rendering the entire multilayer highly reflective. The time t_s before the transition starts is inversely proportional to the incident intensity, t_s ∝ 1/I₀, after which the multilayer is brought to equilibrium by a combination of positive and negative feedbacks between mm-wave absorption and heating of VO₂. For a given intensity I₀ ≥ I_t, the equilibrium is determined by the fraction of the VO₂ layer transformed into the metallic phase. At that point, the limiter is capable of safely dissipating a small portion of the incident power absorbed by the limiter, while reflecting the rest of the energy back to space. The high reflectivity (as opposed to absorptance) prevents the limiter from overheating. Moreover, a combination of the resonant conditions and the high contrast in electrical conductivity between the two phases of VO₂ results in a substantial enhancement of the limiter extinction ratio and allows marked reduction in the limiting threshold—both highly desirable features in limiting applications.

The limiter properties, such as operating frequency, bandwidth, threshold level, and switching time, are determined by the limiter design, ambient conditions, and incident power density. In particular, as long as the VO₂ nanolayer is in the dielectric phase, most of the resonant absorption occurs in the sapphire substrate, while the VO₂ contributions to the absorption and heating processes remain negligible. The relatively large thickness of the sapphire substrate (~0.5 mm) results in its large heat capacity, which explains the long switching times of the limiter. If the damage inflicted by HPM is thermal in origin, then a critically important characteristic of the free-space limiter is the energy density passed through the limiter before the limiter blocks the input radiation, U = I₀t_s, where t_s is given by Eq. 5. It thus turns out that if the incident intensity I₀ is well above the limiting threshold, the value of U is virtually independent of I₀, U ≈ C(θ_c − θ₀)/A, provided that t_s is much shorter than the temperature relaxation time of the limiter. Given the specific parameters of our limiter and the ambient temperature, the total transmitted energy density U during the limiter switching time t_s is ~22.5 J/cm². One way to substantially reduce both the switching time t_s and the passed energy density U would be to deposit a resistive nanolayer or nanostructure (43) on the top of the VO₂. The heat capacity of the resistive nanolayer can be much smaller than that of the sapphire substrate (e.g., by four orders of magnitude in the case of In₂O₅Sn), and the heat released in the resistive nanolayer will be almost instantly transferred to the VO₂ nanolayer. Preliminary estimates show the reduction in t_s and U of more than three orders of magnitude, particularly for the incident intensity I₀ well above the limiting threshold (it can still be well below the damage threshold). The limiter performance is also determined by spatial and temporal characteristics of the incident radiation. In particular, in the case of CW Gaussian beam, the output power of the limiter operating above the threshold appears virtually independent of the input power because of nonuniform heating of the VO₂ layer.

MATERIALS AND METHODS

Thin-film deposition and structural analysis

The VO₂ thin film was deposited in a Neocera Pioneer 180 Pulse Laser Deposition system with a KrF excimer laser (Coherent COMPexPro 110, λ = 248 nm, 10-ns pulse duration, 10-Hz repetition rate) applied for the ablation of a high-purity vanadium disk. The chamber base pressure of a 5% O₂/95% Ar gas mixture was maintained at 25 mtorr during the deposition. The 76.2-mm double-side-polished C-cut (006) sapphire substrate was held at 600° C. X-ray diffraction (XRD) analysis of the VO₂ films was carried out using a PANalytical X’Pert diffractometer with a hybrid monochromator for Cu Kα₁ radiation (λ = 1.54056 A) at room temperature. The presence of highly oriented monoclinic VO₂ crystalline phase is indicated by the characteristic XRD peaks (020) and (040) at 39.87° and 85.97°, respectively (fig. S1) (44). The average VO₂ crystalline grain size about 110 nm was found from the Scherrer equation for the FWHM (β) of the (020) peak (45). A VO₂ film thickness of approximately 150 nm was measured with SEM.

Mm-wave spectral measurements

Mm-wave field spectra of the photonic limiter and complex permittivities of its constitutive components were obtained using a W-band, high-temperature, free-space measurement apparatus (46). The measurement system consisted of an Agilent 5222A performance network analyzer (PNA), N5261A millimeter head controller, and a set of OML V10VNA-T/R frequency extender heads (one for each port) serving to boost the output of the PNA base unit to the W-band frequencies (75 to 110 GHz). A matched set of custom-designed, lensed horn antennas was used for launching and receiving a Gaussian mm-wave beam (waist radius of 16.5 mm) transmitted via and reflected from the sample. The sample was located in the center of a Mellen tube furnace with an overall length and diameter of 32 and 15 cm, respectively, and a 15-cm-long, uniform heating region centered along the axial length of the furnace. A silicon carbide composite sample holder was used for the measurements. The temperature was controlled with an E-type thermocouple embedded in the sample holder immediately adjacent to the outer radius of the sample. In the temperature range from 27° to 110° C, the thermocouple had an accuracy of 1.0° C.

High-power mm-wave measurements

For higher-power free-space measurements, a CPI VKB2463L2 Extended Interaction Klystron (EIK) power amplifier was used to provide a CW 95-GHz signal. EIK input and output mm-wave power was sampled using calibrated directional couplers and then measured using diode-based detectors. The input mm-wave drive signal was controlled with a LabVIEW-based feedback circuit to maintain a consistent mm-wave power output over extended periods of time, which could otherwise drop because of heating of components. The EIK mm-wave output was coupled into the same lensed antenna that was used with the network analyzer measurement setup, to form a Gaussian beam directed into a shielded anechoic chamber and focused at the center of the sample being interrogated. At a peak power gain, the maximum incident power of the Gaussian mm-wave beam was 55 W.

MULTIPHYSICS simulations

Equation 2 was solved numerically, using the coupled Microwave and Heat Transfer modules of a finite-element software package from COMSOL MULTIPHYSICS (41) and a 2D axisymmetric model, capturing all the features of the 3D problem with axial (cylindrical) symmetry. In the simulations, we used a varying mesh density (fig. S4). The thin sapphire and air-gap layers were partitioned with the mesh density increased toward the center of the limiter, while the center sapphire and air-gap layers toward the VO₂ layer. The convergence of the results has been evaluated with a tolerance factor of 0.1%. We then repeated the calculations by doubling the number of mesh points to guarantee the accuracy of the converged numerical solutions. The mm-wave source was modeled with a surface current density line producing the Gaussian beam, which was located 1.5 mm away from the front end of the multilayer inside the far-field air domain. The wave propagation was modeled using PML boundary conditions to avoid the back reflections from the boundaries of the geometry.

Supplementary Materials

This PDF file includes:

Figs. S1 to S4

Table S1

Legends for movies S1 and S2

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 and S2