Resource planning strategies for healthcare systems during a pandemic

Abstract

We study resource planning strategies, including the integrated healthcare resources’ allocation and sharing as well as patients’ transfer, to improve the response of health systems to massive increases in demand during epidemics and pandemics. Our study considers various types of patients and resources to provide access to patient care with minimum capacity extension. Adding new resources takes time that most patients don't have during pandemics. The number of patients requiring scarce healthcare resources is uncertain and dependent on the speed of the pandemic's transmission through a region. We develop a multi-stage stochastic program to optimize various strategies for planning limited and necessary healthcare resources. We simulate uncertain parameters by deploying an agent-based continuous-time stochastic model, and then capture the uncertainty by a forward scenario tree construction approach. Finally, we propose a data-driven rolling horizon procedure to facilitate decision-making in real-time, which mitigates some critical limitations of stochastic programming approaches and makes the resulting strategies implementable in practice. We use two different case studies related to COVID-19 to examine our optimization and simulation tools by extensive computational results. The results highlight these strategies can significantly improve patient access to care during pandemics; their significance will vary under different situations. Our methodology is not limited to the presented setting and can be employed in other service industries where urgent access matters.

1. Introduction

COVID-19 was first identified in Wuhan, China in December 2019 and it has since become a global pandemic (Ferreira, Kannan, Meidutė-Kavaliauskienė & Vale, 2022). As of December 2021, there have been more than 250 million reported COVID-19 cases worldwide. As the result of the COVID-19 pandemic, the world has seen more than five million deaths until now; most healthcare systems have faced extraordinary challenges. As one of the most important challenges, outbreaks of the SARS-CoV-2 infection in local communities yield a massive increase in demand for limited resources such as intensive care unit (ICU) beds, healthcare personnel, and mechanical ventilators. Several governments established widespread closures and stay-at-home orders to intervene in this issue (Govindan, Mina & Alavi, 2020; Mervosh, Lu & Swales, 2020; Ferreira et al., 2022). However, the accelerated number of COVID-19 cases forced many hospitals to discharge existing patients earlier to preserve care capacity for COVID-19 patients (Parker, Sawczuk, Ganjkhanloo, Ahmadi & Ghobadi, 2020; Tonna et al., 2020) as part of the guidelines from the Centers for Disease Control and Prevention (CDC, 2020). Although these approaches were effective to treat a greater number of COVID-19 patients, they resulted in poor outcomes for non-COVID-19 patients and a substantial financial loss for healthcare systems.

Extending healthcare resources’ capacity is impossible for many countries in a short time, according to Adelman (2020). Ramping up production of complex medical equipment, such as ventilators, in facilities configured for other products will require time that several COVID-19 patients don't have. In such critical situations, two other primary strategies are resource sharing and demand redistribution, which can minimize shortages in response to massive hospitalization demand with the minimum extension of resources’ capacity. Some facts demonstrate the applicability of these strategies in countries or local communities. Indeed, the infection spreads at varying rates in different regions, and COVID-19 cases peak at different times in different regions. This variance provides an opportunity for sharing some scarce resources such as ventilators; these devices can be transported over large distances or within regions to reduce capacity shortfalls caused by an epidemic surge in a particular area. In addition, regarding demand redistribution, patients tend to select hospitals/healthcare centers in accordance with their reputation or distance on a local level, which leads to unbalanced patient loads across hospitals/healthcare centers and a decrease in the overall quality of patient care (Drevs, 2013; Varkevisser, van der Geest & Schut, 2012). Parker et al. (2020) demonstrated that the operationally feasible redistribution of newly admitted patients through the network of healthcare systems can reduce the patients’ overflow. Healthcare systems can consider system-level interventions and patient transfers to maximize the utilization of available resources.

From the medical literature, qualitative studies propose some strategies to deal with the capacity shortage under a potential surge in demand (Mills, Helm & Wang, 2020). This study is motivated by the healthcare capacity concerns created during the COVID-19 pandemic. Its theory and practice are directly relevant to the capacity planning through healthcare systems, and the objective is to optimize the use of resources during a pandemic by various strategies. We develop a novel data-driven multi-stage stochastic programming approach for managing healthcare resources as well as demand redistribution to provide care for patients during a pandemic. In particular, we provide an answer to the question, “what could have been done to mitigate shortages due to a massive increase in the demand for limited resources during a pandemic such as COVID-19?”

Our decision-making framework considers two types of healthcare resources: 1) direct, in use resources (such as ICU beds and ventilators) and 2) service resources (such as personnel and laboratories). We also then explore various possible capacity planning options for healthcare resources, including capacity extension and relocation, as well as demand redistribution strategies that are modeled to provide hospitalization services to patients. This methodology considers uncertainty in the disease spread and, therefore, demand for healthcare resources in various regions or hospitals. We deploy a simulation approach based on an agent-based continuous-time stochastic model to capture the COVID-19 spread providing a daily forecast for the hospitalization demand over time, and this model can be adapted to any county or geographical region. Our modeling study provides critical insights into how regions or hospitals could cope with a surge in demand for healthcare resources.

The existing scientific literature suffers from a lack of decision support tools for managing healthcare resources during a pandemic, which simultaneously considers the above-mentioned strategies and demand uncertainty. In this study, the proposed data-driven decision-making tool encompasses a large scope of operational situations. The proof of concepts will be given for allocation and relocation of ventilators among several healthcare regions of the US and, secondly, allocation of resources and demand redistribution among hospitals in an area of Iran. A summary of the contributions of this work is as follows:

• •We propose a multi-stage stochastic program (MSSP) for the integrated healthcare resources planning and demand redistribution during a pandemic. This model accounts for various patient types and healthcare resources during pandemics.
• •We extend our model into a data-driven resource planning approach by developing a rolling horizon procedure, which will help decision-makers make real-time decisions.
• •We deploy an agent-based continuous-time stochastic model for modeling the COVID-19 transmission and then a scenario tree construction approach to capture the stochasticity of the number of infected individuals requiring hospitalization.
• •We investigate two different case studies by our proposed tools.

The organization of the paper is as follows: Section 2 provides the literature review. In Section 3, the problem definition and MSSP are described. The data-driven decision-making approach based on the rolling horizon approach is explained in Section 4. The agent-based simulation approach and scenario tree construction approaches are presented in Section 5. Computational results based on two case studies are provided in Section 6. Several managerial insights derived from our computational results are presented in Section 7. Finally, Section 8 concludes the paper.

2. Literature review

Regarding disaster management and humanitarian operations, abundant literature exists (see e.g., Altay & Green III, 2006; Gupta, Starr, Farahani & Matinrad, 2016; Rodríguez-Espíndola, Albores & Brewster, 2018; Wex, Schryen, Feuerriegel & Neumann, 2014) and several papers investigate the healthcare operations for emergency situations (see e.g., Adan, Bekkers, Dellaert, Jeunet & Vissers, 2011; Chi, Li, Shao & Gao, 2017; Luscombe & Kozan, 2016; Sung & Lee, 2016). However, the nature of epidemic outbreaks and pandemics are meaningfully different from other disasters in terms of their dynamic nature, resources’ demand, global scale, and length. The World Health Organization has defined practical phases in epidemics and pandemics management: Anticipation, Early detection, Containment, Control and mitigation, and Elimination or eradication (World Health Organization, 2018). Literature focusing specifically on the allocation of healthcare resources during emergencies often concentrates on the distribution of life-saving medical devices (Dasaklis, Pappis & Rachaniotis, 2012). Resource allocation helps in Containment and Control and mitigation phases when it comes to healthcare resources planning. Generally, the resource allocation problem has been deeply investigated since the 1990s by the operations research community (see e.g., Bakuli & Smith, 1996; Elmaghraby, 1993; Fiedrich, Gehbauer & Rickers, 2000; Hegazy, 1999).

Mills et al. (2020) investigated possible actions of hospitals to provide immediate additional healthcare services in the case of urgent massive demand. They focused on strategies related to the Containment and Control and mitigation phases. Further, in the medical literature, there are some research studies, such as Hick et al. (2004), Kaji, Koenig and Bey (2006), and Rothman, Hsu, Kahn and Kelen (2006), which identified response components and developed conceptual frameworks to propose qualitative methods for creating the surge capacity without quantification of capacity allocation and relocation approaches. Practical reports in the healthcare systems of the Netherlands indicated that the lack of cooperation between hospitals is a major cause for trauma patients to be transported outside the region because of shortages in ICU capacity and their corresponding nurses (Litvak, Van Rijsbergen, Boucherie & van Houdenhoven, 2008). Litvak et al. (2008) addressed the capacity problem related to ICU beds, in which many hospitals in a geographical region reserve a small number of ICU beds for the regional emergency patients. Scheduling of nurse shifts and planning of workforce are also addressed by Otegbeye, Scriber, Ducoin and Glasofer (2015) and Willis, Cave and Kunc (2018), respectively. Farley et al. (2013) highlighted that emergency department information systems constitute a unique and important role in hospitals’ electronic health records, and the information system performance affects physician clinician workflow, decision-making, communication, overall patient safety, and quality of care. Most research works in resource planning in healthcare systems deal with standard and forecastable leadwork of a single healthcare center. Some other studies address mass casualty incidents that demonstrate short-term effects on hospitals, but those works contrast with the long-lasting effects of a pandemic outbreak.

During the influenza pandemic preparedness, Toner and Waldhorn (2006) emphasized the significance of cooperation between different healthcare centers to decrease the extreme healthcare system stress. Bertsimas et al. (2020) showed the advantages of inter-regional collaboration in sharing ventilators across states in the U.S. Assuming a perfect demand forecast, their deterministic optimization model allocates the federal stockpile of ventilators and determines how many ventilators to transfer between states to minimize ventilator shortage costs. Considering the same problem, but with stochastic demand, Mehrotra et al. (2020) presented a two-stage stochastic model for allocating and sharing ventilators. They demonstrated that sharing ventilators across states could reduce shortages. Parker et al. (2020) studied the problem of finding demand and healthcare resource transfers between hospitals during the COVID-19 pandemic to minimize the required new capacity and shortage for healthcare resources. They used robust optimization to address demand uncertainty. The concern of this study, resource planning strategies for healthcare systems during epidemics and pandemics, is recently highlighted by the operations research community to improve the response to pandemics, especially to COVID-19. Further, modeling the effects of pandemics on a region's individuals and their progression is also investigated; some of the studies related to COVID-19 are Lewnard et al. (2020), Parker et al. (2020), Levin et al. (2020), Nabi (2020), Silva et al. (2020), and Reddy et al. (2020).

Methodologically, in the healthcare operations management area, the two-stage stochastic programming approach is commonly employed to formulate various problems that incorporate uncertainty (see e.g., Mehrotra et al., 2020). However, the uncertainty in stochastic parameters such as the number of patients is usually realized progressively and the decisions at each period or stage are a function of uncertainty observations, previous decisions, and observed feedback outcomes up to that stage (Erdogan et al., 2013; Govindan, Fattahi & Keyvanshokooh, 2017). Therefore, multi-stage stochastic programming will be a more suitable optimization tool that we utilize in this work.

There are key differences between the above papers and ours. First, the focus of most studies in resource planning during a pandemic is a single mitigation strategy to improve the healthcare systems’ response; however, our model with realistic features considers various patient types, demand redistribution, and different capacity planning options aligned with the type of healthcare resources. Second, an MSSP is developed to incorporate the uncertain number of patients requiring treatment during a pandemic. Third, the decisions made by MSSPs are not implementable in practice, and a data-driven decision-making approach with the help of a rolling horizon procedure is developed to deal with this issue and to determine real-time decisions.

3. Problem formulation

During a pandemic such as COVID-19, surges in demand for the healthcare system often occur; it's common for the healthcare resources of a hospital to be lower than the required capacity. We categorize resources in terms of patients’ usage types. The first is direct in use resources (DUR), which a hospital assigns them to a patient as long as he/she is hospitalized. For example, suitable beds and ventilators are in this category for COVID-19. The second category is service resources (SER) such as personnel or laboratories that a hospital utilizes as needed.

Given the ongoing capacity concerns, based on the types of resources, three main strategies are used by various countries during pandemics (especially COVID-19), as follows:

Demand redistribution: to address the balance of loads, redistribution of patients between hospitals is implemented,

Resource allocation (extension): the government or policy makers provide more external resources for regions or hospitals such as increasing capacity through calling in additional personnel and creating new suitable beds.

Resource relocation (sharing): the sharing of capacity between regions (hospitals) is applicable for portable resources, such as healthcare personnel and ventilators.

In this section, we propose a multi-stage stochastic program (MSSP) to determine the optimal demand redistribution, resource allocation, and sharing decisions to minimize shortages, medical treatment refusals or delays, and resource extension. Following practical requirements, the foremost priority is to minimize shortages (non-accepted patients), and the second goal is to minimize the allocation of new resources to healthcare regions or hospitals.

By using an MSSP, the optimization problem has several decision layers, where random parameters are progressively realized, and decisions should be adapted to this process. Typically, an N-stage stochastic program includes a sequence of stochastic parameters ${\xi }_1,{\xi }_2,\dots ,{\xi }_{N-1}$ with a discrete support. A scenario is a realization of these stochastic parameters over the problem's stages (periods), and a scenario tree represents the progressive observation of these parameters. During a pandemic such as COVID-19, a healthcare system faces various patient types in different regions or hospitals requiring treatment (unlike healthcare equipment). The number of patients in various types at different regions or hospitals is a stochastic parameter in our study, which is thought of as the healthcare system's demand.

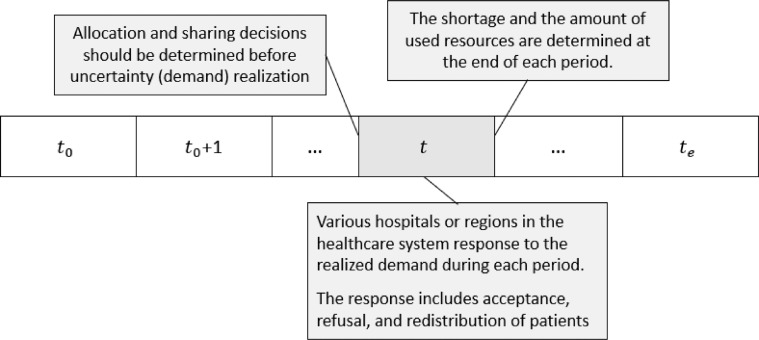
The decisions in each stage of an MSSP can be categorized into two groups: (i) the decisions that are made before the uncertainty realization at that stage, (ii) the decisions that are made based on the uncertainty realization. In our problem setting, both resource sharing and extension belong to the first group of decisions, and other decisions, including the acceptance or refusal of patients and demand redistribution, belong to the second group. Fig. 1 illustrates these decisions in our problem in period $t\in T$ where $T=\left\{t_0,t_0+1,\dots ,t_e\right\}$ is the set of time periods.

Fig. 1.

Different decision types and the decision-making process over $\left|T\right|$ period.

A policy should be non-anticipative in an MSSP, which means the decisions made at each stage must not be dependent on the future realization of stochastic parameters. There are two common ways to formulate an MSSP (Dupačová, 1995; Kall & Wallace, 1994). In the first, an MSSP is formulated as a sequence of nested two-stage stochastic programs in which non-anticipativity is implicitly imposed. In the second (used in this paper), a set of non-anticipativity constraints (NAC) is explicitly modeled and these constraints should be considered for the decisions that are determined before uncertainty realization (Dupačová, 1995; Erdogan & Denton, 2013; Kall & Wallace, 1994).

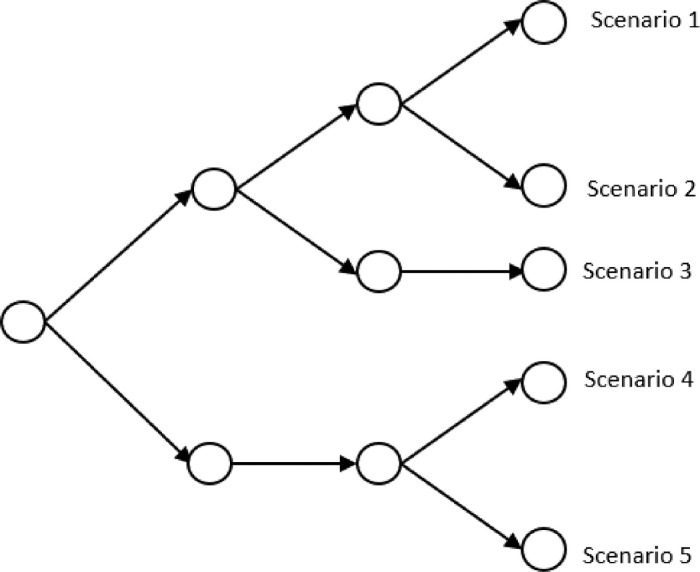
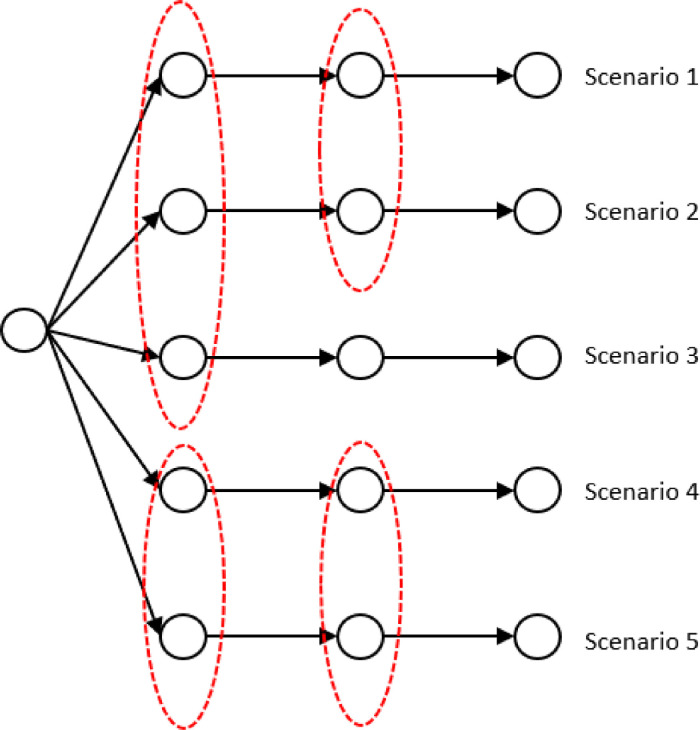
To model stochasticity related to various patient types in healthcare regions or hospitals as a scenario tree, a set of scenarios $S$ with countable size $\left|S\right|$ is taken into account. The corresponding scenarios’ probabilities are ${\pi }_1,{\pi }_2,\dots ,{\pi }_{\left|S\right|}.$ If we denote a realization for patient number of type $k\in K$ at region $i\in I$ on period $t\in T$ under scenario $s\in S$ by $D_{ikt}^s$ and ${\xi }_t^s=\left(D_{ikt}^s:i\in I,k\in K\right)$, then the realization of stochastic parameters in scenario $s\in S$ from period $t_0$ to period $t_e$ is $\left({\xi }_{t_0}^s,{\xi }_{t_0+1}^s,\dots ,{\xi }_{t_e}^s\right)$. Fig. 2a shows an example of a scenario tree with three periods and five scenarios for our problem with three regions. As an example, for scenario s and period t, $\left(|D_{11t}^s|,|D_{21t}^s|,|D_{31t}^s|\right)$ is a realization related to the number of patients in type 1 and $|D_{11t}^s|,|D_{21t}^s|$ and $|D_{31t}^s|$ are corresponding to region 1, 2, and 3, respectively. Fig. 2b is an alternative representation of the scenario tree, which is called scenario fan, where the individual scenarios observed in the particular stages are disaggregated to form five scenarios.

Fig. 2a.

A scenario tree example.

Fig. 2b.

The corresponding scenario fan.

In this section, the proposed MSSP is presented. However, the solution obtained from solving the MSSP is scenario-dependent and, hence, it is not implementable in the real-world practice and does not allow the information attained over time to be used. Indeed, the critical limitation of scenario-based stochastic programs is that their optimal policy is only valid for a limited set of scenarios. To resolve this issue, we develop a new data-driven Rolling Horizon Procedure (RHP). Our approach, presented in Section 4, addresses this issue and provides real-time day-to-day sharing policy and demand redistribution in a rolling horizon manner. The required notations for presenting the mathematical model are defined in Table 1 .

Table 1.

Notations.

Sets and indices
$T$	The set of periods indexed by $t,t^{\prime }\in T.$
$S$	The set of scenarios $s,s^{\prime }\in S.$
$I$	The set of regions $i,i^{\prime }\in I$ (it is possible to consider hospitals set instead of regions based on the problem setting).
$R$	The set of healthcare resources $r\in R.$$R_{DUR}$ and $R_{SER}$ denote the direct in use and service resources, respectively. $R_{EX}$ and $R_{TR}$ denote the set of resources with the possibility of capacity extension and sharing, respectively. Finally, $R_{EX}^c$ and $R_{TR}^c$ are the complement of set $R_{EX}$ and $R_{TR}$, respectively.
$K$	The set of patient types, $k\in K.$
$R\left(k\right)$	The set of required healthcare resources for patient type k.
$I\left(i,r\right)$	The set of regions, which can receive (forward) resource $r\in R$ from (to) region $i\in I.$
$I\left(i,k\right)$	The set of regions, which can receive (forward) patient type $k\in K$ from (to) region $i\in I.$ It is assumed the patient transfer should be done by a lead time of less than one day (period).

Parameters
$D_{ikt}^s$	The number of patients’ arrival in type $k\in K$ at region $i\in I$ in period $t\in T$under scenario $s\in S$.
${\Gamma }_k$	Average discharge time of an accepted patient in $k\in K$.
$L_{ri{i}^{\prime }}$	Lead time for transshipment of resource $r\in R_{TR}$ between regions $i\text{and}{i}^{\prime }\in I,L_{ri{i}^{\prime }}\ge 1,\forall i,i^{\prime }\in I$.
${\lambda }_{ri}$	Lead time of adding resource $r\in R_{EX}$ at region $i,\forall i\in I$
${\overline{X}}_{ik{t}_0}$	The number of hospitalized patients in type $k\in K$ at region $i\in I$ at the beginning of planning horizon.
${\tilde{X}}_{ikt}$	The number of accepted patients in type $k\in K$ in region $i\in I$ in periods before $t_0$, which they will be discharged at period $t$ based on ${\Gamma }_k$. This parameter is zero for $t\ge t_0+{\Gamma }_k.$
${\overline{E}}_{ir{t}_0}$	The number of available resources $r\in R_{DUR}$ in region $i\in I$ at the beginning of planning horizon.
${\overline{C}}_{ir{t}_0}$	The capacity of resource $r\in R_{SER}$ in region $i\in I$ at the beginning of planning horizon.
${\phi }_{kr}$	The capacity usage coefficient of patient type $k\in K$ for resource $r\in R_{SER}$.

Decisions
$n_{irt}^s$	The number of added healthcare resources $r\in \left(R_{DUR}\cap R_{EX}\right)$ at region $i\in I$ in period $t\in T$under scenario $s\in S$.
$c_{irt}^s$	The amount of new capacity for healthcare resource $r\in \left(R_{SER}\cap R_{EX}\right)$ added at region $i\in I$ in period $t\in T$under scenario $s\in S$.
$q_{i{i}^{\prime }rt}^s$	The number of healthcare resource $r\in R_{TR}$, which are transshipped from region $i\in I$ to $i^{\prime }\in I$ at the beginning of period $t\in T$ under scenario $s\in S$.
$v_{irt}^s$	The capacity of healthcare resource $r\in R_{SER}$ at region $i\in I$ in period $t\in T$under scenario $s\in S$.
$x_{ikt}^s$	The number of accepted patients in type $k\in K$ in region $i\in I$ during period $t\in T$ under scenario $s\in S$.
$w_{ikt}^s$	The number of non-accepted patients in type $k\in K$ in region $i\in I$ in period t under scenario $s\in S.$
$w_{ikt}^{{}^{\prime }s}$	The number of non-accepted patients in type $k\in K$ in region $i\in I$ in period t under scenario $s\in S$that cannot be met even with transferring them to other regions, so sent to the next period.
$k{b}_{irt}^s$	The number of available healthcare resource $r\in R_{DUR}$ in region $i\in I$ at the beginning of period $t\in T$ under scenario $s\in S$.
$k{e}_{irt}^s$	Secondary variable that represents the number of healthcare resource $r\in R_{DUR}$ in region $i\in I$ at the end of period $t\in T$ under scenario $s\in S$.
$p_{i{i}^{\prime }kt}^s$	The number of patients in type $k\in K$, which are sent from region $i\in I$ to $i^{\prime }\in I$ at period $t\in T$ under scenario $s\in S$.
$a_{ikt}^s$	Auxiliary binary variable that represents the refusal of patients is occurred in region $i\in I$ at period $t\in T$ under scenario $s\in S$.

The MSSP is presented as follows:

$$\begin{array}{ccc}& & Min:\sum _{s\in S}{\pi }_s[\alpha \left(\sum _{i\in I}\sum _{t\in T}\sum _{k\in K}{w}_{ikt}^{{}^{\prime }s}\right)+\sum _{i\in I}\sum _{t\in T}\sum _{r\in R_{DUR}}\left(\left|T\right|+1-t\right)n_{irt}^s\hfill \\ & & +\sum _{i\in I}\sum _{t\in T}\sum _{r\in R_{SER}}\left(\left|T\right|+1-t\right)c_{irt}^s+\beta \left(\sum _{i^{\prime }\in I}\sum _{i\in I}\sum _{t\in T}\sum _{r\in R}{q}_{i^{\prime }irt}^s\right)\hfill \\ & & +\gamma \left(\sum _{i^{\prime }\in I}\sum _{i\in I}\sum _{t\in T}\sum _{k\in K}{p}_{i^{\prime }ikt}^s\right)]\hfill \end{array}$$ (1)

$$k{b}_{ir{t}_0}^s={\overline{E}}_{ir{t}_0}\forall i\in I,\forall r\in R_{DUR},\forall s\in S$$ (2-1)

$$k{b}_{irt}^s=k{e}_{ir\left(t-1\right)}^s\forall i\in I,\forall t\in T\setminus \left\{t_0\right\},\forall r\in R_{DUR},\forall s\in S$$ (2-2)

$$\begin{array}{ccc}\hfill k{e}_{irt}^s& =& k{b}_{irt}^s+\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i^{\prime }ir\left(t-L_{r{i}^{\prime }i}\right)}^s+n_{ir(t-{\lambda }_{ir})}^s-\sum _{k\in K:r\in R\left(k\right)}{x}_{ikt}^s\hfill \\ & & +\sum _{k\in K:r\in R\left(k\right)}{\tilde{X}}_{ikt}+\sum _{k\in K:r\in R\left(k\right)}{x}_{ik\left(t-{\Gamma }_k\right)}^s-\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i{i}^{\prime }rt}^s\hfill \\ & & \forall i\in I,\forall t\in T,\forall r\in R_{DUR},\forall s\in S\hfill \end{array}$$ (2-3)

$$n_{irt}^s=0\forall i\in I,\forall t\in T,\forall r\in R_{EX}^c,\forall s\in S$$ (2-4)

$$q_{i{i}^{\prime }rt}^s=0\forall i\in I,\forall i^{\prime }\in I,\forall t\in T,\forall r\in R_{TR}^c,\forall s\in S$$ (3)

$$\begin{array}{ccc}\hfill v_{irt}^s& =& {\overline{C}}_{ir{t}_0}+\sum _{t^{\prime }\le t}{c}_{ir(t^{\prime }-{\lambda }_{ir})}^s+\sum _{t^{\prime }\le t}\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i^{\prime }ir\left(t^{\prime }-L_{r{i}^{\prime }i}\right)}^s\hfill \\ & & -\sum _{t^{\prime }\le t}\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i{i}^{\prime }r{t}^{\prime }}^s\forall i\in I,\forall t\in T,\forall r\in R_{SER},\forall s\in S\hfill \end{array}$$ (4-1)

$$c_{irt}^s=0\forall i\in I,\forall t\in T,\forall r\in R_{EX}^c,\forall s\in S$$ (4-2)

$$\begin{array}{ccc}& & \sum _{k\in K:r\in R\left(k\right)}{\phi }_{kr}\left({\overline{X}}_{ik{t}_0}^s+\sum _{t^{\prime }\le t}{x}_{ik{t}^{\prime }}^s-\sum _{t_0+{\Gamma }_k\le t^{\prime }\le t}{x}_{ik\left(t^{\prime }-{\Gamma }_k\right)}^s-\sum _{t^{\prime }\le t}{\tilde{X}}_{ik{t}^{\prime }}\right)\hfill \\ & & \le v_{irt}^s\forall i\in I,\forall t\in T,\forall r\in R_{SER},\forall s\in S\hfill \end{array}$$ (5)

$$\begin{array}{ccc}& & x_{ikt}^s+w_{ikt}^s-\sum _{i^{\prime }\in I\left(i,k\right)}{p}_{i{i}^{\prime }kt}^s=D_{ikt}^s+\sum _{i^{\prime }\in I\left(i,k\right)}{p}_{i^{\prime }ikt}^s+w_{ik\left(t-1\right)}^{{}^{\prime }s}\hfill \\ & & \forall i\in I,\forall k\in K,\forall t\in T,\forall s\in S\hfill \end{array}$$ (6-1)

$$w_{ikt}^{{}^{\prime }s}\ge w_{ikt}^s-\sum _{i^{\prime }\in I\left(i,k\right)}{p}_{i{i}^{\prime }kt}^s\forall i\in I,\forall k\in K,\forall t\in T,\forall s\in S$$ (6-2)

$$w_{ikt}^s\le \underset{s^{\prime }\in S}{max}\left\{D_{ikt}^{s^{\prime }}\right\}\times a_{ikt}^s\forall i\in I,\forall k\in K,\forall t\in T,\forall s\in S$$ (6-3)

$$\sum _{i^{\prime }\in I\left(i,k\right)}{p}_{i^{\prime }ikt}^s\le \underset{s^{\prime }\in S}{max}\left\{D_{ikt}^{s^{\prime }}\right\}\times \left(1-a_{ikt}^s\right)\forall i\in I,\forall k\in K,\forall t\in T,\forall s\in S$$ (6-4)

$$\begin{array}{ccc}\hfill n_{irt}^s& =& n_{irt}^{s^{\prime }}\forall i\in I,\forall r\in \left(R_{DUR}\cap R_{EX}\right),\forall t\in T,\hfill \\ & & \forall s,s^{\prime }\in S:\left({\xi }_{t_0}^s,{\xi }_{t_0+1}^s,\dots ,{\xi }_{t-1}^s\right)=\left({\xi }_{t_0}^{s^{\prime }},{\xi }_{t_0+1}^{s^{\prime }},\dots ,{\xi }_{t-1}^{s^{\prime }}\right)\hfill \end{array}$$ (7-1)

$$\begin{array}{ccc}\hfill c_{irt}^s& =& c_{irt}^{s^{\prime }}\forall i\in I,\forall r\in \left(R_{SER}\cap R_{EX}\right),\forall t\in T,\hfill \\ & & \forall s,s^{\prime }\in S:\left({\xi }_{t_0}^s,{\xi }_{t_0+1}^s,\dots ,{\xi }_{t-1}^s\right)=\left({\xi }_{t_0}^{s^{\prime }},{\xi }_{t_0+1}^{s^{\prime }},\dots ,{\xi }_{t-1}^{s^{\prime }}\right)\hfill \end{array}$$ (7-2)

$$\begin{array}{ccc}\hfill v_{irt}^s& =& v_{irt}^{s^{\prime }}\forall i\in I,\forall r\in R_{SER},\forall t\in T,\hfill \\ & & \forall s,s^{\prime }\in S:\left({\xi }_{t_0}^s,{\xi }_{t_0+1}^s,\dots ,{\xi }_{t-1}^s\right)=\left({\xi }_{t_0}^{s^{\prime }},{\xi }_{t_0+1}^{s^{\prime }},\dots ,{\xi }_{t-1}^{s^{\prime }}\right)\hfill \end{array}$$ (7-3)

$$\begin{array}{ccc}\hfill k{b}_{irt}^s& =& k{b}_{irt}^{s^{\prime }}\forall i\in I,\forall r\in R_{DUR},\forall t\in T,\hfill \\ & & \forall s,s^{\prime }\in S:\left({\xi }_{t_0}^s,{\xi }_{t_0+1}^s,\dots ,{\xi }_{t-1}^s\right)=\left({\xi }_{t_0}^{s^{\prime }},{\xi }_{t_0+1}^{s^{\prime }},\dots ,{\xi }_{t-1}^{s^{\prime }}\right)\hfill \end{array}$$ (7-4)

$$\begin{array}{ccc}\hfill q_{i{i}^{\prime }rt}^s& =& q_{i{i}^{\prime }rt}^{s^{\prime }}\forall i\in I,\forall i^{\prime }\in I,\forall r\in R,\forall t\in T,\hfill \\ & & \forall s,s^{\prime }\in S:\left({\xi }_{t_0}^s,{\xi }_{t_0+1}^s,\dots ,{\xi }_{t-1}^s\right)=\left({\xi }_{t_0}^{s^{\prime }},{\xi }_{t_0+1}^{s^{\prime }},\dots ,{\xi }_{t-1}^{s^{\prime }}\right)\hfill \end{array}$$ (7-5)

$$\mathit{n},\mathit{c},\mathit{v},\mathit{kb},\mathit{ke},\mathit{q},\mathit{w},{\mathit{w}}^{\prime },\mathit{p},\mathit{x},\mathit{q}\ge 0\text{and}\mathit{a}\in {\left\{0,1\right\}}^{\left|I\right|\times \left|K\right|\times \left|T\right|\times \left|S\right|}.$$ (8)

Our main goal in relation (1) is to minimize the amount of cumulative non-accepted patients in the considered healthcare system over the planning horizon, the total number of added DUR resources, the total number of added SER resources, and the total amount of patient transfers and resource sharing. According to the practical aspects, the weights $\alpha ,\beta$, and $\gamma$ are set such that the minimization of non-accepted patients has the highest priority. The second priority is to minimize the total number of new resources. Since the supply of new resources is time-consuming for policy makers, it is desirable to have as much time as possible before new supplies of healthcare resources. In order to account for this aspect in our formulation, the weight $\left|T\right|+1-t$ is considered for new resources in each period t. Furthermore, this weight can be interpreted as some rental cost per day in the objective function. Finally, we minimize the amount of resource sharing and patients’ transfer, by considering coefficients $\beta$ and $\gamma$, respectively, with the lowest priority in comparison with other goals. In practice, policy makers can set coefficients $\beta$ and $\gamma$ based on their necessities. It is worth noting that in the results, the mentioned parameters are tuned so that the amount of shortages be reasonable and manageable for the healthcare system.

Based on constraints (2-1)-(2-4), the available DUR at the beginning and end of each time period are calculated. The possibility of the extension of DUR resources and resource sharing over the planning horizon are considered by constraints (2-4) and (3), respectively. In addition, relations (4-1) show the available capacity of SER resources in each period and under each scenario. The possibility of adding SER resources over the planning horizon is considered by constraints (4-2). For the acceptance of patients’ hospitalization, constraints (5) guarantee the available capacity for serving them in terms of SER resources. Based on constraints (6-1)-(6-4), the amount of patients’ acceptance, non-acceptance, and redistribution are calculated. Constraints (6-2) obtain the number of refused patients that cannot be met even by transferring them to other regions (hospitals). Further, constraints (6-3) and (6-4) guarantee that a region (hospital) can accept the patients from other regions (hospitals) in each period if it does not refuse any patients at that period. Constraints (7-1)-(7-5) are NACs in our MSSP, which are considered for the decisions that are made before uncertainty realization at each stage. Variable types and ranges are defined in constraints (8). It is worth noting that the proposed model is flexible to be used for a set of regions as well as hospitals.

4. Data-driven decision-making by the RHP

Here, we propose a data-driven resource planning framework under uncertainty by using an RHP to implement our MSSP in real time. The rolling horizon approach makes the obtained policy implementable in practice and evaluates the policy empirically. By this approach, the latest data that is revealed as time progresses enables us to adjust our decisions over time. In other words, we observe the realization of the uncertain parameters in one period and, then, dynamically update the uncertainty for the following periods and input parameters of the MSSP.

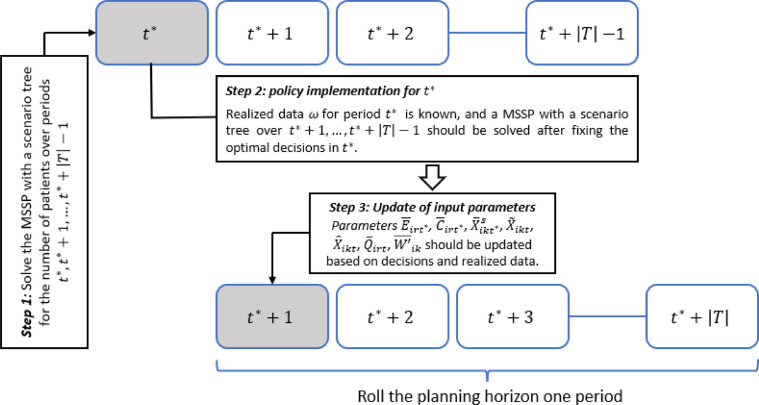
To explain how the proposed approach works for the real data over a horizon of $\left|T\right|$ periods (days), we consider a sample path, denoted by $\omega$, as real data. The sample path includes the realized number of patients and discharge of accepted patients over $\left|T\right|$ periods. In planning horizon $=\left\{t_0,t_0+1,\dots ,t_e\right\}$, to obtain a policy for $t^{*}\in T$, we solve the MSSP with a scenario tree for the number of patients over periods $t^{*},t^{*}+1,\dots ,t^{*}+\left|T\right|-1$. Then for the implementation of the obtained policy, we solve the MSSP with a horizon of $\left|T\right|$ periods in which for the first period $t^{*}$, the uncertain parameters are known (based on sample path $\omega$) and the optimal decisions are fixed. For the next period, we update some input parameters of the stochastic model and in addition to model's parameters that should be updated in each period, we repeatedly update the uncertainty after a predetermined number of periods by calibrating parameters of our simulation model based on our observations (See the RHP in Fig. 3 ).

Fig. 3.

The RHP in this study.

The explained procedure should be repeated in each period, and we roll the patients’ arrival planning horizon forward one day by adding a new period to the calendar at every step. In obtaining policy in each specific period $t^{*}$, we should update some parameters of the stochastic model and consider some modification in the presented model to capture the impacts of previous realized data and decisions. In Table 2 , we provide the definition of some parameters, which are used for the model's modifications, and we entitle this model the rolling horizon model. It is worth noting that period $t^{*}$ is the first period of the horizon in the rolling horizon model.

Table 2.

Parameters for updating the rolling horizon model.

${\overline{E}}_{ir{t}^{*}}$	The amount of resource $\in R_{DUR}$, which are available in region $i\in I$ at the beginning of period $t^{*}$.
${\overline{C}}_{ir{t}^{*}}$	The capacity of resource $r\in R_{SER}$ in region $i\in I$ at the beginning of period $t^{*}$.
${\overline{X}}_{ik{t}^{*}}^s$	The number of hospitalized patients in type $k\in K$ at region $i\in I$ at the beginning of period $t^{*}$.
${\tilde{X}}_{ikt}$	The number of accepted patients in type $k\in K$ in region (hospital) $i\in I$ in periods before $t^{*}$, which they will be discharged at period $t$ based on ${\Gamma }_k$. This parameter is zero for $t\ge t^{*}+{\Gamma }_k.$
${\widehat{X}}_{ikt}$	The number of accepted patients in type $k\in K$ in region (hospital) $i\in I$ in periods before $t^{*}$, which is supposed to be discharged in period $t$ based on ${\Gamma }_k$, but they are discharged in periods before $t^{*}$.
${\overline{Q}}_{irt}$	The number of healthcare resources $r\in R_{TR}$, which are transshipped from other regions to region $i\in I$ in periods before $t^{*}$ and will be available at the beginning of period $t\in T$.
${\overline{W{}^{\prime }}}_{ik}$	The number of patients in type $k\in K$ at region $\in I$, which are not accepted in any regions in period $t^{*}-1$ (previous period of the beginning period).

In the rolling horizon model, parameters ${\overline{E}}_{ir{t}_0}$ and ${\overline{C}}_{ir{t}_0}$ should be changed to ${\overline{E}}_{ir{t}^{*}}$ and ${\overline{C}}_{ir{t}^{*}}$, respectively, and their values are based on the available information at the beginning of each period. Constraints (2-3) should be updated as follows:

$$\begin{array}{ccc}\hfill k{e}_{irt}^s& =& k{b}_{irt}^s+\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i^{\prime }ir\left(t-L_{r{i}^{\prime }i}\right):\left(t-L_{r{i}^{\prime }i}\right)\ge t^{*}}^s\hfill \\ & & +{\overline{Q}}_{irt}+n_{ir(t-{\lambda }_{ir})}^s-\sum _{k\in K:r\in R\left(k\right)}{x}_{ikt}^s\hfill \\ & & +\sum _{k\in K:r\in R\left(k\right)}{x}_{ik\left(t-{\Gamma }_k\right):\left(t-{\Gamma }_k\right)\ge t^{*}}^s+\sum _{k\in K:r\in R\left(k\right)}{\tilde{X}}_{ikt}-\sum _{k\in K:r\in R\left(k\right)}{\widehat{X}}_{ikt}\hfill \\ & & -\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i{i}^{\prime }rt}^s\hfill \\ & & \forall i\in I,\forall t\in T,\forall r\in R_{DUR},\forall s\in S\hfill \end{array}$$ (9)

By constraints (9) in the rolling horizon model, the impact of patients’ acceptance, resource sharing decisions, and realized uncertainty will be captured. Furthermore, constraints (4-1) should be modified as follows:

$$\begin{array}{ccc}\hfill v_{irt}^s& =& {\overline{C}}_{ir{t}^{*}}+\sum _{t^{\prime }\le t}{c}_{ir(t^{\prime }-{\lambda }_{ir})}^s+\sum _{t^{\prime }\le t}\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i^{\prime }ir\left(t^{\prime }-L_{r{i}^{\prime }i}\right):\left(t^{\prime }-L_{r{i}^{\prime }i}\right)\ge t^{*}}^s+\sum _{t^{\prime }\le t}{\overline{Q}}_{ir{t}^{\prime }}\hfill \\ & & -\sum _{t^{\prime }\le t}\sum _{i^{\prime }\in I\left(i,r\right)}{q}_{i{i}^{\prime }r{t}^{\prime }}^s\hfill \\ & & \forall i\in I,\forall t\in T,\forall r\in R_{SER},\forall s\in S\hfill \end{array}$$ (10)

Constraints (5) is also modified in the rolling horizon model as follows:

$$\begin{array}{ccc}& & \sum _{k\in K:r\in R\left(k\right)}{\phi }_{kr}\left({\overline{X}}_{ik{t}^{*}}^s+\sum _{t^{\prime }\le t}{x}_{ik{t}^{\prime }}^s-\sum _{t^{\prime }\le t}\left({\tilde{X}}_{ik{t}^{\prime }}-{\widehat{X}}_{ik{t}^{\prime }}\right)-\sum _{t^{*}+{\Gamma }_k\le t^{\prime }\le t}{x}_{ik\left(t^{\prime }-{\Gamma }_k\right)}^s\right)\hfill \\ & & \le v_{irt}^s\forall i\in I,\forall t\in T,\forall r\in R_{SER},\forall s\in S\hfill \end{array}$$ (11)

Finally, the patients which are not accepted in any region before period $t^{*}$ should be considered in constraints (6-1) for the first period by substituting parameter ${\overline{W{}^{\prime }}}_{ik}$ instead of $w{{}^{\prime }}_{ik\left(t^{*}-1\right)}^s$.

The RHP has been applied for MSSPs in a few studies (Fattahi & Govindan, 2018, 2020) and one can refer to these studies for more information about the estimation of the true objective function in real time by rolling horizon simulation. In other words, by assuming enough realized sample paths, we can evaluate the policies from MSSPs by the rolling horizon simulation. Fig. 3 shows the RHP in this study.

5. Scenario tree construction for multivariate stochastic parameters

In this study, we focus on one category of COVID-19 pandemic patients, those who get the SARS-CoV-2 virus from infected individuals in a cohort. This group includes patients with a critical state who will die if they remain untreated. These patients should be hospitalized, and their treatments, including an ICU with mechanical ventilation, can prevent a subset of deaths among them. To construct a scenario tree for the MSSP, we follow the approach presented by Ekici, Keskinocak and Swann (2014) for the simulation of the number of patients who need hospitalization in a region with insights from experts in a medical school. Accordingly, an agent-based continuous-time stochastic model is constructed for the COVID-19 transmission.

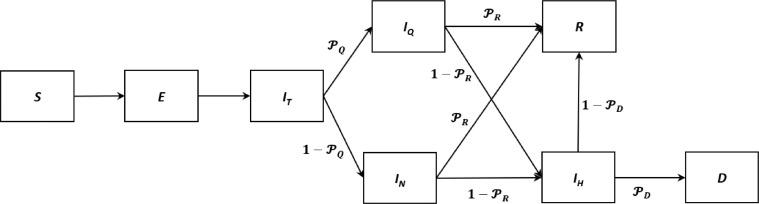
Firstly, the entire population is divided into three age groups (0–19y, 20–59y, or ≥60y), that helps model the various types of interactions between people in the population. The population in a region is classified into Susceptible (S), Exposed (E), Infected (I_T), Quarantined (I_Q), Hospitalized at the critical stage (I_H), Recovered (R), and Deceased (D). In our model, a proportion of the exposed individuals in an age subgroup are quarantined as soon as they get into the Infected stage, which means they are isolated from the population and do not infect additional individuals. Our simulation network related to defined compartments is illustrated in Fig. 4 .

Fig. 4.

The simulation network of our model.

We construct the base model for each group and the disease spread is modeled through two main parts: 1) the disease progress for an infected individual, and 2) the spread of the disease between the members of the population. In other words, we assume that each individual will lie in one of the compartments in Fig. 4. ${\mathcal{P}}_Q,{\mathcal{P}}_R,$and ${\mathcal{P}}_D$ are the probabilities of self-quarantine of an infected individual, recovery of an infected individual without hospitalization, and death of a hospitalized individual, respectively. In the model, we assume 80% of 0–19y group, 50% of 20–59y, and 90% of ≥60y group quarantine themselves after getting the infection. Generally, we model a defined cohort of individuals (e.g., population of a region) for a given number of days (simulation horizon). The simulation time unit is one day. Susceptible individuals can acquire SARS-CoV-2 infection from infected individuals in the cohort. Once an individual is infected, he/she progresses through various infection states until either recovery or death. The severity of disease and the length of stay in each disease state are based on age-specific transition probabilities of COVID-19 natural history, estimated from historical data and scientific reports (Haridy, R., 2020; Hu et al., 2020; Liu, Gayle, Wilder-Smith & Rocklöv, 2020; Mizumoto, Kagaya, Zarebski & Chowell, 2020; Wang et al., 2020; Yang et al., 2020; Zhou et al., 2020; Perc, Gorišek Miksić, Slavinec & Stožer, 2020). In this study, we considered that the individuals who are in the critical disease state should be managed in an ICU with mechanical ventilation.

Effective reproduction number (R₀) is another important parameter of our model which is the average number of secondary cases caused by an infectious individual; it determines the infectivity of the virus. We update the input parameters each week to account for the variation of effective reproduction number. By consultation from partner medical schools, we have obtained the other parameters and constructed the described disease spread model.

By running the simulation model, we obtain the number of patients in critical state at each region/hospital over a planning horizon. The results of the simulation model depend on the values of ${\mathcal{P}}_Q,{\mathcal{P}}_R,{\mathcal{P}}_D$, and R₀, which can change within some small intervals based on the literature's data. Therefore, by running the simulation model several times, we can obtain a set of discrete scenarios for the stochastic parameter as a scenario fan. We then construct a scenario tree based on the generated scenario fan and reduce the number of scenarios in order to avoid computationally intractable stochastic programs. To do so, we deploy a forward scenario tree construction method proposed by Heitsch and Romisch (2005) based on the proposed heuristics by Dupačová, Gröwe-Kuska and Römisch (2003). They proposed two approaches to transform a scenario fan into a scenario tree called as the forward and backward constructions. The generated scenario fan follows a probability distribution $F$ and if we transform it into a scenario tree with probability distribution $F^T$, the Kantorovich distance ($D^K$) between $F$ and $F^T$ should be less than a predetermined value $\epsilon$. In other words, the reduction algorithms apply maximal reduction strategy such that $D^K\left(F,F^T\right)<\epsilon$.

We use forward scenario tree construction approach in this paper and bundle the scenarios for each period $t\in T$. For detailed explanations related to the scenario construction approach, one can refer to Fattahi and Govindan (2018), Fattahi, Govindan and Keyvanshokooh (2018), and Fattahi and Govindan (2020). Further, parameter $\epsilon$is considered as ${\epsilon }_r\times {\epsilon }_{max}$ where ${\epsilon }_r$ is a constant value between zero and one representing a scale for the amount of reduction in the initial scenario fan and ${\epsilon }_{max}$ is the minimum distance between $F$ and one of its scenarios with probability one. It is worth noting that by increasing the reduction scale ${\epsilon }_r$, the number of obtained scenarios decreases, so the information loss increases. However, as the number of scenarios decreases, we have a better computational tractability for solving the MSSP. Therefore, there is a trade-off between the number of scenarios and computational tractability.

The RHP enables us to deal with the uncertainty realization over time. The uncertainty vector at each time period $t^{*}$, ${\mathit{\xi }}_{t^{*}}=\left({\mathit{\xi }}_{t^{*}},{\mathit{\xi }}_{t^{*}+1},\dots ,{\mathit{\xi }}_{t^{*}+\left|T\right|-1}\right)$, depends on uncertainty at periods before time period $t^{*}$. If we consider the realized uncertainty before $t^{*}$ as ${\overline{\mathit{\xi }}}_{\left[t^{*}-1\right]}$, the dependency of ${\mathit{\xi }}_{t^{*}}$ to ${\overline{\mathit{\xi }}}_{\left[t^{*}-1\right]}$ can be presented as ${\mathit{\xi }}_{t^{*}}\left({\overline{\mathit{\xi }}}_{\left[t^{*}-1\right]}\right)$. During any pandemic, many parameters can affect disease spread and transmission and we capture ${\mathit{\xi }}_{t^{*}}\left({\overline{\mathit{\xi }}}_{\left[t^{*}-1\right]}\right)$ by our simulation model and update the scenario trees in predetermined time periods over the planning horizon.

6. Computational results

We will give a proof of concept for our data-driven MSSP methodology using two case studies during COVID-19 pandemic: 1) sharing mechanical ventilators among a subset of regions in the U.S., 2) sharing nurses and ventilators and demand transfers between hospitals in a geographical area of Iran.

6.1. Case study 1: sharing ventilators among a subset of U.S. healthcare regions

In this case study, we address sharing of ventilators among healthcare regions in an area of the USA based on Keyvashokooh, Fattahi, Zokaeinikoo, Freedberg and Kazemian (2020). During each peak of the pandemic, additional ventilators were obtained from the government to cope with the surge in ventilator demand. Our data-driven optimization model informs an optimal ventilator allocation and relocation policy so that the uncertain demand can be satisfied with the fewest possible ventilators. This ensures that hospitals can better serve non-COVID patients and potentially cancel fewer procedures by accommodating the needs of patients with as few ventilators as possible. It should be mentioned, in this case study, we address one type of critical patients needing ventilators, and patient transfer between regions is not reasonable and applicable since we have not considered hospitals in this case study.

In solving the MSSP, 150 scenarios in the form of a scenario fan are simulated by using the agent-based continuous-time stochastic model for COVID-19 transmissions, and then the scenarios are reduced and converted into a scenario tree by the forward scenario construction approach. In our implementations, parameter ${\epsilon }_r$ is set to 0.7. It is worth noting for setting the value of ${\epsilon }_r$, we have done stability analysis based on the approaches proposed by Fattahi and Govindan (2018), and the in-sample and out-of-sample stability error are 2.2% and 1.8%, respectively. Regarding computational tractability, in examined case studies, our model is solvable with various settings by the CPLEX solver in less than 5 min.

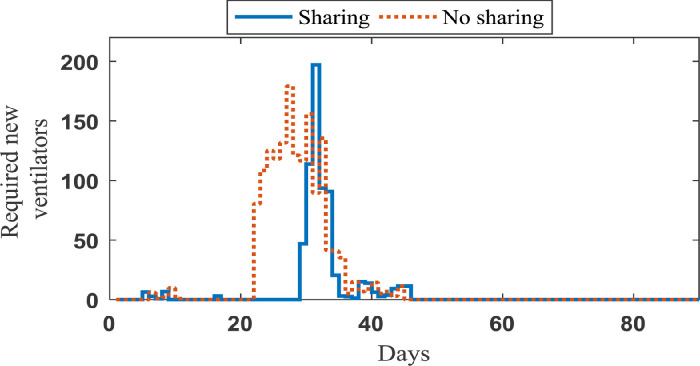
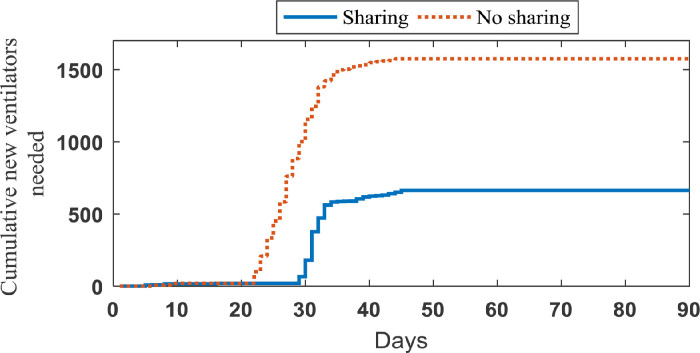
The impact of sharing ventilators strategy. In order to investigate the importance of sharing strategies, 20 sample paths are generated based on our simulation model that represent the realized number of new patients in need of ventilators on each day over the planning horizon (90 days) and the length of ventilator use for each patient. Considering this set of samples, we implement our data-driven approach to obtain the optimal sharing policy corresponding to each sample path. The average number of new ventilators required to cope with the demand and its cumulative value under two strategies (sharing and no sharing strategies) are shown in Figs. 5 and 6 , respectively.

Fig. 5.

Average number of required ventilators in each day in Case study 1.

Fig. 6.

Average cumulative number of required ventilators in Case study 1.

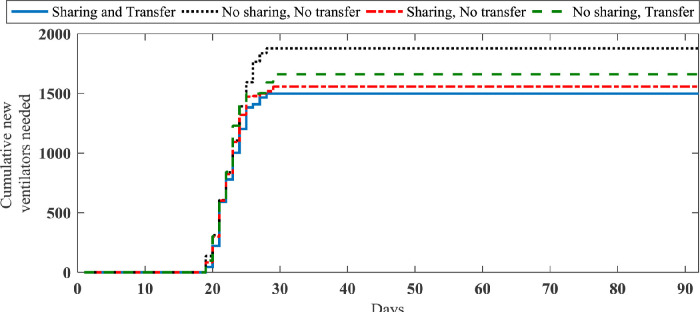
As seen in Fig. 5, when resource sharing is not done, a new supply of ventilators is needed earlier than when ventilators are shared. Under the sharing strategy, some of the early shortages can be eliminated by moving ventilators from regions with excess ventilators to those experiencing a shortfall. More importantly, we can see in Fig. 6 that the no sharing strategy requires significantly higher number of additional ventilators to cope with the demand. While 1574.7 additional ventilators are needed in average to avoid refusal of patients’ care as much as possible across this US area under the no sharing strategy, this area under the sharing strategy requires only 662.5 additional ventilators to achieve the same outcome. The more details of information obtained from simulating case study 1 are reported in Table 3 . Through solving our case study by the RHP over 90 days, we have constructed a scenario tree for each day and updated the input parameters of our agent-based simulation model, weekly. It is worth noting that the average number of scenarios in the constructed scenario trees by ${\epsilon }_r=$ 0.7 is 22.8.

Table 3.

Ventilator needs and sharing outcomes under two strategies.

	Total new ventilators required, Mean (SD)	Total transshipments between regions, Mean (SD)	Total shortages (non-accepted patients), Mean (SD)	Maximum number of shortages (non-accepted patients) over scenario paths
No sharing	1574.7 (114.4)	0 (0)	16.1 (8.1)	34
Sharing	662.5 (21.2)	2898 (132.1)	14.8 (7.9)	27

From Table 3, we can see the amount of sharing between the regions is significant under the sharing strategy. In addition, although the impact of sharing strategy on the non-accepted patients’ number is not meaningful based on our mathematical modeling, the total number of needed ventilators in the case of no sharing increases significantly. In other words, in our optimization problem, we have assumed the needed ventilators will be supplied by the government in the US and because of this issue, we have not any significant increase in the value of shortages.

6.2. Case study 2: demand redistribution and sharing resources among a subset of Iranian hospitals

In this case study, main hospitals in some cities of Iran are considered during the COVID-19 pandemic that contains 20 hospitals in a healthcare region. Each hospital has an initial capacity of ventilators, ICU beds, and medical personnel (nurses). The ICU beds and ventilators correspond to the DUR and medical personnel relate to the SER. Here, sharing of ventilators and medical personnel and patients’ transfer are possible to provide services to infected patients requiring the hospitalization. The horizon of three months in the third peak of COVID-19 is considered for this case study. Our data-driven model optimizes various strategies such that demand can be satisfied with fewest resources possible.

6.2.1. The impact of sharing resources and patients transfer strategies

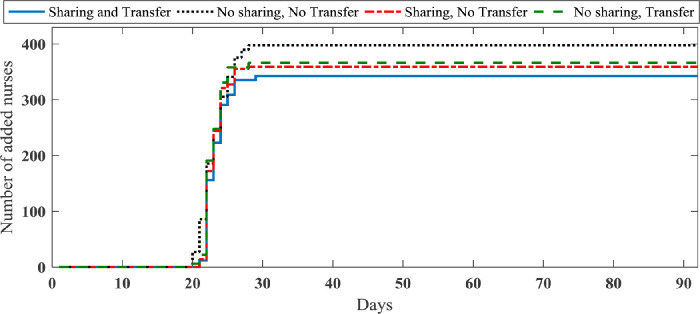
We investigate the importance of our strategies in this section. Considering a set of samples as realized uncertainty, we implement our data-driven approach to obtain the optimal resource planning corresponding to each sample path. The average total number of new nurses and ventilators required to cope with the demand under four strategies (no sharing and no patient transfer, sharing and no patient transfer, no sharing and patients transfer, sharing and patients transfer strategies) are shown in Figs. 7 and 8 , respectively. More details of information obtained from simulating case study 2 are reported in Table 4 . It is worth noting that through solving case study 2 by the RHP over 90 days, the average number of scenarios in the constructed scenario trees by ${\epsilon }_r=$ 0.7 is 24.1.

Fig. 7.

Average total number of required nurses in case study 2.

Fig. 8.

Average total number of required new ventilators in case study 2.

Table 4.

Ventilators and nurses needed under four strategies.

	Total new ventilators required, Mean (SD)	Total new nurses required, Mean (SD)	Total shortages (non-accepted patients) Mean (SD)	Maximum number of shortages (non-accepted patients) over scenario paths
No sharing, No patients transfer	1877.1 (129.2)	397.8 (28.9)	18.8 (9.9)	27
Sharing, Patients transfer	1498.1 (112.7)	342.5 (26.1)	2.1 (1.01)	5
Sharing, No patients transfer	1558.5 (113.1)	359.3 (27.9)	9.3 (3.7)	14
No sharing, Patients transfer	1661 (115.4)	366.2 (25.0)	7.4 (2.8)	10

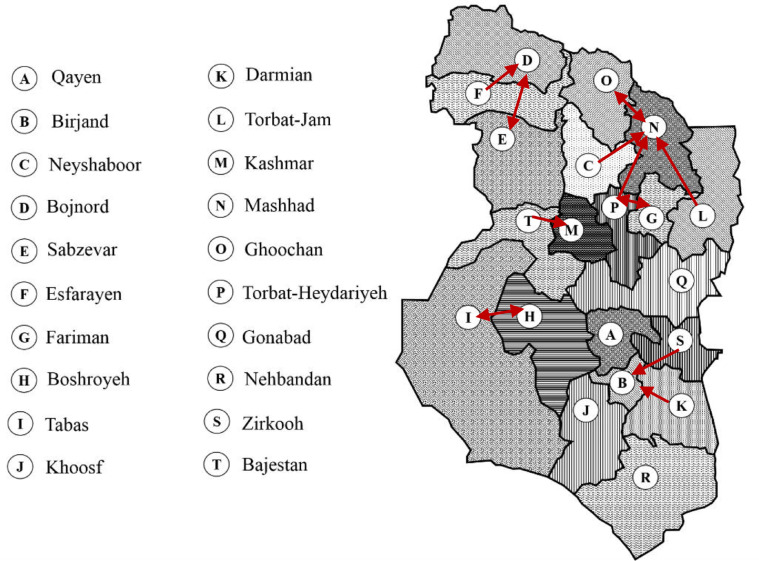
Presented results in Table 4 show that we can improve the required ventilators and nurses by about 20% and 14%, respectively, by using both sharing and patients’ transfer strategies. Further, the sharing strategy in this case study is more effective than patients transfer strategy in terms of required new resources. However, patients transfer strategy has a better impact on the reduction of non-accepted patients in compared to the sharing strategy. Fig. 9 shows the main patients transfer through the considered region in the sharing and patients transfer strategy.

Fig. 9.

Main patients’ transfers through the considered region in case study 2 (more than 10 over the planning horizon in average).

6.2.2. Demand redistribution vs resource sharing

The presented results in the previous section highlight the importance both of resource sharing and demand redistribution strategies. However, some policy makers may have different priorities in using these strategies based on the existing healthcare infrastructure. In this sub-section, we investigate how different priorities can be embedded in our model.

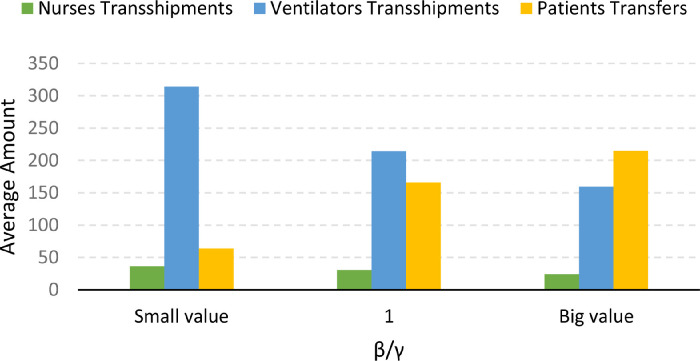
In our results in the previous sub-section, the same weights are considered for $\beta$ and $\gamma$ in the sharing and patients transfer strategy. Here, we report the sensitivity of the average amount of ventilators transshipments, nurses’ transshipments, and patients transfers in this strategy to $\frac{\beta }{\gamma }$ in Fig. 10 .

Fig. 10.

The sensitivity of the average amount of nurses’ transshipments, ventilators transshipments, and patients transfers to $\frac{\beta }{\gamma }$.

As shown in Fig. 10, the sensitivity of nurses and ventilators transshipments to $\frac{\beta }{\gamma }$ value are relatively the same. On the other hand, we can obtain various policies in terms of using resource sharing and patients transfer by setting parameters $\beta$ and $\gamma$.

6.3. The significance of data-driven decisions

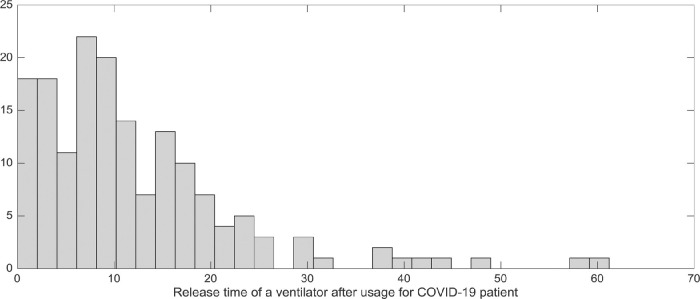
One of the main advantages of our proposed data-driven methodology is the progressive information update based on uncertainty realization over time. In this sub-section, we assess the impact of data-driven decision-making in terms of one aspect. The discharge time of a patient, denoted by $\Gamma$, has a significant impact on the optimal decisions. In this paper, we have assumed that the discharge time of patients in critical state and the resources’ release are the same. Using published data on the duration of ventilator use for patients with COVID-19, we used a lognormal distribution for $\Gamma$ (Ludwig, Jacob, Basedow, Andersohn & Walker, 2021). Based on our historical data, the value of $\Gamma$ follows log-normal distribution and $ln\left(\Gamma \right)$ has normal distribution with mean 2.5 and standard deviation 0.93. Fig. 11 shows the release time of ventilators in our historical data.

Fig. 11.

The release time of ventilators after usage for the COVID-19 patients.

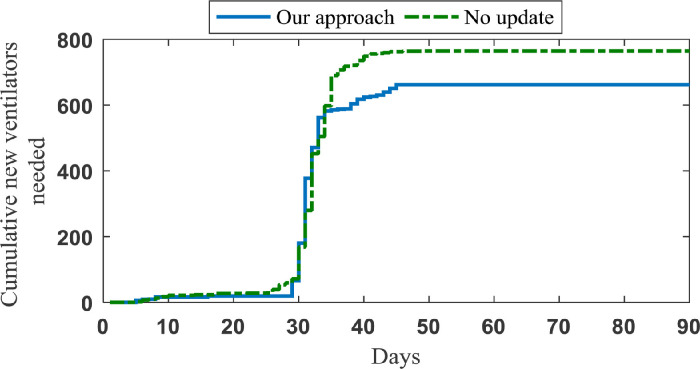
In the optimization model, we set the value of $\Gamma$ to the mean duration of ventilator use (14 days). Then, by implementation of our data-driven approach, we account for the released ventilators in each region on each day. In order to investigate the importance of this data-driven approach, we assume that all ventilators will be released after 14 days and use our model without updating released ventilators on each day. As shown in Fig. 12 , without a data-driven approach in case study 1, 764.5 additional ventilators are called on to ensure demand is met as much as possible, whereas with a data-driven approach, the same is achieved with only 662.5 ventilators. Further, in case study 2, the average amount of required ventilators and nurses increase about 11% and 9%, respectively, if we assume a constant value for $\Gamma$ and do not update the input parameters based on the obtained information.

Fig. 12.

Average number of required ventilators in case study 1 and in the case of no update, which is assumed that ventilators would be released after 14 days.

Note we have only examined the importance of parameter $\Gamma$ in this sub-section, and in our data-driven model, we update the discharge of patients as well as the uncertainty through our data-driven RHP.

6.4. Risk-averse decisions

Here, we determine a risk-management policy by using the Conditional Value at Risk (CVaR) as a well-defined risk measure. Linear programming techniques are used for formulating the problem by this risk measure (Ahmed, 2006). By assuming the cumulative distribution function of random variable Q as ${\mathcal{F}}_Q(.)$, the Value at Risk at the confidence level c ($Va{R}_c$) is $Va{R}_c\left(\mathcal{F}\right)=\text{inf}\left\{\theta \in R|{\mathcal{F}}_Q\left(\theta \right)\ge c\right\}$ and hence $CVa{R}_c\left(\mathcal{F}\right)=\mathbb{E}\left(Q|Q\ge Va{R}_c\left(\mathcal{F}\right)\right)$. Additionally, based on the formulation presented by Rockafellar and Uryasev (2002), $CVa{R}_c\left(\mathcal{F}\right)=\underset{z\in R}{inf}\left\{z+\frac{1}{1-c}\mathbb{E}\left[{\left(F-z\right)}^{+}\right]\right\}$.

One important issue related to the risk-averse MSSPs is the time consistency. Recently, it has been highlighted by several studies as a desirable property of a problem. Informally, in order to preserve the time consistency in MSSPs, by given the available information at the time when a policy is determined, the optimality of the policy should only be with respect to possible future realizations (Homem-de-Mello & Pagnoncelli, 2016). Ruszczyński (2010) defined the time consistency in dealing with sequences of random variables in the dynamic programming approach, and Shapiro (2009) focused on the stability of decision variables at each stage in risk-averse MSSPs.

We consider $CVa{R}_c$ of total non-accepted patients instead of its expected value and, we have used the approach of Yin and Büyüktahtakin (2021)) for modeling the risk-averse MSSP. Yin and Büyüktahtakin (2021)) confirmed that their modeling approach preserves the time consistency. In other words, our formulation enforces the time consistency by non-anticipativity constraints.

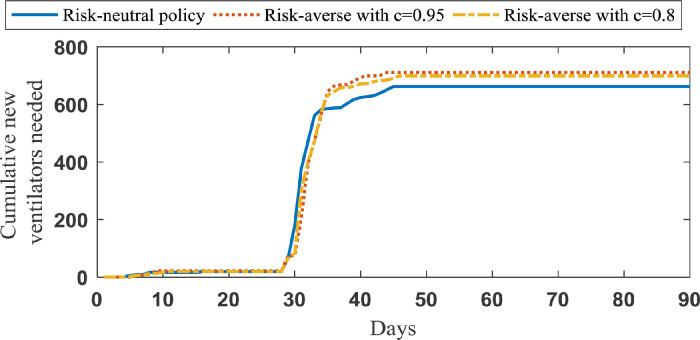
In case study 1, we examine the total number of new ventilators over 90 days for risk-averse decisions where c is equal to 0.8 and 0.95. In Fig. 13 , the needed ventilators for risk neutral and risk-averse decisions are illustrated.

Fig. 13.

Average total number of required ventilators in case study 1 for risk-neutral and risk-averse policies.

As shown in Fig. 13, the risk management policies call for about 8% more ventilators. However, this comes with the benefit of fewer non-accepted patients and standard deviation of new ventilators in practice. $CVa{R}_c$ quantifies the expected value of the worst $\left(1-\alpha \right)\%$ non-accepted patients. If we increase the value of parameter c, $CVa{R}_c$ accounts for the risk of higher number of non-accepted patients. As a consequence, larger values for parameter c result in larger values for $CVa{R}_c.$ Here, we have investigated two values for c, including 0.8 and 0.95, in case study 1, and the corresponding results are reported in Table 5 .

Table 5.

New ventilators required and the number of non-accepted patients with the risk-neutral and risk-averse policies.

	New ventilators required, Mean (SD)	Total non-accepted patients, Mean (SD)	Maximum of non-accepted patients over scenarios
Risk-averse Policy with c =0.95	710.8 (16.7)	3.2 (2.7)	9
Risk-averse Policy with c = 0.8	699.8 (17.2)	4.3 (2.2)	11
Risk-neutral Policy	662.5 (21.2)	14.8 (7.9)	27

Here, we report the new resources allocation as well as the number of non-accepted patients in both of case study 1 and 2 under risk-averse and risk-neutral policies. Furthermore, we compare our results by the obtained policies from two-stage stochastic programming and deterministic models to highlight the importance of the uncertainty consideration and multi-stage stochastic programming approach. In the two-stage stochastic model, all allocation and sharing decisions should be made at the beginning of the planning horizon. In Tables 6 and 7 , the results related to case study 1 and 2 are reported, respectively.

Table 6.

New ventilators required and non-accepted patients with the risk-averse, stochastic, and deterministic policies in case study 1.

	New Ventilators Required, Mean (SD)	Total non-accepted patients, Mean (SD)	Maximum non-accepted patients over scenarios
Risk-averse Policy with c = 0.95	710.8 (16.7)	3.2 (2.7)	9
Risk-neutral policy by MSSP approach	662.5 (21.2)	14.8 (7.9)	27
Risk neutral policy by two-stage stochastic programming approach	677.2 (23.7)	15.1 (9.2)	27
Deterministic Policy	619.3 (24.9)	26.2 (15.3)	53

Table 7.

New ventilators and nurses required and non-accepted patients with the risk-averse, stochastic, and deterministic policies in case study 2.

	New ventilators required, Mean (SD)	New nurses required, Mean (SD)	Total non-accepted patients, Mean (SD)	Maximum non-accepted patients over scenarios
Risk-averse Policy with c = 0.95	1541.7 (78.1)	355.1 (14.8)	0.81 (0.22)	2
Risk-neutral policy by MSSP approach	1498.1 (112.7)	342.5 (26.1)	2.1 (1.01)	5
Risk neutral policy by two-stage stochastic programming approach	1589.4 (128.1)	353.8 (32.9)	2.9 (0.92)	6
Deterministic Policy	1382 (189.7)	307.9 (48.1)	16.7 (2.9)	24

From Table 6, we can see about 2.4% improvement of the MSSP in compared with the two-stage stochastic program in terms of the total number of new ventilators in case study 1. In addition, as shown in Table 7 for case study 2, the improvement of required ventilators and nurses are 5.7% and 3.2%, respectively. In the two-stage stochastic model, all allocation and sharing decisions should be made at the beginning of the planning horizon. Additionally, the poor performance of the deterministic policy is highlighted in terms of the amount of non-accepted patients in which the average number of patients is considered instead of stochastic patients’ number.

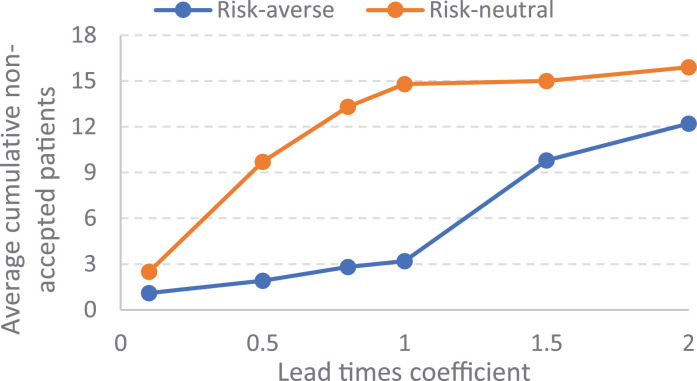
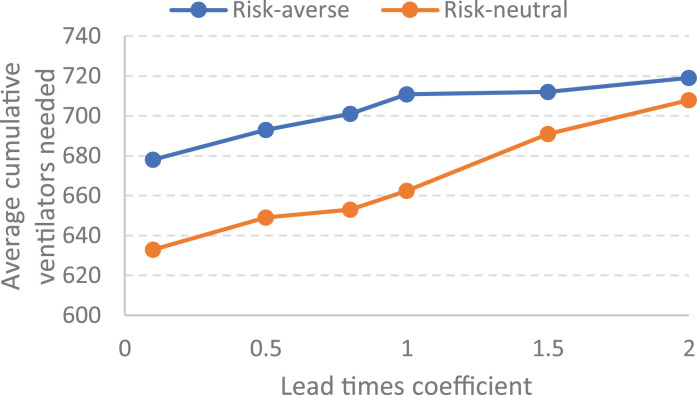
The importance of lead times. Our extensive computational experiments indicate that the number of non-accepted patients is mainly dependent on lead-times in both of risk-neutral and risk-averse policies. For case study 1, Fig. 14a presents the sensitivity of the average non-accepted patients on lead time values related to the risk-neutral and risk-averse policies, and Fig. 14b illustrates the sensitivity of the average cumulative new ventilators’ requirement on lead time values. In the sensitivity analysis various multiplier coefficients are considered for lead times.

Fig. 14a.

Sensitivity of non-accepted patients to lead-times.

As shown in Fig 14 , the lead time values has a main negative impact on the output of resource planning during a pandemic in both of risk-averse and risk-neutral policies. However, presented results show that the risk-averse policy has a more stability against the increase of lead times in terms of non-accepted patients amount. If policy makers are able to decrease the lead time values, the responsiveness of healthcare systems would be improved during a pandemic.

Fig. 14b.

Sensitivity of resource allocation to lead-times.

6.5. The impacts of interventions on resources need

Regarding case study 2, on several occasions, Iranian governors announced stay-at-home orders aimed to slow the spread of COVID-19. The policy makers' orders were effective in reducing transmissions and can be captured by the reduction in estimated effective reproduction number of the disease.

In this part, we investigate the effect of these interventions on optimal policy and resources need. In particular, we model two scenarios in which the transmission rate from the considered horizon is 50% higher or lower compared to the observed rate. If interventions were less effective, ventilator and nurse needs derived from our optimal policy would increase 18% and 12%, respectively. This is because less effective interventions would result in more infections and, subsequently, a higher demand for resources. On the other hand, if interventions were more effective, the need for ventilators and nurses from our optimal policy would decrease 7% and 5%, respectively.

7. Managerial insights

To meet potential surges in healthcare resources’ demand under pandemics, our optimization model considers various types of patients as well as resources (DUR and SER) simultaneously for the first time in the literature. Further, the model considers the sharing strategy and patients’ transfers to avoid non-accepted patients as much as possible by using the fewest additional resources. The presented optimization setting is flexible and applicable for different healthcare resources planning problems, which is confirmed by our computational results for two real examples.

Our empirical results provide insight into how hospitals in different regions could cope with the increase in demand for healthcare resources, which results from local surges in infections during COVID-19. Based on the computational results, by sharing ventilators among regions of an area of the USA, the average number of ventilators allocation to regions decreases about 58%. In the second case study (hospitals of a healthcare region of Iran), it decreases about 17%. The main reason for different significance of the ventilators sharing strategy between these two cases is that the infection spreads at varying rates in different regions in case study 1. Therefore, this provides an opportunity for sharing scarce resources such as ventilators, which can be transported over large distances within regions to alleviate capacity shortfalls caused by an epidemic surge in a region. More importantly, governors and decision makers have to ‘find’ significantly more ventilators to cope with the demand in the absence of sharing, which will take time; several patients don't have time during pandemics.

Based on our results from solving case study 2, we can find patients’ transfer as another efficient strategy in reducing the total required capacity in hospitals. In order to facilitate patients’ transfer between hospitals to manage the healthcare systems’ capacity, an infrastructure is necessary for transshipping patients between hospitals in a short time. Since the patients’ transfer has not any lead time compared with resource transshipments in our case study, it is more impactful in terms of the minimization of non-accepted patients (See Table 4). On the other hand, the integrated use of sharing resources and demand redistribution strategies improve the required resources about 21% while the improvement related to the usage of the single resource sharing and patients’ transfer strategy are about 17% and 12%, respectively.

The proposed data‐driven decision-making framework can help decision makers adjust their decisions in real-time based on the past observation of uncertain parameters and their prior decisions. We highlight the importance of the information update related the release time of healthcare resources. In the accessible historical data, the release time of ventilators used for the COVID-19 patients follows a log-normal distribution and varies largely in different cases; our data-driven decision-making framework improves the additional capacity allocation in both case study 1 and 2 by real-time decisions.

We highlight the significance of the MSSP in compared with deterministic and two-stage stochastic programming model. Further, by developing the risk-averse MSSP with the CVaR of non-accepted patients instead of its expected value, we investigate the risk‐neutral and risk‐averse decision-making in healthcare resources planning. Our experimental results show that the risk‐averse decisions make the expected allocation of additional resources worse, its standard deviation lower, and reduces the amount of non-accepted patients in our case studies. Therefore, in many practical situations, we can increase the robustness of our decisions by employing a risk-averse objective function.

Finally, interventions like closure of non-essential business, mask wearing, and social distancing protocols are very effective in reducing transmissions. Such mandates are captured by considering different values for the effective reproduction number in our simulator, and we show these strategies can meaningfully reduce the required additional resources in hospitals.

8. Conclusion

We introduce a new integrated resource sharing and demand redistribution problem during pandemics. Our optimization is applicable for various patient types and required healthcare resources. Under a multi‐period setting, an MSSP with non‐anticipativity constraints is developed to obtain the optimal sharing, patients’ transfer, and capacity allocation decisions.

Methodologically, we formulate our problem as a mixed-integer linear programming model, which is solvable by the CPLEX as a commercial solver. The real‐world applicability of the proposed MSSP is deeply investigated by two real case studies. A new data‐driven decision‐making approach is developed to implement the decisions made by the MSSP in real-time. This approach enables decision-makers to employ the data that is realized over time and to adjust the corresponding decisions in a rolling horizon framework.

In the computational results, we illustrate the validity of our model and its importance in resource planning during COVID-19 pandemic. Further, the significance of the MSSP is compared with both deterministic and two-stage stochastic programming models, data‐driven decisions, the sharing of healthcare resources, the demand redistribution, and risk-averse decisions are discussed and analyzed. Our decision-making framework showcases its capabilities and flexibility with its exceptional performance in reducing required new healthcare resources during pandemics.

To capture the demand uncertainty and create an efficient scenario tree in our optimization problem, a simulation approach based on an agent-based continuous-time stochastic model is used to model the disease spread. Next, by applying the forward scenario tree construction technique, we reduce the scenarios’ number and convert them into a scenario tree. The efficiency of this method is confirmed by in‐sample and out‐of‐sample stability analysis.

Although our work is motivated by healthcare operations management under pandemics, our models and insights can also be applied to other service industries under massive increases in demand. Moreover, this study has a few limitations, which can be addressed by future researches. In our model, we do not consider priorities in responding to patients in the case of shortfalls and patients’ preferences in selecting hospitals.