Abstract
These are unprecedented times while the world weathers the highly infectious respiratory pandemic caused by coronavirus disease-19 (COVID-19). Humanity has experienced other cataclysmic events, but something as novel as this pandemic cannot be easily described. A safe COVID-19 vaccine is often hailed as the only effective public health method to prevent the further spread of this virus. New vaccines’ cost has increased even as policymakers struggle with limited resources and budget constraints. Thus, more decision-support tools are needed to facilitate the selection of vaccine manufacturers as part of a global immunization strategy against COVID-19 or other epidemics and pandemics. This study sought to address this issue by combining three well-established operational research methods (i.e., cognitive mapping, decision-making trial and evaluation laboratory, and the Choquet integral). Based on the insights provided by a panel of experts on vaccination and infectious diseases, a vaccine manufacturer selection mechanism was developed that incorporates the World Health Organization’s guidelines. This approach facilitated the identification of multiple selection criteria regarding vaccine manufacturers, their allocation into six major clusters (i.e., soundness of scientific approach and technology used; speed of delivery; cost; liability and risk sharing; ability to supply sufficient quantities through production capacity development; and global solidarity), and subsequent analysis of the respective cause-and-effect relationships. The results of a real-life application of the proposed selection system were further consolidated by a member of Saint Francisco Xavier Hospital Infectious Diseases Unit in Lisbon, Portugal. The mechanism’s advantages and limitations are also discussed.
Keywords: Coronavirus disease-19 (COVID-19), Epidemics and pandemics, Multiple criteria analysis, Operational research, Vaccine manufacturer selection
Introduction
The World Health Organization (WHO) endorsed the 2011–2020 Global Vaccine Action Plan (GVAP), which includes six strategic objectives related to global immunization. The first is for all countries to commit to making vaccination a priority, while the second is for individuals and communities to understand vaccines’ value and demand immunization as both their right and responsibility. The third objective is to ensure that vaccines’ benefits are equitably extended to all people. The fourth is to establish strong immunization systems that are an integral part of fully functional health systems, and the fifth is to create vaccination programs that have sustainable access to predictable funding, quality supplies, and innovative technologies. The last objective is to stimulate country, regional, and global research on—and development of—innovations to maximize immunization benefits (WHO, 2020).
The coronavirus-19 (COVID-19) pandemic has put extra pressure on this already-fragile vaccine action plan. According to the WHO (2020), only one out of the six strategic objectives was being addressed before the current crisis. The pandemic is inflicting extensive human life and economic losses worldwide and further exposing the 2011–2020 GVAP’s weaknesses. Immunization has, however, become an even more critical issue because this crisis’ permanent solution is most likely to be found through the development and deployment of an effective, safe COVID-19 vaccine.
The crisis’s scale means that time pressures on vaccine manufacturers are unprecedented. Every month gained by a vaccine’s deployment will save many lives, jobs, and billions of dollars. Léon et al., (2020, p. 2457) assert that: “there is a virtuous cycle showing how vaccination leads to health-related benefits, to increase[s] in productivity, to community or health systems’ externalities and to broader economic improvements in [… areas such as] public budget[s] or changes to national income or production”. Given that vaccine development usually takes more than 10 years, the quest for effective COVID-19 vaccines is particularly challenging due to their urgency. Teams are working worldwide to deliver successful vaccines within a very short timeline.
With effective vaccines available, hundreds of millions—or even billions—of doses need to be produced in order to cover needs around the globe: all without compromising the production of other essential vaccines. This quest is a global challenge primarily because every region worldwide has been affected and the virus’s spread has proved that no areas are safe until COVID-19 is under control everywhere. Three interrelated questions thus need to be answered:
How can vaccine manufacturers be evaluated to ensure the best candidate is selected?
What objective and subjective metrics should be used to ensure more accurate assessments of vaccine manufacturers and to facilitate the selection process?
How can multiple criteria be aggregated to obtain a synthetic indicator of each vaccine manufacturer’s effectiveness?
Given the importance of these questions, the present study assumed a constructivist stance and sought to combine cognitive mapping, decision-making trial and evaluation laboratory (DEMATEL), and the Choquet integral (CI). The proposed methodology was designed to support the selection of the most appropriate vaccine manufacturers from among those who share an interest in implementing an immunization strategy against COVID-19. Due to the process-oriented framework of the proposed approach, this methodology can also be applied to deal with future epidemics and pandemics.
Cognitive maps are an extremely useful and effective tool when decision problems need to be structured (Eden, 2004). These maps allow decision makers to deal with uncertainty, such as contrasting perspectives, making problem visualization quite intuitive. The DEMATEL technique, in turn, facilitates causal analyses of links between variables via matrices, thereby also revealing the interdependence between factors and facilitating the development of cause-and-effect diagrams of these relationships (Govindan et al., 2021). Finally, the CI is a non-additive measure that ranks alternatives (i.e., vaccine manufacturers in the current research) based on an overall score calculated by quantifying criteria’s interactions. Additionally, the procedural steps followed by this methodology focuses on supporting interactive learning and a fruitful elaboration of recommendations for vaccine manufacturer selection. As such, the combined use of cognitive mapping, DEMATEL and CI promotes exchange of ideas and experiences, boosts a deeper understanding of decision situations, and uncovers the cause-and-effect relationships among criteria. This facilitates questions such as “why does this happen?” to be answered.
Following this, we believe our study makes important theoretical and practical contributions. Theoretically, although the findings are idiosyncratic in nature, they can be an important starting point for other researchers and practitioners who analyze determinants of vaccine manufacturer selection. Thus, our contribution will be available as a springboard for additional studies, and complements previous contributions in the field. From a methodological point of view, our contribution is two-fold: one coming from the combination of methodologies used, which we believe to be novel in this study context, and second from the description of the process followed, which allows for replications in other contexts and/or with different groups of experts, due to the process-oriented nature of the framework. This methodology facilitated the development of a system that identifies determinants of vaccine manufacturer selection in a simple, transparent, and structured approach. A review of the literature uncovered no evidence of a prior use of these three operational research (OR) techniques in this context, which means that the proposed methodology constitutes a valuable contribution to the existing knowledge about both OR and epidemic and/or pandemic vaccination programs.
This paper is organized into five sections. The next section contextualizes the study and presents a concise summary of the relevant literature. Section three discusses the methodologies applied (i.e., cognitive mapping, DEMATEL, and the CI), while section four describes the development of the decision-support system and the results of a practical application, including their consolidation. The final section highlights the research’s contributions and limitations, followed by suggestions for future studies.
Background and research gap
Many extraordinary measures have been taken to deal with the COVID-19 pandemic and its impacts. In particular, a global effort has been made to accelerate the development, manufacture, and deployment of COVID-19 vaccines. Experts agree that an effective, safe vaccine is humanity’s best bet to find a permanent solution for the pandemic. This strategy has, according to Wijhe et al., (2019, p. 5704), widespread support since “vaccines are often hailed as one of the most effective public health methods in preventing infectious diseases”.
Time is of the essence, so efforts to accelerate the development and availability of safe and effective vaccines need to receive full support to ensure a vaccine is made available within a very short timeframe. However, vaccine development is a complex, lengthy process (Duijzer et al., 2018; Shedrawy et al., 2018). This intricate undertaking requires manufacturers to run clinical trials while investing in production capacity to be able to deliver millions or even billions of doses of a successful vaccine. Making a vaccine universally available constitutes a global challenge (Enayati & Özaltın, 2020; Ravensbergen et al., 2019; Vrdelja et al., 2020). An important step toward multiple countries taking joint action has been the Inclusive Vaccines Alliance formed by France, Germany, Italy, and the Netherlands. The European Union’s (EU) strategy is thus to implement a cooperative approach to achieving specific goals. These are to: (1) ensure COVID-19 vaccines’ quality, safety, and efficacy; (2) secure immediate access to vaccines for EU populations even while Europe leads global solidarity efforts; and (3) guarantee equitable access to an affordable vaccine as early as possible (European Commission, 2020a).
The EU’s strategy, therefore, rests on two pillars. The first is to secure the EU’s production of vaccines and adequate supplies through advance purchase agreements (APAs) with manufacturers. Further financing and support can be associated with these agreements. The second pillar is to adjust the EU’s regulatory framework to deal with the present crisis and harness the existing structure’s flexibility to speed up the vaccine’s development, approval, and distribution while ensuring high standards of excellence, safety, and efficacy (European Commission, 2020a, 2020b; Vrdelja et al., 2020). This process raises critical questions: How can the best widely available vaccine candidate and its manufacturer be selected, what criteria should be applied during the selection process, and how do these criteria interact with each other?
When making financial decisions about which vaccine programs to support, the European Commission (2020a) recommends that multiple criteria be taken into consideration. These should include the soundness of the scientific approach and technology applied, agile delivery at scale, cost effectiveness, shared risk and liability, reliance on varied technologies, continuous consultation with regulators, a global team spirit, and the ability to supply sufficient quantities through a well-developed production capacity. Governmental and non-governmental partners should be committed to the principle of universal, equitable, and affordable access to vaccines, especially for the most vulnerable countries (European Commission, 2020c; Mipatrini et al., 2017).
Despite all the care taken to select the right manufacturers, the risk always exists that supported candidates will fail to produce a vaccine during clinical trials. Thus, the recommended strategies are similar to an insurance policy by which some risks are transferred from the industry to public authorities in return for assurance that the relevant countries will have equitable, affordable access to any successful vaccines. The European Commission’s (2020a) criteria for choosing the best vaccine manufacturers are also non-exhaustive, so decision makers need to consider other factors and their respective interdependencies (Léon et al., 2020; Wijhe et al., 2019). It is worth noting, however, that the current practices used to address vaccine manufacturer selection still display limitations in how these models identify the decision criteria to be incorporated in the selection process (cf. Enayati & Özaltın, 2020; Vrdelja et al., 2020). Another issue is the analysis of the cause-and-effects relationships among decision criteria, which should be carried out in a dynamic manner (cf. Vrdelja et al., 2020). Problem structuring methods (PSMs) and multiple criteria decision analysis (MCDA) can bring more robustness and clarity to the literature on this topic. This is precisely what the present study sought to do by combining cognitive mapping, DEMATEL, and the CI.
Cognitive mapping facilitates the identification of criteria that reflect different perspectives and reduces the number of variables omitted from the decision-making process. DEMATEL supports causal analyses of links between variables via matrices, as well as highlighting factors’ interdependence and permitting cause-and-effect diagrams to be developed that represent these connections. The CI, in turn, is a non-additive measure that uses overall scores based on criteria’s interactions to rank alternatives (i.e., vaccine manufacturers). As mentioned previously, no prior evidence was found of these OR techniques being applied in this research context, which means the results of the proposed methodology add significantly to the literature on OR and epidemic and/or pandemic immunization.
Methodology
The OR field has branched into research on, among other techniques, PSMs and MCDA, which have gained prominence as ways to deal with complex decision problems in recent years (Ackermann, 2012; Marttunen et al., 2017; Mingers, 2008; Rosenhead, 2013; Zavadskas et al., 2014). One of the main objectives of these two methodological approaches is to construct or create support mechanisms that help decision makers to model complex problems, thereby altering these individuals’ preferences and/or helping them to make decisions congruent with their values (Belton & Stewart, 2002; Howick & Eden, 2011; Smith & Shaw, 2019). These values are subjective, but disregarding them during the modeling process does not eliminate their effects (Keeney, 1992, 1994).
Belton and Stewart (2002) state that the MCDA-based decision-support process has three phases. The first is structuring, which, in the present study, involved applying cognitive mapping to identify the selection criteria and their most significant clusters. The second phase is evaluation, which, in this research, relied on DEMATEL to analyze the criteria’s interdependence and the CI to aggregate partial performances and rank real vaccine manufacturers. The last phase is recommendations, in which suggested improvements to the proposed methodology were elicited.
Cognitive mapping
This knowledge-intensive interdisciplinary methodology can solve applied decision problems using cognitive maps. These maps are models of the structure of cause-and-effect links within mapped situations, objects, or systems. This technique can be used by individuals or groups (Assunção et al., 2020; Eden & Ackermann, 2004; Simões et al., 2020). The construction of cognitive maps can thus be a collective process involving various decision makers that facilitates the organization of ideas to clarify objectives and identify potential actions and that avoids potential flaws in the structuring procedure (Belton & Stewart, 2002). As a PSM, cognitive mapping provides inputs to decision makers who need to decide which strategies to implement regarding unclear decision problems or solutions (Ackermann & Eden, 2001).
The model basic format is a directed graph with nodes that are associated with concepts and arches. The latter are interpreted as causal relationships between concepts (Fonseca et al., 2020; Martins et al., 2020) and given influence signs (i.e., + or –) or influence weights, which results in a signed or weighted map, respectively. The cognitive mapping technique facilitates groups of actors’ efforts to manage complex decision problems more effectively (Eden & Ackermann, 2004; Paes de Faria et al., 2020). This method—also called mental modeling—has been applied in varied contexts to analyze and understand disorganized decision problems (Kolkman et al., 2005; Natividade et al., 2020). According to Vaz de Almeida et al., (2019, p. 362), cognitive maps “depict the problem and/or subject within a network reflecting means and goals or causes and effects as perceived by the decision makers”. This method thus constitutes a metacognitive, constructivist tool to harness a specific group of specialists’ opinions on a topic, which expediates technical discussions.
Over time, cognitive mapping has been found to be a truly potent collaboration technique in groupwork, facilitating a fuller understanding of participants’ perspectives. The present study applied this tool to vaccine manufacturer selection for three reasons. The first was to promote productive debate among participants in this decision-support procedure. The second reason was to decrease the number of relevant criteria omitted, while the last was to stimulate an expanded learning process based on a deeper comprehension of the criteria’s cause-and-effect links (Eden, 2004; Martins et al., 2020).
DEMATEL
DEMATEL was created in the 1970s by the Battelle Memorial Institute Research Center in Geneva to represent complex causal relationship structures using matrices or digraphs (cf. Gabus & Fontela, 1972, 1973). Dalvi-Esfahani et al., (2019, p. 5) report that this method focuses on resolving “real-world complex problems” such as political, economic, or scientific issues by analyzing different dimensions and factors encompassing many stakeholders (Dalvi-Esfahani et al., 2019; Falatoonitoosi et al., 2013).
Si et al. (2018) note that DEMATEL’s application involves five steps. After information is gathered from experts on the relevant topic, the first step is to construct the direct influence matrix Z. To define the connections between a system’s n factors F = , l specialists in a decision team E = need to indicate the direct influence of a factor/criterion Fi on factor/criterion Fj. The specialists should use a scale ranging from 0 to 4 (i.e., 0 = “no influence”; 1 = “weak influence”; 2 = “medium influence”; 3 = “strong influence”; 4 = “very strong influence”). The individual direct influence matrix provided by the specialist kth can then be created so that all the components of the main diagonal are equal to 0 and is decision maker ’s judgement about the degree to which factor influences factor . Using the total value of the l experts’ opinions, the direct influence group matrix can be generated with Eq. (1) to construct the matrix in Eq. (2):
| 1 |
| 2 |
DEMATEL’s second step is to create normalized direct influence matrix X. After the direct group influence matrix Z is developed, normalized matrix can be generated through Eq. (3):
| 3 |
in which All elements of matrix X should be in accordance with 0 ≤ < 1, 0 ≤ , and at least one i should comply with .
The third step comprises developing total influence matrix T. Using matrix X, matrix T = is estimated by obtaining the total of direct and indirect effects by means of Eq. (4):
| 4 |
in which and I is denoted the identity matrix.
In the fourth step, the threshold value is calculated by averaging the influence values of matrix T. This value functions as a reference point when selecting the most significant effects within the matrix so that values below the threshold value are excluded. The threshold value can be obtained using Eq. (5):
| 5 |
The last step is to create an influential relation map (IRM). Vectors R and C stand for the totals of matrix T’s lines and columns, respectively. These vectors are defined by Eqs. (6) and (7):
| 6 |
| 7 |
in which is the total of matrix T’s ith line, thus representing the total of direct and indirect effects of factor on the other factors. Similarly, is the total of the jth column in matrix T, which describes the total of direct and indirect effects of the other factors on factor .
In this step, i = j and i, j ∈ {1, 2,..., n}, and the vector R + C stands for the horizontal axis, for which the term “prominence” is used, and represents the strength of the overall influence a specific factor gives and receives. That is, R + C denotes the degree of importance of a relevant factor in the decision-support system. Vector R − C is the vertical axis—known as “relationship”—and represents the net effect the same factor has within the system. If () has a positive value, then factor overall influences the other factors, so it can be considered part of the causes group. If () has a negative value, this factor is overall being affected by the other factors, so it is placed in the effects group. The resulting IRM can be divided into four quadrants (i.e., I, II, III, and IV) that each correspond to a specific kind of factor. QI comprises central factors that are highly prominent and strongly connected. QII contains determinant factors that are not prominent but that are quite influential. QIII covers independent factors that are not prominent and that have weak relationships. Finally, QIV includes impact factors that are quite prominent but that have weak connections. The IRM is thus generated via the data set of (R + C; R–C), which provides decision makers with important information. Figure 1 shows how the indicators were categorized according to where they appear in the IRM.
Fig. 1.
Interpretation of DEMATEL diagram.
Source: Si et al. (2018)
DEMATEL, therefore, not only identifies the criteria’s degree of interdependence but also reveals which criteria have an impact on other factors, which depend on others, and which are affected by others (Kijewska et al., 2018). This method was applied in the present study because of DEMATEL’s ability to explore “intertwined cluster problems” in conjunction with an IRM (Govindan & Chaudhuri, 2016, p. 181).
Choquet integral
Choquet (1954) developed the CI as an information aggregator primarily to synthesize the partial scores of each decision criterion into one overall score for a given option (i.e., a vaccine manufacturer) (Krishnan et al., 2015). Grabisch (1997), Grabisch et al. (2002), and Krishnan et al. (2015) also found that the CI can be used as a fuzzy integral because it can be utilized to model fuzzy measures. On a more technical level, work done by Bottero et al. (2018), Choquet (1954), Ferreira et al. (2018), Shieh et al. (2009), Silva et al. (2021), and Tan and Chen (2010) confirmed that a fuzzy measure in universe X represents function . However, this is only true if—and only if—the measure complies with the conditions described in Eqs. (8) and (9):
| 8 |
| 9 |
Ralescu and Adams (1980) and Castanho et al. (2021) also assert that, for to be deemed a non-additive measure, the premises in Eqs. (10) and (11) must also be respected:
| 10 |
| 11 |
In addition, Brito et al. (2019) and Torra et al. (2016) affirm that denotes a measure that is submodular and non-additive if and one that is supermodular and non-additive if for A, B P, respectively. Thus, the CI of in terms of in A is represented as and defined using Eq. (12) (Ouyang & Li, 2004):
| 12 |
in which stands for a non-negative, measurable, and real-valued function defined in X and when .
If , then is considered integrable (Wang, 2011). As a result, if (X, P, ) stands for a fuzzy measure space with , Fx is the set of all non-negative, measurable, and real-valued functions defined by X. The CI will have the properties itemized in Eqs. (13) to (18) (Wang, 2011):
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
in which c denotes a positive constant. Wang (2011) notes that, since the CI combines a set of monotone, non-linear, and non-additive integrals, the CI’s most significant property is the non-additivity of as defined by Eq. (19):
| 19 |
in which f and g F. Finally, Murofushi and Sugeno (1991) assert that the CI’s underlying monotony can also be expressed as Eq. (20):
| 20 |
whenever f ≤ g.
One of this integral’s key features is that it can handle criteria coalition (i.e., decision criteria’s interdependence). Thus, the CI produces more up-to-date, realistic results because it can aggregate cardinal information (Brito et al., 2019; Demirel et al., 2010; Ferreira et al., 2017; Krishnan et al., 2015). In the present study, a literature review uncovered no prior research combining cognitive mapping, DEMATEL, and the CI to facilitate vaccine manufacturer selection. As mentioned previously, the proposed framework contributes significantly to the extant body of literature on both OR and epidemic and/or pandemic vaccination programs.
System development and practical application
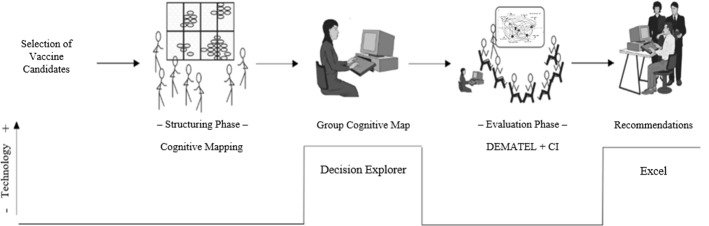
Cognitive mapping, DEMATEL, and the CI have been frequently used in varied decision-making contexts, in which each has functioned well as a decision-support tool. These methods’ integrated use, however, is scarcer, and no documented evidence exists of its prior use by decision makers selecting vaccine manufacturers during epidemics or pandemics. This approach is thus an apparent novelty. Figure 2 depicts the procedures followed in the present study. It is worth noting that all the data and results were obtained and analyzed in close interaction with a panel of immunization experts during intense collective discussion and negotiation. An important feature of this procedure is that it allows for an interactive exploration of changes in the inputs to the model, such that the impact of such changes can be seen immediately, offering opportunities for further discussion (again, a reflection of the recursive and constructivist nature of the framework) (Belton & Stewart, 2002).
Fig. 2.
Methodology adopted.
Source: adapted from Ackermann and Eden (2010)
As Fig. 2 shows, the procedures were organized into the three main phases described in the previous section (Belton & Stewart, 2002). The first phase involved structuring the decision problem and using cognitive mapping. This process facilitated the identification—and organization into clusters—of multiple selection criteria regarding vaccine manufacturers. The second phase was the evaluation, which concentrated on applying DEMATEL and the CI to elucidate the dynamics of the criteria’s causal interrelationships and to aggregate partial performances, respectively. This phase resulted in the categorization and ranking of actual vaccine manufacturers. Finally, the recommendations phase generated suggestions of how best to facilitate vaccine candidate selection. These phases are described in more detail in the next subsections.
Structuring phase
Participants
To apply the proposed methodology, decision makers were recruited from among specialists with practical know-how in infectious diseases and immunization. The relevant literature neglects to mention an ideal decision group size, but the general consensus among researchers is between 5 and 12 members (cf. Bana e Costa et al., 2002). As a result of the invited experts’ availability or lack thereof, the panel consisted of nine professionals with varied positions in hospitals, infectious disease units, and vaccination laboratories. More specifically, the specialists were two public health doctors, a senior member of Portugal’s Directorate General of Public Health, two virologists, one senior vaccination technician, two vaccination laboratory technicians, and a COVID-19 emergency team coordinator.
The panel recruitment process was designed to ensure the participants filled important positions and came from relevant and diverse categories of stakeholders, whilst simultaneously considering gender and age diversity. These criteria were applied to maximize the panel’s credibility and representativeness to ensure different perspectives would emerge (Eden & Ackermann, 2001). However, the specialists were not ultimately chosen to guarantee representativeness but instead to focus more strongly on process (Ormerod, 2013, 2020). This means that the present study’s results are context specific, but the procedures can function equally well with other experts and in other immunization contexts because the proposed methodology is process oriented (cf. Ackermann, 2019; Bell & Morse, 2013; Ferreira et al., 2017).
Group cognitive map and vaccine manufacturer selection criteria
The first face-to-face meeting lasted around three hours and concentrated on structuring the decision problem in question. This session was conducted as a videoconference on the Zoom platform (see www.zoom.us) to respect the WHO’s recommendations at the time. In addition to the experts, this meeting also involved a facilitator to improve communication by raising relevant issues and fostering a feeling of mutual commitment among the participants. The session started with a brief explanation of the study primary goals and the methodology used throughout the decision process.
After the panel members had overcome any initial shyness, the facilitator asked the following trigger question: “Based on your knowledge and professional experience, how would you describe the best vaccine manufacturer in epidemic and/or pandemic contexts?”. This question stimulated the participants to identify the most important variables (i.e., selection criteria), and to understand the significance of the selection process. After the brainstorming process was completed, the criteria were put into clusters. The specialists were next asked to structure the selection variables by degree of importance within their respective clusters, placing the criteria considered the most significant at the clusters’ top and less important variables at the bottom (i.e., base) (Ackermann & Eden, 2001; Estevão et al., 2019).
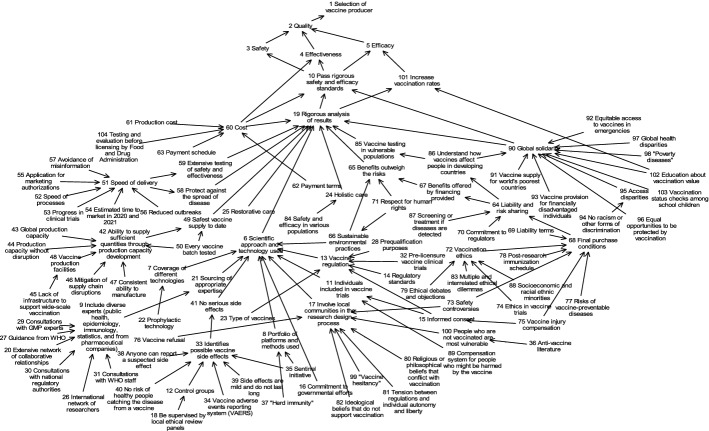
After the first group session ended, the structured criteria were used to generate a collective cognitive map. The Decision Explorer software was used to achieve this step (see www.baxia.com). Figure 3 contains the map’s final version after the participants validated it via an intense group discussion at the beginning of the second group session.
Fig. 3.
Group cognitive map
Figure 3 shows the cognitive map created with the information gathered from the selected infectious diseases and immunization experts, namely structured criteria supporting the choice of vaccine manufacturers. Although cognitive maps are deeply affected by the decision makers’ perceptions (Tegarden & Sheetz, 2003), these maps provide added value by visualizing the group’s perspectives and real-life experience, thereby overcoming various limitations of purely statistical approaches (cf. Martins et al., 2020; Paes de Faria et al., 2020). For example, the issue of religious or philosophical beliefs opposing immunization is often omitted from discussions, but the cognitive mapping process was able to detect the effect of this issue. Many academic and medical studies have found that individuals who ask for exemptions for religious and/or philosophical reasons run a greater risk of being infected, which endangers these people and their communities (Feikin et al., 2000; Schwartz & Caplan, 2017). Thus, medical and public health promoters frequently struggle to find a balance between protecting individuals’ beliefs and their communities’ wellbeing. This perceived dilemma was overtly mentioned in the collective cognitive map generated for the present study.
In addition, the European Commission’s (2020a) recommendations regarding financing decisions about which vaccine manufacturers to back were meticulously taken into account. As suggested by Eden (2004), the group cognitive map was subsequently structured into clusters labeled CTR1 through 6.
CTR1: soundness of scientific approach and technology used
Based on the European Commission’s (2020a) advice, this cluster includes drawing on the available evidence about vaccines’ quality, safety, and efficacy already generated during the development phase. This cluster further contains coverage of different technologies used to develop vaccines that rely on a variety of platforms and production methods. To maximize the chances of producing an efficacious, safe vaccine, APA portfolios need to cover different technologies.
CTR2: speed of delivery
This cluster includes decision criteria that focus on the progress made during clinical trials. Another important aspect is the manufacturers’ ability to deliver sufficient quantities of the vaccine in 2020 and 2021.
CTR3: cost
This cluster considers cost variables. Some examples are the amount of financing requested, overall schedule, and relevant payment conditions.
CTR4: liability and risk sharing
Benefits offered in exchange for financing are considered in this cluster. These advantages include situations of either a successful vaccine or no vaccine (e.g., potential flexibility in manufacturing capacity use). The funding given can be considered a down payment on the vaccines that will actually be bought, so financial support will be reflected in the specifications made regarding the vaccines’ final purchase. This cluster also incorporates any special liability coverage that companies may require.
CTR5: ability to supply sufficient quantities through production capacity development
The current pandemic-related crisis has highlighted the advantages of having diverse sources of supply. Most countries remain deeply committed to international trade and development of global supply chains, but this cluster covers the efforts made to attract manufacturers with a more easily accessible vaccine production capacity to diminish disruptions to immunization supply chains.
CTR6: global solidarity
This cluster contains decision criteria reflecting a commitment to making future supplies of vaccines available to all countries to end the pandemic worldwide. The output of these production sites will not be reserved for a few populations. Thus, the candidate vaccine manufacturers’ early efforts to engage with regulators in order to apply for marketing authorization are also included in this cluster.
After discussing and validating the collective map, the panel moved on to the next phase. The second part of the proposed methodology comprised applying DEMATEL and the CI to analyze dynamically and quantitatively the causal connections between the components of the decision-support system.
Evaluation phase
DEMATEL application
The second session was attended by the same decision makers (i.e., nine participants), with the additional presence of a technical assistant to record the results. This second meeting began with the process of carefully analyzing the cognitive map in order to provide a solid basis for the application of the DEMATEL technique. More specifically, the expert panel scored the influence exerted by all the relationships between the different clusters and criteria on a nominal scale of 0–4 (i.e., no influence = 0; very strong influence = 4). These values were used to fill in seven main matrices (i.e., a general matrix for all clusters and a matrix for each cluster). The most influential criteria in each cluster were selected using nominal group and multi-voting techniques.
DEMATEL application to clusters
Following the analysis of inter-cluster cause-and-effect relationships, the first matrix in Table 1 was constructed based on the panel’s collective perception. This matrix represents the effect that the clusters have on each other.
Table 1.
Inter-cluster initial matrix
| CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | TOTAL | |
|---|---|---|---|---|---|---|---|
| CTR1 | 0.0 | 4.0 | 4.0 | 4.0 | 4.0 | 3.2 | 19.2 |
| CTR2 | 3.2 | 0.0 | 4.0 | 3.7 | 3.6 | 3.9 | 18.4 |
| CTR3 | 3.8 | 3.8 | 0.0 | 3.8 | 3.4 | 3.8 | 18.6 |
| CTR4 | 3.7 | 4.0 | 4.0 | 0.0 | 3.9 | 4.0 | 19.6 |
| CTR5 | 3.9 | 4.0 | 4.0 | 3.5 | 0.0 | 4.0 | 19.4 |
| CTR6 | 3.9 | 3.8 | 4.0 | 4.0 | 3.7 | 0.0 | 19.4 |
| Total | 18.5 | 19.6 | 20.0 | 19.0 | 18.6 | 18.9 |
| Max | 20.0 | 19.6 |
|---|---|---|
| 1/max | 0.05 | 0.05106 |
| 1/s | 0.05 | |
As Table 1 shows, the initial matrix is nonsymmetric, so each cluster affects and is affected by another cluster differently. The results show that CTR4, CTR5, and CTR6 are those that have the most influence on the other clusters. CTR3 and CTR2, in turn, are the most affected by the others, which means they are also an extremely important part of the findings. After the first matrix was generated, it was normalized using Eq. (3) (see Sect. 3.2). Table 2 presents the normalized matrix generated by the inter-cluster analysis.
Table 2.
Inter-cluster normalized matrix
| CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | |
|---|---|---|---|---|---|---|
| CTR1 | 0.0000 | 0.2000 | 0.2000 | 0.2000 | 0.2000 | 0.1600 |
| CTR2 | 0.1600 | 0.0000 | 0.2000 | 0.1850 | 0.1800 | 0.1950 |
| CTR3 | 0.1900 | 0.1900 | 0.0000 | 0.1900 | 0.1700 | 0.1900 |
| CTR4 | 0.1850 | 0.2000 | 0.2000 | 0.0000 | 0.1950 | 0.2000 |
| CTR5 | 0.1950 | 0.2000 | 0.2000 | 0.1750 | 0.0000 | 0.2000 |
| CTR6 | 0.1950 | 0.1900 | 0.2000 | 0.2000 | 0.1850 | 0.0000 |
The next step was to apply Eq. (4) (see Sect. 3.2) to create the total influence matrix T. Vectors R and C (see Eqs. (6) and (7) in Sect. 3.2) were then calculated to produce the DEMATEL diagram. Table 3 presents the steps in the construction of matrix T and the results of the inter-cluster analysis for the matrix vectors.
Table 3.
Inter-cluster total influence matrix and intermediate calculations
| CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | |
|---|---|---|---|---|---|---|
| I | ||||||
| CTR1 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| CTR2 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| CTR3 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 |
| CTR4 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| CTR5 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| CTR6 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 |
| CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | |
|---|---|---|---|---|---|---|
| I–X | ||||||
| CTR1 | 1.0000 | − 0.2000 | − 0.2000 | − 0.2000 | − 0.2000 | − 0.1600 |
| CTR2 | − 0.1600 | 1.0000 | − 0.2000 | − 0.1850 | − 0.1800 | − 0.1950 |
| CTR3 | − 0.1900 | − 0.1900 | 1.0000 | − 0.1900 | − 0.1700 | − 0.1900 |
| CTR4 | − 0.1850 | − 0.2000 | − 0.2000 | 1.0000 | − 0.1950 | − 0.2000 |
| CTR5 | − 0.1950 | − 0.2000 | − 0.2000 | − 0.1750 | 1.0000 | − 0.2000 |
| CTR6 | − 0.1950 | − 0.1900 | − 0.2000 | − 0.2000 | − 0.1850 | 1.0000 |
| CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | |
|---|---|---|---|---|---|---|
| (I − X)^ − 1 | ||||||
| CTR1 | 4.2952 | 3.6269 | 3.6868 | 3.5383 | 3.4757 | 3.4977 |
| CTR2 | 3.3185 | 4.3388 | 3.5635 | 3.4099 | 3.3454 | 3.4051 |
| CTR3 | 3.3692 | 3.5296 | 4.4285 | 3.4439 | 3.3684 | 3.4312 |
| CTR4 | 3.5099 | 3.6880 | 3.7492 | 4.4316 | 3.5307 | 3.5856 |
| CTR5 | 3.4871 | 3.6567 | 3.7173 | 3.5502 | 4.3375 | 3.5548 |
| CTR6 | 3.4890 | 3.6516 | 3.7192 | 3.5697 | 3.4956 | 4.3900 |
| CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | R | |
|---|---|---|---|---|---|---|---|
| Matrix T | |||||||
| CTR1 | 3.2952 | 3.6269 | 3.6868 | 3.5383 | 3.4757 | 3.4977 | 21.1205 |
| CTR2 | 3.3185 | 3.3388 | 3.5635 | 3.4099 | 3.3454 | 3.4051 | 20.3811 |
| CTR3 | 3.3692 | 3.5296 | 3.4285 | 3.4439 | 3.3684 | 3.4312 | 20.5709 |
| CTR4 | 3.5099 | 3.6880 | 3.7492 | 3.4316 | 3.5307 | 3.5856 | 21.4949 |
| CTR5 | 3.4871 | 3.6567 | 3.7173 | 3.5502 | 3.3375 | 3.5548 | 21.3036 |
| CTR6 | 3.4890 | 3.6516 | 3.7192 | 3.5697 | 3.4956 | 3.3900 | 21.3152 |
| C | 20.4689 | 21.4916 | 21.8644 | 20.9437 | 20.5532 | 20.8645 | |
Values highlighted in bold are selected for analysis
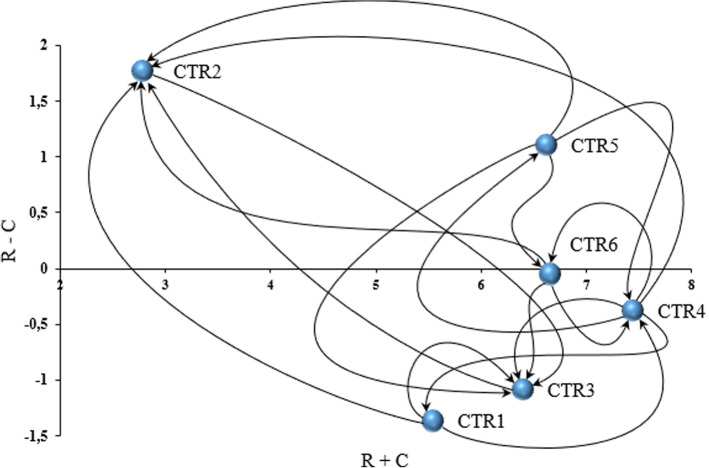
The threshold value α was obtained based on the total influence matrix (i.e., 3.5052 according to Equation (5) in Sect. 3.2). This α is the average of the matrix values, which is used to select the most significant relationships to construct the final diagram. These latter are shaded in matrix T in Table 3. To construct the IRM, only the R + C and R − C values were estimated. The first set of values represents the degree of importance that cluster i has in the decision-support system, while the second set gives this cluster’s net effect upon the system, thereby segmenting the clusters into causes or effects. Table 4 is the total influence matrix of the inter-cluster analysis, while Fig. 4 shows the IRM generated.
Table 4.
Total influence and causal inter-cluster relationships matrix
| R | C | R + C | R − C | |
|---|---|---|---|---|
| CTR1 | 2.0858 | 3.453257974 | 5.5391 | − 1.3675 |
| CTR2 | 2.2746 | 0.505681085 | 2.7803 | 1.7689 |
| CTR3 | 2.6546 | 3.737707867 | 6.3923 | − 1.0831 |
| CTR4 | 3.5321 | 3.908852984 | 7.4409 | − 0.3768 |
| CTR5 | 3.8621 | 2.754973472 | 6.6171 | 1.1071 |
| CTR6 | 3.3026 | 3.351284826 | 6.6539 | − 0.0487 |
Fig. 4.
Inter-cluster IRM
As Fig. 4 reveals, CTR2, CTR5, and CTR6 are categorized as causes (i.e., positive R − C values), while CTR1, CTR3, and CTR4 are effects (i.e., negative R − C values). Regarding this relationship vector, CTR2 has the strongest overall effect and contributes the most to the decision-support system (R–C = 1.7689). CTR3 has the lowest value (R − C = − 1.3675). CTR4 is the most prominent (R + C = 7.4409), so this cluster is the most important in the system. CTR2, in turn, is the least prominent (R + C = 2.7803). These results do not diminish the significance of speed of delivery in pandemics, but a slower yet more reliable vaccine is preferable to a speedy but less reliable one. The final ranking of the clusters by importance was CTR4 > CTR6 > CTR5 > CTR3 > CTR1 > CTR2.
DEMATEL application to most influential criteria
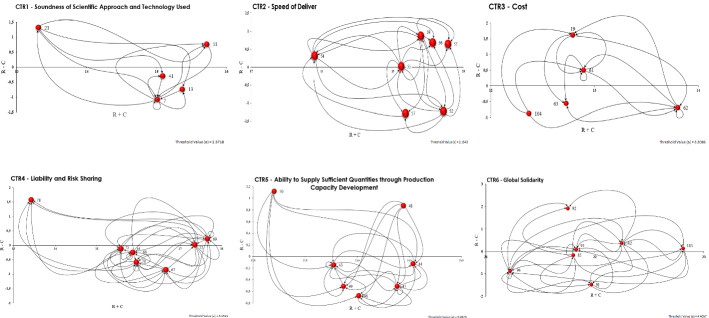
For each cluster, the expert panel selected the most significant criteria using nominal group and multi-voting techniques. The intra-cluster analysis followed the same procedures as the inter-cluster analysis. The first matrices generated are shown in Table 5, in which the numbers in the axes represent the criteria chosen. The respective correspondence appears in Table 6. Figure 5 presents the IRMs for the six clusters.
Table 5.
Direct-influence matrix Z for each cluster
| CTR1: Scientific approach and technology used | |||||
|---|---|---|---|---|---|
| 7 | 11 | 13 | 21 | 41 | |
| 7 | 0.0 | 3.9 | 3.5 | 3.8 | 4.0 |
| 11 | 4.0 | 0.0 | 2.8 | 3.2 | 4.0 |
| 13 | 4.0 | 3.5 | 0.0 | 3.8 | 2.8 |
| 21 | 3.9 | 3.8 | 3.9 | 0.0 | 3.7 |
| 41 | 4.0 | 3.6 | 4.0 | 3.1 | 0.0 |
| CTR2: Speed of delivery | |||||||
|---|---|---|---|---|---|---|---|
| 52 | 53 | 54 | 55 | 56 | 57 | 59 | |
| 52 | 0.0 | 3.9 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 |
| 53 | 4.0 | 0.0 | 4.0 | 3.9 | 3.8 | 3.9 | 3.9 |
| 54 | 3.5 | 3.8 | 0.0 | 3.9 | 3.8 | 3.8 | 3.9 |
| 55 | 3.2 | 3.6 | 3.5 | 0.0 | 3.7 | 3.4 | 3.6 |
| 56 | 3.7 | 3.7 | 3.6 | 3.4 | 0.0 | 3.2 | 3.3 |
| 57 | 3.8 | 3.6 | 3.9 | 3.6 | 3.4 | 0.0 | 3.7 |
| 59 | 3.9 | 4.0 | 4.0 | 3.8 | 3.7 | 3.5 | 0.0 |
| CTR3: Cost | |||||
|---|---|---|---|---|---|
| 19 | 61 | 62 | 63 | 104 | |
| 19 | 0.0 | 3.8 | 4.0 | 3.8 | 3.6 |
| 61 | 3.9 | 0.0 | 4.0 | 3.7 | 3.9 |
| 62 | 3.8 | 3.6 | 0.0 | 4.0 | 3.6 |
| 63 | 3.7 | 3.5 | 3.7 | 0.0 | 2.5 |
| 104 | 3.5 | 4.0 | 3.9 | 3.0 | 0.0 |
| CTR4: Liability and risk sharing | |||||||
|---|---|---|---|---|---|---|---|
| 67 | 68 | 69 | 70 | 72 | 75 | 78 | |
| 67 | 0.0 | 3.9 | 3.6 | 3.9 | 3.4 | 3.6 | 2.5 |
| 68 | 3.7 | 0.0 | 3.9 | 4.0 | 3.7 | 4.0 | 3.5 |
| 69 | 3.5 | 3.8 | 0.0 | 3.8 | 3.9 | 4.0 | 3.6 |
| 70 | 3.7 | 3.7 | 4.0 | 0.0 | 3.7 | 3.9 | 3.6 |
| 72 | 3.3 | 3.6 | 4.0 | 3.8 | 0.0 | 4.0 | 3.8 |
| 75 | 3.0 | 3.9 | 3.9 | 3.8 | 3.9 | 0.0 | 3.7 |
| 78 | 2.3 | 3.3 | 3.3 | 3.2 | 3.5 | 3.2 | 0.0 |
| CTR5: Ability to supply sufficient quantities through production capacity development | |||||||
|---|---|---|---|---|---|---|---|
| 43 | 44 | 46 | 47 | 48 | 49 | 50 | |
| 43 | 0.0 | 4.0 | 4.0 | 3.9 | 3.7 | 3.8 | 3.8 |
| 44 | 3.9 | 0.0 | 4.0 | 4.0 | 3.7 | 3.6 | 3.5 |
| 46 | 3.8 | 3.9 | 0.0 | 3.9 | 3.5 | 3.7 | 3.8 |
| 47 | 4.0 | 3.9 | 4.0 | 0.0 | 3.6 | 3.9 | 3.7 |
| 48 | 3.9 | 3.9 | 3.7 | 3.8 | 0.0 | 4.0 | 3.8 |
| 49 | 3.7 | 3.4 | 3.8 | 3.7 | 3.7 | 0.0 | 3.8 |
| 50 | 4.0 | 3.9 | 3.9 | 3.9 | 3.5 | 4.0 | 0.0 |
| CTR6: Global solidarity | |||||||
|---|---|---|---|---|---|---|---|
| 85 | 91 | 92 | 93 | 94 | 102 | 103 | |
| 85 | 0.0 | 3.9 | 3.8 | 3.9 | 3.9 | 3.8 | 3.9 |
| 91 | 3.8 | 0.0 | 3.7 | 3.8 | 3.8 | 4.0 | 3.7 |
| 92 | 3.5 | 3.5 | 0.0 | 3.7 | 3.8 | 3.7 | 3.9 |
| 93 | 3.6 | 4.0 | 3.6 | 0.0 | 3.9 | 3.8 | 3.7 |
| 94 | 4.0 | 4.0 | 3.9 | 4.0 | 0.0 | 3.8 | 3.9 |
| 102 | 3.9 | 3.9 | 3.9 | 3.6 | 3.9 | 0.0 | 3.8 |
| 103 | 3.6 | 3.4 | 3.8 | 3.9 | 4.0 | 4.0 | 0.0 |
Table 6.
Direct and indirect effects of criteria in each cluster
| Criteria | (R + C) | (R − C) | |
|---|---|---|---|
| CTR1: Scientific approach and technology used | |||
| 7 | Coverage of different technologies | 15.01012977 | − 1.069650646 |
| 11 | Individuals included in vaccine trials | 15.71545595 | 0.767706886 |
| 13 | Vaccine regulation | 15.3660784 | − 0.732049227 |
| 21 | Sourcing of appropriate expertise | 13.30900535 | 1.327549866 |
| 41 | No serious side effects | 15.08626407 | − 0.293556879 |
| CTR2: Speed of delivery | |||
| 52 | Speed of processes | 19.71803677 | − 1.228229698 |
| 53 | Progress in clinical trials | 19.11957218 | 0.018927311 |
| 54 | Estimated time to market in 2020 and 2021 | 17.89725139 | 0.309802989 |
| 55 | Application for marketing authorizations | 19.78167492 | 0.640193116 |
| 56 | Reduced outbreaks | 19.56403032 | 0.682856467 |
| 57 | Avoidance of misinformation | 19.17961015 | − 1.290898621 |
| 59 | Extensive testing of safety and effectiveness | 19.39656537 | 0.867348437 |
| CTR3: Cost | |||
| 19 | Rigorous analysis of results | 12.78867858 | 1.619404715 |
| 61 | Production cost | 12.89344839 | 0.502080687 |
| 62 | Payment terms | 13.80189928 | − 0.691757682 |
| 63 | Payment schedule | 12.72568174 | − 0.553306233 |
| 104 | Testing and evaluation before licensing by Food and Drug Administration | 12.36781638 | − 0.876421487 |
| CTR4: Liability and risk sharing | |||
| 67 | Benefits offered by financing provided | 16.65697865 | − 0.84739254 |
| 68 | Final purchase conditions | 15.86153375 | − 0.248925465 |
| 69 | Liability terms | 17.65648392 | 0.219894345 |
| 70 | Commitment to regulators | 15.94897471 | − 0.583497016 |
| 72 | Vaccination ethics | 17.35307759 | 0.014091765 |
| 75 | Vaccine injury compensation | 15.58030584 | − 0.122424521 |
| 78 | Post-research immunization schedule | 13.42471281 | 1.568253432 |
| CTR5: Ability to supply sufficient quantities through production capacity development | |||
| 43 | Global production capacity | 13.04860795 | − 0.147709773 |
| 44 | Production capacity without disruptions | 14.57094816 | − 0.12889826 |
| 46 | Mitigation of supply chain disruptions | 13.52509107 | − 0.679156463 |
| 47 | Consistent ability to manufacture | 14.263633 | − 0.51660328 |
| 48 | Vaccine production facilities | 14.3857391 | 0.871495514 |
| 49 | Safest vaccine supply to date | 13.2375538 | − 0.516982925 |
| 50 | Every vaccine batch tested | 11.90515624 | 1.117855186 |
| CTR6: Global solidarity | |||
| 85 | Vaccine tests in vulnerable populations | 21.80083619 | − 0.166287667 |
| 91 | Vaccine supply for world’s poorest countries | 21.96719102 | − 1.481635453 |
| 92 | Equitable access to vaccines in emergencies | 21.75202149 | 1.92394612 |
| 93 | Vaccine provision for financially disadvantaged individuals | 21.82751528 | 0.092452284 |
| 94 | No racism or other forms of discrimination | 21.22157512 | − 0.879315539 |
| 102 | Education about vaccination value | 22.24485781 | 0.375208736 |
| 103 | Vaccination status checks among school children | 22.80895714 | 0.13563152 |
Fig. 5.
IRMs for the six clusters
The R − C values were used to divide the six clusters into two categories. The first is a causes group of clusters mostly containing criteria with positive R − C values and thus factors that directly influence the others. The second is an effects group of clusters with the most criteria presenting negative R − C values, which are largely affected by other factors. In the causes group, the five criteria with the highest positive R − C values are equitable access to vaccination in emergencies, rigorous analysis of results, post-research immunization schedule, sourcing of appropriate expertise, and every vaccine batch tested. These criteria have R − C values of 1.9239, 1.6194, 1.5683, 1.3275, and 1.1179, respectively. The five criteria are considered causes that most influence other criteria in this model. In the effects group, the criteria with the highest negative R − C values are avoidance of misinformation, speed of processes, coverage of different technologies, testing and evaluation before licensing by Food and Drug Administration, and benefits offered by financing provided. Their values are − 1.2909, − 1.2282, − 1.0697, − 0.8764, and − 0.8474, respectively. These criteria are thus the most affected by the other factors.
On the R + C axis, the model’s five most important criteria are vaccine supply for world’s poorest countries, vaccine provision for financially disadvantaged individuals, vaccination status checks among school children, vaccine tests in vulnerable populations, and equitable access to vaccines in emergencies. These criteria have R + C values of 21.9672, 21.8275, 22.8090, 21.8008, and 21.7520, respectively. The DEMATEL’s results were used in the next step to calculate the CI in order to facilitate the selection of the best vaccine manufacturer.
Vaccine manufacturer selection using CI
Every vaccine manufacturer must have the ability to deliver the necessary volume of vaccines within the required timelines. An initial list of candidates should be drawn up quickly to begin negotiations, but the list has to be updated as more information is made available, especially from clinical trials. Among the many vaccine manufacturers available, many are known worldwide (e.g., GlaxoSmithKline, Merck Group, Pfizer, Novavax, Emergent BioSolutions, Commonwealth Serum Laboratories, Inovio Pharmaceuticals, Bavarian Nordic, and Mitsubishi Tanabe Pharma). However, for the present study purposes, only three candidates (hereafter called “alphas” to avoid any associations with famous brands) were assessed.
The expert panel was shown a matrix with all the possible criteria combinations. Choquet (1954) states that the potential combinations are specified based on 2n parameters, which, in the present case, indicate that 64 combinations are possible (i.e., 2*6 = 64). Table 7 shows the matrix of potential interactions among clusters, with “bad” representing a deficient performance and “good” an excellent performance (see full version in Appendix). The matrix combinations were identified by the panel based on the group cognitive map information on how the six clusters are interconnected.
Table 7.
Matrix of interactions
| # | CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | Score |
|---|---|---|---|---|---|---|---|
| 1 | Bad | Bad | Bad | Bad | Bad | Bad | 0 |
| 2 | Good | Bad | Bad | Bad | Bad | Bad | 2 |
| 3 | Bad | Good | Bad | Bad | Bad | Bad | 1 |
| 4 | Bad | Bad | Good | Bad | Bad | Bad | 2 |
| 5 | Bad | Bad | Bad | Good | Bad | Bad | 2 |
| 6 | Bad | Bad | Bad | Bad | Good | Bad | 1 |
| 7 | Bad | Bad | Bad | Bad | Bad | Good | 1 |
| 8 | Good | Good | Bad | Bad | Bad | Bad | 3 |
| 9 | Good | Bad | Good | Bad | Bad | Bad | 3 |
| – | – | – | – | – | – | – | – |
| 55 | Good | Good | Bad | Bad | Good | Good | 6 |
| – | – | – | – | – | – | – | – |
| 64 | Good | Good | Good | Good | Good | Good | 10 |
To complete the last column in Table 7, the facilitator asked the decision makers various questions. For example, one question fielded by the panel was as follows: “How would you assess the hypothetical scenario of a vaccine manufacturer for which only the criterion of scientific approach and technology used is considered good while the other criteria are rated bad?”. The experts’ judgments were assigned a value on a 10-point scale, on which 0 is an extremely poor performance and 1 is an extremely strong performance.
The importance of group dynamics and negotiation in this context needs be highlighted because they forced the specialists to deal with contrasting opinions and thus formulate more consensual solutions. This process allowed the panel members to experience decision dimensions that would not have been accessible through other methodologies. The exercise was conducted using the alphas to compare the attractiveness of the clusters’ “swings”, thereby avoiding the most common significant mistake in decision analysis. According to Keeney (1992), this is evaluating criteria entirely based on decision makers’ intuitive rating of the factors’ importance and ignoring their interdependence. Although the present study approach was non-linear and intrinsically subjective, it facilitated a collaborative exploration of variations in the relevant inputs so that the impacts of each change could be detected instantly. This procedure offered further opportunities for discussion, which again reflected the constructivist, sociotechnical nature of the framework adopted.
Table 7 offers a few instances of the combinations assessed by the panel. For example, the fifty-fifth line has a good-good-bad-bad-good-good pattern, which was given six points. The expert panel was thus asked: “How would you assess the hypothetical scenario of a vaccine manufacturer in which only the criteria of scientific approach and technology used, speed of delivery, ability to supply sufficient quantities through production capacity development, and global solidarity are rated good while the criteria of cost and liability and risk sharing are appraised as bad?”. The results show that the panel overrated the value of this combination as the score assigned (i.e., 6 points) was higher than the total of the values given to each cluster on its own (i.e., 2 + 1 + 1 + 1 = 5). A comparison matrix was created, and similar steps were taken for the criteria the specialists had selected from each cluster, providing the basis for the CI estimation. A file containing all the combinations generated is available upon request. Table 8 provides the performance evaluations for three alphas with regard to each criterion.
Table 8.
Overall results of vaccine manufacturer evaluation
| Cluster | Criteria | Alpha 1 | Alpha 2 | Alpha 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CTR1 | 7 | 8 | 90 | 848 | 9 | 93 | 864 | 9 | 88 | 844 |
| 11 | 7 | 8 | 7 | |||||||
| 13 | 9 | 9 | 8 | |||||||
| 21 | 10 | 10 | 9 | |||||||
| 41 | 10 | 10 | 10 | |||||||
| CTR2 | 52 | 7 | 75 | 9 | 85 | 7 | 74 | |||
| 53 | 6 | 8 | 7 | |||||||
| 54 | 6 | 8 | 7 | |||||||
| 55 | 8 | 8 | 7 | |||||||
| 56 | 8 | 8 | 6 | |||||||
| 57 | 9 | 9 | 7 | |||||||
| 59 | 10 | 10 | 10 | |||||||
| CTR3 | 19 | 8 | 75 | 8 | 75 | 8 | 79 | |||
| 61 | 8 | 7 | 8 | |||||||
| 62 | 8 | 8 | 8 | |||||||
| 63 | 7 | 8 | 8 | |||||||
| 104 | 7 | 7 | 7 | |||||||
| CTR4 | 67 | 9 | 85 | 9 | 87 | 8 | 84 | |||
| 68 | 8 | 9 | 8 | |||||||
| 69 | 9 | 9 | 8 | |||||||
| 70 | 9 | 9 | 9 | |||||||
| 72 | 8 | 8 | 9 | |||||||
| 75 | 9 | 9 | 9 | |||||||
| 78 | 8 | 8 | 9 | |||||||
| CTR5 | 43 | 10 | 93 | 10 | 97 | 10 | 87 | |||
| 44 | 9 | 9 | 9 | |||||||
| 46 | 9 | 10 | 8 | |||||||
| 47 | 9 | 10 | 8 | |||||||
| 48 | 10 | 10 | 10 | |||||||
| 49 | 9 | 9 | 8 | |||||||
| 50 | 9 | 9 | 8 | |||||||
| CTR6 | 85 | 8 | 90 | 8 | 91 | 9 | 94 | |||
| 91 | 9 | 9 | 10 | |||||||
| 92 | 10 | 10 | 10 | |||||||
| 93 | 9 | 9 | 9 | |||||||
| 94 | 8 | 8 | 10 | |||||||
| 102 | 10 | 10 | 9 | |||||||
| 103 | 9 | 10 | 9 | |||||||
After the CI was calculated using the formulas discussed in Sect. 3.3, Alpha 2 was ranked first with a total score of 864 points. A file containing all the calculations is also available upon request. This ranking process was the last part of the evaluation phase, which meant the next phase/procedures could be carried out, namely, validating the results and assessing the decision-support system generated.
Discussion, consolidation, implications, and recommendations
A final session was held to confirm the results obtained and the assessment system’s potential applicability and impact. This last meeting was attended by a staff member of the Saint Francisco Xavier Hospital Infectious Diseases Unit in Lisbon, Portugal. This expert is an experienced virologist who is responsible for the public sector vaccine purchases. The interviewee’s opinion was deemed to be of profound importance as he has specialized knowledge about the subject in question, and he had not joined any of the panel previous sessions, making him a neutral participant.
The meeting lasted about one hour, during which five objectives were achieved. The first was to provide briefly a context for the present study in terms of the available evaluation techniques used to select vaccine manufacturers. The second objective was to elicit feedback on the ability of the methodology combining cognitive maps, DEMATEL, and the CI to strengthen the current understanding of this decision problem. The third was to discuss the results, and the fourth was to compare the advantages of the proposed assessment system with other evaluation techniques. The last objective was to verify the proposed decision support system’s potential application by practitioners, as well as what would be required to implement it.
After the meeting purpose was clarified for the interviewee, the limitations of existing assessment practices were briefly discussed and the proposed methodology was summarized. A breakdown followed of both the collective cognitive map and the cluster interactions matrix generated in the second group session. The final session then moved on to the interviewee’s analysis of and reactions to the results. This expert said that he “would have given the same scores or something very similar to the results” (in his words). The interviewer subsequently explained that, because of this study constructivist approach, the proposed methodology focuses on process and improvements can be made at any time to the decision support system to strengthen the results. The interviewee then identified five advantages of applying cognitive mapping, DEMATEL, and the CI together, which are as follows:
First, the fact that this approach seeks a solution that starts with the people involved; second, the relevance of the process itself, which increases the decision makers’ level of interest and involvement through sharing know-how acquired through both personal and professional experiences in the field; third, the flexibility of the results achieved due to the constructivist logic [applied]; fourth, the combination of quantifiable and non-quantifiable criteria; [and,] last, greater specificity and focus on vaccine manufacturers’ current reality compared to the models already developed (in his words).
This specialist noted that the analysis system developed depends on each decision maker’s value judgments and/or opinions and their personal and professional experience but that the process-orientation of the proposed approach also has benefits. It allows adjustments whenever these are considered pertinent or the expert panel changes. This part of the final meeting thus proved to be particularly valuable as a confirmation of the decision-support system’s practical value.
Despite the popularity of the methods applied (i.e., cognitive mapping, DEMATEL, and the CI), their combined use is rare, and no evidence was found of their application to assessments of vaccine manufacturers. The proposed methodology addressed some limitations of prior approaches mentioned in the literature (e.g., the ways assessment models select the criteria included in evaluation mechanisms and the [non]modeling of multi-criteria coalition). In addition, by using expert opinions, the methodology proposed in our study assumes a different stance, and we were able to bring added realism into our framework, as the use of cognitive mapping brought new insights to the analysis processes based on the experts’ know-how, which would not have been detected through the use of statistical methods alone. The issues of “ideological beliefs that do not support vaccination”, “anti-vaccine literature” and/or “vaccine refusal”, for instance, can be easily overlooked, but are not without consequence. DEMATEL and the CI also facilitated modeling the criteria’s interdependencies.
Conclusion
Immunization against epidemic and/or pandemic viruses is, in general, thought to be the best long-term solution. In this context, the global vaccines industry is expected to grow rapidly, spearheaded by the foremost manufacturers worldwide who make a variety of vaccines. The COVID-19 global pandemic has thus had an extensive, positive effect on this market as many top companies are now concentrating on creating the most effective vaccine to fight against this highly infectious, life-threatening disease and spending heavily to produce a viable COVID-19 vaccine. The global vaccine market will likely experience strong growth in the next five years due to intense competition among vaccine manufacturers. Selecting the overall best manufacturer is, therefore, of great interest to society at large.
Joint EU action on a global scale could significantly enhance the chances of a COVID-19 vaccine and a return to socioeconomic normalcy worldwide. The European Commission plans to implement the EU strategy in conjunction with the member states, thereby increasing the probability that all those who need vaccines will gain equitable, affordable access to these vaccines as soon as possible. To this end, the EU will deploy the available regulatory, financial, and advisory tools, among others. Wijhe et al., (2019, p. 5705) report: “the success of vaccination programmes is inherently tied to the willingness of policy makers to finance the purchase and delivery of vaccines, the monitoring of their effects in terms of coverage, adverse events, and the occurrence of the target diseases”.
By combining cognitive mapping, DEMATEL, and the CI, the present study developed a novel assessment system allowing vaccine manufacturers to be vetted based on the European Commission’s (2020a) suggestions. The findings include the following dimensions: (1) soundness of scientific approach and technology used; (2) speed of delivery; (3) cost; (4) liability and risk sharing; (5) ability to supply sufficient quantities through production capacity development; and (6) global solidarity. The existing literature provides no evidence of other research in this context using these methodologies. Notably, the proposed approach was designed to complement rather than substitute the available evaluation models, thus enhancing the significance of this study contributions on both a theoretical and practical level.
Although the findings are context-specific, they could function as an important starting point for researchers and practitioners seeking to assess vaccine manufacturers, and the results should improve on previous field studies and practices. The present study makes two specific contributions to methodology. Its main value lies in the techniques applied, which are an apparent innovation in this research context. The second contribution is the detailed description of the proposed mechanism, provided so that this can be replicated in other contexts and/or with different groups of experts based on the sociotechnical and process-oriented nature of the framework (Bell & Morse, 2013; Ormerod, 2018).
Due to the idiosyncratic nature of the proposed approach, any extrapolations to other contexts need to be analyzed and adapted carefully. As mentioned previously, this study sought not so much to obtain the best model as to foster new approaches to selecting vaccine manufacturers during epidemics and pandemics. Future research along the same lines may benefit from considering other techniques capable of generating structured models of decision makers’ interactions and preferences (e.g., see Belton and Stewart (2002) and Zhou et al. (2009)). Another option is comparative studies involving other techniques. Methodological comparisons are important, so they should be encouraged in further research. However, the present study complementary stance needs to be emphasized again as the goal was not to substitute previous methods or models but rather to add to them. In terms of methodology, more useful results could thus be achieved by applying the proposed approach in varied contexts. Any contributions that increase the empirical robustness of the present findings and provide further advances in this field will always be seen as timely additions to the literature on OR.
Acknowledgements
This work was partially funded by the Portuguese Foundation for Science and Technology (Grant UIDB/00315/2020). Records from the expert panel meetings, including photographs, software output, and non-confidential information, can be obtained from the authors upon request.
Appendix
| # | CTR1 | CTR2 | CTR3 | CTR4 | CTR5 | CTR6 | Score |
|---|---|---|---|---|---|---|---|
| 1 | Bad | Bad | Bad | Bad | Bad | Bad | 0 |
| 2 | Good | Bad | Bad | Bad | Bad | Bad | 2 |
| 3 | Bad | Good | Bad | Bad | Bad | Bad | 1 |
| 4 | Bad | Bad | Good | Bad | Bad | Bad | 2 |
| 5 | Bad | Bad | Bad | Good | Bad | Bad | 2 |
| 6 | Bad | Bad | Bad | Bad | Good | Bad | 1 |
| 7 | Bad | Bad | Bad | Bad | Bad | Good | 1 |
| 8 | Good | Good | Bad | Bad | Bad | Bad | 3 |
| 9 | Good | Bad | Good | Bad | Bad | Bad | 3 |
| 10 | Good | Bad | Bad | Good | Bad | Bad | 3 |
| 11 | Good | Bad | Bad | Bad | Good | Bad | 3 |
| 12 | Good | Bad | Bad | Bad | Bad | Good | 3 |
| 13 | Bad | Good | Good | Bad | Bad | Bad | 3 |
| 14 | Bad | Good | Bad | Good | Bad | Bad | 4 |
| 15 | Bad | Good | Bad | Bad | Good | Bad | 3 |
| 16 | Bad | Good | Bad | Bad | Bad | Good | 3 |
| 17 | Bad | Bad | Good | Good | Bad | Bad | 5 |
| 18 | Bad | Bad | Good | Bad | Good | Bad | 4 |
| 19 | Bad | Bad | Good | Bad | Bad | Good | 4 |
| 20 | Bad | Bad | Bad | Good | Good | Bad | 4 |
| 21 | Bad | Bad | Bad | Good | Bad | Good | 5 |
| 22 | Bad | Bad | Bad | Bad | Good | Good | 4 |
| 23 | Good | Good | Good | Bad | Bad | Bad | 5 |
| 24 | Good | Good | Bad | Good | Bad | Bad | 5 |
| 25 | Good | Good | Bad | Bad | Good | Bad | 5 |
| 26 | Good | Good | Bad | Bad | Bad | Good | 4 |
| 27 | Good | Bad | Good | Good | Bad | Bad | 6 |
| 28 | Good | Bad | Good | Bad | Good | Bad | 5 |
| 29 | Good | Bad | Good | Bad | Bad | Good | 5 |
| 30 | Good | Bad | Bad | Good | Good | Bad | 6 |
| 31 | Good | Bad | Bad | Good | Bad | Good | 6 |
| 32 | Good | Bad | Bad | Bad | Good | Good | 5 |
| 33 | Bad | Good | Good | Good | Bad | Bad | 7 |
| 34 | Bad | Good | Good | Bad | Good | Bad | 6 |
| 35 | Bad | Good | Good | Bad | Bad | Good | 6 |
| 36 | Bad | Good | Bad | Good | Good | Bad | 6 |
| 37 | Bad | Good | Bad | Good | Bad | Good | 6 |
| 38 | Bad | Good | Bad | Bad | Good | Good | 6 |
| 39 | Bad | Bad | Good | Good | Good | Bad | 7 |
| 40 | Bad | Bad | Good | Good | Bad | Good | 7 |
| 41 | Bad | Bad | Good | Bad | Good | Good | 6 |
| 42 | Bad | Bad | Bad | Good | Good | Good | 6 |
| 43 | Good | Good | Good | Good | Bad | Bad | 8 |
| 44 | Good | Good | Good | Bad | Good | Bad | 7 |
| 45 | Good | Good | Good | Bad | Bad | Good | 8 |
| 46 | Good | Bad | Good | Good | Good | Bad | 8 |
| 47 | Good | Bad | Good | Good | Bad | Good | 8 |
| 48 | Good | Bad | Good | Bad | Good | Good | 7 |
| 49 | Good | Bad | Bad | Good | Good | Good | 7 |
| 50 | Bad | Good | Good | Good | Good | Bad | 7 |
| 51 | Bad | Good | Good | Good | Bad | Good | 8 |
| 52 | Bad | Good | Good | Bad | Good | Good | 8 |
| 53 | Bad | Good | Bad | Good | Good | Good | 7 |
| 54 | Bad | Bad | Good | Good | Good | Good | 8 |
| 55 | Good | Good | Bad | Bad | Good | Good | 6 |
| 56 | Good | Good | Bad | Good | Bad | Good | 7 |
| 57 | Good | Good | Bad | Good | Good | Bad | 7 |
| 58 | Bad | Good | Good | Good | Good | Good | 9 |
| 59 | Good | Bad | Good | Good | Good | Good | 9 |
| 60 | Good | Good | Bad | Good | Good | Good | 7 |
| 61 | Good | Good | Good | Bad | Good | Good | 8 |
| 62 | Good | Good | Good | Good | Bad | Good | 9 |
| 63 | Good | Good | Good | Good | Good | Bad | 9 |
| 64 | Good | Good | Good | Good | Good | Good | 10 |
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Ackermann F. Problem structuring methods ‘in the Dock’: Arguing the case for soft OR. European Journal of Operational Research. 2012;219(3):652–658. [Google Scholar]
- Ackermann F. PSMs are dead; long live PSMs. Journal of the Operational Research Society. 2019;70(8):1396–1397. [Google Scholar]
- Ackermann F, Eden C. SODA – Journey making and mapping in practice. In: Rosenhead J, Mingers J, editors. Rational Analysis for a Problematic World Revisited: Problem Structuring Methods for Complexity. John Wiley & Sons; 2001. pp. 43–60. [Google Scholar]
- Ackermann F, Eden C. Strategic options development and analysis. In: Reynolds M, Holwell S, editors. Systems Approaches to Managing Change: A Practical Guide. Springer; 2010. pp. 135–190. [Google Scholar]
- Assunção E, Ferreira F, Meidutė-Kavaliauskienė I, Zopounidis C, Pereira L, Correia R. Rethinking urban sustainability using fuzzy cognitive mapping and system dynamics. International Journal of Sustainable Development and World Ecology. 2020;27(3):261–275. [Google Scholar]
- Bana e Costa C, Corrêa E, De Corte J, Vansnick J. Facilitating bid evaluation in public call for tenders: A socio-technical approach. Omega the International Journal of Management Science. 2002;30(3):227–242. [Google Scholar]
- Bell S, Morse S. Groups and facilitators within problem structuring processes. Journal of the Operational Research Society. 2013;64(7):959–972. [Google Scholar]
- Belton V, Stewart T. Multiple Criteria Decision Analysis: An Integrated Approach. Kluwer Academic Publishers; 2002. [Google Scholar]
- Bottero M, Ferreti V, Figueira J, Greco S, Roy B. On the Choquet multiple criteria preference aggregation model: Theoretical and practical insights from a real-world application. European Journal of Operational Research. 2018;271:120–140. [Google Scholar]
- Brito V, Ferreira F, Pérez-Gladish B, Govindan K, Meidutė-Kavaliauskienė I. Developing a green city assessment system using cognitive maps and the Choquet integral. Journal of Cleaner Production. 2019;218:486–497. [Google Scholar]
- Castanho M, Ferreira F, Carayannis E, Ferreira J. SMART-C: Developing a “smart city” assessment system using cognitive mapping and the Choquet integral. IEEE Transactions on Engineering Management. 2021;68(2):562–573. [Google Scholar]
- Choquet G. The theory of capacities. Annales De L’institute Fourier. 1954;5:131–295. [Google Scholar]
- Dalvi-Esfahani M, Niknafs A, Kuss D, Nilashi M, Afrough S. Social media addiction: Applying the DEMATEL approach. Telematics and Informatics. 2019;43:1–14. [Google Scholar]
- Demirel T, Demirel N, Kahraman C. Multi-criteria warehouse location selection using Choquet integral. Expert Systems with Applications. 2010;37(5):3943–3952. [Google Scholar]
- Duijzer L, Jaarsveld W, Dekker R. Literature review: The vaccine supply chain. European Journal of Operational Research. 2018;268(11):174–192. [Google Scholar]
- Eden C. Analyzing cognitive maps to help structure issues or problems. European Journal of Operational Research. 2004;159(3):673–686. [Google Scholar]
- Eden C, Ackermann F. SODA – The principles. In: Rosenhead J, Mingers J, editors. Rational Analysis for a Problematic World Revisited: Problem Structuring Methods for Complexity. John Wiley & Sons; 2001. pp. 21–40. [Google Scholar]
- Eden C, Ackermann F. Cognitive mapping expert views for policy analysis in the public sector. European Journal of Operational Research. 2004;152(3):615–630. [Google Scholar]
- Enayati S, Özaltın O. Optimal influenza vaccine distribution with equity. European Journal of Operational Research. 2020;283(21):714–725. [Google Scholar]
- Estêvão R, Ferreira F, Rosa A, Govindan K, Meidutė-Kavaliauskienė I. A socio-technical approach to the assessment of sustainable tourism: Adding value with a comprehensive process-oriented framework. Journal of Cleaner Production. 2019;236:1–11. [Google Scholar]
- European Commission (2020a). Coronavirus: Commission unveils EU Vaccines Strategy, retrieved from https://ec.europa.eu/commission/presscorner/detail/en/ip_20_1103 [July 2021].
- European Commission (2020b). EU Strategy for COVID-19 Vaccines: Communication from the Commission to the European Parliament, the European Council, the Council and the European Investment Bank, retrieved from https://ec.europa.eu/info/sites/info/files/communication-eu-strategy-vaccines-covid19_en.pdf [July 2021].
- European Commission (2020c). Investment Plan for Europe: European Investment Bank to Provide BioNTech with up to €100 Million in Debt Financing for COVID-19 Vaccine Development and Manufacturing, retrieved from https://ec.europa.eu/commission/presscorner/detail/en/ip_20_1034 [July 2021].
- Falatoonitoosi E, Leman Z, Sorooshian S, Salimi M. Decision-making trial and evaluation laboratory. Research Journal of Applied Sciences, Engineering and Technology. 2013;5(13):3476–3480. [Google Scholar]
- Feikin D, Lezotte D, Hamman R, Salmon D, Chen R, Hoffman R. Individual and community risks of measles and pertussis associated with personal exemptions to immunization. Journal of the American Medical Association. 2000;84:3145–3150. doi: 10.1001/jama.284.24.3145. [DOI] [PubMed] [Google Scholar]
- Ferreira F, Jalali M, Zavadskas E, Meidutė-Kavaliauskienė I. Assessing payment instrument alternatives using cognitive mapping and the Choquet integral. Transformations in Business and Economics. 2017;16:170–187. [Google Scholar]
- Ferreira J, Jalali M, Ferreira F. Enhancing the decision-making virtuous cycle of ethical banking practices using the Choquet integral. Journal of Business Research. 2018;88:492–497. [Google Scholar]
- Fonseca J, Ferreira F, Pereira L, Govindan K, Meidutė-Kavaliauskienė I. Analyzing determinants of environmental conduct in small and medium-sized enterprises: A sociotechnical approach. Journal of Cleaner Production. 2020;256:1–13. [Google Scholar]
- Gabus, A. & Fontela, E. (1972). World Problems: An Invitation to Further Thought Within the Framework of DEMATEL, Geneva, Switzerland: Battelle Geneva Research Centre.
- Gabus, A. & Fontela, E. (1973). Perceptions of the World Problematique: Communication Procedure, Communicating with Those Bearing Collective Responsibility, Geneva, Switzerland: Batelle Geneva Research Center.
- Govindan K, Chaudhuri A. Interrelationships of risks faced by third party logistics service providers: A DEMATEL-based approach. Transportation Research Part E Logistics and Transportation Review. 2016;90:177–195. [Google Scholar]
- Govindan K, Dhingra Darbari J, Kaul A, Jha PC. Structural model for analysis of key performance indicators for sustainable manufacturer–supplier collaboration: A grey-decision-making trial and evaluation laboratory-based approach. Business Strategy and the Environment. 2021;30(4):1702–1722. [Google Scholar]
- Grabisch M. K-order additive discrete fuzzy measures and their representation. Fuzzy Sets and Systems. 1997;92(2):167–189. [Google Scholar]
- Grabisch M, Duchêne J, Lino F, Perny P. Subjective evaluation of discomfort in sitting position. Fuzzy Optimization and Decision Making. 2002;1(3):287–312. [Google Scholar]
- Howick S, Eden C. Supporting strategic conversations: The significance of a quantitative model building process. Journal of the Operational Research Society. 2011;62(5):868–878. [Google Scholar]
- Keeney R. Value-Focused Thinking: A Path to Creative Decision Making. Harvard University Press; 1992. [Google Scholar]
- Keeney R. Creativity in decision making with value-focused thinking. MIT Sloan Management Review. 1994;35(4):33–41. [Google Scholar]
- Kijewska K, Torbacki W, Iwan S. Application of AHP and DEMATEL methods in choosing and analysing the measures for the distribution of goods in Szczecin region. Sustainability. 2018;10(7):1–26. [Google Scholar]
- Kolkman M, Kok M, Van der Veen A. Mental model mapping as a new tool to analyse the use of information in decision-making in integrated water management. Physics and Chemistry of the Earth. 2005;30(4):317–332. [Google Scholar]
- Krishnan A, Kasim M, Bakar E. A short survey on the usage of Choquet integral and its associated fuzzy measure in multiple attribute analysis. Procedia Computer Science. 2015;59:427–434. [Google Scholar]
- Léon T, Liern V, Pérez-Gladish B. A multicriteria assessment model for countries’ degree of preparedness for successful impact investing. Management Decision. 2020;58(11):2455–2471. [Google Scholar]
- Martins S, Ferreira F, Ferreira J, Marques C. An artificial-intelligence-based method for assessing service quality: Insights from the prosthodontics sector. Journal of Service Management. 2020;31(2):291–312. [Google Scholar]
- Marttunen M, Lienert J, Belton V. Structuring problems for multi-criteria decision analysis in practice: A literature review of method combinations. European Journal of Operational Research. 2017;263(1):1–17. [Google Scholar]
- Mingers J. Reaching the Problems that Traditional OR/MS Methods Cannot Reach. University of Kent Canterbury; 2008. [Google Scholar]
- Mipatrini D, Stefanelli P, Severoni S, Rezza G. Vaccinations in migrants and refugees: A challenge for European health systems—A systematic review of current scientific evidence. Pathogens and Global Health. 2017;111:59–68. doi: 10.1080/20477724.2017.1281374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murofushi T, Sugeno M. A theory of fuzzy measures: Representations, the Choquet integral, and null sets. Journal of Mathematical Analysis and Applications. 1991;159(2):532–549. [Google Scholar]
- Natividade J, Ferreira F, Zopounidis C, Pereira L, Çipi A, Ferreira J. Developing a composite index for intrapreneurial orientation in small and medium-sized enterprises: A comprehensive dual methodology. Journal of the Operational Research Society. 2020 doi: 10.1080/01605682.2020.1730715. [DOI] [Google Scholar]
- Ormerod R. Logic and rationality in OR interventions: An examination in the light of the ‘critical rationalist’ approach. Journal of the Operational Research Society. 2013;64(4):469–487. [Google Scholar]
- Ormerod R. The logic and methods of OR consulting practice: Towards a foundational view. Journal of the Operational Research Society. 2018;69(9):1357–1378. [Google Scholar]
- Ormerod R. The pragmatic logic of OR consulting practice: Towards a foundational view. Journal of the Operational Research Society. 2020;71(11):1691–1709. [Google Scholar]
- Ouyang Y, Li J. A note on the monotone set functions defined by Choquet integral. Fuzzy Sets and Systems. 2004;146(1):147–151. [Google Scholar]
- Paes de Faria A, Ferreira F, Dias P, Çipi A. A constructivist model of bank branch front-office employee evaluation: An FCM-SD-based approach. Technological and Economic Development of Economy. 2020;26(1):213–239. [Google Scholar]
- Ralescu D, Adams G. The fuzzy integral. Journal of Mathematical Analysis and Applications. 1980;75(2):562–570. [Google Scholar]
- Ravensbergen S, Nellums L, Hargreaves S, Stienstra Y, Friedland J. National approaches to the vaccination of recently arrived migrants in Europe: A comparative policy analysis across 32 European countries. Travel Medicine and Infectious Disease. 2019;27(1):33–38. doi: 10.1016/j.tmaid.2018.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenhead J. Problem structuring methods. In: Gass S, Fu M, editors. Encyclopedia of Operations Research and Management Science. Springer; 2013. pp. 46–64. [Google Scholar]
- Schwartz J, Caplan A. Vaccination Ethics and Policy: An Introduction with Readings. MIT Press; 2017. [Google Scholar]
- Shedrawy J, Henriksson M, Hergens M, Askling H. Estimating costs and health outcomes of publicly funded tick-born encephalitis vaccination: A cost-effectiveness analysis. Vaccine. 2018;36(50):7659–7665. doi: 10.1016/j.vaccine.2018.10.086. [DOI] [PubMed] [Google Scholar]
- Shieh J, Wu H, Liu H. Applying a complexity-based Choquet integral to evaluate students’ performance. Expert Systems with Applications. 2009;36(3):5100–5106. [Google Scholar]
- Si S, You X, Liu H, Zhang P. DEMATEL Technique: A systematic review of the state-of-the-art literature on methodologies and applications. Mathematical Problems in Engineering. 2018;2018:1–33. [Google Scholar]
- Silva A, Ferreira F, Carayannis E, Ferreira J. Measuring SMEs’ propensity for open innovation using cognitive mapping and MCDA. IEEE Transactions on Engineering Management. 2021;68(2):396–407. [Google Scholar]
- Simões J, Ferreira F, Peris-Ortiz M, Ferreira J. A cognition-driven framework for the evaluation of startups in the digital economy: Adding value with cognitive mapping and rule-based expert systems. Management Decision. 2020;58(11):2327–2347. [Google Scholar]
- Smith C, Shaw D. The characteristics of problem structuring methods: A literature review. European Journal of Operational Research. 2019;274(2):403–416. [Google Scholar]
- Tan C, Chen X. Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Systems with Applications. 2010;37(1):149–157. [Google Scholar]
- Tegarden D, Sheetz S. Group cognitive mapping: A methodology and system for capturing and evaluating managerial and organizational cognition. Omega the International Journal of Management Studies. 2003;31(2):113–125. [Google Scholar]
- Torra V, Narukawa Y, Yager R. On a relationship between fuzzy measures and AIFS. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. 2016;24(6):847–858. [Google Scholar]
- Vaz de Almeida M, Ferreira J, Ferreira F. Developing a multi-criteria decision support system for evaluating knowledge transfer by higher education institutions. Knowledge Management Research and Practice. 2019;17(4):358–372. [Google Scholar]
- Vrdelja M, Učakar V, Kraigher A. From mandatory to voluntary vaccination: Intention to vaccinate in the case of policy changes. Public Health. 2020;180:57–63. doi: 10.1016/j.puhe.2019.10.026. [DOI] [PubMed] [Google Scholar]
- Wang R. Some inequalities and convergence theorems for Choquet integrals. Journal of Applied Mathematics and Computing. 2011;35(1/2):305–321. [Google Scholar]
- WHO – World Health Organization (2020). The Global Vaccine Action Plan 2011–2010: Review and Lessons Learned, retrieved from https://www.who.int/immunization/global_vaccine_action_plan/GVAP_review_lessons_learned/en/ [July 2020].
- Wijhe M, Boer P, Jong H, Vliet H, Wallinga J, Postma M. Trends in governmental expenditure on vaccination programmes in the Netherlands: A historical analysis. Vaccine. 2019;37(38):5698–5707. doi: 10.1016/j.vaccine.2019.07.097. [DOI] [PubMed] [Google Scholar]
- Zavadskas E, Turskis Z, Kildienė S. State of art surveys of overviews on MCDM/MADM methods. Technological and Economic Development of Economy. 2014;20(1):165–179. [Google Scholar]
- Zhou P, Ang B. Comparing MCDA aggregation methods in constructing composite indicators using the Shannon-Spearman measure. Social Indicators Research. 2009;94(1):83–96. [Google Scholar]