Superconductivity in nickel-based 112 systems

Abstract

Superconductivity has been discovered recently in infinite-layer nickel-based 112 thin films R_1−xA_xNiO₂ (R = La, Nd, Pr and A = Sr, Ca). They are isostructural to the infinite-layer cuprate (Ca,Sr)CuO₂ and are supposed to have a formal Ni 3d⁹ valence, thus providing a new platform to study the unconventional pairing mechanism of high-temperature superconductors. This important discovery immediately triggers a huge amount of innovative scientific curiosity in the field. In this paper, we try to give an overview of the recent research progress on the newly found superconducting nickelate systems, both from experimental and theoretical aspects. We mainly focus on the electronic structures, magnetic excitations, phase diagrams and superconducting gaps, and finally make some open discussions for possible pairing symmetries in Ni-based 112 systems.

Graphical abstract

Public summary

• •The infinite-layer nickel-based 112 thin films R_1−xA_xNiO₂ can host superconductivity up to 15 K
• •R_1−xA_xNiO₂ is a multiband system, in which the short-range antiferromagnetic fluctuations can be detected
• •R_1−xA_xNiO₂ has an unconventional superconducting pairing sate with a robust d-wave gap and a full gap without unified understanding
• •The nickelate system provides a new platform for researching unconventional superconductivity

Introduction

In 1986, Bednorz and Müller¹ in IBM Zürich Research Laboratory discovered the high-temperature superconductivity (HTS) in Ba doped insulating cuprate system La_2−xBa_xCuO₄, and they were awarded the Nobel Prize in Physics for this important discovery. Soon after, the critical temperature (T_c) in YBa₂Cu₃O_7−δ system was found to be as high as 93 K,^2,3 which broke through the Macmillan limit⁴ and the boiling temperature of liquid nitrogen, starting a new era of intensive research on HTS. Scientists discovered more and more cuprate systems5, 6, 7, 8 and continuously renewed the records of the highest superconducting transition temperatures at ambient pressure.^9,10 However, the pairing mechanism in HTS remains controversial and elusive.11, 12, 13 It seems that the superconducting states can coexist or compete with different kinds of emergent intertwined orders, which leads to a complicated phase diagram.14, 15, 16, 17, 18 Since 2008, the discovery of iron-based superconductors (FeSCs)^19,20 gives us some new hints for investigating the pairing mechanism of HTS and exploring superconductors with higher T_c. Scientists have made great achievements in this fast-developing field of superconductivity during the last few decades.21, 22, 23 For now, cuprate and FeSCs are recognized as the only two systems of HTS under ambient pressure, and it seems to be a long-standing pursuit to realize room temperature superconductors.24, 25, 26, 27 The most essential consensus that has been achieved is that HTS should have layered structures and 3d orbital electrons of transition metals with appropriate electron correlation. It has been widely perceived that the pairing may be established through exchanging antiferromagnetic (AF) spin fluctuations or superexchange effect.

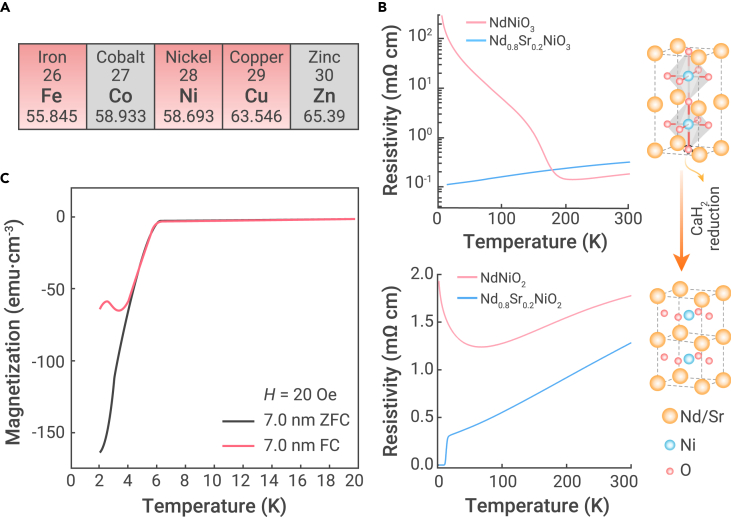
Many experimental and theoretical efforts have been devoted to searching HTS in the analogous compounds without copper. For example, bulk superconductivity was found in Sr₂RuO₄ with a very low T_c,²⁸ and electron-doped Sr₂IrO₄ exhibits plausible spectroscopic signatures of superconducting gaps.²⁹ As shown in Figure 1A, the Ni element locates just between Fe and Cu, and scientists are curious about whether HTS can be realized in the Ni-based materials. In this regard, LaNiO₃/LaAlO₃ superlattice has been proposed as a potential candidate for high-temperature superconductivity;30, 31, 32 here, Ni has a 3d⁷ orbital configurations, and the $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital is lower in energy compared with the $d_{{\mathrm{z}}^2}$ orbital. This will lead to a half-filled $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital, mimicking the electron occupation of undoped cuprates. However, the most stable nickelates in nature have a formal valence of Ni²⁺ with a d⁸ electronic configuration, such as in NiO and La₂NiO₄. In spite of the same structure as La₂CuO₄, investigators failed to find any trace of superconductivity in the hole doped system La_2−xSr_xNiO₄.^33,34 In addition, the multilayer nickelate Ruddlesden-Popper phase^35,36 R_n+1Ni_nO_3n+1 (R = La, Nd, Pr) possesses a high-valence state of Ni. The apical oxygen can be removed using a soft-chemistry topotactic reduction method, resulting in the phase of R_n+1Ni_nO_2(n+1) with a relatively lower valence state.37, 38, 39 Their Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ band is expected to be close to half-filled as the number of layers (n) increases.⁴⁰ However, researchers found some other exotic physics involving charge and spin orders instead of superconductivity in this family of materials.40, 41, 42, 43 In particular, when n approaches infinity, it can be reduced to infinite-layer RNiO₂ with 3d⁹ configuration of Ni¹⁺ valence.^44,45 With the dedicated efforts over the decades, in 2019, superconductivity was finally discovered in Nd_1−xSr_xNiO₂ (x = 0.2) thin films deposited on SrTiO₃ substrates.⁴⁶ Figure 1B gives a schematic for removing the apical oxygen of Nd_1−xSr_xNiO₃ by using CaH₂ reduction at a high temperature, forming a superconducting phase, Nd_1−xSr_xNiO₂. Bulk NdNiO₃ is a nearly standard perovskite structure with room temperature lattice parameters 3.81 Å, and Sr doping gives negligible influence on the lattice parameter.⁴⁷ The reduction will lead to an expansion of the in-plane lattice constant to about 3.92 Å and a reduced c axis lattice constant to about 3.31 Å, which is the distance between adjacent NiO₂ planes.³⁸ NdNiO₂ is composed by the stacking of alternating NiO₂ planes (superconducting layer) and Nd planes, forming the so-called infinite-layer structure. In the resistivity measurements, the undoped NdNiO₃ shows the characteristic first-order phase transition from a high-temperature paramagnetic metal to a low-temperature AF insulator.^48,49 Sr doping makes it change into a good metal in the whole temperature region. After the reduction, NdNiO₂ displays metallic behavior at high temperatures, with a resistive upturn below about 70 K. This unexpected feature will be discussed in the following section. Upon 20% Sr doping, Nd_0.8Sr_0.2NiO₂ exhibits a superconducting transition with an onset at 14.9 K and zero resistance at 9.1 K. Furthermore, perfect diamagnetism was observed recently on Nd_0.8Sr_0.2NiO₂ thin films with different thicknesses ranging from 6 to 17 nm.⁵⁰ Figure 1C shows the direct current (DC) magnetization measured under zero field cooling (ZFC) and field cooling (FC) modes on the thin film with typical thickness of 7 nm. It is found that T_c of diamagnetism is slightly lower than the one of zero resistance, suggesting the presence of inhomogeneity of the superconducting phase in the thin films. The phase coherence can occur in the entire films only when it is well below the zero resistance temperature, and the Meissner effect can thus happen. Combined with the fact of considerable critical current density up to 170 kA/cm²,⁴⁶ we may conclude that the Nd_0.8Sr_0.2NiO₂ thin films have bulk superconductivity instead of interface effect. Another two systems, namely, hole doped LaNiO₂ and PrNiO₂, were synthesized successfully and found to be superconductive as well.51, 52, 53, 54 Accordingly, the nickelate system is considered to be a promising candidate to be expanded into a large family, providing a new route to research and explore HTS. Based on the current experimental results, one can see that these three systems, La, Pr, Nd 112 phases, share similar electronic structures and superconducting properties. Thus, in the following sections of this review, we mainly focus on discussing the representative NdNiO₂ system, including the calculated electronic structures with multiband features, spin configurations, magnetic excitations, phase diagrams, and the measurement of single-particle tunneling spectrum; finally, we make some open discussions for the possible pairing symmetries and pairing mechanism in the newly found Ni-based superconductors.

Figure 1.

Discovery of superconductivity in nickelate Nd_1−xSr_xNiO₂ thin films

(A) Some elements of transition metals in the periodic table. Fe and Cu are two basic elements in cuprate and iron-based superconductors, respectively.

(B) The temperature-dependent resistivity of Nd-113 and Nd-112 films. Due to CaH₂ reduction, the perovskite structure of NdNiO₃ is changed into an infinite-layer NdNiO₂. The shaded region shows that Ni is located at the center of NiO₆ octahedral. Adapted from Li et al.⁴⁶

(C) ZFC and FC modes of DC magnetization on the Nd_0.8Sr_0.2NiO₂ thin film with typical thickness of 7 nm under the magnetic field of 20 Oe. Adapted from Zeng et al.⁵⁰

Electronic structures

As we know, the parent compounds of cuprates may be described as a Mott insulator with an AF long-range order,55, 56, 57, 58, 59 and superconductivity occurs upon chemical doping.⁶⁰ Due to the strong p-d orbitals hybridization,⁶¹ the doped holes enter into the oxygen sites in the CuO₂ planes. It was proposed that the doped holes on the p-orbital of oxygens combine with the $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ spins of Cu ions to form the Zhang-Rice singlets,⁶² moving through the square lattice, and exchange with their neighboring Cu spins. This theoretical proposal sets cuprates into a single band limit and naturally renders an effective two-dimensional (2D) t-J model to describe the low-energy physics of cuprates. In FeSC, the situation becomes more complex because the As/Se atoms locate alternatively above and below the center of the Fe squares. The crystalline environment experienced by Fe atoms is somewhat in between a tetrahedral one, in which the energy of the t_2g orbitals is higher than that of the e_g orbitals, while for an octahedral one as in cuprates, the energy of the t_2g orbitals is lower. As a result, the crystal splitting between the orbitals is weakened, and all five d-orbitals give a considerable contribution to the low-lying energy of electronic states.⁶³ As for the newly found Ni-based superconductors, many papers have made detailed theoretical calculations of the electronic structures, demonstrating the multiorbital features in the Nd/La 112 system within the low-energy region and pointing out both similarities and differences between nickelates and cuprates.64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75

Mott insulator, self-doping effect, and possible Kondo coupling

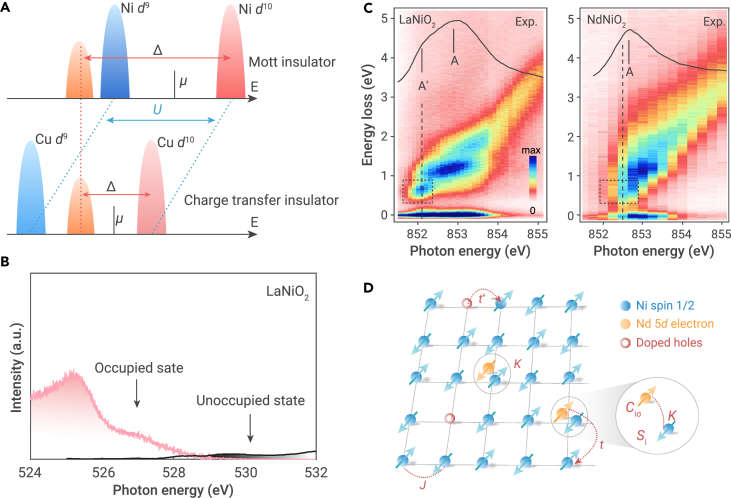
When we compare the NiO₂ layer in nickelate and CuO₂ layer in cuprates, a major difference becomes immediately obvious. As shown by the sketch in Figure 2A, a charge-transfer energy is estimated to be Δ ≈ 9 eV in NiO₂ and Δ ≈ 3 eV in CuO₂. According to the Zaanen-Sawatzky-Allen (ZSA) scheme,⁷⁶ cuprates locate in the regime of charge transfer insulator, while nickelates belong to the system of Mott insulator.⁷⁷ The holes doped in a Mott insulating NiO₂ layer would reside on the Ni-derived bands, not in the O 2p one. Because Ni²⁺ (3d⁸) with S = 1 is very common in all the known Ni²⁺ oxides, this makes the appearance of rather high-T_c superconductivity very puzzling and definitely unlike that in cuprates. In experiments, Hepting et al.⁷⁸ conduct X-ray absorption spectroscopy (XAS) and emission spectroscopy (XES) measurements near the O K-edge in parent phase RNiO₂ (R = La, Nd), and the results roughly reflect the unoccupied and occupied oxygen partial density of state (PDOS), respectively. As shown in Figure 2B, the oxygen PDOS exhibits a diminished weight near the Fermi energy, especially in the unoccupied states; this indicates that the O 2p orbitals carry less weight in the expected upper Hubbard band by comparison. All these are consistent with the calculated oxygen PDOS from the calculation of local density approximation (LDA) + U method. In addition, Figure 2C shows the results of resonant inelastic X-ray scattering (RIXS) at the Ni L₃-edge (a core-level 2p to valence 3d transition). The markers A indicate the main absorption peak of LaNiO₂ and NdNiO₂, which resembles the single peak associated with the 2p⁶3d⁹–2p⁵3d¹⁰ transition in cuprates.⁷⁹ The A′ labels highlight the hybridization between the Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ and R 5d orbitals. In this configuration, the Ni state can have a charge transfer to the rare-earth cation, thus leaving holes in Ni orbitals and electrons in R 5d orbitals, this is the so-called self-doping effect. In NdNiO₂, the similar feature caused by the Nd–Ni hybridization is also revealed by RIXS measurements, but its resonance energy A′ almost coincides with the main peak A. Based on above experimental results, one can naturally understand that in parent phase, the singly occupied Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital with strong correlation may give rise to a local spin 1/2 and a Mott insulator state with an AF long-range order. However, the parent compound NdNiO₂ displays metallic behavior at high temperatures (see Figure 1B) and shows no sign of any magnetic long-range order in the whole measured temperature range.^37,38 Similar results have also been found previously in LaNiO₂.⁸⁰ These experimental observations show an obvious contradiction to the naive expectations. It is therefore important to address what is the nature of the parent compounds and how the AF long-range order is suppressed. Zhang et al.⁸¹ made a detailed analysis of resistivity data as functions of temperature for both parent compounds NdNiO₂ and LaNiO₂. When the data are put on a semi-logarithmic scale, they find that the resistivity ρ upturn in the low-temperature region well obey a logarithmic temperature (ln T) dependence below about 40 K down to 4 K for NdNiO₂ and below about 70 K down to 11 K for LaNiO₂. This is supposed to be the evidence of magnetic Kondo scattering, which is further supported by the Hall effect data with the same ln T dependence at low temperatures.^46,80 Considering the existence of self-doping effect and the more itinerant R 5d electrons, a schematic picture is plotted in Figure 2D. The presence of both Kondo singlets and holons can suppress very efficiently the AF long-range order and cause a phase transition from the Mott insulating state to a metallic state. However, we would like to remind that the correlation effect will also induce a low-temperature upturn of resistivity, as that occurring in underdoped cuprates.^82,83 Thus, it remains interesting to unravel whether the Kondo scattering mechanism is the dominant one to interpret this low-temperature upturn of resistivity.

Figure 2.

Mott insulator, self-doping effect, and possible Kondo coupling in nickelates RNiO₂

(A) Sketch of a Mott insulator and a charge transfer insulator. The blue and pink domes stand for the lower and upper Hubbard bands, while the orange one shows the O 2p band, assuming no p-d hybridization.

(B) XES and XAS in the pre-edge region of LaNiO₂, roughly reflecting the occupied and unoccupied oxygen PDOS, respectively.

(C) RIXS intensity map of LaNiO₂ and NdNiO₂. The corresponding XASs are superimposed as a solid black line in each map. The dashed boxes highlight the 0.6 eV features of LaNiO₂ and NdNiO₂ that are associated with the Ni–La and Ni–Nd hybridizations, respectively. Adapted from Hepting et al.⁷⁸

(D) Illustration of the effective model on a two-dimensional square lattice of NiO₂ plane in RNiO₂. The blue ball with an arrow represents the local spin 1/2 on Ni site, which interacts with its neighboring spin by AF coupling J. The yellow ball with an arrow denotes a Nd 5d electron, which couples to Ni spin by the Kondo coupling K, to form a Kondo singlet. Red open circle represents Ni 3d⁸ configuration, or a holon. The t and t∗ are the hopping integrals of Kondo singlet and holon, respectively. Adapted from Zhang et al.⁸¹

Two orbitals, three orbitals, or more

For modeling the realistic electronic structure in the Nd/La 112 system, the first question appears to be how many orbitals should be considered to capture the basic features of both the normal state and the superconducting state. Kitatani et al.⁸⁴ propose that RNiO₂ can be described by one band Hubbard model, albeit with an additional electron reservoir, which is used to calculate the T_c. Hepting et al.⁷⁸ construct a two-orbital model of Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital and an R-$d_{{\mathrm{z}}^2}$ orbital to study the hybridization effects between them. Some researchers propose different types of two-orbital models consisting of two Ni-d orbitals. Hu et al.⁸⁵ include Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ and Ni-d_xy orbitals, while Zhang et al.,⁸⁶ Werner and Hoshino,⁸⁷ and Wan et al.⁸⁸ include Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ and Ni-$d_{{\mathrm{z}}^2}$ orbitals. These types of two-orbital models are aimed to study the competition of high-spin (HS) S = 1 triplet and low-spin (LS) S = 0 singlet when the system is hole doped.⁸⁹ Some other researchers construct three-orbital models. Wu et al.⁹⁰ include Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$, Nd-d_xy, and Nd-$d_{{\mathrm{z}}^2}$ orbitals. This model is further used to calculate the spin susceptibility and robust d-wave pairing symmetry in Nd_1−xSr_xNiO₂. Nomura et al.⁹¹ include Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital, R-$d_{{\mathrm{z}}^2}$ orbital, and a bonding orbital made from interstitial-s orbital in the Nd layer and the Nd 5d_xy orbital, which is used to study the metallic screening effects of the Nd-layer states on the Hubbard U between Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ electrons. Gao et al.⁹² construct a general four-orbital model that consists of two Ni-d orbitals and two R-d orbitals. The model is used to calculate the topological property of the Fermi surface. Jiang et al.⁹³ use a tight-binding model that consists of five Ni-d orbitals and five R-d orbitals to comprehensively study the hybridization effects between Ni-d and R-d orbitals. Jiang et al. also highlight that the f orbital of Nd hybridizes with Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$, which is a non-negligible ingredient for transport and even HTS. Botana et al.,⁹⁴ Lechermann,⁹⁵ and Karp et al.⁹⁶ consider more orbitals (including Nd-d, Ni-d, and O-p states) in the modeling of NdNiO₂ with the influence on the Ni-d orbitals and make a comparison to infinite-layer cuprates. Botana et al.⁹⁴ extract longer-range hopping parameters and the e_g energy splitting. Lechermann⁹⁵ studies hybridization and doping effects. Karp et al.⁹⁶ calculate the phase diagram and estimate the magnetic transition temperature.

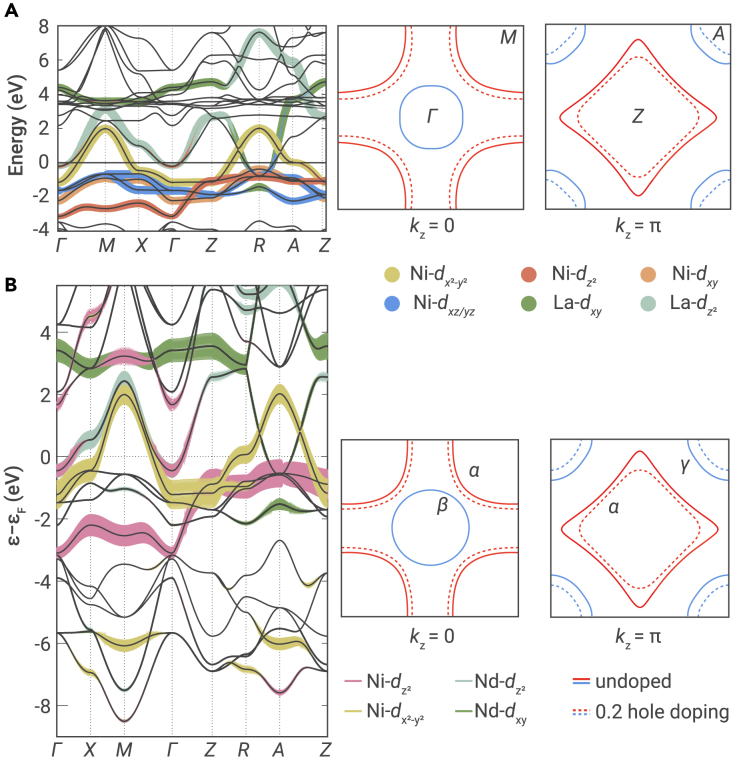
Sakakibara et al.⁹⁷ made the first-principles calculation in LaNiO₂, modeled by seven orbitals constituted by five Ni 3d orbitals ($3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$, $3d_{{\mathrm{z}}^2}$, 3d_xz, 3d_yz, 3d_xy) and two La 5d orbitals (5d_xy, $5d_{{\mathrm{z}}^2}$). Figure 3A shows the band structure based on the first-principles calculations on LaNiO₂, superposed by Wannier-orbital weight. The corresponding Fermi surfaces at k_z = 0 and k_z = π planes are also plotted both for parent phase (solid lines) and 20% hole doping (dashed lines). The main Fermi surface in the system named by α is constructed from Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital, which plays the dominant role in the low-lying energy of the system. It displays a van Hove feature evolving from the k_z = 0 cut to the k_z = π cut with the evolution from a hole pocket around the M point to an electron pocket around the Z point. One can also see two small electron-like pockets, β and γ, around the Γ and A points, which are contributed mainly from La-derived orbitals. These self-doping bands are crucially originated from the hybridization between La 5d and Ni 3d orbitals. More specifically, β pocket around the Γ point has the mixture of La $5d_{{\mathrm{z}}^2}$ and Ni $3d_{{\mathrm{z}}^2}$, while γ pocket around the A point has the mixture of La 5d_xy and Ni 3d_xz/yz. The similar band structure of NdNiO₂ can be obtained in density functional theory (DFT),⁹⁵ as shown in Figure 3B. The DFT calculation⁹⁸ suggests that with hole doping, R 5d band rises up much faster than Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ band. Therefore, at the doping level around 20%, the β pocket has disappeared almost completely, and it leaves a diminished γ pocket around the A point in both compounds.

Figure 3.

Orbital resolved band structures of LaNiO₂ and NdNiO₂ in parent phase and 20% hole doping

(A) Band structure of LaNiO₂ from the first-principles (solid lines). The band structure of the seven-orbital model is superposed, where the Wannier-orbital weight is represented by the thickness of lines with color-coded orbital characters. Adapted from Sakakibara et al.⁹⁷

(B) DFT band structure of NdNiO₂. Adapted from Lechermann et al.⁹⁵ Right panels display cross sections of the Fermi surfaces at k_z = 0 (left) and k_z = π (right), where the red and blue lines depict Ni and La/Nd-dominant Fermi surfaces, respectively. Undoped and 20% hole doped cases are plotted by solid lines and dashed lines, respectively. The Fermi surfaces of La-112 and Nd-112 are adapted from Sakakibara et al.⁹⁷ and Petocchi et al.⁹⁹, respectively.

We want to emphasize that the band structures and Fermi surfaces discussed above are calculated within a weak coupling scenario. It can help us to obtain the noninteracting Fermi surfaces and random phase approximation (RPA) spin susceptibility. We need also notice that the parent phase RNiO₂ starts with the description of self-doping Hubbard-Mott insulator, which should be naturally categorized into a strong coupling limit. Therefore, it becomes necessary to calculate the more correlated electronic structures within the scheme of LDA + U, in which the strength of interaction is mainly determined by the value of Hubbard U. Many theoretical papers have put forward that the multiorbital picture in RNiO₂ is not only depicted based on the localized Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ and R-dominated self-doping bands, but also the Ni $3d_{{\mathrm{z}}^2}$ band in a Hund-assisted manner, so U is defined as the on-site Hubbard interaction of Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}/3d_{{\mathrm{z}}^2}$ orbitals. Lechermann⁹⁵ pioneers the doping-dependent competition between Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ versus Ni $3d_{{\mathrm{z}}^2}$ and first describes the flat band feature of Ni $3d_{{\mathrm{z}}^2}$ states at the Fermi level with hole doping. In the large-U limit (larger than 10 eV), such a model at a quarter filling by holes (three-electron filling) is expected to exhibit a Mott insulator for the Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ band. Because the self-doped character remains robust up to large interaction strengths, the nickelate compound avoids an insulating state for even larger U = 15 eV. Compared to the LDA result in the undoped case, the size of the electron pocket around A is reduced, but the many-body calculation intensifies the stronger Ni $3d_{{\mathrm{z}}^2}$/Nd $5d_{{\mathrm{z}}^2}$ hybridized electron pocket around Γ. At about 0.2 hole doping, the role of the self-doping band is depleted already. Therefore, Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ and $3d_{{\mathrm{z}}^2}$ compete at energies close to the Fermi level, and the spectral weight close to ε_F is strongly Ni-e_g orbitals dominated.

To conclude, for the mother compound, a small number of holes are self-doped into the Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital because of the presence of electron pockets. These electron pockets may have relevance to the metallic behavior observed experimentally, while the electronic state of the $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ band with a hole self-doping may be close to that of the heavily underdoped cuprates with no magnetism or superconductivity.100, 101, 102, 103 Furthermore, the superconductivity in thin films of Nd_1−xSr_xNiO₂ may share some similarities like that of the single-orbital cuprates, while more distinctions are expectable, providing a new fascinating platform on the research of unconventional correlated superconducting materials.

Transport measurements and phase diagram

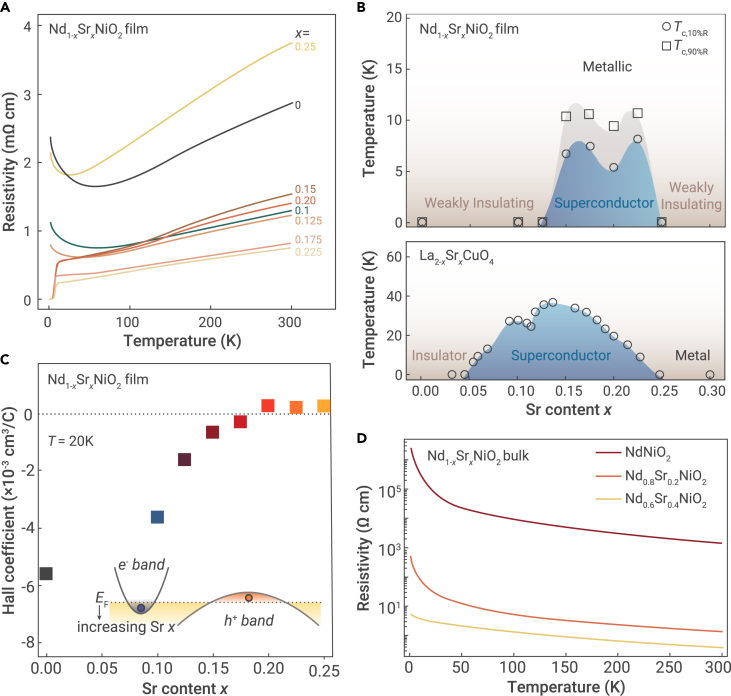
Considering the difficulty in synthesizing the high-quality superconducting nickelate thin films, we just make a brief review on the transport data and the related phase diagram. Li et al.¹⁰⁴ have made a detailed study on resistivity and Hall effect measurements on the typical system of infinite-layer Nd_1−xSr_xNiO₂. Figure 4A displays the temperature-dependent in-plane resistivity ρ_xx across the doping series. The films with x = 0.15, 0.175, 0.2, and 0.225 show varying T_c, while for x = 0, 0.1, 0.125, and 0.25, a weakly insulating feature emerges at low temperatures, as shown in the upper panel of Figure 4B. These data indicate a superconducting dome that is similar to hole-doped cuprates^105,106 in the lower panel, but approximately half as wide in the doping regime. Furthermore, an approximately linear T dependence of ρ_xx is observed across a wide temperature range above T_c, similar to that found in cuprates (known as the “strange metal” phase107, 108, 109) and other strongly correlated systems, suggesting a similar possible origin for ρ_xx(T) despite different underlying electronic structures.¹¹⁰ As for the noticeable upturn in ρ_xx(T) for nonsuperconducting compositions (x = 0, 0.1, 0.125, and 0.25), it is not simply identified as weak localization. Also, the lack of strongly insulating behavior has already been widely reported for the undoped compounds.⁴⁶ It can be possibly attributed to the self-doping bands and Kondo effect. They further find that the “overdoped” regime does not appear to approach the Fermi liquid ending point commonly understood in the hole-doped cuprates.111, 112, 113, 114 Overall, the relevance of “hole doping” remains an open question for Nd_1−xSr_xNiO₂. They also measure the evolution of the normal state Hall effect in this series of samples. Figure 4C shows that R_H(20 K) monotonically increases from negative to positive values, crossing zero between x = 0.175 and 0.2. While in La_2−xSr_xCuO₄, R_H was found to be large and positive in the undoped case and as systematically varied as ∼1/x with initial doping.^105,115 The distinctive doping dependence of R_H in the nickelates is clearly inconsistent with single-band hole doping. A simple explanation that can be considered is a two-band model with both electron-like and hole-like Fermi surfaces. With increasing hole doping, a predominantly electron-like Hall effect will undergo a transition to a hole-like one, followed by the reduced Fermi level. This two-band picture is well corroborated by many recent electronic structure calculations, which are discussed in detail in the former section. The general consensus is that band structures for NdNiO₂ is the presence of a large hole pocket with Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ character near the k_z = 0 cut, and two-electron pockets with the dominant characters of Nd $5d_{{\mathrm{z}}^2}$ and 5d_xy orbitals near Γ(0,0,0) and A(π,π,π), respectively.

Figure 4.

Transport measurements and the related phase diagram

(A) Temperature-dependent resistivity (2–300 K) measured for representative samples with different doping levels.

(B) Top: phase diagram of Nd_1−xSr_xNiO₂. Open circles (squares) represent T_c of 10% R (T_c of 90% R), as defined to be the temperatures at which the resistivity is 10% (90%) of the one at 20 K. Bottom: phase diagram of La_2−xSr_xCuO₄.

(C) Hall coefficient as a function of x at 20 K, crossing zero between x = 0.175 and 0.2. The inset displays a two-band schematic (electron pocket, e⁻ band; hole pocket, h⁺ band). The arrow indicates the downward shift of the Fermi level E_F with increasing x. Adapted from Li et al.¹⁰⁴

(D) Temperature dependence of resistivity for Nd_1−xSr_xNiO₂ (x = 0, 0.2, 0.4) bulk samples. Adapted from Li et al.¹¹⁶

In addition, it should be noted that bulk samples with the same Nd-112 structure and proper Sr-doping, as well as Sm_0.8Sr_0.2NiO₂, have been made by some of us,^116,117 but no superconductivity was observed, as shown in Figure 4D. The absence of superconductivity in bulk samples has recently been repeated by another group.¹¹⁸ In addition, the bulk samples of Nd_1−xSr_xNiO₂ exhibit very strong insulator-like behavior even under a pressure up to 50.2 GPa. It was argued that the absence of superconductivity in bulk samples may be induced by the deficiency of Ni or caused by the significant influence of physical properties by the subtle change of the structure and doping level between the bulk and film samples. The Ni deficiency can either strongly lower down the hole doping or act as strong scattering centers that localize the mobile electrons and thus diminish superconductivity. It seems to be physically unreasonable of attributing the absence of superconductivity in bulk samples to intercalating extra hydrogen,¹¹⁹ because both the superconducting thin films and the bulk samples are treated with CaH₂ in exactly the same way. Furthermore, we also successfully synthesize 112 phase using a non-hydrogen reducing medium zirconium and find that although the 112 phase has a better crystallinity, the insulating behavior seems to be even stronger, and superconductivity remains absent. Despite a lot of challenges, it is still worth making more efforts to figure out the unsettled issue.

Spin configurations and magnetic excitations

As we know, the parent phase of cuprates is depicted as a charge transfer insulator with an AF order,120, 121, 122, 123 where the Cu²⁺ ions have one active $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital hybridized with the p orbitals of the neighboring in-plane oxygens.^124,125 Upon hole doping, because of the negative charge-transfer gap, the holes predominantly go to the O-p orbitals. Thus, it will give rise to the spin configuration of 3d⁹ Cu²⁺, surrounded by a ligand hole on oxygen. This is the formation of Zhang-Rice singlets.⁶² In inelastic neuron-scattering measurements, a square-shaped continuum of excitations peaked at incommensurate positions, and an “hourglass” shape of the magnetic dispersions in the superconducting state of cuprates has been extensively observed.126, 127, 128, 129 These excitations are regarded as a general property of cuprates and a promising candidate for magnetically mediated electron pairing. Moreover, when revisiting the phase diagrams of temperature versus doping level both in cuprates and FeSC, we can find that the occurrence of superconductivity is intimately correlated with the disappearance of AF long-range order and the occurrence of AF spin fluctuations.¹³⁰ As a result, it may lead to the unconventional pairing state of d wave in cuprates¹³¹ and s^± in FeSC.¹³² Accordingly, it is highly desirable to address the spin configurations and magnetic excitations in nickel-based superconductors.

Competition between HS and LS states

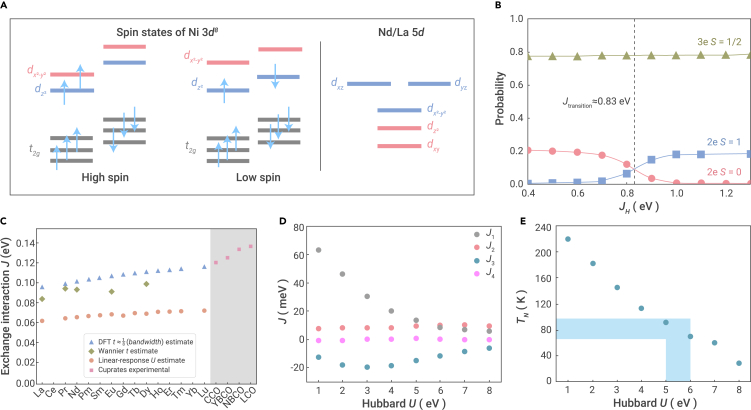
Because the charge-transfer energy is much larger in the nickelates, one may expect the doped holes to reside dominantly on the Ni site, rather than in the O-p band. Moreover, many theoretical papers have proposed that the two orbitals of Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}/3d_{{\mathrm{z}}^2}$ are essential for the multiorbital process in the nickelate system because of Hund’s coupling. For example, Werner and Hoshino⁸⁷ use dynamical mean field theory (DMFT) calculations for the two-orbital Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}/3d_{{\mathrm{z}}^2}$ system and argue that a multiorbital description of nickelate superconductors is warranted. Lechermann^95,133 pioneers the doping-dependent competition between Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ versus Ni $3d_{{\mathrm{z}}^2}$ orbitals. Accordingly, in a square lattice environment as depicted in Figure 5A, the e_g states of Ni²⁺ may be energetically arranged in two different ways, which depends on the limit whether the Hund’s rule coupling is larger than the crystal-field splitting between the two e_g orbitals. For the high-spin (HS) state, the electron from the $d_{{\mathrm{z}}^2}$ orbital is removed, in which case the resultant configuration is ${\left(t_{2\mathrm{g}}\right)}^6{\left(d_{{\mathrm{z}}^2}\right)}^1{\left(d_{{\mathrm{x}}^2-{\mathrm{y}}^2}\right)}^1$, with S = 1; for the low-spin (LS) state, the electron from the $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital is removed, in which case the configuration is ${\left(t_{2\mathrm{g}}\right)}^6{\left(d_{{\mathrm{z}}^2}\right)}^2$, with S = 0.

Figure 5.

Spin configurations and possible AF state

(A) Left panel: spin configurations of Ni 3d⁸ in a square-planar environment. High-spin state with S = 1 and low-spin state with S = 0. Right panel: crystal field splitting on Nd.

(B) Calculated probabilities for the three-electron S = 1/2, two-electron S = 0 and 1 states as a function of Hund’s coupling J_H. Adapted from Wan et al.⁸⁸

(C) Exchange interaction of RNiO₂ calculated by 4t²/U, based on different schemes of theoretical methods DFT, Wannier, and linear response theory, compared with the cuprate exchange interactions that are taken from some experimental results. Adapted from Been et al.¹³⁴

(D) The Hubbard U dependent of exchange coupling parameters.

(E) The estimated T_N. Adapted from Liu et al.¹³⁵

Concerning that the Ni²⁺ ions are commonly found to be spin-triplet state in most of the nickel compounds, it has recently been argued in several theoretical works^99,133 that hole-doping Nd_1−xSr_xNiO₂ should produce Ni²⁺ with spin S = 1. Based on the HS state, Zhang et al.⁸⁶ propose a variant of t-J model and find two distinct mechanisms for d-wave superconductivity. However, as early as in 1959, Ballhausen and Liehr¹³⁶ have discussed the S = 0 spin singlet state in the planar Ni(II) complexes based on the theory of ligand field. Recently, Jiang et al.¹³⁷ first point out that the S = 1 state may be incompatible with robust superconductivity, and a number of many-body calculations using LDA and DMFT pointed to the formation of intraorbital singlets.^95,96 Krishna et al.¹³⁸ find that from the first-principles calculations of explicit Sr doping in RNiO₂ (R = La, Nd) supercells, an LS state is favored. From experimental measurements, Rossi et al.¹³⁹ use a combination of high-resolution XAS and RIXS, and find that doped holes are primarily introduced in the Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ Hubbard band in a LS configuration. Wan et al.⁸⁸ discuss the solutions of an effective two-band model, including Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}/3d_{{\mathrm{z}}^2}$ orbitals on the basis of DMFT. As shown in Figure 5B, whether an S = 0 or 1 state emerges depends on a precise value of the intra-atomic Hund’s coupling J_H in the vicinity of its commonly accepted range of values 0.5–1 eV. Until now, we cannot make a definite conclusion about whether the S = 0 or 1 scenario is realized for doped nickelates. The key issue is the competition between Hund’s coupling and the crystal field splitting. Because of the considerable hybridizations between the itinerant Nd 5d and Ni 3d orbitals, the values of J_H and crystal field splitting based on DFT simulations may be questionable. Therefore, the spin state of Ni²⁺ in hole-doping Nd_1−xSr_xNiO₂ remains highly debatable and worthy of more attention.

AF magnetic excitation

Most intriguingly, one key experimental observation for the infinite-layer NdNiO₂ is that its resistivity exhibits a minimum at about 70 K and an upturn at a lower temperature. Meanwhile, the Hall coefficient drops toward a larger value, signaling the loss of charge carriers. More interestingly, no long-range magnetic order has been observed in powder neutron diffraction on LaNiO₂ and NdNiO₂ when temperature is lowered down to 5 and 1.7 K, respectively.^37,38,80 This greatly challenges the existing theories, because it is generally believed that magnetism is essential for the emergence of unconventional superconductivity. Therefore, it is highly desirable to study the magnetic properties of undoped parent NdNiO₂ and elucidate its experimental indications.

In theoretical aspects, there are still some debates on the estimation of exchange coupling strength J in nickelates; some theories suggest J to be one order of magnitude smaller than in cuprates because of the large charge transfer energy,^135,137 whereas some others argue it could be comparable to that in cuprates.^88,134,140 Been et al.¹³⁴ calculate the exchange interaction J = 4t²/U in RNiO₂ based on the different schemes of theoretical methods, as shown in Figure 5C. They conclude that the magnitude and nature of the superexchange interactions in the nickelate are predicted to be similar to the spin-spin interactions in the cuprates. Liu et al.¹³⁵ present a first-principles calculation for the electronic and magnetic structure of undoped parent NdNiO₂. By taking relevant interaction strength found experimentally into account, they find that the AF order with (π, π, π) vector in NdNiO₂ is a compensated bad metal with small Fermi pockets. The calculated exchange coupling parameters as a function of Hubbard U are shown in Figure 5D. The main finding is that the estimated magnetic exchange interaction is around J₁ ∼ 10 meV, J₂ ∼ 10 meV. This indicates that effective exchange interactions in NdNiO₂ are about one order of magnitude smaller than those of cuprates ∼112 meV.141, 142, 143 Also, it results in a relatively weaker magnetic ordering and lower Néel temperature, T_N, in NdNiO₂ compared with cuprates. Furthermore, the infinite-layer nickelate is believed to be a worse metal compared to elemental nickel with Hubbard U about 3 eV,¹⁴⁴ which can be considered as a lower boundary of U. The Coulomb interaction in infinite-layer nickelates should be smaller than that in the charge-transfer insulator NiO with U about 8 eV,¹⁴⁵ which can be considered as an upper boundary of U. Therefore, a reasonable value of U in NdNiO₂ can be estimated around 5–6 eV. As shown in Figure 5E, there could exist a transition from normal metal to bad AFM metal around T_N ∼ 70–90 K, which provides a plausible understanding of minimum of resistivity and drop of Hall coefficient in infinite-layer NdNiO₂.

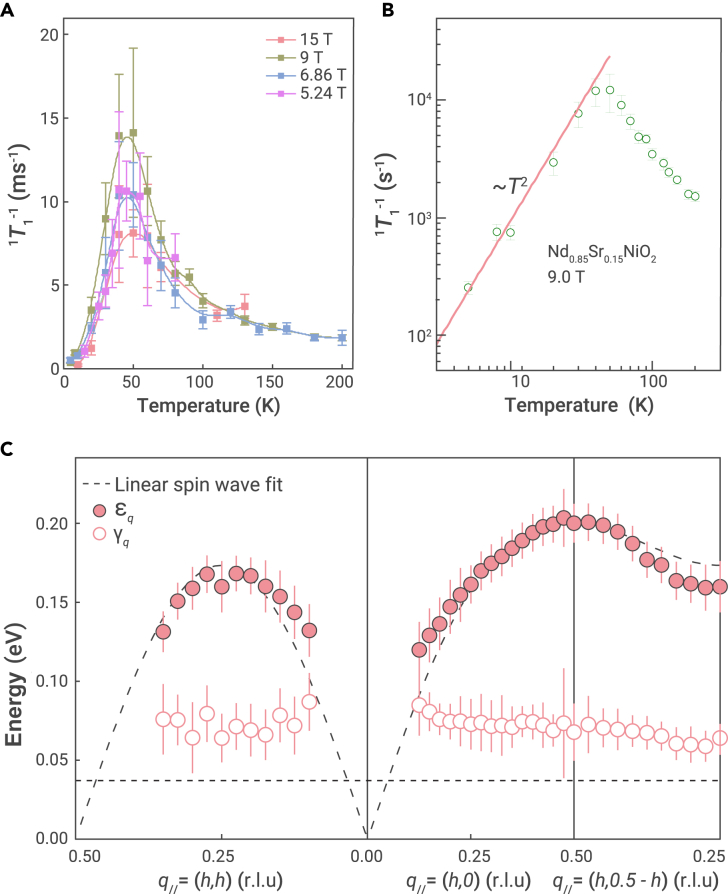
From experimental aspects, Cui et al.¹⁴⁶ report the ¹H nuclear magnetic resonance (NMR) measurements on powdered Nd_0.85Sr_0.15NiO₂ samples by taking advantage of the enriched proton concentration after hydrogen annealing. The spin-lattice relaxation rate T₁⁻¹ is a sensitive probe of low-energy spin fluctuations.^147,148 The temperature-dependent ¹T₁⁻¹ under various fields is plotted in Figure 6A. From 2 K, the ¹T₁⁻¹ first increases dramatically, then forms a peaked feature at T ∼ 40 K, and finally flattens out at temperatures above 100 K. A sharp peak in ¹T₁⁻¹ is usually a signature of magnetic phase transition, while the broad one at about 40 K suggests the onset of a short-range glassy AF order in bulk Nd_0.85Sr_0.15NiO₂, which is similar to underdoped cuprate superconductor.¹⁴⁹ Furthermore, the plot of a log-log scale is shown in Figure 6B. Below 40 K, ¹T₁⁻¹ ∝ T^α, following a power-law behavior with a low-power-law exponent α = 2, much smaller than that caused by AF spin-wave excitations (α = 5).¹⁵⁰ This indicates the onset of low-energy spin fluctuations and remaining spin excitations extending to much higher temperatures. The finding of strong AF fluctuations reveals the strong electron correlations in bulk Nd_0.85Sr_0.15NiO₂ and paves the way for understanding the relationship between magnetism and superconductivity in nickelates. Lu et al.¹⁵¹ measure the dispersion of magnetic excitations in undoped NdNiO₂ by using RIXS at the Ni L₃-edge. Figure 6C plots a summary of fitted magnetic mode energy ε (filled red circles) and damping factor γ (empty red circles) versus in-plane momentum transfers q_// along high-symmetry directions. NdNiO₂ possesses a branch of dispersive excitations with a bandwidth of approximately 200 meV, which can be fitted to the linear spin wave theory of a 2D AF Heisenberg model with J₁ ∼ 63.6 meV, J₂ ∼ −10.3 meV. These results can clarify that the exchange interaction in NdNiO₂ is comparable to that in cuprates. Besides, the significant damping and rather constant γ_q of these modes indicates that rare-earth itinerant electrons play a role here, which are highly coupled to Ni-3d orbitals.

Figure 6.

Magnetic excitations

(A) Temperature-dependent ¹T₁⁻¹ of Nd_0.85Sr_0.15NiO₂ under different magnetic fields.

(B) Temperature-dependent ¹T₁⁻¹ is plotted in a log-log scale, with a fitting of low-temperature data to ¹T₁⁻¹ ∝ T². Adapted from Cui et al.¹⁴⁶

(C) Dispersion of magnetic excitations in NdNiO₂ and fitted to the linear spin wave theory. Magnetic mode energy ε is denoted by filled red circles and damping factor γ is denoted by empty red circles versus projected in-plane momentum transfers q_// along high-symmetry directions. Adapted from Lu et al.¹⁵¹

To reconcile the discrepancy between the observed paramagnetic metallic state (only the remaining AF excitations) of RNiO₂ and the measured considerable exchange interaction J, along with the theoretically predicted AF transition nearby 90 K, one fact that needs to be noticed is that the estimation of T_N in Figure 5E has not taken the influence of conduction electrons into account. As Gu et al.¹⁵² point out, the hybridization between Ni-$d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital and itinerant electrons in RNiO₂ is substantially stronger than previously thought. Because of that, Ni local moment is screened by itinerant electrons, and the critical U_Ni for long-range magnetic ordering is increased. As a result, the local magnetic AF ordering below the T_N should be very weak, which may be hard to be visualized in the magnetic related measurements, such as NMR and neutron scattering. Instead, only the remaining AF fluctuations can be detected.

Superconducting state

The foregoing sections are mainly focused on the electronic structures and magnetic excitations of normal state in RNiO₂, now we will turn to discussing the superconducting properties of this newly discovered superconducting nickelate Nd_1−xSr_xNiO₂ thin film, including upper critical field, superconducting gap, and possible pairing symmetries.

Isotropic Pauli-limited pairing state

As we know, in most superconductors,¹⁵³ the superconducting gap (Δ) and the pairing strength may be linked to the upper critical field H_c2 via the Pippard relation, ξ = ℏv_F/πΔ and μ₀H_c2 = Φ₀/2πξ² (orbital de-pairing), where ξ is the coherence length, v_F is the Fermi velocity, and Φ₀ is the flux quantum. However, in a few superconductors, Cooper pairs can be broken mainly because of the Zeeman-split effect,¹⁵⁴ and thus the upper critical field is dominated by Pauli paramagnetic limit μ₀H_P = √2Δ/gμ_B. Here, μ_B is the Bohr magneton, and g is the Landé factor. Therefore, it is worthy to measure the upper critical field to obtain the information of the pairing strength for this new superconducting system. More generally, the Nd_1−xSr_xNiO₂ system can be regarded as layered superconductor, in which case one may naturally wonder whether there is some anisotropy in Γ = H_c2||/H_c2⊥, where H_c2|| and H_c2⊥ represent the upper critical fields when it is along the ab plane and the crystal c axis direction, respectively. The case for the nickelates is a priori interesting: although it shares the same crystal structure as the infinite-layer cuprates, calculations indicate that both a quasi-2D hole band and three-dimensional (3D) electron bands are present in the nickelates for a broad range of electron interactions.^64,94 The relative importance of these bands is a subject of much interest with respect to the superconducting state. Moreover, the reported Nd_1−xSr_xNiO₂ thin film can be synthesized as thin as only about 5 nm,¹⁵⁵ thus providing a new system to explore long-standing debates on the role of dimensionality for superconductivity.

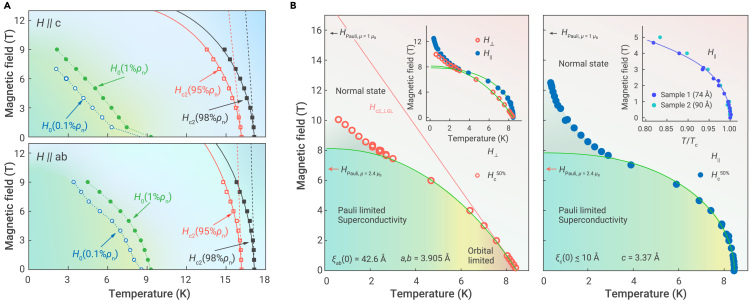
Xiang et al.¹⁵⁶ extract H_c2||(T) and H_c2⊥(T) from ρ(T) curves under different magnetic fields on Nd_0.8Sr_0.2NiO₂ thin films by using two different criteria of 95% ρ_n(T) and 98% ρ_n(T), where ρ_n(T) is the linear extrapolation of the normal-state resistivity. Because the normal-state residual resistivity is large for this film, they attempt to use the Werthamer, Helfand, and Hohenberg (WHH) theory¹⁵⁴ in the dirty limit for a superconductor with a single s-wave gap to fit the data, as shown in Figure 7A. They achieve several interesting experimental observations. First, the Maki parameter α ranges from 13 to 42, when the magnetic field is applied within ab plane or along c axis and under different criteria. The obtained very large α here is very rare, even much larger than that in the most well-known Pauli-limited systems, such as heavy-fermion and organic superconductors.157, 158, 159, 160, 161, 162, 163 Meanwhile, a very large value of α indicates the possible existence of the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state in the high-magnetic-field region at low temperatures.164, 165, 166 Because the FFLO state is fragile in the presence of disorders,^160,167 the existence of this state in the Nd_1−xSr_xNiO₂ thin film requires further investigation via high-magnetic-field experiments. Second, the value of Γ approaches to 1 when the temperature is well below T_c, namely, the very small anisotropy between ξ_ab and ξ_c (equivalent to the effective mass ratio of m_c^1/2/m_ab^1/2). This provides strong evidence that the existence of two 3D electron pockets makes the electronic structures more isotropic, when compared to the only one single band of quasi 2D Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$. Third, H₀(T) values are determined using the criteria 0.1% ρ_n(T) and 1% ρ_n(T), in order to extract the irreversibility field of the thin film.

Figure 7.

Upper critical field and Pauli-limited superconductivity

(A) Superconducting phase diagram H(T). Symbols used here denote the temperature-dependent μ₀H_c2 and μ₀H₀ obtained from ρ-T curves, measured at different magnetic fields. The solid (dashed) lines show the fitting results (theoretical curves) obtained from the WHH theory. Adapted from Xiang et al.¹⁵⁶

(B) Superconducting H_c2-T phase diagrams for magnetic fields along the c axis and in the ab plane. The regions above H_c2 (open and filled circles) are shaded orange, representing the normal state, while the regions under H_c2 are shaded as a transition from red regions near T_c to green regions near 0 K, representing a transition from superconductivity limited by orbital de-pairing to Pauli-limited superconductivity. The solid green lines are WHH fits of the H_c2 data above the low-temperature upturn. Adapted from Wang et al.¹⁶⁸

Wang et al.¹⁶⁸ have conducted similar measurements to probe the anisotropy in Nd_0.775Sr_0.225NiO₂ with a slightly lower T_c. Figure 7B plots superconducting H_c2-T phase diagrams for magnetic fields along the c axis and in the ab plane, including many intriguing phenomena. First, the key observation is a T-linear dependence of H_c2⊥ and a (T_c − T)^1/2 dependence of H_c2||. First of all, they rule out the possibility of 2D superconductivity. The main reason is that they deduce a thickness to be 2.3–3 times larger than the observed one, if adopting the linearized Ginzburg–Landau model of 2D superconductor.¹⁶⁹ Another plausible origin is that a Pauli-limited superconductor can also give a (T_c − T)^1/2 dependence of H_c2||.170, 171, 172 Second, high values of Maki parameter α for both orientations are obtained, which indicates the presence of the paramagnetic pairing breaking effect. Third, the phase diagram shows a crossover from superconductivity limited by orbital pair-breaking to Pauli-limited one. The upturn of H_c2(T) deviates from the WHH fits, suggesting an increasing role of the paramagnetic effect at the low-temperature region. This anomalous feature may also indicate the occurrence of two-band superconductivity.¹⁷³ The high values of α suggests possible existence of FFLO state at low temperatures and high magnetic fields, which seems to be consistent with the upturn of H_c2 data below 4 K. However, the fact that the film lies in the dirty limit is inconsistent with anticipated expectations.

To draw a conclusion about the magnetotransport measurements of the two works above, they both point out the isotropic Pauli-limited superconductivity with unconventional pairing in the newly found nickelate superconducting film. This provides strong evidence that two small 3D electron-like pockets β and γ contributed mainly from Nd-derived orbitals to play a non-negligible role here. In addition, a very large value of Maki parameter α indicates possible existence of the very interesting FFLO state in the high-magnetic-field region at low temperatures under the condition that the system can be pushed into a clean limit.¹⁶⁰

Single-particle tunneling spectrum measurement

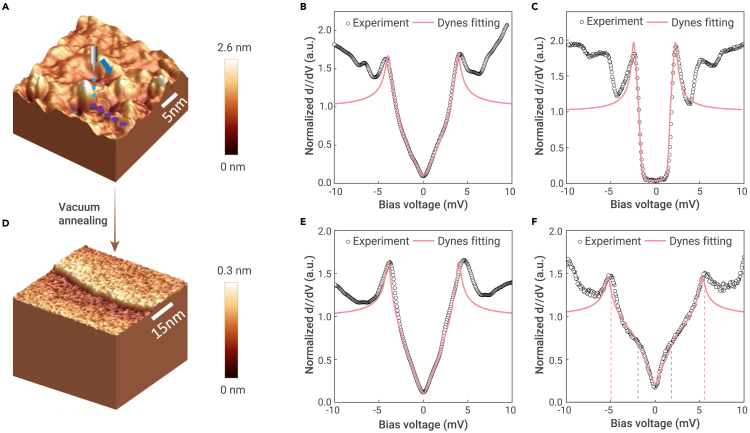
Concerning the pairing mechanism of nickel-based 112 systems, the core issue is to know the superconducting gap function that measures the pairing interaction of the two electrons of a Cooper pair. However, the research is very rare on physical properties of this material, especially for angle-resolved photoemission spectroscopy (ARPES) and scanning tunneling microscopy (STM) measurements. Thus, it is urgent to conduct spectroscopic measurements to directly determine the gap structure. In this section, we introduce the first investigation of single-particle tunneling measurements on the superconducting Nd_1−xSr_xNiO₂ thin films.¹⁷⁴ Figure 8A shows the surface of the film just after annealing by the soft-chemistry method. One can see that the surface is not atomically flat, showing a roughness of about 1–2 nm. This large roughness may be induced by a drastic reaction of the 113 film with hydrogen during the post-annealing process. However, if we take a long time vacuum annealing (at about 180°C in a vacuum of 10⁻⁹ torr for 12 h) on the film with this type of rough surface, some areas of the surface show layer-by-layer structure with terraces, and a typical surface morphology is shown in Figure 8D. Now the roughness becomes much smaller, in which case the tip can have a better stability during the tunneling process. We have conducted measurements of scanning tunneling spectroscopy (STS) on the surfaces with these two different morphologies, one is called rough surface and another one is called smooth surface. We find that the superconducting spectra predominantly show two types of features on the rough surfaces. One type shows a typical V-shape feature, which is shown in Figure 8B. By doing the Dynes model fitting,^175,176 as displayed by the red curve, we find that the spectrum can be nicely fitted with a d-wave gap of Δ = 3.9cos2θ (meV). The other one shows a full gap feature plotted in Figure 8C, with a Dynes fitting of Δ = 2.35(0.85 + 0.15cos4θ) (meV). A slight anisotropy (about 15% weight of the differential conductivity) is added to the gap function in order to have a good fit. This may suggest that at least one of the bands is fully gapped. On the smooth surface, we find dominant V-shape spectra as shown in Figure 8E. It needs to be emphasized that this type of full gap is hardly observed on the smooth surface. Instead, we can easily observe a mixture of the two-gap features on the spectra, as shown in Figure 8F. The Dynes fitting is Δ₁ = 5.3(0.8cos2θ+0.2cos6θ) (meV), taking a dominant weight of p₁ = 85% and Δ₂ = 2 meV.

Figure 8.

STM measurement of topography and tunneling spectra on Nd_1−xSr_xNiO₂ film

(A) 3D illustration of the topographic image after topotactic reaction method; one can see the surface roughness about 1–2 nm.

(B) A tunneling spectrum with a V-shape, which is measured on the rough surface. The Dynes model fitting yields a gap function Δ = 3.9cos2θ (meV).

(C) A tunneling spectrum with full gap feature, which is measured on the rough surface. The Dynes model fitting is Δ = 2.35(0.85 + 0.15cos4θ) (meV).

(D) 3D illustration of the topographic image after a long-time vacuum annealing. The roughness becomes much smaller. We can see a clear step with the height about 0.17 nm, being consistent with half of the unit cell height.

(E) A typical V-shape spectrum measured on the smooth surface. A gap function Δ = 3.95(0.95cos2θ + 0.05cos6θ) (meV) is used in the fitting.

(F) A mixture of the two-gap features on the spectrum is measured on the smooth surface. Dynes fitting results, Δ₁ = 5.3(0.8cos2θ + 0.2cos6θ) (meV), Δ₂ = 2 meV, p₁ = 85%, and p₂ = 15%. Adapted from Gu et al.¹⁷⁴

Furthermore, one can note that the topographic image in Figure 8A shows strong roughness, which provides the possibility for the STM tip to detect tunneling behavior along different directions at different positions. This may give us the advantage to detect the superconducting gap features derived from different bands, which could be the reason for us to see two distinct gap structures at different positions.^177,178 The same situation occurs in the STM measurements of MgB₂ bulk and film.¹⁷⁹ The STM tip can detect the gap with a magnitude of about 7.1 meV on the σ-band on some grains and can also measure the gap on the π-band with the value of 2.3 meV on other grains. However, as mentioned above, on the smooth surface, it is hard to observe a “clean” full gap feature. Most times the spectrum shows a mixture of the two, and a robust V-shape feature appears near zero bias. This may be understood in the way that, now the tunneling current mainly goes along c axis direction, with a reduced side tunneling component that would occur in the measurements on the rough surface at some locations. Based on the above discussion and the multiband features in Nd_1−xSr_xNiO₂, one may naturally conclude that the two kind of features on the measured spectra correspond to the gaps on different Fermi surfaces.

Robust d-wave pairing and possible explanations for full gap

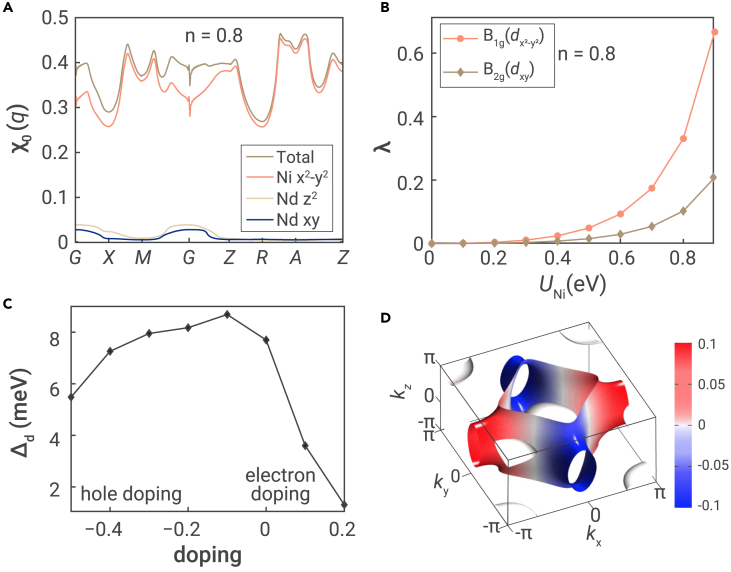
Considering the common feature of V-shape spectra measured on superconducting thin films, we first discuss the possibility of a d-wave gap. It has been extensively demonstrated in many theoretical papers that the Nd_1−xSr_xNiO₂ system has a robust d-wave pairing, in both limits using a weak-coupling approach of RPA and strong coupling of the t-J model. Wu et al.⁹⁰ find that, in all instances, the dominant pairing tendency is in the $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ channel. In analogy with cuprates,^12,131 pnictides,^27,132 and heavy-fermion superconductors,^180,181 superconductivity in the present compound is assumed to be mediated by spin fluctuation. Based on the multiorbital fluctuation exchange approximation, the effective pair interaction vertex Γ(k,k’) is determined by RPA susceptibility. By solving the dimensionless pairing strength functional, the largest pairing eigenvalue λ will lead to the highest transition temperature, and its eigenfunction determines the symmetry of the gap.182, 183, 184 Figure 9A displays the bare susceptibilities for n = 0.8 filling. The dominant peaks locate around the M and A points, indicating intrinsic AF fluctuations. The prominent features in the orbital-resolved susceptibility are that the peaks around M and A are mainly attributed to the Ni $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital, which will further promote the dominant $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$-wave pairing state. As the effective low-energy interaction parameters remain undetermined for Nd_1−xSr_xNiO₂, a large region of parameter space has been calculated within RPA calculations. The obtained pairing eigenvalues as a function of interaction strength U_Ni for n = 0.8 are displayed in Figure 9B. One can find that the $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ pairing state is dominant over other competing ones, for example, for d_xy state. This is consistent with the fact that both the dominant density of states and pairing interactions reside on the Ni $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital.

Figure 9.

Robust d-wave pairing

(A) Bare susceptibility for n = 0.8.

(B) The pairing eigenvalues as a function of the interaction U_Ni for n = 0.8.

(C) The $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$-wave gap as a function doping with J₁ = J₂ = 0.1 eV. Positive (negative) values relate to electron (hole) doping.

(D) 3D illustration of $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$-wave gap. Adapted from Wu et al.⁹⁰

The nickelate system seems to belong to the intermediate coupling one; it thus becomes important to resolve the pairing mechanism. From a strong-coupling perspective, concerning the nickelate system, the t-J model can be reduced to one single Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital for simplicity. Wu et al.⁹⁰ investigate the pairing state for an extended range of doping levels. Figure 9C plots the representative superconducting gap of the $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ pairing versus different dopings. It shows that there is a superconducting dome, and the gap reaches the maximum at a doping of 0.1 hole/Ni. Moreover, the 3D gap function of the obtained $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$-wave pairing is displayed in Figure 9D at 0.2 hole doping, without considering the contribution of Nd orbitals. The main findings from a t-J model analysis are consistent with the RPA analysis.

Now it can be understood that the measured V-shape spectra that featured a d-wave gap mainly originated from the Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital; meanwhile, several theoretical assumptions are proposed to explain the observed full gap. The first picture is that this full gap may just simply reflect the gap function on the hybridized orbitals of the Ni $3d_{{\mathrm{z}}^2}$, 3d_xz,yz mixed with the Nd $5d_{{\mathrm{z}}^2}$, 5d_xy, namely, on the β and γ Fermi pockets. However, if we just simply follow the $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ notation for the gaps in the whole momentum space, the nodal line will cut the two electron pockets, which is not consistent with our observation of a full gap. Theoretically, Adhikary et al.¹⁸⁵ propose a two-orbital model consisting of Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ and an axial orbital that is constructed out of Nd 5d, Ni $3d_{{\mathrm{z}}^2}$, and Ni s characters. Considering the crucial role of the interorbital Hubbard interaction in superconductivity, it turns out to be orbital selective electron pairing in Nd_1−xSr_xNiO₂. Furthermore, Bandyopadhyay et al.¹⁸⁶ point out that the f-orbital of R element has an important role in the electronic structure of RNiO₂. The f-orbital can pull down the d-orbital to the Fermi level in Nd- and Pr-based nickelates compared with in the La-one. This difference shows up in computed doping-dependent superconducting properties of the three compounds within a weak coupling theory, which finds two-gap superconductivity for NdNiO₂ and PrNiO₂ and the possibility of a single-gap superconductivity for LaNiO₂.

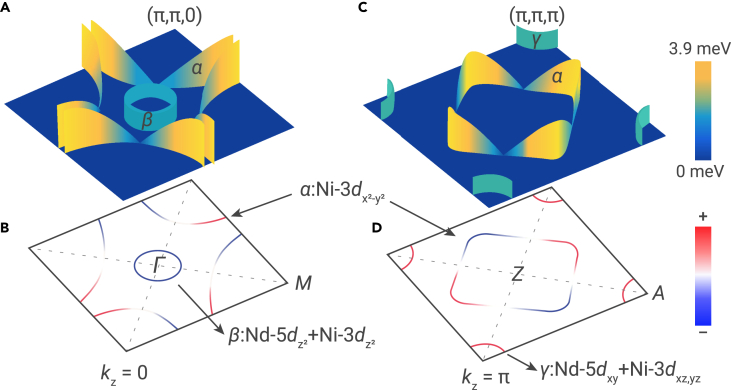
Based on the proposal of the orbital selective pairing, we can plot a cartoon picture for the Fermi surfaces and the gap structure on different cuts of k_z in the weak coupling scenario, as depicted in Figure 10. Concerning the interorbital Hubbard interaction between different orbitals, we expect not only a d-wave gap on the α pocket but also full gaps on the β and γ ones with opposite gap signs. The latter is a bit like the s^± pairing in many pnictides. This scenario is quite interesting and tells that not only the intra-pocket interaction but also the inter-pocket interaction plays an important role here, leading to the orbital selective pairing. The second one to interpret this full gap relies on a recent theoretical calculation about the doping-dependent phase evolutions of the pairing symmetries.¹⁸⁷ This phase diagram is established based on the proposed picture of self-doped Mott insulator,⁸¹ which shows an evolution from a d-wave dominant region to an s-wave region with the intermediate phase of d+is wave. To satisfy this model, we need to postulate that the doping level is not homogeneous in the film; thus, somewhere the system shows a d-wave gap, somewhere s-wave, and somewhere a mixture of the two. This seems compatible with our results; however, according to our experience of MBE growth, the doping level of Sr may not vary too much in the deposition region (5 × 5 mm²) of the thin film, but rather the local clustering or reconstruction may give more influential effects. The third one suggests that the full gap of the tunneling spectrum may arise from the NiO₂ terminated surface, which has natural buckling planes of NiO₂.¹⁸⁸ This picture is also interesting, which can be checked out on a surface with atomically resolved morphology. The fourth one proposes that the experimental observation can be simply explained within a pairing scenario characterized by a $d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$-wave gap structure with lowest harmonic on the Ni-band and higher harmonics on the Nd-band.¹⁸⁹ This scenario can be tested in future STM experiments with improved sample quality where the position of STM tip with respect to the Nd_1−xSr_xNiO₂ unit cell can be precisely determined. Last but not the least, the full gap feature may just be induced by the tunneling matrix problem. The symmetry of superconductor gap function refers to its transformation under crystal symmetry operations. In this general point of view, even a p-wave or a time-reverse-symmetry breaking d-wave would also produce the spectrum with a full gap feature. Because the V-shape spectra have been widely observed in our experiment, we thus believe that the d-wave gap should be a dominant one. And this is consistent with many theoretical calculations.

Figure 10.

Cartoon picture for the Fermi surfaces and gap structures

(A and B) The Fermi surfaces and the gap amplitude at the cut k_z = 0. A d-wave gap is formed on the α Fermi pocket centered around Γ, and a full gap may appear on the β pocket. Actually, the Fermi surface on the α pocket at this cut looks very similar to that of underdoped cuprates.

(C and D) The Fermi surfaces and the gap amplitude at the cut k_z = π. A d-wave gap is formed on the α Fermi pocket centered around Z, now the Fermi surface becomes a closed square like mimicking that of overdoped cuprates, and a full gap may appear on the γ pocket around A. The height of the colored walls in (A) and (C) indicates the gap magnitude on each Fermi surface. The blue and red colors in (B) and (D) represent the gap signs. Adapted from Gu et al.¹⁷⁴

Intuitively, the pairing form in Nd_1−xSr_xNiO₂ may serve as a bridge between the cuprates and the FeSC. Because the former has a single band feature and only the intraorbital interaction as the driving force for pairing, leading to the d-wave gap, while the latter is a multiband system, one needs not only intraorbital but also the interorbital interaction for pairing, resulting in the orbital selective pairing and s-wave gaps with opposite signs on different Fermi pockets.190, 191, 192, 193 At the moment, we do not know whether the gaps on the hybridized-orbital-derived β and γ pockets are really fully gapped and whether these gaps have opposite signs. The direct experimental evidence of the d-wave gap on the α pocket is also lacking. To resolve this issue, we need to do further phase-referenced quasiparticle interference experiments194, 195, 196, 197 on single-crystal samples when they are available, which has been conducted successfully in FeSC^190,198, 199, 200 and cuprates.²⁰¹ Clearly, more efforts are desired in order to pin down the assignment of the superconducting gaps on different Fermi pockets.

Outlook

The discovery of superconductivity in infinite-layer nickelate thin films paves a new path in the field of superconductivity. In this brief review, we focus mainly on the electronic structures, magnetic excitations, and superconducting pairing. Meanwhile, we also point out both similarities and distinctions between nickelates and cuprates.

First, RNiO₂ definitely has a multiorbital feature, which is different from the single-band cuprate system. Due to the hybridizations between Ni 3d and R 5d orbitals, a small number of holes are self-doped into Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital, forming a dominant Fermi pocket originating from Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital and two extra small electron pockets derived mostly from R 5d orbitals.

Second, the parent compound RNiO₂ locates in the regime of Mott insulator; one can naturally infer that the singly occupied Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ will possibly form a local spin and AF long-range order. However, it shows no sign of any long-range magnetic order in the magnetic-related measurements. Generally, the R 5d itinerant electrons can actively couple to Ni 3d orbitals and screen the local spin of Ni, increasing the critical value of U_Ni that is necessary to induce long-range magnetic ordering. Moreover, upon hole doping, the spin configuration of Ni 3d⁸ may be energetically arranged in two different ways, which depends on the limit whether the Hund's coupling is dominant over the crystal-field splitting (HS state) or the opposite situation (LS state). It remains highly debatable and worthy of more attention.

Third, Pauli-limited superconductivity with a very large value of Maki parameter α has been found in Nd_1−xSr_xNiO₂ superconducting film, indicating unconventional pairing in the system. The Pauli-limited scenario is not really compatible with pairing of a triplet origin. Instead, this should point to a singlet related and even-parity pairing. The tunneling spectra on Nd_1−xSr_xNiO₂ thin films show predominantly two types of features, one has a V-shape, another a full gap. The measured V-shape spectra featuring a d-wave gap is the dominant pairing instability and mainly originated from Ni $3d_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ orbital, which has been extensively demonstrated in many theoretical papers. Meanwhile, the full gap may have several possible explanations.

As for a future perspective, despite the discovery of superconductivity in all the three kinds of Nd, Pr, La based 112 systems, T_c is still too low compared to that of cuprates. Strictly speaking, nickelates may not be categorized into the family of high-temperature superconductors for now. We need to find out the reason and make an effort to increase T_c. Furthermore, bulk samples with the same structure and proper doping have no trace of superconductivity. It remains very elusive and needs enduring efforts toward resolving the problem. Concerning the phase diagram, we need to focus on whether there are emergent intertwined orders just like that in cuprates, especially for the relationship between AF spin fluctuations and superconductivity. The direct experimental evidence of the d-wave gap on α pocket is also lacking. With the development of sample synthesis and continuous accumulation of experimental results, we will find the answers to these challenging issues.

In conclusion, at the moment, it is just the beginning of research on superconductivity in the nickelate system. The phenomena observed so far show some similarities with cuprates, but more distinctions. Thus, the nickelate system provides a new platform for exploring unconventional superconductivity. The establishment and understanding of superconductivity in nickelates will shed new light on resolving the elusive pairing mechanism in high-temperature superconductors.

Published Online: December 24, 2021