Abstract
We investigate how politico-economic factors shaped government responses to the spread of COVID-19. Our simple framework uses epidemiological, economic and politico-economic arguments. Confronting the theory with US state level data we find strong evidence for partisanship even when we control for fundamentals including the electorate’s political views. Moreover, we detect an important role for the proximity of elections which we interpret as indicative of career concerns. Finally, we find suggestive evidence for complementarities between voluntary activity reductions and government imposed restrictions.
Keywords: COVID-19, Lockdown, Politics
1. Introduction
Confronted with the sudden spread of COVID-19 infections, governments across the world faced new tradeoffs in the early months of 2020. At their core, these tradeoffs concerned the choice between “lives” and “livelihoods”—health risks for broad segments of the population could only be contained by reducing social and economic activity. Governments responded differently to these tradeoffs, with some countries choosing a more light-handed approach and relying on individuals and firms to voluntarily adjust their behavior while others imposed harsh lockdowns and social distancing measures.
These differences reflected “fundamentals:” Not all populations were equally at risk, nor did economic activity in all regions equally depend on social interaction. Plausibly, they were also the consequence of politico-economic factors: Even with similar fundamentals, political incentives led policy makers to assess the relative costs and benefits of lives and livelihoods differently, and to act accordingly.
In this paper, we investigate how politico-economic factors shaped early-stage government responses to COVID-19 in US states. Our contribution is, first, to use epidemiological, economic and politico-economic arguments to derive a simple framework to analyze the incentives of policy makers. Second, we confront the theory with data to identify the role of political determinants of government choices.
An empirical analysis of the determinants of government choices in response to COVID-19 infections faces several challenges. Most importantly, governments operated in environments that varied along numerous dimensions of which many are unobserved or difficult to quantify. For example, cultural factors, social capital or family structures which might affect individual behavior and thus the costs and benefits of government interventions, differ across countries but are hard to measure, such that omitted variables are a natural concern.
We address this problem by focusing on a set of governments—state governments in the US—that act within relatively similar environments.1 While there are, undoubtedly, differences between how communities operate in Minnesota or Texas these differences (as well as differences between political parties and government institutions) are minor when compared with cross-country differences. For related reasons, we focus on state-government responses during a relatively short time period, namely March to June 2020. By restricting the analysis to a quarter of a year we do not have to control for factors that changed between the first and subsequent waves of infections and did so asymmetrically across states, for instance due to different capabilities to implement test-and-trace strategies.
Another challenge when trying to identify the determinants of government interventions concerns anticipation effects. When individuals expect governments to act in certain ways and change their behavior accordingly then it is difficult to distinguish between direct and indirect effects of policy. An advantage of the COVID-19 setting that we analyze is that anticipatory effects can plausibly be excluded. While epidemiologists had warned for years that sooner or later a global epidemic would strike, policy makers and the media in the US and in other countries not affected by SARS or MERS did not prioritize this threat. With memories of the Spanish Flu having faded both US state governments and the broader public were largely caught unaware when COVID-19 struck.
In Section 2, we document the heterogeneous policy interventions in US states and in Section 3, we lay out the epidemiological, economic, and politico-economic model that guides our analysis. As far as epidemiology is concerned we focus on two specifications, the canonical and the modified SIR model (Bailey, 1975, Kermack, McKendrick, 1927). We emphasize the advantages and disadvantages of both specifications and extract their robust features, arguing that only such robust features might plausibly have guided policy choices.
In addition we emphasize various politico-economic factors which imply that the tradeoff between lives and livelihoods as perceived by a policy maker differs from the one faced by a Ramsey planner. In particular, we argue that partisanship and re-election concerns of governors in combination with the time lag between the onset of the pandemic and the election date affect the political valuation of lives vs. livelihoods. Different politico-economic theories make contrasting predictions about the election effect. When campaign contributions are a major concern theory predicts policy makers to put more emphasis on livelihoods rather than lives as the election date approaches. Less emphasis on livelihoods, in contrast, is consistent with career concerns of policy makers that want to signal competence. Our setup is agnostic about which channel dominates.
The model predicts that in addition to these political factors, fundamentals such as health care quality, the age structure of the population and its density, the industry structure, unemployment benefits, and ideological views of the electorate determine equilibrium economic activity. The latter, in turn, is a function both of the restrictions that policy makers impose and the voluntary activity choices of individuals. Both elements might interact, reflecting complementarities or substitutabilities.
Against this theoretical background we present the empirical analysis in Section 4. We aim at identifying how the political factors—party affiliation of the state governor and proximity of the next election—determine the government imposed restrictions. In line with common wisdom we find that Republican governors tended to impose shorter and less harsh lockdowns. The effect is robust and quantitatively important even when we control for the electorate’s political views, among the other fundamentals. Moreover, we find that proximity of the next election has the opposite effect: An upcoming election tended to cause stricter restrictions. We interpret this as evidence for career concerns and against the importance of campaign contributions.
Digging deeper we hypothesize that career concerns should matter most when elections are close and the governor is legally able and chooses to run for re-election. Taking this qualification into account we find indeed that the effect we identify becomes stronger. The estimated coefficients of interest are statistically significant and quantitatively important, independently of whether we rely on OLS (in a subsample of states that imposed restrictions) or Tobit regressions (in the full sample including states that did not impose lockdowns).
We also estimate specifications in which we try to control for voluntary activity reductions, using Google mobility data just before state governments started to impose restrictions as proxy. Interestingly, we find suggestive evidence that points to complementarities between voluntary and government imposed activity reductions: Governors found it more beneficial to impose restrictions where the population voluntarily reduced activity. In contrast, we do not find convincing evidence for important roles played by state legislatures; knife-edge political races; the governor’s gender; or differences in career concerns across party lines.
Section 5 concludes and the appendix collects proofs and further discussion.
Related literature
Since mid March 2020 there has been an explosion of papers focusing on the intersection of epidemiological dynamics and economic cost-benefit analysis. Early contributions include Atkeson (2020) and Eichenbaum et al. (2020) or, among the much fewer works preceding the pandemic, Gersovitz and Hammer (2004).2 Our paper adopts a positive rather than normative perspective. In addition, it confronts theory with data, provides evidence for an important role of elections in disciplining policy makers, and suggests that voluntary and mandatory activity reductions may be complements.
We also contribute to the politico-economic literature on elections and career concerns according to which elections discipline politicians in office (Alesina, Cukierman, 1990, Barro, 1973, Ferejohn, 1986); with imperfect information about politicians’ competence, career concerns give rise to policy cycles (Rogoff, 1990); and office holders sacrifice rents before election to signal competence to voters.
Using cross-country data, Herrera et al. (2020) document that infection dynamics, and government responses to them, affect political approval ratings. For the US there is clear evidence that government imposed restrictions did reduce economic activity (e.g. Baek et al., 2021) and the spread of COVID-19 (e.g. Dave et al., 2021), giving rise to a (short-term) tradeoff between lives and livelihoods. Dingel and Neiman (2020) and Aum et al. (2020) document industry-level differences in the ability to let employees work from home, and Allcott et al. (2020) find evidence of partisan beliefs about the personal and social risks of COVID-19, factors that we account for when analyzing the variation of policy choices across states. Baccini and Bradeur (2021) find evidence that Democratic governors imposed more restrictive COVID-19 policy measures. Our results support this finding even when we condition on the political views among the electorate (and other fundamentals).
Iaryczower et al. (2021) provide evidence that US senators made policy concessions to increase their chances for re-election. In a similar vein, our analysis suggests that governors running for re-election chose to impose longer and more stringent lockdowns but only when they were more than half way through their terms. Pulejo and Querubín (2021) analyze cross-country data and find that restrictions were weaker when incumbent presidents faced re-election, a result that contrasts with our finding that career concerns fostered government imposed activity restrictions. Pulejo and Querubín (2021, p. 7) acknowledge that their cross-country results should be interpreted with caution and they argue in favour of within-country studies like ours.
2. US state interventions
In March 2020, US states responded to the spread of COVID-19 infections with various nonpharmaceutical interventions including social distancing restrictions. Our first measure of such restrictions is lockdown, a dummy variable that takes the value one if a state imposed a lockdown between March and June 2020 and zero otherwise. We refer to the 50 US states plus Washington, DC and Puerto Rico as “states” such that our sample includes 52 states, and we define a lockdown as a situation where “stay-at-home orders” are in place or “non-essential businesses” have to close. With this definition, 45 states instituted lockdowns while seven states did not. The latter are Arkansas, Iowa, Nebraska, North Dakota, South Dakota, Utah, and Wyoming; all had a Republican governor.
Fig. 1 illustrates the (effective) start and end dates of the lockdowns in the 45 states (see Table A.1 in the appendix for the exact dates). We define the beginning of a lockdown as the first day at which “stay-at-home orders” came into effect or “non-essential businesses” had to close, and similarly the end of a lockdown as the last day at which either restriction was in place. The figure shows that there is significant heterogeneity, with states that started the lockdown later often ending it earlier. The average lockdown among the 45 states lasted about 53 days, with a minimum of 24 days (Alaska) and a maximum of 93 days (Puerto Rico). Puerto Rico was the first state to impose a lockdown (March 15) and Oregon the last one to lift restrictions (June 19). Most states both declared “stay-at-home orders” and closed “non-essential businesses;” 11 states resorted only to the former intervention and three only to the latter.
Fig. 1.
Start and end dates for lockdowns across US states.
Fig. 2 illustrates the severity of restrictions over time according to the “stringency index” of the Oxford COVID-19 Government Response Tracker (Hale et al., 2021). The index is computed daily and accounts for eight containment and closure measures as well as one health policy measure.3 The figure plots the index values for each of the 45 states that imposed a lockdown. Note that the severity of restrictions increases rapidly from mid March as most states instituted lockdowns, and decreases slowly after mid April with wide variation across states.
Fig. 2.
Severity of restrictions across states during their lockdowns.
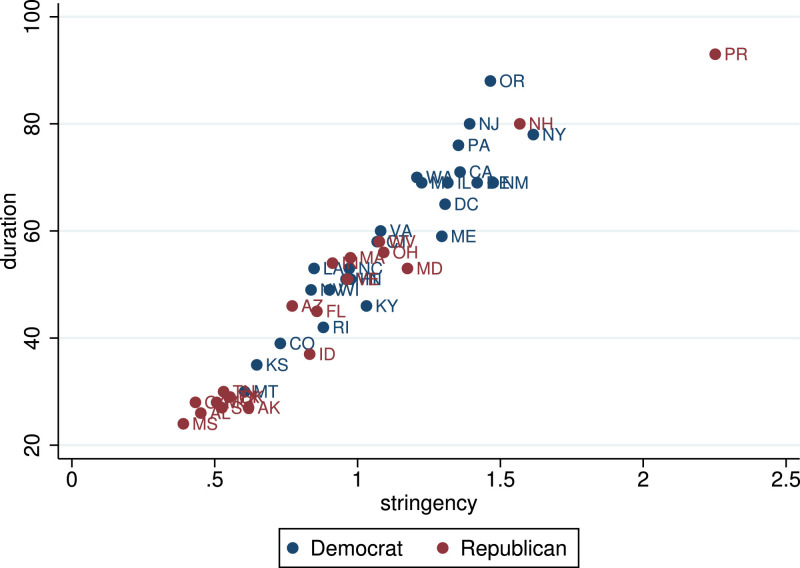
For our empirical analysis we condense these raw data into two further measures of state-level restrictions in addition to lockdown: The duration of lockdowns according to our definition given above. And the stringency of restrictions, defined as the normalized integral of the Oxford stringency index over the duration of the lockdown in the respective state.4 Fig. 3 illustrates the stringency measure across the 45 states that had a lockdown. Fig. 4 shows that duration and stringency are strongly correlated. It also shows that states with Republican governors tended to have weaker restrictions. Table 1 reports summary statistics for our three measures of state-level restrictions.
Fig. 3.
Stringency of restrictions across states.
Fig. 4.
Duration and stringency of restrictions are strongly correlated.
Table 1.
Summary statistics of restriction measures.
| Mean | SD | Min | Max | N | |
|---|---|---|---|---|---|
| lockdown | 0.87 | 0.35 | 0.00 | 1.00 | 52 |
| duration | 52.33 | 18.36 | 24.00 | 93.00 | 45 |
| stringency | 1.00 | 0.38 | 0.39 | 2.25 | 45 |
3. The model
To rationalize the observed differences in state interventions we merge basic epidemiological, economic, and politico-economic theories.
On the epidemiological side we emphasize that social interaction between infected and susceptible persons, which we refer to as “activity,” fosters infections. We use a standard epidemiological framework to capture the time-varying dynamics. On the economic side we emphasize restrictions on activity that state governments can impose. Such restrictions have economic costs because citizens value the income and consumption that activity generates; and they have benefits because by depressing activity the restrictions slow down infection dynamics and reduce health costs. Finally, we emphasize that the restrictions are imposed by self interested policy makers, not a hypothetical social planner or Ramsey government. We argue that this has implications for the objectives and instruments of state level policy makers at the onset of the pandemic.
3.1. Epidemiology
We base our analysis on a setup that nests the canonical SIR model due to Kermack and McKendrick (1927) and the modified SIR model due to Bailey (1975). Both models specify laws of motion in continuous time for the state-population shares of three groups that differ with respect to their health status. The three groups are the “susceptible,” the “infected” or “infectives,” and the “removed,” and their respective population shares in state at time are denoted by , , and , respectively, where .5 We normalize the mass of the total population at time 0 to unity. Accordingly, the three population shares correspond to the mass of susceptible, infected, and removed citizens.
At time 0 the state’s population consists of susceptible citizens and a few infected citizens, . There are no removed citizens at this time, . Subsequently infected citizens transmit the disease to members of the susceptible group and a share of the infected dies while a share recovers and develops immunity. Formally,
| (1) |
| (2) |
| (3) |
According to Eq. (1) the rate at which susceptible citizens are infected depends on their number, ; the possibly time-varying infection rate, ; and a measure of the infected population. We allow for two such measures depending on the binary parameter . When then the measure equals the population share of the infected population, . When , in contrast, then the measure equals the number of infected citizens relative to the number of susceptible or infected citizens, .
Eq. (2) describes the dynamics of the infected pool. The gross flow into infections corresponds to the outflow from the susceptible pool, . The net flow equals the gross flow minus the mass of citizens who die or recover. We assume that , which determines the exit rate from infections, is invariant across states. Finally, Eq. (3) states that the measure of the removed population, which equals , increases corresponding with the gross outflows from the infected pool.
Eqs. (1)–(3) with represent the canonical SIR model due to Kermack and McKendrick (1927). To understand its dynamic properties suppose that is constant at value and note from Eqs. (1) and (2) (subject to ) that for the share of infected citizens increases until it reaches a maximum when ; thereafter, the share declines. Intuitively, once falls short of (the “herd immunity level”) there are fewer new infections of susceptible citizens than outflows from the infected pool due to recoveries and death. In what follows we assume that , consistent with the COVID-19 experience in the US.
One noteworthy feature of the canonical SIR model is that the time path of determines the long-run population shares and ( always equals 0). When restrictions reduce the infection rate this implies that the time path of restrictions affects both transition dynamics and the steady state. The following well-known epidemiological result (e.g., Theorem 2.1 in Hethcote, 2000), which is proved in the appendix, formally describes some of the model’s implications:
Proposition 1
In the canonical SIR model with,
Accordingly, the maximum value ofequals
and the long-run share of the susceptible population,, solves the equation
such thatis strictly increasing in.
Eq. (1) with implies that a doubling of the population shares and leads to a quadrupling of new infections, . This is different in the modified SIR model due to Bailey (1975), which follows from Eqs. (1)–(3) when is set to 0. With Eq. (1) implies that a doubling of and only leads to a doubling, not a quadrupling of new infections.6 An advantage of the modified SIR model lies in its tractability: System (1)–(3) with can easily be solved, see the appendix. We have the following result which also is proved in the appendix:
Proposition 2
Consider the modified SIR model and let. Then,attains the maximum value
after the duration
A less appealing feature of the modified SIR model is that, contrary to the canonical SIR model, it predicts exogenous levels of and . In the modified SIR model restrictions imposed by policy makers therefore affect health outcomes only during the transition. In fact, the modified SIR model predicts that eventually, the whole population gets infected before recovering or dying, . As we discuss in Gonzalez-Eiras and Niepelt (2020c) this latter, implausible feature can easily be rectified by specifying a hybrid model which combines features of the canonical and modified SIR model.
Fortunately, the advantages and drawbacks of the two specifications do not give rise to a difficult modeling trade off for our analysis because they generate very similar dynamics during the early stage of a COVID-19-like epidemic, see Fig. 5 .7 In fact, given the uncertainty that policy makers faced at the beginning of the pandemic the differences between the two predictions are second or third order. We will therefore use both specifications to capture how restrictions affect infection dynamics, focusing on the specification with to represent long-run implications and on either specification to represent short-run dynamics.
Fig. 5.
Dynamics in the canonical (blue) and modified (red) SIR models: (dotted), (solid), and (dashed). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.2. Economics
State-level activity, , affects the infection rate according to
| (4) |
Here, denotes an epidemiological constant and represents state characteristics that determine how elastically activity affects the infection rate.
Activity, in turn, is affected by state-level restrictions, , and by the activity level that citizens would choose in the absence of restrictions, .8 We do not take a stance on the form of the interaction between the two factors, allowing for both substitutability or complementarity between and . (Local) substitutability could be present if unwillingness of citizens to restrain their social interaction increased the marginal effect of government restrictions on activity. The opposite effect, (local) complementarity, could be present if government restrictions without supportive actions on the part of citizens were less effective. Formally, we let
| (5) |
for some aggregator function . The derivative of with respect to its first and second argument, respectively, is positive and negative; the cross-partial may have either sign.
Citizens value net benefits of activity (e.g., utility from consumption net of disutility from labor supply) and dislike costs of infection such as from death. We assume that the flow net benefits of citizen in state are a concave function of state-level activity,
| (6) |
Note two properties of this formulation. First, absent any infection related costs of activity the utility maximizing activity choice would equal unity. Second, the net benefits depend on the parameter which we introduce to capture differences in the degree that citizens can substitute away from infection prone activity, reflecting for instance different exposure to infection risk across professions or preconditions or different opportunities to substitute types of activity that are particularly affected by restrictions.9
We refer to the net benefits in (6) as livelihoods and the (expected) benefit of avoiding infections and lost lives (to be specified more precisely below) as lives. The indirect utility function of citizen in state aggregates the expected discounted utility flows from livelihoods and lives for all subject to Eqs. (1)–(5).
Ramsey program
A quickly growing literature summarized in the introduction has analyzed how a Ramsey government resolves the tradeoff between lives and livelihoods. Let denote the social welfare function of state that results when the indirect utility functions are aggregated according to a given set of welfare weights. The Ramsey program as of time then consists of selecting an admissible path of restrictions to maximize . In particular, at the onset of the epidemic (at time 0) the Ramsey government maximizes .
Let denote the “fundamentals” in state which determine and therefore the Ramsey planner’s choice of restrictions. From the model presented so far we conclude that includes the following elements:
-
•
The quality of the state’s health care infrastructure. This quality determines the (expected) rate at which infected persons die. Formally, in Eq. (3) is a decreasing (and an increasing) function of health care quality.
-
•
The population share of the elderly. Since the elderly are particularly strongly affected by the pandemic a high share of the elderly increases the state’s in Eq. (3) (and decreases ).
-
•
The state characteristics determining how elastically activity affects the infection rate, . From Eq. (4) these characteristics influence the costs of activity in terms of induced infections.
-
•
Opportunities to work from home. These opportunities determine the possibility to substitute infection prone activity by other forms of activity which is captured by the parameter in Eq. (6); see Dingel and Neiman (2020) or Aum et al. (2020).
-
•
The state’s unemployment or social welfare benefits. The size of these benefits, which again is captured by the parameter in Eq. (6), determines how strongly reductions in infection prone activity affect livelihoods.
-
•
The initial share of the infected population, . This share affects the relationship between lives and livelihoods because for a given path of activity it determines the infection dynamics, see Eqs. (1)–(3) as well as Propositions 1 and 2.10
-
•
Finally, political beliefs or ideology, for instance regarding the adequate balance between personal safety and freedom or the proper role of government. These beliefs directly affect citizens’ relative valuations of lives and livelihoods; see Allcott et al. (2020).
3.3. Political economy
Political economy factors distort the program of politically motivated decision makers relative to the Ramsey program. We emphasize four such factors. The first three imply that the objective maximized at time 0, say, differs from . The fourth factor concerns admissibility constraints.
Modified welfare weights
When office motivated candidates with commitment compete for votes they have an incentive to propose platforms that gain a majority. Under assumptions about voter preferences the winning platform only represents the interests of the median voter (Downs, 1957, Hotelling, 1929). In a probabilistic voting environment, in contrast, candidates have incentives to cater to “swing voters” that respond particularly elastically to changes in the policy platform as opposed to other, ideological considerations (Lindbeck and Weibull, 1987), or to better organized lobbies (Baron, 1994, Olson, 1965). How electoral competition distorts away from is ambiguous. A median voter perspective would suggest a moderating effect of electoral competition while a high degree of swing voting or lobbying on behalf of citizens with extreme preferences could induce the opposite.
The presence of partisan rather than office motivated candidates may further distort relative to . The extent to which this occurs depends on whether candidates can commit or not, or similarly, whether the policy platform is determined pre or post election. In the former case, with commitment, partisanship may or may not imply policy divergence, i.e., equilibrium policies that reflect the winning candidate’s preferences; in the latter case partisanship implies divergence unless middle-ground policies can be sustained in a cooperative equilibrium (Alesina, 1988). When “citizen-candidates” strategically select into running for office such that the degree of partisanship is endogenous a multiplicity of equilibria and potentially winning policy platforms arises, even when voters vote sincerely rather than strategically (Besley, Coate, 1997, Osborne, Slivinski, 1996). Finally, post-election bargaining within a group of policy makers, e.g., a governor and the state legislature, can introduce further distortions.11
In summary, pre- and post-election competition as well as legislative bargaining give rise to a multitude of potential mechanisms that distort relative to . In general, the distribution of voter preferences, the format of elections, and legislative bargaining protocols, among other factors, shape . We drastically simplify and account for these factors by allowing for two types of changes relative to : First, may depend on the fundamentals in different ways than depends on them. And second, may reflect the party affiliation of the governor. In the following we denote by the “political factors” that shape but not and which contain the governor’s party affiliation.
Modified reference date
A Ramsey government maximizes the objective function as of time 0, . In contrast, a policy maker maximizes the probability of winning the upcoming election when she is office motivated and she maximizes subject to mustering sufficient political support in the legislature or the next election when she is partisan. Suppose for simplicity that only the next election (rather than legislative bargaining up to the election) is of concern for ; that this election is scheduled for time ; and that all factors discussed above (related to modified welfare weights) are absent. The concern of then is to affect —not . Moreover, when voters are forward looking their expected utility and thus, political support at will be a function of the state at that time as well as of the policy platforms on offer. This implies that ’s objective at time 0 reduces to optimally manipulating the time- state. This may occur through several intertemporal links:
First, punishment. When there is no direct connection between the policy choices prior to the election and the payoff relevant state at time (for instance because elections lie far in the future) and when voters are fundamentally indifferent between candidates at the time of election then a punishment motive may lead them to vote against the incumbent if they perceive her to have mismanaged the epidemic in retrospective. This effect can discipline the policy maker.
Second, signaling. When voters care about the competence of elected officials but cannot directly observe it and when policy makers have career or re-election concerns the state at time includes voter beliefs about the policy maker’s type.12 As the competence beliefs are continuously updated the policy maker has a stronger incentive to act competently or pretend competence when the election is near. Accordingly, rent seeking is less pronounced closely before an election.
A final intertemporal link arises because of campaign contributions. When the incumbent’s contributions constitute a relevant state variable at the time of the election then the interests of those contributing to the campaign may guide the policy maker’s actions before the election; our previous discussion about lobbying applies. Effectively, reflects the preferences of the contributors in this case.
In our context the punishment mechanism appears of limited relevance for policy choices early in the epidemic. In contrast, the implications of the campaign contributions channel seem clear: Since campaign contributions are positively correlated with economic activity13 an important campaign-contributions channel would increasingly shift the political objective in favor of livelihoods as opposed to lives as the election date draws nearer. That is, when campaign contributions lay at the center of intertemporal links then proximity of the election would tend to reduce the incentives to impose restrictions.
As for the signaling channel the effect of proximity of the next election on the relative weight attached to lives vs. livelihoods is less clear. If officials can more easily engage in rent seeking when activity is high then a closer election date makes restrictions relatively more attractive (by diminishing incentives for rent seeking); if rent seeking mainly occurs through mechanisms that also benefit lives the reverse is the case. In our view, the former is much more plausible, for similar reasons as campaign contributions are more closely related to activity. An important signaling channel thus should most likely increase the incentives to impose restrictions when the election date comes closer.
In summary, the time lag between the onset of the pandemic and the election date affects the political valuation of lives relative to livelihoods because it is the state at the time of the election that an optimizing policy maker targets (see also Mian et al., 2010).14 To account for this we allow the relative valuation to be affected by the distance to the next state election, i.e., the time to the next election is an element of . An empirical finding of a positive relationship between proximity of the next election and restrictions only is consistent with a signaling motive.
The time before the next state election also matters insofar as it reduces the dimensionality of the argument of the political objective function: It is not necessarily the whole time path of restrictions (or implied activity levels) which matters for but rather any sufficient statistic of this path for the state at the time of the election. We account for this by representing the lives-vs-livelihoods tradeoff by way of robust summary statistics of the health dynamics, which apply in either epidemiological specification (see below).
Lack of information
Especially at the onset of an epidemic policy makers face severe information problems. Both epidemiological and economic aspects are highly uncertain, that is, the constraints (1)–(5) may be understood in principle but their exact form is unknown. Against this background policy makers may opt for robust strategies (Gilboa, Schmeidler, 1989, Hansen, Sargent, 2011, Knight, 1921). Also the information problems of policy makers are aggravated by those of voters who may only pay attention to a small set of issues at a given time.
For our purposes this has two implications which reinforce some of the conclusions we have already drawn. First, the policy maker’s objective relates to robust statistics. And second, the relative valuation of lives and livelihoods varies depending on the time lag between the onset of the pandemic and the election.
Admissibility constraints
Constitutions, legislative procedures and other factors constrain which policy instruments are admissible and how flexibly policy makers can adjust them. In our analysis we only allow for a single choice of instrument, namely “the” (average) level of restrictions. Since the political objective depends on the state at the time of election rather than the whole path of variables up to that time, this reduction in the dimensionality of the instrument space appears relatively innocuous.
3.4. Implications
We draw three main conclusions from the foregoing discussion. First, a state governor’s valuation of lives relative to livelihoods depends on fundamentals, , and political factors, . Second, proximity to the next election may increase the weight that policy makers attach to the lives goal when the signaling channel is key while it has the opposite effect when campaign contributions lie at the center of intertemporal links. And third, the arguments of the governor’s objective function as well as her instruments are simple, robust statistics.
We operationalize the simplicity feature by restricting attention to constant rather than time-varying paths of and (and thus ).15 Moreover, we assume that only depends on average fundamentals. That is, we restrict to include the average value of in the state rather than the full distribution and similarly for the political views or ideology.
Since several plausible measures of the pandemic’s health costs are increasing functions of we operationalize the robustness feature by letting represent the lives objective. A first such measure is the maximal stress in the health care system, which in the modified SIR model is related to peak infections, . Peak infections also correspond to the integral of net flows into infection up to . A second measure is related to the integral of gross flows into the infected pool up to the time of peak infections or equivalently, to one minus the share of susceptible citizens at the time when infections peak. In the canonical SIR model this measure equals , see the text before Proposition 1. And yet another measure is related to one minus the share of the population that avoids infection in the long run, , which is known in the canonical SIR model. All these measures increase in (the first for plausible parameter values), see Propositions 1 and 2. This motivates our choice of as a robust statistic. The livelihoods objective is given by the function of activity given in (6).16
Against this background, the indirect utility function of the governor in state aggregates the indirect utility functions of citizens as
| (7) |
The first argument of , which enters positively, represents the concern for livelihoods. The second, which enters negatively and incorporates the epidemiological constraints (1)–(3) in reduced form, represents the concern for lives. The function also depends on all fundamentals other than and (these two fundamentals directly enter in the constraint (4) and the first argument, respectively) and the political factors.
For simplicity, we abstract from nonlinear effects of the first two arguments of ; then is strictly concave in because the livelihood costs of restrictions are convex while the lives benefits are concave. The first-order condition with respect to (or ) reads
| (8) |
where denotes a weight function.
Note that the optimal strictness of restrictions induces an activity level that decreases in as long as . Unambiguously, better substitutability of infection prone activity (higher ) or a higher weight on lives, , reduce . When a signaling channel is operative a shorter duration to the next election (which is an element of ) increases and therefore implies lower activity; the opposite mechanism is present when campaign contributions are key such that a shorter duration decreases . The decomposition of changes in activity into changes of and depends on the functional form of .
4. Empirical analysis
In this section we confront the theory with data. We are particularly interested in the “political determinants” of restrictions, i.e., in how the political factors affected policy choices. We first discuss our measures of the theoretical concepts before turning to the econometric approach and the estimation results.
4.1. Measures
The theoretical analysis in Section 3 relates restrictions, , the voluntary activity level in the absence of restrictions, , and equilibrium activity, , to a set of determinants: Fundamentals, , and political factors, . We have already introduced our three measures of , namely lockdown, duration, and stringency (see Section 2).
Voluntary activity
In some of our specifications we try to control for voluntary activity choice, , which is unobserved. We proxy by relying on Google COVID-19 Community Mobility Reports from early in the pandemic, before state government imposed restrictions came into effect (LLC, 2020). The reports contain daily data by geographical area and distinguish between locations and areas such as retail and recreation, groceries and pharmacies, parks, transit stations, workplaces, or residential areas. Mobility is measured in percent relative to a baseline value.17 We focus on workplace mobility, consistent with our interpretation of activity as economic activity.18 Denoting Google workplace mobility in state at day by we define as
Only Puerto Rico had imposed a lockdown prior to March 18. The mean of early_activity excluding Puerto Rico is 0.71; its minimum and maximum values are given by 0.44 (Washington, DC) and 0.81 (North Dakota). This is consistent with findings in earlier work that substantial behavioral changes preceded restrictions (see, e.g., Goolsbee and Syverson, 2021 or Krueger et al., 2020).
Fundamentals,
At the onset of the pandemic, health authorities across the world emphasized ICU beds and respirators as key tools to deal with surging COVID-19 related hospitalizations. Since respirators can relatively easily be relocated their number does not constitute a reliable measure of state level health care capacities. Accordingly, we associate the quality of the state’s health care infrastructure with the number of ICU beds per 10,000 inhabitants (2018 population), and we denote the empirical measure by icu. The data for icu comes from the Kaiser Family Foundation and uses American Hospital Association Annual Survey data and population data from the US Census Bureau.19
We measure the population share of the elderly by the share of the state population aged 65 or above. We associate , which determines how elastically activity affects the infection rate, with the urbanization rate, i.e., the share of the state’s population that lives in urban areas. The data source for our two empirical measures, and , is the US Census Bureau.
We measure opportunities to work from home by an index based on Dingel and Neiman (2020), .20 We associate unemployment benefits with two measures, namely and . The former measures the state’s average unemployment replacement rate in the year 2019, and the latter measures the replacement rate in the second quarter of 2020, including the 600 USD supplement granted by the CARES Act of March 27, 2020. We explain below when we use either of the two measures. The data comes from the Department of Labor’s Employment and Training Administration.21
We associate the share of the infected population in the state at March 15, , with the empirical measure initial_infections (number of infected persons per million inhabitants) which is based on New York Times data which in turn is based on reports by state and local health agencies. Population data comes from the US Census Bureau. Finally, we associate the predominant ideological views of the state’s electorate with the vote share for Donald Trump in the 2016 presidential election. The data sources for our empirical measure ideology are Ballotpedia22 and other online sources.
Political factors,
We associate the party affiliation of the state governor with the empirical measure republican, which takes the value one if the governor is Republican and zero otherwise. Finally, we associate the time to the next gubernatorial election with a dummy variable, early_election, that takes the value one if the state faces an election in the years 2020 or 2021 and zero otherwise.23 The data sources for our measures republican and early_election are Ballotpedia and other online sources.
Table 2 reports summary statistics of our activity measure and the explanatory variables.
Table 2.
Summary statistics of empirical measures.
| Mean | SD | Min | Max | N | |
|---|---|---|---|---|---|
| early_activity | 0.71 | 0.07 | 0.44 | 0.81 | 51 |
| republican | 0.52 | 0.50 | 0.00 | 1.00 | 52 |
| early_election | 0.27 | 0.45 | 0.00 | 1.00 | 52 |
| wfh | 0.36 | 0.05 | 0.30 | 0.60 | 52 |
| ui_replacement | 0.45 | 0.06 | 0.31 | 0.54 | 52 |
| ui_supplement | 1.08 | 0.15 | 0.85 | 1.77 | 52 |
| ideology | 0.48 | 0.11 | 0.24 | 0.68 | 52 |
| urbanization | 74.50 | 15.00 | 38.70 | 100.00 | 52 |
| share65+ | 16.50 | 2.00 | 11.10 | 20.70 | 52 |
| icu | 2.68 | 0.82 | 0.67 | 6.00 | 52 |
| initial_infections | 3.80 | 6.25 | 0.00 | 36.00 | 52 |
4.2. Estimates: determinants of restrictions
Empirical specification
Eq. (8) implies that the activity level in a state is a function of and . Moreover, from Eq. (5) activity is an increasing function of and a decreasing function of . Assuming (approximate) linearity, we represent these theoretical relationships by the reduced-form estimating equation
| (9) |
where denotes an affine function and indicates an error term that is uncorrelated with the arguments of . Eq. (9) constitutes our core empirical specification once we replace the theoretical concepts , and with empirical counterparts.
We note two points. First, Eq. (9) admits a causal interpretation of the effects of as long as the specification does not suffer from an omitted variables bias. We return to this point below when we check the robustness of the coefficient estimates across different specifications. Second, our main regressions only include the 45 states that implemented a lockdown, in order to minimize the risk of mismeasuring the dependent variable. On the one hand, it is not clear whether an observation of zero restrictions reflects an interior optimal choice rather than a corner solution.24 On the other hand, fixed costs of imposing and lifting restrictions might have prevented some states from instituting short lockdowns, i.e., a politically preferred brief lockdown may not have been imposed. Below, we return to this point as well when we run Tobit regressions based on observations for all 52 states.
Baseline
In a first step, we use the measures described in the previous subsection except that we do not yet rely on the measure early_activity for . Instead, we adopt the identifying assumption that is an arbitrary (linear) function of the fundamentals—but not the political factors—such that, from Eq. (9),
| (10) |
Under this identifying assumption we can estimate the effect of the political factors by regressing our restriction measure on the measures of and .
How plausible is this identifying assumption? To answer this question we regress early_activity, which is our best measure of , on a set of covariates without and with the political measures; if the identifying assumption is correct then the political measures should not add significant explanatory power. The results reported in Table 3 support that view.25 They show in column (1) that wfh and ideology explain nearly of the variation in early_activity while the other variables including the political measures do not add meaningful explanatory power (see column (2)).26 Here and in all subsequent tables we report robust standard errors.
Table 3.
Determinants of early_activity.
| (1) | (2) | |
|---|---|---|
| early_activity | early_activity | |
| wfh | -0.818 | -0.620 |
| (-5.09) | (-2.74) | |
| ideology | 0.279 | 0.248 |
| (3.64) | (2.77) | |
| republican | 0.00815 | |
| (0.93) | ||
| early_election | -0.00955 | |
| (-0.87) | ||
| ui_replacement | -0.195 | |
| (-1.88) | ||
| urbanization | -0.000938 | |
| (-2.21) | ||
| share65+ | 0.00275 | |
| (0.90) | ||
| icu | -0.0113 | |
| (-1.35) | ||
| initial_infections | 0.0000273 | |
| (0.04) | ||
| constant | 0.864 | 0.949 |
| (9.13) | (7.97) | |
| N | 51 | 51 |
| Adj. | 0.789 | 0.835 |
OLS regressions, robust t statistics in parentheses , , .
We note three points. First, we use the measure ui_replacement rather than ui_supplement because, plausibly, voluntary activity reductions in March 2020 reflected insurance benefit rules that were in place at the time, not the benefits that were enacted later in the year. Second, multicollinearity is not a problem although several covariates including wfh, ideology and urbanization are strongly correlated.27 Third, one might suspect that early_activity misrepresents voluntary activity reductions because some government imposed restrictions were already in place around March 18, but we do not capture them by focusing on the restrictions discussed in Section 2. But this appears not to be the case; when we include candidates for such early government imposed restrictions they do not enter with a significant coefficient.28
Evidently, the measures of the fundamentals do not perfectly explain . Our complete identifying assumption therefore is that is not affected by the political measures and that any omitted explanatory factor of (including measurement error) is uncorrelated with the measures of . Under this assumption, regression (10) yields unbiased estimates of the coefficients on the -measures which can be interpreted causally. In contrast, the estimated coefficients on the measures of do not admit structural interpretations because they may reflect both direct effects on restrictions and indirect effects operating through voluntary activity changes.
Table 4 presents the results of regression (10) for each of our restriction measures. We now use ui_supplement rather than ui_replacement as the measure of state level unemployment benefits because these benefits had changed, or were about to change (reflecting federal policy changes such as the CARES Act29 ) when state restrictions were in place.
Table 4.
Determinants of restrictions.
| (1) | (2) | (3) | |
|---|---|---|---|
| lockdown | duration | stringency | |
| republican | -0.117 | -10.41 | -0.177 |
| (-1.76) | (-2.20) | (-1.74) | |
| early_election | -0.0175 | 10.03 | 0.163 |
| (-0.16) | (1.99) | (1.60) | |
| wfh | 0.498 | 90.93 | 2.869 |
| (0.47) | (1.28) | (2.09) | |
| ideology | -1.724 | -63.85 | -1.091 |
| (-2.65) | (-1.53) | (-1.26) | |
| ui_supplement | -0.289 | 0.388 | 0.415 |
| (-0.90) | (0.02) | (0.87) | |
| urbanization | -0.00316 | 0.161 | 0.00266 |
| (-0.92) | (1.07) | (0.84) | |
| share65+ | 0.0446 | 3.057 | 0.0636 |
| (1.54) | (2.53) | (2.48) | |
| icu | 0.132 | -0.610 | -0.0433 |
| (2.00) | (-0.16) | (-0.54) | |
| initial_infections | -0.0230 | -0.692 | -0.0126 |
| (-3.08) | (-1.25) | (-1.28) | |
| constant | 1.135 | -7.903 | -1.030 |
| (1.18) | (-0.17) | (-0.97) | |
| N | 52 | 45 | 45 |
| Adj. | 0.260 | 0.487 | 0.504 |
OLS regressions, robust t statistics in parentheses , ,
Across all three specifications, we estimate a negative coefficient for republican. With lockdown as the dependent variable the coefficient estimate indicates that a Republican governor is about less likely to impose a lockdown.30 Note that this estimated coefficient is substantially smaller than , the coefficient in a regression of lockdown only on republican or equivalently, the share of Republican governed states without a lockdown. This highlights that it is important to control for other covariates when trying to identify the partisan effect on restrictions.
In the specification with duration a Republican governor is associated with a shortening of lockdown duration of around ten days and in the specification with stringency, a reduction in the index by about 0.18; in either case this amounts to roughly half a standard deviation of the dependent variable. The estimated coefficient on early_election is positive but only in the specification with duration is it significant at the level. On average, states with upcoming gubernatorial elections in 2020 or 2021 experienced lockdowns that were about 10 days longer (with an increase of stringency by 0.16).
Partisanship
One interpretation of the negative effect of republican is that Republican governors personally prefer weaker restrictions, independently of the preferences of their constituencies which presumably reflect fundamentals including ideology. Alternatively, these governors could be more open to lobbying by business interests, maybe because of party pressure within or outside of the state. Yet another interpretation is that Republican governors perceive their constituencies to be less exposed to infection risk, or at least perceive their constituencies to hold such a view.31
Career concerns
Whether or not such lobbying channels are strong, the positive coefficient on early_election suggests that they are checked by an election channel which operates through signaling/career concerns (see the discussion in Section 3.3). Pursuing this signaling aspect further we note that signaling that is motivated by career concerns should only be operative if the incumbent is allowed to seek re-election and willing to do so. Against this background we construct a modified measure, career_concerns, to replace early_election. Variable career_concerns takes the value one when a state has a gubernatorial election in the year 2020 or 2021 and the incumbent seeks re-election, and zero otherwise.32
The estimated coefficients in regression (10) with the modified election measure support our interpretation of career concerns, see Table 5 . In the specifications for duration and stringency the estimated coefficients on republican and career_concerns are significant at the or level and have the expected signs. They imply that Republican governors imposed lockdowns that were shorter by 13 days and less stringent by 0.22. Governors seeking re-election imposed lockdowns for 15 days longer and more stringent by 0.27. The estimated coefficients on the other covariates barely change relative to the earlier regressions with early_election rather than career_concerns among the covariates.
Table 5.
Determinants of restrictions: career concerns.
| (1) | (2) | (3) | |
|---|---|---|---|
| lockdown | duration | stringency | |
| republican | -0.123 | -12.58 | -0.216 |
| (-1.86) | (-3.25) | (-2.51) | |
| career_concerns | 0.0360 | 15.13 | 0.271 |
| (0.32) | (2.76) | (2.44) | |
| wfh | 0.450 | 112.2 | 3.213 |
| (0.47) | (1.74) | (2.59) | |
| ideology | -1.701 | -57.71 | -1.003 |
| (-2.70) | (-1.59) | (-1.28) | |
| ui_supplement | -0.282 | 1.867 | 0.446 |
| (-0.92) | (0.11) | (1.05) | |
| urbanization | -0.00292 | 0.130 | 0.00215 |
| (-0.90) | (0.94) | (0.73) | |
| share65+ | 0.0419 | 2.805 | 0.0579 |
| (1.41) | (2.64) | (2.54) | |
| icu | 0.132 | -0.727 | -0.0428 |
| (2.09) | (-0.20) | (-0.55) | |
| initial_infections | -0.0230 | -0.818 | -0.0151 |
| (-3.11) | (-1.53) | (-1.55) | |
| constant | 1.152 | -12.43 | -1.087 |
| (1.24) | (-0.30) | (-1.13) | |
| N | 52 | 45 | 45 |
| Adj. | 0.262 | 0.552 | 0.559 |
OLS regressions, robust t statistics in parentheses , ,
There is another indication for a signaling rather than campaign contribution channel. According to Lott (2000) campaign contributions are larger where state governments are bigger, for instance because campaign contributors expect to be rewarded with rents which increase in the size of the public sector. If a mechanism along these lines were strongly operative we would expect states with bigger governments to impose fewer and weaker restrictions, in particular when the state held an election in 2020 or 2021. To test this we run a regression in which we replace the variable early_election with a new variable that interacts early_election and the size of the state’s government.33 We find that the estimated coefficient on this new variable is positive—unlike what an operative campaign contributions channel would suggest—but not statistically significant. In regressions including both the new variable and career_concerns only the latter variable enters significantly.
Robustness: Omitted variables
As mentioned before, the coefficients on the political factors would be estimated with a bias if the regression (10) omitted relevant determinants of restrictions that are correlated with republican or career_concerns. To test whether this is likely to be the case we introduce a series of candidate variables in the regression and check whether the estimated coefficients on republican or career_concerns change. Among the candidate covariates we consider are: Income per capita, share of population under age 18, rainy-day funds of the state, gun ownership, share of the population with bachelor or higher education, coverage of health insurance before Medicaid expansion, and share of representatives with a Tea Party affiliation in the 2010 election.34 While some of the candidate variables are correlated with republican we find that none of them enters significantly and that adding them to the regression does not importantly change the estimated coefficients on republican or career_concerns.35
To check for possible regional effects, for instance due to climatic differences, we introduce dummy variables for the US Census Regions Northeast, Midwest, West, and South.36 These dummies are not statistically significant and introducing them has no effect on the estimated coefficients of the political measures of interest when the dependent variable is duration or stringency. For lockdown as the dependent variable the dummy for the Midwest region is statistically significant at the 10% level and negative; the probability that a state with a Republican governor does not impose a lockdown slightly increases to 14.7%.37
Robustness: Tobit regressions
As a further robustness check we perform Tobit regressions for lockdown and stringency as the dependent variables where we now include the seven states without lockdowns which we excluded so far out of concern about mis-measurement (see the discussion above). The results are reported in Table E.1 in the appendix. As expected, the estimated coefficients on republican are now more negative, indicating that Republican governors imposed on average lockdowns that were 18 days shorter with their stringency reduced by 0.32. The estimated coefficients on career_concerns barely change.
We conclude that specifications using the variable career_concerns generate robust, significant and plausible results. This reinforces our interpretation of meaningful effects of career concerns which induce governors, by reducing their incentives to seek activity-related rents, to attach more weight to lives relative to livelihoods when elections are near and they want to be re-elected.
Complementarities Between Voluntary and Mandatory Activity Reductions
So far we have assumed that voluntary activity is a linear function of the fundamentals, see Eq. (10). Under our identifying assumption, this allowed us to interpret the coefficients on causally.
We now relax this assumption and directly include a measure for , as in Eq. (9), in order to estimate the effect of voluntary activity choices on politically motivated restrictions. Recall from Eq. (8) that activity reflects both voluntary individual choices and government imposed restrictions and that and may be substitutes or complements. There is little empirical evidence so far on the importance of substitutability or complementarity but some suggestive evidence exists. For example, Frey et al. (2020) find in cross-country data that some (more democratic) societies impose less stringent lockdowns than other (more autocratic) countries while the citizens of the former reduce mobility by more than those of the latter; this might suggest substitutability. Our data, which is less marred by cross-country cultural and other differences, admits an alternative testing ground.
We thus use early_activity as a proxy of and given our previous results on the explanatory power of wfh and ideology for early_activity (see Table 3), we exclude wfh and ideology from the set of measures of . That is, we assume that opportunities to work from home and ideological views affect restrictions only indirectly, through their effect on . The estimation results are reported in Table 6 . We find that the coefficient on early_activity is significant at the level and negative, suggesting strategic complementarity between and . The estimated coefficients on republican and career_concerns change slightly relative to the baseline specification and they remain significant. We find similar results when we measure not by early_activity but by its projection on wfh and ideology.
Table 6.
Determinants of restrictions: voluntary activity reductions.
| (1) | (2) | |
|---|---|---|
| duration | stringency | |
| republican | -11.11 | -0.209 |
| (-3.14) | (-2.67) | |
| career_concerns | 12.98 | 0.189 |
| (2.98) | (2.14) | |
| early_activity | -166.9 | -2.904 |
| (-4.45) | (-3.79) | |
| urbanization | 0.000843 | -0.000498 |
| (0.01) | (-0.19) | |
| share65+ | 2.612 | 0.0507 |
| (3.45) | (3.00) | |
| icu | -3.016 | -0.0818 |
| (-1.38) | (-1.65) | |
| initial_infections | -0.613 | -0.00589 |
| (-1.93) | (-0.85) | |
| constant | 137.8 | 2.504 |
| (4.11) | (3.57) | |
| N | 44 | 44 |
| Adj. | 0.592 | 0.521 |
OLS regressions, robust t statistics in parentheses , ,
4.3. Extensions
Finally, we use our baseline specification (10) to check whether the policy responses to the spread of COVID-19 provide some evidence for additional political-economy channels or the role of specific groups. We focus on four narratives. First, we investigate whether it is governors or rather the interplay between governors and the state legislators that matters. Since stay-at-home orders and closures of non-essential businesses came into effect through executive orders we expect the former.38 To test the alternative hypothesis we investigate the role of divided government by including the variable divided, a dummy variable that takes the value one when at least one chamber in the state’s legislature was under the control of the governor’s opposition and zero otherwise.39
Second, we investigate the degree of political competition which has been shown to matter for policy choices across US states (Besley et al., 2010). To capture effects of political competition we include the variable close, a dummy variable that takes the value one when the difference between the winner and the runner-up in the state’s last gubernatorial election fell short of five percentage points, and zero otherwise.40 And third, we investigate whether female governors systematically behaved differently in the face of COVID-19. This is motivated by evidence that female leaders cater more to the needs of women,41 and that men and women plausibly perceive different tradeoffs between lives and livelihoods. We therefore include the dummy variable female_governor in the regression.
Table E.2 in the appendix reports the results, both for duration (columns (1)–(3)) and stringency (columns (4)–(6)) as the dependent variable.42 None of the three variables enters significantly and none of them, when introduced in the baseline regression, importantly affects the estimated coefficients on the other controls.43 We conclude that state legislatures, knife-edge political races, and the governor’s gender play at most minor roles in the determination of early COVID-19 interventions.
Fourth and finally, we test whether the role of career concerns differs across party affiliations. To do so, we include the interaction of republican and career_concerns as an additional regressor. Given the small sample size, it is difficult to make conclusive statements but Table E.3 in the appendix reports the results: We find no evidence for a difference in the importance of career concerns across party lines although the estimated coefficients on career_concerns are slightly smaller and no longer significant in the specification with stringency as the dependent variable.44
5. Conclusion
We have shown that in the early stage of the COVID-19 epidemic in the US, state governments responded quite differently both in terms of the restrictiveness of their measures and the duration of lockdowns. Based on a simple model that merges epidemiological, economic, and politico-economic arguments we have proposed a framework to rationalize these differences. The framework links government imposed restrictions on activity, which slow down infections, to fundamentals that affect the societal tradeoffs between lives and livelihoods, and to political factors that modify these tradeoffs.
We have been careful to conceptually distinguish between adjustments in activity that individuals undertake voluntarily and those that are a consequence of government imposed restrictions. To identify the effects of political factors in the data we have made the assumption that those factors did not affect how individuals would have chosen their activity in the absence of restrictions. Under this identifying assumption we find that Republican party affiliation substantially reduced the restrictiveness of government measures, even when we control for the political views among the electorate.
In addition, we find evidence for a career-concerns channel: Governors that sought re-election in the near future imposed substantially harsher restrictions. There is also evidence of complementarities between voluntary and government imposed activity reductions. This could suggest that factors such as interpersonal networks and narratives constitute important elements of successful government campaigns to check infections. Other factors such as divided government, gender of the governor, or closeness of elections do not appear to have played an important role for the early COVID-19 response.
Our analysis constitutes a first step. Better data or more specific theories could be used to improve upon it. For example, a more reliable measure of voluntary activity reductions in the absence of government restrictions could help refine the identification of complementarities. And a theory of how industry structure interacts with campaign contributions and career concerns could help identify the role of these two dynamic political channels separately. Of course, the analysis could also be extended to other federalist countries. We leave these next steps for future research.
For valuable comments and discussions we thank Yongseok Shin and Guillaume Vandenbroucke as well as our discussant Sang Yoon (Tim) Lee, Agustín Casas, Carlos Sanz, and participants at the Gerzensee/JEDC/SNB/St. Louis Fed/University of Bern conference.
The federal government faced legal hurdles with respect to its ability to impose national or regional lockdowns. On March 28, president Trump considered ordering a two-week quarantine of New York, New Jersey, and parts of Connecticut. However, he later backed away because of doubt about enforceability. Instead, the Centers for Disease Control and Prevention issued a domestic-travel advisory for the area. See “Why There’s No National Lockdown,” The Atlantic, March 31, 2020.
Other recent papers include Alvarez et al. (2021), Farboodi et al. (2021), Garibaldi et al. (2020) or Toxvaerd (2020) and the references cited therein.
The former measures are school closing, workplace closing, cancellation of public events, restrictions on gathering size, closure of public transport, stay-at-home requirements, restrictions on internal movement, and restrictions on international travel; and the latter concerns state-wide public information campaigns.
To normalize the integral value of a state we divide by the average integral value across the 45 states that had a lockdown.
We follow the notation introduced by Kermack and McKendrick (1927).
For a discussion, see Hethcote (2000, p. 602).
The simulation is based on parameter values which reflect the scientific consensus in spring 2020. See Gonzalez-Eiras and Niepelt (2020c) for details.
We disregard that the epidemiological state might affect .
See for example Eichenbaum et al. (2021).
For a discussion, see for example Persson and Tabellini (2000, 5.4).
For a discussion of punishment and career concerns, see Barro (1973), Ferejohn (1986), Alesina and Cukierman (1990), Rogoff (1990) or Persson and Tabellini (2000, 4.4, 4.5).
Using state level data on campaign contributions between 1998 and 2021 from https://www.followthemoney.org/ we find that campaign contributions are negatively correlated with state-level unemployment when controlling for state and time fixed effects.
Mian et al. (2010) study the support by politicians for the American Housing Rescue and Foreclosure Prevention Act and the Emergency Economic Stabilization Act of 2008. They find that the choices of policy makers reflected ideology, interests of the constituency, and the interests of donors in the financial industry; and that only senators running for re-election responded to constituency interests and financial sector campaign contributions.
Note that even Ramsey optimal-lockdown programs may yield paths that are not that different from largely constant paths, see e.g. Alvarez et al. (2021) or Gonzalez-Eiras and Niepelt (2020a).
Note that (6) increases in (when which holds true in equilibrium) and that the positive relation between and the livelihoods objective is also plausible for other reasons: Lower activity lowers the infection rate and thereby extends the period up to peak infections which constitutes a plausible ex-ante measure of the duration of activity reductions. This follows from Proposition 2 for plausible parameter values. Even if restrictions are not lifted after duration the actual duration may still be proportional to . Peak infections also are a time when voters’ attention is likely to divert from the pandemic to other issues. In conclusion, lower activity plausibly increases livelihood losses in size and expected duration.
E.g., a value of indicates that mobility fell short of its baseline value. The baseline value for a particular weekday is the median value for the corresponding weekday during the 5-week period January 3–February 6, 2020.
We find similar results when we use an average mobility measure. This average includes workplace, retail and recreation, transit stations, and residential mobility.
See https://www.kff.org/other/state-indicator/icu-beds/. For Puerto Rico we use a report by America’s Emergency Care Environment for 2014 showing that ICU beds per capita were of the average in the U.S. at the time. See http://www.emreportcard.org/Puerto-Rico/.
The index uses two-digit NAICS industry-level data on the share of jobs that can be done from home constructed by Dingel and Neiman (2020). The code is due to Ole Agersnap. Data is available online at https://github.com/jdingel/DingelNeiman-workathome/blob/master/state_measures.
For details see https://oui.doleta.gov/unemploy/ui_replacement_rates.asp.
See www.ballotpedia.org.
There are fourteen states that held scheduled gubernatorial elections in 2020 or 2021. In New Hampshire and Vermont governors are elected for two years. In both states elections were held in November 2020 so the governors were more than half-way through their terms when they imposed lockdowns. Accordingly, we assign a value of one to the variable early_election in these states.
In certain phases of a pandemic a government might want to institute an “inverse lockdown”, i.e. stimulate rather than restrict activity, see Gonzalez-Eiras and Niepelt (2020b).
We exclude Puerto Rico where the lockdown started on March 15.
According to the point estimates, the two political variables account for less than one percent of activity change, much less than one standard deviation (see Table 2).
The highest variance inflation factor is 3.43 for wfh.
In particular, we consider school closures, restrictions on restaurant businesses, and gathering limitations, all of which varied across states by March 18. None of these three variables, nor an index that combines them, turns out to be statistically significant.
The Act was signed into law on March 27, 2020. It included a federal supplement of $600 per week for recipients of state unemployment benefits. As can be seen from Table 2 the supplement significantly increased unemployment replacement rates.
We do not estimate a Probit specification because the variable republican would be dropped from the regression as predicts perfectly. If a Probit specification could be estimated without dropping observations the marginal effects would be close to the OLS estimates (Angrist and Pischke, 2009).
This perception might be correct; some groups with low earnings and members of traditionally Democratic-voting minority groups have been more affected by the pandemic, see e.g. Chen and Krieger (2020). However, such asymmetric exposure might not have been evident in the early days of the pandemic when decisions about lockdowns were taken.
In the United States, 36 states impose term limits for governors. Of the 52 states, 41 governors could seek re-election. The only governor who was legally able to seek re-election but chose not to do so was Gary Herbert in Utah. The filing deadline for gubernatorial candidates was March 19, 2020. The decision not to seek re-election therefore was taken prior to the pandemic and independently of the governor’s handling of it. Variable career_concerns takes the value 1 for 11 states among which 10 instituted a lockdown.
We measure the size of the government by per capita spending in the fiscal year 2017. The data source is www.ballotpedia.org which uses the State Expenditure Reports (2015–2017) from the National Association of State Budget Officers.
Note that all these candidate variables plausibly were determined before the party affiliation of the governor such that the added controls in the estimating equation are not endogenous. See Angrist and Pischke (2009).
Adding the measure for education gives rise to a potential collinearity problem, however. The variance inflation factor of our measure of education is close to 10.
We group Puerto Rico with the South.
We obtain similar results in Tobit regressions, reported below.
Only in Wisconsin did the Supreme Court overturn the state’s stay-at-home order when ruling on a lawsuit started by the leaders of the state’s Republican legislature.
For an analysis of the role of divided government see e.g. Alesina and Rosenthal (1996).
The difference is measured in percentage points and the data source is Ballotpedia.
See, for example, Chattopadhyay and Duflo (2004).
Of the 52 states, 14 had close elections, 13 featured a divided government and 11 had female governors. For the 45 states that instituted a lockdown, the corresponding numbers are 12, 13, and 10, respectively.
The point estimates for female_governor are the only ones that are economically significant.
Furthermore, the variance inflation factor for ideology is relatively large (5.27) in this regression.
We disregard discrepancies without effect on our measure of lockdown duration. A situation with “irrelevant” discrepancies occurs, for example, when both data sources imply that a stay-at-home order came into effect on March 25, while there is disagreement about the fact whether businesses were closed three or five days later.
There is no need to also include in the fundamentals because, anticipating the empirical implementation, does not exhibit any meaningful relative variation across states.
Appendix A. Data and data sources
Data on lockdown duration stems from executive or public health orders or proclamations. Our primary source is the Council of State Governments, web.csg.org/covid19/executive-orders/. We also use information from state government websites. There is significant heterogeneity with respect to the kind of businesses that were closed. Where a distinction is possible we prioritize restrictions on manufacturing over those on retail businesses. Table A.1 lists the start and end dates we identify.
Table A1.
Beginning and end dates of lockdowns.
| State | Stay at home | Non-essential | End stay at | End non-essential |
|---|---|---|---|---|
| business closure | home | business closure | ||
| Alabama | 4/4 | 4/30 | ||
| Alaska | 3/28 | 3/28 | 4/24 | 4/24 |
| Arizona | 3/31 | 5/16 | ||
| California | 3/19 | 5/29 | ||
| Colorado | 3/26 | 3/26 | 4/27 | 5/4 |
| Connecticut | 3/23 | 5/20 | ||
| Delaware | 3/24 | 3/24 | 6/1 | 5/22 |
| District of Columbia | 4/1 | 3/25 | 5/29 | 5/29 |
| Florida | 4/3 | 5/18 | ||
| Georgia | 4/3 | 5/1 | ||
| Hawaii | 3/25 | 3/25 | 5/15 | |
| Idaho | 3/25 | 3/25 | 5/1 | 5/1 |
| Illinois | 3/21 | 3/21 | 5/29 | 5/29 |
| Indiana | 3/25 | 3/25 | 5/18 | 5/18 |
| Kansas | 3/30 | 3/30 | 5/4 | 5/4 |
| Kentucky | 3/26 | 5/11 | ||
| Louisiana | 3/23 | 3/23 | 5/15 | 5/15 |
| Maine | 4/2 | 5/31 | ||
| Maryland | 3/30 | 3/23 | 5/15 | 5/15 |
| Massachusetts | 3/24 | 5/18 | 5/18 | |
| Michigan | 3/24 | 3/24 | 6/1 | 5/26 |
| Minnesota | 3/28 | 5/18 | 4/27 | |
| Mississippi | 4/3 | 4/3 | 4/27 | 4/27 |
| Missouri | 4/6 | 5/4 | 5/4 | |
| Montana | 3/28 | 3/28 | 4/26 | 4/27 |
| Nevada | 3/31 | 3/21 | 5/9 | 5/9 |
| New Hampshire | 3/28 | 3/28 | 6/16 | 5/11 |
| New Jersey | 3/21 | 3/21 | 6/9 | 5/18 |
| New Mexico | 3/24 | 3/24 | 6/1 | 5/15 |
| New York | 3/22 | 3/22 | 6/8 | 5/26 |
| North Carolina | 3/30 | 3/30 | 5/22 | 5/8 |
| Ohio | 3/24 | 3/24 | 5/19 | 5/4 |
| Oklahoma | 3/25 | 4/24 | ||
| Oregon | 3/23 | 6/19 | ||
| Pennsylvania | 4/1 | 3/21 | 6/5 | 6/5 |
| Puerto Rico | 3/15 | 3/15 | 6/16 | 5/10 |
| Rhode Island | 3/28 | 3/30 | 5/9 | 5/9 |
| South Carolina | 4/7 | 5/4 | ||
| Tennessee | 4/2 | 4/1 | 5/1 | 5/1 |
| Texas | 4/2 | 4/2 | 4/30 | 5/1 |
| Vermont | 3/25 | 3/25 | 5/15 | 4/27 |
| Virginia | 3/30 | 5/29 | ||
| Washington | 3/23 | 3/25 | 6/1 | 5/21 |
| West Virginia | 3/24 | 3/24 | 5/4 | 5/21 |
| Wisconsin | 3/25 | 3/25 | 5/13 | 5/11 |
Source: State executive or public health orders or proclamations. See the explanations in the text.
Raifman et al. (2020) also determine start and end dates of restrictions. In the following we highlight differences in the identified start or end dates and we explain the reasons for our timing assumptions:45
-
•
California: Business reopening started on May 8. By May 29, most counties had reached “phase 2” and curbside retail, dine-in restaurants, shopping malls, manufacturing, business offices and some other services resumed operation. We view this as the de facto end of the lockdown although the stay-at-home order remained in place until 2021.
-
•
Colorado: Retail and personal services could reopen on May 1, when they implemented best practices. Non-critical offices could open on May 4, subject to a 50 percent capacity cap. We use the latter date.
-
•
Hawaii: The stay-at-home order was not formally relaxed for a long time. But businesses started to reopen on May 7, (Seventh Supplementary Emergency Proclamation). We use May 15, as the reopening date, the day retail businesses reopened in Honolulu City and County, and we treat this as the de facto end of the lockdown.
-
•
Illinois: Businesses reopened after executive order 2020-38 of May 29.
-
•
Maine: Executive order 28 ordered to stay at home effective of at 12:01 a.m. on April 2. Executive order 49 extended the stay-at-home order until May 31.
-
•
Michigan: Executive order 2020-110 lifted the stay-at-home order at June 1.
-
•
New Hampshire: The stay-at-home order expired on June 15.
-
•
New Jersey: The stay-at-home order was lifted on June 9.
-
•
New Mexico: Public health order 060120 of June 1, extended the stay-at-home order but relaxed a number of additional restrictions on restaurants, retail businesses, exercise facilities, pools, and places of lodging. We treat this as the de facto end of the lockdown.
-
•
New York: Executive order 202–31 set a time table and contingencies for reopening. By June 8, Mid-Hudson entered phase 1, so all regions except New York City and Long Island could reopen. On June 8, reopening started in New York City. We treat this as the de facto end of the lockdown.
-
•
Ohio: The stay-at-home order was lifted on May 19, although it was originally set to expire by May 29.
-
•
Oklahoma: The Fourth Amended Executive Order 2020–07 closes businesses on March 25.
-
•
Oregon: On June 19, all counties entered phase 1 of reopening. We treat this as the de facto end of the lockdown.
-
•
Pennsylvania: Executive order 2020–0319 closing businesses established two start dates: March 19, 8 p.m. for indoors dinning, and March 21, 12:01 a.m. for non-life sustaining businesses. We use the latter as the start date of the lockdown. According to the Department of Health’s Yellow Phase Order, reopening started on May 8. All counties were considered to be in the Yellow phase by June 5. We treat this as the de facto end of the lockdown.
-
•
Texas: Executive order GA-14 of March 31, ordered non-essential businesses to close and became effective on April 2.
-
•
Virginia: Executive orders 61 and 62 set time tables and contingencies for reopening. Northern Virginia shifted to Phase One by May 29. We treat this as the de facto end of the lockdown.
-
•
Washington: The stay-at-home order expired on June 1.
-
•
West Virginia: Executive order 32-20 set rules and a timetable for reopening. The reopening dates were May 5, for small businesses, restaurants (outdoor dining), religious entities, personal care; May 18, for gyms; and May 21, for restaurants (indoor dining), large retail stores and indoor malls. We treat the last date as the end date for business closures and thus the end of the lockdown.
Appendix B. Proof of Proposition 1
Dividing Eq. (2) by Eq. (1) (subject to ) yields
Integrating yields . Since and are given the constant equals and the first result follows. The second result follows from the fact that reaches a maximum when as argued in the text. The third equation follows since . Totally differentiating that equation and collecting terms yields
Since we conclude that is increasing in .
Appendix C. Solving the modified SIR model
Let . Following Bohner et al. (2019), let for . We have
such that
where . Substituting into Eq. (1) yields
which has the solution
| (C.1) |
Accordingly, we can solve Eq. (2) for
| (C.2) |
and Eq. (3) for
| (C.3) |
where we use the fact that the population size equals unity.
When is constant at value the solution reduces to
| (C.4) |
| (C.5) |
| (C.6) |
where .
Appendix D. Proof of Proposition 2
From Eq. (1) with and (2), implies . Using Eqs. (C.4) and (C.5) this implies
The result for then follows. Substituting into Eq. (C.5) yields the result for .
Appendix E. Robustness checks
Table E1.
Determinants of restrictions: Tobit regressions.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| duration | duration | stringency | stringency | |
| republican | -15.75 | -17.78 | -0.284 | -0.321 |
| (-3.27) | (-4.21) | (-2.81) | (-3.57) | |
| early_election | 8.084 | 0.139 | ||
| (1.29) | (1.11) | |||
| career_concerns | 15.69 | 0.297 | ||
| (2.44) | (2.33) | |||
| wfh | 111.0 | 130.8 | 3.246 | 3.507 |
| (1.33) | (1.86) | (2.09) | (2.56) | |
| ideology | -125.5 | -119.8 | -2.431 | -2.248 |
| (-3.29) | (-3.48) | (-3.18) | (-3.25) | |
| ui_supplement | -13.98 | -10.78 | 0.138 | 0.190 |
| (-0.53) | (-0.47) | (0.23) | (0.36) | |
| urbanization | 0.0445 | 0.000120 | 0.000220 | |
| (0.24) | (0.03) | (0.07) | ||
| share65+ | 5.278 | 4.567 | 0.107 | 0.0939 |
| (3.05) | (3.16) | (2.95) | (3.00) | |
| icu | 4.393 | 3.859 | 0.0685 | 0.0563 |
| (1.11) | (1.07) | (0.83) | (0.73) | |
| initial_infections | -1.519 | -1.634 | -0.0307 | -0.0319 |
| (-3.54) | (-4.52) | (-3.74) | (-4.02) | |
| constant | -10.16 | -6.626 | -1.018 | -1.023 |
| (-0.16) | (-0.13) | (-0.76) | (-0.88) | |
| N | 52 | 52 | 52 | 52 |
| Adj. | 0.12 | 0.13 | 0.55 | 0.61 |
Tobit regressions, robust t statistics in parentheses , ,
Table E2.
Close elections, divided government and governor gender.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| duration | duration | duration | stringency | stringency | stringency | |
| republican | -12.48 | -12.42 | -11.37 | -0.212 | -0.217 | -0.192 |
| (-3.14) | (-3.30) | (-2.86) | (-2.42) | (-2.54) | (-2.15) | |
| career_concerns | 15.10 | 15.14 | 16.99 | 0.270 | 0.271 | 0.308 |
| (2.70) | (2.71) | (3.17) | (2.39) | (2.41) | (2.78) | |
| wfh | 113.2 | 111.5 | 103.9 | 3.254 | 3.219 | 3.050 |
| (1.72) | (1.72) | (1.55) | (2.55) | (2.55) | (2.49) | |
| ideology | -59.06 | -57.28 | -54.57 | -1.056 | -1.007 | -0.940 |
| (-1.70) | (-1.49) | (-1.47) | (-1.40) | (-1.23) | (-1.22) | |
| ui_supplement | 1.619 | 1.901 | -11.46 | 0.437 | 0.446 | 0.182 |
| (0.09) | (0.11) | (-0.60) | (1.04) | (1.03) | (0.42) | |
| urbanization | 0.123 | 0.140 | 0.134 | 0.00186 | 0.00206 | 0.00223 |
| (0.84) | (0.94) | (0.86) | (0.61) | (0.67) | (0.77) | |
| share65+ | 2.768 | 2.803 | 2.572 | 0.0565 | 0.0579 | 0.0533 |
| (2.56) | (2.60) | (2.56) | (2.42) | (2.51) | (2.54) | |
| icu | -0.705 | -0.715 | -1.739 | -0.0419 | -0.0429 | -0.0629 |
| (-0.19) | (-0.19) | (-0.45) | (-0.55) | (-0.55) | (-0.81) | |
| initial_infections | -0.824 | -0.811 | -0.951 | -0.0154 | -0.0152 | -0.0178 |
| (-1.57) | (-1.47) | (-1.56) | (-1.62) | (-1.48) | (-1.66) | |
| close | 1.031 | 0.0406 | ||||
| (0.20) | (0.37) | |||||
| divided | 0.728 | -0.00712 | ||||
| (0.16) | (-0.08) | |||||
| female_governor | 9.887 | 0.196 | ||||
| (1.42) | (1.57) | |||||
| constant | -11.09 | -13.50 | 7.204 | -1.034 | -1.077 | -0.698 |
| (-0.26) | (-0.31) | (0.18) | (-1.07) | (-1.09) | (-0.80) | |
| N | 45 | 45 | 45 | 45 | 45 | 45 |
| Adj. | 0.539 | 0.539 | 0.575 | 0.549 | 0.547 | 0.579 |
OLS regressions, robust t statistics in parentheses , ,
Table E3.
Partisan effects of career concerns.
| (1) | (2) | |
|---|---|---|
| duration | stringency | |
| republican | -15.70 | -0.287 |
| (-3.63) | (-3.01) | |
| career_concerns | 8.394 | 0.117 |
| (1.72) | (1.55) | |
| republican*career_concerns | 13.26 | 0.304 |
| (1.39) | (1.54) | |
| wfh | 112.9 | 3.229 |
| (1.73) | (2.59) | |
| ideology | -49.99 | -0.826 |
| (-1.36) | (-1.04) | |
| ui_supplement | -0.767 | 0.386 |
| (-0.05) | (1.05) | |
| urbanization | 0.177 | 0.00323 |
| (1.27) | (1.11) | |
| share65+ | 2.550 | 0.0521 |
| (2.66) | (2.55) | |
| icu | -1.348 | -0.0570 |
| (-0.37) | (-0.76) | |
| initial_infections | -0.806 | -0.0149 |
| (-1.47) | (-1.50) | |
| constant | -10.05 | -1.033 |
| (-0.26) | (-1.15) | |
| N | 45 | 45 |
| Adj. | 0.563 | 0.576 |
OLS regressions, robust t statistics in parentheses , ,
References
- Alesina A. Credibility and policy convergence in a two-party system with rational voters. Am. Econ. Rev. 1988;78(4):796–805. [Google Scholar]
- Alesina A., Cukierman A. The politics of ambiguity. Q. J. Econ. 1990;105(4):829–850. [Google Scholar]
- Alesina A., Rosenthal H. A theory of divided government. Econometrica. 1996;64(6):1311–1341. [Google Scholar]
- Allcott H., Boxell L., Conway J., Gentzkow M., Thaler M., Yang D. Polarization and public health: partisan differences in social distancing during the coronavirus pandemic. J. Public Econ. 2020;191:104254. doi: 10.1016/j.jpubeco.2020.104254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez F., Argente D., Lippi F. A simple planning problem for COVID-19 lockdown. Am. Econ. Rev. Insights. 2021;3(3):367–382. [Google Scholar]
- Angrist J.D., Pischke J.S. Princeton University Press, Princeton; 2009. Mostly Harmless Econometrics. [Google Scholar]
- Atkeson, A., 2020. What will be the economic impact of COVID-19 in the US? Rough estimates of disease scenarios. Working Paper 26867, NBER, Cambridge, Massachusetts.
- Aum, S., Lee, S. Y., Shin, Y., 2020. Who should work from home during a pandemic? The wage-infection trade-off. Working Paper 27908, NBER, Cambridge, Massachusetts.
- Baccini L., Bradeur A. Explaining governors’ response to the COVID-19 pandemic in the United States. Am. Polit. Res. 2021;49(2):215–220. [Google Scholar]
- Baek C., McCrory P.B., Messer T., Mui P. Unemployment effects of stay-at-home orders: evidence from high-frequency claims data. Rev. Econ. Stat. 2021:1–15. [Google Scholar]
- Bailey N.T.J. 2nd ed. Hafner Press, New York; 1975. The Mathematical Theory of Infectious Diseases and its Applications. [Google Scholar]
- Baron D.P. Electoral competition with informed and uninformed voters. Am. Polit. Sci. Rev. 1994;88(1):33–47. [Google Scholar]
- Barro R.J. The control of politicians: an economic model. Public Choice. 1973;14(1):19–42. [Google Scholar]
- Besley T., Coate S. An economic model of representative democracy. Q. J. Econ. 1997;112(1):85–114. [Google Scholar]
- Besley T., Persson T., Sturm D.M. Political competition, policy and growth: theory and evidence from the us. Rev. Econ. Stud. 2010;77(4):1329–1352. [Google Scholar]
- Bohner M., Streipert S., Torres D.F.M. Exact solution to a dynamic SIR model. Nonlinear Anal. Hybrid Syst. 2019;32:228–238. [Google Scholar]
- Chattopadhyay R., Duflo E. Women as policy makers: evidence from a randomized policy experiment in India. Econometrica. 2004;72(5):1409–1443. [Google Scholar]
- Chen J.T., Krieger N. Revealing the unequal burden of COVID-19 by income, race/ethnicity, and household crowding: US county versus zip code analyses. J. Public Health Manag. Pract. 2020;27(1):S43–S56. doi: 10.1097/PHH.0000000000001263. [DOI] [PubMed] [Google Scholar]
- Dave D., Friedson A.I., Matsuzawa K., Sabia J.J. When do shelter-in-place orders fight COVID-19 best? Policy heterogeneity across states and adoption time. Econ. Inq. 2021;59(1):29–52. doi: 10.1111/ecin.12944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dingel J.I., Neiman B. How many jobs can be done at home. J. Public Econ. 2020;189:104235. doi: 10.1016/j.jpubeco.2020.104235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downs A. Harper and Row, New York; 1957. An Economic Theory of Democracy. [Google Scholar]
- Eichenbaum, M. S., Rebelo, S., Trabandt, M., 2020. The macroeconomics of epidemics. Working Paper 26882, NBER, Cambridge, Massachusetts.
- Eichenbaum, M. S., Rebelo, S., Trabandt, M., 2021. Inequality in life and death. Working Paper 29063, NBER, Cambridge, Massachusetts.
- Farboodi M., Jarosch G., Shimer R. Internal and external effects of social distancing in a pandemic. J. Econ. Theory. 2021;196(C):105293. [Google Scholar]
- Ferejohn J. Incumbent performance and electoral control. Public Choice. 1986;50:5–26. [Google Scholar]
- Frey C.B., Chen C., Presidente G. Democracy, culture, and contagion: political regimes and countries’ responsiveness to COVID-19. Covid Econ. 2020;18:222–238. doi: 10.1016/j.jebo.2023.04.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garibaldi, P., Pissarides, C., Moen, E. R., 2020. Static and dynamic inefficiencies in an optimizing model of epidemics. Discussion Paper 15439, CEPR, London, UK.
- Gersovitz M., Hammer J.S. The economical control of infectious diseases. Econ. J. 2004;114:1–27. [Google Scholar]
- Gilboa I., Schmeidler D. Maxmin expected utility with non-unique prior. J. Math. Econ. 1989;18(2):141–153. [Google Scholar]
- Gonzalez-Eiras M., Niepelt D. On the optimal ‘lockdown’ during an epidemic. Covid Econ. 2020;7:68–87. [Google Scholar]
- Gonzalez-Eiras, M., Niepelt, D., 2020b. Optimally controlling an epidemic. Discussion Paper 15541, CEPR.
- Gonzalez-Eiras, M., Niepelt, D., 2020c. Tractable epidemiological models for economic analysis. Discussion Paper 14791, CEPR.
- Goolsbee A., Syverson C. Fear, lockdown, and diversion: comparing drivers of pandemic economic decline 2020. J. Public Econ. 2021;193:104311. doi: 10.1016/j.jpubeco.2020.104311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hale T., Angrist N., Goldszmidt R., Kira B., Petherick A., Phillips T., Webster S., Cameron-Blake E., Hallas Laura Majumdar S., Tatlow H. A global panel database of pandemic policies (Oxford COVID-19 government response tracker) Nat. Hum. Behav. 2021;5(4):529–538. doi: 10.1038/s41562-021-01079-8. [DOI] [PubMed] [Google Scholar]
- Hansen L.P., Sargent T.J. In: Handbook of Monetary Economics, Vol. 3B. Friedman B.M., Woodford M., editors. Elsevier, Amsterdam; 2011. Wanting Robustness in Macroeconomics; pp. 1097–1157. [Google Scholar]; Chapter 20
- Herrera, H., Konradt, M., Ordoñez, G., Trebesch, C., 2020. Corona politics: the cost of mismanaging pandemics. Unpublished.
- Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653. [Google Scholar]
- Hotelling H. Stability in competition. Econ. J. 1929;39(153):41–57. [Google Scholar]
- Iaryczower, M., Lopez-Moctezuma, G., Meirowitz, A., 2021. Career concerns and the dynamics of electoral accountability. Unpublished, Princeton University.
- Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Ser. A. 1927;115(772):700–721. [Google Scholar]
- Knight F.H. Houghton Mifflin Company, Boston and New York; 1921. Risk, Uncertainty and Profit. [Google Scholar]
- Krueger, D., Uhlig, H., Xie, T., 2020. Macroeconomic dynamics and reallocation in an epidemic: evaluating the “Swedish Solution”. Working Paper 27047, NBER, Cambridge, Massachusetts.
- Lindbeck A., Weibull J.W. Balanced-budget redistribution as the outcome of political competition. Public Choice. 1987;52:273–297. [Google Scholar]
- LLC, G., 2020. Google COVID-19 community mobility reports. https://www.google.com/covid19/mobility/, accessed April 27, 2020.
- Lott J.R. A simple explanation for why campaign expenditures are increasing: the government is getting bigger. J. Law Econ. 2000;43(2):359–393. [Google Scholar]
- Mian A., Sufi A., Trebbi F. The political economy of the US mortgage default crisis. Am. Econ. Rev. 2010;100(5):1967–1998. [Google Scholar]
- Olson M. Harvard University Press, Cambridge, Massachusetts; 1965. The Logic of Collective Action: Public Goods and the Theory of Groups. [Google Scholar]
- Osborne M.J., Slivinski A. A model of political competition with citizen-candidates. Q. J. Econ. 1996;111(1):65–96. [Google Scholar]
- Persson T., Tabellini G. MIT Press, Cambridge, Massachusetts; 2000. Political Economics. [Google Scholar]
- Pulejo M., Querubín P. Electoral concerns reduce restrictive measures during the COVID-19 pandemic. J. Public Econ. 2021;198:104387. doi: 10.1016/j.jpubeco.2021.104387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raifman, J., Nocka, K., Jones, D., Bor, J., Lipson, S., Jay, J., Chan, P., Galea, S., 2020. COVID-19 US state policy database. Ann Arbor. https://tinyurl.com/statepolicysources.
- Rogoff K. Equilibrium political budget cycles. Am. Econ. Rev. 1990;80:21–36. [Google Scholar]
- Toxvaerd F. Cambridge Institute for New Economic Thinking, Cambridge; 2020. Equilibrium Social Distancing. [Google Scholar]; Working Paper 2020/08