Abstract
In the context of the outbreak of coronavirus disease (COVID-19), this paper proposes an innovative and systematic decision support model based on Bayesian networks (BNs) to identify and control the risk of COVID-19 patients spreading the virus, which requires the following three steps. First, by consulting the related literature and combining this with expert knowledge, we identify and classify the characteristics (risk factors) of COVID-19 and obtain a conceptual framework for COVID-19 Risk Assessment Bayesian Networks (CRABNs). Second, data on COVID-19 patients with expert scoring results on patient risk levels were collected from hospitals in Hubei Province of China and are used as the training set, and the structure and parameters of the CRABNs model are obtained through machine learning. Finally, we propose two indicators, namely, Model Bias and Model Accuracy, and use the remaining data to verify the feasibility and effectiveness of the CRABNs model to ensure that there are no significant differences between the predicted results of the model and the actual results provided by experts who have relevant experience in treating COVID-19. At the same time, we compared the CRABNs model with the support vector machine (SVM), random forest (RF), and k-nearest neighbour (KNN) models through four indicators: accuracy, sensitivity, specificity, and F-score. The results suggest the reliability of the model and show that it has promising application potential. The proposed model can be used globally by doctors in hospitals as a decision support tool to improve the accuracy of assessing the severity of COVID-19 symptoms in patients. Furthermore, with the further improvement of the model in the future, it can be used for risk assessments in the field of epidemics.
Keywords: Decision support analysis, Bayesian networks (BNs), COVID-19, Risk identification and control, Machine learning
1. Introduction
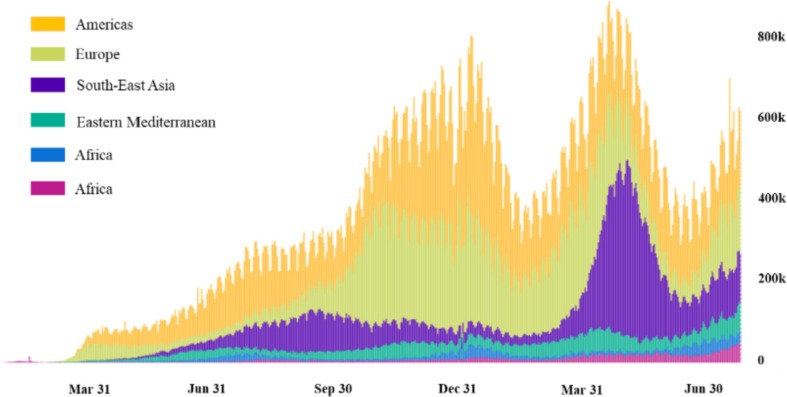
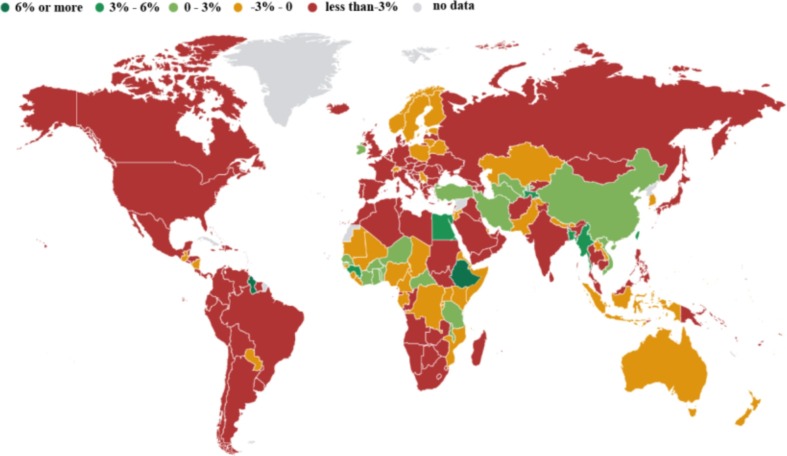
At the end of 2019, coronavirus disease 2019 (COVID-19) swept the world. As of November 27, 2020, the cumulative number of patients and deaths stemming from COVID-19 worldwide were 60,534,526 and 1,426,101, respectively (WHO, 2020). At present, except for a few countries, the epidemic situation in most countries has not been completely alleviated or has become even more serious. Fig. 1 presents the daily increase in the number of confirmed COVID-19 cases in different countries and regions from January 2020 to June 2021 (WHO, 2021). The current epidemic situation is still very serious and is not optimistic. The spread of COVID-19 has caused various economic recession in various countries; Fig. 2 presents annual percentage of GDP growth of each country in the previous year by the beginning of 2021 (IMF, 2021). COVID-19 has caused a recession of the global economy, which is of public concern. With the continuous spread of the epidemic, medical resources have inevitably become strained or have even collapsed (Armocida, et al., 2020), and many patients cannot receive timely diagnoses or treatment. Because of the uncertainty regarding the risk of COVID-19, public concern has also intensified. In general, due to its severe contagiousness, COVID-19 has not only caused a national economic recession but also a shortage of medical resources, which have caused social instability. Therefore, it is necessary to analyse the severity of symptoms of patients who are affected by COVID-19.
Fig. 1.
Data map of newly confirmed cases from January 2020 to June 2021.
Fig. 2.
Annual percentage of GDP growth of each country in the previous year by the beginning of 2021.
Although PCR or lateral flow COVID-19 test is an efficient method for COVID-19 detection, the application of these two methods is basically in the form of detection reagent, and it is more difficult than conventional blood routine test. Especially in some underdeveloped areas, it is difficult to obtain enough nucleic acid detection reagents to detect COVID-19 patients. Therefore, in some places where there are insufficient numbers of diagnostic kits and a lack of nucleic acid detection equipment, the identification of COVID-19 patients still depends on the judgement of doctors. Based on certain surface characteristics and laboratory results, doctors can judge whether a patient is sick and the severity of their symptoms. However, the shortage of medical resources not only affects the detection progress of doctors but also causes a waste of medical resources if the symptom severities of patients are misjudged. Therefore, it is necessary to establish a mechanism or model to predict the risk level of COVID-19 patients to help doctors make decisions and improve diagnosis efficiency. In particular, after accurately judging the degree of the patient's disease, doctors can provide more targeted treatment to them, which not only contributes to the rational use of medical resources, but also helps to control of the spread of COVID-19.
Although many scholars have conducted related research on epidemics, including clinical and epidemiological investigations (Alhazzani et al., 2020, Zhou et al., 2020), viral genome analysis (Zhang, et al, 2020), vaccine development (Ahn, et al, 2020), establishment of evolution and transmission models (Yadav et al., 2020, da Silva et al., 2020), and public sector epidemic management mechanisms (Fu, et al, 2020), there are relatively few studies on the COVID-19 risk for patients (De Nardo et al., 2020, Williams et al., 2020, Zhang et al., 2020). At the same time, although big data technology has been widely used in the medical field, neural networks and support vector machines are often used in medical imaging and text recognition (Sergio and Patricia, 2021, Mohammad and Shamim Hossain, 2020, Shaban et al., 2020), while Bayesian networks (BNs) are relatively less frequently used for analysis (Nour, Cömert, & Polat, 2020). Risk control is a dynamic identification process in which the relevant parameters change with changes in time and space, and the medical field is uncertain. With the ability to integrate prior knowledge and sample data, BNs can provide a strong tool for knowledge representation and reasoning in a dynamic environment and provide a coherent and intuitive representation of uncertain domain knowledge (Bucci et al., 2011, Nikovski, 2000). Compared with neural networks and support vector machines, BNs perform more effectively in advanced classification tasks, such as data mining, fault monitoring, and bioinformatics (Xu, 2012). Therefore, this study applies the Bayesian network concept in its analysis.
The purpose of this study was to construct a BN model to analyse the severity of COVID-19 patient symptoms by identifying the characteristics associated with COVID-19. Therefore, we (a) find and classify the characteristics of COVID-19 patients, (b) build a BN model through machine learning and simultaneously determine the parameters of the model, and (c) verify the accuracy of the model through patient data that were collected from Hubei.
2. Research method and framework
2.1. Bayesian networks
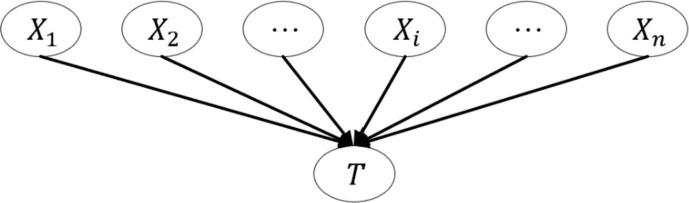
Bayesian networks provide a method for the expression and reasoning of uncertain knowledge in the medical field and have been widely used in clinical diagnosis and risk prediction (Velikova, Lucas, Samulski, & Karssemeijer, 2013). A BN is a directed acyclic graph (DAG), where each node represents an attribute (data variable), and the directed edges between nodes represent the probability dependences between nodes (from a parent node to its child node), which indicate that the value of one node will affect the value of another node. Fig. 3 presents a simple BN model with n attributes, where represents n different variables (child nodes) and T represents an event (parent node). Event T is simultaneously affected by n variables; that is, if T is regarded as a risk event, then are the risk factors for event T.
Fig. 3.
A simple BN model with n attributes.
2.2. Model design
The design of a BN model includes two elements: structure learning and parameter learning. The purpose of structure learning is to find a suitable DAG and determine the relationships among nodes, while the purpose of parameter learning is to determine the conditional probability distribution of each node in the established BN model (Cooper and Herskovits, 1992, Oniśko et al., 2001). In general, three methods can be used to design a BN model: (a) structure and parameter learning that completely rely on expert knowledge; (b) structure and parameter learning that completely rely on training data; and (c) a BN structure that is designed by using expert prior knowledge, and the parameters are obtained through training data learning.
Because of the uncertainty of COVID-19 itself, the results of a BN model that is designed using the first method may not match the outcomes of the actual situation (Cano, Masegosa & Moral, 2011). The second method involves using real data to obtain the model through machine learning, which may exhibit strong adaptability in result predictions. However, a BN structure that is established by data learning is often difficult to understand and has significant requirements regarding the quantity and quality of the training data (Amyotte, 2011). The third method represents a compromise between the first two methods, and it can improve the learning speed if the relationships among variables are obvious. Although there are currently no effective drugs for COVID-19, doctors have gained much knowledge regarding some of its symptoms, such as its pathogenesis and characteristics, during the several months of fighting the virus. These experiences are used as prior knowledge to help facilitate the structural learning of the BN model. On this basis, relatively little training data needs to be collected from hospitals to meet the requirements for parameter learning. This characteristic not only can improve the applicability of the model results but can also reduce the subjectivity of the BN design (Zhang, Wu, Ding, Skibniewski & Yan, 2013).
2.3. Model validation
The node variables in a BN model are independent of each other (Robertson, et al, 2009), so their conditional probabilities do not affect each other. Before using a model in practice, it is necessary to verify its feasibility. By using a portion of the collected data as the test set, the performance of the BN model is evaluated by two indicators: Model Bias and Model Accuracy. The specific method involves comparing the predicted results of the model with the scores provided by experts (actual results). At the same time, we also use the accuracy, sensitivity, specificity, and F-score which are commonly used in the field of statistical classification to further verify the model more comprehensively.
2.3.1. Predicted and actual results of the model
The predicted results of a BN model are a series of probability values and are not specific values (Borsuk, Stow & Reckhow, 2004); however, the actual real result is a single value. To compare the predicted results with the actual results, we must first understand how to characterize the predicted and actual results. When using a BN model to predict the risk event T, it is assumed that there are p cases in event T, and each case is divided according to a different value range, as shown in Eq. (1), where and represent the upper and lower bounds of case i (i = 1, 2…, p), respectively. The prediction result of a BN model for event T is the possible probability value of each situation, which is represented by the vector o, and the cumulative vector of o is represented by O, as shown in Eq. (2).
| (1) |
| (2) |
In Eq. (2), represents the probability that a BN model predicts the occurrence of event T and is . The actual result of the test data that are used to verify the model can be represented by a vector s, and the cumulative vector s is represented by S, as shown in Eq. (3).
| (3) |
2.3.2. Model Bias
Model Bias is used to judge the consistency between the central trend of the BN model prediction results and the real results. The central trend of the model can be reflected by the median (or 50th percentile), which is the number in the middle of a group of numbers that are sorted by size. When the predicted results of the model are close to the actual results, the bias is approximately zero.
To obtain the Model Bias, we assume that the model obeys a uniform probability distribution in each case and the linear interpolation between and , which are the lower and upper boundaries of for and , respectively. The median value () of a BN model is estimated by Eq. (4). When there are n sets of data, the Model Bias can be obtained by drawing a scatter plot. If the intercept of the regression line is zero and the slope is one, this indicates that the model prediction result is reliable.
| (4) |
2.3.3. Model accuracy
Model Accuracy is used to judge the approximation between the predicted results and actual results. Here, we use the mean probability error (MPE) and mean square probability error (MSPE) to judge the accuracy of the BN model.
The MPE is used to describe the average deviation between the predicted probability of the model and the actual probability. When the model prediction is sufficiently accurate, the value of the MPE is zero, and when there is a deviation between the predicted possibility and actual possibility, the value of the MPE is not equal to zero. Eq. (5) and Eq. (6) are used to calculate the MPE value of a single prediction and N sets of prediction results.
| (5) |
| (6) |
The MSPE is used to describe the average error between the predicted probability and actual probability. When the predicted result is completely consistent with the actual result, the value of the MSPE is 0; otherwise, it is greater than 0. Eq. (7) and Eq. (8) are used to calculate the MSPE value of a single prediction and N groups of prediction results. The parameter N in Eq. (6) and Eq. (8) refers to the number of prediction samples, that is, the number of samples that have actual results and are predicted by the model.
| (7) |
| (8) |
To obtain the significance of the MPE and MSPE, we compare them with the expected distribution of the mean probability error () and mean square probability error (), respectively. (or ) can be obtained by the following methods: (a) randomly take a set of data from N sets of data; (b) calculate with Eq. (5) (or Eq. (7)) to obtain (or ); and (c) repeat (a) and (b) 10,000 times to obtain the expected (or ) distribution. According to the expected distribution, we can obtain the possibility of MPE (or MSPE). If the possibility is within the acceptable range, it is considered that there is no significant difference between the MPE (or MSPE) and the expected result, and the prediction result of the model is reliable. If the possibility exceeds the acceptable range, then the model is considered to be problematic. We chose the acceptable range to be [0.025, 0.095] since p < 0.05 is the most commonly recognized indicator of a significant difference.
2.3.4. Statistical classification indicators
Accuracy (Acc), sensitivity (Se), specificity (Sp), and F-score are commonly used in classification. Especially in the medical field, accuracy can reflect the overall classification performance, while sensitivity and specificity can reflect the missed diagnosis rate and misdiagnosis rate, respectively. They are calculated from the four parameters of true positive (TP), true negative (TN), false positive (FP), and false negative (FN). The specific calculation is as follows:
| (9) |
| (10) |
| (11) |
| (12) |
Here, TP and TN represent the number of positive and negative samples that are predicted correctly, while FP and FN represent the number of positive and negative samples that are predicted incorrectly, respectively.
2.4. Research framework
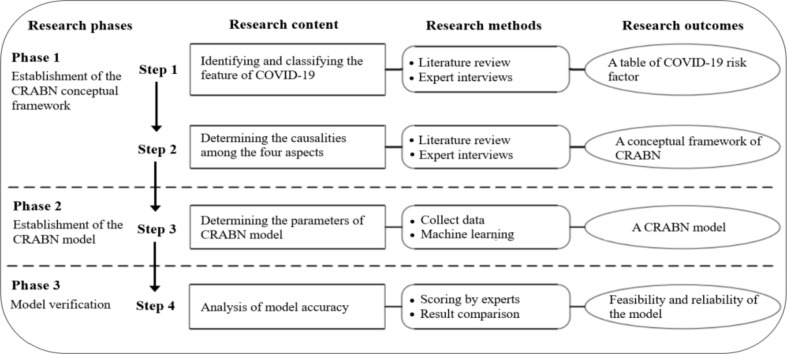
The research consists of three phases, namely, the establishment of the COVID-19 Risk Assessment Bayesian Networks (CRABNs) conceptual framework (phase 1), the establishment of the CRABNs model (phase 2), and the model verification (phase 3). The specific research stages and corresponding research contents and methods are shown in Fig. 4 .
Fig. 4.
Research framework.
3. Building a BN model for COVID-19 risk assessment
3.1. COVID-19 risk factor identification and classification
Currently, the detection of COVID-19 is mainly divided into four aspects in hospitals. According to the diagnosis process of the hospital, the sequence is: epidemiological history, clinical symptoms, imaging examination, and laboratory examination. To identify and classify the risk factors, we used a combination of a literature review and expert interviews, which is a very common method used in factor identification. The specific steps are as follows:
Step 1: We searched the literature related to the risks of COVID-19 features in the Web of Science, Google Scholar and Wiley Interscience databases, and then the 6 authors of this paper independently read these studies and extracted the risk indicators.
Step 2: To verify the accuracy of the classification and enrich the kinds of the characteristics of COVID-19, in September 2020, we invited five experts and doctors from the Tianjin Medical University General Hospital, Tianjin First Central Hospital, and Tianjin University of Traditional Chinese Medicine to a separate conference room for 90 min semi-structured interview, all of whom had relevant experience in treating COVID-19. First, one of the authors, as the leader, guided the experts to discuss the rationality of the existing indicators, retained the indicators that were deemed reasonable by the experts, and eliminated them otherwise. Then, the experts were invited to supplement the existing indicators with others that they considered important. Through the above steps, the proposed indicators were screened.
Step 3: To better distinguish between the different disease characteristics, we merged similar characteristics, and the remaining indicators were systematically integrated to obtain the final risk factor indicator system. At the same time, based on different interval values, the risk of disease under each characteristic could be divided into three categories: high, medium, and low.
Specifically, we first extracted 23 risk characteristics and after merging, we were left with 16, which belong to four different categories: epidemiological history (), clinical symptoms (), imaging examination (), and laboratory examination (). includes age (), comorbidity (), body mass index (), and living with vulnerable people (). includes temperature (), respiratory rate (), heart rate (), and the duration of symptoms (). includes the degree of opacity for lung (), the extent of lung involvement (), concomitant signs (), and the number of damaged lobes (). includes the number of immune cells (), myocardial index (), protein content (), and blood oxygen level (). To construct the CRABNs model, we assume that all risk characteristics are independent (Wang and Yang, 2018, Fu et al., 2020). The specific description is as follows.
Epidemiological history is an important part of preventive medicine and includes parameters such as age, comorbidity, body mass index, and living with vulnerable people (De Nardo et al., 2020, Krishnan et al., 2018). Generally, physical fitness and age show an inverted U-shaped curve. Comorbidity refers to the existence of some related diseases, such as diabetes, respiratory or cardiovascular diseases, and tumour and haematological diseases. The body mass index is the ratio of weight to height and is used to assess whether one is overweight or underweight. Living with vulnerable people refers to whether patients have been exposed to people who are susceptible to infection or who have been infected.
Clinical symptoms refers to a series of symptoms that occur in the body after one contracts a certain illness, and its parameters include temperature, respiratory rate, heart rate, and the duration of symptoms (Xu et al., 2020, Moon et al., 2011). COVID-19 can cause pneumonia; so, temperature, respiratory rate, and heart rate are important parameters in this case.
Imaging examination refers to a chest X-ray examination used for further diagnosis and is mainly based on lung images to determine the degree of opacity of the lungs, extent of lung involvement, concomitant signs, and the number of damaged lobes (Yang, et al, 2020; Cohen et al., 2020). In this case, the degree of lung opacity was scored as follows: 0 = no opacity, 1 = ground glass opacity, 2 = consolidation, and 3 = white-out, and the total opacity score ranged from 0 to 6 (when the results for the right and left lung were added). The extent of lung involvement was scored as follows: 0 = no involvement, 1 = <25% involvement, 2 = 25–50% involvement, 3 = 50–75% involvement, and 4 = >75% involvement. The total score ranged from 0 to 8 (when the results for the right and left lung were added).
The main test parameters used in the laboratory examination included the number of immune cells, myocardial index, protein content, and blood oxygen level, where the number of immune cells includes the number of white blood cells, neutrophils, and lymphocytes (Khanday, et al, 2020). Since the numbers of the three kinds of cells are of the same magnitude, their units are the same, and their weights in medical testing are the same; thus, the average number of the three cell types was directly used for division in this study. The myocardial index includes myoglobin, creatine kinase band, cardiac troponin I, and the N-terminal pre-B-type natriuretic peptide. The importance of each feature is approximately the same. Except for myoglobin, the other three features are of the same magnitude, so the myoglobin value is divided by 100, and then the average value is taken for division. The protein content consists of determinations of a C-reactive protein (CRP) biomarker and serum amyloid A (SAA) (Li & Chen, 2020). Similar to the myocardial index, the SAA protein content is divided by 10 and then summed with the CRP to obtain the average value to obtain the corresponding range of protein contents. Blood oxygen includes measuring the blood oxygen partial pressure and blood oxygen saturation (McRae et al., 2020, Caputo et al., 2020). Although the units of these two parameters are not the same, the blood oxygen partial pressure was selected here because of the positive correlation between blood oxygen partial pressure and blood oxygen saturation. (Julie-Ann, et al, 2015).
Table 1 presents these variables and the descriptions of the classification criteria, where the information source of the root nodes () comes from the literature search and expert inquiry, and the information source of the intermediate nodes () was obtained by experts based via the hundred-mark system.
Table 1.
Parameter variables and related status descriptions in CRABNs.
| Parameter variable | State description | Parameter variable | State description |
|---|---|---|---|
| : Age | Low: 18–50 | : Concomitant signs | Low: 0–1 |
| Medium: 51–70 | (numbers) | Medium: 2–3 | |
| High: >70 or < 18 | High: >3 | ||
| : Comorbidities | Low: No | : Number of damaged lobes | Low: 0–1 |
| (kinds) | Medium: 1 | Medium: 2–3 | |
| High: >1 | High: 4–5 | ||
| : Body Mass Index | Low: <30 | : Number of immune cells | Low: 2.2–5.1 |
| Medium: 31–40 | (*10E9/L) | Medium: 5.1–12.1 | |
| High: >40 | High: 12.1–22.8 | ||
| : Living with vulnerable people | Low: 0 | : Myocardial index | Low: 0.5–1.9 |
| (numbers) | Medium: 1 | (ug/ml) | Medium: 1.9–4.3 |
| High: >1 | High: >4.3 | ||
| : Temperature | Low: 35–38.5 | : Protein content | Low: 0.1–9.8 |
| (℃) | Medium: 38.6–40 | (mg/l) | Medium:9.8–24.1 |
| High: >40 | High: >24.1 | ||
| : Respiratory rate | Low: <20 | : Blood oxygen | Low: >80 |
| (breaths/min) | Medium: 20–24 | (mmHg) | Medium: 70–80 |
| High: >24 | High: 65–70 | ||
| : Heart rate | Low: 50–100 | : Epidemiological History Variables | Good: 80–100 |
| (bpm) | Medium: 111–130 | Moderate: 60–80 | |
| High: >130 | Poor: 0–60 | ||
| : Duration of symptoms | Low: <3 | : Clinical Symptoms Variables | Good: 80–100 |
| (days) | Medium: 4–7 | Moderate: 60–80 | |
| High: >7 | Poor: 0–60 | ||
| : Degree of opacity for lung | Low: 0–2 | : Imaging Examination Variables | Good: 80–100 |
| Medium: 2–4 | Moderate: 60–80 | ||
| High: 4–6 | Poor: 0–60 | ||
| : Extent of lung involvement | Low: 0–3 | : Laboratory Examination Variables | Good: 80–100 |
| Medium: 3–5 | Moderate: 60–80 | ||
| High: 5–8 | Poor: 0–60 |
3.2. Model of COVID-19 risk assessment Bayesian networks
After categorizing the risk factors for COVID-19, these four categories were divided into an internal factor group and external factor group. The internal factors included the laboratory examination variables and imaging examination variables, while the external factors included the epidemiological history variables and clinical symptom variables. Fig. 5 presents the conceptual framework of the CRABNs. In the past month, we collected 300 diagnosis reports of patients with COVID-19 from hospitals in Wuhan. After careful extraction, classification, and inspection, we obtained 300 corresponding pieces of data. The final severity of each patient's illness, T, was obtained after evaluation and diagnosis by doctors. According to the experts’ assessment of each patient’s conditions, the COVID-19 risk degree, T, was divided into the following four grades: I(0–25), II(26–50), III(51–75), and IV(76–100). The higher the score, the higher the severity.
Fig. 5.
Conceptual framework of risk factors in CRABNs.
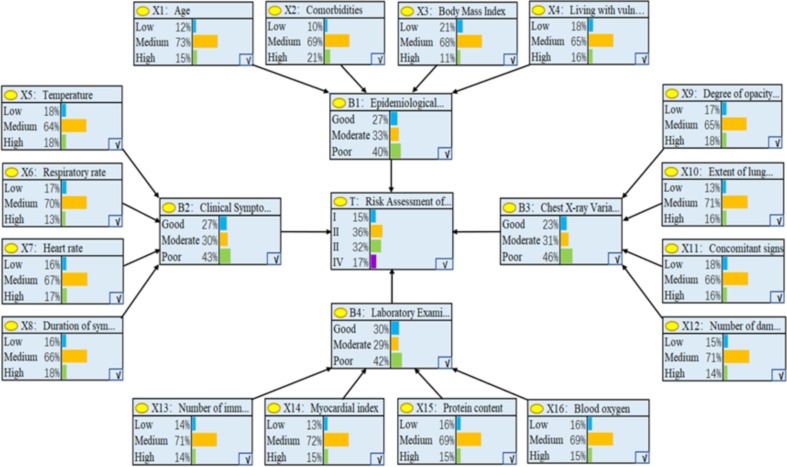
From the 300 pieces of collected data, 250 were randomly selected as the training set. Then, the K2 algorithm, a classic algorithm for BN model learning, was used to calculate the parameters of the CRABNs model. Finally, we obtained the established CRABNs model, as shown in Fig. 6 . In Fig. 6, the outermost layer consists of the 16 obtained variables (child nodes) that are represented by that have an impact on event T; the middle layer consists of the 4 intermediate variables (intermediate nodes) that are represented by after further categorization of 16 variables based on expert experience and the diagnostic process; and the central variable T (parent node) represents the risk of COVID-19 patients. It can be seen that the variable acts on event T by acting on the intermediate variable .
Fig. 6.
Established CRABNs model.
4. Verifying the effectiveness of CRABNs
We established the CRABNs model above, but the model can only be used for predictions when the accuracy of the model is verified to be within an acceptable range. To verify the validity of the CRABNs model, the remaining 50 medical records were used as test samples, and the collected medical records were independent of each other. Table 2 presents the 50 data samples that were used for testing.
Table 2.
Test samples for CRABNs.
| Data | T | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 35 | 1 | 33 | 0 | 37.3 | 21 | 102 | 5 | 3 | 3 | 2 | 2 | 5.3 | 2.2 | 10.23 | 71 | 31 |
| 2 | 48 | 1 | 35 | 1 | 37.6 | 21 | 105 | 4 | 2 | 4 | 2 | 2 | 6.6 | 2.5 | 14.78 | 72 | 42 |
| 3 | 17 | 0 | 50 | 1 | 38.1 | 23 | 80 | 3 | 1 | 2 | 1 | 1 | 3.2 | 1.7 | 9.85 | 80 | 23 |
| 4 | 60 | 0 | 25 | 3 | 36.2 | 25 | 118 | 4 | 3 | 4 | 3 | 2 | 9.7 | 3.6 | 22.56 | 78 | 63 |
| 5 | 57 | 0 | 32 | 2 | 39.0 | 26 | 120 | 5 | 3 | 3 | 2 | 3 | 8.5 | 3.4 | 19.79 | 73 | 53 |
| 6 | 55 | 1 | 30 | 1 | 37.9 | 23 | 126 | 4 | 3 | 3 | 3 | 2 | 7.9 | 2.6 | 20.02 | 75 | 58 |
| 7 | 40 | 0 | 33 | 1 | 37.0 | 22 | 116 | 5 | 3 | 4 | 2 | 3 | 7.3 | 3.1 | 12.56 | 70 | 55 |
| 8 | 75 | 2 | 20 | 2 | 38.3 | 28 | 135 | 8 | 5 | 6 | 3 | 4 | 11.8 | 4.2 | 27.0 | 62 | 77 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 50 | 52 | 1 | 28 | 0 | 37.5 | 18 | 113 | 5 | 4 | 5 | 2 | 3 | 7.0 | 2.5 | 14.37 | 73 | 60 |
4.1. Assessment of model Bias
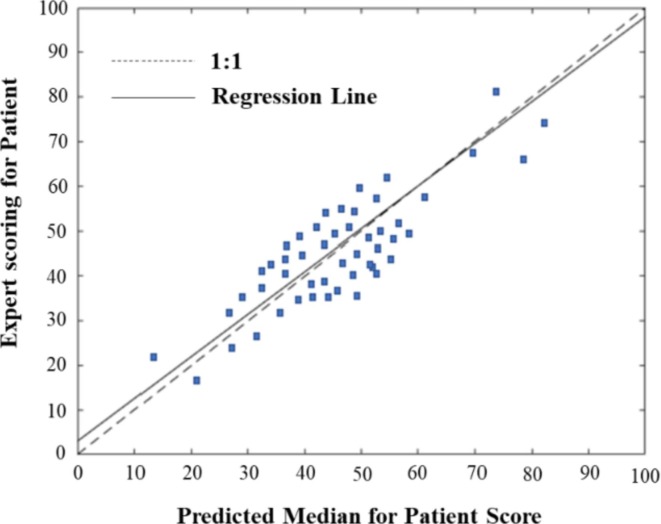
We first input the value of each risk factor, , for the 50 test samples into the CRABNs model in turn, and, according to Eq. (1), the probability distribution of the COVID-19 risk degree for each patient T was obtained. Then, we extracted the median of the probability distribution that was predicted by the model according to Eq. (4), and the Model Bias was obtained by comparing the actual value given by the doctors with the predicted median, as shown in the scatter plot in Fig. 7 . The horizontal coordinates in the graph represent the predicted risk scores, and the vertical coordinates represent the experts’ actual scores. The regression line and ideal regression line were used to evaluate the consistency between the actual and predicted results.
Fig. 7.
Scatterplot of predicted and actual values of COVID-19 risk.
As shown in Fig. 7, when the expert scores were low, the predicted median values were low; similarly, when the expert scores were high, the predicted median values were also high. The slope of the regression line was 0.95 and approached 1, which indicates that the CRABNs model is very effective in assessing the risk of COVID-19. In other words, there were no significant differences between the central tendency predicted by the model and the actual results.
4.2. Assessment of model accuracy
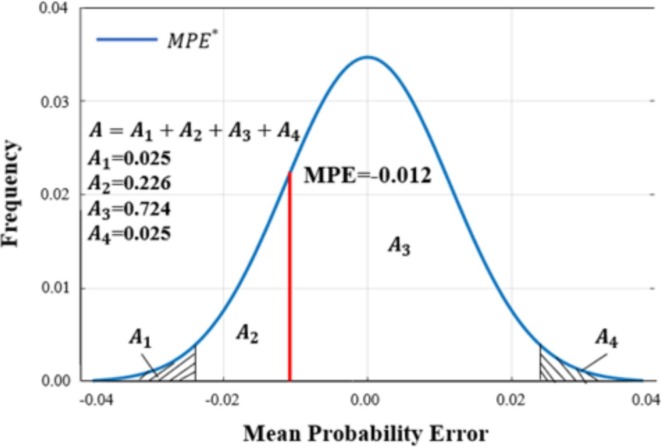
Model Accuracy is judged by two indicators: MPE and MSPE. The MPE result after calculating the 50 pieces of test data via Eq. (6) was −0.012. Fig. 8 presents the frequency curve of , where (i = 1,2,3,4) represents the calculated frequency in each range. The probability of the MPE, which is greater than in the figure, is 0.774 ( in Fig. 8), which is within the acceptable range [0.025, 0.975]. The results showed that there was no significant difference between the actual MPE and the expected value.
Fig. 8.
Frequency plot of expected mean probability error () for risk of COVID-19 patients.
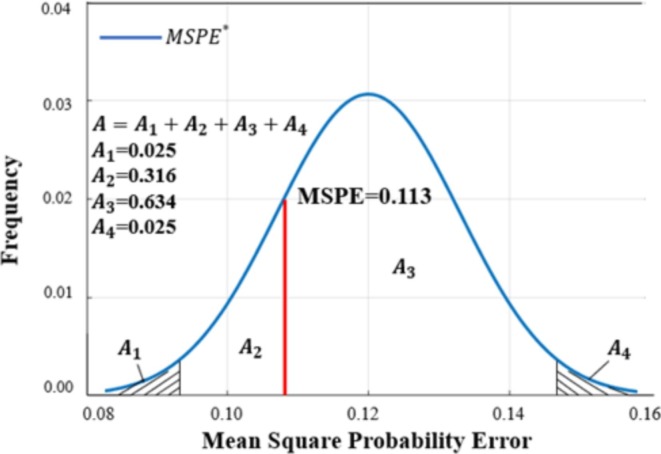
Using Eq. (8) to calculate the MSPE value of the 50 data points, we obtained a value of 0.113. Fig. 9 shows the frequency curve of , where (i = 1,2,3,4) represents the calculated frequency in each range. The probability of the MSPE, which is greater than in the figure, is 0.749 ( in Fig. 9), and this value is also within the acceptable range [0.025, 0.975]. The results show that there was no significant difference between the actual MSPE and the expected value.
Fig. 9.
Frequency plot of expected mean square probability error () for risk of COVID-19 patients.
Based on the analysis of MPE and MSPE, there were no significant differences between the predicted values and the actual scores of risk uncertainty, and the accuracy of the model was therefore verified.
4.3. Model comparisons
The accuracy of the model was verified by testing the Model Bias and Model Accuracy. To further verify the reliability of the proposed model, we compared it with three commonly used classification algorithms: support vector machine (SVM), random forest (RF), and k-nearest neighbour (KNN). Because this study is a multiclassification problem, we calculated each indicator (e.g., Acc, Se, Sp, and F-score) in each category with Eqs. (9), (10), (11), (12) on the basis of the traditional two-classification problem and then calculated the weighted average values of the same index in different categories to obtain the final data for each indicator (Zheng, 2015). For the COVID-19 epidemic, sensitivity is a very important indicator, and the higher the risk level of COVID-19 patients, the greater the risk due to a missed diagnosis. Therefore, we assigned weighting coefficients of 0.15, 015, 0.3 and 0.4 to the four levels of I, II, III, and IV, respectively. The models all use 300 collected data points, of which 250 were used as the training set and 50 were used as the test set. Table 3 shows a comparison of models. It can be seen from the table that the CRABNs model that was constructed in this paper has a good classification effect.
Table 3.
Comparison of models.
| Model | Acc | Se | Sp | F-score |
|---|---|---|---|---|
| SVM | 0.91 | 0.90 | 0.96 | 0.90 |
| RF | 0.88 | 0.82 | 0.97 | 0.85 |
| KNN | 0.90 | 0.84 | 0.94 | 0.88 |
| CRABNs | 0.94 | 0.92 | 0.98 | 0.93 |
5. Discussion
In this study, we constructed a Bayesian network model to assess the risk levels of patients affected by COVID-19. The established CRABNs model was tested by two indicators, Model Bias and Model Accuracy, and the feasibility of the model was verified. Finally, the CRABNs model was compared with other three models to further verify the reliability of the model.
5.1. Theoretical implications
In this paper, through the recognition and integration of COVID-19 features, 16 risk factors were extracted and further divided into four intermediate modules. At the same time, a Bayesian network was used to better predict the severity of COVID-19 patients. In the past, many studies have analysed the risk factors for COVID-19, and some of our research results have been verified in other studies. For example, the older the patient, the higher the risk of COVID-19, which is consistent with the conclusion of Guan et al. (Guan, Ni, Hu, & Liang, 2020). The positive correlation between the number of comorbidities and risk of COVID-19 is similar to the conclusion of Wang et al. (Wang, et al, 2020). However, at the same time, past studies have neglected to assess the comprehensive impact of the epidemiology, clinical symptoms, imaging tests, and laboratory factors on the risk of COVID-19. Compared with previous studies (Majid et al., 2020, Cahan et al., 2020, Zhao et al., 2020), our study classified the disease characteristics more systematically to assess the risk of COVID-19 patients. In particular, real data and quantitative methods were used to establish a CRABNs model and calculate its parameters through machine learning algorithms. Finally, we proposed two indicators, Model Bias and Model Accuracy, to evaluate the effectiveness of the model and compared this model with other classification models to show the reliability of the model.
5.2. Practical implications
COVID-19 has affected many people, but there is still a lack of large datasets that have been marked by relevant experts, and it is difficult to rely on doctors to diagnose all COVID-19 patients. At the same time, in the process of consulting with the experts, we found that there is currently a lack of quantitative tools for the risk diagnosis of COVID-19 patients in China to quickly assess patient risk levels. The CRABNs model, which was constructed in this study, can improve this deficiency. It can be used to assist doctors in decision-making, improve diagnostic efficiency, and reduce diagnosis times. Specifically, this study developed a prediction model that can effectively predict the risk levels of COVID-19 patients. The model can solve the problem of insufficient detection capabilities caused by the lack of COVID-19 nucleic acid detection kits in underdeveloped areas to a certain extent. In the future, if the model is further simplified, it could be used to construct an app, which could then be used more widely and conveniently by nonprofessional people.
5.3. Limitations and future research
Despite the above contributions, this study has some shortcomings. First, in this study, the sample data collected were not sufficient. Therefore, we suggest that more data be collected in the future to build a more applicable model. Second, when using the constructed CRABNs model for risk assessments, the patients’ main risk factors were not considered. Therefore, we recommend analysing the impact of disease risk factors in the future. Third, when collecting samples, we did not consider the demographic differences among patient groups. Since the main risk factors for different groups are different, we could consider these different groups (e.g., teenagers, young people, and the elderly) for future analysis. Fourth, although we have tried our best to avoid any correlations between the risk factors and draw lessons from some hypotheses in the literature, there may still be some correlations between some risk factors. Therefore, we suggest that a more appropriate method (e.g., combining Copula function with BN model) should be adopted to deal with the correlation between factors when building a similar BN model in the future.
6. Conclusion
The risk identification and assessment of COVID-19 patients can effectively prevent the spread of COVID-19, while incorrect judgements can cause a waste of medical resources and even greater COVID-19 spread. In this study, we constructed a CRABNs model to assess the risk of COVID-19 patients and used real sample data to verify the feasibility of this model. This research contributes to the development of epidemic assessment tools, which will help doctors better conduct decision-making analyses and risk assessments in the field of epidemics.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Acknowledgments
This research was supported by the National Natural Science Foundation of China (Grant No.: 71971123). We sincerely thank the participants who contributed to this research.
The authors dedicate this research to all medical workers who are at the forefront of the fight against COVID-19 as well as to those who have lost their lives in the fight against COVID-19.
References
- Ahn D.-G., Shin H.-J., Kim M.-H., Lee S., Kim H.-S., Myoung J., et al. Current status of epidemiology, diagnosis, therapeutics, and vaccines for novel coronavirus disease 2019 (COVID-19) Journal of Microbiology and Biotechnology. 2020;30(3):313–324. doi: 10.4014/jmb.2003.03011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alhazzani W., Møller M.H., Arabi Y.M., Loeb M., Gong M.N., Fan E., et al. Surviving sepsis campaign: Guidelines on the management of critically ill adults with coronavirus disease 2019 (covid-19) Intensive Care. 2020;46(5):854–887. doi: 10.1007/s00134-020-06022-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amyotte K.P. Safety analysis in process facilities: Comparison of fault tree and bayesian network approaches. Reliability Engineering & System Safety. 2011 [Google Scholar]
- Armocida, B., Formenti, B., Ussai, S., Palestra, F., & Missoni, E. (2020). The Italian health system and the COVID-19 challenge. The Lancet Public Health. [DOI] [PMC free article] [PubMed]
- Borsuk M.E., Stow C.A., Reckhow K.H. A bayesian network of eutrophication models for synthesis, prediction, and uncertainty analysis. Ecological Modelling. 2004;173(2-3):219–239. [Google Scholar]
- Bucci G., Sandrucci V., Vicario E. 44th Hawaii International Conference on Systems Science (HICSS-44 Proceedings, 4–7 January 2011, Koloa, Kauai, HI. IEEE Computer Society; USA: 2011. Ontologies and Bayesian Networks in Medical Diagnosis. [Google Scholar]
- Cahan A., Gottesman T., Katz M.T., et al. Development and validation of a knowledge-driven risk calculator for critical illness in covid-19 patients. The American Journal of Emergency Medicine. 2020 doi: 10.1016/j.ajem.2020.09.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cano A., Masegosa A.R., Moral S. A method for integrating expert knowledge when learning bayesian networks from data. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society. 2011;41(5):1382–1394. doi: 10.1109/TSMCB.2011.2148197. [DOI] [PubMed] [Google Scholar]
- Caputo N.D., Strayer R.J., Levitan R., Kline J. Early self-proning in awake, non-intubated patients in the emergency department: A single ed's experience during the covid-19 pandemic. Academic Emergency Medicine. 2020;27(5):375–378. doi: 10.1111/acem.13994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen, J. P., Dao, L., Morrison, P., Roth, K., Bengio, Y., & Shen, B. et al. (2020). Predicting covid-19 pneumonia severity on chest x-ray with deep learning. arXiv e-prints. [DOI] [PMC free article] [PubMed]
- Cooper G.F., Herskovits E. A bayesian method for the induction of probabilistic networks from data. Machine Learning. 1992;9(4):309–347. [Google Scholar]
- da Silva R.G., Ribeiro M.H.D.M., Mariani V.C., Coelho L.D.S. Forecasting brazilian and american covid-19 cases based on artificial intelligence coupled with climatic exogenous variables. Chaos Solitons & Fractals. 2020;139:110027. doi: 10.1016/j.chaos.2020.110027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu L., Wang X., Wang D., Griffin M.A., Li P. Human and organizational factors within the public sectors for the prevention and control of epidemic. Safety ence. 2020;131:104929. doi: 10.1016/j.ssci.2020.104929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan, W. J., Ni, Z. Y., Hu, Y., Liang, W. H., & Zhong, N. S, et al. (2020). Clinical characteristics of 2019 novel coronavirus infection in China. medRxiv.
- Julie-Ann, Collins, Aram, Rudenski, John, & Gibson, et al. (2015). Relating oxygen partial pressure, saturation and content: the haemoglobin-oxygen dissociation curve. Breathe (Sheffield, England). [DOI] [PMC free article] [PubMed]
- Khanday A.M.U.D., Rabani S.T., Khan Q.R., Rouf N., Mohi Ud Din M. Machine learning based approaches for detecting covid-19 using clinical text data. International Journal of Information. 2020;12(3):731–739. doi: 10.1007/s41870-020-00495-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan B., Isabel D.-S.-S., David A., et al. Association of BMI with overall and cause-specific mortality: A population-based cohort study of 3·6 million adults in the UK. Lancet Diabetes & Endocrinology. 2018 doi: 10.1016/S2213-8587(18)30288-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L., Chen C. The contribution of acute phase reaction proteins to the diagnosis and treatment of 2019 novel coronavirus disease (covid-19) Epidemiology and Infection. 2020;148:1–21. doi: 10.1017/S095026882000165X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IMF. (2021). World Economic Outlook. Available from: https://www.imf.org/external/datamapper/datasets/WEO.
- Majid N., Zafer C., Kemal P. A novel medical diagnosis model for COVID-19 infection detection based on Deep Features and Bayesian Optimization. Applied Soft Computing. 2020;97 doi: 10.1016/j.asoc.2020.106580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams M., Mi E., et al. Estimating the risk of death from COVID-19 in adult cancer patients. Clinical Oncology. 2020 doi: 10.1016/j.clon.2020.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mcrae, M. P., Simmons, G. W., Christodoulides, N. J., ZhibingLu, Kang, S. K., & DavidFenyo, et al. (2020). Clinical decision support tool and rapid point-of-care platform for determining disease severity in patients with covid-19. Lab on a Chip, 20. [DOI] [PMC free article] [PubMed]
- Mohammad S., Shamim Hossain M. Metacovid: A siamese neural network framework with contrastive loss for n -shot diagnosis of covid-19 patients. Pattern Recognition. 2020 doi: 10.1016/j.patcog.2020.107700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moon A., Cosgrove J.F., Lea D., Fairs A., Cressey D.M. An eight year audit before and after the introduction of modified early warning score (mews) charts, of patients admitted to a tertiary referral intensive care unit after cpr. Resutation. 2011;82(2):150–154. doi: 10.1016/j.resuscitation.2010.09.480. [DOI] [PubMed] [Google Scholar]
- De Nardo P., Gentilotti E., Mazzaferri F., Cremonini E., Hansen P., Goossens H., et al. Multi-criteria decision analysis to prioritize hospital admission of patients affected by covid-19 in low-resource settings with hospital-bed shortage. International Journal of Infectious Diseases. 2020;98:494–500. doi: 10.1016/j.ijid.2020.06.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikovski D. Constructing bayesian networks for medical diagnosis from incomplete and partially correct statistics. Knowledge & Data Engineering IEEE Transactions on. 2000;12(4):509–516. [Google Scholar]
- Nour M., Cömert Z., Polat K. A novel medical diagnosis model for covid-19 infection detection based on deep features and bayesian optimization. Applied Soft Computing. 2020;97:106580. doi: 10.1016/j.asoc.2020.106580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oniśko A., Druzdzel M.J., Wasyluk H. Learning bayesian network parameters from small data sets: Application of noisy-or gates. International Journal of Approximate Reasoning. 2001;27(2):165–182. [Google Scholar]
- Robertson D.E., Wang Q.J., Mcallister A.T., Abuzar M., Malano H.M., Etchells T. A bayesian network approach to knowledge integration and representation of farm irrigation: 2. model validation. Water Resources Research. 2009;45(2):142–143. [Google Scholar]
- Sergio V.S., Patricia M. A new approach for classifying coronavirus COVID-19 based on its manifestation on chest X-rays using texture features and neural networks. Information Sciences. 2021:403–414. doi: 10.1016/j.ins.2020.09.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaban W.M., Rabie A.H., Saleh A.I., Abo-Elsoud M.A., et al. Detecting COVID-19 patients based on fuzzy inference engine and Deep Neural Network. Applied Soft Computing. 2020 doi: 10.1016/j.asoc.2020.106906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velikova M., Lucas P.J.F., Samulski M., Karssemeijer N. On the interplay of machine learning and background knowledge in image interpretation by bayesian networks. Artificial Intelligence in Medicine. 2013;57(1):73–86. doi: 10.1016/j.artmed.2012.12.004. [DOI] [PubMed] [Google Scholar]
- Wang, D., Hu, B., Hu, C., Zhu, F., Liu, X., & J Zhang, et al. (2020). Clinical Characteristics of 138 Hospitalized Patients With toy Novel Coronavirus-Infected Pneumonia in Wuhan, China. JAMA The Journal of the American Medical Association. [DOI] [PMC free article] [PubMed]
- Wang L., Yang Z. Bayesian network modelling and analysis of accident severity in waterborne transportation: A case study in china. Reliability Engineering and System Safety. 2018;180(DEC.):277–289. [Google Scholar]
- WHO. (2020). Coronavirus disease (COVID-19) pandemic Coronavirus disease (COVID-19) pandemic – situation report. Available from: https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
- WHO. (2021). WHO Coronavirus (COVID-19) Dashboard. Available from: https://covid19.who.int/.
- Xu B.G. Intelligent fault inference for rotating flexible rotors using bayesian belief network. Expert Systems with Applications. 2012;39(1):816–822. [Google Scholar]
- Xu J.J., Yin Z.R., Liu Y., Wang S.F., Duan L.M., et al. Clinical characteristics and outcomes of severe or critical covid-19 patients presenting no respiratory symptoms or fever at onset. Engineering. 2020 doi: 10.1016/j.eng.2020.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadav M., Perumal M., Srinivas M. Analysis on novel coronavirus (COVID-19) using machine learning methods. Chaos Solitons & Fractals. 2020;139 doi: 10.1016/j.chaos.2020.110050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W., Sirajuddin A., Zhang X., Liu G., Teng Z., Zhao S., et al. The role of imaging in 2019 novel coronavirus pneumonia (covid-19) European Radiology. 2020;30(9):4874–4882. doi: 10.1007/s00330-020-06827-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Wu X., Ding L., Skibniewski M.J., Yan Y. Decision support analysis for safety control in complex project environments based on bayesian networks. Expert Systems with Applications An International Journal. 2013;40(11):4273–4282. [Google Scholar]
- Zhang P.E., Wang M.M., Wang Y., Wang Y.F., Li T., et al. Risk factors associated with the progression of covid-19 in elderly diabetes patients. Diabetes Research and Clinical Practice. 2020 doi: 10.1016/j.diabres.2020.108550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J., Li X., Huang W., Zheng J. Potential risk factors for case fatality rate of novel coronavirus (covid-19) in china: A pooled analysis of individual patient data. American Journal of Emergency Medicine. 2020;38(11):2374–2380. doi: 10.1016/j.ajem.2020.08.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., et al. Clinical course and risk factors for mortality of adult inpatients with covid-19 in Wuhan, China: A retrospective cohort study. The Lancet. 2020;395(10229):1054–1062. doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]