Abstract
Purpose
The purpose of this work was twofold: (a) To provide a robust and accurate method for image segmentation of dedicated breast CT (bCT) volume data sets, and (b) to improve Hounsfield unit (HU) accuracy in bCT by means of a postprocessing method that uses the segmented images to correct for the low‐frequency shading artifacts in reconstructed images.
Methods
A sequential and iterative application of image segmentation and low‐order polynomial fitting to bCT volume data sets was used in the interleaved correction (IC) method. Image segmentation was performed through a deep convolutional neural network (CNN) with a modified U‐Net architecture. A total of 45 621 coronal bCT images from 111 patient volume data sets were segmented (using a previously published segmentation algorithm) and used for neural network training, validation, and testing. All patient data sets were selected from scans performed on four different prototype breast CT systems. The adipose voxels for each patient volume data set, segmented using the proposed CNN, were then fit to a three‐dimensional low‐order polynomial. The polynomial fit was subsequently used to correct for the shading artifacts introduced by scatter and beam hardening in a method termed “flat fielding.” An interleaved utilization of image segmentation and flat fielding was repeated until a convergence criterion was satisfied. Mathematical and physical phantom studies were conducted to evaluate the dependence of the proposed algorithm on breast size and the distribution of fibroglandular tissue. In addition, a subset of patient scans (not used in the CNN training, testing or validation) were used to investigate the accuracy of the IC method across different scanner designs and beam qualities.
Results
The IC method resulted in an accurate classification of different tissue types with an average Dice similarity coefficient > 95%, precision > 97%, recall > 95%, and F1‐score > 96% across all tissue types. The flat fielding correction of bCT images resulted in a significant reduction in either cupping or capping artifacts in both mathematical and physical phantom studies as measured by the integral nonuniformity metric with an average reduction of 71% for cupping and 30% for capping across different phantom sizes, and the Uniformity Index with an average reduction of 53% for cupping and 34% for capping.
Conclusion
The validation studies demonstrated that the IC method improves Hounsfield Units (HU) accuracy and effectively corrects for shading artifacts caused by scatter contamination and beam hardening. The postprocessing approach described herein is relevant to the broad scope of bCT devices and does not require any modification in hardware or existing scan protocols. The trained CNN parameters and network architecture are available for interested users.
Keywords: dedicated breast CT, deep learning, image segmentation, shading artifacts
1. Introduction
Dedicated computed tomography of the breast (bCT) is an imaging modality devised to improve the diagnostic accuracy of breast cancer screening and diagnosis by rendering a high‐resolution volumetric image of breast anatomy. The technology of bCT has undergone multiple engineering iterations, incorporating ever advancing constituent hardware components and resolving engineering challenges in different ways. Accordingly, several generations and designs of bCT devices exist.1, 2, 3, 4 Reducing and resolving artifacts known to arise in bCT is critical for improving imaging for breast cancer detection.
Artifacts related to Hounsfield unit (HU) biasing and shading, such as cupping and capping, are common and have previously been well described.5, 6 It is the case for bCT, as it is for computed tomography in general, that scatter and beam hardening of the x‐ray beam as it interacts with the breast tissue can result in a nonuniform bias of HU values. HU biasing of the breast anatomy results in a “cupping” artifact in the reconstructed coronal images. Specifically, the HU values in voxels near the center of the breast decrease relative to voxels at the periphery. Different bCT system designs may employ different device‐specific rationale and approaches for cupping corrections in patient images. A simplification of breast shape or anatomical composition used in existing correction methods can result in residual cupping or overcorrection of cupping which in turn introduces what is essentially reverse cupping — or “capping” — to the bCT image.7, 8, 9 An additional artifact of concern specific to cone beam geometry CT systems is the decrease in HU voxel values that occurs in coronal planes parallel to the central coronal slice for increasing cone angles. This artifact, commonly referred to as HU drop,10 originates from incomplete sampling of the Radon space data induced by the cone beam geometry. Beyond causing image distortions, these artifacts can impact patient diagnosis and consequently treatment. Uncalibrated or poorly calibrated HU values can reduce the diagnostic value of the images.11 The presence of artifacts can also affect CT density‐based conversion tables,12 which in turn may result in inaccurate dose calculations and technique factors used for treatment planning in radiation therapy.13
For a fixed scanner geometry and imaging protocol, scatter distribution on projection images is dependent on the size, shape, and glandular distribution of the breast positioned in the field of view (FOV). Previous studies showed that the scatter‐to‐primary ratio (SPR) in cone beam bCT varies between 0.1 and 1.6.14, 15, 16, 17 Strategies in scatter management in cone beam CT in general — and bCT in particular — include hardware modifications, software‐based prospective or retrospective algorithms, or knowledgeable combinations of these methods. These approaches include changing scanner geometry,1, 18, 19 utilization of anti‐scatter grids,20, 21, 22, 23, 24 utilization of beam stopping arrays or strips (BSA),18, 25, 26, 27, 28, 29 or beam passing arrays (BPA)30, 31 followed by sinogram‐domain image processing, Monte Carlo (MC) simulation approaches,8, 15, 16, 18, 32, 33 or purely postprocessing image domain techniques.34, 35, 36, 37, 38 A brief discussion of these methodologies is presented in the following three paragraphs.
One can reduce photon scatter contamination by simply increasing the gap between the x‐ray detector and the breast; however, this approach may decrease breast coverage and increase focal spot blur. Using anti‐scatter grids is another option in reducing the SPR; however, the dose penalty in using a grid system for a low dose x‐ray imaging modality such as bCT in addition to the technical difficulties in correcting for the septal shadow in the projections makes this a prohibitive option. These methods are commonly referred to as scatter rejection techniques where both high‐ and low‐frequency contributions of the scattered photons are decreased. The goal of the other proposed methods, commonly referred to as scatter corrections techniques, is to correct the effects of scatter contamination in either the projection or reconstruction domain.
MC simulation is a powerful tool in exploring and understanding the characteristics and contributions of x‐ray scatter. However, the strategies in evaluating MC‐based correction techniques often involve assumptions made to increase computational efficiency and versatility of the developed techniques. For example, the assumption of a simple breast model which is cylindrical in shape3, 14, 39, 40, 41 or homogenous in composition.16 The result of these simplifications is a suboptimal correction of the cupping artifact leading to residual cupping or capping. In comparison with MC‐based solutions, BSA or BPA approaches provide object‐specific scatter information via direct measurement of the scattered signal in the shadows of the beam stop or collimator and result in improved scattered correction outcome. However, incorporating BSA or BPA approaches into a scanner requires additional dose to the breast, hardware modifications, and results in an increased overall scan time.
Several retrospective methods have been reported to effectively reduce the predominant low‐frequency effects of x‐ray scatter and beam hardening in the reconstructed images (image domain). Studies performed on the voxel intensity values of bCT images42, 43 and the postmortem anatomical analysis of breast tissues44, 45 have shown that the adipose voxel CT numbers can be treated as a narrowly spread normal distribution around a peak value. This unique property of breast tissue can be leveraged to correct for shading artifacts in the image domain. Such methods require segmentation to classify only the adipose voxels, an algorithm for parameterizing the distribution of the cupping in the segmented adipose voxels, and an algorithm for flattening the shading artifact (i.e., flat fielding) so that the average CT number of the adipose voxels match a predefined value. Altunbas et al.34 introduced the concept of fitting two‐dimensional polynomials to features extracted from the spatial location of the adipose voxels in bCT coronal slices. This was followed by stacking the two‐dimensional models to generate a three‐dimensional fit, and a smoothing operation was performed to correct for the discrepancies between the neighboring individual models. The extracted background volume was then used to flatten the adipose field; however, assumptions made regarding the shape and positioning of the breast voxels in a bCT image limit the utility and practice of this method. These simplifications include assuming the breast is circularly symmetric in the coronal plane, assuming the adipose tissue values are radially symmetric, and assuming that the center of the circular coronal slice coincides with the gantry's isocenter.
In this work, we propose a generalized low‐order polynomial correction for shading artifacts in bCT reconstructions that is independent of the breast shape, size, composition, and position in the scanner geometry. The interleaved correction (IC) method consists of two parts. First, all reconstructed images are segmented into air, adipose, fibroglandular, and skin types using a deep convolutional neural network (CNN) which was designed and trained using a large cohort of bCT data sets. The large size of the training data set allows for a realistic feature extraction in different layers of the CNN. The network architecture and the optimization parameters were carefully selected according to the size of the reconstructed images, voxel types, and their prevalence in the bCT images. The advantage of the proposed semantic segmentation technique in comparison with regional intensity or overall histogram‐based unsupervised learning methods is its dependency on both the voxel intensities and morphological variations and gradients within the reconstructed image. We introduce a regularization mechanism to compensate for the large gap between the number of overrepresented voxels such as air and adipose and underrepresented voxels such as fibroglandular. The second step in the IC method following the segmentation is to use the geometrical position of the adipose voxels for defining a convex feature space. The feature space and adipose voxel values are used through a nine‐step process to find a three‐dimensional, low‐order polynomial fit analytically. This polynomial model is independent of the convexity of the shading artifacts in the reconstructed images, and therefore, the same methodology can be used for cupping, capping, or axial HU drop correction.
The utility of the IC method was evaluated through mathematical and physical phantoms. In addition, the quantitative and qualitative gains in adopting this method were investigated in eight patient scans acquired using four different bCT scanner systems.
2. Materials and methods
The bCT systems referred to herein were designed and developed in our laboratory at UC Davis. The systems are code‐named Albion, Bodega, Cambria, and Doheny, where the alphabetical order of the names indicates their chronological development.1 Scanner parameters, as they relate to this study, are listed in Table 1. Clinical patient images referenced in the validation sections were acquired during two separate clinical trials.11, 46, 47 The Albion and Bodega scanners are similar in design, differing only in the amount of filtration and the use of dynamic gain for the flat panel detector installed on Bodega. Cambria and Doheny differ more substantially across scanner characteristics.
Table 1.
Dedicated breast computed tomography systems used in this study along with the corresponding x‐ray beam characteristics
| Scanner | kV | Filtration | 1st HVL (mm AL) | Effective energy (keV) | Theoretical 100% adipose tissue HU |
|---|---|---|---|---|---|
| Albion | 80 | 0.30 mm Cu | 5.7 | 45 | −89 |
| Bodega | 80 | 0.20 mm Cu | 5.0 | 42 | −110 |
| Cambria | 65 | 0.25 mm Cu | 4.0 | 39 | −128 |
| Doheny | 60 | 0.20 mm Gd | 3.6 | 36 | −151 |
The capping artifact cases discussed in this study stem from a MC‐based HU calibration method previously published8 that tends to over correct the cupping artifact for some patient cases. This previous method computes the dimensions of the largest water cylinder that can fully encompass the breast volume and then implements a MC simulation program48 to generate a scatter signal distribution for each corresponding projection of the modeled cylinder. The final HU calibration is carried out by a logarithmic subtraction between the projection image of the breast and the simulated water phantom. As discussed in the introduction, this oversimplification of the breast shape and size results in residual shading artifacts. In a realistic patient acquisition where the breast diameter generally decreases anteriorly, the modeled water cylinder (and hence MC simulated scatter distribution) is much greater than the true breast diameter and this results in the observed capping artifact. These capping artifact cases are introduced in the present study only to demonstrate the feasibility and flexibility of the proposed IC method for sufficiently correcting existing images that suffer from residual shading artifacts (i.e., capping).
2.1. CT image segmentation
A semantic segmentation architecture can be broadly thought of as an encoder network (learning a discriminative feature space) followed by a decoder network (learning a transfer operation mapping the feature space elements onto voxel space). The details of the architecture, however, are highly application specific. The input to the proposed CNN is a two‐dimensional coronal image from a three‐dimensional bCT volume data set. The input image undergoes multiple levels of convolutional and nonlinear operations during which the image domain information becomes encoded into a set of features. The encoding process must be followed by a decoding mechanism to project the discriminative features learned during the encoding process onto voxel space. The depth and width of the encoder–decoder chain and the definition of the loss function are dependent on the type and complexity of the features embedded in the image. The following section describes the rationale behind the choices made in designing a CNN for bCT image segmentation.
2.1.1. Network architecture
The overall network architecture is shown in Fig. 1. A modified U‐Net49 architecture was designed consisting of two “wings”: the encoder and decoder wings. We reduced the convolution/nonlinearity operations during the decoder wing of the standard U‐Net to amplify the magnitude of the backpropagated error tensors. The size of the arrays in the coarsest level of the encoder is . Given the average fibroglandular breast density of 19.3%,50, 51 adding more layers to the encoder wing results in disappearing features representing fibroglandular tissue composition, especially in fatty breasts where fibroglandular tissue is more sparse. Furthermore, adding convolutional layers in the decoding wing reduces the impact of low‐density or sparse fibroglandular tissue on the forward propagating tensors resulting in an overestimation of dense fibroglandular tissues. Therefore, additional convolution layers and activation gates were avoided in the decoding wing. Linear rectified activation functions were used to induce nonlinearity and to speed up the learning process.52 A residual learning paradigm53 was introduced to the encoder wing to boost the error backpropagation of underrepresented voxel types.
Figure 1.
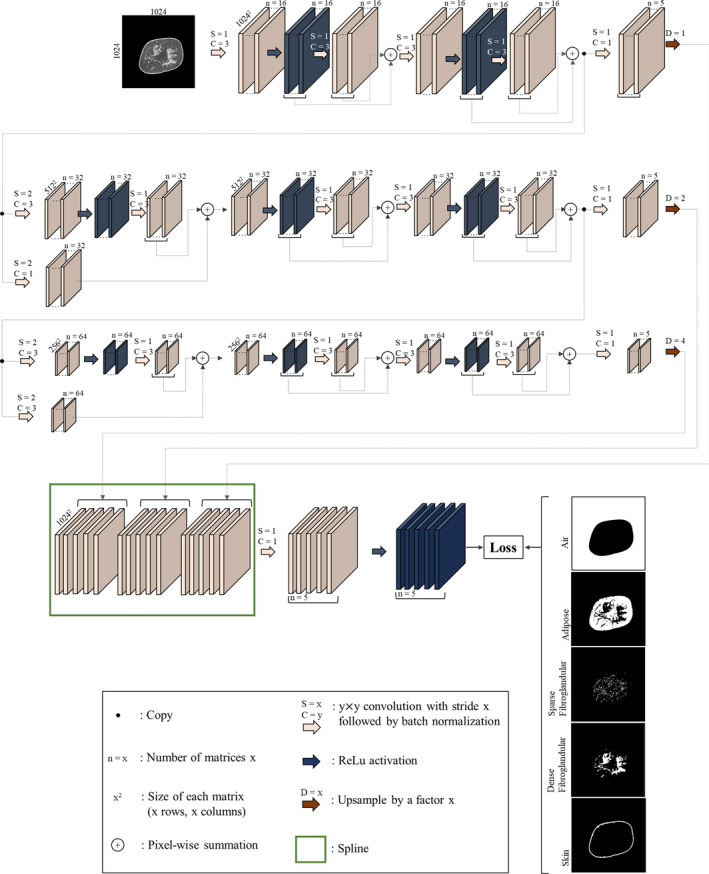
Architecture of the convolutional neural network used for semantic image segmentation of the breast computed tomography images. [Color figure can be viewed at wileyonlinelibrary.com]
The input to the network is a coronal image section of a reconstructed breast CT image. The corresponding segmented image is one‐hot‐encoded54 into five image arrays, collectively called the input label matrix. One‐hot encoding is the process of converting categorical data (such as the segmented images) into binary data where each binary value is representative of one and only one category. As such, image arrays contained in the label matrix have the same size and spacing as the input image, each representing air, adipose, sparse fibroglandular (low‐density fibroglandular, we refer to this voxel type as sparse due to the existing high sparsity in the corresponding classified matrix), dense fibroglandular, or skin.
During a training attempt, the resulting output label matrix contains values between zero and one, which is interpreted as the predicted label image probability density function. This enables the use of the cross‐entropy metric55 as the loss function in the classification task at hand:
| (1) |
where is the ground truth label matrix, is the input image section, θ denotes the network's trainable parameters, index spans all elements (N) of the label image arrays, and is the predicted posterior probability (output label) matrix. The loss function defined in Eq. (1) penalizes different classification errors equally. In a typical bCT image, there is a significantly lower number of fibroglandular and skin voxels compared to air or adipose voxels. Hence, this loss function generates backpropagation gradients that force the network to misclassify fibroglandular and skin voxels in favor of the air or adipose voxels. We utilized the following weighted loss metric within which the individual classification errors were penalized differently. The weighted loss was defined as follows:
| (2) |
where Ij is a binary indication function indicating whether this voxel belongs to category and is the penalization weight associated with the category . Hyper‐parameter is used to find a trade‐off between the error term and the ‐norm regularization term to avoid overfitting.56 The five voxel categories are air , adipose , sparse fibroglandular , dense fibroglandular , and skin . Since the fibroglandular and skin voxel types are underrepresented in a breast CT image, Eq. (2) penalizes the misclassification of these voxels more than the other voxel types. Fibroglandular density in an average breast was reported to be between 9 and 24%,50, 51 implying that the majority (78% chosen in this study) of an average breast volume is composed of adipose tissue and the rest (22%) is composed of fibroglandular tissue and skin. In an empirical test of 111 ground truth bCT data sets used to train the network, on average 63% of the CT image voxels are classified as air and the rest (37%) are breast tissue voxels. Based on these numbers, was set to , to and , and to . The hyper‐parameter was found via cross‐validation and was set to 0.0005 by monitoring the cross‐entropy value to avoid under or overfitting.
During the convolution steps, the input image arrays were zero‐padded and shifted to enable one‐to‐one correspondence between the input image matrix and the output label matrix. The output number of the matrices in each operation of the encoder wing was set to a power of two to accommodate more efficient memory management on the Graphics Processing Unit (GPU). An Adaptive Moment Estimation (Adam) stochastic optimization algorithm57 was implemented because of its computational and memory management efficiency. The batch size was set to 16, epoch number to 20, learning rate to 0.0001, and constant momentum to 0.95. The network parameters were initialized to a random‐draw from a Gaussian distribution with mean 0 and standard deviation which was inversely proportional to the square root of the inputs of layer operations.58 Training was implemented using Microsoft's Cognitive Toolkit Application Programming Interface59 running on a system with an Intel CoreTM i7‐6850K @3.60 GHz processor, 64 GB RAM, and an NVIDIA Quadro P5000 GPU.
2.1.2. Image preprocessing
Several preprocessing steps were applied before the start of the network training. All bCT images at UC Davis were reconstructed into matrix sizes of (for scanners Albion, Bodega or Cambria) and for scanner Doheny. This difference in reconstruction matrix size is due to the inherent limiting spatial resolution of each scanner (0.9 lp/mm in Albion and Bodega, 1.7 lp/mm in Cambria and 3.6 lp/mm in Doheny). To maintain consistency for the input image size, all coronal bCT images used in this study were isotropically reconstructed into a 512 × 512 matrix using a variation of the Feldkamp filtered back‐projection algorithm and a Shepp‐Logan filter. The input image to the network during training or deployment was scaled to zero and one by finding 1% and 99% grayscale values of the overall CT image histogram and using those values as minimum and maximum levels, respectively. In each bCT data set, the most posterior coronal image used for network training was manually determined as the image that does not contain partial volume artifacts. In addition, slices that contain metal artifacts (usually caused by markers in a breast) were also excluded from this study.
2.1.3. Training and validation
A total of 45 621 coronal bCT images were used for training. These images were reconstructed from 11, 83, 7, and 10 patient scans performed using scanners Albion, Bodega, Cambria, and Doheny, respectively (111 data sets in total). The images were divided into three subsets used for training (70% of images), test (20% of images), and validation (10% of images). The training and test subsets were disjunctive, as they contained images from different patients, to ensure generalization capability of the found solution. The ground truth segmented images were generated automatically using a previously developed and tested expectation‐maximization based segmentation methodology42, 60 followed by manual review from an experienced breast CT research scientist.
The overall memory required to train the network at once exceeds the capacity of the hardware used in this study. Therefore, a tenfold memory management paradigm was used to cover the entire cohort of images in the training set. First, the slices from each patient scan were divided randomly into ten sets. Second, one set from each patient scan was randomly selected and aggregated with the other sets selected from other scans to generate a batch of 4562 slices. This batch was used to train the network. Following this paradigm, all patient data sets were included in each training attempt. At the end of training each image batch, the network parameters were saved and used to initialize the network for the training of the next batch of images. Hence, all the slices available for training were used to train the network without a bias for a patient scan or scanner type.
The error in the classification task was measured using the Sorensen–Dice similarity coefficient (DSC) defined as follows:
| (3) |
where is the Jaccard similarity coefficient61 defined as the intersection of ground truth and resulting label matrices divided by their union. The intersection of two label images was defined as an element‐wise multiplication of the two label matrices followed by summation of all elements of the resulting product matrix. Union of two matrix matrices was calculated by first finding the summation of all elements of each matrix and then adding up the results. In addition, two confusion matrix‐based metrics — precision and recall defined based on true positive (TP), false‐positive (FP), and false‐negative (FN) quantities — were considered for evaluating the classification task,
| (4) |
and
| (5) |
Using Eqs. (4) and (5), we calculated the score, a measure of accuracy, as follows:
| (6) |
2.1.4. Postprocessing and deployment
The output labeled image of the trained network is a matrix where the third dimension comes from the five probabilities for each class assigned to each voxel. The class with the highest probability is selected and assigned a value 0, 1, 2, 3, or 5, depending on whether the pixel is classified as air, adipose, sparse fibroglandular, dense fibroglandular, or skin, respectively. The output of the segmentation routine is a grayscale image corresponding to the input slice to the network.
2.2. CT image shading correction
Following the bCT reconstruction, all voxels in the images are converted to HU. The effective energy of the beam in each bCT system was found by utilizing the measured first HVL (Table 1) and the TASMICS62 x‐ray spectral model. The expected HU values for 100% adipose tissue in different scanners were found using the calculated effective energy.63 Adipose HU values are canonically treated as uniform, and this assumption was leveraged in the following description of the methodologies used for flat fielding of the bCT images.
Let be the HU value of the voxel located at the Cartesian location in the reconstructed image where x, y, and z are the indices of a voxel along row, column, and slice, respectively. Let a subset of containing only the adipose voxel values be . The objective of the regression model is to find the parameters () of a deterministic function such that the values of all voxels classified as adipose are modeled within an error ,
| (7) |
where is a set of features with members and is a set of unknown parameters associated with the regression model . The error term was assumed to be a zero mean Gaussian random variable with standard deviation , since the adipose voxel values are generally assumed to have a unimodal distribution.50, 64, 65, 66 Therefore, is defined as a probabilistic function dependent on y with standard deviation of ,
| (8) |
where denotes conditional probability and is the normal distribution.
Following the linear regression paradigm,67 was defined as the inner product of the features () and unknown parameters (. The classification of one voxel in an image as adipose has no bearing on the classification of another voxel. Individual adipose voxel HU values are therefore assumed to be uncorrelated. This property of the CT image enables us to derive a solution for by maximizing the likelihood function. A likelihood function () is a function of unknown parameters and in the following form:
| (9) |
where is the total number of adipose voxels in the reconstructed breast CT image volume, is the CT number of the nth adipose voxel located at and . Maximizing the likelihood function defined in Eq. (9) with respect to results in deriving (the parameters corresponding to the Maximum Likelihood solution).56 The analytical solution is the result of the inner product of and the Moore‐Penrose pseudo‐inverse () of the adipose features matrix , that is,
| (10) |
is defined as:
| (11) |
The analytical solution found in Eq. (10) fully describes the fit within the feature space. The DC component of the parameter set, , plays an important role in determining the convergence of the cupping/capping correction algorithm. Setting the derivative of the likelihood function [Eq. (9)] with respect to to zero leads to being equal to the average value of adipose voxels CT numbers. If is within 1 HU to the theoretical value of the 100% adipose tissue stated in Table 1, a convergence for IC has been reached. Otherwise, the fit is not optimal, and another iteration of the fit must be performed until reaching the convergence criterion.
The number of features , defined by the order of the polynomial, is an important parameter that is dependent on the nature of x‐ray scatter and beam hardening and its propagation in the reconstruction pipeline. These physical phenomena result in artifacts manifested as low‐frequency degradation of CT numbers at the center of mass of the reconstructed image. With this in mind, the proposed method (IC) implemented a quadratic (second order) fit. For the mathematical derivation, refer to the supplemental material included in the Appendix S1.
The following steps outline the IC methodology of fitting a three‐dimensional second‐order polynomial model to the adipose system matrix and using the derived model to flat field a bCT image:
Segment the bCT image using the CNN described in Section 2.A.
Define an adipose features matrix of size (10 × ) as follows:
| (12) |
where x A, y A, and z A are the elements of the position of the considered adipose voxel in the Cartesian coordinate system. Use the segmented image volume to form .
Form using the original and segmented image volumes.
Derive the Moore‐Penrose pseudo‐inverse of the adipose system matrix using Eqs. (10) and (11) as follows:
| (13) |
where βML is a column vector with 10 elements. Note that the first element of this vector () is a bias term independent of the spatial location of the voxels. As the algorithm converges, this parameter approaches the theoretical adipose value listed in Table 1. Later in step 7, we use this term to determine the convergence of the HU calibration algorithm.
is a subset of a feature matrix spanning all voxels of the reconstructed CT image volume. Form this matrix as
| (14) |
| (15) |
where is a vector containing the same number of elements as the CT image volume. Due to the second‐order feature space and fitting algorithm, the background fit is convex with a single global minimum and it describes the CT volume as if it entirely consisted of adipose voxels.
Use the modeled background matrix [Eq. (15)], to calculate the background‐corrected matrix using the following equation:
| (16) |
where is a vector consisting of all CT image numbers.
Let HUTA be the theoretical HU of 100% adipose tissue at a given effective energy. The HU‐calibrated CT matrix () can then be formed as,
| (17) |
Following the above steps, one can derive a corrected version of the original reconstructed CT image. The resulting HU‐calibrated image, , is in turn used to generate a segmented image using the CNN described in Section 2.A. The new segmented image and are used to generate a new flat‐fielded CT image. This iterative process continues until a convergence is reached. Because of the convexity of the model used for fitting, it is expected that converges to the theoretical adipose HU value as listed in Table 1. Convergence is defined to be achieved when is within 1 HU from the expected adipose value.
2.3. Validation using mathematical breast phantoms
The percentage and distribution of fibroglandular tissue affect the performance of the proposed IC method. To remove this variability and validate the segmentation and flat fielding parts of the IC method with respect to a known distribution of fibroglandular tissue, we used a series of previously reported numerical homogenous phantoms68, 69 and scans of the corresponding physical phantoms to construct mathematical phantoms. Details regarding the design and fabrication of the breast phantoms have been previously published, and therefore, only details pertinent to this work are discussed herein.
The size and shape of the numerical and physical breast phantoms were derived from a large cohort of 215 breast CT volume data sets. This cohort of data sets was grouped by total breast volume (excluding skin) into one of five volume‐specific breast phantom sizes defined as V1 (small) through V6 (extra‐large). The average radius profile was then determined for each size group resulting in a total of six numerical and physical breast phantoms. A subsequent study utilized the size‐specific breast phantoms and cohort of bCT volume data sets to quantify the statistical distribution of fibroglandular tissue on a size‐specific basis.70 For the present study, the V1 (small), V3 (median), and V5 (large) physical and numerical breast phantoms were used for validation of the IC method. Figure 2(a) is a representation of the V3 (median‐sized) numerical breast phantom with a heterogenous fibroglandular distribution.
Figure 2.

Generation of the V3 (median‐sized) phantom used for IC validation. In each case, the coronal view is shown in left and sagittal view in right. A heterogenous phantom with volume glandular fraction corresponding to 50% of pollution used in modeling is shown in (a). The corresponding physical V3 phantom (b) is scanned twice. The reconstructed images are subtracted and normalized to form realistic quantum noise distribution (c). The physical phantom is also cupping corrected to simulate a “ground truth” background model (d). The background and noise images are added to the original heterogenous image to generate the V3 mathematical phantom (e).
In order to replicate a realistic bCT case, the V1, V3, and V5 physical breast phantoms were positioned in scanner Doheny's FOV, aligned with the isocenter axis and scanned twice with the technique factors used for routine patient scans. An example scan of the V3 phantom is shown in Fig. 2(b). In each case, the two reconstructed image data sets were subtracted and voxel‐wise normalized by , resulting in a realistic quantum noise distribution observed in bCT images as shown in Fig. 2(c). The noise images were then added to the mathematical heterogenous phantom [Fig. 2(b)] to generate a noisy mathematical phantom model [Fig. 2(e)]. In the next step, one of the data sets for each physical V‐phantom was randomly selected and corrected for the cupping artifact following the nine‐step IC method described above. The resulting background image [Fig. 2(d)] serves as a known ground truth and was added to the corresponding numerical noisy phantom to generate a mathematical breast phantom that realistically resembles a bCT data set. This process was identically repeated for all three V‐phantoms. The IC method was used to correct for the shading artifacts in the three mathematical phantoms, resulting in segmentation and background modeling of the data sets that are compared to the ground truth segmentation and background images for validation.
2.4. Validation using physical breast phantom
The phantom setup outlined in this section characterizes the proposed IC method's ability to remove cupping artifact with respect to radial distance from the center of mass of each coronal slice and to correct for axial HU drop. Three uniform cylindrical polyethylene phantoms with diameters of 10.2, 12.7, and 15.2 cm were positioned in the FOV of scanner Doheny and scanned with the x‐ray techniques listed in Table 1. Under these conditions, the theoretical value for polyethylene HU is −198.71 CT image volumes were reconstructed and HU‐calibrated using the nine‐step IC method described earlier in this section to generate cupping‐corrected data sets. Multiple bands were used at different radial distances from the center of mass in coronal slices, each having an equal radial thickness of 1 cm (refer to Fig 3). Band averaging was applied before and after application of the IC method to minimize noise. Band averaging implies averaging through all the voxels within a predefined distance from the center of mass of an image section. The width of the bands (in the anterior‐posterior direction) was set to 1 cm, and in doing so a single value is calculated for each band in a coronal image section. This process was repeated for all coronal sections of a bCT volume data set. An aggregate of these values for a specific band provides intuition into how HU values change as the cone angle increases. Since air voxels are present near the cylindrical phantom periphery, they may be included in the outer band. To mitigate this, band averaging was not calculated in regions within 1cm of the edge of the phantom.
Figure 3.
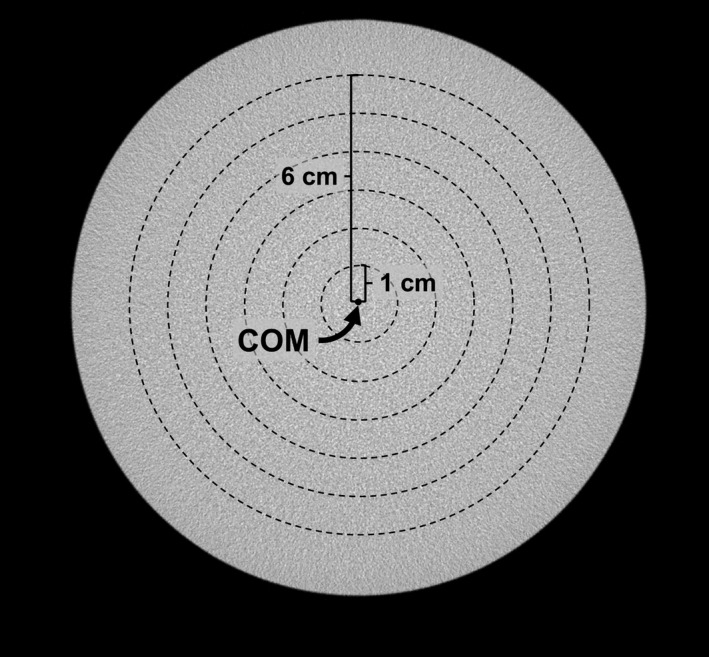
Band averaging used in physical phantom experiment. A coronal slice of a 15.2‐cm cylindrical phantom image is shown. Six bands are shown, each 1 cm thick in the radial direction and positioned radially symmetric from the center of mass (COM) of the image. The voxel values within each band were averaged to generate six values.
Two metrics of uniformity7 were used to assess the shading artifact, the integral nonuniformity (INU) metric defined as:
| (18) |
and the Uniformity Index (UI) defined as:
| (19) |
where and are the maximum and minimum of the radial bands. The band containing the center of mass (called center band) has an average CT number of and the most peripheral band has an average CT number of .
2.5. Patient scan validation
Volume data sets from eight patient scans — two for each scanner listed in Table 1 — were used to evaluate the performance of IC on real patient images. These data sets were not used for CNN training. Patients for whom images were utilized exhibited variations in breast size and density, spanning patient self‐reported cup‐size of A to D, and average glandular fractions of 12% to 29%. The aggregate adipose values of each data set, before and after cupping/capping correction, were collected and compared to study the standard deviation of adipose voxels values.
3. Results
Figure 4 displays the progression of the network training during multiple epochs (top row), and a sequence of an example input image, ground truth, and the output segmented image (middle row). The input test image is from a patient data set acquired using scanner Bodega. The breast diameter is 14.5 cm, and the breast glandular fraction is 21%. The five images captured during the training at epochs 1, 4, 8, 12, and 16 display that the network gradually learns features from the volume data sets, starting from the easy to classify regions (i.e., air and adipose), and building up with each iteration to the more complex features. One important observation from the CNN segmentation is that the small fibroglandular fibers in the reconstructed image [Fig. 2(b)–2(c); middle column] are segmented as predominantly sparse fibroglandular [Figs. 2(b)–2(c); right column]; whereas in the ground truth segmentation [Figs. 2(b)–2(c); left column], these small fibers are segmented predominantly as adipose tissue — highlighting one of the advantages of implementing a CNN algorithm for segmentation.
Figure 4.
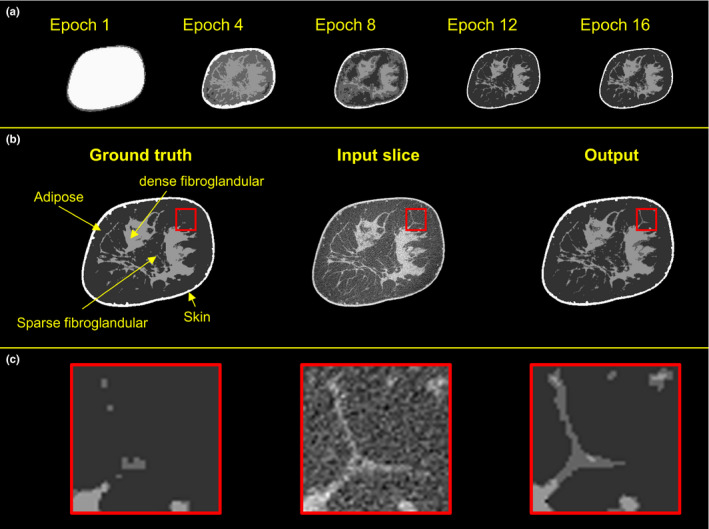
Examples of the progression of the network training. Top row shows the output of the network during training. The input coronal image, input segmented image, and the output of the trained network are shown in the middle row. The bottom row displays the zoomed‐in views of the regions of interest. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 5 shows the average error quantified in terms of cross‐entropy (H) between the network output and the ground truth that was generated during the training. The average DSC value of the test data set along different epochs is also shown in Fig. 5. Error bars display the maximum and minimum of the entropy and DSC values in each epoch.
Figure 5.
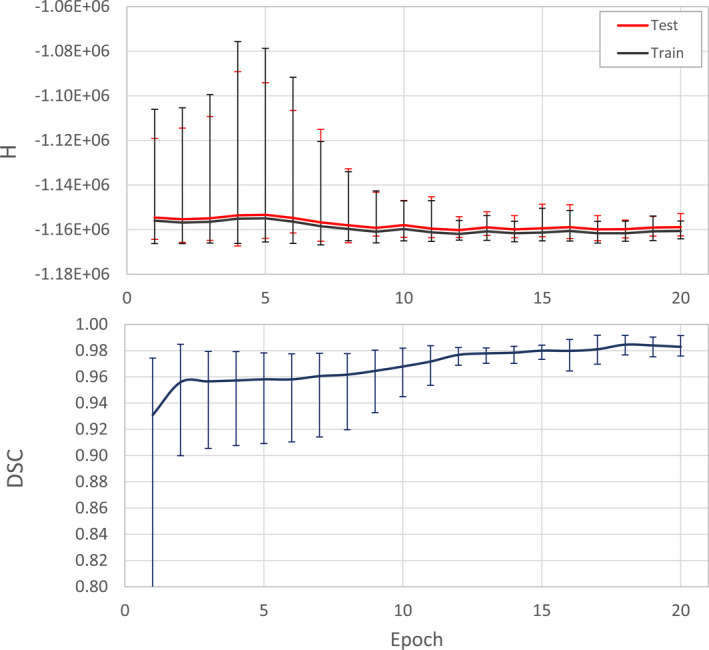
The progression of average error during network training. The cross‐entropy (H) between the output of the network and the input image is shown. The Dice similarity coefficient (DSC) between output and the reference segmentation masks in the test set is shown in the bottom graph. Error bars display the minimum and maximum values in each epoch. [Color figure can be viewed at wileyonlinelibrary.com]
Three metrics were used in evaluation of the trained neural network's ability to segment different tissue types — precision, recall, and F1 score. Referring to Fig. 6, the drop observed in precision, recall, and consequently F1 score from 1 (the ideal value) is mainly due to misclassification of the sparse fibroglandular tissue voxels. Air voxels are almost unanimously predicted correctly as indicated by the near unity value for all three metrics. The adipose voxels show a small decrease (precision = 0.98, recall = 0.96 and F1 = 0.97), while the large drops are observed in the case of sparse fibroglandular (precision decrease = 8.3% relative to unity, recall decrease = 3.9%, F1 decrease = 2.8%), dense fibroglandular (precision decrease = 3.4% relative to unity, recall decrease = 1.5%, F1 decrease = 2.4%), and skin (precision decrease = 3.5% relative to unity, recall decrease = 4.7%, F1 decrease = 4.2%).
Figure 6.
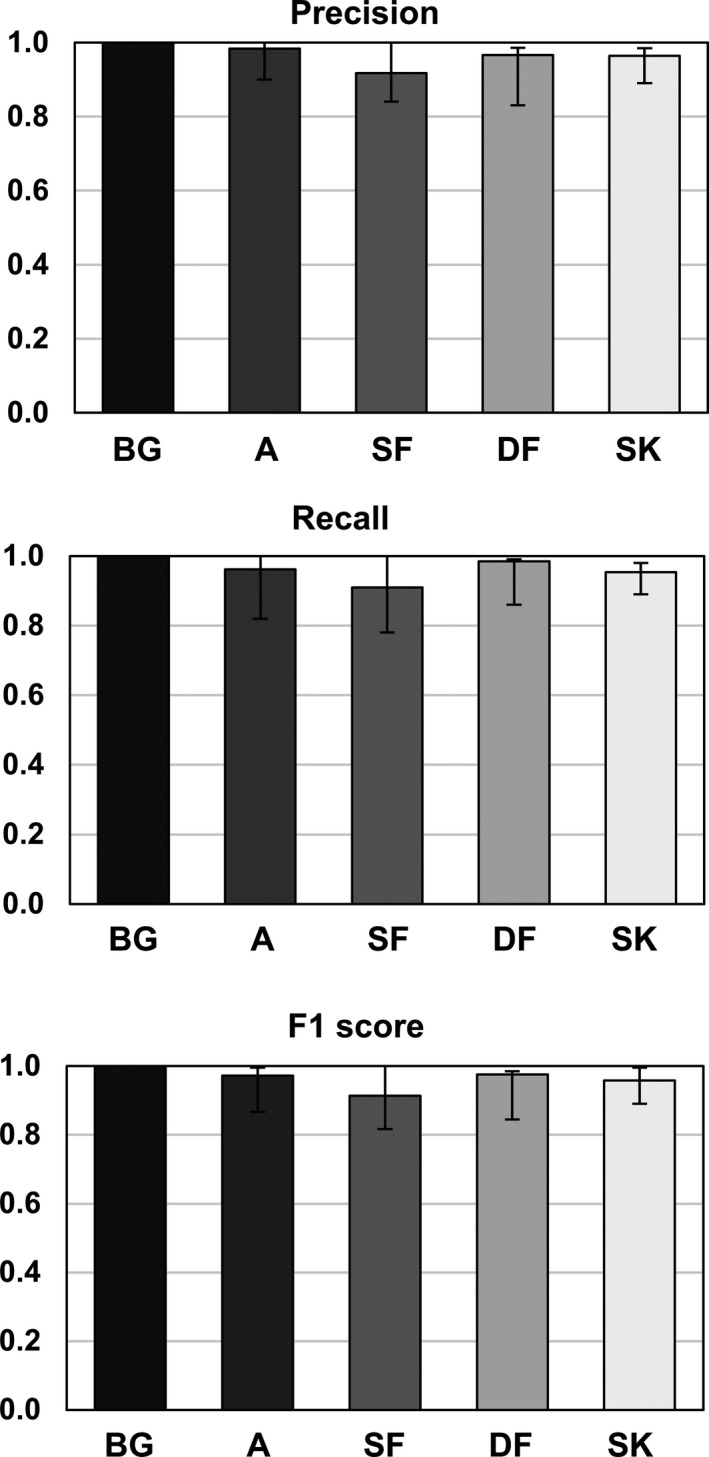
Results of the precision, recall, and F1 score metrics used to evaluate the trained network's ability to correctly classify the test image voxels according to the corresponding ground truth. The voxel types are denoted as air (background‐BG), adipose (A), sparse fibroglandular (SF), dense fibroglandular (DF), and skin (SK).
Figure 7 displays the segmentation results for three different sized mathematical phantoms. The CNN segmentation consistently outperforms the k‐means clustering segmentation method across all phantoms. The largest difference between the known phantom voxel types, and either CNN or 2‐means clustering results is observed in the case of glandular and adipose voxels. There are consistently more adipose voxels than glandular voxels across all phantoms as indicated by the volumetric glandular fractions of 19.9%, 9.5%, and 3.8% for V1, V3, and V5 phantoms, respectively. Therefore, the difference between the ground truth (mathematical phantoms) and the other segmentation methods is greater for adipose than for either skin or fibroglandular tissue types. The error in estimating the ground truth background, defined as the absolute difference between the voxels of the ground truth and the estimated background, was 11.19 ± 4.91 (mean ± standard deviation) HU.
Figure 7.
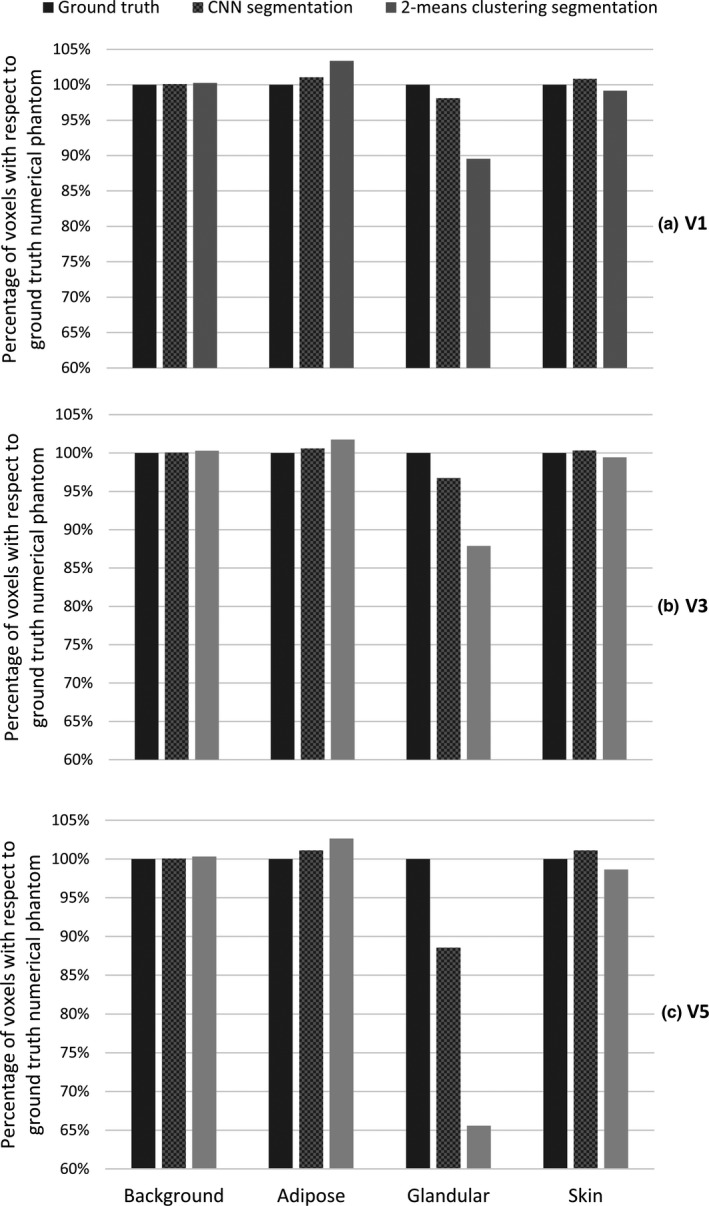
Mathematical phantom segmentation results using the proposed convolutional neural network (CNN) or 2‐means clustering segmentation processes. The type of voxel is already known in the ground truth image (generated mathematical phantom). Different types of voxels are extracted after segmentation via each method and compared to the ground truth. The V1 (a), V3 (b), and V5 (c) mathematical phantom results are shown in top, middle, and bottom rows, respectively.
The segmentation method outlined in Section 2.A is utilized during the CT image flat fielding described in Section 2.B. Figure 8 presents six different box‐whisker plots showing the results of separately applying IC to CT images of three uniform cylindrical polyethylene phantoms. The boxes highlight the median and the high (75th %) and low two quartiles (25th %) of the coronal band averages (see Fig. 3) throughout the image sections. The reconstructed images were first segmented and then flat‐fielded using the segmentation results. In the case of phantom experiments, segmentation does not change after completion of the flat fielding due to the phantom's simple shape and composition. The IC therefore converges in a single iteration. In each case, cupping and capping artifacts were substantially reduced. Band average values converged to the expected polyethylene HU, an indication that the voxel HU values were properly calibrated. The relative consistency of the HU values along the axial direction after implementation of the IC is indicated in Fig. 8 by a significant decrease in the HU variance for each box — implying satisfactory correction for the axial HU drop. In summary, Fig. 8 demonstrates that implementation of the IC method results in mitigation of axial HU drop and the cupping artifact inherent in cone beam breast CT reconstructions. In addition, these results demonstrate that the residual artifact (i.e., capping), which is the result of over correcting for the cupping artifact, can also be mitigated.
Figure 8.
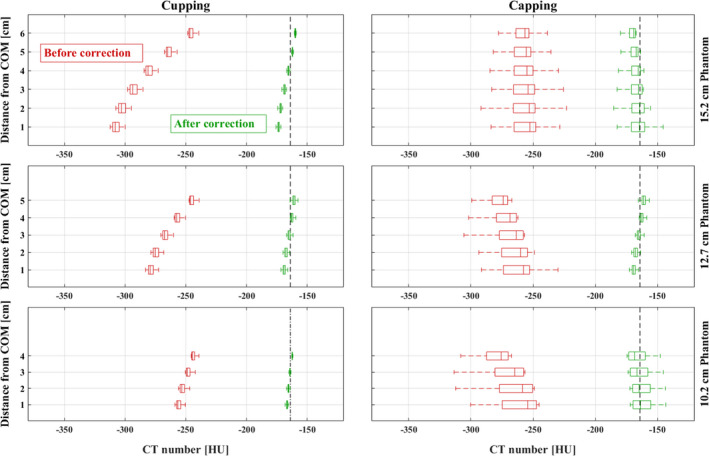
Box‐whisker plots presenting phantom experiment results in evaluation of IC for the correction of cupping, capping, and cone beam HU drop artifacts in addition to HU miscalibration for a 15.2 cm (top row), 12.7 cm (middle row), and 10.2 cm (bottom row), 12.7 cm (middle row), and 10.2 cm (bottom row) diameter polyethylene phantom. In each of the 6 plots, the leftmost “Box” edge represents the first quantile boundary, the vertical line inside of the box represents the median, and the rightmost edge represents the third quantile boundary. The left and right columns show the results of using IC in cupping and capping cases, respectively, across phantom sizes. The change in the average HU band values along the axial axis is demonstrated through the size of each box. In each case, the quantile variance is reduced (the box width shrinks) after flat fielding, indicating a correction of HU change in axial direction. [Color figure can be viewed at wileyonlinelibrary.com]
Uniformity metrics of the phantom scan experiments are reported in Tables 2 and 3. The UI metric, an index of the extent of curvature in cupping or capping artifacts, was reduced in all but one case (15.2 cm phantom — capping). The INU metric results imply that the HU drop in the axial direction was reduced with implementation of the proposed IC.
Table 2.
Uniformity Index metric of phantom scans before and after IC application. Positive UI values indicate cupping, negative UI valued indicate capping
| Phantom size | UI (%) | |||
|---|---|---|---|---|
| Cupping | Capping | |||
| Before | After | Before | After | |
| 15.2 cm | −19.92 | −6.00 | −1.53 | −1.92 |
| 12.7 cm | −11.86 | −2.77 | 6.32 | 3.02 |
| 10.2 cm | −4.69 | −1.54 | 8.39 | 2.87 |
Table 3.
Integral nonuniformity metric of phantom scans before and after IC. The standard error of the integral nonuniformity (INU) index in each case is stated in parenthesis
| Phantom size | INU | |||
|---|---|---|---|---|
| cupping | capping | |||
| Before | After | Before | After | |
| 15.2 cm | −0.0087 (0.0012) | −0.0029 (0.0010) | −0.0294 (0.0056) | −0.0235 (0.0074) |
| 12.7 cm | −0.0074 (0.0007) | −0.0057 (0.0006) | −0.0335 (0.0074) | −0.0076 (0.0008) |
| 10.2 cm | −0.0062 (0.0010) | −0.0018 (0.0008) | −0.0444 (0.0097) | −0.0426 (0.0017) |
Figure 9 shows the example of CT images from one of the patient scan cases. The displayed image data set was acquired using scanner Bodega. Image sections from anatomical regions and circumstances containing visible levels of shading artifacts are displayed in this figure. Both artifacts, cupping and capping, are treated with the same IC methodology. The line profiles of through the image sections display a visual comparison between the quality of the images before and after shading correction.
Figure 9.
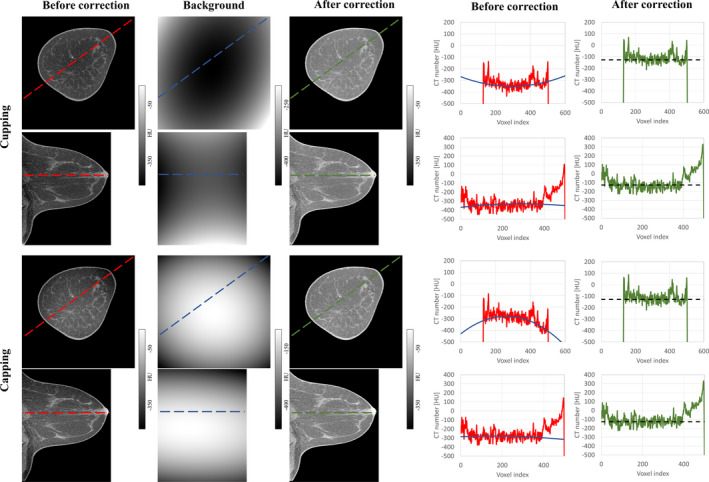
Evaluation of the IC for an example patient scan on the Bodega scanner. Shown in red in each coronal or sagittal view are the line profiles along the longest axes containing the breast tissue. Blue and green lines show the line profiles along the modeled background and corrected images, respectively. The theoretical adipose HU value (−110 HU as mentioned in Table 1) is shown in dotted black. [Color figure can be viewed at wileyonlinelibrary.com]
The change in the overall values of the adipose tissue in each patient scan case is shown in Fig. 10. In each data set, the adipose tissue variation is reduced as is appreciated by comparing the size of boxes before and after applying IC.
Figure 10.
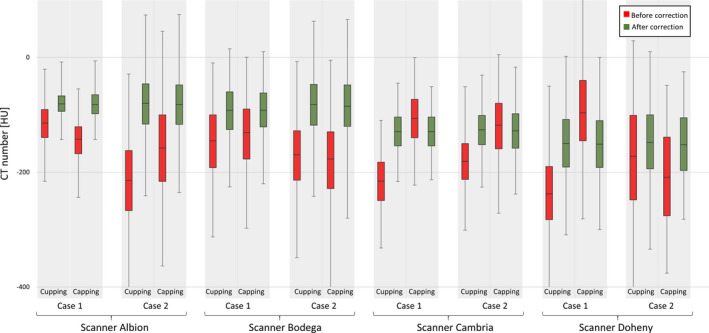
Change in adipose tissue voxels before and after correction. Eight total cases from four scanner are selected. The median, first, and third quantile of adipose voxels in each data sets are displayed. The 1% and 99% of the histogram are shown using error bars. [Color figure can be viewed at wileyonlinelibrary.com]
4. Discussion
Clinical studies are heavily dependent on quantitative analysis of HU values, and their accuracy impacts the quality of a diagnostic study. The focus of this work was on developing a postprocessing shading artifact correction method for bCT. The proposed IC method consists of two parts: image segmentation and CT image flat fielding. These two tasks are highly interdependent. Accurate flat fielding of the CT image depends on correct image segmentation. The accuracy of the segmentation task is in turn highly dependent on shading artifacts and HU calibration. This interdependency is escalated in the case of large and dense breasts, because of the increased amount of x‐ray scatter and beam hardening. For instance, the fibroglandular tissue voxels may be wrongly classified as adipose in cases that suffer from cupping artifact, especially in region near the center of mass in the coronal plane. Similarly, a severe capping results in classification of adipose voxels as fibroglandular. These misclassifications lead to an erroneous definition of the feature space used for polynomial flat fielding and consequently a reduced convexity in the cupping modeled fit or an enhanced concavity in the capping modeled fit. Therefore, the modeled fits are not truly representative of the background of the bCT images. To address this, sequential utilization of the two parts (segmentation and flat fielding) is repeated until the HU of adipose tissue matches an expected HU. This value is calculated with knowledge of the x‐ray beam quality used for each scan.
The parameters of the neural network architecture used for segmentation were carefully selected to accommodate the requirements of the bCT image classification. The cost function was modified from the classical cross‐entropy form to penalize the misclassification of underrepresented voxels types more than the overrepresented voxels. The graphs shown in Fig. 5 demonstrate a training saturation after approximately epoch 15. It is important to note that training of the network beyond epoch 20 does not yield worthwhile improvement as the cost function defined in Eq. (2) is restrained to avoid overfitting. Therefore, the number of epochs was set to 20.
Increasing the number of voxels classified as sparse fibroglandular in the segmented image implies a reduction in the number of dense fibroglandular or adipose voxel types. This is what leads to the difference in the magnitude of error bars in Fig. 6. The variations in the metric values are highest in the case of fibroglandular tissue types highlighting the fact that a portion of the voxels previously classified as adipose in the ground truth is now classified as sparse fibroglandular, the effect that is visible in images shown in Fig. 6. The same conclusion is made by comparing the percentage of fibroglandular voxels that were correctly classified in the mathematical phantom study. Voxel classification using the proposed CNN is much closer to the true category for each voxel than the results gained from the histogram‐based 2‐means clustering method. This is likely due to the fact that the blurring used in 2‐means clustering results in the sparse fibroglandular tissue voxel values being in the adipose tissue territory and being classified as such which gave rise to the adipose classified voxels in 2‐means clustering as shown in Fig. 7.
The nine steps outlined in Section 2.B provide a systematic methodology for removing cupping or capping from the bCT image. The objective is to find an analytical solution to the background fitting problem in all three dimensions which is provided by Eq. (13). The flat fielding step of the IC was evaluated using mathematical and physical phantoms of various sizes and corresponding size‐specific fibroglandular distributions. In each of the four experimental physical phantom cases, both cupping and capping were successfully reduced. Application of the IC method in each of the eight independent patient scan experiments resulted in improvement as depicted in Fig. 10.
Among all cases of phantom and patient scan experiments, no bias was observed for the algorithm's performance in resolving cupping or capping as the algorithm tries to fit a second order polynomial to the adipose feature space. The algorithm does not favor concavity or convexity of the feature space. The cupping/capping is not fully resolved, as shown in Fig. 7. This is most likely due to the variations in the adipose CT values throughout the CT volume as it affects the fitting model. One can apply a low‐pass filter to the adipose voxel CT number vectors to reduce this variation. Another potential solution would be to statistically track the HU values of adipose voxels, pick outliers, and remove them from the feature space to avoid a potential skewing of the fitting process.
The drop in HU along the axial direction was reduced significantly after implementation of the IC method which was an unintended, yet advantageous consequence of the developed flat fielding method that was developed for correction of the cupping artifact. The low‐frequency HU drop is a well‐studied artifact of circular cone beam CT systems. In circular trajectory breast CT systems — such as the ones used in this study — the Radon space data of a breast cannot be completely measured as the image acquisition does not meet the requirements of Tuy's data sufficiency condition.72 The average intensity of the reconstructed adipose voxels in coronal planes consistently drops moving away from the central coronal plane. Results shown in Fig. 8 demonstrate that applying the IC method on CT images reduces the variation in adipose voxel values throughout the CT image — indicative of a correction for axial HU drop.
Patient scans from four different scanners were used to test the robustness of the flat fielding. In all cases, the cupping/capping artifacts were resolved, and the HU values were properly calibrated. The relative HU values of the adipose and fibroglandular tissues were not affected by applying the IC method. This is consistent with other previously reported image domain correction methods.34, 37 The importance of this characteristic for the proposed IC method is in contrast‐enhanced breast CT applications. The iodine contrast uptake in tumors — quantified as enhanced HU values — has been shown to correlate with conspicuity of malignant breast masses,11 and therefore, preserving the contrast between the iodinated tumor and the adipose background is crucial.
5. Conclusion
Introduced herein are two novel methods for image segmentation and background fitting, which coupled, result in correction for shading artifacts in dedicated breast CT. First, we present the design and utilization of a convolutional neural network specific to breast CT. Following segmentation is the application of an analytical approach to three‐dimensional image background fitting. These two methods, implemented as an iterative two‐step process, correct for shading artifacts that are ubiquitous in breast CT. The accuracy of the presented method was demonstrated through mathematical and physical phantom experiments and a pilot study of eight patient scans acquired using four differently designed breast CT scanner systems.
Supporting information
Appendix S1: Mathematical derivation of a 3D quadratic fit to bCT shading artifact.
Acknowledgments
This work was supported by research grants (Grants No. R01 CA181081, R01 CA214515, P30 CA093373, P30 CA093373) from National Institutes of Health.
References
- 1. Gazi PM, Yang K, Burkett GW, Aminololama‐Shakeri S, Anthony Seibert J, Boone JM. Evolution of spatial resolution in breast CT at UC Davis. Med Phys. 2015;42:1973–1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Logan‐young W, Lin CL, Sahler L, et al. Cone‐beam CT for breast imaging: Radiation dose, breast coverage, and image quality. Am J Roentgenol. 2010;195:496–509. [DOI] [PubMed] [Google Scholar]
- 3. Kalender WA, Beister M, Boone JM, Kolditz D, Vollmar SV, Weigel MCC. High‐resolution spiral CT of the breast at very low dose: Concept and feasibility considerations. Eur Radiol. 2012;22:1–8. [DOI] [PubMed] [Google Scholar]
- 4. Shah JP, Mann SD, McKinley RL, Tornai MP. Three dimensional dose distribution comparison of simple and complex acquisition trajectories in dedicated breast CT. Med Phys. 2015;42:4497–4510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Rührnschopf EP, Klingenbeck K. A general framework and review of scatter correction methods in x‐ray cone‐beam computerized tomography. Part 1: Scatter compensation approaches. Med Phys. 2011;38:4296–4311. [DOI] [PubMed] [Google Scholar]
- 6. Rührnschopf EP, Klingenbeck K. A general framework and review of scatter correction methods in cone beam CT. Part 2: scatter estimation approaches. Med Phys. 2011;38:5186–5199. [DOI] [PubMed] [Google Scholar]
- 7. Bissonnette JP, Moseley DJ, Jaffray DA. A quality assurance program for image quality of cone‐beam CT guidance in radiation therapy. Med Phys. 2008;35:1807–1815. [DOI] [PubMed] [Google Scholar]
- 8. Yang K, Kwan A, Burkett G, Boone J. SU‐FF‐I‐05: Hounsfield units calibration with adaptive compensation of beam hardening for a dose limited breast CT system. Med Phys. 2006;33:1997. [Google Scholar]
- 9. Barrett JF, Keat N. Artifacts in CT: recognition and avoidance. Radiographics. 2004;24:1679–1691. [DOI] [PubMed] [Google Scholar]
- 10. Zhu L, Starman J, Fahrig R. An efficient estimation method for reducing the axial intensity drop in circular cone‐beam CT. Int J Biomed Imaging. 2008;2008:1‐11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Prionas ND, Lindfors KK, Ray S, Beckett LA, Monsky WL, Boone JM. Contrast‐enhanced dedicated breast CT: initial clinical experience 1 purpose: methods: results: Radiology. 2010;256:714–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Boone JM, Nelson TR, Lindfors KK, Seibert JA. Dedicated breast CT: Radiation dose and image quality evaluation. Radiol Brook. 2001;221:657–667. [DOI] [PubMed] [Google Scholar]
- 13. Hatton J, McCurdy B, Greer PB. Cone beam computerized tomography: The effect of calibration of the Hounsfield unit number to electron density on dose calculation accuracy for adaptive radiation therapy. Phys Med Biol. 2009;54:N329–N346. [DOI] [PubMed] [Google Scholar]
- 14. Kwan ALC, Boone JM, Shah N. Evaluation of x‐ray scatter properties in a dedicated cone‐beam breast CT scanner. Med Phys. 2005;32:2967–2975. [DOI] [PubMed] [Google Scholar]
- 15. Chen Y, Liu B, O'Connor JM, Didier CS, Glick SJ. Characterization of scatter in cone‐beam CT breast imaging: comparison of experimental measurements and Monte Carlo simulation. Med Phys. 2009;36:857–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Shi L, Vedantham S, Karellas A, Zhu L. Library based x‐ray scatter correction for dedicated cone beam breast CT. Med Phys. 2016;43:4529–4544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Liu B, Glick SJ, Groiselle C. Characterization of scatter radiation in cone beam CT mammography. 2005;36:818. [Google Scholar]
- 18. Bootsma GJ, Verhaegen F, Jaffray DA. The effects of compensator and imaging geometry on the distribution of x‐ray scatter in CBCT. Med Phys. 2011;38:897–914. [DOI] [PubMed] [Google Scholar]
- 19. Jaffray DA, Siewerdsen JH. Cone‐beam computed tomography with a flat‐panel imager.pdf. Med Phys. 2000;27:1311–1323. [DOI] [PubMed] [Google Scholar]
- 20. Patel T, Peppard H, Williams MB. Effects on image quality of a 2D antiscatter grid in x‐ray digital breast tomosynthesis: initial experience using the dual modality (x‐ray and molecular) breast tomosynthesis scanner. Med Phys. 2016;43:1720–1735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Altunbas C, Kavanagh B, Alexeev T, Miften M. Transmission characteristics of a two dimensional antiscatter grid prototype for CBCT. Med Phys. 2017;44:3952–3964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Schafer S, Stayman JW, Zbijewski W, Schmidgunst C, Kleinszig G, Siewerdsen JH. Antiscatter grids in mobile C‐arm cone‐beam CT: effect on image quality and dose. Med Phys. 2012;39:153–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Endo M, Tsunoo T, Nakamori N, Yoshida K. Effect of scattered radiation on image noise in cone beam CT. Med Phys. 2001;28:469–474. [DOI] [PubMed] [Google Scholar]
- 24. Shen SZ, Bloomquist AK, Mawdsley GE, Yaffe MJ, Elbakri I. Effect of scatter and an antiscatter grid on the performance of a slot‐scanning digital mammography system. Med Phys. 2006;33:1108–1115. [DOI] [PubMed] [Google Scholar]
- 25. Maltz JS, Gangadharan B, Vidal M, et al. Focused beam‐stop array for the measurement of scatter in megavoltage portal and cone beam CT imaging. Med Phys. 2008;35:2452–2462. [DOI] [PubMed] [Google Scholar]
- 26. Lazos D, Williamson JF. Impact of flat panel‐imager veiling glare on scatter‐estimation accuracy and image quality of a commercial on‐board cone‐beam CT imaging system. Med Phys. 2012;39:5639–5651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Ning R, Tang X, Conover D. X‐ray scatter correction algorithm for cone beam CT imaging. Med Phys. 2004;31:1195–1202. [DOI] [PubMed] [Google Scholar]
- 28. Niu T, Zhu L. Scatter correction for full‐fan volumetric CT using a stationary beam blocker in a single full scan. Med Phys. 2011;38:6027–6038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Lai CJ, Chen L, Zhang H, et al. Reduction in x‐ray scatter and radiation dose for volume‐of‐interest (VOI) cone‐beam breast CT – a phantom study. Phys Med Biol. 2009;54:6691–6709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Yang K, Burkett G, Boone JM. A breast‐specific, negligible‐dose scatter correction technique for dedicated cone‐beam breast CT: a physics‐based approach to improve Hounsfield Unit accuracy. Phys Med Biol. 2014;59:6487–6505. [DOI] [PubMed] [Google Scholar]
- 31. Sechopoulos I. TU‐E‐217BCD‐02: an x‐ray scatter correction method for dedicated breast computed tomography. Med Phys. 2012;39:3914. [DOI] [PubMed] [Google Scholar]
- 32. Gao H, Zhu L, Fahrig R. Modulator design for x‐ray scatter correction using primary modulation: material selection. Med Phys. 2010;37:4029–4037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Bhagtani R, Schmidt TG. Simulated scatter performance of an inverse‐geometry dedicated breast CT system. Med Phys. 2009;36:788–796. [DOI] [PubMed] [Google Scholar]
- 34. Altunbas MC, Shaw CC, Chen L, et al. A post‐reconstruction method to correct cupping artifacts in cone beam breast computed tomography. Med Phys. 2007;34:3109–3118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Yang X, Wu S, Sechopoulos I, Fei B. Cupping artifact correction and automated classification for high‐resolution dedicated breast CT images. Med Phys. 2012;39:6397–6406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Xie S, Li C, Li H, Ge Q. A level set method for cupping artifact correction in cone‐beam CT. Med Phys. 2015;42:4888–4895. [DOI] [PubMed] [Google Scholar]
- 37. Qu X, Lai CJ, Zhong Y, Yi Y, Shaw CC. A general method for cupping artifact correction of cone‐beam breast computed tomography images. Int J Comput Assist Radiol Surg. 2016;11:1233–1246. [DOI] [PubMed] [Google Scholar]
- 38. Shi L. X‐ray scatter correction for dedicated cone beam breast CT using a forward‐ projection model. [DOI] [PMC free article] [PubMed]
- 39. Hunter AK, Mcdavid WD. Characterization and correction of cupping effect artefacts in cone beam CT. Dentomaxillofac Rad. 2012;41:217–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Boone JM, Kwan ALC, Seibert JA, Shah N, Lindfors KK, Nelson TR. Technique factors and their relationship to radiation dose in pendant geometry breast CT. Med Phys. 2005;32:3767–3776. [DOI] [PubMed] [Google Scholar]
- 41. Boone JM, Shah N, Nelson TR. A comprehensive analysis of DgNCT coefficients for pendant‐geometry cone‐beam breast computed tomography. Med Phys. 2004;31:226–235. [DOI] [PubMed] [Google Scholar]
- 42. Gazi PM, Aminololama‐Shakeri S, Yang K, Boone JM. Temporal subtraction contrast‐enhanced dedicated breast CT. Phys Med Biol. 2016;61:6322–6346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Michael O'Connor J, Das M, Dider CS, Mahd M, Glick SJ. Generation of voxelized breast phantoms from surgical mastectomy specimens. Med Phys. 2013;40:041915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Molloi S, Ducote JL, Ding H, Feig SA. Postmortem validation of breast density using dual‐energy mammography. Med Phys. 2014;41:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Ding H, Klopfer MJ, Ducote JL, Masaki F, Molloi S. Breast tissue characterization with photon‐counting spectral CT imaging: a postmortem breast study. Radiology. 2014;272:731–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Lindfors KK, Boone JM, Nelson TR, Yang K, Kwan ALC, Miller DF. Dedicated breast CT: Initial Clinical methods: results: conclusion. Radiology. 2008;246:725–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Lindfors KK, Boone JM, Newell MS, D'Orsi CJ. Dedicated breast CT: The optimal cross sectional imaging solution? Radiol Clin North Am. 2011;48:1043–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Boone JM, Lindfors KK, Cooper VN, Seibert JA. Scatter/primary in mammography: comprehensive results. Med Phys. 2000;27:2408–2416. [DOI] [PubMed] [Google Scholar]
- 49. Ronneberger O, Fischer P, Brox T. U‐net: convolutional networks for biomedical image segmentation. Nat Methods. 2015;9351:234–241. [Google Scholar]
- 50. Yaffe MJ, Boone JM, Packard N, et al. The myth of the 50–50 breast. Med Phys. 2009;36:5437–5443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Huang SY, Boone JM, Yang K, et al. The characterization of breast anatomical metrics using dedicated breast CT. Med Phys. 2011;38:2180–2191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Agarap AF. Deep Learning using Rectified Linear Units (ReLU); 2018. 10.1249/01.MSS.0000031317.33690.78 [DOI]
- 53. Wu S, Zhong S, Liu Y. Deep residual learning for image steganalysis. Multimed Tools Appl. 2017;77:1–17. [Google Scholar]
- 54. Guo C, Berkhahn F. Entity Embeddings of Categorical Variables; 2016;1–9. 10.1109/ICCV.2017.324 [DOI]
- 55. Phan H, Krawczyk‐Becker M, Gerkmann T, Mertins A. DNN and CNN with Weighted and Multi‐task Loss Functions for Audio Event Detection. 2017. http://arxiv.org/abs/1708.03211
- 56. Bishop CM. Pattern recognition and machine learning. J Electron Imaging; 2006. 10.1017/CBO9781107415324.004 [DOI]
- 57. Kingma DP, Adam Ba J. A Method for stochastic Optimization; 2014;1–15. http://doi.acm.org.ezproxy.lib.ucf.edu/10.1145/1830483.1830503
- 58. He K. Delving deep into rectifiers: Surpassing human‐level performance on imagenet classification; 2014. https://doi.org/10.1.1.725.4861
- 59. Yu D, Eversole A, Seltzer M, et al. Introduction to Computational Networks and the Computational Network Toolkit. Microsoft Research;2014. https://www.microsoft.com/en-us/research/publication/an-introduction-to-computational-networks-and-the-computational-network-toolkit/
- 60. Packard N, Boone JM, Packard N, Boone JM, Packard N, Boone JM.Glandular segmentation of cone beam breast CT volume images; 2019. 10.1117/12.713911 [DOI]
- 61. Thada V, Jaglan D. Comparison of jaccard, dice, cosine similarity coefficient to find best fitness value for web retrieved documents using genetic algorithm. Int J Innov Eng Technol. 2013;2:202–205. [Google Scholar]
- 62. Hernandez AM, Boone JM. Tungsten anode spectral model using interpolating cubic splines: unfiltered x‐ray spectra from 20 kV to 640 kV. Med Phys. 2014;41:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Hubbell JH, Seltzer SM.Tables of X‐Ray mass attenuation coefficients and mass energy‐absorption coefficients 1 keV to 20 MeV for Elements Z=1 to 92 and 48 Additional substances of Dosimetric Interest; 1995. http://physics.nist.gov/xaamdi
- 64. Kim WH, Kim CG, Kim DW. Optimal CT number range for adipose tissue when determining lean body mass in whole‐body F‐18 FDG PET/CT studies. Nucl Med Mol Imaging. 2010;2012:294–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. McEvoy FJ, Madsen MT, Svalastoga EL. Influence of age and position on the CT number of adipose tissues in pigs. Obesity. 2008;16:2368–2373. [DOI] [PubMed] [Google Scholar]
- 66. Juneja P, Evans P, Windridge D, Harris E. Classification of fibroglandular tissue distribution in the breast based on radiotherapy planning CT. BMC Med Imaging. 2016;16:4–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Bishop CM.Pattern recognition and machine learning; 2006. 10.1017/CBO9781107415324.004 [DOI]
- 68. Hernandez AM, Boone JM. Average glandular dose coefficients for pendant‐geometry breast CT using realistic breast phantoms. Med Phys. 2017;44:5096–5105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Hernandez AM, Seibert JA, Boone JM, Seibert JA, Boone JM. Breast dose in mammography is about 30 % lower when realistic heterogeneous glandular distributions are considered Breast dose in mammography is about 30 % lower when realistic heterogeneous glandular distributions are considered. Med Phys. 2015;42:6337–6348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Hernandez AM, Becker AE, Boone JM. Updated breast CT dose coefficients (DgNCT) using patient‐derived breast shapes and heterogeneous fibroglandular distributions. Med Phys. 2019;46:1455–1466. [DOI] [PubMed] [Google Scholar]
- 71. Hubbell JH, Seltzer SM.Tables of X‐Ray Mass Attenuation Coefficients and Mass Energy‐Absorption Coefficients 1 KeV to 20 MeV for Elements Z = 1 to 92 and 48 Additional Substances of Dosimetric Interest; 1995.
- 72. Katsevich A. Implementation of Tuy's cone‐beam inversion formula. 1994. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Mathematical derivation of a 3D quadratic fit to bCT shading artifact.


