Abstract
We document the impact of COVID-19 on inflation modelling within a vector autoregression (VAR) model and provide guidance for forecasting euro area inflation during the pandemic. We show that estimated parameters are strongly affected, leading to different and sometimes implausible projections. As a solution, we propose to augment the VAR by allowing the residuals to have a fat-tailed distribution instead of a Gaussian one. This also outperforms with respect to unconditional forecasts. Yet, what brings sizeable forecast gains during the pandemic is adding meaningful off-model information, such as that entailed in the Survey of Professional Forecasters. The fat-tailed VAR loses part, but not all of its relative advantage compared to the Gaussian version when producing conditional inflation forecasts in a real-time setup. It is the joint fat-tailed errors and multi-equation modelling that manage to robustify models against extreme observations; in a single-equation model the same solution is less effective.
Keywords: COVID-19, Forecasting, Student’s t errors, Tilting, Inflation, VAR
1. Introduction
‘In reality, however, the distribution of shocks hitting the economy is more complex.... [The shocks] might exhibit excess kurtosis, commonly referred to as “tail risk” in which the probability of relatively large disturbances is higher than would be implied by a Gaussian distribution.’
As the pandemic unfolded worldwide, macroeconomists struggled to make sense of their models after adding the new COVID-19 observations. The variation exhibited by some macroeconomic series was so large (e.g. real activity and labour market indicators) that this sufficed to distort the estimated coefficients since March 2020. This was shown for the U.S. (Carriero et al., 2021, Lenza and Primiceri, 2020, Schorfheide and Song, 2020) and we show that this is also true for the euro area.
In this paper we investigate the impact of the COVID-19 shock on one of the most popular time series models—Sims’ vector autoregression (VAR) model—and discuss the results by focusing on euro area inflation. Our lessons are valid for a wide range of empirical analyses, but we choose to focus on inflation because this has been a particularly hard-to-grasp indicator since the Great Financial Crisis on both sides of the Atlantic. In the decade prior to the pandemic, inflation across advanced economies consistently surprised economists on the downside. The euro area in particular struggled with low inflation to the extent that inflation expectations became less well anchored to the ECB’s inflation aim, adding to existing disinflationary pressures (Baumann et al., 2021). Inflation continued to surprise during the pandemic, starting in 2020. Initially, while energy inflation fell quickly, the response of euro area core inflation was modest relative to the decline in activity. From the middle of the year onwards, headline inflation fell further as core inflation increasingly reflected disinflationary tendencies, and overall inflation surprised on the downside. Starting in 2021, the situation completely reversed and inflation once again took centre stage in the economic debate, as its surge took central banks and other professional forecasters by surprise. The normalisation of the economy, ensuing supply-side bottlenecks, and rising commodity prices put upward pressure on prices. In this context of highly atypical economic developments—marked by the economic lockdown and the subsequent re-opening—the question is which tools can be still employed to model inflation.
We show that using a standard Gaussian BVAR to model inflation distorts economic inference. The incoming data after March 2020 heavily impact the parameters of conventionally estimated models and this is something to be aware of when forecasting or conducting empirical analyses covering this period, irrespective of the scope. Here we focus on the analysis of inflation, but the critique is generally valid.
The contribution of our paper is twofold: (i) first, we propose solutions for the problem that the change in parameters poses for both in-sample and out-of-sample inference; (ii) second, we show what brings forecast gains when trying to project inflation during the pandemic. To the best of our knowledge, we are the first to discuss real-time inflation forecasting for the euro area for this particular abnormal period. We validate our proposed model by looking at a longer period of time (in a pseudo-real-time inflation forecasting exercise) and by providing evidence for a large set of advanced economies.
We tackle the problem of VAR parameters becoming unstable when adding the COVID-19 observations by proposing a tractable and elegant solution, namely to relax the assumption that the errors are normally distributed and assume instead that they follow a Student’s -distribution. Intuitively, unusually large shocks are more likely to occur under -errors as Gaussian errors, since the former has fatter tails. This allows the residuals to soak up the abnormal variation, stabilising the parameter estimates.
Our paper is related to the strand of literature emerging after the Great Recession trying to accommodate tail events in macro-models. For DSGEs, Chib and Ramamurthy, 2014, Cúrdia et al., 2014, and Ascari et al. (2015) argue that models with a -distributed shock structure are strongly favoured by the data over standard Gaussian ones.
For VARs, Chiu et al. (2017) and Chan (2020) show that allowing for fat-tailed errors improves in-sample fit and forecasting properties.1 We show that euro area macroeconomic data exhibit substantial tail risk even before the pandemic. Moreover, this extension suffices to deal with the impact of the pandemic (which is a more rare and extreme event than recessions).
We also contribute to the rising literature on how standard models can be adapted to withstand the impact of the COVID-19 observations. Lenza and Primiceri (2020) and Carriero et al. (2021) propose downweighing the impact of abnormal observations through assumptions on the associated variance of the residuals. Our solution is similar in spirit. We believe it is still too soon to ascertain a break in the economic transmission mechanisms, and thus parameters should not display dramatic changes with respect to pre-COVID-19 times, especially if a normalisation in economic developments is to be expected. At the same time, we do not exclude the possibility that the COVID-19 observations might affect macroeconomic relationships in the future (as reflected by model parameters). From this point of view, our approach is more flexible than simply cutting the sample to the pre-COVID-19 period or including dummy variables for each quarter over the pandemic. The observations in 2020 will remain an issue for time series models going forward, so time series models have to be adapted for a longer period of time.
In a standard Gaussian BVAR, the response of inflation to a shock in real activity gradually weakens and appears to be stabilising at lower levels compared to the pre-pandemic period. In our fat-tailed BVAR there is still some weakening, but to a smaller extent. There are several reasons that call for caution when it comes to ascertaining changes in established economic relationships, such as the one between inflation and real activity, for instance, known as the Phillips curve. The pandemic is not the usual macroeconomic shock when it comes to its composition and its size. In terms of its composition, it is a multifaceted shock, actually a combination of demand and supply shocks acting at the same time. In terms of its size, it is an abnormally large shock which distorts any estimate not equipped to deal with tail events. On top, there have been unusual data distortions and unusually high uncertainty regarding slack.
We show that it is the joint multivariate and fat-tailed errors that manage to robustify models against extreme observations; in a single-equation model the same solution is less effective. We take a simple Phillips curve model and show that estimated parameters change notably when adding the COVID-19 observations to the sample, implying a drastic flattening in the euro area. A fat-tailed error distribution does not appear to be a panacea this time around. In the multiple-equation system of a VAR the fatness of tails pertaining to the error distribution (and hence the extent to which the errors can soak up abnormal observations in order not to distort coefficients) is informed by the simultaneous developments in all variables. In single-equation models it is the development of the dependent variable that matters more in informing the properties of the residuals; extreme developments occurred in the first part of the pandemic on the real activity front and less so on the nominal side of the economy. Thus, the residuals of a Phillips curve do not have such fat tails as the residuals of the inflation equation in a VAR model that also includes GDP, for instance. Hence, multi-equation models are more flexible and better equipped to deal with the impact of abnormal observations.
As an alternative to fat-tailed errors, we find that adding more variables to the Gaussian BVAR, together with a reasonably tighter prior to control for the larger dimension, yields more stable results than a smaller-scale BVAR. This suggests that in large-dimensional models the impact of variables with abnormal dynamics is mitigated; also, an appropriately informative prior helps in disciplining the results. Still, the model with -distributed errors outperforms in delivering more stable parameters.
The pandemic-related change in coefficients also mechanically affects unconditional forecasts in a Gaussian BVAR. The fat-tailed and the large-scale BVAR alleviate this problem. Yet, we find that this problem of parameter and forecast instability is also mitigated in a standard Gaussian BVAR when relevant off-model information is included, as conditional forecasts appear to be well behaved.
Turning to the second contribution on how our proposed fat-tailed BVAR would have fared when forecasting euro area inflation in real time in this turbulent period, we find that a fat-tailed BVAR produces more accurate forecasts than a Gaussian BVAR. Our results also hold when performing a forecast evaluation over a longer period (but in a pseudo-real-time fashion due to data constraints) and are confirmed for a large set of advanced economies. Yet, in abnormal times unrecorded in the available estimation sample, it is hard to trust forecasts based solely on exploring historical regularities. We argue that these times are best suited to add information from outside the model to inform purely model-based results. Lenza and Primiceri, 2020, Primiceri and Tambalotti, 2020, also incorporate some kind of off-model information to produce more plausible forecasts during the pandemic.
We find that, indeed, including off-model information brings sizeable gains to forecasting inflation during the pandemic. We make use of the information included in the ECB Survey of Professional Forecasters (SPF), first by looking at ‘hard conditional’ forecasts where we impose the expected GDP path (together with a constant exchange rate and oil price futures), and second by looking at ‘soft conditional’ forecasts where we tilt the unconditional forecasts towards expectations of inflation and growth from the SPF. Tilting towards SPF expectations can be a valid way to provide the model with some degree of informed judgement, as professional forecasters do not solely rely on models (which might have been affected by COVID-19 observations), but use a substantial degree of judgement when forming their beliefs about the future. Also, there is evidence that such tilting improves inflation forecasting in certain challenging times, such as in the post-Great Recession period, as a way of indirectly accommodating structural changes (see Tallman and Zaman (2020) and Ganics and Odendahl (2021)). Both the considered hard and soft conditional inflation forecasts would have been superior to unconditional ones in a standard Gaussian BVAR. Compared to these, the BVAR with fat-tailed errors largely loses its comparative advantage, suggesting that, indeed, meaningful off-model information makes a difference in forecasting in a standard BVAR.
Notwithstanding our documented forecast gains over a standard Gaussian BVAR, also in our best models, in the first phase of the pandemic, inflation tended to surprise on the downside, and subsequently it turned out to be notably higher than foreseen.2 The puzzling behaviour of inflation during the pandemic is also reflected in the marked revisions in short-term inflation expectations of professional forecasters. Throughout 2020, analysts lowered their inflation expectations, particularly for the short term. Part of this revision was driven by oil price developments. In addition, in the perceptions of SPF panellists, demand factors were largely considered dominant relative to possible supply-side and scarcity effects. In the second year of the pandemic, professional forecasters, who revised their near-term outlooks quite markedly, were caught off guard by the extent of the inflationary pressures that global supply-side bottlenecks and increases in input costs created. This pattern in the revision of expectations is also valid for other advanced economies, such as the U.S. (see the discussion in Meyer et al. (2021)).
The rest of the paper is structured as follows. Section 2 discusses parameter instability in VAR models when the abnormal COVID-19 observations are added to the sample. Section 3 assesses the impact of this parameter instability on unconditional and conditional inflation forecasts, and Section 4 conducts a formal forecast evaluation for euro area inflation during the pandemic. Section 5 explains why multi-equation models (such as VARs) are better equipped to deal with the impact of abnormal observations than single-equation models (such as Phillips curves), and Section 6 concludes.
2. The impact of the COVID-19 shock on estimates within VAR models
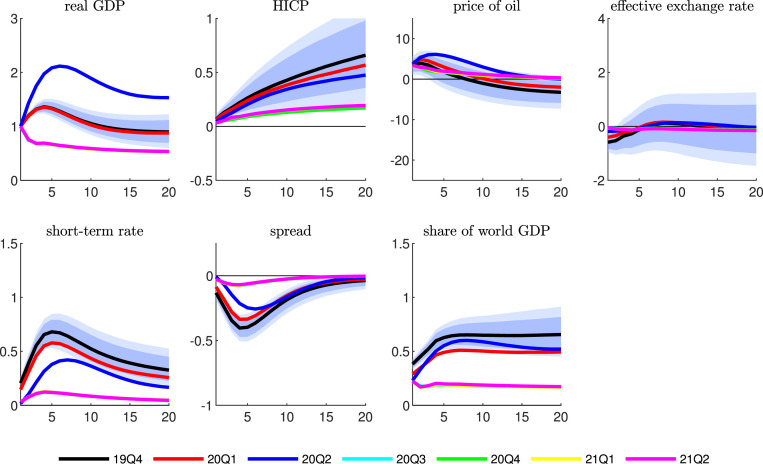
In this section we consider one of the most popular models employed in macroeconomics, namely Sims’ vector autoregression (VAR) model. For our analysis, we use the small-scale VAR that was employed to understand the drivers of euro area inflation by Bobeica and Jarociński (2019). Fig. 1 shows the data over the sample 1980:Q1–2021:Q2. There is some variation during the COVID-19 crisis in the considered variables, but nothing unprecedented, with the exception of the real GDP and the euro area share in world GDP. The existing literature dealing with the impact of the pandemic on time series modes has focused on the U.S., where some economic variables, in particular the unemployment rate, have recorded formidable spikes. Yet, we show that the variation recorded by the euro area variables, even if less pronounced than in the U.S. case, is large enough to distort the parameter estimates in a standard BVAR.
Fig. 1.
Data set for the baseline small-scale euro area BVAR. Note: Real GDP, HICP, price of oil, and nominal effective exchange rate are in log-levels times 100; short-term rate, 10-year government bond spread, and share in world GDP are in percentage points.
Fig. 2 shows impulse response functions (IRFs) to a one-standard-deviation shock in real GDP estimated over an expanding window until 2019:Q4, 2020:Q1, …, 2021:Q2, starting in 1980:Q1.3 Estimates are obtained using a Sims and Zha (1998) prior; which we label as ’Sims and Zha prior’.4 The inclusion of the COVID-19 observation substantially affects the IRF estimates as compared to the pre-COVID-19 times. Specifically, with the inclusion of the 2020:Q2 observation, the IRF of real GDP changes substantially, first it becomes more persistent, afterwards it subsides. The transmission of the shock to inflation gradually weakens and appears to be stabilising at lower levels; the reaction of inflation to the generic GDP shock is flattened. The impact on financial variables is also dampened. This illustrates that parameter estimates are sensitive to unusually large innovations in a standard Gaussian BVAR, which is a major shortcoming for analysis in times of COVID-19, even after the large swings in real activity have passed.
Fig. 2.
Impulse response functions in a small BVAR with Gaussian errors. Note: Impulse response functions to a one-standard-deviation shock in real GDP from a BVAR with Gaussian errors using a Sims and Zha prior. Coloured thick lines are median estimates, and the dark (light) blue area is the 68% (90%) credible interval for the estimation window until 2019:Q4.
The prior choice makes a difference, with more informative priors having an upper hand in delivering more stable coefficients once the COVID-19 observations are added. Lenza and Primiceri, 2020, Schorfheide and Song, 2020, and Carriero et al. (2021) document using monthly U.S. data that estimated VAR models are explosive when the recent COVID-19 observations are included. While the estimated IRFs in Fig. 2 are sensitive to the inclusion of the COVID-19 observations, they are not explosive for our chosen prior specification. In Online Appendix B, Panel (a) in Fig. B.1 shows that this explosive behaviour is present in the euro area case as well if we adopt a weakly informative prior for the VAR coefficients.5 This suggests that the design of the prior, the chosen amount of shrinkage, as well as the data set at hand dictate whether a Bayesian VAR model becomes explosive once COVID-19 observations are included in the sample. Moreover, we also explore whether a higher degree of shrinkage applied to our baseline Sims and Zha prior dampens the impact of COVID-19 on the change in the VAR coefficient estimates; we label this the ‘strong Sims and Zha prior’.6 Panel (b) in Fig. B.1 shows that the higher degree of shrinkage mechanically disciplines the coefficients in the VAR to some extent, but there is still notable instability in the IRFs once the COVID-19 period is included in the sample, which stems from a change in residual correlations.7 Yet, imposing a very dogmatic prior comes with the drawback of silencing the information coming from the data.
2.1. Solutions for estimation within a VAR
2.1.1. Accommodating COVID-19 observations via alternative error structures
Several proposals on how to tackle the problem of changing parameters due to the COVID-19 observations have been put forward in the literature.8 The approach taken by Lenza and Primiceri (2020) and Carriero et al. (2021) have in common the belief that macroeconomic relationships which held in the past are assumed to be still informative. That is, they propose downweighing the abnormal observations by allowing the variance of the residuals to adjust quickly to the COVID-19 observations.
Lenza and Primiceri (2020) propose an explicit volatility model for the residuals corresponding to the COVID-19 observations. Their solution is tractable and easy to understand, but requires specifying exactly when the abnormal observations start and estimating the decay of volatility based on few observations (especially when working with quarterly data). Carriero et al. (2021) propose a more flexible solution that allows for variable-specific outliers in the volatility process, leaving fewer choices to the modeller. Here volatility is a function of its past values, but it is also allowed to jump with abnormal observations with a certain probability. One possible limitation of this model class is related to the sensitivity to the ordering of variables (see Primiceri (2005) and Cogley and Sargent (2005)). Specifically, when volatility changes idiosyncratically, estimates of the time-varying covariance matrix may be extremely sensitive to the ordering of variables, due to the structure imposed by the triangular factorisation of the time-varying covariance matrix in their model, see Hartwig (2020).
Our proposal does not involve making ad hoc choices and is thus more in line with the approach of Carriero et al. (2021). We propose to abandon the Gaussian error structure and assume a multivariate -distribution for the errors instead; see Ni and Sun (2005) and Chan (2020). Intuitively, extremely large shocks are more likely to occur under the Student’s t-distribution, as it has fatter tails than the Gaussian one. Consequently, not all observations are equally informative for the parameter estimates, and the impact of rare observations such as those related to the COVID-19 pandemic are downweighed, which stabilises the relationship between variables. The idea that the data might favour models with errors that haver fatter tails is inspired by the literature emerging after the Great Recession (see Chan, 2020, Chiu et al., 2017, Cúrdia et al., 2014), when Gaussian models failed to properly account for the strong variation in some variables; we show that -distributed errors work also during the pandemic. This solution shares the spirit of the aforementioned ones in the sense that the COVID-19 observations are downweighed by some form of conditional variance within the estimation framework. Similar to Lenza and Primiceri (2020), we treat the change in shock volatility as being common across all variables instead of considering variable-specific volatility as in Carriero et al. (2021). This is a simple and tractable assumption but neglects potential change of the residual correlations during the pandemic. As opposed to the latter paper, in our VAR, residuals have constant second-order moments (see Appendix A for more technical details on the VAR with -errors).9 Compared to standard stochastic volatility models, we argue that Student’s -distributed errors—or other fat-tailed error distributions—are better suited during the pandemic, as the COVID-19 observations may inflate the volatility process for too long in widely employed stochastic volatility models (without outlier correction or -distributed errors). This may lead to rather imprecise density forecasts; see Carriero et al. (2021) and Hartwig (2021).10
Fig. 3 shows the counterpart to Fig. 2 under the assumption that the errors in the Bayesian VAR are multivariate t-distributed. In general, the IRFs are much more stable across different estimation samples compared to their Gaussian version.11 Thus, this solution allows for the impact of COVID-19 observations to be soaked up by the heavy tails of the VAR residuals, leaving parameter estimates largely unaffected.12 Zooming in on inflation, for the pre-COVID-19 sample, the reaction of inflation to real GDP is somewhat weaker in the VAR with fat-tailed errors compared to the one with Gaussian residuals. When adding the COVID-19 observations, the response of inflation to a shock in real GDP also weakens, but to a lesser extent than in the Gaussian VAR case.
Fig. 3.
Impulse response functions in a small BVAR with fat-tailed errors. Note: Impulse response functions to a one-standard-deviation shock in real GDP from a BVAR with fat-tailed errors using a Sims and Zha prior. Coloured thick lines are median estimates, and the dark (light) blue area is the 68% (90%) credible interval for the estimation window until 2019:Q4.
We estimate the Bayesian VAR with -errors by making use of an equivalent scale mixture of normal representations of the VAR model (see Appendix A). This estimation technique yields, as a by-product, an interesting latent variable, which we label lambda.13 This variable reflects the common volatility of the VAR residuals and is independently inverse-gamma distributed. As such, is a noisy variable that can be interpreted as the high-frequency common volatility of the data (Chiu et al., 2017) or used as an outlier detection tool (Jacquier et al., 2004).14 15
Panel (a) of Fig. 4 depicts the latent high-frequency volatility in our data set alongside a measure of macroeconomic uncertainty.16 Lambda spiked during the Great Recession and sky-rocketed during the COVID-19 crisis, capturing the fact that there was abnormal variation or statistical outliers in the data. The timing of these spikes coincides with the peaks in measured macroeconomic uncertainty.17 Lambda capturing the spikes in macroeconomic uncertainty is another argument in favour of allowing for heavy tails: the model with -distributed errors identifies these periods to be less informative for the parameter estimates compared to the Gaussian model, which treats all observations equally. Therefore, standard Gaussian models may yield distorted estimates of macroeconomic relationships in turbulent times.
Fig. 4.
Macroeconomic uncertainty and tail risk. Note: (a) Posterior median and 90% credible interval of the high-frequency volatility lambda in the BVAR with -distributed errors and Sims and Zha prior. (b) Posterior distribution of the degrees-of-freedom parameter estimated on an expanding sample.
Did the euro area economy exhibit heavy-tailed errors prior to the pandemic? Panel (b) of Fig. 4 shows that the posterior distribution of the degrees-of-freedom parameter () becomes sharper and shifts to the left once the COVID-19 observations are included, indicating a higher tail risk. However, the decline of the posterior median for is moderate, from 4.6 in the pre-COVID-19 period to 3.5 in 2021:Q2. Therefore, the tail risk in the euro area economy increases somewhat with the COVID-19 observations.18 We interpret these findings as evidence that the data not only exhibit fat tails due to the extreme COVID-19 observations but also exhibited substantial tail risk even before, which speaks in favour of the -distribution assumption as a more appropriate treatment of the data in general.
An alternative way to check whether the data ask for fat-tailed errors is to compare the log marginal likelihood of the Bayesian VARs with Gaussian and -distributed errors. Table 1 shows these estimates for various prior specifications and on an expanding estimation window.19 By comparing the log marginal likelihood figures in Panels (a) and (b) we find decisive evidence in favour of fat tails both before and during the COVID-19 pandemic, as well as across all different prior specifications.
The optimal degree of parameter shrinkage is not affected by the COVID-19 observations. Specifically, both models favour our standard calibration for the Sims and Zha prior over the weakly informative or the strong Sims and Zha prior with a higher degree of parameter shrinkage.20 This is in contrast to the result reported in Lenza and Primiceri (2020), who document that the Gaussian VAR model likes less shrinkage after COVID-19.
Table 1.
Log marginal likelihood for the small BVAR model.
| Weak | SZ | Strong SZ | Weak | SZ | Strong SZ | |||
|---|---|---|---|---|---|---|---|---|
| 19Q4 | −1748.65 | −1336.97 | −1440.18 | 19Q4 | −1686.01 | −1261.99 | −1381.34 | |
| 20Q1 | −1791.18 | −1376.40 | −1475.32 | 20Q1 | −1707.68 | −1283.12 | −1402.46 | |
| 20Q2 | −1886.03 | −1484.85 | −1585.18 | 20Q2 | −1740.65 | −1315.44 | −1434.05 | |
| 20Q3 | −1966.81 | −1539.32 | −1631.13 | 20Q3 | −1772.91 | −1348.37 | −1463.95 | |
| 20Q4 | −1986.24 | −1550.60 | −1642.30 | 20Q4 | −1786.26 | −1359.18 | −1475.18 | |
| 21Q1 | −2003.93 | −1568.70 | −1658.81 | 21Q1 | −1802.27 | −1374.57 | −1490.36 | |
| 21Q2 |
−2016.85 |
−1577.25 |
−1667.85 |
21Q2 |
−1813.50 |
−1384.72 |
−1501.50 |
|
| (a) BVAR with Gaussian errors | (b) BVAR with fat-tailed errors | |||||||
Note: The bold figure indicates the maximum log marginal likelihood for each model in a selected estimation window. ‘Weak’ stands for a weakly informative prior, and ‘SZ’ stands for Sims and Zha.
2.1.2. Expanding the data set by adding more variables
As an alternative to fat-tailed errors in the VAR, we investigate whether employing a larger model ensures more stable parameters during the pandemic. Intuitively, in large-dimensional models, the impact of variables with abnormal dynamics might be mitigated. A larger set of data might offer a hedge when it comes to estimation and forecasting in the presence of instabilities; see Rossi (2020). To explore this possibility, we estimate our BVARs with 23 variables used in Bobeica and Jarociński (2019) to understand inflation dynamics in the euro area.21
Fig. 5 shows the impulse response functions for real GDP and HICP inflation to a one-standard-deviation shock in real GDP for both the Gaussian and fat-tailed BVAR with more variables, using the two variants of the Sims and Zha prior.22 The IRFs of the large Gaussian BVAR with a Sims and Zha prior exhibit substantial instability as soon as the COVID-19 observations are included and become explosive in 2020:Q2; see Panel (a). The change in the IRFs persists after the initial COVID-19 shock. When imposing more shrinkage, as recommended for larger models, the BVAR coefficients become better behaved; see Panel (b). Compared to Fig. 2, the IRFs of this large BVAR are somewhat more stable when adding the COVID-19 observations. Nevertheless, the covariance matrix is still substantially affected by the extreme observation, which leads to a different propagation of the shock. In contrast, estimates from a large BVAR with heavy-tailed errors are well behaved across different prior specifications; see Panels (c) and (d). Therefore, even in large VARs, fat-tailed errors are a sufficient extension to make the model robust against the extreme variations triggered by the pandemic.
Fig. 5.
Selected impulse response functions in a large BVAR. Note: Impulse response functions to a one-standard-deviation shock in real GDP from the large BVAR with Gaussian (BVAR) and fat-tailed errors (BVAR-t) using various priors. Coloured thick lines are median estimates, and the dark (light) blue area is the 68% (90%) credible interval for the estimation window until 2019:Q4.
Since the large Gaussian BVAR produces more stable dynamics only with the strong Sims and Zha prior, a natural question is whether the marginal likelihood would also favour this model. Table 2 shows the log marginal likelihood for these VARs. Again, the models with fat-tailed errors yield higher marginal likelihoods, suggesting that they are preferred by the data. At the same time, the standard Sims and Zha prior, which was used for the small-scale BVAR, is preferred over its strong variant for all estimation samples. This criterion would thus guide us to choose an explosive over a stable model, which is a clear caveat when selecting an appropriate model for inference. This suggests that model diagnostics cannot be blindly trusted in the case when the error distribution is heavily mis-specified—as it is in the case with the abnormal observations during the pandemic (see also Section 4.2). Therefore, we argue that in times of COVID-19, one has to consider other aspects as well when selecting the most appropriate model.
Table 2.
Log marginal likelihood for the large BVAR.
| Weak | SZ | Strong SZ | Weak | SZ | Strong SZ | |||
|---|---|---|---|---|---|---|---|---|
| 19Q4 | −6480.35 | −3756.80 | −3918.06 | 19Q4 | −5915.25 | −3485.19 | −3695.15 | |
| 20Q1 | −6615.97 | −3864.18 | −4021.19 | 20Q1 | −5982.10 | −3539.20 | −3751.03 | |
| 20Q2 | −6756.28 | −3978.87 | −4151.69 | 20Q2 | −6062.13 | −3608.26 | −3810.56 | |
| 20Q3 | −6889.06 | −4067.78 | −4233.83 | 20Q3 | −6152.90 | −3717.54 | −3905.92 | |
| 20Q4 | −6964.35 | −4114.55 | −4298.21 | 20Q4 | −6190.53 | −3766.41 | −3957.56 | |
| 21Q1 | −7049.20 | −4151.13 | −4334.66 | 21Q1 | −6299.66 | −3807.15 | −4000.44 | |
| 21Q2 |
−7134.59 |
−4199.77 |
−4388.15 |
21Q2 |
−6323.87 |
−3852.67 |
−4045.27 |
|
| (a) BVAR with Gaussian errors | (b) BVAR with fat-tailed errors | |||||||
Note: The bold figure indicates the maximum log marginal likelihood for each model in a selected estimation window. ‘Weak’ stands for weakly informative, and ‘SZ’ stands for Sims and Zha.
3. The impact of the COVID-19 shock on forecasts within VAR models
It is difficult to ascertain what works in forecasting during the pandemic, as there are only a few observations available as yet. To provide some guidance for inflation forecasters, we first investigate how unconditional and conditional forecasts are affected by the change in parameters previously documented. Then we study how our proposed models fare in a real-time forecasting exercise during the pandemic. We also check whether our extension to the standard VAR model of allowing for fat-tailed errors affects unconditional forecasts before and after the pandemic. Finally, we show in a real-time setup that bringing off-model information to our VAR model would have improved the inflation forecast during the pandemic.
3.1. Impact of COVID-19 observations on unconditional forecasts
The change in parameters generated by the COVID-19 observations in traditional Gaussian VAR models has an impact on the forecast paths as well. Focusing again on inflation, Fig. 6 shows the unconditional forecasts starting 2021:Q3 for the BVAR models previously described. In producing these forecasts, the data and the starting date of the forecast are the same. The only thing that differs is the sample on which the coefficients have been estimated. In other words, the change in the forecast path solely reflects revisions in VAR parameter estimates. Panels (a) and (b) show that in the case of the small-scale VAR, unconditional forecasts for both a weakly informative prior and the Sims and Zha prior exhibit visible variation once the COVID-19 observations are added to the estimation sample. Specifically, the short-run and long-run forecasts for inflation bounce down when the abnormal 2020:Q2 observation is included in the sample (blue line) and up again when including more quarters over the pandemic period. The effect of changing parameters on the forecast path is more pronounced for the weakly informative prior. In contrast, unconditional forecasts are only mildly affected in the BVAR with fat-tailed errors (Panel (c)) or in the large-scale Gaussian BVAR with a strong Sims and Zha prior (Panel (d)).
Fig. 6.
Unconditional forecasts starting in 2021:Q3. Note: The forecast starts in 2021:Q3; parameters are estimated on an expanding estimation window. Coloured thick lines are median estimates, and the (overlapping) light blue areas are the 68% credible interval for each respective estimation window.
Interestingly, the projected paths of inflation are quite similar for both the small-scale fat-tailed BVAR and the large-scale Gaussian BVAR. With actual data up to 2021:Q2, both models predict that inflation would eventually normalise after the spike in 2021. The forecast bands are somewhat wider for the fat-tailed BVAR than for the large-scale Gaussian model. Also, the bands under the fat-tailed BVAR become wider (hardly visible in the figures) as soon as the COVID-19 observations are included in the estimation sample. This is due to the fact that the estimated degrees-of-freedom parameter declines, which increases the unconditional variance of the forecast errors.
3.2. Impact of COVID-19 observations on conditional forecasts
Most policy institutions rely on some type of conditional forecast in order to form an opinion on the likely future inflation path. The previous section showed that the unconditional forecast paths are sensitive to the change in parameters brought about by the inclusion of the pandemic observations. A natural question arises whether the inclusion of off-model information while producing conditional forecasts mitigates this forecast instability problem.
‘Hard conditioning’ using external projections
We illustrate how the change in coefficients brought about by the COVID-19 shock affects conditional forecasts for euro area inflation when taking into account external projections. Specifically, we condition on a set of off-model projected paths for the following variables: real GDP growth based on the Survey of Professional Forecasters,23 the price of oil based on futures contracts,24 and the nominal effective exchange rate, which is kept constant over the projection horizon, mimicking a common practice in policy circles. The path of the variables is strictly imposed using the algorithm of Waggoner and Zha (1999) without the updating step. Again, as in the exercise showing unconditional forecasts, the aim is to study the change in the forecast path coming solely from the revisions in VAR parameters; the starting date of the forecast, the actual data, and the conditioning data are the same across all the coloured lines in the figure.
Fig. 7 shows that conditional forecasts using the small-scale Gaussian BVAR are now less sensitive to the change in parameter estimates over the expanding estimation window for all prior specifications, even for the weakly informative one; see Panels (a) and (b). Including the 2020:Q2 information does not result in an explosive or a dramatically changed forecast anymore. Thus, the problem of unstable forecasts can be mitigated by conditioning on a sufficient set of variables that exhibit well-behaved future paths and are strongly interlinked with the target variable. Similarly, the conditional forecasts of the BVAR with fat-tailed errors are not sensitive to the inclusion of the pandemic observations in the estimation sample (Panel (c)). This model yields a slightly higher medium-term inflation outlook than the Gaussian one, and compared to its unconditional version, inflation is now expected to stabilise at somewhat higher levels. Conditional forecasts are also stable for the large BVAR (Panel (d)). Overall, this suggests that conditioning on a relevant information set alleviates the problem of in-sample parameter instability.
Fig. 7.
‘Hard conditioning’ forecasts starting in 2021:Q3. Note: Forecasts conditional on real GDP growth (as in the 2021:Q3 ECB Survey of Professional Forecasters), oil price futures (as of 16 August 2021), and a constant nominal effective exchange rate; parameters are estimated on an expanding window. Coloured thick lines are median estimates, and the (overlapping) light blue areas are the 68% credible interval for each respective estimation window.
‘Soft conditioning’ using expectations of the Survey of Professional Forecasters
Using the previously described methodology of producing conditional forecasts, the imposed future paths of the conditioning variables always hold exactly. However, in particularly uncertain times, one may want to consider off-model information with some degree of uncertainty around it. This is known as ‘soft conditioning’; see the relative entropy method proposed by Robertson et al. (2005). The main idea of this approach is to derive a new predictive distribution ‘tilted’ to the mean or median of the distribution of the off-model information (and possibly also to some quantile values) that is as close as possible to the initial unconditional forecast distribution (which might not be the case in the approach by Waggoner and Zha (1999)).
In principle, one can apply this procedure to produce forecasts for any variable included in the VAR by ‘tilting’ its unconditional forecast to some off-model information regarding its future path. Here we illustrate this approach by considering expectations of the Survey of Professional Forecasters (SPF) for the euro area.25 This alternative approach alleviates the issue of having to come up with a set of strong assumptions, as in Primiceri and Tambalotti (2020), interpolation issues in case forecasts are available only for some quarters, and the problem of imposing the future path of many variables included in the model. It can also constitute a valid crosscheck for hard conditional forecasts.
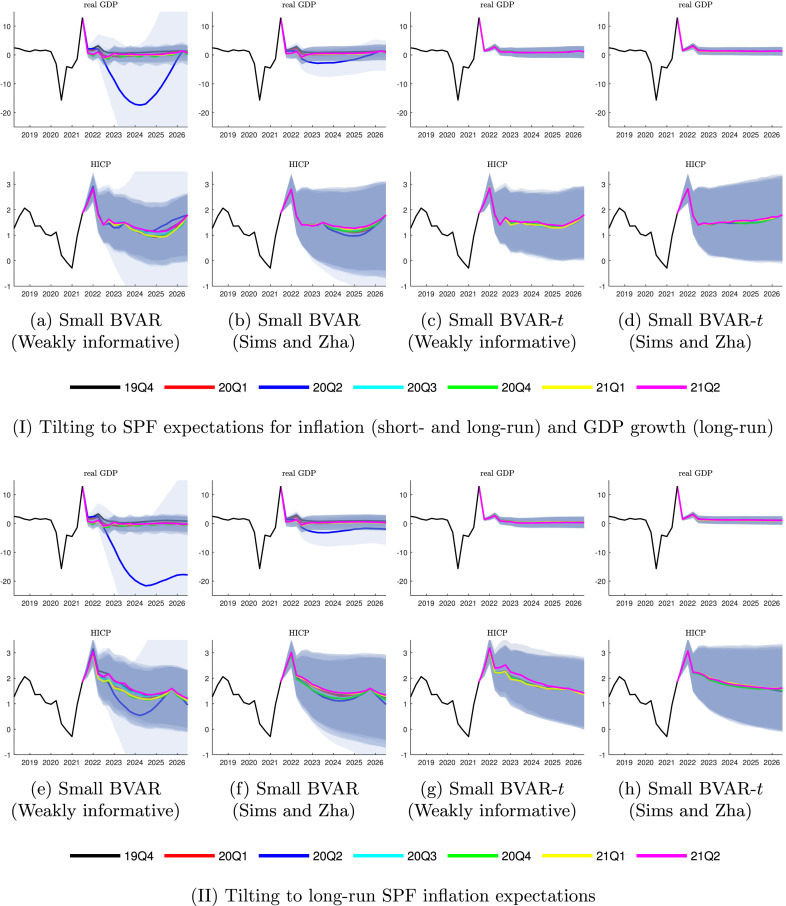
We produce soft conditional forecasts by considering the median SPF inflation expectations for one, two, and five years ahead, but also long-term real GDP growth expectations; see Fig. 8. Panel (a) shows that tilting the unconditional inflation forecasts to median SPF values for inflation and GDP yields inflation forecasts which are robust to the parameter change induced by the COVID-19 observations.26 Nevertheless, these conditions are not sufficient to ensure overall stability in the Gaussian VAR with a weakly informative prior. Furthermore, Panel (b) shows forecasts when the unconditional distribution is tilted to five-year-ahead inflation only. Thus, whereas long-run expectations are crucial to ensure stability, short-run expectations are important to ensure an informed profile of the future inflation path.
Fig. 8.
Conditional forecasts based on tilting to SPF expectations. Note: Forecasts tilted to SPF expectations for inflation and real GDP growth starting in 2021:Q3 and using parameters from an expanding window estimation. Coloured thick lines are median estimates, and the (overlapping) light blue areas are the 68% credible interval for each respective estimation window.
4. Forecasting inflation during the pandemic
The previous section documented the sensitivity of unconditional and conditional forecasts with respect to changing VAR parameters during the pandemic. In this section, we study how our proposed models would have fared when forecasting inflation in real time. We also investigate the comparative forecasting advantage of the fat-tailed BVAR model by looking at a longer period of time and at a larger set of countries in a pseudo-out-of-sample forecast evaluation.
4.1. Real-time forecast evaluation
Would a forecaster have been better equipped by using our fat-tailed BVAR compared to using a standard Gaussian model when trying to forecast inflation during the pandemic? We investigate this question by looking at our benchmark small-scale BVAR.27
Table 3 shows the root mean squared forecast error (RMSFE) for inflation over the period from 2020:Q1–2021:Q2. Given the very short period, the results can only provide some hints towards promising avenues to explore when forecasting inflation during the pandemic. The first column shows the figures corresponding to unconditional forecasts within a standard Gaussian BVAR. Compared to this model, it would have paid off to employ a model with fat-tailed errors, as doing so would have produced a smaller RMSFE over the pandemic period (second column). As an additional benchmark to the Gaussian BVAR, we employ the same VAR model augmented with dummy variables for each quarter during the pandemic, which we label dummy BVAR.28 This can appear to be a simple fix to the problem of changing parameters when including the COVID-19 observations in the sample, as it basically fixes the parameter estimates to the pre-pandemic period (as done in Schorfheide and Song (2020)).29 This benchmark has the advantage that the dummy variables are able to absorb the variation induced by the COVID-19 observations, leaving the remaining parameters of the BVAR largely unchanged. Nevertheless, it has the disadvantage that, unlike the BVAR with fat-tailed errors, it requires several ad hoc choices from the modeller, such as when pandemic observations start and when the pandemic will be over (which would be an indication to stop including dummy variables). Also, it is not a priori clear how an informative prior should be formulated for the dummies such that economic relations might be affected by the COVID-19 shock during the pandemic. Table 3 shows that unconditional forecasts based on a dummy BVAR would have outperformed the ones based on an unadjusted Gaussian BVAR, but the BVAR with fat-tailed errors beats this benchmark—especially at longer horizons.
Table 3.
Real-time forecast evaluation for euro area inflation: RMSFE.
| Unconditional |
Hard conditioning |
Soft conditioning |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| BVAR | BVAR | BVAR | BVAR | BVAR | BVAR | BVAR | BVAR | BVAR | |
| 0.61 | 0.58 | 0.60 | 0.47 | 0.50 | 0.62 | 0.56 | 0.56 | 0.55 | |
| 1.07 | 0.98 | 1.02 | 0.84 | 0.91 | 1.05 | 0.88 | 0.91 | 0.88 | |
| 1.41 | 1.13 | 1.17 | 0.93 | 0.91 | 1.01 | 0.99 | 0.98 | 0.96 | |
| 1.66 | 1.19 | 1.25 | 1.01 | 0.96 | 0.94 | 1.01 | 1.01 | 1.00 | |
Note: RMSFE during COVID-19 pandemic for HICP inflation. BVAR denotes a standard Gaussian BVAR, BVAR is the fat-tailed BVAR, and BVAR is the BVAR augmented with dummy variables each quarter over the COVID-19 period. The evaluation sample covers the period from 2020:Q1–2021:Q2.
Including off-model information brings sizeable gains to forecasting inflation during the pandemic. Unconditional forecasts based on models that only look at past historical patterns of the data are hard to trust during the pandemic, as COVID-19 is an unprecedented macroeconomic shock. It has complex effects on the demand- and supply-side of the economy (Guerrieri et al., 2020)), highly heterogeneous impacts across sectors and agents, and unknown behavioural consequences. For a stylised representation of the channels through which the COVID-19 shock affects inflation; see Fig. B.7 in Online Appendix B. As such, these times are ideally suited to adding information from outside the model to inform purely model-based forecasts, as also argued by Primiceri and Tambalotti (2020). Both the considered hard and soft conditional inflation forecasts would have been superior to unconditional ones in a Gaussian BVAR (columns 4 and 7, compared to column 1). Compared to these, the BVAR with fat-tailed errors largely loses its comparative advantage, suggesting that, indeed, meaningful off-model information makes a difference in forecasting in a standard VAR, as discussed in the previous section.
While the forecast gain from bringing in meaningful off-model information to the VAR is notable, our exercise suggests that it does not make a big difference whether one does this via hard conditioning on several variables (including real GDP, as in the SPF) or via soft conditioning on the inflation expectations of professional forecasters. It is clear in any case that the expectations of professional forecasters can discipline econometric models in turbulent times. This is also because professional forecasters do not solely rely on models, which have likely been adversely affected by COVID-19 observations, but use judgement when submitting their forecasts (see the discussion in de Vincent-Humphreys et al. (2019)). In a special ECB SPF questionnaire (see ECB (2019)), respondents indicated that a sizeable share of their forecast can be attributed to their judgement, especially when it comes to long-term forecasts; see Fig. 9.
Fig. 9.
Information used by professional forecasters of inflation at various forecast horizons. Note: Professional forecasters’ response to the question: To what extent are your point forecasts model- or judgement-based? (percent of responses) .
Tilting model-based inflation forecasts to SPF expectations has been investigated recently, but for somewhat different reasons. Ganics and Odendahl (2021) focus on the euro area and show that survey forecasts can help mitigate the effects of structural breaks on the forecasting performance in a VAR. They also find that professional forecasters are better at forecasting than a standard Bayesian VAR model around the two recent euro area recessions, as well as the slow recovery thereafter. This is a particularly challenging period for forecasting euro area inflation as reduced-form time series models have a hard time providing accurate forecasts (as also discussed in Bańbura and Bobeica (2020)). Similarly, Tallman and Zaman (2020) show that such tilting produces superior inflation forecasts after the Great Recession in the U.S., acting as a way of indirectly accommodating structural changes (and mitigating misspecification issues in a VAR). Bańbura et al. (2021) document forecast gains for euro area inflation and GDP when an optimal forecast combination from many models is tilted to the more subjective SPF mean. It is worth noting that when tilting to both first and second moments of the SPF, there is a general worsening of the forecasting performance, so the authors recommend tilting only to the mean.
Fig. 10 shows the real-time predictions of euro area inflation during the COVID-19 crisis using both unconditional and conditional forecasts. Panels (c) and (d) show that incorporating alternative information brings the projection for euro area inflation closer to its actual level, which is consistent with the RMSFE analysis. In addition to the information included in Table 3, it becomes obvious that in the first phase of the pandemic, inflation tended to surprise on the downside, and subsequently, it turned out to be notably higher than foreseen. The puzzling behaviour of inflation during the pandemic is also reflected in the marked revisions to the short-term inflation expectations of professional forecasters (see Fig. 11).
Fig. 10.
Real-time inflation forecast. Note: Real-time forecast for inflation estimated over an expanding window. The thick black line is the actual inflation, the coloured dashed lines are median estimates, and the (overlapping) light blue areas are the 68% credible interval for each respective estimation window.
Fig. 11.
Revisions in short- and long-term euro area inflation expectations for various forecast horizons. Note: ECB Survey of Professional Forecasters.
Throughout 2020, analysts lowered their inflation expectations, particularly for the short term. Part of this revision was driven by oil price developments. In addition, in the perceptions of SPF panellists (see ECB (2020)), demand factors were largely considered dominant relative to possible supply-side and scarcity effects. The combination of lower oil price assumptions and the drop in demand led SPF respondents to revise HICP inflation expectations down sharply for shorter horizons, and the downward adjustment also involved expected core inflation. The second year of the pandemic marked a reversal in inflation dynamics. Inflation in the euro area (and in other advanced economies) surged, on the back of the rebound in oil prices and rising cost pressures from supply-side bottlenecks which accompanied the reopening of the economies. Inflation exceeded the expectations of professional forecasters, who revised their near-term outlooks quite markedly (see Fig. 11). This pattern is valid also for other advanced economies, such as the U.S. (see the discussion in Meyer et al. (2021)). At the same time, despite the large swings in near-term inflation expectations, long-term expectations remained fairly stable. This is also reflected in Fig. 10, Panel (d), where soft conditioning disciplines inflation forecasts beyond the near term.
4.2. Pseudo-forecast evaluation and cross-country evidence
Our assessment over the pandemic period is that the solution that we propose for disciplining BVAR parameters in abnormal times is also superior to a standard Gaussian BVAR when it comes to unconditional forecasts. Caution is warranted, of course, given the very short available pandemic sample. In order to form a better view of whether this model is a valid solution in general, we conduct a forecast evaluation over a longer sample (starting in 1995), where we compare the fat-tailed BVAR with its Gaussian counterpart. For the euro area, such an exercise can be done only using a pseudo-real-time setup, due to the lack of real-time vintages going so far back into the past.
Specifically, we evaluate the accuracy of unconditional forecasts in the small BVAR with the Sims and Zha prior on the pre-pandemic sample from 1995:Q1 until 2019:Q4, and during the COVID-19 period from 2020:Q1 until 2021:Q2. To do so, we re-estimate each model over an expanding window using 1980:Q1 as a starting date, simulate a forecast, and evaluate the horizons from one quarter to four quarters ahead. The forecast performance is measured in terms of point and density predictions.30 For the point prediction, we compute the root mean squared forecast error (RMSFE) using the posterior mean of the predictive distribution. The performance of density forecasts is judged by two commonly used scoring rules: the average continuous ranked probability score (ACRPS), for which the lower the value the better; and the average log predictive likelihood (ALPL), for which the higher the value the better.31 Even though various authors have argued in favour of either ACRPS or ALPL, Krüger et al. (2021) stress that this choice appears ultimately subjective. Particularly, we consider both scoring rules because they may yield different answers regarding the best performing model in the event of extreme observations; see Bjerregård et al. (2021). The CRPS measures the quadratic difference between the predicted and empirical cumulative distribution function. By construction, this metric rewards observations close to the median and is less sensitive to extreme observations. The log predictive likelihood, on the other hand, evaluates the likelihood of the observation based on its predictive density. As such, extreme observations are particularly punished if the tails of the predictive density are too thin.
Table 4 reports the outcome of this forecast evaluation for real GDP growth and HICP inflation. Prior to the pandemic period, the BVAR with fat-tailed errors produces slightly more accurate point and density predictions for both real GDP growth and HICP inflation as compared to the standard Gaussian BVAR. During the pandemic, the fat-tailed model exhibits a clear upper hand over the standard Gaussian model. It produces substantially more accurate point and density predictions for real GDP growth and HICP inflation, especially at longer forecast horizons. Therefore, the unconditional forecast accuracy of a Gaussian BVAR model suffers particularly when extreme observations distort parameter estimates.
Table 4.
Pseudo-out-of-sample forecast evaluation.
| (a) Real GDP growth | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSFE |
ACRPS |
ALPL |
||||||||||
| BVAR | 0.52 | 0.95 | 1.37 | 1.75 | 0.26 | 0.48 | 0.71 | 0.93 | −0.83 | −1.38 | −1.77 | −2.07 |
| BVAR | 0.51 | 0.94 | 1.36 | 1.74 | 0.25 | 0.46 | 0.69 | 0.90 | −0.74 | −1.24 | −1.64 | −1.92 |
| (I) Pre-COVID-19 period: 1995:Q1–2019:Q4 | ||||||||||||
| BVAR | 9.03 | 11.72 | 13.07 | 14.79 | 5.73 | 7.14 | 8.22 | 9.26 | −34.09 | −63.40 | −55.06 | −44.43 |
| BVAR | 7.38 | 8.71 | 8.90 | 9.69 | 5.01 | 5.61 | 6.13 | 7.35 | −6.67 | −6.72 | −7.43 | −8.89 |
| BVAR | 7.49 | 8.93 | 9.04 | 9.77 | 5.05 | 5.76 | 6.08 | 7.04 | −61.45 | −80.80 | −69.11 | −63.25 |
| (II) COVID-19 period: 2020:Q1–2021:Q2 | ||||||||||||
| (b) HICP inflation | ||||||||||||
| RMSFE |
ACRPS |
ALPL |
||||||||||
| BVAR | 0.30 | 0.54 | 0.75 | 0.99 | 0.16 | 0.28 | 0.39 | 0.52 | −0.25 | −0.82 | −1.12 | −1.39 |
| BVAR | 0.30 | 0.53 | 0.72 | 0.96 | 0.16 | 0.28 | 0.38 | 0.50 | −0.22 | −0.72 | −1.03 | −1.33 |
| (I) Pre-COVID-19 period: 1995:Q1–2019:Q4 | ||||||||||||
| BVAR | 0.61 | 1.06 | 1.35 | 1.56 | 0.32 | 0.66 | 0.78 | 0.80 | −1.09 | −1.90 | −1.68 | −1.59 |
| BVAR | 0.58 | 0.99 | 1.12 | 1.14 | 0.31 | 0.64 | 0.71 | 0.67 | −0.86 | −1.71 | −1.67 | −1.58 |
| BVAR | 0.59 | 1.02 | 1.16 | 1.21 | 0.31 | 0.63 | 0.68 | 0.67 | −1.05 | −1.82 | −1.55 | −1.48 |
| (II) COVID-19 period: 2020:Q1–2021:Q2 | ||||||||||||
Note: Forecast evaluation metrics prior to and during the COVID-19 pandemic for (a) real GDP growth and (b) HICP inflation. BVAR denotes a standard Gaussian BVAR, BVAR is the fat-tailed BVAR, and BVAR is the BVAR augmented with dummy variables for each quarter in the COVID-19 period.
The dummy-augmented BVAR, on the other hand, is a competitive benchmark during the pandemic. Overall, the accuracy of point predictions is at a similar level to that of the fat-tailed BVAR, though the latter is somewhat more accurate at longer horizons. One driving force behind this relative improvement of the fat-tailed BVAR might be that it implies less persistent propagation of macroeconomic shocks as compared to the dummy-augmented Gaussian BVAR. In terms of density predictions, the evidence is more mixed. The ACRPS suggests that the quality of the density predictions is of similar accuracy for both real GDP and HICP inflation. However, the ALPL draws a different picture. Under this metric, the dummy-augmented BVAR produces the worst density forecast for real GDP, while the figures for HICP inflation are comparable. The reason behind this seemingly unintuitive result is that the predictive distribution of the dummy BVAR (excluding the dummies from the forecast exercise) is too far away from the actual realisation of real GDP. In other words, the tails of the predictive distribution are too thin to rationalise these abnormal observations. Updating the VAR parameters helps in this respect, but generates unreasonable forecasts, as discussed above. Thus, the log predictive likelihood may discard a very competitive forecast model, as the predictive distribution is heavily mis-specified. Since the predictive likelihood and the marginal likelihood are closely connected (Geweke and Amisano, 2010, Geweke and Amisano, 2011), this also explains why the marginal likelihood may favour an overall explosive model—specifically, because it is unable to rationalise extreme observations with more stable parameters. Similar messages arise based on the large VAR. The forecast evaluation is presented in Table B.1 in Online Appendix B.
While the pandemic was a global shock, each country reacted differently when it came to containment measures. So one might ask whether the findings for the euro area are also valid for other countries. This is also a way to check the robustness of the finding that the BVAR with fat-tailed errors is a viable alternative to Gaussian BVARs when it comes to inflation forecasting before and after the pandemic. We found that for major euro area countries (France, Germany, Italy, and Spain), and for Canada, the United Kingdom, the U.S., and Japan, the model with fat-tailed errors is a valid alternative tool to a standard Gaussian BVAR when it comes to forecasting inflation. The differences in forecasting performance are marginal in the pre-COVID-19 period, but as soon as the extreme observations kick in, the model equipped with fat-tailed residuals outperforms; see Tables B.2, B.3, and B.4 in Online Appendix B.
5. Modelling the COVID-19 shock with univariate and multivariate -distributed errors
A relevant question is whether the solution of relaxing the normality assumption of the residuals works only for multi-equation systems such as VARs, or whether it also works for single-equation models. We show that it actually is the joint multivariate and fat-tailed errors that manage to robustify models against extreme observations. We illustrate this by taking a simple Phillips curve model, a key macroeconomic relationship used to gauge past and future inflation dynamics. In central banking, it is one of the pillar frameworks in thinking about inflation, with reduced-form models often employed to grasp the link between inflation and real activity (see Yellen (2015) and Eser et al. (2020)).
In the single-equation framework, fatter tails are less effective at mitigating the impact of extreme observations, as they primarily capture abnormal variations associated with the dependent variable, but not so much those induced by an exogenous regressor (since its coefficients can always be shrunk to zero to mitigate the impact on the errors). Intuitively, in the multivariate setup, all variables are re-scaled by a common volatility factor, which is informed by the innovations in all endogenous variables, while in the single-equation setup, this volatility factor is informed only by the residuals of the dependent variable. For technical details; see Appendix A.
To illustrate this point, consider the following example with a simple Phillips curve model, using real GDP growth as a measure of slack, its own lag, and no other exogenous regressor (such as external price pressures or inflation expectations):
where is the seasonally adjusted quarterly growth rate of inflation excluding energy and food (HICPx), and is the seasonally adjusted quarterly growth rate of the real gross domestic product (RGDP).
We estimate the coefficients using system and single-equation techniques. For the system estimation, we use: (i) a Bayesian VAR with Gaussian errors, (ii) a Bayesian VAR with multivariate -distributed errors, and (iii) a counterfactual BVAR with exogenous time-varying variance (as detailed below). For the single-equation estimation, we use a univariate version of the three models listed above. As a prior distribution, we assume a diffuse (non-informative) prior for all parameters. We obtain different estimates of from the models with -errors: the BVAR- () and the single-equation regression of the VAR equation for the output gap () and HICP inflation excluding energy and food (), respectively. Subsequently, the posterior medians of these ’s are fed into the model with exogenous time-varying variance to study the impact of allowing for fat tails on the coefficient estimates.
Fig. 12 shows the implied volatility by these ’s. Both and spike when the COVID-19 pandemic wreaks havoc on the euro area, whereas remains relatively flat during this period. This illustrates that different information sets may crucially affect these ’s in the multi- and univariate setup with -errors.
Fig. 12.
Implied volatility under multivariate and univariate errors. Note: Coloured thick lines are posterior median estimates of implied volatility in the following models with -errors: (i) BVAR- using one lag (BVAR-) and the single-equation regression of the VAR model for (ii) real GDP growth (SgEq RGDP) and (iii) inflation (SgEq HICPx).
How do these different estimates of affect the inference about the coefficients in Eq. (5)? Table 5 shows the posterior mean of the coefficients using the estimation choices described above for (a) the pre-COVID-19 sample and (b) with the COVID-19 observations included in the estimation sample.
Table 5.
Simple Phillips curve coefficients with real GDP growth (qoq, sa).
| Gaussian |
Fat-tailed |
Gaussian() |
Gaussian() |
Gaussian() |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coeff. | System | SgEq | System | SgEq | System | SgEq | System | SgEq | System | SgEq | ||||
| 0.041 | 0.042 |  |
 |
 |
 |
0.040 | 0.041 |  |
 |
|||||
| 0.945 | 0.945 |  |
 |
 |
 |
0.951 | 0.951 |  |
 |
|||||
| 0.031 | 0.030 |  |
 |
 |
 |
0.029 | 0.028 |  |
 |
|||||
| (a) Simple Phillips curve estimated until 2019:Q4 | ||||||||||||||
| Gaussian |
Fat-tailed |
Gaussian() |
Gaussian() |
Gaussian() |
||||||||||
| Coeff. | System | SgEq | System | SgEq | System | SgEq | System | SgEq | System | SgEq | ||||
| 0.088 | 0.090 |  |
 |
 |
 |
0.070 | 0.069 |  |
 |
|||||
| 0.943 | 0.942 |  |
 |
 |
 |
0.947 | 0.948 |  |
 |
|||||
| 0.006 | 0.006 |  |
 |
 |
 |
0.020 | 0.020 |  |
 |
|||||
| (b) Simple Phillips curve estimated until 2021:Q2 | ||||||||||||||
Note: Posterior mean of Phillips curve coefficients based on various modelling assumptions. The first top row denotes the class of the error distribution—i.e. Gaussian is normal errors, Fat-tailed is -errors, and Gaussian() is normal errors with exogenous time-varying variance—and the second row describes whether the equation was estimated as a system (System) or as single equation (SgEq).
Focusing on the pre-COVID-19 sample (Panel (a)), the estimated slope of the Phillips curve is the same for the Gaussian model estimated as a system or as a single equation (column ‘Gaussian’). The slope coefficients of the fat-tailed model (column ‘Fat-tailed’) are also very similar. However, other coefficients such as the intercept and persistence differ slightly between the two versions. These differences can be explained by the fact that the ’s differ across the two options (multi- versus univariate -errors), mainly because of differences during the financial crisis; see Fig. 12.
The COVID-19 observations lead to a decrease in the Phillips curve slope by about 80% for real GDP growth; see Panel (b) (columns ‘Gaussian’ and ‘Fat-tailed, SgEq’). This strong parameter revision in the univariate fat-tailed model (but also in the Gaussian model) occurs because the COVID-19 observations are not heavily discounted, since the remains rather flat. In contrast, when is estimated under multivariate -distributed errors (column ‘Fat-tailed, System’), the slope coefficient changes considerably less, by about 30%. In addition, when estimating this equation with a known from the VAR (column ‘Gaussian()’) or the real GDP growth equation (column ‘Gaussian()’), the slope coefficients also change by a similar amount as compared to the system estimation, whereas when plugging in , they change substantially (column ‘Gaussian()’).
6. Conclusions
The parameters of Gaussian VAR models, frequently employed to analyse inflation by central bankers and other practitioners, are strongly affected by the COVID-19 observations and this has a bearing on the inflation forecast path.
We showed that relaxing the assumption of normal errors and allowing them to follow a multivariate -distribution appear to tackle the parameter instability problem. In this way, tail events are accommodated by the residuals, and this diminishes the impact on the parameters. We also showed that it is the joint multivariate and fat-tailed error modelling that manages to robustify models against extreme observations. In a single-equation setup such as a Phillips curve, the fat-tailed error solution is less effective.
Within a standard Gaussian Bayesian VAR, the choice of prior matters, with more informative specifications or a higher degree of prior shrinkage (more suitable for larger BVARs) acting in favour of stabilising the results after the COVID-19 shock. Both a fat-tailed BVAR and a large Gaussian BVAR with more prior shrinkage ensure stable unconditional forecasts. Nevertheless, as past data do not record an event similar to COVID-19, adding relevant off-model information to the purely model-based forecast is crucial for producing more trustworthy forecasts.
In a real-time forecast exercise, we found that the fat-tailed BVAR is notably superior to its Gaussian counterpart. Also, including off-model information, such as that in the ECB’s Survey of Professional Forecasters, brings sizeable gains to forecasting inflation during the pandemic. Both the considered hard and soft conditional inflation forecasts would have been superior to unconditional ones in a standard Gaussian BVAR. Compared to these, the BVAR with fat-tailed errors loses part, but not all of its comparative advantage.
Notwithstanding our documented forecast gains over a standard Gaussian BVAR, also in our best models, in the first phase of the pandemic, inflation tended to surprise on the downside, and subsequently it turned out to be notably higher than foreseen. The puzzling behaviour of inflation during the pandemic is also reflected in the marked revisions to the short-term inflation expectations of professional forecasters, who were surprised by inflation, first on the downside (in the first year of the pandemic) and then on the upside (in the second pandemic year).
As a lesson for practitioners, we suggest that before deriving conclusions based on existing models, one has to check and be aware of how the COVID-19 observations affect the parameter estimates and the implied forecasts. Also, adding meaningful off-model information to the model, such as that in the Survey of Professional Forecasters, brings forecast gains when forecasting inflation in turbulent times such as the pandemic. As new observations pile up, the distortion of traditionally estimated parameters diminishes. Yet, a simple model with Gaussian and homoscedastic errors cannot account for the extreme observations in COVID-19 times.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
We thank Marek Jarociński, Michele Lenza, Chiara Osbat, and one anonymous referee for their valuable comments. We also want to express our gratitude and thanks for the feedback we received from the participants in the 9th ECB Near Term Inflation Projection Workshop, the DG-ECFIN internal seminar, the 2021 Annual Conference of the International Association for Applied Econometrics, the 7th RCEA Time Series Workshop, and the SEACAN-CAMA webinar. The views expressed in this paper are of the authors only and do not necessarily reflect those of the European Central Bank or the Eurosystem.
Even before the Great Recession some economists warned that the unconditional distribution of macro-variables is not Gaussian (see Christiano (2007) or Fagiolo et al. (2008)).
In 2020, the sharp fall in oil prices was a result of global lockdowns and not captured by oil price futures. In 2021, apart from the economic drivers, a set of statistical effects (e.g. changes in the weights of the consumption basket and the reversal of a value-added tax decrease in Germany) not captured by our model significantly increased inflation.
We do not attach any structural interpretation to this shock, but merely use it to study the dynamic properties.
We construct dummy observations along the lines of Bańbura et al. (2010) and Doan et al. (1983), which reflect Minnesota-type shrinkage on VAR coefficients coupled with two sum-of-coefficients restrictions. For estimation, we use dummy observations to construct the moments of the implied normal-inverse-Wishart prior.
The weakly informative prior is calibrated by centring the VAR coefficients around zero and setting the variance of all coefficients to one, except for the constant, which we set to 10. The scale of the inverse Wishart distribution is set to the identity matrix.
Specifically, we divide the prior variances for the coefficients by a factor of four. A higher level of shrinkage is typically recommended for very large VARs with over 100 variables; see Bańbura et al. (2010).
For brevity, we do not report changes in the residual correlation structure for our considered VAR models.
See Carriero et al., 2021, Huber et al., 2020, Lenza and Primiceri, 2020, and Ng (2021) in the context of VARs, and Antolín-Díaz et al. (2021) for dynamic factor models.
Antolín-Díaz et al. (2021) suggest that the typical comovement between different variables changed with the pandemic, and within a dynamic factor model, the authors distinguish between persistent increases in aggregate volatility and transitory ones specific to individual variables. We do not account for such change explicitly; indirectly, while conducting conditional forecasting, we also inform the comovement between certain variables.
Inference about macroeconomic volatility also changes, as the COVID-19 observations inflate the estimated error volatility of the stochastic volatility process due to the ex post smoothing of the spike during the pandemic.
The IRFs of the fat-tailed VAR are stable under the weakly informative prior and under the strong Sims and Zha prior; see Panels (a) and (b) in Fig. B.2 in Online Appendix B.
The dynamic propagation of the shock is somewhat dampened due to the revised prior distribution—which implies a tighter prior for some variables—in the expanding sample estimation; see also Hartwig (2021). Fig. B.3 shows that under a pre-COVID-19 Sims and Zha prior, the IRFs of the Gaussian model become even more unstable (Panel (a)), while those of the fat-tailed model are virtually unchanged (Panel (b)).
In Appendix A, is defined in the variance scale. In the text, we use . Technically, this variable mixes multivariate normal distributions such that it mimics the multivariate -distribution with a particular degree of freedom; see Geweke (1993) and Ni and Sun (2005).
Importantly, is used as an estimation device to simulate the fat tails of the -distribution. It is not to be confused with a traditional model for time-varying volatility such as stochastic volatility or GARCH.
Since , …, are conditionally independent given the model parameters and the data, we sample each of them independently, as in Chan (2020). The information sources used to estimate at each quarter are the sum of squared normalised VAR residuals for that quarter (the residuals are conditional on the VAR parameters utilising the entire sample), the number of variables included in the VAR, the degrees of freedom of the -distribution, and the assumed prior inverse-gamma distribution; see the conditional posterior distribution of lambda in Eq. (9) in Appendix A. The influence of this prior specification on the width of the estimated uncertainty band for lambda depends on the degrees-of-freedom parameter (see Eq. (5) in Appendix A), which ensures that the errors are -distributed (see Geweke (1993)). The lower the degrees-of-freedom parameter (), the more widespread the prior inverse-gamma distribution of lambda. Our chosen prior distribution for the degrees-of-freedom parameter is uninformative about the posterior shape of the -distribution, as we assume a uniform prior distribution (see Appendix A). Therefore, we are agnostic about the heavy-tailedness of the -distribution.
We use the U.S. macroeconomic uncertainty index of Jurado et al. (2015) as an imperfect proxy for the euro area because the available Economic Policy Uncertainty index for the euro area derived by Baker et al. (2016) focuses too much on policy and does not reflect the macroeconomic uncertainty embedded in our variables.
By construction, our measure of high-frequency volatility (lambda) is of a short-lived nature, as under -errors, large shocks are modelled as independent events and are not allowed to be serially correlated. This can explain why during the Great Recession, the proxy for macroeconomic uncertainty was elevated for longer than what lambda would imply. The same applies for the case of the COVID-19 shock.
Nevertheless, the log probability of large tail events is rather similar for a degrees-of-freedom parameter between and , while for larger values of , the tails become substantially thinner. Compared to the Gaussian case, a ten-standard-deviation shock receives a log probability of , i.e. percentage points, which practically means that such an event will never materialise. Under -errors with a degrees-of-freedom parameter between and , the probability of such an event is roughly comparable to a four-standard-deviation shock under normal errors, which is about 0.0134 percentage points..
For the VAR with -errors, we use the algorithm in Chan (2020).
We also conducted a more granular grid search on the tightness of the dummy observation prior and found that the -error model generally favours a lower level of tightness as compared to the Gaussian model.
The VAR includes HICP, real GDP, real private consumption, real private investment, total employment, unemployment rate, capacity utilisation, consumer confidence, PMI, the rest-of-the-world real GDP, nominal effective exchange rate, EUR/USD exchange rate, the oil price in dollars, non-energy commodity prices, U.S. real GDP, U.S. CPI, U.S. short-term interest rate, EONIA, two-year government bond spread, 10-year government bond spread, mortgage bank lending spread, VSTOXX index of financial volatility, and economic policy uncertainty. See Bobeica and Jarociński (2019) for details regarding the data set.
In Online Appendix B, Figs. B.4, B.5, and B.6 show the IRFs for all variables and for all prior specifications.
We use the one-, two-, and five-year-ahead real GDP growth expectations of the ECB SPF 2021:Q3 round (i.e. the latest available when the ECB projected inflation as of 2021:Q3) and we interpolate linearly for missing quarters.
As of 16 August 2021, corresponding to the cut-off of the ECB inflation projections starting in 2021:Q3.
Grothe and Meyler (2018) show that these expectations have a non-negligible predictive power for euro area inflation developments, as compared to statistical benchmark models.
Our codes adjust the tilting function included in the BEAR toolbox; see Dieppe et al. (2016).
All vintages for the seven variables included in the benchmark BVAR (real GDP, HICP, price of oil, nominal effective exchange rate, short-term rate, 10-year government bond spread, and share in world GDP), as well as the conditioning variables coming from the Survey of Professional Forecasters and the oil price futures, correspond to the official ECB’s macroeconomic projection cut-off dates.
For the dummy variables, we assume an uninformative prior with mean zero and variance of .
Carriero et al. (2021) also explore the workings of a VAR augmented with dummy variables for each month since March 2020. The dummies fully absorb the variation induced during the pandemic, leaving all parameters unchanged. Though this strategy stabilises the parameters of the VAR model, the authors note that stochastic volatility remains at pre-pandemic levels, which yields implausibly narrow forecast bands..
Appendix A provides some computational details for the evaluation metrics.
For recent applications; see e.g., Chan, 2020, Clark and Ravazzolo, 2015, and Carriero et al. (2021).
Note that this posterior mean is equivalent to the generalised least squares estimate.
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.ijforecast.2022.01.002.
Appendix A. The proposed econometric solution for estimating BVARs after March 2020. Errors with a t-distribution and dummy observation prior
Bayesian VAR with multivariate -distributed errors
Let be an vector of variables that is observed over the periods . Consider the following generic VAR(p) model with independent multivariate -errors:
| (1) |
where is an vector of intercepts and are coefficient matrices. Let be a vector of an intercept and lags with , and let be a matrix. The error term follows an independent multivariate -distribution with covariance matrix of dimension and degrees of freedom .
The multivariate -distribution of the error term can be represented by a scale mixture of normal distributions; see Geweke (1993) and Ni and Sun (2005):
| (2) |
where is a latent state variable that is inverse-gamma distributed, i.e. .
Next, we stack the observation over , which yields
| (3) |
where , , and are respectively of dimensions , , and . denotes the matric-variate normal distribution, is the Kronecker product, and is of dimension .
We assume that the priors for , , and are independent. For we adopt a standard normal-inverse-Wishart prior:
| (4) |
For , we assume that is independently inverse-gamma distributed:
| (5) |
and for we follow (Chan & Hsiao, 2014) and assume a uniform prior:
| (6) |
where is sufficiently large to approximate normal errors.
Because of the prior structure, the posterior draws can be obtained by sequentially sampling from: (1) ; (2) and (3) . As detailed in Chan (2020), natural conjugacy of the prior survives even with a general covariance structure in . Therefore, one can derive conditional posterior quantities for that are still normal-inverse-Wishart distributed. The conditional posterior is given by
| (7) |
| (8) |
where
The posterior distribution for can be easily derived, as the are conditionally independent given the data and . Therefore, one can show that the posterior of is given by
| (9) |
Next, the posterior distribution for conditional on is independent from the data and . As shown by Chan and Hsiao (2014), the conditional posterior for is given by
| (10) |
for , and otherwise. This density is non-standard and we use the independence-chain Metropolis–Hastings algorithm of Chan and Hsiao (2014) to sample .
To summarise, we can sequentially sample the parameters using a Gibbs sampler with a Metropolis–Hasting step:
-
1.
Draw from an distribution
-
2.
Draw from an
-
3.
Draw from an for
-
4.
Draw from a proposal distribution and accept/reject using a Metropolis–Hasting step
Inference in the BVAR model with -errors.
To conduct inference in the BVAR model with -errors, it is convenient to work with the normal mixture representation of (1):
| (11) |
where . Thus, conditional on , the BVAR with -errors can be represented as a standard Gaussian VAR with independent but not identically distributed errors. Specifically, the error term exhibits idiosyncratic heteroscedasticity, which is controlled by .
To compute impulse response functions and unconditional and conditional forecasts from (11), we follow the exposition of Jarociński (2010) and derive impulse response coefficients as well as the projection matrices for the variables and for the residuals of the BVAR model with -errors. We start by simplifying the derivation and define the VAR in terms —with deviations of from the central level defined as:
The VAR in the companion form is
| (12) |
where
Take and, using (12), recursively substitute . In the first rows we obtain expressed in terms of data up to and subsequent errors
| (13) |
where is the upper-left block of ( to the power ). is the matrix of orthogonalised impulse response after periods. is the matrix composed of the first rows of . The stacked vector of can be written as
| (14) |
or shortened as
| (15) |
The above derivations are very similar to those of standard stationary VARs. The only difference is that the forecast errors are now conditionally heteroscedastic on the sequence of , which follows directly from the normal mixture representation of the multivariate -distribution.
Forecast evaluation metrics
Root mean squared forecast error (RMSFE):.
Lower values indicate that the forecast is close to the actual value.
where is the predictive mean forecast.
Average log predictive likelihood (ALPL):.
Higher values indicate that actual observations are more likely under the predictive density.
where is the predictive density.
Average continuous ranked probability score (ACRPS):.
Lower values indicate that actual observations are more likely under the predictive distribution.
where , and denotes the cumulative distribution function associated with the predictive density , denotes an indicator function taking the value if and otherwise, and and are independent random draws from the posterior predictive density.
Heavy tails in single- and multiple-equation models
To understand the effect of univariate and multivariate -distributed errors on the coefficients of a (multivariate) linear regression model, consider the VAR in (3) and rewrite it in seemingly unrelated regression form using the scale-mixture Gaussian representation of the -distribution:
| (16) |
where , , , is an identity matrix of dimension , and is a diagonal covariance matrix. For simplicity it is instructive to focus on the conditional posterior mean of the coefficients under a diffuse (non-informative) prior.32
The conditional posterior mean of is given by
where and denote the generalised and ordinary least squares estimates, respectively.
These formulas reveal two interesting properties. First, given , the system estimation (System) is equivalent to single-equation estimation (SgEq). Second, given , then (the error term is homoscedastic and independently Gaussian distributed). Note that under -distributed errors , and hence, .
Because of the first property, if the system estimation does not yield the same estimate as an equation-by-equation estimation, then it must be the case that the implied volatility is different in the univariate setting as compared to the multivariate setting, i.e. .
To see this, suppose and are fixed. Using (16), the error is . The conditional posterior of from a regression with univariate -distributed errors for variable is given by
whereas the conditional posterior of with multivariate -distributed errors for is given by
Thus, depends on different information sets (abstracting from distributional differences). Particularly, depends only on the forecast error of the th variable () in the univariate settings, while under the multivariate distribution, depends on the vector of forecast errors (, scalar).
For instance, suppose there is a large shock in the th variable but not in the th variable. Heuristically, the posterior of will be larger than because there was no unusually large forecast error in the th variable. As a consequence, when the parameters are updated in the next iteration of the Gibbs sampler, the data will be downweighed more strongly in the multivariate setup as opposed to the univariate setup. The estimated coefficients are then different because .
Appendix B. Supplementary data
The following is the Supplementary material related to this article.
.
References
- Antolín-Díaz J., Drechsel T., Petrella I. 2021. Advances in nowcasting economic activity: Secular trends, large shocks and new data. Mimeo. [Google Scholar]
- Ascari G., Fagiolo G., Roventini A. Fat-tail distributions and business-cycle models. Macroeconomic Dynamics. 2015;19:465–476. [Google Scholar]
- Baker S., Bloom N., Davis S. Measuring economic policy uncertainty. Quarterly Journal of Economics. 2016;131:1593–1636. [Google Scholar]
- Bańbura M., Bobeica E. Does the Phillips curve help to forecast euro area inflation? International Journal of Forecasting. 2020 forthcoming. [Google Scholar]
- Bańbura M., Brenna J., Paredes F., Ravazzolo F. European Central Bank; 2021. Combining bayesian vars with survey density forecasts: does it pay off? [Google Scholar]
- Bańbura M., Giannone D., Reichlin L. Large Bayesian vector auto regressions. Journal of Applied Econometrics. 2010;25:71–92. [Google Scholar]
- Baumann U., Darracq Pariès M., Westermann T., Riggi M., Bobeica E., Meyler A., Böninghausen B., Fritzer F., Trezzi R., Jonckheere J. European Central Bank; 2021. Inflation expectations and their role in eurosystem forecasting. [Google Scholar]
- Bjerregård M., Mller J., Madsen H. An introduction to multivariate probabilistic forecast evaluation. Energy and AI. 2021;4 [Google Scholar]
- Bobeica E., Jarociński M. Missing disinflation and missing inflation: A VAR perspective. International Journal of Central Banking. 2019;15:199–232. [Google Scholar]
- Carriero A., Clark T., Mertens E. Federal Reserve Bank of Cleveland; 2021. Addressing COVID-19 outliers in BVARs with stochastic volatility. [Google Scholar]
- Chan J. Large Bayesian VARs: A flexible Kronecker error covariance structure. Journal of Business & Economic Statistics. 2020;38:68–79. [Google Scholar]
- Chan J., Hsiao C. Bayesian inference in the social sciences. John Wiley & Sons Ltd; 2014. Estimation of stochastic volatility models with heavy tails and serial dependence; pp. 155–176. chap 6. [Google Scholar]
- Chib S., Ramamurthy S. DSGE models with Student-t errors. Econometric Reviews. 2014;33:152–171. [Google Scholar]
- Chiu C.-W., Mumtaz H., Pinter G. Forecasting with VAR models: Fat tails and stochastic volatility. International Journal of Forecasting. 2017;33:1124–1143. [Google Scholar]
- Christiano L. Comment on ‘on the fit of New Keynesian models’. Journal of Business & Economic Statistics. 2007;25:143–151. [Google Scholar]
- Clark T., Ravazzolo F. Macroeconomic forecasting performance under alternative specifications of time-varying volatility. Journal of Applied Econometrics. 2015;30:551–575. [Google Scholar]
- Cogley T., Sargent T. Drifts and volatilities: Monetary policies and outcomes in the post WWII US. Review of Economic Dynamics. 2005;8:262–302. [Google Scholar]
- Cúrdia V., Del Negro M., Greenwald D. Rare shocks, great recessions. Journal of Applied Econometrics. 2014;29:1031–1052. [Google Scholar]
- de Vincent-Humphreys R., Dimitrova I., Falck E., Henkel L., Meyler A. Economic Bulletin 1, Article 1. European Central Bank; 2019. Twenty years of the ECB Survey of Professional Forecasters. [Google Scholar]
- Dieppe A., van Roye B., Legrand R. European Central Bank; 2016. The BEAR toolbox. [Google Scholar]
- Doan T., Litterman R., Sims C. National Bureau of Economic Research; 1983. Forecasting and conditional projection using realistic prior distributions. [Google Scholar]
- ECB T. European Central Bank; 2019. Results of the third special questionnaire for participants in the ECB Survey of Professional Forecasters. [Google Scholar]
- ECB T. European Central Bank; 2020. The ECB Survey of Professional Forecasters- Second quarter of 2020. [Google Scholar]
- Eser F., Karadi P., Lane P., Moretti L., Osbat C. European Central Bank; 2020. The Phillips curve at the ECB. [Google Scholar]
- Fagiolo G., Napoletano M., Roventini A. Are output growth-rate distributions fat-tailed? Some evidence from OECD countries. Journal of Applied Econometrics. 2008;23:639–669. [Google Scholar]
- Ganics G., Odendahl F. Bayesian VAR forecasts, survey information and structural change in the euro area. International Journal of Forecasting. 2021;37:971–999. [Google Scholar]
- Geweke J. Bayesian treatment of the independent Student-t linear model. Journal of Applied Econometrics. 1993;8:19–40. [Google Scholar]
- Geweke J., Amisano G. Comparing and evaluating Bayesian predictive distributions of asset returns. International Journal of Forecasting. 2010;26:216–230. Special Issue: Bayesian Forecasting in Economics. [Google Scholar]
- Geweke J., Amisano G. Hierarchical Markov normal mixture models with applications to financial asset returns. Journal of Applied Econometrics. 2011;26:1–29. [Google Scholar]
- Grothe M., Meyler A. Inflation forecasts: Are market-based and survey-based measures informative? International Journal of Financial Research. 2018;9:171–188. [Google Scholar]
- Guerrieri V., Lorenzoni G., Werning I. National Bureau of Economic Research; 2020. Macroeconomic implications of COVID-19: Can negative supply shocks cause demand shortages? [Google Scholar]
- Hartwig B. Deutsche Bundesbank; 2020. Robust inference in time-varying structural VAR models: The DC-Cholesky multivariate stochastic volatility model. [Google Scholar]
- Hartwig B. 2021. Bayesian VARs and prior calibration in times of COVID-19. Mimeo. [Google Scholar]
- Huber F., Koop G., Onorante L., Pfarrhofer M., Schreiner J. Nowcasting in a pandemic using non-parametric mixed frequency VARs. Journal of Econometrics. 2020 [Google Scholar]
- Jacquier E., Polson N., Rossi P. Bayesian analysis of stochastic volatility models with fat-tails and correlated errors. Journal of Econometrics. 2004;122:185–212. [Google Scholar]
- Jarociński M. Conditional forecasts and uncertainty about forecast revisions in vector autoregressions. Economics Letters. 2010;108:257–259. [Google Scholar]
- Jurado K., Ludvigson S., Ng S. Measuring uncertainty. American Economic Review. 2015;105:1177–1216. [Google Scholar]
- Krüger F., Lerch S., Gneiting T. Predictive inference based on Markov chain Monte Carlo output. International Statistical Review. 2021;89:274–301. [Google Scholar]
- Lenza M., Primiceri G. National Bureau of Economic Research; 2020. How to estimate a VAR after March 2020. [Google Scholar]
- Meyer B., Prescott B., Sheng X. The impact of the COVID-19 pandemic on business expectations. International Journal of Forecasting. 2021 doi: 10.1016/j.ijforecast.2021.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishkin F. National Bureau of Economic Research; 2011. Monetary policy strategy: Lessons from the crisis. [Google Scholar]
- Ng S. National Bureau of Economic Research; 2021. Modeling macroeconomic variations after COVID-19. [Google Scholar]
- Ni S., Sun D. Bayesian estimates for vector autoregressive models. Journal of Business & Economic Statistics. 2005;23:105–117. [Google Scholar]
- Primiceri G. Time varying structural vector autoregressions and monetary policy. Review of Economic Studies. 2005;72:821–852. [Google Scholar]
- Primiceri G., Tambalotti A. Manuscript 2020. Northwestern University; 2020. Macroeconomic forecasting in the time of COVID-19. [Google Scholar]
- Robertson J., Tallman E., Whiteman C. Forecasting using relative entropy. Journal of Money, Credit and Banking. 2005;37:383–401. [Google Scholar]
- Rossi B. Center for Economic Policy Research; 2020. Forecasting in the presence of instabilities: How do we know whether models predict well and how to improve them. [Google Scholar]
- Schorfheide F., Song D. Federal Reserve Bank of Philadelphia.; 2020. Real-time forecasting with a (standard) mixed-frequency VAR during a pandemic. [Google Scholar]
- Sims C., Zha T. Bayesian methods for dynamic multivariate models. International Economic Review. 1998;39:949–968. [Google Scholar]
- Tallman E., Zaman S. Combining survey long-run forecasts and nowcasts with BVAR forecasts using relative entropy. International Journal of Forecasting. 2020;36:373–398. [Google Scholar]
- Waggoner D., Zha T. Conditional forecasts in dynamic multivariate models. The Review of Economics and Statistics. 1999;81:639–651. [Google Scholar]
- Yellen J. Speech at the Philip Gamble Memorial Lecture, University of Massachusetts, Amherst, Massachusetts, 24 2015. Federal Reserve System; 2015. Inflation dynamics and monetary policy. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
.