Computational design of a cutinase for plastic biodegradation by mining molecular dynamics simulations trajectories

Graphical abstract

Abstract

Polyethylene terephthalate (PET) has caused serious environmental concerns but could be degraded at high temperature. Previous studies show that cutinase from Thermobifida fusca KW3 (TfCut2) is capable of degrading and upcycling PET but is limited by its thermal stability. Nowadays, Popular protein stability modification methods rely mostly on the crystal structures, but ignore the fact that the actual conformation of protein is complex and constantly changing. To solve these problems, we developed a computational approach to design variants with enhanced protein thermal stability by mining Molecular Dynamics simulation trajectories using Machine Learning methods (MDL). The optimal classification accuracy and the optimal Pearson correlation coefficient of MDL model were 0.780 and 0.716, respectively. And we successfully designed variants with high ΔT_m values using MDL method. The optimal variant S121P/D174S/D204P had the highest ΔT_m value of 9.3 °C, and the PET degradation ratio increased by 46.42-fold at 70℃, compared with that of wild type TfCut2. These results deepen our understanding on the complex conformations of proteins and may enhance the plastic recycling and sustainability at glass transition temperature.

1. Introduction

Polyethylene terephthalate (PET) is one of the most widely used man-made synthetic plastics worldwide, with an annual production of nearly 70 million tons used in textiles and packaging [1]. However, its excellent durability has now become an environmental hazard. To solve or attenuate these environmental problems, a variety of chemical and physical technologies have been developed to treat plastic waste; however, the byproducts resulting from this processing also contribute to environmental pollution [2], [3]. Therefore, using keratinase and lipase to biodegrade plastics has become an important research focus [4], [5], [6], [7], [8]. However, the glass transition temperature of PET plastics is high, at which the plastic degradation enzyme is easily inactivated, and the PET degradation enzyme needs a high temperature of about 70℃ to carry out their activity [9], [10], [11], [12], [13]. Therefore, it is very important to improve the thermal stability of the PET degradation enzyme for the realization of plastic biodegradation.

At present, researchers have proposed several computational methods to design, test, and track conformations or mutations that improve thermal stability. Several methods are developed based on sequence information. iPTREE-STAB uses a decision tree method to predict the effects of single-point variations on protein stability and considers the physicochemical properties and interactions between substituted amino acids and their adjacent amino acids [14]. SIFT (Sorts Invarierant From Tolerant) uses sequence homology to explore the effects of sequence variations on protein function to identify beneficial and harmful variations in target sequences by multiple sequences alignment analysis [15]. Similarly, several methods have been developed based on structural information. I-Mutant2.0 uses a support vector machine (SVM) method to predict stable or unstable amino acid variations based on free energy changes (ΔΔG) [16]. SDM (Site-directed Mutator) [17] predict protein stability based on the statistical derivation of force field potential energy using changes in relatively free energy. FoldX use the empirical force field to calculate relative free energy differences caused by changes in interactions within the variant structure [18]. Rosetta is a modeling software library based on Monte Carlo simulated annealing algorithm, and Rosetta ddg_monomer can be used to predict the thermal stability of protein mutants (ΔΔG) [19]. The DeepDDG can predict the stability change of protein point mutations using neural networks [20]. Almost all of these structure-based protein stability predication methods rely on protein crystal structure data. The protein crystal structure provided by protein data bank (PDB) only represents the conformation of a protein under specific conditions but does not reflect the fact that the conformation of a protein is complex and constantly changing. Therefore, it is necessary to introduce other conformations of proteins into the thermal stability design of PET degradation enzymes.

Molecular dynamics (MD) modeling has developed into a mature technique capable of analyzing protein structure [21]. Molecular dynamics simulations can capture a variety of important biomolecular processes, including conformational changes, ligand binding, and protein folding, revealing the positions of all atoms at femtosecond temporal resolution [22], [23], [24]. Using MD to simulate the structural changes of proteins in a specific solution and at a specific temperature will help to further understand the dynamic properties of proteins [25], [26], [27], [28], [29]. MD simulation can provide subtle and dynamically changing high-dimensional structural information of proteins in solution, which requires an analytical method to analyze the relationship between the high-dimensional dynamic structural characteristics of proteins and their thermal stability. The development of machine learning technology (ML) provides an effective means for the analysis of high-dimensional data, which can be used to construct the classification or regression model of protein thermal stability based on the information of multi-dimensional structural characteristics [30], [31]. In this study, we integrated MD simulations and ML (named the MDL method) to predict protein variants with improved thermal stability. The MD simulations provided sufficient structural features as input for the ML algorithms, and the classification and regression results showed that the MDL method performed well. Currently, researchers focus on PETase from Ideonalla sakaiensis (IsPETase), but the amount of degradation product of IsPETase is μM grade [6], [8], [32]. Cutinase from thermobifida fusca KW3 (TfCut2) can degrade PET plastic, and the amount of degradation products reached mM grade. But TfCut2 loses 100% of its activity after 1 h at 65.6 ℃ [33]. A thermal stabilization of the enzyme is therefore required to increase its efficiency for PET degradation. Here, TfCut2 was modified with the MDL method, the thermal stability and PET degradation ability of the variants were significantly improved.

2. Materials and methods

2.1. Dataset

Thermodynamics Database for Proteins and Mutants (ProTherm) is a collection of numerical data of thermodynamic parameters [34], [35], [36]. From the ProTherm dataset, we gathered 1293 single point mutations (M1293) in 86 wild type proteins with the experimentally measured thermal related parameters. Among them, 389 mutants with improved thermal stability were used as positive samples and 905 mutants without improvement in thermal stability as negative samples. The 3D structures of these 86 wild type proteins used for MD simulation were downloaded from the Protein Data bank, http://www.rcsb.org. And the real experimental ΔT_m value of these 1293 single point mutants ranges from −53 ℃ to 40 ℃. The training and test data sets are listed in the Supporting Information Excel file.

2.2. MD simulations

The 3D structures of these 86 wild type proteins were downloaded from the PDB database [37]. All non-protein and hydrogen atoms were removed and hydrogens were added back with Discovery studio 2.5.5. For residues with multiple conformations, the “A” conformation was used. Protein molecules were placed in cubic box at a minimum of 12 Å distances from the edge and solvated with TIP3P explicit water and chloride counter-ions using VMD 1.9.2 [38], where the approximate density of which is determined by the liquid water density at the corresponding temperature.

MD simulations were performed using NAMD 2.12 with the CHARMM22 force field [39], [40], [41], [42], [43]. All simulations were carried out with periodic boundary conditions, a 12 Å cut-off for nonbonded interactions, and Particle Mesh Ewald for long-range electrostatics. 2 fs was used as the time step and snapshots were saved every 1 ps. Each system was equilibrated using the following protocol. The protein was fully constrained and the solvent was minimized for 2000 steps using a conjugate gradient algorithm. Under the NPT condition, the solvent was equilibrated for 100 ps. The solvent was then fully constrained and the protein was minimized for 2000 steps. The entire system was then minimized for 2000 steps. Finally, the system was equilibrated for 100 ps under the same NPT conditions. Then, all simulations were carried out at 400 K in the NVE ensemble (20 ns each), with the box size fixed at its final size from the equilibration.

2.3. Computational framework for the predicting models

As one of the state-of-the-art statistical methods, the logistic regression (LR) model was used for calculation of the classification and regression models. In this study, the R package glmnet was used as the LR machine learning package [44]. To obtain the optimal lambda parameter, the prediction effect was tested by iterating the lambda values. Finally, the optimal lambda value was obtained for the LR machine learning models.

To build suitable SVM machine learning models, the R package e1071 was selected as the SVM machine learning package [45]. The grid search was used for the parameter optimization of SVM machine learning, and the Gaussian kernel was used as its kernel function. As for parameter cost and gamma, they were optimized using a grid search method and the optimal range of them were [2⁰, 2¹⁰] and [2⁻¹³,1] respectively. Finally, the optimal cost parameter and gamma parameter were used for the SVM machine learning models.

As an important part of machine learning, RF is widely used in various classification and regression problems. Here, R package Randomforest was used for classification and regression of mutant databases [46]. To get a RF model with excellent performance, the grid search was used to optimize parameters and the optimal ntree and mtry were used for the RF machine learning models. The optimization range of ntree is [10², 10⁴], and the step size is 100. The optimization range of mtry varies according to the dimension of the eigenvector. Compared with the other two machine learning algorithms, RF model shows better predictive performance. Therefore, RF is finally selected as the algorithm for classification model and regression model construction in this study.

2.4. Enzyme activity assay using bis-hydroxyethyl terephthalate

Bis-hydroxyethyl terephthalate (BHET) was used as a substrate to detect enzyme activity [47], and BHET was purchased from Sigma-Aldrich Co. (St. Louis, MO, USA) and the purity (GC) is 94.5%. The enzyme was heat-inactivated at two kinds of temperatures (65℃ and 70℃) for different time (from 0 to 5 h) and then mixed with BHET in a phosphate buffer (100 mM phosphate buffer, 100 mM NaCl, pH 8.0). The reaction system containing 50 μg/ml enzyme and 2 mg/ml BHET was incubated at 50 °C for 1 h. Add one volume of acetonitrile to stop the reaction. Use high performance liquid chromatography (HPLC, Shimadzu) to detect the substrate and product (mono-(2-hydroxyethyl) terephthalic acid (MHET) and terephthalic acid (TPA)) concentration [6].

2.5. Enzyme activity assay using PET powder

PET powder (crystallinity: 35.5%) was also used for enzyme activity detection, and PET powder was got from AIMPLAS after grinding (size 500um). The reaction system (100 mM phosphate buffer, 100 mM NaCl, pH 8.0) containing 50 μg/ml enzyme and 10 mg/ml substrate was reacted for 48 h at 70 ℃. The reaction was terminated by adding one volume of acetonitrile, and the product (BHET, MHET, and TPA) concentration was detected by HPLC [6].

2.6. Melting temperature (T_m) measurement

Thermal stability of TfCut2 proteins was determined by measuring melting curves at pH 8.0 with the Protein thermal shift dye (Applied Biosystems) in a QuantStudio 3 Real-Time PCR System (Thermo Fisher Scientific) [8]. Data analysis using Protein Thermal Shift™ software. Refer to the instruction manual for the specific operation.

3. Results

3.1. MDL rational design strategy

We proposed an integrated MDL approach and used it to design potential protein variants with improved thermal stability. As shown in Fig. 1, the MD simulated the complex and dynamic structural conformations of proteins. Three different ML algorithms were used to learn how the protein thermal stability and structural characteristics of the conformations from the MD trajectories were related. The learned rules were used to build models for predicting thermal stability changes induced by sequence variations. Finally, the conserved domain search tool (CD-search) [48], [49] was used to exclude the conserved functional sites and detect variations that could potentially improve the thermal stability without affecting catalyzing function (Fig. 4).

Fig. 1.

Flow chart of MDL rational design strategy. On the left is the extraction of molecular dynamics simulation features and the construction of machine learning prediction models. On the right is the prediction of mutant with the improved thermal stability of new proteins and rational screening of mutant sites.

Fig. 4.

Analysis of conserved domain of TfCut2. COG4188 is the conserved domain sequence found in the conserved database. The amino acid residue sites with strong conserved values are marked in red, and the amino acid residue sites circled in blue are the selected mutation sites. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In the MDL design strategy, the key is to shift the usual paradigm of structural bioinformatics from studying mainly single structures to analyze conformational ensembles. We simulated 86 wild type proteins at 400 K with the NAMD v2.12 program [43]. Subsequently, root mean square deviation (RMSD) in the simulation trajectories were calculated to understand the structural changes in the protein unfolding process. As shown in Fig. S1, the protein unfolding process was roughly classified as one-step or multi-step unfolding. In the one-step unfolding process, the three-dimensional structure of the protein was stretched continuously during the simulation process, and finally reached a stable unfolded state (Fig. S1a). In the multi-step unfolding process, the protein reached a stable unfolded state through a cyclic process of “extension-equilibrium-extension” of the structure (Fig. S1b). Especially for the multi-step unfolding process, the conformations of the protein in different equilibrium states were very variable. Therefore, if only one of the conformations was used to design the variations and the other conformations were ignored, only partial structural information would be considered, which would make it difficult to identify key variations that contribute positively to protein stability. The RMSD analysis confirmed that the conformation ensembles provided by the MD simulations were necessary for studying the relationship between protein structure and thermal stability.

3.2. Quality assessment of the models

To design variants with improved thermal stability, we constructed RF prediction model with every single structural feature. The Receiver Operating Characteristic Curve (ROC) and Precision Recall Curve (PRC) of each model in the 10-fold cross-validation are illustrated in Fig. S2, we found that the area under the ROC curve (AUROC) values ranged from 0.571 to 0.777 (Fig. S2a) and the area under the PRC (AUPRC) values ranged from 0.728 to 0.886 (Fig. S2b) using the different structural features. Compared with the models constructed with valence bond data, the models constructed with unfolding free energy and amino acid interaction network parameters had better AUROC values and AUPRC values. Among these features, the amino acid network parameter (degree) was the most outstanding feature.

To improve prediction performance, two-feature predictive models were constructed. The ROC curves and PRC curves of each model in the 10-fold cross-validation are illustrated in Fig. S3, due to the addition of valence bond data, the AUROC values were improved from 0.767 (ΔΔG) to 0.774 (ΔΔG/hbond) (Fig. S3a) and the AUPRC values were also improved from 0.871(ΔΔG) to 0.876 (ΔΔG/sbond) (Fig. S3b). The addition of amino acid network parameter data has a similar enhancement effect. The AUROC values were improved from 0.767(ΔΔG) to 0.812(ΔΔG/degree) (Fig. S3a) and the AUPRC values were also improved from 0.871(ΔΔG) to 0.899(ΔΔG/degree) (Fig. S3b). Compared with the valence bond data, the addition of amino acid network parameter data is more effective in improving the performance of the predictive model.

On the basis of the above results, we constructed four multi-feature combination prediction models: features combination of ΔΔG and four amino acid network parameters (ΔΔG/nets), features combination of ΔΔG, four amino acid network parameters, and hydrogen bond (ΔΔG/nets/hbond), features combination of ΔΔG, four amino acid network parameters, and salt bond (ΔΔG/nets/sbond), and features combination of ΔΔG, four amino acid network parameters, hydrogen bond, and salt bond (ΔΔG/nets/hsbond). As shown in Fig. 2, the addition of four amino acid network parameters improved the performance of the prediction model significantly. The AUROC values increased from 0.767 (ΔΔG) to 0.824 (ΔΔG/nets) (Fig. 2a) and the AUPRC values increased from 0.871 (ΔΔG) to 0.913 (ΔΔG/nets) (Fig. 2b). Based on these results, we continued to provide the valence bond data as input features and found that despite the performance still improved, but not noticeably. In conclusion, the classification prediction performance of the model constructed by the feature combination ΔΔG/nets/sbond is the best.

Fig. 2.

Effects of the integration of ΔΔG, network parameters, and valence bond on the performance of RF models. RF classification models of 10-fold cross-validation: (a) ROC curves and their corresponding AUROC values. (b) PRC curves and its corresponding AUPRC values. RF regression models of 10-fold cross-validation: (c) Regression model of ΔΔG. (d) Regression model of ΔΔG/nets. (e) Regression model of ΔΔG/nets/hbond. (f) Regression model of ΔΔG/nets/sbond. (g) Regression model of ΔΔG/nets/hsbond.

Then, we used RF regression models to predict the Melting temperature variation (ΔT_m) of the protein variants. The Pearson correlation coefficient (PCC) between experimentally measured ΔT_m values and predicted ΔT_m values was calculated. As shown in Fig. 2, when only the predicted ΔΔG is used as input, the PCC value was 0.565 (Fig. 2c), whereas when the predicted ΔΔG and four amino acid network parameters were used as input, the PCC value significantly improved to 0.712 (Fig. 2d). After adding hydrogen bond data or ionic bond data, the PCC values improved to 0.712 and 0.716, respectively (Fig. 2e, f). When all the features were integrated into the prediction model, the predictive performance was not further improved and the PCC value dropped to 0.712 (Fig. 2g). These results indicated that the four network parameters greatly improved the prediction performance of models and, compared with hydrogen bond data, the addition of ionic bond data was more effective in improving the performance of the prediction models.

To further improve the prediction performance, including RF, we also used other two different ML methods, logistic regression (LR) and SVM, to build the prediction models. As shown in Table S1, RF prediction model have the best performance, the most optimal AUROC and AUPRC values were 0.826 and 0.913, respectively. We also analyzed the classification accuracy of the different ML methods. As shown in Table S2, the RF model has the highest classification accuracy of 0.780. In addition to classification models, regression models were also constructed. As shown in Table S3, RF model outperformed the other two ML methods, the optimal PCC value for RF method was 0.716.

3.3. Blind test and comparison with four traditional thermostability prediction methods

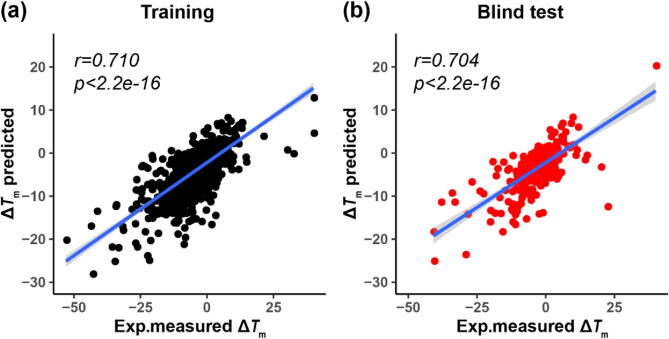
A blind test was used to evaluate the generalization of the MDL approach. The dataset M1293 were divided into two datasets: 1000 single-point variants (M1000), which were used for the 10-fold cross-validation test and model construction, and other 293 single-point variants (B293), which were used as an independent test set. Our results validated our approach. The PCC values corresponding to M1000 set and B293 set are 0.710 and 0.704, respectively (Fig. 3).

Fig. 3.

Blind test for MDL method. (a) M1000 was used for the 10-fold cross-validation. (b) B293 was used as an independent test set.

900 single-point variants with ΔΔG data (M900) isolated from dataset M1293 were divided in 630 variants (M630) and 270 variants (B270). M630 was used to construct an MDL prediction model to predict ΔΔG, and B270 was used as independent test set for performance comparison between different prediction methods. As shown in Table 1, for the existing methods, the optimal PCC value among the predicted and actual ΔΔG values was 0.492, and for the MDL method, the optimal PCC value was 0.725. When 10% of the outliers were removed, the PCC value for the MDL method reached 0.755, whereas the optimal PCC value among the other methods increased to only 0.642. In the MAE (mean absolute error) comparison, the MDL method had a smaller MAE value than the other four methods (1.456, 0.979). The MDL method also performed well in predicting ΔT_m values (PCC: 0.726, 0.827), but the MAE values were relatively high (3.048, 2.109).

Table 1.

Results for MDL models and four traditional thermostability prediction methods for the independent test set B270.

Method	Predict type	No. of predictions	PCC	MAE
SDM	ΔΔG	270/243	0.323/0.383	1.992/1.307
Foldx	ΔΔG	270/243	0.407/0.534	1.853/1.171
Rosetta	ΔΔG	270/243	0.492/0.579	3.001/2.390
Deepddg	ΔΔG	270/243	0.484/0.642	1.636/0.950
MDL	ΔΔG	270/243	0.725/0.755	1.456/0.979
MDLa	ΔTm	270/243	0.726/0.827	3.048/2.109

^aMDL algorithm for ΔT_m prediction.

3.4. Improved thermal stability and enzyme activity of TfCut2 variants

We used MDL model to design variants of TfCut2 with improved thermal stability. A total of 177 variants with predicted ΔT_m > 1℃ were analyzed for conserved domains and variation hotspots, and variants were selected for experimental verification as follows. 177 positive single-point variants were distributed on 53 amino acid residue sites, among which Asp174, Asp204, Trp234, Trp183, Glu253, Glu254, and Trp61 were the variation hotspots that produce positive variants, as shown in Fig. S5. After considering the results of the conserved domain analysis, we selected eight positive variants with predicted ΔT_m > 1℃ for experimental verification, namely D174S (1.2℃), S121P (1.6℃), E202L (2.6℃), S113P (3.7℃), S113E (3.2℃), S163K (1.0℃), S194P (1.8℃), and A55V (1.9℃) (Fig. 4). Because the largest number of predicted positive variants were on Asp204, we also selected the D204P variant, giving us a total of nine variants for experimental verification.

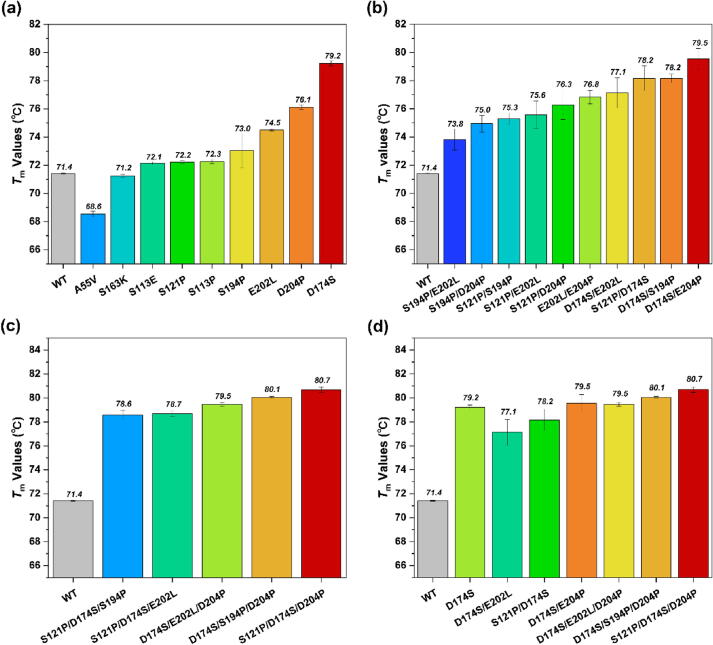
Among the nine variants, the T_m values of seven variants were higher than that of the wild type TfCut2 (Fig. 5a). While only A55V and S163K variants had the lower T_m values than the wild type. We combined the five single-point variants (S121P, D174S, S194P, E202L, D204P) that showed significantly improved thermal stability to randomly construct 10 double-point variants. The T_m values of all the double-point variants ranged from 73.8℃ to 79.5℃, which were significantly higher than that of wild type TfCut2 with the T_m value of only 71.4℃ (Fig. 5b). To generate more thermally stable variants, we combined three of the double-point variants (S121P/D174S, D174S/S194P, D174S/E204P) to construct triple-point variants (Fig. 5c). The T_m values of all the triple-point variants further improved the T_m values of TfCut2, and the D174S/S194P/D204P and S121P/D174S/D204P variants had T_m values of 80.1℃ and 80.7℃ respectively. Among these variants, we selected the seven variants (D174S, S121P/D174S, D174S/E202L, D174S/D204P, S121P/D174S/D204P, D174S/S194P/D204P, D174S/E202L/D204P) that had the most notable improvement of thermal stability for the subsequent polyethylene terephthalate (PET) degradation experiments (Fig. 5d).

Fig. 5.

T_m values of wild type (WT) TfCut2 and mutants. (a) T_m values of nine single mutants. (b) T_m values of ten double mutants. (c) T_m values five triple mutants. (d) Seven mutants with significantly improved thermal stability were used in subsequent enzyme activity and PET plastic degradation experiments. The redder the color, the higher the T_m value, and the bluer the color, the lower the T_m value.

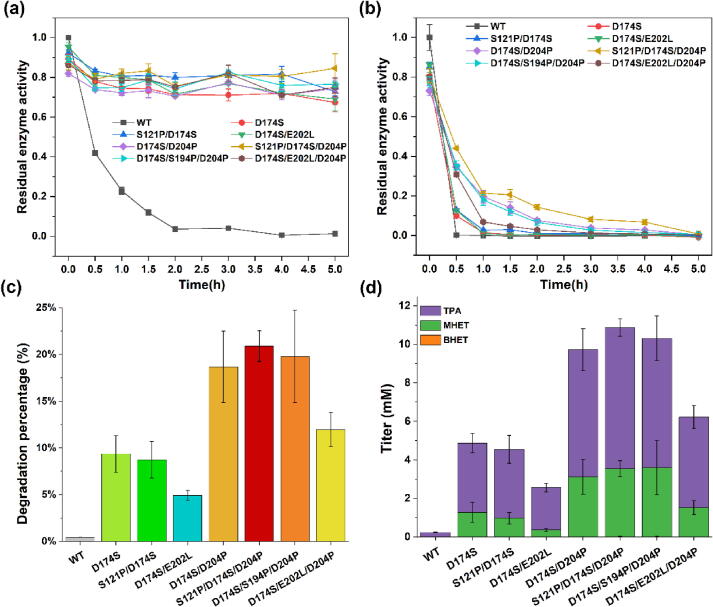
Interestingly, we found that the enzyme activity of TfCut2 variants was also improved with BHET as substrate. After treatment at 65℃ for 2 h, the residual enzyme activity of the wild type TfCut2 has been almost lost, but all of the variants still have at least 60% of the activity, and the best one S121P/D174S/D204P retains 80% of the residual enzyme activity (Fig. 6a). Moreover, the activity of this variant was higher than 80% even after the treatment at 65 ℃ for 5 h. Since the glass transition temperature (T_g) of PET plastic is >70℃, polyester hydrolases for PET degradation need to be thermally stable at ≥ 70℃. The enzyme activity of wild type TfCut2 and its variants was measured at 70℃ (Fig. 6b). After treatment at 70℃ for 0.5 h, the enzyme activity of wild type TfCut2 was lost, but the residual enzyme activity of the variants was more than 10%. And the S121P/D174S/D204P variant had the highest residual enzyme activity, which reached more than 44%. After treatment at 70℃ for 2 h, the S121P/D174S/D204P variant still had a residual enzyme activity above14%.

Fig. 6.

Residual enzyme activity and PET degradation ability of wild type (WT) TfCut2 and mutants. (a) Residual enzyme activity at 65℃ with BHET as substrate for different treatment times. (b) Residual enzyme activity at 70℃ with BHET as substrate for different treatment times. (c) Using PET powder with a crystallinity of 35.5% as the substrate, degradation rate of PET plastics treated with wild type TfCut2 and seven mutants respectively. The redder the color, the higher the degradation rate of PET plastic, and the bluer the color, the lower the degradation rate of PET plastic. (d) Using PET powder with a crystallinity of 35.5% as the substrate, determination of degradation products of PET plastics by HPLC, after treated with wild type TfCut2 and seven mutants respectively. Here purple stands for TPA, green for MHET, and orange for BHET. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.5. Enhanced PET powder degradation by TfCut2 variants

To further investigate the PET degradation properties, we measured the PET degradation of wild type TfCut2 and its variants at 70℃ using PET powder with a crystallinity of 35.5% as the substrate. The wild type TfCut2 only degraded 0.45% of the PET powder, while the degradation ratio of PET powder for the D174S, D174S/D204P, S121P/D174S, D174S/E202L, D174S/S194P/D204P, S121P/D174S/D204P, and D174S/E202L/D204P variants were 9.35%, 18.66%, 8.73%, 4.93%, 19.79%, 20.89%, and 11.95%, respectively (Fig. 6c). For the optimal S121P/D174S/D204P variant, the PET degradation ratio is 46.42 folds higher than that of the wild type TfCut2.

The PET degradation products were detected by HPLC, and the result showed that the PET powder was completely degraded to MHET and TPA, and BHET was barely detectable. Wild type TfCut2 degraded the PET powder to 0.23 mM TPA, and no BHET or MHET was detected. The D174S variant degraded the PET powder to 1.27 mM MHET and 3.60 mM TPA, and no BHET was detected. Among the three D174S-derived double-point variants, the D174S/D204P variant degraded the PET powder to 0.02 mM BHET, 3.11 mM MHET, and 6.60 mM TPA, which is an improvement over the degradation ability of D174S. Among the three D174S/D204P-derived triple-point variants, the degradation ability of the D174S/S194P/D204P and S121P/D174S/D204P variants was further improved. And the optimal S121P/D174S/D204P variant degraded the PET powder to 0.02 mM BHET, 3.52 mM MHET, and 7.34 mM TPA (Fig. 6d). There were few BHET in degradation products of PET plastics.

3.6. Mutant-induced changes in the distribution of hydrogen bonds

To explore the mechanism of thermal stability improvement of TfCut2 variants, we analyzed structure changes of the wild type and TfCut2 variants. Considering that the mutant sites are distributed on the surface of the protein structure, we analyzed the hydrogen bond distribution between each amino acid site of the protein and the surrounding solvent environment. As shown in Fig. 7, When Ser121, Asp174, Ser194, Glu202, and Asp204 were mutated into Pro, Ser, Pro, Leu, and Pro, respectively, the number of hydrogen bonds between the mutant site and the surrounding environment decreased to varying degrees. This result means that the region where these amino acid residues are located become more hydrophobic, facilitating a more compact structure in the region where they are located.

Fig. 7.

Cluster analysis of hydrogen bond distribution. The horizontal axis represents wild type and different mutant proteins and the vertical axis represents different amino acid residue sites. The bluer the color the less hydrogen bonds there are, the redder the color the more hydrogen bonds there are. The black arrow represents the amino acid residue sites where the mutations occurred.

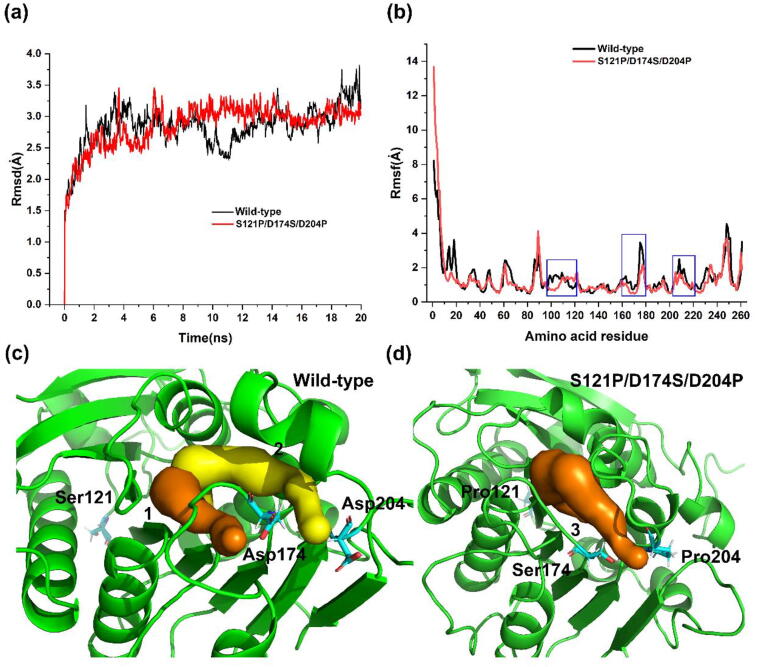
Then, the MD simulation trajectory of the S121P/D174S/D204P variant and its structure was analyzed. As shown in Fig. 8a, the RMSD value of the wild type TfCut2 did not stabilize and showed a further upward trend after the end of 20 ns simulation, while the RMSD value of the variant was stable and finally lower than that of the wild type TfCut2. RMSF analysis was also performed, compared with the wild type TfCut2, the variant had a lower RMSF value near the mutant residues site region (Fig. 8b). The last frame structure of the MD simulation trajectories of wild type TfCut2 and the variant were used for further analysis. For the wild type TfCut2, Ser121, Asp174, and Asp204, they can form 3, 5, and 5 hydrogen bonds with the surrounding solvent environment, respectively. After mutation, Pro121, Ser174, and Pro204 can form 1, 2, and 1 hydrogen bonds with the surrounding solvent environment, respectively (Fig. S4). The three mutation sites all occurred in the loop region of the protein. Proline mutations limit the conformational flexibility of surrounding amino acid residues, thus improving the thermal stability of proteins. The decrease in the number of hydrogen bonds with the surrounding environment makes these three regions more hydrophobic, making the structure of these regions more compact, which is conducive to the improvement of protein stability. There are cavities near residues 174 and 204, and the reduction of hydrogen bonds with the surrounding environment makes this region more hydrophobic and compact, which contributes to the narrowing of the cavity and thus improves the thermal stability of the protein (Fig. 8c-8d).

Fig. 8.

Structural analysis of variant S121P/D174S/D204P. (a) RMSD analysis of MD simulation trajectories, the structural stability of the variant S121P/D174S/D204P was superior to that of the wild type. (b) RMSF analysis of MD simulation trajectories, the thermal stability of the variant region is improved. (c) The numbers 1 and 2 represent the two cavities that exist around Asp174 and Asp204 and are marked orange and yellow, respectively. (d) The number 3 represents the cavity that exist around Ser174 and Pro204 and is marked orange. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

In this study, we constructed a database of MD simulation trajectories of 86 proteins and explored the internal relationship between the complex dynamic protein conformations and the thermal stability. On the basis of the dynamic conformational characteristics, we constructed a predictor to predict the changes in thermal stability of proteins induced by sequence variations. We found that 1) the predictor based on the unfolding free energy predicted the impact of the variations on thermal stability well, 2) the introduction of dynamic protein conformational characteristics significantly improved the predictive performance of the predictor, and 3) introduction of amino acid interaction network parameters further significantly improved the predictive performance of the predictor. Our results are consistent with earlier reports that there is a strong correlation between the unfolding free energy and protein thermal stability [50], [51]. Unlike previous studies, we combined MD simulations and ML to include the dynamic structural conformation of proteins and the amino acid interaction network in a model to predict the thermal stability of proteins.

The combination of MD simulations and ML models to predict the effects of amino acid modifications on protein thermal stability is an important highlight of this study. We used mainly ΔΔG as the input feature to build the ML model, and the PCC values between experimentally measured and predicted ΔT_m values were used as the performance evaluation criteria. The changes in PCC values with simulation time are shown in Fig. 9. The starting point for each protein structure was the PCC value calculated using FoldX before beginning the MD simulations (crystal structure PCC 0.423). When the MD simulation was introduced into the ML model, the PCC values increased with the simulation time. These results show that the introduction of MD simulations was important in improving the performance of the ML model.

Fig. 9.

Effects of MD simulation time on the performance of ML regression models. ML methods: (a) LR, (b) SVM, (c) RF.

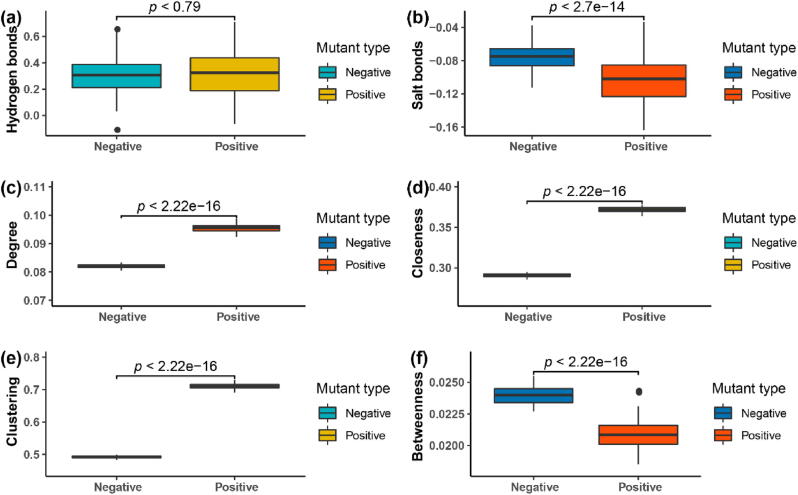
The introduction of hydrogen and ionic bonds into ML models was previously shown to have inconsistent effects on model performance [52], [53]. Therefore, we analyzed the differences in the number of hydrogen and ionic bonds between variant and wild type proteins. Compared with the wild type protein structure, 0.32 hydrogen bonds were increased in the positive variants and 0.31 hydrogen bonds were increased in the variants with lower thermal stability, but the Wilcoxon test showed that the hydrogen bond changes between the positive and negative variants were not significant (p = 0.79) (Fig. 10a). For the ionic bonds, 0.10 ionic bonds were reduced in the variants with improved thermal stability, and 0.07 ionic bonds were reduced in the variants with reduced thermal stability (Fig. 10b), and the Wilcoxon test showed that the ionic bond changes between the positive and negative variants were extremely significant (p = 2.7E − 14). The significant difference in numbers of ionic bonds between the positive and negative variants is consistent with the observed improved performance of the ML models with the introduction of ionic bond data.

Fig. 10.

Difference analysis of positive and negative mutation sites. (a) The differences in the number of hydrogen bonds between mutants and wild type proteins. (b) The differences in the number of salt bonds between mutants and wild type proteins. (c) The distribution difference in the degree of network parameter between positive and negative mutation sites. (d) The distribution difference in the closeness of the network parameter between positive and negative mutation sites. (e) The distribution difference in the clustering of network parameters between positive and negative mutation sites. (f) The distribution difference in the betweenness of the network parameter between positive and negative mutation sites.

Biomolecular networks, which describe interactions between biological molecules, are increasing being used to discover the basic molecular processes and rules that underlie biological system such as growth, development, aging, and disease [54], [55], [56]. Here, several topology properties of the amino acid interaction network were used to analyze the positive and negative protein variants. As shown in Fig. 10c–f, the distribution of positive and negative variant sites in the networks was significantly different in the centrality assessment parameters of these networks (Wilcoxon test: p < 2.22e − 16). The degree values of the positive and negative variation sites were 0.096 and 0.082 respectively (Fig. 10c), which reflected that the positive variation sites were more likely to be distributed on the core residue sites of the network or the core nodes of a module in the network than the negative variation sites. The parameter clustering coefficient values of positive and negative variation sites were 0.71 and 0.49 respectively (Fig. 10e), which also reflected that the positive variation sites were more likely to be distributed on the central residual sites in a local region of the network (subnetwork). The centrality closeness values of positive and negative variation sites were 0.37 and 0.29 respectively (Fig. 10d), which indicates that positive variation sites tend to be distributed on the core residue sites of the network. Compared with these three network parameters, betweenness centrality indicates the probability of the shortest path through residue X between any two residues other than residue X. This means that residues with high betweenness centrality are generally the key hub residues between the amino acid interaction networks that connect different network nodules. The betweenness centrality of positive and negative variation sites was 0.020 and 0.024 respectively (Fig. 10f). The negative variation sites were more likely to be distributed on the connecting nodes between the residue network modules than the positive variant sites. In summary, positive variant residues tended to be distributed in the core sites of the amino acid interaction network or the core sites of a module of the amino acid interaction network, whereas negative variant residues tend to be distributed in the channels connecting different amino acid interaction network modules.

The distribution of predicted positive variants at amino acid residues sites was analyzed when selecting suitable variation sites. Three important Ca²⁺ binding residues (Asp174, Asp204, Glu253) were identified as positive variation hotspots (Fig. S5), which is consistent with the findings of previous studies [13]. Then et al. [57] focused on these hotspots and significantly improved the thermal stability of TfCut2 by introducing a disulfide bridge (D204C/E253C) to replace the Ca²⁺ binding function. Tournier et al. [7] also found three corresponding residues in leaf-branch compost cutinase, namely two acidic residues (Glu208 and Asp238) and neutral Ser283, and replaced the divalent metal binding site with a disulfide bridge (D238C/S283C) to improve the thermal stability of the leaf-branch compost cutinase. Moreover, the MDL method accurately predicted additional positive variation hotspots, which were modified to design more positive variants (Fig. S5). However, the MDL method can be further improved to predict multi-point variants. For example, the predicted ΔT_m values of variants D204C and E253C were 1.8 °C and 0.4 °C respectively, but the ΔT_m values of the D204C/E253C variant could not be predicted; thus, disulfide bond design prediction could not be conducted. In future studies, we plan to further improve the MDL method to increase the prediction accuracy and include a wider application range.

5. Data availability

All data supporting the results are available within the paper and its supplementary information files.

CRediT authorship contribution statement

Qingbin Li: Investigation, Software, Methodology, Formal analysis, Visualization, Writing – original draft. Yi Zheng: Investigation, Validation, Formal analysis, Visualization. Tianyuan Su: Validation, Visualization, Writing – review & editing. Qian Wang: Resources, Writing – review & editing. Quanfeng Liang: Resources, Visualization, Writing – review & editing. Ziding Zhang: Conceptualization, Resources, Software, Writing – review & editing. Qingsheng Qi: Conceptualization, Resources, Validation, Writing – review & editing. Jian Tian: Conceptualization, Resources, Methodology, Software, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: