Violations of proportional hazard assumption in Cox regression model of transcriptomic data in TCGA pan-cancer cohorts

Graphical abstract

Abstract

Background

Cox proportional hazard regression (CPH) model relies on the proportional hazard (PH) assumption: the hazard of variables is independent of time. CPH has been widely used to identify prognostic markers of the transcriptome. However, the comprehensive investigation on PH assumption in transcriptomic data has lacked.

Results

The whole transcriptomic data of the 9,056 patients from 32 cohorts of The Cancer Genome Atlas and the 3 lung cancer cohorts from Gene Expression Omnibus were collected to construct CPH model for each gene separately for fitting the overall survival. An average of 8.5% gene CPH models violated the PH assumption in TCGA pan-cancer cohorts. In the gene interaction networks, both hub and non-hub genes in CPH models were likely to have non-proportional hazards. Violations of PH assumption for the same gene models were not consistent in 5 non-small cell lung cancer datasets (all kappa coefficients < 0.2), indicating that the non-proportionality of gene CPH models depended on the datasets. Furthermore, the introduction of log(t) or sqrt(t) time-functions into CPH improved the performance of gene models on overall survival fitting in most tumors. The time-dependent CPH changed the significance of log hazard ratio of the 31.9% gene variables.

Conclusions

Our analysis resulted that non-proportional hazards should not be ignored in transcriptomic data. Introducing time interaction term ameliorated performance and interpretability of non-proportional hazards of transcriptome data in CPH.

1. Introduction

As sequencing costs decreased in recent years, transcriptomic sequencing is an efficient and increasingly popular approach to characterize complex biological pathways of tumors [1]. Numerous studies have demonstrated the possibility of transcriptomic signatures as prognostic markers, which is often achieved based on Cox proportional hazard regression (CPH) [2], [3], [4].

The main premise of CPH is the proportional hazard (PH) assumption [5], [6]. Specifically, the model assumes that the hazard of each covariate does not change over time. Violation of the PH assumption may lead to misleading and erroneous scientific findings [7], [8]. If the hazard of variable increases or decreases over time, the usual CPH model will ignore these time-dependent changes. Bellera et al. found that the negative status of hormone receptors increased the risk of metastasis at early stages but was protective thereafter in breast cancer [9]. Moreover, Shintani et al. demonstrated that time-fixed CPH could have a considerable bias in analyzing the relationship between delirium and ICU length of stay [10].

However, verification of the PH assumption has not received sufficient attention. Only a small proportion of studies relying on Cox models have validated the PH assumption [8], [11]. Unlike clinical data, the transcriptomic data consisted of high-throughput RNA signatures. Compliance with the PH assumption in transcriptomic data is to be investigated. On the other hand, the CPH with the time-dependent term can deal with the non-proportional hazards of variables [5]. The effects of CPH with the time-dependent term for transcriptomic data are still uncertain.

The Cancer Genome Atlas (TCGA) is one of the most comprehensive tumor omics projects containing over 20,000 samples spanning 33 cancer types [12]. The high-quality sequencing data of TCGA provide an opportunity to systematically characterize the non-proportional hazards of each transcriptomic gene. This study aimed to construct a CPH model for overall survival (OS) prediction at the RNA level for each gene and answer the following 5 questions using TCGA cohorts: 1) What proportions of single-gene CPH models violate the PH assumption in different tumors; 2) How important are these genes with non-proportional hazards in CPH; 3) Are these genes very different across cohorts of the same tumors; 4) The CPH with the time-dependent term is an approach to explain the non-proportional hazards of covariates. Which form of the time-interaction term works better in time-dependent CPH; 5) Does the time-dependent CPH change the significance of the log hazard ratio (HR) of genes compared with the usual CPH.

2. Material and methods

Assessing the association of RNA levels of genes in cancer patients with survival times had important implications for the prognostic markers' identification. In this study, we aimed to fit cancer patients' OS (outcome variable) using univariate CPH. Models included only gene RNA level as an independent variable unless otherwise specified.

2.1. Data collection and standardization

We collected 9,056 patients from 32 cohorts with complete RNA sequencing (RNA-seq) of primary tumors and OS annotations (patients with 0 survival time were excluded) from TCGA [12]. The RNA-seq of TCGA was normalized by TPM & log₂(x + 1) and downloaded by Xena database [13]. We removed RNAs that had the same expression values in more than 80% of the patients. Finally, we included 38,154 RNAs in TCGA cohorts.

Three independent transcriptomic datasets of NSCLC were collected from the Gene Expression Omnibus (GEO) database: GSE68465 (lung adenocarcinoma, LUAD, n = 442) [14], GSE37745 (non-small cell lung cancer, NSCLC, n = 196) [15], GSE50081 (NSCLC, n = 172) [16]. Their microarray data were normalized by log₂ RMA [17]. The basic information of included cohorts was shown in Tab. S1.

2.2. Schoenfeld residual test

Schoenfeld residual test was an effective and widely used method for the diagnosis of PH assumption [7], [6]. The Schoenfeld residuals were defined as the following functions [18]:

$$\mathrm{M}\left(\mathrm{\beta },{\mathrm{t}}_{\mathrm{k}}\right)=\sum _{\mathrm{s}\in \mathrm{R}\mathrm{s}}{\mathrm{Z}}_{\mathrm{s}}\ast {\mathrm{e}}^{\mathrm{\beta }\ast {\mathrm{Z}}_{\mathrm{s}}}/\sum _{\mathrm{s}\in \mathrm{R}\mathrm{s}}{\mathrm{e}}^{\mathrm{\beta }\ast {\mathrm{Z}}_{\mathrm{s}}}$$

$${\mathrm{r}}_{\mathrm{k}}\left(\mathrm{\beta }\right)={\mathrm{Z}}_{\mathrm{k}}-\mathrm{M}(\mathrm{\beta },{\mathrm{t}}_{\mathrm{k}})$$

where Rs denotes the risk set at time t_k, Z_s is the covariate of the patient with an event at time t_k, β is the coefficient of Z_s, $\mathrm{M}(\mathrm{\beta },{\mathrm{t}}_{\mathrm{k}})$ is the conditional weighted mean of covariate at time t_k. Schoenfeld residuals were scaled using the average variance matrix [19]. Under the assumption of PH, the scaled Schoenfeld residuals were a mean of 0 and independent of time. We used R 'cox.zph' function to performed Schoenfeld residual test [19].

2.3. Time-dependent CPH model

Introducing a time-dependent variable in CPH provided a flexible method to evaluate non-proportionality [20]. In this study, we constructed an interaction term between gene expression and time function (t, log(t), t², sqrt(t), or e^t) in time-dependent CPH:

$${\mathrm{h}}_{\mathrm{x}}\left(\mathrm{t}\right)={\mathrm{h}}_0\left(\mathrm{t}\right)\ast {\mathrm{e}}^{(\mathrm{\beta }\mathrm{x}+\mathrm{\delta }\ast \mathrm{x}\ast \mathrm{f}(\mathrm{t}))}$$

Where ${\mathrm{h}}_{\mathrm{x}}(\mathrm{t})$ is the hazard of gene ×, ${\mathrm{h}}_0(\mathrm{t})$ represents baseline hazard, and f(t) is time function, β is the coefficient of ×, and δ is the coefficient of time-interaction term. The CPH was performed by R 'coxph' function, and interaction term was realized by the time-transform functionality of 'coxph' [21].

2.4. Performance evaluation of CPH model

Log-likelihood and Akaike information criterion (AIC) were used to assess the fitting capability of models. Log-likelihood was positively associated with favourable fitting performance, while AIC was negatively linked to fitting performance. We used R 'logLik' and 'AIC' functions to calculate the Log-likelihood and AIC of CPH models [22], [23].

2.5. Protein-protein interaction network and node importance assessment

STRING was a protein–protein interaction (PPI) database that contained 7 kinds of interaction evidence (fusion evidence, neighborhood evidence, co-occurrence evidence, experimental evidence, textmining evidence, database evidence, and co-expression evidence) [24]. We constructed PPI networks consisting of 17,399 genes overlapped with TCGA RNA signatures and 496,557 edges with confidence greater than 0.6 from STRING.

Betweenness, closeness, and degree were indexes reflecting node importance of PPI networks and calculated by R 'igraph' package (https://igraph.org/). Betweenness was the proportion of the shortest path through a certain node [25]. Closeness measured the reciprocal distances to all other nodes. Degree measured the number of directly connected nodes. Genes with all betweenness, closeness and degree above the median were identified as hubs, and others were non-hubs.

2.6. Exploring potential factors associated with non-proportionality in CPH

For genes with non-proportional hazards in a CPH model, since each patient corresponded to one survival time, there were 2 patient sets (corresponded to the 2-time sets) in which genes were inversely related to prognosis. We first constructed the risk scores for each patient using multivariable Cox regressions for fitting OS from a random set of 2000 genes in each cohort. Next, we divided the patients into two groups for each gene: group A, [rank(gene expressions) - median(rank(gene expressions))] and [rank(risk scores) - median(rank(risk scores))] have the same sign; group B, [rank(gene expressions) - median(rank(gene expressions))] and [rank(risk scores) - median(rank(risk scores))] have the different sign. Hierarchical clustering of the matrix [genes, patient groups] resulted in non-proportional related patient clusters. Hierarchical clustering was realized by R 'hclust' function [26].

MCPcounter was an algorithm for calculating microenvironmental cell infiltration scores based on ssGSEA [27]. We performed statistical analysis to explore infiltration score related and clinical factors associated with the above clusters. In order to identify cluster-related genes, we performed differential expressed gene analysis for each cluster vs. others via R 'limma' package [28].

2.7. Concordance regression

Concordance regression (CON) was an algorithm that used all available patient pairs (omit censored pairs) to model C' [29]. The C' was developed from the c-index to be generalized to continuous data: ${\mathrm{c}}^{\text{'}}=P\left(T_i<T_j\right|x_i=x_j+1)$

Where X is gene expression value, T is survival time, and i, j were patients. We used R 'concreg' package to construct CON model [29].

2.8. Generation of simulated datasets

Simulated expression matrices for 10,000 genes *100 samples were derived from a standard normal distribution via R 'rnorm' function [30]. Generalized gamma distributions are flexible distributions fitted to survival times that incorporate commonly used distributions (exponential, Weibull, log normal, and gamma) [31]. The mu, sigma, Q parameters were used to characterize the survival curves, which were realized by R 'flexsurv' package [32]. We performed 40 experiments with 8 typically shaped survival curves using different parameters of the generalized gamma distribution and 5 event rates (10%, 25%, 50%, 75%, and 90%).

2.9. Statistical analysis

All statistical analysis was performed by R 3.6.1. Survival analysis was performed by R 'survival' package [21]. Randomly distributed P values were generated for each gene with the following formula: rank(P)/gene number. The rank(P) is descending ranking of Schoenfeld residuals test P value. Kolmogorov-Smirnov test was performed by R 'ks.test' function [33]. The R 'pracma' package was used to calculate the area under the curves [34]. Fleiss' kappa was calculated by R 'irr' package [35]. R 'stats' package was used to perform chi-square and analysis of variance (ANOVA) tests. Parallel computing was performed by R 'parallel' package [36]. Multiple tests were adjusted by Benjamini and Hochberg method in gene enrichment analysis [37]. P < 0.05 was considered as statistical significance in hypothesis tests. All the P values were 2-sided.

3. Results

3.1. Landscapes of violations of the PH assumption for CPH with transcriptome genes in TCGA pan-cancer cohorts

The study design was shown in Fig. 1. A total of 9,056 samples with complete RNA-seq (TPM) and OS information from 32 cancers were collected from TCGA. Overall, the mean follow-up time in TCGA was 2.75 years, with death events observed in a total of 29.5% patients (Tab. S1). The verification of PH assumption was based on Schoenfeld residual test, which identified the non-proportional characteristic of variables in CPH models fitted OS. Through the parallel strategy of R 'parallel' package, Schoenfeld residual test of univariate CPH for each gene was performed in different tumors, respectively. The distributions of Schoenfeld test P values were left-skewed and light-tail in most tumors (Fig. 2A & Fig. S1). In all tumors, an average of 8.5% gene CPH models violated the PH assumption. The above proportions were the highest in LGG (29.3%), LIHC (23.0%), and READ (19.2%) and the lowest in TGCT (1.4%), THCA (2.4%), and THYM (3.1%). Furthermore, 66.2% of the gene CPH models violated the PH assumption in at least one tumor, but only 7% of the gene CPH models violated PH in more than 5 tumors (Fig. 2B). The Quantile-Quantile (QQ) plot revealed that the p values from the Schoenfeld residual test were significantly better than that from a random distribution in the 81.25% (26/32) tumors (Fig. 2C), except PRAD, SKCM, TGCT, THCA, THYM, and UCS. To explore potential factors, we analyzed the shape of the tumor survival curve, median follow-up time, and number of events as independent variables. The mu, sigma, Q parameters of generalized gamma distributions were used to characterize the survival curves. We included 5 variables (mu, sigma, Q, median follow-up time and number of events) for multivariable linear regression. Only median follow-up time and number of events showed significant positive coefficients in linear models fitted the area under the curve of the QQ plot and the proportion of p value better than random distribution (log₁₀(proportion*30000)), respectively (Fig. 2D & E).

Fig. 1.

Study design. PH, proportional hazards; CPH, Cox proportional hazard regression; TCGA, The Cancer Genome Atlas; AIC, Akaike information criterion; GO, Gene Ontology.

Fig. 2.

The landscape of violations of the PH assumption for transcriptome genes in TCGA pan-cancer cohorts. (A) Skewness and kurtosis of distribution of P values of Schoenfeld residual test; (B) Plot of tumor numbers and numbers of non-proportional hazard genes; (C) QQ plot of Schoenfeld residuals test P value and expected P value. The red dotted line represents y = x; (D) Multivariable linear regression fitted the area under the curve of the QQ plot; (E) Multivariable linear regression fitted the proportion of p value better than expected value (log10(proportion*30000)); (F-H) Scaled Schoenfeld residual plot of RPL7A gene. QQ, Quantile-Quantile; PH, proportional hazard; AUC, area under the curve. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Scaled Schoenfeld residual plot (Fig. 2F-H) showed that the prognostic effect of RPL7A varied significantly over time in KIRC, KIRP, and LGG. For LGG, the residual plot showed a strong effect of RPL7A expression in the first 2 years, and then the effect tends to weaken.

3.2. Both hub and non-hub genes in the interaction networks possibly had non-proportional hazards in CPH models

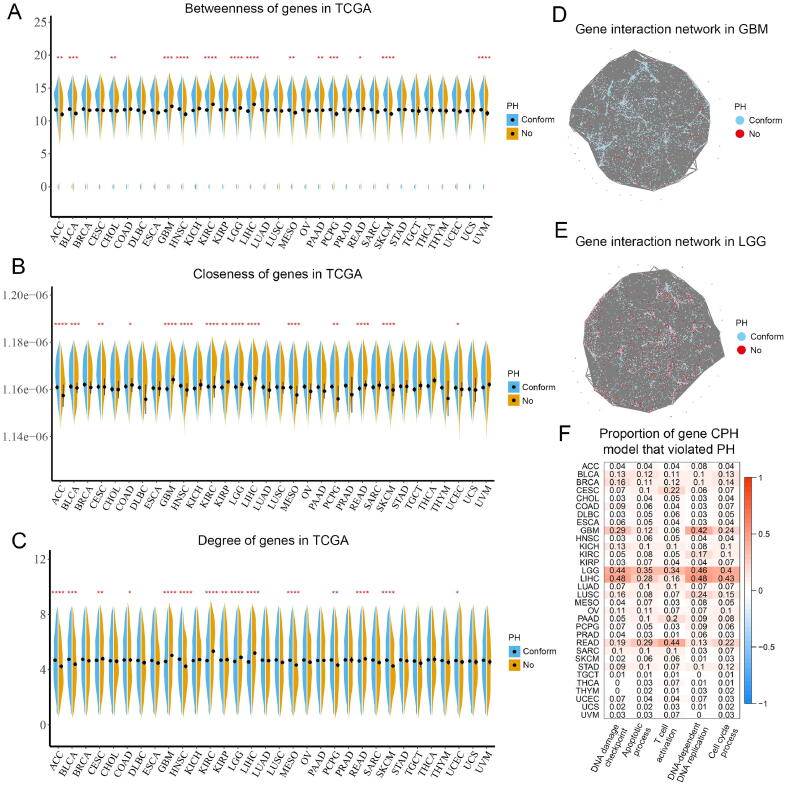
We used network analysis to assess the importance of genes using PPI networks identified by STRING database. PPI networks consisted of 17,399 genes overlapped with TCGA RNA signatures and 496,557 edges with confidence greater than 0.6. In GBM, KIRC, LGG, LIHC, and READ, genes with non-proportional hazards in CPH models had higher betweenness, closeness, and degree, which were linked to hub positions (Fig. 3A-C). However, the above relevance was reversed in ACC, BLCA, HNSC, MESO, and SKCM. We next defined hub genes as possessing betweenness, closeness, and degree values above the median, and a total of 6357 hub genes were identified. We similarly found that hub genes had a higher proportion of non-proportional hazards in ACC, BLCA, ESCA, OV, HNSC, PCPG, MESO, SARC, STAD, SKCM and THYM, whereas more non-hub genes had non-proportional hazards in GBM, KICH, KIRC, LGG, LIHC, and READ (Table 1).

Fig. 3.

Topological characteristics of proportional and non-proportional genes in TCGA pan-cancer cohorts. (A) Betweenness of proportional and non-proportional genes; (B) Closeness of proportional and non-proportional genes; (C) Degree of proportional and non-proportional genes; (D & E) Gene interaction networks in GBM and LGG; (F) Proportion of gene CPH model that assumption violated PH in the 5 important biological processes. CPH, Cox proportional hazard regression; PH, proportional hazard; TCGA, The Cancer Genome Atlas.

Table 1.

Proportions of hub and non-hub genes with non-proportional hazards in CPH model.

TCGA ID	PH-Nhub	PH-hub	NPH-Nhub	NPH-hub	hub (NPH%)	Nhub (NPH%)	Chi-Square P
ACC	9161	5787	534	195	3.26%	5.51%	<0.0001
BLCA	7787	5137	1302	649	11.22%	14.33%	<0.0001
BRCA	7294	4889	1160	714	12.74%	13.72%	0.1
CESC	8535	5325	699	485	8.35%	7.57%	0.09
CHOL	9655	5845	575	344	5.56%	5.62%	0.8936
COAD	8686	5538	532	346	5.88%	5.77%	0.8075
DLBC	9235	5730	547	294	4.88%	5.59%	0.05758
ESCA	9423	5810	533	270	4.44%	5.35%	0.01128
GBM	8762	5074	1059	946	15.71%	10.78%	<0.0001
HNSC	8211	5443	617	270	4.73%	6.99%	<0.0001
KICH	8630	5264	926	663	11.19%	9.69%	0.003137
KIRC	8241	5114	547	601	10.52%	6.22%	<0.0001
KIRP	8410	5346	679	433	7.49%	7.47%	0.9857
LGG	6209	3705	2763	2029	35.39%	30.80%	<0.0001
LIHC	6622	3752	1955	1928	33.94%	22.79%	<0.0001
LUAD	8410	5326	859	526	8.99%	9.27%	0.582
LUSC	8183	5197	1074	631	10.83%	11.60%	0.1506
MESO	9134	5705	753	351	5.80%	7.62%	<0.0001
OV	8163	5239	1038	581	9.98%	11.28%	0.01339
PAAD	8732	5416	1054	652	10.74%	10.77%	0.9807
PCPG	8787	5635	566	274	4.64%	6.05%	0.000219
PRAD	8528	5506	257	182	3.20%	2.93%	0.3734
READ	7500	4505	2203	1529	25.34%	22.70%	0.0001699
SARC	8471	5429	949	487	8.23%	10.07%	0.0001544
SKCM	9010	5691	703	280	4.69%	7.24%	<0.0001
STAD	8220	5326	1000	578	9.79%	10.85%	0.04084
TGCT	10,221	6113	136	72	1.16%	1.31%	0.4472
THCA	8390	5475	191	123	2.20%	2.23%	0.9562
THYM	9489	5840	294	145	2.42%	3.01%	0.03506
UCEC	9327	5712	528	310	5.15%	5.36%	0.591
UCS	10,226	6088	307	162	2.59%	2.91%	0.2389
UVM	8876	5651	345	186	3.19%	3.74%	0.07955

Note: PH, proportional hazards; NPH, non-proportional hazards; Nhub, non-hub; CPH, COX proportional hazards.

The specific PPI networks in GBM and LGG were presented in Fig. 3D & E. Next, we investigated genes from 5 Gene Ontology (GO) terms[38] with important biological processes: DNA damage checkpoint, apoptotic process, T cell activation, DNA-dependent DNA replication, and cell cycle process (Fig. 3F). The 15/32 cancers had a proportion exceeding 10% of gene CPH models that violated the PH assumption in at least one important process. The above results indicated that both hub or non-hub genes had the potential to have non-proportional hazards.

3.3. The non-proportional hazards of genes varied widely across cohorts of the same tumors

To investigate the consistency of non-proportional hazards of genes in different datasets, we collected five NSCLC transcriptomic datasets containing TCGA LUAD (n = 500), TCGA LUSC (n = 491), GSE68465 (n = 442) [14], GSE37745 (n = 196) [15] and GSE50081 (n = 172) [16]. Violations of the PH assumption of CPH models fitted survival times in these datasets ranged from 3.3% to 22% (Fig. 4A). The matrix of Schoenfeld test P value was next converted to a binary matrix (1, significant; 0 non-significant). However, overlapping patterns of the binary matrix in 5 datasets were scarce (Fig. 4B). Violations of the PH assumption across the 5 datasets were also highly inconsistent (Fig. 4C).

Fig. 4.

The non-proportional hazards of genes varied widely across cohorts of the same tumors. (A) The proportion of non-proportional in 5 NSCLC datasets; (B) Overlapping patterns of non-proportional genes; (C) Kappa coefficient matrix of panel B; (D) Design of exploring potential factors associated with non-proportionality; (E) Plot of beta value of univariate Cox regression in patient A and patient B groups (see methods); (F) The 4 patient clusters had differentiated patterns; (G) Boxplot of patient clusters and cellular scores of microenvironment; (H) Differently expressed genes for each patient cluster. NSCLC, non-small cell lung cancer; LUAD,

We next explored potential factors associated with non-proportionality. Using our unique strategy (see methods, Fig. 4D), patients were divided into the 2 groups for each non-proportional gene in CPH (patient A and patient B, see methods) and further clustered into different clusters. In TCGA LUAD, all genes had positive significant beta value of univariate Cox regression in patient A group and negative value in patient B group (Fig. 4E). Moreover, the 4 patient clusters had differentiated patterns (Fig. 4F). Through the MCPcounter algorithm, we constructed the cellular scores of microenvironment. However, the non-proportionality related clusters were not related to microenvironment scores (Fig. 4G). Furthermore, these clusters also were not associated with clinical characters (gender, age, pathologic stage, treatment outcome of first course, Tab. S2). At the transcriptome level, the clusters also showed scarce differential genes (Fig. 4H). In the other 4 NSCLC cohorts (TCGA LUSC, GSE68465, GSE37745 and GSE50081), the non-proportionality clusters were also independent of clinical characters and microenvironment scores (Fig. S2-5 & Tab. S3-6), which suggested that non-proportional hazards may be due to other unknown causes.

Fig. 5.

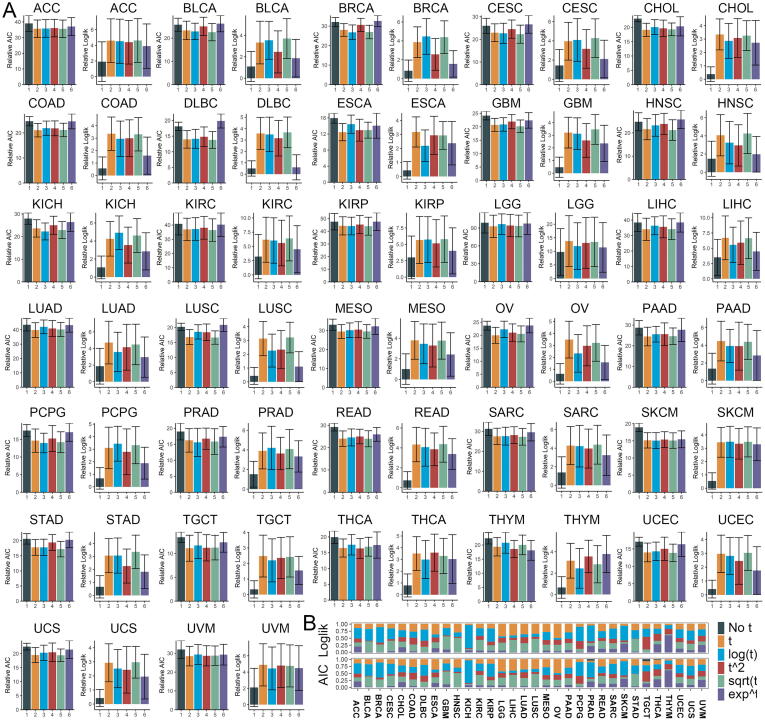
CPH with the time-dependent variables allowed for a better fit of the prognosis. (A) The Log-likelihood and AIC of CPH with different time functions in TCGA pan-cancer cohorts; (B) Proportions of max Log-likelihood value for gene CPH model violated PH assumption in CPH with different time functions. CPH, Cox proportional hazard regression; AIC, Akaike information criterion.

3.4. CPH with the time-dependent variables allowed for a better fit of OS

Introducing time-dependent variables was an effective method to analyze non-proportional hazards in CPH. Introducing one of the 5 time functions (f(t) = t, log(t), t², sqrt(t), e^t) of the time-dependent variables increased the Log-likelihood value and reduced AIC of CPH in all tumors (Fig. 5A). The e^t function performed worse than the other 3 time functions. For gene CPH violated PH assumption, the CPH with log(t) function had the highest proportions of maximum Log-likelihood value in the 14/32 tumors (Table 2, Fig. 5B). For instance, among the 5,086*6 CPH models composed of 5,086 genes with non-proportional hazards in BRCA, 53.3% of the genes in log(t) function model had the largest Log-likelihood. Moreover, the proportions of maximum Log-likelihood and minimum AIC in different datasets were similar. However, CPH of the 7.6% gene CPH models that violated the PH assumption fitted better without time-dependent variable in TGCT. In general, for gene CPH violated the PH assumption, introducing log(t), t, and sqrt(t) functions had a superior performance in most tumors. In particular, for AIC, 60.2% non-proportional CPH models in THYM benefited from e^t.

Table 2.

Proportions of maxima Log-likelihood and minima AIC for non-proportional genes in CPH with different time functions.

TCGA ID	Patient number	Proportions of gene CPH model violated PH (%)	Maxima Log likelihood (Proportions %)						Minima AIC (Proportions %)
			Non-t	t	log(t)	t^2	sqrt(t)	exp^t	Non-t	t	log(t)	t^2	sqrt(t)	exp^t
ACC	77	5.34%	0.00%	15.12%	36.36%	13.57%	14.09%	20.87%	0.00%	15.12%	36.36%	13.57%	14.09%	20.87%
BLCA	405	12.44%	0.00%	18.18%	40.87%	2.35%	36.48%	2.12%	0.19%	18.18%	40.76%	2.35%	36.40%	2.12%
BRCA	1077	13.33%	0.00%	12.06%	53.27%	6.70%	26.90%	1.06%	0.00%	12.06%	53.27%	6.70%	26.90%	1.06%
CESC	291	7.91%	0.00%	16.27%	37.30%	5.39%	36.28%	4.76%	0.06%	16.27%	37.30%	5.39%	36.22%	4.76%
CHOL	36	5.64%	0.00%	22.61%	24.32%	15.56%	19.21%	18.30%	0.00%	22.55%	24.32%	15.44%	19.21%	18.48%
COAD	282	5.87%	0.00%	27.59%	20.91%	23.61%	23.46%	4.42%	0.00%	27.59%	20.91%	23.61%	23.46%	4.42%
DLBC	46	5.59%	0.00%	20.55%	38.55%	20.82%	18.54%	1.54%	0.13%	20.28%	38.35%	21.36%	18.33%	1.54%
ESCA	181	4.82%	0.00%	37.12%	10.55%	16.83%	20.22%	15.28%	0.00%	37.12%	10.55%	16.83%	20.22%	15.28%
GBM	152	9.67%	0.00%	15.33%	25.33%	3.51%	45.51%	10.32%	0.04%	15.29%	25.33%	3.47%	45.27%	10.60%
HNSC	517	7.48%	0.00%	30.29%	15.55%	3.55%	49.86%	0.75%	0.07%	30.15%	15.55%	3.55%	49.80%	0.89%
KICH	65	10.92%	0.00%	4.46%	80.29%	3.16%	4.03%	8.06%	0.00%	4.43%	80.29%	3.16%	4.07%	8.06%
KIRC	528	7.61%	0.00%	16.00%	26.13%	14.15%	36.84%	6.88%	0.00%	16.00%	26.13%	14.15%	36.84%	6.88%
KIRP	285	8.68%	0.00%	16.50%	45.82%	12.71%	18.71%	6.25%	0.00%	16.50%	45.82%	12.71%	18.71%	6.25%
LGG	504	29.31%	0.00%	43.85%	5.43%	16.60%	27.45%	6.67%	0.00%	43.85%	5.43%	16.60%	27.45%	6.67%
LIHC	363	23.01%	0.00%	40.65%	8.29%	7.54%	41.69%	1.83%	0.00%	40.65%	8.29%	7.54%	41.69%	1.83%
LUAD	500	9.09%	0.00%	36.78%	10.04%	20.79%	29.14%	3.25%	0.15%	36.58%	10.04%	20.44%	29.04%	3.75%
LUSC	491	11.89%	0.00%	34.87%	10.56%	7.08%	45.43%	2.07%	0.00%	34.87%	10.56%	7.08%	45.39%	2.11%
MESO	85	7.79%	0.00%	28.74%	27.92%	16.19%	20.47%	6.68%	0.05%	28.69%	27.92%	16.05%	20.47%	6.82%
OV	418	11.31%	0.00%	49.54%	6.33%	17.55%	22.24%	4.34%	0.16%	49.42%	6.33%	17.55%	22.20%	4.34%
PAAD	177	10.75%	0.00%	30.10%	22.21%	15.03%	24.14%	8.52%	0.15%	30.10%	22.21%	15.03%	24.03%	8.48%
PCPG	177	5.56%	0.00%	10.65%	49.66%	27.22%	9.89%	2.59%	0.15%	10.27%	49.20%	27.83%	9.73%	2.81%
PRAD	495	3.66%	0.00%	6.29%	54.75%	5.89%	10.31%	22.76%	5.49%	5.76%	53.28%	5.22%	9.91%	20.35%
READ	91	19.22%	0.00%	26.04%	23.51%	10.34%	27.34%	12.76%	0.00%	26.04%	23.51%	10.34%	27.34%	12.76%
SARC	258	9.16%	0.00%	16.87%	36.01%	14.78%	20.16%	12.19%	0.00%	16.87%	36.01%	14.78%	20.16%	12.19%
SKCM	101	5.54%	0.00%	7.46%	50.71%	5.97%	5.40%	30.47%	0.00%	7.46%	50.71%	5.97%	5.40%	30.47%
STAD	388	9.32%	0.00%	22.51%	29.49%	0.90%	43.92%	3.18%	0.05%	22.51%	29.49%	0.90%	43.87%	3.18%
TGCT	132	1.41%	0.00%	17.26%	28.17%	43.91%	9.39%	1.27%	7.61%	14.21%	21.83%	36.29%	6.35%	13.71%
THCA	503	2.35%	0.00%	17.46%	17.67%	24.35%	11.64%	28.88%	2.16%	16.59%	17.46%	23.92%	11.21%	28.66%
THYM	118	3.14%	0.00%	5.05%	12.76%	19.01%	3.25%	59.93%	0.00%	5.05%	12.76%	18.77%	3.25%	60.17%
UCEC	178	6.15%	0.00%	19.62%	30.29%	14.25%	22.62%	13.23%	0.64%	19.55%	30.16%	13.74%	21.98%	13.93%
UCS	56	3.24%	0.00%	23.82%	33.89%	12.07%	22.04%	8.18%	0.10%	23.82%	33.89%	11.86%	21.93%	8.39%
UVM	79	4.26%	0.00%	19.62%	22.40%	19.43%	12.39%	26.16%	0.00%	19.62%	22.40%	19.43%	12.39%	26.16%

Concordance regression (CON) provided by Dunkler et al. [29] was an alternative approach to survival analysis which was not constrained by PH assumption. We constructed CPH with time interaction term and CON models for each gene in the TCGA tumor datasets, and used C-index as the evaluation index. We selected the best performing time function in Table 2 for each tumor. More gene CON models were inferior to CPH models with time-interaction term, which may be influenced by high censoring rate of real datasets (Fig. S6).

The e^t and t² performed better in TGCT, THCA, THYM and UVM, and these datasets were highly censored: 3% events in TGCT, 3.2% events in THCA, 6.8% events in THYM, 27.8% events in UVM. In order to explore the factors that influence the performance of the time function, we performed 40 simulation experiments (8 survival curve shapes*5 event rates for 10,000 genes*100 patients, see methods, Fig. S7). We found that highly censored datasets had unusually lower proportions of the log(t) and sqrt(t) function with minimum AIC (Fig. S8 & Tab. S7).

3.5. CPH with the time-dependent variables changed the significance of log HR of the genes with non-proportional hazards

Whether the introduction of time-dependent variables changed the significance of gene variables in CPH was next examined. There were 2 parameters (β and δ) in time-dependent CPH model (see methods). For β parameter (log HR), the changes of significance in non-proportional hazard genes with different time-dependent functions in BRCA were presented in Fig. 6A. The CPH with sqrt(t) function had the highest proportion (74.5%) of significant changes of log HR. The significant changes of gene log HR with a time-dependent variable of CPH in different tumors were shown in Tab. S8-12. For CPH model with t function, overall 39.8% of CPH models changed the significance of log HR, 46.4% of the non-prognostic genes became significantly prognostic genes after introducing the time-interaction term in CPH, and 21.2% of the significantly prognostic genes became non-prognostic genes. In terms of other time functions (t, log(t), t², sqrt(t), and e^t), there were significant changes log HR in 15.3%, 22.4%, 52.3%, and 10.8% CPH models violated PH assumption, respectively. Furthermore, pooling results across all time functions, a total of 31.9% genes' log HR changed significance, including 27.7% non-significant genes became significant, while 4.2% genes were opposite. These results suggested that non-time-dependent CPH may underestimate the number of prognosis related transcriptome genes. For δ parameter, overall 26.5%, 70.7%, 56.8%, 42.3%, 76.5% and 8.8% of CPH models with non-proportional genes had significant time interaction term with t, ln(t), t^2, sqrt(t) and e^t functions, respectively (Tab. S13).

Fig. 6.

CPH with the time-dependent variables changed the significance of logHR of the genes. (A) Changes of logHR significance in non-proportional hazard genes with different time-dependent functions in BRCA; (B) Scaled Schoenfeld residual plot of BCL2 in BRCA; (C) CPH of BCL2 in BRCA; (D) Scaled Schoenfeld residual plot of VEGFA in BRCA; (E) CPH of VEGFA in BRCA. CPH, Cox proportional hazard regression.

Next, we tentatively illustrated with 2 specific examples that these significant changes in time-dependent CPH might be compatible with factual evidence. BCL2 was a BCL family member that regulated apoptosis. A Meta-analysis [39] included 17 studies with over 100 cases of breast cancer that showed that positive BCL2 was significantly linked to a favourable prognosis. In this study, after the introduction of the time-gene interaction term, BCL2 expression became a significant prognostic factor, and its positive prognostic effects decreased in the first 4 years (Fig. 6B & C, Fig. S9), which was consistent with the previous study [40]. Another example was VEGFA, an important gene inducing angiogenesis and lymphangiogenesis, which was identified as an unfavourable prognostic factor in BRCA [41]. In this study, VEGFA also had a non-proportional effect in BRCA (Fig. 6D, Fig. S10), it was a significant prognostic factor in time-dependent CPH rather than general CPH (Fig. 6E).

4. Discussion

Using the 32 TCGA cohorts, we investigated non-proportional hazards of transcriptomic data. An average of 8.5% of single-gene CPH models violated the PH assumption, and 66.2% of the models violated the PH assumption in at least one tumor, suggesting that non-proportional hazards of transcriptome should not be overlooked. Furthermore, according to the network analysis of PPI, both hub and non-hub genes potentially had non-proportional hazards. In at least one of the 5 important biological processes, more than 10% of the genes in 46.9% of cancers had non-proportional hazards in CPH models.

Although the comprehensive investigation of non-proportionality of gene-based CPH was lacking, some clinical studies provided examples of genes with non-proportional hazards. Werdyani et al. found that GUSBP1 and PDLIM3 copy number variations were significantly associated with prognosis only within the first 3 years after diagnosis in COADREAD [42]. Moreover, Candido-dos-Reis et al. found that patients with BRCA1 mutation had better short-term survival, this prognostic advantage was lost over time and converted to the opposite direction after 5 years [43].

Time-dependent CPH contributed to assessing non-proportional hazards and quantifying hazards of the gene over time. In this study, we compared the 5-time functions (t, log(t), t², sqrt(t), e^t) in time-dependent CPH. The log(t), and sqrt(t) functions performed well in most tumors. Other strategies also could account for non-proportionality. For instance, perform CPH by stratifying time-dependent variables [44], however, gene expression was not the stratified categorical variable. Moreover, the stratified CPH was linked to lower power than the general CPH. Another strategy was to use intervals of time to code time-dependent variables. Quantin et al. proved that this piecewise model depended on the number of time intervals and the specific parametric function [45]. Furthermore, some non-Cox models could also consider time-varying effects. Accelerated failure time model was a parametric model without considering the PH assumption. Some studies proved the effectiveness of accelerated failure time model in survival analysis [46], [47], but the model needed to specify the probability distribution of survival times. Moreover, additive model and regression splines model were also the flexible and interpretable prognostic models [48], [49]. Still, CPH remained the most commonly used prognostic model.

The non-proportional risk of genes meant that the survival curve may cross under a certain threshold. Therefore, the results of Cox regression with time-interaction terms should be interpreted carefully. The optimal grouping threshold of variables under nonproportional risk needs further studies.

In this study, we found that the genes' CPH model that violated the PH assumption in 5 NSCLC datasets had a very low kappa coefficient (all < 0.2), suggesting that the non-proportionality of genes in CPH models was dataset-dependent. The different time-varying effects of genes might be explained by the heterogeneity of datasets. TCGA was next-generation sequencing, while GEO data were microarrays based on different platforms (GSE68465, Affymetrix Human Genome U133A Array; GSE37745, Affymetrix Human Genome U133 Plus 2.0 Array; GSE50081, Affymetrix Human Genome U133 Plus 2.0 Array). Moreover, the clinical baseline might be unbalanced in the 5 datasets. According to our results, the PH assumption should be tested for gene expression data, even if this gene had been tested in previous studies.

This study had some limitations. The main results of this study were based on TCGA cohorts, and there was still no investigation of other large cohorts. We did not investigate the non-proportionality of genes under multivariable CPH. In addition, the patient clusters of non-proportional risk were not associated with clinical features and microenvironment infiltration. The reason for non-proportionality of genes in CPH models needed further study.

In this study, we didn't perform multiple testing in Schoenfeld residual test. Transcriptomic data were ultrahigh dimensional data characterized by the dimension being much larger than the sample size. The RNAs included in this study were greater than 30000, and significant genes obtained using BH correction were very rare (zero in 22/32 tumors, Tab. S14). There were extensive regulatory relationships and collinearity among genes, and perhaps not all tests were independent. In addition, this paper was an exploratory study, strict adjustment will reduce the sensitivity.

In summary, non-proportional hazards were widespread across the transcriptome, and the tests of PH assumption in the transcriptome were not only the statistical premise of CPH but also facilitated the exploration of specific temporal patterns of gene hazards.

5. Conclusions

This study was original to investigate the non-proportionality of genes in CPH models fitted survival times using transcriptomic data in TCGA pan-cancer cohorts. Non-proportional hazards were widespread across transcriptomic genes. Introducing the time-gene interaction term improved model performance and changed the significance of gene variables in CPH model.

Data availability

The data underlying this article are available in GEO Database at https://www.ncbi.nlm.nih.gov/geo/, and can be accessed with accession number: GSE68465, GSE37745, GSE50081, and Xena, at https://xenabrowser.net/datapages/?cohort = TCGA%20Pan-Cancer%20(PANCAN).

Funding

This work was supported by National Natural Science Foundation of China (81773236, 81800429 and 81972852), Key Research & Development Project of Hubei Province (2020BCA069), Nature Science Foundation of Hubei Province (2020CFB612), Health Commission of Hubei Province Medical Leading Talent Project, Young and Middle-Aged Medical Backbone Talents of Wuhan (WHQG201902), Application Foundation Frontier Project of Wuhan (2020020601012221), Zhongnan Hospital of Wuhan University Science, Technology and Innovation Seed Fund (znpy2019001, znpy2019048, and ZNJC201922), Medical Sci-Tech Innovation Platform of Zhongnan Hospital, Wuhan University (PTXM2019026), and Chinese Society of Clinical Oncology TopAlliance Tumor Immune Research Fund (Y-JS2019-036).

Authors' contributions

ZZ, YGong and CX designed this study. ZZ, YGao, JL and GZ collected TCGA and GEO data. ZZ, YGao, SS and QW analyzed all the data. ZZ and YGao drafted the manuscript. YGong and CX revised the manuscript and supervised this study. All authors read and approved the final manuscript.

Appendix A. Supplementary data

The following are the Supplementary data to this article: