High Indirect Energy Consumption in AEM-Based CO₂ Electrolyzers Demonstrates the Potential of Bipolar Membranes

Abstract

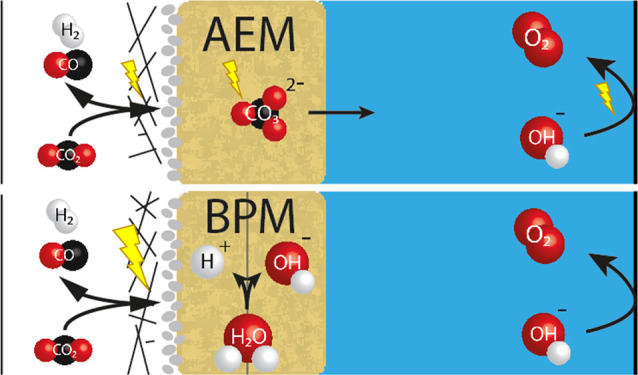
Typically, anion exchange membranes (AEMs) are used in CO₂ electrolyzers, but those suffer from unwanted CO₂ crossover, implying (indirect) energy consumption for generating an excess of CO₂ feed and purification of the KOH anolyte. As an alternative, bipolar membranes (BPMs) have been suggested, which mitigate the reactant loss by dissociating water albeit requiring a higher cell voltage when operating at a near-neutral pH. Here, we assess the direct and indirect energy consumption required to produce CO in a membrane electrode assembly with BPMs or AEMs. More than 2/3 of the energy consumption for AEM-based cells concerns CO₂ crossover and electrolyte refining. While the BPM-based cell had a high stability and almost no CO₂ loss, the Faradaic efficiency to CO was low, making the energy requirement per mol of CO higher than for the AEM-based cell. Improving the cathode–BPM interface should be the future focus to make BPMs relevant to CO₂ electrolyzers.

Introduction

To mitigate global warming, political and industrial stakeholders have embraced technologies that recycle emitted CO₂, such as the electrochemical reduction of CO₂. Via this electrochemical reaction of CO₂ (CO₂ER), (hydro)carbon building blocks (e.g., CO, C₂H₄) are produced for downstream processes.¹ In order for this reaction to be sustainable, they should be coupled to renewable energy sources. However, to be industrially competitive with already-existing processes based on fossil fuels, a higher energy efficiency is mandatory given that the electricity costs currently dominate the expected operating costs for practical CO₂ electrolysis.^1,2

To reach higher performance in terms of product selectivity, energy efficiency, and stability, the reactor configurations for CO₂ER have progressed throughout the years. To overcome the mass transport limitations of CO₂ in aqueous environments, a compartment with gaseous CO₂ implemented alongside a gas diffusion electrode (GDE) has been proven effective following mature fuel cell technology. As the diffusion coefficient in a gas environment is four orders of magnitude higher than in a liquid environment, it allows operation at high current densities (≥100 mA cm^–2).³ In addition to eliminating Ohmic losses, a zero-gap electrolyzer configuration is attractive to reach higher current densities with the same cell potential as it allows to further reduce the ion path.⁴ In this configuration, an ion exchange membrane is sandwiched between the cathode and anode, resulting in lower Ohmic losses.

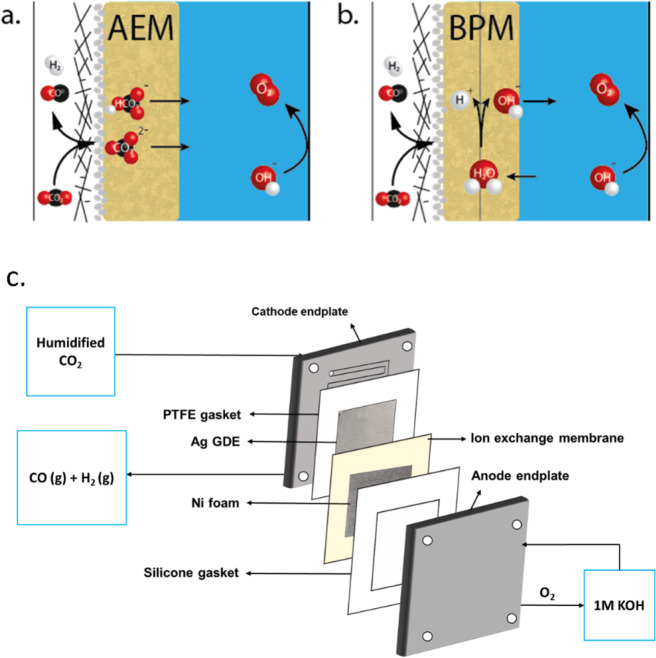
Typically, an anion exchange membrane (AEM) is used in such an MEA configuration for CO₂ reduction (see Figure 1a) as it has a high ionic conductivity and limits the crossover of cations from the anolyte. Using an alkaline anolyte also enables us to use earth-abundant materials like NiFe-based catalysts for the oxygen evolution reaction (OER). A disadvantage of this configuration is the reaction of gaseous CO₂ from the cathode feed with hydroxide ions in the membrane, forming carbonate or bicarbonate ions.⁵ Those (bi)carbonate ions cross over to the anolyte via migration and diffusion. Even the use of a KHCO₃ electrolyte as anolyte also does not circumvent this problem since the interfacial pH at the cathode is sufficiently high at high current densities; thus, CO₂ is transported to the anode in the form of (bi)carbonate across the AEM.⁶ Moreover, KHCO₃ electrolyte disables the use of highly active NiFe-based catalysts for the OER. The carbonate formation (or carbon crossover) is unwanted since it reduces the chemical potential of hydroxide ions at the anode, which increases the required thermodynamic potential for oxygen evolution. This implies that the strong alkaline electrolyte should be either regenerated or disposed as waste. Therefore, the CO₂ crossover in AEM electrolyzers needs two additional processes to increase CO₂ conversion rate and long-term operation: (1) additional CO₂ needs to be captured as the CO₂ conversion rate is low, and (2) the alkalinity of the anolyte needs to be constantly restored to run the electrolyzer with long stability.

Figure 1.

Schematic illustration of (a) an AEM-based cell versus (b) one with a BPM. The BPM-based cell performs a water dissociation reaction at the internal interface of the BPM, of which the produced proton will be transported to the cathode and a hydroxide ion will be transported toward the anode. (c) Schematic of the electrochemical cell. CO₂ gas feed is presented on the left, where the CO₂ has to diffuse through the GDE in order to reach the cathode and can be converted into products (for example, CO), with hydrogen evolution reaction as a competing side reaction. The AEM-based cell will transport anions (e.g. CO₃^2–) toward the anode, where oxygen is generated.

The extent of the carbon crossover depends on the membrane properties. Although the new class of AEMs, like Sustainion⁷ or PiperION,⁸ are highly conductive and configurations with these membranes have proven to reach high partial current densities for making CO, these membranes are strong carbonate (CO₃^2–) conductors as well. The mass transfer coefficient of the carbonate species depends on the membrane affinity (e.g., cross-linking or type of fixed charges) and thickness, with the extreme case of having no membrane (i.e., only a GDE) where the carbon crossover is maximized.^9,10 Also, cation exchange membranes, like Nafion, neither provide a solution to the carbon crossover. These membranes strongly suffer from ion crossover (e.g., K⁺), leading to salt formation at the cathode catalyst and high hydrogen evolution rates.^11,12 While CEM-based MEA might potentially alleviate the indirect energy losses due to CO₂ crossover, the higher proton flux transporting to the cathode would result in hydrogen evolution dominating, as has been shown previously by Shafaque et al., where a low CO selectivity of 4.3% was achieved.¹³

The high carbon crossover can be prevented with the use of a bipolar membrane (BPM) as it consists of two membrane layers with opposite fixed charges. In between these layers is an interface layer where the water dissociation reaction (WDR) occurs (see Figure 1b). The reaction, H₂O → H⁺ + OH^–, maintains an alkaline environment around the anode as the hydroxide ions are migrated toward the anode. To drive this reaction, a thermodynamic potential of 0.83 V is required at standard conditions. Although, in theory, this required water dissociation potential can be gained back in the created chemical potential (i.e., a pH gradient), previous work has shown that this does not fully balance out,^14,15 presumably because the environment of the cathode is not at pH 0 while the environment of the WDR is.¹⁶ This leads to a higher cell potential, which has held back the use of bipolar membranes as serious competitors to be used in a CO₂ electrolyzer.

Having established that both AEM-based and BPM-based CO₂ reduction cells face limitations in cell voltage and crossover, a comparison of those systems on a single metric would help to assess their potential for practical applications. In this letter, we perform a study to compare those systems based on direct and indirect energy consumption. From an energy consumption point of view, we can weigh the loss of CO₂ and spent anolyte in an AEM-based MEA against the additional cell potential in a BPM-based MEA. Therefore, we studied two MEA systems for CO₂ to CO conversion, one with an AEM and one with a BPM, to quantify the direct and indirect energy required to produce CO and to determine whether the increase of potential in BPMs is justified as the CO₂ and OH^– loss is minimized.

Materials and Methods

All experiments were performed in a 5 cm² area membrane electrode assembly (MEA) having a serpentine flow channel on both the anode and cathode endplates (Dioxide Materials cell), as illustrated in Figure 1C. A Sigracet 38 BC gas diffusion layer (GDL) of 6.25 cm² area (2.5 cm × 2.5 cm) was used as the porous transport layer. An Ag catalyst layer was deposited on top of microporous layer of GDL by direct current magnetron sputtering to obtain a thickness of 100 nm. Nickel foam (3 cm × 3 cm, Recemat BV) was used as the anode. Ag GDE and Ni foam were combined with an oversized 16 cm² (4 cm × 4 cm) Sustainion anion exchange membrane (X37-50 Grade RT) to assemble the MEA.

Between the BPMEA and the anode, an anolyte (1 M KOH, volume of 60 mL) was flushed around (0.667 cm³ s^–1). In the anodic reservoir, a pH meter was inserted to continuously measure the OH^– concentration. Humidified CO₂ at an inlet flow rate of 40 sccm was used. The gas flow rate at the outlet of the reactor was measured using a mass flow meter (Bronkhorst) in order to estimate the Faradaic efficiency of the products accurately (see Figure S1 for a schematic of the setup), which was measured with a gas chromatograph (every 5 min injection). A constant current density of 100 or 300 mA/cm² was imposed at both cells. The total cell voltage was continuously monitored, as well as the anolyte pH and periodic gas compositions. The calculation of the obtained Faradaic efficiency is described in the Supporting Information (eq S1–S5).

Results and Discussion

To quantify the required energy for the production of CO, three contributions are considered: (1) electrical energy to operate the electrochemical cell, (2) energy to recover OH^– ions in the anolyte to maintain the chemical potential of the system, and (3) energy to capture or recover CO₂ that has crossed over from the inlet stream to the anolyte. To evaluate the energy performance, each contribution is expressed in kJ per mol produced CO, which means that the Faradaic efficiency is automatically taken into account.

To determine the energy to operate the electrochemical cell, constant current electrolysis experiments were performed in an MEA setup. In this setup, a GDE with Ag as catalyst was pressed on the AEM (Sustainion) with a Ni mesh as anode surrounded by 1 M KOH (see the SI for more details). The experiments were performed for two hours at 100 and 300 mA cm^–2. To compare its performance with a bipolar membrane, another series of experiments were performed with the same setup using a Fumatech BPM instead of the AEM. For further experimental details, see the SI.

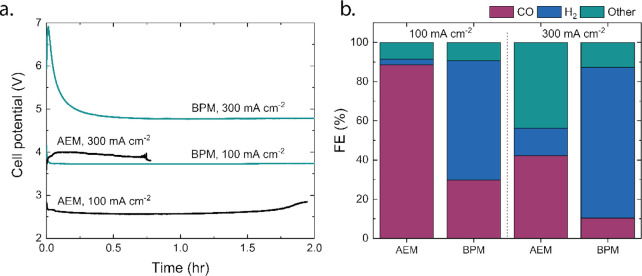
The classic comparison in both configurations focuses on the applied potential and the product distribution. In this case, the total cell potential for the AEM-based cell reaches a minimum of 2.6 V, while the BPM-based cell (3.7 V) requires more than 1 V extra to reach 100 mA cm^–2 (Figure 2a). The obtained products at the cathode depend on the membrane type (Figure 2b). The obtained Faradaic efficiency (FE) for CO is 88.5% (±0.3%) for CO with the AEM-based cell, with little H₂ produced (2.8% ± 0.1%). In the BPM-based cell, a FE of 31.5 (±1.7%) toward CO is achieved, with a H₂ production twice of the CO production (59.7% ± 1.2%). The small error margins reflect the virtually constant Faradaic efficiency over the measurement series of 2 h (see Figure S3). For both cases, similar values have been reported previously.⁹ Roughly 10% of the FE remains undetected in both cases. As Ag is known to produce formic acid at this current density, which ends up being decomposed at the anode, this could explain the undetected products.⁹ At 300 mA cm^–2, the total cell potential is 3.9 and 4.7 V while the FE to CO drops to 42 and 11% for AEM and BPM-based cells, respectively. In the AEM-based cell, more than 40% of the products are undetected and are ascribed again to, e.g., formic acid being decomposed, as reported in the literature before.⁹ In the BPM-based cells, the majority of the produced products is hydrogen as the BPM impedes the crossover of anionic products like formate.

Figure 2.

(a) Cell potential of MEA setup with AEM and BPM at 100 and 300 mA cm^–2. (b) Faradaic efficiency of MEA with AEM and BPM at 100 and 300 mA cm^–2, where “other” stands for carbon products that are liquid or decomposed at the anode.

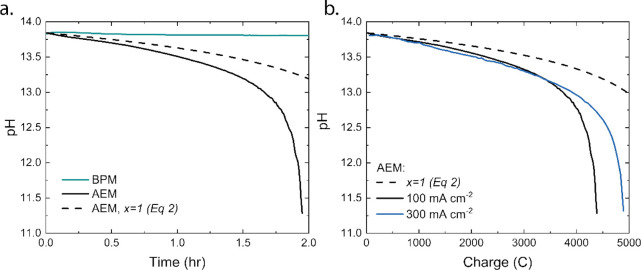
In this batch-type experiment of Figure 2a, the cell potential of the AEM-based cell is not stable over time. This is due to the change in pH of the anolyte (initially 60 mL of 1 M KOH) caused by the carbon (CO₃^2–) crossover. The pH drops in almost 2 h from 13.8 to 11.3 (Figure 3a) for the AEM-based cell at 100 mA cm^–2, after which the experiment was stopped to prevent degradation of the Ni mesh. After 1.75 h, a sudden jump is visible in the cell potential, indicating that the concentration of OH^– becomes too low to perform the OER from the OH^– pathway, and the reaction starts to shift to the pathway where H₂O serves as reactant. This requires a higher cell potential (as seen in Figure 2a).

Figure 3.

(a) pH of the anolyte in AEM- and BPM-based cells at 100 mA cm^–2, with the simulation-based pH for AEM if the consumed OH^– was sourced only from the CO₂ER and (b) the pH drop of the KOH anolyte of the AEM-based cell in function of the applied charge for 100 and 300 mA cm^–2 in comparison to the simulation-based pH (calculated based on x = 1, where pH is determined by the loss of OH^– molecules due to applied charge) if the consumed OH^– was sourced only from the CO₂ER.

This pH shift is caused by the consumption of OH^– at the anode (for the OER) as well as at the cathode (reacting with CO₂). Given the high alkaline environment at the cathode, carbonate is formed, which requires two hydroxide ions¹⁷ (eq 1).

1

These hydroxide ions can come from two sources: either from diffusion of OH^– from the electrolyte to the gas–liquid interface or via CO₂ER, where the produced OH^– is immediately converted with an additional CO₂ molecule. The latter process of combined CO₂ER and CO₂ scavenging can be described by eq 2, where x describes the ratio between dissolved and converted CO₂.

2

Here, x = 1 (when all and only the produced OH^– from the CO₂ER is used for CO₂ scavenging), 0 < x < 1 (for partial OH^– consumption), or x > 1 (when additional OH^– from the anolyte is used to scavenge CO₂). The net OH^– consumption in the latter case, for x > 1, is reflected in a negative OH^– production at the right side of the reaction, which is equivalent to (net) OH^– consumption at the left side.

With x, we can also define the CO₂ utilization efficiency that describes the ratio between the moles of CO₂ converted into CO (only product of interest for us) and the used moles of CO₂ (those converted to CO and those that cross over to the anolyte), with n being the amount of moles.

3

To differentiate between the mechanisms of OH^– consumption, the pH was calculated if only the OH^– production from the CO₂ER were to be consumed (i.e., x = 1; dashed line in Figure 3a). For that case, the pH for the AEM-based cell would not drop below 13.2 in this experiment, indicating that additional carbon crossover also occurs. A carbon balance was determined via the chemical equilibrium software VisualMINTEQ as presented in an earlier reported article,¹⁸ indicating that the total carbon concentration is 0.5 M at the end of the experiment, corresponding with an average molar flux of 2.5 mmol cm^–2 h^–1 (15% of the inlet CO₂ at 40 mL min^–1). If we look at the CO₂ utilization efficiency (see eq 3, with n_CO determined via the GC and n_crossover determined via the VisualMINTEQ results and the measured pH), we obtained 40%. This means that x = 1.5 in this case, and thus, 2.5 CO₂ molecules are required to produce 1 CO molecule. Further analysis on the OH^– source shows that 67% of the OH^– comes from the CO₂ER and the remaining part comes from the electrolyte. If the same experiment would be performed while keeping the anolyte pH constant (refreshing the anolyte continuously), the crossover is expected even higher as the CO₂ crossover rate (including (bi)carbonates) decreases over time in a batch-type reactor as the anolyte saturates.¹⁸

The pH of the anolyte of the AEM-based cell operated at 300 mA cm^–2 has a similar shape as the pH drop when operated at 100 mA cm^–2 (see Figure S2) but reaches the cutoff value already after 45 min. If the two curves are compared as a function of charge, we obtain a good agreement between the curves, indicating that the CO₂ crossover and, thus, the consumption of OH^– is rather independent of the current density (Figure 3b) and the corresponding Faradaic efficiency (Figure 2b). This implies a regime in which CO₂ scavenges all produced OH^– even at a current density of 300 mA cm^–2. The slightly earlier decrease in pH at 100 mA/cm² can be ascribed to the diffusion of uncharged species (H₂CO₃) at the cathode, which is less prominent for the 300 mA cm^–2 case as the experiment was roughly three times shorter.

Although the CO₂ crossover is even a bit slower for higher current density when normalizing on the transferred charge (Figure 3b), the crossover per produced mol of CO is significantly higher when operating at 300 mA cm^–2 because of the decreased FE. The contribution of formate (of which the majority is expected to decompose at the anode) will affect the pH similarly as for the CO₂ crossover itself, as the decomposed products will be converted into (bi)carbonate species and therefore be included in the crossover component. This together yields an increase to x = 3, which means 75% of the consumed CO₂ is dissolved in the anolyte (in this case 40% of the CO₂ inflow), and the CO₂ utilization efficiency is only 25%.

In the literature, little information can be found on x or CO₂ utilization efficiency. Larrazabal et al. describe a CO₂ utilization efficiency of 50 and 40% at 100 and 300 mA cm^–2. Thus, the respective x is then 1 and 1.5, which is in both cases lower than in our study (see for comparison Table S1) but demonstrating a similar trend as in our experiments that higher current densities reach a higher x. Weng et al. describe in a modeling study a CO₂ utilization efficiency of 35% at 100 mA cm^–2, resulting in an x of 2.¹⁹ This modeling study also shows that x decreases at higher current densities if the FE remains stable (which is not the case in the experimental cases). The comparison suggests that the exact value of x depends on the cell type (such as membrane thickness and type) or operational parameters (such as flow rates) and that all cases demonstrate CO₂ utilization efficiencies of ≤50% when using an AEM-based MEA.

The pH drop in the AEM-based cell is in stark contrast with the pH of the anolyte in the BPM-based cell, which remains practically stable throughout the experiment (Figure 3a). This indicates that barely any dissolved inorganic carbon is crossing over through the BPM. Recent literature has shown that, depending on the type of membrane and production method, some BPMs also suffer from CO₂ crossover.¹⁸

From the experimental data presented so far, the energy consumption to produce CO via CO₂ER was calculated. The first component, the direct energy consumption coming from the electrochemical cell E_electrolysis (in kJ/mol), was determined based on the cell voltage and Faradaic efficiency (eq 4)

4

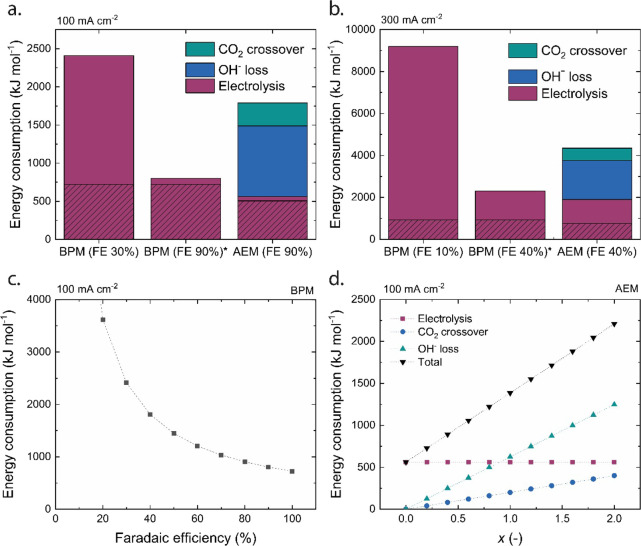
where n is the amount of electrons required for CO₂ER, F is the Faraday constant, U is the cell potential, and FE_CO is the Faradaic efficiency toward CO. In this calculation, the contribution of hydrogen (side reaction) or oxygen (anodic reaction) is ignored as CO is of main interest for this study. E_electrolysis is presented in the red bars in Figure 4, in which the red shaded portion indicates the energy required if the FE would be 100%.

Figure 4.

Energy consumption for the production of CO for BPM-based and AEM-based cells for MEA configurations operating at (a) 100 mA/cm² and (b) 300 mA/cm². The electrolysis component is separated into two parts; the shaded section is the minimal energy needed to produce CO at a FE of 100%. For comparison, the hypothetical energy consumption for a BPM electrolyzer is plotted at a similar FE as for the AEM-based cell at the respective current density. (c) Simulation of the total energy consumption of the BPM-based cell at 100 mA/cm² in function of the Faradaic efficiency toward CO (following eq 4). (d) Simulation of the distribution of the total energy consumption of the AEM-based cell at 100 mA/cm² in function of the ratio of dissolved vs converted carbonic species (x) assuming a FE of 90% toward CO.

The second component to the total energy consumption is due to the neutralization of OH^– by inorganic carbon, which implies the necessity of regenerating the OH^– solution to operate in a steady state. To regenerate these ions, the minimum required energy for this process is 0.83 eV per OH^– ion to drive the water dissociation reaction (eq 4 with U = 0.83 V). However, this value does not include Ohmic losses and energy losses at the electrode. Hong et al. (2014) report a value of 312 kJ mol^–1 OH^– for the industrial production of OH^– via electrolysis of sodium chloride.²⁰ To normalize that to the produced CO, one has to multiply this value with the ratio of consumed OH^– of the electrolyte and produced CO (3.0 mol OH^– per 1.0 mol CO), resulting in 928 kJ mol^–1 CO for regenerating OH^– in the 100 mA cm^–2 case. When operating at 300 mA cm^–2 these values are 5.9 mol OH^– per 1.0 mol CO, resulting in 1848 kJ mol^–1 CO.

The third component is the loss of dissolved CO₂, which implies the need for a larger supply of CO₂ feed. The energy consumption for capturing additional CO₂ depends on the process to capture and purify the CO₂. The state-of-the-art CO₂ capture via bipolar membrane electrodialysis requires at the moment around 200 kJ per mol CO_2.²¹ This value should then be converted to the amount of CO₂ that crosses over per mol of produced CO by multiplying with x, i.e., the ratio of dissolved CO₂ per converted CO₂ (which is the same as produced CO).

The total required (direct + indirect) energy is plotted in Figure 4a,b and differentiated for each component. For the BPM-based cell, only the direct energy consumption from the electrolysis cell contributes. As no carbon crossover occurs, there is no CO₂ loss. Additionally, at this current density, there is little (other) ion crossover, and the selectivity of the water dissociation reaction is nearly 100% (see Figure 3a), which allows us to neglect OH^– replenishment. The electrolysis component suffers in the BPM-based cell from the low FE toward CO (30 and 10% at 100 and 300 mA cm^–2), leading to high values per mol of CO. This is illustrated in Figure 4c, where a simulation is made for the total energy consumption in function of FE toward CO. The most sensitive lever to reduce the energy consumption in this BPM electrolyzer configuration is via increasing the FE, as the minimal required energy (at 100% Faradaic efficiency) for the production of CO in these conditions is 720 and 920 kJ mol^–1 at 100 and 300 mA cm^–2, respectively. This would require a BPM–catalyst interaction that is designed for this specific reaction and environment. Recent literature reports have shown promising results by inserting a buffering layer,^22,23 which prevents the formation of hydrogen. A more detailed discussion on improving the BPM–catalyst interaction can be found in a recent perspective.²⁴ At a current density of 300 mA cm^–2, the energy analysis is even more outspoken due to the low FEs for both the AEM and BPM-based cell caused by the catalyst–membrane interaction and CO₂ diffusion limitations at higher current densities.²⁵

In contrast, for the AEM case, the indirect energy consumption due to CO₂ crossover and OH^– regeneration exceeds the direct energy consumption for electrolysis in the AEM electrolyzer. The simulation of the energy consumption in function of the ratio of dissolved versus converted carbonic species (x) shows that if x > 0.7, the indirect components exceed the direct ones (Figure 4d). The impact of the CO₂ and, more importantly, OH^– loss reduces the energy efficiency of the AEM-based cell with 68% at 100 mA cm^–2 when x = 1.5. For every mol of CO produced, 1.5 mol of CO₂ diffused into the electrolyte, which neutralized 3 mol of OH^–. Reducing these indirect energy losses in AEM electrolyzers is not straightforward. AEMs that conduct preferentially hydroxide ions may prevent excessive carbon crossover, although it may compromise the membrane conductivity as (bi)carbonate is formed anyway at the cathode interface. In a more quantitative fashion, we can assess what improvements are required for the BPM-based electrolyzer to better the total energy consumption of the AEM electrolyzer. If the FE of the BPM-based cell would be 42% for the 100 mA cm^–2 case, the total energy required for the production of CO would be already similar as the (direct + indirect) energy needed in the AEM-based cell (at an FE of 90%). Similarly, the gain in the AEM-based cell if the FE were further increased up to 100% would only lead to just a 5% reduction in energy consumption. When the Faradaic efficiency is equal in both cases (FE 90%; Figure 4a), the BPM-based cell is favored due to the minimized CO₂ crossover (i.e., stable electrolyte and absence of indirect energy losses) despite its higher voltage in the electrolysis cell. This means that with a BPM-based cell, significant performance gains can be achieved for CO₂ER. With this comparison between two ion-exchange membranes, there is more than ever a need for new BPM configurations with a focus on the cathode–membrane interface.

Conclusions

In this study, the energy consumption required to electrochemically produce CO from CO₂ was investigated in a membrane electrode assembly with either an anion-exchange membrane or bipolar membrane. To fairly address the indirect energy losses due to inorganic carbon crossover, anolyte degradation, and side reactions such as hydrogen evolution, we propose to benchmark CO₂ conversion systems including the indirect energy consumption for CO₂ replenishment and anolyte purification. Although the direct cell voltage required for this operation was lower for the anion exchange membrane, the CO₂ loss to OH^– and the consequent drop in anolyte pH resulted in poor stability of AEM when operated for 2 h. In contrast, the MEA operated with a bipolar membrane showed a steady cell potential and no drop in anolyte pH over time, indicating its relevance in minimizing the carbon crossover to the anode. For the present state-of-the-art BPMs, the poor product selectivity of CO at 100 mA cm^–2 for the BPM cell (30%, against 90% for the AEM-based cell) brings the total (direct + indirect) energy consumption for BPM-based cells higher than that of AEM-based cells. However, the total energy required for the BPM would be lower than that of the AEM if it produces CO with more than 42% FE, leveraging its advantage in minimizing the CO₂ losses to electrolyte and increasing the CO₂ utilization rate. Hence, future work on BPM-based cells should be directed to increase Faradaic efficiencies, e.g., via adding a buffer layer on the cathode to minimize the hydrogen evolution and maximize CO production in a BPM-operated MEA configuration.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.1c16513.

• Electrochemical setup, pH for electrochemical experiments at 300 mA/cm², literature comparison, calculation of Faradaic efficiency, and outlet flow rate measurements (PDF)

The authors declare no competing financial interest.