Energy vs Charge Transfer in Manganese-Doped Lead Halide Perovskites

Abstract

Mn-doped lead halide perovskites exhibit long-lived dopant luminescence and enhanced host excitonic quantum yield. The contention between energy and charge transfer in sensitizing dopant luminescence in Mn-doped perovskites is investigated by state-of-the-art DFT calculations on APbX₃ perovskites (X = Cl, Br, and I). We quantitatively simulate the electronic structure of Mn-doped perovskites in various charge and spin states, providing a structural/mechanistic analysis of Mn sensitization as a function of the perovskite composition. Our analysis supports both energy- and charge-transfer mechanisms, with the latter probably preferred in Mn:CsPbCl₃ due to small energy barriers and avoidance of spin and orbital restrictions. An essential factor determining the dopant luminescence quantum yield in the case of charge transfer is the energetics of intermediate oxidized species, while bandgap resonance can well explain energy transfer. Both aspects are mediated by perovskite host band edge energetics, which is tuned in turn by the nature of the halide X.

Doping semiconductors by transition metal ions has been widely proved to impart specific optical and magnetic properties to the semiconducting host. In particular, Mn²⁺ doping has been successfully implemented in binary semiconductor nanocrystals (NCs), such as CdSe, ZnS, ZnSe, and ZnO, with a direct impact on their stability and optoelectronic properties.¹⁻³ As an example, doping CdSe NCs by Mn²⁺ substantially increases the excitonic photoluminescence (PL) lifetime. Another behavior which is also typically observed is the appearance of two PL features, i.e., the excitonic CdSe band at ∼2.4 eV and the typical ⁴T₁→⁶A₁ ligand field transition of the Mn²⁺ ion at ∼2 eV.⁴ Of technological relevance for optoelectronics and biomedical applications, the dopant emission is usually confined to a narrow energy range; thus, a variable Stokes shift can be realized by playing with both the size and the composition of the NC host. Furthermore, incorporation of manganese ions into the crystal lattice imparts magnetic properties to the host, clearly manifested at cryogenic temperatures.^5,6

Metal halide perovskites (MHPs) are a game-changer class of materials in photovoltaics and optoelectronics.⁷⁻¹⁶ Besides their success in solar cells, perovskite NCs have shown outstanding optical properties in light-emitting diodes, with near unity emission quantum yield and wide color tuning.¹⁷⁻²⁴ To further diversify the emission color gamut of MHP NCs, Mn²⁺ doping has been successfully implemented.^5,25,26 Mn doping can be introduced in variable concentrations, covering a range up to ∼10%.^5,25−31 Previous studies indicate incorporation of the transition metal in the bulk of the material rather than on the NC surface, with the transition metal located in a lead substitutional position within an octahedral coordination environment.^25,29,31,32

Similar to what is observed in binary semiconductors, in MHPs a dual-color emission from the perovskite host exciton is observed, along with a broad Mn²⁺ (⁴T₁→⁶A₁) ligand field transition. The PL decay of the Mn emission is single exponential with a ∼ms lifetime,^{27,30,32−34} and it is moderately tunable by playing with the dopant content, varying from the yellow–orange region (2.14 eV) to the orange–red one (1.98 eV).^5,33,35,36 Mn doping was also reported to enhance the MHP band gap PL quantum yield.^{13,25,28,30,25,31,37−43} The possible mechanism behind the dopant-induced PL quantum yield increase has been ascribed in some cases to dopant-to-material back transfer, although a plausible explanation is also defect passivation, e.g., Mn→Pb vacancy filling,⁴⁴ which coherently suppresses material degradation and progressively stabilizes the host’s cohesive energy.⁴⁵

Most notably, the Mn²⁺ luminescence quantum yield in perovskite NCs is strongly halide-dependent, with lead bromide perovskites showing a significantly less intense emission intensity compared to their lead chloride counterpart, while, to our knowledge, Mn²⁺ luminescence is not detected in lead iodide perovskites.^{37−40,5,25,41−43} This peculiar behavior raises questions about the interplay between dopant and host electronic energy levels and how this would affect the population of dopant states from initially populated host states. It is generally accepted that population of the ⁴T₁ excited Mn²⁺ state occurs through energy transfer from the host exciton to the Mn dopant. In this framework, Liu et al. proposed that the more intense Mn²⁺ luminescence of lead chloride perovskites, compared to lead bromide and lead iodide compounds, can be ascribed to the progressively less resonant band gap of the perovskite host with the ligand field dopant transition.⁵ Pinchetti et al. pointed out the presence of a dopant sensitization process in CsPbCl₃ occurring via an intermediate step which involves a long-lived shallow trap state mediating excitation of the Mn²⁺ center by the host band-edge excitons.³⁰ Consistent with the proposed mechanism, an activation energy of ∼0.3 eV was measured for the sensitization process. Sun et al. confirmed the presence of an activation barrier for Mn²⁺ luminescence, though these authors found a smaller barrier of ∼0.1 eV.²⁹ A similar effect was also detected by Zeng et al., with Mn²⁺ luminescence quantum yield decreasing with temperature.⁴⁶

Despite available information, the nature of the mechanism responsible for the possible sensitization of the excited manganese ⁴T₁ state remains elusive. Temperature-dependent Raman spectroscopy performed by Pradeep et al. on Mn:CsPb(Cl/Br)₃ shows a progressive sharpening of the 132 cm^–1 Pb–Br stretching phonon mode with increasing temperature, which is strongly coupled to Mn dopant modes.⁴¹ The presence of a transient Mn³⁺ species in Mn²⁺-doped II–IV semiconducting NCs was proposed by Gahlot et al.⁴⁷ The presence of Mn³⁺ in perovskite samples was also invoked to rationalize the ferromagnetic coupling in MAPb_1–xMn_xI₃, proposed to arise from Mn²⁺–I^––Mn³⁺ motifs.⁴⁸ Very recently, Babu et al. revealed the formation of a transient charge-transfer state in Mn:CsPbBr₃, suggesting that a spin-allowed charge-transfer process (concurrent to energy transfer) related to Mn³⁺ formation is likely to occur.⁴⁹

Motivated by the huge interest in Mn-doped MHPs and by the puzzling mechanism of Mn²⁺ sensitization, we here explore the structural and electronic properties of Mn-doped APbX₃ perovskites (X = Cl, Br, and I) by state-of-the-art first-principles modeling studies based on hybrid density functional theory (DFT) and spin–orbit coupling (SOC) on fairly large perovskite models, Figure 1a. We accurately simulate the alignment of host/dopant energy levels in both Mn²⁺ and Mn³⁺ states considering different electronic and spin states and the associated structural rearrangement. Based on this data we provide an in-depth analysis on both the possible energy- and charge-transfer processes in Mn:APbX₃ perovskites, highlighting points in favor of the former or the latter. In the framework of a hole (h) charge transfer to Mn²⁺ in CsPbCl₃, we found a thermally activated mechanism with a barrier in fair agreement with that reported by Pinchetti et al.³⁰ This suggests the same mechanism to be a major pathway in lead chloride perovskites, proposing Mn itself as a shallow trap mediating the sensitization of ⁴T₁, later decaying to ⁶A₁. We finally investigate the charge transfer/energy transfer dependency on different halides, extending our study to lead bromide and lead iodide perovskites.

Figure 1.

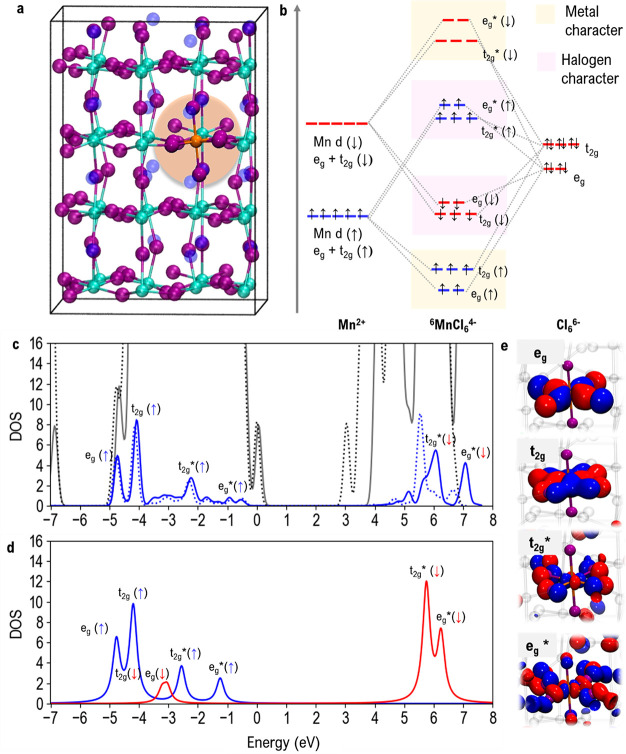
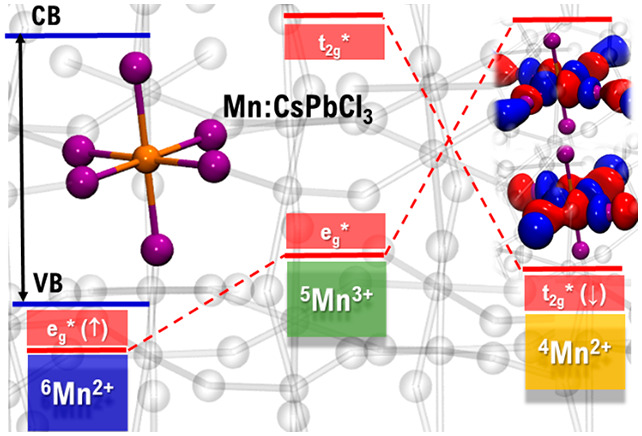
(a) Tetragonal 2×2×2 supercell (32 formula units) employed to model Mn:CsPbCl₃. Orange, Mn; purple, Cl; cyan, Pb; and blue, Cs atoms. (b) Qualitative molecular orbital scheme for the complex with spin (↑) (blue) and spin (↓) (red) manifolds. (c) Total (gray) and manganese (blue) density of states (DOS) of ⁶Mn²⁺:CsPbCl₃ computed at the PBE0 and PBE0-SOC levels (solid and dashed lines, respectively), with Mn molecular orbitals labeled. (d) Aligned manganese DOS for the ⁶MnCl₆^4– model complex. (e) Isodensity plots of representative ⁶Mn²⁺:CsPbCl₃ spin α single-particle states with e_g, t_2g, t_2g*, and e_g* character.

We model three key states of Mn-doped APbX₃ perovskites. While the perovskite host has an even number of electrons, paired to form a singlet ground state, Mn doping introduces additional d-states of the dopant which can give rise to different electronic patterns, namely the sextet ground state of the Mn²⁺ ion with five Mn d-unpaired electrons (⁶A₁, t_2g³e_g², hereafter ⁶Mn²⁺), the quartet excited state (⁴T₁, t_2g⁴e_g¹, hereafter ⁴Mn²⁺) obtained by pairing two electrons from the high-spin sextet, and an oxidized state obtained by removing an electron from the sextet ground state, formally corresponding to a Mn³⁺ ion with a quintet ground state (t_2g³e_g¹, hereafter ⁵Mn³⁺), which may account for hole trapping at the Mn²⁺ site.

We immediately face an issue with the coherent description of the electronic structure of the perovskite host—which requires the inclusion of SOC—and the interest in various local Mn spin multiplet states, which are not purely defined in the presence of SOC. In addition, we need to combine SOC with a hybrid functional, such as PBE0,^50,51 for a correct description of the perovskite band edge energies and band gap. At the same time, a hybrid functional is required to correctly describe the energetics of the dopant d-shell orbitals and the structural relaxation associated with the various local Mn spin states.⁵² As a practical solution, by taking Mn:CsPbCl₃ as a benchmark, we first calculate the electronic structure at the PBE0-SOC level, which provides results in quantitative agreement with the experiment (e.g., a host band gap of 3.04 eV, Figure 1c).⁵³ Based on this analysis, we notice that unoccupied Mn states lie sufficiently above the host conduction band (CB) edge (>2 eV) that they are less likely to intrude in the gap when neglecting SOC (SOC basically downshifts the host CB states by ∼1 eV, while its effect on the valence band (VB) is negligible in this case, Figure 1c). We thus confidently employ PBE0 with no SOC for structural optimizations and for electronic structure analysis, checking the impact of SOC in selected cases.

The local electronic structure of ⁶Mn²⁺:CsPbCl₃ shares many analogies with that typical of octahedral transition metal complexes with π-donor ligands,⁵⁴ as schematized in Figure 1b, where a qualitative molecular orbital diagram for a ⁶MnCl₆^4– model complex is reported. In the octahedral symmetry (O_h), the Mn d orbitals labeled as e_g (d_x²–y², d_z²) and t_2g (d_xy, d_xz, d_yz), Figure 1b, interact with the halogen orbitals of the same symmetry, generating bonding molecular orbitals, i.e., t_2g and e_g, and antibonding ones, i.e., t_2g* and e_g*, Figure 1e. The molecular orbitals with spins α and β are shown separately, referred to as (↑) and (↓) respectively, Figure 1b. The Mn contributions to the density of states (DOS) of Figure 1c for ⁶Mn²⁺:CsPbCl₃ can be classified by comparison with the ones of ⁶MnCl₆^4– in Figure 1d as following: e_g (↑) orbitals at ∼ –4.77 eV below the VB maximum, which are originated from the σ bonding interaction between the Mn d_x²–y², d_z² and Cl p orbitals, followed at ∼ –4.13 eV by t_2g (↑) orbitals, which originate from the π bonding interaction between the Mn d_xy, d_xz, d_yz and Cl p orbitals. Corresponding antibonding interactions can be found at ∼  −2.29 eV (t_2g* (↑) orbitals) and at ∼ –0.70 eV (e_g* (↑) states). Antibonding e_g* and t_2g* unoccupied (↓) states are found 1.63 eV above the SOC-calculated CB edge, Figure 1c. Notice that, in agreement with the model complex (Figure 1b–d), while the α bonding combinations show a predominant Mn character, α antibonding states have more halide character. The computed energy of occupied Mn (↑) 3d levels with respect to the material band edges appears in good accordance with that found for typical Mn-doped binary semiconductors like Cd_1–xMn_xTe. The 3d⁵ levels of Mn(II)-doped Cd_1–xMn_xTe are empirically located at 9.7 eV vs vacuum; thus, for a given work function (Wf, eV), subtract the Wf from 9.7 eV to find the binding energy (BE) of the Mn(II) levels below the Fermi level.^55,56 In our case, with an experimental VB for CsPbCl₃ located at −5.82 eV.⁵⁷ we can expect the Mn levels to be 3–4 eV below the VB, in line with the calculated position of the t_2g (↑) and e_g (↑) states.

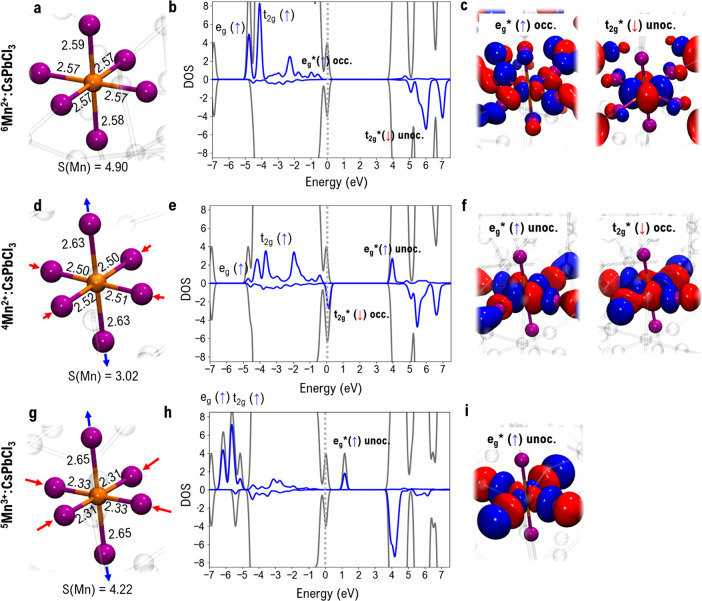
The ⁶Mn²⁺:CsPbCl₃ ground state has an almost symmetric Mn–ligand coordination environment, Figure 2a, with average Mn–Cl distances of 2.57 Å, in good agreement with previous results reported by Ma et al.⁵⁸ Significant structural differences in the MnCl₆ coordination sphere are calculated for ⁴Mn²⁺:CsPbCl₃ and ⁵Mn³⁺:CsPbCl₃, Figure 2d–g, with compression (elongation) along the equatorial (axial) bond distances in ⁴Mn²⁺, Figure 2d, and average distances of 2.51 Å (2.63 Å). These structural differences can be understood in terms of the variation in the electronic structure associated with the different spin/charge states. ⁴Mn²⁺:CsPbCl₃ is originated from ⁶Mn²⁺:CsPbCl₃ by promotion of an electron from an e_g* (↑) to an unoccupied t_2g* (↓) state, initially lying within the perovskite host CB, Figure 2e,f. Although the octahedral symmetry is not retained, we continue to use octahedral labels for simplicity rather than D_4h labels; see Figure S1 in the Supporting Information.

Figure 2.

Structural properties, DOSs with Mn contributions, and key orbitals involved in spin/charge transitions for Mn:CsPbCl₃. (a) ⁶Mn²⁺:CsPbCl₃ first coordination sphere with distances in Å and spin moments from Mulliken population analysis. Orange spheres represent Mn atoms, purple ones chloride atoms; species outside the Mn first coordination shell are transparent. (b) Total (gray) and manganese (blue) DOS (with negative/positive spin differentiation) for ⁶Mn²⁺:CsPbCl₃ computed at the PBE0 level of theory, with Mn active molecular orbitals labeled. The dashed vertical bar represents the Fermi level. (c) Isodensity plots of orbitals involved in spin/charge transitions for occupied e_g* (↑) and unoccupied t_2g* (↓) single-particle states of ⁶Mn²⁺:CsPbCl₃. (d) ⁴Mn²⁺:CsPbCl₃ first coordination sphere. (e) Total (gray) and manganese (blue) DOS for ⁴Mn²⁺:CsPbCl₃. (f) Isodensity plot of orbitals involved in spin/charge transitions for unoccupied e_g* (↑)and occupied t_2g* (↓) single-particle states of ⁴Mn²⁺:CsPbCl₃. (g) ⁵Mn³⁺:CsPbCl₃ first coordination sphere. (h) Total (gray) and manganese (blue) DOS for ⁵Mn³⁺:CsPbCl₃. (i) Isodensity plot of orbitals involved in spin/charge transitions for unoccupied e_g* (↑) single-particle state of ⁵Mn³⁺:CsPbCl₃.

The PBE0-calculated energy difference between the optimized ⁴Mn²⁺ and ⁶Mn²⁺ structures is 2.05 eV, in excellent agreement with the ⁴T₁→⁶A₁ PL recorded experimentally.^{5,25,30,34,59,60} A value of 1.48 eV was calculated by using the non-hybrid PBE functional, confirming the importance of the use of a hybrid functional for a quantitative assessment of Mn²⁺ electronic state energetics (see the related section in the Supporting Information to look for further GGA-hybrid comparative data).^52,61−63 The charge hole left on the e_g*(↑) state in ⁴Mn²⁺:CsPbCl₃ is largely destabilized, now lying 0.01 eV above the CB, while the occupied t_2g*(↓) state is strongly stabilized, now lying 0.13 eV above the VB; compare the DOS for the two states in Figure 2b–e and Figure S2 in the Supporting Information for additional analyses. A significant orbital reorganization occurs in parallel for e_g (↑) and t_2g (↑) states, whose density significantly decreases in ⁴Mn²⁺:CsPbCl₃ compared to that in ⁶Mn²⁺:CsPbCl₃, Figure 2b–e.

Upon removing one electron from the ⁶Mn²⁺:CsPbCl₃ ground state, we find two structural minima with different energies and electronic structures; see Figure 2g and Figure S3a in the Supporting Information. The most stable oxidized species has a geometry similar to that of ⁶Mn²⁺:CsPbCl₃, and inspection of the DOS (Figure S3b, Supporting Information) shows that it indeed corresponds to removal of one electron from the perovskite host VB, leading to a [⁶Mn²⁺/h⁺:CsPbCl₃] electronic structure; i.e., the host rather than the dopant is oxidized. A secondary minimum corresponding to manganese oxidation, ⁵Mn³⁺:CsPbCl₃, is calculated 0.18 eV above [⁶Mn²⁺/h⁺:CsPbCl₃], which shows a significant equatorial compression (average Mn–Cl distance of 2.31 Å), Figure 2g, due to the typical Jahn–Teller effect of ⁵Mn³⁺ ions in weak ligand fields. The electronic structure of the ⁵Mn³⁺:CsPbCl₃ DOS is reported in Figure 2h,i, which clearly shows hole localization in the e_g* state, along with energy relaxation of bonding manganese states by ∼1.5 eV due to the increased manganese effective charge. It is interesting to notice that the [⁶Mn²⁺/h⁺:CsPbCl₃] and ⁵Mn³⁺:CsPbCl₃ minima are connected by an energy barrier of 0.33 eV, Figure 3, as determined by a linear transit calculation. On overall, while in ⁴Mn²⁺:CsPbCl₃ a significant orbital reorganization occurs compared to ⁶Mn²⁺:CsPbCl₃, in ⁵Mn³⁺:CsPbCl₃ the distribution of t_2g (↑)(↓) and e_g (↑)(↓) states is almost unaltered, except for the aforementioned energy shift, Figure 2h. This behavior parallels what was found for the model complexes ⁴MnCl₆^4– and ⁵MnCl₆^3– (Figure S1, Supporting Information).

Figure 3.

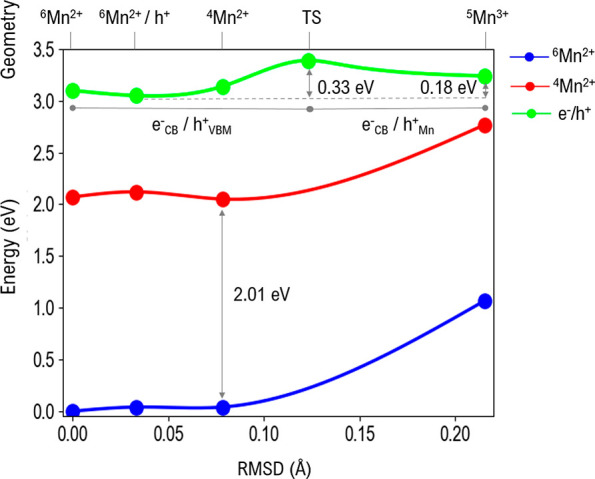
Configurational energy diagram of Mn:CsPbCl₃. The energies of the sextet state (blue dots/lines), quartet state (red dots/lines), and electron/hole pair (green dots) are plotted against the root-mean-square deviation (RMSD) of the MnCl₆ moiety in the perovskite. The reference is set as the sextet ground state. Larger values of RMSD correspond to MnCl₆ equatorial bond compression and axial bond elongation.

In Figure 3 we propose a global spin/charge configurational diagram for Mn-doped CsPbCl₃, with the three involved potential energy surfaces, i.e., ⁶Mn²⁺, ⁴Mn²⁺, and that obtained upon band gap excitation, lying 3.04 eV above the ground state. In this latter case we aim at describing the formation of an electron/hole pair, where the electron is delocalized into a host CB state, while the hole can be either VB-delocalized, as in [⁶Mn²⁺/h⁺:CsPbCl₃], or trapped by manganese in ⁵Mn³⁺:CsPbCl₃.

The potential energy surface of the three considered states is almost flat for low root-mean-square deviation (RMSD) values of MnCl₆ (i.e., small structural distortions from the sextet ground-state geometry), while the total energy significantly increases when the Mn–Cl equatorial distances are compressed, moving to the ⁵Mn³⁺:CsPbCl₃ minimum region, Figure 3. While the energies of the ⁶Mn²⁺:CsPbCl₃ and ⁴Mn²⁺:CsPbCl₃ states increase, that of the ⁵Mn³⁺:CsPbCl₃ state goes through a transition state (TS) (0.33 eV above the [⁶Mn²⁺/h⁺:CsPbCl₃] minimum) and then reaches a local minimum corresponding to hole trapping at the Mn center, which we calculate to be 0.18 eV higher than [⁶Mn²⁺/h⁺:CsPbCl₃], Figure 3.

Upon band gap excitation of the CsPbCl₃ perovskite host, there are two possible decay pathways involving the dopant:

• (i)energy transfer from the host to the excited ⁴Mn²⁺:CsPbCl₃ state;
• (ii)hole trapping to form ⁵Mn³⁺:CsPbCl₃, followed by non-radiative decay to ⁴Mn²⁺:CsPbCl₃.

While the decay channel (i) requires negligible structural deformation, similar to band gap recombination, pathway (ii) requires overcoming an energy barrier associated with hole trapping with significant structural deformation. Previous literature typically ascribed population of the ⁴Mn²⁺ state to pathway (i), i.e., band gap exciton to manganese dopant energy transfer. A factor in favor of this mechanism is the small required structural rearrangement. An experimental finding which is also a point in favor of energy transfer is the mono-exponential Mn luminescence decay, suggesting the absence of intermediates.²⁷ The different local Mn spin states could, however, hinder such a process; as a matter of fact, the direct ⁶T₁→⁴T₁ excitation has a negligible cross section due to the spin-forbidden nature of this process. Also, the significant orbital reorganization associated with the inner manganese shell discussed above could further inhibit such a process. Pathway (ii) requires a significant structural reorganization but no spin restriction, as ⁵Mn³⁺:CsPbCl₃ can accept one electron in the t_2g* state to form ⁴Mn²⁺:CsPbCl₃, keeping the e_g* orbital unoccupied. This mechanism of manganese ⁴T₁ sensitization is associated with a calculated activation barrier of 0.33 eV, corresponding to the evolution of the transient ⁵Mn³⁺ species, which is in good agreement with the activation energy measured by Pinchetti et al.³⁰ and consistent with the behavior of Mn:ZnSe NCs reported by Gahlot et al.⁴⁷ The shallow trap in our case is represented by hole trapping at ⁵Mn³⁺:CsPbCl₃. Coherently, Pradeep et al. reported temperature-dependent Raman spectra with sharpening of the 132 cm^–1 peak (Mn/Pb–Br stretching mode) on Mn:CsPb(Cl/Br)₃ NCs at temperatures >173 K, consistent with the occurrence of a significant Jahn–Teller distortion related to Mn oxidation.⁴¹

Since both energy- and charge-transfer processes are strongly dependent on the dopant/host relative energy levels, energetic overlap variations in the perovskite composition, in particular in terms of the halide nature, could afford significantly different electronic structures with different associated decay channels. To evaluate the electronic and structural changes occurring in different halide perovskites, we carried out a comparative study on CsPbCl₃ and MAPbBr₃/MAPbI₃. The impact of A-site cations on the electronic structure is minimal; as a matter of fact, the ⁴T₁→⁶A₁ Mn luminescence is still observed,⁶⁴ so we used pre-existing models for the bromide and iodide perovskites. Structural analyses indicate a progressive Mn–X bond increase with the series Mn–Cl ∼ 2.57 Å > Mn–Br ∼ 2.74 Å > Mn–I ∼ 2.98 Å, Table 1, in line with the increasing ionic radii trend.

Table 1. Averaged Mn–X Axial (d_Mn-X(ax)) and Equatorial (d_Mn-X(eq)) Distances (Å), Mn Spin from Mulliken Population Analysis (e), Band Gaps (ΔE_gap, V), and ⁴T₁→⁶A₁ Spin Gaps (ΔE⁴ T₁/⁶A₁, eV).

CsPbCl3
	ΔEgap = 3.03		ΔE4T1/6A1 = 2.05
	dMn-X(ax)	dMn-X(eq)	Mn spin
6Mn2+	2.58	2.57	4.90
4Mn2+	2.63	2.51	3.02
6Mn2+/h+	2.59	2.56	4.90
TS	2.64	2.42	4.74
5Mn3+	2.65	2.32	4.22

MAPbBr3
	ΔEgap = 2.34		ΔE4T1/6A1 = 2.04
	dMn-X(ax)	dMn-X(eq)	Mn spin
6Mn2+	2.77	2.72	4.92
4Mn2+	2.83	2.65	3.07
6Mn2+/h+	2.77	2.73	4.92
TS	2.83	2.56	4.62
5Mn3+	2.85	2.52	4.48

MAPbI3
	ΔEgap = 1.80		ΔE4T1/6A1 = 1.99
	dMn-X(ax)	dMn-X(eq)	Mn spin
6Mn2+	3.04	2.95	4.92
4Mn2+	3.09	2.89	3.15
6Mn2+/h+	3.04	2.95	4.92
5Mn3+	3.09	2.72	4.59

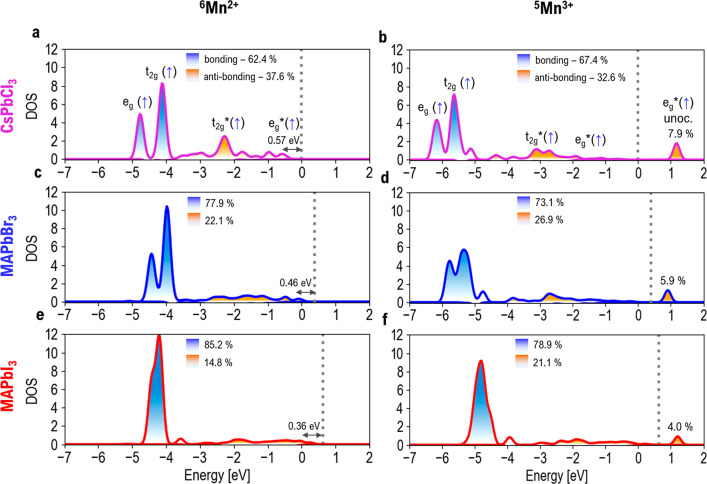
We notice that our calculations retrieve the experimental trend of VB rising and band gap closing observed for the Cl → Br → I series, while the electronic structure of the Mn-doped systems is qualitatively similar along the halide series, although quantitative differences are found in the distribution of the bonding/antibonding states. Figure 4, panels a, c, and e, clearly show that the Mn–Cl bonding states, i.e., e_g and t_2g, contain progressively smaller halide contributions when moving from Cl to I, in line with ⁶MnX₆^4– models (Figure S4, Supporting Information). This could be ascribed to the reduced covalency in the Mn–X bond and to the reduced ligand field strength. The inner manganese states become harder because of the combined less covalent character of the chemical bond and weaker ligand field provided by the halides according to the I^– < Br^– < Cl^– trend.

Figure 4.

Manganese DOS contribution in ⁶Mn²⁺ and ⁵Mn³⁺ electronic states for Mn-doped CsPbCl₃, MAPbBr₃, and MAPbI₃ perovskites. The manganese–halide bonding (antibonding) states are highlighted in blue (orange), and the percentage weight of each region compared to the total is also reported. The VB of CsPbCl₃ is set to zero, while the energies of Mn-doped MAPbBr₃ and MAPbI₃ perovskites are aligned to that of Mn-doped CsPbCl₃. The dashed lines represent the aligned VB edges.

In line with results on CsPbCl₃, in the bromide and iodide perovskites, the ⁴Mn²⁺ structures present a slight equatorial compression and axial expansion; see Table 1. The energy of the quartet ⁴T₁ vs ⁶A₁ is ∼2 eV for the three perovskites, irrespective of the nature of the halide. These values well agree with the emission detected experimentally,^5,41,65 confirming the insensitivity of the Mn-dopant emission energy to the host chemical structure. A significantly higher energy state is found in the case of Mn:MAPbI₃, characterized by a Mn spin moment of 1.12 (see results in the Supporting Information), related to the reduced covalency and ligand strength of the Mn–X bond.

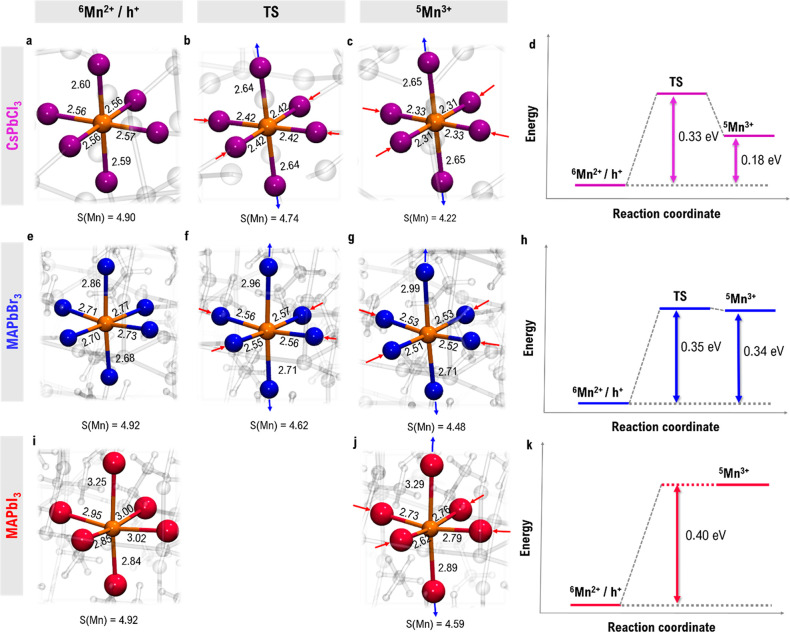
Similar to what has already been discussed for CsPbCl₃, when a positive charge is allocated to the lead bromide or lead iodide perovskites, a global minimum is found where the perovskite host VB is oxidized, followed by a higher energy local minimum where Mn is oxidized, with subsequent equatorial (axial) compression (elongation), Figure 5g–j. In the case of bromide, the ⁵Mn³⁺ minimum is 0.34 eV above the ⁶Mn²⁺/h⁺ state, and it can be reached by overcoming a barrier of 0.35 eV, while in the case of the iodide, ⁵Mn³⁺ minimum is 0.40 eV above ⁶Mn²⁺/h⁺, Figure 5h–k.

Figure 5.

Mn coordination spheres and energy features of key species along the route of Mn oxidation in the quintet spin state: ⁶Mn²⁺/h⁺ with a free hole delocalized in the material VB, the transition state (TS) connecting ⁶Mn²⁺/h⁺ to ⁵Mn³⁺, and ⁵Mn³⁺ corresponding to the oxidized manganese. Mn spin moments are reported along with octahedron distances in Å. Orange spheres represent manganese atoms, purple ones chloride atoms, blue ones bromide atoms, and red ones iodide atoms; species outside the Mn first coordination shell are transparent.

The energy difference between ⁵Mn³⁺ and ⁶Mn²⁺/h⁺ increases when moving from Cl (0.18 eV) to Br (0.34 eV) and I (0.40 eV), highlighting a progressive thermodynamical destabilization of the oxidized form, although their kinetic barriers are similar. Considering the energy-transfer process of pathway (i), we should expect, as proposed by Liu et al.,⁵ to observe a band-gap-dependent Mn-dopant luminescence. Basically, to observe Mn PL, the host band gap should be larger than ∼2.0 eV, i.e., the energy of the (⁴T₁→⁶A₁) ligand field transition. The charge-transfer pathway (ii) is instead modulated by the different thermodynamic stability of the oxidized forms and the corresponding kinetic barriers, Figure 5. We predict that formation of ⁵Mn³⁺ requires similar activation energies in the three materials, which should induce a similar PL quantum yield temperature trend for the three halides. The reduced stability of ⁵Mn³⁺ in the order Cl > Br > I, however, indicates that the concentration of dopant luminescent centers is significantly reduced in the latter two cases, progressively hindering the dopant PL quantum yield.

To sum up, our accurate theoretical analysis has allowed us to quantify the dopant/host alignment of energy levels for a series of manganese-doped lead halide perovskites, identifying the key factors responsible for energy- vs charge-transfer population of the ⁴Mn²⁺ excited state. Our analysis supports both energy-transfer and charge-transfer mechanisms, with the latter probably preferred in Mn:CsPbCl₃ due to avoidance of spin and orbital restrictions, though requiring a significant structural modification at the dopant site. Also in favor of a charge-transfer mechanism in this case is the calculated activation energy for manganese sensitization, agreeing with experimental data for the ⁴T₁→⁶A₁ luminescence. The reported quantitative comparison of the electronic structure of different halide perovskites may well rationalize the progressive disappearance of dopant luminescence on the basis of both energy-transfer and charge-transfer mechanisms. For the latter we found that an essential factor in determining the Mn quantum yield, in addition to the host band gap/Mn ⁴T₁→⁶A₁ resonance, is provided by the thermodynamics/kinetics of ⁵Mn³⁺ formation. The kinetics is similar, and this predicts PL temperature trends analogous to those of to Mn:CsPbCl₃, but the Mn oxidized species is thermodynamically more stable in chloride than in bromide or iodide perovskites, implying a reduced concentration of Mn chromocenters in the latter two systems.

Computational Details

Mn-doped perovskites CsPbCl₃, MAPbBr₃, and MAPbI₃ were modeled in the 2×2×2 supercell of tetragonal APbX₃. The dopant Mn was disposed in a substitutional position, in place of the metal lead, assuming a doping concentration of 3.12%. Equilibrium structures were found by relaxing ion positions in the supercell defects by using the PBE0 functional and fixing cell parameters to the experimental values: for CsPbCl₃, a = b = 15.811 Å, c = 22.520 Å; for MAPbBr₃, a = b = 16.690 Å, c = 23.604 Å; and for MAPbI₃, a = b = 17.711 Å, c = 25.320 Å.^66,67 Hybrid functional PBE0 calculations were performed by using the CP2K code,^68,69 keeping the fraction of Fock exchange α at its original value (0.25). Calculations were carried out with Goedecker–Teter–Hutter pseudopotentials, six double-ζ polarized basis sets for the wave functions, and a cutoff of 500 Ry for the expansion of the electron density in plane waves.⁷⁰ We used the auxiliary density matrix method with the cFIT auxiliary basis set to speed up the hybrid functional calculations. To simulate the different spin properties of our systems, the calculations were all performed with the local spin density (LSD) approximation by fixing the spin multiplicity to the respective value, i.e., 6 for ⁶Mn²⁺:APbX₃, 4 for ⁴Mn²⁺:APbX₃, and 5 for ⁵Mn³⁺:APbX₃ and ⁶Mn²⁺+h⁺:APbX₃. The atomic Mn spin moments of the minima were calculated by employing the Mulliken population analysis.⁷¹

Additional PBE0-SOC calculations for ⁶Mn²⁺:CsPbCl₃/MAPbBr₃/MAPbI₃ were performed by means of single points on the PBE0 structures using a PBE0 hybrid functional^50,51 together with SOC corrections.⁷² Norm-conserving pseudopotentials were used with a cutoff on the wave function of 40 Ry and a cutoff on the Fock grid of 80 Ry, sampling at the Γ point of the Brillouin zone. The fraction of exact exchange was kept to its original value of α = 0.25. To this aim we used the Quantum Espresso package.⁷³

To compare energy values of positively charged systems, such as ⁵Mn³⁺ and ⁶Mn²⁺+h⁺, to those of the neutral ground state, we computed the respective redox level (0/+),⁴⁴ making use of the Freysoldt approach for the finite size correction.⁷⁴

The alignment of valence bands and Mn levels for different halides perovskites in Figure 4 was achieved using the tridimensional averaged Hartree potential.

Comparative molecular calculations on the model complexes MnX₆^4–/MnX₆^3– were carried out by employing the Amsterdam Density Functional program (ADF) using the PBE0 functional,⁵⁰ a Slater-type triple-zeta basis set augmented with two polarization functions (TZ2P), and a scalar Zero Order Regular Approximation to the Dirac Equation (ZORA) Hamiltonian.^75,76 Molecular orbital diagrams were constructed through the symmetrized fragment orbital approach by dividing the complex in two fragments, i.e., Mn²⁺/Mn³⁺ and 6Cl^–. We applied octahedral (O_h) molecular symmetry for ⁶MnX₆^4– and tetragonally distorted (D_4h) symmetry for ⁴MnX₆^4– and ⁵MnX₆^3–.⁷⁵

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsenergylett.1c00553.

• Structures, DOS, and orbitals of Mn:APbX₃ and MnX₄^– (PDF)

The authors declare no competing financial interest.