An explanatory machine learning framework for studying pandemics: The case of COVID-19 emergency department readmissions

Abstract

One of the major challenges that confront medical experts during a pandemic is the time required to identify and validate the risk factors of the novel disease and to develop an effective treatment protocol. Traditionally, this process involves numerous clinical trials that may take up to several years, during which strict preventive measures must be in place to control the outbreak and reduce the deaths. Advanced data analytics techniques, however, can be leveraged to guide and speed up this process. In this study, we combine evolutionary search algorithms, deep learning, and advanced model interpretation methods to develop a holistic exploratory-predictive-explanatory machine learning framework that can assist clinical decision-makers in reacting to the challenges of a pandemic in a timely manner. The proposed framework is showcased in studying emergency department (ED) readmissions of COVID-19 patients using ED visits from a real-world electronic health records database. After an exploratory feature selection phase using genetic algorithm, we develop and train a deep artificial neural network to predict early (i.e., 7-day) readmissions (AUC = 0.883). Lastly, a SHAP model is formulated to estimate additive Shapley values (i.e., importance scores) of the features and to interpret the magnitude and direction of their effects. The findings are mostly in line with those reported by lengthy and expensive clinical trial studies.

1. Introduction

Hospital readmission bears significance in both institutional quality and cost of care [1]. Prediction of rehospitalization enables early intervention, which is crucial to preventing more serious or life-threatening events [2]. Readmissions also comprise a significant portion of total medical expenses [3]. Recent studies show that as much as 27% of hospital readmissions are potentially preventable [4], costing Medicare alone $26 billion annually [5]. In recent years, and especially after the initiative by the U.S. Centers for Medicare and Medicaid Services (CMS) that penalizes hospitals for avoidable readmissions, readmission rates have increasingly been used as a quality benchmark for assessment of hospitals and health systems in certain contexts [6]. According to a former director of CMS' quality measurement and health assessment group, early rehospitalizations are mainly driven by “defects in care, medication errors, failure to plan for necessary equipment, and shortcomings in the preparation of the patient and family for his or her care outside of the hospital” [7].

While cost and quality of care have been the main drivers of interest among scholars in hospital readmissions, the recent global COVID-19 pandemic has revealed a lesser-known problem of healthcare that can be aggravated by high hospital readmission rates: The unusual decision many doctors and healthcare providers had to make to prioritize intensive care unit (ICU) facilities for patients with higher chances of survival [[8], [9], [10]]. A similar situation holds in the emergency department (ED), where physicians have to prioritize patients with higher risks of developing complications to be hospitalized and discharge low- to moderate-risk patients. This poses another perspective to the study of hospital and ED readmissions: To determine the principal factors that lead to readmissions among patients of novel viruses (including SARS-CoV-2) to minimize the ethical and professional burden on hospitals and doctors. Such an endeavor is crucial for two reasons. First, when a pandemic is caused by a novel pathogen, our understanding of the disease's primary readmission risk factors is minimal or anecdotal. Second, even though we learn more about these risk factors as the number of affected citizens increases, we need to establish a reliable framework to identify the risk factors as early as possible such that the adverse effects of hospital readmissions can be minimized in an ongoing or a future pandemic. This study seeks to tackle these concomitant problems. Specifically, we use artificial intelligence (AI) and data analytics to implement a clinical decision support system (DSS) to predict readmission and to discover the prominent factors among COVID-19 patients.

Our study aims to make two main contributions. From the methodological perspective, we use evolutionary algorithms, deep artificial neural networks (DNN), and eXplanatory Artificial Intelligence (XAI) to develop a hybrid data analytics (i.e., an exploratory/predictive/explanatory) framework. This framework can be used to accelerate the development of clinical DSS, which in turn facilitates the process of understanding novel diseases. To evaluate the proposed framework from a practical perspective, we identify the risk of readmission in early COVID-19 patients using their electronic health records. Particularly, we aim at providing the practitioners with a tool to gain insight about novel diseases within a reasonable time frame (as opposed to running lengthy clinical trials) and to enable them to adjust their treatment protocols accordingly. While a large number of studies have been published on the COVID-19 pandemic, we argue that a majority of those studies have mainly focused on only one of the aspects incorporated in our proposed framework (i.e., either exploration, prediction, or explanation). Specifically, explanatory studies on COVID-19 have mostly relied on lengthy clinical trials that used limited samples, and therefore, led to hardly generalizable results. The Shapley Additive exPlanations (SHAP) approach employed in our proposed framework, however, not only provides more generalizable insights at the aggregate (population) level, but also enables the practitioners to analyze the specific risk factors that are associated with each individual subject.

We organize the remainder of the manuscript into four sections. In the following section, we review the recent work on the use of data analytics for the analysis and identification of risk factors that lead to ED or hospital readmissions. Next, we describe our data processing and data engineering steps. Subsequently, we propose our framework and evaluate it by building a clinical DSS to predict hospital readmissions in COVID-19 patients where the related data is obtained from Cerner's HealthFacts data warehouse. Finally, we discuss our findings and conclude the manuscript with a summary of our contributions and avenues for future research.

2. Prior work

Two approaches have generally been used to predict hospital readmissions. In real-time models, predictors are available on or shortly after the index hospitalization, whereas in retrospective studies, features used to predict rehospitalization are mostly known after the patient is discharged [11]. Since most electronic medical records (EMR) aggregate data on various aspects of hospital encounters, including variables on administration, demographics, visit, laboratory, medication, and discharge processes, models built using such data are considered to belong to the retrospective category [12].

Various retrospective studies in the literature have tried to predict hospital readmissions; however, a majority of them do not divide the data into training and validation sets for an objective evaluation and/or do not evaluate the prediction models using appropriate assessment metrics. As a result, these studies have a descriptive perspective rather than a predictive focus [13]. Logistic regression and survival analysis have been the most common modeling methods in these descriptive studies [14]. A smaller number of studies have adopted the predictive approach and used machine learning techniques for the prediction of hospital readmissions.

While predictive analytics approaches have been widely used for studying hospital readmissions, ED readmission studies have primarily focused on determining explanatory variables instead of building predictive models. Nevertheless, it would be especially important for the emergency clinicians to identify particularly high-risk patients who may not only come back in a more critical state, but also may die even before returning to the hospital. Obermeyer et al. [15] examined Medicare claims from 2007 to 2012 and found that among patients discharged from the ED, 0.12% died within seven days, representing 10,093 cases per year nationally. Gunnarsdottir and Rafnsson [16], who found a mortality rate of 208.5 per 100,000 ED visits within eight days after discharge, attribute this rate to a misjudgment of patients' conditions at the time of discharge. Another study asserts that 3-day ED readmissions account for around 30% of unexpected intensive care unit (ICU) admissions [17].

Table 1 provides a summary of the relevant predictive studies on ED and hospital readmissions.

Table 1.

Predictive studies on hospital and ED readmissions.

Study	Readmission facility	Disease(s)a	Sample size (patients)	Period	Best performing method	Metric	Value
[68]	Hospital	COPD	106	30 days	Random Forest	AUC	0.720
[69]	Hospital	Multiple	92,530	30 days	LASSO & SVM	AUC	0.680
[70]	Hospital	PN COPD CHF AMI THA/TKA	40,442 31,457 25,941 29,060 23,128	30 days	Deep Neural Network (DNN)	AUC	0.734 0.711 0.676 0.649 0.638
[71]	Hospital	HF AMI PN	4210 2379 2825	30 days	SVM	AUC	0.660 0.650 0.630
[72]	Hospital	CHF	1641	30 days	PSO-SVM	Accuracy Sensitivity Specificity	0.784 0.973 0.086
[73]	Hospital	Multiple	64,912	3 days 7 days 15 days 30 days	Ensemble	AUC	0.666 0.681 0.700 0.720
[74]	Hospital	CHF	4840	30 days	CHAID Decision Tree	AUC	0.707
[75]	Hospital	Diabetes	Not Given	30 days	Recurrent NN	AUC	0.800
[76]	Hospital	Multiple	32,718	30 days	DNN	AUC	0.780
[77]	Hospital	Multiple	304,888	30 days	Ensemble	AUC	0.771
[78]	Hospital	Lupus	9457	30 days	DNN	AUC	0.700
[2]	Hospital	Multiple	700	30 days	DNN	AUC	0.730
[12]	Hospital	CHF COPD	32,350 31,070	30 days	Random Forest	AUC	0.742 0.754
[79]	Hospital	COPD	111,992	30 days	Gradient Boosting Tree	AUC	0.653
[80]	Hospital	Multiple	38,597	30 days	DNN	AUC	0.714
[81]	ED	Multiple	279,611	30 days	Decision Tree	Accuracy Sensitivity AUC	0.772 0.402 0.732
[82]	ED	Multiple	330,631	3 days	Gradient Boosting	Sensitivity Precision AUC	0.16 0.75 0.76
[83]	ED	Multiple	120,000	3 days	DNN	Accuracy Sensitivity AUC	0.680 0.679 0.755
[48]	ED	Multiple	290,000	3 days	Ensemble	Accuracy AUC	0.957 0.610

*AUC stands for Area Under the (Receiver Operating Characteristic) Curve.

^aCOPD: Chronic Obstructive Pulmonary Disease; PN: Pneumonia; CHF: Congestive Heart Failure; AMI: Acute Myocardial Infarction; THA/TKA: Total Hip/Knee Arthroplasty.

A review of the studies listed in Table 1 reveals three major gaps. First, all of these studies focus on known, chronic conditions, and therefore, their main focus is on improving the performance of the predictive models through a combination of novel modeling techniques and more effective data engineering processes. COVID-19, however, is an acute condition for which the identification of the risk factors and their significance is as equally important as the prediction accuracy. In other words, the descriptive and prescriptive components of the analytical models are as critical as their predictive angle. Second, most of the extant work in the literature focuses on 30-day readmission of patients; however, early readmissions (i.e., 7-day) are better indicators of quality of care [18] and are more likely to be preventable and amenable to hospital-based interventions [19]. Prediction of early readmissions is especially important for hospitals dealing with COVID-19 patients because it can inform clinical practice, discharge disposition decisions, and health care planning to ensure the availability of resources needed for acute and follow-up care of discharged patients [20]. Third, ED readmissions are relatively understudied from a predictive analytics point of view. Since prior research argues that a considerable fraction of ED discharges each year leads to death or early readmission of critically ill patients, COVID-19 patients are expected to be at a higher risk due to the novelty and less-known nature of the disease. Our goal in this research effort is to address these three gaps for COVID-19 patients simultaneously.

Our attempt is guided by the existing descriptive studies on COVID-19 rehospitalizations. Recent studies on hospital readmissions that are related to COVID-19 have identified various risk factors. While these studies differ on sample characteristics - such as size and geographic location – they point out certain factors as common risk factors for hospital readmission among COVID-19 patients. For instance, certain underlying diseases such as diabetes, COPD, diseases of the genitourinary system (e.g., chronic kidney disease), hypertension, cancer, and liver diseases, as well as older age (typically higher than 65) are found to be more common among those who were re-hospitalized due to post-discharge COVID-19 complications. Table 2 provides a summary of these studies. We draw on these findings to guide our data preprocessing and feature selection in the following section.

Table 2.

Risk factors for readmission among COVID-19 patients.

Study	Location	Sample size	Readmission rate	Risk factors
[84]	USA	279	6.8%	Comorbidity (hypertension, diabetes, COPD, liver disease, cancer, substance abuse)
[85]	South Korea	7590	4.5%	Gender (men), age, medical aid subscription, comorbidity, chest radiographs, computed tomography (CT) scans, HIV antivirals
[20]	USA	106,543	9%	Discharge disposition, age, comorbidity (COPD, CHF, diabetes, chronic kidney disease, obesity)
[86]	Spain	1368	4.4%	Weakened immune system, having fever within 48 h prior to discharge
[87]	Turkey	154	7.1%	Malignant tumor, Hypertension
[88]	USA	1775	19.9%	Age

*AUC stands for Area Under the (Receiver Operating Characteristic) Curve.

3. Methods and materials

3.1. Data

Emergency department (ED) visits recorded in the “Cerner Health Facts” data warehouse between November 30, 2019 (around the date when the first signs of the novel virus were noticed in China), and June 9, 2020, were used. We excluded visits by non-adult (< 18 years of age) patients. The resulting raw data set contained 27,215 visits made by 22,963 unique patients. We further refined our data set by only keeping those patients who tested positive for COVID-19 in at least one of their visits to the ED. For this group of patients, we retained the first visit with a positive test, as well as all their following visits (i.e., 6620 unique patients who made 7373 ED visits). We excluded other patients and all their visits from the data set.

In the next step, we performed one-hot encoding for every comorbidity/symptom diagnosed in at least 50 patients during their visits (based on the ICD-10 coding system). This resulted in 729 binary variables where each variable represented the existence of one of the comorbid conditions in a patient. Similarly, 1487 unique medications (each being taken by at least 50 patients) were identified and one-hot encoded. Additionally, patients' demographic and visit-specific information (i.e., age, gender, race, admission type, and payer type) were included for further analyses.

Finally, we derived a binary response variable indicating whether each visit was followed by another one (by the same patient) within a period of 7 days (i.e., response = 1) or not (i.e., response = 0). Our records showed that 1358 out of 7373 (18.4%) COVID-19 related visits were followed by another visit within 7 days of discharge. This rate is far away from the 3–4% average rate for 7-day readmission to the emergency department reported in the literature [21,22] but is partly anticipated due to the novelty and mysterious nature of COVID-19 (at the time of visits). Table 3 shows the demographics of the final data set.

Table 3.

Summary statistics of the patients.

Variable	Average (std dev) / proportion
Age	45.81 (17.03)
Race	White 39.8% Black 28.3% Latino 19.7% Other 12.2%
Gender	Male 53.1% Female 46.7% Other 0.02%

3.2. Methodology

3.2.1. Feature selection

Since very little is known about the mechanism and confounders of the novel coronavirus disease, we chose to employ an exploratory approach to select comorbidity/symptom and medication features that affected the likelihood of post-COVID 7-day ED readmissions. Even though we employed a fully exploratory approach and did not make the algorithm to include any specific feature in the final feature set, we made sure that the relevant risk factors already identified in the literature (see Table 2) are present in the initial feature set (even if they did not meet the minimum frequency threshold of 50 instances).

A forward feature selection genetic algorithm (GA) was developed to refine the feature set. GA is a heuristic, evolutionary-based random-search approach that mimics the process of natural selection. It begins by the random generation of a large number (i.e., population) of feasible solutions (i.e., chromosomes). Each solution will then be scored using a fitness function that quantifies the desirability of the solution. The fittest solutions from each generation will then mate (a.k.a., crossover) to produce offspring of the next generation. The process of reproducing new generations continues until the algorithm converges in terms of the fitness of the top solutions.

We developed a GA with a population size of 1000 solutions in each iteration (i.e., generation). Each solution in the initial population involved a random set including 200 to 220 features from the 2221 features contained in the initial data set (i.e., around 10%). In each iteration, using the selected set of features for that iteration, we trained a basic Random Forest (RF) model1 with 80% of the data and tested the model on the remaining 20%. The Area Under the Receiver Operating Characteristic curve (AUC) of the trained RF model was used as the fitness function to identify the top feature set in each generation. We chose AUC as the fitness function since this measure indicates the distinctive power of each feature set in distinguishing visits that lead to readmissions from those that do not. A tournament selection strategy was defined for the algorithm such that at the end of each iteration, it keeps 30% top solutions, discards 30% worst solutions, and generates new solutions by performing crossover among the top 30% (with a crossover rate of 20%). Also, a 5% mutation rate was considered to prevent the algorithm from getting stuck in a limited area of the solution space. A maximum of 100 generations was set for the algorithm, with the possibility of an early stop in case of no AUC improvement in 10 consecutive generations.

In the end, the selected set of features associated with the highest AUC was retained to be used for further training and eventual testing of the predictive models.

3.2.2. Predictive modeling

A fully-connected multilayer perceptron (MLP) deep artificial neural network - a representation learning method [23] - was employed for building the predictive model. In addition to finding the mapping from features to the output, which is done by classic machine learning (ML) methods, representation learning techniques operate by learning and discovering the data features as well [24]. In other words, a deep network, through multiple hidden layers incorporated in its architecture, first derives complex features from simple concepts and then maps those advanced features to the output.

Regarding the network elements (i.e., weight functions, transfer functions, etc.), MLP networks (a.k.a., deep feedforward networks) are the most similar type of deep networks to the typical neural network models used in classic ML [24]. They are called feedforward because no feedback connections (i.e., feeding outputs of a perceptron back to it as input) are allowed for the signals in their architecture [23,25]. A fully-connected (a.k.a., dense) MLP is one in which every unit (perceptron) from a layer is connected to all units from the preceding and succeeding layers. While MLP networks, technically, have no limitation in terms of the number of input features, incorporating more features requires providing the network with a large number of instances for decent training. Otherwise, the model may either not converge at all or overfit the training data quickly and perform poorly in classifying new, unseen cases. That is why we began with an exploratory feature selection approach to reduce the dimensionality by around 90%, yet trying to retain the most distinctive subset of features.

An MLP network with four hidden dense layers was developed to train the predictive model. The model (Fig. 1 ) involves a total of 89,793 trainable parameters (i.e., connection weights).

Fig. 1.

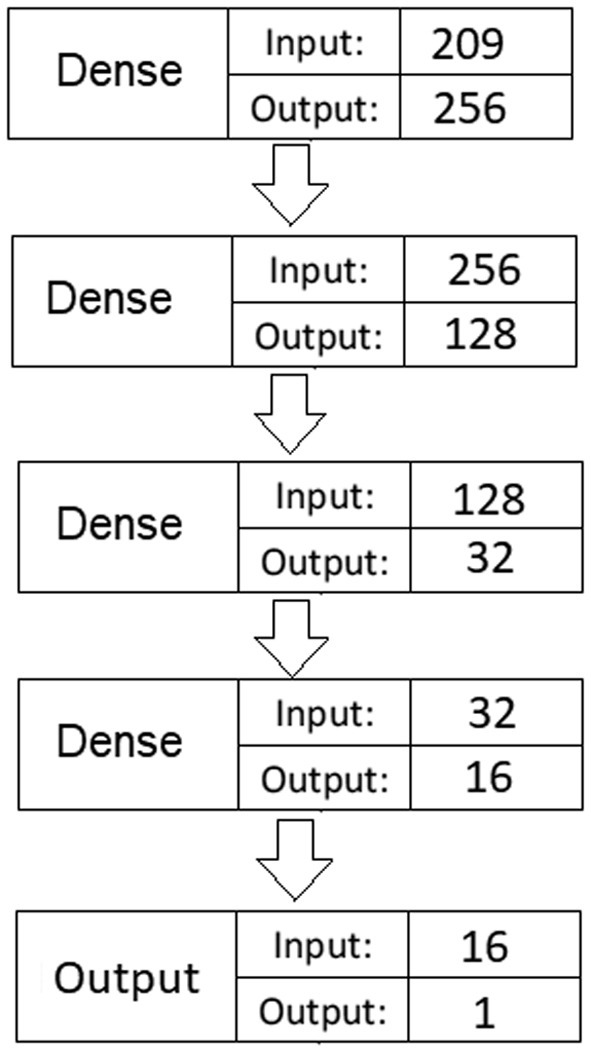
Deep fully-connected MLP network architecture.

For each hidden dense layer, we used Rectified Linear Units (ReLU) as the activation (transfer) function. ReLU is shown to be highly efficient with deep learning (DL) applications since, unlike other common functions (e.g., linear or hyperbolic tangent), it does not suffer from the vanishing gradient problem [26]. This problem occurs in the gradient descent optimization process when the derivation of the transfer function for a given input becomes very small through the backpropagation of error. As a result, the weights of such inputs will not be updated during the training process. The literature suggests that He’s initialization schema [27] is the best parameter initialization method for hidden layers that involve the ReLU activation function [28] as it maintains the variance of weights high and compensates for the amount of variance decreased as a result of applying ReLU. Additionally, given the binary nature of the response variable, a sigmoid transfer function was used for the output layer.

Regarding the relatively large number of parameters compared to the available instances for training the model, there were fairly high odds of overfitting the model to the training data and poor generalizability. To address that issue, we used a combination of three strategies suggested in the literature: learning rate decay, L1 regularization, and L2 regularization.

The learning rate decay strategy simply reduces the learning rate (i.e., the proportion of error that backpropagates through the network to tune up weights) after each epoch. This leads to faster convergence of the network weights at the beginning and then gradually slows down their changes as the model output becomes closer to the real value of the response variable. Otherwise, the weight optimization algorithm would quickly use all noises to tune up the weights and would create a model that would perfectly predict the outcome for all instances in the training data (i.e., overfitting). Various methods have been proposed for scheduling the decay, such as the exponential schedule [29,30], step-based schedule [31], and non-monotonic schedule [32] to obtain the best training performance in complex DL applications, such as image analysis or voice recognition. However, since our MLP network has a relatively simple architecture (compared with convolutional or recurrent neural networks, which are used for more complex tasks), we employed a simple linear decay schedule with a fixed decay rate per each epoch to avoid any additional parameterization.

L1 and L2 regularization strategies each add a penalty term to the loss function of the weight optimization algorithm. Specifically, L1 regularization adds a proportion of the sum of absolute network weights to the loss function, while L2 regularization adds a proportion2 of the sum of squared network weights to that function. Generally speaking, they both prevent the algorithm from assigning large weights to any feature during the learning process, as large weights make the network unstable and result in large differences in the output by small changes in the input features [33]. This is particularly important when the trained model sees new data with somewhat different values for the features weighted heavily, leading to poor performance in predicting their outcomes. More technically speaking, L1 regularization (a.k.a., Lasso regression) encourages sparsity by making the weights to be zero when possible. Hence, it can be thought of as a feature selection approach that removes less important features by encouraging their weights (i.e., contribution) in calculating the outcome to be zero. L2 regularization (a.k.a., Ridge regression), on the other hand, is a more nuanced approach that encourages small weights for features by pushing them towards zero, but not necessarily making them be zero. For a more detailed discussion on DL regularization methods, see Goodfellow et al. [34].

Practical DL guidelines suggest using both L1 and L2 regularizations simultaneously to make a balance between the sparsity offered by L1 and the nuance offered by L2. Following these guidelines, we took advantage of both methods in training our network.

3.2.2.1. Cost-sensitive learning

Given the imbalanced nature of our data set (i.e., containing less than 20% positive cases) and the majority class's high degree of bias, using regular classification procedures did not yield acceptable per-class accuracy results. To address the data imbalance issue, several approaches are suggested in the literature, such as under- and over-sampling. Under-sampling generally leads to losing some information and may not be a good option in cases where the data is severely imbalanced, as is the case in the current study. Also, popular over-sampling approaches, such as SMOTE [35], typically require the majority of features to be continuous variables to perform well with minimum bias; hence, they are deemed improper choices for our data.

Another approach to address the data imbalance issue is to employ a cost-sensitive learning approach [36,37]. This approach is essentially designed for classification problems in which catching a specific outcome correctly by the algorithm involves a much higher financial cost/benefit than incorrectly predicting the opposite outcome. As such, a higher cost is assigned to instances of the more important class in the data to make the algorithm produce a smaller number of false predictions for that class (i.e., the minority class). Similarly, for an imbalanced classification problem, we may give a higher weight to the minority class instances in the loss function to compensate for the bias caused by different class proportions. Although several methods are suggested for calculating weights for different classes, we used a simplistic approach by assuming an equal cost for false negative and false positive predictions. That is, given the 1000:226 ratio of negative and positive instances in the data, we used the cost matrix shown in Table 4 to customize the classification algorithm's loss function.

Table 4.

Classification cost function weights.

	Actual negative	Actual positive
Predict negative	0	1
Predict positive	0.226	0

3.2.2.2. Optimization of hyperparameters

One of the challenges in working with deep networks is numerous hyperparameters that must be specified by the user. These include the network architecture hyperparameters (such as number of layers, number of neurons in each layer, and activation functions) and training hyperparameters (such as the optimizer algorithm, learning rate and its decay rate, batch size, number of epochs, loss function, and the regularization weights). A specific choice for each of these factors may work differently when combined with different values of other hyperparameters in the training phase of the network, and sometimes, slight changes can easily lead to over- or under-fitting of the predictive model. Hence, choosing a good combination of values for the hyperparameters is itself seen as a standalone optimization problem. To address this issue, a variety of approaches have been proposed in the literature, such as grid search [38], random search [39], Gaussian process [40], and sequential model-based optimization [41], just to name a few.

For this study, we employed a grid search approach to optimize the training hyperparameters (i.e., learning rate and its decay, batch size, epochs, and optimizer method), while keeping the network architecture hyperparameters fixed. We purposely did not consider varying every hyperparameter to keep the number of permutations in a reasonable range. This allowed the grid search to be completed in a reasonable time given the technical computing limitations. The specific grid search settings are elaborated in the Results Section.

3.2.3. Model interpretation

Machine learning techniques in general, and artificial neural networks in particular, have long been known as “black box” approaches with decent predictive power, but little to no interpretability. In recent years, however, there has been a surge of studies proposing various approaches, such as LIME [42], DeepLIFT [43], and Layer-Wise Relevance Propagation [44], to improve the interpretability aspect of ML.3 Most of these methods aim at estimating the classic Shapley regression values [45] (i.e., feature importance for linear models in the presence of multicollinearity) for complex ML models using cooperative game theory equations [46]. Assuming each feature value of a given instance as a “player” and the prediction for that instance as the “payout” in a game, Shapley values determine how to fairly divide the payout among the features.

Lundberg and Lee [46] propose an intuitive approach called SHaply Additive exPlanations (SHAP) to interpret complex predictive models, such as ensemble and deep learning models. SHAP combines the classic Shapley values approach with a couple of other agnostic methods (including LIME and DeepLIFT) and assigns each feature in the model an additive importance score. The importance score for each feature represents the change in the expected model prediction when conditioning on that feature.

To calculate the importance score of any given instance i of feature X (i.e., X(i)), the SHAP approach considers all feature subsets (not including X itself), then computes the effect on predictions (i.e., deviation from the average of all predictions) of adding X(i) to all those subsets. Essentially, one important difference between SHAP and the classic Shapley values approach is the “local accuracy” property involved in SHAP, which enables it to explain every instance of a factor in the data by calculating a single marginal contribution for that instance, whereas Shapley values just assign an importance score to the whole factor (and not to each instance of data) [46]. As a result, using SHAP we have an additive set of marginal contributions for each instance whose aggregation yields the prediction for that instance. Hence, in the specific context of this study, each patient's readmission probability (prediction) can be explained in terms of the additive marginal contributions of her corresponding health factors. Also, the overall importance score of each factor is simply the average of its marginal contributions across all instances (i.e., all patients in our context).

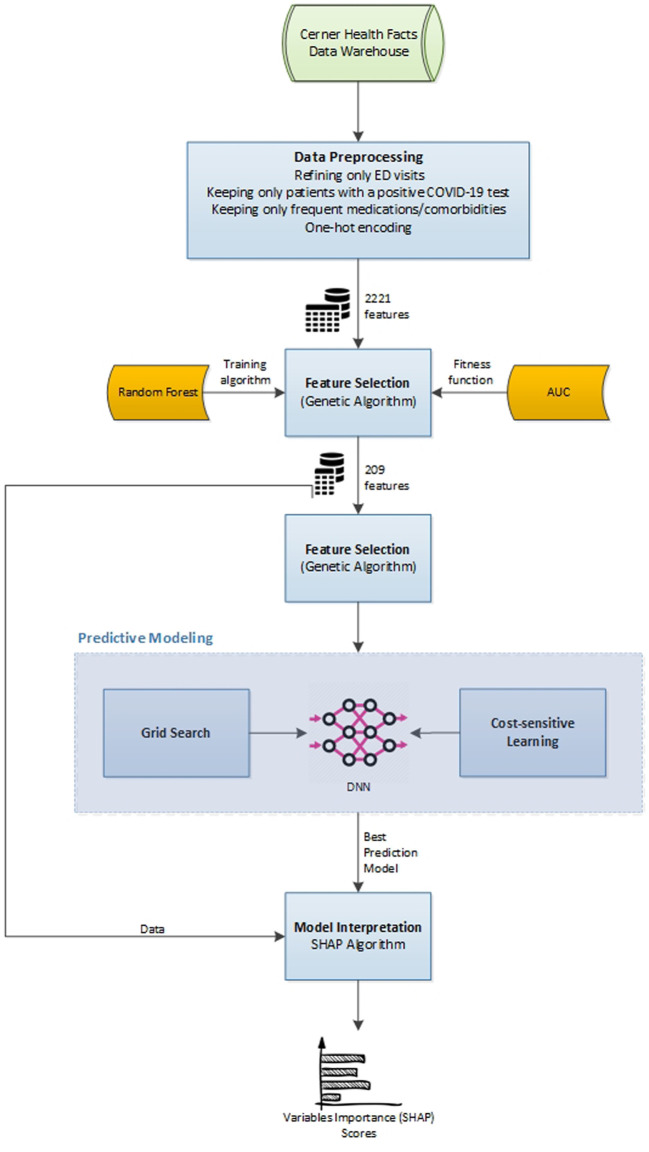
In the last stage of our proposed framework, and after developing a predictive model (stage 2) using the optimally selected features (stage 1), we employed SHAP to interpret the complex DL model we trained and to identify the major factors that contributed to one's readmission to the ED within a week after discharge. Fig. 2 summarizes our proposed framework.

Fig. 2.

Summary of the proposed framework.

4. Results

4.1. Feature selection

We ran the GA model on a computer with i9 2.90 GHz 8 Core processing power and a 64GB memory. The model converged after 42 generations, which took around 36 h of processing.4 The optimized feature set involved a total of 209 variables and the basic random forest model trained by those features had an AUC of 0.812 (accuracy: 0.79; sensitivity: 0.61; F1-score: 0.54). From the selected features, 81 were comorbidity/symptom-related, 123 were medication indicator variables, and the remaining 5 were all the demographic features existing in the original data.

4.2. Prediction model

In this study, while holding the hyperparameters of the network architecture fixed (i.e., the number of hidden layers, the number of neurons, and activation functions), we employed a grid search approach to optimize the training hyperparameters such that they would work best with the selected network architecture and would minimize the weighted binary cross-entropy loss function. Table 5 indicates the values used for each of the training hyperparameters in the grid search.

Table 5.

Grid search settings for hyperparameter optimization.

Hyperparameter	Range of values	Number of values tested
Optimizer	[Adam, Nadam, RMSProp]	3
Learning rate	[0.005, 0.05]	10
Decay rate	[0.05, 0.30]	6
Batch size	[4, 8, 16, 32]	4
Epochs	[100, 200, 300]	3
Regularization weight	[0.0001, 0.001, 0.01]	3
	Total number of permutations	6480

For each permutation, the neural network was trained using 80% of the data and was validated on the remaining 20% (a random stratified sampling approach was used for partitioning). We used the TensorFlow package (with Keras backend) in Python to perform the model training. The grid search optimization was managed using the Talos package5 in Python, which works seamlessly with TensorFlow.

We ran the algorithm on a workstation with two NVIDIA TITAN XP GPUs (working in parallel) and 64GB of memory. It took around 110 h for the algorithm to run all the 6480 permutations of the grid search (i.e., around 0.61 s per epoch). The (nearly) optimal hyperparameter settings obtained from the grid search are shown in Table 6 .

Table 6.

Optimal set of hyperparameters.

Hyperparameter	Optimal value
Optimizer	Adam
Learning rate	0.01
Decay rate	0.25
Batch size	8
Epochs	300
Regularization weight	0.0001

Since a grid search strategy does not exhaust the entire solution space, after obtaining the nearly optimal set of hyperparameters, we performed a manual search in the vicinity of each of the hyperparameters (except the optimizer) by slightly changing them one at a time and observing the model outcome. We realized that a learning rate of 0.007 with a decay rate of 0.2 led to a relatively steadier training process with better performance on the validation data set.

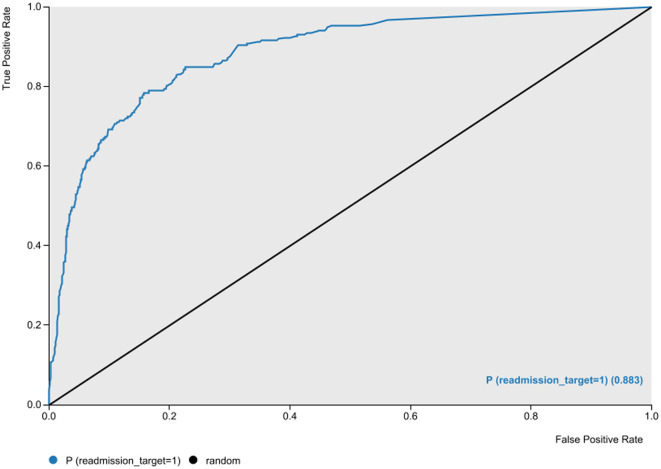
With a dichotomous target variable indicating whether a patient with a positive COVID-19 test returned to the ED within 7 days after discharge (1) or not (0), our best artificial neural network achieved an accuracy of 87.4% with an area under the Receiver Operating Characteristic (ROC) curve value of 0.883 (Fig. 3 ), a sensitivity of 71.9%, a specificity of 91.5%, and an F-1 measure of 70.4%.

Fig. 3.

The Receiver Operating Characteristic (ROC) curve of the best ANN model.

For severely imbalanced classification problems, Sánchez-Hernández et al. [47] suggest G-mean, the geometric mean of true positive rate (TPR) and true negative rate (TNR) (Eq. (1)), as an objective measure of predictive power. They maintain that G-mean is more indicative of the performance of such classification models than F-measure or precision; two metrics that are basically designed for classification tasks with fairly balanced data. In our model, the G-mean measure was 81.2%.

$$G-\mathit{mean}=\sqrt{\mathit{TPR}\ast \mathit{TNR}}$$ (1)

While, to the best of our knowledge, the ED readmission prediction for COVID-19 patients has not been addressed in any prior study, we believe a comparison between our model with similar recent ED readmission studies in other contexts could demonstrate the utility of our proposed predictive approach. This comparison is given in Table 7 .

Table 7.

Prediction model results comparison with similar studies.

Article	Context	Readmission window	Approach	Model metrics
Present study	COVID-19	7-day	GA + DNN	Acc = 0.874 Sens = 0.719 Precision = 0.691 F1 = 0.704 G-mean = 0.812 AUC = 0.883
[81]	General	30-day	Decision Tree	Acc = 0.772 Sens = 0.402 F1 = 0.494 AUC = 0.732
[82]	General	3-day	Gradient Boosting	Sens = 0.16 Precision = 0.75 AUC = 0.76
[82]	General	9-day	Gradient Boosting	Sens = 0.23 Precision = 0.70 AUC = 0.75
[83]	General	3-day	DNN	Acc = 0.680 Sens = 0.679 AUC = 0.755
[48]	General	3-day	Ensemble	Acc = 0.957 AUC = 0.61

Particularly, the difference between sensitivity and AUC of the present study with those of other studies is notable, suggesting the remarkably higher distinctive power of our proposed model. Even though the accuracy reported by Sarasa Cabezuelo [48] is considerably high, the AUC reported in that study suggests that the high accuracy is partially due to the use of a highly imbalanced data set (and therefore, a large gap between their model's sensitivity and specificity).

4.3. Model interpretation

The predicted probabilities by the best DNN model, along with the training and test data, were fed into the SHAP algorithm to assess the feature importance scores. The SHAP package6 in Python was employed to perform these analyses. With a large number of features and instances, the runtime for the SHAP algorithm is considerably high. A suggested workaround to deal with this issue is to use a set of weighted k-means of instances (each weighted by the number of instances it represents) rather than the whole training data. Using this approach, we summarized the training data into 4 weighted k-means (using the shap.kmeans() method) and used them to train the SHAP algorithm.

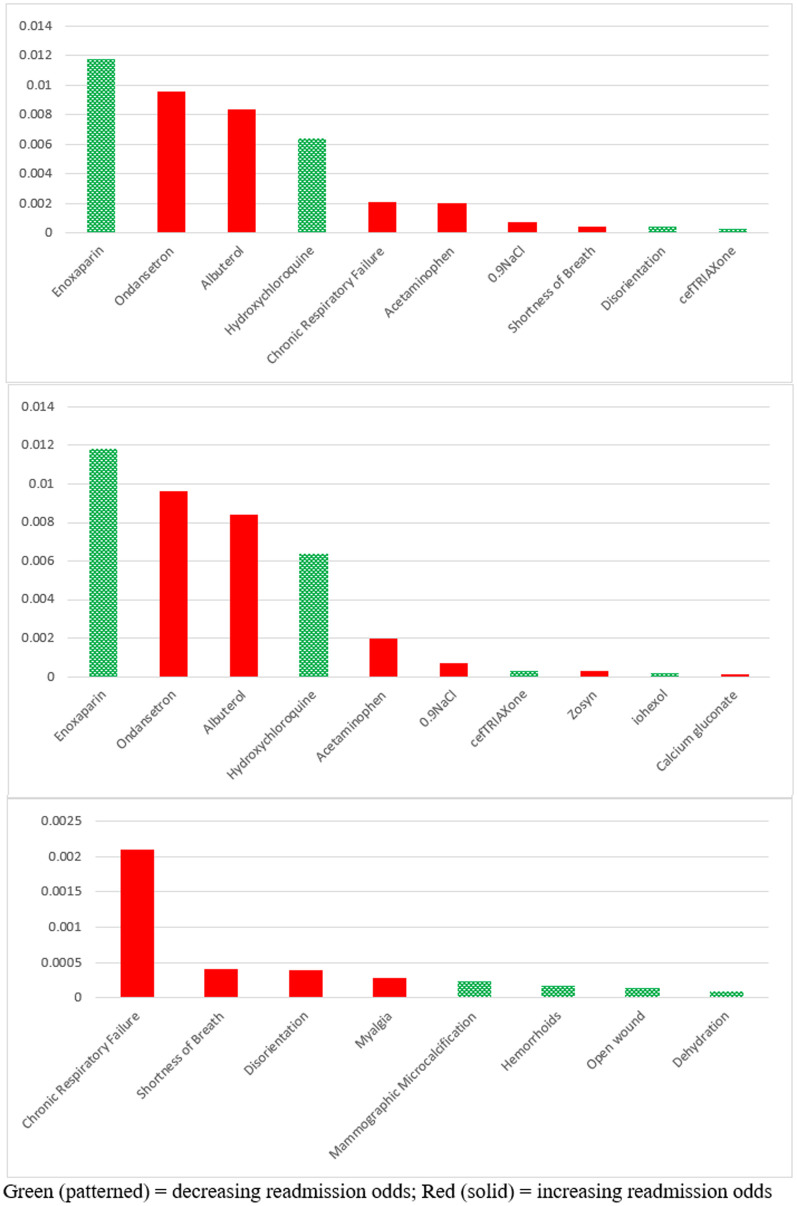
Fig. 4 indicates the most important features in terms of SHAP scores, top medications, and top comorbid conditions, respectively. Bars shown in green/red represent factors that decrease/increase the chances of readmission. As shown in Fig. 4, Enoxaparin, a drug typically used to prevent the formation of blood clots, turned out as the most important factor in decreasing the chances of readmission. Several studies have reported a suspiciously significant association between COVID-19 and Thromboembolism [[49], [50], [51], [52]]. Our results suggest that, regardless of whether that association is causal, administering blood clot preventive medications could be effective in treating COVID-19 patients and decreasing their chances of returning to ED.

Fig. 4.

SHAP importance scores of top features overall (top), medications (middle), and comorbidities (bottom). Green (patterned) = decreasing readmission odds; Red (solid) = increasing readmission odds.

Another medication shown to decrease the chances of readmission is Hydroxychloroquine (HCQ), a drug well-known for treating malaria. Since the beginning of the pandemic, HCQ has been one of the controversial treatments for COVID-19. Several clinical trials have been conducted to investigate its efficacy, with some reporting positive effects [53], while a larger group reporting no significant effect [[54], [55], [56], [57]]. Mahase [58] argues that while there is no solid proof that HCQ is effective in treating COVID-19, some clinical trials report its efficacy in reducing severe symptoms of the disease.7 ^,. 8 We believe our findings confirm the results of those trials since ED visits are typically initiated after observing severe symptoms in the patients.

On the other hand, administering Ondansetron and Albuterol, two drugs that are typically used to treat nausea and shortness of breath, have turned out to increase the chances of returning to ED. The Centers for Disease Prevention and Control (CDC) has officially listed both conditions as typical symptoms of COVID-19. Since we could not find any notable clinical studies discussing these two drugs as possible treatments of COVID-19, it seems that they were mainly prescribed by doctors to alleviate nausea and dyspnea. However, according to our SHAP importance scores, it appears that these medications do not act as effectively on COVID-19 patients as they do on patients with other conditions.

In terms of comorbidity/symptom factors, the bottom chart in Fig. 4 indicates that chronic respiratory failure and shortness of breath are the most important reasons for patients' readmission to ED. While CDC has identified respiratory failure as a condition with a moderate risk of complication in COVID-19 patients [59], it is surprising to see that some patients with that condition had been discharged from ED after being tested positive for COVID-19. One explanation for this observation could be the limited capacity of health care organizations and the need to prioritize the allocation of hospital beds. This could also justify why high-risk comorbid conditions (e.g., COPD and chronic heart failure) did not turn out among the top factors in our study because patients with those conditions were most likely hospitalized once diagnosed with COVID-19. Our results suggest, however, that when hospital beds are available, patients with COPD or heart diseases are better to be hospitalized because they have a higher probability of returning to the ED within a short time.

Since the outcome of SHAP analysis (as a post-hoc interpretation method) depends generally on the existing features in the model and because we employed an evolutionary approach (with some degree of randomness) for feature selection, some concern may be raised about the robustness of our results. To address such concerns, we repeated the SHAP analysis with 50 and 110 features selected by GA in two separate runs. In both cases, the model converged before reaching the maximum number of generations. We observed that: 1) A majority of the features selected in these extra runs were among the 220 features used in the original run (88% and 87.2% for the 50- and 110-feature re-runs, respectively); 2) except “Ceftriaxone” and “open wound” which were not among the 50 selected features, all top features identified in Fig. 4 were present among the selected features in both new runs.; and 3) after calculating the average SHAP scores for the two new feature sets and sorting the features by their scores, we observed a Spearman's rank-order correlation of 0.92 and 0.89 between the selected features in the two new runs (50 and 110 features, respectively) and the features from the original feature selection run (i.e., 220 features). Overall, we believe that these additional analyses corroborate the robustness of our results. We believe that the reasonable settings we considered for the feature selection step enabled the GA to search the solution space sufficiently and to go through enough iterations to converge.

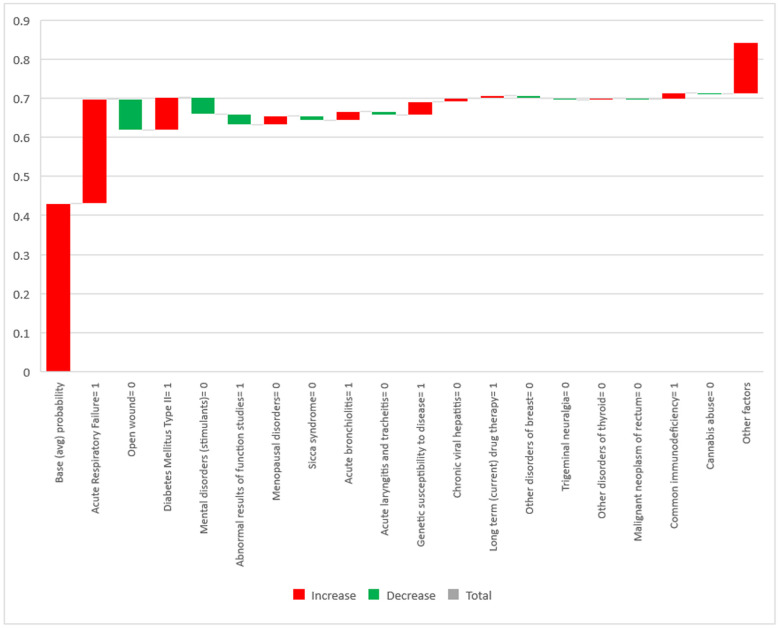
In addition to the insights provided at the aggregate level, the additive nature of SHAP scores enables the practitioners to analyze the patient-specific risk factors at the individual level. In other words, sum of the features' SHAP scores for each patient represents his or her corresponding deviation from the average (across the entire sample) probability of readmission. In addition, every single feature's SHAP score for a specific patient represents the contribution of that feature to the patient's total deviation from the average readmission probability. The waterfall chart in Fig. 5 shows the contributing risk factors (and the extent of their contribution) to the probability of readmission for a sample patient. The column on the left shows the average probability of readmission across all patients, serving as a baseline for interpreting the additive SHAP scores. Fig. 5 only displays diagnosis- or symptom-related factors because these factors are present at the time of a patients' initial visit and are the main criteria for physicians to decide on the hospitalization of the patient.

Fig. 5.

SHAP feature importance scores of a sample patient (individual level).

The figure shows the important factors specific to a female patient (63 years old) who returned to the ED within a week after her initial visit. The predicted probability by the model for the patient's readmission was 0.842, which is 0.411 higher than the average probability across all patients. The length of the bar associated with each factor explains how much of that gap is attributable to that factor (red/green bars for increasing/decreasing effects). In line with the aggregate findings (Fig. 4), acute respiratory failure is a major factor for this patient's return to the ED (this condition has increased her chances of readmission by around 0.27). This strongly suggests that patients experiencing this symptom at the time of their first visit to the ED should be given a high priority for hospitalization. Thus, we are able to confirm the findings of previous studies (e.g., [60]) in which respiratory failure at the time of admission was identified as a major mortality risk factor. Moreover, Fig. 5 suggests that diabetes mellitus type II, genetic susceptibility to diseases, and deficiency of the immune system are the other important risk factors leading this particular patient to be readmitted. A review of the relevant literature reveals that these results confirm the findings by several clinical trial studies investigating the association between diabetes [[61], [62], [63]], genetic susceptibility [64,65], and immunodeficiency [66,67] with the severity of COVID-19.

Clearly, since the risk factors may differ from patient to patient, several factors identified in Fig. 4 (at the aggregate level) are not present in Fig. 5 for this particular patient. This sheds light on the importance of studying risk factors at the patient level in addition to the cohort level. Although the risk factors identified in cohort-level studies (especially clinical trials) are typically more common and generalizable, investigating those factors at the patient level may reveal somewhat rare risk factors as well as capture the effect of comorbidities (i.e., coexistence of multiple risk factors).

5. Summary and conclusion

In this study, we proposed an exploratory/predictive/explanatory machine learning framework that can be employed as a decision support tool to help clinicians identify high-risk patients and critical medical factors in a reasonable timeframe during pandemics.

The mysterious nature of novel viral diseases in their early stages of outbreak makes clinical predictive analytics a challenging activity mainly because such analyses rely on prior knowledge about the potential predictors of the outcome to limit the feature space and to reduce the dimensionality. In the absence of such knowledge, an exploratory effort is needed to identify the highly relevant factors. Additionally, a purely predictive machine learning approach barely provides insights for clinicians to gain a better understanding of the disease; hence, a predictive effort should ideally be followed by an explanatory one to simplify the complexity of predictive models and to provide intuitive guidelines. Our proposed framework offers such a holistic package to clinical decision-makers and enables them to make informative decisions even in the early stages of a pandemic.

While we tested our framework in the specific context of pandemic-related ED readmissions, we believe that it is highly generalizable to other, even non-pandemic, contexts where both prior knowledge and historical data are limited. We encourage future research to validate the applicability of this framework to other contexts.

Declaration of Competing Interest

None.

Biographies

Behrooz Davazdahemami is an Assistant Professor of Information Technology and Supply Chain Management (IT&SCM) at University of Wisconsin-Whitewater. He received his M.S. in Industrial Engineering from University of Tehran and his Ph.D. in Management Science and Information Systems from Oklahoma State University. His research interests include health analytics, business analytics, IT privacy, and technology addiction. He is a member of the Association for Information Systems, The Institute for Operations Research and the Management Sciences, and the Decision Sciences Institute. Behrooz has published in journals such as Journal of the American Medical Informatics Association (JAMIA), Information & Management, Journal of Business Research, International Journal of Medical Informatics, and Expert Systems with Applications, as well as IS proceedings such as the Hawaii International Conference on System Sciences (HICSS) and the International Conference on Information Systems (ICIS).

Hamed M. Zolbanin is an assistant professor of information systems at the University of Dayton. Prior to this position, he served as the director of the business analytics program at Ball State University. He had several years of professional experience as an IT engineer prior to receiving his Ph.D. in Management Science and Information Systems from Oklahoma State University. His research has been published in such journals as Decision Support Systems, Information & Management, Information Systems Frontiers, Communications of the Association for Information Systems, and the Journal of Business Research. His main research interests are healthcare analytics, online reviews, sharing economy, and digital entrepreneurship.

Dursun Delen is the holder of Spears and Patterson Endowed Chairs in Business Analytics, Director of Research for the Center for Health Systems Innovation, and Regents Professor of Management Science and Information Systems in the Spears School of Business at Oklahoma State University. He has authored/co-authored more than 120 journal papers and numerous peer-reviewed conference proceeding articles. His research has appeared in major journals including Decision Sciences, Journal of Production Operations Management, Decision Support Systems, Communications of the ACM, Computers and Operations Research, Computers in Industry, Journal of the American Medical Informatics Association, Artificial Intelligence in Medicine, International Journal of Medical Informatics, Health Informatics Journal, among others. He has published 11 books/textbooks in the broad area of Business Intelligence and Business Analytics. He is often invited to national and international conferences and symposiums for keynote addresses, and companies and government agencies for consultancy/education projects on data science and analytics related topics. Dr. Delen served as the general co-chair for the 4th International Conference on Network Computing and Advanced Information Management (held in Soul, South Korea), and regularly chairs tracks and minitracks at various information systems and analytics conferences. He is currently serving as the editor-in-chief, senior editor, associate editor and editorial board member of more than a dozen academic journals.