Predictive models for cochlear implant outcomes: Performance, generalizability, and the impact of cohort size

Abstract

While cochlear implants have helped hundreds of thousands of individuals, it remains difficult to predict the extent to which an individual’s hearing will benefit from implantation. Several publications indicate that machine learning may improve predictive accuracy of cochlear implant outcomes compared to classical statistical methods. However, existing studies are limited in terms of model validation and evaluating factors like sample size on predictive performance. We conduct a thorough examination of machine learning approaches to predict word recognition scores (WRS) measured approximately 12 months after implantation in adults with post-lingual hearing loss. This is the largest retrospective study of cochlear implant outcomes to date, evaluating 2,489 cochlear implant recipients from three clinics. We demonstrate that while machine learning models significantly outperform linear models in prediction of WRS, their overall accuracy remains limited (mean absolute error: 17.9-21.8). The models are robust across clinical cohorts, with predictive error increasing by at most 16% when evaluated on a clinic excluded from the training set. We show that predictive improvement is unlikely to be improved by increasing sample size alone, with doubling of sample size estimated to only increasing performance by 3% on the combined dataset. Finally, we demonstrate how the current models could support clinical decision making, highlighting that subsets of individuals can be identified that have a 94% chance of improving WRS by at least 10% points after implantation, which is likely to be clinically meaningful. We discuss several implications of this analysis, focusing on the need to improve and standardize data collection.

Introduction

Worldwide, hundreds of thousands of people have been able to regain hearing thanks to cochlear implants (CIs). While most people who meet the criteria for a CI will benefit from implantation, it remains difficult to accurately predict the extent to which an individual’s hearing will benefit from the procedure prior to implantation. There have been numerous studies of the factors that may influence the chances of success, typically with a relatively small number of predictive factors that are consistently collected in clinical settings (Blamey et al.,1992; Plant et al.,2016; Roditi et al.,2009). Such studies have found strong evidence that factors such as prelingual hearing loss, underlying etiology, and the pre-operative pure-tone average of the implanted ear (PTA) impact post-implantation performance, with further factors showing lower levels of evidence for association (Blamey et al.,2013; Boisvert et al.,2020; Zhao et al.,2020; Lazard et al.,2012).

Given the difficulty in predicting who will benefit from cochlear implantation, it has long been hoped that robust decision making tools could be constructed to provide further evidence to clinicians by combining multiple predictive factors Crowson et al. (2020c). Linear models are often used to combine such factors, but their ability to explain variance of hearing outcome is limited, with most models explaining between 8% and 60% of variance in hearing outcome (Roditi et al.,2009; Lazard et al.,2012), with higher results typically only observed in small sample sizes. However, it is important to note that metrics such as accuracy or the proportion of variance explained do not give any indication of a model’s ability to make predictions on previously unseen new individuals, where predictions are typically less accurate (Siontis et al.,2015; Ramspek et al.,2021). Given this, it is important to explicitly evaluate how well models generalize when assessing predictive ability.

Given the limited utility of multivariate linear models to predict cochlear implant outcome, there have been numerous explorations of prognostic modelling of hearing outcome Crowson et al. (2020b,2020a). Using a Random Forest (Breiman,2001), Kim et al. (2018) report a Pearson’s correlation of 0.91 for the WRS of 120 adult CI recipients (in this case equivalent to explaining approximately 83% of variance in hearing outcome). However, they observed a significant drop in the strength of the correlation to a Pearson’s correlation of 0.6 (approximately 36% of variance explained) when evaluating the model on 38 individuals from clinics not used to construct the model. Using deep learning neural networks, Crowson et al. (2020c) report a RMSE of 0.57 (in this case equivalent to an almost perfect Pearson’s correlation of 0.99 or 98% variance explained) when predicting Hearing in Noise Test (HINT) scores for 1,604 patients across a single cohort. However, given this degree of error is below the test-retest variability of such scores (Bentler,2000), it remains unclear how this model would perform on a new dataset. These results highlight the potential of machine learning, while simultaneously demonstrating the need for robust evaluations across multiple datasets.

In this study, we systematically explore the performance of machine learning algorithms for the prediction of WRS one year after implantation. Using data from 2,489 cochlear implant recipients from across three globally dispersed clinics, the largest retrospective study of cochlear implant outcomes in adults with post-lingual hearing loss to date, we explore the predictive performance of four commonly used machine learning techniques, emphasizing the evaluation of model generalizability through internal and external validation. First, we examine whether the use of machine learning based models achieve significantly better prediction of hearing outcomes compared to standard linear models used in audiology domain. We extend this analysis to focus on the generalizability of the models, considering different training and evaluation regimes, that increasingly require the model to account for inter-clinic differences. We evaluate the impact of increasing the amount of data, varying the amount of data used to train each model and estimating their performance if the available datasets could be increased to 5000 samples. Finally, we examine whether the accuracy of the predictive models developed in this work are sufficient to help inform clinical decision making, in particular identifying subgroups of patients that are highly likely (or highly unlikely) to meet a clinically meaningful level of improvement. Observations from these models highlight several future directions that might help improve predictive accuracy, focusing on the need to improve and standardize data collection, and raise questions about how such modelling might best be translated into clinical practice.

Methods

Cohort description

The cohort analyzed in this study was initially comprised of 6,500 patients from three clinics: Vanderbilt University Medical Center (VUMC), Ear Science Institute Australia (ESIA), and Medizinische Hochschule Hannover (MHH). Ethics approvals and data privacy protection practices were implemented. All patient data were de-identified and met data compliance requirements for local patient data privacy laws and international law for General Data Protection Regulation (GDPR). Each clinic used their own standard practice and pre-implantation test protocol for CI candidacy and post-implantation evaluations. We note that these protocols have evolved over time.

The study focuses on adults with post-lingual hearing loss that received a single cochlear implant. To ensure that the patient records met this criteria across the clinics, we removed any individual where:

• age at implantation was less than 18 years.

• a second CI was received sooner than 12 months after the first implant.

• implantation was conducted between 2003 and 2018.

• data entered were spurious (e.g., incorrect age, missing surgery date).

• post-operative WRS was not recorded between 6 and 24 months.

To ensure consistency across clinics, individuals with better hearing (those with records with a PTA of lower than 60 dB or a pre-operative WRS greater than 50%) were not included in the study. Therefore, there were 2,489 patients remaining after these criteria were applied. Table 1 provides an overview of the patient numbers and demographics of our cohort. The dataset in this study is the same as dataset in Goudey et al. (2021) except for the exclusion of individuals with confirmed prelingual hearing loss, which resulted in the removal of 38 records in VUMC, 47 records in ESIA and 161 records in MHH.

Table 1.

Cohort demographics: including the total number of patients, and the reported distribution by gender (with number of females and their percentage in the brackets). For the following statistics, the reported number of patients with the mean and standard deviation are provided in brackets: word score recognition (WRS), with CI and HA, pure tone average (PTA), and years of severe to profound deafness (YRS-D) for the implanted and contralateral ears. All individuals in this study were implanted between 2003 and 2018.

	VUMC	ESIA	MHH	Combined dataset
Number of patients	453	246	1790	2489
Number of female	453 (199, 43.9%)	NA	1790 (986, 55.1%)	2243(1185, 47.6%)
Age(CI)	453 (65.7, 13.8)	246 (64.7, 14.0)	1790 (57.3, 16.7)	2489 (59.6, 16.3)
WRS(CI)	453 (45.0, 22.6)	246 (42.8, 23.1)	1790 (53.5, 28.0)	2489 (50.9, 26.9)
WRS(HA)	376 (8.4, 12.3)	238(7.0, 11.4)	709(4.2, 9.5)	1323 (5.9, 10.9)
PTA ${}_i$	450 (97.7, 19.3)	246 (116.7, 14.1)	1771 (98.5, 17.6)	2467(100.2, 18.4)
PTA ${}_c$	450 (83.4, 25.5)	246 (85.5, 29.0)	1740 (76.3, 28.6)	2436 (78.5, 28.3)
YRS-D ${}_i$	396 (24.9, 17.1)	230 (27.2, 18.3)	1373 (8.1, 12.5)	1999(13.7, 16.5)
YRS-D ${}_c$	58 (26.9, 14.9)	62 (28.3, 17.0)	592 (11.6, 17.0)	712 (14.3, 17.8)

Hearing outcomes

This study focuses on monosyllabic word recognition score (WRS) tests in the implanted ear as it is the most common method to evaluate a patient’s hearing performance and was recorded across all clinics. There were notable differences between the WRS tests used across the clinics. Consonant-Nucleus-Consonant (CNC) (Peterson and Lehiste,1962) score tests were used for data acquired in Australia (ESIA) and the United States of America (VUMC), and the Freiburg monosyllable score tests was used for data collected in Germany (MHH) (Hahlbrock,1953, 1960). Across all clinics, WRS tests were conducted under free-field conditions at conversational level (ranging from 60 to 65 dB SPL RMS) with a hearing aid (HA) before and a CI after implantation. During the test, each clinic masked the contralateral ear where this was required. Monosyllabic word recognition tests vary across clinics in language, words, and number of words tested, but are all scores at the word level and were consistent across assessments within each clinic. Any missing pre-operative WRS(HA) values were imputed to be 0 if all measured pure tone average (PTA) values were equal to or above 110 dB HL, mimicking the situation in which a patient does not provide any correct answers during a word recognition task Goudey et al. (2021). All WRS are normalized between 0 and 100 to account for the difference in the number of words tested across clinics. We use WRS(HA) to denote the latest WRS prior to implantation while WRS(CI) denotes the value most closely recorded to the one-year mark after implantation. Additionally, we consider prediction of the quartiles of WRS, breaking the scores into four equally sized groups, to determine if this removes variability and hence improves our predictive ability.

Factors considered

Since this study is concerned with the prediction of performance from the information available at the time of implantation, we concentrate our analysis on pre-operative features. Factors of interest that are available to us can be grouped into four categories: demographic factors, audiological and hearing-related metrics, a patient’s clinical history, and etiology.

• Demographic: We include the age of a patient at the time of implantation (Age-CI). Where available, we include whether the patient natively speaks the test language and a patient’s gender.

• Audiological and hearing-related: We include the pure tone average of hearing frequencies of 0.5 kHz, 1 kHz, 2 kHz and 4 kHz for the ear chosen for implantation (PTA ${}_i$ ) and the contralateral ear (PTA ${}_c$ ). In cases, where PTA measurements indicated that the patient reached the limit of particular frequency (a non-numeric value), we replaced the value 125 dB HL, the maximum possible frequency. The PTA for the better ear (PTA ${}_{min}$ ) is calculated as the minimum of PTA ${}_i$ and PTA ${}_c$ . We include pre-operative word recognition tests which were conducted under free-field conditions at natural level (60 dB - 65 dB) on the to-be-implanted ear in the best aided condition (WRS(HA) ${}_i$ ), the contralateral ear (WRS(HA) ${}_c$ ), and both ears simultaneously (WRS ${}_b$ ). The maximum score obtained by a patient with headphones and varying loudness levels (PB ${}_{max}$ ) is also included.

• Clinical history: Factors pertaining to the patient history in this analysis are the duration of severe to profound hearing loss or deafness (in years, YRS-D), patient age at deafness (Age-D), the duration of hearing aid use prior to implantation (in years, YRS-HA), the nature of hearing loss (progressive or sudden), and the side chosen for implantation. Most of these (YRS-D, Age-D, nature of hearing loss) are self-reported and based on the information collected to a series of questions (e.g. when did the patient stop using the phone?). Such self-reported questions have been shown to have increased variability compared to more objective measures Tsimpida et al. (2020).

• Etiology: We grouped available etiologies in the following 13 categories: noise induced, otosclerosis, Meniere’s disease, congenital syndrome, childhood or congenital illness, genetics, (chronic) otitis media & infections, trauma, sudden hearing loss, ototoxicity & streptomycin, meningitis, others (containing all recorded etiologies that did not fit into a category with sufficient values to be meaningful or were recorded as ’other’ in the original datasets), and unknown (if etiology was recorded as unknown in the original datasets or was missing). Etiology is mostly patient-reported (similar to other clinical history measures) and the few patients with multiple etiologies were placed into a single category after discussing with subject matter experts.

Not all features included in this study are available in all datasets and further details around the individual features are described in Goudey et al. (2021).

Machine learning models

Artificial Neural Networks

Artificial Neural Networks (ANN) and deep learning architectures have become extremely popular in the last decade but their increased predictive power comes at the cost of a large number of parameters, and hence require large amounts of data. Given this, debate remains around their applicability for relatively small datasets. To explore these models, we implement two feed forward neural networks using Keras (Chollet et al.,2015) for regression and classification. For regression tasks, we use a network with with two hidden layers and Mean Absolute Error (MAE) as the loss function. For the classification of WRS quartiles, we use a feed forward neural network that has three hidden layers with categorical cross-entropy as the loss function and a softmax activation function in the last layer. Both models use the ReLU activation function (Glorot et al.,2011), Adam optimizer, have a batch size of 5 and are trained for 50 epochs.

Random Forest

Random Forests (RF) are a widely-used ensemble method that builds many simple classifiers (decision trees) in the training phase, each constructed over different sample “bags” (a set of samples randomly selected with replacement) and different subsets of features. After training, predictions for unseen samples are made by averaging over all individual trees, taking either the mean or the mode for regression or classification tasks respectively. Herein, we use the Random Forest regressor from the scikit-learn library (Breiman,2001; Pedregosa et al.,2011) with 100 estimators and MAE as the criterion.

Gradient Boosting

Gradient Boosting are another ensemble method which sequentially fits weak predictive models using information from the previously trained models to improve performance (Friedman,2001). In particular, each consecutive model is fit to the previous model’s residuals, trying to account for errors in the previous model. Gradient boosting has been shown to be extremely effective for many predictive tasks. In this work, we use the eXtreme Gradient Boosting (XGBoost) package (Chen and Guestrin,2016) using either linear models (denoted as XGB-Lin) and Random Forest (denoted as XGB-RF) as the base models, using the default parameters. Note that XGB-RF can naturally handle incomplete samples with missing measures without the need for imputation or exclusion.

Baseline models

It is difficult to form a direct comparison of our machine learning based models to those that have been previously reported in the literature, as such models have not been made public or make use of measurements that are unavailable in this dataset. Instead, we implemented three baseline models that take inspiration from three previously reported models (Blamey et al.,2013; Lazard et al.,2012; Kim et al.,2018) but are implemented using the data available to this study. Given these are new models, we denote them Baseline models A, B and C and indicate their respective features in Table 2. These models allow us to (i) compare non-linear and linear models; (ii) contrast performance of different feature sets; and (iii) explore different modelling approaches.

Table 2.

Features included or excluded in the baseline models and in the novel models developed in this work. These features have been found to significantly impact post-implantation hearing performance in previous studies. Here, ✓indicates the feature is used in the model, and - indicates the feature is not used in the model. ${}^{*}$ Calculated as the difference of Age-CI and YRS-D. ${}^{**}$ Both WRS(HA) and PB ${}_{max}$ are used as pre-operative speech test measures.

Feature description	Baseline model A	Baseline model B	Baseline model C	Models in this work
Age at onset of s/p deafness (Age-D) ${}^{*}$	✓	✓	✓	✓
Duration of HA use (YRS-HA)	-	-	✓	✓
Etiology	✓	✓	-	✓
PTA ${}_i$	-	-	✓	✓
PTA ${}_{min}$	-	✓	-	✓
PTA ${}_c$	-	-	✓	✓
Duration of s/p deafness (YRS-D)	✓	✓	✓	✓
Age-CI	✓	✓	✓	✓
Pre-operative speech test ${}^{**}$	-	-	✓	✓
Native speaker	-	-	-	✓
Implant side	-	-	-	✓

Baseline model A in Table 2 is inspired on the multivariate regression developed by Blamey et al. (2013), which made use of duration of severe to profound deafness, age at onset of severe to profound deafness, underlying etiology, and the duration of cochlear implant experience (YRS-CI). In our analysis, we implement this linear model using years of pre-implantation deafness (YRS-D) as a substitute for the duration of severe to profound deafness. We compute age at onset of deafness by subtracting the number of years of pre-implantation severe to profound deafness from the age of the recipient at CI implantation. The duration of CI experience is not included in our model as patient performance is evaluated at the closest recording to one year after implantation, resulting in approximately one year implant experience for each implantee. We include etiology as previously described in section 2.3.

Baseline model B is inspired on the work by Lazard et al. (2012), which extended the work of Blamey et al. (2013) making use of pure tone average of the better ear, the duration of HA use prior to implantation, the duration of moderate hearing loss, the percentage of active electrodes and CI brand as significant. The latter three features are unavailable in our data, so they are not included in Baseline model B. We compute PTA of the better ear as ${\mathrm{PTA}}_{min}=min({\mathrm{PTA}}_i,{\mathrm{PTA}}_c)$ , given that its unclear from the available data whether the better ear was the one chosen to be implanted or not. The resulting features are shown in Table 2.

The final baseline model, Baseline model C, is inspired by the Random Forest of Kim et al. (2018), used to predict post-operative sentence recognition score. This previous study includes the following features: the PTA of the ear chosen for implantation (PTA ${}_i$ ), the PTA of the contralateral ear (PTA ${}_c$ ), patient age at implantation, the best-aided pre-operative sentence recognition score, the duration of HA use, and the duration of deafness. Similarly, Baseline model C is a Random Forest model and includes PTA ${}_i$ , PTA ${}_c$ , and age at implantation. In addition, we substitute sentence recognition score with a word recognition score, WRS(HA) and PB ${}_{max}$ where available.

Model setup and evaluation

Across the different experiments in this paper we consider four machine learning models, RF, XGB-Lin, XGB-RF, and ANN, and three baseline models, Baseline A, B and C. As the implementations of RF and ANN used in this work only allow for the inclusion of complete data points, we replace all missing values with a constant value (specifically -1) for these models. In contrast, XGBoost models allow us to use all available data, even where a feature was not recorded. A one-hot encoding scheme (i.e., a dummy coding) is used to encode the categorical feature (i.e., etiology) as a set of binary columns for all models. All models are evaluated in one of two ways: (i) using 10 repeats of 10-fold stratified cross-validation (testing where each of 10 folds are iteratively held-out as the test sample and the process is repeated 10 times), either the combined data from all clinics or on each clinic independently; (ii) constructing models using training data from two clinics and evaluated performance in the held-out clinic. In both instances, evaluation is conducted over a set of patients that were not used to train the model. This quantifies the model’s generalizability, its ability to make accurate predictions on data not used for model construction.

Depending on the framing of the prediction task, different metrics are used. When predicting continuous outcomes (WRS(CI) or delta WRS(CI)), we report mean absolute error (MAE), which measures the average magnitude of the errors in a set of prediction (e.g., if MAE of predicted WRS is 20, real WRS will be predicted WRS +/- 20 points). For classification tasks (WRS(CI) quartiles), we report accuracy, proportion of true positive predictions. When comparing distributions of scores (such as those from cross-validation), we evaluate the significance of improvement using a two-sided Wilcoxon signed rank test (Woolson,2007). To go beyond just summary statistics of model performance, and given the difficulty in computing 95-CI from cross-validation Bates et al. (2021), we provide graphical representation of model performance and distribution across the different folds. This is achieved primarily through boxplots with boxes showing median, first and third quartile, while the whiskers show interquartile range.

Experiments

Motivated by the need for improved decision making around cochlear implantation and common challenges in clinical applications of machine learning, this work focuses on predicting WRS at approximately 12 months after implantation, using only measurements available pre-implantation. If robust and accurate predictions could be made, it would indicate that decision support tools for identifying cochlear implantation candidates are viable. This work explores the feasibility of such models by addressing the following questions: (i) Using the largest combined dataset, can our model perform as well as or better than the baseline models that are based on previously published literature? (ii) Can our model generalize to data from new clinics? (iii) Will increasing the amount of data but maintaining the same quality and measurements likely lead to improved performance? (iv) Will the prediction of discretized outcomes (specifically quartiles) improve model performance and/or provide different insights? (v) Using the subsets of individuals, can hearing outcome be predicted with high confidence?

Predicting WRS(CI)

To analyze the performance of different machine learning algorithms and the impact of different feature sets to predict WRS(CI), we evaluate MAE of all seven models considered in this work in 10 repeats of 10 fold cross-validation on the combined cohort. We examine the distribution of MAE resulting from cross-validation and evaluate whether these differences are significant using a Wilcoxon signed-rank test.

Assessing generalizability to other clinics

To assess whether our model has the ability to generalize to unseen data, in particular the data which is collected at a different clinic, we investigate different training/test data splits. We use the best-performing model from the first experiment (Section 2.7.1) in terms of median MAE, to predict WRS(CI) and compare the following scenarios:

• Single clinic cross-validation: Training and testing are performed separately on each clinics’ dataset in 10 times repeated 10-fold cross-validation. All clinics cross-validation: Training and testing are done on data from all clinics in combination using 10 repeats of 10-fold cross-validation, which is the same protocol as used in Section 2.7.1. Here, the model is trained using individuals from all clinics, but we assess the model’s prediction on each of the different clinics’ held-out samples separately.

• External validation: Model training is conducted using data from two clinics and evaluated on the individuals in the held-out clinic. This is performed once for each combination of clinics.

Sample size analysis

To analyze the impact of sample size in our particular task, we vary the amount of data used to train the model from 10% and 90% of the combined data from all clinics, evaluating its performance on the remaining 10% of individuals. In assessing the model trained on the combined dataset, we evaluate the average performance across all held-out individuals, regardless of clinic. To estimate performance as sample size increases beyond that in the data, we compute the line of best fit using an inverse power law Figueroa et al. (2012), allowing us to extrapolate the impact that more data may have on model performance.

Predicting discretized outcomes

WRS measurements are inherently noisy, with previous studies estimating that there can be up to 30% variability between tests (Moulin et al.,2017). Given this, we speculate that a model trained on discrete classes may be more robust to noise. To evaluate this, we repeat experiment (i) as a classification task with WRS(CI) discretized into quartiles. In line with the previous experiments, we use 10 times repeated 10-fold cross-validation and use the same sets of models, albeit focusing on prediction of a discrete output. Since we are conducting a classification task, we are reporting the accuracy of our predictions, rather than the MAE.

Using predictive models to predict individual level outcomes

We illustrate how the output of predictive models with imperfect accuracy might be used to help inform clinical decision making by predicting the improvement, delta WRS, and examine properties of individuals in seven risk categories based on their predicted delta WRS values. We examine the distribution of actual delta WRS outcomes to examine how much variability is in any group.

We use these ranges to define sets of individuals who will treat as likely to achieve a delta WRS of 10 and then consider the positive predictive value (PPV): the proportion of individuals in the group predicted to achieve a delta WRS of 10 that actually achieve a delta WRS of 10 or more. Conversely, we may also consider the negative predictive value: the proportion of individuals in a group predicted to achieve a delta WRS less than 10 that actually achieve a delta WRS less than 10. The criteria are useful for determining whether subgroups of individuals exist that are likely to meet a defined level of clinical improvement, or conversely whom we can state are unlikely to meet such a level.

We note that the required increase of 10 is a parameter that can be altered but was selected here as we believe it indicates a meaningful improvement in hearing when considering only WRS.

Results

Performance of different models to predict WRS(CI)

Our initial experiment compares the performance of several models to predict WRS(CI) at around 12 months after implantation. Different machine learning algorithms, trained using all available features, are compared with three models that represent re-implementations of published models using our dataset. As highlighted in Table 2, not all features used in the previously published models were available in this study and hence these re-implementations may be weaker than the originally reported results.

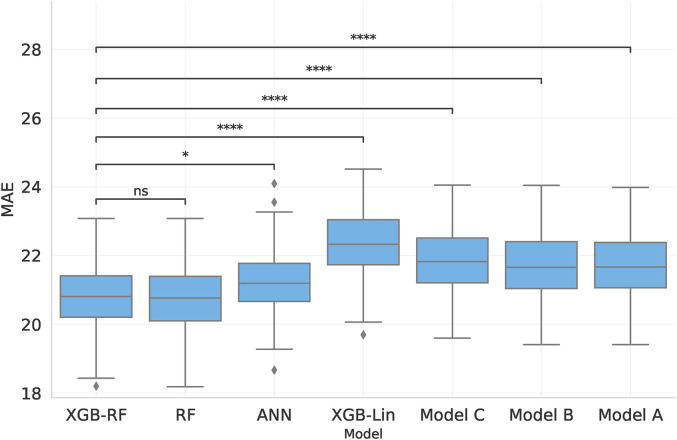
Figure 1 shows the resulting model MAEs when training on the combination of all datasets and evaluating performance in cross-validation. We find that the strongest predictive performance is obtained using XGB-RF and all available features (median MAE: 20.81), with similar results obtained for RF (median MAE: 20.76). The XGB-RF has a significantly better performance than either the ANN and XGB-Lin models (two-sided Wilcoxon signed rank test $p<0.0075$ and $4.4\times {10}^{-19}$ , respectively). We similarly find that re-implementations of previously published models perform worse than XGB-RF (median MAE: 21.8, 21.6, 21.6 for all three baseline models, with $p<{10}^{-11}$ for all compared with XGB-RF).

Figure 1.

Comparison of the MAE of predicting the post-operative WRS on all datasets combined using four novel models and three baseline models, where Models A and B are linear and Model C is a Random Forest. The first four boxes use all features in our dataset, while the remaining boxes are the baseline models. Statistical significance of the drop in performance compared to XGB-RF is shown by lines above the bars, where symbols correspond to the following p-values: ns : p > 0.05, * : p ≤ 0.05, **: p ≤ 0.01, *** : p ≤ 0.001, ****: p ≤ 0.0001.

Assessing generalizability to other clinics

Measured hearing outcomes can change across different clinics due to differences in factors such as experimental setup or cohort demographics. Moreover, as machine learning models grow in complexity, they have a tendency to overfit to the given dataset, memorizing both the true signal and the noise specific to the data used to construct the model. These two concerns mean it is unclear whether predictive models of WRS are likely to remain accurate when the model is trained on one cohort of patients and evaluated on another. To explore this, we examine the performance of the XGB-RF model (which had the highest median MAE in Figure 1) in three scenarios described in Section 2.7.2 that increasingly require a more robust model: single clinic cross-validation, all clinics cross-validation, and external validation. In the case of external validation, if the differences across the clinics are substantial, we might expect significant drops in performance compared to the cross-validation scenarios.

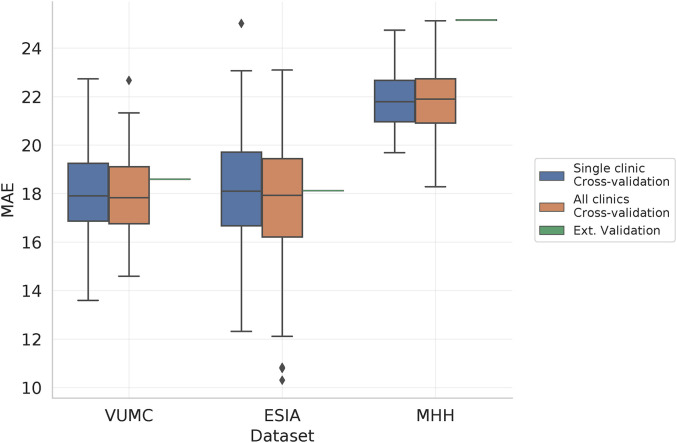
Figure 2 shows the MAE of each dataset under the three training scenarios, with lower MAE indicating that predictions are closer to the true values. In all configurations, there are clear differences between the different datasets, with VUMC and ESIA showing a median MAE of 17.9 and 18.1 in single-clinic cross-validation, and MHH shows increased error (MAE: 21.8). While these differences indicate differences between the clinics, we see little change in predictive performance when constructing the predictive model using data from two clinics and validating on the third, with VUMC and ESIA showing a MAE of 18.6 and 18.12 respectively compared to the single clinic setting (an increase of 0.07 and 0.02), and MHH has a more substantial increase to a MAE of 25.2 (an increase of 3.4), which may be reflective of differences in setup between the cohorts (Goudey et al.,2021). Interestingly, when we train over all datasets combined and test on subsets of each of the individual datasets, model performance only varies slightly, increased amount of data available for training. Overall, these results highlight that the trained models are likely to perform similarly when evaluated on cohorts of patients not used for model construction. This is a key clinical challenge.

Figure 2.

Evaluation of XGB-RF predictive performance under increasingly stringent validation settings. We consider single clinic and all-clinics cross-validation, where models are trained and evaluated in a cross-validation framework using data from either a single clinic or all clinics combined, with results from the latter stratified across the three datasets. As multiple models are constructed, we show the distribution of these results. Finally, external validation, shows the result of training a model on two cohorts and evaluating on the remaining cohort. These results are a single score for a single model and hence are shown as a horizontal line.

Sample size analysis

Machine learning approaches are known to greatly benefit from large sample sizes. Indeed, a key aspect of the performance improvements of machine learning in the last decade has been the availability of ever-growing datasets, typically of high dimensional (i.e., consisting of many measurements) (Jordan and Mitchell,2015). However, there is no clear evidence how sample size impacts the ability to predict hearing outcome, and hence whether effort should be placed on increasing clinical data collection, as opposed to improving quality or collecting additional measurements. To address these questions, we explore the impact of varying the amount of training data in each different dataset, and in combination, to evaluate their performance. Furthermore, we project how the observed trends might extend as the number of samples are increased from that available in this study.

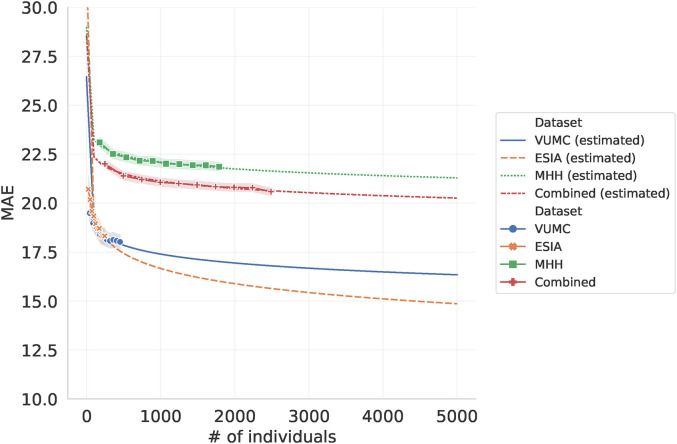
Figure 3 shows that for ESIA, the smallest dataset, the MAE sharply decreases by 2.0 when increasing the number of samples for training from 24 samples to 246 (from MAE of 20.2 down to 18.2). But for the largest dataset, MHH, the decreases in MAE only drops by 1.3 when increasing sample size from 179 to 1,790 (from MAE of 23.1 to 21.8), with similar trends shown in VUMC and the combined analysis. Fitting a logarithmic curve to each of these error profiles, we estimate that even if we increase the number of samples in the combined analysis from 2,489 to 5,000, we may only see a decrease in MAE of 0.3 (from 20.5 to 20.2). While these are only estimates, they highlight the need for improvements in data quality and for novel features rather than simply increasing the number of observations.

Figure 3.

Impact of adjusting training dataset size on MAE. Here, the amount of data used to train the model is varied, leaving a fixed 10% of each dataset withheld to evaluate the model. Estimated dataset in dot lines are fitted logarithmic curve in order to extrapolate the impact additional training data of the same quality on the model performance.

Predicting discretized outcomes

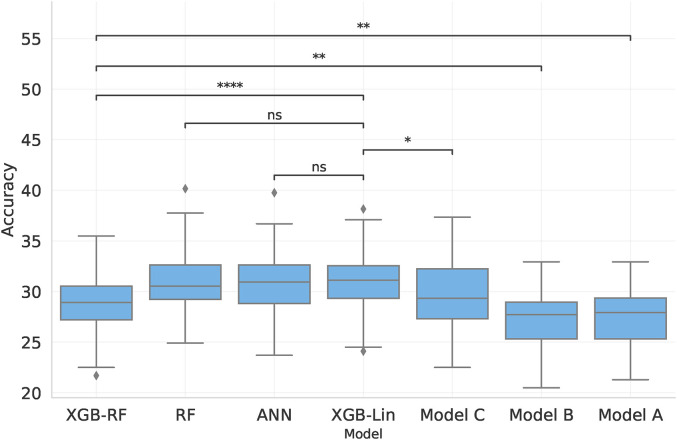
Given the inherent noise in WRS, we explore whether prediction of discrete WRS outcomes substantially changes the predictive performance. To be more specific, can we predict which WRS(CI) quartile an individual belongs to? Figure 4 replicates Figure 1 but here shows the seven models’ accuracies for the classification task of different WRS(CI) classes, rather than MAE. Hence higher values indicate a better performance here.

Figure 4.

Comparison of the accuracy of predicting discretized post-operative WRS using four machine learning models and the three baseline models. The first four boxes use all features in our dataset, while the remaining boxes are the baseline models, where Models A and B are linear and Model C is a Random Forest. Statistical significance of drop in performance compared to XGB-Lin is shown by lines above the bars, where symbols correspond to the following p-values: ns : p > 0.05, *: p ≤ 0.05, ** : p ≤ 0.01, *** : p ≤ 0.001, ****: p ≤ 0.0001.

The models which yield the best predictions are RF using all available features, ANN, and XGB-Lin. This result differs from that obtained through regression analysis (see Section 2.7.1), where XGB-RF performed better than XGB-Lin. For all models, accuracy is low when predicting discretized WRS in all models.

Identifying sub-groups that can be confidently predicted

The previous experiments consider the overall predictive performance of machine learning models, highlighting how well we can predict the results for any individual. However, it is unclear from such summary statistics whether the error rates of these models are low enough to help decision making in a clinical setting. An alternative exploration that may aid clinical translation of these models is to ask whether we can identify subsets of individuals that are highly likely to benefit from cochlear implants (or conversely, for whom cochlear implants will lead to no benefit).

To address this question, we alter the predictive task from predicting absolute WRS(CI) at 12 months, to predicting delta WRS, the improvement of WRS(CI) above pre-implantation WRS(HA). Using the XGB-RF model on the combined dataset, individuals were stratified into seven groups based on their predicted delta WRS, ranging from the lowest to highest. Figure 5 shows the distribution of actual outcomes for each group.

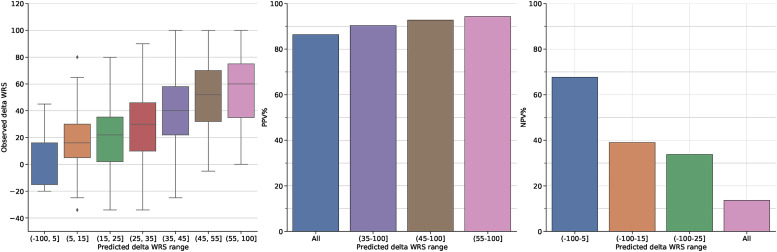
Figure 5.

a) Distribution of actual delta WRS (WRS(CI)-WRS(HA)) for individuals predicted to fall within seven predicted WRS ranges. b) Positive predictive value (PPV) of achieving a post-implantation delta WRS of 10 considering different prediction intervals: all predictions, and the three highest risk groups in subplot a). c) Negative predictive value (NPV) of achieving a post-implantation delta WRS of 10 considering different prediction intervals: the three lowest risk groups in subplot a) and all predictions. Note the colour of the bars correspond to those in subplot a).

Figure 5a shows strong differences in actual outcome between the different groups. Individuals who are predicted to have a delta WRS of less than 5, have a median outcome of 7, with 50% of individuals having a change in WRS between -15 and 15. In contrast, those individuals predicted to have a delta WRS greater than 55 have a median improvement in WRS of 60, with 50% of individuals having an improvement between 35 and 75, indicating almost all individuals in this group are likely to receive significant improvements. While these wide outcome ranges reflect the limited predictive accuracy of the model, they also highlight strong differences between individuals at the extreme ends of the predicted scores for whom we may be able to make strong claims about their likely range of possible outcomes.

To explore this idea further, we consider the positive or negative predictive value (PPV, NPV respectively) of these groups given a criteria of interest, namely whether WRS will improve by 10 points after implantation. For PPV, Figure 5b shows that there is a high chance of any individual having a positive outcome with 86% of patients achieving a delta WRS of 10 regardless of their predicted delta WRS. However, if we only consider the highest predictive group as the likely implant group (predictions between (55-100]), we see that PPV increases substantially to 94%. PPV remains strong if we expand this range to consider individuals predicted to have a WRS greater than 45 (PPV of 94%) or even 35 (PPV of 90%). In contrast, the NPV of the individuals with low predicted delta WRS is substantially lower with Figure 5c showing those with predicted WRS in the range (-100,5] have an NPV of 68% for achieving an increase of 10 points. This drops further to 40% and 34% as we consider individuals with WRS less than 15 or 25 respectively. Exploration of different thresholds for improvement (20 and 30) revealed similar trends, albeit with lower PPV and higher NPV (for the highest range PPV/NPV is 88%/21% and 82%/32% for thresholds of 20 and 30 respectively). This is expected given that each increase in the threshold is more difficult to predict given the target subpopulations are smaller (i.e., the number of individuals with WRS improving by at least 10 is larger the number whose WRS improves by at least 30). The results indicate that we can make more definitive statements about positive outcomes with further work required to more accurately identity those individuals who will not substantially improve from implantation.

Discussion

In this work, we have explored the use of machine learning algorithms to predict post-operative word recognition score across the largest retrospective, multi-centre cohort to date. Evaluating seven different models, we find that gradient boosting based approaches have the best predictive performance, in both predicting continuous and discretized WRS outcomes. Moreover, we find the performance of these models is robust when trained on one cohort and evaluated on another. The overall predictive performance is relatively weak, with a mean absolute error between 18 and 24 points. Analysis of sample size indicates that improving the number of available patients alone is unlikely to dramatically improve performance. While these analyses indicate that predicting hearing outcome for all individuals remains difficult to do with high precision, current models may be able to identify subsets of patients that have a very high probability of substantial improvement, highlighting a possible direction for translating this modelling approach towards clinical decision support.

The comparison of different machine learning algorithms and sets of baseline features revealed that the use of gradient boosting, or similar ensemble-based Random Forest, with all available features provides the best performance, significantly stronger than that of commonly used linear models. This is consistent with many other studies which have typically found these ensemble-based models to provide the strongest predictive performance without a need to manually select features (Tang et al.,2018). However, if we consider the absolute difference in MAE, we see that the median MAE of the XGB-RF model is 20.81 compared to 21.66 for the 3-feature linear regression baseline (Model A). While the difference in performance are statistically significant, it is less clear that these differences are clinically significant. Similar trends are observed when we treat the problem as a discrete task, where we try to predict the quartile of hearing outcome that a patient will achieve. While these gains in performance are modest, they do consistently indicate that the non-parametric machine learning models modestly outperform linear models. These differences may be due to the ability of the more complex models to account for interaction effects, which have recently been shown to have significant associations with WRS (Goudey et al.,2021).

One of the strengths of this study is the strong focus on model generalizability, examining how well we can make predictions about individuals that were not used to construct the models. A common concern in the development of clinical predictive models is whether they suffer from overfitting (Royston et al.,2009; Bleeker et al.,2003; Siontis et al.,2015), learning not only the true signal in the data but also the dataset-specific idiosyncrasies and noise (Royston et al.,2009). Given this, we evaluated two forms of validation to ensure that we gain reasonable estimates of model performance that is reflective of their behaviour on unseen individuals. The first is through the use of cross-validation, which is commonly used when only a single dataset is available. While this approach is an unbiased approach that can provide a reasonable estimate of how well a model would perform given an individual who is very similar compared to the training population (Harrell Jr,2015), it is generally expected that model performance will significantly worsen given an entirely independent set of data (Ramspek et al.,2021; Bleeker et al.,2003). Thus, a critical step in the development of predictive models is external validation on an independent dataset (Siontis et al.,2015). Using data from three large independent datasets, we conducted external validation by training the model on data from two clinics and evaluating performance on the held out data from the third clinic, thus demonstrating that predictive performance remains relatively robust regardless of which datasets were used to train the model. This focus on generalizability is critical in the development of models that may be used to help guide decision supports tools in clinics but is rarely conducted, especially when considering external validation (Siontis et al.,2015). While some of the previously published studies of machine learning models appear to achieve very strong, and in some cases almost perfect, prediction of post-operative hearing outcomes, they have lacked rigorous investigation of model generalizability. This makes it likely that there is some degree of overfitting (Ramspek et al.,2021). The external validation performed here also provides evidence that the important features in our models are not significantly different between clinics. In future work, it would be interesting to explore generalizability of our models temporally, given the changes in cohort definitions over time. This could be done by training the model on the past data from a specified range (e.g., 2003 - 2015) and testing on more recent data (2016 onwards). Such an approach is outside of the current scope but would reflect real world usage where the collection of clinical data and implant criteria evolve over time.

An important consideration when developing predictive models is their possible context of use in any future clinical application. The identification of groups of individuals who are highly likely to obtain weak, or conversely strong, hearing outcomes after implantation is one possible path for using such models to aid clinical interpretation. The identification of potentially ”at risk” individuals requiring additional counseling and clinical care could help segment and streamline clinical care and increase the effectiveness of patient care. The use of machine learning models playing the role of support for decision makers, rather than directly determining a decision, is similar to a long history of statistical screening tests (Moons et al.,2009; Collins et al.,2015; Bouwmeester et al.,2012). In other domains, such as radiology, AI-based algorithms have been used to provide additional support to a clinical decision maker (Wright et al.,2016; Lim et al.,2020), especially in situations where clinicians may have low confidence in their ability to make a diagnosis (Marchetti et al.,2020). Despite the limited predictive power across all patients, identification of groups of individuals whose outcomes are likely to be at the extreme ends represent the most immediate uses-case for such predictive models. This is an interesting direction to consider and the analysis performed here requires further exploration. In particular, our estimates of PPV and NPV depend on a specific definition of clinical success and will vary depending on the dataset being considered, in this case individuals who all received a cochlear implant. Given these results are only based on adults with post-lingual hearing loss who received their first CI, other scenarios that exist in a clinical environment (for example, individuals who are receiving a second cochlear implant) need to be examined. More systematic exploration of the the impact of changing success criteria and the cutoffs for the highest and lowest risk groups also highlight the need for further research in this space (Smulders et al.,2018).

While machine learning can be a powerful tool, performance is often constrained by three issues related to data: (i) the number of observations; (ii) the quality of data used to build the model; (iii) the quality of the label to be predicted (Roh et al.,2021). We explicitly studied the impact of sample size in this study, finding that model performance on the combined dataset only improves from MAE of 22.4 to 20.5 when the number of records is increased from 249 to 2240. This modest improvement in model accuracy, despite a 9-fold increase in sample size, indicates that the current bottleneck is unlikely to be sample size. While data is likely to be the biggest bottleneck, there may be opportunities for further improvements in terms of optimizing models for use on tabular data, making use of transfer learning if relevant data is available or focusing efforts to develop more parsimonious models. But we suspect that the benefits from such modelling approaches will be limited without access to improved data.

Our conclusions regarding the impact of increasing the dataset size lead us to speculate that the quality and type of collected measurements, both the features used to build the model and WRS outcome being predicted, require attention to dramatically improve predictive performance. Such observations have been made in a variety of domains (Cortes et al.,1995; Sheng et al.,2008), especially in the clinical space (Obermeyer and Emanuel,2016). In the audiology domain, there is known variation in all measurements across the different clinics, differences in data collection processes leading to significant amount of missingness, and limits to the number of features about implantation performance that are being collected. These issues are true of many studies related to cochlear implantation (Zhao et al.,2020; Boisvert et al.,2020), and in clinical research more broadly (Agrawal and Prabakaran,2020), and reflect the difficulties of patient data collection in clinical settings. As with many discussions of predictive factor analysis (Zhao et al.,2020; Goudey et al.,2021; Boisvert et al.,2020), the ideal solution to improve both data quality and quantity, and hence improve predictive modelling, is to standardize data collection across clinics performing cochlear implantation. Examples of such standardization can be seen in oncology, where improving data collection practices have lead to successful insights into how to improve clinical practices that would not have otherwise been obtained (Srigley et al.,2009; Williams et al.,2015). The utilization of tests that can be performed outside the traditional clinical setting can also provide access to higher resolution data (Botros et al.,2013; Ching et al.,2018). Such a solution is likely to dramatically improve the quality of available data, which will also improve the performance of data-driven predictive models.

There are several limitations to this study. The generalizability and potential bias of the models need to be even further assessed on data from different clinics, beyond the three clinics analyzed here. As already highlighted, there is variability across the data collected from the three clinics, including cohort differences, testing protocol, language differences, testing material differences, and/or setup differences, and patient selection criteria, due to differing regulatory rules across countries. While these represent the complexities of real-data in this domain, it is likely that collecting data from yet more clinics may increase this variability. Moreover, translation of these types of models not only requires greater validation of their predictive capacity, but also an understanding of the health and economic consequences (i.e., the implications of over- or under-diagnosis) Kelly et al. (2019). A further limitation to the predictive power of the models was the set of features that were available in the datasets. We only included a limited set of pre-operative features, but there are additional measurements that are known to be associated with hearing outcome. These include known peri-operative factors, such as the as electrode placement (Holden et al.,2013), insertion depth (James et al.,2019), brand and model of the CI implant and the number of active electrodes during stimulation (Lazard et al.,2012), as well as under-explored factors such as social support, social engagement, motivation or cognitive ability. Moreover, measures of the implantation itself or post-operative information, including whether the electrode is optimally placed, the electro-neural interface/cochlear health, rehab or training process, are also likely to impact implantee’s hearing performance. The inclusion of such criteria will depend on the expected use case of a model, with a subset relevant to determine cochlear implant candidacy, while the expanded subset can be used to refine patient expectations over time. All models were run with default parameters and while we do not believe a more through exploration of the hyper-parameter space would impact results, this was not conducted as part of this analysis. Some variables, such as age of onset, are often based on patient recollections and hence can be quite variable. However, the measurements available to this study are collected in a clinical setting and also reflect the real world challenges that predictive methodologies will need to overcome. A final challenge is that the chosen hearing outcome, WRS, is known to have significant variability between patient visits (Moulin et al.,2017), and in this study has additional temporal variability, given the outcome visit varied between 6 and 24 months after implantation. One potential direction for future work would be to consider multiple hearing outcomes as a composite and/or considering prediction of outcomes longitudinally. The additional measurements may serve to reduce the variance of the outcome measure and lead to increased predictive performance, as well as a more holistic measure of hearing outcome success.

Conclusion

In this work, we use the largest retrospective cohort of adult cochlear implantees to explore the accuracy and generalizability of machine learning algorithms when predicting WRS after implantation. While machine learning approaches yield improved results compared to linear models, the gains are modest and are unlikely to be improved with collection of more data if the type and quality of input measures remain the same, highlighting that further work is required relating to standardization of data collection. Despite this, we provide evidence that our models are able to identify subsets of individuals that are highly likely to have strong improvements in hearing, with similar, though weaker, results for patients who will achieve poorer outcomes. Our results highlight the potential for prognostic machine learning models for guiding clinical decision support related to cochlear implantation.