Unveiling whole‐brain dynamics in normal aging through Hidden Markov Models

Abstract

During normal aging, the brain undergoes structural and functional changes. Many studies applied static functional connectivity (FC) analysis on resting state functional magnetic resonance imaging (rs‐fMRI) data showing a link between aging and the increase of between‐networks connectivity. However, it has been demonstrated that FC is not static but varies over time. By employing the dynamic data‐driven approach of Hidden Markov Models, this study aims to investigate how aging is related to specific characteristics of dynamic brain states. Rs‐fMRI data of 88 subjects, equally distributed in young and old were analyzed. The best model resulted to be with six states, which we characterized not only in terms of FC and mean BOLD activation, but also uncertainty of the estimates. We found two states were mostly occupied by young subjects, whereas three other states by old subjects. A graph‐based analysis revealed a decrease in strength with the increase of age, and an overall more integrated topology of states occupied by old subjects. Indeed, while young subjects tend to cycle in a loop of states characterized by a high segregation of the networks, old subjects' loops feature high integration, with a crucial intermediary role played by the dorsal attention network. These results suggest that the employed mathematical approach captures the complex and rich brain's dynamics underpinning the aging process.

Normal aging is associated with brain structural and functional changes. In this study, we applied the dynamic data‐driven approach of Hidden Markov Models on resting state functional MRI data of 88 subjects, equally distributed in young and old, to investigate how aging is related to specific characteristics of dynamic brain states. After estimating six states, we found that two states were mostly occupied by young subjects, whereas three other states by old subjects. A decrease in strength with the increase of age, and an overall more integrated topology of states occupied by old subjects were also observed.

1. INTRODUCTION

In the last decades, rs‐fMRI has been widely used to study the spatio‐temporal network organization of spontaneous brain activity. Across different brain regions, rs‐fMRI BOLD signals exhibit temporal synchronization (Biswal, Zerrin Yetkin, Haughton, & Hyde, 1995) which gives rise to resting state networks (RSNs), composed of distributed regions that demonstrate coherent activity (Beckmann, DeLuca, Devlin, & Smith, 2005; Fox, Snyder, Vincent, Corbetta, & Raichle, 2005).

rs‐fMRI studies have investigated the effects of aging in healthy subjects, showing that the brain undergoes both structural and functional alterations (Betzel et al., 2014; Damoiseaux, 2017; Ferreira, 2013; Wang, Su, Shen, & Hu, 2012). The undoubtedly strongest result found among rs‐fMRI studies performed at the network level, is a reduced functional segregation (Chan, Park, Savalia, Petersen, & Wig, 2014; Song et al., 2014) and increased between‐network connectivity (Betzel et al., 2014) which underlines the tendency of RSNs to reorganize in a more integrated topology (Bagarinao et al., 2019) with the increase of age. Specifically, several works reported a weaker within‐network functional connectivity (FC) with age in the default mode, (Andrews‐Hanna et al., 2007; Betzel et al., 2014; Damoiseaux et al., 2008; Geerligs, Renken, Saliasi, Maurits, & Lorist, 2015; Song et al., 2014; Tomasi & Volkow, 2012; Varangis, Habeck, Razlighi, & Stern, 2019; Zonneveld, 2019), ventral‐attention (Andrews‐Hanna et al., 2007; Betzel et al., 2014; Tomasi & Volkow, 2012; Zonneveld, 2019) and executive networks (Betzel et al., 2014; Geerligs et al., 2015; Varangis et al., 2019). Regarding sensorimotor and visual networks, the results were quite inconsistent among studies. Indeed, within the sensorimotor network, many groups found a FC increase (Song et al., 2014; Tomasi & Volkow, 2012), other a decrease (Zonneveld, 2019) or even no changes (Geerligs et al., 2015). FC was found to be increased with older age within the visual network in (Betzel et al., 2014; Chan et al., 2014; Yan et al., 2011), decreased in (Zonneveld, 2019), or to remain stable across age (Geerligs et al., 2015; Varangis et al., 2019).

Although these studies have investigated how RSNs are distributed across the lifespan, they assume that FC is stationary. However, recent research has proven that even in resting conditions, FC among brain networks varies over time bringing to a dynamic reconfiguration during the rs‐fMRI scan (Allen et al., 2014; Hutchison et al., 2013). With the purpose of overcoming traditional approaches based on static FC, many methods have been introduced to study dynamic FC (dFC) (see Lurie et al., 2020 for a review). Focusing on approaches which aim to identify FC states directly from the measured data, we can distinguish two main methods: sliding windows followed by clustering (Allen et al., 2014) and Hidden Markov Model (HMM; Vidaurre, Smith, & Woolrich, 2017).

To our knowledge, only a few studies (Chen et al., 2019; Tian, Li, Wang, & Yu, 2018; Xia et al., 2019) have investigated the relationship between aging and dFC. Both studies are based on sliding windows followed by clustering approach in healthy subjects. Despite using comparable populations and the same methodological approach, the three studies reached conflicting results. Specifically, a different number of states were identified: three in Tian et al. (2018) and five in the other two studies. In addition, concerning the dwelling time (i.e., the duration of each state throughout the scanning time) and the number of transitions between states as a function of age, Chen and colleagues did not find any differences in the dwelling time, whereas both in Tian et al. (2018) and Xia et al. (2019), significant differences were reported. In particular, Tian and colleagues observed a positive correlation between age and the dwell time of the “loose interaction state,” characterized by an overall weak connectivity, whereas Xia and colleagues found a positive correlation between dwelling time and age. The number of transitions between states was found to be mostly negatively correlated with age in Xia et al. (2019), whereas in Chen et al. (2019) an opposite direction was observed. Given the discordant results of previous studies, in this work, we attempt to understand the properties of dFC states in young and old people using the model‐based method of HMM. This method overcomes the limitations of clustering and sliding‐window approaches regarding the selection of the optimal window size and clustering dimensionality (Hutchison et al., 2013; Rousseeuw, 1987), but raises the problem of the choice of the model order, which, however, can be chosen quantitatively (Rezek & Roberts, 2005). In addition, HMM allows to capture the heterogeneity of the time‐dynamic variation of the FC by considering in the same framework of analysis the variability between individuals in a population. In this context HMM uses temporally concatenated resting state fMRI data to determine, in a full probabilistic approach, the time‐varying neural processes represented as discrete brain states and their transition over time. Although its mathematical complexity, in recent years, HMM has been applied for characterizing brain states in healthy subjects during rest (Vidaurre et al., 2017) and tasks (Vidaurre et al., 2018), as well as in patients (Cao, 2019; Kottaram et al., 2019; Van Schependom et al., 2019), demonstrating its ability to exploit and summarize the richness of the rs‐fMRI data. Given these premises, in this study, we investigated the developmental trajectories of brain states employing resting state data of 88 healthy subjects, equally divided in young and old. We first applied an independent component analysis (ICA) to obtain a whole‐brain high‐resolution functional parcellation, then we used the time courses of these components within the HMM framework and we estimated the model parameters. Contrary to previous studies based on sliding window and correlation techniques, the choice of the number of states in the model was based on a quantitative approach: after introducing a new index to quantify the precision of the estimates, the goodness of the fit and the precision were assessed as the model order varied. Finally, to investigate the effects of aging on dynamic properties of brain states, we characterized the age‐relation of temporal variability and organization of the states, using temporal metrics, derived from single‐subject sequences of visited states, and a graph‐theory approach.

This study was divided into two parts: (1) methodological considerations related to the application of HMM and (2) assessment of the differences in brain states properties between young and old subjects.

2. MATERIAL AND METHODS

2.1. Participants

Magnetic resonance imaging (MRI) data from 88 healthy participants from the publicly available MPI‐Leipzig Mind‐Brain–Body dataset (Arno Villringer, 2020; Mendes et al., 2019) were analyzed. The data selection was performed after excluding from the original dataset consisting of 318 subjects, 10 subjects due to scanner artifacts or unavailability of rs‐fMRI data or corrupted structural scans or failure of the pre‐processing stages. Inclusion criteria were: (1) no SKID diagnoses; (2) no drug abuse; (3) mean framewise displacement smaller than 0.3 mm (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). Subjects were then divided into two groups: the young group (Y: n = 44; 20 females, 24 males; age range = 20–25 years) and the old group (O: n = 44; 22 females, 22 males; age range = 60–80 years).

2.2. Data acquisition

Full details on MRI data are provided in (Mendes et al., 2019). In brief, data acquisition was performed with a 3T Siemens Magnetom Verio scanner, equipped with a 32‐channel head coil. The protocol included a T1‐weighted 3D magnetization‐prepared 2 rapid acquisition gradient echoes (MP2RAGE; TR = 5,000 ms, TE = 2.92 ms, TI1 = 700 ms, TI2 = 2,500 ms, first flip angle = 4°, second flip angle = 5°, FOV = 256 × 240 × 176 mm, voxel size = 1 × 1 × 1 mm, multiband acceleration factor [MBAccFactor] = 3), rs‐fMRI scans (TR = 1,400 ms, TE = 39.4 ms, flip angle = 69°, FOV = 202 × 202 mm, voxel size = 2.3 × 2.3 × 2.3 mm, volumes = 657, MBAccFactor = 4) and two spin echo acquisitions (TR = 2,200 ms, TE = 52 ms, flip angle = 90°, FOV = 202 × 202 mm, voxel size = 2.3 × 2.3 × 2.3 mm). During rs‐fMRI scans, the subjects were asked to keep their eyes opened and to lie down as still as possible.

2.3. MRI data pre‐processing

A structural pre‐processing was applied on the pseudo‐T1w image, obtained by multiplying the T1w 3D‐MP2RAGE image with its second inversion time image. The pipeline included bias field correction (N4BiasFieldCorrection [Tustison et al., 2010]), skull‐stripping (MASS [Doshi, Erus, Ou, Gaonkar, & Davatzikos, 2013]) and nonlinear diffeomorphic registration (Avants et al., 2011) to the symmetric MNI152 2009c atlas (Fonov et al., 2011).

Pre‐processing of rs‐fMRI data included slice timing (Smith et al., 2004), distortion (TOPUP [Andersson, Skare, & Ashburner, 2003]) and motion correction (MCFLIRT [Jenkinson, Bannister, Brady, & Smith, 2002]) and nonlinear registration to the symmetric MNI atlas (Fonov et al., 2011) passing through the single subject pseudo‐T1w image (boundary‐based registration [Greve & Fischl, 2009]). As a second step, the GIFT toolbox (http://trendscenter.org/software/gift/) was used to decompose the functional pre‐processed data into independent components (ICs) and thus to reduce their dimensionality. To obtain a high‐resolution functional parcellation of the main RSNs, we performed a group spatial‐ICA, setting the number of ICs to 180. Among these, those related to banding artifacts, vascular or noise components were discarded, resulting in a set of 46 components (M = 46). The ICs were manually classified by visual inspection of both the spatial maps and the source power spectra, in accordance with (Damaraju et al., 2014; Griffanti et al., 2014). The RSNs were grouped into 11 functional domains: visual (VIS), sensorimotor (SMN), auditory (AUD), cingolo‐opercularis (CON), dorsal‐attention (DAN), fronto‐parietal (FPN), default‐mode (DMN), cognitive‐control (CCN), frontal (FRN), cerebellum (CER), and basal ganglia (BG).

The group‐information guided ICA (GIG‐ICA) back‐reconstruction algorithm (Du & Fan, 2013) was used to estimate the subject‐specific spatial maps and time series of each independent component.

The following steps were performed on the time courses of the 46 ICs as additional denoising step: (1) despiking, applied with the icatb_despike_tc function of the GIFT toolbox, (2) multiple regression of the six head motion parameters, their temporal derivatives, mean WM and mean CSF signals (Jo et al., 2013), (3) high‐pass filtering (cut‐off frequency = 1/128 Hz). No global signal regression was applied.

2.4. Part 1: Methodological considerations related to HMM

2.4.1. Hidden Markov Model—Overview

Following the approach previously described by Vidaurre et al. (2017), we applied HMM to the time courses of the 46 ICs. Prior to running the inference, the subject‐specific time courses were standardized, so each IC has mean equal to zero and SD equal to one. Then, the standardized time series of both the populations of young and old subjects were temporally concatenated, yielding a data matrix of dimensions 88 subjects × 46 ICs × 657 time points. Stacking all subjects together allowed us to make the model inference at the group‐level. The HMM was inferred using the HMM‐MAR toolbox (Vidaurre et al., 2016), available in MATLAB in a public repository (https://github.com/OHBA-analysis/HMM-MAR).

2.4.2. Hidden Markov Model—Inference

The HMM describes the data (IC time series) as a hidden sequence of K states, where K must be set a priori. A multivariate Gaussian observation model assumes that the probability of the data at time point t (X _t ) given a certain state k at time point t (S _t ), follows a multivariate Gaussian distribution with mean activity μ _k ([M × 1] vector) and precision Ω _k ([M × M] matrix):

$$X_t\mid S_t=k\sim N\left({\mu }_k,{\mathrm{\Omega }}_k\right)$$

Since the inference is performed on the demeaned and standardized ICs time courses, μ _k describes a change away from the grand‐average zero activity level. Two ICs that both have a positive or negative μ _k , are therefore functionally connected. For each state, the observational model is hence parametrized by these two variables.

Another property of the state sequence resides in the transition probability between states, represented by the matrix Θ _l,k , that describes how likely is to be in specific state k at time point t, if we were in state l at time point t−1. Finally, the probability of each state being active at the initial time point must be estimated. Given that the HMM was applied to the data concatenated across subjects, the parameters describing the states were defined at the population level, whereas the probability of each state being active at each time point was subject‐specific and described by:

$$\mathit{\text{Gamma}}=\mathit{Pr}\left(S_t=k\right)={\sum }_l{\mathrm{\Theta }}_{l,k}\mathit{Pr}\left(S_{t-1}=l\right)$$

An analytical approach, defined within the Variational Bayes (VB) framework, was employed to obtain an approximation of the model posterior distributions. As described in (Vidaurre et al., 2016), this VB approach infers the parameters of the model alternating a variational expectation‐step and maximization‐step. The first step deals with the estimation of the hidden states probabilities and the second step estimates the model parameters. The aim of the VB inference is to minimize a cost function, called Free Energy (FE), which includes three terms: the average log‐likelihood (avLL, i.e., how well the model fits the data), the Kullback–Leibler divergence (how divergent are the approximate posterior distributions from the priors) and the negative entropy, computed for the distribution of the hidden states. The number of repetitions of the initialization algorithm was set to 5 and out of these, the best in terms of FE was used as starting point for the inference run. Since there is not a gold standard to perform the initialization of the hidden states probabilities, we tried both a random initialization and an initialization with a mixture of Gaussian models. Given the nonlinear nature of the VB algorithm, and therefore the possibility of reaching a local minimum of the cost function, 200 realizations of the model were performed for each of the two types of initializations. Then, the 200 realizations were sorted on the basis of the FE and the one with the lowest value of FE was chosen. This procedure was performed for the two different initializations and the best realization in terms of FE was kept. Further analysis, presented in Supporting Information, was then performed to ensure that the type of initialization did not lead to a large variation in the estimates results.

2.4.3. Hidden Markov Model—Choice of model size

In the HMM framework, the number of states (K) assumed to model the signal dynamics must be specified before running the inference. Given the dimensionality of our dataset, we fit the model with a number of states from 2 to 8 and evaluated for each model order the following indices: the FE and the avLL, as indices of fit goodness; the AIC (Hero Akaike, 1973) and the Bayes Information Criterion (BIC; Schwarz, 1978) as parsimony indices.

In addition, for each model order and for each IC within each state, we assessed the uncertainty of the μ _k estimates, by evaluating its coefficients of variation (CVs), defined as:

$${\mathit{CV}}_k=100\times {\sqrt{\mathit{diag}\left({\mathrm{\Omega }}_k\right)}}^{-1}$$

The CV value ranges from 0 to 100, where 0 represents no uncertainty.

To summarize the uncertainty associated with the μ _k estimates as the model order K increased, for each K, we computed the average and the SD of the CV inside each state. Then, for each K, the ratio between the CV's mean SD and CV's average value across states was evaluated.

Therefore, the choice of the number of states was made taking into account not only the FE, avLL, AIC, and BIC, but also the CV's ratio index. Moreover, after fixing the model order, to highlight the less and more precise μ _k estimates, we also computed the ΔCV, defined as the distance between each IC's CV and the average CV ($\overline{\mathit{CV}}$) among ICs within the same state:

$$\Delta \mathit{CV}={\mathit{CV}}_{{\mathit{IC}}_m}-\overline{\mathit{CV}}m=1,..,M$$

2.5. Part 2: Differences between young and old subjects

2.5.1. Hidden Markov Model—Chronnectome

In addition to the HMM estimates, the model allows to obtain for each subject the probability of each state being active at each time point, $\mathit{\text{Gamma}}.$ This probability was then exploited as input to the Viterbi algorithm, to find the most likely sequence of states for each subject.

To describe subject‐specific temporal characteristics of brain states, three metrics, that defined the so called “chronnectome,” were evaluated starting from the Viterbi path:

• the fractional occupancy (FO), defined as the proportion of time that each subject spends in each state,

• the lifetime (LT) of each state, defined as the duration of the visits to that particular state,

• the switching rate (SR), defined as the frequency of transitions between different states.

These subject‐specific metrics were then averaged between young and old subjects and, given their non‐Gaussian distribution, a two‐sample Kolmogorov–Smirnov (K–S) test followed by multiple comparison correction (False Discovery Rate‐FDR, α = .05) was applied for statistical testing of differences between the two groups.

Finally, to investigate the relation between SR and behavior, we performed a logistic regression analysis to predict individual SR from the pattern of behavioral scores covering different domains (see Supporting Information for further details).

2.6. Brain states graph metrics

To detect the network organization of the estimated brain states, firstly the states Pearson's correlation matrices were derived from the corresponding covariance matrices ∑ _k (∑ _k  = Ω _k ⁻¹ ). Then, a graph theory‐based approach was exploited to summarize the FC properties. Two metrics were used: the strength (STR) to describe FC global properties, and the local efficiency (EL) to quantitatively investigate the behavior at the local level. The computation was performed with the Brain Connectivity Toolbox (BCT; Rubinov & Sporns, 2010). Before evaluating the graph measures, a proportional threshold approach (Achard & Bullmore, 2007) was applied to FC of each state. The 20% of the strongest edges were retained ensuring equal density across states.

A two‐sample K‐S test followed by multiple comparison correction (FDR, α = .05) was applied to test for significant differences between states graph metrics. This analysis allowed us to characterize the topological properties of the states FC at the whole brain level, but it was blind to graph measures differences at the level of single RSNs. For this reason, to compare STR and EL across RSNs, we introduced two novel measures, $\mathit{\text{nSTR}}$ and $\mathit{nEL}$, that were evaluated for each graph metric within each of the 11 functional domains ($i$), normalizing each measure specific for one state with respect to those computed across all the states:

$$\mathit{\text{nSTR}}=\frac{\overline{{\mathit{STR}}_{k,i}}-\overline{{\mathit{STR}}_{\mathit{all},i}}}{\mathit{std}\left({\mathit{STR}}_{\mathit{all},i}\right)}\mathit{nEL}=\frac{\overline{{\mathit{EL}}_{k,i}}-\overline{{\mathit{EL}}_{\mathit{all},i}}}{\mathit{std}\left({\mathit{EL}}_{\mathit{all},i}\right)}k=1:6;i=1:11$$

Furthermore, to investigate the organization of RSNs in each state at the functional module level, we applied the Louvain's community detection algorithm (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008) on the thresholded FCs. Given the non‐deterministic nature of the algorithm, we repeated the community assignment 50,000 times. Then, to obtain the most representative modularity, we first created for each state and each of the 50,000 iterations, the corresponding modular matrix, assigning to each node the index of the module in output by the function, then, from these 50,000 matrices, we computed the mode matrix and a binary matrix indicating the assignments which were present in more than 95% of the realizations. The final modular matrix of each state was hence obtained by multiplying the binary and the mode matrix. Further analyses on the integration and segregation of RSNs based on the modularity matrices are reported in Supporting Information. To quantify the similarity of the community assignment obtained for each state, after binarizing the modular matrices, we computed the Sorensen‐Dice similarity coefficient between each pair of states matrices both considering the intra‐domains connections (intra‐Dice) and considering the inter‐domains ones (inter‐Dice).

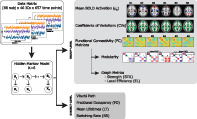
The schematic workflow followed for the analysis is reported in Figure 1. A glossary table is reported in Supporting Information.

FIGURE 1.

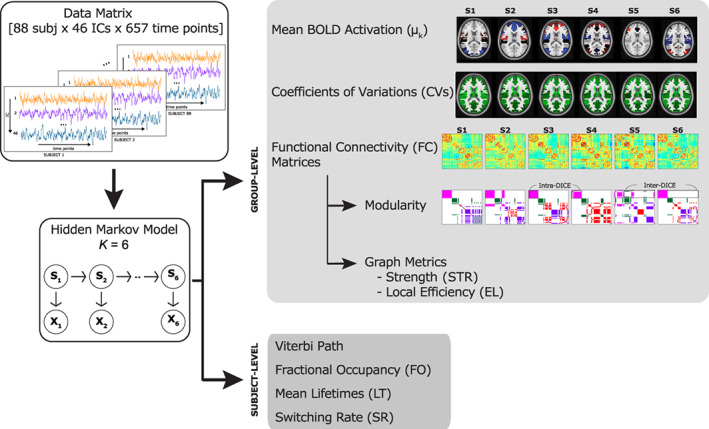
Scheme of the processing workflow employed for the analysis. Starting from the data (matrix of dimensions 88 subjects × 46 independent components (ICs) × 657 time points) a Hidden Markov Model with six states was inferred

3. RESULTS

3.1. Part 1: Methodological considerations related to HMM

3.1.1. Choice of initialization algorithm

After testing the two initialization algorithms with different model orders, we detected negligible differences: the results obtained for the μ _k estimates and for $\mathit{\text{Gamma}}$ were not affected by this choice. Therefore, the HMM‐MAR initialization (i.e., the toolbox default option) was employed for further analysis and the results presented in the following sections are based on this type of initialization adopted. Further comparisons of the interplay between the initialization algorithm and the model orders are reported in Supporting Information.

3.1.2. Choice of the model order

Table 1 reports the values of the indices evaluated for the choice of the model order. The FE had a decreasing trend as the number of states increased, showing no negative peaks, thus it was not informative for model selection purposes. Both AIC and BIC were not informative too, as they suggest the lowest order (K = 2). The avLL always assumed negative values. This is also the reason why, when implementing AIC and BIC formula, both the indices suggested the lowest order. However, the avLL showed a non‐monotonous trend, with a maximum peak value reached for K = 6, corresponding to the maximization of the log‐likelihood in the tested range of K.

TABLE 1.

Different indices for the choice of the model order obtained after the inference at the group level (i.e., combining young and old subjects together) are reported

Model order	FE	avLL	AIC	BIC	SD/mean
2	2767676	−18285	276680	1352976	0.17
3	2746036	−21496	403162	2017627	0.19
4	2734664	−28209	536653	2689307	0.19
5	2725354	−27130	654562	3345422	0.19
6	2717131	−26139	772651	4001735	0.19
7	2709337	−29693	899836	4667162	0.20
8	2702429	−28785	1018101	5323687	0.20

Note: In the first column the lowest free energy value, obtained among the 200 realizations is reported. Starting from this value, we computed the average log‐likelihood (second column), Akaike (third column), Bayes Information Criterion (fourth column), and ratio between the SD and mean values computed on the averaged CVs within a state (fifth column). The two indices that were informative for the model selection are marked in bold.

To investigate if the model with six states led to reliable estimates of the parameters, we also quantified the CVs of the estimates as the model order increases and then we computed the ratio between the SD of the CVs and their average value, obtained by averaging across ICs and states. As shown in the last column of Table 1, among different model orders, the ratio was almost comparable, and, as expected, showed an increasing trend as K increased. In terms of homogeneity within each state, the configuration with K = 6 resulted the best. Thus, considering avLL and the reliability of the estimates through the CVs, we set K equal to 6.

3.1.3. Group‐level characteristics of brain states

Mean activation (μ _k )

For each brain state (henceforth referred to as S1, S2, S3, S4, S5, and S6), Figure 2 shows the spatial distribution of the μ _k estimates at the whole‐brain level. For visualization purposes, the spatial map of each state was thresholded by setting the lower threshold to half of the maximum absolute mean value and the higher one to the maximum absolute mean value, respectively for positive and negative μ _k values in that particular state. Negative activations are displayed in blue‐scale and positive activations in red‐scale. The highest positive values in S1 are associated with the AUD and CON domains, whereas the negative with the VIS and DAN (Figure 2a). In S2, the SMN, AUD, and CON show higher positive deviations from the average, whereas the DMN, FRN, and CER higher negative ones (Figure 2b). S3 highlights positive values for the DMN, FRN, and CER, whereas negative values are associated with SMN, AUD, DAN (Figure 2c). In S4, positive values are associated with the AUD, FPN, FRN, and CER, whereas negative values with the BG (Figure 2d). S5 shows positive values associated with AUD, CON, FPN, CCN, and FRN and negative values associated with DMN, CER, BG (Figure 2e). S6 highlights positive values for the DAN, CER and for most ICs of the VIS and DMN. Negative mean values are associated with the AUD, CON, FRN, BG (Figure 2f).

FIGURE 2.

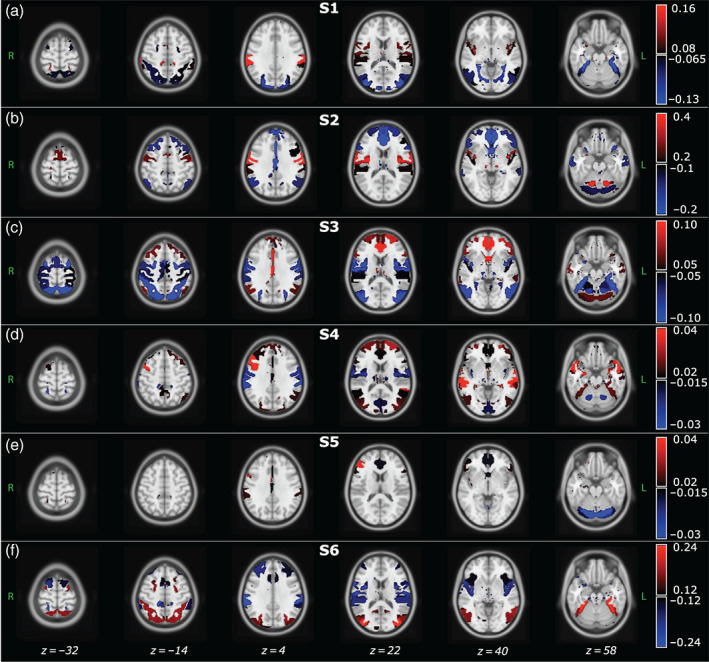
Each panel shows the axial view of the spatial distribution of the mean BOLD activation (μk) estimates, obtained for each brain state. Since the HMM was inferred at the population level, that is, concatenating the IC time courses of young and old participants, the μk values are group‐level estimates. Color bar values range from half of the maximum absolute mean value to the maximum absolute mean value, respectively for positive and negative μk values obtained in each state. ICs with mean activation values out of these bounds are not displayed. Negative values are displayed in blue‐scale, whereas positive values in red‐scale. The spatial distributions are overlaid to the MNI atlas, shown in gray scale. The labels S1, S2, and so forth refer to State 1, State 2, and so forth

Further details on μ _k estimates are provided in Figure S1, where for each IC and brain state we show the associated mean activation value.

Reliability of the states

To quantify the precision of the μ _k estimates presented above, we computed the CVs. Figure 3 shows the spatial distribution of the ΔCVs in green scale and, for a better comparison between the six states, the color bar values range from −35 to 35% with respect to the average CV value within each state. Ranking the most reliable states in terms of CVs, resulted in S4 ($\overline{\mathit{CV}}$= 47.6%), S3 ($\overline{\mathit{CV}}$= 51%), S5 ($\overline{\mathit{CV}}$= 51.5%), S1 ($\overline{\mathit{CV}}$= 53%), S6 ($\overline{\mathit{CV}}$= 60.4%), and finally S2 ($\overline{\mathit{CV}}$= 70.4%). Overall, when comparing the reliability across states and within functional domains, the μ_k values associated with the DAN show the highest reliability, whereas those associated with FRN, CER, and BG are the least reliable in all the states with CVs above the average level, as shown in Figure 3 in bright green. These results imply that the DAN network is, among all, the most reliable, in terms of precision of the estimates, in its representation within each state. Although CV values of all the SMN components were over the average in S1, S2, and S6, for all the other functional domains the trend of the CVs could not be summarized among states. Further details on the CVs patterns across RSNs are provided in Figure S2, where for each IC and brain state we show the associated CV.

FIGURE 3.

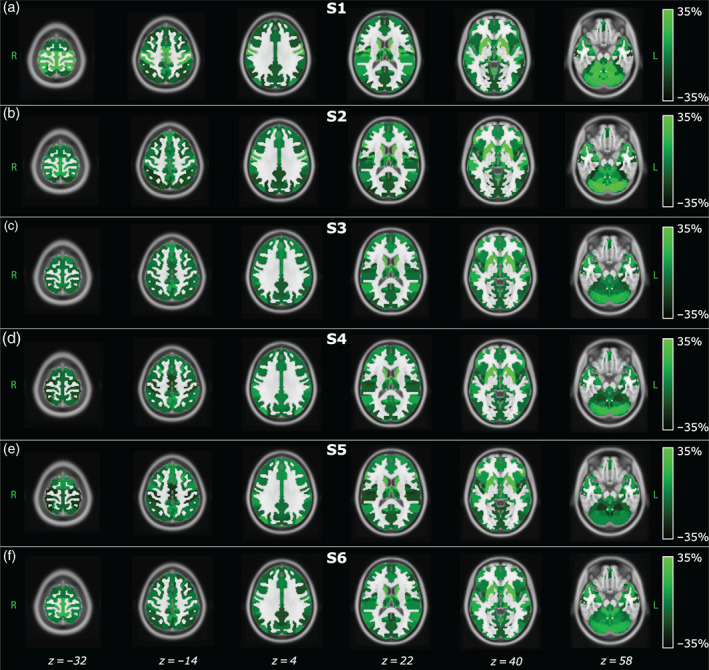
Spatial distribution of the distance between each IC's CV and the average CV among ICs within the same state (ΔCVs) obtained for each brain state. Since the model was inferred at the population level, that is, concatenating the IC time courses of young and old participants, these maps represent group‐level estimates. Positive values represent an increment in CV with respect to the mean value of the CVs obtained in each state. Therefore, bright colors are associated with more uncertain ICs. The spatial distributions are overlaid to the MNI atlas, shown in gray scale. The labels S1, S2, and so forth refer to State 1, State 2, and so forth

3.2. Part 2: Differences between young and old subjects

3.2.1. Subject‐specific temporal characteristics

Transition probabilities matrices

In Figure 4, the probabilities of transition, without considering the probabilities of persistence in the same state (i.e., the diagonal of the Θ_k matrix), are reported for the two groups separately. Particularly for the young subjects (Figure 4a,b), the probabilities are higher among S6 and S1 (prob = 0.56), S4 and S1 (prob = 0.48), S1 and S6 (prob = 0.45). Whereas for the old subjects (Figure 4c,d), the transition probabilities are higher among S2 and S3 (prob = 0.63), S6 and S3 (prob = 0.49), S3 and S2 (prob = 0.47). Interestingly, both the dynamic of the transitions is characterized by the presence of one loop, composed by different states through the young and old, but with the same behavior, that is, when a young subject reaches S1, he seems to circle between S6 and S1 in a closed loop, while, when and old subject reaches S3, he holds in a circle between S2 and S3. As highlighted in the corresponding spatial maps, the first set of loops (Figure 4b) involved mainly occipital and parietal regions, while the second set (Figure 4d) frontal regions.

FIGURE 4.

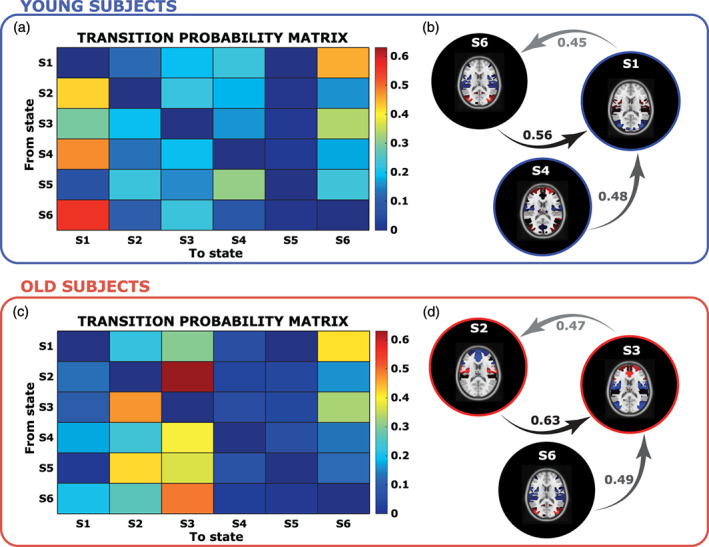
In Panels (a) and (c), the transition probabilities from one state (y‐axis) to another (x‐axis), for the young and O, are reported. Finally, Panels (b) and (d) show the three top most likely transition probabilities and links

Chronnectome

The differences between the two groups are evident when comparing the aforementioned state‐relevant temporal metrics. In Figure 5a, we show the fractional occupancy distribution, obtained for the two groups in each brain state. On average, the time spent from the young subjects in S1 was 39% of total rs‐acquisition and in S4 28%. While the old subjects spent 20% of the time in S2, 39% in S3 and 12% in S5. Instead, S6 was characterized in equal proportion by both the groups: 18% by young and 19% by old. The K–S test pointed out statistical differences (p‐value < .01) between groups: young subjects spend more time in S1 and S4, whereas old subjects in S2, S3, and S5. Instead, the time spent in S6 did not significantly differ between young and old.

FIGURE 5.

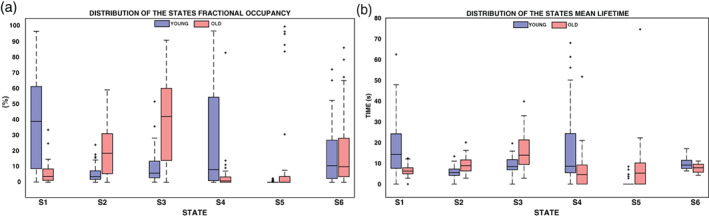
In Panels (a) and (b), the distribution in different states of fractional occupancy and mean LT, respectively, is reported in blue for the young subjects and in red for the old subjects. The bottom and top edges of each box indicate the 25th and 75th percentiles. The outliers are represented by the “+” symbol. In each boxplot, the solid line indicates the median, so for example, the median value of the FO for young subjects in S1 is 39%

In Figure 5b, the distributions of the mean lifetime, ranging from seconds to tens of seconds, are represented by boxplots. For this metric, statistical differences between groups were found in S1 (p‐value = 1e−07), S2 (p‐value = 1.6e−04), and S3 (p‐value = 1.7e−04).

Lastly, we evaluated for each subject his switching rate among states and then we computed the median value for the young and the old groups, respectively equal to 0.10 Hz and 0.11 Hz. No statistical difference was found between the two groups.

3.2.2. Brain states graph metrics

In Figure 6, we report the states FC matrices, from which, after proportional thresholding, we computed the STR, EL, and modularity indices. Since the FC matrices were obtained at the group‐level, without distinction between the two subgroups of young and old subjects, the graph metrics and modularity indices are representative of the whole population.

FIGURE 6.

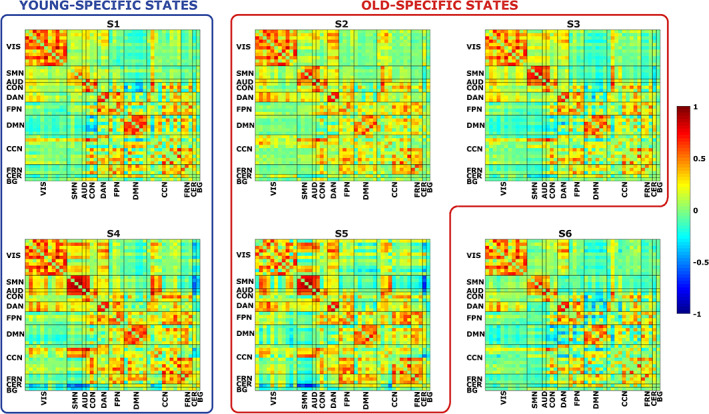
Each panel represents the FC matrix associated to a particular brain state (S1, S2, etc.). In both the x‐ and y‐axis, we have the 46 ICs, divided in the 11 functional domains. Warm colors represent high positive correlations values between ICs, whereas cool colors represent high anti‐correlations values. We grouped together states mostly populated by young subjects (blue box) and by old subjects (red box)

The states did not differ in terms of global properties of the associated graph: no statistically significant difference was found in the node strength distribution. Nonetheless, for this metric, S4 and S5 resulted to have the highest values (on average: STR_S1 = 4.1, STR_S2 = 4.02, STR_S3 = 3.93, STR_S4 = 4.73, STR_S5 = 4.46, and STR_S6 = 3.73). On the contrary, statistically significant differences (p‐value <0.01) were found at the local level, where the local efficiency of states S4 and S5 was significantly greater than in states S2, S3 (on average: EL_S1 = 0.36, EL_S2 = 0.34, EL_S3 = 0.34, EL_S4 = 0.42, EL_S5 = 0.38, and EL_s6 = 0.33).

In Figure 7, we report the results of the analysis carried out at the functional domain level, for the STR and the EL measures, respectively. Taking into account only the extreme values exceeding ±1.5SD, we found that in S1 the STR of DMN was significantly higher than in the remaining domains; in S4 the same happened for the VIS domain and in S5 in FPN domain, whereas negative deviations from the average (i.e., low STR) were found for S2 in FPN and for S6 in CON. Considering the EL, we found only positive deviations and in particular for S4 in AUD, CON and CCN, for S5 in FRN. Taken together, these results confirmed our hypothesis that moving to a more detailed characterization of the graph represented by the specific domains, a better description of the states in terms of STR and EL is possible. In particular, we were able to capture specific properties, especially for three states (S1, S4, and S5), that presented more integrated behavior in different functional domains. Furthermore, this analysis confirmed the added value of the information provided by the BOLD activation parameter (μ _k ), with others derived from a deeper investigation of some properties of the nodes at the graph‐level. In fact, even if some functional domains did not exhibit a high BOLD activation, they resulted to play a crucial role at the graph‐level. For example, while the DMN showed low BOLD activation in S1, it was the only domain to present the highest STR, suggesting its potential role of hub in that particular state.

FIGURE 7.

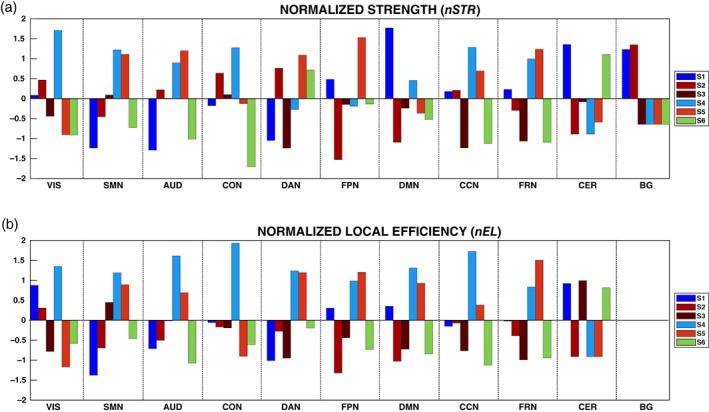
In Panels (a) and (b), we show the normalized values of the strength (nSTR) and local efficiency (nEL) for the states, colored differently, and in the functional domains. Given that, after proportional thresholding of the FC matrices, the local efficiency resulted to be 0 for the basal ganglia (BG) in all the states, in Panel (b) no values of nEL are reported for the BG. The labels S1, S2, and so forth refer to State 1, State 2, and so forth

In Figure 8, for each state, we depict the modular organization derived from multiple repetitions of the Louvain's community detection algorithm. Instead of the classical graph representation for the module assignment, we arrange the results in a matrix form to better highlight the assignment of each IC to a specific module and how this relates to the assignment of the other ICs. In the same figure, we also report the states modularity index, obtained by averaging across the 50,000 realizations. Even if no differences were found in this metric, we can notice a trend in our results, in particular, S5 assumes the lowest value of modularity, reflecting a situation of integration between networks, whereas S1 shows the highest value, reflecting a segregation of the networks, which is confirmed by the number of detected communities that resulted to be 4 for this state and 5 for all the others. Interestingly, even if S5, an old‐specific state, followed by S4, a young‐specific state, presented a low modularity in comparison to the others, they also exhibited the highest values for STR and EL, as reported before.

FIGURE 8.

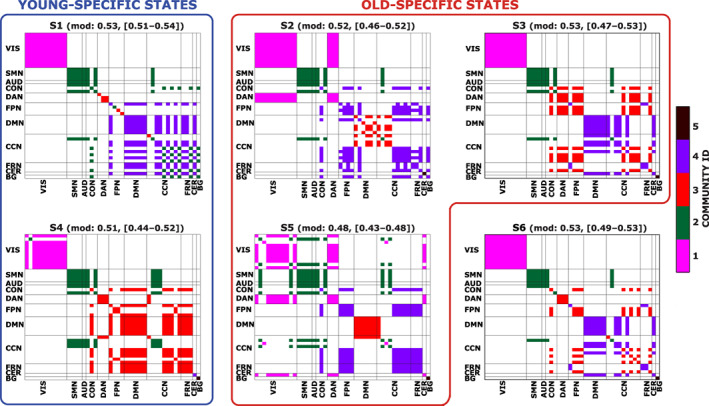
Each figure represents the modular organization of a brain state (S1, S2, etc.) obtained as explained in the main text. Different colors are representative of a distinct community. In both the x‐ and y‐axis, we have the 46 ICs, divided in the 11 functional domains. In the title, we also report the mean modularity value, obtained across the 50,000 realizations, together with the minimum and maximum values. We grouped together states mostly populated by young subjects (blue box) and by old subjects (red box)

A detailed description of the results of intra/inter Dice computation to detect integration/segregation of the RSNs is provided in Supporting Information.

We summarize the main findings for each state:

• S1: state with the highest segregation of the RSNs; loss of segregation of the FPN; DAN completely segregated; BG highly integrated; CER highly integrated.

• S2: loss of segregation of the DMN; DAN completely integrated with VIS; CER completely segregated; BG highly integrated.

• S3: DAN integrated with many ICs of cognitive RSNs; CER highly integrated.

• S5: state with the highest integration between RSNs, especially for VIS, DAN, and CER; DMN completely segregated.

• S6: DAN completely segregated; CER highly integrated; BG completely segregated.

4. DISCUSSION

In this article, we have explored the effects of normal aging in the spatiotemporal organization of brain states, carrying out a data‐driven analysis based on HMMs. After modeling the ICs time courses obtained at the whole‐brain level, we implemented a novel method to select the optimal order of HMM in a quantitative manner by balancing the model complexity with the precision of the hidden parameter estimates. Then, we derived six states and characterized them by evaluating the properties of FC matrix of each state, and the mean level of BOLD activation of each RSN. In contrast to other approaches, one of the advantages of using this method is in that it allows the quantification of the CVs, an index about how uncertain the estimates of specific brain regions are.

At the temporal scale, the states were described by the most frequent transition patterns between them. In this way, we could derive the time spent in each state, the average duration of the state visits, and the frequency of transitions between different states. These metrics were compared between young and old subjects to investigate possible links between aging and temporal dynamics of brain states. From this analysis, we could observe that two states, namely, S1 and S4, were mostly occupied by young subjects, while three states, namely, S2, S3, and S5, by old subjects. The remaining state, S6, was populated in equal proportion by the two groups. Moreover, given the extensive literature supporting the theory of increasing functional integration between networks with increasing age, we conducted a graph‐based analysis that allowed us to distinguish states characterized by high network segregation rather than high integration. In particular, we found that old‐specific states exhibited an overall more integrated topology with respect to a more segregated in young‐specific states.

The findings reported are not expected to be driven by arousal differences between young and old subjects. Indeed, a recent study (Daneault et al., 2021) has found no statistically significant differences in FC between young and old people and no interaction with age when comparing wakefulness and N1 during 100 minutes of eye‐closed acquisition. It is of note that the subjects employed in our study were asked to keep their eyes‐open for the entire duration of the acquisition and this should prevent N1 stage (Gu, Han, & Liu, 2019). However, even if we assume that some of them fell into a N1 sleep stage, it does not foresee significant differences in FC between young and old, based on (Daneault et al., 2021).

4.1. Model order choice

The choice to adopt HMM instead of others approaches to study dynamic FC, was driven by the possibility to select the model order in a quantitative way, exploiting the principle of parsimony that seeks to balance the goodness of the fit with the precision of the estimates. In fact, relying only on the free energy cost function, the optimal model would not be found, since with the increase of the model order, the free energy decreased, without showing minimum values able to lead us in the model selection. In contrast with free energy results, AIC and BIC indices showed their maximum value for model order equal to 2. To find the optimal model, it was therefore necessary to introduce and evaluate other indices for different model orders, which are the average log‐likelihood, as indicator of the goodness of the fit, and the CVs, as indicators of reliability of the estimates. To our knowledge, this is the first study that attempts to solve the model selection issue, making a compromise between the free energy, which pushes towards a hyper parameterized model and indices of parsimony that push towards a simplification of the model, also adding information about uncertainty of the estimates.

4.2. Group‐level characteristics of brain states

At the spatial level, we obtained the maps of the mean level of BOLD activation, which allow us to distinguish high activation states (S1, S2, S3, and S6) from baseline states (S4 and S5) in which the RSNs present a mean level of activation. Almost all the spatial maps here presented show patterns in line with a previous work (Vidaurre et al., 2018) that employed UK Biobank data and inferred 8 states, indicating that even with our small sample size, HMM application leads to reproducible results. Comparing our results with (Vidaurre et al., 2018), we observed a match between: S2 and the SMN state; S3 and the DMN; S6 and the VIS state. The only exception was for the primary visual that in our case are mapped in another state. This mismatch can be explained not only by the different sample sizes, but also by the different age of the sample and the different number of inferred states.

The choice of the HMM for the study of the dynamic connectivity, also allowed us to quantify the uncertainty of the estimates through the CVs. Thanks to the introduction of this index in the study, we were able to distinguish areas associated with higher uncertainty, such as FRN, CER, and BG, that were also consistent across brain states. As these three functional domains were found to be associated with worse CVs, the conclusions drawn about these domains in specific states should thus be taken with caution. From a physiological standpoint these results are not unexpected, as the BOLD signal in the basal ganglia and cerebellum has a quite different underpinning structure in comparison with cortical regions, both in terms of neuroreceptors (Palomero‐Gallagher & Zilles, 2018) and iron content (Cherubini, Péran, Caltagirone, Sabatini, & Spalletta, 2009).

4.3. Subject‐specific temporal characteristics

In line with the study of Xia et al. (2019), we found that the occupancy of the two groups in each state was statistically different: S1 and S4 populated mainly by young subjects, whereas S2, S3, and S5 by old subjects. This finding suggests a clear separation between occurring patterns of mean BOLD activations as well as FC in young people rather than in elderly.

Even if no significant differences were found in the SR, we can note a positive trend with increasing age. This result is well in line with previous studies, which observed an increased SR in healthy elderly subjects (Malagurski, Liem, Oschwald, Mérillat, & Jäncke, 2020) or a significant association between aging and SR increase in less performant older adults with low cognitive performances (Cabral et al., 2017).

Moreover, in relation to the transition probabilities between states, we found for young subjects a main loop between S1 and S6 with high probability to remain in S1, the state with the highest segregation of RSNs, and on the other hand for old subjects, a main loop between S2 and S3, two very integrated states, where the DAN serves as a bridge for the integration between RSNs of different functional domain.

4.4. Brain states graph metrics

The graph‐based analysis carried out on the sparse FC matrices, pointed out very interesting results, both considering the entire network or specific domains. Previous studies (Andrews‐Hanna et al., 2007; Damoiseaux et al., 2008) suggested that the DMN components undergo a FC modification during aging. This result was confirmed by our analysis conducted at the functional domain level. Indeed, young‐specific states had a much higher strength in the DMN with respect to old‐specific states.

Many deviations from the average level were also found in the two baseline states: S4 exhibited the highest strength values in the VIS, and also local efficiency values in the AUD, CON, and CCN. Instead, S5 revealed higher strength in the FPN and local efficiency in the FRN. The other two old‐specific states, S2 and S3, did not show strongly above average behaviors, in fact both the strength and the local efficiency were in general below the average level, with a significant decrease of strength for S2 in the FPN. This network plays a central role in the executive functions, attentional processes and working memory, and many studies found an increased functional activity in the FPN during cognitively demanding tasks (Fox, Corbetta, Snyder, Vincent, & Raichle, 2006; Smith et al., 2009), but also a positive correlation between ageing and weaker within network connectivity (Betzel et al., 2014) and decreased local efficiency (Geerligs et al., 2015). Moreover, many groups detected an altered activation of the FPN both in mild cognitive impairment and Alzheimer disease (Agosta et al., 2012; Wang et al., 2012) that led to an impairment of the performances during cognitive tasks (Yetkin, Rosenberg, Weiner, Purdy, & Cullum, 2006; Zanchi et al., 2017). Therefore, we suppose that the weak strength and local efficiency of the FPN in S2, could be associated with a cognitive decline due to age progression.

In general, in literature, an increased FC between RSNs in elderly has been reported (Betzel et al., 2014; Chan et al., 2014; Geerligs et al., 2015; Song et al., 2014) and it is hypothesized that this change is due to a loss of modularity and segregation between networks (Chan et al., 2014; Song et al., 2014). Our modularity analysis revealed that while S1, a young‐specific state, was mostly characterized by a greater segregation of the networks, S5, populated only by the elderly, was the one that presented more integration between networks. The intra‐Dice results highlighted loss of segregation in the CCN for S1, S4, and in the FPN for S1. This loss of FPN integrity together with the interaction between the BG and many ICs of cognitive domains could shed light on the compensatory role of the BG for the maintenance of general cognition.

Interestingly, in line with previous studies (Chong et al., 2019; Damoiseaux et al., 2008) that reported the association between older age and lower functional integrity in the DMN, we detected a loss of integrity of the DMN only for the old‐specific S2.

In summary, we found that young‐specific states presented low segregation in the FPN and CCN, and high integration of the DMN, while old‐specific states an overall more‐integrated topology, especially between the DAN and many other domains, but also different patterns of integration rather than segregation of the DMN. The organization of RSNs in a more integrated‐topology is confirmed by a previous study (Bagarinao et al., 2019), which performed analysis at the network‐level and found a decrease in the shortest path length and an increase in global efficiency with age (Song et al., 2014, p. 201).

4.5. Limitations

This study is not exempt from limitations. First, we inferred HMM to the time series of all the subjects together, without distinction between young and old, thus obtaining parameters estimates at the group‐level. An alternative approach would have been to fit the model separately for the two groups and thus to describe properties specific to the population of interest. However, this would have significantly increased the number of parameters to be estimated and, with the relatively low sample size at disposal, no such reliable estimates would have been obtained. Moreover, it would not have allowed a direct comparison between state metrics of the two different models.

Regarding limitations, some might raise the issue that movement may affect the results. However, we found low values of FD in both the groups (on average 0.11 mm for young people and 0.17 mm for old people) and the pre‐processing we followed through ICA included discarding motion‐related components and a subsequent despiking step on the IC's time courses. Thus, we cannot find any reason to support that our findings are driven by motion differences between young and old people.

5. CONCLUSIONS

In this study, we performed a whole‐brain dynamic FC analysis, through Hidden Markov Models, to characterize brain states in the healthy aging population. This approach embeds the entire population heterogeneity in the model and allows to decode the dynamics of the time‐varying FC and to capture the individual transitions between brain states. We selected the best model in an automatic and mathematically reliable way and, to our knowledge for the first time, we provided a tool to quantify the uncertainty of the estimates. The results showed that different states and within them specific brain regions, have distinct levels of accuracy, therefore caution must be paid in the physiological interpretation of the results. Indeed, among the six inferred states, we found the DAN associated to the most accurate μ _k estimates, while the FRN, CER, and BG to the least ones. Moreover, we found that the time spent in each state was different among groups, in fact in terms of fractional occupancy, a clear separation between states was observed. This allowed us to define young‐specific states rather than old‐specific states. The graph‐based and modularity analysis revealed an overall more integrated networks topology in old‐specific states. We also found an increase in strength with increasing age in the DMN, which can be explained by the highly integrated topology of this network in young‐specific states. On the contrary, in old‐specific states, the DMN was found to be highly segregated or to lose its integrity. Furthermore, we observed that the transitions between states were not random, but more likely to occur between specific states and following preferential paths. For young subjects, these paths were characterized by states at high segregation of the networks. On the contrary, old subjects fell in a loop of states where the networks were very integrated, and the DAN acted as a connecting point for the network communication.

Although previous studies assumed the stationarity of FC during the resting acquisition, our results instead suggested a continued transition between states, characterized by different patterns of connectivity between networks. Therefore, static approaches cannot be sufficient to capture the rich dynamics governing transient brain states in the aging population.

AUTHOR CONTRIBUTIONS

Manuela Moretto: Conceptualization, software, methodology, formal analysis, data curation, writing—original draft, writing—review & editing, visualization. Erica Silvestri: Conceptualization, software, methodology, formal analysis, data curation, writing—review & editing. Andrea Zangrossi: Formal analysis, writing. Maurizio Corbetta: Writing—review & editing. Alessandra Bertoldo: Conceptualization, methodology, writing—review & editing, supervision, project administration.

Supporting information

Appendix S1: Supporting Information

Moretto, M. , Silvestri, E. , Zangrossi, A. , Corbetta, M. , & Bertoldo, A. (2022). Unveiling whole‐brain dynamics in normal aging through Hidden Markov Models. Human Brain Mapping, 43(3), 1129–1144. 10.1002/hbm.25714

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.