Abstract
Numerical estimation of arrays of objects is faster and more accurate when items can be clustered into groups, a phenomenon termed “groupitizing.” Grouping can facilitate segregation into subitizable “chunks,” each easily estimated, then summed. The current study investigates whether spatial grouping of arrays drives specific neural responses during numerical estimation, reflecting strategies such as exact calculation and fact retrieval. Fourteen adults were scanned with fMRI while estimating either the numerosity or shape of arrays of items, either randomly distributed or spatially grouped. Numerosity estimation of both classes of stimuli elicited common activation of a right lateralized frontoparietal network. Grouped stimuli additionally recruited regions in the left hemisphere and bilaterally in the angular gyrus. Multivariate pattern analysis showed that classifiers trained with the pattern of neural activations read out from parietal regions, but not from the primary visual areas, can decode different numerosities both within and across spatial arrangements. The behavioral numerical acuity correlated with the decoding performance of the parietal but not with occipital regions. Overall, this experiment suggests that the estimation of grouped stimuli relies on the approximate number system for numerosity estimation, but additionally recruits regions involved in calculation.
Keywords: angular gyrus, approximate number system (ANS), calculation, groupitizing, numerosity perception
Numerosity estimation is more accurate when items can be clustered into groups.
Common frontoparietal areas are activated by different spatial arrangements.
Estimation of grouped stimuli recruits additional areas such as angular gyrus.
1. INTRODUCTION
Humans can quantify the number of objects in a scene at a glance with reasonable accuracy (Dehaene, 2011; Jevons, 1871). This ability is seen across the animal kingdom and thought to rely on a non‐verbal approximate number system that is faster but less accurate than verbal counting (Dehaene, 2011; Nieder, 2016). However, recent behavioral studies have shown that participants are faster and more precise when estimating the numerosity of briefly presented arrays when the items can be easily grouped into small clusters (2–4), within or around the subitizing range (Anobile, Castaldi, Moscoso, Burr, & Arrighi, 2020; Ciccione & Dehaene, 2020; Maldonado Moscoso, Castaldi, Burr, Arrighi, & Anobile, 2020). Several cues can aid grouping, including color, spatial and temporal distribution, and the effect generalize to other sensory modalities, including auditory sequences (Anobile, Castaldi, Maldonado Moscoso, Arrighi, & Burr, 2021). This phenomenon has been termed groupitizing and shown to depend on subitizing and calculation abilities (Anobile et al., 2020, 2021; Beckwith & Restle, 1966; Ciccione & Dehaene, 2020; Starkey, Spelke, & Gelman, 1990; Wege, Trezise, & Inglis, 2021; Wender & Rothkegel, 2000). While preschoolers do not benefit from grouping strategies, school‐age children do, and the grouping advantage parallels the development of their arithmetical abilities (Starkey & McCandliss, 2014). Recently, Maldonado Moscoso et al. (2020) showed that like subitizing, groupitizing is an attention‐based process, annulled in adults during an attention‐grabbing double task. The study also showed that participants with better calculation skills benefit more from grouping, suggesting that they might spontaneously apply summation and multiplication strategies to solve the task. Most likely, when presented with groupable stimuli, participants automatically parse the array into subitizable groups and then sum the subitized estimates.
Overall, these behavioral results suggest that numerosity estimation may rely on different strategies, depending on the spatial arrangement of the visual arrays. While ungrouped arrays may favor approximate or gross numerosity estimation, grouped arrays may automatically elicit the use of exact calculation and fact‐retrieval strategies (such as recall of rote‐learned multiplication tables or simple additions). Do the neural responses underlying the numerical estimation process also depend on the spatial arrangement of the array, especially in cortical regions known to be involved in arithmetical calculation? Imaging studies have identified an extended network that is activated during arithmetical calculation, comprising the left or bilateral superior and inferior parietal lobules, which delimit the intraparietal sulcus (IPS), the angular gyri, the inferior and middle temporal lobes, the prefrontal cortex, the cingulate gyrus and the insula (Amalric & Dehaene, 2016; Arsalidou & Taylor, 2011; Bugden, Woldorff, & Brannon, 2019; Chochon, Cohen, Moortele, & Dehaene, 1999; De Smedt, Holloway, & Ansari, 2011; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Grabner et al., 2007; Grabner, Ansari, et al., 2009; Holloway, Price, & Ansari, 2010; Ischebeck, Zamarian, Schocke, & Delazer, 2009; Kong et al., 2005; Lee, 2000; Menon, Rivera, White, Glover, & Reiss, 2000; Piazza, Mechelli, Price, & Butterworth, 2006; see also: Dehaene, Piazza, Pinel, & Cohen, 2003; Nieder & Dehaene, 2009, for a review). Within this network, some studies have reported that the frontoparietal areas showed more right‐lateralized activation when participants engaged in approximate numerical estimates and approximate calculation, and more left‐lateralized when participants performed exact calculations (Chochon et al., 1999; Dormal, Andres, Dormal, & Pesenti, 2010; Dormal, Dormal, Joassin, & Pesenti, 2012; Kucian, Von Aster, Loenneker, Dietrich, & Martin, 2008; Piazza et al., 2006; Pinel & Dehaene, 2010). At the level of the parietal lobe two key regions are known to be involved in arithmetical calculation: the region within and around the intraparietal sulcus and the angular gyrus. Calculation‐related activation of IPS has been reported both in adults and in children, and fine scale mapping localized this activation more precisely in the inferior‐lateral part of IPS (here named IPS excluding IPS0‐5; Amalric & Dehaene, 2016; Arsalidou, Pawliw‐Levac, Sadeghi, & Pascual‐Leone, 2018; Arsalidou & Taylor, 2011; Bugden et al., 2019; Castaldi, Vignaud, & Eger, 2020; Chochon et al., 1999; De Smedt et al., 2011; Kaufmann, Wood, Rubinsten, & Henik, 2011; Kawashima et al., 2004; Kong et al., 2005; Kucian et al., 2008; Menon et al., 2000; Peters, Polspoel, Op de Beeck, & De Smedt, 2016; Pinel & Dehaene, 2010; Venkatraman, Ansari, & Chee, 2005; Zhou et al., 2007; see also: Harvey, 2016; Nieder & Dehaene, 2009, for a review). IPS seems to be especially recruited more for procedural strategies, as opposed to fact retrieval (Polspoel, Peters, Vandermosten, & De Smedt, 2017; Tschentscher & Hauk, 2014). On the other hand, neuropsychological and other imaging studies have highlighted the role of the left angular gyrus during exact calculation and arithmetic fact retrieval (Cipolotti, Butterworth, & Denes, 1991; Dehaene et al., 1999; Gerstmann, 1940; Grabner et al., 2007; Grabner, Ansari, Koschutnig, Reishofer, & Ebner, 2013; Grabner, Ansari, et al., 2009; Grabner, Ischebeck, et al., 2009; Jackson & Warrington, 1986; Menon et al., 2000; Stanescu‐Cosson et al., 2000; Van Harskamp & Cipolotti, 2001; see also: Dehaene et al., 2003; Seghier, 2013, for a review).
To investigate the neural mechanisms underlying the groupitizing phenomenon, we scanned with fMRI participants while they estimated the numerosity of briefly presented grouped or ungrouped arrays. If participants use calculation strategies when estimating numerosity of grouped stimuli, we expect to find the areas involved in arithmetical computation and fact retrieval to be most strongly activated compared to when the same task is performed on ungrouped stimuli. The results show that numerosity estimation of grouped stimuli recruited regions that partially overlap with those involved in numerosity estimation of ungrouped stimuli, but with the additional contribution of the left hemisphere and the angular gyrus bilaterally. Moreover, the numerosity of grouped stimuli was best decoded from parietal areas, and classification accuracy in these areas, but not in primary visual cortex, correlated with behavioral numerical acuity of grouped stimuli (Weber fraction).
2. MATERIALS AND METHODS
2.1. Subjects and MRI acquisition procedure
Fifteen adult volunteers (10 males and 5 females, 28.2 ± 6.2 years old) with normal or corrected‐to‐normal vision participated in the study, both behavioral and fMRI scanning. The study was approved by the ethics committee of the University of Regensburg, and all participants gave written informed consent before commencing. Due to technical problems during the data acquisition, one participant could not complete the study and his data were therefore discarded from the analysis.
Functional images were acquired on a Prisma 3T scanner (Siemens, Erlangen, Germany) using 64 channel head coil (Erlangen, Germany) as T2*‐weighted fast‐saturation echo‐planar image (EPI) volumes with 2 mm isotropic voxels (slices number: 72; multiband factor: 3; repetition time [TR] = 2000 ms, echo time [TE] = 30, flip angle [FA] = 52). T1‐weighted anatomical images were acquired at 0.8 mm isotropic resolution (repetition time [TR] = 2,400, echo time [TE] = 2.18, flip angle [FA] = 8; 208 transversal slices were acquired). During the scanning head movements were minimized by padding and tape.
Visual stimuli were viewed through a mirror mounted on the head coil, which provided the participant with a full view of back‐projected stimuli (1,024 × 768 pixels subtending 40° × 30°) projected from a remote LCD projector (PROPixx, VPixx Technologies, Quebec, CA) onto a translucent screen located at the end of the scanner bore. Viewing distance was constant at 95 cm. Participants were instructed to provide occasional responses by pressing one of three buttons on an MRI‐compatible response box (Celeritas Fiber Optic Response System PS T‐101458, Psychological Software, Pittsburgh, PA).
2.2. Stimuli and experimental design
Prior to scanning participants were tested with a behavioral numerosity estimation task (following Maldonado Moscoso et al. (2020)) to measure the strength of the groupitizing effect in these participants. Participants estimated the numerosity of centrally presented arrays of items (numerosity range 5–17), either grouped or ungrouped. In the grouped conditions, each numerosity was organized into 2 to 4 clusters, each comprising a variable number items (between 2 and 6), resulting in the following configurations: 2, 2, 1; 3, 3; 3, 3, 1; 2, 2, 2, 2; 4, 4; 3, 3, 3; 3, 3, 3, 1; 3, 3, 3, 2; 3, 3, 3, 3; 4, 4, 4; 5, 5, 3; 4, 4, 3, 3; 4, 4, 4, 3; 4, 4, 4, 4; 5, 5, 6; 5, 4, 4, 4. All clusters except three (13 = 5, 5, 3; 16 = 5, 5, 6; 17 = 5, 4, 4, 4) contained 1 to 4 elements. Arrays were white items (0.4° × 0.4°) with black borders displayed, with overall luminance matched to the gray background. All but one item were squares, with the odd shape randomly selected to be a diamond, a triangle or a circle (with total area matched to that of the squares). Item location within each array was either randomly selected from 106 possible coordinates within the 6° × 6° stimulus area (ungrouped spatial arrangement) or selected within a maximum of 4 groups (each group spanning 1° × 1.5° and being located at 3° from the central fixation point), so that the items were grouped (grouped spatial arrangement). In the latter case, locations of individual items were selected out of the 12 possible coordinates included in the selected quadrant and each group of items was randomly assigned to one quadrant.
Participants sat at 57 cm from a 19″ screen monitor (60 Hz), in a quiet and dimly light room, and estimated the numerosity of grouped (3 blocks) or ungrouped (3 blocks) arrays. The presentation of the conditions was counterbalanced across participants, and they were not informed about the different spatial arrangement of the stimuli. Each trial started with a black central fixation point that turned white after 1 s and remained on the screen for the entire experiment. The first array was centrally presented after 1 s, followed by a blank screen. Participants called out the numerosity of the array as quickly and accurately as possible, neglecting the shape of the individual items. The experimenter entered the response on the numerical keypad and initiated the following trial. The numerosities and configuration patterns were randomly selected on every trial. Each participant performed 150 trials for each condition (ungrouped and grouped), with each numerosity presented on average 12 times, for a total of 300 trials for the entire numerosity estimation task. After the behavioral experiment, the experimenter debriefed the participants. All participants reported that they had spontaneously used arithmetical strategies (addition and/or multiplication of the subgroups) when the stimuli were grouped, while they mostly used estimation strategies when the stimuli were ungrouped. After the debriefing, participants were asked to use the same strategies they used during the psychophysical tasks during the scanning. At no stage during instruction was there any mention of “calculation strategies.”
During the fMRI scanning participants were centrally presented with arrays of 8, 12, or 16 items (similar to those used in the behavioral experiment: Figure 1a). Grouped stimuli were created with two different configurations, so that there was no systematic association between the numerosity shown within each group and the overall numerosity. Each 10‐min run was divided into two parts, in which participants performed a numerosity and a shape control estimation task on exactly the same stimuli, following the instructions (Figure 1b). The order of the two tasks was counterbalanced between participants. Instructions were displayed for 2 s before the first and the second half of the run, and specified whether participants had to attend to the number of items (number task) or to the shape oddball presented on every trial (shape control task). Four seconds after the instructions were turned off, the first array was briefly presented for 200 ms and participants attended to the cued dimension, and held this information in memory until the following trial was presented. After a variable ISI of 3.8–5.8 s, either a new array or a signal to respond – “Number?” or “Shape?”—was presented. If a new array was presented, participants had to update their memory with the new stimulus and no response was required. If the question appeared, participants had to either estimate the numerosity or the shape of the odd item. Responses were provided by pressing one of three buttons of the response box.
FIGURE 1.
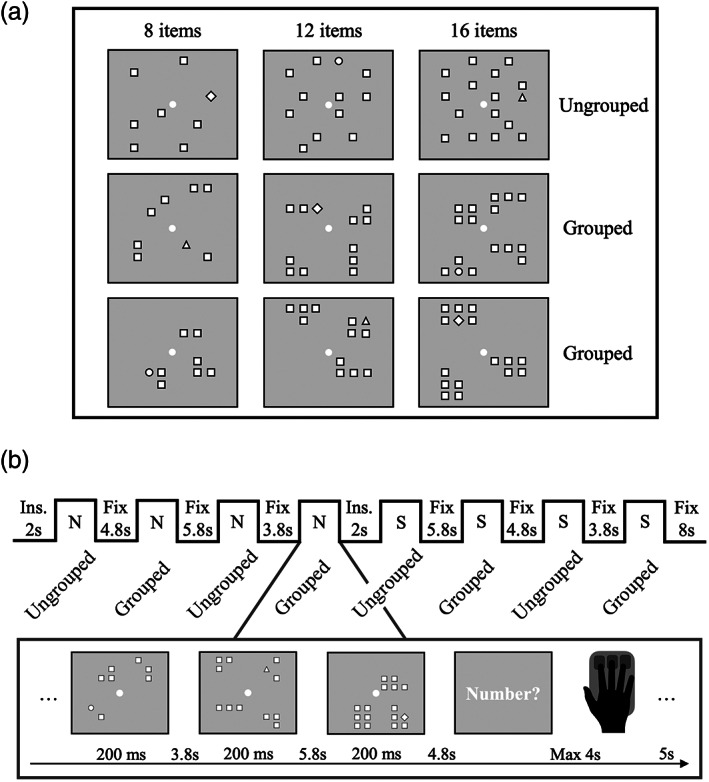
Stimulus configuration and overview of the experimental design. (a) Examples of stimulus configurations. (b) One run comprised eight blocks with either grouped or ungrouped stimuli. Participants estimated either numerosity (N) or shape (S), as specified by the instructions (Ins.) presented at the beginning of the first and second half of the run
For each task, both grouped and ungrouped arrays were shown in different blocks, but the change in spatial arrangement was not explicitly signaled (Figure 1b). For each task, 48 trials were presented: 6 trials for each of the 6 conditions (3 numerosities × 2 spatial arrangements) and 12 signals to respond. Within each scanning session participants performed eight runs, each including 8 blocks where the two tasks alternated. The type of task at run onset was balanced across runs and participants. Stimuli were generated and presented using PsychToolbox routines (Brainard, 1997), operating under Matlab (ver. R2016b. 9.1.0.441655, The Mathworks, Inc., http://mathworks.com).
2.3. Data analysis
For the psychophysical experiment prior to scanning, we calculated the average perceived numerosity and the response SD, separately for each participant, numerosity and condition. We then calculated Weber fraction (Wf) by dividing the SDs by the corresponding perceived numerosity. A repeated measures ANOVA was performed on Wfs and perceived numerosity with numerosity and spatial arrangement as factors. Effect size (η 2) was also reported when appropriate. η 2 indicates a small (0.01), a medium (0.06), and a large (0.14) effect.
The behavioral performance on both numerosity estimation and shape control task measured during the scanning was analyzed by a repeated measures ANOVA, performed on inverse efficiency score (IES). The IES was calculated for each subject and each numerosity dividing the RT by the proportion of correct response (accuracy). The IES between grouped and ungrouped were then averaged in order to obtain a single value for each numerosity and task. Effect size (η 2) was also reported when appropriate.
EPI images were preprocessed and analyzed with FSFAST tools of Freesurfer 6.0 (https://surfer.nmr.mgh.harvard.edu/). Preprocessing included motion correction and smoothing with a 3D Gaussian kernel (FWHM = 5 mm). We performed surface‐based reconstruction and individual participants' data were sampled to the left and right hemisphere of fsaverage (the surface area of the Freesurfer average subject).
The preprocessed EPI images were entered into two general linear models estimated on subject's volume and on fsaverage surface space. Predictors were convolved with the SPM canonical hemodynamic response function. In the first General Linear Model (GLM), for each participant we separately modeled the following six regressors: 4 conditions (2 spatial arrangements × 2 tasks), the instruction and the response trials. To identify which brain regions were involved in numerosity estimation of ungrouped and grouped arrays, for each participant we contrasted the activity elicited during the number task (separately when performed on ungrouped and grouped arrays) against that elicited during the respective control conditions (i.e., “Ungrouped number task > Ungrouped shape control task”; and “Grouped number task > Grouped shape control task”). We then performed a random effects group analysis. The resulting statistical maps were thresholded at p < .001, using correction for multiple comparison at cluster level (Hagler, Saygin, & Sereno, 2006) with a cluster forming threshold p < .001. Next, to reveal regions that responded more to the number task than to their respective control conditions, both when the arrays were ungrouped and grouped, we performed a conjunction of random effect analysis across the two contrasts: “(Grouped number task > Grouped shape control task) ∩ (Ungrouped number task > Ungrouped shape control task)”. This analysis showed the brain regions that were activated for both contrasts (not just either). Finally, for each participant we determined whether there were brain regions that showed greater activation specifically (and not shared) for the number task when the arrays were grouped or ungrouped after subtracting out activity associated with their control tasks: “(Grouped number task > Grouped shape control task) > (Ungrouped number task > Ungrouped shape control task)”; and “(Ungrouped number task > Ungrouped shape control task) > (Grouped number task > Grouped shape control task)”. We then performed a random effects group analysis, as described above.
In the second GLM we additionally modeled the effect for each numerosity separately, resulting in 14 regressors: 12 conditions (i.e., 3 numerosities × 2 spatial arrangements × 2 tasks), the instruction and the response trials. The beta estimates for the 12 conditions were entered into pattern classification analysis. For each participant we anatomically defined regions of interest (ROIs) from V1 to IPS5 derived from a surface based probabilistic atlas (Wang, Mruczek, Arcaro, & Kastner, 2015) and other ROIs derived from the Freesurfer atlas (Destrieux, Fischl, Dale, & Halgren, 2010). ROIs were created on Freesurfer gray matter surface and were back projected onto each participant's volume space. The left and right hemisphere for each ROI were merged. ROIs from V1 to IPS5 were further merged into three ROIs corresponding to early (V1 to V3), intermediate (V3A, V3B and V7 also known as IPS0) and higher‐level (IPS1 to IPS5) ROIs. We also defined a region called IPS excluding IPS0‐5 by excluding the ROIs from IPS0 to IPS5 from the intraparietal and transverse parietal sulcus ROI as defined by the Freesurfer atlas. This region was found to be specifically involved during calculation and numerosity comparison as opposed to numerosity perception (Castaldi et al., 2020). The angular gyrus ROI was defined based on the Freesurfer atlas.
Within each of these bilateral ROIs we selected on a subject‐by‐subject basis an equal number of 1,000 voxels that responded most strongly to the orthogonal contrast (“all numerosities > baseline”) for pattern classification analysis. Pattern classification analysis was performed in sckit‐learn (Pedregosa et al., 2011) using beta estimates after subtracting the voxel‐wise mean across conditions. Linear support vector machines (SVM) with regularization parameter C = 1 was applied. Classification analysis was performed following a leave‐one‐run‐out cross‐validation scheme. Classification accuracy obtained from each cross‐validation cycle were then averaged together. We performed pairwise classification on trials recorded during the number task, for both spatial arrangements and for all pairs of numerosities, keeping patterns separated by spatial arrangement “(Train ungrouped ⇒Test ungrouped; and Train grouped ⇒ Test grouped)”. We then tested generalization of the classifier across spatial arrangements. Significance against the theoretical chance level (50%) was tested with one‐sample t‐tests, and significance reported after correction for multiple comparisons. We also report log10 Bayes Factors (logBF), which should be interpreted as lending positive (0–0.5), substantial (0.5–1), strong (1–1.5), very strong (1.5–2) support to the alternative hypothesis, with negative values within these ranges supporting the null hypothesis. Repeated measures ANOVA and Bonferroni corrected t test were performed on classification accuracy with ROIs and spatial arrangements as factors. Greenhouse–Geisser was applied when sphericity was violated. Effect size (η 2) was also reported when appropriate.
3. RESULTS
3.1. Psychophysics
Prior to scanning, participants were tested with a behavioral experiment to measure Weber fractions (Wfs) for numerosity estimation of stimuli with different spatial arrangements to quantify the groupitizing effect in the participant sample. The results replicated previous findings, by showing that Wfs were lower when stimuli were grouped (mean = 0.11, SD = 0.03) compared with when they were displayed randomly (mean = 0.13, SD = 0.03), for all numerosities tested (Figure 2a). Repeated measures ANOVA, with spatial arrangement (ungrouped or grouped) and numerosity (from 5 to 17) as factors, revealed a significant main effect of spatial arrangements (F(1,13) = 10.74, p = .006, η 2 = 0.07) suggesting that numerical estimates were significantly more precise when items were grouped compared to when they were ungrouped. The groupitizing advantage was about 15% on average, in line with previous studies (Anobile et al., 2020; Maldonado Moscoso et al., 2020), average results are shown by the bars of Figure 2b.
FIGURE 2.
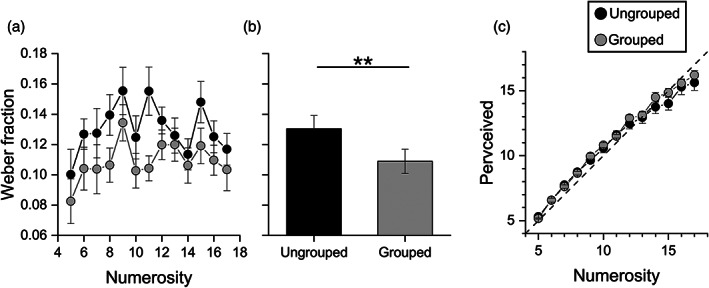
Psychophysics experiment. Sensory precision and perceived numerosity for grouped and ungrouped stimuli. (a) Average Weber fraction as a function of numerosity for ungrouped (black circles) and grouped (gray circles) stimuli. (b) Average Weber fraction for the two conditions showing the main effect of spatial arrangements. (c) Perceived numerosity averaged across participants as a function of numerosity for ungrouped (black circles) and grouped (gray circles) stimuli. Error bars represent ±1 s.e.m. ** p ≤ .01
We also evaluated the effect of grouped stimuli on the accuracy of perceived numerosity estimation. Repeated measures ANOVA, with spatial arrangement (ungrouped and grouped) and numerosity (from 5 to 17) as within subject factors, shows that perceived numerosity did not significantly differ between grouped and ungrouped stimuli (F(1,13) = 0.82, p = 0.38, η 2 = 0.001; Figure 2c), in line with previous studies.
3.2. fMRI univariate analysis
Having verified the effect of the groupitizing behaviorally, we used a sub‐sample of the same stimuli to scan participants with fMRI. In the scanner participants viewed arrays of 8, 12 or 16 items, grouped or ungrouped, and judged either their numerosity or the shape of the odd item, as specified by the instructions. Behavioral performance during the scanning did not differ between tasks, suggesting that difficulty was balanced (see Table S1).
We first performed a surface‐based group analysis to identify brain regions that showed greater activity during the numerosity task compared with the shape control task (separately for ungrouped and grouped stimuli). The contrast “Ungrouped numerosity > Ungrouped shape control” (red activation in Figure 3a) revealed greater activation for processing numerosity compared with the shape control task of ungrouped stimuli in parietal and frontal cortex. Significant activations included the right superior and transverse occipital sulcus, right intraparietal and transverse parietal sulcus, right superior parietal gyrus and the bilateral postcentral sulcus. In the frontal cortex activations were found in the right inferior precentral sulcus and superior frontal gyrus.
FIGURE 3.
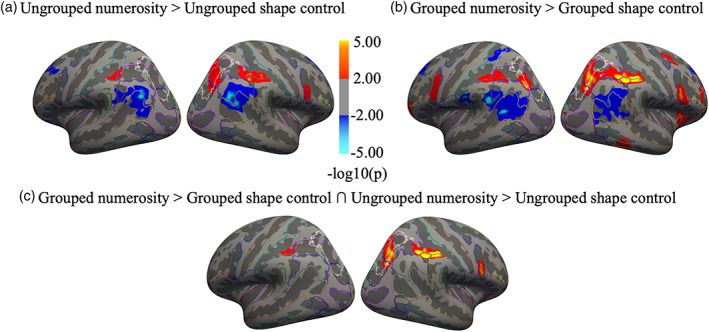
Neural activation for ungrouped and grouped stimuli relative to their respective shape control tasks and conjunction analysis. Activation maps obtained from the surface‐based group analysis (n = 14) showing the activation elicited by numerosity relative to the shape control task when items in visual arrays were randomly scattered in space (a) or grouped (b). Red and blue clusters respectively indicate greater activity for the numerosity relative to the control task and for the shape control relative to the numerosity task. (c) Brain regions activated in both contrasts shown in (a) and (b). Red clusters represent the conjunction of the numerosity estimation task performed on both ungrouped and grouped stimulus arrays greater than their respective control conditions. Maps are thresholded at p < .001, uncorrected for multiple comparison and displayed on Freesurfer's fsaverage surface. Color outlines mark anatomical sulci and gyri according to the Destrieux Atlas (Fischl et al., 2004). White outlines identify the region IPS0‐5 based on visual topography (Wang et al., 2015). Table S2 of supplementary materials lists the cluster summary tables for both contrasts and the conjunction analysis
The contrast “Grouped numerosity > Grouped shape control” (red activation in Figure 3b) revealed activation in similar regions, and additionally recruiting much more of the left hemisphere. Additional activations were also observed in right insula and in right inferior temporal gyrus.
The reverse contrasts, “Ungrouped shape control > Ungrouped numerosity” and “Grouped shape control > Grouped numerosity” (blue activations in Figure 3a,b) revealed activations in several bilateral parieto‐occipital and superior temporal areas. Widespread activation was also observed bilaterally in the frontal cortex (mainly in the superior and middle frontal gyrus and cingulate gyrus).
We then performed a conjunction analysis to reveal regions that were more active for both the ungrouped and grouped numerosity tasks than for their respective controls. The conjunction analysis “(Grouped number task > Grouped shape control task) ∩ (Ungrouped number task > Ungrouped shape control task)” highlighted the regions activated by the number task on both grouped and ungrouped stimuli, relative to their respective controls. The results shown in Figure 3c revealed that common neural activation was found for grouped and ungrouped number tasks in the right superior occipital and transverse occipital sulcus, right intraparietal and transverse parietal sulcus, right superior parietal gyrus and in the postcentral sulcus bilaterally. Activation was observed also in the frontal cortex, specifically in the right precentral sulcus and right superior frontal gyrus. The results suggest that these regions play an important role in the estimation of non‐symbolic quantities irrespective of spatial configuration.
Finally, we looked for regions specifically activated for the number task for grouped compared to ungrouped arrays, after subtracting out activity associated with their control tasks: “(Grouped numerosity > Grouped shape control) > (Ungrouped numerosity > Ungrouped shape control)”. This contrast elicited activations in bilateral angular gyrus and in left frontal regions covering the lateral orbital sulcus, and middle frontal gyrus (red activations in Figure 4). On the other hand, no brain regions showed greater activation specifically for the number task when the arrays were ungrouped compared to grouped: “(Ungrouped numerosity > Ungrouped shape control) > (Grouped numerosity > Grouped shape control)”.
FIGURE 4.
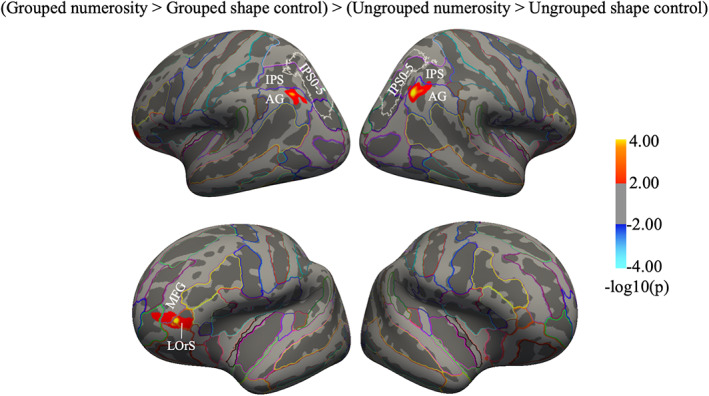
Neural activation for grouped compared to ungrouped stimuli after subtracting out activity associated with the respective shape control tasks. Statistical results obtained from the surface‐based group analysis showing distinct neural activity for the numerosity task when it was performed on grouped compared to ungrouped arrays. The maps show the regions with greater activations for numerosity estimation of grouped compared to ungrouped arrays, after subtracting out activity associated with their respective shape control tasks. The reverse contrast (greater activations for numerosity estimation of ungrouped compared to grouped arrays, after subtracting out activity associated with the respective shape control tasks) did not yield significant activation. The cluster summary table is in Table S2. White outlines identify the region IPS0‐5 based on visual topography (Wang et al., 2015); AG, angular gyrus; IPS, intraparietal sulcus; LOrS, lateral orbitofrontal sulcus; MFG, middle frontal gyrus
3.3. fMRI multivariate analysis
The results so far suggest that estimating the numerosity of ungrouped and grouped arrays elicits activation in partially overlapping cortical areas. However, the fact that ungrouped and grouped arrays activate similar or overlapping regions does not necessarily imply that the same shared neural mechanisms are recruited in both cases: it could reflect functionally different neural patterns within the same brain regions. We therefore analyzed further the pattern of activity elicited by different spatial arrangements along the dorsal pathway using classification techniques.
We defined five different regions in each participant (V1–V3, V3AB‐V7, IPS1‐5, IPS excluding IPS0‐5 and angular gyrus; Figure 5a). Within each region we selected the 1,000 most activated voxels in the contrast “all numerosities > baseline” and used these voxels to train and test classifiers discriminating between spatial arrangement (ungrouped vs grouped) irrespective of numerosity, and between numerosities within and across spatial arrangements during the numerosity estimation task.
FIGURE 5.
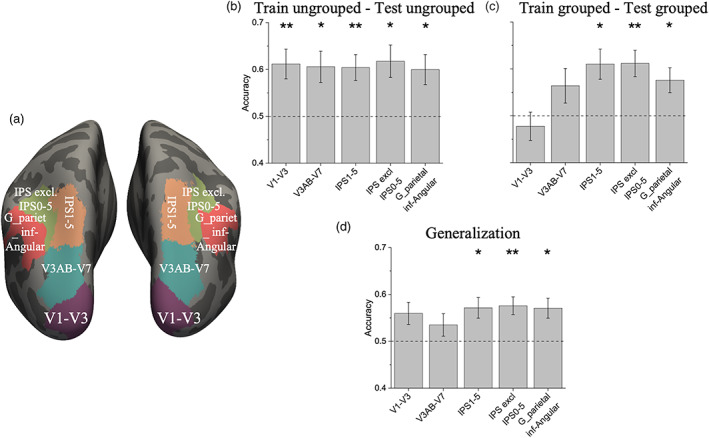
ROIs illustration and results of multivariate pattern analysis. ROI localization of the occipital and parietal regions pooled over both hemisphere and results of multivariate classification for discrimination between numerosities when participants were performing the numerosity task on items with different spatial arrangements. (a) Color‐coded ROIs on the inflated brain template. (b,c) Average decoding accuracy for different numerosities when training and testing the classifier with the pattern of activity elicited by the ungrouped (b) and grouped (c) arrays. (d) Average decoding accuracy for three different pairwise set‐size comparisons when the classifier was trained on the pattern of activity elicited by one given spatial arrangement and tested on the pattern of activity elicited by the other. Bars show mean classification accuracy across subjects ± s.e.m of mean (star marks indicate significance against chance (0.5), after correction for multiple comparisons: 0.05/5 = 0.01. * p < .01; ** p < .001)
The classifier performance in discriminating between spatial arrangements irrespective of numerosity was highest in the primary visual areas and progressively decreased along the dorsal stream (Figure S1, Table S3), probably due to the different retinotopical organization of the stimuli.
Figure 5b,c shows the performance of the classifier when discriminating between numerosities of ungrouped and grouped arrays. When the different set sizes of 8, 12 or 16 items were presented in ungrouped arrays, the different numerosities could be decoded significantly above chance in all ROIs (Table 1). On the other hand, when numerosities were shown with grouped arrays the decoding accuracy was above chance in the parietal but not in the early and intermediate ROIs (Table 1). Bayes factors provided substantial evidence in favor of no significant difference from chance in the primary visual ROI, and positive and strong evidence in favor of significant differences in intermediate and parietal ROIs respectively. When doing the shape estimation task, classification accuracies for numerosity in all areas were at chance, confirming that the control task directed attention away from the numerical content of the array
TABLE 1.
Classification performance within and across spatial arrangements
| ROIs | Train ungrouped—Test ungrouped | Train grouped—Test grouped | Generalization | ||||||
|---|---|---|---|---|---|---|---|---|---|
| t‐value | p | LogBF | t‐value | p | LogBF | t‐value | p | Log BF | |
| V1–V3 | 3.65 | .001** | 1.5 | −0.77 | .77 | −0.77 | 2.63 | .01 | 0.79 |
| V3AB‐V7 | 3.28 | .003* | 1.24 | 1.8 | .05 | 0.26 | 1.51 | .078 | 0.09 |
| IPS1‐5 | 3.92 | <.001** | 1.68 | 3.55 | .002* | 1.42 | 3.39 | .002* | 1.31 |
| IPS excl IPS0‐5 | 3.53 | .002* | 1.41 | 4.1 | <.001** | 1.81 | 4.17 | <.001** | 1.86 |
| Angular gyrus | 3.22 | .003* | 1.19 | 2.96 | .006* | 1.07 | 3.45 | .002* | 1.35 |
Note: Student's t‐values, p‐values and LogBF for classification accuracy against chance (0.5) in each ROI. Stars indicate significance against chance (0.5), after correction for multiple comparisons: 0.05/5 = 0.01.
p ≤ .01.
p < .001.
Classification accuracies were analyzed with repeated measures ANOVA with ROIs (5 levels) and spatial arrangements (2 levels) as factors. The results showed a significant interaction between ROIs and spatial arrangements (F(4,52) = 3.70, p = .01, p = .02 after Greenhouse–Geisser sphericity correction, η 2 = 0.06). Post‐hoc comparisons revealed that the difference in classification accuracy between V1–V3 ungrouped and V1–V3 grouped was at significance (t = 3.53, p = .05), and clearly significant for V1–V3 grouped and IPS 1–5 grouped and for V1–V3 grouped and IPS excluding IPS 0–5 grouped (respectively t = 4.10, p = .004; t = 4.14, p = .003). There was no significant main effect of ROIs and spatial arrangements (F(4,52) = 2.36, p = .06, p = .07 after Greenhouse–Geisser sphericity correction, η 2 = 0.06; F(1,4) = 2.06, p = .17, η 2 = 0.04, respectively for ROIs and spatial arrangements).
We then tested for generalization of classification performance across spatial arrangements (Figure 5d). Significant generalization was observed in the parietal but not in the intermediate ROIs nor in the primary visual ROIs after correction for multiple comparisons (Table 1).
3.4. Correlational analysis
We then correlated the Weber fraction measured psychophysically outside the scanner for grouped arrays against the classification accuracy for grouped arrays, measured from the different ROIs (from the primary visual areas to the angular gyrus). To this aim, we averaged for each participants the Wfs measured during the psychophysical experiment when the stimuli were grouped across numerosity levels in order to obtain a summary precision index. There were no significant correlations in primary and intermedial visual areas nor in IPS1‐5 (V1–V3: r = −.44, p = .11, LogBF = 0.02, Figure 6a; V3AB‐V7: r = −.26, p = .37, LogBF = −0.32; IPS1‐5: r = −.34, p = .24, LogBF = −0.21, Figure S2A,B). Correlations were significant in IPS excluding IPS0‐5 and angular gyrus; however, only the latter remained significant after Bonferroni correction (0.05/5 = 0.01; IPS excluding IPS0‐5: r = −.55, p = .043, LogBF = 0.32, Figure S2C; angular gyrus: r = −.67, p = .009, LogBF = 0.86, Figure 6b).
FIGURE 6.
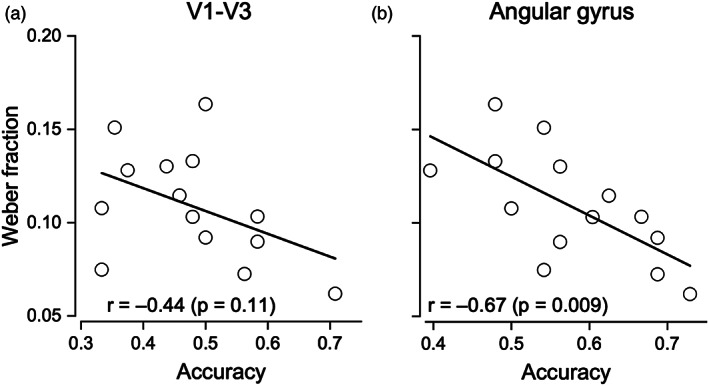
Relationship between behavioral Wfs and classification accuracy in the numerosity grouped condition. (a) Weber fractions measured in a separate experiment plotted against classification accuracy in the primary visual areas (V1–V3) and (b) in the angular gyrus ROI
4. DISCUSSION
This study explored the neural resources underlying numerosity estimation when stimuli were grouped into small clusters to facilitate “groupitizing,” a strategy known to improve rapid estimation of numerosity. The results showed that the numerosity estimation of ungrouped and grouped stimuli both activated a similar right lateralized frontoparietal network. However, estimation of grouped stimuli additionally activated regions in the left hemisphere, and specifically recruited the angular gyrus. Multivariate pattern analysis showed that classifiers trained with the pattern of neural activations read out from parietal regions, but not from the primary visual areas, can decode different numerosities both within and across spatial arrangements. fMRI decoding performance of the angular gyrus (and to some extent of the IPS excluding IPS0‐5), but not of the other ROIs, correlated with the behavioral Wfs measured in a separate experiment with the estimation task.
The results from the univariate analysis of the fMRI data showed that numerosity estimation of ungrouped and grouped stimuli activated both common (mostly right‐lateralized) and specific cortical areas within the frontoparietal network when compared with the respective control conditions, which could not be explained by differences in task difficulty. The activation of the right lateralized network has been reported previously in neuroimaging studies investigating the neural correlates of approximate numerosity perception (Chassy & Grodd, 2012; Dormal et al., 2010, 2012; Piazza et al., 2006; Piazza, Mechelli, Butterworth, & Price, 2002).
In the current experiment, we found that compared with the control task, numerosity estimation of grouped stimuli activated similar regions in the right hemisphere but additionally recruited corresponding areas in the left hemisphere, suggesting that participants might employ different strategies to enumerate grouped stimuli, such as simple calculations. Much evidence in the literature from brain‐damaged patients and fMRI studies on neurologically intact participants, suggests that the left hemisphere is involved in mental arithmetic (Chochon et al., 1999; Cipolotti et al., 1991; Dehaene et al., 1999; Delazer et al., 2003; Gerstmann, 1940; Grabner et al., 2007; Grabner, Ansari, et al., 2009; Jackson & Warrington, 1986; Pesenti, Thioux, Seron, & De Volder, 2000; Piazza et al., 2006; Pinel & Dehaene, 2010; Stanescu‐Cosson et al., 2000; see also: Dehaene et al., 2003, for a review). Interestingly, the activation observed here in left parietal areas mainly includes the lateral and inferior part of IPS (IPS excluding IPS0‐5), a region previously found to be more strongly activated by calculation relative to reading (Castaldi et al., 2020).
Areas in the frontal, temporal and insular cortices were also more activated by numerosity estimation of grouped stimuli than by the control task. The frontal gyrus has been repeatedly found to be activated during symbolic mental calculation tasks and to reflect the calculation procedure, working memory and executive attention (Chochon et al., 1999; Dehaene et al., 1999; Gruber, Indefrey, Steinmetz, & Kleinschmidt, 2001; Kong et al., 2005; Kuo, Yeh, Chen, Liang, & Chen, 2008; Lee, 2000; Menon et al., 2000; Zhou et al., 2007). The frontal gyrus, together with the intraparietal and inferior temporal regions, has also been reported to be more strongly activated during high‐level mathematical judgments compared with non‐mathematical judgments in mathematicians (Amalric & Dehaene, 2016). Moreover, the activation of the inferior temporal gyrus for grouped stimuli is in line with recent studies highlighting the role of this region in symbolic and non‐symbolic calculation tasks in adults and children (Bugden et al., 2019; Kawashima et al., 2004; Lee, 2000). In this region fMRI and electrocorticographic (ECoG) studies have identified a population of neurons that selectively respond to visual presentation and identification of numerals relative to letters and scrambled symbols; it has been termed the “visual number form area” (NFA; Grotheer, Herrmann, & Kovács, 2016; Shum et al., 2013). Interestingly, activity recorded from the NFA was functionally coupled with that recorded from the intraparietal sulcus during arithmetic verification tasks, suggesting that these two regions support arithmetical processing through multiple feedback loops (Daitch et al., 2016; Pinheiro‐Chagas, Daitch, Parvizi, & Dehaene, 2018). Insular activation has been reported during approximate and exact calculation in adults and children, potentially reflecting a domain general contribution related to error processing and switching between the executive‐control and the default‐mode network (Arsalidou et al., 2018; Grabner et al., 2007; Ischebeck et al., 2009; Kong et al., 2005). Overall, the major involvement of the network engaged in calculation during numerosity estimation of grouped items suggests deployment of mental arithmetic strategies.
Interestingly, the network recruited for estimating numerosities of grouped arrays is not completely different from that for estimating random arrays. The conjunction analysis showed that the neural network in the right hemisphere is largely shared between numerosity estimation of grouped and ungrouped arrays. Beyond this commonly shared system, we observed areas that were more strongly activated during numerosity estimation of grouped than ungrouped stimuli, after subtracting out activity for their respective control tasks: areas that were specifically activated during numerosity estimation of grouped stimuli. These areas were the bilateral angular gyrus, the left orbital sulcus and the left middle frontal gyrus. Although the angular gyrus has been shown to be activated in various cognitive domains (perceptual and motor reorienting, number processing, attention and spatial cognition, episodic memory retrieval and encoding, language processing, theory of mind; Cabeza, Ciaramelli, & Moscovitch, 2012), fMRI and neuropsychological studies have shown that the left angular gyrus plays an important role also during calculation processing, in particular during multiplication and arithmetical fact retrieval from memory (Chochon et al., 1999; Delazer et al., 2003; Gerstmann, 1940; Grabner et al., 2007, 2013; Grabner, Ansari, et al., 2009; Grabner, Ischebeck, et al., 2009; Ischebeck, Zamarian, Egger, Schocke, & Delazer, 2007; Lee, 2000; Stanescu‐Cosson et al., 2000; see also: Dehaene et al., 2003, for a review). However, some studies have reported bilateral activation of the angular gyrus during exact calculation tasks, suggesting that also the right angular gyrus has a role in arithmetic processing, although the left hemisphere showed a larger effect (Göbel, Walsh, & Rushworth, 2001; Menon et al., 2000; Stanescu‐Cosson et al., 2000). Interestingly, activation of the left inferior and middle frontal regions was found in studies that investigated the neural substrates of symbolic and non‐symbolic exact calculations, compared with approximate calculations. It has been suggested that this left lateralized parieto‐frontal network may play an important role for arithmetic fact retrieval (Piazza et al., 2006; Prado et al., 2011; Prado, Mutreja, & Booth, 2014; Stanescu‐Cosson et al., 2000). The activity revealed during estimation of grouped stimuli may implicate the automatic use of multiplication strategies or retrieval of arithmetic facts (i.e., basic addition) to solve the task.
Overall, the results from the univariate analysis showed that numerosity estimation of both ungrouped and grouped stimuli activated similar regions in the frontoparietal network, although with different lateralization. Numerosity estimation of grouped stimuli further recruited additional areas of the calculation network—temporal, cingulate and insular cortices—and specifically the angular gyrus.
The fact that different stimuli activated overlapping regions, however, does not necessarily imply that the same neural mechanisms are recruited, and may rather reflect the existence of intermingled neural populations that are differentially recruited for the different tasks. We therefore tested whether numerosity estimation of arrays with different spatial arrangements elicited similar patterns of neural activation. The results of the multivariate pattern analysis showed that the difference between spatial arrangements was decoded most strongly in primary visual areas and all along the dorsal stream. This was probably mostly due to the different locations of the items within the array, giving rise to different retinotopical signals that are encoded by all visual areas (from the early to the parietal ones).
We also found that numerosities could be read out from brain activity during numerosity estimation of ungrouped arrays all along the visual stream, in line with previous studies (Castaldi, Piazza, Dehaene, Vignaud, & Eger, 2019; Cavdaroglu & Knops, 2019; Eger, 2016; Eger, Pinel, Dehaene, & Kleinschmidt, 2015; Lasne, Piazza, Dehaene, Kleinschmidt, & Eger, 2019). However, when training the classifiers with the pattern of activity elicited by estimation of grouped stimuli, numerosity could be decoded above chance only in parietal regions. In this study, the total visual field area was matched between ungrouped and grouped stimuli, but within this area, the location of the individual items was more scattered in the ungrouped than in the grouped arrays (by definition). This may have elicited a more distinct pattern of activity in the primary visual areas for the ungrouped compared to the grouped stimuli, therefore explaining the higher decoding performance for ungrouped stimuli.
Decoding in parietal, but not early visual, ROIs successfully generalized across spatial arrangements, suggesting that numerosity information is similarly encoded in the parietal cortex, independently of whether stimuli were ungrouped or grouped. One possibility is that the pattern of activity in these regions represents the final numerical estimate, regardless of the strategy by which this estimate was computed. Future studies that characterize the temporal course of neural activity associated with numerosity estimation may verify this possibility.
Another possibility is that the classification is based on non‐numerical visual features (such as the total number of pixels), which were not controlled across number in the current experiment. However, this possibility is unlikely. First, much evidence suggests that numerosity, especially for the low numbers tested here, is perceived independently of non‐numerical visual features (Anobile, Cicchini, & Burr, 2014; Castaldi, Mirassou, Dehaene, Piazza, & Eger, 2018; Zimmermann, 2018; Zimmermann & Fink, 2016), and that the pattern of activation read out from parietal areas encodes numerosity directly (Castaldi et al., 2019; Harvey & Dumoulin, 2017). Second, decoding in parietal areas successfully generalized across spatial arrangements only when classifiers were trained and tested with trials recorded while participants judged numerosity: performance was at chance when they judged shape. Given that the stimuli presented in both tasks were identical, any non‐numerical difference across stimuli should have allowed for classification also in the control task, while this is not what we observed.
Finally, we tested the behavioral relevance of the pattern of activity read out from early, intermediate and parietal areas. A previous study found that the behavioral numerical acuity correlated with performance of a classifier discriminating ungrouped numbers when this was trained and tested with the pattern of activity read out from the parietal but not from the early visual areas (Lasne et al., 2019). Here we measured the correlation between numerical acuity for grouped stimuli and decoding accuracy in several ROIs across the dorsal stream. Participants with higher acuity (lower Weber fractions) showed higher decoding accuracy in the angular gyrus and to some extent also in IPS excluding IPS0‐5, pointing to a more precise neural representation of numerosity. This suggests that these regions may play an important role in the estimation of grouped stimuli.
5. CONCLUSIONS
In conclusion, we used fMRI to explore the activation elicited by numerosity estimation of grouped stimuli. Univariate analysis provided evidence that estimation of both ungrouped and grouped stimuli activates a similar right‐lateralized frontoparietal network. However, the possibility of grouping items may automatically elicit a different strategy for numerosity estimation, which results in the additional recruitment of a network that is typically involved in calculation, mostly including regions in the left hemisphere and specifically the angular gyrus. Moreover, the numerosity of grouped stimuli could be best decoded from parietal areas, and classification performance in the angular gyrus correlated with psychophysical measures of numerosity estimation of grouped stimuli. Overall, the present experimental results support the hypothesis that the estimation of grouped stimuli relies on the system for numerosity estimation that additionally recruits regions involved in calculation, thereby enabling a more precise and rapid estimate of the numerosity of grouped arrays.
CONFLICT OF INTEREST
The authors declare no competing interests.
AUTHOR CONTRIBUTIONS
All authors contributed to the study concept and design. Testing and data collection were performed by Paula A. Maldonado Moscoso, who also analyzed the data together with Elisa Castaldi. All authors contributed to the interpretation of results and to the writing of the manuscript.
ETHICS APPROVAL
The study was approved by the Committee for Research Ethics of the University of Regensburg; all participants gave informed consent in agreement with the ethical principles for research involving human subjects (Declaration of Helsinki).
Supporting information
Appendix S1: Supporting Information
ACKNOWLEDGMENTS
We thank W. Malloni, M. Becker and A. Beer for support during fMRI acquisition and advice on fMRI analysis. We also thank E. Eger for helpful comments on an earlier draft of this article. This research was supported by the European Union (EU) and Horizon 2020—Grant Agreement No 832813—ERC Advanced “Spatio‐temporal mechanisms of generative perception—GenPercept”; the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska‐Curie grant agreement No 885672—DYSC‐EYE‐7T—“The neural substrate of numerical cognition in dyscalculia revealed by eye tracking and ultra‐high field 7T functional magnetic imaging”; the Italian Ministry of Education, University, and Research under the PRIN2017 program (Grant number 2017XBJN4F—“EnvironMag” and Grant number 2017SBCPZY—“Temporal context in perception: serial dependence and rhythmic oscillations”); M. W. G. was supported by the German Research Foundation (DFG, INST 89/393‐1 and GR988/25‐1). P. A. M. M. was supported by the Erasmus+ Exchange Program of the EU during her stay in Regensburg, Germany.
Maldonado Moscoso, P. A. , Greenlee, M. W. , Anobile, G. , Arrighi, R. , Burr, D. C. , & Castaldi, E. (2022). Groupitizing modifies neural coding of numerosity. Human Brain Mapping, 43(3), 915–928. 10.1002/hbm.25694
Funding information Deutsche Forschungsgemeinschaft, Grant/Award Numbers: GR988/25‐1, INST 89/393‐1; H2020 European Research Council, Grant/Award Number: 832813; H2020 Marie Skłodowska‐Curie Actions, Grant/Award Number: 885672; Ministero dell'Istruzione, dell'Università e della Ricerca, Grant/Award Numbers: 2017SBCPZY, 2017XBJN4F
DATA AVAILABILITY STATEMENT
Due to data‐privacy protection issues, the collected MRI dataset cannot be made available in public repositories. In particular, public sharing was not requested in the proposal for the Ethical Committee (University of Regensburg) and participants were not explicitly asked for their permission. The pseudo‐anonymized dataset will be stored on the UR‐lab server and the corresponding author can provide access to the data on reasonable requests and upon a formal data‐sharing agreement with the Ethical Committee of the University of Regensburg. Codes used for the implementation of the analyses are publicly available in scientific publications that are appropriately cited in the manuscript.
REFERENCES
- Amalric, M. , & Dehaene, S. (2016). Origins of the brain networks for advanced mathematics in expert mathematicians. Proceedings of the National Academy of Sciences of the United States of America, 113(18), 4909–4917. 10.1073/pnas.1603205113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anobile, G. , Castaldi, E. , Maldonado Moscoso, P. A. , Arrighi, R. , & Burr, D. (2021). Groupitizing improves estimation of numerosity of auditory sequences. Frontiers in Human Neuroscience, 15, 339. 10.3389/fnhum.2021.687321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anobile, G. , Castaldi, E. , Moscoso, P. A. M. , Burr, D. C. , & Arrighi, R. (2020). “Groupitizing”: A strategy for numerosity estimation. Scientific Reports, 10(1), 1–9. 10.1038/s41598-020-68111-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anobile, G. , Cicchini, G. M. , & Burr, D. C. (2014). Separate mechanisms for perception of numerosity and density. Psychological Science, 25, 265–270. 10.1177/0956797613501520 [DOI] [PubMed] [Google Scholar]
- Arsalidou, M. , Pawliw‐Levac, M. , Sadeghi, M. , & Pascual‐Leone, J. (2018). Brain areas associated with numbers and calculations in children: Meta‐analyses of fMRI studies. Developmental Cognitive Neuroscience, 30, 239–250. 10.1016/j.dcn.2017.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arsalidou, M. , & Taylor, M. J. (2011). Is 2+2=4? Meta‐analyses of brain areas needed for numbers and calculations. NeuroImage, 54(3), 2382–2393. 10.1016/j.neuroimage.2010.10.009 [DOI] [PubMed] [Google Scholar]
- Beckwith, M. , & Restle, F. (1966). Process of enumeration. Psychological Review, 73(5), 437–444. 10.1037/h0023650 [DOI] [PubMed] [Google Scholar]
- Brainard, D. H. (1997). The psychophysics toolbox. Spatial Vision, 10, 433–436. 10.1163/156856897X00357 [DOI] [PubMed] [Google Scholar]
- Bugden, S. , Woldorff, M. G. , & Brannon, E. M. (2019). Shared and distinct neural circuitry for nonsymbolic and symbolic double‐digit addition. Human Brain Mapping, 40(4), 1328–1343. 10.1002/hbm.24452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabeza, R. , Ciaramelli, E. , & Moscovitch, M. (2012). Cognitive contributions of the ventral parietal cortex: An integrative theoretical account. Trends in Cognitive Sciences, 16(6), 338–352. 10.1016/j.tics.2012.04.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castaldi, E. , Mirassou, A. , Dehaene, S. , Piazza, M. , & Eger, E. (2018). Asymmetrical interference between number and item size perception provides evidence for a domain specific impairment in dyscalculia. PLoS One, 13, e0209256. 10.1371/journal.pone.0209256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castaldi, E. , Piazza, M. , Dehaene, S. , Vignaud, A. , & Eger, E. (2019). Attentional amplification of neural codes for number independent of other quantities along the dorsal visual stream. eLife, 8, e45160. 10.7554/eLife.45160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castaldi, E. , Vignaud, A. , & Eger, E. (2020). Mapping subcomponents of numerical cognition in relation to functional and anatomical landmarks of human parietal cortex. NeuroImage, 221, 117210. 10.1016/j.neuroimage.2020.117210 [DOI] [PubMed] [Google Scholar]
- Cavdaroglu, S. , & Knops, A. (2019). Evidence for a posterior parietal cortex contribution to spatial but not temporal numerosity perception. Cerebral Cortex, 29(7), 2965–2977. 10.1093/cercor/bhy163 [DOI] [PubMed] [Google Scholar]
- Chassy, P. , & Grodd, W. (2012). Comparison of quantities: Core and format‐dependent regions as revealed by fMRI. Cerebral Cortex, 22(6), 1420–1430. 10.1093/cercor/bhr219 [DOI] [PubMed] [Google Scholar]
- Chochon, F. , Cohen, L. , Moortele, P. V. D. , & Dehaene, S. (1999). Differential contributions of the left and right inferior parietal lobules to number processing. Journal of Cognitive Neuroscience, 11(6), 617–630. [DOI] [PubMed] [Google Scholar]
- Ciccione, L. , & Dehaene, S. (2020). Grouping mechanisms in numerosity perception. Open Mind, 4, 102–118. 10.31234/osf.io/p6ryv [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cipolotti, L. , Butterworth, B. , & Denes, G. (1991). A specific deficit for numbers in a case of dense acalculia. Brain, 114(6), 2619–2637. 10.1093/brain/114.6.2619 [DOI] [PubMed] [Google Scholar]
- Daitch, A. L. , Foster, B. L. , Schrouff, J. , Rangarajan, V. , Kaşikçi, I. , Gattas, S. , & Parvizi, J. (2016). Mapping human temporal and parietal neuronal population activity and functional coupling during mathematical cognition. Proceedings of the National Academy of Sciences of the United States of America, 113(46), E7277–E7286. 10.1073/pnas.1608434113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Smedt, B. , Holloway, I. D. , & Ansari, D. (2011). Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency. NeuroImage, 57(3), 771–781. 10.1016/j.neuroimage.2010.12.037 [DOI] [PubMed] [Google Scholar]
- Dehaene, S. (2011). The number sense: How the mind creates mathematics. New York, NY: Oxford University Press. [Google Scholar]
- Dehaene, S. , Piazza, M. , Pinel, P. , & Cohen, L. (2003). Three parietal circuits for number processing. Cognitive Neuropsychology, 20(3–6), 487–506. 10.1080/02643290244000239 [DOI] [PubMed] [Google Scholar]
- Dehaene, S. , Spelke, E. , Pinel, P. , Stanescu, R. , & Tsivkin, S. (1999). Sources of mathematical thinking: Behavioral and brain‐imaging evidence. Science, 284(5416), 970–974. 10.1126/science.284.5416.970 [DOI] [PubMed] [Google Scholar]
- Delazer, M. , Domahs, F. , Bartha, L. , Brenneis, C. , Lochy, A. , Trieb, T. , & Benke, T. (2003). Learning complex arithmetic – An fMRI study. Cognitive Brain Research, 18(1), 76–88. 10.1016/j.cogbrainres.2003.09.005 [DOI] [PubMed] [Google Scholar]
- Destrieux, C. , Fischl, B. , Dale, A. , & Halgren, E. (2010). Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. NeuroImage, 53(1), 1–15. 10.1016/j.neuroimage.2010.06.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dormal, V. , Andres, M. , Dormal, G. , & Pesenti, M. (2010). Mode‐dependent and mode‐independent representations of numerosity in the right intraparietal sulcus. NeuroImage, 52(4), 1677–1686. 10.1016/j.neuroimage.2010.04.254 [DOI] [PubMed] [Google Scholar]
- Dormal, V. , Dormal, G. , Joassin, F. , & Pesenti, M. (2012). A common right fronto‐parietal network for numerosity and duration processing: An fMRI study. Human Brain Mapping, 33(6), 1490–1501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eger, E. (2016). Neuronal foundations of human numerical representations. Progress in Brain Research, 227, 1–27. 10.1016/bs.pbr.2016.04.015 [DOI] [PubMed] [Google Scholar]
- Eger, E. , Pinel, P. , Dehaene, S. , & Kleinschmidt, A. (2015). Spatially invariant coding of numerical information in functionally defined subregions of human parietal cortex. Cerebral Cortex, 25(5), 1319–1329. 10.1093/cercor/bht323 [DOI] [PubMed] [Google Scholar]
- Fischl, B. , Van Der Kouwe, A. , Destrieux, C. , Halgren, E. , Ségonne, F. , Salat, D. H. , … Dale, A. M. (2004). Automatically parcellating the human cerebral cortex. Cerebral Cortex, 14(1), 11–22. 10.1093/cercor/bhg087 [DOI] [PubMed] [Google Scholar]
- Gerstmann, J. (1940). Syndrome of finger agnosia, disorientation for right and left, agraphia and acalculia: Local diagnostic value. Archives of Neurology and Psychiatry, 44(2), 398–408. 10.1001/archneurpsyc.1940.02280080158009 [DOI] [Google Scholar]
- Göbel, S. , Walsh, V. , & Rushworth, M. F. S. (2001). The mental number line and the human angular gyrus. NeuroImage, 14(6), 1278–1289. 10.1006/nimg.2001.0927 [DOI] [PubMed] [Google Scholar]
- Grabner, R. H. , Ansari, D. , Koschutnig, K. , Reishofer, G. , & Ebner, F. (2013). The function of the left angular gyrus in mental arithmetic: Evidence from the associative confusion effect. Human Brain Mapping, 34(5), 1013–1024. 10.1002/hbm.21489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabner, R. H. , Ansari, D. , Koschutnig, K. , Reishofer, G. , Ebner, F. , & Neuper, C. (2009). To retrieve or to calculate? Left angular gyrus mediates the retrieval of arithmetic facts during problem solving. Neuropsychologia, 47(2), 604–608. 10.1016/j.neuropsychologia.2008.10.013 [DOI] [PubMed] [Google Scholar]
- Grabner, R. H. , Ansari, D. , Reishofer, G. , Stern, E. , Ebner, F. , & Neuper, C. (2007). Individual differences in mathematical competence predict parietal brain activation during mental calculation. NeuroImage, 38(2), 346–356. 10.1016/j.neuroimage.2007.07.041 [DOI] [PubMed] [Google Scholar]
- Grabner, R. H. , Ischebeck, A. , Reishofer, G. , Koschutnig, K. , Delazer, M. , Ebner, F. , & Neuper, C. (2009). Fact learning in complex arithmetic and figural‐spatial tasks: The role of the angular gyrus and its relation to mathematical competence. Human Brain Mapping, 30(9), 2936–2952. 10.1002/hbm.20720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grotheer, M. , Herrmann, K.‐H. , & Kovács, G. (2016). Neuroimaging evidence of a bilateral representation for visually presented numbers. The Journal of Neuroscience, 36(1), 88–97. 10.1523/JNEUROSCI.2129-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber, O. , Indefrey, P. , Steinmetz, H. , & Kleinschmidt, A. (2001). Dissociating neural correlates of cognitive components in mental calculation. Cerebral Cortex, 11(4), 350–359. 10.1093/cercor/11.4.350 [DOI] [PubMed] [Google Scholar]
- Hagler, D. J. , Saygin, A. P. , & Sereno, M. I. (2006). Smoothing and cluster thresholding for cortical surface‐based group analysis of fMRI data. NeuroImage, 33(4), 1093–1103. 10.1016/j.neuroimage.2006.07.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey, B. M. (2016). Quantity cognition: Numbers, numerosity, zero and mathematics. Current Biology, 26(10), R419–R421. 10.1016/j.cub.2016.03.059 [DOI] [PubMed] [Google Scholar]
- Harvey, B. M. , & Dumoulin, S. O. (2017). Can responses to basic non‐numerical visual features explain neural numerosity responses? NeuroImage, 149, 200–209. 10.1016/j.neuroimage.2017.02.012 [DOI] [PubMed] [Google Scholar]
- Holloway, I. D. , Price, G. R. , & Ansari, D. (2010). Common and segregated neural pathways for the processing of symbolic and nonsymbolic numerical magnitude: An fMRI study. NeuroImage, 49(1), 1006–1017. 10.1016/j.neuroimage.2009.07.071 [DOI] [PubMed] [Google Scholar]
- Ischebeck, A. , Zamarian, L. , Egger, K. , Schocke, M. , & Delazer, M. (2007). Imaging early practice effects in arithmetic. NeuroImage, 36(3), 993–1003. 10.1016/j.neuroimage.2007.03.051 [DOI] [PubMed] [Google Scholar]
- Ischebeck, A. , Zamarian, L. , Schocke, M. , & Delazer, M. (2009). Flexible transfer of knowledge in mental arithmetic – An fMRI study. NeuroImage, 44(3), 1103–1112. 10.1016/j.neuroimage.2008.10.025 [DOI] [PubMed] [Google Scholar]
- Jackson, M. , & Warrington, E. K. (1986). Arithmetic skills in patients with unilateral cerebral lesions. Cortex, 22(4), 611–620. 10.1016/S0010-9452(86)80020-X [DOI] [PubMed] [Google Scholar]
- Jevons, W. S. (1871). The power of numerical discrimination. Nature, 3(67), 281–282. [Google Scholar]
- Kaufmann, L. , Wood, G. , Rubinsten, O. , & Henik, A. (2011). Meta‐analyses of developmental fMRI studies investigating typical and atypical trajectories of number processing and calculation. Developmental Neuropsychology, 36(6), 763–787. 10.1080/87565641.2010.549884 [DOI] [PubMed] [Google Scholar]
- Kawashima, R. , Taira, M. , Okita, K. , Inoue, K. , Tajima, N. , Yoshida, H. , … Fukuda, H. (2004). A functional MRI study of simple arithmetic – A comparison between children and adults. Cognitive Brain Research, 18(3), 227–233. 10.1016/j.cogbrainres.2003.10.009 [DOI] [PubMed] [Google Scholar]
- Kong, J. , Wang, C. , Kwong, K. , Vangel, M. , Chua, E. , & Gollub, R. (2005). The neural substrate of arithmetic operations and procedure complexity. Cognitive Brain Research, 22(3), 397–405. 10.1016/j.cogbrainres.2004.09.011 [DOI] [PubMed] [Google Scholar]
- Kucian, K. , Von Aster, M. , Loenneker, T. , Dietrich, T. , & Martin, E. (2008). Development of neural networks for exact and approximate calculation: A fMRI study. Developmental Neuropsychology, 33(4), 447–473. 10.1080/87565640802101474 [DOI] [PubMed] [Google Scholar]
- Kuo, B. C. , Yeh, Y. Y. , Chen, D. Y. , Liang, K. C. , & Chen, J. H. (2008). The capacity constraint in the prefrontal and parietal regions for coordinating dual arithmetic tasks. Brain Research, 1199, 100–110. 10.1016/j.brainres.2007.12.070 [DOI] [PubMed] [Google Scholar]
- Lasne, G. , Piazza, M. , Dehaene, S. , Kleinschmidt, A. , & Eger, E. (2019). Discriminability of numerosity‐evoked fMRI activity patterns in human intra‐parietal cortex reflects behavioral numerical acuity. Cortex, 114, 90–101. 10.1016/j.cortex.2018.03.008 [DOI] [PubMed] [Google Scholar]
- Lee, K. M. (2000). Cortical areas differentially involved in multiplication and subtraction: A functional magnetic resonance imaging study and correlation with a case of selective acalculia. Annals of Neurology, 48(4), 657–661. [DOI] [PubMed] [Google Scholar]
- Maldonado Moscoso, P. A. , Castaldi, E. , Burr, D. C. , Arrighi, R. , & Anobile, G. (2020). Grouping strategies in number estimation extend the subitizing range. Scientific Reports, 10(1), 1–10. 10.1038/s41598-020-71871-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon, V. , Rivera, S. M. , White, C. D. , Glover, G. H. , & Reiss, A. L. (2000). Dissociating prefrontal and parietal cortex activation during arithmetic processing. NeuroImage, 12(4), 357–365. 10.1006/nimg.2000.0613 [DOI] [PubMed] [Google Scholar]
- Nieder, A. (2016). The neuronal code for number. Nature Reviews Neuroscience, 17(6), 366–382. 10.1038/nrn.2016.40 [DOI] [PubMed] [Google Scholar]
- Nieder, A. , & Dehaene, S. (2009). Representation of number in the brain. Annual Review of Neuroscience, 32, 185–208. 10.1146/annurev.neuro.051508.135550 [DOI] [PubMed] [Google Scholar]
- Pedregosa, F. , Varoquaux, G. , Gramfort, A. , Michel, V. , Thirion, B. , Grisel, O. , … Duchesnay, E. (2011). Scikit‐learn: Machine learning in Python. Journal of Machine Learning Research, 12, 2825–2830. [Google Scholar]
- Pesenti, M. , Thioux, M. , Seron, X. , & De Volder, A. (2000). Neuroanatomical substrates of Arabic number processing, numerical comparison, and simple addition: A PET study. Journal of Cognitive Neuroscience, 12(3), 461–479. 10.1162/089892900562273 [DOI] [PubMed] [Google Scholar]
- Peters, L. , Polspoel, B. , Op de Beeck, H. , & De Smedt, B. (2016). Brain activity during arithmetic in symbolic and non‐symbolic formats in 9‐12 year old children. Neuropsychologia, 86, 19–28. 10.1016/j.neuropsychologia.2016.04.001 [DOI] [PubMed] [Google Scholar]
- Piazza, M. , Mechelli, A. , Butterworth, B. , & Price, C. J. (2002). Are subitizing and counting implemented as separate or functionally overlapping processes? NeuroImage, 15(2), 435–446. 10.1006/nimg.2001.0980 [DOI] [PubMed] [Google Scholar]
- Piazza, M. , Mechelli, A. , Price, C. J. , & Butterworth, B. (2006). Exact and approximate judgements of visual and auditory numerosity: An fMRI study. Brain Research, 1106(1), 177–188. 10.1016/j.brainres.2006.05.104 [DOI] [PubMed] [Google Scholar]
- Pinel, P. , & Dehaene, S. (2010). Beyond hemispheric dominance: Brain regions underlying the joint lateralization of language and arithmetic to the left hemisphere. Journal of Cognitive Neuroscience, 22(1), 48–66. 10.1162/jocn.2009.21184 [DOI] [PubMed] [Google Scholar]
- Pinheiro‐Chagas, P. , Daitch, A. , Parvizi, J. , & Dehaene, S. (2018). Brain mechanisms of arithmetic: A crucial role for ventral temporal cortex. Journal of Cognitive Neuroscience, 30(12), 1757–1772. 10.1162/jocn_a_01319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polspoel, B. , Peters, L. , Vandermosten, M. , & De Smedt, B. (2017). Strategy over operation: Neural activation in subtraction and multiplication during fact retrieval and procedural strategy use in children. Human Brain Mapping, 38(9), 4657–4670. 10.1002/hbm.23691 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado, J. , Mutreja, R. , & Booth, J. R. (2014). Developmental dissociation in the neural responses to simple multiplication and subtraction problems. Developmental Science, 17(4), 537–552. 10.1111/desc.12140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado, J. , Mutreja, R. , Zhang, H. , Mehta, R. , Desroches, A. S. , Minas, J. E. , & Booth, J. R. (2011). Distinct representations of subtraction and multiplication in the neural systems for numerosity and language. Human Brain Mapping, 32(11), 1932–1947. 10.1002/hbm.21159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seghier, M. L. (2013). The angular gyrus: Multiple functions and multiple subdivisions. The Neuroscientist, 19(1), 43–61. 10.1177/1073858412440596 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shum, J. , Hermes, D. , Foster, B. L. , Dastjerdi, M. , Rangarajan, V. , Winawer, J. , … Parvizi, J. (2013). A brain area for visual numerals. Journal of Neuroscience, 33(16), 6709–6715. 10.1523/JNEUROSCI.4558-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanescu‐Cosson, R. , Pinel, P. , Van De Moortele, P. F. , Le Bihan, D. , Cohen, L. , & Dehaene, S. (2000). Understanding dissociations in dyscalculia: A brain imaging study of the impact of number size on the cerebral networks for exact and approximate calculation. Brain, 123(11), 2240–2255. 10.1093/brain/123.11.2240 [DOI] [PubMed] [Google Scholar]
- Starkey, G. S. , & McCandliss, B. D. (2014). The emergence of “groupitizing” in children's numerical cognition. Journal of Experimental Child Psychology, 126, 120–137. 10.1016/j.jecp.2014.03.006 [DOI] [PubMed] [Google Scholar]
- Starkey, P. , Spelke, E. S. , & Gelman, R. (1990). Numerical abstraction by human infants. Cognition, 36(2), 97–127. 10.1016/0010-0277(90)90001-Z [DOI] [PubMed] [Google Scholar]
- Tschentscher, N. , & Hauk, O. (2014). How are things adding up? Neural differences between arithmetic operations are due to general problem solving strategies. NeuroImage, 92, 369–380. 10.1016/j.neuroimage.2014.01.061 [DOI] [PubMed] [Google Scholar]
- Van Harskamp, N. J. , & Cipolotti, L. (2001). Selective impairments for addition, subtraction and multiplication. Implications for the organisation of arithmetical facts. Cortex, 37(3), 363–388. 10.1016/S0010-9452(08)70579-3 [DOI] [PubMed] [Google Scholar]
- Venkatraman, V. , Ansari, D. , & Chee, M. W. L. (2005). Neural correlates of symbolic and non‐symbolic arithmetic. Neuropsychologia, 43(5), 744–753. 10.1016/j.neuropsychologia.2004.08.005 [DOI] [PubMed] [Google Scholar]
- Wang, L. , Mruczek, R. E. B. , Arcaro, M. J. , & Kastner, S. (2015). Probabilistic maps of visual topography in human cortex. Cerebral Cortex, 25(10), 3911–3931. 10.1093/cercor/bhu277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wege, T. E. , Trezise, K. & Inglis, M. (2021). Finding the subitizing in groupitizing: Evidence for parallel subitizing of dots and groups in grouped arrays. 10.31234/osf.io/x2ztc. [DOI] [PMC free article] [PubMed]
- Wender, K. F. , & Rothkegel, R. (2000). Subitizing and its subprocesses. Psychological Research, 64(2), 81–92. 10.1007/s004260000021 [DOI] [PubMed] [Google Scholar]
- Zhou, X. , Chen, C. , Zang, Y. , Dong, Q. , Chen, C. , Qiao, S. , & Gong, Q. (2007). Dissociated brain organization for single‐digit addition and multiplication. NeuroImage, 35(2), 871–880. 10.1016/j.neuroimage.2006.12.017 [DOI] [PubMed] [Google Scholar]
- Zimmermann, E. (2018). Small numbers are sensed directly, high numbers constructed from size and density. Cognition, 173, 1–7. 10.1016/j.cognition.2017.12.003 [DOI] [PubMed] [Google Scholar]
- Zimmermann, E. , & Fink, G. (2016). Numerosity perception after size adaptation. Scientific Reports, 6, 32810. 10.1038/srep32810 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supporting Information
Data Availability Statement
Due to data‐privacy protection issues, the collected MRI dataset cannot be made available in public repositories. In particular, public sharing was not requested in the proposal for the Ethical Committee (University of Regensburg) and participants were not explicitly asked for their permission. The pseudo‐anonymized dataset will be stored on the UR‐lab server and the corresponding author can provide access to the data on reasonable requests and upon a formal data‐sharing agreement with the Ethical Committee of the University of Regensburg. Codes used for the implementation of the analyses are publicly available in scientific publications that are appropriately cited in the manuscript.


