Significance
Prochlorococcus is the smallest and most abundant photosynthetic organism on Earth and is thought to be confined to low-latitude regions by its requirement for warm waters. Latitudinal transects in the North Pacific, however, demonstrate that the poleward decrease of this species occurs across a wide range of temperatures. An additional mechanism is likely required. We use theory, computational models, and additional observational data to suggest that the poleward decrease is caused by an ecological interaction: a shared predator which consumes both Prochlorococcus and similar-sized heterotrophic bacteria. Understanding the fate of this organism requires a knowledge of the interconnected ecosystem of other organisms, where both direct and indirect interactions control community structure.
Keywords: Prochlorococcus, biogeography, trophic interactions
Abstract
Prochlorococcus is both the smallest and numerically most abundant photosynthesizing organism on the planet. While thriving in the warm oligotrophic gyres, Prochlorococcus concentrations drop rapidly in higher-latitude regions. Transect data from the North Pacific show the collapse occurring at a wide range of temperatures and latitudes (temperature is often hypothesized to cause this shift), suggesting an ecological mechanism may be at play. An often used size-based theory of phytoplankton community structure that has been incorporated into computational models correctly predicts the dominance of Prochlorococcus in the gyres, and the relative dominance of larger cells at high latitudes. However, both theory and computational models fail to explain the poleward collapse. When heterotrophic bacteria and predators that prey nonspecifically on both Prochlorococcus and bacteria are included in the theoretical framework, the collapse of Prochlorococcus occurs with increasing nutrient supplies. The poleward collapse of Prochlorococcus populations then naturally emerges when this mechanism of “shared predation” is implemented in a complex global ecosystem model. Additionally, the theory correctly predicts trends in both the abundance and mean size of the heterotrophic bacteria. These results suggest that ecological controls need to be considered to understand the biogeography of Prochlorococcus and predict its changes under future ocean conditions. Indirect interactions within a microbial network can be essential in setting community structure.
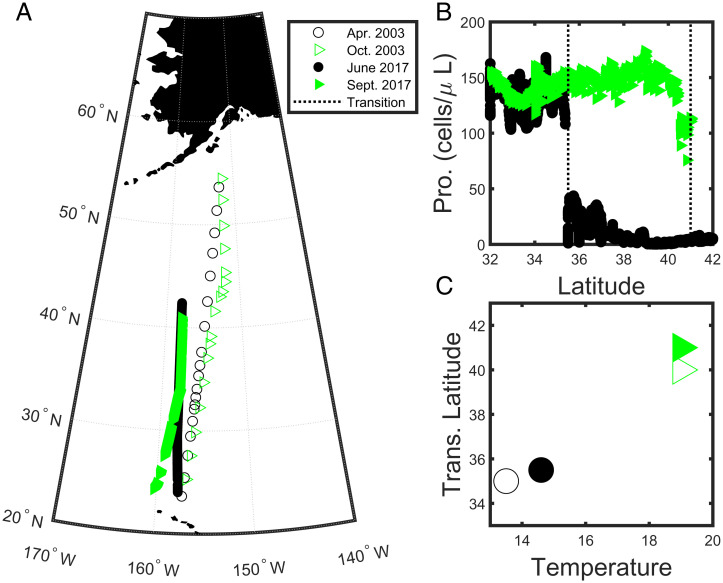
Prochlorococcus is the world’s smallest photosynthetic organism and is found ubiquitously in the global ocean equatorward of about 45∘ latitude (1). In regions where it occurs, Prochlorococcus tends to numerically dominate the photosynthetic community. Understanding what sets its biogeography is critical because of its important impact on global primary production and biogeochemical cycling. A striking feature of Prochlorococcus biogeography is its absence from higher latitudes (2) and regions of high chlorophyll concentrations (3), and, in particular, the rapidness of decline (Fig. 1). This collapse has been become even more clear with new high spatial resolution SeaFlow data (4) (Fig. 1B). This “collapse” at high latitudes is often ascribed to temperature sensitivity: Prochlorococcus fails to grow below ∼8 ∘C in the laboratory (5). Indeed, global distributions of Prochlorococcus appear to be well captured by simple parametric models including only temperature and light (photosynthetically available radiation) (2). This has led some authors (2, 6) to conclude that the biogeography of Prochlorococcus will expand poleward under climate change–induced ocean warming.
Fig. 1.
Cruise transect data: The transition from relatively stable to very few Prochlorococcus occurs at different latitudes over the seasons, and at different temperatures. (A) Cruise tracks for four latitudinal cruises across the northeast Pacific Ocean from April 2003, October 2003, April 2016, and September 2017. Black circles represent spring, and green triangles represent fall. Filled symbols are measurements from cruises associated with the Simons Collaboration on Ocean Processes and Ecology (SCOPE)-Gradients (7) cruise campaign, and open symbols are associated with cruises as part of the Comprehensive Oligotrophic Ocean Knowledge-Biogeochemical Observations Oahu-Kodiak (COOK-BOOK) program (8). (B) Mixed layer abundances of Prochlorococcus (cells per microliter) along the transect of the two cruises in June 2017 and September 2017. The dashed vertical lines indicate the latitude of the abrupt drop in cell numbers. (C) The corresponding latitude (y axis) and temperature (x axis) where the transition occurs.
We explore this temperature-driven hypothesis of the collapse of Prochlorococcus by examining observations from several cruises in the northeast Pacific Ocean (Fig. 1). We plot an estimate for the latitudinal location of the collapse of Prochlorococcus populations for each of four cruises (7, 8), as well as the temperature at that location. Three things are clear: the decrease in cell abundance can happen over a short distance; the location of the collapse moves by at least 6∘ latitude over the year; and the collapse occurs at different temperatures. This final point is the most critical. The temperature of the cell abundance transition for Prochlorococcus appears to span ∼7∘ of temperature, some of which are within Prochlorococcus’ optimal temperature range (9). This suggests that an additional factor contributes to the collapse of Prochlorococcus in this region.
We pose that an ecological interaction might be important, leveraging the knowledge that Prochlorococcus and similarly sized phytoplankton and heterotrophic bacteria share common predators (10–14). We hypothesize that this indirect interaction leads to the decline of Prochlorococcus as heterotrophic bacterial populations increase in regions of higher nutrient supply. Indeed, although temperature effects could not be excluded, heterotrophic bacteria have been invoked in this fashion as a possible explanation for observed decreases in Prochlorococcus indicator pigments at high chlorophyll concentrations (3). In ecological theory, this mechanism is known as “apparent competition” (15), defined as the “negative indirect interactions between victim species that arise because they share a natural enemy” (16). Here we refer to the mechanism as “shared predation” since the term “competition” is strongly associated with nutrient limitation and “bottom-up” controls in plankton ecology.
We provide a size-based theory for how shared predation works in this system. In this model, a critical size emerges that separates the size spectrum into heterotroph-dominated and photoautotroph-dominated sections. We show that this critical size increases as a function of resource supply, demonstrating how Prochlorococcus-like cells could be excluded in favor of heterotrophic bacteria in regions with sufficiently high resource supply. This theory therefore contains both top-down (e.g., grazers) and bottom-up (e.g., rate of supply of limiting nutrient) components. After showing how this theory works in simplified models, we implement it in a fully coupled global ecosystem model. The transition naturally emerges, solving outstanding issues with our ability to simulate and interpret Prochlorococcus globally. Finally, we return to transect data, showing that the trends in Prochlorococcus and heterotrophic bacterial abundance as well as their size agree with our predictions.
Theoretical Framework for Plankton Community Size Structure
Previous theoretical frameworks to explore the controls on size structuring of phytoplankton assemblages have highlighted the important interaction between predator and prey, and the supply rate of the limiting resource (3, 17–20). To illustrate these ideas, we first consider the following set of equations (schematically shown with black arrows in Fig. 2A):
| [1] |
| [2] |
| [3] |
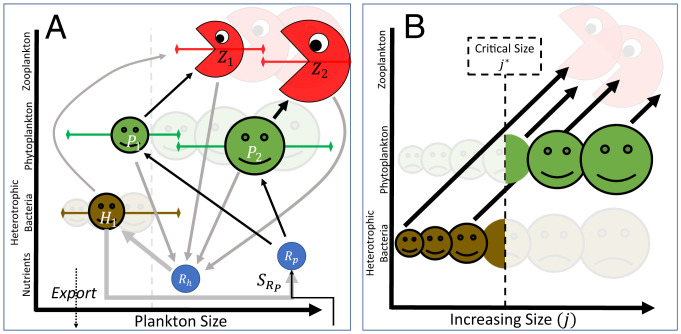
Fig. 2.
Ecosystem schematics. (A) Heterotrophic bacteria, Hj, phytoplankton, Pj, and zooplankton, Zj, along with their required resources Ri () are shown with arrows representing the elemental flow. The earlier size-based PZ model (Eqs. 1–3) formulation with two sizes is represented by the black arrows. The addition of a heterotroph, H1 and organic matter resource Rh shown with gray arrows (i.e., the system represented by Eqs. 6–10), allows for the exclusion of P1 at large enough resource supplies (). (B) The mechanism for exclusion can be described in terms of a critical size class, , separating a heterotroph-dominated from an autotroph-dominated section of the size spectrum. This critical size increases as a function of inorganic resource supply.
Here Rp is the limiting resource for the phytoplankton (e.g., nutrient such as nitrate), Pj is the biomass of the phytoplankton j, and Zj is the zooplankton that grazes on the jth phytoplankton. The resource is supplied to the system at rate . Plankton growth (μpj) is considered a function of a maximum growth rate, , a half-saturation constant κpj, and the limiting resource in a Monod kinetics,
Zooplankton graze with a per capita rate gj, and assimilate a fraction γ of the prey biomass. Both plankton have a linear loss rate (mp, mz). Here we consider a simple food chain with a range of phytoplankton sizes (j = 1 is the smallest) that are preyed on by a size range of zooplankton (j = 1 is the smallest). We assume that the smallest phytoplankton has the highest affinity, , for the resource, the second smallest has the next highest affinity, and so on, as suggested empirically (21) (see Materials and Methods).
Although highly simplified, these equations provide a clear illustration of the mechanisms at play, especially when we consider steady state (see Materials and Methods, Eqs. M1–M3). In particular, the nonzero steady-state solution for resource and phytoplankton are (where * indicates the steady state solution)
| [4] |
| [5] |
Following the terminology of resource competition theory (22, 23), the phytoplankton type with the lowest subsistence resource concentration (Eq. 4) is the fittest. In the absence of grazing, the smallest phytoplankton with highest affinity has the lowest and will outcompete all others (Fig. 3A). This occurs when resource supplies are very low. As one transitions to regions of higher and higher nutrient supplies, the grazer biomass increases (when only one zooplankton exists, ; see Materials and Methods, Eq. M4), and, subsequently, increases. It eventually reaches the value of (in the absence of grazing), and the two smallest phytoplankton can coexist (second vertical dashed line in Fig. 3A). The smallest phytoplankton biomass, P1, is capped as given in Eq. 5. Additional resource supply goes into the biomass of the next largest phytoplankton (P2) and its paired zooplankton (Z2) and so on for additional size classes. This inclusion of larger and larger phytoplankton transitioning from oligotrophic to increasingly eutrophic (higher ) waters is a well-known phenomenon observed in the world’s oceans (24, 25).
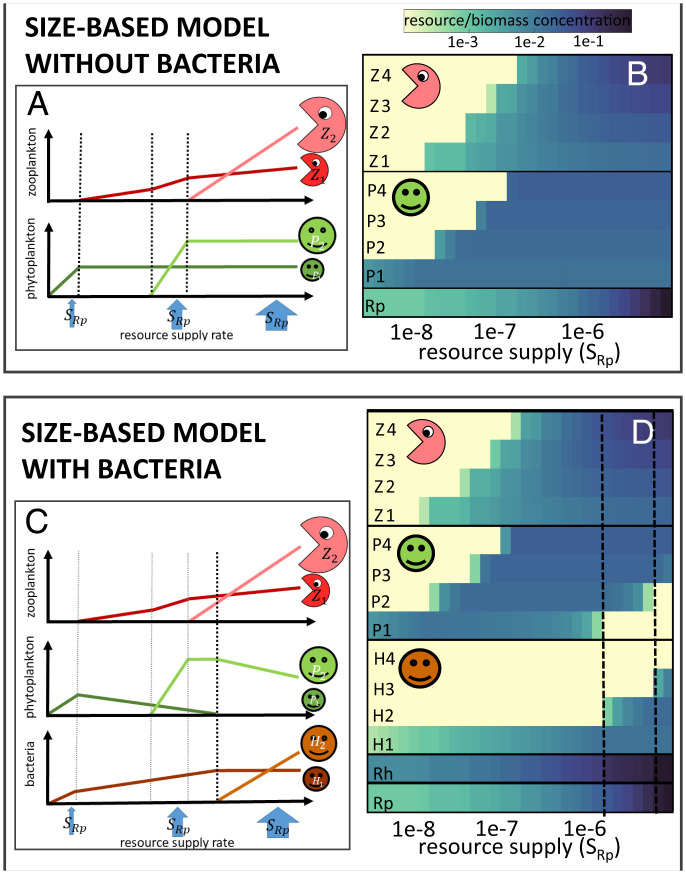
Fig. 3.
(A and C) Schematic of the theoretical steady-state results for different resource rates (SR) for (A) simple Rp, Pj, Zj size structured model (Eqs. 1–3) and (C) the more complex model including size classes of heterotrophic bacteria Hj (Eqs. 6–10). (B and D) Solutions for zero-dimensional numerical model for different resource supply rates for (B) Eqs. 1–3 and (D) Eqs. 6–10. Solutions are steady state for low resource supply rates, and are averages over several cycles of predator–prey oscillations that occur for higher resource supply rates in the simplified equations.
However, in the simplified theory, P1 persists with biomass (Eq. 5) no matter the resource supply. Thus, there is no mechanism in this theory to explain the collapse of Prochlorococcus as shown in Fig. 1.
Shared Predation between Prochlorococcus and Heterotrophic Bacteria Causes the Collapse.
We introduce into this framework heterotrophic bacteria, Hj, which are consumed along with similar size phytoplankton, Pj, by zooplankton, Zj (Fig. 2A; gray lines indicate the additional flows of matter),
| [6] |
| [7] |
| [8] |
| [9] |
| [10] |
Heterotrophic bacteria are assumed to consume detrital matter, Rh,
The constant is the maximum growth rate and κhj is the detritus half-saturation rate for bacteria j. Only a small fraction of the detrital matter taken up by heterotrophic bacteria goes into biomass growth (26), and the excess matter (, where ) is remineralized to the inorganic resource, Rp. Detrital matter is supplied by the ecosystem loss terms , although it could also include some of the nonconsumed grazed plankton. For ease of illustration, we do not express this term explicitly, but do note that increases with increased total biomass.
The steady-state subsistence solutions (see Materials and Methods, Eqs. M5–M9) for inorganic resource are the same as in the simpler model (Eq. 4), but the analogous equation to Eq. 5 has a significant difference,
| [11] |
| [12] |
The predator-mediated, “apparent” competition manifests in Eq. 12 where declines as increases (and vice versa). By having a shared predator, similarly sized phytoplankton and heterotrophic bacteria negatively impact each other.
The steady-state solution for detrital matter has a similar form to the inorganic resource,
| [13] |
If we assume [as suggested empirically (27, 28), and see Materials and Methods] that smaller bacteria have a higher affinity for dissolved organic matter than larger bacteria, these equations suggest an increase in size classes of bacteria across a gradient of increasing supply of resource, (schematically shown in Fig. 3C). Zj concentrations increase with higher inorganic and organic resource supply (in the case of a single size class ; see Materials and Methods, Eq. M9). Thus, with increasing resource supply, increases until another size class of bacteria can be supported. Instead of the bacteria being capped at a constant value, it is the sum of the similar-sized phytoplankton and bacteria (j) that is held at (Fig. 3B and Eq. 12). As detrital matter accumulates in regions with higher inorganic resource supply, heterotrophic bacterial biomass increases, to the detriment of the similar-sized phytoplankton. As Hj approaches , the phytoplankton are excluded (black dashed vertical line in Fig. 3C). This provides an ecological mechanism for the demise of a size class with increased resource supply.
A Size-Based Ecological Transition from Heterotrophs to Autotrophs.
The steady-state solutions for Eqs. 7 and 8 provide two constraints on the zooplankton biomass (Materials and Methods, Eq. M7). To match these constraints simultaneously (if we assume that the death rate constants for Hj and Pj equate, mh = mp), coexistence in steady state occurs only when the growth rates of the similar size bacteria and phytoplankton are equal,
| [14] |
This suggests that a tight coupling between accumulation of detrital matter and supply of inorganic resources is necessary for the coexistence of the two prey. For how many sizes classes, (j), is this condition met?
We have assumed here that the growth rate constants μmax and κ are functions of the organism type (subscripts p or h) and increasing size, j. There is strong theoretical and empirical evidence to suggest that the size-dependent growth rate constants μmax and κ for phytoplankton can be expressed as power law functions of size (21, 29), and, for simplicity, here we assume the growth of heterotrophic bacteria scales similarly (see Materials and Methods). Given these scalings, we can write μmax and κ as separable functions; a function of size (, which are independent of type) multiplied by type-dependent constants ( or ). We expand Eq. 14 with these functions,
| [15] |
which can be solved for the size-dependent portion of the half-saturation function,
| [16] |
The half-saturation constant is a monotonically increasing function of size (see Materials and Methods), and the right-hand side of Eq. 16 is independent of size. Thus, there is, at most, a single size class (i.e., single j, which we will refer to as ) which contains both plankton types for any fixed combination of and (set by the resource supply, ). As the derivative of the right-hand side of Eq. 16 is negative under our conditions, size classes of phytoplankton will be systematically eliminated with increasing nutrient supplies.
Numerical Simulations Support Theory
The theory we lay out above suggests that smaller phytoplankton will be eliminated with higher resource supply due to shared predation with similar-sized heterotrophic bacteria. The theory also suggests that only one sized pair of bacteria and phytoplankton can coexist at any resource supply rate. The number of size classes of the eliminated phytoplankton increases with higher resource supply. Here we demonstrate these findings with two sets of numerical simulations.
The first model setup encodes the exact equations as laid out in Theoretical Framework for Plankton Community Size Structure (see Materials and Methods; parameters are provided in SI Appendix, Table S1), and we solve the solutions for parcels of water (we will call this the zero-dimensional model setup) with different resource supply rates . First, we show the solutions for Eqs. 1–3 for the size-based model including only phytoplankton and zooplankton (Fig. 3B) represented by the black arrows in Fig. 2A for four size classes. Nutrient affinity decreases with size, although note that we employ a unimodal distribution for maximum growth rates (30), such that the smallest type has a low rate as observed for Prochlorococcus (9) (see Materials and Methods). The anticipated increase in the number of coexisting phytoplankton size classes with increasing resource supply is evident. The resource supply at which any size class of phytoplankton j can coexist is higher than the resource supply rate where the smaller-size class grazer (j – 1) is supported, indicating that grazer control of a smaller phytoplankton size class allows the next larger phytoplankton size class to survive. Once the jth grazer can survive, the prey j has its biomass capped. These results support the finding of previous size-based models (e.g., refs. 17 and 19).
In Fig. 3D, we show the results for the system extended to include heterotrophic bacteria and detrital matter (Eqs. 6–10, additional gray arrows in Fig. 2A). Again, we see the increase of coexisting phytoplankton size classes and their grazers with increasing resource supply (). Additionally, several size classes of heterotrophic bacteria can coexist at larger resource supply rates. Increasing resource supply leads to increased detrital supply, which, in turn, leads to increased bacterial biomass in the jth size class at the expense of the jth phytoplankton. At a critical resource supply rate (vertical black dashed lines in Fig. 3D), when the heterotrophic bacteria reach its maximum biomass (), the jth phytoplankton is eliminated. Additionally, we see that only one size class of phytoplankton and bacteria can coexist. Moving along the axis of resource supply rate, we see each new size class j + 1 of bacteria emerge only after the smaller phytoplankton j no longer coexists.
This computational examination of Eqs. 6–10 provides evidence that indirect competition due to a shared predator can cause the collapse of a phytoplankton size class. However, this setup is highly simplistic, and we now put these ideas in the context of the Prochlorococcus collapse seen in Fig. 1. First, we note that the smallest heterotrophic bacteria (e.g., SAR11) are smaller than Prochlorococcus. For instance, SAR11 have been found to have cell diameters between about 0.3 and 0.45 m (28), while Prochlorococcus has been observed with diameters varying between about 0.45 and 0.8 m (5, 9, 31, 32). Additionally, the carbon cell quota of SAR11 has been shown to be ∼10 times less than for Prochlorococcus (33). We repeat the experiment seen in Fig. 3D with the smallest size class only consisting of bacteria, and find, qualitatively, the same results (SI Appendix, Fig. S1A). Nevertheless, the model described by the set of Eqs. 6–10 is extremely simplified, neglecting the many additional complexities of the real ocean, including influences of seasonality, light, temperature, multiple limiting nutrients, more complex food web dynamics (e.g., inclusion of viruses), and constant mixing and transport by the three-dimensional fluid flow. We now consider a second set of numerical experiments using a more complex three-dimensional global biophysical model.
We use a modified version of the size-based numerical ecosystem model used in ref. 34. The model includes 31 phytoplankton types (Fig. 4 A and C) covering 15 size classes from 0.6 mm to 104 m equivalent spherical diameter (ESD). The phytoplankton are additionally split into functional groups including diatoms, coccolithophores, prokaryotes, picoeukaryotes, diazotrophs, and mixotrophs. The smallest phytoplankton (with ESD of 0.6 m) is an analog of Prochlorococcus. Phytoplankton growth (and sinking) parameters are allometrically defined similarly to the simple zero-dimensional model shown in Fig. 3, but with functional group specifics (see ref. 35, Materials and Methods, and SI Appendix, Table S1). Growth rates are also a function of multiple potential limiting nutrients (dissolved inorganic nitrogen, phosphate, iron, and silicic acid), spectral light, photoacclimation, and temperature. The model includes a size range of zooplankton that graze on plankton 5 to 15 times smaller than themselves, but, preferentially, 10 times smaller (36–38). We additionally include three heterotrophic bacteria, ranging from smaller than to the same size as the two smallest phytoplankton, following ref. 26. This complex ecosystem, along with inorganic, dissolved, and particulate material, is advected and mixed within a three-dimensional global ocean model (see Materials and Methods).
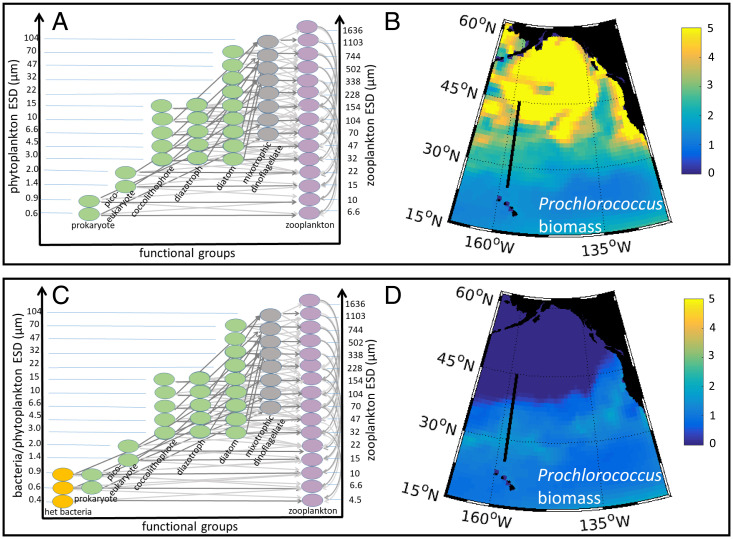
Fig. 4.
Global biophysical model. (A and C) Schematic of the ecosystem structure with y axis representing the size of organisms and x axis representing their functional type. In A, remineralization is parameterized as a rate, while, in C, three heterotrophic bacteria size classes are explicitly included in the food web. (B and D) Modeled surface biomass (milligrams C per cubic meter) of the model Prochlorococcus analogs for the case with no explicit bacteria (B) and the case with bacteria (D).
We run two experiments: one where we explicitly include the heterotrophic bacteria and another where we exclude the bacteria and approximate remineralization as a rate-specific function of the detrital matter’s concentration. Both models capture similar (and reasonable) patterns of total chlorophyll a concentrations (Chl), size distribution of phytoplankton, and functional groups (SI Appendix, Figs. S2 and S3). The patterns of high and low total Chl are realistic, including the sharp increase in Chl and size classes in the transition from subtropical to subpolar conditions in the North Pacific covered by the shipboard transects (Fig. 1 and SI Appendix, Fig. S2). In the simulation with explicit bacteria, the smallest bacteria type is ubiquitous, with an increase in larger types also occurring in the transition zone (SI Appendix, Fig. S4).
In the model without explicit bacteria, Prochlorococcus analogs continue to exist in poleward regions (Fig. 4B), in strong contrast to the version with explicit bacteria (Fig. 4D). With the explicit bacteria, Prochlorococcus biomass is relatively uniform in the subtropical regions, with a sharp decrease in the midlatitudes similar to that suggested by the observations. The collapse in the population occurs slightly poleward from where the total phytoplankton biomass increases dramatically, coincident with the grow-in of the larger heterotrophic bacteria (SI Appendix, Fig. S4). Over this region (several degrees of latitude, shifting between 30∘N and 40∘N seasonally), the environment shifts from oligotrophic conditions with relatively uniform nutrient supplies (i.e., constant; SI Appendix, Fig. S5) via remineralization to a region of seasonally large fluxes of nutrients from upwelled waters at higher latitudes (see, e.g., ref. 39). This increase in resource supply rates (at least seasonally) increases dramatically over a very short distance (i.e., the x axis, , of Fig. 3D is collapsed over just a few degrees of latitude). This sharp increase in resource supply rate promotes the sharp increase in total phytoplankton biomass (i.e., more size classes), increases supply of organic matter, and thus allows the coexistence of the larger bacteria size class (SI Appendix, Fig. S4). Shared predation with these larger heterotrophic bacteria driven by the 6.6-m grazer leads to the collapse of the Prochlorococcus analog. The simulation without explicit bacteria shows no such collapse (Fig. 4B). These results suggest that, even in a much more realistic environment (multiple limitations on growth, lack of steady state) and far more complex food web dynamics, the insight from the theoretical framework of shared predation can explain the collapse of Prochlorococcus.
Data Comparison and Summary
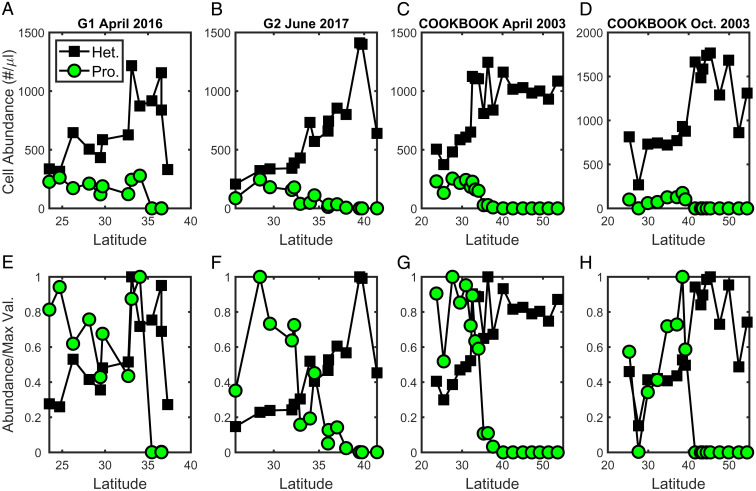
We have developed a theory that combines size-based predator–prey interactions (19, 40), including shared predation [known as “apparent competition” in classical ecological theory (15)], to consider the controls on community structure. The theory, by including both bottom-up (e.g., supply of nutrients) and top-down (e.g., grazing pressure) processes, lays out a set of predictions that can be evaluated with observed data from latitudinal surface transects in the North Pacific. The simplest prediction from apparent competition is that the abundance of heterotrophic bacteria should increase as the abundance of Prochlorococcus decreases, clearly seen in the zero-dimensional simulation results (Fig. 3D). However, growth rates in the real ocean will be affected by a number of factors other than a single resource, including temperature and, in the case of phytoplankton, light, while grazing rarely manifests as food chains. The global biophysical models suggest that a more complex marine food web with multiple limitations to growth, and subject to physical advection and mixing (i.e., never in steady state), provides similar results (Fig. 4D and SI Appendix, Fig. S4). We also see that this prediction is consistent with the surface data from four different cruise transects (Fig. 5). These transects are from different times of year and span almost 15 y. We find that the relative cell abundance of heterotrophic bacteria undergoes a strong increase coincident with the strong decrease in Prochlorococcus. Across this transect, nutrient supply rates increase poleward (as shown in the model; SI Appendix, Fig. S5). Surface nutrient concentrations also increase (SI Appendix, Fig. S7) (39), as suggested by increasing R. The increased nutrient supply leads to higher primary production and higher biomass of larger phytoplankton (Fig. 6A) poleward. As a result, more organic matter is produced, which, in turn, supports more heterotrophic bacteria. The theory of shared predation predicts such a pattern; as both the mutual grazer and the bacteria population increase, the loss of Prochlorococcus increases until it no longer coexists.
Fig. 5.
Observed surface data for Prochlorococcus (green circles) and heterotrophic bacteria (black squares). (A–D) Cell abundance (cells per microliter) across four different transects spanning 2003–2016. Cruises in B–D are the same as in Fig. 1. Additional cruise information is available for the SCOPE-Gradients cruises 1 and 2 (A and B; see ref. 7) and the COOK-BOOK cruises (C and D; see ref. 8). (E–H) Cell abundance normalized to the maximum value of that type on that transect (above, A–D).
Fig. 6.
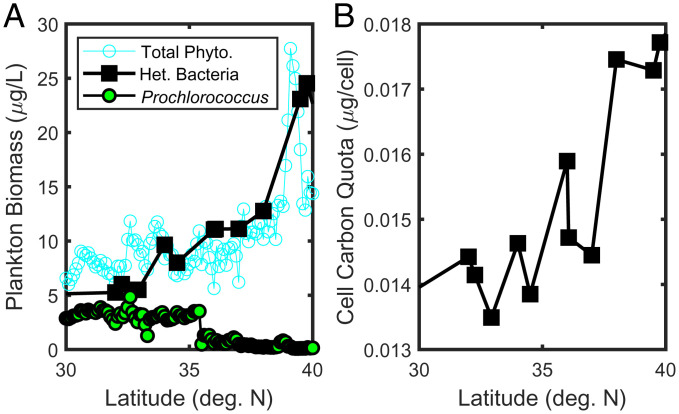
Observed surface data from the June 2017 north–south transect near 158∘W (MGL1704, SCOPE-Gradients 2; also see Fig. 1). (A) Total estimated carbon biomass (micrograms C per liter; see Materials and Methods) for heterotrophic bacteria (black squares), Prochlorococcus (green circles), and total phytoplankton (blue open circles). (B) Mean cell mass (micrograms C per cell) of heterotrophic bacteria.
The theory also suggests that only a single size class of mutual prey can coexist, and that this critical size, , is a function of resource supply. This result is illustrated in the more abstract zero-dimensional model (Fig. 3D). Allowing for the different ranges in sizes of phytoplankton and heterotrophic bacteria, our global model results also suggest that it is, in fact, increases in larger bacteria that force the collapse of Prochlorococcus (SI Appendix, Fig. S4B). The smallest heterotrophic bacteria are ubiquitous in the model ocean, similar to the wide distribution of SAR11 (28). It is only as the larger bacteria grow, supported in regions of higher plankton biomass and nutrient supply rates, that Prochlorococcus is eliminated. We find that this additional component of the theory/model is also consistent with observations from cruise results. Not only does the biomass of bacteria increase just south of the collapse of Prochlorococcus (Fig. 6A), but the average cell size of the bacteria also increases significantly moving poleward (Fig. 6B). The cell size increase closely follows the increase in total phytoplankton biomass, and hence the increase in production of organic matter and supply of inorganic resource.
Here we have focused on the decrease of Prochlorococcus abundance moving poleward in surface waters of the North Pacific, but similar patterns of declining Prochlorococcus cell abundances have also been observed in the Atlantic (5, 41) in both northern and southern gyre transitions. Coincidentally, increasing bacterial cell abundances have been observed across these transitions (41). Thus, we believe that this theoretical understanding is not restricted to the North Pacific and has a larger application to understanding global Prochlorococcus distributions.
We do not preclude a role for temperature, as Prochlorococcus does indeed fail to grow in cold water (5). Prochlorococcus also has a low maximum growth rate relative to eukaryotic phytoplankton (9), consistent with its very small size (30). It will have a growth disadvantaged relative to others, particularly with a combination of higher nutrients and low temperatures (42). However, its ability to avoid predation due to its small size remains, which is why this mechanism fails to cause the collapse in models (as in Fig. 4). Our work suggests that shared predation may be a leading process in determining the spatial distribution of Prochlorococcus. In addition to explaining the demise of Prochlorococcus at high latitudes, we believe that shared predation with bacteria may also partially explain the demise of Prochlorococcus with depth. Similar to the poleward decrease of Prochlorococcus growth rate with temperature, the relative growth rates of Prochlorococcus and other autotrophs decline significantly with depth as the amount of available light decreases. In this case, the demise could be set by a balance between organic material sinking from above and the decreasing light intensity.
We have focused on shared predation with bacteria. However, shared predation could also be at play with similar-sized phytoplankton or even between phytoplankton and generalist viruses. For instance, some predators can consume (11, 12) and some cyanophages can infect (43–45) both Prochlorococcus and Synechococcus. There are, indeed, some interesting shifts in Prochlorococcus distributions that may be related to indirect competition with Synechococcus (SI Appendix, Fig. S6 and Fig. 3D), although we note that the relationship between these two populations is less clear. Nonetheless, expanding the concept of shared predation to other functional types and size classes (e.g., Synechococcus and a similar-sized heterotrophic bacteria) could very likely help explain these nuances.
We contend that the observational data are consistent with the theoretical framework of shared predation combined with size class grazing that can explain the decreases of Prochlorococcus in higher latitudes. This theory does not require any assumption about how Prochlorococcus growth is impacted by temperature. However, we do note that the theory is, by design, extremely simple in order to illustrate key concepts. Indeed, the real world is far more complex, and growth rates are impacted by other factors, such as temperature, nutrients, and light. These complexities are captured in the more complex global biophysical model (Fig. 4 C and D), but the theoretical ideas of the collapse still hold, showing that the underlying mechanism is robust. However, even the three-dimensional model is simplified with regard to the real ocean. Here we have, for instance, assumed heterotrophic bacteria and phytoplankton do not compete for resources, and the food web remains relatively simple. Nonetheless, the observations in the real world are consistent with the theoretical insight, suggesting that shared predation plays an important role in the dramatic collapse of Prochlorococcus populations (Fig. 1). Further observational exploration of these ideas, especially those focused on the seasonal progression of these ecological transitions (39), should help quantify the importance of shared predation and related mechanisms in structuring plankton biogeography.
Understanding what sets the biogeography of plankton and their dynamics has become additionally important under a changing climate. These organisms set the foundation for global fisheries and are the conduits for long-term carbon storage in the deep ocean. Current methods for predicting the range shifts of phytoplankton are often based on assuming that current correlations with temperature are predictive in a future ocean. Ecological mechanisms, such as shared predation, show how small changes in our understanding can lead to large changes in our predictions into the future. If we want to correctly project and understand how the ocean ecosystem will evolve moving forward, it is critical that we build a mechanistic understanding of how the community structure currently functions. The controls of Prochlorococcus distributions are important to understand, given this species’ numerical dominance in many regions of the ocean. Currently suggested controls based on a thermal growth threshold (5) are insufficient to explain the species’ collapse at high latitudes (Fig. 1). We utilize a bacteria-driven mechanism (3), which allows for decreasing Prochlorococcus abundance at higher production rates. We provide theoretical, numerical, and observational support for the idea that shared predation with heterotrophic bacteria controls the range of Prochlorococcus. In our theory, size-based predation leads to the emergence of a critical size separating heterotrophic bacteria from phytoplankton. This size increases with nutrient supply, eventually eliminating the smallest phytoplankton, Prochlorococcus, from the ecosystem. This same mechanism is likely to play a role in the dynamics of the next largest phytoplankton, Synechococcus, and the formulation may prove useful for simplifying our understanding of the relationships between other functional groups of plankton.
While the importance of direct interactions such as grazing have been established (18, 19, 40) and included in models, the role of indirect interactions such as shared grazing is often ignored. Yet, as we show here, these interactions may be crucial to understanding Prochlorococcus distributions. Thus, the knowledge of the microbial network of interactions, including processes such as shared grazing and other indirect interactions (e.g., refs. 3 and 46–50), is essential for being able to understand and predict community structure and its changes in the future. Equally important are frameworks, like the one presented here, which allow quantification of the broader effects of these interactions across the plankton size spectrum.
Bottom-up resource controls and top-down predator controls conspire to set the biogeography of plankton in the sea. The simplest, size-based theories suggest that, as nutrient supplies increase, larger phytoplankton grow in while the smaller phytoplankton remain. For the smallest, and arguably most critical, phytoplankton Prochlorococcus, this prediction is broken, as Prochlorococcus populations collapse at high latitudes. The location of this collapse in the North Pacific is difficult to explain with temperature but emerges naturally if shared predation with similarly sized heterotrophic bacteria is considered. Under the theory posed here, heterotrophic bacteria increase with nutrient supplies along with higher biomass of larger phytoplankton and higher primary production. If heterotrophic bacteria and Prochlorococcus share a grazer, this increase in bacterial populations can lead to a collapse of Prochlorococcus. This study highlights that the marine ecosystem needs to be understood, and modeled, as an interconnected network of organisms where both direct and indirect interactions control community structure.
Materials and Methods
Observational Data.
Cell count data used in Fig. 5 were provided by discrete samples collected in surface water ( ∼5 m depth), fixed with glutaraldehyde (0.25% final concentration), and analyzed by Influx’s cell sorter. Prochlorococcus was discriminated based on forward light scattering and red autofluorescence emitted by pigments. Total bacteria counts were obtained by staining the sample with SYBR Green I (0.01% final concentrations), and heterotrophic bacteria counts were calculated by subtracting Prochlorococcus cell counts from total bacteria counts (51). Biomass estimates in Fig. 6 use diameters and carbon quotas of individual cells estimated by the Influx (heterotrophic bacteria) and SeaFlow flow cytometers (Prochlorococcus and total phytoplankton) from forward light scatter measurements by the application of Mie theory for spherical particles, calibrated using particles of known refractive indices and several phytoplankton species of known carbon content (4). Data were averaged across tenth-of-a-degree bins. All data used in this study are publicly available. Data for the COOK-BOOK cruises [April and October 2003 (8)] can be found at https://hahana.soest.hawaii.edu/cookbook/cookbook.html; data for the SCOPE-Gradients cruises (April 2016, May/June 2017) are available via the open access data repository Zenodo: Influx 2016: 10.5281/zenodo.4085858; Influx 2017: 10.5281/zenodo.4085873; SeaFlow: 10.5281/zenodo.3994953.
Steady-State Solutions of Theoretical Frameworks.
An informative set of nonzero steady-state results for the size-based model without bacteria (Eqs. 1–3) are
| [M1] |
| [M2] |
| [M3] |
| [M4] |
Solutions for the more complex system including heterotrophic bacteria and an organic detrital pool (Eqs. 6–10) are
| [M5] |
| [M6] |
| [M7] |
| [M8] |
And, if we assume mh = mp, we additionally find
| [M9] |
Allometric Scaling of Plankton Growth and Grazing.
In both zero-dimensional and the global three-dimensional model, we follow the allometric scaling used in ref. 35. Phytoplankton and heterotrophic maximum growth rate, nutrient affinity, grazing, and sinking (in the three-dimensional model), as well as zooplankton maximum grazing rates, are parameterized as power law functions of cell volume V: aVb. Thus, many size classes can be described by just two coefficients (a, b) per parameter (SI Appendix, Table S1). Plankton smaller than 3 m have an increase of growth rate with size, and those larger than 3 m have a decrease of growth rate with size. This unimodal distribution has been observed (30, 52–55) and explained as a trade-off between replenishing cell quotas versus synthesizing new biomass (56, 57). Thus the b for maximum growth rates are different below and above 3 m ESD. The intercept a depends on the functional group of phytoplankton in the three-dimensional model (see discussion below, and SI Appendix, Table S1). The smallest phytoplankton have the highest affinity for nutrients (21), as a result of the lower surface to volume ratio found in larger cells (52, 58).
The choice of allometric scaling parameters for the heterotrophic bacteria is less clear, as fewer laboratory studies have examined the size dependence of growth as compared to phytoplankton and zooplankton. Additionally, different bacteria may consume a variety of types of organic matter (59, 60). However, it is generally recognized that larger bacteria (copiotrophs) grow significantly faster than smaller oligotrophs (59–61), and also that smaller oligotrophs have high nutrient affinities (27, 60). Without better constraints, we chose to use the same power exponent for growth rate and uptake as for phytoplankton (although this is not a requirement; see additional extra zero-dimensional experiment discussed below). The intercept a value was chosen to provide the smallest bacteria types with maximum growth rates on the order of 0.1 per day (62, 63).
Zero-Dimensional Model.
The model simulation results presented in Fig. 3 B and D represent a parcel of water (i.e., zero-dimensional) with an influx of resource . We integrate the two sets of equations (Eqs. 1–3 and 6–10) from initial conditions (set by the grazing-free steady-state analytical solutions) until a (quasi-) steady state is reached using a fourth-order Runge–Kutta scheme (64). We include 10 size classes (j) in the simulations, but show only the 4 smallest for simplicity. Size spacing was the same as in the global model (Fig. 4D). Plankton growth and grazing parameters are allometrically based, as discussed above, and are provided in SI Appendix, Table S1. We run individual simulations with different values of spanning from very low values through values typical of the subtropical gyres ( mmol N×m-3 ×s-1, as suggested by the global numerical model) to high values more typical of seasonal higher latitudes. Each grid in Fig. 3 B and D shows the final solution of each of these experiments. At low values of , these results are the steady-state solution. At higher supply rates, the simulations develop predator–prey oscillations, and here we present the average of these cycles.
We perform a number of additional simulations to test parameter choices as well as sensitivity to resource supply assumptions. We show three additional results in SI Appendix. We repeat the experiment seen in Fig. 3D with the smallest size class only consisting of bacteria, and find, qualitatively, the same results (SI Appendix, Fig. S1B). Additionally, for ease in the theoretical proof showing that only one size class of phytoplankton and heterotrophic bacteria can coexist, we assumed that there is no external supply rate (i.e., was entirely due to remineralization of detrital matter) and that the allometric relationships for bacteria and phytoplankton growth parameters were identical. We perform two additional numerical experiments that show that these assumptions are not critical to the qualitative behavior described above (SI Appendix).
The Global Biophysical Ocean Model.
The biogeochemical/ecosystem model captures the cycling of C, N, P, Si, and Fe as they pass through inorganic and (dead and living) organic pools (35, 65). The specific details of the ecosystem follow from ref. 34 (see SI Appendix for the exact differences from that model) and resolves 31 phytoplankton (2 picoprokaryotes, 2 picoeukaryotes, 5 coccolithophores, 5 diazotrophs, 9 diatoms, 8 mixotrophic dinoflagellates), 16 zooplankton, and 3 heterotrophic bacteria. Phytoplankton have size resolution spanning from 0.6 m to 140 m ESD, zooplankton spanning 4.5 μm to 1,636 m, and bacteria spanning 0.4 μm to 0.9 m (Fig. 4C). The new component of the model relative to ref. 34 is the inclusion of the heterotrophic bacteria component. We follow ref. 26 in parameterizing the bacteria as consuming dissolved organic matter with a Michaelis–Menten function. A fraction of the uptake goes to bacteria growth, and the remainder is remineralized to inorganic nutrients.
Parameters influencing phytoplankton growth, grazing, and sinking are related to size (35, 66), with specific differences between the six functional groups (35) (SI Appendix, Table S1, and discussion above). Phytoplankton growth is limited by multiple nutrients (N, P, Fe, and Si in the case of diatoms), light (following ref. 67), and temperature (following refs. 68 and 69). Grazing is parameterized using a Holling II function (70) and is size specific such that grazers can prey upon plankton 5 to 15 times smaller than themselves, with an optimal size of 10 times smaller (36–38). The emergent size distribution of the simulated plankton populations is strongly controlled both by the rate of supply of limiting nutrients (bottom up) and by grazing (top down) (19, 35).
The biogeochemical and biological tracers are transported and mixed by the Massachusetts Institute of Technology (MIT) general circulation model (MITgcm) (71), constrained to be consistent with altimetric and hydrographic observations (72). This three-dimensional configuration has coarse resolution (1∘ by 1∘ horizontally) and 23 levels ranging from 10 m in the surface to 500 m at depth.
Two simulations are presented: one with explicit bacteria and the other where organic matter remineralized to inorganic nutrients with a temperature-dependent rate, as used in previous versions of this model (e.g., ref. 35). The two simulations were run for 10 y. The ecosystem quickly (within 2 y) reaches a quasi-steady state. Here we show results from the 10th year of the simulations.
The latitudinal distribution and seasonality of bulk ecosystem properties such as chlorophyll (SI Appendix, Fig. S2), as well as distributions of size classes and functional groups, are plausible in comparison with satellite and in situ observations (73, 74) (SI Appendix, Figs. S2 and S3). The model results are similar to those in previous studies, with slight modification in the model (e.g., with a slightly different number of larger size classes) and different physical frameworks that have conducted additional evaluation (e.g., refs. 35, 75, and 76). As in those studies, we find that our model Chl a compares well to satellite estimates, although we note that the satellite estimates have large uncertainties (77) (more than 35% errors). The coarse resolution of the model does not capture important physical processes near coastlines, and lack of sedimentary and terrestrial supplies of nutrients and organic matter lead to Chl a being too low in these regions. Chl a is underestimated by the model in the subtropical gyres, likely due to lack of mesoscale processes in the model that would supply additional nutrients in these regions (78). The model results have the observed ubiquitous picophytoplankton and the limitation of the larger size classes to the more productive regions. The model picophytoplankton size class Chl a is potentially slightly too low, and the nano size class is potentially too high. However, we note that, if we set the pico/nano break at the model fifth size class (just under 3 m) instead of at the fourth (2 m) size class, the relative values are much more in line with the satellite product. We suggest that the satellite product division might not be that accurate.
We also compare to a synthesis of phytoplankton abundances (world atlas of MARine Ecosystem DATa [MAREDAT]) (74) (SI Appendix, Fig. S3). Although the observations are sparse, we do capture the ubiquitous nature of the picophytoplankton, the limited domain of the diazotrophs (including observed lack of diazotrophs in the South Pacific gyre), and the pattern of enhanced diatom biomass in high latitudes and low diatom biomass in subtropical gyres. We overestimate the coccolithophore biomass relative to MAREDAT in many regions, but note that the conversion from cells to biomass in that compilation was estimated to have uncertainties of several 100% (79). The MAREDAT compilation did not include a category for dinoflagellates.
Model code and parameters (80) and model biomass output (81) are available online (see Data Availability).
Supplementary Material
Acknowledgments
We thank all the members of the Simons Collaboration on Ocean Processes and Ecology (SCOPE)-Gradients program for conversation about this region of the ocean, and the identification of the “Propocalypse.” We also thank John MacMillan, Kelsy Cain, and Annette Hynes for processing and curating flow cytometry data from SCOPE-Gradient cruises. This work was supported by multiple grants from the Simons Foundation. The Simons Collaboration on Computational Biogeochemical Modeling of Marine Ecosystems (CBIOMES) supported S.D. and M.J.F. on CBIOMES Grant 549931 and supported C.L.F. on CBIOMES Grants 827829 and 553242. F.R. was funded on Simons Life Sciences Project Award 574495. SCOPE funded D.C., E.V.A., and M.J.F. on SCOPE Award 329108. E.Z. was funded by the Simons Postdoctoral Fellowship in Marine Microbial Ecology. Additional support came from NASA (Grant 80NSSC17K0561, S.D., F.R., E.V.A., and M.J.F.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2110993118/-/DCSupplemental.
Data Availability
The csv files from flow cytometer data have been deposited in Zenodo (10.5281/zenodo.4085858; 10.5281/zenodo.4085873; 10.5281/zenodo.3994953). Data for the COOK-BOOK cruises [April and October 2003 (8)] can be found at https://hahana.soest.hawaii.edu/cookbook/cookbook.html. All data used can be accessed directly through the Simons CMAP project, https://simonscmap.com/, for download (82). The physical model used here is available through mitgcm.org, and the generic ecosystem code used in this study is available through https://github.com/darwinproject/darwin3. The specific modifications for the setup used here, and all parameter values, are available via Harvard Dataverse https://doi.org/10.7910/DVN/ISJQ1W, and the model output used in this manuscript is available at https://doi.org/10.7910/DVN/FEWXB4.
References
- 1.Partensky F., Garczarek L., Prochlorococcus: Advantages and limits of minimalism. Annu. Rev. Mar. Sci. 2, 305–331 (2010). [DOI] [PubMed] [Google Scholar]
- 2.Flombaum P., et al., Present and future global distributions of the marine Cyanobacteria Prochlorococcus and Synechococcus. Proc. Natl. Acad. Sci. U.S.A. 110, 9824–9829 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Goericke R., The structure of marine phytoplankton communities—Patterns, rules, and mechanisms. CCOFI Rep. 52, 182–197 (2011). [Google Scholar]
- 4.Ribalet F., et al., SeaFlow data v1, high-resolution abundance, size and biomass of small phytoplankton in the North Pacific. Sci. Data 6, 277 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Johnson Z. I., et al., Niche partitioning among Prochlorococcus ecotypes along ocean-scale environmental gradients. Science 311, 1737–1740 (2006). [DOI] [PubMed] [Google Scholar]
- 6.Flombaum P., Wang W. L., Primeau F. W., Martiny A. C., Global picophytoplankton niche partitioning predicts overall positive response to ocean warming. Nat. Geosci. 13, 116–120 (2020). [Google Scholar]
- 7.Juranek L. W., et al., The importance of the phytoplankton “middle class” to ocean net community production. Global Biogeochem. Cycles 34, e2020GB006702 (2020). [Google Scholar]
- 8.Church M. J., Björkman K. M., Karl D. M., Saito M. A., Zehr J. P., Regional distributions of nitrogen-fixing bacteria in the Pacific Ocean. Limnol. Oceanogr. 53, 63–77 (2008). [Google Scholar]
- 9.Moore L. R., et al., Culturing the marine cyanobacterium Prochlorococcus. Limnol. Oceanogr. Methods 5, 353–362 (2007). [Google Scholar]
- 10.Caron D. A., et al., Grazing and utilization of chroococcoid cyanobacteria and heterotrophic bacteria by protozoa in laboratory cultures and a coastal plankton community. Mar. Ecol. Prog. Ser. 76, 205–217 (1991). [Google Scholar]
- 11.Christaki U., Jacquet S., Dolan J. R., Vaulot D., Rassoulzadegan F., Growth and grazing on Prochlorococcus and Synechococcus by two marine ciliates. Limnol. Oceanogr. 44, 52–61 (1999). [Google Scholar]
- 12.Christaki U., et al., Dynamic characteristics of Prochlorococcus and Synechococcus consumption by bacterivorous nanoflagellates. Microb. Ecol. 43, 341–352 (2002). [DOI] [PubMed] [Google Scholar]
- 13.Sakka Hlaili A., Legendre L., Gosselin M., Delesalle B., Structure of the oligotrophic planktonic food web under low grazing of heterotrophic bacteria: Takapoto Atoll, French Polynesia. Mar. Ecol. Prog. Ser. 197, 1–17 (2000). [Google Scholar]
- 14.Strom S., Novel interactions between phytoplankton and microzooplankton: Their influence on the coupling between growth and grazing rates in the sea. Hydrobiologia 480, 41–54 (2002). [Google Scholar]
- 15.Holt R. D., Predation, apparent competition, and the structure of prey communities. Theor. Popul. Biol. 12, 197–29 (1977). [DOI] [PubMed] [Google Scholar]
- 16.Holt R. D., Bonsall M. B., Apparent competition. Annu. Rev. Ecol. Evol. Syst. 48, 447–471 (2017). [Google Scholar]
- 17.Armstrong R. A., Stable model structures for representing biogeochemical diversity and size spectra in plankton communities. J. Plankton Res. 21, 445–464 (1999). [Google Scholar]
- 18.Poulin F. J., Franks P. J., Size-structured planktonic ecosystems: Constraints, controls and assembly instructions. J. Plankton Res. 32, 1121–1130 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ward B. A., Dutkiewicz S., Follows M. J., Modelling spatial and temporal patterns in size-structured marine plankton communities: Top-down and bottom-up controls. J. Plankton Res. 36, 31–47 (2014). [Google Scholar]
- 20.Follows M. J., Dutkiewicz S., Ward B., Follett C., “Theoretical interpretations of subtropical plankton biogeography” in Microbial Ecology of the Oceans, Gasol J., Kirchman D., Eds. (John Wiley, Hoboken, NJ, ed. 3, 2018), pp. 467–494. [Google Scholar]
- 21.Edwards K. F., Thomas M. K., Klausmeier C. A., Litchman E., Allometric scaling and taxonomic variation in nutrient utilization traits and maximum growth rate of phytoplankton. Limnol. Oceanogr. 57, 554–566 (2012). [Google Scholar]
- 22.Tilman D., Resource competition between plankton algae: An experimental and theoretical approach. Ecology 58, 338–348 (1977). [Google Scholar]
- 23.Tilman D., Sterner R. W., Invasions of equilibria: Tests of resource competition using two species of algae. Oecologia 61, 197–200 (1984). [DOI] [PubMed] [Google Scholar]
- 24.Marañón E., Cermeño P., Latasa M., Tadonléké R. D., Resource supply alone explains the variability of marine phytoplankton size structure. Limnol. Oceanogr. 60, 1848–1854 (2015). [Google Scholar]
- 25.Acevedo-Trejos E., Marañón E., Merico A., Phytoplankton size diversity and ecosystem function relationships across oceanic regions. Proc. Biol. Sci. 285, 20180621 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zakem E. J., et al., Ecological control of nitrite in the upper ocean. Nat. Commun. 9, 1206 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Noell S. E., Giovannoni S. J., SAR11 bacteria have a high affinity and multifunctional glycine betaine transporter. Environ. Microbiol. 21, 2559–2575 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Giovannoni S. J., SAR11 bacteria: The most abundant plankton in the oceans. Annu. Rev. Mar. Sci. 9, 231–255 (2017). [DOI] [PubMed] [Google Scholar]
- 29.Litchman E., Klausmeier C. A., Schofield O. M., Falkowski P. G., The role of functional traits and trade-offs in structuring phytoplankton communities: Scaling from cellular to ecosystem level. Ecol. Lett. 10, 1170–1181 (2007). [DOI] [PubMed] [Google Scholar]
- 30.Marañón E., et al., Unimodal size scaling of phytoplankton growth and the size dependence of nutrient uptake and use. Ecol. Lett. 16, 371–379 (2013). [DOI] [PubMed] [Google Scholar]
- 31.Casey J. R., Björkman K. M., Ferrón S., Karl D. M., Size dependence of metabolism within marine picoplankton populations. Limnol. Oceanogr. 64, 1819–1827 (2019). [Google Scholar]
- 32.Morel A., et al., Prochlorococcus and Synechococcus: A comparative study of their optical properties in relation to their size and pigmentation. J. Mar. Res. 51, 617–649 (1993). [Google Scholar]
- 33.White A. E., Giovannoni S. J., Zhao Y., Vergin K., Carlson C. A., Elemental content and stoichiometry of SAR11 chemoheterotrophic marine bacteria. Limnol. Oceanogr. Lett. 4, 44–51 (2019). [Google Scholar]
- 34.Dutkiewicz S., Boyd P. W., Riebesell U., Exploring biogeochemical and ecological redundancy in phytoplankton communities in the global ocean. Glob. Change Biol. 27, 1196–1213 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dutkiewicz S., et al., Dimensions of marine phytoplankton diversity. Biogeosciences 17, 609–634 (2020). [Google Scholar]
- 36.Hansen P. J., Bjørnsen P. K., Hansen B. W., Zooplankton grazing and growth: Scaling within the 2-2,000-m body size range. Limnol. Oceanogr. 42, 687–704 (1997). [Google Scholar]
- 37.Kiørboe T., A Mechanistic Approach to Plankton Ecology (Princeton University Press, 2019). [Google Scholar]
- 38.Schartau M., Landry M. R., Armstrong R. A., Density estimation of plankton size spectra: A reanalysis of IronEx II data. J. Plankton Res. 32, 1167–1184 (2010). [Google Scholar]
- 39.Follett C. L., Dutkiewicz S., Forget G., Cael B. B., Follows M. J., Moving ecological and biogeochemical transitions across the North Pacific. Limnol. Oceanogr. 66, 2442–2454 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Armstrong R. A., Grazing limitation and nutrient limitation in marine ecosystems: Steady state solutions of an ecosystem model with multiple food chains. Limnol. Oceanogr. 39, 597–608 (1994). [Google Scholar]
- 41.Zubkov M. V., Sleigh M. A., Burkill P. H., Leakey R. J., Picoplankton community structure on the Atlantic Meridional Transect: A comparison between seasons. Prog. Oceanogr. 45, 369–386 (2000). [Google Scholar]
- 42.Casey J., et al., Basin-scale biogeography of marine phytoplankton reflects cellular-scale optimization of metabolism and physiology. Sci. Adv., in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sabehi G., et al., A novel lineage of myoviruses infecting cyanobacteria is widespread in the oceans. Proc. Natl. Acad. Sci. U.S.A. 109, 2037–2042 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sullivan M. B., Waterbury J. B., Chisholm S. W., Cyanophages infecting the oceanic cyanobacterium Prochlorococcus. Nature 424, 1047–1051 (2003). [DOI] [PubMed] [Google Scholar]
- 45.Weigele P. R., et al., Genomic and structural analysis of Syn9, a cyanophage infecting marine Prochlorococcus and Synechococcus. Environ. Microbiol. 9, 1675–1695 (2007). [DOI] [PubMed] [Google Scholar]
- 46.Larsen A., et al., Contrasting response to nutrient manipulation in Arctic mesocosms are reproduced by a minimum microbial food web model. Limnol. Oceanogr. 60, 360–374 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pree B., et al., Dampened copepod-mediated trophic cascades in a microzooplankton-dominated microbial food web: A mesocosm study. Limnol. Oceanogr. 62, 1031–1044 (2017). [Google Scholar]
- 48.van Someren Gréve H., Kiørboe T., Almeda R., Bottom-up behaviourally mediated trophic cascades in plankton food webs. Proc. Biol. Sci. 286, 20181664 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sundt-Hansen L. E., Olsen Y., Stibor H., Heldal M., Vadstein O., Trophic cascades mediated by copepods, not nutrient supply rate, determine the development of picocyanobacteria. Aquat. Microb. Ecol. 45, 207–218 (2006). [Google Scholar]
- 50.Thingstad T. F., et al., Nature of phosphorus limitation in the ultraoligotrophic eastern Mediterranean. Science 309, 1068–1071 (2005). [DOI] [PubMed] [Google Scholar]
- 51.Marie D., Partensky F., Vaulot D., Brussaard C., Enumeration of phytoplankton, bacteria, and viruses in marine samples. Curr. Protoc. Cytom. 10, 11–15 (2001). [DOI] [PubMed] [Google Scholar]
- 52.Raven J. A., Carbon fixation and carbon availability in marine phytoplankton. Photosynth. Res. 39, 259–273 (1994). [DOI] [PubMed] [Google Scholar]
- 53.Bec B., Collos Y., Vaquer A., Mouillot D., Souchu P., Growth rate peaks at intermediate cell size in marine photosynthetic picoeukaryotes. Limnol. Oceanogr. 53, 863–867 (2008). [Google Scholar]
- 54.Finkel Z. V., et al., Phytoplankton in a changing world: Cell size and elemental stoichiometry. J. Plankton Res. 32, 119–137 (2010). [Google Scholar]
- 55.Sommer U., Charalampous E., Genitsaris S., Moustaka-Gouni M., Benefits, costs and taxonomic distribution of marine phytoplankton body size. J. Plankton Res. 39, 494–508 (2017). [Google Scholar]
- 56.Verdy A., Follows M., Flierl G., Optimal phytoplankton cell size in an allometric model. Mar. Ecol. Prog. Ser. 379, 1–12 (2009). [Google Scholar]
- 57.Ward B. A., Marañón E., Sauterey B., Rault J., Claessen D., The size dependence of phytoplankton growth rates: A trade-off between nutrient uptake and metabolism. Am. Nat. 189, 170–177 (2017). [DOI] [PubMed] [Google Scholar]
- 58.Kiørboe T., Turbulence, phytoplankton cell size, and the structure of pelagic food webs. Adv. Mar. Biol. 29, 1–72 (1993). [Google Scholar]
- 59.Luo H., Moran M. A., How do divergent ecological strategies emerge among marine bacterioplankton lineages? Trends Microbiol. 23, 577–584 (2015). [DOI] [PubMed] [Google Scholar]
- 60.Weissman J. L., Hou S., Fuhrman J. A., Estimating maximal microbial growth rates from cultures, metagenomes, and single cells via codon usage patterns. Proc. Natl. Acad. Sci. U.S.A. 118, e2016810118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Koch A. L., Bacterial Growth and Form (Kluwer Academic, Dordrecht, The Netherlands, 2001). [Google Scholar]
- 62.Dolan J. R., Microbial ecology of the oceans. J. Plankton Res. 40, 500–502 (2018). [Google Scholar]
- 63.Lauro F. M., et al., The genomic basis of trophic strategy in marine bacteria. Proc. Natl. Acad. Sci. U.S.A. 106, 15527–15533 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Runge C., Ueber die numerische Auflösung von Differentialgleichungen [in German]. Math. Ann. 46, 167–178 (1895). [Google Scholar]
- 65.Dutkiewicz S., et al., Capturing optically important constituents and properties in a marine biogeochemical and ecosystem model. Biogeosciences 12, 4447–4481 (2015). [Google Scholar]
- 66.Ward B. A., Dutkiewicz S., Jahn O., Follows M. J., A size-structured food-web model for the global ocean. Limnol. Oceanogr. 57, 1877–1891 (2012). [Google Scholar]
- 67.Geider R. J., MacIntyre H. L., Kana T. M., A dynamic regulatory model of phytoplanktonic acclimation to light, nutrients, and temperature. Limnol. Oceanogr. 43, 679–694 (1998). [Google Scholar]
- 68.Eppley R., Temperature and phytoplankton growth in the sea. Fish. Bull. 70, 1063–1085 (1972). [Google Scholar]
- 69.Anderson S. I., Barton A. D., Clayton S., Dutkiewicz S., Rynearson T. A., Marine phytoplankton functional types exhibit diverse responses to thermal change. Nat. Commun. 12, 6413 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Holling C. S., The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 97, 5–60 (1965). [Google Scholar]
- 71.Marshall J., Adcroft A., Hill C., Perelman L., Heisey C., A finite-volume, incompressible navier stokes model for, studies of the ocean on parallel computers. J. Geophys. Res. Oceans 102, 5753–5766 (1997). [Google Scholar]
- 72.Wunsch C., Heimbach P., Practical global oceanic state estimation. Physica D 230, 197–208 (2007). [Google Scholar]
- 73.Ward B. A., Temperature-correlated changes in phytoplankton community structure are restricted to polar waters. PLoS One 10, e0135581 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Buitenhuis E. T., et al., MAREDAT: Towards a world atlas of MARine ecosystem DATa. Earth Syst. Sci. Data 5, 227–239 (2013). [Google Scholar]
- 75.Sonnewald M., Dutkiewicz S., Hill C., Forget G., Elucidating ecological complexity: Unsupervised learning determines global marine eco-provinces. Sci. Adv. 6, eaay4740 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kuhn A. M., Fennel K., Evaluating ecosystem model complexity for the northwest North Atlantic through surrogate-based optimization. Ocean Model. 142, 101437 (2019). [Google Scholar]
- 77.Moore T. S., Campbell J. W., Dowell M. D., A class-based approach to characterizing and mapping the uncertainty of the MODIS ocean chlorophyll product. Remote Sens. Environ. 113, 2424–2430 (2009). [Google Scholar]
- 78.Clayton S., et al., Biogeochemical versus ecological consequences of modeled ocean physics. Biogeosciences 14, 2877–2889 (2017). [Google Scholar]
- 79.O’Brien C. J., et al., Global marine plankton functional type biomass distributions: Coccolithophores. Earth Syst. Sci. Data 5, 259–276 (2013). [Google Scholar]
- 80.Dutkiewicz S., Jahn O., Darwin3 31 + 16+3 model code, datafiles and parameters. Harvard Dataverse. 10.7910/DVN/ISJQ1W. Deposited 2 December 2021. [DOI]
- 81.Dutkiewicz S., Darwin3 31 + 16+3 model output: annual mean surface plankton biomass. Harvard Dataverse. 10.7910/DVN/FEWXB4. Deposited 2 December 2021. [DOI]
- 82.Ashkezari M. D., et al., Simons Collaborative Marine Atlas Project (Simons CMAP): An open-source portal to share, visualize, and analyze ocean data. Limnol. Oceanogr. Methods 19, 488–496 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The csv files from flow cytometer data have been deposited in Zenodo (10.5281/zenodo.4085858; 10.5281/zenodo.4085873; 10.5281/zenodo.3994953). Data for the COOK-BOOK cruises [April and October 2003 (8)] can be found at https://hahana.soest.hawaii.edu/cookbook/cookbook.html. All data used can be accessed directly through the Simons CMAP project, https://simonscmap.com/, for download (82). The physical model used here is available through mitgcm.org, and the generic ecosystem code used in this study is available through https://github.com/darwinproject/darwin3. The specific modifications for the setup used here, and all parameter values, are available via Harvard Dataverse https://doi.org/10.7910/DVN/ISJQ1W, and the model output used in this manuscript is available at https://doi.org/10.7910/DVN/FEWXB4.