Disentangling direct from indirect relationships in association networks

Significance

Networks are fundamental units for studying complex systems, but reconstructing networks from large-scale experimental data is very challenging in systems biology and microbial ecology, primarily due to the difficulty in unraveling direct and indirect interactions. By tackling several mathematical challenges, this study provides a conceptual framework for disentangling direct and indirect relationships in association networks. The application of iDIRECT (Inference of Direct and Indirect Relationships with Effective Copula-based Transitivity) to synthetic, gene expression, and microbial community data demonstrates that it is a powerful, robust, and reliable tool for network inference. The framework developed here will greatly enhance our capability to discern network interactions in various complex systems and allow scientists to address research questions that could not be approached previously.

Abstract

Networks are vital tools for understanding and modeling interactions in complex systems in science and engineering, and direct and indirect interactions are pervasive in all types of networks. However, quantitatively disentangling direct and indirect relationships in networks remains a formidable task. Here, we present a framework, called iDIRECT (Inference of Direct and Indirect Relationships with Effective Copula-based Transitivity), for quantitatively inferring direct dependencies in association networks. Using copula-based transitivity, iDIRECT eliminates/ameliorates several challenging mathematical problems, including ill-conditioning, self-looping, and interaction strength overflow. With simulation data as benchmark examples, iDIRECT showed high prediction accuracies. Application of iDIRECT to reconstruct gene regulatory networks in Escherichia coli also revealed considerably higher prediction power than the best-performing approaches in the DREAM5 (Dialogue on Reverse Engineering Assessment and Methods project, #5) Network Inference Challenge. In addition, applying iDIRECT to highly diverse grassland soil microbial communities in response to climate warming showed that the iDIRECT-processed networks were significantly different from the original networks, with considerably fewer nodes, links, and connectivity, but higher relative modularity. Further analysis revealed that the iDIRECT-processed network was more complex under warming than the control and more robust to both random and target species removal (P < 0.001). As a general approach, iDIRECT has great advantages for network inference, and it should be widely applicable to infer direct relationships in association networks across diverse disciplines in science and engineering.

Real-world systems in all areas of human endeavor, from biology to medicine, economy, and climate change, are complex dynamical systems in which various components (e.g., members in a community) interact with one another through extensive exchange of materials, energy, and/or information (1–3). Such complex systems can be represented as networks with components modeled as nodes and their connections as links or edges, which are typically weighted according to the strengths of the relationships (2, 4). Networks are fundamental units for understanding the dynamics and properties of complex systems (5). However, reconstructing networks (e.g., regulatory networks or microbial interaction networks) from large-scale datasets is a long-standing challenge in systems biology and microbial ecology (6). It is often unclear how accurately the reconstructed networks represent the real-world systems (7). One of the major problems is that networks reconstructed with statistical approaches (e.g., Pearson correlation, mutual information, and other similarity metrics) contain both direct and indirect associations (8) (Fig. 1A). Furthermore, even if there is a true association between a pair of nodes, the strength of such an association might be overestimated due to the influences of additional transitive associations from indirect relationships (indirect paths) at different orders (e.g., second, third, and higher orders) (4). The number of indirect relationships increase exponentially as the network size increases, and such a transitive problem appears intractable with traditional approaches in network inference. All of these could result in biased network structures with many spurious links and inaccurate weights in various practical applications (4, 7, 9).

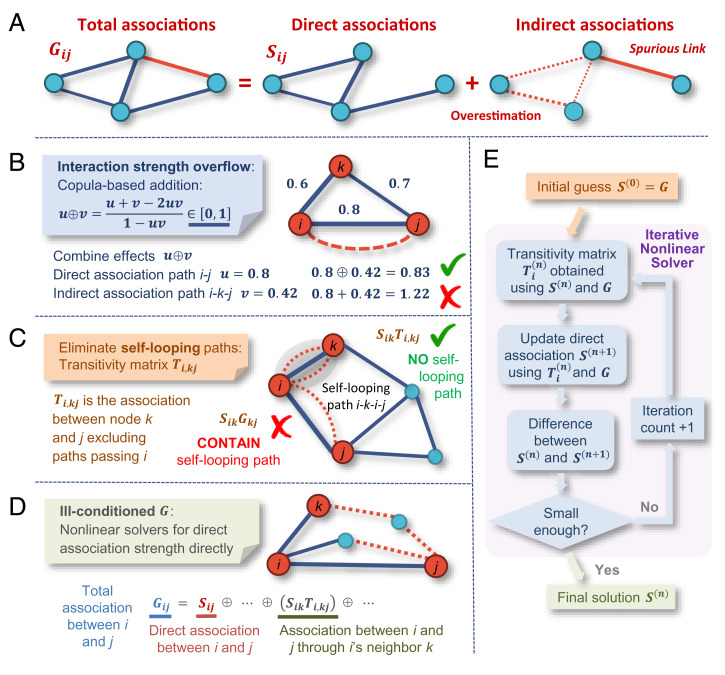
Fig. 1.

Overview of iDIRECT. (A) An association network contains both direct (blue) and indirect (red) associations. Indirect associations include spurious links (solid lines) and overestimated direct links (dotted lines). (B) iDIRECT uses a copula-based addition ⊕ to combine association between two nodes through different paths, ensuring the interaction strengths to be within the range [0,1]. (C) iDIRECT introduces a transitivity matrix T_i,kj (association between k and j excluding paths passing i) and uses S_ikT_i,kj to calculate indirect association strength between i and j, eliminating spurious self-looping paths like i–k–i–j. (D) iDIRECT uses nonlinear solvers to obtain direct association strengths of each link, without inverting the ill-conditioned association matrix. (E) Overall workflow for iDIRECT.

Disentangling direct associations from indirect associations is a pervasive problem in network science because experimental techniques often have difficulty in distinguishing between direct and indirect effects (9). Various approaches have been developed to infer direct associations among measured variables (3, 4, 6, 10, 11), such as partial correlation (PC) (12–14), Granger causality (15, 16), conditional mutual information (17), part mutual information (8), and Bayesian networks (18). However, the performance of individual inference methods varies substantially depending on different implementations and/or datasets (6). Furthermore, these methods are usually either time-consuming, restricted to specific applications, or limited to low-order indirect associations. Thus, more effective and general approaches are desperately needed (6). Several more general approaches that use the inverse of the association matrix were developed to better estimate direct dependencies, such as network deconvolution (ND) (3, 4), global silencing (GS) (19), and SPIEC-EASI (Sparse Inverse Covariance Estimation for Ecological Association Inference) (20). Although ND, GS, and SPIEC-EASI have several advantages over traditional approaches in terms of accuracy, generality, and efficiency (SI Appendix, section A.1), they suffer from inaccurate estimation of indirect relationships due to several problems related to ill-conditioning, self-looping, and interaction strength overflow (see SI Appendix, sections A.2–A.4 for details). Specifically, ill-conditioning means that the association matrix is close to singular and is highly unreliable to invert (SI Appendix, Fig. S1A). Self-looping refers to spurious indirect paths passing a node multiple times, leading to overestimation of the corresponding indirect association (SI Appendix, Fig. S1B). Interaction strength overflow indicates that the values of the total interaction strengths are outside their natural range (SI Appendix, Fig. S1C) because simple addition (+) is not appropriate to combine direct and indirect associations.

The objective of this study was to develop a mathematically sound, general approach to disentangle direct from indirect relationships in association networks; we refer to this approach as iDIRECT (Inference of Direct and Indirect Relationships with Effective Copula-Based Transitivity). First, we developed mathematical and computational strategies to minimize or eliminate several problems associated with the ND and GS approaches. We then compared our method to ND and GS, as well as PC (7), based on synthetic network data. In addition, we used our approach to reconstruct gene regulatory networks in two applications: Escherichia coli using gene-expression data and microbial ecological networks for a grassland soil microbial community from a long-term warming site. Our results indicate that iDIRECT can distinguish direct and indirect relationships of arbitrary orders with high precision and sensitivity, and, hence, it is an effective, reliable, and robust approach for inferring direct relationships and their strengths in association networks.

Results

Overview of iDIRECT.

To ameliorate the problems encountered in ND (3, 4), GS (19), and SPIEC-EASI (20), such as interaction strength overflow, self-looping, and ill-conditioning, a general framework, iDIRECT, was developed (Fig. 1 B–D). First, iDIRECT addresses the interaction strength overflow problem by introducing a copula-based addition ⊕, which guarantees u ⊕ v ∈ [0,1] for all u,v ∈ [0,1] (Fig. 1B and SI Appendix, section B.1). iDIRECT also introduces a transitivity matrix (T_i) to eliminate self-looping-induced indirect paths by considering the indirect association between two nodes i and j through one of i’s neighbors, k (Fig. 1C). The indirect association strength between i and j through k is S_ikT_i,kj, where S_ik is the direct association strength between i and k, and T_i,kj is the association strength between nodes k and j, excluding paths passing i. S_ikT_i,kj does not include any self-looping-induced indirect paths because they are explicitly excluded from T_i,kj (SI Appendix, section B.2). Finally, combining the results above, the total association G_ij between nodes i and j is the sum of the direct association S_ij between i and j and the indirect association S_ikT_i,kj between i and j through one of i’s neighbors, k (Fig. 1D). To obtain the direct association S_ij, iDIRECT uses two sets of nonlinear solvers (see SI Appendix, section B.3 for details) with the goal of not inverting the association matrix, which is ill-conditioned and highly unreliable. As a result, iDIRECT provides a comprehensive, mathematically sound framework for disentangling direct from indirect effects in any association network. The overall workflow of iDIRECT is shown in Fig. 1E.

Simulated Synthetic Association Networks.

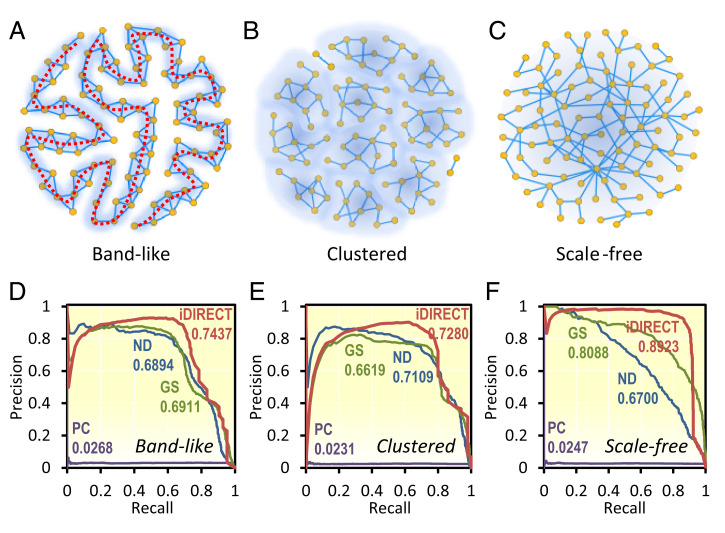
Since there is no gold-standard experiment for establishing a true network structure, using simulated networks and data is the dominant approach for assessing the performance of various network inference methods (6, 20, 21). In a simulated network, the ground truth of network structure is known a priori, and hence predictions can be systematically evaluated. To determine the performance of iDIRECT, we used synthetic 500-node networks with three distinct topologies: band-like, clustered, and scale-free (Fig. 2 A–C; see details in Materials and Methods). iDIRECT yielded a higher average precision (0.79) than ND (0.69), GS (0.72), and PC (0.02) for all three types of networks (Fig. 2 D–F) in terms of the Area Under PR curves (AUPR), which represents the average precision when recall varies from zero to one (see details in Materials and Methods). The above results indicate that iDIRECT yielded more consistent results with the simulated synthetic networks than ND, GS, and PC. Because of the poor performance of PC, we did not include PC in the following examples.

Fig. 2.

Performance of iDIRECT on simulated networks in comparison with other methods. (A–C) Synthetic networks with three distinct topologies. (A) Band-like. All the nodes are connected to form a long, band-like structure. The dotted red line indicates the band. (B) Clustered. All nodes are clustered into several disjointed groups. (C) Scale-free. The degree distribution of the nodes follows the power law. (D–F) Comparison of PR curves with varying network topologies: band-like (D), clustered (E), and scale-free (F). Pearson’s correlation coefficients were used to calculate the association matrix. Red, iDIRECT; blue, ND; green, GS; and purple, PC. The numbers indicate the AUPR, with values ranging from zero to one. AUPR represents the average precision when recall varies from zero to one.

Simulated Gene Regulatory Network from DREAM5.

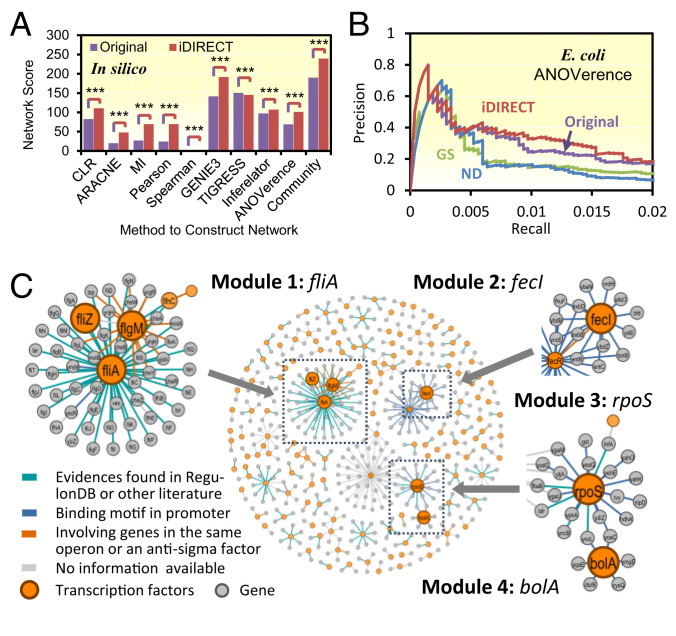
The performance of iDIRECT and the other methods were further tested with an in silico gene regulatory network from the DREAM5 (Dialogue on Reverse Engineering Assessment and Methods project, #5) Network Inference Challenge (22). Its corresponding gene-expression data were simulated by using GeneNetWeaver (GNW) version 3.0 (gnw.sourceforge.net/). We applied iDIRECT to the 100,000 links with the highest weights from 10 submissions that were among the best-performing Challenge participants and reweighted those links based on direct association strength. Those links were then scored based on the true network using the Challenge organizer’s script (details in Materials and Methods), which was just −log(p) of the empirical P values of the predicted AUPR from 1,000 random simulations. The same 10 submissions were also used in ND (4). iDIRECT performed better than all original submissions except for TIGRESS (trustful inference of gene regulation using stability selection), with the average AUPR score of 31% higher than the original submissions (Fig. 3A), although wide variations were observed. For examples, iDIRECT had 187% and 156% improvement over the Pearson and MI, but only 10.0% over Inferator, but −3.5% over TIGRESS (Fig. 3A).

Fig. 3.

Regulatory networks from DREAM5 network inference challenge. (A) In silico network score. iDIRECT (red) was compared with original submissions (purple). ***P < 0.001. Note that the numbers for Spearman (2.26 × 10⁻⁵ for original and 2.90 × 10⁻³ for iDIRECT) are too small to show. (B) PR curve for the E. coli network. (C) Top 500 links in the E. coli networks obtained by iDIRECT. Four modules with one principal hub were highlighted. Nodes with orange color represent transcriptional factors, and those with gray color mean the regulated genes. Colors of the edges represent different types of supporting evidences: Cyan means links with evidences found in literature; blue means having a binding motif found in promoter; orange means involving either genes in the same operon or an antisigma factors; and gray means no information.

Since different network inference methods are complementary, having different advantages and limitations in different contexts, it is expected that combining the results of multiple inference methods would be a good strategy for improving predictions (6). Thus, community networks were constructed by integrating the predictions of all participating teams across all methods (6). Previous analysis indicated that community networks outperformed individual inference methods, and community-based methods provide a powerful, robust, preferred tool for inferring transcriptional gene regulatory networks (6). Consistent with the comparable results from individual inference methods, iDIRECT considerably improved (26%) the community network (6). Similar results were obtained when only a subset of submissions was included in the community network integration (SI Appendix, Fig. S2).

We also applied ND and GS to process these submissions. The average increase was 18.8% for ND and 17.2% for GS over the original submissions (SI Appendix, Fig. S3). Although the performance of iDIRECT over ND and GS was less consistent across different submissions (SI Appendix, Fig. S3), both ND and GS had poorer performance than iDIRECT for the community networks. ND had only a 0.4% increase, and GS had a 13.8% decrease over the original community network (SI Appendix, Fig. S3), which were much lower than the improvement by iDIRECT. Collectively, our results indicated that iDIRECT was generally better at distinguishing direct from indirect relationships in the in silico gene regulatory network.

Application to a Gene Regulatory Network in E. coli.

The DREAM5 Challenge (22) also included reconstruction of genome-scale transcriptional regulatory networks in E. coli from chip-based gene-expression data. We applied iDIRECT to rerank the 100,000 edges submitted by the best-performing method, ANOVerence (23), based on direct association strength. Due to the lack of overlap between ANOVerence and other methods, such as TIGRESS, we could not perform a detailed analysis for other top-performing methods. Since the DREAM5 project was accomplished several years ago, we updated the gold standard compiled from an updated version of RegulonDB (24) (version 10.0; Materials and Methods) to reassess iDIRECT, as well as ND and GS. Application of iDIRECT to these 100,000 edges from ANOVerence resulted in an average 12.5% increase in precision. In contrast, the average precision of ND and GS decreased by 30.9% and 27.0%, respectively, compared to ANOVerence (23) (Fig. 3B). These results also suggested that iDIRECT was more effective in distinguishing true direct links from spurious/indirect links.

We further manually examined whether the links identified by iDIRECT were consistent with biological evidence by focusing on the top 500 links. Overall, there were 28.0% of these links supported by RegulonDB (SI Appendix, Fig. S4), 7.6% by online databases or by experimental evidence in the literature, and 14.0% by the presence of a transcriptional factor binding motif in the promoter region (25); also, 4.8% of these links contained genes that were in the same transcriptional unit (TU), and 3.6% were between an antisigma factor and a target gene of the corresponding sigma factor. About 40% of these links had no supporting evidence available. For comparison, the top 500 links from ND and GS were also examined and compared with those from iDIRECT (SI Appendix, Fig. S4). The percentage of links that were most likely true (listed in RegulonDB, found in online databases or literature, or having a binding motif in the promoter region) was substantially higher in iDIRECT (49.4%) than ND (25.2%) or GS (31.0%). These results further supported that iDIRECT had a higher prediction power than ND and GS.

To demonstrate the effectiveness of iDIRECT, four modules in the iDIRECT network were examined in detail. The hubs of these modules were extensively studied regulatory factors, fliA, fecI, rpoS, and bolA (Fig. 3C), allowing us to retrieve experimental evidence and computational data. FliA (σ²⁸) in Module 1 (49 links) is a minor sigma factor required for flagellin production. Among these, 34 links had experimental evidence in RegulonDB; 15 links contained the binding motif of σ²⁸ upstream of the target gene. Among these 15 links, experimental evidence was found in the literature for three target genes, yjdA (26), flgA (27), and yhjH (28), and nine target genes encoding flagellar biosynthesis-related proteins according to sequence annotation (SI Appendix, Table S1). FecI (σ¹⁹) in Module 2 (25 links) is a sigma factor that regulates genes involved in the transportation of ferric citrate from the periplasmic space to the cytoplasm. No experimental evidence was found for these links, but the FecI binding motif (29) was found upstream of all 25 target genes, and most of these genes were related to ferric transport based on sequence annotation (SI Appendix, Table S1). RpoS (σ³⁸) in Module 3 (18 links) is the master regulator of general stress response, regulating up to 10% of the genes in E. coli directly or indirectly (30, 31). Experimental evidence was found for 1 target gene, yncL, in the literature (27), and the RpoS binding motif was found upstream of all 18 target genes (SI Appendix, Table S1). BolA in Module 4 (11 links) is a transcriptional factor regulating genes involved in a range of cellular processes, including bacterial morphology, membrane permeability, motility, and biofilm formation (32). No experimental evidence was found for these links, but the perfect BolA core binding motif (GCCAG) (32) was found upstream of nine target genes, and imperfect core binding motifs (GCCA or CCAG) were found upstream of two target genes (SI Appendix, Table S1). The consensus sequences of the binding motifs of FliA, FecI, or RpoS were consistent with the literature (29) (SI Appendix, Fig. S5). Collectively, the above results suggested that iDIRECT had high accuracy when applied in reconstruction of bacterial regulatory networks.

Application to Microbial Community Networks in Response to Warming.

To further explore whether iDIRECT was useful for analyzing microbial molecular ecological networks (MENs) (33, 34), iDIRECT was applied to analyze the MENs of soil microbial communities in response to in situ experimental warming. Our previous studies indicated that warming shifted the microbial community structure dramatically, led to divergent succession (35), accelerated microbial temporal turnover (36), and enhanced network complexity and stability (37). Thus, this experimental dataset was ideal to evaluate the performance of iDIRECT on community networks.

Two phylogenetic MENs under warming and control were constructed, respectively, using the random matrix theory (RMT)-based network approach (38). iDIRECT was then applied to these two MENs to remove spurious indirect links in the original networks. A considerable portion of the links were removed in networks under warming (27.5%) (SI Appendix, Table S2) or control (20.8%) (SI Appendix, Table S3). Consequently, the average connectivity significantly decreased under warming (18%) or control (10.1%) compared to the corresponding original networks (SI Appendix, Tables S2 and S3). Various network topological metrics were significantly (P < 0.001) different between the iDIRECT-derived networks and the original networks (SI Appendix, Tables S2 and S3). Most interestingly, the relative modularity of the iDIRECT-derived networks increased significantly compared to the original networks (SI Appendix, Tables S2 and S3). In addition, the OTU (operational taxonomic unit) composition of network/module hubs and connectors were considerably different between the iDIRECT-derived networks and the original networks (SI Appendix, Table S4). These results suggested that use of iDIRECT effectively removed spurious/indirect links in the MEN analysis. ND and GS were not used for comparison in this application because they do not provide a clear cutoff for network reconstruction.

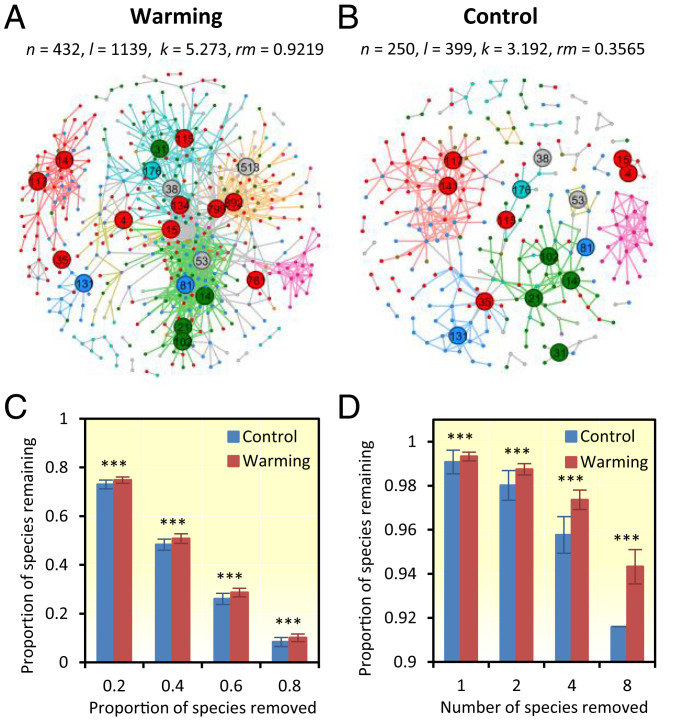
Both networks generated by iDIRECT were scale-free (33, 34, 39) and exhibited small-world behavior (SI Appendix, Table S5 and Fig. S6), which are characteristics consistent with most molecular biology and technology networks (39–41). The iDIRECT-derived network was more complex under warming than control in terms of the number of nodes, links, and average connectivity (Fig. 4 A and B and SI Appendix, Table S5). Also, there were 166 nodes shared under warming and control, but no significant correlations of the connectivity were observed between shared OTUs (r = 0.2775, P = 0.7817). All topological attributes were significantly (P < 0.05) different between warming and control, as well as from their corresponding random networks (SI Appendix, Table S5), suggesting that the network composition and structure were not conserved between warming and control. In addition, a total of 12 and 10 modules with more than five members were detected under warming and control, respectively. Fisher’s exact test (42) showed that many modules (14 of 22, 63.6%) could be paired together. Within the paired modules, only 22.9% of the total nodes shared between these two networks were identical (SI Appendix, Table S6). Eigengene network analysis showed that the eigengenes from the nine paired modules were clustered differently with other eigengenes (SI Appendix, Fig. S7), suggesting that these two networks were even less conserved at the modular level. Finally, a total of 8 and 22 keystone taxa were detected under warming and control, respectively (SI Appendix, Fig. S8), but very few of these (3, or 11.1%) were shared between warming and control (SI Appendix, Table S4). The keystone taxa from iDIRECT-processed networks had higher correlations with more soil, plant, and ecosystem functioning variables (8.4% more for warming and 2.4% more for control; SI Appendix, Fig. S9). The same was observed between several key network properties and soil, plant, and ecosystem functioning variables under warming (4.4% more; SI Appendix, Fig. S10). Collectively, the above results indicated that warming substantially altered the overall network composition, structure, higher-order organization, and topological roles of individual populations, which is in agreement with our previous analyses (37) and similar to what we observed under elevated CO₂ (33, 34).

Fig. 4.

Soil microbial networks in response to experimental warming. (A and B) Visualization of the microbial MENs under warming or control. n, node number; m, edge number; k, average connectivity; rm, relative modularity. Network nodes were colored at the phylum level; edges were colored based on their module memberships. OTUs identified as module hubs or network hubs were labeled by numbers. (C) Robustness to species removal of iDIRECT-processed networks when 50% of the taxa were randomly removed. (D) Robustness to target taxa removal of iDIRECT-processed networks when four module hubs were removed. The error bars represent SD of 100 repetitions of each simulation. Significant differences are expressed. ***P < 0.001. Detailed simulation results of robustness for both original iDIRECT-processed networks were seen in SI Appendix, Fig. S11.

Since relative modularity of the network under warming was more than two times higher than that under control (SI Appendix, Table S5), it is expected that the network under warming was more robust than that under control because the effects of a local perturbation on the whole system should be minimized if the network had high modularity (43–45). To test this prediction, robustness analysis was performed. Our results indicated that the robustness of the networks generated by iDIRECT to both random and targeted species removal was significantly higher (P < 0.01) under warming than control (Fig. 4 C and D), which is consistent with our general expectation. However, the robustness of the networks prior to applying iDIRECT to random and target species removal was lower under warming than control (13.5% for random and 15.6% for targeted) (SI Appendix, Fig. S11B), even though the relative modularity was higher under warming than control, countering our general expectation. These results further suggested the importance of removing spurious/indirect linkages in network analysis.

Discussion

One of the main challenges in network sciences is how to disentangle direct and indirect relationships in a complex system. Although network studies have received great attention recently (46, 47), studies to effectively recognize and eliminate the effects of indirect interactions at a global scale are in their infancy (9). In this study, we developed iDIRECT to infer direct dependences in association networks by overcoming various mathematical problems inherent to the existing methods. Analyses with simulation, microbial gene expression, and microbial community data demonstrate that iDIRECT is a powerful, robust, and reliable tool in distinguishing direct and indirect relationships. Thus, we expect that iDIRECT will greatly enhance our capability to discern network interactions in microbial systems.

iDIRECT has several advantages over previous approaches. First, iDIRECT is more rigorous in its formulation than those from existing methods, such as ND, GS, and SPIEC-EASI. As the total association matrix G tends to be singular or ill conditioned (48) due to the underdetermined nature of network inference (10, 19, 20), iDIRECT avoids inverting G directly and solves the direct association strengths through a set of nonlinear equations to minimize the impact of underdetermination. In contrast, ND (4), GS (19), and SPIEC-EASI (20) all use G⁻¹ in their formulations. When the singularity or ill-conditioning of G becomes a problem during implementation, other approaches use generic numerical analysis techniques to invert the association matrix G. For instance, ND uses a scaling factor and an eigen-decomposition-based pseudoinverse. GS modifies G using a bootstrap randomization, and SPIEC-EASI follows an optimization approach using the sparsity of G. These approaches failed to utilize the intrinsic network structure provided in G, which is used by iDIRECT. Second, by introducing a copula-based addition, a two-step product-assembly strategy, and a transitivity matrix, iDIRECT eliminates the problems of self-looping and interaction strength overflow. With these mathematical improvements, it is expected that iDIRECT will perform better in distinguishing direct from indirect relationships than previous approaches. This is supported by both synthetic and empirical data. Third, the copula-based addition adopted by iDIRECT is designed for a variety of association metrics. iDIRECT performs especially well with association metrics based on correlation, mutual information, and certain other approaches. In addition, the computation-efficiency enhancement techniques based on generator functions of Archimedean copulas is very effective, so that iDIRECT is able to process synthetic and experimental datasets comprising hundreds to thousands of nodes. Finally, iDIRECT provides a robust and reliable framework to calculate both direct and indirect association strength in an association network. Therefore, it not only allows us to analyze the direct association network, but also the indirect association network, which can be useful in ecology (49, 50) and evolutionary biology, such as mutualistic coevolution (51).

For iDIRECT, several further improvements are needed. First, iDIRECT uses nonlinear solvers extensively, in calculating both the transitivity matrix and the direct association strength. Despite developments in recent decades, nonlinear solvers are still time-consuming and can fail to yield a converged solution when the initial guess is not close enough. Also, the introduction of the transitivity matrix costs more storage space and slows down computation. If the problem is scaled up to tens or even hundreds of thousands of nodes, and the maximal connectivity substantially increases, the increase in storage and computational time may pose serious problems. In addition, the implementation of the binary operator u ⊕ v is relatively slow when compared with ordinary addition +, despite the fact that we have accelerated it using the generator function of the corresponding Archimedean copula. In addition, it would be of interest to extend iDIRECT to directed networks that can describe asymmetric relationships in a community. In directed networks, the two combinatorial rules used in this paper, u ⊗ v = uv and u ⊕ v = (u + v − 2uv)/(1 − uv), might not be applicable, and some of the key equations, such as the definition of the transitivity matrix, might need to be modified due to loss of symmetry. All these issues need to be addressed to further realize the full power of iDIRECT.

In conclusion, iDIRECT is a robust, reliable, and general tool to infer direct association networks from the total association matrix. By testing it against synthetic, experimental gene expression and microbial community data, we demonstrate that iDIRECT is not only capable of effectively removing spurious links, but also overcoming overestimated direct association strength caused by indirect influences. iDIRECT improves the prediction accuracy of a wide variety of association measures in synthetic and experimental systems. Therefore, it is expected that iDIRECT is generally applicable to many other association-based networks, as well as other types of networks, across different research fields. We expect that iDIRECT will have broad applications in network science, systems biology, and microbiome research.

Materials and Methods

Mathematical Framework.

iDIRECT aims to separate direct associations from indirect associations without suffering problems in the existing approaches, such as ill-conditioning, self-looping, and interaction strength overflow (see SI Appendix, section A for details). To address the interaction strength overflow problem, we improved the algorithms to calculate indirect association from direct association by considering the ways how two nodes in a network are indirectly linked together (see SI Appendix, section B.1 for details). Basically, there are two ways through which two nodes are indirectly connected. One is sequential paths, i.e., two nodes are indirectly linked through a third node (SI Appendix, Fig. S12A and section B.1.1 for details). Let u and v be the direct association strength, the indirect association strength u ⊗ v = uv intuitively. The other is parallel paths, i.e., two nodes are linked through two different paths (SI Appendix, Fig. S12B and section B.1.2 for details). Let u and v be the association strength of those two paths; the combined association strength is termed as u ⊕ v. An intuitive choice u ⊕ v = u + v was used in previous approaches, such as ND and GS, resulting in the undesirable interaction strength overflow. To address this problem, iDIRECT uses the following formula (Eq. 1) based on copulas from the probability theory, which guarantees u ⊕ v ∈ [0,1] for all u,v ∈ [0,1] (see SI Appendix, section C.1 for details).

$$u\oplus v=\frac{u+v-2uv}{1-uv}.$$ [1]

This copula-based addition is developed from Archimedean copulas (SI Appendix, section C.2). Archimedean copulas are associative and commutative, and they help to enhance the computational efficiency (SI Appendix, section C.3), which is very important when the sum contains lots of terms, as in the case of complex networks.

Based on the basic algorithms, the total association between two nodes i and j (G_ij) is the sum (using ⊕) of their direct association (S_ij) and indirect association. The indirect association between i and j consists of many parallel paths, each of which passes one of i’s neighbors (k₂, k₃, …, k_d; SI Appendix, Fig. S12C). Therefore, the indirect association between i and j can be calculated as the sum (using ⊕) of the indirect association through each of i’s neighbors k (k = k₂, k₃, …, k_d). The indirect association through k appears to be the product of the direct association between i and k (S_ik) and the association strength between k and j (G_kj), i.e., S_ik ⊗ G_kj = S_ikG_kj. But this actually overestimates the indirect association through k because spurious indirect paths passing i twice are also included, i.e., the self-looping problem (SI Appendix, section A.3).

To eliminate all self-looping-induced indirect paths, iDIRECT introduced a transitivity matrix (see SI Appendix, section B.2 for details), whose (i, k, j)-th component T_i,kj is the association strength between node k and j, excluding paths passing i. Therefore, the indirect association through k is S_ik ⊗ T_i,kj = S_ikT_i,kj, which contains no self-looping indirect paths, because we explicitly exclude them in the definition of T_i,kj. The transitivity matrix T_i,kj can be calculated with an indirect approach. Consider three nodes i, j, and k in a network (SI Appendix, Fig. S12D). The total association between k and j is G_kj. G_kj is expressed as the sum (using ⊕) of T_i,kj (the association strength of paths not passing i) and T_j,kiT_k,ij (the association strength of paths passing i). In the same way, G_ki and G_ij are expressed in terms of the transitivity matrix:

$$\{\begin{array}{c}{G}_{kj}=T_{i,kj}\oplus (T_{j,ki}{T}_{k,ij});\\ G_{ki}=T_{j,ki}\oplus (T_{k,ij}{T}_{i,kj});\\ G_{ij}=T_{k,ij}\oplus (T_{i,kj}{T}_{j,ki}),\end{array}$$ [2]

which contain three equations to solve three unknown variables (T_i,kj, T_j,ki, and T_k,ij). For each node i, we can iterate j and k over all i’s neighbors to obtain the rest of the equations to solve all entries of each transitivity matrix. Combining the results above, we calculate the total association G_ij from S_ij, S_ik, and T_i,kj:

$$G_{ij}=S_{ij}\oplus S_{i{k}_2}{T}_{i,k_{2}j}\oplus S_{i{k}_3}{T}_{i,k_{3}j}\oplus \dots \oplus S_{i{k}_d}{T}_{i,k_{d}j}.$$ [3]

Iterating j over all i’s neighbors will give us all the equations we need to solve all the direct association strength S_ij (collectively as a matrix S) from G_ij (collectively as a matrix G) and T_i,kj (collectively as T_i). Eq. 3 and its derived forms are the foundation of iDIRECT.

To ameliorate the problem of ill-conditioning caused by underdetermination of network inference, unlike previous methods such as ND (4), GS (19), and SPIEC-EASI (20), iDIRECT does not explicitly use G⁻¹ in the formulation (SI Appendix, section B.3). The formulation starts from dividing the whole system into small subsystems. For a given node i, first, we select two of i’s neighbors, j and k, and calculate the transitivity matrix T_i,jk by solving Eq. 2; then, we select all of i’s neighbors, k_l (l = 1,2,…, d) and calculate the direct association strength S_ikl by solving Eq. 3. The nonlinear systems in Eqs. 2 and 3 are solved by two nonlinear solvers (T-solver, using G to compute T_i, and S-solver, using G and T_i to compute S) without calculating G⁻¹. The T-solver is applied first (SI Appendix, section B.3.2):

$$\{\begin{array}{c}\psi \left(1-G_{kj}\right)=\psi \left(1-T_{i,kj}\right)+\psi \left(1-T_{j,ki}{T}_{k,ij}\right);\\ \psi \left(1-G_{ki}\right)=\psi \left(1-T_{j,ki}\right)+\psi \left(1-T_{k,ij}{T}_{i,kj}\right);\\ \psi \left(1-G_{ij}\right)=\psi \left(1-T_{k,ij}\right)+\psi \left(1-T_{i,kj}{T}_{j,ki}\right),\end{array}$$ [4]

where ψ(t) is the generator function associated with the corresponding copula of ⊕. Eq. 4 is solved by using Newton’s method, where an initial guess is made, and the solution is iteratively improved until further improvement is too small (SI Appendix, section B.3.2). Then, the S-solver is applied,

$$\{\begin{array}{l}\psi \left(1-G_{i{k}_1}\right)=\psi \left(1-S_{i{k}_1}\right)+\psi \left(1-T_{i,k_1{k}_2}{S}_{i{k}_2}\right)+\dots +\psi \left(1-T_{i,k_1{k}_d}{S}_{i{k}_d}\right);\hfill \\ \psi \left(1-G_{i{k}_2}\right)=\psi \left(1-T_{i,k_2{k}_1}{S}_{i{k}_1}\right)+\psi \left(1-S_{i{k}_2}\right)+\dots +\psi \left(1-T_{i,k_2{k}_d}{S}_{i{k}_d}\right);\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \hfill \\ \psi \left(1-G_{i{k}_d}\right)=\psi \left(1-T_{i,k_d{k}_1}{S}_{i{k}_1}\right)+\psi \left(1-T_{i,k_d{k}_2}{S}_{i{k}_2}\right)+\dots +\psi \left(1-S_{i{k}_d}\right).\hfill \end{array}$$ [5]

Again, Newton’s method is used for the S-solver (SI Appendix, section B.3.3). In brief, iDIRECT accepts the observable total association matrix G as input and returns the direct association matrix S as output. iDIRECT finished running in minutes for each network considered in this study.

Network Simulation.

We developed a network simulator to generate abundance profiles when an overall network topology is given. We tested three different network topologies: band-like (all nodes are connected to form a long band-like structure; Fig. 2A), clustered (all nodes are clustered into several disjoint groups; Fig. 2B), and scale-free [the degree distribution of nodes follow the power-law (20); Fig. 2C]. The generated abundance profiles of two nodes are designed to have high Pearson’s correlation coefficients when those two nodes are directly linked. Therefore, we can directly use Pearson’s correlation coefficients to measure the association strength. The network simulator provides suitable synthetic datasets for inferring direct and indirect relationships in association networks.

The first step of the network simulator is to generate an undirect unweighted network. We set the size (number of nodes, n) and average connectivity (k, between two and three) of the network and choose a network topology: band-like, clustered, or scale-free (20). For a band-like network (Fig. 2A), we label all nodes from 1 to n. We connect node i to node i + 1 and randomly connect node i and node i + 2 with a probability of k − 2. For a clustered network (Fig. 2B), we divide all nodes into several clusters. Each cluster contains about 10 nodes. We connect nodes in each cluster into a circle, then add more edges (to reach an average connectivity k) and rewire existing edges randomly. For a scale-free network (Fig. 2C), we start from one node, followed by consecutive random attachment of additional nodes (52). The probability of a new node attaching to an existing node is proportional to the cubic root of the connectivity of the existing node; that is, P_i ∼ (k_i)^1/3. After enough nodes are attached, random edges are added, with the goal to reach an average connectivity k and to make the node degree distribution fitting the power law better.

The second step is to assign direction and weight to all edges of the obtained undirect unweighted network. The direction of an edge is always from high-connectivity node to low-connectivity node, avoiding any loops to make the algorithm in the third step feasible. The weight of an edge is randomly selected from an interval that represents association strengths in real microbial communities.

The third step is to generate abundance profiles based on the directed weighted network obtained in step 2. We first locate nodes in the network that only have edges pointing from them and assign random values as their observed abundance across different samples. Then, we locate nodes that satisfy the following conditions: 1) All the edges pointing to the node are from nodes that already have their abundance profiles, and 2) the remaining edges pointing away from the node. Then, we generate abundance profiles across different samples for those nodes. For instance, let the abundance profiles of node A and B be vectors x and y, respectively, and node A and B has two edges pointing to node C. The association strength of A–C and B–C are u and v, respectively. To generate the abundance profile z of node C, let z = αx + βy + w, where α and β are variables to be determined, and w contains random values. To determine α and β, we use the requirements that the correlation of A–C is u, and the correlation of B–C is v. There are two equations to uniquely determine two unknown variables (α and β). This can be extended to cases when a node has n edges pointing to it; we can always construct n equations originating from the correlation requirement to uniquely determine n unknown variables. We repeat this process until we obtain the abundance profiles for all the nodes. Because the network was constructed to contain no loops in step 2, this approach is always feasible. Because the AUPR results become stable after the sample size exceeds 100 (SI Appendix, Fig. S13), 100 samples were used in the analysis, with the networks containing 500 nodes.

Precision-Recall and Receiver Operating Characteristics Curves.

Precision-Recall (PR) curves and Receiver Operating Characteristics (ROC) curves are utilized to evaluate the performance of network inference as described (4, 6, 19). First, the precision, recall (true-positive rate), and false-positive rates are calculated as follow:

$$\begin{array}{rrr}\hfill \text{Precision}& \hfill =& \hfill \frac{TP}{TP+FP};\\ \hfill \text{Recall/true} \text{positive} \text{rate}& \hfill =& \hfill \frac{TP}{TP+FN};\\ \hfill \text{False} \text{positive} \text{rate}& \hfill =& \hfill \frac{FP}{FP+TN},\end{array}$$ [6]

where TP, FP, TN, and FN are true-positive, false-positive, true-negative, and false-negative link numbers, respectively. A link with association strength above a certain threshold is counted as true positive if the link is a true interaction; otherwise, it is false positive. In contrast, a link with association strength below a certain threshold is false negative if the link is a true interaction; otherwise, it is true negative.

For each network, a series of precision, recall, and false-positive rates are generated by varying the threshold used in defining TP, FP, TN, and FN above. Then, the PR curve is obtained by plotting precision (y axis) against recall (true-positive rate, x axis); the ROC curve is obtained by plotting the true-positive rate (y axis) against the false-positive rate (x axis). PR and ROC curves provide an overall evaluation of the trade-off between type I errors (false positive) and type II errors (false negative). The quality of the prediction can be further quantified by AUPR and Area Under ROC curves (AUROC), both of which range within [0, 1]. AUPR represents the average precision when recall (true-positive rate) varies from zero to one, and AUROC represents the average true positive rate when the false-negative rate varies from zero to one.

Gene Regulatory Networks: DREAM5 Network Inference Challenge.

The DREAM5 network inference challenge (22) (https://www.synapse.org/#!Synapse:syn2820440/wiki/) is a benchmark example used in ND (4) and GS (19). The challenge organizer provided microarray compendia of four networks (6) for the participants to infer the structure of the underlying transcriptional regulatory networks, including an in silico network (53) and an E. coli network. For the in silico network, the corresponding gene-expression data were generated by GNW version 3.0 (gnw.sourceforge.net/). For in vivo E. coli networks, a set of experimentally validated interactions from the RegulonDB database (24) (regulondb.ccg.unam.mx, version 7.0) were provided as a gold standard. RegulonDB is a database of transcriptional regulation in E. coli manually curated from the literature, high-throughput datasets, and computational predictions. Each predicted interaction is classified into one of three categories: weak (single evidence with ambiguous conclusions), strong (single evidence with direct physical interaction or solid genetic evidence), and confirmed (independent strong evidences with mutually excluding false positives). The classification of RegulonDB evidence types can be found in regulondb.ccg.unam.mx/evidenceclassification. The database includes interactions between transcription factor (TF)–gene, TF–operon, TF–TF, sigma factor–gene, and small RNA binding sites. Only those interactions that contained at least one strong evidence were included (2,066 interactions) in the DREAM5 challenge gold standard. Each participant in the challenge was asked to submit 100,000 edges with the highest confidence level. Each submission was compared to the gold standards and scored based on AUPR and AUROC. The final score was a logarithmic-scaled probability of achieving the same AUPR or AUROC based on 1,000 random simulations:

$$\begin{array}{lll}{\theta }_{PR}\hfill & =\hfill & -{\log }_{10}{p}_{PR},\hfill \\ {\theta }_{\mathit{ROC}}\hfill & =\hfill & -{\log }_{10}{p}_{\mathit{ROC}},\hfill \\ {\theta }_{\mathit{total}}\hfill & =\hfill & \left({\theta }_{PR}+{\theta }_{\mathit{ROC}}\right)/2.\hfill \end{array}$$ [7]

In Eq. 7, p_PR and p_ROC are the P values with respect to AUPR and AUROC values; θ_PR, θ_ROC, and θ_total are the corresponding scores. RegulonDB has been updated several times since the DREAM5 challenge. Therefore, we collected all the edges in the latest version of RegulonDB (version 10.0, containing 2,692 interactions; compare with 2,066 interactions from version 7.0) that have at least one strong evidence. We then compiled them into an updated gold standard that was used to evaluate the performances of iDIRECT, ND, and GS.

In the evaluation (22), the submitted 100,000 edges from each participant were treated as the observable total association matrix. iDIRECT, ND (4), and GS (19) were applied to the first 3,000 edges to obtain their direct association strength, which were used to rerank those 3,000 edges in a descending order. These reranked edges, together with the remaining edges, were scored by using the same scoring script provided by the challenge organizer (6). This procedure was consistent with the practice of ND (4). ND- and GS-processed direct association strength were obtained by using the scripts posted online (4, 19). The community networks were integrated from the predictions of all participants by rescoring interactions according to their average rank and are the best performer in the DREAM5 challenge (6). iDIRECT, ND, and GS were applied to individual submissions before community integration instead of being directly applied to the integrated community networks. Because only interactions between a transcriptional factor and a gene were considered, and the entailing association matrix was rectangular, PC was not applicable and was excluded in the comparison. To evaluate the significance of the difference between the AUPR scores obtained from each submission after processed by iDIRECT, ND, and GS for the in silico network, we randomly switched the weights of the true links and randomly switched the weights of the false links in the first 3,000 edges from each submission. The SDs of the AUPR scores obtained from 100 such randomizations were used as a proxy for the SD for the AUPR scores for each submission and method combination. Then, Student’s t test was performed to evaluate whether the AUPR scores obtained from iDIRECT, ND, and GS were significantly different (SI Appendix, Fig. S3).

To assess whether edges identified by iDIRECT in the E. coli network from the DREAM5 challenge are biologically meaningful, we examined the top 500 links with the highest direct association strengths from iDIRECT (Fig. 3C). For the links without any evidence in RegulonDB, we manually searched each predicted interaction to find supporting evidence by the following steps: 1) We manually searched online databases, including RegulonDB (54), EcoCyc (55) (a biological database of E. coli K-12 containing transcriptional regulation), RegPrecise (56) (a database of manually curated TF regulons reconstructed by comparative genomic approaches in prokaryotic genomes), and TEC (57) (transcription profile of E. coli) to see whether these regulatory relationships were described in these databases; 2) if no evidence was found in these databases, we searched through the literature for experimental support; 3) if no evidence was found in any database or in the literature, we searched for the presence of a binding motif of the TF in the promoter region of the target genes; and 4) lastly, if the predicted interaction involved two genes in the same operon, it was classified as the same TU and was unlikely a true direct link, but the expression level of each gene in a TU tends to change in the same direction as they are cotranscribed. If the link involved an antisigma factor, and supporting evidence was available for the interaction between the corresponding sigma factor and the target gene, it was classified as an antisigma factor interaction. These links might be true, but lack direct experimental evidence. If the target gene was involved in the same specific cellular pathway or stress-response pathway based on annotation, it was considered as supportive evidence of the predictive power of iDIRECT.

Microbial Community Network.

We applied iDIRECT to MENs in microbial communities from a long-term experimental warming site of native Oklahoma grasslands (38). A total of 240 surface soil samples were collected from 24 warmed (+2 °C) plots and 24 unwarmed plots once a year for 5 y. DNA extraction, 16S ribosomal ribonucleic acid (rRNA) gene sequencing, and data processing were performed as described (35, 36). The sequences were rarefied to the same sequencing depth in each sample (25,986 sequences per sample), and OTUs were generated with 97% identity. OTUs observed in less than 75% of samples were removed. Previously, we showed that the effects of the compositional bias on the network structure of highly diverse microbial communities could be negligible (37), as evidenced by the very strong correlations of various topological properties between the networks based on log-transformation and central log-ratio transformation, which is expected to mitigate the bias induced by compositionality (58, 59). Thus, log-transformation of OTU abundances was used for calculating pairwise Spearman correlations. To minimize the influence of missing values on network construction, an OTU was removed from the calculation if it was missing from both samples. A small value 0.01 was used to avoid indefinite value in the log-transformation if an OTU was missing only from one sample. Two MENs were constructed based on pairwise Spearman correlations. Each MEN contains edges with association strength above a certain threshold. The threshold was determined objectively by RMT (34). We applied iDIRECT to separate direct and indirect relationships in each MEN and focused on the direct associations in the network. Direct links are those with direct association strengths significantly (P < 0.05) different from background noises, which are estimated by computing the differences between the observed indirect association strengths and the iDIRECT-predicted indirect association strengths of random links below the RMT-determined cutoff.

Topological properties of the networks were calculated as reported (38, 60, 61). Random networks were generated by following the Maslov–Sneppen procedure (62). We used the greedy modularity optimization (63) to divide the whole network into modules. The higher-order organization of the constructed direct MENs is revealed by eigengene network analysis (60, 64). The nodal topological role was defined by the within-module connectivity (Z_i; how well a node is connected to other nodes in the same module) and intermodule connectivity (P_i; how well a node is connected to different modules) (65). The nodes are divided into four categories (66), including peripheral nodes (low Z_i and low P_i), connector (low Z_i but high P_i), module hub (high Z_i and low P_i), and network hub (high Z_i and high P_i).

The robustness of a network represents its resistance to external perturbation and can be quantified as the proportion of remaining species in the network after targeted or random species removal (67). In the targeted species removal, species with significant topological roles (e.g., module hubs) in the network were removed; in random species removal, species to be removed were randomly selected. After initial species removal, a species was considered extinct when it became isolated and lost all its connections to other species; then, this species was removed from the network. This process continued until all remaining species were connected to at least one other species, and the proportion of remaining species was recorded.

We have also attempted to apply ND and GS to the MENs for comparative purposes. For ND, we followed the procedure outlined in the coauthor collaboration network example (4). First, we removed nodes that had no links to other nodes; then, we constructed an unweighted input association matrix by setting the corresponding entries to one when two nodes are connected and setting them to zero when two nodes are not connected. Then, we ran the ND script to obtain a weighted ND-processed direct association matrix. The obtained direct association strengths varied from 0.5612 to 1 under control and from 0.6424 to 1 under warming. For GS, because using unweighted input association matrix resulted in singularity error, we used a weight-input association matrix, with weights being the absolute value of the correlation coefficients. The obtained weight for the GS-processed direct association strength varied from 0.2438 to 0.9656 under control and varied from 0.4707 to 1 under warming. In both ND and GS, there were no clear cutoff values for the direct association strengths to qualitatively distinguish direct links from indirect links. Therefore, we could not construct ND-processed direct networks or GS-processed direct networks for the microbial community under experimental warming.

Data Availability

The method has been incorporated with our Molecular Ecological Network Analysis Pipeline (http://ieg4.rccc.ou.edu/mena/login.cgi). The Python code is available for download at GitHub (https://github.com/nxiao6gt/iDIRECT) (68). Previously published data were used for this work (22, 36). The DNA sequences of the 16S rRNA gene and ITS amplicons were deposited in the National Center for Biotechnology Information (accession no. PRJNA331185).

Change History

January 17, 2022: The byline has been updated.