Improvement of Spatial Resolution with Iterative PET Reconstruction using UltraFast TOF

Abstract

The impact of Time-of-Flight (TOF) on positron emission tomography (PET) spatial resolution is generally considered negligible. In this work, a two-step approach based on simulations of two-dimensional scanner configurations is taken to show that ultra-fast TOF has the potential to overcome the limitation induced by the physical size of detectors on spatial resolution. An estimation of the lower bound on spatial resolution using point sources is provided, followed by a qualitative assessment of the resolution obtained using a Hot Spot phantom. The impact of detector width, TOF resolution and TOF binning on the achieved spatial resolution is also studied. While gain beyond the expected blur due to detector size is demonstrated, the detector size remains one limiting factor albeit less prominent. The dependence on acquisition statistics to reach the full potential of TOF-induced gain in spatial resolution is demonstrated. A simulated brain phantom acquired with a fictive three-dimensional PET scanner was qualitatively analyzed and structures smaller than the typical limit are clearly made visible by reconstructing the images with a ∼13-ps TOF resolution. A potential application of this feature of ultra-fast TOF would be the design of clinical PET scanners achieving spatial resolution beyond the current state-of-the-art.

I. Introduction

THE multiple benefits that Time-of-Flight (TOF) provides to Positron Emission Tomography (PET), including a gain in signal-to-noise ratio, reduction of artifact propagation, and faster reconstruction, are demonstrated extensively in the literature [1], [2]. Yet, PET scanners featuring TOF started to become available clinically only about 15 years ago [3]–[5]. This was made possible by developments in detector technology that enabled achieving usable TOF resolution with viable detection efficiency [6], [7]. Currently, the TOF resolution of clinical PET scanners is approaching 200 ps Full Width at Half Maximum (FWHM) [8].

The benefits provided by TOF derive from the ability to circumscribe the origin of an annihilation event to a portion of the tube of response (TOR) defined by the coincident detectors, which adds a new dimension in the PET acquisition sampling scheme [9]. A Coincidence Time Resolution (CTR) of 30 ps would enable direct image formation without loss of image resolution since most clinical PET scanners achieve a spatial resolution in the range of 4–6 mm [10]. The feasibility of ultra-fast TOF-PET detectors has yet to be proven [11], [12], but the roadmap towards 10 ps CTR has already been laid out [13]. Recently, a CTR of 58 ps was achieved with current state-of-the-art LSO:Ce:0.4%Ca detectors albeit with short crystals [14].

Up to now, the effect of TOF on PET spatial resolution has been mostly neglected due to the exceptional gain in sensitivity and contrast recovery that it provides. However, as the TOF resolution improves and becomes comparable to the spatial resolution of current PET scanners, it might be instructive to investigate the potential benefits in terms of spatial resolution of images reconstructed with ultra-fast TOF information. The spatial resolution of a PET scanner in FWHM, Γ, can be approximately described by

$$\Gamma =\alpha \sqrt{{\left(\frac{d}{2}\right)}^2+b^2+\frac{{\left(12.5r\right)}^2}{r^2+R^2}+{\left(0.0044R\right)}^2+s^2},$$ (1)

with the reconstruction factor (α), the detector width (d), the detector decoding error (b), the annihilation photon penetration inside the detectors (r: radial distance of the source from the center, R: scanner radius), the annihilation photon acolinearity and the positron range (s) [15]. A complete explanation of each factor is given in [15]. Currently, the scanner CTR is not considered as a contributing factor in (1).

We hypothesize that TOF, with a good enough CTR, can mitigate the limitation induced by the discrete nature of the PET acquisition sampling scheme. If this holds true, it means that the spatial resolution of a TOF-PET scanner, when combined with a model describing every source of spatial blur, would only be limited by the statistics of the acquisition. The main focus of this paper is to show that, when ultra-fast TOF is available, the blur induced by the detectors can be mitigated depending on the acquisition statistics. The experiments in this study are accomplished via simulation since PET scanner offering ultra-fast (<100 ps) TOF resolution are not yet available.

In this work, fictive two-dimensional scanners that differ by their detector width and TOF resolution are studied. They are simulated such that the only source of spatial blur is their detectors width. This investigation is broadened, in part, to a range of TOF discretization level to show its effect on the achieved spatial resolution. The spatial resolution lower bound of these scanners is evaluated and compared to the spatial resolution qualitatively extracted from a custom Hot Spot phantom. We also qualitatively show the gain in resolution that a cylinder-type PET scanner with excellent TOF resolution would provide in the imaging of a brain phantom with a typical fluorodeoxyglucose-like (¹⁸FDG) distribution. Overall, the results of this study are in agreement with the hypothesis that ultra-fast TOF will eventually make it possible to achieve spatial resolution beyond the blur induced by the detector size and that this gain is dependent on the acquisition statistics.

II. Simulation setup

First, we describe the scanners under study and how acquisitions were simulated. Then, the reconstruction tool used, which affects the analysis of the spatial resolution, is presented. The approach we used to study the gain in resolution provided by ultra-fast TOF is divided in three steps: evaluation of the scanner spatial resolution lower bound with point sources, comparison with a structured phantom and application to a realistic 3D phantom.

A. Simulation configuration

PET acquisitions were simulated with Geant4 Application for Tomographic Emission (GATE) v.8.0 [16]. Unless otherwise stated, back-to-back sources, referring to a source of annihilation photons that is not affected by positron range and acolinearity, were used in this work. Only the photoelectric detection process was activated for the annihilation photons from those sources. Scattered coincidences were thus not included in the simulations. The back-to-back emission angle was limited to the transverse plane. In all simulated acquisitions, the emission rate was chosen such as to minimize the rate of random coincidences. In all the scanners studied, the detectors were shaped as right rectangular prisms and their depth was fixed at 10 µm to limit the impact of depth of interaction on TOF resolution [17]. A fictitious high-density material was created for the detectors to reduce simulation time by ensuring that incident annihilation photons would almost certainly be detected. In this work, a scanner with a single detector ring along the axial axis was referred to as a two-dimensional (2D) scanner.

Scanner models in 2D were created to study the interplay between detector width and TOF resolution on the image spatial resolution. All scanners shared the same shape, which is a gap-less regular polygon with an inner diameter of ≈80 cm and 40 panels each 64 mm in width. Three uniform subdivision of the panels were considered: 8, 16 and 32 resulting in detector width of 8, 4 and 2 mm hereafter referred to using the width of their detectors, e.g., “4-mm Det. geometry” (Top of Table I). The detectors were 4 mm wide in the axial direction for all these geometries. CTR of 13.3, 26.6 and 53.3 ps FWHM, corresponding to TOF spatial resolution of 2, 4 and 8 mm FWHM respectively, were studied for the three geometries. From here on, they will be referred to using their CTR value converted to the spatial domain, e.g., “4-mm TOF scanners” (bottom of Table I). The term configuration was used to refer to a scanner with a specific CTR and geometry. Thus, three TOF resolutions and three geometry variants yielding nine configurations were considered in this study. One three-dimensional (3D) scanner was studied. It consisted of duplicating 64 times the 4-mm Det. geometry along the axial axis without gaps. The resulting scanner had 40,960 detectors and a 25.6 cm axial FOV. Its TOF resolution was fixed at 2 mm FWHM (∼13 ps).

TABLE I.

(Top) Instrumental spatial resolution limit of the geometries (Bottom) CTR of the studied scanners

Geometry	2-mm Det.	4-mm Det.	8-mm Det.
Resolution limit	1.0 mm	2.0 mm	4.0 mm
TOF resolution	2-mm TOF	4-mm TOF	8-mm TOF
CTR	13.3 ps	26.6 ps	53.3 ps

The value of (1) for a given configuration will be referred to as its instrumental spatial resolution limit. In this study, there were no detector decoding, nor depth of interaction. Also, α was fixed to 1.0 since iterative reconstructions were used until asymptotic convergence. Since positron range and annihilation photon acolinearity were only included for the 3D configuration, the two last factors in (1) do not apply for the 2D configurations. The instrumental spatial resolution limit for each 2D geometry and TOF resolution corresponding to CTR are summarized in Table I.

B. Image reconstruction

The simulated acquisitions were reconstructed using the MLEM algorithm without ordered subsets, inclusion of image priors or correction factors.

The system matrices of the 2D configurations were precomputed. For each scanner geometry, a TOF-less system matrix was computed using the geometric probabilities at the center of each image pixel to approximate the pixel response function. This can be computed accurately since the emission lies in a 2D plane and the depth of interaction is negligible. The TOF system matrices were built by duplicating the corresponding TOF-less system matrix with the number of TOF bins and weighting each copy with the TOF response function of the corresponding TOF bin. The TOF response function of a TOR was approximated by assuming it only varies along the TOR following a Gaussian distribution of fixed FWHM determined by the CTR. Thus, the binned TOF response function was defined as the convolution of the TOF response function with the rectangular function of the TOF bin along the TOR. The same TOF binning was used for every TOR of a given configuration and it was defined as the uniform partition of the largest TOF domain possible for the image domain. The image domain was a plane of 8.0 × 8.0 cm² discretized in 256 × 256 pixels, which resulted in an in-plane pixel width of 0.3125 mm.

The 3D scanner acquisition was reconstructed with the CASToR software v.3.0.1 [18]. All the TORs that intersected the image domain were included for fully 3D image reconstruction. The multiSiddon projector with 100 samples was used for the on-the-fly approximation of the system matrix. When TOF information was exploited, it was in its continuous form with the default options [19]. The image domain was a volume of 23.36 × 23.36 × 18.96 cm³ discretized in 584×584×474 voxels. The resulting voxel width was 0.4 mm isotropic.

C. Scanner spatial resolution lower bound

A phantom made of point-like sources, referred to as MultiDots, was created to evaluate the lower bound on the spatial resolution of the 2D configurations. It consisted of seven line sources of 2 µm in diameter and 4 mm in height. They were placed at a distance of 5 mm to 35 mm from the center with a step of 5 mm along the principal axes of the FOV to maximize the distance between each source (Fig. 1a). Each source was centered on the nearest image pixel that fitted the specified distance in order to simplify the study of the resulting point spread function. Approximately one million coincidence events were acquired for each simulation.

Fig. 1.

The three phantoms used: (a) MultiDots phantom with the distance of the line sources from the center; (b) HotSpots phantom with the rod diameter in each sector; (c) a mid-brain transversal slice through the BigBrain phantom.

The spatial resolution for each scanner configuration was evaluated with the methodology described in [20]. As suggested, the uniform background value was chosen such that the contrast between the point sources and the background was lower than 0.1 at convergence. The spatial resolution at a given distance from the center was defined as the mean of the FWHM along the x and the y axes.

With the 2-mm TOF configurations, 40k iterations were sometimes required to ensure that the resolution gain per 10k iterations became negligible. For TOF-less reconstructions, resolution stability was achieved way before 5k iterations. Thus, the resolution for TOF and TOF-less reconstructions were evaluated respectively at 50k and 5k iterations. The simulations obtained from the 2-mm TOF scanners were reconstructed over a range of TOF discretizations while the other simulations were reconstructed with 1 and 128 TOF bins.

D. Qualitative evaluation of spatial resolution

The spatial resolution of the 2D configurations was also evaluated from the reconstruction of a Hot Spot phantom, referred to as HotSpots (Fig. 1b). It consisted of a 60 mm diameter, 4 mm high cylinder in which six sectors were populated with spots spaced at a distance equal to their diameters of 1.0, 1.5, 2.0, 2.5, 3.0, 3.5 mm. The activity in the phantom was distributed such that the expected spot-to-background ratio would be equal to four. Two acquisitions of the phantom were simulated for each 2D configurations: one with 7 million coincidence events and another with 0.7 million coincidence events. All of them were reconstructed with 128 TOF bins. TOF-less reconstruction of each geometry was also included.

This analysis was based on the method proposed in [21]. The spatial resolution achieved by a configuration was evaluated from the image obtained at the best iteration, defined as the one reaching the minimum mean squared difference with the ground truth, which is available with GATE. From that image, the peak-to-valley ratio (PVR) of the six sectors was computed. The sectors for which their PVR satisfied the Rayleigh resolution criterion with an intensity dip of 26.5% were defined as resolved [22]. Thus, a scanner configuration was described as achieving a resolution of at least d if the sector composed of spots with diameter d was resolved.

The PVR of a sector was defined as the median PVR of the lines profiles (intensity ratio between the pixels of the spots and the background) of the sector (Fig. 2a). Pixels affected by partial volume effect due to discretization, detected from the ground truth by using a high threshold and a low threshold, were excluded from the evaluation (Fig. 2b). If any line profile of a sector had a PVR of one or less, the sector was defined as not resolved.

Fig. 2.

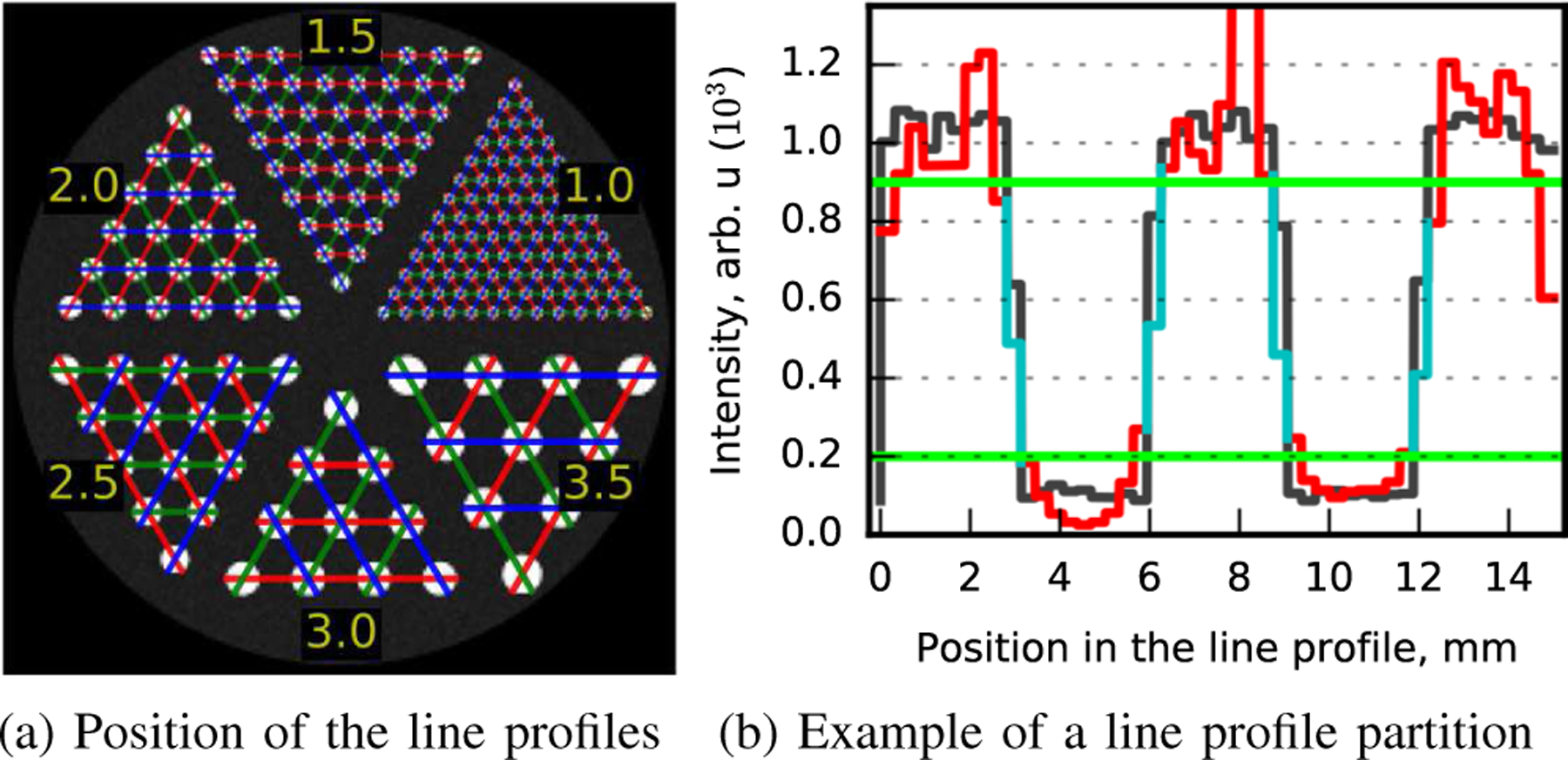
(a) Line profiles overlayed on the HotSpots phantom. The green, red and blue colors were used for better visualization. (b) Example of partition applied for peak-to-valley ratio evaluation. The black line shows the line profile for the ground truth of the reconstructed image. The green lines are the thresholds applied on the ground truth line profile to find pixels affected by partial volume effect. The red line shows the pixels extracted from the reconstructed image while the cyan line shows those that were excluded.

E. Brain phantom

The acquisition of the BigBrain, a voxelized phantom of the human brain [23], was simulated with the 3D scanner. The BigBrain version used in this study was the ‘2015 3D Classified Volumes, MNI ICBM 152 Space’ with 0.4 mm isotropic voxels. The simulation was made with a ¹⁸F positron source having a distribution derived from a typical ¹⁸F-FDG PET scan of the human brain. All relevant physical processes were activated for the simulation. Fig. 1c shows a transaxial view of the resulting source distribution. The phantom was defined as being composed of water. Approximately 60 million coincidence events were acquired. The instrumental spatial resolution limit of this scanner was around 2.7 mm since the positron range and annihilation photon acolinearity of ¹⁸F were incorporated in the simulation.

III. Results

First, the spatial resolution lower bound of the 2D configurations were evaluated with the MultiDots phantom. Then, these data were qualitatively compared with the HotSpots phantom. Finally, the 3D scanner resolving power was qualitatively analyzed with the BigBrain phantom.

A. Scanner spatial resolution lower bound

The spatial resolution of the point sources as a function of their radial position is shown in Fig. 3 for the nine 2D configurations. For all of them, the resolution obtained was significantly better than their respective instrumental spatial resolution limit (Table I). The spatial resolution lower bound for all TOF resolutions is approximately four-fold better than the expected values. These results show a dependence on the scanner geometries whereas the TOF resolution has a more limited impact. Non-monotonic variation of the resolution as a function of radial position were observed, which suggests that the gain in resolution provided by TOF varies over the image domain.

Fig. 3.

FWHM spatial resolution for the nine 2D configurations as a function of radial position. For all cases, 128 TOF bins were used. The instrumental spatial resolution limit at the center are respectively 1, 2 and 4 mm for the 2-mm Det., 4-mm Det. and 8-mm Det. geometries (Table I). The black line shows the width of an image pixel.

Fig. 4a shows the resolution obtained for the point source positioned at 5 mm from the center as a function of the number of TOF bins for the three geometries with 2-mm TOF. As expected, the resolutions achieved with one TOF bin were lower-bounded by their respective half detector width. We also observed that fine TOF discretization were not a requirement to reach the best spatial resolution. Indeed, even when using 32 TOF bins, which had a spatial TOF binning width of ∼4 mm (magenta dashed line), the values obtained were mostly equivalent to their 256 TOF bins counterparts. Furthermore, a significant gain in the reconstructed spatial resolution was observed even with only four TOF bins.

Fig. 4.

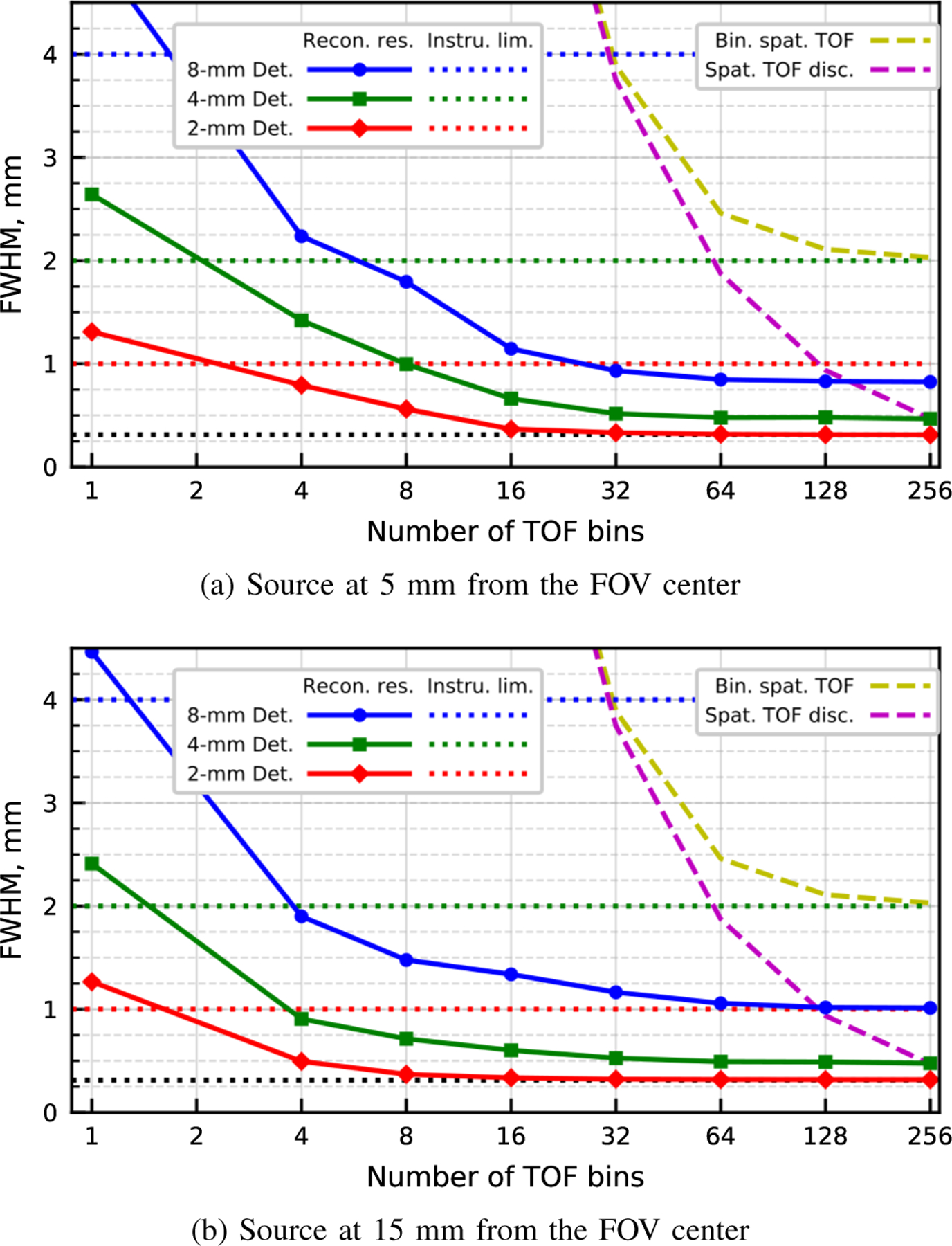
FWHM spatial resolution for the three geometries with 2-mm TOF as a function of TOF binning are shown with the solid lines. The dotted lines show the half detector width for each geometry. The yellow and magenta dashed line respectively show the TOF binning width and the FWHM of the TOF response function over the number of TOF bins. The black dotted line show the width of the image pixel.

Fig. 4b shows the resolution obtained for the point source positioned at 15 mm from the center as a function of the number of TOF bins for the three geometries with 2-mm TOF. The observations made for the previous position (5 mm) also apply here: TOF provided a significant gain in the reconstructed spatial resolution and ultra-fine TOF discretization was not needed to achieve the best spatial resolution. However, the resolutions obtained for lower number of TOF bins, including the TOF-less case, were slightly better at this position than the ones obtained for the source at 5 mm from the center.

B. Qualitative evaluation of spatial resolution

Fig. 5 shows the best images obtained for the two acquisitions of the HotSpots phantom on each of the geometries with 2-mm TOF. For the 8-mm Det. and 4-mm Det. configurations, we can distinguish spots that are smaller than their respective instrumental spatial resolution limit. We also observe that images obtained from acquisition with less statistics (right) have poorer resolution than the ones obtained with more coincidence events (left).

Fig. 5.

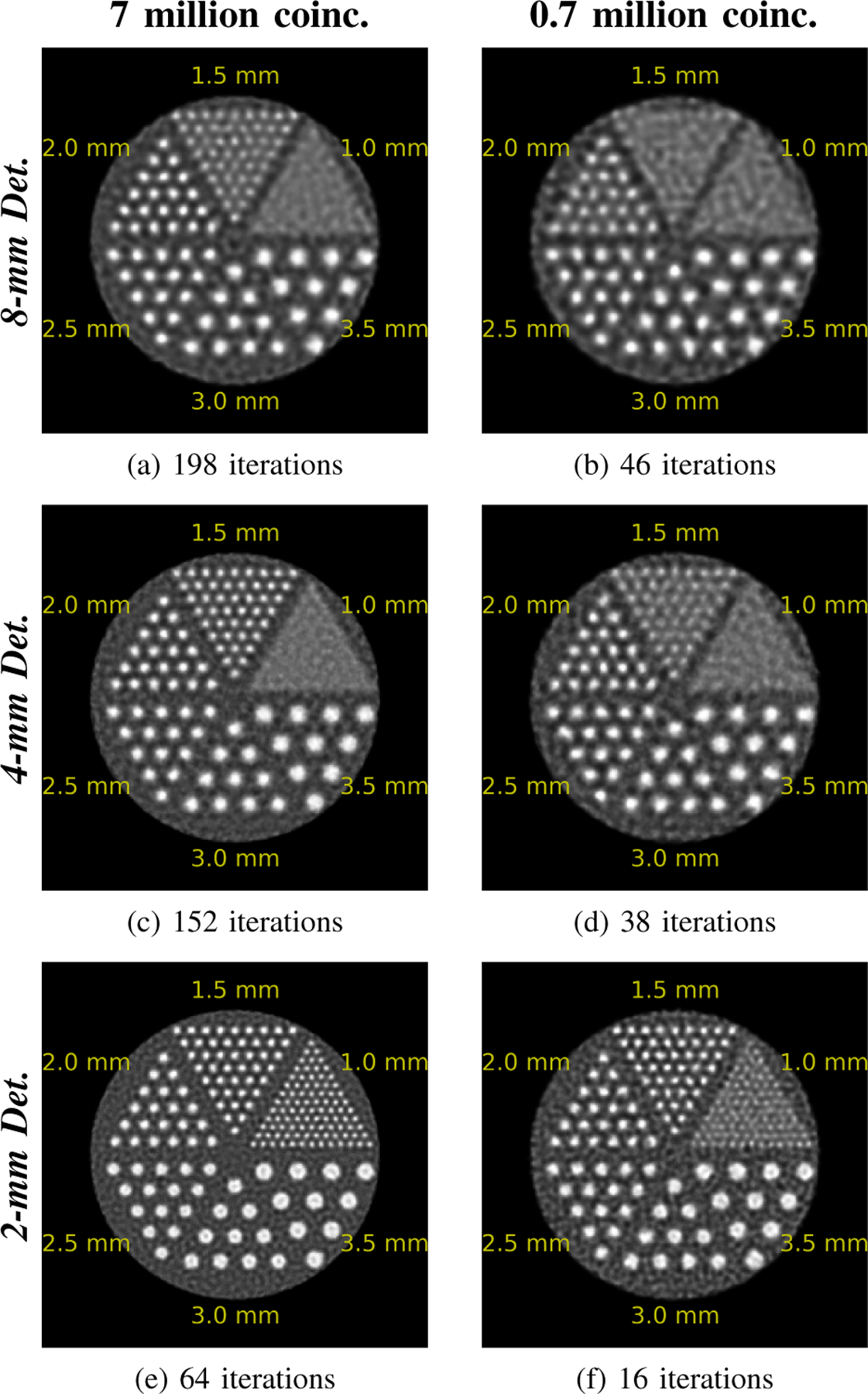
Reconstructions of the HotSpots phantom with 2-mm TOF. The number of iterations used for each of these images is shown beneath them. All images of a column are displayed with the same maximum value.

The left side of Fig. 6 displays the PVRs extracted from the reconstruction of the HotSpots acquisitions with 7.0 million coincidence events. The black dashed line in each figure indicates the resolving threshold based on Rayleigh criterion. When TOF information was ignored, the resolving power was worse than half their detector width, which follows their instrumental spatial resolution limit and fits with our previous observations. In most cases that exploited TOF information, the resolving power was better than the resolution predicted by their instrumental spatial resolution limit. Moreover, better TOF resolution provided greater gain in spatial resolution or at the very least an increase in PVR.

Fig. 6.

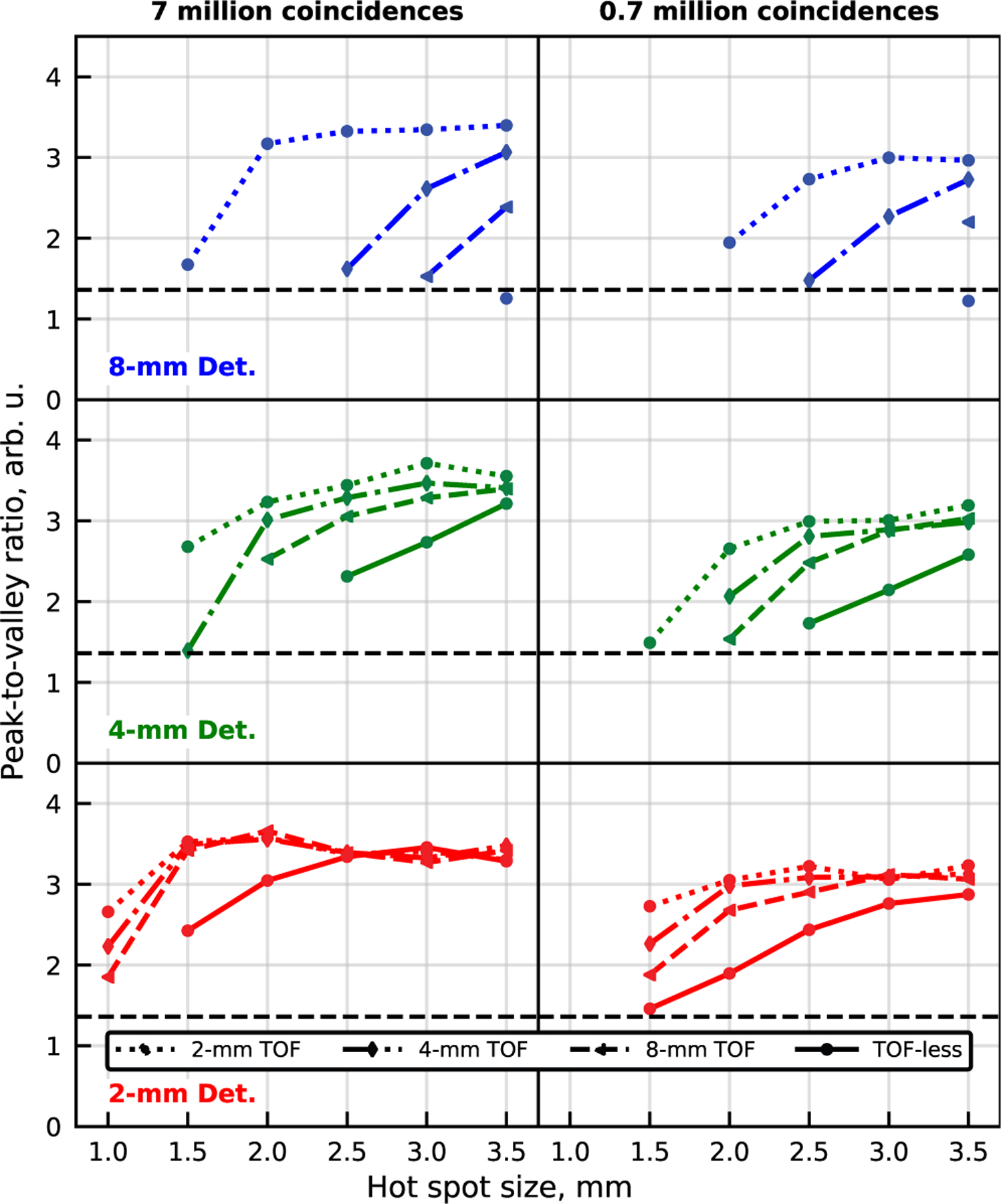
Peak-to-valley ratio of the sectors of the HotSpots phantom are shown for the best images obtained with the nine 2D configurations. The results are shown for simulations of 7.0 (left) and 0.7 (right) million coincidence events. From top to bottom, the results are shown for the 8-mm Det., the 4-mm Det. and the 2-mm Det. geometries. The dotted, dash-dotted and dashed lines respectively refer to the 2-mm TOF, 4-mm TOF and 8-mm TOF scanners. The solid lines are TOF-less reconstructions. The black dashed line shows the chosen Rayleigh resolution criterion. Missing values are cases where at least one line profile had a peak-to-valley ratio of one or less.

The right side of Fig. 6 displays the PVRs extracted from the acquisitions with 0.7 million coincidence events. Again, we observe that the achieved resolutions in some of the reconstructions that exploited the TOF information were better than the ones predicted by their respective instrumental spatial resolution limit. However, we also noticed that in most of them at least one sector was no longer resolved when compared to the reconstructions obtained from acquisition with 7.0 million coincidences. In the other cases (e.g. 1.5 mm sector of the (4-mm Det. & 2-mm TOF) configuration), the PVR of the smallest resolved sector was diminished significantly suggesting that some lost of resolving power can be expected if less coincidences were available.

C. Brain phantom

Fig. 7 shows a sagittal slice for three images created from the acquisition of the BigBrain phantom simulated with the 3D scanner. The images are, from left to right, the TOF-less reconstruction, the ground truth and the TOF reconstruction. For the reconstructions, we selected the iteration number that had the best resolving power according to our own judgment. The TOF-less reconstruction and the ground truth were post-smoothed with a 3D isotropic Gaussian kernel of respectively 0.4 mm and 1.0 mm sigma for visual appreciation. The sigma values were chosen such as they were sufficient to mitigate local intensity fluctuations caused by the relatively low total number of coincidence events on the finely discretized image space.

Fig. 7.

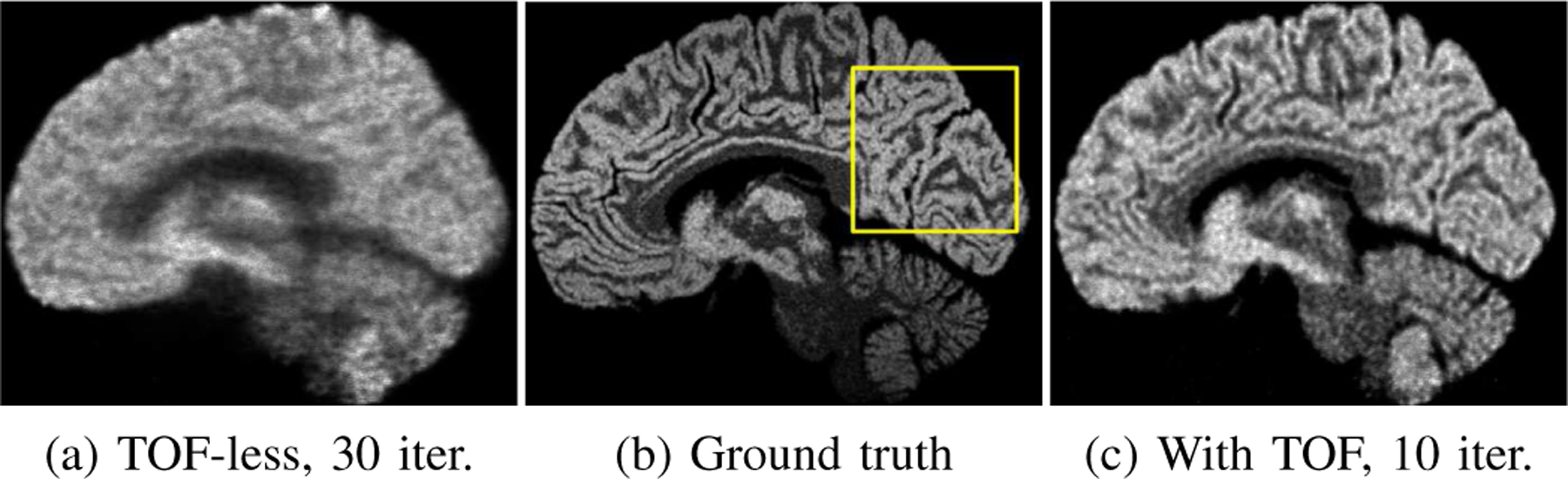
Sagittal slice of three images produced from the acquisition of the BigBrain phantom with the 3D scanner: (a) TOF-less reconstruction; (b) simulation ground truth; (c) TOF reconstruction. The slices are extracted at the same position for the three images and they are slightly offsetted from the FOV center. (a) and (b) were smoothed with a 3D isotropic Gaussian kernel of respectively 0.4 and 1.0 mm sigma. The maximum value for visualization was fixed at ∼90% of their respective cumulative intensity histogram.

As expected, fewer iterations were required for the TOF reconstruction compared to the TOF-less reconstruction (10 vs 30 iter.). The TOF reconstruction (Fig. 7c) better matches the ground truth (Fig. 7b) compared to the TOF-less reconstruction (Fig. 7a). Furthermore, multiple structures, mostly in the white matter, were made clearly visible by the introduction of TOF, displaying its capability to enhance the contrast recovery.

An expanded 5.9 × 5.9 cm² area of these images is shown in Fig. 8. The position was chosen to highlight the gain in resolution provided by ultra-fast TOF. Again, the TOF reconstruction had better contrast recovery than the TOF-less one. Yellow circles of 2.7 mm in diameter were added to illustrate the instrumental spatial resolution limit for the 3D scanner (Sec. II-E). Green arrows highlight some of the structures that can be resolved in the TOF image even though they were smaller than the expected resolution limit of 2.7 mm. This again suggests that TOF does provide a gain in resolution beyond the instrumental spatial resolution limit. As expected, these structures were not resolved in the TOF-less reconstruction. We also observed that some structures were still not visible even with the TOF reconstruction (red arrows).

Fig. 8.

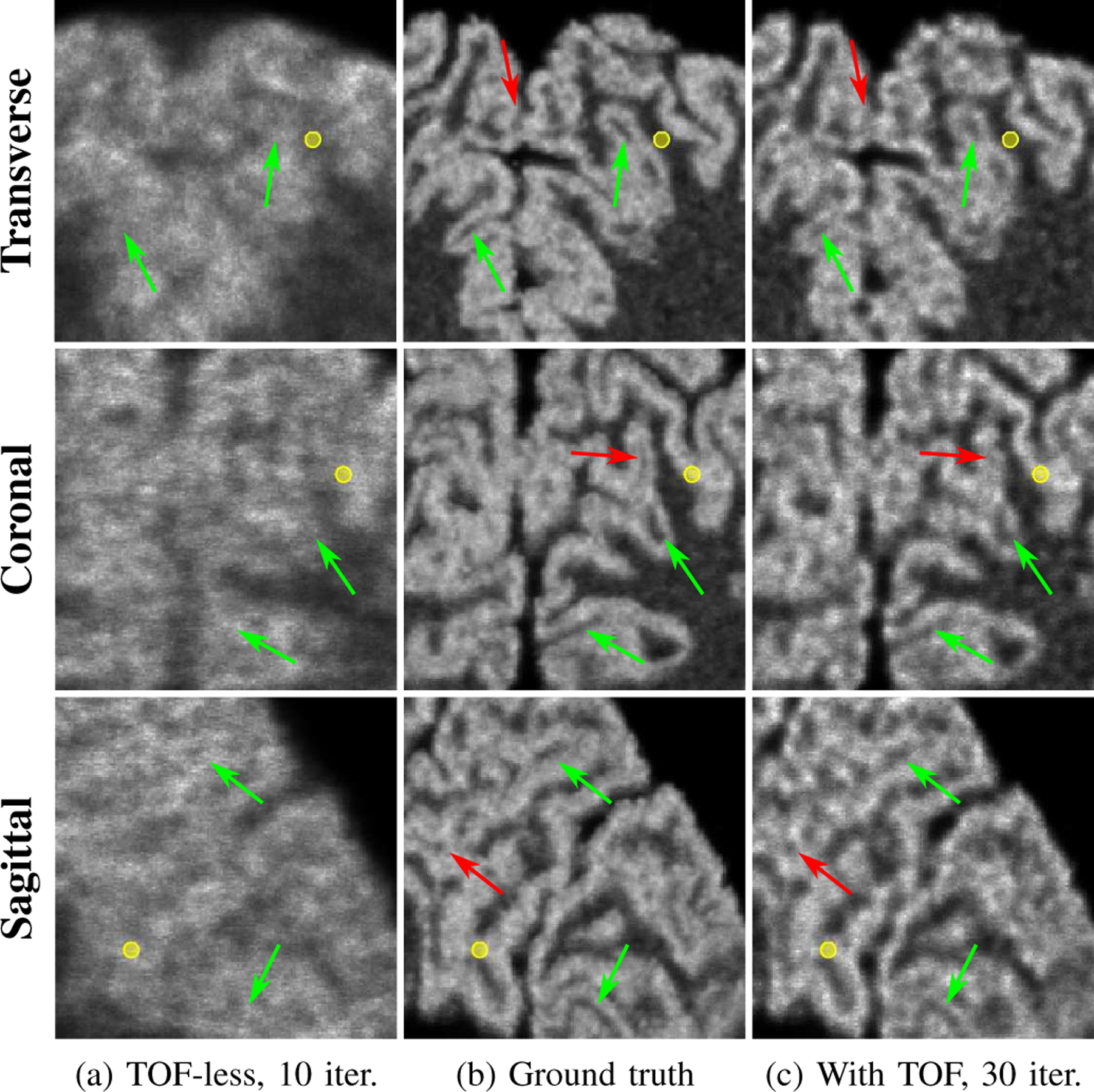
Expanded 5.9 × 5.9 cm² areas indicated by the yellow square in Fig. 7 centered at ∼54 mm from the FOV center. The yellow circles are 2.7 mm in diameter, representing the instrumental spatial resolution limit of the 3D scanner. The green arrows highlight structures smaller than the instrumental spatial resolution limit that are visible in the TOF reconstruction while red arrows highlight structures that are not resolved in the TOF reconstruction.

IV. Discussion

Our aim was to demonstrate and describe the gain in spatial resolution that ultra-fast TOF can provide to the PET image reconstruction. This study was based on clinical size PET scanners with ultra-fast TOF albeit mostly limited to 2D configurations. First, the MultiDots phantom was used to evaluate the spatial resolution limit of the studied 2D scanners. The reported resolutions were significantly better than their respective instrumental spatial resolution limit given by (1) which, in this study, was only affected by the detector width. It was also observed that reducing the detector width remains a means for improving resolution even with ultra-fast TOF.

Reconstructions of the HotSpots phantom were then used to evaluate qualitatively the spatial resolution of the scanners via spots resolvability. Again, resolutions better than the ones predicted by the instrumental spatial resolution limit were observed, but some discrepancies becoming more prominent with lower statistics were noted when compared to the resolution data obtained with the MultiDots phantom. The image reconstructed from the simulation of the BigBrain phantom with a 3D scanner also clearly demonstrated the capability of TOF to provide some gain in spatial resolution beyond the instrumental spatial resolution limit. Overall, these results are in accordance with the hypothesis that an ultra-fast TOF resolution mitigates the limitation induced by the discrete nature of the PET reconstruction scheme, thus compensating for the effect of detector width on the achievable spatial resolution.

A. Further analysis of the results

The 8-mm Det. and 4-mm Det. geometries had fewer TORs than the number of pixels, which means that the reconstruction problem was undetermined when TOF information was ignored since the number of equations (TORs) was strictly lower than the number of variables (pixels). Undetermined inverse problems do not have a unique solution, therefore there is a class of images that are optimal for the corresponding reconstruction problem. For the 2-mm Det. geometry, the number of TORs was slightly higher than the number of pixels. However, this does not ensure by itself that the reconstruction problem is overdetermined since some of the TORs could be redundant. Future investigation, currently limited by the extremely large size of the system matrices, could be made to evaluate the smallest eigenvalue of the hessian matrix resulting from each reconstruction problem to confirm, or infirm, if any of them are overdetermined.

Non-monotonic variations of the resolution as a function of radial position were observed for all the configurations (Fig. 3). While more TOF bins increases the sampling density of the image space, this does not guarantee that the resulting reconstruction problem has a unique solution. Indeed, the additional information it provides is only along the TORs without increasing the angular sampling of the pixels. A clean representation of the nonuniform pixel sampling provided by the TORs of a typical 2D scanner is shown in Fig. 3 of [15]. Thus, the non-monotonic behavior of the spatial resolution resulting from the undersampling of the image space with wide detectors can be mitigated, but not completely eliminated, by the TOF sampling along TORs. We expect that this behavior will be less prominent with a 3D scanner since the angular sampling provided by the TORs are denser.

Several tests (not shown) were done to ascertain that the lower bounds in spatial resolution reported in Sec. III-A were not limited by the methodology. These tests consisted of using finer discretization of the reconstruction parameters (e.g. more TOF bins, smaller image pixels, etc.) which could not be applied for all the configurations due to hardware limitations. No significant gain in resolution was observed with these tests, suggesting that the results reported in Sec. III-A are not limited by the choice of reconstruction parameters.

B. Review of the methodology

The estimation of the lower bound on spatial resolution was based on the technique proposed in [20], which details a convenient procedure for evaluating the spatial resolution with iterative reconstruction. Although this technique was not validated for PET scanners having ultra-fast TOF, the TOF reconstruction of the MultiDots phantom followed a similar pattern: a contrast of 0.1 or less produced stable FWHM value while far higher contrast resulted in resolution converging to the pixel width. Further lowering the contrast did not change the observed resolution (ignoring cases where numerical errors dominated the reconstruction). Since TOF reconstructions are known to converge faster, it is surprising that ten times more iterations than for TOF-less reconstructions were sometimes required to achieve spatial resolution convergence. However, the gain in convergence speed provided by TOF might not apply to the study of spatial resolution. The most reassuring support of the validity of this technique in the context of the current study is that gain in spatial resolution beyond the instrumental spatial resolution limit was also clearly observed with reconstructions of the HotSpots phantom. Overall, the results observed in the present work suggest that the technique proposed in [20] is valid to study the lower bound on spatial resolution of PET scanner with ultra-fast TOF.

The evaluation of the spatial resolution achieved by the 2D configurations was based on the Rayleigh resolution criterion for two points combined with the HotSpots phantom. While it seemed in agreement with our capability to visually resolve the spots (Fig. 5), it remains to be proven that it is viable for PET imaging. Furthermore, there might have been better choices of algorithm and stopping criterion to study the resolving limit of the different configurations. MLEM is known to converge to a noisy solution and the mean squared difference metric could have favored solutions with lower overall noise over ones having more spots resolved. For example, the 1.0 mm sector was resolved for iterations beyond 40 with the (2-mm Det. & 2-mm TOF) configuration, but the 16^th iteration was selected by the metric (Fig. 5f). These could explain, in part, the discrepancies observed between the results obtained from the MultiDots phantom and those from the HotSpots phantom. Nevertheless, these choices do have the advantage of not depending upon hyper-parameters calibration (e.g., penalized MLEM weights and noise tolerance level). Also, the number of coincidences was high considering the size of the phantom and the 2D scanner configurations. These should not be considered as fundamental limitations when the goal is to grasp the potential of ultra-fast TOF to provide a gain in spatial resolution, but it needs to be kept in mind when considering the requirements for practical applications.

C. Limitations of the methodology

As stated previously, some of the reconstruction problems studied in this work were undetermined, which might be the cause of the non-monotonic variation observed in Sec. III-A. A coarser image domain discretization would mitigate this concern, but the capability to evaluate the spatial resolution would have been further limited. We hypothesize that it only broadened the spatial resolution lower bound of the studied configurations since MLEM reconstructions are known to recover low-frequency structures first. In other words, we expect that the reconstructed image for a given undetermined reconstruction problem is the solution with the worst resolution among all the optimal solutions of that reconstruction problem. If this hypothesis holds, the values reported in this work would be worse than what could be achieved with the 3D counterparts of the studied configurations since they would have more TORs. Note that all the reconstructions made in this study were initialized with a constant value. When a reconstruction was initialized using the ground truth of the simulation (not shown), the reconstructed image was the ground truth, showing that a class of images would be optimal for this specific reconstruction problem.

Another concern is the possibility of an ‘inverse’ parallax effect due to the absence of depth-of-interaction in the detectors, resulting in finer TORs for off-center positions. The width of the TORs that intersected the image domain for the three geometries were computed and most matched their detector width. The largest variation observed was around ∼0.2 mm for the 8-mm Det. geometry. It was expected that this ‘inverse’ parallax effect would not have much impact in this study since the 8.0 × 8.0 cm² reconstructed region is a small portion of the FOV of the studied scanners.

Even with the simple 2D configurations studied, the system matrices remained a bottle-neck. The inter-pixel variation of the geometric response function was neglected. More samples per pixel would have provided a better approximation. However, the gain that it could provide would likely be marginal since the pixels (0.3125 mm in width) were small compared to the other sources of blur. The size of the system matrices also limited the image domain and the number of TOF bins that could be studied. The chosen image domain is too small to extrapolate the observed gain over the full FOV of a clinical scanner. We expect a more significant gain further along the radial axis. This is based on the fact that TOF spatial resolution is the same over all projections irrespective of their position in the FOV while parallax induces a broadening of the TOR with off-center positions. The observation that the point source at 15 mm required less TOF bins than the point source at 5 mm to achieve its best spatial resolution supports this claim. We also expect that the spatial resolution will still degrade along the radial axis since the angular sampling (i.e. TORs sampling) is less dense away from the scanner center [15].

The inclusion of TOF information into the system matrix was also an approximation of the scanner TOF response function. The weighting of the pixel geometric response with the TOF response at its center disregarded the inter-pixel variation of the TOF response function. We also assumed that the TOF response function varies along but not across the TORs, which is not accurate especially for scanners with wider detectors, like the 8-mm Det. geometry. Thus, the TOF blur of the studied configurations were underestimated. Both of these assumptions should have a rather limited impact considering the significant difference between the detector sizes and the scanner radius. However, we suspect that this might be another cause of some of the discrepancies observed between the results obtained from the MultiDots phantom and those from the HotSpots phantom. Both of these sources of blur can be modeled in the system matrix and they are not fundamental limitations of the PET spatial resolution.

CASToR, the tool used to reconstruct the 3D simulation, approximates the system matrix on-the-fly [19], resulting in a trade-off between the quality of the approximation and computation time. For this study, the multiSiddon projector with 100 random samples was chosen, giving at best one sample per 0.4 × 0.4 mm² on the 4 × 4 mm² face of the detectors. This sampling might be good enough for the 0.4 mm isotropic voxels of the image. Nevertheless, the obtained images, shown in Fig. 7, were already satisfactory. Further improvements could be achieved with more accurate system matrices, however at the cost of higher computational resources.

D. Considerations for practical application

The results of this study are based on fictive scanners with 13.3 to 53.3 ps CTR, which is not currently achievable in TOF-PET. However, such ultra-fast TOF might not be necessary to observe some gain in spatial resolution. Data in Fig. 4 indicate that coarser binning of the TOF information down to 8 bins along TORs, artificially mimicking a ∼100 ps precision, still improves the resolution beyond the instrumental resolution limit. While this might not be achievable from a PET scanner with corresponding CTR, it does indicate that there is some latitude in the requirements to achieve a spatial resolution beyond the instrumental spatial resolution.

With realistic detectors having up to 20 mm or more in length, TOF resolution will be limited by the bias induced by coincidences occurring at different DOIs [17] and off-center spatial resolution will be affected by parallax. From the results of the 2-mm Det. configuration shown in Fig. 6, we observe that an acquisition with 53.3 ps CTR (8-mm TOF) can provide a better spot resolvability than an acquisition with 13.3 ps CTR (2-mm TOF) and 10 times less statistics. As a crude estimate, this would be representative of L(Y)SO detectors 4 mm in length (∼8% coincidence efficiency) compared to detectors 20 mm in length (∼80% coincidence efficiency). In that situation, the configuration with 20 mm detectors and 53.3 ps CTR would be a better choice for spatial resolution. Despite the much simplified analysis, it does indicate that there is some leeway in the requirements to achieve a gain in spatial resolution with TOF. It is worth mentioning that recent advances in DOI measurements of TOF detectors are likely to make such TOF resolution achievable in the foreseeable future.

E. Spatial resolution limit with ultra-fast TOF

We hypothesize that ultra-fast TOF could mitigate the limitation, in terms of spatial resolution, induced by the discrete nature of the reconstruction problem. There are at least two consequences that would follow if the hypothesis holds true. First, any source of blur that is properly modeled in the reconstruction process would not represent a lower bound to the spatial resolution. Second, the critical factor that would affect the achieved spatial resolution would be statistics, if the reconstruction model accurately describes all the sources of blur. For the 2D configurations studied, the only source of blur simulated and modeled was the detector width, and the results obtained are in agreement with our hypothesis. While we expect the same conclusion with the other factors of (1), since these sources of blur can be modeled in the system matrix, it remains to be proven.

One could conjecture that the detector size and the TOF resolution share an equivalent and interchangeable role in limiting the achievable spatial resolution. In other words, the reconstructed spatial resolution would be lower bounded by the smaller of the two. However, the results of this study show that spatial resolution better than both the TOF resolution and instrumental resolution (half detector size here) can be achieved in the TOF reconstructed image. This observation represents an additional support to our hypothesis stating that ultra-fast TOF can mitigate the limitation of spatial resolution induced by the discrete nature of the reconstruction problem.

Discrete deconvolution of a signal affected by a continuous blur is limited by the discrepancies induced by the discretization. However, this limitation becomes irrelevant when these discrepancies are not perceptible for the application of interest. This is an important consideration of our hypothesis about ultra-fast TOF in PET reconstruction: its capability to mitigate the discrete nature of the sampling relative to the application.

The idea that TOF information could provide a gain in spatial resolution when used in the reconstruction model can be motivated from one of its properties already described in the literature. Indeed, it has been shown that TOF information induces data redundancy which makes the reconstruction problem more robust to data inconsistencies and improves contrast-to-noise ratio [24], [25]. This property of TOF supports the hypothesis that TOF can mitigate the discrete nature of the iterative reconstruction problem. After all, the size of the detectors restricts the density of the sampling scheme but TOF provides a supplementary sampling dimension along the TOR that induces data redundancy, and therefore, improves the sampling density.

This feature can also be motivated without TOF. In a separate study (not shown), we analyzed a TOF-less reconstruction of the 8-mm Det. geometry in which the scanner was translated nine times during the acquisition (combination of three translations in the x and y axes) and a resolution of 1.6 mm was achieved for a source at 5.0 mm from the center. This gain in TORs sampling, which was modeled in the system matrix, enables the reconstruction scheme to circumvent the limitation in sampling induced by the detectors width in classical acquisitions. Enhancing TORs sampling with TOF information provides a gain that is analog to this sampling scheme.

While the spatial resolution of the studied configurations was indeed shown to be better than the instrumental spatial resolution limit, we also observed that the detector width and the TOF resolution still influence the spatial resolution lower bound of these configurations. As discussed in Sec. IV-C, we expect that 3D configurations will mitigate their influence on the spatial resolution limit since it provides a better angular sampling of the pixels.

This simulation study showed the potential of ultra-fast TOF to provide a gain in spatial resolution. Further investigation will be required to confirm that it can be achieved with a real ultra-fast TOF-PET clinical scanner. The requirements in terms of statistics, TOF discretization and TOF resolution are bound to vary depending on the application. An important reminder, however, is that achieving the full potential is not essential: even a partial gain could be a highly rewarding feature.

V. Conclusion

The gain in spatial resolution provided by ultra-fast TOF was studied for 2D clinical size PET scanners. The lower bound on spatial resolution of these scanners was shown to be significantly better than their respective conventional limit derived from their detector width. These gains were validated qualitatively from reconstructions of a Hot Spot phantom. A human brain phantom reconstructed with a fictive 3D scanner having ultra-fast TOF resolution also demonstrated the potential brought by TOF to resolve features below the conventional resolution limit. These results show that ultra-fast TOF mitigates the lower bound in spatial resolution induced by the discrete nature of PET reconstruction sampling scheme. We expect this to hold for all sources of spatial blur if they are modeled in the reconstruction process, which would imply that spatial resolution would be mostly limited by statistics. A potential benefit of this feature of ultra-fast TOF would be to enable clinical PET scanners to reach spatial resolution beyond the current state-of-the-art.