Abstract
Strong gradient systems can improve the signal-to-noise ratio of diffusion MRI measurements and enable a wider range of acquisition parameters that are beneficial for microstructural imaging. We present a comprehensive diffusion MRI dataset of 26 healthy participants acquired on the MGH-USC 3 T Connectome scanner equipped with 300 mT/m maximum gradient strength and a custom-built 64-channel head coil. For each participant, the one-hour long acquisition systematically sampled the accessible diffusion measurement space, including two diffusion times (19 and 49 ms), eight gradient strengths linearly spaced between 30 mT/m and 290 mT/m for each diffusion time, and 32 or 64 uniformly distributed directions. The diffusion MRI data were preprocessed to correct for gradient nonlinearity, eddy currents, and susceptibility induced distortions. In addition, scan/rescan data from a subset of seven individuals were also acquired and provided. The MGH Connectome Diffusion Microstructure Dataset (CDMD) may serve as a test bed for the development of new data analysis methods, such as fiber orientation estimation, tractography and microstructural modelling.
Subject terms: Brain imaging, Cognitive ageing, Magnetic resonance imaging
| Measurement(s) | brain measurement |
| Technology Type(s) | diffusion magnetic resonance imaging |
| Factor Type(s) | diffusion time • gradient strength • direction |
| Sample Characteristic - Organism | Homo sapiens |
Machine-accessible metadata file describing the reported data: 10.6084/m9.figshare.16910290
Background & Summary
Diffusion magnetic resonance imaging (MRI) offers a unique and valuable tool for mapping brain tissue microstructure and structural connectivity noninvasively in the living human brain. Diffusion MRI benefits from strong gradient systems that achieve more efficient diffusion-encoding1–3, resulting in decreased echo time and higher signal-to-noise ratio (SNR), and also enabling a larger diffusion measurement space to be probed in vivo. As part of the Human Connectome Project (HCP), the MGH-USC Consortium engineered the first 3 T whole-body Connectome MRI scanner equipped with 300 mT/m maximum gradient system – the strongest gradients ever built for a human MRI scanner1,2. Such high gradient strengths have benefited diffusion tractography by enhancing the resolution of complex fiber configurations for improved reconstruction of white matter fiber pathways4–9. An important by-product of such dedicated high gradient systems is the unparalleled assessment of brain tissue microstructure in vivo through sensitizing the diffusion MRI signal to water diffusion within highly restricted compartments, thereby enabling the mapping of microstructural properties such as axon diameter, density and g-ratio7,10–22. In recognition of the importance of high gradient strengths for in vivo tissue microstructural mapping, an ultra-strong gradient human MRI scanner with even higher maximum amplitude of 500 mT/m is currently being developed as part of the NIH BRAIN Initiative-funded Connectome 2.0 Project23,24.
Despite the advantages of strong gradient systems for human imaging, data acquisition on such systems requires specialized expertise and resources, rendering the data less accessible. Currently, only four Connectome MRI scanners have been installed worldwide1–3. As part of the efforts of the HCP, we previously released the MGH–USC Adult Diffusion Dataset from 35 healthy adult participants8, which consisted of four b-values up to 10,000 s/mm2 acquired at a single diffusion time with relatively dense angular sampling that was mainly designed for mapping the human structural connectome25–30. In this work, we leverage the high gradient strengths and wide range of diffusion times accessible on the Connectome scanner to acquire the MGH Connectome Diffusion Microstructure Dataset (CDMD) consisting of data from 26 healthy adult participants, which samples a wider range of b-values up to ~18,000 s/mm2 and multiple diffusion times. This comprehensive dataset will benefit the development of new analytic frameworks and models for mapping human brain tissue microstructure, as well as serving as a normative high-gradient strength dataset for exploring changes in brain tissue microstructure and structural connectivity across the lifespan.
The acquisition protocol was designed to sample the available diffusion measurement space. Specifically, the hour-long acquisition included two diffusion times (19 and 49 ms), eight shells corresponding to gradient strengths linearly spaced between 30 mT/m and 290 mT/m per diffusion time, and maximum b-value of 17,800 s/mm2. The acquisition used a custom-built 64-channel phased-array head coil to boost image SNR31, cutting-edge in-plane acceleration incorporating a Fast Low angle Excitation Echo Train to suppress parallel imaging artifacts due to breathing and head motion during the auto-calibration signal acquisition32, simultaneous multi-slice (SMS) for accelerated whole-brain coverage33–37, and an expert diffusion-weighted pulse sequence enabling independent control of different sequence parameters, and reconstruction of magnitude and phase images. Moreover, scan/rescan data in a subset of seven healthy individuals were acquired to assess the variability in diffusion MRI estimates extracted from this protocol38.
Portions of the dataset have been used to develop new methods for mapping axon diameter and density17,19,38 and to investigate alterations in axonal microstructure in multiple sclerosis10,39 and the aging brain12, as well as explore the diffusion time dependence of estimated microstructural metrics and fiber orientations24,40. This high-quality dataset may be used as a test bed for the development of new fiber orientation estimation, tractography and microstructural modelling methods, including methods for probing gray matter microstructure such as soma and neurite density imaging (SANDI)41 that may benefit from data acquired with high gradient strengths, which are often developed and initially tested in small animals on preclinical scanners. The MGH CDMD thus provides an important opportunity for the translation of such methods to human imaging. The two diffusion times sampled in the acquired diffusion dataset may be employed to explore diffusion time dependence in different tissues42–46 and the effects of inter-compartmental water exchange in gray matter47–49. Finally, atlases of microstructural metrics derived from high-gradient diffusion MRI can be created using the group data.
Methods
Participants
The institutional review board of Mass General Brigham approved the study protocol and ensured that all relevant ethical regulations were complied with. Written informed consent was obtained from all participants. Data were acquired in 26 healthy, cognitively normal adults (22 to 72 years old, 36.8 ± 14.6 years old, 17 females and 9 males). Seven out of 26 participants (22 to 72 years old, 37.1 ± 18.4 years old, 4 females) were scanned twice in the same day. For the scan/rescan experiments, participants were removed from the scanner after the first scan session and were given a rest period of approximately one hour38. They were then repositioned within the scanner for the second scan session.
Data acquisition
All data were acquired on the 3 T Connectome MRI scanner (Magnetom CONNECTOM, Siemens Healthineers) equipped with a maximum gradient strength of 300 mT/m and maximum slew rate of 200 mT/m/ms. The slew rate was de-rated to a maximum of 62.5 mT/m/ms during diffusion encoding to prevent peripheral nerve stimulation. A custom-built 64-channel phased array head coil31 was used for signal reception.
Diffusion MRI data were acquired using a two-dimensional single-refocused diffusion-weighed pulsed-gradient spin-echo echo planar imaging (EPI) sequence50,51 with anterior-to- posterior phase-encoding direction. For each participant, 66–70 contiguous sagittal slices were acquired with the center slice placed along the midline corpus callosum to achieve symmetric whole brain coverage. The imaging parameters are as follows: repetition time (TR) = 3800 ms, echo time (TE) = 77 ms, field of view (FOV) = 216 × 216 mm, matrix size = 108 × 108, slice thickness = 2 mm, voxel size = 2 × 2 × 2 mm3, diffusion time (Δ) = 19 or 49 ms, diffusion-encoding gradient duration (δ) = 8 ms, eight diffusion-encoding gradient strengths evenly spaced between 30 and 290 mT/m (i.e., 31, 68, 105, 142, 179, 216, 253, 290 mT/m) for each diffusion time corresponding to 16 different b-values (i.e., 50, 350, 800, 1500, 2400, 3450, 4750, and 6000 s/mm2 for Δ = 19 ms; 200, 950, 2300, 4250, 6750, 9850, 13,500, 17,800 s/mm2 for Δ = 49 ms), 32 diffusion encoding directions uniformly distributed on a sphere for b < 2400 s/mm2 and 64 uniform directions for b ≥ 2400 s/mm2 respectively, one interspersed b = 0 image volume for every 16 diffusion-weighted images (DWIs) (i.e., 50 b = 0 images and 800 DWIs in total), parallel imaging using generalized autocalibrating partially parallel acquisitions (GRAPPA)32,52 with an acceleration factor R = 2, simultaneous multislice33,35–37 (SMS) acceleration factor = 2, partial Fourier factor = 7/8, bandwidth = 2315 Hz/pixel. The choice of δ = 8 ms was based on limitations to the accessible rise time imposed by the scanner hardware and the need for sufficiently long delta to achieve high b-values > 10,000 s/mm2. The 32 and 64 diffusion-encoding directions were identical for each diffusion time and each gradient strength. Five b = 0 image volumes with reversed phase-encoding direction (posterior-to-anterior) were also acquired to correct for susceptibility-induced image distortions. The acquisition time for the entire diffusion MRI protocol was 55 minutes.
In 14 participants (a total of 21 scan or rescan sessions), an adapted version of the same diffusion MRI sequence was used for acquisition to enable the export of the phase images in addition to the magnitude images. Real-valued diffusion data were derived by removing the nuisance background phase (reflecting contributions from physiological noise, motion, and instrumental imperfections such as inhomogeneity in the B1-transmit field) from the raw complex image data and then taking the real part following previous studies19,53–55.
T1-weighted structural MRI data were acquired using a 3-dimensional multi-echo magnetization-prepared gradient echo (MEMPRAGE) sequence56 with whole-brain coverage. The imaging parameters are as follows: TR = 2530 ms, TE = 1.15, 3.03, 4.89, 6.75 ms, inversion time (TI) = 1100 ms, flip angle = 7°, 176 contiguous sagittal images, FOV = 220 × 220 mm, matrix size = 220 × 220 mm, 1 mm isotropic resolution, GRAPPA R = 3, bandwidth = 650 Hz/pixel, acquisition time = 4 minutes.
Data processing
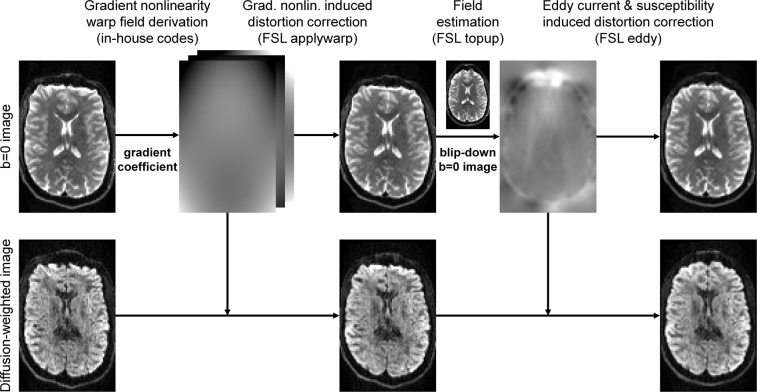
The diffusion data processing pipeline is outlined in Fig. 1. The diffusion data were first corrected for gradient nonlinearity-induced image distortions using in-house Matlab codes8 and the proprietary gradient coefficients provided by Siemens. The corrected images were computed using the derived warp fields and the “applywarp” function from the FMRIB Software Library (FSL)57 with the cubic spline interpolation.
Fig. 1.
Diffusion data processing pipeline. Diffusion data were corrected for gradient nonlinearity, susceptibility and eddy current induced image distortions and co-registered.
The diffusion data were then corrected for susceptibility and eddy current-induced image distortions and co-registered using the TOPUP58 and EDDY59,60 functions (i.e., the GPU version “eddy_cuda9.1”) from FSL (version v6.0.4). The TOPUP function was performed with default parameters and the pre-defined configuration file “b02b0.cnf” provided by FSL. The pre-defined configuration file was slightly modified to adjust the spatial resolution of the warp field for the last two iterations from 4 mm isotropic to 2 mm isotropic, the native spatial resolution of the diffusion MRI data. Specifically, the line “--warpres = 20,16,14,12,10,6,4,4,4” in the “b02b0.cnf” file was modified to “--warpres = 20,16,14,12,10,6,4,2,2”. The EDDY function was performed with dynamic susceptibility correction61, slice-to-volume motion correction62 and default parameters except for the cubic eddy current model, eight iterations, and considering both positive and negative outliers (i.e., “--ol_pos option” option). Since the EDDY function treats data as separate shells only when their b-values differ by more than 100 s/mm2, the acquired b-values of 50, 200 and 2400 s/mm2 were slightly modified to 101, 202 and 2401 s/mm2 respectively to enforce differentiation between shells with b-values of 0, 101 and 2300 s/mm2, such that the data from each acquired shell could be separately modelled and corrected for eddy current effects. The modified b-values were only used for the purpose of utilizing the EDDY function properly in the step of data pre-processing and the b-values released in the data sharing repository are true to the acquisition. The brain mask used for the EDDY function was obtained by binarizing the sum of all brain masks created from each interspersed b = 0 image volume using FSL’s “bet2”63 function with the fractional intensity threshold set to 0.1. The modified diffusion-encoding directions from EDDY (i.e., provided by the “my_eddy_output.rotated_bvecs” output file) were used to account for the head motion of participants, resulting in slightly varying diffusion-encoding directions for each participant.
For the slice-to-volume motion correction in the EDDY function, the “--mporder” was set to the number of excitations in a volume (i.e., number of image slices in a volume over 2 due to the SMS acceleration factor equal to 2) over 2 and the “--s2v_lambda” was set to 1. The EDDY function was designed to be more sensitive to outliers at lower b-values (i.e., 50, 200, 350 s/mm2 in this work) and was sometimes too sensitive to find any image volumes without outlier slices as the shape reference volume for the slice-to-volume motion correction. To circumvent algorithm abortions, the image volumes at b-values of 50, 200, 350 s/mm2 were first replaced with outlier-free image volumes generated by a “pre-run” of EDDY correction, where EDDY function was performed in the same way as described earlier, but with the “–repol” option and without slice-to-volume correction.
The T1-weighted data were first corrected for the gradient nonlinearity induced image distortion in the same way as was performed for the diffusion data. For de-identification, facial features were obscured in each image volume64. Spatially varying intensity biases were then corrected using the unified segmentation routine65 implementation in the Statistical Parametric Mapping software (SPM) with a full-width at half-maximum of 30 mm and a sampling distance of 2 mm66. Finally, cerebral cortical surface reconstruction and volumetric segmentation were performed using the “recon-all” function of the FreeSurfer software67–69 (stable version v6.0.0). The volumetric segmentation results (i.e., aparc + aseg.mgz) were resampled to the diffusion image space using the affine transformation derived using the boundary-based registration70 implemented in FreeSurfer’s “bbregister” function and the averaged b = 0 image with the nearest neighbor interpolation.
Diffusion model fitting
As an initial demonstration of the variety of analyses that can be performed with this comprehensive dataset, several diffusion models were fitted for estimating fiber orientations and microstructural metrics. These models are widely adopted in clinical and neuroscientific studies with publicly available software and open-source codes. Many other models such as diffusion basis spectrum imaging (DBSI)71,72 and soma and neurite density imaging (SANDI)41 can be also fitted, potentially on data from different diffusion times to explore the diffusion time dependence. The dataset also provides a unique opportunity for advancing the integration of diffusion MRI-based microstructural imaging and tractography, e.g., microstructure-informed tractography25,73–75 or tractography-informed microstructural imaging76. Despite recent interest in multi-modal data acquisition, i.e., combining diffusion MRI data with other MRI contrasts such as relaxometry and myelin-sensitive imaging measures, the focus of the current dataset is on the strengths of high-gradient diffusion MRI for microstructural imaging and thus does not include data from other contrasts, which has been explored in other complementary studies14.
Specifically, fiber orientation estimation was performed using six different methods. Diffusion tensor imaging77,78 model fitting was performed using the “dtifit” function from FSL on the b = 800 and 1500 s/mm2 data from the Δ = 19 ms acquisition. The multi-shell multi-tissue constrained spherical deconvolution79–81 (MSMT-CSD) was performed using the “dwi2response” function with the “msmt_5tt” option and the “dwi2fod” function with the “msmt_csd” option from the MRtrix3 software on the b = 800, 1500, 2400, 3450 s/mm2 data from the Δ = 19 ms acquisition. The segmentation of five tissue types was performed on the T1-weighted data using MRtrix3’s “5ttgen” function with the “fsl” option. All and stick (three sticks) model82,83 was fitted using FSL’s “BEDPOSTX” function on the b = 800, 1500, 2400, 3450 s/mm2 data from the Δ = 19 ms acquisition. The constant solid angle q-ball imaging84 (CSA-QBI) and the generalized q-space imaging85 (GQI) reconstruction was performed using the “CsaOdfModel” and “GeneralizedQSamplingModel” models from the Diffusion Imaging In Python (DIPY) software86, respectively, on the b = 6000 s/mm2 data from the Δ = 19 ms acquisition. Generalized diffusion spectrum imaging27 (GDSI) reconstruction was performed on the b = 50, 350, 800, 1500, 2400, 3450, 4750, 6000 s/mm2 data from the Δ = 19 ms acquisition using in-house Matlab codes. Default parameters of fitting/reconstruction functions were employed for all models.
In addition to DTI, multi-shell data from Δ = 19 ms acquisition (b = 800, 1500, 2400, 3450 s/mm2) were used to derive the microstructural metrics pertaining to five exemplary diffusion models as described below. Diffusion kurtosis imaging87,88 (DKI) and white matter tract integrity89 (WMTI) imaging model fitting was performed using the “dki_fit” function from the DESIGNER software. DKI and WMTI metrics were then derived using DESIGNER’s “dki_parameters” and “wmti_parameters” functions, respectively. The neurite orientation dispersion and density imaging (NODDI)90 metrics were derived using the NODDI Matlab toolbox. Microscopic DTI91 (MicroDTI) and Multi-compartment microscopic diffusion imaging92 (MCMicro) metrics were derived using the “fitmicrodt” and “fitmcmicro” functions from the SMT software.
Data Records
The preprocessed diffusion MRI data and the T1-weighted MRI data of 26 healthy participants and the preprocessed rescan diffusion MRI data and the T1-weighted MRI data from seven of the 26 participants are publicly available through the figshare repository93. For participants sub_001 to sub _007, the rescan data are available (i.e., sub_001_rescan to sub _007_rescan). For participants sub_001 to sub_014, the real-valued diffusion data are available. The data of each participant are organized into a folder with 2 (participants with only magnitude-valued data) or 3 (participants with both magnitude-valued and real-valued data) folders as described below.
Folder 1: anat: T1-weighted MRI data corrected for gradient nonlinearity induced image distortion as well as a copy also corrected for spatially varying intensity bias. The estimated spatially varying intensity bias, brain mask, and volumetric segmentation results from FreeSurfer reconstruction (i.e., aparc + aseg.mgz) are also provided.
Folder 2: dwi: The pre-processed magnitude-valued diffusion MRI data along with the corresponding b-value and b-vector files. The brain mask, FreeSurfer volumetric segmentation results (i.e., aparc + aseg.mgz) resampled to the diffusion image space are also provided.
Folder 3: diff_real: The pre-processed real-valued diffusion MRI data, along with the corresponding b-value and b-vector files. The brain mask, FreeSurfer volumetric segmentation results (i.e., aparc + aseg.mgz) resampled to the diffusion image space are also provided.
In addition, the FreeSurfer reconstruction results and the image co-registration results (i.e., affine transformation matrices) between the diffusion and T1-weighted image space derived using boundary-based registration of each participant are provided in the “derivatives” folder.
Technical Validation
Assessment of diffusion data quality
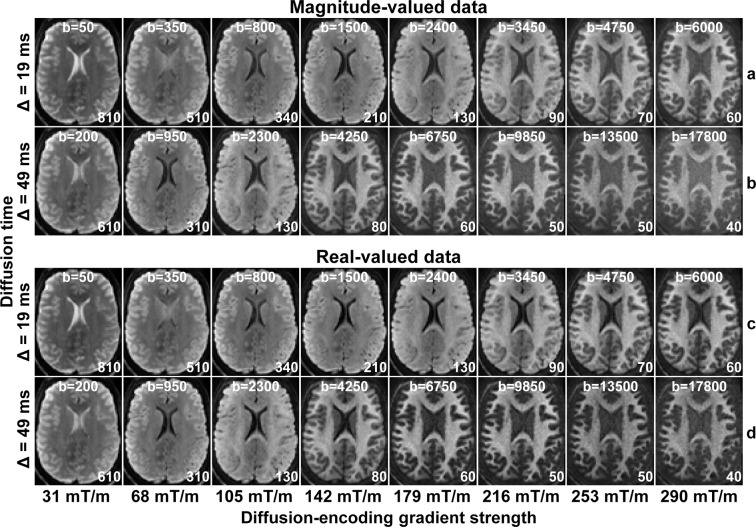
The magnitude-valued and real-valued spherical mean DWIs from each diffusion time and gradient strength of a representative participant are shown in Fig. 2. There were no significant ghosting or reconstruction artifacts by visual inspection. The image data for all participants were visually inspected for quality control. The difference between the magnitude-valued and real-valued spherical mean DWIs becomes visually discernible at b = 3450 s/mm2 and becomes increasingly prominent with increasing b-value. Specifically, the elevated Rician noise floor in the magnitude-valued data is removed in the real-valued data, which is characterized by a Gaussian noise distribution. The temporal signal-to-noise ratio (tSNR) quantified using the 50 interspersed b = 0 images, defined as the mean of time-series values over the standard deviation of time-series values at each voxel, was estimated in each participant and shown to be consistent across participants. The mean tSNR within the white matter was estimated to be 22.2 in a representative participant shown in Fig. 2. The group mean and group standard deviation of white matter-averaged tSNR was estimated to be 23.1 ± 2.46.
Fig. 2.
Spherical mean diffusion-weighted images. Spherical mean diffusion-weighted images for magnitude-valued (rows a, b) and real-valued (rows c, d) diffusion MRI data for each diffusion time (Δ) and diffusion-encoding gradient strength of a representative healthy participant. The images are windowed individually for improved visualization, between 0 and a higher image intensity listed at the bottom right of each sub-figure.
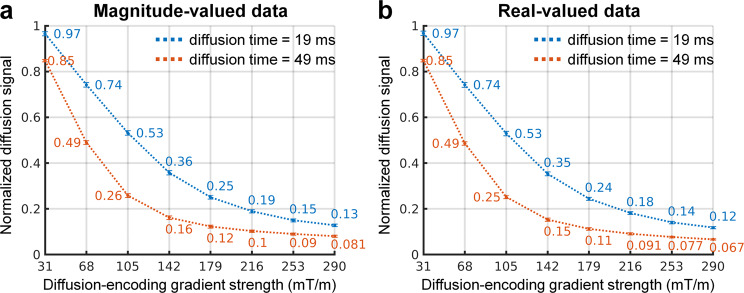
The group mean and group standard deviation of the white matter-averaged normalized diffusion signal for each diffusion time and gradient strength are shown in Fig. 3. The normalized diffusion signal smoothly decays with increasing diffusion-encoding gradient strength. The real-valued signal is slightly lower than the magnitude-valued signal, and the difference is greater for longer diffusion times and higher diffusion-encoding strengths.
Fig. 3.
Normalized diffusion signal attenuation. The group mean (numbers below and above curves) and group standard deviation of the white matter-averaged normalized diffusion signal for each diffusion time and diffusion-encoding gradient strength.
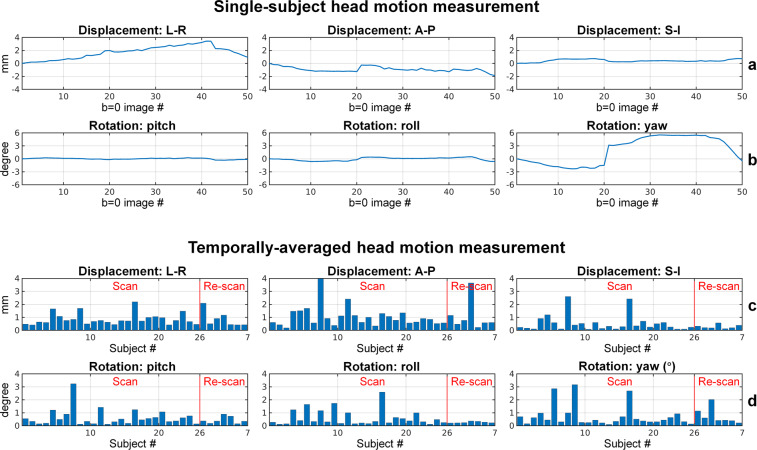
Assessment of participant head motion
Participant head motion during the scan was evaluated, as shown in Fig. 4. The motion parameters estimated by FSL’s EDDY function from the rigid-body co-registration between the interspersed b = 0 image volumes and the first b = 0 image volume include the translation along the left-right (L-R), anterior-posterior (A-P), superior and inferior (S-I) direction (Fig. 4, row a), as well as the rotation around the L-R axis (pitch), A-P axis (roll) and S-I axis (yaw) (Fig. 4, row b). The temporally averaged absolute values of the motion measurements, which reflect the overall participant motion during the approximately one-hour scan, were relatively low. For most participants, the mean absolute translations along the L-R and A-P direction were confined within 1 mm, and the translation along S-I direction was within 0.5 mm. The group mean and group standard deviation for the translations along L-R, A-P and S-I directions were 0.86 ± 0.47 mm, 1.06 ± 0.93 mm and 0.49 ± 0.58 mm, respectively. For most participants, the mean absolute rotations were within 1 degree. The group mean and group standard deviation for the rotations around the L-R, A-P and S-I axis were 0.59 ± 0.59 degree, 0.54 ± 0.56 degree and 0.74 ± 0.79 degree.
Fig. 4.
Participant head motion measurement. Head motion measurement estimated from the rigid-body co-registration between the 49 interspersed b = 0 image volumes and the first b = 0 image volume of a representative participant, quantified in the translation along the left-right (L-R), anterior-posterior (A-P), superior and inferior (S-I) direction (row a), as well as the rotation around the L-R axis (pitch), A-P axis (roll) and S-I axis (yaw) (row b). The temporally averaged absolute values of head motion parameters are used to reflect the overall head motion of each participant (rows c, d).
The small to moderate motion and image distortions were successfully corrected by the pre-processing pipeline, quantified by the image correlation between the interspersed b = 0 image volumes and the first b = 0 image volume. For all participants, the image correlation between any b = 0 image volume and the first b = 0 image volume was higher than 0.95. The group mean and group standard deviation of the temporally averaged b = 0 image correlation was 0.84 ± 0.11 and 0.99 ± 0.0051 before and after the pre-processing.
Assessment of diffusion modelling outcomes
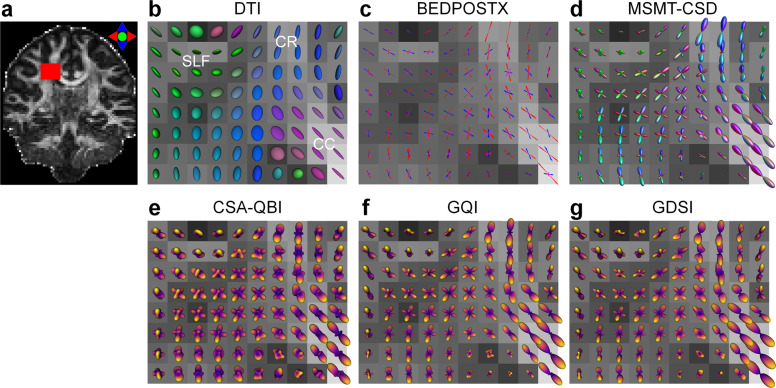
The quality of the diffusion MRI data is also assessed by evaluating the diffusion modelling outcomes using different methods. In terms of fiber orientation estimation, Fig. 5 shows the fiber orientation distributions within the right centrum semiovale of a representative participant estimated using six methods, including DTI, MSMT-CSD, BEDPOSTX, CSA-QBI, GQI and GDSI. These methods have different data requirements for the estimation, which are all satisfied by this comprehensive dataset. Except for DTI, which can only recover a single orientation, all other methods successfully recovered the fiber crossing at the intersecting region of three major fiber bundles: the corpus callosum, the corona radiata, and the superior longitudinal fasciculus. The mapped crossing fiber orientations from different methods were visually similar.
Fig. 5.
Fiber orientation estimation results. The diffusion tensor derived using the diffusion tensor imaging (DTI) (b), fiber orientation samples estimated from the BEDPOSTX method (10 randomly selected samples, stick length proportional to the fiber volume fraction) (c), and the orientation distribution functions (ODFs) reconstructed using the multi-shell multi-tissue constrained spherical deconvolution (MSMT-CSD) (d), the constant solid angle q-ball imaging (CSA-QBI) (e), the generalized q-space imaging (GQI) (f), and the generalized diffusion spectrum imaging (GDSI) (g) in the right centrum semiovale region (red rectangle in a) of a representative participant. The centrum semiovale region contains intersection of the corpus callosum (CC), the corona radiata (CR), and the superior longitudinal fasciculus (SLF). The diffusion tensors and MSMT-CSD ODFs are color coded based on orientation (red: left-right, green: anterior-posterior, blue: superior-inferior). The red, blue and magenta vectors from BEDPOSTX represent the primary, secondary and tertiary diffusion orientations, respectively. All reconstruction results are displayed on top of the DTI fraction anisotropy map (windowed between 0 and 1).
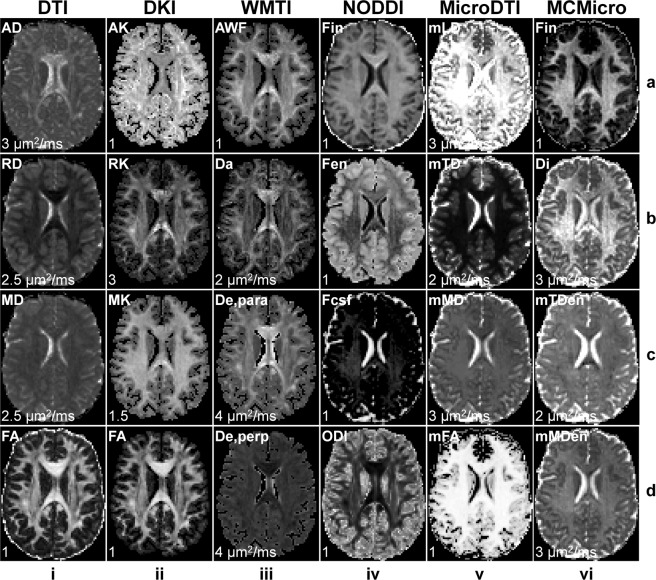
Figure 6 shows maps of different microstructural metrics derived from six distinct diffusion modelling methods, including DTI, DKI, WMTI, NODDI, MicroDTI, and MCMicro. Specifically, maps of axial diffusivity (AD), radial diffusivity (RD), mean diffusivity (MD) and fractional anisotropy (FA) are displayed for DTI. Maps of axial kurtosis (AK), radial kurtosis (RK), mean kurtosis (MK), and FA from the tensor component are displayed for DKI. Maps of axonal water fraction (AWF), intra-axonal diffusivity (Da), axial extra-axonal diffusivity (De, para), and radial extra-axonal diffusivity (De, perp) are displayed for WMTI imaging. Maps of intra-neurite volume fraction (Fin), extra-neurite volume fraction (Fen), cerebrospinal fluid volume fraction (Fcsf), and orientation dispersion index (ODI) are displayed for NODDI. Maps of microscopic longitudinal diffusivity (mLD), microscopic transverse diffusivity (mTD), microscopic mean diffusivity (mMD), and microscopic FA (mFA) are displayed for MicroDTI. Maps of intra-neurite volume fraction (Fin), intrinsic diffusivity (Di), microscopic extra-neurite transverse diffusivity (mTDen), microscopic extra-neurite mean diffusivity (mMDen) are displayed for MCMicro imaging. These metrics are consistent with the expected results of respective models.
Fig. 6.
Microstructural modelling results. Maps of metrics estimated using various microstructural models of a representative participant. For diffusion tensor imaging (DTI) (column i), maps of axial diffusivity (AD), radial diffusivity (RD), mean diffusivity (MD) and fractional anisotropy (FA) are displayed. For diffusion kurtosis imaging (DKI), maps of axial kurtosis (AK), radial kurtosis (RK), mean kurtosis (MK), and FA from the tensor component are displayed. For white matter tract integrity (WMTI) imaging (column iii), maps of axonal water fraction (AWF), intra-axonal diffusivity (Da), axial extra-axonal diffusivity (De, para), and radial extra-axonal diffusivity (De, perp) are displayed. For neurite orientation dispersion and density imaging (NODDI) (column iv), maps of intra-neurite volume fraction (Fin), extra-neurite volume fraction (Fen), cerebrospinal fluid volume fraction (Fcsf), and orientation dispersion index (ODI) are displayed. For microscopic diffusion tensor imaging (MicroDTI) (column v), maps of microscopic longitudinal diffusivity (mLD), microscopic transverse diffusivity (mTD), microscopic mean diffusivity (mMD), and microscopic FA (mFA) are displayed. For multi-compartment microscopic diffusion (MCMicro) imaging (column vi), maps of intra-neurite volume fraction (Fin), intrinsic diffusivity (Di), microscopic extra-neurite transverse diffusivity (mTDen), microscopic extra-neurite mean diffusivity (mMDen) are displayed. The maps are windowed individually for improved visualization, between 0 and a higher intensity listed at the bottom left of each sub-figure.
Acknowledgements
This work was supported by the NIH Grants P41-EB015896, P41-EB030006, U01-MH093765, U01-EB026996, R01-NS118187, R01-EB006847, R00-EB015445, K23-NS096056, K23-NS078044, K99-AG073506, S10-RR023401, S10-RR023043, and S10-RR019307. Funding support was also received from the National Multiple Sclerosis Society, the American Heart Association Postdoctoral Fellowship Award (17POST33670452) and the MGH Claflin Distinguished Scholar Award.
Author contributions
Q.T. contributed to the conception of the study, processed and analyzed the data, and wrote the manuscript. Q.F. contributed to the conception of the study, acquired, processed and analyzed the data, and wrote the manuscript. T.W. provided imaging sequences and maintained the scanner and hardware. M.N.P. and N.A.O. recruited participants and acquired the data. C.N., A.W.R., N.M., and K.B. acquired the data. F.W. contributed to participant motion characterization. K.S. contributed to the real diffusion data derivation. J.R.P. contributed to gradient nonlinearity correction. B.K. provided the 64-channel head coil. L.L.W. and B.R.R. contributed to the conception of the study. E.C.K. contributed to the conception of the study and supervised the data acquisition. A.N. contributed to the conception of the study and designed the data acquisition protocol. S.Y.H. contributed to the conception of the study, designed the data acquisition protocol, supervised the data acquisition and processing, and wrote the manuscript.
Code availability
The Matlab codes for gradient nonlinearity correction have been modified into Python codes, which are publicly available (https://github.com/ksubramz/gradunwarp). The FMRIB Software Library used in the diffusion data pre-processing and DTI and BEDPOSTX model fitting is publicly available (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FslInstallation). The FreeSurfer software is publicly available (https://surfer.nmr.mgh.harvard.edu/fswiki/DownloadAndInstall). The software used for face masking is publicly available (https://nrg.wustl.edu/software/face-masking). The SPM software for image intensity bias correction is publicly available (https://www.fil.ion.ucl.ac.uk/spm). The MRtrix3 software for the constrained spherical deconvolution is publicly available (https://www.mrtrix.org). The DIPY software used for the CSA-QBI and GQI reconstruction is publicly available (https://www.dipy.org). The codes for the GDSI reconstruction are publicly available (https://github.com/qiyuantian/GDSI). The DESIGNER software for the DKI and WMTI model fitting is publicly available (https://github.com/NYU-DiffusionMRI/DESIGNER). The NODDI Matlab toolbox is publicly available (http://mig.cs.ucl.ac.uk/index.php?n=Tutorial.NODDImatlab). The SMT software for the MicroDTI and MCMicro model fitting are publicly available (https://github.com/ekaden/smt).
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Setsompop K, et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. NeuroImage. 2013;80:220–233. doi: 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.McNab JA, et al. The Human Connectome Project and beyond: initial applications of 300 mT/m gradients. NeuroImage. 2013;80:234–245. doi: 10.1016/j.neuroimage.2013.05.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jones DK, et al. Microstructural imaging of the human brain with a ‘super-scanner’: 10 key advantages of ultra-strong gradients for diffusion MRI. NeuroImage. 2018;182:8–38. doi: 10.1016/j.neuroimage.2018.05.047. [DOI] [PubMed] [Google Scholar]
- 4.Wedeen VJ, et al. The geometric structure of the brain fiber pathways. Science. 2012;335:1628–1634. doi: 10.1126/science.1215280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fan Q, et al. Investigating the capability to resolve complex white matter structures with high b-value diffusion magnetic resonance imaging on the MGH-USC connectom scanner. Brain connectivity. 2014;4:718–726. doi: 10.1089/brain.2014.0305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tian Q, et al. Q-space truncation and sampling in diffusion spectrum imaging. Magnetic Resonance in Medicine. 2016;76:1750–1763. doi: 10.1002/mrm.26071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fan Q, et al. HIgh b-value and high Resolution Integrated Diffusion (HIBRID) imaging. NeuroImage. 2017;150:162–176. doi: 10.1016/j.neuroimage.2017.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fan Q, et al. MGH–USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. NeuroImage. 2016;124:1108–1114. doi: 10.1016/j.neuroimage.2015.08.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Movahedian Attar F, et al. Mapping short association fibers in the early cortical visual processing stream using in vivo diffusion tractography. Cerebral Cortex. 2020;30:4496–4514. doi: 10.1093/cercor/bhaa049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huang SY, et al. Corpus callosum axon diameter relates to cognitive impairment in multiple sclerosis. Annals of clinical and translational neurology. 2019;6:882–892. doi: 10.1002/acn3.760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang SY, et al. Characterization of axonal disease in patients with multiple sclerosis using high-gradient-diffusion MR imaging. Radiology. 2016;280:244–251. doi: 10.1148/radiol.2016151582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fan Q, et al. Age-related alterations in axonal microstructure in the corpus callosum measured by high-gradient diffusion MRI. NeuroImage. 2019;191:325–336. doi: 10.1016/j.neuroimage.2019.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Veraart J, et al. Noninvasive quantification of axon radii using diffusion MRI. Elife. 2020;9:e49855. doi: 10.7554/eLife.49855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yu F, et al. Imaging G-Ratio in Multiple Sclerosis Using High-Gradient Diffusion MRI and Macromolecular Tissue Volume. American Journal of Neuroradiology. 2019;40:1871–1877. doi: 10.3174/ajnr.A6283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Duval T, et al. g-Ratio weighted imaging of the human spinal cord in vivo. NeuroImage. 2017;145:11–23. doi: 10.1016/j.neuroimage.2016.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Duval T, et al. In vivo mapping of human spinal cord microstructure at 300 mT/m. NeuroImage. 2015;118:494–507. doi: 10.1016/j.neuroimage.2015.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huang SY, et al. High-gradient diffusion MRI reveals distinct estimates of axon diameter index within different white matter tracts in the in vivo human brain. Brain Structure and Function. 2020;225:1277–1291. doi: 10.1007/s00429-019-01961-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huang SY, et al. The impact of gradient strength on in vivo diffusion MRI estimates of axon diameter. NeuroImage. 2015;106:464–472. doi: 10.1016/j.neuroimage.2014.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fan, Q. et al. Axon Diameter Index Estimation Independent of Fiber Orientation Distribution Using High-Gradient Diffusion MRI. NeuroImage, 117197 (2020). [DOI] [PMC free article] [PubMed]
- 20.Fan Q, et al. Validation of diffusion MRI estimates of compartment size and volume fraction in a biomimetic brain phantom using a human MRI scanner with 300 mT/m maximum gradient strength. NeuroImage. 2018;182:469–478. doi: 10.1016/j.neuroimage.2018.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dell’Acqua, F. et al. Temporal Diffusion Ratio (TDR): A Diffusion MRI Technique to Map the Fraction and Spatial Distribution of Large Axons in the Living Human Brain. In Proceedings of the 27th Annual Meeting of the International Society for Magnetic Resonance in Medicine, 0064 (2019).
- 22.Tax CM, Szczepankiewicz F, Nilsson M, Jones DK. The dot-compartment revealed? Diffusion MRI with ultra-strong gradients and spherical tensor encoding in the living human brain. NeuroImage. 2020;210:116534. doi: 10.1016/j.neuroimage.2020.116534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yendiki, A., Witzel, T. & Huang, S. Y. Connectome 2.0: Cutting-Edge Hardware Ushers in New Opportunities for Computational Diffusion MRI. InProceedings of the Medical Image Computing and Computer Assisted Intervention Society Workshop on Computational Diffusion MRI, 3–12 (2020).
- 24.Huang, S. Y. et al. Connectome 2.0: Developing the next-generation ultra-high gradient strength human MRI scanner for bridging studies of the micro-, meso-and macro-connectome. NeuroImage, 118530 (2021). [DOI] [PMC free article] [PubMed]
- 25.Girard G, et al. AxTract: Toward microstructure informed tractography. Human Brain Mapping. 2017;38:5485–5500. doi: 10.1002/hbm.23741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Siless V, Chang K, Fischl B, Yendiki A. AnatomiCuts: Hierarchical clustering of tractography streamlines based on anatomical similarity. NeuroImage. 2018;166:32–45. doi: 10.1016/j.neuroimage.2017.10.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tian Q, et al. Generalized diffusion spectrum magnetic resonance imaging (GDSI) for model-free reconstruction of the ensemble average propagator. NeuroImage. 2019;189:497–515. doi: 10.1016/j.neuroimage.2019.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Farooq H, Chen Y, Georgiou TT, Tannenbaum A, Lenglet C. Network curvature as a hallmark of brain structural connectivity. Nature communications. 2019;10:1–11. doi: 10.1038/s41467-019-12915-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Maffei C, Sarubbo S, Jovicich J. Diffusion-based tractography atlas of the human acoustic radiation. Scientific reports. 2019;9:1–13. doi: 10.1038/s41598-019-40666-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tristán-Vega A, Aja-Fernández S. Efficient and accurate EAP imaging from multi-shell dMRI with micro-structure adaptive convolution kernels and dual Fourier Integral Transforms (MiSFIT) NeuroImage. 2020;227:117616. doi: 10.1016/j.neuroimage.2020.117616. [DOI] [PubMed] [Google Scholar]
- 31.Keil B, et al. A 64-channel 3T array coil for accelerated brain MRI. Magnetic Resonance in Medicine. 2013;70:248–258. doi: 10.1002/mrm.24427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Polimeni JR, et al. Reducing sensitivity losses due to respiration and motion in accelerated echo planar imaging by reordering the autocalibration data acquisition. Magnetic resonance in medicine. 2016;75:665–679. doi: 10.1002/mrm.25628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Setsompop K, et al. Blipped‐controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g‐factor penalty. Magnetic Resonance in Medicine. 2012;67:1210–1224. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Larkman DJ, et al. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. Journal of Magnetic Resonance Imaging. 2001;13:313–317. doi: 10.1002/1522-2586(200102)13:2<313::aid-jmri1045>3.0.co;2-w. [DOI] [PubMed] [Google Scholar]
- 35.Feinberg DA, Setsompop K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. Journal of magnetic resonance. 2013;229:90–100. doi: 10.1016/j.jmr.2013.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Feinberg DA, et al. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PLoS One. 2010;5:e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Setsompop K, et al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. NeuroImage. 2012;63:569–580. doi: 10.1016/j.neuroimage.2012.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fan Q, et al. Scan-rescan repeatability of axonal imaging metrics using high-gradient diffusion MRI and statistical implications for study design. NeuroImage. 2021;240:118323. doi: 10.1016/j.neuroimage.2021.118323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ngamsombat C, et al. Axonal Damage in the Optic Radiation Assessed by White Matter Tract Integrity Metrics is Associated with Retinal Thinning in Multiple Sclerosis. NeuroImage: Clinical. 2020;27:102293. doi: 10.1016/j.nicl.2020.102293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Avram, A. V., Tian, Q., Fan, Q., Huang, S. Y. & Basser, P. J. The diffusion time dependence of MAP-MRI parameters in the human brain. In Proceedings of the 29th Annual Meeting of the International Society for Magnetic Resonance in Medicine, 2465 (2021).
- 41.Palombo M, et al. SANDI: a compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. NeuroImage. 2020;215:116835. doi: 10.1016/j.neuroimage.2020.116835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Burcaw LM, Fieremans E, Novikov DS. Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage. 2015;114:18–37. doi: 10.1016/j.neuroimage.2015.03.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fieremans E, et al. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. NeuroImage. 2016;129:414–427. doi: 10.1016/j.neuroimage.2016.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lee H-H, Fieremans E, Novikov DS. What dominates the time dependence of diffusion transverse to axons: Intra-or extra-axonal water? NeuroImage. 2018;182:500–510. doi: 10.1016/j.neuroimage.2017.12.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lee H-H, Papaioannou A, Kim S-L, Novikov DS, Fieremans E. A time-dependent diffusion MRI signature of axon caliber variations and beading. Communications biology. 2020;3:1–13. doi: 10.1038/s42003-020-1050-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Harkins KD, Beaulieu C, Xu J, Gore JC, Does MD. A simple estimate of axon size with diffusion MRI. NeuroImage. 2021;227:117619. doi: 10.1016/j.neuroimage.2020.117619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jelescu, I. O., de Skowronski, A., Palombo, M. & Novikov, D. S. Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange. Preprint at https://arxiv.org/abs/2108.06121 (2021). [DOI] [PMC free article] [PubMed]
- 48.Olesen, J. L., Østergaard, L., Shemesh, N. & Jespersen, S. N. Diffusion time dependence, power-law scaling, and exchange in gray matter. Preprint at https://arxiv.org/abs/2108.09983 (2021). [DOI] [PMC free article] [PubMed]
- 49.Jelescu, I. O. & Novikov, D. S. Water exchange time between gray matter compartments in vivo. In Proceedings of the 29th Annual Meeting of the International Society for Magnetic Resonance in Medicine, 0715 (2020).
- 50.Tanner JE, Stejskal EO. Restricted self‐diffusion of protons in colloidal systems by the pulsed‐gradient, spin‐echo method. The Journal of Chemical Physics. 1968;49:1768–1777. [Google Scholar]
- 51.Stejskal E, Tanner J. Spin diffusion measurements: spin echoes in the presence of a time‐dependent field gradient. The journal of chemical physics. 1965;42:288–292. [Google Scholar]
- 52.Griswold MA, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magnetic Resonance in Medicine. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 53.Eichner C, et al. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. NeuroImage. 2015;122:373–384. doi: 10.1016/j.neuroimage.2015.07.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Setsompop K, et al. High‐resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (g S lider‐SMS) Magnetic resonance in medicine. 2018;79:141–151. doi: 10.1002/mrm.26653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wang F, et al. Motion‐robust sub‐millimeter isotropic diffusion imaging through motion corrected generalized slice dithered enhanced resolution (MC‐gSlider) acquisition. Magnetic resonance in medicine. 2018;80:1891–1906. doi: 10.1002/mrm.27196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.van der Kouwe AJ, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. NeuroImage. 2008;40:559–569. doi: 10.1016/j.neuroimage.2007.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. FSL. NeuroImage. 2012;62:782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- 58.Andersson JL, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20:870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- 59.Andersson JL, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016;125:1063–1078. doi: 10.1016/j.neuroimage.2015.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Andersson JL, Graham MS, Zsoldos E, Sotiropoulos SN. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage. 2016;141:556–572. doi: 10.1016/j.neuroimage.2016.06.058. [DOI] [PubMed] [Google Scholar]
- 61.Andersson JL, Graham MS, Drobnjak I, Zhang H, Campbell J. Susceptibility-induced distortion that varies due to motion: Correction in diffusion MR without acquiring additional data. NeuroImage. 2018;171:277–295. doi: 10.1016/j.neuroimage.2017.12.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Andersson JL, et al. Towards a comprehensive framework for movement and distortion correction of diffusion MR images: Within volume movement. NeuroImage. 2017;152:450–466. doi: 10.1016/j.neuroimage.2017.02.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Smith SM. Fast robust automated brain extraction. Human brain mapping. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Milchenko M, Marcus D. Obscuring surface anatomy in volumetric imaging data. Neuroinformatics. 2013;11:65–75. doi: 10.1007/s12021-012-9160-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ashburner J, Friston KJ. Unified segmentation. NeuroImage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- 66.Uwano I, et al. Intensity inhomogeneity correction for magnetic resonance imaging of human brain at 7T. Medical Physics. 2014;41:022302. doi: 10.1118/1.4860954. [DOI] [PubMed] [Google Scholar]
- 67.Fischl B. FreeSurfer. NeuroImage. 2012;62:774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis: II: inflation, flattening, and a surface-based coordinate system. NeuroImage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- 69.Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. Segmentation and surface reconstruction. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 70.Greve DN, Fischl B. Accurate and robust brain image alignment using boundary-based registration. NeuroImage. 2009;48:63–72. doi: 10.1016/j.neuroimage.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Wang Y, et al. Quantification of increased cellularity during inflammatory demyelination. Brain. 2011;134:3590–3601. doi: 10.1093/brain/awr307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wang Y, et al. Differentiation and quantification of inflammation, demyelination and axon injury or loss in multiple sclerosis. Brain. 2015;138:1223–1238. doi: 10.1093/brain/awv046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Schiavi S, et al. A new method for accurate in vivo mapping of human brain connections using microstructural and anatomical information. Science Advances. 2020;6:eaba8245. doi: 10.1126/sciadv.aba8245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Daducci A, D Palù A, Lemkaddem A, Thiran J-P. COMMIT: convex optimization modeling for microstructure informed tractography. IEEE transactions on medical imaging. 2014;34:246–257. doi: 10.1109/TMI.2014.2352414. [DOI] [PubMed] [Google Scholar]
- 75.Pestilli F, Yeatman JD, Rokem A, Kay KN, Wandell BA. Evaluation and statistical inference for human connectomes. Nature methods. 2014;11:1058–1063. doi: 10.1038/nmeth.3098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Barakovic, M. et al. Bundle-specific axon diameter index as a new contrast to differentiate white matter tracts. Frontiers in neuroscience15 (2021). [DOI] [PMC free article] [PubMed]
- 77.Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophysical journal. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- 79.Tournier JD, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. NeuroImage. 2004;23:1176–1185. doi: 10.1016/j.neuroimage.2004.07.037. [DOI] [PubMed] [Google Scholar]
- 80.Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. NeuroImage. 2007;35:1459–1472. doi: 10.1016/j.neuroimage.2007.02.016. [DOI] [PubMed] [Google Scholar]
- 81.Jeurissen B, Tournier J-D, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage. 2014;103:411–426. doi: 10.1016/j.neuroimage.2014.07.061. [DOI] [PubMed] [Google Scholar]
- 82.Behrens T, et al. Characterization and propagation of uncertainty in diffusion‐weighted MR imaging. Magnetic resonance in medicine. 2003;50:1077–1088. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- 83.Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TE. Model‐based analysis of multishell diffusion MR data for tractography: How to get over fitting problems. Magnetic Resonance in Medicine. 2012;68:1846–1855. doi: 10.1002/mrm.24204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Aganj I, et al. Reconstruction of the orientation distribution function in single‐and multiple‐shell q‐ball imaging within constant solid angle. Magnetic Resonance in Medicine. 2010;64:554–566. doi: 10.1002/mrm.22365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Yeh F-C, Wedeen VJ, Tseng W. Generalized q-sampling imaging. IEEE transactions on medical imaging. 2010;29:1626. doi: 10.1109/TMI.2010.2045126. [DOI] [PubMed] [Google Scholar]
- 86.Garyfallidis, E. et al. Dipy, a library for the analysis of diffusion MRI data. Frontiers in neuroinformatics8 (2014). [DOI] [PMC free article] [PubMed]
- 87.Lu H, Jensen JH, Ramani A, Helpern JA. Three‐dimensional characterization of non‐gaussian water diffusion in humans using diffusion kurtosis imaging. NMR in Biomedicine. 2006;19:236–247. doi: 10.1002/nbm.1020. [DOI] [PubMed] [Google Scholar]
- 88.Wu EX, Cheung MM. MR diffusion kurtosis imaging for neural tissue characterization. NMR in Biomedicine. 2010;23:836–848. doi: 10.1002/nbm.1506. [DOI] [PubMed] [Google Scholar]
- 89.Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. NeuroImage. 2011;58:177–188. doi: 10.1016/j.neuroimage.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage. 2012;61:1000–1016. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]
- 91.Kaden E, Kruggel F, Alexander DC. Quantitative mapping of the per‐axon diffusion coefficients in brain white matter. Magnetic resonance in medicine. 2016;75:1752–1763. doi: 10.1002/mrm.25734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Kaden E, Kelm ND, Carson RP, Does MD, Alexander DC. Multi-compartment microscopic diffusion imaging. NeuroImage. 2016;139:346–359. doi: 10.1016/j.neuroimage.2016.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Tian Q, 2021. Comprehensive diffusion MRI dataset for in vivo human brain microstructure mapping using 300 mT/m gradients. figshare. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Tian Q, 2021. Comprehensive diffusion MRI dataset for in vivo human brain microstructure mapping using 300 mT/m gradients. figshare. [DOI] [PMC free article] [PubMed]
Data Availability Statement
The Matlab codes for gradient nonlinearity correction have been modified into Python codes, which are publicly available (https://github.com/ksubramz/gradunwarp). The FMRIB Software Library used in the diffusion data pre-processing and DTI and BEDPOSTX model fitting is publicly available (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FslInstallation). The FreeSurfer software is publicly available (https://surfer.nmr.mgh.harvard.edu/fswiki/DownloadAndInstall). The software used for face masking is publicly available (https://nrg.wustl.edu/software/face-masking). The SPM software for image intensity bias correction is publicly available (https://www.fil.ion.ucl.ac.uk/spm). The MRtrix3 software for the constrained spherical deconvolution is publicly available (https://www.mrtrix.org). The DIPY software used for the CSA-QBI and GQI reconstruction is publicly available (https://www.dipy.org). The codes for the GDSI reconstruction are publicly available (https://github.com/qiyuantian/GDSI). The DESIGNER software for the DKI and WMTI model fitting is publicly available (https://github.com/NYU-DiffusionMRI/DESIGNER). The NODDI Matlab toolbox is publicly available (http://mig.cs.ucl.ac.uk/index.php?n=Tutorial.NODDImatlab). The SMT software for the MicroDTI and MCMicro model fitting are publicly available (https://github.com/ekaden/smt).