Computational modeling of aberrant electrical activity following remuscularization with intramyocardially injected pluripotent stem cell-derived cardiomyocytes

Abstract

Acute engraftment arrhythmias (EAs) remain a serious complication of remuscularization therapy. Preliminary evidence suggests that a focal source underlies these EAs stemming from the automaticity of immature pluripotent stem cell-derived cardiomyocytes (PSC-CMs) in nascent myocardial grafts. How these EAs arise though during early engraftment remains unclear. In a series of in silico experiments, we probed the origin of EAs—exploring aspects of altered impulse formation and altered impulse propagation within nascent PSC-CM grafts and at the host-graft interface. To account for poor gap junctional coupling during early PSC-CM engraftment, the voltage dependence of gap junctions and the possibility of ephaptic coupling were incorporated. Inspired by cardiac development, we also studied the contributions of another feature of immature PSC-CMs, circumferential sodium channel (NaCh) distribution in PSC-CMs. Ectopic propagations emerged from nascent grafts of immature PSC-CMs at a rate of <96 bpm. Source-sink effects dictated this rate and contributed to intermittent capture between host and graft. Moreover, ectopic beats emerged from dynamically changing sites along the host-graft interface. The latter arose in part because circumferential NaCh distribution in PSC-CMs contributed to preferential conduction slowing and block of electrical impulses from host to graft myocardium. We conclude that additional mechanisms, in addition to focal ones, contribute to EAs and recognize that their relative contributions are dynamic across the engraftment process.

Graphical Abstract

1. Introduction:

Remuscularization of the ventricles via intramyocardial injections of pluripotent stem cell-derived cardiomyocytes (PSC-CMs) holds immense promise in halting or even reversing heart failure (HF) progression following cardiac injuries, such as myocardial infarction (MI), if only the emergence of engraftment arrhythmias (EAs) can be addressed. Injected PSC-CMs have demonstrated the ability to form stable, electromechanically integrated myocardial grafts that enhance ventricular contractility[1–5]. However, transient ventricular tachyarrhythmias (VTs) remain widespread across published studies using large, preclinical animal models[3, 6–8]. These EAs were especially prevalent several days (4-21) following PSC-CM injection during early PSC-CM engraftment. Preliminary evidence from electroanatomical mapping, clinical pacing maneuvers, and cardioversion suggests that the mechanism underlying these EAs is a graft-induced, focal source[7, 8]. Exactly how graft-induced focal EAs arise during early PSC-CM engraftment remains unclear in part because the electromechanical integration of PSC-CMs and its dynamics remain under characterized in vivo [9].

To study this, we used a computational modeling approach that incorporated key biophysical details in the intercellular electrotonic junctions between adjacent CMs. These included the voltage dependence of gap junctions[10, 11] and the possibility of a cardiac ephapse[12–18]. Both have been observed to impact impulse formation and impulse propagation when gap junctional coupling (GJC) is especially poor, a condition that manifests during the initial stages of PSC-CM engraftment when EAs are just starting to emerge[6–8]. In the former, gap junctional channels inactivate or close in response to large transjunctional voltage differences [10]. In the latter, cardiac ephapse or ephaptic coupling (EpC) is made possible in part because the membranes of adjacent CMs are brought into close proximity (<30 nm) at the intercalated disc (ID). The ID is an important intercellular nanodomain at the longitudinal ends of CMs responsible for the electrotonic coupling and mechanical anchoring of adjacent CMs[15, 19]. EpC is also made possible in the adult heart because sodium channels (NaChs) localize at the ID in mature ventricular CMs[19]. In immature PSC-CMs however, NaChs are circumferentially distributed because complete PSC-CM maturation in vitro remains elusive[20, 21]. PSC-CM maturation, including NaCh localization to the ID, has been shown to occur in vivo though[7, 8, 22]. The functional impact of NaCh distribution in PSC-CMs on electrical impulse formation and propagation during remuscularization has not been studied.

Thus, the current study aimed to address two principal gaps of knowledge. First and foremost, we sought to determine whether and how a graft-induced focal mechanism could underlie EAs during early PSC-CM engraftment. Secondly, we sought to probe the contributions of NaCh localization at the ID, a feature of PSC-CM maturation, on EA dynamics. In a series of in silico experiments, we explored the contributions of altered impulse formation (Fig. 1A, left) and altered impulse propagation (Fig. 1A, right) on the emergence and dynamics of EAs. Within nascent myocardial grafts comprised of PSC-CMs with different intrinsic spontaneous beating rates, the dynamics of beating rate and beating synchrony was studied. At the host-graft interface, the effect of several PSC-CMs on the emergence and rate of spontaneous ectopic beats in a host ventricular CM was studied. The effect of different NaCh distributions among mature, host ventricular CMs and immature graft PSC-CMs (localization to the ID and no localization, respectively) on electrical conduction at the host-graft interface was also studied. Combining all these elements, we observed how spontaneous ectopic propagations emerged from a contiguous PSC-CM graft in a myocardial ring model.

Figure 1: Overview of study and computational model schematic.

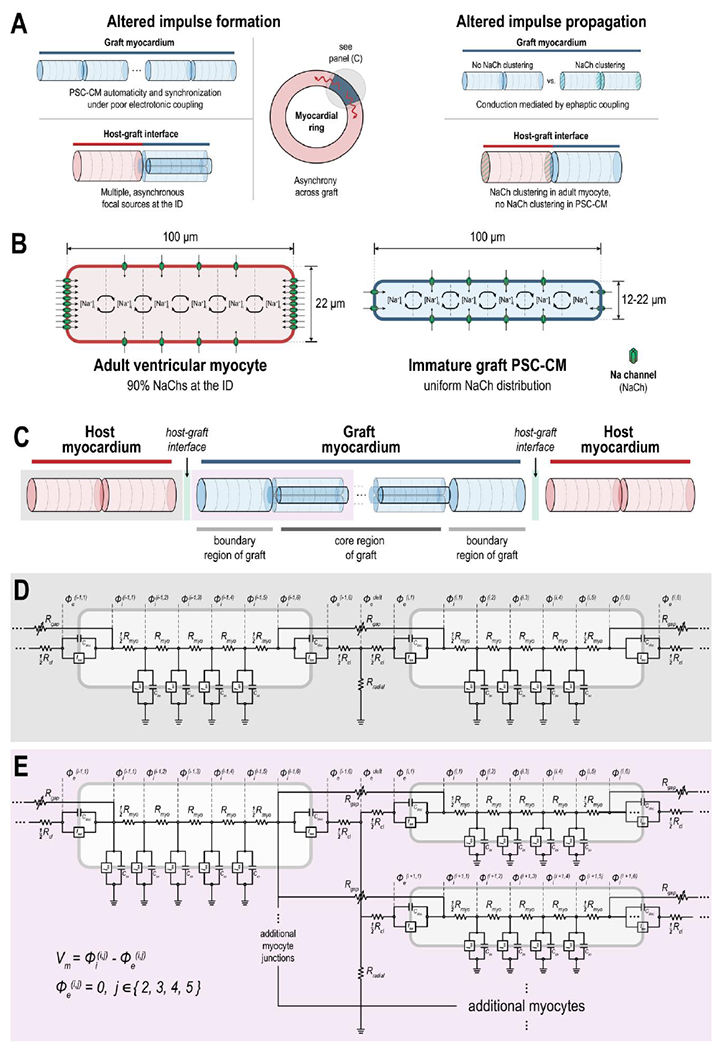
(A) Graphical abstract of study. The biophysical mechanisms underlying engraftment arrhythmias (EAs) following injections of pluripotent stem cell-derived cardiomyocytes (PSC-CMs) was studied with respect to altered electrical impulse formation (left) and altered impulse propagation (right). Several hypotheses were systematically tested with respect to each; the effect of sodium channel (NaCh) distribution (clustered or not clustered at the longitudinal ends), a feature of PSC-CM maturation, was also determined. (B) Individual cardiomyocytes (CMs) were idealized as cylinders. Adult ventricular host CMs had radius = 11 μm and length = 100 μm with nonuniform distribution of NaChs; specifically, 90% NaChs were localized to the longitudinal ends. Graft PSC-CMs had variable radius (ranging from 6-11 μm) and length = 100 μm; NaChs were either uniformly or nonuniformly distributed. (C) At the tissue scale, 20 host and 42 graft CMs were arranged into a myocardial ring with junctional coupling occurring at the longitudinal ends of abutting myocytes. The graft myocardium was comprised of a core (4 linear strands of 10 PSC-CMs each with radius = 8 μm) and boundary region (2 PSC-CMs with radius = 11 μm, one on either end); the degree of junctional coupling at the host-graft interface and between PSC-CMs in the graft were studied with respect to the emergence of EAs. Electrical circuit representation of (D) two or (E) more coupled myocytes at a shared junctional cleft. Adjacent cells interacted either through intracellular current flowing across the gap-junctional resistor (R_gap) or extracellular cleft current flowing across the T-shaped network of axial (R_cl) and radial (R_radial) resistors. Gap junctions exhibited dynamic voltage-gating. See text for additional details.

2. Materials and Methods:

2.1. The computational model

Individual CMs were discretized in order to account for NaCh localization to the ID. To do this, both adult ventricular CMs and graft PSC-CMs were idealized as symmetric cylinders and subdivided into 6 patches along the longitudinal axis (Fig. 1B: 4 axial membrane patches and 2 disc or junctional patches) like previous studies[12, 23]. Adult ventricular CMs (length: 100 μm, radius: 11 μm) were typically larger than graft PSC-CMs (length: 100 μm, radius: 8 or 11 μm) with NaChs distributed nonuniformly; specifically, 90% of NaChs were localized at the disc patches. In PSC-CMs, NaChs were either distributed uniformly or nonuniformly, the former simulating a more immature cytoarchitecture[22, 24, 25]. The membrane kinetics of host and graft CMs at each patch were modeled using the Luo-Rudy I (LR1) for a guinea pig ventricular myocyte[26]. While the LR1 lacks the biophysical detail of newer cardiac action potential (AP) models, the LR1 enabled us to simulate the general dynamics between excitable (host) and oscillatory (graft) CMs in a computationally tractable way. A constant depolarizing current (I_d), analogous to the funny current (I_f), was added to simulate automaticity in graft PSC-CMs; both I_f and I_Na have been implicated in PSC-CM automaticity[27, 28]. I_d also elevated the maximum diastolic potential (MDP), another electrophysiological characteristic of immature PSC-CMs[29]. Consistent with previous findings[30], the magnitude of I_d altered the automaticity rate (Fig. S1). With 6 membrane patches, there was no difference in beating rate when NaChs were distributed uniformly or nonuniformly (Fig. S1A). Moreover, automaticity rate did not change with graft myocyte size (Fig. S1B) and never exceeded 83 bpm. This latter observation, taken together with the fact that the membrane kinetics between host and graft differed only by a single current (I_d), suggest that our graft PSC-CMs are reasonably representative of late-stage PSC-CMs or late embryonic/neonatal myocytes.

Graft PSC-CMs and host adult ventricular CMs were subsequently coupled into various configurations of increasing structural complexity across a series of experiments that probed the dynamics of altered impulse formation and impulse propagation during early PSC-CM engraftment. These were studied within nascent PSC-CM grafts, at the host-graft interface, and between host and graft myocardium during early engraftment. In each coupling configuration, CMs were organized end-to-end and electrotonically coupled at the ID. At a particular ID, adjacent CMs could be coupled in either 1:1 (Fig. 1C, highlighted in grey) or 1:4 ratios (Fig. 1C, highlighted in purple). These basic organizational units were subsequently integrated into a myocardial ring model (Fig. 1C), the details of which are described later. For each of these coupling ratios (Fig. 1D and Fig. 1E, respectively), the intracellular spaces of the corresponding disc patches of juxtaposed CMs were resistively coupling (R_gap). R_gap was scaled based on the degree of voltage-dependent gating inactivation. Connexins, including connexin-43 (Cx43) or the isoform predominantly expressed in the ventricles, and the gap junctional channels that they form are known to exhibit voltage-dependent gating[11, 31, 32]; large transjunctional voltage differences result in gap junction inactivation[10]. The voltage-dependence of gap junctions was modeled using a previously published two-state dynamic gating model[33]. While not known to significantly alter electrical conduction in well-coupled myocardium[17], voltage-dependence would play an important role in the emergent electrical dynamics during the initial stages of PSC-CM engraftment when GJC is being established[10]. A T-shaped resistor junction (R_cl and R_radial) in the intercellular cleft space mediated EpC between adjacent CMs (Fig. 1D, E); R_cl and R_radial were proportional and inversely proportional to ID cleft width, respectively[34].

Complete details of the computational model can be found in the Supplementary Materials; all model parameters are given in Tables I and II in the Supplementary Materials.

2.2. Quantification of synchrony

The average beating synchrony across all graft PSC-CMs was quantified by the Z statistic[35]. Z was computed as the time average of instantaneous z statistics (z_t), or

$$Z=\sum _{t=1}^T{z}_t$$

Each z_t was defined as the beating synchrony across a given population of N PSC-CMs at time t. Specifically,

$$z_t=\frac{1}{N}\left|\sum _{j=1}^N{e}^{i{\theta }_j}\right|$$

where θ_j is the phase of a particular myocyte j. For each myocyte j, the phase at time t was computed as θ_j = 2πx_j, where x_j is defined as the progression through the current cycle length (CL) at time t (i.e., bounded on the interval [0,1]); CLs were defined as the interval between adjacent upstrokes of spontaneous beats.

2.3. Computation of conduction velocity

Conduction velocity (CV) across the myocardial strand was computed by linear regression of the activation times as previously described[23].

3. Results:

3.1. Graft dynamics are predominantly determined by GJC as opposed to EpC because I_Na is reduced in spontaneously beating PSC-CMs.

In the first set of experiments, we sought to determine how the synchronization and automaticity of graft PSC-CMs changed with respect to electrotonic coupling and NaCh distribution. 20 PSC-CMs (radius=8 μm) were arranged into a linear strand, all coupled in 1:1 ratios (Fig 1C, highlighted in grey). For each PSC-CM, the intrinsic beating rate (42-82 bpm) was determined by uniformly sampling a value of I_d between 2.3 and 3.7 μA/μF; the initial state of each PSC-CM was also randomized by uniformly sampling from steady-state single cell dynamics. Different stages of engraftment were simulated by altering gap junctional resistance (R_gap) and ID cleft width between PSC-CMs in the strand. ID cleft width, or the distance between adjacent CM membranes at the ID, is a key determinant of EpC. A wide range of R_gap (1×10⁴ to 1×10¹⁶ kΩ) and cleft widths (10 to 100 nm) were sampled, because the progression of electromechanical coupling during PSC-CM engraftment has not been characterized. Moreover, it is unknown whether ID clefts are enlarged or contracted across this process. In addition to proximity, a high density of NaChs at the ID has also been shown to be integral for EpC[12–15]. Thus, we also tested the effects of NaCh distribution (uniform vs. nonuniform); we wanted to determine whether nonuniform NaCh distribution could enhance graft synchrony and facilitate impulse propagation in nascent myocardial grafts.

Reducing R_gap increased the average synchrony of PSC-CMs across the linear myocardial graft strand (Fig. 2A). The relationship between R_gap and synchrony was sigmoidal. There was little change in synchrony (^~0.22) between R_gap values of 1×10⁸ and 1×10¹⁶ kΩ, but dramatically increased from 0.29 to 1.00 when R_gap was reduced from 1×10⁷ to 1×10⁵ kΩ. Cleft width had minimal effect on average PSC-CM synchrony except for one notable case—when cleft width was 10 nm, and R_gap and NaCh distribution were 1×10⁶ kΩ and nonuniform, respectively. Visualizing the action potentials (APs) at this configuration (Fig. 2B, middle bottom), we identified that PSC-CMs were only partially synchronized. The last 4 myocytes (myocytes 16-19) were asynchronous to the remaining myocytes (myocytes 0-15). This was not the case when NaChs were uniformly distributed (Fig. 2B, middle top). The earliest activation occurred at myocyte 19 with subsequent activations occurring sequentially along the linear strand; out of all the myocytes in the strand, myocyte 19 had the largest value of I_d (3.45 μA/μF) and thus fastest intrinsic beating rate. In contrast, PSC-CMs were not only synchronized but activation occurred simultaneously when R_gap was reduced to 1×10⁵ kΩ (Fig. 2B, left). When R_gap was increased to 1×10⁷ kΩ (Fig. 2B, right), PSC-CMs were no longer synchronized and the activation of adjacent PSC-CMs were distinct from one another.

Figure 2: Graft dynamics with respect to gap junctional coupling, ID cleft width, and NaCh distribution.

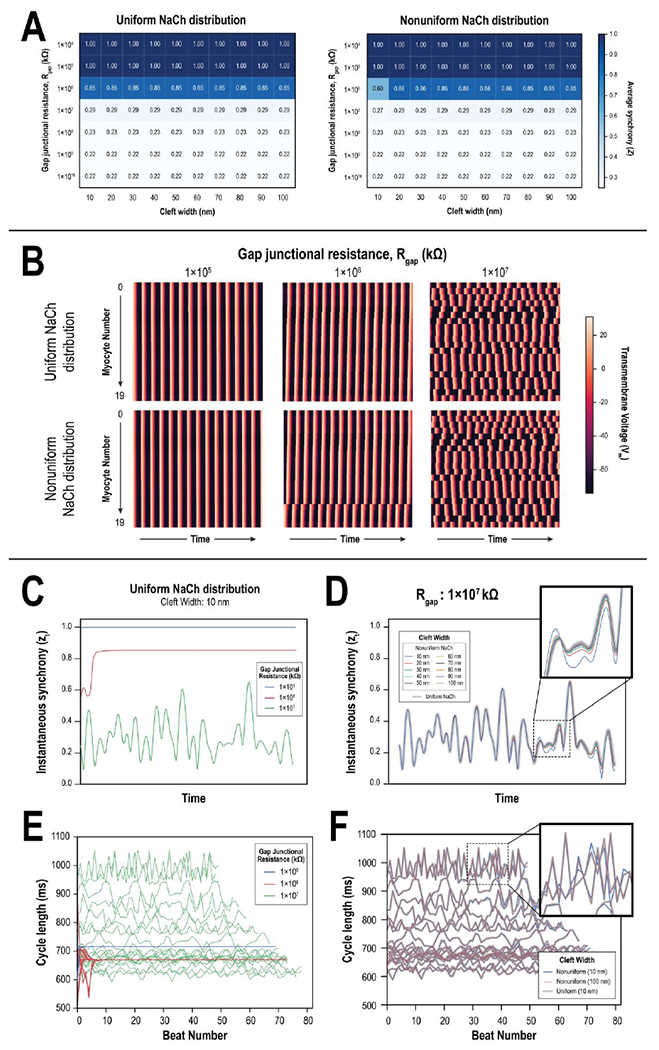
(A) Heat maps of average synchrony across combinations of gap junctional resistances (R_gap) and cleft widths for 20 linearly coupled PSC-CMs with either uniform (left) and nonuniform (right) NaCh distributions. (B) Color maps denote the temporal evolution of transmembrane potential (V_m) across all 20 PSC-CMs at 3 different levels of R_gap (1×10⁵ kΩ, left; 1×10⁶ kΩ, middle; 1×10⁷ kΩ, right) when NaChs were distributed uniformly (top) and nonuniformly (bottom); cleft width was 10 nm. When R_gap=1×10⁶ kΩ and NaChs were nonuniformly distributed (middle, bottom), myocytes 16-19 were synchronized but remained asynchronous from the rest. (C) Instantaneous synchrony vs. time across R_gap values in panel (B); NaChs were uniformly distributed, and cleft width was 10 nm. (D) Instantaneous synchrony vs. time across different cleft widths when R_gap=1×10⁷ kΩ and NaChs were uniformly and nonuniformly distributed. Differences between the traces were more pronounced at particular instances in time (inset). (E) Line plots of individual PSC-CM cycle length (CL) vs. beat number across R_gap values in panel (B); NaChs were uniformly distributed, and cleft width was 10 nm. (F) Line plots of cycle length vs. beat number demonstrating slight changes between uniform and nonuniform NaCh distributions when R_gap=1×10⁷ kΩ. Differences were more pronounced for slower beating PSC-CMs (inset).

The aforementioned graft dynamics were reflected in the time course of instantaneous synchrony, z_t (Fig. 2C, 2D). When R_gap was 1×10⁵ kΩ, z_t was constant and equal to 1 because all PSC-CMs were synchronized and activated simultaneously (blue trace). When R_gap was 1×10⁶ kΩ, z_t slightly fluctuated before increasing to a steady-state value of 0.85 (red trace). After an initial adjustment period, PSC-CMs entrained with the fastest beating PSC-CM (myocyte 19) and sequentially activated across the strand; z_t was not 1.0 because PSC-CMs did not all simultaneously excite. When R_gap was 1×10⁷ kΩ, z_t fluctuated significantly across time (green trace). Instantaneous synchrony had only a small dependence on EpC (Fig. 2D); z_t exhibited slight deviations across different cleft widths when NaCh was nonuniformly distributed (Fig. 2D, inset).

At the cell scale, individual PSC-CMs exhibited beat-to-beat fluctuations at R_gap values that enabled electrotonic interactions between adjacent PSC-CMs without achieving synchrony (Fig. 2E). The electrotonic influence of neighboring myocytes contributed to fluctuations in the cycle lengths (CLs) of spontaneous beats reminiscent of previous foundational work in sinoatrial pacemaker cells[36, 37]. Beat-to-beat cycle CL fluctuations were the largest when R_gap was 1×10⁷ kΩ (green trace) and for slower beating PSC-CMs; average beating rates for individual PSC-CMs ranged from 624 to 1038 ms (58 to 96 bpm) (Fig. S3 and S4). When R_gap was reduced to 1×10⁶ kΩ, PSC-CMs synchronized to a beating CL of 670 ms (89.6 bpm) after an initial adjustment period (red trace). Notably, the synchronized CL increased to 714 ms (84.0 bpm) when R_gap was reduced further to 1×10⁴ kΩ (blue trace); this trend continued when R_gap was reduced further yet to 1×10⁴ kΩ (CL was 720 ms or 83.3 bpm; Fig. S3 and S4). EpC only slightly altered beat-to-beat fluctuations (Fig. 2F) and were most pronounced for slower beating PSC-CMs (Fig. 2F, inset). When NaChs were distributed nonuniformly, CL fluctuations changed slightly when cleft width was increased from 10 to 100 nm (blue and pink, respectively). At 100 nm cleft width, CL fluctuations were identical to those when NaChs were distributed uniformly (grey). CL fluctuations did not change with cleft width when NaChs were uniformly distributed, indicating that the effects of EpC was negligible in this setting. Because CL fluctuations were so minimal, the average CLs of PSC-CMs were essentially identical between uniform and nonuniform NaCh distributions (Fig. S3 and S4). The impact of EpC was diminished because I_Na, the predominant depolarizing current, was blunted in spontaneously beating PSC-CMs (Fig. S5A). I_Na showed a dependence on I_d (Fig. S5A, middle). While I_d determined automaticity rate (Fig. S1), it also set the maximum diastolic potential (MDP); larger I_d values increased the MDP (Fig. S5A, left). Consequently, reactivation of h and j inactivation gates in I_Na remained incomplete (Fig. S5A, right). In paced beats however (Fig. S5B), I_Na was significantly larger (^~230 μA/μF vs. <50 μA/μF), because electrical stimulation enabled rapid depolarization to threshold (Fig. S5, middle).

Because I_Na was significantly larger when excitation was evoked, we next tested the hypothesis that EpC could drive synchronization and electrical propagation across the graft in conditions of poor GJC. We electrically stimulated the linear strand along one side (myocyte 0) at a basic CL of 400 ms (150 bpm) to simulate the effects of a fast-rate focal source. We rationalized that this could arise because of the presence of faster beating nodal-like subtypes[38] or because of triggered activity occurring within a PSC-CM graft due to poor vascularization[39]. In any case, these rapid excitations would need to propagate across the graft and into the host myocardium for EAs to be driven by a purely focal mechanism. Compared to when the strand was not stimulated, average synchrony across the stimulated strand remained essentially unchanged and was even diminished (0.76 vs 0.85) when R_gap=1×10⁶ kΩ (Fig. S6). Paced beats failed to propagate or synchronize across PSC-CMs in the strand, indicating that EpC remained insufficient. This further indicated that electrical conduction of spontaneous PSC-CM beats across the strand when not stimulated (Fig. 2B, middle) was only “apparent”; instead, PSC-CMs were mutually entrained via phase resetting[36, 37].

Overall, these results demonstrate that the degree of GJC plays a dominant role in the synchronization and average beating rate of coupled PSC-CMs as opposed to EpC. In one instance (nonuniform NaCh distribution, R_gap=1×10⁶ kΩ, and 10 nm cleft width) however, EpC did appear to play a role in promoting graft asynchrony. While moderate to low GJC gave rise to modest reductions in average spontaneous CL (^~110 ms) in coupled PSC-CMs (Fig. S3 and S4), they did not give rise to significantly accelerated automaticity across the graft overall (89.6 bpm vs. 83.3 bpm). Moreover, rapid pacing that simulated a fast-rate, focal source within the graft was unable to entrain PSC-CMs at low GJC despite enhanced EpC because of a more than a 4-fold increase in I_Na. In total, this suggests that enhanced or altered automaticity alone contribute to EAs.

3.2. Source-sink effects and gap junctional voltage gating impact PSC-CM automaticity and the emergence and rate of graft-induced spontaneous ectopic beats

To probe how source-sink interactions between host and graft CMs impact the emergence and rate of graft-induced ectopic beats at the host-graft interface, adult ventricular CMs were coupled to PSC-CMs in simplified host-graft tandems in 1:4 ratios. In this configuration, the effect of several asynchronous PSC-CMs—each with different intrinsic beating rates (I_d = 3.1, 3.3, 3.5, and 3.7 μA/μF)—on the emergence and rate of spontaneous ectopic beats in a host ventricular CM was studied. While PSC-CMs spontaneously beat, host ventricular CMs remain quiescent unless depolarized to threshold. They thus act as an electrotonic sink to suppress PSC-CM automaticity. The rates of PSC-CM automaticity and graft-induced ectopic beats were observed across a range of R_gap (1.6×10⁵ to 2.5×10⁵ kΩ) and ID cleft widths (10 to 100 nm). PSC-CM radius was maximal (11 μm) to simulate the worst-case source-sink conditions (i.e., maximal electrotonic source). PSC-CM size impacts both the magnitude of depolarizing ionic membrane current sources and excitability via membrane surface area and capacitance.

Asynchronous PSC-CMs with heterogeneous spontaneous beating rates gave rise to additional complexity in host-graft dynamics (Fig. 3) not observed in initial characterizations (Fig. S2). Elicited APs in the host CM occurred for an even smaller subset of the coupling parameter space (Fig. 3A, left compared to Fig. S2E, top). PSC-CM automaticity rate and the rate of elicited spontaneous ectopic beats in the host CM were affected by both R_gap and ID cleft width (Fig. 3A). At narrow cleft widths and high GJC, automaticity across all PSC-CMs was suppressed altogether (Fig. 3A, right) demonstrating the combined effects of increased electrotonic load and I_Na attenuation. I_Na is attenuated in EpC because large negative deflections in the cleft potential (ϕ_e,cleft) increase V_m of all the CMs at that particular junction; this in turn reduces the I_Na driving force or (E_Na-V_m). (ϕ_e,cleft deflections increase for smaller cleft widths. The magnitude of I_d played a role in both the persistence and rate of automaticity of individual PSC-CMs for a given R_gap and cleft width (Fig. 3A, right). In the simplest case, 1:1 host-graft coupling occurred (Fig. 3B). The rate of elicited spontaneous ectopic beats was driven predominantly by the fastest beating PSC-CM (graft PSC-CM 4 with I_d=3.7 μA/μF); the gating of junction 4 fluctuated the most because transjunctional voltage differences between graft PSC-CM 4 and host CM were the largest (Fig. 3B, right). However, instances of 3:1 (Fig. 3C), 5:1 (Fig. 3D), and 11:1 (Fig. 3E) capture were also observed. Junctional gating inactivation was prominent across all host-graft junctions in instances where spontaneous beats did not capture. When the host CM captured, graft PSC-CM 4 again provided the most gap junctional current via the corresponding junction (junction 4). Although gating inactivation was the largest in junction 4, graft PSC-CM 4 still provided the largest total depolarizing junctional current. This arose because gating inactivation kinetics were delayed and slower than membrane AP kinetics. Consequently, gating inactivation blunted peak junctional current (i.e., when one CM is depolarized but the other is not) but did not change the relative contribution of depolarizing junctional current provided by each PSC-CM. Depending on the coupling configuration however, different graft PSC-CMs provided the largest supplementary junctional current. For example, graft PSC-CM 3 provided the second most electrotonic current when R_gap=2.1×10⁵ kΩ and cleft width was 60 nm (Fig. 3C). Meanwhile, graft PSC-CM 1 provided the second largest electrotonic current when R_gap=2.4Ω10⁵ kΩ and cleft width was 70 nm (Fig. 3D). Prior to a captured beat, a noticeable subthreshold depolarization occurred in graft PSC-CM 1 which drove its V_m to a more depolarized value prior to the next spontaneous beat. These subthreshold depolarizations were driven by potential changes in the shared cleft because individual PSC-CMs were not coupled to one another (electrotonic coupling occurred only at the ID; Fig 1E).

Figure 3: Heterogeneity of beating rates among graft PSC-CMs can give rise to inconsistent graft-induced spontaneous ectopic beats in a host CM.

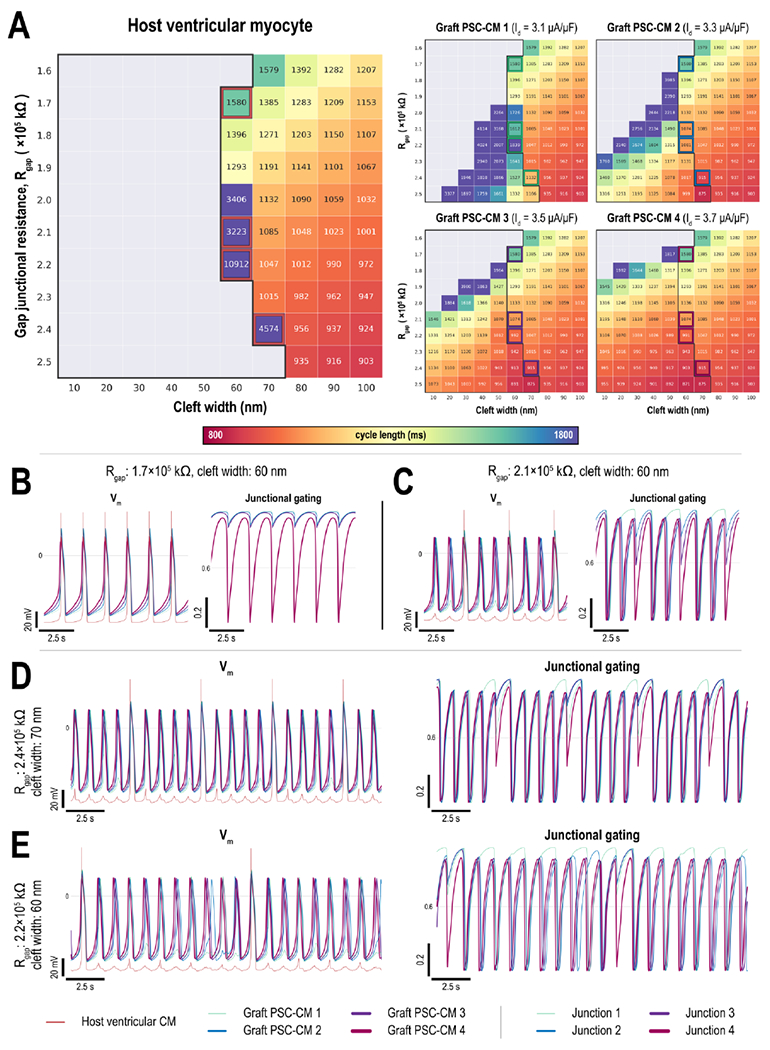
(A) Heat maps show how the cycle lengths of graft-induced ectopic beats in a host ventricular CM (left) and spontaneously beating graft PSC-CMs (right) change with gap junctional resistance (R_gap) and cleft width for 1:4 host-graft coupling configuration; PSC-CMs had a range of I_d (3.1, 3.3, 3.5, and 3.7 μA/μF) with initial states randomized. (B-E) Representative V_m traces of host and graft CMs (left) and junctional gating (right). A wide range of activation patterns were observed from (B) 1:1 capture and instances of (C) 3:1, (D) 5:1, and (E) 11:1 block. Across all traces, junction 4 exhibited the largest gating fluctuations.

In summary, we demonstrated how host-graft electrotonic coupling altered PSC-CM automaticity and the emergence graft-induced ectopic beats. Interestingly, PSC-CM automaticity and the emergence of graft-induced spontaneous ectopic beats were altered by cleft width only when multiple PSC-CMs were coupled at a single shared cleft ID. At high GJC and small cleft widths, PSC-CM automaticity could be suppressed altogether. When PSC-CMs had different intrinsic beating rates, a wide range of intermittent host CM capture was observed; both cleft width and junctional gating played a role in these emerging dynamics. Graft PSC-CM 4, the fastest beating graft CM, always contributed the most junctional current source. More importantly however, the rate of graft-induced ectopic propagations was at most equivalent to that of the fastest beating PSC-CM; the rate of graft-induced ectopic propagations across these simulations never exceeded 73 bpm (822 ms CL). No instances of dynamic asynchrony between host and graft CMs were observed when PSC-CMs had intrinsically different beating rates. Whenever the host CM captured, all graft CMs depolarized which served to resynchronize PSC-CMs (Fig. 3C–E). This suggested that multiple focal sources at the ID alone do not contribute to EAs.

3.3. Electrical impulses from host to graft myocardium can exhibit preferential conduction delay and conduction block at the host-graft interface compared to electrical impulses from graft to host.

Cognizant that conduction delay at the host-graft interface in addition to conduction slowing across the graft could contribute to unidirectional conduction block and reentry, we also sought to investigate the role of different NaCh distribution between host and graft CMs on electrical conduction across the host-graft interface. To simulate this, 30 host CMs were arranged in a linear strand (all coupled in a 1:1 ratio) with myocyte 15 altered in a particular way (Fig. 4A). NaChs were distributed uniformly on the left half but were distributed nonuniformly on the right half. A range of cleft widths and gap junctional resistances (R_gap) at junction 14 between myocytes 14 and 15 were simulated to capture the possible progression of electrotonic coupling at the host-graft interface; the cleft width and junctional coupling at all other IDs were 20 nm and 1×10⁴ kΩ, respectively. The linear strand was subsequently paced from either the left or right ends at a constant pacing interval of 1000 ms; stimulating from the left simulated a sinus beat propagating across the host myocardium prior to encountering the host-graft discontinuity, while stimulating from the right simulated an ectopic beat propagating across the graft myocardium. Subsequently, we quantified CV and observed for instances of conduction block.

Figure 4: Direction-dependent conduction delay and conduction block at the host-graft interface.

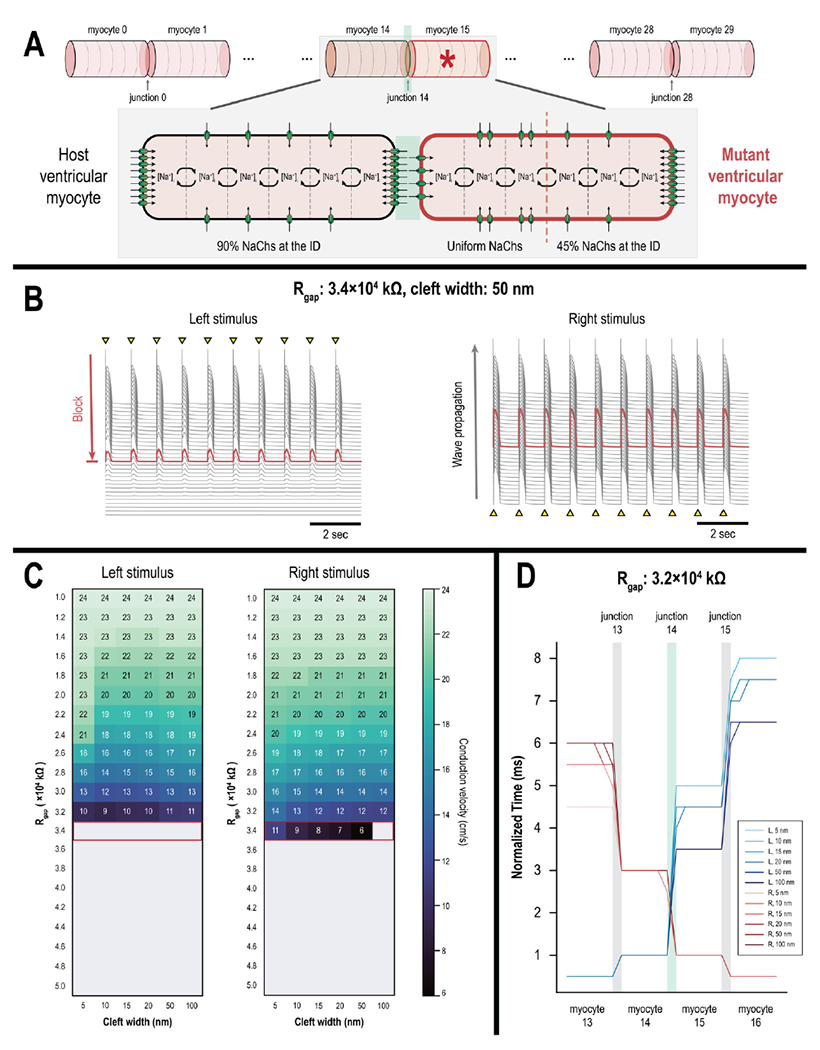
(A) Linear strand of 30 host CMs with a single junctional discontinuity (junction 14) around a single mutant CM (myocyte 15, starred). The mutant CM has uniform NaCh distribution on the left half but nonuniform NaCh distribution on the right half. (B) Action potential (AP) traces of all 30 myocytes demonstrate an instance of asymmetrical conduction. Electrical conduction failed at myocyte 15 (red) when the strand was stimulated from the left end (left). When stimulated from the right end however, electrical conduction successfully propagated across the strand (right). (C) Heat map of conduction velocities across the linear strand when stimulating from the left vs. right ends (left and right, respectively). Unidirectional conduction occurs when gap junctional resistance (R_gap) was 3.4×10⁴ kΩ (outlined in red). (D) Activation profiles of myocytes 13-16 when the strand was stimulated from the left (blue) versus the right (red) end; R_gap=3.2×10⁴ kΩ at the host-graft interface (junction 14). Across all cleft widths, conduction delays at junction 14 were more pronounced when the myocardial strand was stimulated from the left as opposed to the right end.

When R_gap was 3.6×10⁵ kΩ or higher, conduction block occurred regardless of the stimulus location. Electrical conduction was only possible when stimulating from the right but not the left side when R_gap was reduced to 3.4×10⁵ kΩ, however (Fig. 4B). When stimulating from the left, conduction block occurred at myocyte 15 (red AP trace). When R_gap was further reduced and electrical propagation across the strand was successful, CV was noticeably faster when stimulating from the right versus the left (Fig. 4C); this was especially noticeable at low levels GJC and small cleft widths. Slowed CV when stimulating from the left was due in part to more significant conduction delays at junction 14 (Fig. 4D, blue versus red traces). Conduction delays at junction 14 were no more than 4.5 ms when the strand was stimulated from the right but were greater than 5.0 ms when stimulated from the left.

In summary, we showed that PSC-CM grafts are prone to entrance block under low but sufficient levels of GJC; sinus impulses propagating through host myocardium could block at the host-graft interface while graft-induced ectopic beats would propagate outwards. Asymmetrical NaCh distribution at IDs at the host-graft interface—whereby NaChs are distributed uniformly in PSC-CMs but nonuniformly in host CMs—contributed to preferential conduction out of the graft due to differences in local excitability. This difference would be further exacerbated when taken with previous results indicating that the magnitude of I_Na is blunted when PSC-CMs spontaneously beat.

3.4. Spontaneous ectopic propagations emerge from different and changing sites along a contiguous PSC-CM graft embedded within a myocardial ring

In the final experiment, we combined all these previous components and simulated the engraftment of a contiguous nascent graft of PSC-CMs in a myocardial ring model (Fig. 1C). Ectopic beats emerging from one end of the graft could propagate around to the other end and influence the timing and emergence of ectopic beats from this distal site. The myocardial ring comprised of 62 CMs: 20 host CMs and 42 graft PSC-CMs. The graft consisted of two distinct regions: an immature core and a partially matured boundary region. This setup was chosen in part because PSC-CMs along the edges of graft myocardium have been observed to mature much more than those in the interior in vivo[3, 6–8]. PSC-CMs in the core region were organized as 4 linear bundles and were smaller compared to boundary PSC-CMs (8 μm vs. 11 μm radius, respectively) to reflect localized hypertrophy of PSC-CMs along the graft edges. The boundary region consisted of individual PSC-CMs, one at either end of the graft, that interfaced with a host ventricular CM at the host-graft interface. In both core and boundary regions, NaChs in PSC-CMs were distributed uniformly. Individual PSC-CMs in the graft had different intrinsic spontaneous beating rates (I_d uniformly sampled between 3.0 and 3.7 μA/μF) and randomized initial states. Three different levels of GJC between PSC-CMs (1×10⁵, 1×10⁶, and 1×10⁷ kΩ) were simulated; PSC-CM synchrony was previously observed to change the most across these values of R_gap (Fig. 2A). At the host-graft interface, R_gap was 3.4×10⁴ kΩ. ID cleft widths of 10 and 100 nm, both between PSC-CMs in the graft and at the host-graft interface, were tested. In host myocardium, R_gap between adjacent ventricular CMs was 1×10⁴ kΩ (conductance: 0.1 μS) and ID cleft width was 20 nm. These values were based on previously published studies of human atrial biopsies[40] and ex vivo measurements of guinea pig ventricles[23]; this gave rise to a conduction velocity (CV: 22.2 cm/s) across the host myocardial strand comparable to estimates of slowed CV in peri-infarcted myocardium[41, 42]. Subsequently, the emergence and rate of graft-induced ectopic propagations across host myocardium was observed for.

The magnitudes of R_gap and cleft width between PSC-CMs in the graft altered the emergent dynamics of graft-induced spontaneous ectopic propagations. In the simplest case (Fig. 5A), ectopic beats emerged from both ends of the graft nearly simultaneously; electrical waves (Fig. 5A, inset) elicited from both ends of the graft (red and blue AP traces) collided in the host myocardium (grey traces). This occurred when R_gap and cleft width were 1×10⁵ kΩ and 100 nm, respectively. Ectopic beats also consistently emerged from one side of the graft (Fig. 5B, red trace) and propagated across the host myocardium to the other side of the graft (blue trace). This occurred when cleft width within the graft was 10 nm for all simulated R_gap values. In the third and most proarrhythmic case, the direction of ectopic propagations was not consistent. The first ectopic beat emerged from one particular side of the graft (Fig. 5C, left inset) and triggered an electrical wave across the host myocardium before the distal graft site could trigger an ectopic beat. Subsequent ectopic beats would however emerge from this distal graft site (Fig. 5C, right inset) and electrical activation would be retrograde. Moreover, the rate of these spontaneous ectopic propagations was a fraction (1284 vs. ^~630 ms CL) of those previously highlighted (Fig. 5A, 5B). Across all simulations (Fig. 5D, 5E). the cycle lengths of spontaneous ectopic propagations never exceeded 626 ms (95.8 bpm). When cleft width within the graft was 10 nm (Fig. 5D), 1:1 capture between host and graft was observed. When cleft width within the graft was 100 nm however (Fig. 5E), 2:1 capture and complete block was observed between the spontaneously beating core PSC-CMs and boundary PSC-CMs.

Figure 5: Graft-induced spontaneous ectopic propagations in a myocardial ring model.

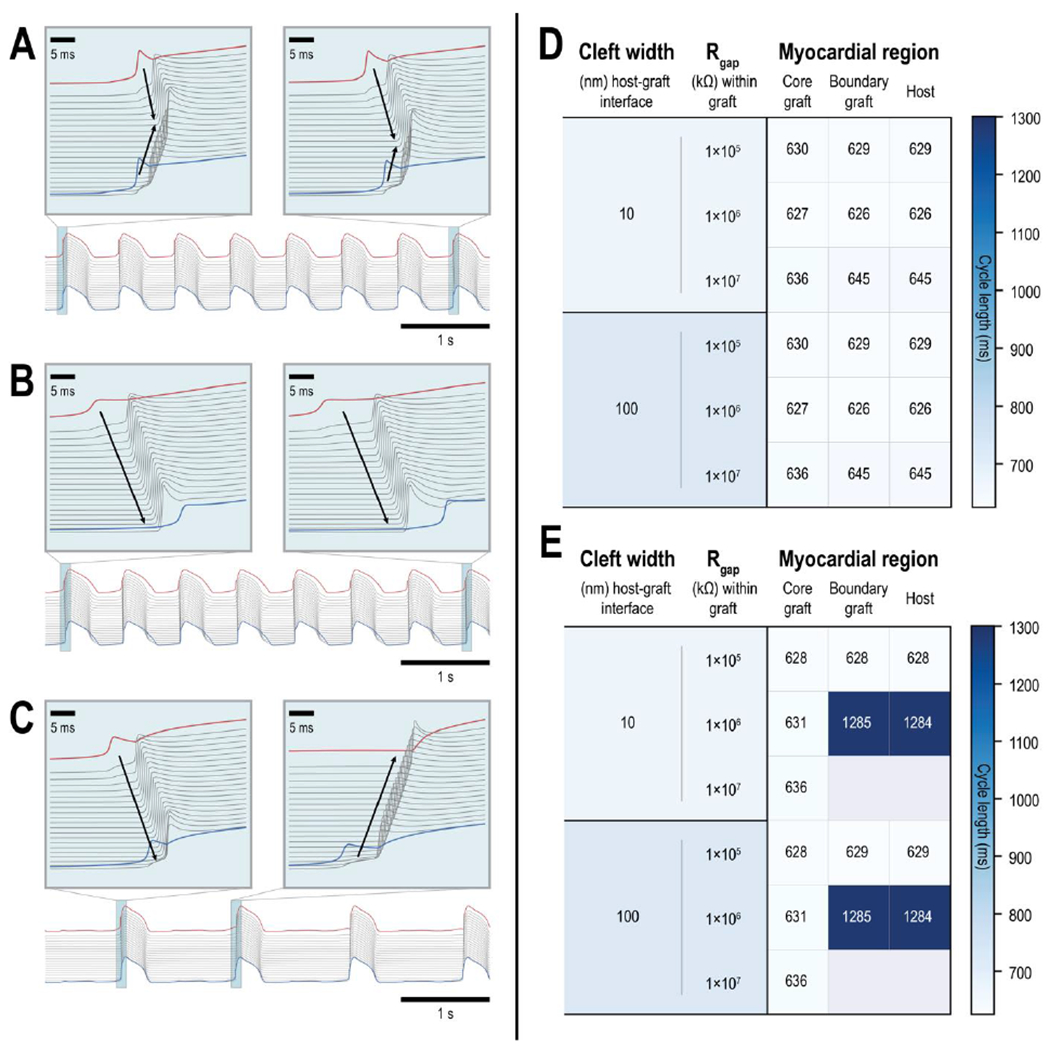
(A-C) Action potential (AP) traces of the 2 boundary graft PSC-CMs (one at either end of the graft, red and blue traces) and all 20 host CMs (grey) demonstrate a variety of graft-induced spontaneous ectopic propagations. (A) An instance where ectopic beats emerged from both ends of the graft myocardium; electrical waves consistently emerged from distal ends of the graft and collide in the host myocardium (inset). (B) An instance where ectopic beats only emerged from one side of the graft; ectopic beats (inset) were triggered by a particular boundary PSC-CM (red) and electrical waves propagated across the host myocardium to the other distal boundary PSC-CM (blue). (C) An instance where ectopic beats emerged from different ends of the graft. The first ectopic beat (inset, left) was triggered by a particular boundary PSC-CM (red) but subsequent ectopic beats (inset, right) emerged from the other boundary PSC-CM (blue). (D-E) Heat maps show the average cycle lengths of spontaneously beating core and boundary PSC-CMs (left and middle columns, respectively) and graft-induced ectopic propagations across ventricular CMs in the host myocardium (right column) across different graft coupling configurations. Within the graft, three different values of gap junctional resistance (1×10⁵, 1×10⁶, and 1×10⁷ kΩ) were tested in combination with ID cleft widths of (D) 10 and (E) 100 nm. Gap junctional resistance at the host graft interface was 3.4×10⁴ kΩ and ID cleft widths of 10 and 100 nm (top and bottom, respectively) were also tested. (E) Instances of 2:1 capture and complete block were observed between core and boundary PSC-CMs when ID cleft width was 100 nm between PSC-CMs in the graft.

In summary, we showed that a single contiguous nascent myocardial graft of PSC-CMs can generate a diverse array of proarrhythmic spontaneous ectopic propagations. Ectopic propagations were observed to emerge from several or a single distinct site along the host-graft interface. Moreover, the site where graft-induced ectopic beats emerged was also observed to change between consecutive beats. 2:1 capture and complete block between host and graft were observed when ID cleft width between PSC-CMs was 100 nm.

4. Discussion:

This study provides a comprehensive in silico investigation of the biophysical mechanisms that could underlie EAs—specifically those of altered impulse formation and impulse propagation within the graft, at the host-graft interface, and between host and graft myocardium. In a series of experiments spanning various scales of structural hierarchy, we first sought to determine whether and how a graft-induced focal driver could underlie EAs—as concluded in two recently published in vivo studies[7, 8]. New key biophysical details were integrated into the representation of intercellular electrotonic junctions because PSC-CM engraftment following their injection does not resemble any pathophysiological or developmental process in vivo. These included the voltage dependence of gap junctions and the formation of a cardiac ephapse. Both could impact emergent dynamics of EAs during the initial stages of engraftment when GJC is extremely poor. The possibility of EpC was considered in part because the spacing between adjacent PSC-CMs during the initial stages of engraftment remains unknown in the absence of extracellular matrix scaffolding and mechanical fascia adherens and desmosomal junctions. It was also inspired in part by the fact that NaChs become localized at the ID in maturing PSC-CMs, similar to that during normal cardiac development and maturation[19]. Thus, we secondly sought to determine the effect of NaCh localization in PSC-CMs on the beating rate, synchrony, and electrical conduction within the graft and at the host-graft interface. We summarize and discuss our key findings below.

4.1. Mechanism(s) and dynamics of EAs following intramyocardial PSC-CM injection: working model

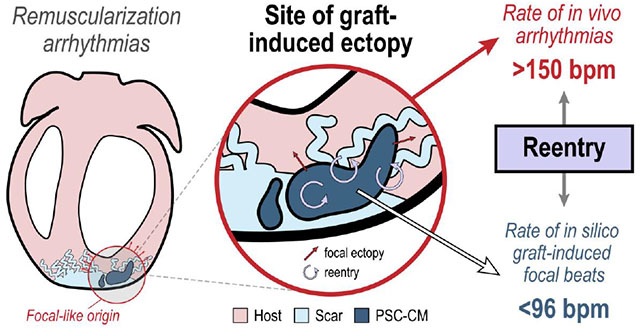
The first key finding is that a reentrant driver mechanism likely contributes to EAs with fast rates. This was highlighted by the fact that the rate of graft-induced focal beats never exceeded 96 bpm across all of our in silico experiments investigating host-graft interactions. The fact that in vitro PSC-CMs spontaneously beat at a fraction of the rate of in vivo EAs (^~60 bpm[43] vs >150 bpm[3, 6–8]) has always perplexed us. While there is little doubt that graft-induced focal triggers occur[7, 8, 27, 44], the incongruence in these two observations highlighted the fact that the underlying mechanism of EAs remained poorly understood. Moreover, the emergence of EAs following intramyocardial PSC-CM injection also drastically differ from observations in the biological pacemaker field[43, 45]. In biological pacemaker studies, spontaneous ectopic beats emerged from transplanted pacemaker cells at or below sinus rate in vivo. Pacemaker cells were also observed to beat faster than ventricular-like PSC-CMs in vitro[43]. One notable difference between in vivo biological pacemaker and remuscularization studies has been in cell dosing (^~1×10⁶ vs. 1×10⁹ cells, respectively), however. Can this alone contribute to EAs? Larger islands of engrafting PSC-CMs would make additional coupling heterogeneity and the emergence of more complex focal dynamics possible[46]; slow conduction through a larger graft would also support reentry though.

In our simulations, spontaneous beats in graft myocardium were also observed to not always elicit ectopic beats in host myocardium. Intermittent capture between host and graft myocardium occurred in part because gap junctional currents were attenuated by voltage dependent inactivation. More complex dynamics did not manifest such that focal beats emerged at rates comparable those of EAs observed in vivo. Asynchrony between PSC-CMs at distal sites of the graft myocardium did not give rise to frequency doubling of elicited ectopic beats as we had originally hypothesized. For example, each PSC-CM might beat at ^~60 bpm but elicited spontaneous ectopic beats could emerge at a rate >120 bpm because asynchronous PSC-CMs at different sites within the graft served as focal triggers each time the host myocardium repolarized. Such dynamics did not emerge because depolarizing current sources provided by PSC-CMs, whether via GCJ or EpC, were not consistently sufficient to depolarize host ventricular CMs to threshold. To the best of our knowledge, there are not significant differences in sodium current dynamics that would affect the excitability of host myocytes across mammalian species. Moreover, source-sink interactions between host and graft CMs only served to depress PSC-CM automaticity even though sufficiently poor electrotonic coupling could entrain PSC-CMs to a slightly faster rate (89.6 vs. 83 bpm). Asynchrony of PSC-CMs at distal sites of graft myocardium did give rise to changing activation sequences of ectopic propagations though (Fig. 5). This result is supported by the observation that in vivo EA morphologies were observed to spontaneously change within a particular subject[8]. In total though, we conclude that a reentrant mechanism is likely to contribute to EAs in order to account for the difference in rate of spontaneous ectopic propagations in our experiments and in vivo VT rates.

Cognizant that our in silico model might not capture the various complexity of in vivo conditions (see Limitations), we propose a more conservative working model—that EAs arise from a combination of focal and reentrant mechanisms (Fig. 6A) and that the contribution of each shifts with time (Fig. 6B). It has been hypothesized that the initially elevated presence of nodal-like PSC-CMs (i.e., selection for a ventricular-like subtype during differentiation is not perfect) can underlie EAs with a focal mechanism[38]. While nodal-like PSC-CMs beat faster than ventricular-like PSC-CMs[38, 43], the question of how such a rapid focal rate arises remains though. Does a single dominant focal source drive EAs or do multiple asynchronous focal sources give rise to EAs with rapid rates? Of the two possibilities, we believe that the latter is more plausible for two reasons. While nodal-like PSC-CMs do spontaneously beat much faster than ventricular-like PSC-CMs, especially under beta-adrenergic stimulation[43], they only make up a very small fraction of the PSC-CMs[38] unless specifically differentiated for[43]. Once electrotonically coupled in vivo, the emergent automaticity rate is affected by source-sink effects—both by slower beating ventricular-like PSC-CMs as well as host CMs in the ventricles[47]. More broadly however, focal EAs could also be driven by triggered activity in PSC-CMs arising from localized hypoxia or adrenergic supersensitivity[48, 49]. However, two observations suggest that these mechanisms do not dominate. First, the remuscularization of a non-infarcted heart in a recent study also resulted in widespread VT that degenerated into ventricular fibrillation[50]. While the non-infarcted heart would have improved vasculature compared to an infarcted heart, we are cognizant that the size of nascent myocardial grafts would play a role though. Second, the administration of metoprolol, a beta-1 blocker, did not have a significant effect on EAs. Progressing from the acute engraftment stage, the improvement of PSC-CM and host-graft coupling would shift EA mechanisms from a focal to a predominantly reentrant one. Improved coupling would have the combined effects of slowing down the rate of graft-induced focal triggers, as well as enabling electrical conduction albeit initially slow. Along this time course where EAs transition from a focal to a predominantly reentrant mechanism, both focal and reentrant drivers could simultaneously exist. The question remains whether engraftment and maturation heterogeneities can give rise to EAs driven by dynamical chaos[51–54]. Exploring this in silico however, would require extensions to 2D[55] and 3D[56] with considerations for differences in the size of host and graft myocytes, which is not trivial. Further improved electrotonic coupling would shift the EA dynamics to that of a focal trigger and reentrant driver. In the chronic PSC-CM engraftment stage however, reentrant mechanisms would dominate. Reentrant pathways sustaining EAs could run through globular islands of engrafting PSC-CMs or around the existing fibrotic substrate of host myocardium. Repolarization dispersion—caused by either localized, slow electrical conduction or adrenergic supersensitivity (graft myocardium is not innervated[57, 58])—across graft myocardium can serve as locations vulnerable to unidirectional conduction block and the initiation of reentry[58–60]. Continued in vivo PSC-CM maturation[6–8, 22, 24, 61] and improvement in host-graft coupling would further reduce the rate of graft-induced focal triggers. This could explain the prolonged persistence of VTs in observed in Shiba et al.[3] that were not observed in other in vivo studies[7, 8, 50].

Figure 6: Working theory of engraftment arrhythmia (EA) mechanisms.

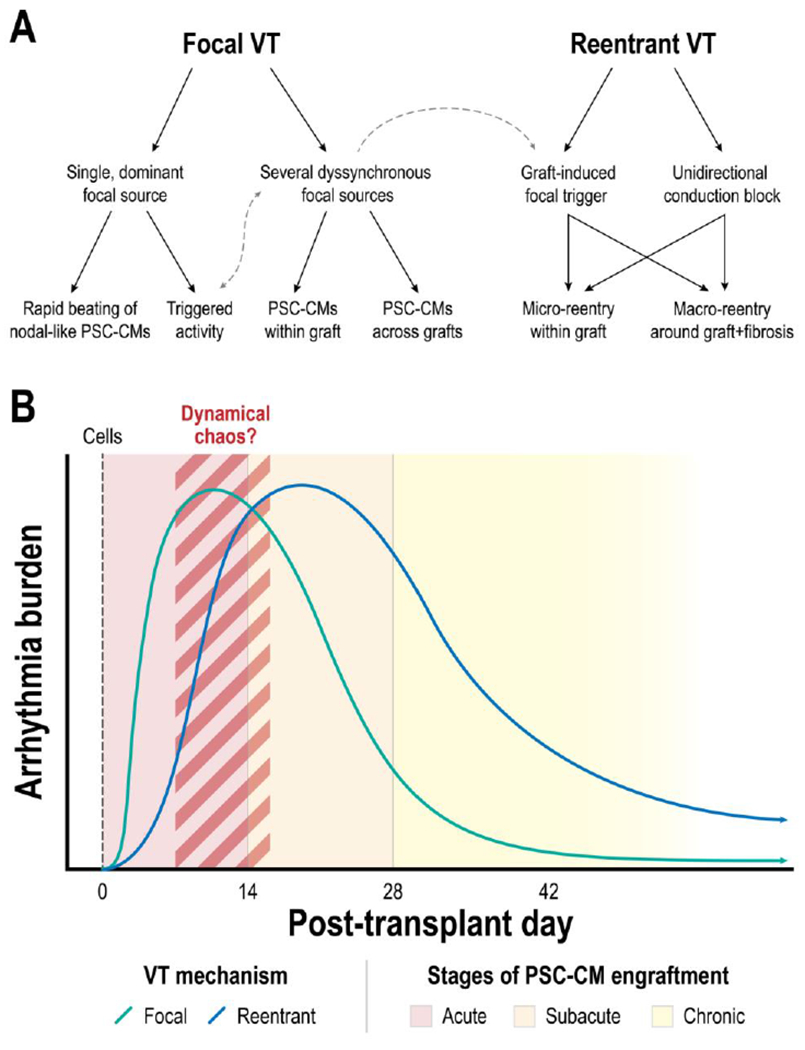
(A) Tree diagram of possible VT mechanisms and their interactions. (B) Time progression of EA mechanism after PSC-CM transplantation. EAs are initially dominated by a focal mechanism but subsequently transitions to a reentrant mechanism.

4.2. GJC dominates over EpC when it comes to dynamics within the graft and across the host-graft interface

The second key finding was that GJC continued to have a dominant effect on graft and host-graft dynamics. Voltage gating of gap junctions played a role in promoting asynchrony within the graft and intermittent propagation of spontaneous ectopic beats at the host-graft interface. NaCh localization at the ID in PSC-CMs had minimal effect on graft dynamics in part because EpC was greatly reduced within the graft. EpC was reduced because peak I_Na was diminished in spontaneously beating PSC-CMs. The latter arose because MDP was elevated in PSC-CMs. The consequence of this was that reactivation of I_Na inactivation gates (h, j) during diastole was incomplete. As a result, EpC was unable to enhance beating synchrony in a graft of PSC-CMs nor facilitate electrical wave propagation, despite localization of NaChs to the ID. Despite this, clustering of NaChs at the ID was observed to promote asynchrony when cleft width was 10 nm and GJC was 1×10⁶ kΩ in a linear strand of PSC-CMs. Differences in NaCh clustering at the host-graft interface promoted entrance block and preferential conduction slowing of electrical impulses into the graft, however. In coupled host-graft tandem simulations, we were intrigued by the fact that cleft width only impacted rates of PSC-CM automaticity and spontaneous ectopic beats in host CMs when coupled in a ratio 1:4 and not 1:1. The former is more representative of the staggered and branching organization of adjacent CMs in the ventricular myocardium in vivo.

4.3. An open question: mechanism of spontaneous, graft-induced ectopic beats between small, spontaneously beating PSC-CMs and large ventricular CMs

To us, the conflict between experimental and in silico[62] research results presents a glaring paradox—that is how are source-sink effects so robustly overcome. We showed that PSC-CM size plays an important role in the ability to elicit spontaneous ectopic beats in a host ventricular CM (Fig. S2). In additional experiments not shown, upwards of 10 PSC-CMs with representative dimensions such as those observed in vitro (radius: 6 μm, length: 18 μm) were unable to generate sufficient inward current to elicit a spontaneous AP in a single host ventricular CM. This would be further exacerbated if we were to consider coupling additional ventricular CMs[62]. Nowhere in heart biology does such a stark transition of myocardial composition occur over such a large area. The sinoatrial node (SAN), the natural pacemaker region of the heart, is electrically isolated from the right atrium due to fibrosis[63, 64]; different cell arrangements have been proposed (i.e., gradient vs. mosaic)[65, 66] to overcome this source-sink effects and enable the formation and propagation of a sinus beat. Similar observations have been observed with transplanted biological pacemaker cells, however; they have been observed to elicit spontaneous ectopic beats in vivo without the addition of some form of electrical insulating[27, 43, 44]. Moreover, a smaller number of cells are transplanted which make the outcome all the more surprising because source-sink effects are further exacerbated. To our knowledge though, we have not found studies where long-term follow-up has been done[45]. In other in vitro studies that have investigated the electrotonic effects of non-myocytes like fibroblasts[67], myofibroblasts[68], and macrophages[69], immature PSC-CMs[70] or neonatal CMs[71] have been employed where cell sizes have been comparable; the electrotonic impact of fibroblast size relative to CMs has been further acknowledge in an in silico study[72].

This modeling and experimental paradox has led us to hypothesize that alternative or compensatory biophysical conduction mechanisms might underlie the emergence of focal beats in remuscularization and biological pacemaker fields that lie outside of what might be observed in physiology or pathophysiology. Could extracellular nanodomains play a role in overcoming source-sink effects in the processes of impulse formation and propagation[73]? Electrical impulses in the sinoatrial node were recently observed to be much more heterogeneous and asynchronous than previously thought[64]. Using high resolution optical mapping, individual pacemaker cells were observed to not spontaneously depolarize adjacent to those that did; moreover, a diverse array of spontaneous intracellular Ca²⁺ oscillations within and among pacemaker cells in the central SAN was observed. Outside the field of cardiac electrophysiology, EpC have been observed to promote synchrony and asynchrony[35, 74] in neuroscience; the biphasic nature of EpC added additional dynamic complexity.

4.4. Clinical and Physiological Implications:

Although a significant challenge to clinical translation, EAs in PSC-CM remuscularization provide a unique opportunity to hone our understanding of electrical impulse formation and propagation in the heart. PSC-CM engraftment in vivo provides an opportunity to bridge disparate experimental observations across different cardiac pathophysiologies, integrate and refine our existing in silico models of electrotonic coupling and electrical wave propagation, and probe the evolving dynamics of electrical communication in the developing and diseased heart. This is due in part because PSC-CM engraftment does not resemble any pathophysiological process; ventricular CMs are mechanically anchored to one another throughout cardiac development. In this context, compensatory or additional biophysical mechanisms could underlie electrotonic interactions that do not manifest in normal physiology and even pathophysiology. A broader and more cohesive understanding of these fundamental principles would certainly help us develop strategies to mitigate EAs. Based on our current findings and analysis, we propose the following areas of exploration in decreasing priority for mitigating EAs: (1) cell dosing, (2) engineered Cx43 with controllable ligand gating, and (3) PSC-CM maturation. Out of the three, testing cell dosing is the easiest. The impact of reducing not just overall cell dose, but dose per injection to a particular site should be studied. This follows from the incongruent observations between the remuscularization and biological pacemaker fields. The motivation for the second strategy is the fact that GJC played a dominant role in graft synchrony and facilitating electrical conduction. Given that PSC-CM maturation in vitro remains elusive, EAs mitigated or reasonably controlled by keeping Cx43 expressed by PSC-CMs inactivated (i.e., unable to pass junctional currents) until sufficient gap junctions have been formed.

4.5. Limitations:

The primary limitation of the present study is the simplification of the cleft shape at the ID. The cleft space at the ID is known to be tortuous and irregular in the adult heart in both physiology and pathophysiology[40]. The dynamics of ID formation between ventricular CMs and PSC-CMs remain uncharacterized but has been shown to occur[7, 8]. The validity of a bulk cleft and homogeneous cleft width assumption for multiple PSC-CMs electromechanically coupled to a single ventricular CM is unknown. Among engrafting PSC-CMs, the ID between amorphous PSC-CMs remains unclear much like in embryonic CMs during cardiac development[19].

Another limitation is the fact that simplified membrane kinetics were implemented for both PSC-CMs and host ventricular CMs. Introduction of a constant depolarizing current (I_d) to the LR1 model was a simplified representation of I_f and captured the essence of PSC-CM automaticity. PSC-CM automaticity in vitro and in vivo has been attributed to interactions between spontaneous sarcoplasmic reticulum (SR) Ca²⁺ release[75] (Ca²⁺ clock) and with membrane ion channels, pumps, and exchangers[27, 28, 76, 77] (membrane clock) much like it is the sinoatrial node[78]. Implementing the added complexity of a biophysically-detail PSC-CM membrane kinetic model such as the Paci et al. formulation[48] that incorporates this resulted in an incredibly stiff numerical system that made numerical integration intractable. Advances on this front would pave the way for more biophysically detailed experiments exploring the added contribution of SR redistribution[77, 79] that occurs in both PSC-CM and in vivo CM maturation.

Finally, we did not incorporate various in vivo spatiotemporal dynamics into our in silico experiments because they have not been characterized. These include the dynamics of GJC, death and proliferation PSC-CMs, local inflammation, and mechanical forces experienced by PSC-CMs in nascent myocardial grafts. While unknown, spatiotemporal heterogeneity of GJC and its dynamics during PSC-CM engraftment could contribute to the emergence of more complex dynamics such as alternans, bistability, periodic spiking, and dynamical chaos[52]. It is known that a significant majority (>90%) of injected PSC-CMs do not survive; some of those that do survive have been observed to proliferate. We chose not to represent this in silico for several reasons. Firstly, it remains unclear how to represent dying or dividing PSC-CMs; these could reasonably impact both individual cell electrophysiology and intercellular coupling. Secondly, where apoptosis and proliferation preferentially occur (i.e., core vs. boundary regions) in nascent grafts and their temporal dynamics has not been characterized. With regards to modeling inflammation, the same reasons apply. Lastly, the mechanical forces experienced by injected PSC-CMs are undoubtably different and more complex than the various in vitro systems that integrate mechanical stretching. The question, however, is whether these mechanical forces promote synchrony[80] or induce dyssynchrony[81] relative to each cardiac cycle.

Non-standard Abbreviations and Acronyms

EA

engraftment arrhythmia

MI

myocardial infarction

VT

ventricular tachycardia

CM

cardiomyocyte

PSC-CM

pluripotent stem cell-derived cardiomyocyte

GJC

gap junctional coupling

EpC

ephaptic coupling

R_gap

gap junctional resistance

Cx43

connexin 43

MDP

maximum diastolic potential