Membership Inference Attacks Against Synthetic Health Data

Abstract

Synthetic data generation has emerged as a promising method to protect patient privacy while sharing individual-level health data. Intuitively, sharing synthetic data should reduce disclosure risks because no explicit linkage is retained between the synthetic records and the real data upon which it is based. However, the risks associated with synthetic data are still evolving, and what seems protected today may not be tomorrow. In this paper, we show that membership inference attacks, whereby an adversary infers if the data from certain target individuals (known to the adversary a priori) were relied upon by the synthetic data generation process, can be substantially enhanced through state-of-the-art machine learning frameworks, which calls into question the protective nature of existing synthetic data generators. Specifically, we formulate the membership inference problem from the perspective of the data holder, who aims to perform a disclosure risk assessment prior to sharing any health data. To support such an assessment, we introduce a framework for effective membership inference against synthetic health data without specific assumptions about the generative model or a well-defined data structure, leveraging the principles of contrastive representation learning. To illustrate the potential for such an attack, we conducted experiments against synthesis approaches using two datasets derived from several health data resources (Vanderbilt University Medical Center, the All of Us Research Program) to determine the upper bound of risk brought by an adversary who invokes an optimal strategy. The results indicate that partially synthetic data are vulnerable to membership inference at a very high rate. By contrast, fully synthetic data are only marginally susceptible and, in most cases, could be deemed sufficiently protected from membership inference.

Graphical Abstract

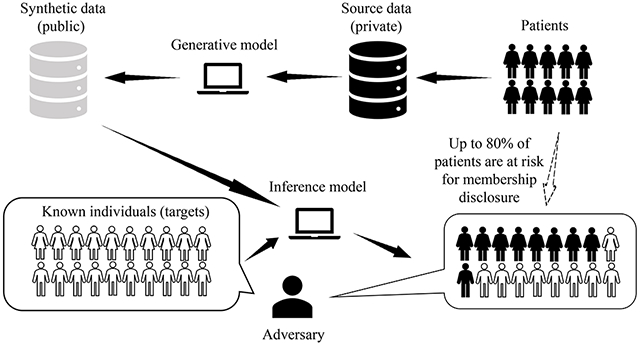
1. Introduction

The quantity and detail of personal health data has grown dramatically over the past decade, providing opportunities to conduct investigations with real-world evidence at scale. These opportunities might be greatly accelerated if the data could be widely shared in its most-specific form, but such efforts are often limited. One of the principal concerns is that the privacy of the patients to whom the data corresponds could be compromised if the data are shared at the level of detail necessary to facilitate a meaningful investigation. While it has been shown that population-level knowledge can be gained in a privacy respective manner by aggregating query responses about the data, many researchers prefer interacting with the individual-level data. In recognition of this preference, over the past several years, the notion of sharing synthetic data as an alternative to real data has gained traction [1–5]. Notably, synthetic data sharing is already taking place at scale with respect to certain collections of data from the healthcare domain (e.g., the U.S. National Institutes of Health-sponsored National COVID Cohort Collaborative (N3C) [6] and the UK Medicines and Healthcare products Agency-sponsored Clinical Practice Research Datalink ¹)

It has been claimed that the use of such approaches poses little risk to the privacy of the individuals whose data are used to compose the models for data synthesis [3, 7]. Such claims are founded on the expectation that synthetic data does not retain an explicit one-to-one match with real individuals (which enables a linkage attack, by which the data are linked to individuals’ identity with the assistance of public sources, such as a publicly accessible voter registration database [8, 9]). However, there is evidence that the models involved in data synthesis can leak information associated with the training samples [10–14], much like how certain types of machine learning models are known to do. For instance, generative models for sequential data can suffer from unintended memorization [15], whereby the synthesized features mimic, or are highly similar to, a specific training sample. As a consequence, an adversary can mount a membership inference attack [16–18], whereby they infer if targets known to the adversary were used in the synthetic data generation process. Membership inference is a privacy violation in its own right as the targets do not necessarily disclose that they visited a particular healthcare organization or participated in a biomedical research study. Moreover, when membership inference occurs, further compromises may arise. For instance, the information associated with these targets reported in the synthetic data, but not known to the adversary a priori, could be revealed as well. We further illustrate how it raises privacy risks by the following example.

Imagine that a malicious attacker Mallory gained access to a patient Bob’s health record history (e.g., via a data broker, self-disclosure by the patient themselves, or a breach of a data warehouse). At some later point in time, Bob received diagnosis x (e.g., HIV-positive) and was treated at a healthcare facility, which Bob intends to keep confidential. Then, a researcher at the facility makes public a synthetic cohort of individuals with diagnosis x based on its set patient records. Now, imagine that Mallory applies a membership inference strategy to learn that Bob’s record was included in the records relied upon to generate the synthetic cohort. At this point, Mallory learns Bob was diagnosed with x, which further compromises Bob’s privacy.

Although it has been shown that the application of statistical perturbation, such as the mechanisms inherent in differential privacy (DP) [19], may assist in the reduction of such risks; generally, they are not preferred from the perspective of the data user. That is because, for generative models, DP can lead to a significant reduction in the utility of the resulting data [4, 20, 21], rendering the synthetic data relatively inadequate for their intended purposes.

Given such problems, it is in the best interest of a data holder to consider the risk that a membership inference attack will be successful. And, based on the analysis, they can then decide if it is appropriate to share the synthesized data or if additional protections (either technical mechanisms, such as DP, or data use agreements) are warranted. It should be recognized that membership inference attacks have received a significant amount of attention over the past several years [18, 22–25]. However, such an attack in the context of sharing synthetic data is quite different from the traditional scenario of targeting models. Notably, potential adversaries can only gain access to a synthetic dataset of a certain number of records, as opposed to the trained model that generates synthetic data. (A summarized illustration of the comparison is provided in Figure 1.) Therefore, most research findings regarding membership inference in the traditional scenario cannot be applied to the synthetic data scenario. Several approaches have been developed to simulate the membership inference attack against synthetic data [10–14]; however, they are limited in several ways when being used for risk evaluation. First, many of these methods rely on assumptions about specific deep learning frameworks, such as generative adversarial networks (GANs [26]) and variational autoencoders (VAEs [27]). Second, these methods tend to assume that the synthetic data has a well-defined structure, such as those encountered in visually inspectable images. Yet data about one’s health are often longitudinal, which are not structured in a perfectly aligned manner. Specifically, each patient’s record includes multiple episodes of care, which are irregularly distributed across a timeline. Additionally, the number of such episodes and events can vary across patient records. As a result, methodology for health data synthesis is increasingly realized in a manner that episodes in the same record are sequentially generated (in a pre-defined order) based on their antecedents rather than being generated altogether at one time by a GAN or VAE [28, 29]. As a consequence, the assumptions inherent in current approaches are not always valid, rendering them less useful.

Figure 1:

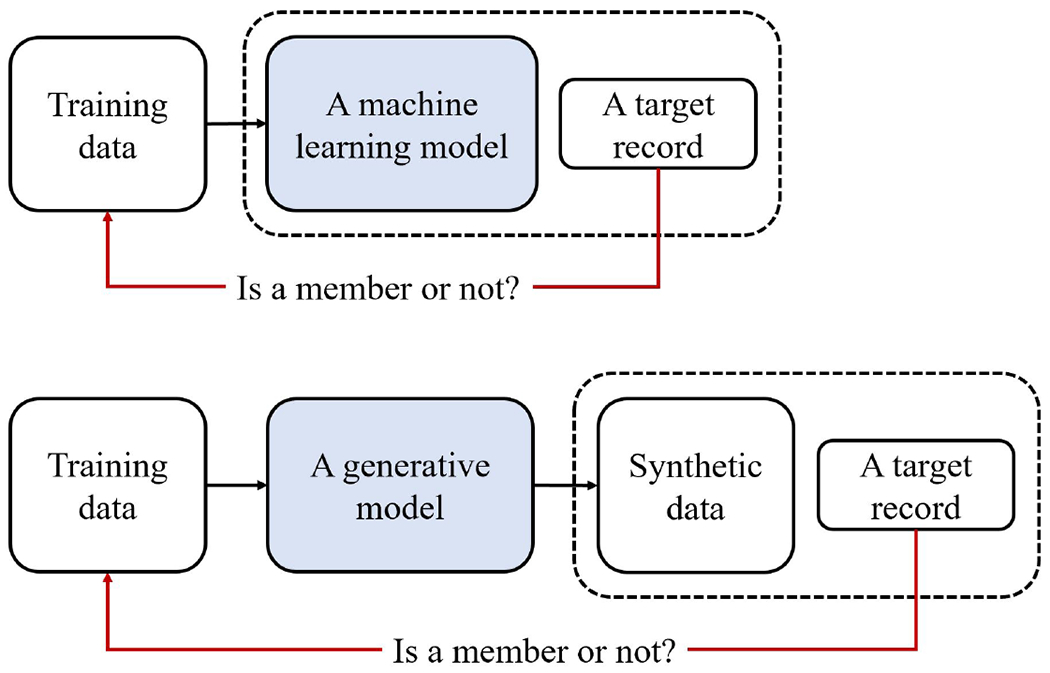
An illustration of membership inference against a machine learning model (upper), and against synthetic data (lower). The dashed box indicates the resource that can be used for inference. The shaded box represents the machine learning models.

In this paper, we introduce a membership inference framework based on representation learning. This framework is independent of the assumptions of the method involved in the synthetic data generation process. We assess the effectiveness of our method through systematic experiments with longitudinally structured diagnosis and procedure code data derived from two large clinical datasets: one from Vanderbilt University Medical Center (VUMC), and the other from the NIH-sponsored All of Us Research Program [30]. Our experimental analysis focuses on two types of synthetic data approaches that have been developed: 1) full, and 2) partial [31] synthesis. In the full synthesis setting, a generative model is learned to simulate the real data distribution and the synthetic data are then sampled from this distribution. The one-to-one association between any synthetic records and real individuals is broken. By contrast, in the partial synthesis setting, a transformation function is learned to map each real record into a synthetic record through feature perturbation. In this situation, each synthetic record has an implicit connection to a real individual. As such, fully and partially synthetic data correspond to the lower and upper bound of privacy risk inherent in synthetic data, respectively. This paper makes the following contributions:

• We empirically demonstrate that partially synthetic data is vulnerable to applications of the proposed framework, while fully synthetic data are substantially more resistant. Specifically, for partially synthetic data, we find that 82% and 44% of the individuals in the VUMC and All of Us datasets, respectively would be subject to membership inference with at least 0.9 precision (i.e., at most 10% false positive rate) if the synthetic data were shared. For fully synthetic data, membership inference can only achieve a maximum precision of 0.55 and 0.64 on any subpopulation that includes more than 2% of the individuals in the VUMC and All of Us datasets, respectively.

• We introduce a contrastive representation learning paradigm as well as a corresponding data augmentation strategy for effective membership inference against partially synthesized health data. The proposed approach exposes the risk of membership inference (i.e., the proportion of compromised individuals in the whole population) that state-of-the art baseline attacks fail to uncover. This work is notable because it shows how risk assessment can be applied before synthetic data sharing takes place. In doing so, it may help bridge the gap between synthetic data methodology and its deployment in real situations.

2. Preliminaries

2.1. Membership inference against synthetic data

In this section, we describe the data holder’s perspective regarding how an adversary conducts membership inference against synthetic data.

We begin by providing context for the adversarial setting. The synthetic health data generation process aims to produce data that serves as a substitute for real patient data. Since the model involved in the synthesis process, referred to as the target model, does not need to be shared, in this paper, we assume that membership inference functions in a black-box setting. Thus, the adversary is provided access to the synthetic dataset only and not the target model. Given this setting, we define membership inference against synthetic data as follows.

We assume the adversary possesses full knowledge for a collection of records $X=\{x_1,x_2,\dots ,x_n\}$, referred to as the known target dataset. X is partitioned into two mutually exclusive datasets. The first dataset, $X_{source}$, is involved in the synthesis process, while the second dataset, $X_{holdout}$ is not. The membership status of each record is maintained in a set of Boolean values $\{m_1,m_2,\dots ,m_n\}$, such that $m_i=1$ if $x_i\in X_{source}$ and m_i = 0 if $x_i\in X_{holdout}$. The adversary’s model is thus defined as:

$$\mathcal{M}:(x_i,X_{syn})\to \{0,1\},$$

where X_syn corresponds to the synthetic dataset.

The adversary’s goal is to resolve a maximal subset of X, $X^{\prime }$, such that

$$\frac{1}{|X^{\prime }|}\sum _{x_i\in X^{\prime }}\mathcal{M}(x_i,X_{syn})\cdot m_i>p,$$

where p is a pre-defined threshold, representing the precision (which equals to 1 – false positive rate) of the adversary’s inference committed against X.

It should further be recognized that in practice, the adversary might have prior knowledge about X_source that could be leveraged for membership inference purposes. We define the adversary model with prior knowledge as:

$${\mathcal{M}}_{aux}:(x_i,X_{syn},X_{aux})\to \{0,1\},$$

where X_aux is a dataset that is not associated with the synthetic data generation process, but is sampled from the same population as X. It is assumed that the adversary has complete knowledge about X_aux. We refer the readers to section 4.3 for a detailed description of X_aux.

2.2. Related research

To date, there have been several investigations into the feasibility of a generic approach to membership inference through models trained in an unsupervised manner - particularly for generative models [26, 27]. The typical approach creates local copies of the generative model, G, with parameter $\theta (X_{syn})$ using the synthetic data. This model is then applied to assign each known record with a likelihood that is either generated or accepted by the local copies [10, 11]. $\mathcal{M}$ is typically formulated as

$$\text{sign}[P(x_i|G_{\theta (X_{syn})})>t],$$

where sign[·] is a signum function that returns either 0 or 1 and t is a pre-defined threshold.

In the attack formulated by Chen and colleagues [12], it is assumed that, if the synthetic data pose a membership inference risk for a known record, then it must be possible to observe that the generative model overfits the record (i.e., the model assigns a higher likelihood to records that are in the training set than those that are not):

$$P(m_i=1|x_i,X_{syn})\propto P(x_i|G_{\theta (X_{syn})}).$$

However, this formulation requires an explicit density function from the generative model, which is not always available. Chen et al. [12], as well as Bilprecht et al. [13], thus propose a more generic membership inference framework. They specifically utilize the property that a membership inference risk can be observed when the synthetic data demonstrate a certain level of similarity to a target record:

$$P(m_i=1|x_i,X_{syn})\propto L(x_i,X_{syn}),$$

where L(·, ·) denotes a general notion of the similarity between x_i and X_syn. Yet, this approach is hindered in practice because it either 1) relies only upon a simple non-parameterized metric for L(·, ·) [13], rendering the approach insufficient for data with complex structure and high dimensionality, or 2) relies on specific assumptions about the target generative model [12].

Recent advancements in representation learning, however, provide an opportunity to alleviate both problems by defining the distance between the latent representations of the records. Typically, the approaches designed to support this endeavor fall into one of two groups: generative or contrastive. The former simulates the data distribution and then derives a latent form that represents the semantic features as decodable factors [32, 33]. Training generative models, which requires simulation of the data in a lossless manner, is often computationally intensive and requires excessively large quantities of data, particularly when in a sequential form (e.g., generative models for natural language: T5 [34] required 34 billion tokens to train 11 billion parameters, while GPT-3 [35] required 300 billion tokens to train 175 billion parameters). Yet, from the perspective of membership inference, acquiring a lossless representation might be unnecessary. A representation composed of a limited number of features may be sufficient to recognize a unique record instance. As such, contrastive learning [36, 37], is well-aligned with the objective of membership inference. Still, one of the challenges in applying a contrastive learning approach is how to design the augmentations (i.e., slightly modified copies of already existing records) needed for training that will maximally promote membership inference as a downstream task of representation learning.

3. A Representation Learning Method for Membership Inference

3.1. General intuition

In this paper, membership inference is accomplished through a two-step process. In the first step, we learn the representations of records that expose only distinctive features that do not replicate across records, which we refer to as a record’s “signature”. In the second step, we apply a measure to calculate the distance between the representation of a known record and the representation of the synthetic records, which can be effectively exploited for membership inference. These two steps collectively represent an implementation of function L() described in section 2.2. Additionally, L() followed by a heuristic algorithm to perform inference based on L() can be regarded as the adversarial model M().

In the synthetic data, it is possible that a record is generated with a signature that corresponds to a real record that the target model (i.e., the model from which the synthetic data are generated) never sees simply by chance. As a result, the membership inference model decision may be misguided. Intuitively, the less a signature correlates with other features, the more likely it would be incidentally replicated by a generative model. This implies that a representation learning framework should not overly focus on such signatures. For presentation purposes, we generally refer to signatures with weak correlations between features as weak-level and those with strong correlations as strong-level. Figure 2 provides an example of signatures.

Figure 2:

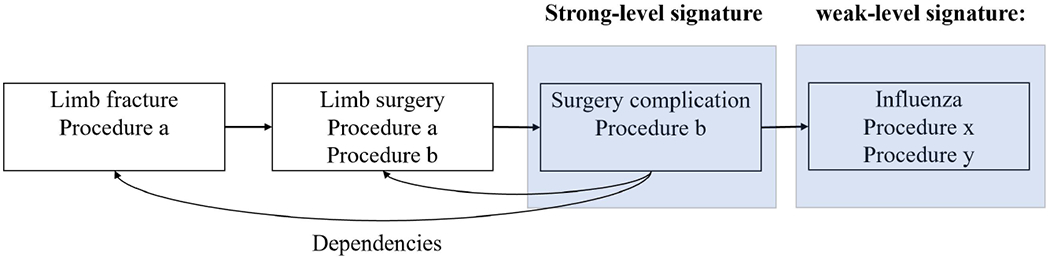
This figure depicts a patient’s health record, in which each box represents an episode, and the horizontal arrows represent the timeline. Suppose both the third and fourth episodes are unique across the dataset. Either can be considered as a signature for the patient with respect to the dataset. However, only the third episode is considered to be strong because the occurrence of this episode depends on the previous two episodes.

It should be noted that, in a contrastive learning process, the model might lack the orientation to learn strong-level signature because weak-level signatures alone may be sufficient to distinguish between records. Thus, inspired by Kobayashi and Lewis and colleagues [38, 39], we reduce the model’s dependence on weak-level signatures by increasing the variability of the augmentations’ weak-level features. Specifically, we create a proxy $\tilde{x}$ for each x, such that $P(\tilde{x})$ is similar to P(x) (Note, in the following subsections, any x without subscript denotes a synthetic record, while $x_i$ denotes a real record from the target set). We refer to this method as contrastive representation learning with proxy for augmentation (CRL-proxy). A flow chart of the membership inference process is shown in Figure 3.

Figure 3:

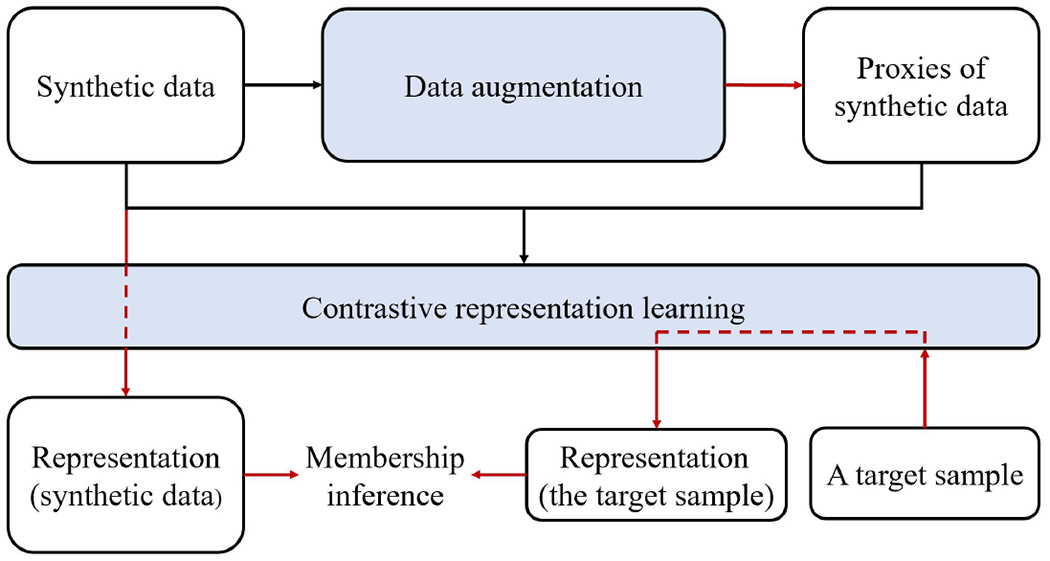
A procedural depiction of the membership inference framework. The black arrows indicate the training process while the red arrows indicate inference using the trained models.

3.2. Self-supervised data augmentation

We first organize each record x as a sequence of consecutive episodes (e.g., outpatient visit or inpatient hospital stay), denoted as $v_1,v_2,\dots ,v_l$, where v_j corresponds to the j^th episode and l is the total number of episodes, which can vary across records.

We represent each x from each v_j’s view as $(v_j^{-},v_j,v_j^{+})$ where $v_j^{-}$ and $v_j^{+}$ represent the previous and following episodes of v_j in the sequence, respectively. We then learn a transformation to map each $(v_j^{-},v_j^{+})$ to a fixed-length vector representation h_j through a pre-training task. Next, we train a conditional generative model to simulate each proxy episode ${\tilde{v}}_j$ of v_j given h_j. For brevity, we represent all of the steps of the process as ${\tilde{v}}_j\sim R(v_j^{-},v_j^{+})$. Appendix A.1 provides details on the model used for this process.

After training, we obtain a proxy $\tilde{x}$ for each x through the process described in Appendix A.2. Briefly, this is accomplished by iteratively replacing v_j with ${\tilde{v}}_j$ for each j in a random shuffling of (1, 2, …, l), where the number of iterations n is determined through empirical calibration. $\tilde{x}$ can be considered as x adding “self-adapted” noise to its features. As n increases, stronger level signatures are affected.

3.3. Contrastive representation learning

We leverage contrastive training to obtain record representations that can be used in downstream membership inference. For each $x\in X_{syn}$, we randomly select a subset X_candidate from X_syn. Next, we generate $\tilde{x}$ (that is, the proxy for x) using the self-supervised augmentation, which we subsequently add to X_candidate. Then, we use an encoder to extract each record’s, as well as each proxy’s, fixed-length vector representation e(x) and $e(\tilde{x})$ (the encoder model is detailed in Appendix A.3). The contrastive training’s objective is to minimize the following function:

$$-{\mathbb{E}}_x\log \frac{\exp (\text{sim}(e(\tilde{x}),e(x)))}{{\sum }_{x_c\in X_{candidate}}\exp (\text{sim}(e(x_c),e(x)))},$$

where $\mathrm{sim}(u,v)=\frac{1}{ϵ}\frac{{\mathit{uv}}^T}{\Vert u\Vert \Vert v\Vert }$ is the scaled dot product between the L2 normalized u and v, and ϵ > 0 is an adjustable hyper-parameter. This objective is precisely the NT-Xent loss as proposed by Chen and colleagues [40] and is equivalent to the infoNCE loss [41], which approximates the negative mutual information between a record and its proxy. In doing so, we can obtain a representation for each record containing information about its weak-level signatures.

3.4. Inference algorithm

In this subsection, we introduce an algorithm to infer the membership status of a known record. For each $x_i\in X$, if $L(x_i,X_{syn})$ is greater than a certain threshold $\tau$, we assert X_syn retain a signature of x_i and further claim x_i is in the source set to generate synthetic data. We consider two heuristics to calculate $L(x_i,X_{syn})$ given $e(x_i)$ and $\{e(x)|x\in X_{syn}\}$.

The first is the mean heuristic [12]:

$$L(x_i,X_{syn})=\frac{1}{|X_{syn}|}\sum _{x\in X_{syn}}\exp (-\text{sim}(e(x_i),e(x)),$$

This function represents an average similarity between $x_i$ and all records in $X_{syn}$.

The second is the maximum heuristic:

$$L(x_i,X_{syn})=\underset{x\in X_{syn}}{\max }\text{sim}(e(x_i),e(x)).$$

This function corresponds to the largest similarity between $x_i$ and all records in $X_{syn}$.

4. Experiments

In this section, we introduce the data relied upon for the empirical investigation. Next, we present the fully and partially synthetic data generation methods. We then describe an additional experimental setup for membership inference with prior knowledge. Finally, we illustrate the risk of membership inference against synthetic data and provide baselines for comparison purposes. Appendix B provides the implementation details of the models involved in the experiments.

4.1. Data

To investigate the performance of the membership inference methodology, we performed an empirical analysis with data derived from two distinct electronic health record (EHR) resources. The first dataset corresponds to de-identified data from VUMC. The second dataset corresponds to the publicly available Registered Tier data from the NIH-sponsored All of Us Research Program.

We structure each individual’s EHR as a sequence of episodes of care. Each episode can include multiple health-related events (e.g., the assignment of a diagnosis), while the number of such episodes and events vary across records. It should be noted that we only consider diagnoses and procedures in this process given that other types of events are not the focus of current longitudinal simulation techniques. However, this setting does not detract from the generalizability of the method or the evaluation process as we process different types of events in the same way. We refined the datasets for this study using the procedure described in Appendix C. The final VUMC and All of Us datasets used in this study were composed of 44,614 and 28,579 distinct patients, respectively. The number of healthcare episodes for each patient is limited to 200 for computational efficiency. It is unlikely that extending beyond 200 would influence the result of our investigation because only a few patients exhibit more than 200 episodes).

4.2. Synthetic data generation

There are several generative frameworks [28, 42] that have been proposed to enable the generation of longitudinal health data. SynTEG [28] supports modeling the longitudinal information (time interval between adjacent episodes) in addition to sequential dependencies between episodes, which we suspect can assist in effective membership inference. Therefore, we used the framework proposed in [28] to generate a synthetic dataset, which we refer to as fully synthetic data, to test the performance of the membership inference methods. We refer the reader to elsewhere [28] for details on the utility of the synthetic dataset generated by this framework (e.g., the extent to which it retains correlations between features and a general representation capacity with respect to building machine learning models).

Alternatively, the data holder may consider another type of synthetic data, namely partially synthetic data, which is expected to retain higher data utility than fully synthetic data. However, though it may not be explicitly revealed by the synthetic data, such superiority is attained at the expense of maintaining a one-to-one relationship between real individuals and synthetic records. To cover a wide variety of scenarios, we also generated a synthetic dataset in this manner. Specifically, we used the multiple imputation strategy proposed by Reiter and colleagues [31, 43], in which the value of each feature (i.e., episode in our case) of a real record is resampled from a posterior distribution of the feature conditioning on other features in a random order. Instead of using the original non-parametric implementation, we used a neural network-based sampling model.

4.3. Membership inference with prior knowledge

In the most challenging attack scenario for an adversary, only the released synthetic data are available. However, it is possible that the adversary has already obtained another data source (e.g., a de-identified public dataset) that is sampled from a similar population that they can use to train the target model. In the worst case scenario (for the data holder), the distributions would be exactly the same, such that membership inference would be assisted by prior knowledge about the source data distribution. This might represent a more similar distribution to the real data than the synthetic data. Moreover, if the known target dataset contains a sufficient number of records, it could provide knowledge about the real population distribution. We performed our experiments in both adversarial settings (i.e., with and without prior knowledge), as outlined in section 2.2.

4.4. Experiment setup for risk assessment

Instead of articulating the risk of membership inference in terms of adverse consequences, we frame it with quantitative values by which the data holder could make decision of whether or not to share the data. This is achieved by providing a topology between the compromised proportion of the population and the attack’s precision.

We randomly split each of All of Us and VUMC datasets into a source set X_source, holdout set X_holdout, and auxiliary set X_aux, all of equal size. The source set is applied to train the generative model, from which a synthetic set X_syn of the same size is generated. We set the size of X_syn to be the same as X_source given that the synthetic data is meant to be a substitution of the real data. We define X_source ∪ X_holdout as the known target set.

Next, we perform proxy generation and contrastive training on the synthetic set and the auxiliary set, respectively. We split the known target set into 10 partitions of the same size, according to the number of episodes associated with each record. It should be noted that the partitioning is only performed across records but not within a record. The intuition behind this step is to investigate how the number of episodes in a record (i.e., the amount of information provided by the record) influences the precision of membership inference. We apply the inference algorithm with the mean heuristic (in section 3.4) to each partition.

We assume the adversary performs an attack on each partition separately for an optimal attack performance. To illustrate the risk, we select the top 10%, 20%, 30%, 40%, and 50% of the records in the known target set with the highest risk score L() (see section 3.4 for the definition) and calculate the proportion of the selected records that are in the source set. In doing so, we obtain a topological depiction of the relationship between the percentage of individuals targeted and the attack’s precision. For instance, a precision of 1 indicates that all of the selected records are correctly inferred as members of the source data, while a precision that is no greater than 0.5 indicates that the adversary is no more successful than a random guess (due to the fact that 50% of the members of the known target set are in the source set).

4.5. Methods for comparison

To assess how well the proposed CRL-proxy performs, we compare with three alternative methods for membership inference. The following provides a summary of the baseline models, while Appendix A.3. provides further details.

Baseline 1: Likelihood estimation (LE).

This baseline is based on a pretext task performed on the synthetic data to detect the target model’s overfitting to the source data. We use the synthetic data to perform masked block modeling (which is based on masked language modeling [44]), with which we calculate the approximated likelihood of each record in the known target dataset, conditioned on the synthetic data:

$$-{\mathbb{E}}_{v_j}\log P(v_j|v_j^{-},v_j^{+};X_{syn}).$$

We claim that a record is in the source data when its likelihood is greater than a predefined threshold. [28] adopted this approach for evaluating the risk of membership inference against longitudinal synthetic data.

Baseline 2: Generative representation learning (GRL).

This method is based on representation learning with a generative model. Given that no specific generative model focusing on representation learning has been proposed for EHR data, we adopt a sequence autoencoder [45]. For each record in the known target set, we infer its membership in the source data by applying the inference algorithm with a maximum heuristic on its learned representation.

Ablation: Contrastive representation learning – local augmentation (CRL-local).

To test the importance of the proposed data augmentation principle for contrastive representation training, we set up an additional baseline where the proposed augmentation is ablated. Instead of using (x, $\tilde{x}$) as the positive-positive pair in the contrastive training process, we use (x, (x_a, …, x_b)), where a and b are random numbers with (b − a)/l being fixed.

Note that for all methods, we use the same longitudinal modeling component as the one used in the generative framework. Therefore, different methods possess equal modeling capacity, which ensures the fairness of the comparison.

4.6. Results

4.6.1. Membership inference risk against synthetic data

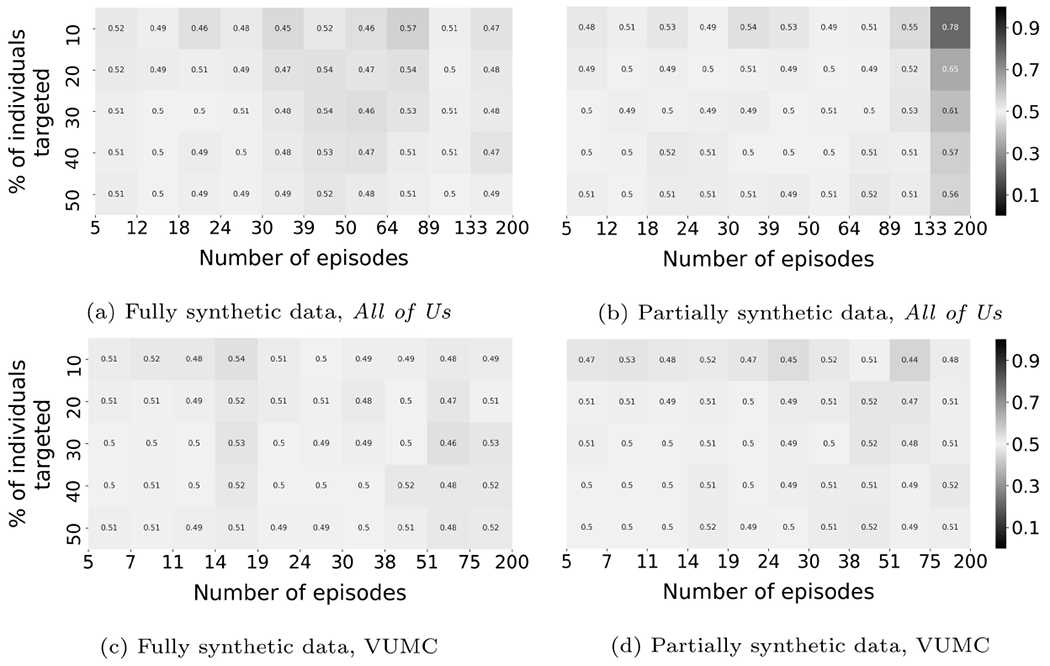
Figure 4 illustrates the membership inference risk based on the experiments with CRL-proxy. In this figure, the x-axis represents the number of episodes exhibited by a patient, while the y-axis represents a cumulative percentage of the patients the adversary conducts a membership inference attack upon. The color in the heatmap corresponds to the inference precision of the targeted subset. For example, in Figure 5a, the cell on the upper left corner represents patients with 5 to 12 episodes. When the top 10% of the targeted patients, ranked according to L(), are inferred as in the source set, the inference precision is 0.47.

Figure 4:

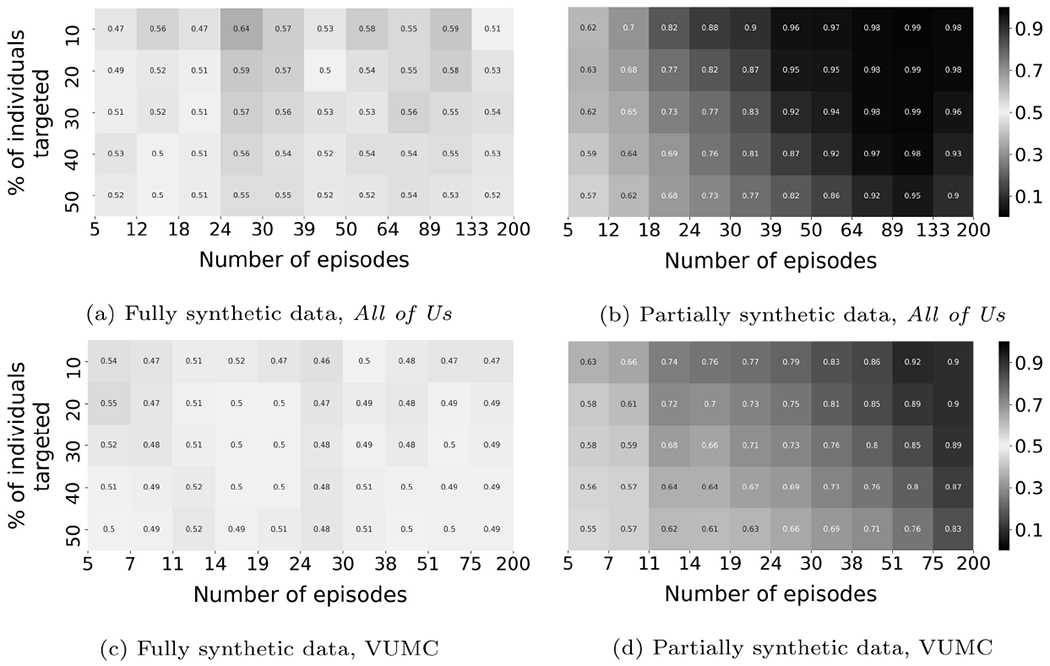
A summary of the membership inference risk against synthetic data (CRL-proxy). Each cell corresponds to a subset of all individuals who could be targeted by the adversary.

Figure 5:

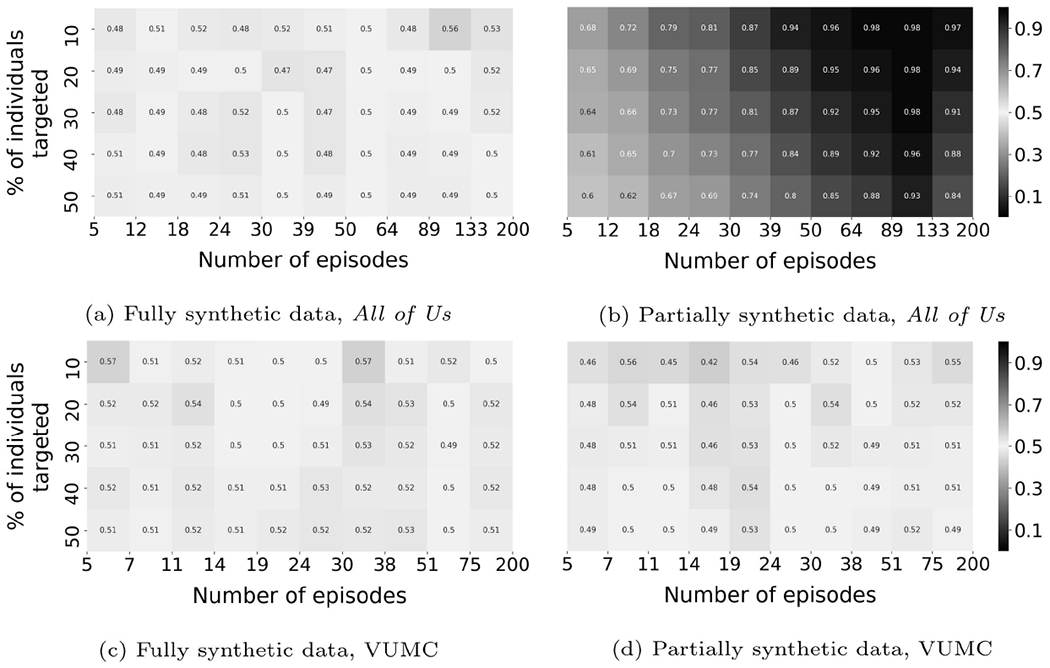
An illustration of membership inference risk against synthetic data (CRL-proxy), where the auxiliary data are used to train the adversarial model.

There are several findings on partially synthetic data worth highlighting. First, it can be seen that the risk of membership inference is non-trivial for both VUMC and All of Us data. As shown in subfigures 4c, and 4d, multiple cells achieve a precision that is significantly greater than 0.5. The size of the subpopulation vulnerable to membership inference (presented as the percentage of the entire population under consideration) with precision beyond 0.9 is 44% for the All of Us data; and 6% for the VUMC data. Now, if the adversary reduces the precision threshold to 0.7, the size of the subpopulation increases to 76% for the All of Us data; and 58% for the VUMC data. Second, the precision for the subpopulation with a greater number of episodes is higher. This is expected and indicates that the records that are more informative are more vulnerable to membership inference. Third, there is a trade-off between the inference precision and the size of the compromised population. The adversary could obtain results with higher confidence by conducting inference on a subpopulation of smaller size.

As for fully synthetic data, the risk of membership inference is substantially insignificant relative to partially synthetic data. The maximum precision that can be achieved on any subpopulation with more than 2% of the individuals is 0.55 and 0.64 for VUMC and All of Us data, respectively.

4.6.2. Membership inference leveraging prior knowledge

Figure 5 illustrates the result when proxy generation and contrastive training are performed on the auxiliary set. For partially synthetic All of Us data, the size of the subpopulation that is vulnerable to membership inference with precision greater than 0.9 is 32%; when the precision threshold is lowered to 0.7, the size of the subpopulation increases to 76%. For the VUMC data, no subpopulation is vulnerable to membership inference risk with precision greater than 0.7.

It can be seen that the inference based on prior information is close to the inference using synthetic data (section 4.6.1) on the All of Us data, but substantially drops for the VUMC data. One possible explanation for this finding is that the adversary’s model is biased to its training dataset. Since the distributions of the real and synthetic data are not exactly the same (due to the imperfect modeling in simulating the data distribution), the inference algorithm relies on different representations given by a model trained with either auxiliary or synthetic data. One of the implications of this finding is that the prior knowledge about the real data’s distribution does not necessarily help an adversary to obtain the best inference.

4.6.3. Comparison between methods

Figures 6 through 8 illustrate the results achieved by the baseline and ablation methods.

Figure 6:

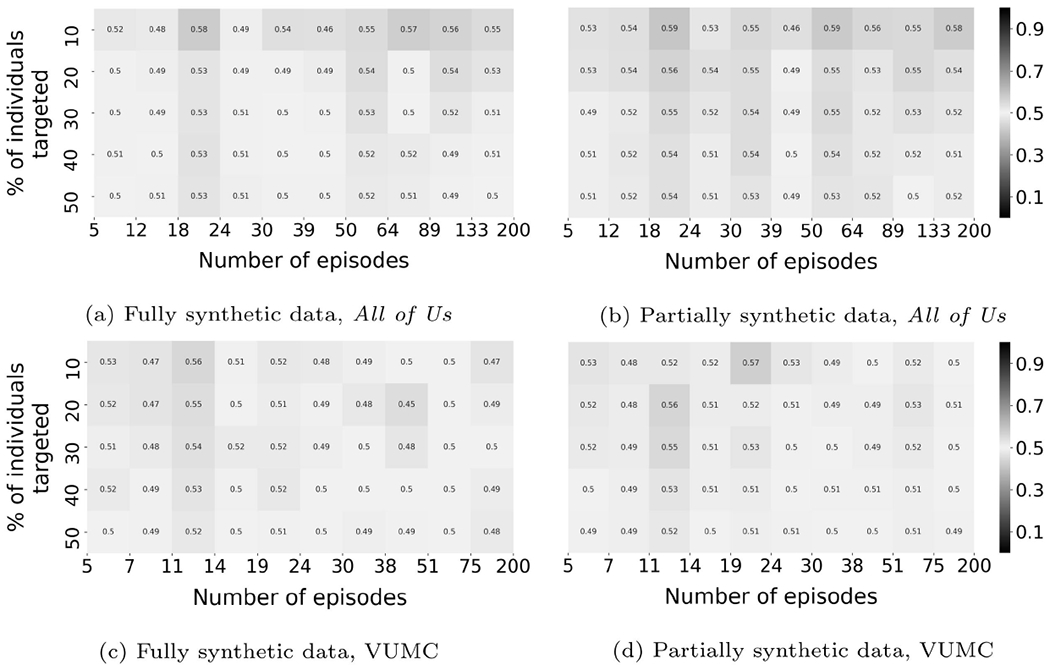
Membership inference results for LE (baseline 1).

Figure 8:

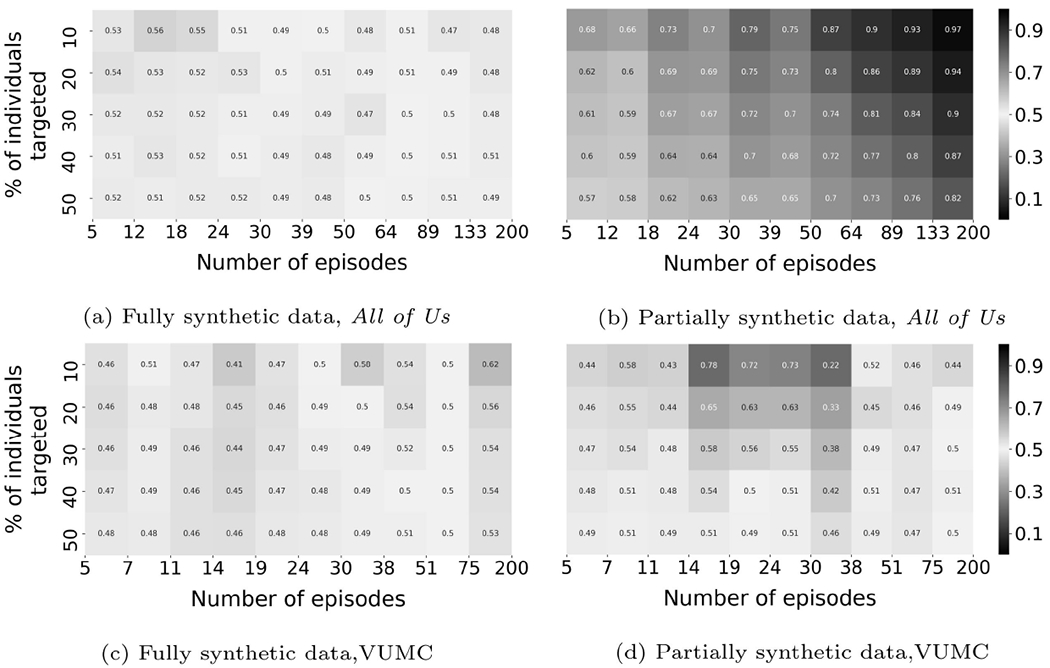
Membership inference results for CRL-local (ablation).

LE (Baseline 1):

For both datasets, no subpopulation is vulnerable to membership inference risk with precision greater than 0.7.

GRL (Baseline 2):

When the precision threshold was 0.7, GRL achieved inferential success on 2% of the population with partially synthetic All of Us data.

CRL-local (Ablation):

When the precision threshold was 0.9, CRL-local achieved inferential success on 8% of the population with partially synthetic All of Us data. When the precision threshold was lowered to 0.7, CRL-local achieved inferential success on 56% and 6% of the population with partially synthetic All of Us and VUMC data, respectively.

CRL-local has the best performance among these methods. However, none reach a performance that rivals CRL-proxy. These findings indicate that the contrastive method is better at learning useful record representations for membership inference and the effectiveness of the proxy generation step to enhance the constrastive method.

5. Discussion and Conclusion

This paper introduced a novel approach for membership inference against synthetic health data. To the best of our knowledge, this is the first approach that is not reliant on assumptions about the model involved in the synthetic data’s generation process. The results of our experiments (with two distinct collections of real world health data) show that partially synthetic data has the potential to be susceptible to membership inference. By contrast, fully synthetic data is substantially more resistant to such an attack such that it would be considered impractical. Further, the method presented in this paper could be applied as a preliminary privacy risk evaluation if any partially synthetic dataset is considered for release.

It should be noted that our model works from the data holder’s perspective. When evaluating the risk reported in the results section, we use the knowledge that an adversary may not possess: 1) the membership distribution in the known target set (e.g., half of the records are in the source set), and 2) prior knowledge about the topological patterns of relationship between the percentage of individuals targeted and inference precision (e.g., the precision of CRL-proxy is higher for records with a larger number of episodes). Therefore, the reported results could lead data holders to slightly overestimate the level of specificity in their synthetic data. A tighter approximation of the risk can be obtained when a better understanding of what knowledge adversaries have access to and what the behavioral limitations of such adversaries are is available.

We also wish to indicate that there are several opportunities for future refinements of this work. First, we relied upon the CCS coding system for EHR data, which has a more coarse feature space in comparison to other systems, e.g., the International Classification of Diseases (Tenth Revision). It is unknown how the experimental results observed in this paper will hold in other coding systems. It also remains to be seen how the size and granularity of the feature space influence the risk of membership inference. Second, our investigation considered only a subset of the available types of health data that are of interest for synthesis purposes. Specifically, we only considered well-structured diagnosis and procedure codes. However, it is important to investigate how our risk estimation methodology fares in the face of other types of medical concepts (e.g., laboratory test results and medications). Third, according to our experimental results, synthetic VUMC data are more resistant to the proposed attack than synthetic All of Us data. We suspect the primary reason for this difference is that the generative models for the datasets suffer from different degrees of overfitting in their training processes. We applied a protocol (in the form of an early stop strategy) to mitigate overfitting; however, its effectiveness varies between the datasets. It is possible that synthetic All of Us data benefits more from this protocol than synthetic VUMC data.

Figure 7:

Membership inference results for GRL (baseline 2).

Highlights (for review).

• Synthetic EHR data is susceptible to privacy intrusions, such as membership inference

• Contrastive representation learning techniques can enhance membership inference attacks

• Data holders can assess privacy risks prior to sharing any synthetic EHR data

Appendices

A. Model details

A.1. Data augmentation

Given the past and future episode of $v_j$, $(v_{j^{-}},v_j^{+})$, we first use a bidirectional language model (biLM [46]) to obtain its contextual representation:

$$\overrightarrow{h_j}=\overrightarrow{\text{LSTM}}(v_j^{-}),\overleftarrow{h_j}=\overleftarrow{\text{LSTM}}(v_j^{+}).$$

Next, we aggregate the representations into a vector:

$$\begin{gathered} h_j=\text{sigmoid}(W_{h1}(\overrightarrow{h_j},\overleftarrow{h_j})+b_{h1})\overrightarrow{h_j} \\ +(1-\text{sigmoid}(W_{h2}(\overrightarrow{h_j},\overleftarrow{h_j})+b_{h2}))\overleftarrow{h_j}, \end{gathered}$$

where $W_{h\ast }$ and $b_{h\ast }$ are trainable weight parameters.

The biLM is jointly trained with a multi-layer perceptron (MLP) to predict each v_j by minimizing the focal loss [47] between MLP(h_j) and v_j. Upon completion of the training process, we build a set of tuples of the learned representations and their corresponding episodes $S=\{(h_j,v_j)|j\}$. Then, we train a conditional generative adversarial network (where D and G denote discriminator and generator, respectively) to simulate each proxy episode ${\tilde{v}}_j$ given h_j with S from the previous step:

$${\tilde{v}}_j=G(z,h_j),z\sim \text{Uniform}(0,1).$$

Specifically, we use the EMR-WGAN implementation proposed by Zhang and colleagues [48], whose optimization objective is

$$\underset{{|D|}_2\le 1}{\max }{\mathbb{E}}_{(h,v)}{\sim }_{S;z}D(h,v)-D(h,G(z,h)).$$

A.2. Proxy generation algorithm

The proxy generation algorithm is shown in Algorithm 1.

A.3. Encoder for representation learning

We extract episode representations with a bidirectional recurrent neural network with long short-term memory unit (BilSTM) [49]:

$$g_1,g_2,\dots ,g_l=\text{BiLSTM}(x),$$

which is represented as a sequence of state outputs. To derive the record representation, we apply an attention mechanism [50] obtain an attentive embedding [51] for each record, specifically,

$$\begin{gathered} u_i=g_i^T{W}_g+b_g; \\ {\alpha }_i=\frac{\exp (u_i)}{{\sum }_j\exp (u_j)}; \\ e(x_i)=\sum _j{\alpha }_j{g}_j, \end{gathered}$$

where W_g and b_g are trainable weight parameters.

Algorithm 1: Proxy Generation

A.4. Baselines

LE:

We build a BiLSTM to predict the likelihood of each episode given its past and future episodes. The record likelihood is approximated by averaging the binary cross-entropy loss for each episode.

GRL:

The encoder-decoder architecture of the sequence autoencoder is as follows. We use a BiLSTM as the encoder to extract the latent representation of records. The records are reconstructed by predicting each episode based on its previous history with the representation as conditional information using a forward LSTM.

B. Implementation details

We implemented all of the deep learning models in this paper using Tensor-flow 2.4. Both the BiLM and the BiLSTM models are composed of 3 LSTM layers with 512 units. We use the Adam optimizer [52] with a mini-batch of 128 records for all models including a LSTM component, and 2000 for GAN models. For contrastive training, we set the size of the candidate set to 100. For all LSTM components, we use dropconnect [53] within a LSTM layer and variational dropout [54] between LSTM layers, both with dropout rate of 0.2. We also apply layer normalization [55] between the LSTM layers.

C. Dataset curation

First, we selected data to cover similar time periods of length, which would sufficiently characterize changes in clinical status for clinical concepts that evolve over time. Specifically, the VUMC data covers January 1, 2005 to December 31, 2011, while the All of Us data covers July 1 2011 to June 30, 2018, as the learning period. We acknowledge that these two resources cover different time periods, but we do not believe this influences our results, as we are not combining these resources for analytic purposes.²

Second, we reduced the dataset to focus on patients with a sufficient number of observations to support machine learning. Specifically, we restricted the set of patients to those who appear to use the healthcare facility as their medical home [56]. It was assumed that the patient used the facility as their medical home if exhibited at least five episodes in the last two years of the observed timeframe.

Finally, in lieu of computational limitations, we randomly selected 50% of the available patient records in the VUMC data.

The selected patients’ diagnosis and procedure codes in both datasets are extracted and mapped into Clinical Classifications Software (CCS)³. Summary statistics about the resulting patient populations are provided in Table 1.

Table 1:

A summary of the datasets used in this in study.

Dataset	Patients (Episodes)	Episodes Per Patient (mean, median)	Age (min, median, max)
VUMC	44,614 (1,539,183)	34, 24	0, 46, 90
All of Us	28,579 (1,037,418)	36, 38	17, 60, 87
Dataset	Gender (Male:Female)	CCS Diagnosis Codes	CCS Procedure Codes
VUMC	44%:56%	262	244
All of Us	38%:62%	282	244