Deep graph convolutional network for US birth data harmonization

Abstract

In this paper, we developed a feasible and efficient deep-learning-based framework to combine the United States (US) natality data for the last five decades, with changing variables and factors, into a consistent database. We constructed a graph based on the property and elements of databases, including variables, and conducted a graph convolutional network (GCN) to learn the embeddings of variables on the constructed graph, where the learned embeddings implied the similarity of variables. Specifically, we devised a loss function with a slack margin and a banlist mechanism (for a random walk) to learn the desired structure (two nodes sharing more information were more similar to each other.), and developed an active learning mechanism to conduct the harmonization. Toward a total of 9,321 variables from 49 databases (i.e., 783 stemmed variables, from 1970 to 2018), we applied our model iteratively together with human reviews for four rounds, then obtained 323 hyperchains of variables. During the harmonization, the first round of our model achieved recall and precision of 87.56%, 57.70%, respectively. Our harmonized graph neural network (HGNN) method provides a feasible and efficient way to connect relevant databases at a meta-level. Adapting to the database’s property and characteristics, HGNN can learn patterns globally, which is powerful to discover the similarity between variables among databases. Our proposed method provides an effective way to reduce the manual effort in database harmonization and integration of fragmented data into useful databases for future research.

Graphical Abstract

INTRODUCTION

In the United States, State laws require birth certificates to be completed for all births; and federal law mandates national collection and publication of births and other vital statistics data [1]. National Center for Health Statistics (NCHS) [2] has published the key statistics of birth data over the years. These data files, from as early as the 1970s, have been released and made publicly available. There are about 3 million new births each year, and every birth is a record in the data set described by hundreds of variables. The total data cover more than half of the current US population, making it an invaluable resource to study and examine birth epidemiology. Using such big data, researchers can ask interesting questions and study longitudinal patterns, for example, the impact of mother’s drinking status on infertility in metropolitans in the last decade or the education level of the biological father to the c-sections over the years.

However, existing published data sets cannot directly support these research questions as there are adjustments to the variables and their categories, which makes these individually published data files fragmented. The information contained in the published data files is highly diverse, containing hundreds of variables each year. Besides minor adjustments like renaming and increasing variable categories, some major updates significantly changed the fields of statistics (including removal, addition, and modification of the variables), making the published data disconnected and ambiguous to use over multiple years. Researchers have previously reconstructed features to study temporal patterns, but the scale is limited (focusing only on a few variables of interest). Many have reinvented the wheels, and such reconstructions lack consistency as different researchers might use different criteria to harmonize variables, leading to inconsistent findings and limiting the reproducibility of research. We believe data is one of the most important aspects of birth epidemiology research [3]. Since there is a database for natality data of each year, it is significant to string variables across databases to provide a unified database to the relative researchers for further and more comprehensive study. Unfortunately, there is no systematic effort to harmonize the variables from natality data of five decades.

The common way to harmonize multiple databases is conducting a manual work. Apparently, it is a daunting job to combine over 9,000 variables across 49 years (1970–2018), i.e., 49 databases, with different names, categories, and contents. To reduce the human burden, we sought automated solutions with the help of machine learning to tackle such challenges. In fact, the variables with different names in databases might indicate the same concept. On the other hand, they might have the same name in different databases. We could regard these two cases as the ‘change’ and ‘keep’ of the names of the variables. Regarding this kind of ‘keep’ or ‘change’ between variable names as a linkage between variables, our goal was to find out all these linkages among variables, and we defined a chain, consisting of all variables indicating the same concept and their linkages, as a ‘hyperchain’ for the concept. For example, Figure 1 shows a hyperchain for the concept ‘Down Syndrome’, including 45 variables from 30 databases and involving four different variable names. To harmonize all variables of databases is to obtain all hyperchains.

Figure 1:

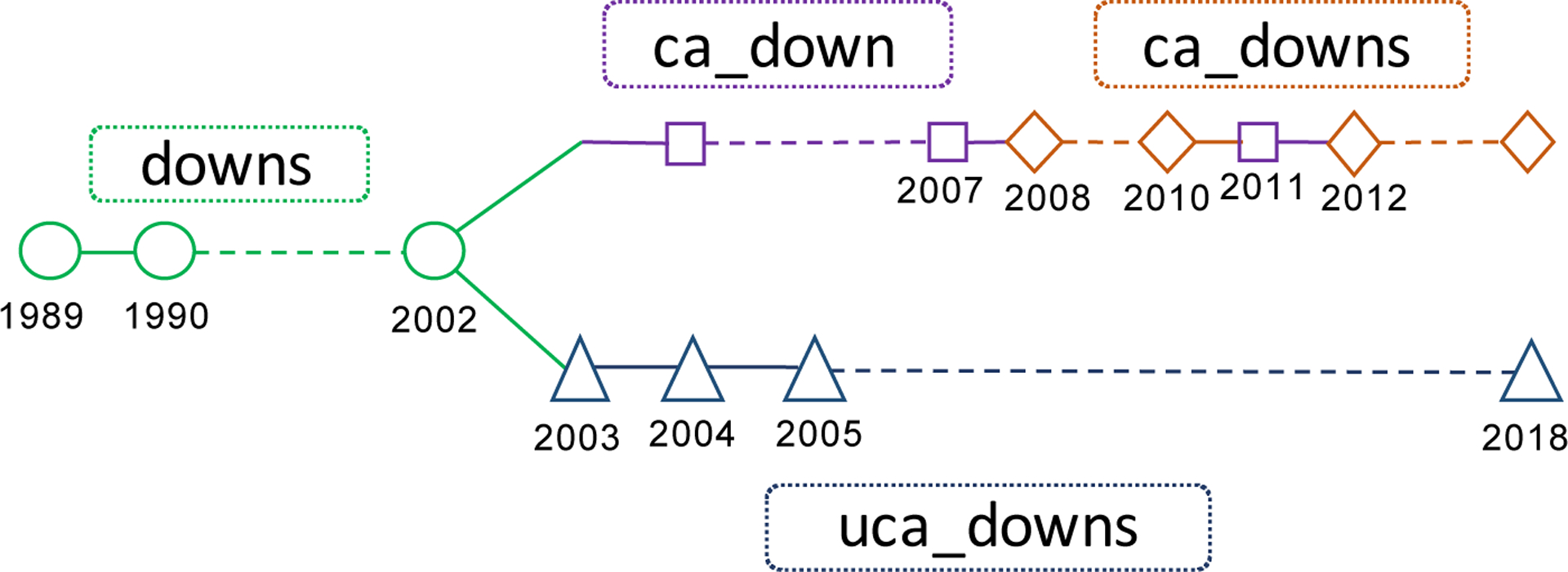
an illustrative variable hyperchain for the concept ‘Down Syndrome’, consisting of 45 variables from 30 databases and their linkages. There are 4 stemmed variable pairs: (‘downs’, ‘ca_down’), (‘downs’, ‘ca_downs’), (‘downs’, ‘uca_downs’) and (‘ca_down’, ‘ca_downs’).

The data harmonization task in this project is different from typical machine learning tasks such as classification and regression. Our task is sort of self-unsupervised (without gold standards), and results have to be confirmed by domain experts for validation of clinical accuracy. The task was challenging, and we had limited clues of linkages between variables for harmonization.

In this paper, we developed an algorithm to minimize the human effort linking variables from multiple years that were highly likely to represent the same concepts, i.e., in the same hyperchains, and verify them by the content expert in an interactive manner. Rather than identifying the local connection between any two variables in successive years, we focused on searching linkages among all variables in 49 years and returned which variables were highly likely to indicate the same concept for experts. This task can be boiled down to node similarity learning in the graph (i.e., the high similarity of variables means a high probability to be in the same hyperchain). We constructed a graph with several different aspects (i.e., variable year, variable name, variable explanation, categories, or levels of each variable), which would help in learning the correlation between variables, and learned the general representation (graph embedding) of variables. Graph neural network (GNN) has been popular since 2017 (i.e., drug repurposing, social network analysis, etc.) [4–7], thanks to its powerful inductive property and good performance in processing the data represented in graph domains[8]. A few studies applied successfully GNN on the medical domain [5,9]. GNN is a deep learning framework that can use rich observation in the network structure of a graph, allowing multiple types of information to be encoded into a general representation for future prediction. We developed a graph convolution network (GCN) [10], a model from the graph neural network family to learn graph embedding of each variable on the constructed global graph containing all variables in the natality database across 49 years, which implied the similarity of variables. We devised a loss function with a slack margin to better learn the similarity of variables and introduced a banlist mechanism to block lots of noise against similarity. We adopted a popular operation for finding similarity of variables as a baseline model. Specifically, since each variable had a phrase to explain itself, we used the off-the-shelf embeddings of words, pre-trained from a large-scale corpus, to generate the embeddings of variables and calculate their similarity. Actually, our baseline method conducted a sematic matching for variable linkages.

Our work is the first deep learning effort to connect variables in different but semantically consistent databases to the best of our knowledge. Our model can save human efforts significantly in the data curation process of linking and harmonizing variables for harmonization.

METHODS

We developed a deep learning methodology to link variables from 49 databases of the birth data for which were obtained from NCHS’ Vital Statistics across 49 years from 1970 to 2018. From the natality data, we determined characteristics of variables that might help to harmonize variables and assumed the variables sharing more characteristics were in a hyperchain with higher probability. Since we had no idea to link different variables directly, the correlation between variables and their characteristics contributed to the similarity between variables. Our basic idea was to capture the similarity between variables based on the entire information included in the 49 years. So we put all variables for harmonization and their characteristics in one graph and built a GCN model to learn their graph embeddings which implied the global correlation among all variables. The model’s key insight was that the graph embedding of variables with more common characteristics would be more similar because, in this case, the variables were expected to be in a hyperchain. Then, we could find the hyperchains by using the similarity of the graph embeddings of variables.

The variables and their characteristics as nodes in the graph formed local communities, i.e., local structure. A loss function with a slack margin and the random walk was devised to allow our method to learn the structural information flexibly (i.e., we learn the graph embedding of each node to keep neighbors in each community closer). Therefore, the variables with more common characteristics, which were likely to represent the same concept, were expected to have similar graph embeddings in the same community. There are two major technical innovations in this work: (1) the re-introduction of a slack margin for loss function (a highly successful in machine learning methods like support vector machines [11]) into a graph convolution neural network framework, and (2) the novel banlist mechanism to discourage wasteful random walks [12] to avoid learning lots of noisy patterns, speed up convergence and discard the linkage between variables with little probability in the same hyperchain.

Natality data for harmonization

From 1979 to 2018, there were 49 natality data files and 49 natality databases, one for each year. Over about half a century, NCHS had applied a lot of changes in the naming and content of its collection. Some information was no longer collected, and other information got expanded (e.g., race and ethnicity). Since some variables in different databases shared the same name and each year had only one database, we differentiate variables by denoting them as ‘Y:year-variable name’. At meanwhile, we used ‘stemmed variable’ to indicate a set of variables in years sharing the same variable name and denoted it as ‘variable name’. Each variable had a short-text label to explain its meaning in the database. A total 49 databases contained 9,321 variables and 783 stemmed variables. Some variables in databases made little sense for harmonization. Flag variable indicates whether or not the specified item is included on the birth certificate of the State of residence or of the MSA of residence (e.g., ‘fmapsrf’ in 1989 is a flag variable to indicate the existence of variable ‘fmaps’) and empty variables in the database contain nothing. After removing 2,438 flag variables and empty variables, we obtained 6,883 non-flag and non-empty variables, 519 stemmed variables. The total number of variables varied in each years’ dataset, and approximated to 140 variables per year.

Here we constructed characteristics of variables indicating the correlations between variables, which help to harmonization work. Each variable had multiple levels, e.g., the levels of the variable indicating ‘mother’s age’ meant different age groups, which were denoted by digits or capitals in the database (we called them ‘level code’). Each level code could be mapped to a level name representing the meaning of level in files. We obtained the level names of all level codes by manual work. During the annotation of level codes, we found two special hyperchains: (frace1e, frace2e, frace3e, frace4e, frace5e, frace6e, frace7e, frace8e) and (mrace1e, mrace2e, mrace3e, mrace4e, mrace5e, mrace6e, mrace7e, mrace8e) from 2003 to 2005, variables of the chains had hundreds of levels with different level codes and names from all other variables’ while other variables had less than a hundred levels. We excluded these two special hyperchains during the harmonization of variables.

Finally, we had 6,835 variables of 503 stemmed variables, containing 93,023 levels, i.e., about 13.6 levels per variable, to start harmonization work. Figure 2 shows the number of variables from 1970 to 2018 for harmonization work. Table 1 shows four variable samples, including their characteristics. eTable 1 shows all variables for harmonization in 2003, 2004, and 2005, and we could see a few variables did not remain the variable names for the three successive years. They might connect with variables with other names to form hyperchains.

Figure 2:

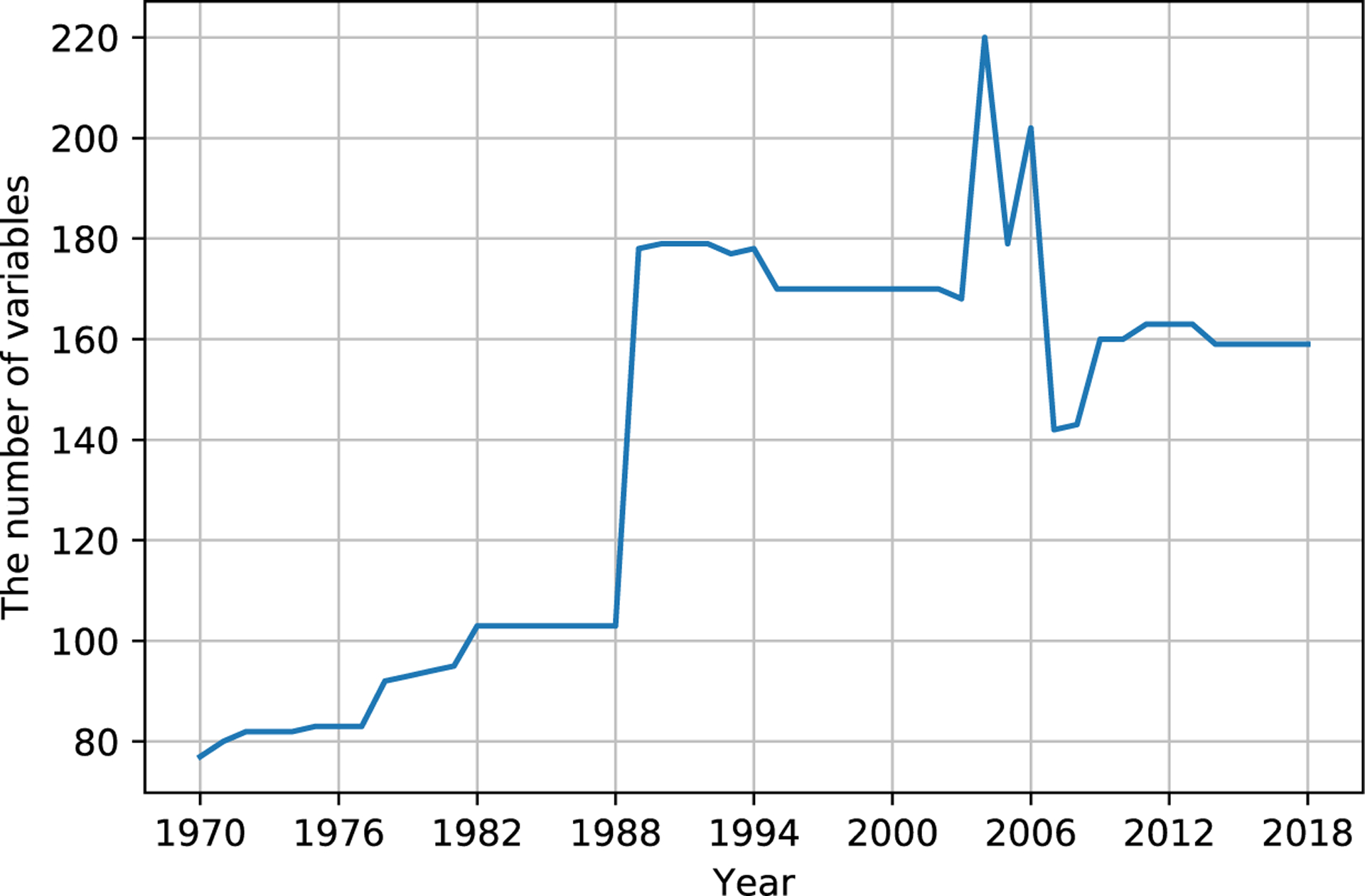
the number of variables for harmonization from 1970 to 2018

Table 1:

Four variable examples, including their stemmed variables, labels, and level codes.

Variable	Stemmed variable	Label	Level code: level name
Y:2000-regnocc	regnocc	Region of Occurrence	1: NORTHEAST 2: NORTH CENTRAL 3: SOUTH 4: WEST
Y:2000-diabetes	diabetes	Diabetes	1: YES 2: NO 8: MISSING 9: UNKNOWN
Y:2013-ab_aven1	ab_aven1	Assisted Ventilation	N: NO U: UNKNOWN Y: YES
Y:2016-ab_aven1	ab_aven1	Assisted Ventilation (immediately) Y Yes	N: NO U: UNKNOWN Y: YES

Introduction of Graph Convolutional Networks (GCN)

GCN was developed by Thomas N. Kipf and Max Welling in 2017 [10] to deal with graph-structured data. Based on the graph $G=(\mathcal{V},\mathcal{E},\mathcal{R})$ with nodes $v_i\in \mathcal{V}$ and edges $\left(v_i,v_j\right)\in \mathcal{E}$, the forward-pass update of one GCN layer is defined as follows:

$$X^{\prime }={\widehat{D}}^{-\frac{1}{2}}\widehat{A}{\widehat{D}}^{-\frac{1}{2}}X\Theta$$

Where $\widehat{A}=A+I$ denotes the adjacency matrix with inserted self-loops and $\widehat{D}$ is the diagonal degree matrix with ${\widehat{D}}_{ii}={\Sigma }_{j=0}{\widehat{A}}_{ij}$, Θ is the weight of the GCN layer, X, and X′ are input and output embedding of nodes for the GCN layer.

The input embedding to the first GCN layer can be chosen as a unique one-hot vector or present node feature, such as the pre-trained embeddings for node ν_i in the graph.

The transformation in GCN is effective in accumulating and encoding features of neighboring nodes in a graph.

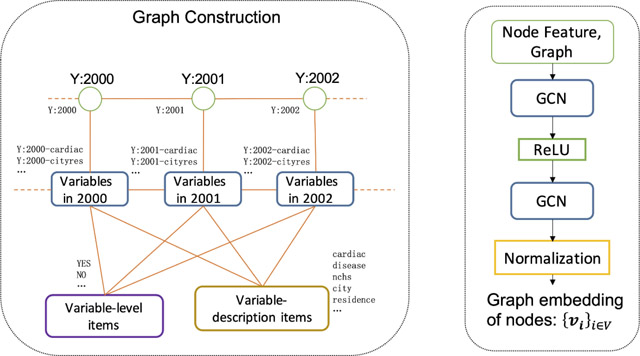
Graph construction

In natality data, there are two main characteristics of variables: (1) data description (label), (2) level name. The more characteristics the variables shared, the higher the possibility that the variables indicated the same information. We took characteristics and variables as nodes of the graph and linked variables to their characteristics to strengthen the correlations between variables. Then, each variable and its associated characteristics formed a subgraph structure in the graph. We used GCN to learn graph embeddings of nodes implying structural information.

Figure 3(a) illustrates the process of graph construction. We defined four types of nodes for graph construction: variables, variable-description items, level items, and years. Each word in the label of the variable was regarded as a variable-description item after striping the suffix ‘s’, except for the special symbols (‘[‘, ‘]’, …), words with a single character, and common words (‘for’, ‘in’, ‘on’ …). Each level name was used as a level item. In order to increase the common characteristics between variables, each word in the level name was also used as a level item after removing the suffix ‘S’ (note: ‘YES’ keep the suffix ‘S’). Table 2 shows samples of four types of nodes in the graph from the databases.

Figure 3:

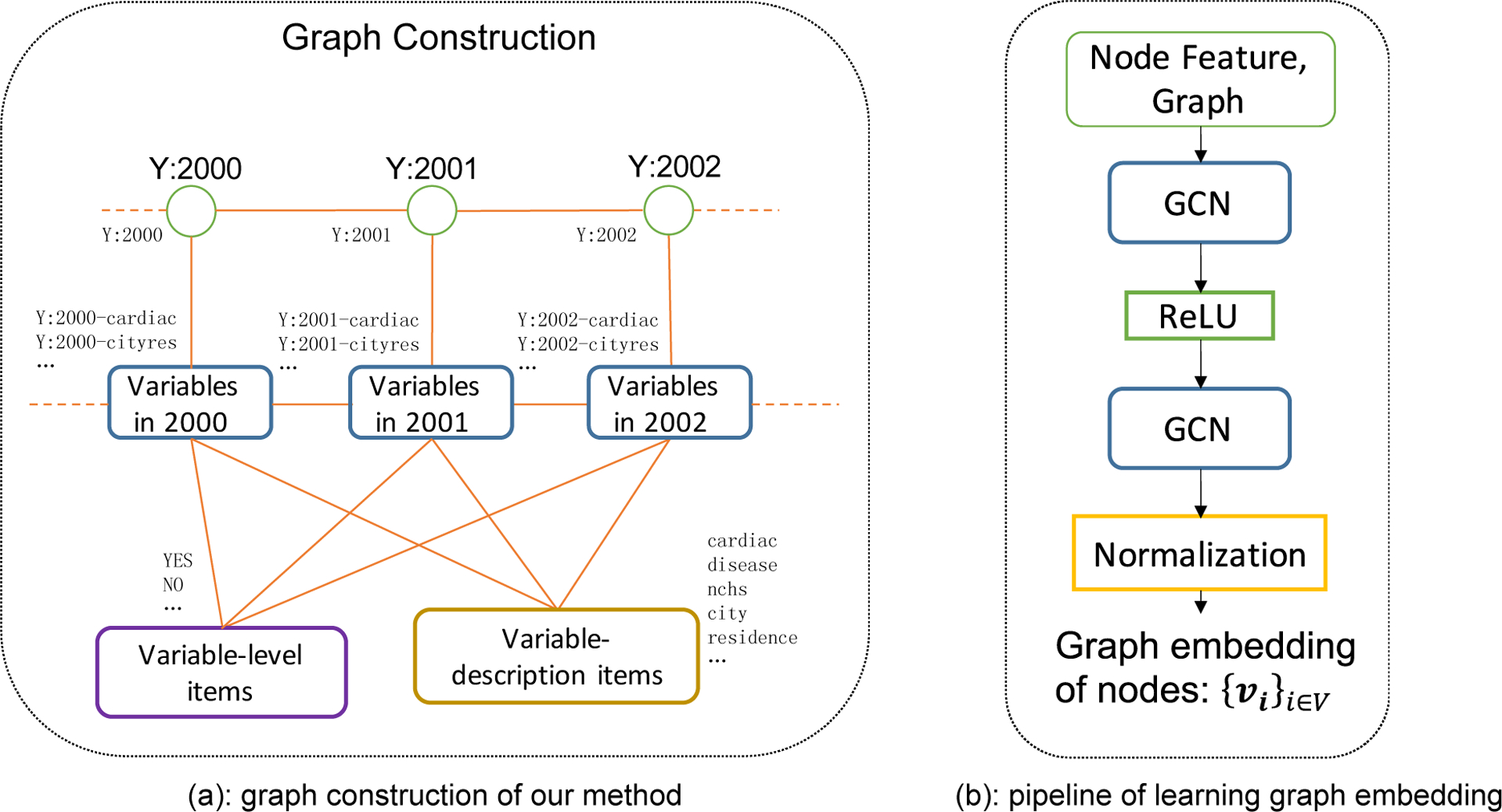
the pipeline of our method: graph construction and model architecture. (a) raw variables are connected to hyperchains over consecutive years, (b) the graph embedding learning process.

Table 2:

samples of four types of nodes in the graph from the databases

Node type	Items in databases	Nodes in graph
Variable	nprev12 (1993), anemia (1991), ume_vac (2013), othermr (2002), monprec (1970)	Y:1993-nprev12, Y:1991-anemia, Y:2013-ume_vac, Y:2002-othermr, Y:1970-monprec
Variable-description item	Detail Month Prenatal Care began (monprec, 1970)	detail, month, prenatal, care, began
Variable-level item	1 (YES) 0 (NO) 0 (FOREIGN RESIDENTS) 2 (MIDDLE ATLANTIC)	ANNO_YES ANNO_NO ANNO_FOREIGN RESIDENTS, ANNO_FOREIGN, ANNO_RESIDENT ANNO_MIDDLE ATLANTIC, ANNO_MIDDLE, ANNO_ATLANTIC
Year	1991, 2000	Y:1991, Y:2000

We linked variables to their characteristics (variable-description items, level items, and years). To improve the graph’s connection, we also linked every two consecutive years and every two successive variables in years sharing the same stemmed variables.

Finally, we have a total of 9,390 nodes, including 6,835 variable nodes, 2,102 variable-level item nodes, 404 variable-description item nodes, and 49 additional nodes indicating each year. We had 158,463 undirected edges.

Development of the GCN model

We developed a GCN model to learn and output each node’s graph embedding by using a banlist mechanism and a loss function with a slack margin.

1). Node feature as input

Each node i has words as its meaning: (1) ‘variable’ node: words in the short-text label, (2) ‘variable-description item’ node: words in node name, (3) ‘level item’ node: words in node name, (4) ‘year’ node: year in node + word ‘year’ (For example, ‘Y:1990’: ‘1990 year’).

We used the average of word embeddings based on pre-trained embeddings available online as node features of each node in the GCN model. All these embeddings were input as node features after normalization, and this paper used a 300-dimensional pre-trained embedding of fastText, which was trained by using Wikipedia and the Crawl dataset [13].

2). Model architecture and graph embeddings

We constructed a two-layer graph convolutional neural network on the constructed graph. As shown in Figure 3(b), a two-layer GCN with a ‘ReLU’ activation function was fed with node feature and graph information (nodes, edges) and followed by a normalization layer, then outputted graph embeddings of each node. For each iterative round, we obtained the graph embeddings of each node and minimized loss regarding k-step random walk and graph embeddings. We expected that the graph embeddings of two variables in a hyperchain were similar.

3). Banlist mechanism, loss function and training samples

We devised a banlist mechanism which worked during a random walk on the graph to avoid marginal linkages. We assumed there is no linkage between any two different variables in the same year since one concept always be indicated by one variable in a natality database, and assumed variables with the same stemmed variable always represent the same concept. According to the assumptions, we constructed a banlist to block the linkage of different variables in the same year, i.e., the banned variables of a variable for linkage were other variables in the same year. We also blocked the connection of variables in other years, sharing the same stemmed variable names with banned variables. The banlist mechanism consists of the definition of hyperchain and helps to reduce low-value linkage.

Each sample for model training consisted of an anchor node, relative nodes from random walking (positive nodes), and nodes from negative sampling (negative nodes). Each anchor node was from a uniform distribution on node-set V. We set the sampling distribution of each step in a random walk as uniform distribution on adjacent nodes of the current nodes, excluding the banned variable nodes of the anchor node. We set negative sampling as uniform distribution on all nodes except the anchor node. We devised a loss function with a slack margin to support graph embedding learning. The optimization on the loss function would result in high similarities between the anchor node and its positive nodes. For an anchor node, positive links were for the positive nodes, while negative links were for negative nodes. We expected that the learned embeddings of two nodes in a hyperchain would have high similarity. In the case that node A linked to multiple nodes in the graph, the similarities between any two of these nodes would be too restrictive if we used a loss function without slack margins. In reality, the existence of linkage does not mean these nodes are definitely included in a hyperchain, while in fact, there might be only a few nodes in a hyperchain. We needed to differentiate the different degree of similarities between node A and its linked nodes. Therefore, we introduced slack margins to release spaces for similarities between nodes. We used two hyperparameters φ_P, φ_N ∈ [−1,1] for the margin of positive and negative links, respectively. For example, for node A linked to node B and node C in the graph, we allow a slack margin so that the graph embedding of node B can be a bit different from that of node C. As shown in the formula, the case where φ_P,φ_N = 1, −1 meant no slack margin since the range of inner product of any two-unit graph embeddings was [−1, 1].

$$\begin{gathered} \mathit{\text{loss }}=-E_{\left\{i~d(V)\right\}}\frac{1}{k}\{\sum _{j\in R{W}_k(G,i)}\mathit{\text{log }}\sigma \left(\mathit{\text{min}}(<{\mathit{v}}_{\mathit{i}},{\mathit{v}}_{\mathit{j}}>,{\phi }_P)\right) \\ +\sum _{z\in Ne{g}_k(G,i)}\mathit{\text{log}}\left[1-\sigma \left(\mathit{\text{max}}\left(<{\mathit{v}}_{\mathit{i}},{\mathit{v}}_{\mathit{z}}>,{\phi }_N\right)\right)\right]\} \end{gathered}$$

where RW_k(G, i) is a k-step random walk on graph G starting from anchor node i, Neg_k(G, i) is k negative samples sampling from a uniform distribution on all other nodes for node i, V is the node set, d(V) is the uniform distribution on V, ν_i is the graph embedding of node i, <, > is an inner product, σ is the sigmoid function, φ_P and φ_N are hyperparameters for the slack margin of the positive and negative links, respectively.

4). Experiment setting

The number of training samples for one epoch was the length of the node set; the batch size was 256. The step of the random walk was 3 (k = 3). The output dimension for GCN was 100. The hyperparameters φ_P, φ_N for the margin of positive and negative links were 0.7 and 0, respectively. We optimized the model using Adam optimizer with a learning rate 0.0001 for 500 epochs to ensure the convergence of loss, then returned the graph embedding of each node.

Similarity between variables for finding hyperchains

We obtained top-N most similar nodes for each variable node by computing the cosine similarity score between graph embeddings and removing non-variable nodes and the banned variables of each variable. The resultant ‘similar’ variable nodes were potential variables representing the same concept. Since variables with the same stemmed variable name always indicate the same concept, i.e., will be in the same hyperchain, we focused on finding two different stemmed variables in a hyperchain in spite of the year of variables. Specifically, we obtained similar stemmed variables by removing years of similar variables and checked every pair of stemmed variables to determine whether their corresponding variables represented the same concept over the years. For checking, we extracted all variables with their labels, level codes, and names of each two similar stemmed variables for experts to identify whether they were in the same hyperchain. Figure 4 shows an example of checking a stemmed variable pair. Each corrected stemmed variable pair meant a part of a hyperchain. By doing this, we made it easier and efficient for the domain experts to verify the pairs and obtain the hyperchain.

Figure 4:

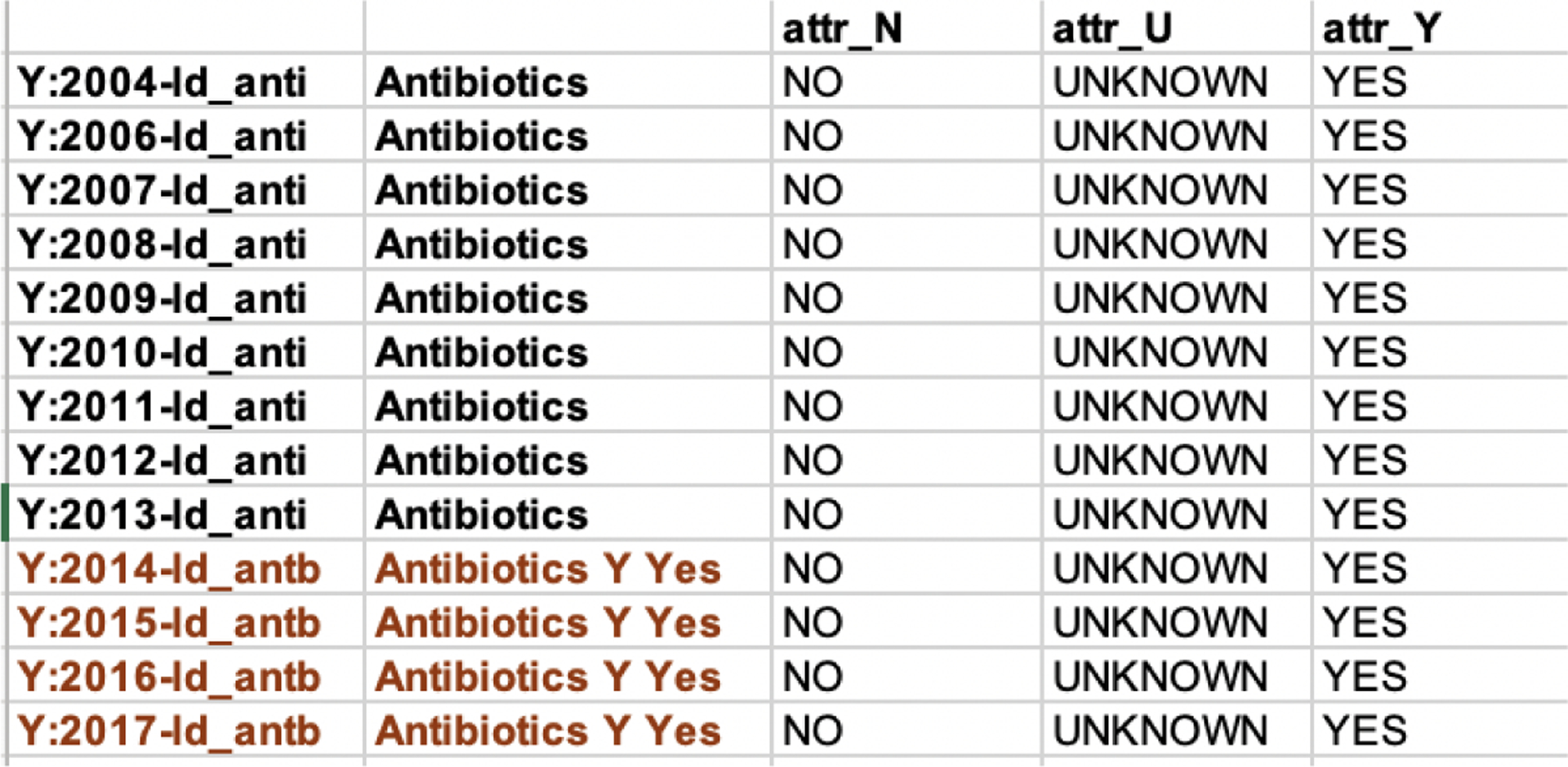
an example of checking variable pair: (ld_anti, ld_antb)

Evaluation

The task was unsupervised, and our objective was to find all hyperchains. In order to evaluate the proposed model performance on the objective, we needed to obtain all harmonized hyperchains, and then conduct a retrospective evaluation of our method. A hyperchain might consist of dozens of variables, which might be several stemmed variables, see Figure 1 & 5. As mentioned above, we found hyperchains by checking pairs of similar stemmed variables. So we would evaluate the ability of the model to find the change of variable names in hyperchains. For a hyperchain, we could convert it into a set of stemmed variable pairs where each pair of different stemmed variables meant a change of variable names of different years. For example, the hyperchain with 4 stemmed variables in Figure 1 was converted into 4 stemmed variable pairs: (‘downs’, ‘ca_down’), (‘downs’, ‘ca_downs’), (‘downs’, ‘uca_downs’) and (‘ca_down’, ‘ca_downs’). We should notice, we determined pairs based on the change of variable names in years. For the hyperchain (A(1970–1980)->B(1981–2000); A(1970–1980)->C(1981–2000)), where A, B, C are different stemmed variables, the pairs are (A, B) and (A, C) without (B, C) since B would not change to C in years (actually B and C changed from A). Then, all harmonized hyperchains were then converted into a set of stemmed variable pairs. Our goal is to find out all these correct pairs, and our method provided candidates stemmed variable pairs for experts to check. Therefore, we could use the recall and precision of stemmed variable pairs to evaluate the performance of the model for finding hyperchains.

Figure 5:

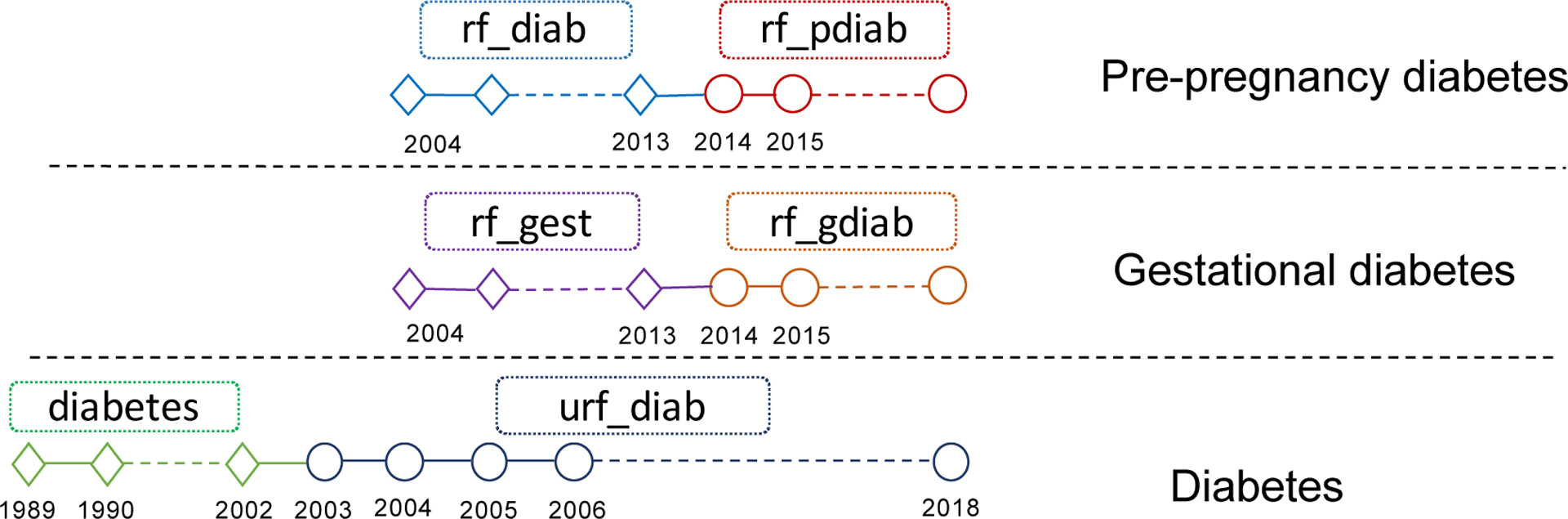
Three hyperchain samples. Each node represents one variable. Each hyperchain has one pair of stemmed variables. The critical judgment is about the connection of these stem variables between consecutive years involving stem variable name/content updates.

Baseline method

We constructed representative vectors describing variables for harmonization by using the fastText embeddings, which were trained from Wikipedia and Crawl corpus[13]. The embedding of each variable was the sum of the fastText embeddings of each word in its label. If labels of variables have a similar meaning, they would have similar embeddings. We computed the cosine similarity score between the embeddings of variables to provide candidate similar stemmed variable pairs.

RESULTS

Iterative rounds and Final variable hyperchains

We conducted our model to obtain the correct stemmed variable pairs for several rounds. Combined with human review, we found the final variable hyperchains by two steps:

1. Using our model to obtain the correct stemmed variable pairs, which were unfolded into hyperchains: We applied our model on all variables for harmonization and obtained 305 candidates of stemmed variable pairs by taking top-20 similar variables. After checking on 305 candidate pairs, we obtained 176 correct pairs, which could reconstruct 129, 15, and 4 hyperchains with 2, 3, and 4 stemmed variables, respectively. Considering stemmed variables outside of the correct pairs might have linkages, we removed all variables of the stemmed variables in the verified-correct pairs and re-ran the algorithm for the rest of the variables with the same model hyperparameters. In the second round, we obtained 37 new candidate pairs after removing the checked pairs, and we found 5 new correct pairs that could reconstruct 5 hyperchains with 2 stemmed variables after checking. We repeated the process for the third round and found 1 new correct pair among 21 new candidate pairs. In the fourth round, we found 0 new correct pairs among 12 new candidate pairs. Then we stopped the iteration. In summary, during the GCN work about the harmonization, we checked 375 candidates of stemmed variable pairs, 182 of which are correct, and found 135, 15, and 4 hyperchains with 2, 3, and 4 stemmed variables, respectively.

2. Human review for completing the hyperchains from step 1: Through human review on the obtained hyperchains, one hyperchain with 3 stemmed variables was completed to a hyperchain with 4 stemmed variables, four hyperchains with 2 stemmed variables were completed to hyperchains with 3 stemmed variables, and 5 hyperchains with 2 stemmed variables were discovered. There were several variables sharing the same variable names but having different levels in years. For this case, they were regarded to represent different concepts, and we put them in different hyperchains. There were four stemmed variables (‘dmeth_rec’, ‘dmar’, ‘attend’, ‘crace’) whose variables did not have the same levels. The variables in these four stemmed variables would be partitioned into several parts in different hyperchains after checking the level names in hyperchains. For example, ‘dmeth_rec’ (2003–2004) and ‘dmeth_rec’ (2005–2018) were different in level names, the former one was in the hyperchain [‘delmeth5’ (1989–2002) -> ‘dmeth_rec’ (2003–2004) -> ‘rdmeth_rec’ (2005–2018); ‘delmeth5’ (1989–2002) -> ‘dmeth_rec’ (2003–2004) -> ‘udmeth_rec’ (2005–2008)] indicating ‘delivery method’ with 5 levels, the latter one consisted another hyperchain indicating ‘delivery method recode’ with 2 levels.

Finally, we confirmed a total of 321 variable hyperchains. Here is a basic summary of our variable hyperchains.

1. 162 hyperchains with only one stemmed variable,

2. 136 hyperchains consisting of two stemmed variables,

3. 18 hyperchains with 3 stemmed variables,

4. 5 hyperchains with 4 stemmed variables.

Focusing on the changes of variable names in the hyperchains, we converted all hyperchains into 201 different stemmed variable pairs for retrospective evaluation of our method. Note that there were two additional special hyperchains with 8 stemmed variables (mrace1e-mrace8e; frace1e-frace8e), which were easily found during the annotation of levels before the harmonized work. In summary, we have 323 hyperchains and 201 correct stemmed variable pairs, as shown in eTable 2.

Model performance

As mentioned above, we had 201 stemmed variable pairs for evaluating the model performance. We expected one implementation round of models could help to find all pairs, so we evaluated the model for one round. Taking N = 20 (see Section Method: Similarity between variables for identifying variable hyperchains), we obtained 305 candidates for stemmed variable pairs, 176 of which were checked as correct pairs. The recall and precision of our method for hyperchains were 87.56% and 57.70%, respectively. We had 503 stemmed variables for harmonization, with a possible total of 126,253 pairs, in our study. Our method provided 305 candidate pairs with high recall, which greatly improved the efficiency of harmonization.

We provided an evaluation table of our method for different N; see Table 3. Obviously, a larger N resulted in an increased number of candidate pairs and lower precision. The recall was considerable for N > 10. Table 3 demonstrates that our model had a wide range of N for a considerate recall and precision, and we could choose an N between 15 and 30. Actually, there is no supervised strategy for choosing N. Our suggestion is to consider the number of candidate pairs. In our case, we selected N for a moderate number of pairs.

Table 3:

The evaluation table of our method for different N.

N	#(CP)	#(TVP in CP)	Recall	Precision
5	109	99	49.25%	90.83%
10	171	141	70.15%	82.46%
15	234	164	81.59%	70.09%
20	305	176	87.56%	57.70%
25	417	180	89.55%	43.17%
30	484	182	90.55%	37.60%

CP: candidate stemmed variable pairs, TVP: true stemmed variable pairs, recall = #(TVP)/ 201, precision = #(TVP in CP)/#(CP). The bold line was the result of our harmonization work.

We evaluated the model for several repeated runs. Table 4 shows the result of repeat experiments with little difference. We could see the model performance was stable.

Table 4:

Result of repeat experiments of our method (N = 20)

#(CP)	#(TVP in CP)	Recall	Precision
305	176	87.56%	57.70%
314	176	87.56%	56.05%
312	173	86.07%	55.45%
304	175	87.06%	57.57%
310	177	88.06%	57.10%

Table 5 shows our model outperformed the baseline method. The baseline provided much more candidate pairs, including fewer correct pairs than our method’s. Although the task was unsupervised and challenging, our GCN model learned the embeddings of variables based on the graph containing the correlations between variables.

Table 5:

Results of our method and the baseline method (N = 20)

	#(CP)	#(TVP in CP)	Recall	Precision
Our method	305	176	87.56%	57.70%
Baseline	900	124	61.69%	13.78%

Impact of banlist mechanism and hyperparameters including slack margin

We conducted an experiment for our method without the ban-list mechanism. From Table 6, the case without ban-list mechanism provided much more candidate pairs with a similar number of correct pairs, compared to that with ban-list. That is, the ban-list mechanism was able to prevent a few invalid variable linkages.

Table 6:

Result of the ablation experiment for the ban-list mechanism (N = 20)

	#(CP)	#(TVP in CP)	Recall	Precision
Our method	305	176	87.56%	57.70%
No ban-list mechanism	695	179	89.05%	25.76%

We show the performance of our method with various random walk steps (K), learning rates (LR), output dimensions for GCN (Dim), and φ_P, φ_N, which were important hyperparameters for our method. Table 7 shows our method was insensitive to the random walk step, the learning rates, and the output dimension.

Table 7:

The evaluation table (N = 20) of our method for random walk step (K), learning rate (LR), output dimension for GCN (Dim), and φ_P, φ_N.

K	LR	Dim	φp, φN	#(CP)	#(TVP in CP)	Recall	Precision
3	0.0001	100	0.7, 0	305	176	87.56%	57.70%
1	0.0001	100	0.7, 0	271	169	84.08%	62.36%
2	0.0001	100	0.7, 0	317	173	86.07%	54.57%
4	0.0001	100	0.7, 0	318	177	88.06%	55.66%
5	0.0001	100	0.7, 0	314	174	86.57%	55.41%
3	0.0005	100	0.7, 0	310	176	87.56%	56.77%
3	0.001	100	0.7, 0	317	172	85.57%	54.26%
3	0.0001	50	0.7, 0	329	174	86.57%	52.89%
3	0.0001	80	0.7, 0	314	177	88.06%	56.37%
3	0.0001	150	0.7, 0	313	174	86.57%	55.59%
3	0.0001	200	0.7, 0	288	174	86.57%	60.42%
3	0.0001	100	1, −1	457	155	77.11%	33.92%
3	0.0001	100	1, 0	336	166	82.59%	49.40%
3	0.0001	100	0.9, 0	333	173	86.07%	51.95%
3	0.0001	100	0.5, 0	288	176	87.56%	61.11%

CP: candidate stemmed variable pairs, TVP: true stemmed variable pairs, recall = #(TVP)/201, precision = #(TVP in CP)/#(CP). The bold line was the result of our harmonization work. Note: the case where φ_P, φ_N = 1, −1 means no slack margin.

Our method introduced a slack margin for loss function to learn graph embedding better. The performance of no slack margin (φ_P, φ_N: 1, −1) and no slack margin for the positive link (φ_P, φ_N: 1, 0) was worse than the slack version. The different slack margin for the positive link φ_P, which were 0.5, 0.7, 0.9, had a similar recall and considerable precision. Actually, we cared about high similarities of the learned embeddings, which might be affected by φ_P, so we paid more attention on the choice of φ_P. Specifically, we expected that two linked variables could have a similarity higher than φ_P, rather than a 100% similarity, and variables in a hyperchain would have higher similarity. As for φ_N, we didn’t need to focus on the degree of similarity of two unlinked nodes, so it was enough to take a negative similarity between two unlinked nodes, and we took φ_N = 0. The experiment demonstrated that the slack margin contributed to the performance, and φ_P could be chosen in a broad range of 0.5~0.9. The comparison result demonstrated that our results are robust at a broad range of slack margins.

DISCUSSION

Longitudinal data analysis is an important area of epidemiological studies. The 49 years of US birth data published by the National Center for Health Statistics (NCHS) offers an important source of information to analyze the trend of birth, disease, and neonatal mortality over 4 decades, which can reflect the important social and economic impact of several generations. However, these data, in their raw format, are not consistently represented. Every researcher who wants to conduct longitudinal research on it needs to spend much effort to string variables in years. It is a tedious job and can lead to replicability (due to human errors or inconsistency in annotation by multiple people when they collaborate). Our graph-based method provides a feasible and efficient way to a harmonized database, which can be used by future researchers. We considered the key property and characteristics of variables in these databases, designed a graph neural network to learn the similarity patterns of variables from the context of a network, and search their relationships in a global manner. The experiments showed our model outperformed the baseline method, which was a vector-based method with the off-the-shelf embeddings learned from large-scale corpora.

The subsequent experiments demonstrated our model was robust in different random walk steps, various learning rates, and different output dimensions. The recall of variable pairs from different slack margins for positive links, φ_P ∈ {0.5, 0.7, 0.9}, was close and higher than that of the model with no slack margin. The experiments demonstrated the model with no slack margin provided more candidate variable pairs but containing less correct pairs comparing the slack margin version. Actually, for the case with no slack margin, optimization on the loss function would force the similarity of the embeddings between the anchor node and each of its positive nodes to approach 1. But for a variable (as an anchor node), not all its correlated variables (as positive nodes) are desired to be equally similar for harmonization. There is a need to differentiate correlated variables for a variable, so we introduced slack margin and let the model decide the desired variables. We expected the similarities of the variables with more common characteristics should be closer through our learning process. The ablation experiment for the banlist mechanism showed that the case without banlist had much more invalid candidate pairs than that with banlist. The banlist mechanism was active in blocking the undesired linkages in a random walk during model training (random walk step > 1), and it screened out the undesired pairs during the generation of candidate pairs, almost all of which were incorrect pairs. We should note that the banlist would not play a part in model training in the case of random walk step = 1 since the variable would not go to its banned variable at one step.

We provided a new solution, an unsupervised graph-based method, for variable linkage tasks or database harmonization. According to the properties of the variables or databases, we constructed a graph with variables and their characteristics helpful for linkages based on limited clues about linkages. Then, our method could generate graph embeddings of variables implying the linkage. Overall, we constructed structural features and devised an integrative model architecture to solve the problem.

Our method had several limitations. There was one special hyperchain during harmonization, i.e., ‘apncu (2004–2008)’ and ‘u_apncu (2004–2008)’ representing the ‘adequacy of prenatal care utilization index,’ whose variables presented in the same year and there is no linkage between two stemmed variables due to no change between variable names. Our model was limited to find this kind of hyperchain. Our model leveraged limited information (level names, variable label) to find similarities between variables and was limited for connecting variables with different characteristics but indicating the same concept. For example, variables ‘legit3’ in 1970–1977 and variables ‘mar2’ in 1978–1988 have only two common characteristics, variable-level items ‘YES’ and ‘NO’, which had been busy in the graph, so it is hard to link them. Incorporating more useful information on variables might improve the efficiency of harmonization. Another limitation of our work is that the choice of hyperparameters (random walk steps) was without supervision, so it was unable to provide the best result for harmonization.

CONCLUSION

Our graph-based method is powerful to discover the linkages among variables in multiple natality databases. The constructed graph with variables and their characteristics contains the correlations between variables. Our GCN model returns graph embeddings of variables that imply the similarities of the variables. The variables with more common characteristics in the graph are expected to be more similar. The experiments demonstrate the banlist mechanism and the loss function with a slack margin increase the efficiency and the performance of the model. The GCN model reaches a correct prediction of 176 out of 201 stemmed variable pairs (N=20), which gives a recall of 87.56% and a precision of 57.70%, respectively. This means that for every 5 pairs of expert reviews, 3 of them are correct. When an expert reviews 305 candidate pairs recommended by our model, it already covered 87.56% of the total correct pairs. This workload is only 0.24% of reviewing the entire 126,253 pairs of nodes for 503 stemmed variables that need to be harmonized. The recall can be further improved if we increase N at the cost of reduced precision.

The unsupervised graph-based method in this paper is capable of harmonizing data sets from the same source. Furthermore, our model might be extended to connect/harmonize variables from different sources (sharing similar contents). One thinking is that Governmental websites also publish mortality data, which can be linked with birth data with a similar strategy. We will explore this problem in future work.

Highlights.

1. an effective way to reduce the manual effort in database harmonization

2. an unsupervised deep-learning framework to combine 49-year US natality databases

3. a slack margin for the loss function benefits learning the similarities of variables

4. a banlist mechanism blocking marginal linkages to increase the efficiency of model