Abstract
Accelerated multi-coil magnetic resonance imaging reconstruction has seen a substantial recent improvement combining compressed sensing with deep learning. However, most of these methods rely on estimates of the coil sensitivity profiles, or on calibration data for estimating model parameters. Prior work has shown that these methods degrade in performance when the quality of these estimators are poor or when the scan parameters differ from the training conditions. Here we introduce Deep J-Sense as a deep learning approach that builds on unrolled alternating minimization and increases robustness: our algorithm refines both the magnetization (image) kernel and the coil sensitivity maps. Experimental results on a subset of the knee fastMRI dataset show that this increases reconstruction performance and provides a significant degree of robustness to varying acceleration factors and calibration region sizes.
Keywords: MRI acceleration, Deep learning, Unrolled optimization
1. Introduction
Parallel MRI is a multi-coil acceleration technique that is standard in nearly all clinical systems [5,15,21]. The technique uses multiple receive coils to measure the signal in parallel, and thus accelerate the overall acquisition. Compressed sensing-based methods with suitably chosen priors have constituted one of the main drivers of progress in parallel MRI reconstruction for the past two decades [4,10,16,25]. While parallel MRI provides additional degrees of freedom via simultaneous measurements, it brings its own set of challenges related to estimating the spatially varying sensitivity maps of the coils, either explicitly [15,25,26] or implicitly [5,21]. These algorithms typically use a fully sampled region of k-space or a low-resolution reference scan as an auto-calibration signal (ACS), either to estimate k-space kernels [5,11], or to estimate coil sensitivity profiles [15]. Calibration-free methods have been proposed that leverage structure in the parallel MRI model; namely, that sensitivity maps smoothly vary in space [16,26] and impose low-rank structure [6,20].
Deep learning has recently enabled significant improvement to image quality for accelerated MRI when combined with ideas from compressed sensing in the form of unrolled iterative optimization [1,7,18,22,23]. Our work falls in this category, where learnable models are interleaved with optimization steps and the entire system is trained end-to-end with a supervised loss. However, there are still major open questions concerning the robustness of these models, especially when faced with distributional shifts [2], i.e., when the scan parameters at test time do not match the ones at training time or the robustness of methods across different training conditions. This is especially prudent for models that use estimated sensitivity maps, and thus require reliable estimates as input.
Our contributions are the following: i) we introduce a novel deep learning-based parallel MRI reconstruction algorithm that unrolls an alternating optimization to jointly solve for the image and sensitivity map kernels directly in k-space; ii) we train and evaluate our model on a subset of the fastMRI knee dataset and show improvements in reconstruction fidelity; and iii) we evaluate the robustness of our proposed method on distributional shifts produced by different sampling parameters and obtain state-of-the-art performance. An open-source implementation of our method is publicly available1.
2. System Model and Related Work
In parallel MRI, the signal is measured by an array of radio-frequency receive coils distributed around the body, each with a spatially-varying sensitivity profile. In the measurement model, the image is linearly mixed with each coil sensitivity profile and sampled in the Fourier domain (k-space). Scans can be accelerated by reducing the number of acquired k-space measurements, and solving the inverse problem by leveraging redundancy across the receive channels as well as redundancy in the image representation. We consider parallel MRI acquisition with C coils. Let and be the n-dimensional image (magnetization) and set of k-dimensional sensitivity map kernels, respectively, defined directly in k-space. We assume that ki, the k-space data of the i-th coil image, is given by the linear convolution between the two kernels as
| (1) |
Joint image and map reconstruction formulates (1) as a bilinear optimization problem where both variables are unknown. Given a sampling mask represented by the matrix A and letting y = Ak + n be the sampled noisy multicoil k-space data, where k is the ground-truth k-space data and n is the additive noise, the optimization problem is
| (2) |
Rm(m) and Rs(s) are regularization terms that enforce priors on the two variables (e.g., J-Sense [26] uses polynomial regularization for s). We let Am and As denote the linear operators composed by convolution with the fixed variable and A. A solution of (2) by alternating minimization involves the steps
| (3a) |
| (3b) |
If ℓ2-regularization is used for the R terms, each sub-problem is a linear least squares minimization, and the Conjugate Gradient (CG) algorithm [19] with a fixed number of steps can be applied to obtain an approximate solution.
2.1. Deep Learning for MRI Reconstruction
Model-based deep learning architectures for accelerated MRI reconstruction have recently demonstrated state-of-the-art performance [1,7,22]. The MoDL algorithm [1] in particular is used to solve (1) when only the image kernel variable is unknown and a deep neural network is used in Rm(m) as
| (4) |
To unroll the optimization in (4), the authors split each step in two different sub-problems. The first sub-problem treats as a constant and uses the CG algorithm to update m. The second sub-problem treats as a proximal operator and is solved by direct assignment, i.e., . In our work, we use the same approach for unrolling the optimization, but we use a pair of deep neural networks, one for each variable in (2). Unlike [1], our work does not rely on a pre-computed estimate of the sensitivity maps, but instead treats them as an optimization variable.
The idea of learning a sensitivity map estimator using neural networks was first described in [3]. Recently, the work in [22] introduced the E2E-VarNet architecture that addresses the issue of estimating the sensitivity maps by training a sensitivity map estimation module in the form of a deep neural network. Like the ESPiRiT algorithm [25], E2E-VarNet additionally enforces that the sensitivity maps are normalized per-pixel and uses the same sensitivity maps across all unrolls. This architecture – which uses gradient descent instead of CG – is then trained end-to-end, using the estimated sensitivity maps and the forward operator Am. The major difference between our work and [22] is that we iteratively update the maps instead of using a single-shot data-based approach [22] or the ESPiRiT algorithm [1,7]. As our results show in the sequel, this has a significant impact on the out-of-distribution robustness of the approach on scans whose parameters differ from the training set.
Concurrent work also extends E2E-VarNet and proposes to jointly optimize the image and sensitivity maps via the Joint ICNet architecture [9]. Our main difference here is the usage of a forward model directly in k-space, and the fact that we do not impose any normalization constraints on the sensitivity maps. Finally, the work in [12] proposes a supervised approach for sensitivity map estimation, but this still requires an external algorithm and a target for map regression, which may not be easily obtained.
3. Deep J-Sense: Unrolled Alternating Optimization
We unroll (2) by alternating between optimizing the two variables as
| (5a) |
| (5b) |
| (5c) |
| (5d) |
where R is defined as
| (6) |
for both m and s, is the Fourier transform, and is the deep neural network corresponding to each variable. Similar to MoDL, we set and across all unrolls, leading to the efficient use of learnable weights. The coefficients λs and λm are also learnable. The optimization is initialized with m(0)and s(0), obtained using a simple root sum-of-squares (RSS) estimate. Steps (5a) and (5c) are approximately solved with n1 and n2 steps of the CG algorithm, respectively, while steps (5b) and (5d) represent direct assignments. The two neural networks serve as generalized denoisers applied in the image domain and are trained in an end-to-end fashion after unrolling the alternating optimization for a number of N outer steps. A block diagram of one unroll is shown in Fig.1.
Fig. 1.
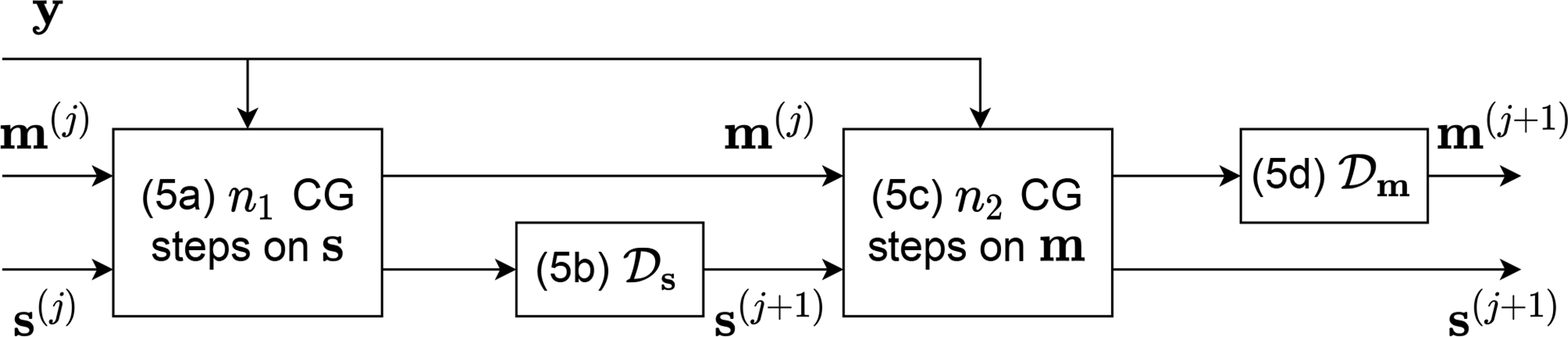
A single unroll of the proposed scheme. The CG algorithm is executed on the loss given by the undersampled data y and the measurement matrices As and Am. Each block is matched to its corresponding equation.
Using the estimated image and map kernels after N outer steps, we train the end-to-end network using the estimated RSS image as
| (7) |
where the supervised loss is the structural similarity index (SSIM) between the estimated image and ground truth image as .
Our model can be seen as a unification of MoDL and J-Sense. For example, by setting n1 = 0 and , the sensitivity maps are never updated and the proposed approach becomes MoDL. At the same time, removing the deep neural networks by setting and removing steps (5b) and (5d) leads to L2-regularized J-Sense. One important difference is that, unlike the ESPiRiT algorithm or E2E-VarNet, our model does not perform pixel-wise normalization of the sensitivity maps, and thus does not impart a spatially-varying weighting across the image. We use a forward model in the k-space domain based on a linear convolution instead of prior work that uses the image domain. This allows us to use a small-sized kernel for the sensitivity maps as an implicit smoothness regularizer and reduction in memory.
4. Experimental Results
We compare the performance of the proposed approach against MoDL [1] and E2E-VarNet [22]. We train and evaluate all methods on a subset of the fastMRI knee dataset [27] to achieve reasonable computation times. For training, we use the five central slices from each scan in the training set, for a total of 4580 training slices. For evaluation, we use the five central slices from each scan in the validation set, for a total of 950 validation slices. All algorithms are implemented in PyTorch [14] and SigPy [13]. Detailed architectural and hyper-parameter choices are given in the material.
To evaluate the impact of optimizing the sensitivity map kernel, we compare the performance of the proposed approach with MoDL trained on the same data, that uses the same number of unrolls (both inner and outer) and the same architecture for the image denoising network We compare our robust performance with E2E-VarNet trained on the same data, and having four times more parameters, to compensate for the run-time cost of updating the sensitivity maps.
4.1. Performance on Matching Test-Time Conditions
We compare the performance of our method with that of MoDL and E2E-VarNet when the test-time conditions match those at training time on knee data accelerated by a factor of R = 4. For MoDL, we use a denoising network with the same number of parameters as our image denoising network and the same number of outer and inner CG steps. We use sensitivity maps estimated by the ESPiRiT algorithm via the BART toolbox [24], where a SURE-calibrated version [8] is used to select the first threshold, and we set the eigenvalue threshold to zero so as to not unfairly penalize MoDL, since both evaluation metrics are influenced by background noise. For E2E-VarNet, we use the same number of N = 6 unrolls (called cascades in [22]) and U-Nets for all refinement modules.
Table 1 shows statistical performance on the validation data. The comparison with MoDL allows us to evaluate the benefit of iteratively updating the sensitivity maps, which leads to a significant gain in both metrics. Furthermore, our method obtains a superior performance to E2E-VarNet while using four times fewer trainable weights and the same number of outer unrolls. This demonstrates the benefit of trading off the number of parameters for computational complexity, since our model executes more CG iterations than both baselines. Importantly, Deep J-Sense shows a much lower variance of the reconstruction performance across the validation dataset, with nearly one order of magnitude gain against MoDL and three times lower than E2E-VarNet, delivering a more consistent reconstruction performance across a heterogeneity of patient scans.
Table 1.
Validation performance on a subset of the fastMRI knee dataset. Higher average/median SSIM (lower NMSE) indicates better performance. Lower standard deviations are an additional desired quality.
| Avg. SSIM |
Med. SSIM |
σ
SSIM |
Avg. NMSE |
Med. NMSE |
σ
NMSE |
|
|---|---|---|---|---|---|---|
| MoDL | 0.814 | 0.840 | 0.115 | 0.0164 | 0.0087 | 0.0724 |
| E2E | 0.824 | 0.851 | 0.107 | 0.0111 | 0.0068 | 0.0299 |
| Ours | 0.832 | 0.857 | 0.104 | 0.0091 | 0.0064 | 0.0095 |
Randomly chosen reconstructions of scans and the estimated sensitivity maps are shown in Fig. 2. We notice that our maps capture higher frequency components than those of MoDL (estimated via ESPiRiT), but do not contain spurious noise patterns outside the region spanned by the physical knee. In contrast, the maps from E2E-VarNet exhibit such patterns and, in the case of the second row, produce spurious patterns even inside the region of interest, suggesting that the knee anatomy “leaks” into the sensitivity maps. Figure 3 shows the projection of the fully-sampled k-space data on the null space of the pixel-wise normalized estimated sensitivity maps. Note that since we do not normalize the sensitivity maps this represents a different set of maps that those learned during training. As Fig. 3 shows, the residual obtained is similar to that of E2E-VarNet.
Fig. 2.
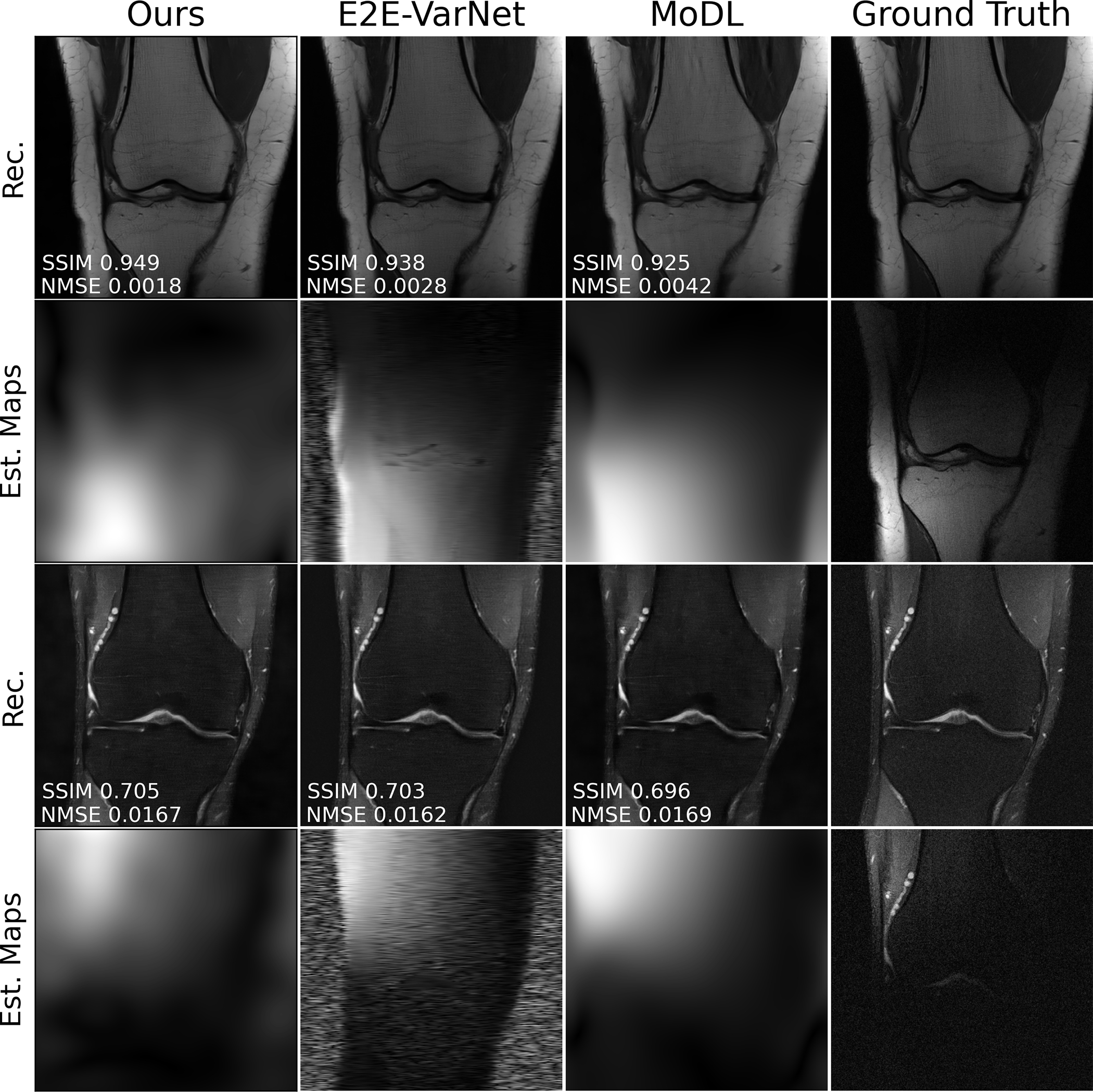
Example reconstructions at R = 4 and matching train-test conditions. The first and third rows represent RSS images from two different scans. The second and fourth rows represents the magnitude of the estimated sensitivity map (no ground truth available, instead the final column shows the coil image) for a specific coil from each scan, respectively. The maps under the MoDL column are estimated with the ESPiRiT algorithm.
Fig. 3.
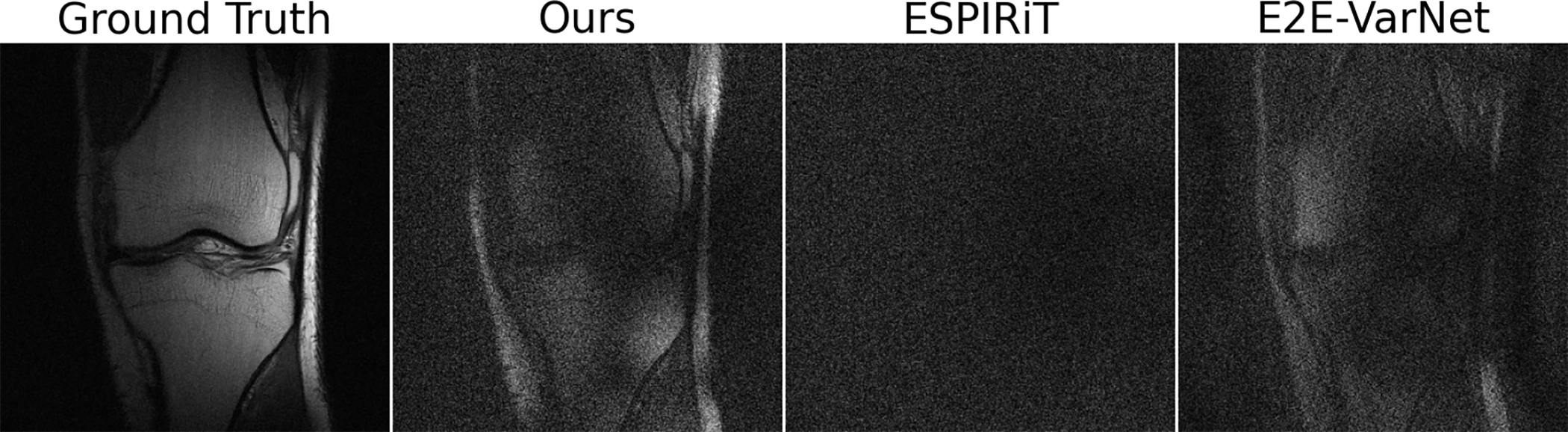
Magnitude of the projection of the ground truth k-space data onto the null space of the normal operator given by the estimated sensitivity maps for various algorithms (residuals amplified 5×). The sample is chosen at random; both Deep J-Sense and E2E-VarNet produce map estimates that deviate from the linear model, but improve end-to-end reconstruction of the RSS image.
4.2. Robustness to Test-Time Varying Acceleration Factors
Figure 4 shows the performance obtained at acceleration factors between 2 and 6, with models trained only at R = 4. The modest performance gain for E2E-VarNet at R < 4 confirms the findings in [2]: certain models cannot efficiently use additional measurements if there is a train-test mismatch. At the same time, MoDL and the proposed method are able to overcome this effect, with our method significantly outperforming the baselines across all accelerations. Importantly, there is a significant decrease of the performance loss slope against MoDL, rather than an additive gain, showing the benefit of estimating sensitivity maps using all the acquired measurements.
Fig. 4.
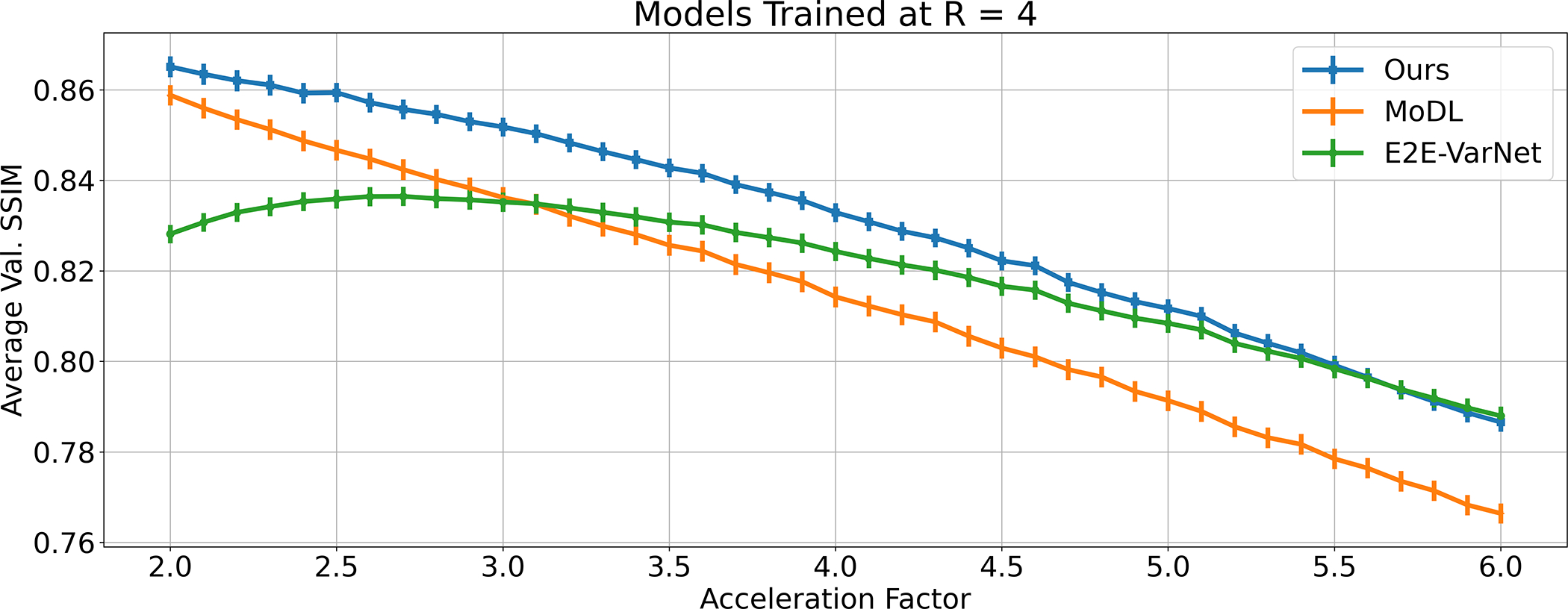
Average SSIM on the fastMRI knee validation dataset evaluated at acceleration factors R between 2 and 6 (with granularity 0.1) using models trained at R = 4. The vertical lines are proportional to the SSIM standard deviation in each case, from which no noticeable difference can be seen.
4.3. Robustness to Train-Time Varying ACS Size
We investigate the performance of the proposed method and E2E-VarNet as a function of the ACS region size (expressed as number of acquired lines in the phase encode direction). All models are trained at R = 4 and ACS sizes {1, 6, 12, 26, 56} and tested in the same conditions, giving a total of ten models. While there is no train-test mismatch in this experiment, Fig. 5 shows a significant performance gain of the proposed approach when the calibration region is small (below six lines) and shows that overall, end-to-end performance is robust to the ACS size, with the drops at 1 and 12 lines not being statistically significant. This is in contrast to E2E-VarNet, which explicitly uses the ACS in its map estimation module and suffers a loss when this region is small.
Fig. 5.
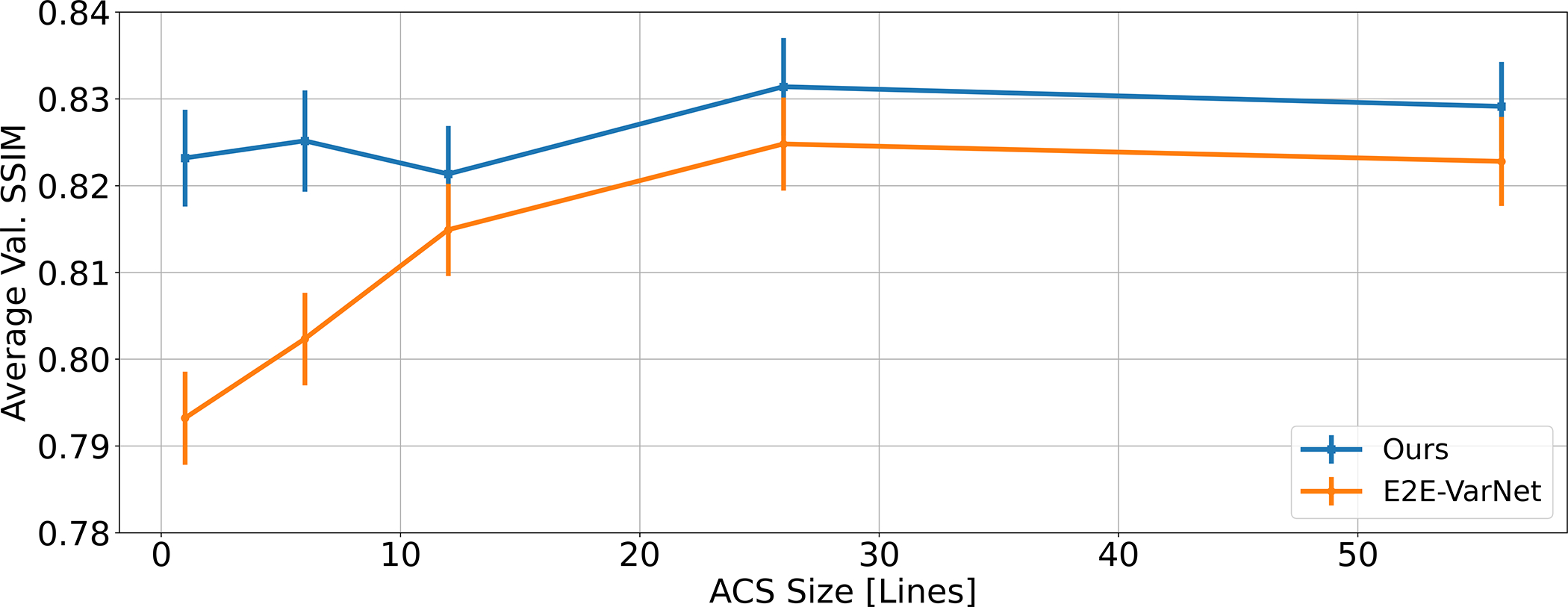
Average SSIM on the fastMRI knee validation dataset evaluated at different sizes of the fully sampled auto-calibration region, at acceleration factor R = 4. The vertical lines are proportional to the SSIM standard deviation. Each model is trained and tested on the ACS size indicated by the x-axis.
5. Discussion and Conclusions
In this paper, we have introduced an end-to-end unrolled alternating optimization approach for accelerated parallel MRI reconstruction. Deep J-Sense jointly solves for the image and sensitivity map kernels directly in the k-space domain and generalizes several prior CS and deep learning methods. Results show that Deep J-Sense has superior reconstruction performance on a subset of the fastMRI knee dataset and is robust to distributional shifts induced by varying acceleration factors and ACS sizes. A possible extension of our work could include unrolling the estimates of multiple sets of sensitivity maps to account for scenarios with motion or a reduced field of view [17,25].
Supplementary Material
Acknowledgments
Supported by ONR grant N00014–19-1–2590, NIH Grant U24EB029240, NSF IFML 2019844 Award, and an AWS Machine Learning Research Award.
Footnotes
Electronic supplementary material The online version of this chapter (https://doi.org/10.1007/978–3-030–87231-1_34) contains supplementary material, which is available to authorized users.
References
- 1.Aggarwal HK, Mani MP, Jacob M: Modl: model-based deep learning architecture for inverse problems. IEEE Trans. Med. Imaging 38(2), 394–405 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Antun V, Renna F, Poon C, Adcock B, Hansen AC: On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc. Natl. Acad. Sci. 117(48), 30088–30095 (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cheng JY, Pauly JM, Vasanawala SS: Multi-channel image reconstruction with latent coils and adversarial loss. ISMRM; (2019) [Google Scholar]
- 4.Deshmane A, Gulani V, Griswold MA, Seiberlich N: Parallel mr imaging. J. Magn. Reson. Imaging 36(1), 55–72 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Griswold MA, et al. : Generalized autocalibrating partially parallel acquisitions (grappa). Magn. Reson. Med.: Off. J. Int. Soc. Magn. Res. Med. 47(6), 1202–1210 (2002) [DOI] [PubMed] [Google Scholar]
- 6.Haldar JP: Low-rank modeling of local k-space neighborhoods (loraks) for constrained MRI. IEEE Trans. Med. Imaging 33(3), 668–681 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hammernik K, et al. : Learning a variational network for reconstruction of accelerated mri data. Magn. Reson. Med. 79(6), 3055–3071 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Iyer S, Ong F, Setsompop K, Doneva M, Lustig M: Sure-based automatic parameter selection for espirit calibration. Magn. Reson. Med. 84(6), 3423–3437 (2020) [DOI] [PubMed] [Google Scholar]
- 9.Jun Y, Shin H, Eo T, Hwang D: Joint deep model-based MR image and coil sensitivity reconstruction network (joint-ICNET) for fast MRI. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5270–5279 (2021) [Google Scholar]
- 10.Lustig M, Donoho D, Pauly JM: Sparse MRI: the application of compressed sensing for rapid mr imaging. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med. 58(6), 1182–1195 (2007) [DOI] [PubMed] [Google Scholar]
- 11.Lustig M, Pauly JM: Spirit: iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 64(2), 457–471 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Meng N, Yang Y, Xu Z, Sun J: A prior learning network for joint image and sensitivity estimation in parallel MR imaging. In: Shen D, et al. (eds.) MICCAI 2019. LNCS. vol. 11767, pp. 732–740. Springer, Cham: (2019). 10.1007/978-3-030-32251-980 [DOI] [Google Scholar]
- 13.Ong F, Lustig M: Sigpy: a python package for high performance iterative reconstruction. In: Proceedings of the ISMRM 27th Annual Meeting, Montreal, Quebec, Canada, p. 4819 (2019) [Google Scholar]
- 14.Paszke A, et al. : Pytorch: an imperative style, high-performance deep learning library. In: Wallach H, Larochelle H, Beygelzimer A, d’ Alché-Buc F, Fox E, Garnett R (eds.) Advances in Neural Information Processing Systems, vol. 32, pp. 8024–8035. Curran Associates, Inc. (2019). http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf [Google Scholar]
- 15.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P: Sense: sensitivity encoding for fast MRI. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Res. Med. 42(5), 952–962 (1999) [PubMed] [Google Scholar]
- 16.Rosenzweig S, Holme HCM, Wilke RN, Voit D, Frahm J, Uecker M: Simultaneous multi-slice MRI using cartesian and radial flash and regularized non-linear inversion: Sms-nlinv. Magn. Reson. Med. 79(4), 2057–2066 (2018) [DOI] [PubMed] [Google Scholar]
- 17.Sandino CM, Lai P, Vasanawala SS, Cheng JY: Accelerating cardiac cine MRI using a deep learning-based espirit reconstruction. Magn. Reson. Med. 85(1), 152–167 (2021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D: A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans. Med. Imaging 37(2), 491–503 (2017) [DOI] [PubMed] [Google Scholar]
- 19.Shewchuk JR, et al. : An introduction to the conjugate gradient method without the agonizing pain (1994)
- 20.Shin PJ, et al. : Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn. Reson. Med. 72(4), 959–970 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sodickson DK, Manning WJ: Simultaneous acquisition of spatial harmonics (smash): fast imaging with radiofrequency coil arrays. Magn. Reson. Med. 38(4), 591–603 (1997) [DOI] [PubMed] [Google Scholar]
- 22.Sriram A, et al. : End-to-end variational networks for accelerated MRI reconstruction. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 64–73 (2020) [Google Scholar]
- 23.Sriram A, Zbontar J, Murrell T, Zitnick CL, Defazio A, Sodickson DK: Grappanet: Combining parallel imaging with deep learning for multi-coil MRI reconstruction. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020) [Google Scholar]
- 24.Tamir JI, Ong F, Cheng JY, Uecker M, Lustig M: Generalized magnetic resonance image reconstruction using the berkeley advanced reconstruction toolbox. In: ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona, AZ (2016) [Google Scholar]
- 25.Uecker M, et al. : Espirit—an eigenvalue approach to autocalibrating parallel MRI: where sense meets grappa. Magn. Reson. Med. 71(3), 990–1001 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ying L, Sheng J: Joint image reconstruction and sensitivity estimation in sense (jsense). Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med. 57(6), 1196–1202 (2007) [DOI] [PubMed] [Google Scholar]
- 27.Zbontar J, et al. : fastMRI: An open dataset and benchmarks for accelerated MRI. ArXiv e-prints (2018) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


