Abstract
Mendelian randomization is a framework that uses measured variation in genes for assessing and estimating the causal effect of an exposure on an outcome. Multivariable Mendelian randomization is an extension that can assess the causal effect of multiple exposures on an outcome, and can be advantageous when considering a set (>1) of potentially correlated candidate risk factors in evaluating the causal effect of each on a health outcome, accounting for measured pleiotropy. This can be seen, for example, in determining the causal effects of lipids and cholesterol on type 2 diabetes risk, where the correlated risk factors share genetic predictors. Similar to univariate Mendelian randomization, multivariable Mendelian randomization can be conducted using two-sample summary-level data where the gene-exposure and gene-outcome associations are derived from separate samples from the same underlying population. Here, we present a protocol for conducting a two-sample multivariable Mendelian randomization study using the ‘MVMR’ package in R and summary-level genetic data. We also provide a protocol for searching and obtaining instruments using available data sources in the ‘MRInstruments’ R package. Finally, we provide general guidelines and discuss the utility of performing a multivariable Mendelian randomization analysis for simultaneously assessing causality of multiple exposures.
Basic Protocol:
Performing a two-sample multivariable Mendelian randomization analysis using the ‘MVMR’ package in R and summarized genetic data
Support Protocol 1:
Installing the ‘MVMR’ R package
Support Protocol 2:
Obtaining instruments from the ‘MRInstruments’ R package
Keywords: causal inference, genetic epidemiology, instrumental variable analysis, mendelian randomization, multivariable, MVMR
INTRODUCTION
Multivariable Mendelian randomization, an extension to the univariate Mendelian randomization approach of instrumenting genetic variants to probe the causal relationship of a single risk factor with an outcome, can simultaneously assess the causal effects of multiple risk factors or exposures on an outcome of interest (Burgess & Thompson, 2015; Sanderson, Davey Smith, Windmeijer, & Bowden, 2019). Multivariable Mendelian randomization allows for a variation of the Mendelian randomization framework to be applied to cases where the assumptions necessary for performing a standard Mendelian randomization analysis do not hold, such as when two or more closely related, potentially correlated risk factors are associated with an outcome or when a risk factor mediates the effect of another risk factor on an outcome (Sanderson et al., 2019).
Rooted in econometric theory for instrumental variable (IV) analysis, Mendelian randomization relies on the random assortment of genetic variants during meiosis to source potential genetic variants as IVs for reliably predicting an exposure (Burgess, Small, & Thompson, 2017). IVs date back to the 1920s, originating from ‘causal path analysis’ developed by economist Philip Wright and his son, statistical geneticist Sewall Wright (Angrist & Krueger, 2001; Stock & Trebbi, 2003), and have since served as an integral part of econometrics for controlling for unmeasured confounding and measurement error bias in observational studies (Greenland, 2018). The concept underlying IV analysis in Mendelian randomization relies on the random assortment of genetic variants during meiosis as stated in Gregor Mendel’s principles of inheritance from the 19th century: namely, the Law of Independent Assortment, which states that alleles of different genes assort independently during gametogenesis, and the Law of Segregation, which states that the two copies or paired alleles of each genetic factor segregate during gametogenesis such that each offspring attains one allele (Davey Smith, 2007).
The random distribution of genetic variants in a population is analogous to the arms of a randomized controlled trial (RCT), the gold standard for evaluating causal relationships between interventions and an outcome, where carriers of the genetic variant can be followed up for an outcome measure which is compared to that of non-carriers (Lawlor, Harbord, Sterne, Timpson, & Davey Smith, 2008). Because genetic variants are fixed at conception and are not modified by the development of the outcome or by external (i.e., environmental) factors, they are largely assumed to be independent of confounding factors and reverse causation. Additionally, in the advanced era of genomic technologies, genotypes are likely not affected by measurement error, minimizing potential bias from measurement error. For these reasons, the implementation of genetic variants for serving as IVs in Mendelian randomization analyses presents a promising avenue for determining exposure-outcome causality, while controlling for biases typically encountered in observational studies (Burgess et al., 2017).
To serve as a valid IV, a genetic variant G must meet criteria for three key assumptions (Fig. 1).
Figure 1.
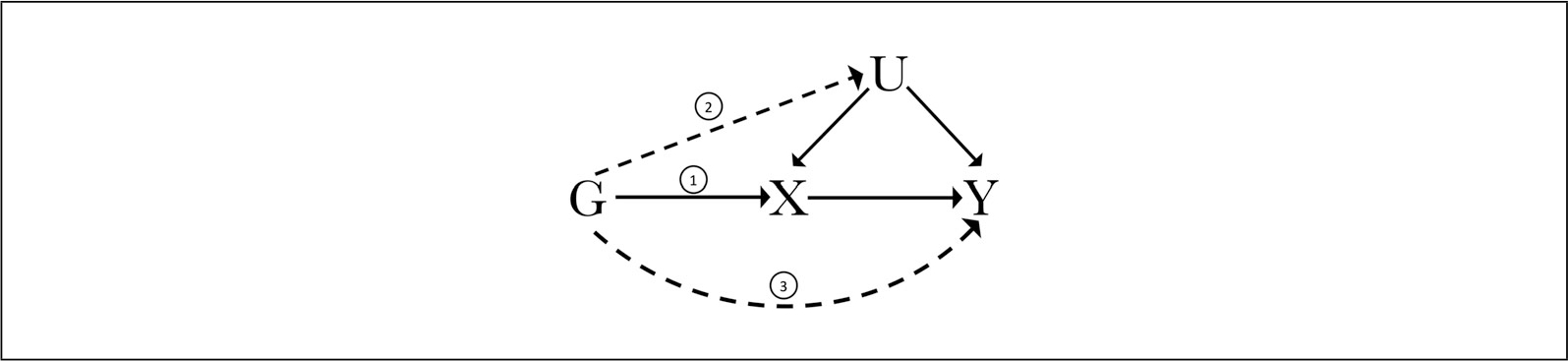
Illustration of the instrumental variable (IV) assumptions for univariate Mendelian randomization as diagrammed by a directed acyclic graph. To be a valid IV, a genetic variant G must be (1) associated with the exposure X, (2) independent of possible confounders U, and (3) not be associated with the outcome Y directly. The three IV assumptions are annotated accordingly, with dotted lines representing violations of the second and third assumptions.
To reliably test for a causal effect of exposure X on outcome Y in the presence of confounder U, the following requisite IV conditions must be confirmed (Lawlor et al., 2008; VanderWeele, Tchetgen Tchetgen, Cornelis, & Kraft, 2014):
Relevance Assumption: The instrument G must be associated with the exposure X.
Independence or Exchangeability Assumption: The instrument G must be independent of all measured or unmeasured confounders U of the exposure-outcome relationship.
Exclusion Restriction Assumption: The instrument G only affects the outcome through the exposure and therefore is independent of the outcome Y given the exposure X and all measured and unmeasured confounders U of the exposure-outcome relationship.
When a genetic variant meets the three requisite IV conditions, then the effect of the exposure on the outcome can be reliably estimated in a Mendelian randomization framework. A genetic variant or set of genetic variants—usually, single nucleotide polymorphisms (SNPs)—can be selected as instruments from genome-wide association studies (GWAS) that detect association between genetic variants and traits. Individual-level GWAS data can be accessed by applying for controlled-access data at the dbGaP (Database of Genotypes and Phenotypes) repository (Tryka et al., 2014), while databases such as the NHGRI-EBI GWAS Catalog (Buniello et al., 2019) and GeneAtlas (Canela-Xandri, Rawlik, & Tenesa, 2018) offer open access to certain summary-level GWAS. Accelerated by the explosive growth in GWAS over the past decade spanning hundreds of complex human traits and diseases across a wide range of domains (Visscher et al., 2017) and the ease in utilizing these rich resources for conducting Mendelian randomization analyses, there has been an ever-increasing number of Mendelian randomization studies and IV approaches applied to medical sciences and public health (Sekula, Del Greco, Pattaro, & Köttgen, 2016).
However, there are also a number of scenarios in which the IV assumptions may be violated, and therefore a genetic variant may not serve as a valid IV for a Mendelian randomization analysis (Palmer et al., 2012; Smith & Ebrahim, 2004; VanderWeele et al., 2014). For example, if a genetic variant G exerts a direct effect on the outcome Y (third assumption shown in Fig. 1), then the exclusion restriction assumption of IV analysis is violated. If a confounding variable U influences the genetic variant G and influences the outcome Y (second assumption shown in Fig. 1), then the independence/exchangeability assumption of IV analysis would be violated. Among the many methodological challenges of Mendelian randomization, a large extent of focus has been centered around pleiotropy—the phenomenon of a single genetic variant affecting two or more phenotypic traits (Paaby & Rockman, 2013).
Classical univariate statistical techniques that model the effect of a single exposure on an outcome can attempt to detect and adjust for certain cases of pleiotropy to quantify an unbiased estimate (Hemani, Bowden, & Davey Smith, 2018). However, pleiotropy is pervasive across the human genome; in fact, the number of phenotypes per gene ranges from 1 to 53, and 44% of genes are associated with more than one phenotype (Chesmore, Bartlett, & Williams, 2018; Jordan, Verbanck, & Do, 2019; Pickrell et al., 2016; Watanabe et al., 2019). Much of method development for Mendelian randomization, therefore, has been focused on adjusting for pleiotropy; for example, MR-Eggar is, one of these methods that has been widely employed and can be used to detect certain violations of the IV assumptions and assess directional pleiotropy to provide an estimate of the causal effect (Bowden, Davey Smith, & Burgess, 2015; Burgess & Thompson, 2017).
Evaluating the mechanisms of different pleiotropic relationships can identify scenarios that may lead to violated IV assumptions. There are two types of pleiotropy of concern in MR analysis: vertical and horizontal pleiotropy. If a genetic variant used as proxy for an exposure affects the outcome first via an effect on another, potentially biologically related exposure, which then has a downstream effect on the outcome (termed ‘vertical pleiotropy’), then the likely case is that the IV assumptions hold, and an unbiased effect estimate can still be obtained (Hemani et al., 2018). If, however, a genetic variant exerts an effect on two different exposures such that the effects of the multiple exposures are independent and each influences the outcome (termed ‘horizontal pleiotropy’), then the IV assumptions do not hold and a causal effect estimate may be biased (Cho et al., 2020). By directly considering associations of genetic variants with a trait such that the genetic variants are also associated with at least another trait included in the model (termed “measured pleiotropy”; Rees, Wood, & Burgess, 2017), multivariable Mendelian randomization presents an avenue for addressing cases where a standard Mendelian randomization technique would fail due to a violation of the exclusion restriction and/or the independence or exchangeability assumptions (Sanderson, 2021).
Genetic variants employed as IVs in a multivariable Mendelian randomization analysis must satisfy a set of assumptions similar to those expected in a univariate Mendelian randomization analysis (Fig. 2). To reliably test for a causal effect of exposures X1…n on outcome Y for n exposures in the presence of potential confounder U, the following IV assumptions must be met for each instrument G for i total number of genetic variants:
Figure 2.
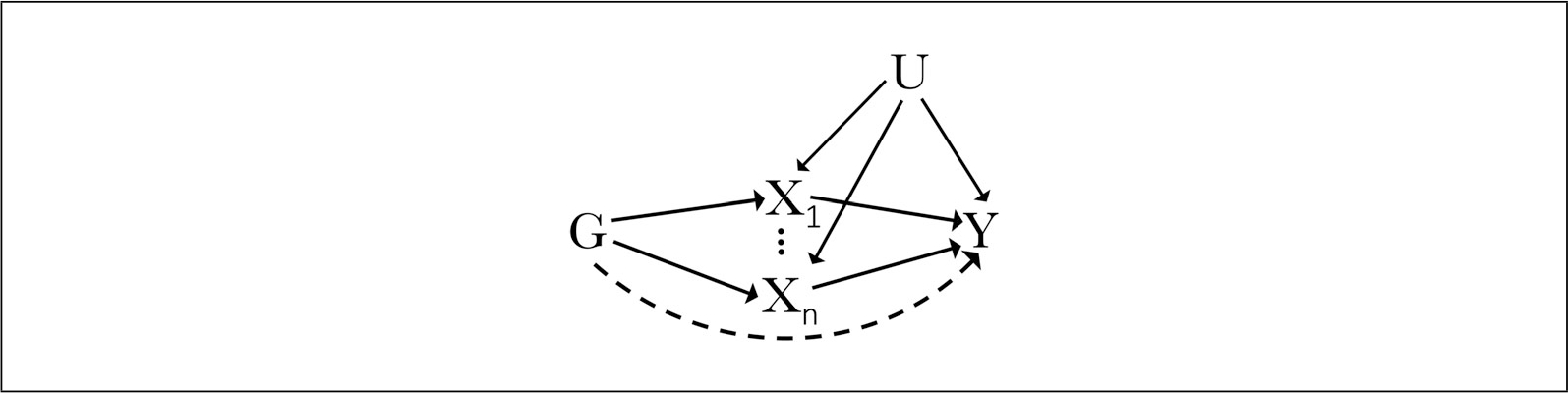
Illustration of the instrumental variable (IV) assumptions for multivariable Mendelian randomization as diagrammed by a directed acyclic graph showing the relationship between genetic variant G, exposures (X through X for n exposures), confounding factor U, 1n, and outcome Y.
The instrument Gi must be associated with each exposure X 1…n given the other included exposures;
the instrument Gi must be independent of all observed or unobserved confounders U of any of the exposure-outcome relationships; and
the instrument Gi is conditionally independent of the outcome Y given all of the exposures and confounders (Burgess & Thompson, 2015; Sanderson, Spiller, & Bowden, 2021).
Like univariate Mendelian randomization, a one-sample or two-sample analysis may be performed. A one-sample study is conducted when individual level data on the genetic variants, exposures, and outcome are all available within the same study (Minelli et al., 2020). If, however, individual data are not available, then a two-sample study can be conducted using summary-level data (including beta coefficients and standard errors) for gene-exposure and gene-outcome associations from separate, non-overlapping studies derived from the same underlying population (Minelli et al., 2020).
Here, we present a protocol for performing a two-sample multivariable Mendelian randomization analysis using summary-level GWAS data. We build on a previous protocol published for performing a univariate two-sample Mendelian randomization analysis using the R package ‘TwoSampleMR’ and GWAS summary statistics (Rasooly & Patel, 2019). In the protocols that follow, we demonstrate how to conduct a multivariable Mendelian randomization analysis using the ‘MVMR’ R package (Sanderson et al., 2021) to calculate inverse-variance weighted causal estimates. In the support protocols that follow, we demonstrate how to install the package ‘MVMR’ and how to extract instruments using available databases accessible through the ‘MRInstruments’ R package. Taken together, our protocols serve to guide you in performing your own two-sample multivariable Mendelian randomization analysis in the R statistical computing environment.
STRATEGIC PLANNING
A number of parameters should be considered when planning a multivariable Mendelian randomization experiment. First, it is necessary that there be at least as many instruments as exposures (Sanderson et al., 2021). Second, it is important to detect weak instruments, similar to a common procedure in univariate Mendelian randomization analysis. This can be done by comparing, for each included exposure, the first-stage F-statistic with a value of 10, such that a value smaller than 10 denotes a weak instrument (Staiger & Stock, 1994). Further, the genetic variables used as IVs should predict each exposure conditional on the other predicted exposures included in the model, to address potential weak instrument bias (Sanderson et al., 2021). We recommend referring to previous articles by Sanderson and colleagues in assessing instrument strength and validity in the one-sample and two-sample multivariable Mendelian randomization settings (Sanderson et al., 2019, 2021).
For analytic guidelines on performing Mendelian randomization investigations, we recommend referring to the flowchart depicted in Figure 1 in an article by Burgess et al. (2019), as well as an article by Gagliano Taliun, and Evans (2021) summarizing ten simple rules for conducting a Mendelian randomization study.
BASIC PROTOCOL
PERFORMING A TWO-SAMPLE MULTIVARIABLE MENDELIAN RANDOMIZATION ANALYSIS USING THE ‘MVMR’ PACKAGE IN R AND SUMMARIZED GENETIC DATA
In this protocol, we show how to perform a two-sample multivariable Mendelian randomization study using available genome-wide association study (GWAS) summary statistics. We provide steps for estimating causal effects using the ‘MVMR’ R package as well as conducting a range of sensitivity analyses for evaluating the IV assumptions in the multivariable scenario.
We thank the developer of the ‘MVMR’ R package, Wes Spiller, for providing an easy-to-use resource and extensive documentation for implementing a multivariable Mendelian randomization study (Sanderson et al., 2021), which this protocol is based on, and the authors of the multivariable Mendelian randomization approach (Burgess & Thompson, 2015; Sanderson et al., 2019, 2021).
The ‘MVMR’ package and related documentation are available at https://github.com/WSpiller/MVMR (Sanderson et al., 2021).
Necessary Resources
Hardware
A computer environment capable of running R/RStudio
Software
R version >3.6, RStudio, ‘MVMR’ R package
Files
Summary statistics for exposures and outcome of interest. The data should include beta coefficient values and standard errors for genetic associations with each exposure, and beta coefficient values and standard errors for genetic associations with the outcome. A vector of names for the genetic variants (e.g., rsID) can also be included.
NOTE: It is important to harmonize the direction of the effects between the exposure and outcome associations of the summary statistic files such that the effect of a genetic variant on the exposure and the effect of that variant on the outcome correspond to the same effect allele. If not harmonized, then the effect allele should be included for harmonization.
-
Obtain summary statistics for your exposures (Fig. 2, X) and outcome (Fig. 2, Y) of interest. These can be obtained through publicly available resources, such as the NHGRI-EBI GWAS Catalog (Buniello et al., 2019), GeneAtlas (Canela-Xandri et al., 2018), or MR-Base (Hemani et al., 2018).
NOTE: Please refer to Support Protocol 2 for detailed steps to obtain instruments using the databases accessible through the R Package ‘MRInstruments’.
- Read in the exposure and outcome GWAS summary statistic data.
exposure_data<-read.table(“exposure_filename.txt”, head=T, sep=“\t”) outcome_data<-read.table(“outcome_filename.txt”, head=T, sep=“\t”)
If using MR-Base (Hemani et al., 2018) to extract data, then the function mrmvinput_to_mvmr_format() can convert data to the ‘MVMR’ readable format. - Determine usability of GWAS summary statistic data by ensuring that, at a minimum, beta coefficients and corresponding standard errors are available for each gene-exposure association and beta coefficients and corresponding standard errors are available for the gene-outcome associations. The rsID column is optional.For the purposes of this illustration (Fig. 3), exposures are triglycerides (Willer et al., 2013), LDL-cholesterol (Willer et al., 2013), and body mass index (BMI; Locke et al., 2015), and outcome is type 2 diabetes (T2D) (Mahajan et al., 2018).
- Identify independent genetic variants that meet a P-value threshold of association (e.g., P < 10−5 for a lenient threshold, P < 10−7 for a more stringent threshold, or P < 5. 0 × 10−8 for genome-wide significance threshold).Independent genetic variants—typically SNPs—that are GWAS-significant for the exposure are instrumented as proxies for the exposure.It is important to ensure that exposure and outcome datasets are harmonized such that the effect alleles from the datasets match.
Determine if the IV assumptions hold for multivariable Mendelian randomization, requiring each variant to be associated with at least one of the exposures, not associated with the outcome through confounders, and not associated with the outcome except through its association with one or more of the exposures included in your model.
- Check if a covariance matrix for the effect of the genetic variants on each exposure is provided.If not, generate a covariance matrix using the phenotypic correlations between the exposures and the standard error of the beta coefficients for genetic associations with the exposure using the function phenocov_mvmr().
- Format summary statistic data to be read by the ‘MVMR’ package.BXG refers to the beta coefficient values for the genetic associations with the exposure. In this example, there are three exposures of interest (i.e., triglycerides, LDL-cholesterol, and body mass index), and therefore three columns representing the beta coefficient values for the three exposures. BYG refers to the beta coefficient values for the genetic associations with the outcome (i.e., type 2 diabetes). seBXG refers to the corresponding standard error values for the beta coefficient values of each of the exposures of interest. As there are three exposures of interest in this example, there are, therefore, three columns representing the standard error values for the three exposures. seBYG refers to the standard errors corresponding to the beta coefficient values for the genetic associations with the outcome. RSID refers to the names of the genetic variants used in this analysis.
MVMR_formatted <- format_mvmr(BXGs = data[,c(1,3,5)], BYG = data[,7], seBXGs = data[,c(2,4,6)], seBYG = data[,8], RSID = data[,9])
- Test the strength of the instruments for each exposure.
strength_mvmr(r_input = MVMR_formatted, gencov = 0)
The F-statistic threshold of 10 can be used to identify weak instruments. Note that with individual-level data (in a one-sample, as supposed to a two-sample experiment as shown here), weak instruments can be tested using the Sanderson-Windmeijer conditional F-statistic Fsw (Sanderson et al., 2019; Windmeijer & Sanderson, 2013). Conditional instrument strength can be tested by calculating the conditional F-statistic, where a threshold of 10 can test for a weak instrument. - Test for horizontal pleiotropy.
pleiotropy_mvmr(r_input = MVMR_formatted, gencov = 0)
If testing for horizontal pleiotropy in the presence of potentially weak instruments (as identified in the previous step), it is advised to perform Q-minimization. Please refer to Sanderson et al. (2021) and the ‘MVMR’ documentation for further details if this is the case (Sanderson et al., 2021). -
Compute effect estimate. This method utilizes the inverse-variance-weighted (IVW) estimator.
ivw_mvmr(r_input = MVMR_formatted)
If there is substantial heterogeneity in your data, compute the effect estimates through Q-statistic minimization.qhet_mvmr(r_input = MVMR_formatted)
Figure 3.

First few rows of an example dataframe in preparation for a multivariable Mendelian randomization study on three exposures. Columns 1, 3, and 5 show the beta coefficient values for the three different exposures (triglycerides, LDL-cholesterol, and body mass index), columns 2, 4, and 6 show the corresponding standard error values, and columns 7 and 8 show the beta coefficient and corresponding standard error of the outcome (type 2 diabetes). Column 9 shows the rsID.
SUPPORT PROTOCOL 1
INSTALLING THE ‘MVMR’ R PACKAGE
This support protocol describes how to install the necessary packages and dependencies for performing a multivariable Mendelian randomization analysis using the “MVMR” R package.
Necessary Resources
Hardware
A compute environment capable of running R/RStudio
Software
R version >3.6, RStudio, “MVMR” R package, “remotes” R package
Files
None
- Install the ‘MVMR’ package.
install.packages(“remotes”) remotes::install_github(“WSpiller/MVMR”)
- Load the ‘MVMR’ package.
library(MVMR)
All functions within the ‘MVMR’package are explained in the R Documentation. Please refer to the R Documentation for ‘MVMR’for a complete list of the parameters, options, and additional details regarding each function within the program. Further details of particular functions can be accessed through the help page. The help page can be accessed by prepending a question mark before the function name within the R interface.
SUPPORT PROTOCOL 2
OBTAINING INSTRUMENTS FROM THE ‘MRInstruments’ R PACKAGE
The R package ‘MRInstruments’ can be utilized to access a number of datafiles from various sources to search for instruments to be used in a two-sample Mendelian randomization study. Contents include methylation QTL data from the ALSPAC Accessible Resource for Integrated Epigenomics Studies (ARIES; Gaunt et al., 2016), the NHGRI-EBI GWAS catalog (Buniello et al., 2019), and GTEx eQTL (Lonsdale et al., 2013). Here, we provide a protocol for obtaining instruments from publicly available GWAS summary statistics from the NHGRI-EBI GWAS catalog (Buniello et al., 2019) for “Type 2 diabetes.”
Necessary Resources
Hardware
A compute environment capable of running R/RStudio
Software
R version >3.6, RStudio, “MRInstruments” R package, “remotes” R package
Files
None
- Install and load ‘MRInstruments’ R package.
install.packages(“remotes”) remotes::install_github(“MRCIEU/MRInstruments”) library(MRInstruments)
- View existing datasets in the ‘MRInstruments’ package (Fig. 4).
data(package = “MRInstruments”)
- Read in GWAS catalog data.
data(gwas_catalog)
- Extract summary statistic data by searching for relevant criteria.
subset(gwas_catalog, Phenotype == “Type 2 diabetes”)
The IEU OpenGWAS project contains a database of genetic associations from GWAS summary statistics that can be queried or downloaded. They are accessible here and also via API: https://gwas.mrcieu.ac.uk/.
Figure 4.

Datasets available in the MRInstruments R package.
GUIDELINES FOR UNDERSTANDING RESULTS
The ‘MVMR’ package outputs estimated causal effects for each of multiple exposures using an inverse-variance-weighted (IVR) model. For example, a study examining three exposures would output three causal effect estimates, where each is interpreted as the direct effect of each exposure on the outcome, conditional on the other exposures included in the model. The direct effect measures the effect of the exposure on the outcome per unit increase of the exposure and absent a mediator. The direct effect sums with the indirect effect, which measures the effect of the exposure on the outcome via the mediator, to equal the total effect of the exposure on the outcome. Multivariable Mendelian randomization contrasts with univariate Mendelian randomization in that the former estimates the direct effect of each exposure included in the model on the outcome while the latter estimates the total effect of the exposure on the outcome (Sanderson, 2021).
In cases where the IV assumptions for performing a multivariable Mendelian randomization experiment are not fully validated, a robust estimate can be derived through Q-statistic minimization (Sanderson et al., 2021). The output of this estimation is interpreted in the same manner, where each effect estimate is interpreted as the direct effect of that exposure on the outcome. It is also imperative to test for possible observed heterogeneity, which would result in a violation of the IV assumptions and therefore bias the estimated causal effect. The critical appraisal checklist (Box 2) provided by Davies and colleagues offers a list of key questions spanning the core IVs assumptions, characteristics of the two sample study populations, data presentation, interpretations, and clinical implications that can assist in evaluating and interpreting Mendelian randomization findings (Davies, Holmes, & Davey Smith, 2018).
COMMENTARY
Background Information
Observational research such as cohort studies or population-based, cross-sectional studies that assess the health status or behavior of a cohort at a single point in time are susceptible to biases such as reverse causation and confounding (Grimes & Schulz, 2002). Stemming from the IV method commonly applied in econometrics, Mendelian randomization presents a strategy for minimizing the effects of unobserved and observed confounding, reverse causation, and measurement error that may bias the effect of an exposure on an outcome of interest. Mendelian randomization provides a method for making causal inferences about the effect of an exposure on an outcome in the presence of confounding and other biases by instrumenting genetic variants, which are randomly distributed at conception and can be reliably associated with risk factors (Davies et al., 2018). Genetic variants that are known to reliably predict the exposure of interest and do not have an effect on the outcome through any other pathway can serve as valid IVs in a Mendelian randomization analysis for obtaining unconfounded estimates of the causal effect of the exposure on the outcome.
As we have previously shown in a protocol, a two-sample Mendelian randomization analysis can be easily conducted using publicly available summary association results from large genome-wide association studies (GWAS; Rasooly & Patel, 2019), where the genotype-exposure and genotype-outcome estimates are derived from separate, non-overlapping cohorts taken from the same underlying population (Hartwig, Tilling, Davey Smith, Lawlor, & Borges, 2021). At the crossroads of genetics and epidemiology, GWAS have revolutionized our understanding of human health and genetic basis of disease, discovering associations between genetic variants—usually single-nucleotide polymorphisms (SNPs)—and phenotypes, and shaping our view of the genetic architecture of complex human traits and diseases (Visscher et al., 2017). The exponential growth in both the number of new GWAS generated as well as new meta-analyzed multi-study GWAS performed, accelerated by the reduction in the cost of genotyping, promises unprecedented opportunities for discovery of causal relationships through Mendelian randomization-based methods, and for realizing yet another avenue for genetics to impact human health and medicine.
Two-sample multivariable Mendelian randomization is an extension to the univariate two-sample Mendelian randomization framework, addressing the use case of simultaneously estimating the effect of multiple exposures or risk factors on an outcome using potentially overlapping sets of genetic variants (Burgess & Thompson, 2015; Sanderson, 2021). A central advantage of applying multivariable Mendelian randomization is examining exposures or risk factors that are a priori hypothesized to be closely related (e.g., effects of lipids and cholesterol on type 2 diabetes). Another advantage of the method is its applicability for investigating a risk factor that mediates the relationship of another risk factor and outcome. This can be further illustrated in the case of horizontal and vertical pleiotropy (Fig. 5).
Figure 5.
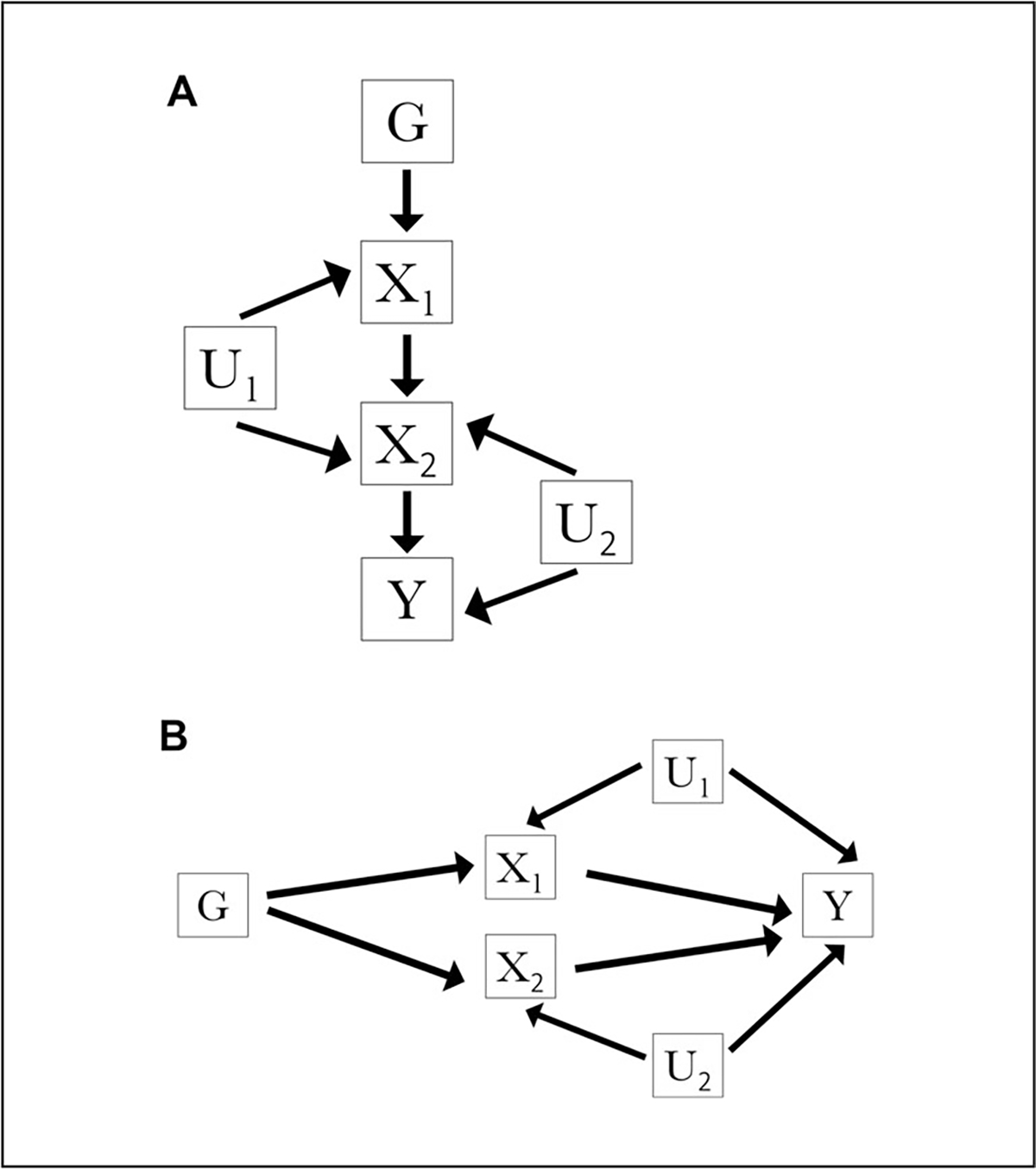
Illustration of vertical (A) and horizontal (B) pleiotropy as diagrammed by directed acyclic graphs. Depiction shown for genetic variant G, exposures X1 and X2, outcome Y, confounder of the X1-outcome association U1, and confounder of the X2-outcome association U2. In the vertical pleiotropy case illustrated in A, genetic variant G is associated with exposure X1, which exerts a downstream causal effect on exposure X2, which then exerts a causal effect on outcome Y. In the horizontal pleiotropy case illustrated in B, genetic variant G is associated with exposure X1 and independently associated with unrelated exposure X2, both exposures of which are associated with outcome Y.
In vertical pleiotropy, a genetic variant is associated with a risk factor that exerts a downstream causal effect on another, potentially closely related risk factor, which then exerts a causal effect on the outcome (Hemani et al., 2018; Fig. 5A). In horizontal pleiotropy, a genetic variant may influence multiple risk factors through independent biological pathways (Hemani et al., 2018; Fig. 5B). While the former may not lead to a violation of the IV assumptions, the latter case of horizontal pleiotropy can violate the IV assumptions, leading to a biased derived causal estimate (Bowden et al., 2015). Multivariable Mendelian randomization can assist in studies susceptible to such circumstances by simultaneously estimating the direct effect of each risk factor on an outcome from a set of two or more risk factors.
To date, several studies have applied the novel multivariable Mendelian randomization approach for jointly estimating multiple causal effects. Davies and colleagues analyzed data from the UK Biobank to study the potential causal effects of intelligence and education, two traits that are phenotypically and genetically correlated, on health outcomes, including mental and physical health, socioeconomic measures, and longevity (Davies et al., 2019). In a multivariable Mendelian randomization study, they estimated the total and direct effect of intelligence and educational attainment on socioeconomic and health outcomes, utilizing genetic variation information that explains a sufficient proportion of the variation in both of the studied risk factors conditional on the other risk factor (Davies et al., 2019). They found that intelligence exhibited a positive direct effect on income and was substantially attenuated compared to the total effects, suggesting that a substantial fraction of the total effects of intelligence on health and social outcomes may be mediated by education (Davies et al., 2019). In another study, the causal effects of educational attainment and intelligence on Alzheimer’s disease were examined; a multivariable Mendelian randomization analysis suggested an independent, causal effect of intelligence in lowering risk for Alzheimer’s disease (Anderson et al., 2020).
Pedron and colleagues performed a joint assessment of the causal effect of body mass index and type 2 diabetes on socioeconomic outcomes, identifying negative effects of body mass index and a null effect of diabetes on household income and regional deprivation (Pedron, Kurz, Schwettmann, & Laxy, 2021). Luo and colleagues studied a dozen red blood cell traits known to be highly genetically and phenotypically correlated in a multivariable Mendelian randomization framework, which suggested that endogenous hemoglobin was the most relevant red blood cell attribute for venous thromboembolism (Luo, Au Yeung, Zuber, Burgess, & Schooling, 2020). Lord and colleagues used knowledge that blood metabolites have been previously associated with midlife cognition to evaluate multiple blood metabolites as causal candidates for Alzheimer disease, identifying glycoprotein acetyls and extra-large high-density lipoproteins as the highest-ranked causal metabolites among 19 studied metabolites (Lord et al., 2021). As can be seen by these recent applications, extending Mendelian randomization analyses from the univariable to the multivariable setting can be a useful tool for disentangling complex relationships involving multiple risk factors and understanding the role each risk factor plays with regards to a health outcome.
Critical Parameters
While multivariable Mendelian randomization offers an attractive approach for estimating causality of multiple exposures simultaneously, there are a number of challenges and limitations that must be considered. Many of the limitations and concerns with respect to the validity of the IV assumptions for multivariable Mendelian randomization are shared with univariate Mendelian randomization and have been discussed at length in other articles (Smith & Ebrahim, 2004; Zheng et al., 2017). An awareness of these limitations is essential in interpreting findings derived from Mendelian randomization-based methods.
For one, it is imperative to conduct a review of the assumptions necessary for conducting a multivariable Mendelian randomization analysis (Fig. 2). These assumptions are largely based on those for univariate Mendelian randomization. Table 1 from Labrecque & Swanson (2018) presents a summary of strategies and related tools for assessing the three core IV assumptions, and provides context for deepening understanding of the assumptions, which can be extended to the multivariable case. Understanding the genetic variants used as IVs and assessing them in the context of the assumptions and prior biological information can further assist in drawing meaningful interpretations from a multivariable Mendelian randomization study.
Further, much attention should be paid to the selection of instruments (e.g., SNPs) and to any underlying biological information and critical parameters that may inform the Mendelian randomization study design as well as any inferences and interpretations drawn from findings. Please refer to the illustrative guide presented in Figure 3 from Swerdlow et al. (2016) that provides an outline of some of the key decisions in the selection of valid instruments. Other limitations include insufficient statistical power and weak instrument bias. To ensure adequate statistical power, Mendelian randomization studies need large sample sizes. To ensure that a genetic variant is not a weak instrument, and that the instrument is strongly associated with the corresponding exposure conditioning on the other exposures, the conditional F-statistic should exceed 10. Further, substantial weak-instrument bias may arise if large numbers of genetic variants are used (Burgess & Thompson, 2015; Burgess et al., 2011). Please refer to Sanderson et al. (2021) for further detail regarding correcting for weak instrument bias in the multivariable Mendelian randomization setting. Further, while multivariable Mendelian randomization accommodates pleiotropy to the extent that it allows for a priori information and known variables inputted in a model, it does not take into account unknown pleiotropy, which may bias the causal estimate (Burgess & Thompson, 2015).
Acknowledgements
GMP is financially supported by NHLBI awards R01HL127564 and R01HL142711. The authors are very grateful to the developer of the ‘MVMR’ R package, Wes Spiller, for providing an easy-to-use resource and extensive documentation for implementing a multivariable Mendelian randomization study (Sanderson et al., 2021), and to the authors of the multivariable Mendelian randomization approach (Burgess & Thompson, 2015; Sanderson et al., 2019, 2021). The ‘MVMR’ package is available for download at: https://github.com/WSpiller/MVMR (Sanderson et al., 2021).
Footnotes
Conflict of Interest
The authors declare no conflict of interest.
Data Availability Statement
The data that support the findings of this study are openly available in the NHGRI-EBI GWAS Catalog at https://www.ebi.ac.uk/gwas/.
Literature Cited
- Anderson EL, Howe LD, Wade KH, Ben-Shlomo Y, Hill WD, Deary IJ, … Hemani G (2020). Education, intelligence and Alzheimer’s disease: Evidence from a multivariable two-sample Mendelian randomization study. International Journal of Epidemiology, 49(4), 1163–1172. doi: 10.1093/ije/dyz280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angrist JD, & Krueger AB (2001). Instrumental variables and the search for identification: From supply and demand to natural experiments. The Journal of Economic Perspectives, 15(4), 69–85. doi: 10.1257/jep.15.4.69. [DOI] [Google Scholar]
- Bowden J, Davey Smith G, & Burgess S (2015). Mendelian randomization with invalid instruments: Effect estimation and bias detection through Egger regression. International Journal of Epidemiology, 44(2), 512–525. doi: 10.1093/ije/dyv080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buniello A, MacArthur JAL, Cerezo M, Harris LW, Hayhurst J, Malangone C, … Parkinson H (2019). The NHGRI-EBI GWAS Catalog of published genome-wide association studies, targeted arrays and summary statistics 2019. Nucleic Acids Research, 47(D1), D1005–D1012. doi: 10.1093/nar/gky1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess S, Davey Smith G, Davies NM, Dudbridge F, Gill D, Glymour MM, … Theodoratou E (2019). Guidelines for performing Mendelian randomization investigations. Wellcome Open Research, 4, 186. doi: 10.12688/wellcomeopenres.15555.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess S, Small DS, & Thompson SG (2017). A review of instrumental variable estimators for Mendelian randomization. Statistical Methods in Medical Research, 26(5), 2333–2355. doi: 10.1177/0962280215597579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess S, & Thompson SG (2015). Multivariable Mendelian randomization: The use of pleiotropic genetic variants to estimate causal effects. American Journal of Epidemiology, 181(4), 251–260. doi: 10.1093/aje/kwu283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess S, & Thompson SG (2017). Interpreting findings from Mendelian randomization using the MR-Egger method. European Journal of Epidemiology, 32(5), 377–389. doi: 10.1007/s10654-017-0255-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess S, & Thompson SG & CRP CHD Genetics Collaboration. (2011) Avoiding bias from weak instruments in Mendelian randomization studies. International Journal of Epidemiology, 40(3), 755–764. doi: 10.1093/ije/dyr036. [DOI] [PubMed] [Google Scholar]
- Canela-Xandri O, Rawlik K, & Tenesa A (2018). An atlas of genetic associations in UK Biobank. Nature Genetics, 50(11), 1593–1599. doi: 10.1038/s41588-018-0248-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chesmore K, Bartlett J, & Williams SM (2018). The ubiquity of pleiotropy in human disease. Human Genetics, 137(1), 39–44. doi: 10.1007/s00439-017-1854-z. [DOI] [PubMed] [Google Scholar]
- Cho Y, Haycock PC, Sanderson E, Gaunt TR, Zheng J, Morris AP, … Hemani G (2020). Exploiting horizontal pleiotropy to search for causal pathways within a Mendelian randomization framework. Nature Communications, 11(1), 1010. doi: 10.1038/s41467-020-14452-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davey Smith G (2007). Capitalizing on Mendelian randomization to assess the effects of treatments. Journal of the Royal Society of Medicine, 100(9), 432–435. doi: 10.1177/014107680710000923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies NM, Hill WD, Anderson EL, Sanderson E, Deary IJ, & Davey Smith G (2019). Multivariable two-sample Mendelian randomization estimates of the effects of intelligence and education on health. eLife, 8, e43990. doi: 10.7554/eLife.43990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies NM, Holmes MV, & Davey Smith G (2018). Reading Mendelian randomisation studies: A guide, glossary, and checklist for clinicians. BMJ, 362, k601. doi: 10.1136/bmj.k601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagliano Taliun SA, & Evans DM (2021). Ten simple rules for conducting a mendelian randomization study. PLoS Computational Biology, 17(8), e1009238. doi: 10.1371/journal.pcbi.1009238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaunt TR, Shihab HA, Hemani G, Min JL, Woodward G, Lyttleton O, … Relton CL (2016). Systematic identification of genetic influences on methylation across the human life course. Genome Biology, 17, 61. doi: 10.1186/s13059-016-0926-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenland S (2018). An introduction to instrumental variables for epidemiologists. International Journal of Epidemiology, 47(1), 358. doi: 10.1093/ije/dyx275. [DOI] [PubMed] [Google Scholar]
- Grimes DA, & Schulz KF (2002). Bias and causal associations in observational research. The Lancet, 359(9302), 248–252. doi: 10.1016/S0140-6736(02)07451-2. [DOI] [PubMed] [Google Scholar]
- Hartwig FP, Tilling K, Davey Smith G, Lawlor DA, & Borges MC (2021). Bias in two-sample Mendelian randomization when using heritable covariable-adjusted summary associations. International Journal of Epidemiology, 50(5), 1639–1650. doi: 10.1093/ije/dyaa266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemani G, Bowden J, & Davey Smith G (2018). Evaluating the potential role of pleiotropy in Mendelian randomization studies. Human Molecular Genetics, 27(R2), R195–R208. doi: 10.1093/hmg/ddy163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemani G, Tilling K, & Davey Smith G (2017). Correction: Orienting the causal relationship between imprecisely measured traits using GWAS summary data. PLoS Genetics, 13(12), e1007149. doi: 10.1371/journal.pgen.1007149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemani G, Zheng J, Elsworth B, Wade KH, Haberland V, Baird D, … Haycock PC (2018). The MR-Base platform supports systematic causal inference across the human phenome. eLife, 7, e34408. doi: 10.7554/eLife.34408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan DM, Verbanck M, & Do R (2019). HOPS: A quantitative score reveals pervasive horizontal pleiotropy in human genetic variation is driven by extreme polygenicity of human traits and diseases. Genome Biology, 20(1), 222. doi: 10.1186/s13059-019-1844-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labrecque J, & Swanson SA (2018). Understanding the assumptions underlying instrumental variable analyses: A brief review of falsification strategies and related tools. Current Epidemiology Reports, 5(3), 214–220. doi: 10.1007/s40471-018-0152-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawlor DA, Harbord RM, Sterne JAC, Timpson N, & Davey Smith G (2008). Mendelian randomization: Using genes as instruments for making causal inferences in epidemiology. Statistics in Medicine, 27(8), 1133–1163. doi: 10.1002/sim.3034. [DOI] [PubMed] [Google Scholar]
- Locke AE, Kahali B, Berndt SI, Justice AE, Pers TH, Day FR, … Speliotes EK (2015). Genetic studies of body mass index yield new insights for obesity biology. Nature, 518(7538), 197–206. doi: 10.1038/nature14177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lonsdale J, Thomas J, Salvatore M, Phillips R, Lo E, Shad S, … Moore HF (2013). The genotype-tissue expression (GTEx) project. Nature Genetics, 45(6), 580–585. doi: 10.1038/ng.2653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lord J, Jermy B, Green R, Wong A, Xu J, Legido-Quigley C, … Proitsi P (2021). Mendelian randomization identifies blood metabolites previously linked to midlife cognition as causal candidates in Alzheimer’s disease. Proceedings of the National Academy of Sciences, 118(16), e2009808118. doi: 10.1073/pnas.2009808118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo S, Au Yeung SL, Zuber V, Burgess S, & Schooling CM (2020). Impact of genetically predicted red blood cell traits on venous thromboembolism: Multivariable mendelian randomization study using UK Biobank. Journal of the American Heart Association, 9(14), e016771. doi: 10.1161/JAHA.120.016771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahajan A, Wessel J, Willems SM, Zhao W, Robertson NR, Chu AY, … McCarthy MI (2018). Refining the accuracy of validated target identification through coding variant fine-mapping in type 2 diabetes. Nature Genetics, 50(4), 559–571. doi: 10.1038/s41588-018-0084-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minelli C, Del Greco MF, van der Plaat DA, Bowden J, Sheehan NA, & Thompson J (2020). The use of two-sample methods for Mendelian randomization analyses on single large datasets. bioRxiv. doi: 10.1101/2020.05.07.082206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paaby AB, & Rockman MV (2013). The many faces of pleiotropy. Trends in Genetics: TIG, 29(2), 66–73. doi: 10.1016/j.tig.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer TM, Lawlor DA, Harbord RM, Sheehan NA, Tobias JH, Timpson NJ, … Sterne JAC (2012). Using multiple genetic variants as instrumental variables for modifiable risk factors. Statistical Methods in Medical Research, 21(3), 223–242. doi: 10.1177/0962280210394459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedron S, Kurz CF, Schwettmann L, & Laxy M (2021). The effect of BMI and type 2 diabetes on socioeconomic status: A two-sample multivariable Mendelian randomization study. Diabetes Care, 44(3), 850–852. doi: 10.2337/dc20-1721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell JK, Berisa T, Liu JZ, Ségurel L, Tung JY, & Hinds DA (2016). Detection and interpretation of shared genetic influences on 42 human traits. Nature Genetics, 48(7), 709–717. doi: 10.1038/ng.3570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasooly D, & Patel CJ (2019). Conducting a reproducible Mendelian randomization analysis using the R analytic statistical environment. Current Protocols in Human Genetics, 101(1), e82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees JMB, Wood AM, & Burgess S (2017). Extending the MR-Egger method for multivariable Mendelian randomization to correct for both measured and unmeasured pleiotropy. Statistics in Medicine, 36(29), 4705–4718. doi: 10.1002/sim.7492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanderson E (2021). Multivariable Mendelian randomization and mediation. Cold Spring Harbor Perspectives in Medicine, 11(2), a038984. doi: 10.1101/cshperspect.a038984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanderson E, Davey Smith G, Windmeijer F, & Bowden J (2019). An examination of multivariable Mendelian randomization in the single-sample and two-sample summary data settings. International Journal of Epidemiology, 48(3), 713–727. doi: 10.1093/ije/dyy262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanderson E, Spiller W, & Bowden J (2021). Testing and correcting for weak and pleiotropic instruments in two-sample multivariable Mendelian randomization. Statistics in Medicine, 40(25):5434–5452. doi: 10.1002/sim.9133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekula P, Del Greco MF, Pattaro C, & Köttgen A (2016). Mendelian randomization as an approach to assess causality using observational data. Journal of the American Society of Nephrology: JASN, 27(11), 3253–3265. doi: 10.1681/ASN.2016010098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith GD, & Ebrahim S (2004). Mendelian randomization: Prospects, potentials, and limitations. International Journal of Epidemiology, 33(1), 30–42. doi: 10.1093/ije/dyh132. [DOI] [PubMed] [Google Scholar]
- Staiger D, & Stock JH (1994). Instrumental Variables Regression with Weak Instruments (No. 151). Cambridge, MA: National Bureau of Economic Research. doi: 10.3386/t0151. [DOI] [Google Scholar]
- Stock JH, & Trebbi F (2003). Retrospectives: Who invented instrumental variable regression? The Journal of Economic Perspectives, 17(3), 177–194. doi: 10.1257/089533003769204416. [DOI] [Google Scholar]
- Swerdlow DI, Kuchenbaecker KB, Shah S, Sofat R, Holmes MV, White J, … Hingorani AD (2016). Selecting instruments for Mendelian randomization in the wake of genome-wide association studies. International Journal of Epidemiology, 45(5), 1600–1616. doi: 10.1093/ije/dyw088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tryka KA, Hao L, Sturcke A, Jin Y, Wang ZY, Ziyabari L, … Feolo M (2014). NCBI’s database of genotypes and phenotypes: DbGaP. Nucleic Acids Research, 42, (Database issue), D975–D979. doi: 10.1093/nar/gkt1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ, Tchetgen Tchetgen EJ, Cornelis M, & Kraft P (2014). Methodological challenges in mendelian randomization. Epidemiology, 25(3), 427–435. doi: 10.1097/EDE.0000000000000081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Wray NR, Zhang Q, Sklar P, McCarthy MI, Brown MA, & Yang J (2017). 10 years of GWAS discovery: Biology, function, and translation. American Journal of Human Genetics, 101(1), 5–22. doi: 10.1016/j.ajhg.2017.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe K, Stringer S, Frei O, Umićević Mirkov M, de Leeuw C, Polderman TJC, … Posthuma D (2019). A global overview of pleiotropy and genetic architecture in complex traits. Nature Genetics, 51(9), 1339–1348. doi: 10.1038/s41588-019-0481-0. [DOI] [PubMed] [Google Scholar]
- Willer CJ, Schmidt EM, Sengupta S, Peloso GM, Gustaffson S, Kanoni S, … Global Lipids Genetics Consortium. (2013) Discovery and refinement of loci associated with lipid levels. Nature Genetics, 45(11), 1274–1283. doi: 10.1038/ng.2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Windmeijer F, & Sanderson E (2013). A weak instrument F-test in linear IV models with multiple endogenous variables. doi: 10.1920/wp.cem.2013.5813. [DOI] [PMC free article] [PubMed]
- Zheng J, Baird D, Borges M-C, Bowden J, Hemani G, Haycock P, … Smith GD (2017). Recent developments in Mendelian randomization studies. Current Epidemiology Reports, 4(4), 330–345. doi: 10.1007/s40471-017-0128-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are openly available in the NHGRI-EBI GWAS Catalog at https://www.ebi.ac.uk/gwas/.


