A Noncontact Ballistocardiography-Based IoMT System for Cardiopulmonary Health Monitoring of Discharged COVID-19 Patients

Abstract

We developed a ballistocardiography (BCG)-based Internet-of-Medical-Things (IoMT) system for remote monitoring of cardiopulmonary health. The system composes of BCG sensor, edge node, and cloud platform. To improve computational efficiency and system stability, the system adopted collaborative computing between edge nodes and cloud platforms. Edge nodes undertake signal processing tasks, namely approximate entropy for signal quality assessment, a lifting wavelet scheme for separating the BCG and respiration signal, and the lightweight BCG and respiration signal peaks detection. Heart rate variability (HRV), respiratory rate variability (RRV) analysis and other intelligent computing are performed on cloud platform. In experiments with 25 participants, the proposed method achieved a mean absolute error (MAE)±standard deviation of absolute error (SDAE) of 9.6±8.2 ms for heartbeat intervals detection, and a MAE±SDAE of 22.4±31.1 ms for respiration intervals detection. To study the recovery of cardiopulmonary function in patients with coronavirus disease 2019 (COVID-19), this study recruited 186 discharged patients with COVID-19 and 186 control volunteers. The results indicate that the recovery performance of the respiratory rhythm is better than the heart rhythm among discharged patients with COVID-19. This reminds the patients to be aware of the risk of cardiovascular disease after recovering from COVID-19. Therefore, our remote monitoring system has the ability to play a major role in the follow up and management of discharged patients with COVID-19.

I. Introduction

The ongoing coronavirus disease 2019 (COVID-19) pandemic has caused tens of millions of people worldwide to be infected. COVID-19 is the result of infection by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2); this virus can cause severe acute respiratory syndrome, which can induce the generalized attenuation of excitatory pathways that regulate the respiratory and cardiovascular systems [1]. SARS-CoV-2 attacks not only the respiratory system but also the cardiovascular system [2]–[5]. Documented evidence has revealed that approximately 20% and 15% of patients with COVID-19 develop acute respiratory distress syndrome and sustain myocardial injury [2], respectively. Patients with cardiopulmonary injury are at risk of chronic cardiopulmonary complications after recovery. Therefore, the physical health of discharged patients who have recovered from COVID-19 should be evaluated to determine the long-term effects of COVID-19.

Heart rate variability (HRV) and respiratory rate variability (RRV) are major indicators of cardiopulmonary health. In addition, the HRV and RRV can be further used for sleep staging modeling and sleep-disordered breathing (SDB) diagnosis. Conventionally, heart rate (HR) and respiratory rate (RR) are monitored using electrocardiogram (ECG) and respiratory signals through contact sensors. However, such monitoring equipment is often limited by patient compliance, analyzable wearing time, electrode skin irritation, and sleep disturbance. Especially for patients with COVID-19, this contact monitoring method can increase the probability of cross-infection and the measurement load. Ballistocardiography (BCG) is a noncontact technique for recording subtle motions of the human body caused by cardiac ejection and breathing. It can be measured using beds [6], [7], wheel chairs [8], [9], and weighting scales [10], [11]. The main advantages of using BCG signal to monitor HR and RR are its convenience, low cost and noncontact monitoring method. In addition, the rapid development of the Internet of Medical Things (IoMT) has increased the use of remote health monitoring systems in home health care. To reduce frequency of contact between patients and doctors, the IoMT-driven remote monitoring system shown in Fig. 1 is a candidate for the follow up of discharged COVID-19 patients.

Fig. 1.

Remote monitoring for discharged COVID-19 patients.

In the IoMT system, the edge device as the node of data collection and processing is the core component of the system. Some BCG-based IoMT systems have been developed for family vital sign parameter monitoring. Various sensors are used to acquire BCG signals. These sensors mainly include polyvinylidene fluoride film (PVDF) [12], electromechanical films (EMFi) [13], hydraulic sensors [14], strain Gauges [15], and fiber Bragg grating sensors (FBGSs) [16]. For example, Brüser et al. [17] used PVDF as a piezoelectric material to develop a film sensor that is placed under the bed sheet where the chest is located to measure pressure changes on the bed attributable to breathing movement and heartbeats. To increase the accuracy of BCG analysis, some studies have designed more complex systems or sensor networks. For example, Kortelainen and Virkkala [18] developed a smart mattress consisting of 160 EMFi sensors distributed throughout it that can obtain a BCG signal from multiple locations. Nevertheless, the improvement of BCG signal quality has remained limited; systems that use multiple BCG signals have increased complexity. The key to BCG measurement system design is not novel sensors or device structures but the stability and reliability of the measuring instrument.

BCG signals are extremely susceptible to interference from various types of noises and motion artifacts. Therefore, research on anti-interference algorithm is the key to improve the accuracy of BCG analysis. For example, Antink et al. [19] used a continuous local interval estimator (CLIE) approach to estimate the beat-to-beat intervals (BBIs). To reduce the influence of frequent motion artifacts on the analysis results, the CLIE method used ultrashort-term HRV analysis. Brüser et al. [20] employed three estimators, namely an autocorrelation function, an average magnitude difference function, and maximum-amplitude pairs, to calculate BBIs by using a sliding time window. Paalasmaa et al. [21] first adaptively inferred the heartbeat shape from the signal by using hierarchical clustering. Subsequently, BBIs were detected by identifying the positions where the heartbeat shape best fits the signal. Although these methods can accurately calculate the average HR per minute, their measurement accuracy for a single heartbeat interval is insufficient. This directly affects the accuracy of HRV measurement.

In this study, we achieved the remote monitoring of users’ cardiopulmonary function through the reasonable allocation of computing resources to edge devices and cloud platform. First, a series of signal preprocessing is performed on the edge device. Then the processed data are uploaded to the cloud platform through the wireless network for further analysis and modeling. Our study has three main contributions.

• 1)The system based on the proposed noncontact method is the first in the world to be used for the cardiopulmonary function monitoring and management in discharged patients who had recovered from COVID-19. This system provides a novel solution for the follow-up and monitoring of these patients.
• 2)To improve the robustness of the HRV analysis algorithm, this study first used approximate entropy to judge signal quality for eliminating signal segments that are severely damaged by interference, thereby improving the accuracy of J-J interval (interval between adjacent J peaks on BCG signal) extraction.
• 3)To reduce the computational load in edge node, this study proposed a lightweight J peaks detection method. The method first used the proposed fuzzy positive and negative slope discrimination (F-PNSD) algorithm to detect peaks in the BCG envelope and then accurately searched for corresponding J peak positions in BCG according to the peak point in the envelope.

In addition, this system can be used for the noncontact monitoring of cardiopulmonary function in patients with COVID-19, which will effectively reduce the contact between doctors and patients.

The remainder of this article is organized as follows. Section II describes BCG mechanism and the proposed IoMT system; Section III presents an anti-interfering BCG and respiration signal peaks detection method, including signal quality assessment (SQA), BCG and respiratory signal separation, and peaks detection; Section IV presents experimental results and discussion; Finally, Section V concludes this article.

II. BCG Mechanism and Proposed IoMT System

A. BCG Mechanism

The BCG signal is caused by the rhythmic systole and diastole of the heart and the resulting periodic pumping in the blood vessels. During ventricular systole, when blood is ejected into the large blood vessels, the body’s center of mass moves toward the body’s head. In the other direction, when blood moves toward blood vessels peripheral to the heart, the center of mass moves toward the feet [22]. A schematic of this process is illustrated in Fig. 2(a). The center of mass shift is caused by the combined forces of heart activity, breathing, and body movement. Therefore, the original signal is mainly composed of the three aforementioned signal components. A standard BCG heartbeat mainly contains H, I, J, K, L, M, N waves, as shown in Fig. 2(b). The signals of the HL interval form a W-shaped wave group that represents heart systole. The L-N waves represent the diastole. Among all waves, the J wave has the largest amplitude, indicating the ejection process after blood enters the descending aorta. The magnitude of I-J wave amplitude reflects the strength of ventricular contractility. Therefore, the BCG signal contains substantial heart activity information.

Fig. 2.

(a) Aortic arch and force vector originating from left ventricular ejection. Image from literature [21] and (b) typical BCG signal waveform.

B. Proposed BCG Sensor

The proposed BCG system uses the piezoelectric ceramic sensor to obtain BCG signals. The piezoelectric effect is a phenomenon in which piezoelectric materials generate electrical charges in response to applied mechanical pressure. The piezoelectric element of a BCG sensor produces the electrical charge signal corresponding to the vertical acceleration of the body’s center of mass. The total charge 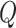is proportional to the external pressure 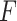applied to the piezoelectric component, defined as

where 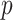is piezoelectric constant, 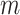and 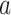are overall body mass and acceleration, respectively.

Because the output of the piezoelectric element is a charge signal, it must be converted into a voltage signal for further processing and analysis. This requires an interface circuit with high input impedance and low input bias [9]. To this end, a piezoelectric sensor and operational amplifier cascade circuit was designed as presented in Fig. 3. The insulation resistance 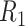of the sensor is high and can be approximated as an open circuit. The capacitor 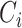passes the alternating current and blocks the direct current. Therefore, only dynamic charges caused by dynamic pressure can enter the interface circuit through 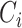. In the integral operation circuit, the conversion relationship between the output voltage 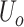and charges 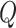is as follows:

In addition, the setting of the parallel resistance 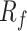can effectively prevent saturation of the operational amplifier caused by major interference from body motion. Because a BCG signal from respiratory activity mainly ranges from 0.1 to 10 Hz, 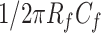is set to be less than the lower limit frequency (0.1 Hz) to ensure the passband range of the signal.

Fig. 3.

BCG sensor interface circuit design.

C. Architecture of BCG-Based IoMT System

Thanks to the development of IoMT technology, the BCG-based IoMT system has been applied to the follow up of discharged patients with COVID-19. As shown in Fig. 4, the proposed IoMT system composes of edge device, transport layer, cloud platform, and application layer.

Fig. 4.

Proposed IoMT system framework.

BCG is collected by the edge sensor placed under the pillow, and then is amplified and processed at the edge node. The amplified signal is converted into a digital signal by an analog-to-digital conversion (A/DC) chip. Finally, the SQA, signal separation, as well as BCG and respiration signal peaks detection are performed sequentially at edge node. In the transport layer, the smartphone or other smart devices receive real-time HR and respiration rate information from edge devices via Bluetooth. Meanwhile, continuous heartbeat and breathing intervals information are uploaded to the cloud platform via wireless network. The cloud platform is first used to store and manage basic user information and physiological data. More importantly, it undertakes the cloud computing task for the further data analysis (HRV, RRV, etc) and modeling (sleep staging, SDB, etc) are performed. The application layer mainly plays the role of interacting with users and doctors. In the doctor-side, the preliminary analysis and diagnosis results are sent to the doctor via the Internet. Based on this information, doctors conduct more in-depth individualized diagnosis, and prescribe individualized prescriptions and rehabilitation guidance to users through Web services. Users can view HR, breathing rate, intelligent analysis reports and doctor’s prescriptions in real time through smart terminals.

III. Anti-Interfering BCG and Respiration Signal Peaks Detection

After the BCG signal is collected by the sensor, it is first preprocessed at the edge device, including SQA, signal separation, as well as BCG and respiration signal peaks detection. Accurate peak point detection is a prerequisite for HRV and RRV analysis, further modeling and intelligent diagnosis. In this section, we present an anti-interfering BCG and respiration signal peaks detection method.

A. Signal Quality Assessment

In automatic health monitoring, the SQA plays a major role in applications such as arrhythmia recognition, HRV analysis, RR detection, and sleep monitoring [23]–[25]. BCG signals are corrupted by various artifacts and noise, including baseline wander (BW) due to breathing and abrupt changes (ACs) due to body movement, power-line interference, and device noise. Artifacts and noise can reduce BCG signal quality. Specifically, ACs may severely corrupt the morphology of the IJK complex wave. The presence of ACs makes it more difficult to determine the feature points of the waveform. The AC component has a higher amplitude than BW does at low frequencies (< 0.8 Hz); the two components merge into abrupt BW in this frequency band.

We extract the abrupt BW by using an infinite impulse response (IIR) low-pass filter with a cutoff frequency of 0.8 Hz. Fig. 5 illustrates the abrupt BW signal separated from the raw BCG signal. The abrupt BW has short-term high-amplitude variation in AC segments. Therefore, the separated abrupt BW signal can be used to determine the quality of the BCG signal. Let 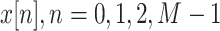be a discrete-time raw BCG signal. The abrupt BW signal is given as

where 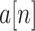is abrupt BW signal and 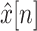is the BCG signal including high frequency noise.

Fig. 5.

Abrupt BW signal separated from the raw BCG signal.

In this study, information entropy is used as signal quality index (SQI). The entropy of a signal represents the average uncertainty of the signal source. As the uncertainty of the information source increases, its entropy value increases. Approximate entropy (ApEn) is an entropy algorithm suitable for processing short-term signals. It is approximately equal to the negative average natural logarithm of the conditional probability of maintaining similarity between a subsequence of length 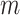and 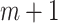[26]. The calculation process of ApEn is presented in Algorithm 1. To determine the signal quality of a short period, the abrupt BW signal 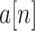is first segmented into continuous blocks of 1 s. Then, the 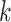th block of 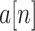is expressed as

where 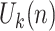is the 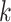th block of 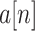and 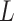is the size of blocks. Subsequently, ApEn is solved in each block. To adaptively detect ACs in BW, signal quality is determined by computing the dynamic ApEn difference between adjacent blocks, calculated as

where 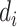is the ApEn difference between 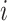th block and 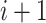th block. The calculated 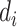is then compared with a preset threshold for AC discrimination in the BW signal. The decision criteria is as follows:

where SQI_i represents the SQI of the 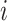th block, 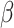is the preset threshold. In this study, BCG signal quality is classified into two grades: good (SQI = 1) versus bad (SQI = 0). Good-grade BCG blocks are further processed, whereas bad-grade blocks are discarded. The dynamic ApEn difference method can effectively avoid BCG block with slowly varying BW being recognized as unacceptable. Moreover, poor-quality signals are not further processed, thereby reducing the computational load of edge devices and increasing signal analysis accuracy in cloud platform.

Algorithm 1 Approximate Entropy Algorithm

• input: 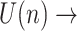abrupt BW signal;

• Output: approximate entropy;

• 1:given a time series 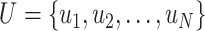, a non-negative integer m ≤ N, and a positive real number 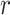, defined the blocks 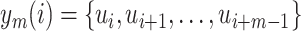and ;
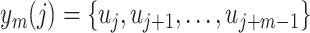• 2:calculate the distance between two blocks as
• 3:calculate the value 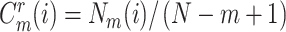, where 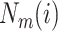is number of ;
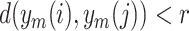• 4:computing:
• 5:increase the space dimensionality to 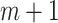, calculate ;
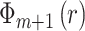• 6:approximate entropy:

B. Separating BCG and Respiratory Signals

The previous section demonstrates that the raw BCG signal is a superposition of the BCG signal, respiratory signal, and noise. The BCG and respiratory signal are important parameters of vital signs that reflect cardiopulmonary function. For further analysis, the extraction of BCG and respiratory signal is necessary. The most important information of these two signals resides in the 1–10 Hz and 0.1–0.5 Hz ranges, respectively. A wavelet transform (WT) can be used to decompose a signal into different frequency bands. Because a wavelet has a flexible shape and short duration, the wavelet signal processing method can accurately capture transient features, such as J-wave. In the traditional WT algorithm (i.e., Mallat algorithm), the input signal is convolved with high-pass and low-pass filters to separate high-frequency and low-frequency information. However, this method is based on the Fourier transform operation, which has strict requirements for the computing power and memory of the edge device. The lifting wavelet scheme (LWS) is a novel wavelet construction method based on the space domain and does not depend on the Fourier transform, also known as second-generation wavelets. It effectively improves the speed of the WT. This scheme reduces the number of arithmetic operations by a factor of nearly two [27]. Therefore, we used the LWS to separate the BCG and respiratory signals and reduce the computational load and memory overhead of the edge devices. Lifting WT (LWT) is divided into two parts: 1) decomposition and 2) reconstruction. Reconstruction is the inverse transformation of decomposition. Decomposition includes the following three main steps.

• 1)
  Splitting: This operation divides the original signal 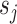into two interrelated odd 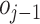and even 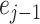samples

  
• 2)
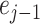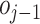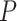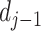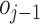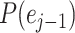  Prediction: This operation uses to predict , the prediction operator is represented by the function . The difference between and represents their similarity. The 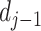is wavelet coefficient, which represents the high frequency component of 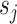. The prediction can be formulated as follows:

  
• 3)
  Updating: This operation first selects an updating operator 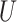, and subsequently updates the even sequence 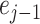to obtain the updated sequence 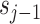, which is called the scale coefficient, as follows:

  

The three aforementioned constitute one iteration of the LWT. The 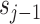represents the smooth part of the input signal, which can be iterated as the input of the subsequent lifting algorithm. The prediction and updating operator are functions that depend on the wavelet family used. The operators used are formulated as follows:

The sampling frequency of the raw BCG signal is 100 Hz. six-layer LWT is used in this study. The BCG and respiratory signals are extracted through the combined reconstruction of wavelet coefficients and scale coefficients in the second, fifth, and sixth layers. The results are showed in Fig. 6.

Fig. 6.

Example of BCG and respiratory signal extraction using LWS.

C. Hilbert Transform

The HRV analysis relies on accurate heartbeat detection. In a typical BCG heartbeat, the J wave has the larger amplitude than other waves. The J peak is usually used as fiducial point for heartbeat segmentation. However, because the BCG waveform can oscillate and have noise interference, directly using the fiducial point detection algorithm on the basis of wave amplitude may cause false detection of the J peak. To overcome this problem, the Hilbert transform (HT) was used in this study to obtain a fundamental frequency that is synchronized with the HR from a BCG signal. The HT of a signal is expressed as

where 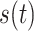is the input signal and 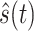represents the output through HT system. After filtering out the respiratory signal, BCG signal can be modeled as

where 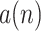represents the heartbeat envelope that models repetition of J wave in a BCG signal. Its frequency spectrum is mainly composed of the fundamental and harmonics frequency corresponding the HR. The 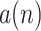is unobservable, and only its version modulated by modulation frequency with 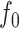can be observed. To obtain the pulse envelope of heartbeats, we perform HT on BCG signal. The HT of a signal is equivalent to inputting the signal to a system with a response function of 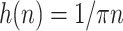. Therefore, HT can produce a phase shift of 90 degrees for input signal. This procedure can be used to approximate the output signal of 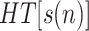by using (15) when noise is negligible

Thus, an analytic signal with the input signal 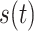as its real component and the output signal 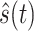as its imaginary component is obtained. The expression is

The heartbeat envelope 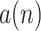can be obtained by calculating the amplitude of 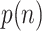, which is expressed as

Fig. 7(a) shows an example of the heartbeat envelope attained using the HT. We further detect the J wave in the BCG signal on the basis of its envelope.

Fig. 7.

Principle diagram of peak detection for BCG and respiration signal. (a) Example of the BCG envelope signal attained using the HT; (b) peak detection in the BCG envelope by comparing the maximum-amplitude points in signal segments with smaller size; (c) peak detection for respiration by comparing the maximum-amplitude points in signal segments with larger size; (d) BCG peak detection by using the envelope peak.

D. BCG and Respiration Signal Peaks Detection

The peak detection is decisive operation for HRV and RRV analyses. To reduce computational complexity, we proposed a lightweight and efficient peak detection algorithm called fuzzy positive and negative slope discrimination (F-PNSD). In this method, the signal is first divided into equal time segments, and the peak points in the signal are detected by identifying the maximum-amplitude points in these signal segments. If the maximum amplitude of any signal segment is lower (higher) than that of the signal segment after it, then the slope of the signal is positive (negative). When the slope switches from positive to negative, the maximum value of the last segment with a positive slope is considered the peak value of the signal. The BCG envelope and respiration signal are separated into segments, as shown in Fig. 7. Switches from a positive to a negative slope are shown in segments S5-S6 and S3-S4 in Fig. 7(b) and (c), respectively. The peak points in S5 and S3 segments with the last positive slope are detected as points P and Q in BCG envelope and respiration signal. The number of peaks detected in the signal depends on the segment size. The smaller the segment size, the more peaks are detected in the signal, and vice versa. Because the heartbeat cycle is shorter than the respiratory cycle, to ensure that the peak point is not missed, the BCG envelope signal has smaller segments. For peak detection in the BCG signal, the peaks of the BCG signal and its envelope do not coincide at the exact same time. Therefore, the peak of the BCG signal must be more accurately identified according to the determined peak point of the envelope signal. In fact, the BCG peak is located near the peak of its envelope signal. The BCG peak location can be expressed as follows:

where 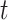represents time interval 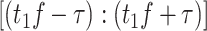, 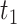represents peak location of the corresponding BCG envelope, 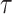is the set search radius, and 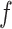is sampling rate of signal. The function 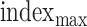returns the index of largest value within search radius. The relative location between the BCG and envelope signal is marked in Fig. 7(d).

IV. Results and Discussion

In this section, the performance of the proposed cardiopulmonary health monitoring system was evaluated and validated. Finally, the system was used to monitor the HRV and RRV of discharged COVID-19 patients, and then to assess their cardiopulmonary function. The experimental setup for cardiopulmonary health monitoring is shown in Fig. 8.

Fig. 8.

Experimental setup for cardiopulmonary health monitoring in participants using the proposed system. (a) Signal measurement scenario. (b) our hardware equipment.

A. Data Sets Acquisition

To evaluate the accuracy of heartbeat and respiration period segmentation, we simultaneously collected golden standard signal (ECG, respiration) and BCG data using BIOPAC MP150 and Witheart Youthope Lite (our BCG monitoring device) from 25 participants with average age in 30.5 ± 5.2 years and average weight in 55.7±10.9 kg. The signals were recorded from each participant for 5 minutes. The sampling frequency of ECG and respiratory signal was 250 Hz, and that of BCG signal was 125 Hz.

To study the cardiopulmonary function of discharged COVID-19 patients, the proposed system was also used to evaluate the cardiopulmonary function of discharged COVID-19 patients during sleep. The experiment was carried out from April 3, 2020 to April 3, 2021. The BCG data were collected from 186 discharged COVID-19 patient (in Wuhan, average age in 49.4 ± 11.4) and 186 healthy volunteers (in Beijing, Guangzhou and Hangzhou, average age in 49.4 ± 11.2). The two groups of participants are matched for age, gender, and underlying diseases. This study was approved by the ethics committee of Wuhan Jinyintan Hospital (Approval number: KY-2020-40.02).

B. Accuracy Evaluation of Period Segmentation

The accuracy of heartbeat and respiration period segmentation is the prerequisite of HRV and RRV analyses. We used four metrics to quantitatively evaluate the performance of the proposed method for BCG J-J interval segmentation. The J-J interval in BCG and the R-R interval in ECG are equivalent, and both represent one heartbeat period, as shown in Fig. 9(a). The four metrics were as follows.

• 1)Mean Absolute Error (MAE): MAE indicates the average value of absolute error between J-J intervals from BCG and R-R intervals from ECG.
• 2)Standard Deviation of Absolute Error (SDAE): SDAE reflects the dispersion of absolute error between J-J intervals and R-R intervals. A low SDAE indicates that the measuring error of J-J intervals fluctuates in small range.
• 3)Coverage: The ratio between the numbers of heartbeat detected from BCG and from ECG. The coverage indicates the heartbeat recall rate from BCG.
• 4)Pearson Correlation Coefficient (PCC): PCC measures the linear correlation between J-J interval sequences from BCG and R-R interval sequences from ECG.

Fig. 9.

Comparison of heartbeat detection based on ECG and BCG signals from a recording with large interference. (a) Definition of J-J interval and R-R interval. (b) J-peaks detection in BCG and R-peaks detection in ECG. (c) tracking comparison of heartbeat interval for five minutes between BCG and ECG.

We compared the performance of the proposed method with other competitive methods using the four aforementioned metrics on our database. The results are summarized in Table I. The proposed method performed the high on the three metrics of MAE (9.6 ms), SDAE (8.2 ms), and PCC (0.993). The coverage of 0.985 is slightly lower than that of 0.987 and 0.992 in [9] and our method without SQA, respectively. It can be seen that the SQA improves the detection accuracy of the J-J interval by discarding poor quality signals, while also reducing the Coverage metric. The accuracy of the J-J interval is more important for HRV analysis than Coverage. Lydon et al. [28] detected the peaks of the envelope obtained by an energy function for heartbeat detection. Lydon et al. [28] used sliding windows to restrict the search range for peak detection in BCG. When signal quality is poor, both methods usually cause the heartbeat to be lost or over-detected. Rosales et al. [30] detected the heartbeat in a sliding window by analyzing the fundamental frequency of the BCG envelope signal. Although this method can prevent interference, the calculated heartbeat interval is actually the average interval of all heartbeats in the window. Thus, the heartbeat intervals extracted by this method are not suitable for HRV analysis. Xie et al. [9] first used the clustering method to automatically learn individualized heartbeat templates and then performed heartbeat recognition based on HT and PCC. The method achieved a coverage of 0.987. This method is advantageous because it can reduce the rate of missed heartbeats, but accurately locating the J peaks in BCG with large body movement interference is difficult. Our method first uses a simple algorithm to perform peak detection on the BCG envelope and then uses these peaks as reference points to further search for corresponding peaks within a small range in BCG. By using the coarse-to-fine peak detection, our method could accurately detect heartbeats even when the BCG signal quality is low. Fig. 9 compares heartbeat detection between BCG and ECG. In this study, the PanTompkins algorithm was utilized to detect R-peak in ECG due to its robustness [31]. Fig. 9(b) indicates that the proposed method accurately detects J peaks in a BCG segment with considerable interference and noise. The tracking comparisons for approximately 5 min between BCG and ECG intervals are illustrated in Fig. 9(c). The blue and orange curves represent the ECG and BCG heartbeat intervals, respectively. We can see that the BCG interval could better track the ECG interval changes except for a few abnormal values. The abnormal values were mainly caused by short-term ACs in the BCG signal that were replaced with the averages of nearby values in subsequent processing. The accuracy of the BCG interval met the requirements for HRV analysis.

TABLE I. Four Metrics for Performance Estimation of Heartbeat Using Different Methods.

Method	Estimation metrics
	MAE±SDAE	Coverage	PCC
Lydon K [28]	31.5±23.7	0.913	0.937
Pino E J [29]	39.3±32.1	0.941	0.926
Rosales L [30]	25.6±19.8	0.939	0.960
Xie Q [9]	11.8±8.7	0.987	0.991
Without SQA	11.1±8.9	0.992	0.990
Proposed method	9.6±8.2	0.985	0.993

To evaluate the accuracy of respiration period segmentation, we utilized two metrics similar to the evaluation for the accuracy of heartbeat period segmentation. The definitions of the two metrics were as follows.

• 1)Mean Absolute Error: MAE indicates the average value of absolute error between respiration intervals from separated respiration signal and gold-standard respiration intervals. The gold-standard respiration intervals are extracted from directly measured respiration signal.
• 2)Standard Deviation of Absolute Error: SDAE reflects the dispersion of absolute error between respiration intervals and gold-standard respiration intervals. A low SDAE indicates that the measuring error of respiration fluctuates in small range.

From Fig. 6, we can see that the respiration signal is similar to the cosine signal. The peak detection of the respiration signal is easier than J-peak detection of the BCG with the complex waveform. We did not detailedly analyze the evaluation results for the accuracy of respiration period segmentation. The proposed method achieved MAE ± SDAE of 22.4±31.1 ms. Therefore, the accuracy met the requirements for RRV analysis.

In addition, the proposed method may have some limitations. In this evaluation experiment, we did not consider the impact of severe heart disease on the accuracy of the algorithm. The BCG signal records the weak body vibrations caused by the rhythmic heartbeat and ejection. However, severe heart diseases (myocardial infarction, arrhythmia, etc.) can cause rhythmic changes in heart beat and ejection, which in turn affect the waveform shape of the BCG signal. The abnormal change of the waveform shape may reduce the accuracy of the J wave detection algorithm. Therefore, we need to evaluate the effectiveness of algorithms for common heart diseases in the next work.

C. HR and RR Monitoring for Discharged COVID-19 Patient

HR and RR are the prerequisites for HRV and RRV analyses. At the same time, medical experts can directly judge the health status of cardiopulmonary function based on the change curve of HR and RR. To facilitate doctors to grasp more comprehensive HR and RR information, we have developed relevant interactive interfaces at the application layer of the system. Fig. 10 presents the monitoring data of a discharged COVID-19 patient in the interactive interfaces. The continuous fluctuation curves of HR and RR at a night is shown in Fig. 10(a). The yellow and blue curve represent HR and RR, respectively. The system automatically determines the bedtime and bed away time according to the detected BCG signal, and recognizes the time to fall asleep and wake up according to HRV and RRV. The sleep staging based on HRV and RRV is shown in bottom of the chart. The HR and RR monitoring data for this volunteer for 30 consecutive days are shown in Fig. 10(b). Here, HR is expressed by the benchmark value of the day, which is obtained by calculating the mode of the continuous HR of the day. The same is true for RR. In the doctor-side, specialists can access this information through the Internet, and then provide patients individualized diagnosis and rehabilitation guidance.

Fig. 10.

Example of HR and RR monitoring using the proposed system: (a) continuous monitoring curves of HR and RR at one of the days; (b) benchmark value of HR and RR at each day.

D. HRV Analysis for Discharged COVID-19 Patients

HRV is the physiological phenomenon of the variation in the time interval between consecutive heartbeats and provides information about the balance between the sympathetic and parasympathetic nervous systems. Low HRV indicates autonomic nervous system dysfunction, which is related to impaired heart function. HRV can be evaluated with various measure. The proposed system analyzed the HRV through SDNN, SDANN, LF, and HF, which are explained in Table II. In this study, a total of 372 participants completed follow-up, and 42 participants of them were excluded because of excessive abnormal values; the monitoring data of 164 discharged patient with COVID-19 and 166 healthy controls were used for HRV analysis. Each participant had at least one continuous monitoring record for more than 10 h. We obtained the long-term HRV by calculating the average value of 5-min HRV over 1 day. Fig. 11 presents boxplots of the four HRV measures for discharged COVID-19 patients and controls. The symbol “+” within boxplots represents the sample mean of HRV. The results show that time domain measures (SDNN, SDANN) and frequency measures (LF, HF) differed significantly between the two groups. The HRV of discharged COVID-19 patients is significantly lower than that of controls. SteelDwass and MannWhitney tests were performed to test for significance. The four measures could be used to separate the two groups in a statistically significant manner (p < 0.001). This indicates that COVID-19 patients have not returned to normal levels on dynamic adjustment of HR after discharge. Currently, two opinions prevail regarding the reasons for HRV reduction after recovery from COVID-19. One opinion is that this is related to direct cardiac injury due to COVID-19. Theoretically, direct injury can damage the cardiac pacing or conduction system, leading to changes in HRV. The second opinion to be considered is an autonomic nervous system. Studies have demonstrated that low HRV is widespread in patients infected with SARS-CoV-2, and the reason may be that the virus can attack the sympathetic and parasympathetic nerve fibers [32], [33]. Weakened sympathovagal activity can reduce HRV. The HRV of patients who recovered from COVID-19 remained lower than that of healthy individuals in this study, indicating that the injury to the heart or autonomic nervous system caused by SARS-CoV-2 is long lasting. Therefore, patients should be aware of the risk of cardiovascular disease after recovering from COVID-19.

TABLE II. Four HRV Measures.

Parameter	Unit	Description
SDNN	ms	Standard deviation of the normal-to-normal sinus node-initiated J-J intervals
SDANN	ms	Standard deviation of average J-J intervals for each 5 min segment of 24 hours HRV
LF	ms2	Absolute power of the low-frequency band (0.04~0.15 Hz)
HF	ms2	Absolute power of the high-frequency band (0.15~0.4 Hz)

Fig. 11.

Comparison of HRV (SDNN, SDANN, LF, HF) between recovered patients with COVID-19 and controls using boxplots.

E. RRV Analysis for Discharged COVID-19 Patient

To assess the recovery of lung function in discharged patients with COVID-19, we used measures similar to those of the HRV analysis to analyze the RR. The four RRV measures are detailed in the Appendix. Fig. 12 presents the comparison of RRV between discharged COVID-19 patient and controls by using boxplots. The RRV analysis also uses four measures of SDNN, SDANN, LF, and HF, which are described in Table III. We can see that RRV did not differ significantly between the recovered patients and the healthy controls. The p-value was considerably higher than 0.05. As far as we know, some studies have shown that the HR and RR irregularities in COVID-19 patients during their illness are significantly higher than those in the normal population [34], [35]. This indicates that respiratory rhythm in patients with COVID-19 can quickly return to normal levels after recovery. In other words, the respiratory rhythm of COVID-19 patients is easier to recover than the heart rhythm. However, this conclusion was obtained from an analysis of single-source data; further medical research is warranted for verification.

Fig. 12.

Comparison of RRV (SDNN, SDANN, LF, HF) between recovered patients with COVID-19 and controls using boxplots.

TABLE III. Four RRV Measures.

Parameter	Unit	Description
SDNN	ms	Standard deviation of respiration intervals
SDANN	ms	Standard deviation of average respiration intervals for 5 min segment of 24 hours RRV;
LF	ms2	Absolute power of the low-frequency band (0.04~0.15 Hz);)
HF	ms2	Absolute power of the high-frequency band (0.15~0.4 Hz))

V. Conclusion

This article proposed a noncontact IoMT system for monitoring cardiopulmonary function. The system can separate BCG and respiration signals from the pressure signal obtained from a BCG sensor placed under the patient’s pillow and further perform HRV and RRV analysis by using the extracted HRs and RRs. A robust method for HR and RR detection was proposed. The experimental results from 25 participants indicated that the accuracy of the proposed method meets the requirements for HRV and RRV analyses. Furthermore, our devices were used to monitor the HRV and RRV of discharged patient with COVID-19. The results indicate that the recovery performance of the respiratory rhythm is better than the heart trhythm among discharged patient with COVID-19. Although this conclusion requires further medical research and verification, the proposed system undoubtedly provides a new solution for the monitoring of discharged patients with COVID-19. In further research, we will continue to monitor the heart recovery of these patients through our system. In addition, our system can be further used to monitor cardiopulmonary function in patients with active COVID-19. Its noncontact remote monitoring feature can effectively reduce contact between doctors and patients, thereby reducing the probability of doctors being infected.

Funding Statement

This work was supported in part by the National Natural Science Foundation of China under Grant U1913210, Grant 61771465, and Grant 62073310; in part by the Strategic Priority CAS Project under Grant XDB38060100; and in part by the COVID-19 Emergency Prevention and Control Special Project of Shenzhen under Grant JSGG20200225153023511.