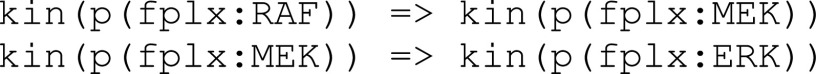Abstract
Counterfactual inference is a useful tool for comparing outcomes of interventions on complex systems. It requires us to represent the system in form of a structural causal model, complete with a causal diagram, probabilistic assumptions on exogenous variables, and functional assignments. Specifying such models can be extremely difficult in practice. The process requires substantial domain expertise, and does not scale easily to large systems, multiple systems, or novel system modifications. At the same time, many application domains, such as molecular biology, are rich in structured causal knowledge that is qualitative in nature. This article proposes a general approach for querying a causal biological knowledge graph, and converting the qualitative result into a quantitative structural causal model that can learn from data to answer the question. We demonstrate the feasibility, accuracy and versatility of this approach using two case studies in systems biology. The first demonstrates the appropriateness of the underlying assumptions and the accuracy of the results. The second demonstrates the versatility of the approach by querying a knowledge base for the molecular determinants of a severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2)-induced cytokine storm, and performing counterfactual inference to estimate the causal effect of medical countermeasures for severely ill patients.
Keywords: Biological expression language, structural causal model, counterfactual inference, causal biological knowledge graph, systems biology, SARS-CoV-2
1. Introduction
Each time a cell senses changes in its environment, it marshals a complex choreography of molecular interactions to initiate an appropriate response. When a virus infects the cell, this delicate balance is disrupted and can result in a cascade of systemic failures leading to disease. In particular, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), the novel pathogen responsible for the COVID-19 pandemic, has a complex etiology that differs in subtle and substantial ways from previously studied viruses. To make informed decisions about the risk that a new pathogen presents, it is imperative to rapidly predict the determinants of pathogenesis and identify potential targets for medical countermeasures. Current solutions for this task include systems biology data-driven models, which correlate biomolecular expression to pathogenicity, but cannot go beyond associations in the data to reason about causes of the disease [1], [2]. Alternatively, hypothesis-driven mathematical models capture causal relations, but are hampered by limited parameter identifiability and predictive power [3], [4].
We argue that counterfactual inference [5] helps bridge the gap between data-driven and hypothesis-driven approaches. It enables questions of the form: “Had we known the eventual outcome of a patient, what would we have done differently?” At the heart of counterfactual inference is a formalism known as a structural causal model [5], [6]. It represents prior domain knowledge in terms of causal diagrams, assumes a probability distribution on exogenous variables, and assigns a deterministic function to endogenous variables. SCM are particularly attractive in systems biology, where structured domain knowledge is extracted from the biomedical literature and is readily available through advances in natural language processing [7], [8], [9], large-scale automated assembly systems [10], and semi-automated curation workflows [11]. This knowledge is curated by multiple organizations [12], [13], [14], [15], [16] and stored in structured knowledge bases [17], [18], [19], [20]. It can be brought to bear for answering causal questions regarding SARS-CoV-2.
This manuscript contributes a three-part algorithm that leverages existing structured biological knowledge to answer counterfactual questions about viral pathogenesis. Algorithm 1 formalizes biologically relevant questions as queries to an existing causal knowledge graph. Algorithm 2 converts the query result into a structural causal model. Algorithm 3 operationalizes the counterfactual inference by interrogating the model with the observed data to estimate a causal effect.
We illustrate the benefits of this approach using two case studies. Case study 1 illustrates the increased precision of counterfactual estimates, as compared to the ODE- and SDE-based forward simulation, in a situation with known ground truth mechanisms of data generation. Case study 2 demonstrates the automated construction of an SCM and the value of counterfactual reasoning in novel situations with limited treatment options (as is the case for SARS-CoV-2). It shows that counterfactual inference enables more precise predictions regarding who would be likely to survive without receiving treatment, who would be likely to die even if they did receive treatment, and who would likely survive only if they received treatment.
2. Background
Biological Signaling Pathways. Signaling pathways are composed of entities that engage in activities [21]. Examples of entities are proteins and metabolites, but also higher level biological processes such as an immune response. Activities are the producers of change. Examples include catalytic activity, kinase activity, or transcriptional activity.
The basic unit of causality in signaling pathways is a directed molecular interaction, where the activity of an upstream molecule increases or decreases the activity of a downstream molecule. For example, the mitogen-activated protein kinase (MAPK) intracellular signaling pathway is a causal chain of directed molecular interactions shown in eq. (1)
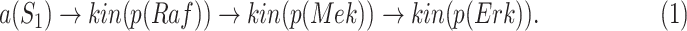
|
The interactions transmit information about a stimulus at the cell surface to the nucleus, where proteins called transcription factors activate an appropriate biological process [22]. A causal diagram of MAPK consists of a signaling molecule  and three proteins
and three proteins 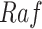 ,
, 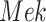 , and
, and 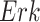 , each of which engage in kinase activity. We represent signaling molecule abundance with
, each of which engage in kinase activity. We represent signaling molecule abundance with 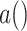 , protein abundance with
, protein abundance with 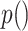 and the kinase activity of a protein with
and the kinase activity of a protein with 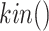 . In the case of MAPK, the abundance or activity of an upstream entity causes the abundance or activity of a downstream entity to increase, and is represented with a sharp edge
. In the case of MAPK, the abundance or activity of an upstream entity causes the abundance or activity of a downstream entity to increase, and is represented with a sharp edge 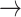 . The diagram is a abstraction showing that the abundance of the signaling molecule
. The diagram is a abstraction showing that the abundance of the signaling molecule 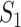 increases the kinase activity of
increases the kinase activity of 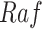 , which increases the kinase activity of
, which increases the kinase activity of 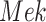 , which increases the kinase activity of
, which increases the kinase activity of 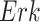 . In other cases, if the abundance or activity of an upstream entity causes the abundance or activity of a downstream entity to decrease, we represent this with a blunt edge.
. In other cases, if the abundance or activity of an upstream entity causes the abundance or activity of a downstream entity to decrease, we represent this with a blunt edge.
Viral Dysregulation. Viral disruptions of a signaling pathway take form of overactivation or repression of its activities. For example, by amplifying the release of intercellular signaling molecules that overstimulate the immune response, known as Cytokine Release Syndrome (cytokine storm), a virus can cause severe system-level cellular damage.
Quantitative Modeling of Biological Processes With ODE/SDE. Temporal dynamics of biological processes can be expressed quantitatively using ordinary (or stochastic) differential equations. A small number of high quality, validated models have been published in the literature and stored in a computable form in repositories such as Biomodels [23], [24]. For example, the MAPK signaling pathway in eq. (1) is well characterized. We denote 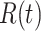 ,
, 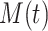 , and
, and 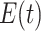 as the respective amounts of active
as the respective amounts of active 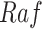 ,
, 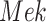 , and
, and 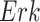 at time
at time 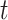 ; We denote
; We denote 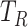 ,
, 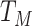 , and
, and 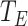 as their total amounts, which we assume do not change during the considered timeframe;
as their total amounts, which we assume do not change during the considered timeframe; 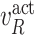 ,
, 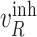 ,
, 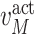 ,
, 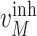 ,
, 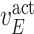 , and
, and 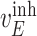 are experimentally derived activation or inhibition kinetic rate constants; and
are experimentally derived activation or inhibition kinetic rate constants; and 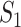 is the amount of the input signal. The system of ordinary differential equations (ODEs) is specified as follows [25], [26]:
is the amount of the input signal. The system of ordinary differential equations (ODEs) is specified as follows [25], [26]:
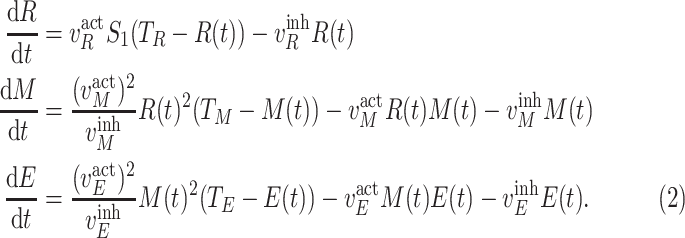
|
Given initial conditions, forward simulations from the ODEs can be used to generate the temporal trajectories of the amounts of activated proteins, such as 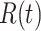 ,
, 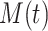 , and
, and 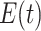 in the MAPK example. In this manuscript we refer to such simulated data as observational data. We define an ideal intervention as an event that fixes the amount of an activated protein. For example, if we fix the kinase acivity of
in the MAPK example. In this manuscript we refer to such simulated data as observational data. We define an ideal intervention as an event that fixes the amount of an activated protein. For example, if we fix the kinase acivity of 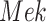 at
at 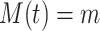 , the second equality
, the second equality 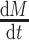 in eq. (2) becomes zero. We can simulate data from eq. (2) with
in eq. (2) becomes zero. We can simulate data from eq. (2) with 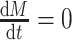 , and refer to these as interventional data. Contrasting observational and interventional data helps evaluate the outcome of the intervention [27].
, and refer to these as interventional data. Contrasting observational and interventional data helps evaluate the outcome of the intervention [27].
The deterministic ODE ignore the fact that at low concentration, stochasticity becomes a significant factor in determining the reaction [28]. As the collisions between molecules participating in biochemical process become stochastic, a stochastic model is required. In contrast to ODE, a stochastic differential equation model or stochastic differential equation (SDE) specifies biological process as a random process. For example, in the case of MAPK, the random process of the reaction 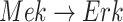 is specified with
is specified with
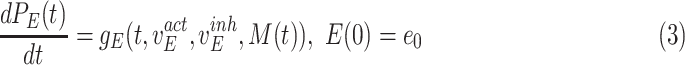
|
where  is marginal probability density of
is marginal probability density of  , function
, function 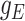 determines the probability of a state change between
determines the probability of a state change between 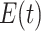 and
and 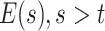 ,
, 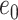 is initial condition, and
is initial condition, and 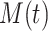 is the value of its parent Mek at
is the value of its parent Mek at 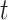 . Once stochastic differential equation are fully specified, one can use, e.g., Gillespie's stochastic simulation algorithm [29] to simulate observational and interventional data, and evaluate the outcomes of interventions.
. Once stochastic differential equation are fully specified, one can use, e.g., Gillespie's stochastic simulation algorithm [29] to simulate observational and interventional data, and evaluate the outcomes of interventions.
Unfortunately, even simple ODEs such as the one in the MAPK example are difficult to build de novo. This is nearly impossible for novel and poorly studied systems that lack the existence or findability of experimental information describing the structure or boundaries of the process, kinetic equations governing their dynamics [30], rate constants for these equations, or rules governing each agents’ states and functions.
Equilibrium Enzyme Kinetics. Simpler and more general quantitative models can be specified when a reaction reaches the state of chemical equilibrium [31]. One commonly used such model is Hill function in the form of

|
where  is the abundance of a protein in a causal diagram (such as
is the abundance of a protein in a causal diagram (such as 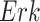 in eq. (1)),
in eq. (1)), 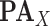 is the set of its parents,
is the set of its parents, 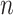 is a parameter interpreted as the number of ligand binding sites of the protein, and
is a parameter interpreted as the number of ligand binding sites of the protein, and 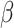 is the total number of molecules of the protein. A special and frequently used case of the Hill function, called Michaelis-Menten function, occurs when
is the total number of molecules of the protein. A special and frequently used case of the Hill function, called Michaelis-Menten function, occurs when 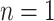 . Although simple to use, these models are deterministic, and do not describe the stochasticity that is a distinctive property of biological systems at low concentrations.
. Although simple to use, these models are deterministic, and do not describe the stochasticity that is a distinctive property of biological systems at low concentrations.
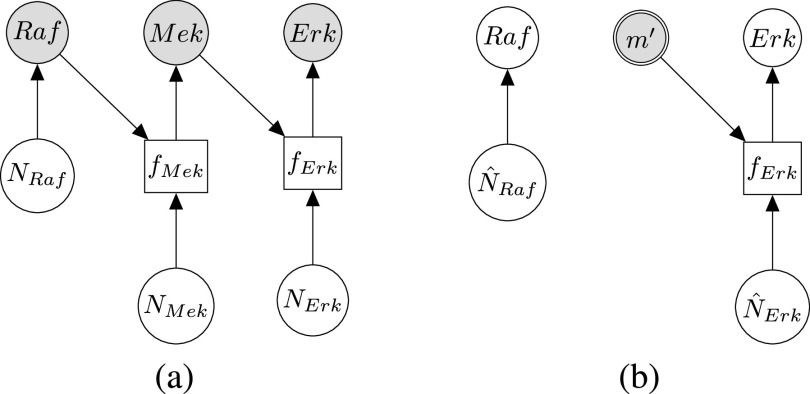
Modeling Biological Processes With Structural Causal Models. The stochastic nature of biological processes at steady-state can be represented by an SCM such as in Fig. 1a
[27], [32]. SCMs represent the dependencies between a child node 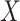 and its parents
and its parents 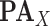 in terms of a deterministic function
in terms of a deterministic function 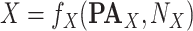 called structural assignment, and a noise variable
called structural assignment, and a noise variable 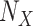 . In Fig. 1a,
. In Fig. 1a, 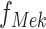 and
and 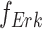 are linear or non-linear structural assignments, and
are linear or non-linear structural assignments, and 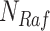 ,
, 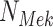 , and
, and 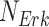 are statistically independent noise variables with defined probability distributions
are statistically independent noise variables with defined probability distributions
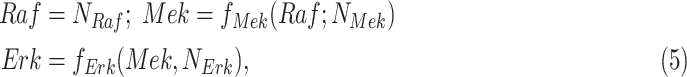
|
An ideal intervention in an SCM is performed on a functional assignment. For example, an ideal intervention on 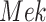 sets
sets 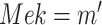 , defining a new SCM
, defining a new SCM
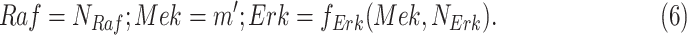
|
An ideal intervention can also be thought of as a process of mutilating the causal graph. For example, intervening on 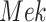 eliminates its dependence upon
eliminates its dependence upon 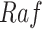 , and therefore the edge from
, and therefore the edge from 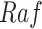 to
to 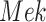 is removed as shown in Fig. 1b.
is removed as shown in Fig. 1b.
Fig. 1.
Causal modeling of MAPK signaling pathway. Circles are variables, double circles are variables intervened upon, squares are deterministic functional assignments, gray nodes are observed variables, and white nodes are hidden variables. (a) Structural causal model. 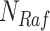 ,
, 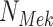 and
and 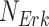 are statistically independent noise variables. Root node
are statistically independent noise variables. Root node 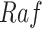 is only dependent on noise variable
is only dependent on noise variable 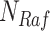 . Non-root nodes
. Non-root nodes 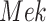 and
and 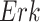 are dependent on their parent and on the associated noise variable. (b) Counterfactual model. The intervention fixes the count of phosphorylated
are dependent on their parent and on the associated noise variable. (b) Counterfactual model. The intervention fixes the count of phosphorylated 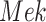 to
to 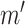 , such that
, such that 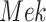 is no longer dependent on
is no longer dependent on 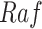 and
and 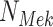 . Given an observed data point, counterfactual inference infers the noise variables
. Given an observed data point, counterfactual inference infers the noise variables 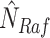 , and
, and 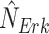 .
.
Counterfactual Inference With SCM. Beyond direct model-based predictions, SCMs enable counterfactual inference, i.e., the process of inferring the unseen outcomes of a hypothetical intervention given data observed in absence of the intervention [5]. In the context of SCM, counterfactuals are defined as operations

|
In other words, the outcome 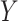 that individual
that individual 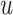 would have had she received treatment
would have had she received treatment 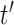 is defined as the value that
is defined as the value that 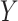 would have in a structural causal model
would have in a structural causal model 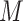 mutilated to replace
mutilated to replace 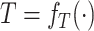 with
with 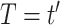 .
.
For example, in the MAPK signaling pathway, we may be interested in the counterfactual question: Having observed the kinase activities of 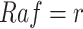 ,
, 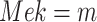 ,
, 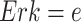 , what would be the kinase activity of
, what would be the kinase activity of 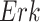 in a hypothetical experiment where the kinase activity of
in a hypothetical experiment where the kinase activity of 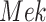 was fixed to
was fixed to 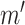 ? This counterfactual query is more formally translated into
? This counterfactual query is more formally translated into
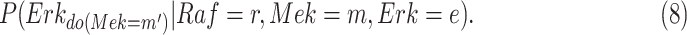
|
The probability distribution in eq. (8) is estimated with the following steps:
-
1)Abduction: Given observational data, estimate the posterior distribution of the noise variables. In the MAPK example, we estimate the posterior distribution of the noise variables:
Several inference algorithms are available for this task, e.g., Markov Chain Monte Carlo [33], Gibbs sampling [34], or no-u-turn Hamiltoninan Monte Carlo (HMC) [35]. In recent years, gradient-based inference algorithms such as stochastic variational inference [36] have become popular, because they can scale to larger models by converting an inference problem into an optimization problem.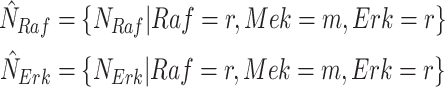
-
2)
Intervention: Apply the intervention to the SCM to generate a mutilated SCM as in Fig. 1b. In the MAPK SCM,
 is replaced with
is replaced with  as shown in Fig. 1b.
as shown in Fig. 1b. -
3)
Prediction: Generate samples from the mutilated SCM using the estimated posterior distribution over the exogenous variables
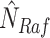 and
and 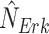 to obtain the counterfactual distribution, as shown in Fig. 1b.
to obtain the counterfactual distribution, as shown in Fig. 1b.
Causal Effects. We distinguish between two causal effects. The first is the average treatment effect (ATE), defined as the difference between the outcome of a hypothetical intervention and the observed outcome in the entire population. In the MAPK example, the ATE of 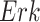 upon an intervention fixing
upon an intervention fixing 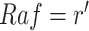 is:
is:

|
This requires no observational data, and therefore the ATE can be inferred with forward simulation.
On the other hand, the individual treatment effect (ITE) is defined as the difference between the outcome of a hypothetical intervention and the observed outcome for a specific individual or context. In the MAPK example, the individual treatment effect of 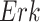 upon an intervention fixing
upon an intervention fixing 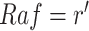 in a context where
in a context where 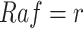 ,
, 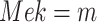 ,
, 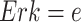 is:
is:
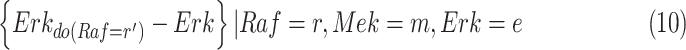
|
The ITE shares stochastic components of the noise variables between observational and interventional data, and is therefore often more precise than a comparison based on a direct simulation [27].
In cases where domain knowledge is available to describe the systems dynamics in the form of an SDE, the system at equilibrium can be translated into an SCM to enable counterfactual reasoning and estimation of the individual treatment effect [27], [37]. Unfortunately, this process is challenging in novel and poorly studied systems, due to our limited ability to establish the structure of the causal graph.
Structured Knowledge Graphs. Although there exist a multitude of biological knowledge bases that are manually curated from the literature [12], [13], [14], [15], [16], the systems biology community has coalesced around a small number of structured knowledge representations that differ mainly in their intended purpose. For example, the Biological Pathway Exchange Language (BioPAX) was designed for pathway database integration [17], and the Systems Biology Graphical Notation (SBGN) was designed for graphical layout [19].
In contrast, the Biological Expression Language (BEL) was specifically designed for manual extraction and automated integration of author statements about causal relationships among biological entities, biological processes, and cellular-level observable phenomena [11]. The syntax of a BEL statement is comprised of a triple in the form of {subject, predicate, object}. Each subject and object represents an activity or abundance whose entities are grounded using terms from standard namespaces. If the subject directly increases the abundance or the activity of the object, we represent this with =>, and for directly decreasing relationships, we use =|. BEL statements can be chained together from the object of the first statement to the subject of the next statement, as shown in Fig. 2 for the case of the MAPK pathway.
Fig. 2.
Example BEL statement. The statement details the processes in the MAPK signaling pathway in eq. (1). The first line states that the kinase activity of RAF directly increases the kinase activity of MEK. The second line states that kinase activity of MEK directly increases the kinase activity of ERK.
BEL provides a number of valuable features for causal modeling. First, the restriction of BEL edges to causal relations implies the topology of the BEL graph can be reflected in the topology of the causal model. Second, the language is expressive enough for humans to manually curate a wide range of biological concepts, but formal enough to serve as a training corpus for corpus for natural language processing of biomedical literature competitions [38]. Third, the BEL ecosystem is sufficiently mature that causal knowledge represented in other languages can be readily converted to BEL [39], [40].
3. Methods
3.1. Notation, Definitions, and Assumptions
Let 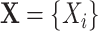 be a set of variables, such as molecular activities in a signaling pathway. Let
be a set of variables, such as molecular activities in a signaling pathway. Let 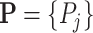 be a set of causal predicates that link these variables, such as increases, or regulates. Using this notation, we define a knowledge graph
be a set of causal predicates that link these variables, such as increases, or regulates. Using this notation, we define a knowledge graph 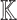 as a set of
as a set of 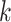 triples
triples
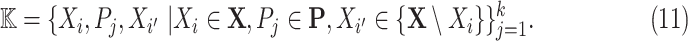
|
We define a causal query 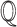 as a set
as a set 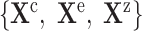 of variables that are potential causes, effects and covariates of interest for the biological investigation, where
of variables that are potential causes, effects and covariates of interest for the biological investigation, where
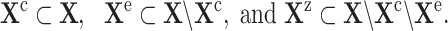
|
A pathway 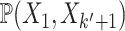 ,
, 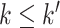 is a sequence of a subset of triples from
is a sequence of a subset of triples from 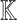 , where the object of the previous triple is subject of the next triple
, where the object of the previous triple is subject of the next triple
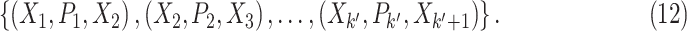
|
Our goal is to query the knowlege graph to generate a qualitative causal model 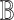 that links the causes, the effects and the covariates of interest. Importantly, the query result
that links the causes, the effects and the covariates of interest. Importantly, the query result 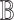 induces a directed acyclic graph
induces a directed acyclic graph 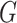 with
with 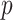 variables from
variables from 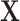 as nodes, and causal relations from
as nodes, and causal relations from 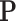 as edges.
as edges.
We assume that every variable in 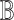 is continuous. We denote
is continuous. We denote 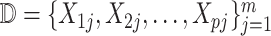 the observational data of
the observational data of 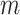 samples from the joint distribution
samples from the joint distribution 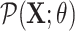 . The distribution is specified in terms of parameters
. The distribution is specified in terms of parameters 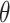 . We denote
. We denote 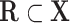 a set of nodes in
a set of nodes in 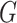 without parents.
without parents.
3.2. Querying a Knowledge Graph to Obtain a Qualitative Causal Model
Given a biological knowledge graph 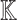 and a causal query of interest
and a causal query of interest 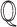 , our first objective is to generate a qualitative causal model
, our first objective is to generate a qualitative causal model 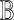 capable of answering the query. To this end, we need to explore all potential directed acyclic paths in
capable of answering the query. To this end, we need to explore all potential directed acyclic paths in 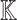 from the cause to the effect in
from the cause to the effect in 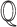 , and then consider all covariates that may act as confounders of the causal question. This is done with the steps in Algorithm 1. The algorithm can be implemented on any knowledge graph that represents causal relationships as directed edges, such as BEL or the Systems Biology Graphical Notation Activity Flow (SBGN-AF) language [41].
, and then consider all covariates that may act as confounders of the causal question. This is done with the steps in Algorithm 1. The algorithm can be implemented on any knowledge graph that represents causal relationships as directed edges, such as BEL or the Systems Biology Graphical Notation Activity Flow (SBGN-AF) language [41].
In the case of MAPK, the qualitative causal model that is capable of answering the counterfactual question in eq. (8) corresponds to the result of this query: 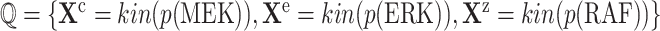 .
.
Algorithm 1. Causal query to Biological Expression Language (QUERY2BEL) algorithm
-
Inputs: knowledge graph
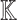
causal query
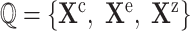
Outputs:
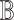
-
1:
procedure query2bel(
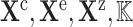 )
) -
2:
 Get all pathways from cause to effect
Get all pathways from cause to effect -
3:
for each cause
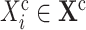 and for each effect
and for each effect 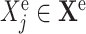 do
do -
4:
find all pathways
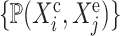
-
5:
 Get all pathways from covariates to causes
Get all pathways from covariates to causes -
6:
for each covariate
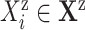 and for each cause
and for each cause 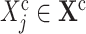 do
do -
7:
find all pathways
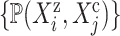
-
8:
 Get all pathways from covariates to effects
Get all pathways from covariates to effects -
9:
for each covariate
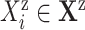 and for each effect
and for each effect 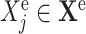 do
do -
10:
find all pathways
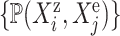
-
11:
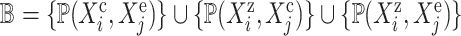
-
12:
return
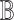
We execute Algorithm 1 step 2 to obtain all pathways from the cause to the effect:
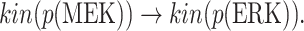
|
We execute Algorithm 1 step 6 to obtain all pathways from the covariate to the cause:
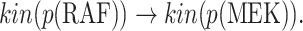
|
We execute Algorithm 1 step 10, but since there are no new pathways from the covariate 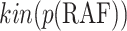 to the effect
to the effect 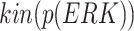 , we obtain the empty set. The final returned model is:
, we obtain the empty set. The final returned model is:
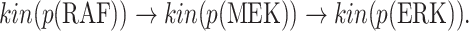
|
3.3. Compiling a Qualitative Causal Model to a Quantitative Structural Causal Model
Our second objective is to express the qualitative causal structure in  into a quantitative SCM, and estimate the parameters of the SCM from experimental data. These steps are described in Algorithm 2.
into a quantitative SCM, and estimate the parameters of the SCM from experimental data. These steps are described in Algorithm 2.
Input. The algorithm takes as input a BEL causal query result  and observed measurements on its variables
and observed measurements on its variables  .
.
Get Network Structure  From
From  (Algorithm 2 Line 3). Since a set of BEL statements identifies parents and children, it induces a causal network structure. We determine this structure by traversing BEL statements with the breadth first search approach, starting with root variables (such as
(Algorithm 2 Line 3). Since a set of BEL statements identifies parents and children, it induces a causal network structure. We determine this structure by traversing BEL statements with the breadth first search approach, starting with root variables (such as 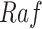 in Fig. 2). For all the non-root variables, the algorithm waits until all the parents are traversed.
in Fig. 2). For all the non-root variables, the algorithm waits until all the parents are traversed.
For Each Root Node 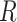 , Use
, Use 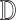 to Estimate Parameters
to Estimate Parameters 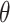 of
of 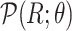 (Algorithm 2 Line 5). In order to specify the SCM, we need to define the type and parameters of the marginal probability distributions of the root variables
(Algorithm 2 Line 5). In order to specify the SCM, we need to define the type and parameters of the marginal probability distributions of the root variables 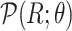 . The BEL statements provide prior knowledge about the distribution in a parametric form. Therefore, this step involves techniques such as maximum likelihood to estimate the parameters of this distribution.
. The BEL statements provide prior knowledge about the distribution in a parametric form. Therefore, this step involves techniques such as maximum likelihood to estimate the parameters of this distribution.
Algorithm 2. Biological Expression Language to Structural Causal Models (BEL2SCM) algorithm
-
Inputs: BEL statements
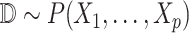
Outputs:
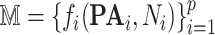
-
1:
procedure bel2scm(
 ,
,  )
) -
2:

-
3:
Get network structure
 from
from  .
. -
4:
for each
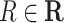 in
in 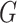 do
do -
5:
 Use
Use  to estimate parameters
to estimate parameters 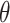 of
of 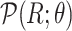
-
6:
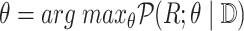
-
7:
 Reparameterize
Reparameterize 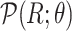 in terms of
in terms of 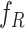 and
and 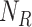
-
8:
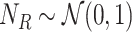
-
9:
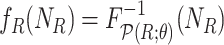
-
10:
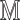 .Add(
.Add(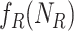 )
) -
11:
for each
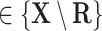 in
in  do
do -
12:
 Estimate parameters
Estimate parameters  and
and  of sigmoid function
of sigmoid function -
13:
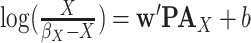
-
14:
 Define distribution of
Define distribution of 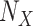 from model residuals.
from model residuals. -
15:
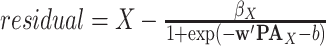
-
16:
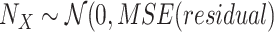 )
) -
17:
 Get
Get 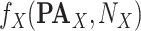 with additive
with additive 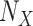 .
. -
18:
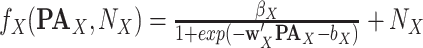
-
19:
 .Add(
.Add( ).
). -
20:
return
For example, in a stochastic MAPK system at equilibrium the root variable the number of active 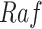 in a cell follows a Binomial distribution. When the maximum number of active or inactive particles in the system is large, the Binomial distribution can be approximated with a Normal distribution with
in a cell follows a Binomial distribution. When the maximum number of active or inactive particles in the system is large, the Binomial distribution can be approximated with a Normal distribution with 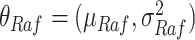 . We then estimate
. We then estimate 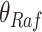 using maximum likelihood from the observed
using maximum likelihood from the observed 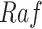 in
in 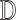 .
.
For Each Root Node 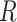 , Reparameterize
, Reparameterize 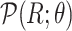 in Terms of
in Terms of 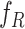 and
and 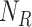 (Algorithm 2 Line 7). The specification of an SCM requires us to separate the deterministic and the stochastic components of variation of each variable as shown in Fig. 1. We accomplish this using a reparameterization technique popularized by variational autoencoders [42], which was shown to make counterfactual inference consistent with core biological assumptions [43]. In the case of root nodes, we reparameterize
(Algorithm 2 Line 7). The specification of an SCM requires us to separate the deterministic and the stochastic components of variation of each variable as shown in Fig. 1. We accomplish this using a reparameterization technique popularized by variational autoencoders [42], which was shown to make counterfactual inference consistent with core biological assumptions [43]. In the case of root nodes, we reparameterize 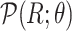 with Uniform(0,1), and then pass it to the inverse CDF of
with Uniform(0,1), and then pass it to the inverse CDF of 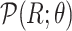 , as follows
, as follows
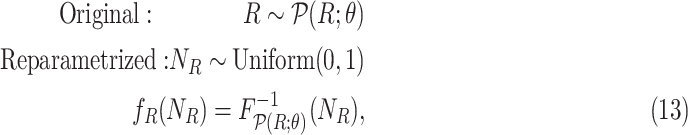
|
where 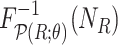 is the inverse cumulative distribution function of
is the inverse cumulative distribution function of 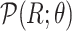 . In the case of MAPK, since
. In the case of MAPK, since  follows a Normal distribution with parameters
follows a Normal distribution with parameters  , the reparameterization simplifies even further to
, the reparameterization simplifies even further to
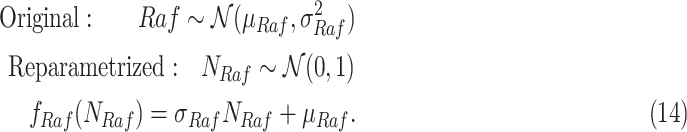
|
Add 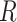 to
to 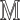 (Algorithm 2 line 10) For each root node, we add the corresponding function
(Algorithm 2 line 10) For each root node, we add the corresponding function 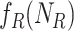 and its noise variable
and its noise variable 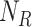 to
to 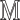 . For example, since MAPK has only one root node
. For example, since MAPK has only one root node 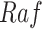 , the Algorithm adds
, the Algorithm adds 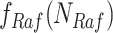 to
to 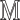 .
.
For Each 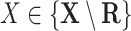 , Estimate Parameters
, Estimate Parameters 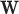 and
and 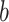 of Sigmoid Function (Algorithm 2 Line 12). In order to specify the SCM for non-root nodes, we need to define the form (polynomial, linear, non-linear, sigmoid, etc.) of functional assignments linking the measurements on the parent nodes to the measurements on the child. We chose the functional assignment in the form of a sigmoid function
of Sigmoid Function (Algorithm 2 Line 12). In order to specify the SCM for non-root nodes, we need to define the form (polynomial, linear, non-linear, sigmoid, etc.) of functional assignments linking the measurements on the parent nodes to the measurements on the child. We chose the functional assignment in the form of a sigmoid function

|
where 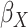 is the maximum number of activated protein molecules. For a node
is the maximum number of activated protein molecules. For a node 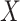 with
with 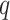 parents,
parents, 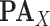 is a
is a 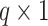 vector of measurements on the parent nodes,
vector of measurements on the parent nodes, 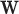 is a
is a 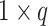 vector of weights,
vector of weights, 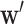 is the transpose of
is the transpose of  , and
, and 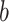 is a scalar bias. Parameters
is a scalar bias. Parameters  and
and 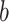 of the sigmoid function are estimated from the data, e.g., using smooth
of the sigmoid function are estimated from the data, e.g., using smooth  loss function.
loss function.
In the example of the MAPK pathway, 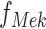 has only one parent. Therefore
has only one parent. Therefore 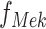 has the form
has the form
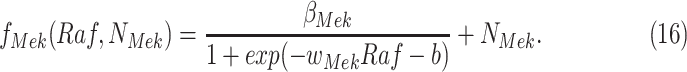
|
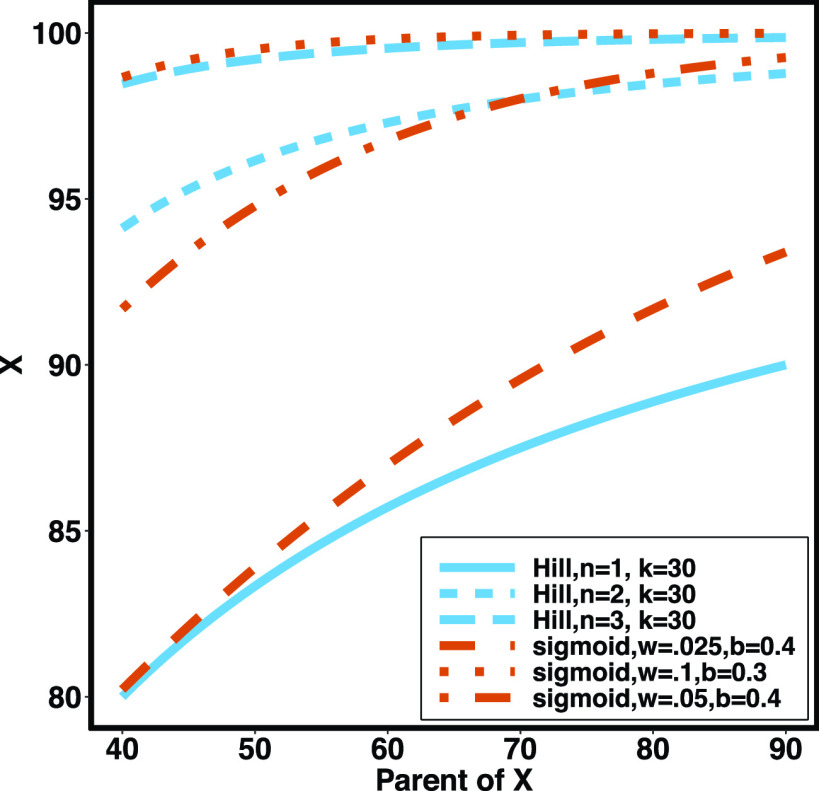
We use the sigmoid function in eq. (15) as a special case of the Hill equation. The full parametric description of the Hill equation has a nuanced precise biochemical interpretation. For example, the parameter 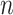 represents the number of times a protein must be phosphorylated before it becomes active and can therefore be obtained from domain knowledge. However, it is difficult to estimate this parameter from data. The sigmoid function maintains the Hill equation's functions, but with a reduced set of parameters that are easier to estimate. Fig. 3 shows that the approximation is reasonable for a range of parameter values.
represents the number of times a protein must be phosphorylated before it becomes active and can therefore be obtained from domain knowledge. However, it is difficult to estimate this parameter from data. The sigmoid function maintains the Hill equation's functions, but with a reduced set of parameters that are easier to estimate. Fig. 3 shows that the approximation is reasonable for a range of parameter values.
Fig. 3.
Examples of hill function and sigmoid function for two variables.
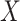 is a single node that has a single parent
is a single node that has a single parent 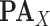 . We use the Hill function (
. We use the Hill function (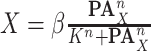 ) and sigmoid function as in eq. (15) to predict the value of
) and sigmoid function as in eq. (15) to predict the value of 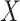 given its parent value. In the Hill function,
given its parent value. In the Hill function, 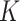 is the activation rate,
is the activation rate, 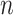 defines the steepness of function and
defines the steepness of function and 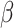 is fixed at 100. Blue lines correspond to Hill equation with
is fixed at 100. Blue lines correspond to Hill equation with 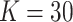 and
and 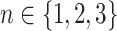 . Brown lines correspond to sigmoid function where
. Brown lines correspond to sigmoid function where 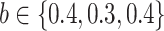 and
and 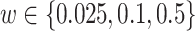 .
.
Define Distribution of 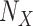 From Model Residuals (Algorithm 2 Line 14). Similarly to the root variables, for non-root variables we assume that the noise variables follow Normal distribution with 0 mean. The variance of this distribution is estimated from the residuals of the model fit in the previous step. For example, in the MAPK pathway,
From Model Residuals (Algorithm 2 Line 14). Similarly to the root variables, for non-root variables we assume that the noise variables follow Normal distribution with 0 mean. The variance of this distribution is estimated from the residuals of the model fit in the previous step. For example, in the MAPK pathway, 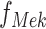 has only one parent
has only one parent 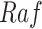 . Therefore, the residuals of the sigmoid curve fit for
. Therefore, the residuals of the sigmoid curve fit for 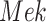 are defined as
are defined as
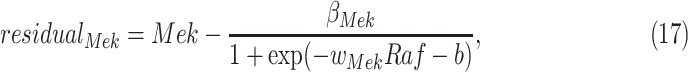
|
and the distribution of the noise variable is defined as 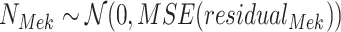
Get 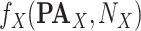 With Additive
With Additive 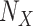 (Algorithm 2 Line 17). The step combines the sigmoid functional assignment and the independent noise variable. In the example of
(Algorithm 2 Line 17). The step combines the sigmoid functional assignment and the independent noise variable. In the example of 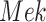 in the MAPK pathway, the step outputs
in the MAPK pathway, the step outputs
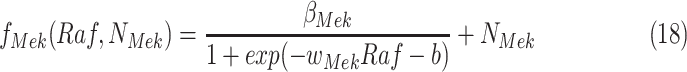
|
Add 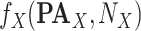 to SCM (Algorithm 2 Line 19). The step iteratively adds
to SCM (Algorithm 2 Line 19). The step iteratively adds 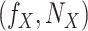 for all
for all 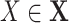 .
.
Output (Algorithm 2 Line 20). The algorithm returns a generative structural causal model 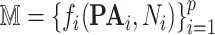 where
where 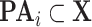 . For example, in the case of the MAPK model, it returns
. For example, in the case of the MAPK model, it returns 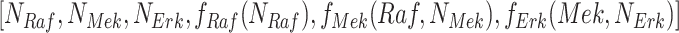 .
.
3.4. Counterfactual Inference Procedure
The generated SCM enables counterfactual inference using a standard procedure [5]. Given a new observation 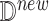 ,
,
-
1)
Abduction: Update the probability
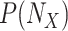 to obtain
to obtain 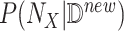 .
. -
2)
Action: Replace the equations determining the variables in set
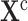 by
by 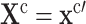 .
. -
3)
Prediction: Sample from the modified model to generate the target distribution
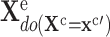 .
.
After generating the target distribution of the intervention model, we estimate causal effects. Algorithm 3 describes the detailed steps of both counterfactual inference (with 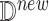 ) and forward simulation (if
) and forward simulation (if 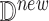 is empty)
is empty)
3.5. Implementation
QUERY2BEL was implemented manually using a publicly available instance of BioDati Studio, then validated using Integrated Dynamical Reasoner and Assembler (INDRA)'s [10] interactive dialogue system Bob with BioAgents [10]. Parameter estimation in BEL2SCM was implemented in PyTorch. Let 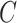 be the number of nodes in causal graph
be the number of nodes in causal graph 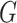 with parents. Let
with parents. Let 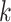 be the number of iterations for gradient descent, let
be the number of iterations for gradient descent, let 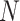 be the number of samples in data, and let
be the number of samples in data, and let 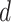 be the maximum number of parents in graph
be the maximum number of parents in graph 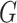 . Computational complexity of parameter estimation step is given by
. Computational complexity of parameter estimation step is given by 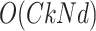 .
.
SCM-based counterfactual inference was performed with Pyro [44], due to its ability to perform interventions on probabilistic models and scalability to larger models, as described in Algorithm 3. Specifically, the implementation relies on the following functionalities in Pyro. The pyro.do method is an implementation of Pearl's do-operator used for causal inference. The pyro.infer.SVI method performs abduction using stochastic variational inference with ELBO loss. The pyro.infer.Importance method performs posterior inference by importance sampling. The pyro.infer.EmpiricalMarginal method performs empirical marginal distribution from the trace posterior's model.
Algorithm 3.
Estimate causal effect on 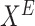 upon intervening on
upon intervening on 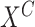
-
Inputs: New data point
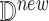
effect node
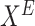
observational data for effect node
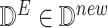
intervention value
node to intervene upon
number of iteration
network structure
SCM
Outputs: Causal Effect
-
1:
procedure getCausalEffect(
 )
) -
2:
-
3:
 Interventional data for effect node
Interventional data for effect node 
-
4:
-
5:
for
 do
do -
6:
for each
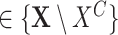 in
in 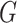 do
do -
7:
 Abduction: Apply stochastic variational inference
Abduction: Apply stochastic variational inference -
8:
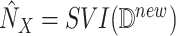
-
9:
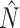 .Add(
.Add(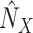 )
) -
10:
 Action: Apply intervention on
Action: Apply intervention on 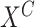
-
11:
-
12:
 Get posterior of
Get posterior of 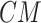 with importance sampling
with importance sampling -
13:
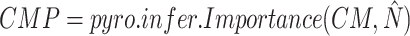
-
14:
 Prediction: Get EmpiricalMarginal (EM) for
Prediction: Get EmpiricalMarginal (EM) for 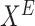
-
15:
-
16:
 .Add(
.Add(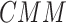 )
) -
17:
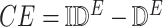
-
18:
return
Experiments in this manuscript took between 13 to 82 seconds depending on the graph size on a system with Intel Core i7 8th Gen CPU, 16 GB RAM and Ubuntu 18.04 Operating System. The code is available at https://github.com/bel2scm.
4. Case Studies
Below we introduce two biological case studies investigated using the approach proposed in this manuscript. The first case study allows us to evaluate the accuracy of the results based on known ground truth. The second uses counterfactual reasoning to pinpoint the mechanism by which SARS-CoV-2 infection can lead to a cytokine storm in severely ill coronavirus disease 2019 (COVID- 19) patients. The details of the case studies, parameter values of the simulations, and of the results are at https://github.com/bel2scm.
4.1. Case Study 1: The IGF Signaling System
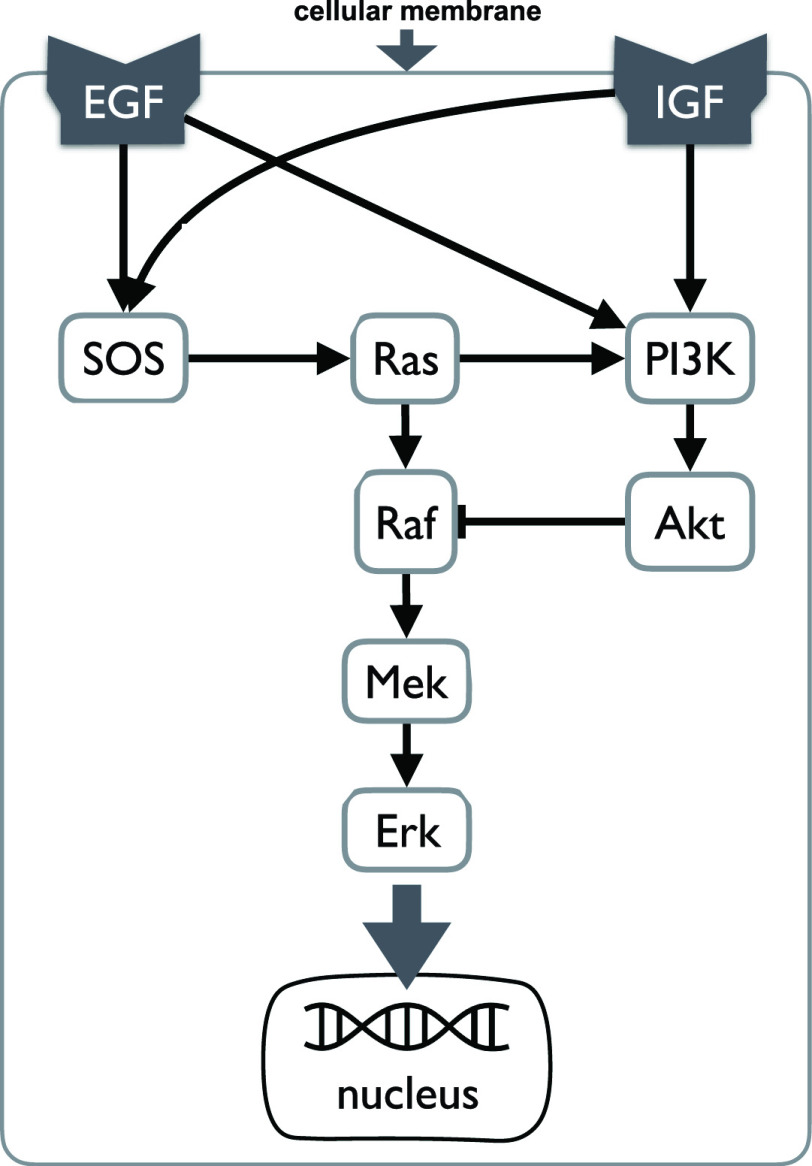
The System. The IGF signaling pathway (Fig. 4) regulates growth and energy metabolism of a cell. The IGF system has been extensively investigated, and its dynamics are well characterized in form of ODE and SDE models [25]. Activated by external stimuli, insulin-like growth factor (IGF) or epidermal growth factor (EGF) triggers a signaling event, which includes the MAPK signaling pathway in eq. (1). Similarly to eq. (1), nodes in the system are kinase activities, and edges represent whether the kinase activity of the upstream protein directly increases or decreases the kinase activity of the downstream protein. However, the system is larger and more complex. It includes two different paths from  to
to 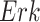 , one direct and the other through
, one direct and the other through 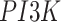 and
and 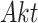 . This challenges estimates of outcomes of interventions. In this case study, we assume that the IGF system has no unobserved confounders.
. This challenges estimates of outcomes of interventions. In this case study, we assume that the IGF system has no unobserved confounders.
Fig. 4.
Case Study 1: the IGF signaling system. The insulin-like growth factor (IGF) and epidermal growth factor (EGF) are receptors of external stimuli, triggering downstream signaling pathways that include the MAPK pathway. All the relationships between abundances of activated proteins in this network are of the type increase, except for the relationship between 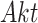 and
and 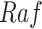 which is of the type decrease.
which is of the type decrease.
Intervention. We considered two interventions. The first fixes the kinase activity of 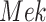 to 40. The second fixes the kinase activity of
to 40. The second fixes the kinase activity of 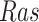 to 30.
to 30.
Causal Effects of Interest. We are interested in two causal questions. First, what would have been the kinase activity of 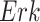 had we intervened to fix the kinase activity of
had we intervened to fix the kinase activity of 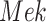 to 40? The second query is as above, but with the intervention fixing the kinase activity of
to 40? The second query is as above, but with the intervention fixing the kinase activity of 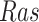 to 30. More formally, we are interested in the average treatment effect
to 30. More formally, we are interested in the average treatment effect

|

|
Next, we introduce a new piece of information about a specific data point generated from the ODE-based simulation. We wish to estimate the causal effect of intervention for this specific data point. More formally, we are interested in the individual treatment effect

|

|
where 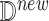 is a new data point. We note that this counterfactual inference can only be performed with an SCM. We wish to compare these estimates of causal effects, in order to characterize the ability of counterfactual inference via
is a new data point. We note that this counterfactual inference can only be performed with an SCM. We wish to compare these estimates of causal effects, in order to characterize the ability of counterfactual inference via 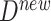 to improve the precision of the estimates.
to improve the precision of the estimates.
Evaluation. The kinetic equations described by the ODE and SDE represent the true underlying dynamics of the IGF signaling pathway. Since the ODE and the SDE can estimate the causal effects by forward simulation, we view the estimates as the ground truth. We then wish to compare the estimates from the SCM against the ground-truth estimates from the ODE and the SDE. Since an SCM represents causal relationships at steady state, we train the parameters of the SCM using data generated from the ground-truth SDE after it has reached steady state.
We consider two types of evaluations. First, we compare the estimates of the forward simulation of the ODE and SDE with the forward simulation of the SCM. This allows us to characterize the impact of SCM specification and estimates of weights on the accuracy of causal effects. We do not expect to see a substantial difference between these two approaches for a correctly specified SCM. We then compare the SCM-based counterfactual inference of causal effects with the estimates based on forward simulation. We expect that the counterfactual inference will provide more precise estimates, illustrating the statistical efficiency of counterfactual inference as compared to the forward simulation.
4.2. Case Study 2: Host Response to Viral Infection
The System. Retrospective studies have indicated that high levels of pro-inflammatory cytokine Interleukin 6 (IL6) are strongly associated with severely ill COVID-19 patients [45]. One recently proposed explanation for this is the viral induction of a positive feedback loop, known as Interleukin 6 Amplifier (IL6-AMP) [46]. IL6-AMP is stimulated by simultaneous activation of nuclear factor kappa-light-chain-enhancer of activated B cell (NF-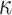 B) and Signal Transducer and Activator of Transcription 3 (STAT3) [47]. This in turn induces various pro-inflammatory cytokines and chemokines, including Interleukin 6, which recruit activated T cells and macrophages. This strengthens the Interleukin 6 Amplifier into a positive feedback loop leading to a cytokine storm [48], which is believed to be responsible for the tissue damage observed in patients with acute respiratory distress syndrome (ARDS) [46].
B) and Signal Transducer and Activator of Transcription 3 (STAT3) [47]. This in turn induces various pro-inflammatory cytokines and chemokines, including Interleukin 6, which recruit activated T cells and macrophages. This strengthens the Interleukin 6 Amplifier into a positive feedback loop leading to a cytokine storm [48], which is believed to be responsible for the tissue damage observed in patients with acute respiratory distress syndrome (ARDS) [46].
Intervention. Originally developed to treat autoimmune disorders such as rheumatoid arthritis [49], Tocilizumab (Toci) is an immunosuppressive drug consisting of a recombinant monoclonal antibody that targets the soluble Interleukin 6 receptor and can effectively block the IL6 signal transduction pathway [50]. Tocilizumab has emerged as a promising drug repurposing candidate to reduce mortality in severely ill COVID-19 patients [51], [52].
Causal Effect of Interest. We define a severely ill COVID-19 patient as someone with CytokineStorm > 65. We are interested in the individual treatment effect (ITE)
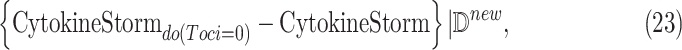
|
where 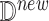 is an observed patient who received Tocilizumab treatment and became severely ill. We wish to characterize the severity of cytokine storm which would have occurred had she not received the treatment. We further wish to compare the ITE with the ATE
is an observed patient who received Tocilizumab treatment and became severely ill. We wish to characterize the severity of cytokine storm which would have occurred had she not received the treatment. We further wish to compare the ITE with the ATE
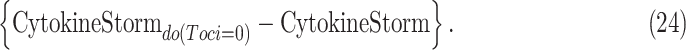
|
Evaluation. Tocilizumab is known to have a strong inhibitory effect on soluble Interleukin 6 receptor. We therefore expect that the severity of the cytokine storm would have been worse had the patient not received treatment. Unfortunately, at the time of writing, there were no ODE or SDE-based models of the pathway, nor were there publicly available COVID-19 datasets quantifying the kinase activity of the Interleukin 6 Amplifier pathway at the single-cell level. Therefore, we simulated data from a “ground-truth” sigmoidal structural causal model, where the topology reflects the causal structure of the pathway, and the numeric values of the parameters were fixed to reflect our prior qualitative knowledge of the IL6-AMP pathway.
We evaluate the ITE the proposed approach in two ways. First, we train the parameters of the SCM using the simulated data, and compare the counterfactual inference of the ITE obtained from the “trained” SCM to the counterfactual inference of the ITE from the “ground-truth” SCM. This comparison allows us to characterize the impact of weight estimation on the accuracy of causal effects. We expect that the need to estimate the weights will inflate the variance of the estimates. Second, we compare the estimates of ITE to the estimates of the ATE using the trained SCM. This comparison allows us to characterize the statistical efficiency of counterfactual inference when estimating causal effects. We expect that the ITE will provide much more precise estimates.
5. Results
5.1. Case Study 1: The IGF Signaling System
Generating BEL Causal Model. The BEL representation of the IGF system was manually curated using PyBEL [40], to match the existing ODE and SDE. The BEL representation of the IGF system specified all the node types as in category abundance. All the relationships between parents and children nodes were of type increase, except for the parent node 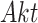 , where the relationship was of type decrease.
, where the relationship was of type decrease.
Observational Data. We mimicked the process of collecting observational data by simulating kinase activity from the corresponding ODE and SDE. The initial number of particles for the receptor was 37 for 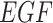 and 5 for
and 5 for 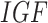 . The deterministic simulation numerically solved the ODE using the deSolve
[53] R package. The stochastic simulation used the Gillespie algorithm [29] from the smfsb
[54] R package.
. The deterministic simulation numerically solved the ODE using the deSolve
[53] R package. The stochastic simulation used the Gillespie algorithm [29] from the smfsb
[54] R package.
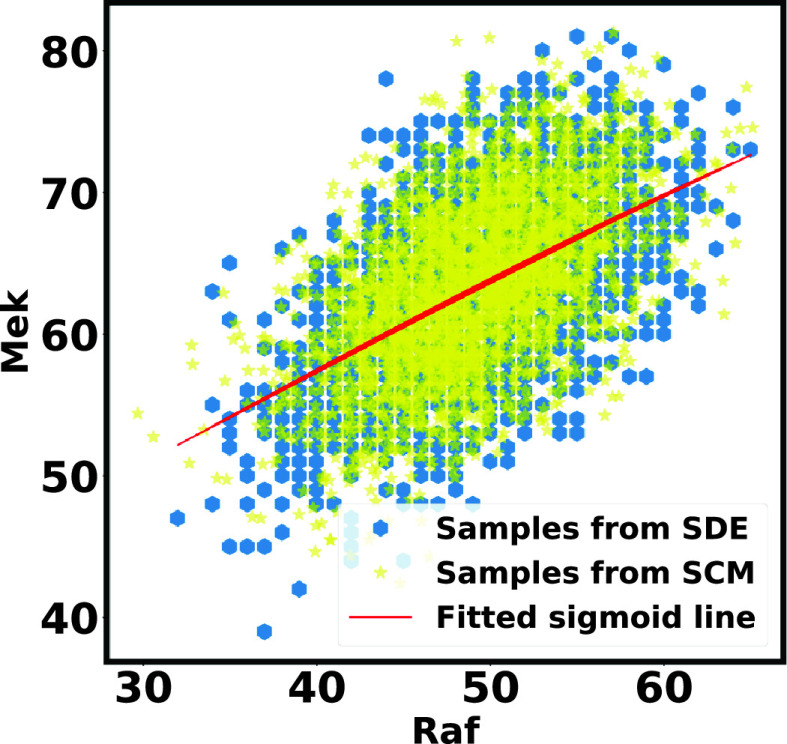
Appropriateness of Model Assumptions. SCM-based estimates of functional assignments with sigmoid approximations were well within the range of the SDE-based data (as shown for 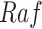 and
and 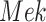 in Fig. 5). Similar results were obtained for estimates of
in Fig. 5). Similar results were obtained for estimates of 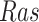 ,
, 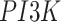 ,
, 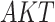 ,
, 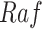 , and
, and 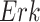 . The fitted functional assignment had little curvature. This indicates that a more complicated function with more parameters, such as Hill equation, was unnecessary in this case.
. The fitted functional assignment had little curvature. This indicates that a more complicated function with more parameters, such as Hill equation, was unnecessary in this case.
Fig. 5.
Case Study 1: IGF Model Scatter Plot of 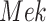 Versus
Versus 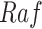 . Blue points are the data points generated by SDE. Yellow points are the estimates from SCM. The red line is the fitted sigmoid curve in Algorithm 2 line 12.
. Blue points are the data points generated by SDE. Yellow points are the estimates from SCM. The red line is the fitted sigmoid curve in Algorithm 2 line 12.
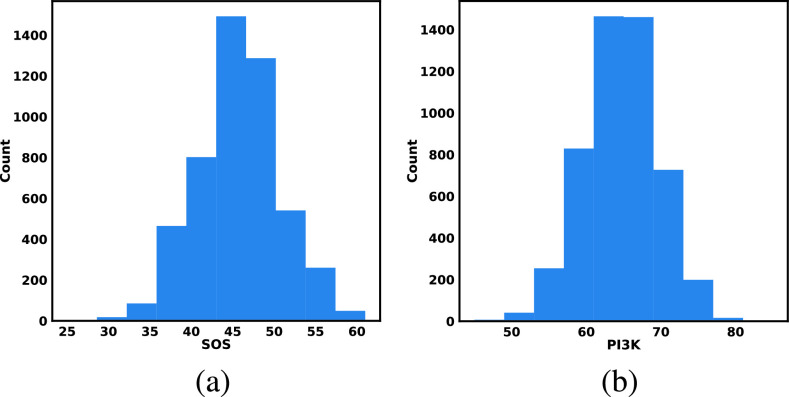
To further evaluate the plausibility of the assumptions, Fig. 6 shows the histograms of the SDE-generated abundances of root nodes, which were not affected by functional assignments in SCM. The shape of the histograms indicate that the assumption of Normal distribution was plausible.
Fig. 6.
Case Study 1: Probability distributions of the root nodes of IGF Model (a) Histogram of 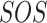 generated from SDE simulation (b) As in (a), for
generated from SDE simulation (b) As in (a), for 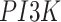 .
.
Accuracy of Causal Effects.
Figs. 7c and 7d show that the average treatment effects (ATEs) on 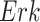 of fixing
of fixing 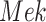 and
and 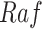 , based on forward simulation of ODE, SDE and SCM, were consistent. Figs. 7a and 7b show that the based on counterfactual inference has a smaller variance than the ATE. Since counterfactual inference reduces nuisance variation by sharing stochastic components in contexts with and without intervention, it increases the statistical efficiency of the estimation.
, based on forward simulation of ODE, SDE and SCM, were consistent. Figs. 7a and 7b show that the based on counterfactual inference has a smaller variance than the ATE. Since counterfactual inference reduces nuisance variation by sharing stochastic components in contexts with and without intervention, it increases the statistical efficiency of the estimation.
Fig. 7.
Case Study 1: Estimated causal effects of the IGF signaling pathway using algorithm 3. The ODE and SDE represent the true underlying dynamics of the IGF signaling pathway. The ODE and SDE-based forward simulation can only estimate the average treatment effect. These estimates are viewed as ground truth. In contrast, an SCM can estimate both the average treatment effect (ATE) and the individual treatment effect (ITE). (a) Comparison of ITE vs ATE for 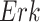 when
when 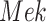 is fixed. (b) Comparison of ITE vs ATE for
is fixed. (b) Comparison of ITE vs ATE for 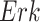 when
when 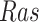 is fixed. (c) Comparison of SCM, SDE and ODE estimates of the ATE for
is fixed. (c) Comparison of SCM, SDE and ODE estimates of the ATE for 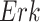 when
when 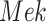 is fixed. (d) Comparison of SCM, SDE and ODE estimates of the ATE on
is fixed. (d) Comparison of SCM, SDE and ODE estimates of the ATE on 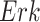 when
when 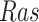 is fixed.
is fixed.
The individual treatment effect on 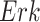 by fixing
by fixing 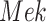 was much stronger than the ITE on
was much stronger than the ITE on 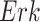 by fixing
by fixing 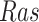 for the following reason. While
for the following reason. While 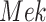 directly influences
directly influences 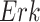 (i.e., there is a single path from
(i.e., there is a single path from 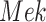 to
to 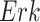 ),
), 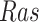 has two pathways to
has two pathways to 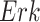 . The path through
. The path through 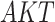 has an inhibiting (deactivation) effect on
has an inhibiting (deactivation) effect on 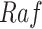 , and estimated negative weights in the sigmoid function in eq. (15). The alternative path, a cascade from
, and estimated negative weights in the sigmoid function in eq. (15). The alternative path, a cascade from 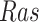 to
to 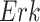 , has the opposite (activating) effect on
, has the opposite (activating) effect on 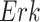 . The two paths mitigate the overall causal effect of
. The two paths mitigate the overall causal effect of 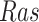 on
on 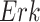 .
.
5.2. Case Study 2: Host Response to Viral Infection
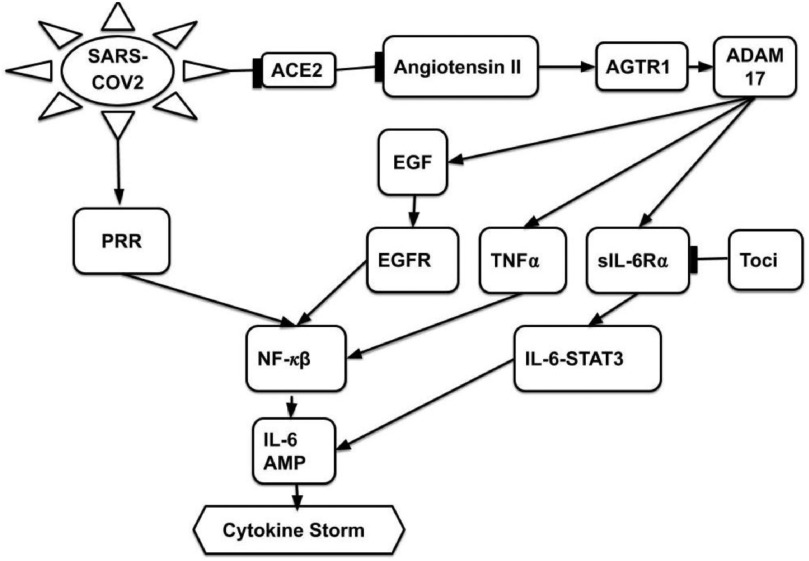
Generating BEL Causal Model. The steps of the proposed Algorithm 1 produced the qualitative causal model in Fig. 8, and the corresponding BEL causal model  , as follows. In accordance with the inputs to Algorithm 1, we defined the knowledge base
, as follows. In accordance with the inputs to Algorithm 1, we defined the knowledge base  as the Covid-19 knowledge network automatically assembled from the Covid-19 document corpus using the INDRA workflow. We defined the cause
as the Covid-19 knowledge network automatically assembled from the Covid-19 document corpus using the INDRA workflow. We defined the cause 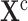 as sIL6R
as sIL6R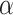 , the effect
, the effect 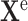 as cytokine storm, and the covariates
as cytokine storm, and the covariates 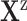 as SARS-CoV- 2 and Toci. Therefore the causal query of interest was defined as
as SARS-CoV- 2 and Toci. Therefore the causal query of interest was defined as  = sIL6R α, CytokineStorm, SARS-CoV-2,Toci}}.
= sIL6R α, CytokineStorm, SARS-CoV-2,Toci}}.
Fig. 8.
Case Study 2: Host response to viral infection pointed edges represent relationships of type increase; flat-headed edges represent relationships of type decrease. Nodes SARS-COV2 and Toci are external stimuli.
Algorithm 1 line 2 generated all pathways from Interleukin 6 to Cytokine Release Syndrome, resulting in 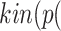 sIL6R α))
sIL6R α))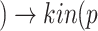 (IL6-STAT3))
(IL6-STAT3)) 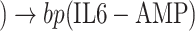 (CytokineStorm), where bp() is a biological process. Next, line 5 generated all pathways from Tocilizumab to Interleukin 6:
(CytokineStorm), where bp() is a biological process. Next, line 5 generated all pathways from Tocilizumab to Interleukin 6: 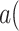 Toci
Toci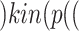 sIL6R
sIL6R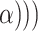 , where
, where  is the dosage level of Tocilizumab. We then generated all pathways from severe acute respiratory syndrome coronavirus 2 to Interleukin 6 receptor:
is the dosage level of Tocilizumab. We then generated all pathways from severe acute respiratory syndrome coronavirus 2 to Interleukin 6 receptor: 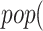 SARS-CoV-2
SARS-CoV-2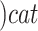 (ACE2)
(ACE2)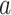 (Angiotensin II)
(Angiotensin II)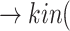 p(AGTR1)
p(AGTR1)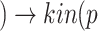 (ADAM17)
(ADAM17)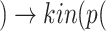 sIL6R
sIL6R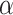 )), where
)), where 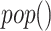 is the viral load of SARS-CoV-2 and
is the viral load of SARS-CoV-2 and 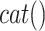 is the normal catalytic activity of Angiotensin Converting Enzyme 2.
is the normal catalytic activity of Angiotensin Converting Enzyme 2.
Line 8 found no new branches from Tocilizumab to Cytokine Release Syndrome. Finally, we generated all pathways from severe acute respiratory syndrome coronavirus 2 to Cytokine Release Syndrome, which resulted in three new branches 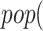 SARS-CoV-2
SARS-CoV-2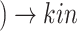 (p(PRR))
(p(PRR))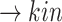 (p(NF-
(p(NF-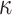 B))
B))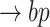 ((IL6-AMP))
((IL6-AMP))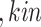 (p(ADAM17))
(p(ADAM17))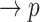 ((EGF))
((EGF))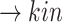 (p(EGFR))
(p(EGFR))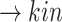 (p(NF-
(p(NF- B))
B)) (pEGFR)
(pEGFR)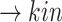 (p(TNF
(p(TNF 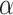 ))
)) 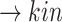 (p(NF-
(p(NF-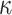 B)).
B)).
Observational Data. We simulated observational data from a “ground-truth” sigmoidal structural causal model, where the topology reflects the causal structure in Fig. 8, and the parameters reflect our prior qualitative knowledge of the IL6-AMP pathway. The root nodes SARS-CoV-2 and Tocilizumab were sampled from a Normal distribution with mean of 50 and standard deviation of 10. The non-root nodes were sampled from a sigmoid function as in eq. (15). Since we have prior qualitative knowledge that IL6-AMP is only activated due to simultaneous activation of NF-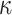 B and IL6-STAT3, we set the threshold for activation above what could be achieved by NF-
B and IL6-STAT3, we set the threshold for activation above what could be achieved by NF-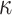 B or IL6-STAT3 alone. Since we also know that Toci is a strong inhibitor of sIL6R
B or IL6-STAT3 alone. Since we also know that Toci is a strong inhibitor of sIL6R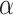 , we set the inhibition coefficient to a large negative number. The parameters of the sigmoid function were chosen to ensure that the variables were in the desired range of 0–100. Finally, we randomly generated two new individuals
, we set the inhibition coefficient to a large negative number. The parameters of the sigmoid function were chosen to ensure that the variables were in the desired range of 0–100. Finally, we randomly generated two new individuals 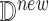 with Cytokine Release Syndrome
with Cytokine Release Syndrome 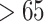 to represent severely ill patients. The first patient had a higher viral load of SARS-CoV-2 and received a lower dose of Toci. The second patient had a lower viral load of and received a higher dose of Toci.
to represent severely ill patients. The first patient had a higher viral load of SARS-CoV-2 and received a lower dose of Toci. The second patient had a lower viral load of and received a higher dose of Toci.
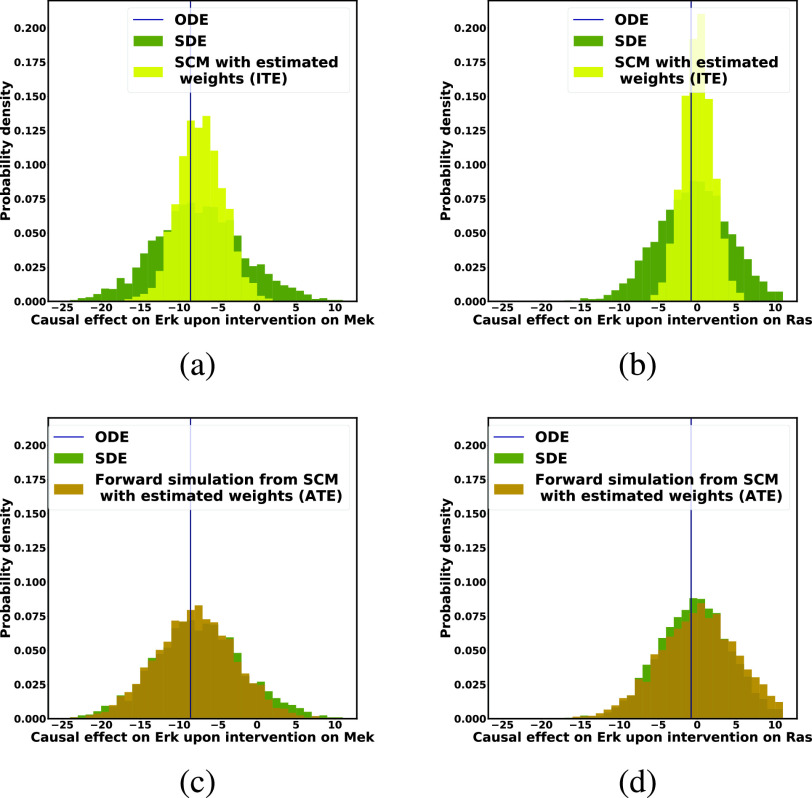
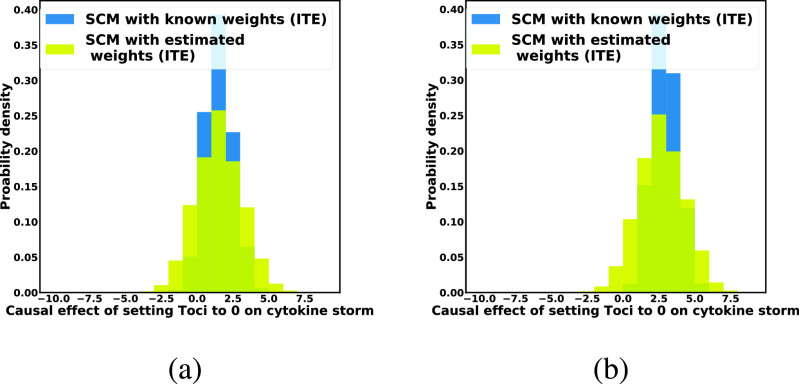
Estimation of Individual-Level Treatment Effect. Fig. 9 evaluates the SCM-based estimates of the individual treatment effect of withholding treatment from two COVID-19 patients who were severely ill. The distribution of the individual treatment effect obtained with the SCM trained using Algorithm 2 was consistent with, but had a slightly larger variance then, the distribution of ITE obtained with the “ground truth” SCM with known weights. Even though both patients had the same severity of illness prior to the intervention, patient B was estimated to have a more severe cytokine storm after Toci was withheld.
Fig. 9.
Case Study 2: SCM-Based estimates of the using algorithm 3. Blue histogram: the ITE estimated from the ground-truth SCM using Algorithm 3. Yellow histogram: the ITE estimated from the Algorithm 3-trained SCM using Algorithm 3. (a) Patient has a high viral load and received a low dose of Tocilizumab. (b) Patient has a low viral load and received a high dose of Tocilizumab. Both patients were severely ill.
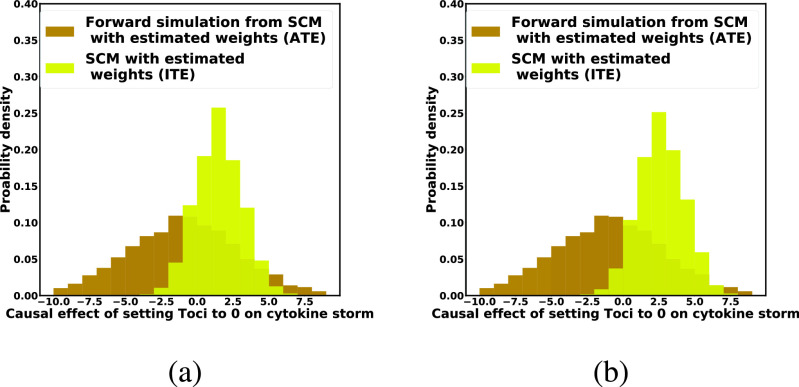
Fig. 10 further compared the individual treatment effect obtained with the SCM trained using Algorithm 2 with the average treatment effect estimated from the same model using forward simulation. The distribution of the individual treatment effect was patient-specific and had smaller variance, thus illustrating the statistical efficiency of counterfactual inference.
Fig. 10.
Case Study 2: SCM-Based estimates of the ATE and of the ITE using algorithm 3. Yellow histogram: the ITE estimated using counterfactual inference. Brown histogram: the ATE estimated using forward simulation. (a) Patient has a high viral load and received a low dose of Tocilizumab. (b) Patient has a low viral load and a received a high dose of Tocilizumab. Both patients were severely ill.
6. Discussion
We proposed a general approach that leverages structured qualitative prior knowledge, automatically generates a quantitative SCM, and enables answers to counterfactual research questions. In both case studies, the use of the Biological Expression Language allowed us to leverage large repositories of structured biological knowledge to specify an SCM and perform counterfactual inference in an automated manner, which would otherwise require a substantial manual effort. The application to the IGF signaling system demonstrated the appropriateness of the underlying assumptions, and the accuracy of the results when compared to ODE- and SDE-based forward simulation. The application to a study of host response to SARS-CoV-2 infection demonstrated the feasibility, versatility and usefulness of this approach as applied to an urgent public health issue. In particular, the approach can help determine the amount of Tocilizumab (Toci) required to reduce the severity of each individual's cytokine storm. Furthermore, in situations where treatment options are limited (as is the case SARS-CoV-2), counterfactual estimates enable a more precise conclusion regarding who would likely live without receiving the treatment, who would likely die even if they did receive the treatment, and who would likely live only after receiving the treatment.
The approach opens multiple directions for future research. In particular, future work can extend the configurability of the BEL2SCM algorithm by incorporating the rich type information in BEL, mapping parent-child type signatures to functional forms such as post-nonlinear models, neural networks, mass action kinetics and Hill equations, and incorporating additional data types such as binary variables, categorical variables, and continuous variables with constraints on their domains. In some cases, the variables in the model may not be directly observable, but may nonetheless be characterized by means of detectable molecular signatures. For example, even if interferon signaling may not be directly observable using transcriptomics measurements, it may still be possible to infer the activity of interferon signaling by an upregulation of interferon stimulated genes (ISG). Future work will focus on leveraging molecular signature databases to infer the activity of variables in the model, and on learning and/or evaluating the models using experimental data [55].
We also note that experimentalists typically formulate biological processes as linear pathways (e.g., from 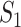 to
to 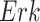 in the MAPK example) that can be effectively perturbed and measured in a laboratory setting. Yet such boundaries of biological processes are quite arbitrary, and are therefore highly susceptible to confounders. One way to address this issue is to search the knowledge graph for all common causes of variables in the causal model, use an identification algorithm [56] to find the minimal valid adjustment set of the augmented model, and then prune all common causes that do not contribute to that set. This approach will require us to tackle the issues of parameter and causal identifiability in the presence of confounders.
in the MAPK example) that can be effectively perturbed and measured in a laboratory setting. Yet such boundaries of biological processes are quite arbitrary, and are therefore highly susceptible to confounders. One way to address this issue is to search the knowledge graph for all common causes of variables in the causal model, use an identification algorithm [56] to find the minimal valid adjustment set of the augmented model, and then prune all common causes that do not contribute to that set. This approach will require us to tackle the issues of parameter and causal identifiability in the presence of confounders.
In addition to unobserved confounders, the validity of causal inferences can be threatened by feedback loops, model misspecification, missing data, and out-of-sample distributions. To address the possibility of feedback loops, we must consider the time scale at which these feedbacks reach steady-state: fast timescale feedback loops can be addressed with the chain graph interpretation of SCMs [57], [58]; intermediate timescale feedbacks can be addressed with non-recursive structural causal models [5]; slow timescale feedback loops can be handled by unrolling the structure of the SCM as is done with dynamic Bayesian networks [59], or simply by representing the entire feedback loop as a biological process, as we did with IL6-AMP. In the case of model misspecification, we will investigate the ability of counterfactual inference to improve the estimation [43]. For missing data, we can leverage causal inference recoverability algorithms that have been published recently [60], and for handling out-of-sample distributions, we can leverage recent results applying causal inference to the problem of external validity [61]. Future work will focus on addressing these threats to validity when applied to real biological data.
Acknowledgments
This work was supported by funds from the PNNL Mathematics and Artificial Reasoning Systems Laboratory Directed Research and Development Initiative. Knowledge curation environments were provided by BioDati.com and Causaly.com. The authors would also like to acknowledge Jessica Stothers and Rose Glavin at CoronaWhy.org and Marek Ostaszewski at the COVID-19 Disease Map Initiative for providing valuable feedback about the IL6-AMP model. Jeremy Zucker, Kaushal Paneri, Sara Mohammad-Taheri contributed equally to this work.
Biographies

Jeremy Zucker is currently the principal investigator for the MARS causal inference for viral pathogenesis project. He has more than 15 years of experience developing causal models to obtain actionable insights from systems biology data to advance knowledge in the study of metabolic engineering, circadian rhythms, evolution, human health and infectious disease.

Kaushal Paneri received the master's degree in data science from Northeastern university. He is a data scientist at Microsoft, currently working on counterfactual platform for Bing Ads Marketplace Optimization. His prominent research interests include causality, optimization and machine learning.

Sara Mohammad-Taheri received the bachelor's and master's degree in mathematics from the Sharif University of Technology. She is currently working toward the PhD degree in computers science with Northeastern University's Khoury College of Computer Sciences, advised by professor Olga Vitek. Her research interest includes causal inference techniques in computational biology and causal discovery of biomolecular data. She is also interested in developing statistical and computational methods and open source software for systems-wide molecular investigations of biological organisms including quantitative genomics, proteomics etc. She is a member of the statistical methods for studies of biomolecular systems group.

Somya Bhargava received the master's degree in data science from Northeastern University. She is currently working with Embedded Healthcare. She's been working in Healthcare industry and is experienced in using natural language processing, machine learning, statistical analysis and causal inference for researching for new products and enhancing existing ones.

Pallavi Kolambkar received the bachelor's degree in computer science, and the master's degree in computer applications, from India. She is majored in data science from Northeastern University and is currently working with Tesla. She has worked with companies from different domains to explore and visualize different dynamics of data.

Craig Bakker received a PhD degree in engineering from the University of Cambridge, where his research focused on optimization algorithms, differential geometry, and computational methods for model decomposition. Following this, he did postdoctoral research in climate change, food security, and economic modelling at Johns Hopkins University. He is currently a research scientist with the Pacific Northwest National Laboratory. He works in game theory, machine learning, and optimal control.

Jeremy Teuton received the PhD degree in cell and molecular biology (virology). He is an experienced interdisciplinary researcher and project leader. He is proficient in experimental design, trouble shooting, data analysis, and interdisciplinary application of scientific principles and approaches including cyber security and signal detection/classification. He excels in challenging environments, where problem-solving skills and experience in adapting technologies, systems and processes/approaches can be of most use.

Charles Tapley Hoyt received the PhD degree in computational life sciences from the University of Bonn. His research interests cover the interface of biocuration, knowledge graphs, and machine learning with systems biology, networks biology, and drug discovery. He is an advocate of open source software, reproducibility, and open science. His open source projects PyBEL and PyKEEN are used by several academic and industrial groups.

Kristie Oxford is a virologist, with expertise in host-pathogen interactions. Her research at Pacific Northwest National Laboratory (PNNL) primarily involves characterizing and interpreting host biomolecular responses to viral infection. She and her team analyze systems biology data from cells infected in vitro and in vivo with mammalian viruses representing many genera and families, in order to understand mechanisms of disease and to identify targets for medical countermeasures. The systems approach interrogates the host transcriptomic response to infection from microarray or RNA sequencing data as well as the proteomic, lipidomic, and metabolomic response from high resolution mass spectrometry analysis. She and her team have studied host-virus interactions from thousands of samples representing more than 12 human viruses, identifying gene, protein, and metabolite candidates for medical intervention and/or mechanistic studies.

Robert Ness received the PhD degree in mathematical statistics from Purdue University, and then he worked as a research engineer in various AI startups. He didn't start in machine learning. He started his career by becoming fluent in Mandarin Chinese and moving to Tibet to do developmental economics fieldwork. He later obtained a graduate degree from Johns Hopkins School of Advanced International Studies. After switching to the tech industry, his interests shifted to modeling data. He has published in journals and venues across these spaces, including Research in Computational Molecular Biology and NeurIPS, on topics including causal inference, probabilistic modeling, sequential decision processes, and dynamic models of complex systems. In addition to startup work, currently he is a machine learning professor with Northeastern University.

Olga Vitek received the PhD degree in statistics from Purdue University. She is currently a professor with the Khoury College of Computer Sciences at Northeastern University. Her research interests include statistical science, machine learning, mass spectrometry and systems biology. Statistical methods and open-source software MSstats and Cardinal developed in her lab are used in academia and industry, and were recently recognized with the Chan Zuckerberg Essential Open Source Software for Science Award. She is a senior member of the International Society for Computational Biology, and an elected member of the Council of HUPO and of the board of directors of USHUPO. She is a member of the editorial advisory board of Molecular and Cellular Proteomics and of Journal of Proteome Research.
Funding Statement
This work was supported by funds from the PNNL Mathematics and Artificial Reasoning Systems Laboratory Directed Research and Development Initiative.
Contributor Information
Jeremy Zucker, Email: jeremy.zucker@pnnl.gov.
Kaushal Paneri, Email: kaushalpaneri@gmail.com.
Sara Mohammad-Taheri, Email: mohammadtaheri.s@northeastern.edu.
Somya Bhargava, Email: bhargavasomyav2@gmail.com.
Pallavi Kolambkar, Email: kolambkar.p@husky.neu.edu.
Craig Bakker, Email: craig.bakker@pnnl.gov.
Jeremy Teuton, Email: Jeremy.Teuton@pnnl.gov.
Charles Tapley Hoyt, Email: charles.hoyt@envedatx.com.
Kristie Oxford, Email: kristie.oxford@pnnl.gov.
Robert Ness, Email: robertness@gmail.com.
Olga Vitek, Email: o.vitek@northeastern.edu.
References
- [1].Pezeshki A., Ovsyannikova I. G., McKinney B. A., Poland G. A., and Kennedy R. B., “The role of systems biology approaches in determining molecular signatures for the development of more effective vaccines,” Expert Rev. Vaccines, vol. 18, 2019, Art. no. 253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Pedragosa M., et al. , “Linking cell dynamics with gene coexpression networks to characterize key events in chronic virus infections,” Front. Immunol., vol. 10, 2019, Art. no. 1002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Nguyen V. K., Klawonn F., Mikolajczyk R., and Hernandez-Vargas E. A., “Analysis of practical identifiability of a viral infection model,” PloS One, vol. 11, 2016, Art. no. e0167568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Arazi A., Pendergraft W. F., Ribeiro R. M., Perelson A. S., and Hacohen N., “Human systems immunology: Hypothesis-based modeling and unbiased data-driven approaches,” Seminars Immunol., vol. 25, 2013, Art. no. 193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Pearl J., Causality: Models, Reasoning and Inference. Cambridge, MA, USA: Cambridge Univ. Press, 2013. [Google Scholar]
- [6].Peters J., Janzing D., and Schölkopf B., Elements of Causal Inference: Foundations and Learning Algorithms. Cambridge, MA, USA: MIT press, 2017. [Google Scholar]
- [7].Allen J. F., Swift M., and De Beaumont W., “Deep semantic analysis of text,” Proc. Conf. Semantics Text Process., 2008, vol. 1, Art. no. 343. [Google Scholar]
- [8].McDonald D. D., “Issues in the Representation of Real Texts: The Design of KRISP,” in Proc. Natural Lang. Process. Knowl. Representation: Lang. Knowl. Knowl. Lang., 2000, pp. 77–110. [Google Scholar]
- [9].Valenzuela-Escárcega M. A., et al. , “Large-scale automated machine reading discovers new cancer-driving mechanisms,” Database, vol. 2018, 2018, Art. no. 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Gyori B. M., Bachman J. A., Subramanian K., Muhlich J. L., Galescu L., and Sorger P. K., “From word models to executable models of signaling networks using automated assembly,” Mol. Syst. Biol., vol. 13, 2017, Art. no. 954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hoyt C. T., et al. , “Re-curation and rational enrichment of knowledge graphs in biological expression language,” Database, vol. 2019, 2019, Art. no. baz068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Cerami E. G., et al. , “Pathway Commons, a web resource for biological pathway data,” Nucl. Acids Res., vol. 39, pp. D685–D690, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Fabregat A., et al. , “The Reactome pathway knowledgebase,” Nucl. Acids Res., vol. 46, pp. D649–D655, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Kanehisa M., Furumichi M., Tanabe M., Sato Y., and Morishima K., “KEGG: New perspectives on genomes, pathways, diseases and drugs,” Nucl. Acids Res., vol. 45, pp. D353–D361, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Perfetto L., et al. , “SIGNOR: A database of causal relationships between biological entities,” Nucl. Acids Res., vol. 44, pp. D548–D554, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Slenter D. N., et al. , “WikiPathways: A multifaceted pathway database bridging metabolomics to other omics research,” Nucl. Acids Res., vol. 46, pp. D661–D667, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Demir E., et al. , “The BioPAX community standard for pathway data sharing,” Nat. Biotechnol., vol. 28, 2010, Art. no. 1308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Hucka M., et al. , “The Systems Biology Markup Language (SBML): Language specification for level 3 version 2 core,” J. Integrative Bioinf., 2018, Art. no. 20170081. [DOI] [PMC free article] [PubMed]
- [19].Le Novere N., et al. , “The systems biology graphical notation,” Nat. Biotechnol., vol. 27, pp. 735–741, 2009. [DOI] [PubMed] [Google Scholar]
- [20].Slater T., “Recent advances in modeling languages for pathway maps and computable biological networks,” Drug Discov. Today, vol. 19, pp. 193–198, 2014. [DOI] [PubMed] [Google Scholar]
- [21].Machamer P., Darden L., and Craver C. F., “Thinking about mechanisms,” Philosophy Sci., vol. 67, 2000, Art. no. 1. [Google Scholar]
- [22].Li Y., Roberts J., AkhavanAghdam Z., and Hao N., “Mitogen-activated protein kinase (MAPK) dynamics determine cell fate in the yeast mating response,” The J. Biol. Chem., vol. 292, pp. 20354–20361, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Chen L., Wang R., Li C., and Aihara K., Modeling Biomolecular Networks in Cells: Structures and Dynamics. Berlin, Germany: Springer, 2010. [Google Scholar]
- [24].Gratie D., Iancu B., and Petre I., “ODE analysis of biological systems,” in International School on Formal Methods for the Design of Computer, Communication and Software Systems. Berlin, Germany: Springer; 2013, Art. no. 29. [Google Scholar]
- [25].Bianconi F., Baldelli E., Ludovini V., Crino L., Flacco A., and Valigi P., “Computational model of EGFR and IGF1R pathways in lung cancer: A systems biology approach for translational oncology,” Biotechnol. Adv., vol. 30, pp. 142–153, 2012. [DOI] [PubMed] [Google Scholar]
- [26].Kim E. K. and Choi E.-J., “Pathological roles of MAPK signaling pathways in human diseases,” Biochimica et Biophysica Acta - Mol. Basis Disease, vol. 1802, pp. 396–405, 2010. [DOI] [PubMed] [Google Scholar]
- [27].Ness R., Paneri K., and Vitek O., “Integrating Markov processes with structural causal modeling enables counterfactual inference in complex systems,” in Proc. Int. Conf. Neural Inf. Process. Syst., 2019, Art. no. 14211. [Google Scholar]
- [28].Paneri K., “Integrating Markov process and structural causal models enables counterfactual inference in complex systems,” Northeastern Univ., 2019.
- [29].Gillespie D. T., “Exact stochastic simulation of coupled chemical reactions,” The J. Phys. Chem., vol. 81, pp. 2340–2361, 1977. [Google Scholar]
- [30].Jha S. K. and Langmead C. J., “Exploring behaviors of stochastic differential equation models of biological systems using change of measures,” BMC Bioinf., vol. 13, 2012, Art. no. S8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Alon U., An Introduction to Systems Biology: Design Principles of Biological Circuits. Boca Raton, FL, USA: CRC press, 2019. [Google Scholar]
- [32].Bongers S. and Mooij J. M., “From random differential equations to structural causal models: The stochastic case,” ArXiv, vol. abs/1803.08784, 2018. [Google Scholar]
- [33].Jerrum M., Sinclair A., and Hochbaum D. S., “The markov chain monte carlo method: An approach to approximate counting and integration,” Approximation Algorithms NP-hard problems, PWS Publishing, 1996.
- [34].Gelfand A. E., “Gibbs sampling,” J. Amer. Statist. Assoc., vol. 95, 2000, Art. no. 1300. [Google Scholar]
- [35].Hoffman M. D. and Gelman A., “The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo,” J. Mach. Learn. Res., vol. 15, pp. 1593–1623, 2014. [Google Scholar]
- [36].Hoffman M. D., Blei D. M., Wang C., and Paisley J., “Stochastic variational inference,” The J. Mach. Learn. Res., vol. 14, pp. 1303–1347, 2013. [Google Scholar]
- [37].Blom T., Bongers S., and Mooij J. M., “Beyond structural causal models: Causal constraints models,” in Proc. 35th Conf. Uncertainty Artif. Intell., 2019, pp. 585–594. [Google Scholar]
- [38].Madan S., et al. , “The extraction of complex relationships and their conversion to biological expression language (BEL) overview of the BioCreative VI (2017) BEL track,” Database, J. Biol. Databases Curation, vol. 2019, 2019, Art. no. baz084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Hoyt C. T., et al. , “Integration of structured biological data sources using biological expression language,” BioRxiv, Cold Spring Harbor Lab., pp. 631812, 2019.
- [40].Hoyt C. T., Konotopez A., Ebeling C., and Wren J., “PyBEL: A computational framework for biological expression language,” Bioinformatics, vol. 34, pp. 703/704, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Mi H., et al. , “Systems biology graphical notation: Activity flow language level 1 version 1.2,” J. Integrative Bioinf., vol. 12, 2015, Art. no. 265. [DOI] [PubMed] [Google Scholar]
- [42].Rezende D. J., Mohamed S., and Wierstra D., “Stochastic backpropagation and variational inference in deep latent gaussian models,” in Proc. Int. Conf. Mach. Learn., vol. 2, 2014. [Google Scholar]
- [43].Ness R., Paneri K., and Vitek O., “Integrating Markov processes with structural causal modeling enables counterfactual inference in complex systems,” in Proc. Int. Conf. Neural Inf. Process. Syst., 2019, Art. no. 14234. [Google Scholar]
- [44].Bingham E., et al. , “Pyro: Deep Universal Probabilistic Programming,” J. Mach. Learn. Res., vol. 20, pp. 1–6, 2018. [Google Scholar]
- [45].Ulhaq Z. S. and Soraya G. V., “Interleukin-6 as a potential biomarker of COVID-19 progression,” Med. Mal. Infect., vol. 50, pp. 382/383, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Hirano T. and Murakami M., “COVID-19: A new virus, but a familiar receptor and cytokine release syndrome,” Immunity, vol. 52, pp. 731–733, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Murakami M. and Hirano T., “The pathological and physiological roles of IL-6 amplifier activation,” Int. J. Biol. Sci., vol. 8, pp. 1267–1280, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Ogura H., et al. , “Interleukin-17 promotes autoimmunity by triggering a positive-feedback loop via interleukin-6 induction,” Immunity, vol. 29, pp. 628–636, 2008. [DOI] [PubMed] [Google Scholar]
- [49].Oldfield V., Dhillon S., and Plosker G. L., “Tocilizumab: A review of its use in the management of rheumatoid arthritis,” Drugs, vol. 69, pp. 609–632, 2009. [DOI] [PubMed] [Google Scholar]
- [50].Zhang C., Wu Z., Li J.-W., Zhao H., and Wang G.-Q., “Cytokine release syndrome in severe COVID-19: Interleukin-6 receptor antagonist Tocilizumab may be the key to reduce mortality,” Int. J. Antimicrob. Agents, vol. 55, 2020, Art. no. 105954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Coomes E. A. and Haghbayan H., “Interleukin-6 in COVID-19: A systematic review and meta-analysis,” MedRxiv, Cold Spring Harbor Lab. Press, 2020. [DOI] [PMC free article] [PubMed]
- [52].Xu X., et al. , “Effective Treatment of Severe COVID - 19 Patients with Tocilizumab,” Proc. Nat. Acad. Sci. USA, vol. 117, pp. 10970–10975, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Soetaert K. E. R., Petzoldt T., and Setzer R. W., “Solving differential equations in R: Package deSolve,” J. Statist. Softw., vol. 33, pp. 77–83, 2010. [Google Scholar]
- [54].Wilkinson D., “Smfsb-stochastic modelling for systems biology,” R Package Version, vol. 1, 2018. [Google Scholar]
- [55].Liu A., Trairatphisan P., Gjerga E., Didangelos A., Barratt J., and Saez-Rodriguez J., “From expression footprints to causal pathways: Contextualizing large signaling networks with CARNIVAL,” Syst. Biol. Appl., vol. 5, 2019, Art. no. 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Tikka S. and Karvanen J., “Identifying causal effects with the R package causal effect,” J. Statist. Softw., vol. 76, 2017, Art. no. 1. [Google Scholar]
- [57].Lauritzen S. L. and Richardson T. S., “Chain graph models and their causal interpretations,” J. Roy. Statist. Soc.: Series B, vol. 64, pp. 321–348, 2002. [Google Scholar]
- [58].Sherman E. and Shpitser I., “Identification and estimation of causal effects from dependent data,” Proc. Int. Conf. Neural Inf. Process. Syst., 2018, vol. 2018, Art. no. 9446. [PMC free article] [PubMed] [Google Scholar]
- [59].Koller D. and Friedman N., Probabilistic Graphical Models: Principles and Techniques - Adaptive Computation and Machine Learning. Cambridge, MA, USA: MIT Press, 2009. [Google Scholar]
- [60].Nabi R., Bhattacharya R., and Shpitser I., “Full law identification in graphical models of missing data: Completeness results,” 2020, arXiv:2004.04872. [PMC free article] [PubMed]
- [61].Bareinboim E. and Pearl J., “Causal inference and the data-fusion problem,” Proc. Nat. Acad. Sci. USA, vol. 113, 2016, Art. no. 7345. [DOI] [PMC free article] [PubMed] [Google Scholar]