Abstract
Computer modeling of complexation of mono- and oligosaccharide ligands with the main (fourth) carbohydrate-binding domain of the mannose receptor CD206 (CRD4), as well as with the model receptor concanavalin A (ConA), was carried out for the first time, using methods of molecular dynamics and neural network analysis. ConA was shown to be a relevant model of CD206 (CRD4) due to similarity of the structural organization of the binding sites and high correlation of the values of free energies of complexation between the literature data and computer modeling (r > 0.9). Role of the main factors affecting affinity of the ligand–receptor interactions is discussed: the number and nature of carbohydrate residues, presence of Me-group in the O1 position, type of the glycoside bond in dimannose. Complexation of ConA and CD206 with ligands is shown to be energetically caused by electrostatic interactions (E) of the charged residues (Asn, Asp, Arg) with oxygen and hydrogen atoms in carbohydrates; contributions of hydrophobic and van der Waals components is lower. Possibility of the additional stabilization of complexes due to the CH–π stacking interactions of Tyr with the Man plane is discussed. The role of calcium and manganese ions in binding ligands has been studied. The values of free energies of complexation calculated in the course of molecular dynamics simulation correlate with experimental data (published for the model ConA): correlation coefficient r = 0.68. The Pafnucy neural network was trained based on the set of PDBbind2020 ligand–receptor complexes, which significantly increased accuracy of the energy predictions to r = 0.8 and 0.82 for CD206 and ConA receptors, respectively. A model of normalization of the complexation energy values for calculating the relevant values of ΔGbind, Kd is proposed. Based on the developed technique, values of the dissociation constants of a series of CD206 complexes with nine carbohydrate ligands of different structures were determined, which were not previously known. The obtained data open up possibilities for using computer modeling for the development of optimal drug carriers capable of active macrophage targeting, and also determine the limits of applicability of using ConA as a relevant model for studying parameters of the CD206 binding to various carbohydrate ligands.
Electronic supplementary material
The online version contains supplementary material available at 10.1134/S0006297922010059.
Keywords: molecular dynamics, artificial neural network, CD206, concanavalin A, macrophages
INTRODUCTION
In the present work the possibilities of molecular dynamics approach and of the Pafnucy artificial neural network [1] for examining regularities in the complexation of the mannose (Man) receptor of macrophages (Mϕ) with carbohydrate ligands are studied that is necessary for constructing drug carriers targeted to mannose receptors (MR) of macrophages.
For creating effective treatment approaches for various diseases, including respiratory diseases, it is important not only to develop new pharmaceuticals, but also their targeted delivery to the affected tissues and cells [2]. Mϕ can serve as targets, which play an important role in the immune response due to recognition and killing pathogens [3]. However, Mϕ can also be a reservoir for growth and reproduction of bacteria and viruses that significantly limits efficiency of antibiotics and of antiviral therapy [4, 5]. The antigen-presenting cells, including Mϕ, are major contributors to creation of the immunosuppressive microenvironment of tumors and concurrently decrease immune response [6]. Repolarization of the immunosuppressive tumor-associated macrophages (M2) to proinflammatory cells (M1) it is a promising pathway for solving this problem [7]. However, the excessive pro-inflammatory activity of macrophages is the cause of autoimmune diseases (rheumatoid arthritis, osteoarthritis, multiple sclerosis). It is thought that specific activation of macrophages can be an effective approach for therapy of neurodegenerative diseases [8]. Based on the above-mentioned knowledge, the targeted delivery of antibacterial preparations or substances capable of regulating the activation of macrophages to macrophages depending on the treatment purpose [9] seems to be a promising approach for increasing effectiveness of therapeutics in various diseases.
Potentially, it is possible to affect macrophages by binding bioactive molecules with pattern recognition receptors, which include toll-like receptors (binding glycolipids, lipopolysaccharides, lipoteichoic acids, peptidoglycans), complement receptors (recognizing the opsonizing fragments C3b, iC3b, and C3dg), scavenger receptors (recognizing glyco- and lipoproteins), and lectin receptors [3]. Influencing lectin receptors during macrophage targeting makes it possible to activate the targeted branches of T-helper lymphocytes: Th1, Th2, or Th17 [10, 11].
It should be noted that targeting Mϕ through mannose receptors recognizing Man-, Fuc-, and GlcNAc-residues of the cell wall oligosaccharides of pathogenic microorganisms [12] has some advantages in comparison with the strategy of targeting other receptors: only the disease-causing macrophages are affected, the risk of resistance and complications is reduced, and effectiveness is increased (https://www.macrophagetx.com). The major mannose receptor of Mϕ is CD206 – a C-type lectin, which is a 175 kDa transmembrane protein. The C-terminal part of CD206 contains a short cytoplasmic part of 45 amino acids (aa) [3]. Carbohydrates of MR are bound due to the C-type lectin-like region consisting of eight domains. However, only the fourth carbohydrate-recognizing domain (CRD4) was shown to have an ability to bind carbohydrates without binding other components [13, 14]. Therefore, the CRD4 was used in the present work for modeling MR features and identifying the most specific mannose ligands. It should be noted that according to the experimental data [15] parameters of oligosaccharide binding by the pair of CRD domains (4-5) are mostly the same as those for the whole mannose receptor of CD206, which was exemplified with the Man23 oligosaccharide (23 mannose residues in the molecule).
However, since the MRs themselves are difficult to access and experimental data on the CD206 complexes are extremely scarce, model receptor proteins are often used for determination of main trends in binding mannose ligands. It is believed that CD206 should be very similar to concanavalin A (ConA) in the regularities of binding carbohydrates [3]. Thus, one of the purposes of the present work was to compare these receptors for detecting the limits of applicability of ConA as a model of MR. ConA consists of four subunits (each of 26.5 kDa, 237 aa), is strongly glycated, binds carbohydrates in the presence of metal cations (usually Mn2+ and Ca2+) [16, 17]. Ca2+ cation coordinates amino acid residues and “prepares” the receptor for recognizing carbohydrates, which is different from concanavalin A as Ca2+ in CD206 participates in the direct complexation with ligands. In the ConA binding site there is another cation, Mn2+ in this case (sometimes this cation is replaced by Co2+, Ni2+, Zn2+), which fixes the position of Ca2+ decreasing mobility of amino acid residues in the binding site. Presence of both cations in ConA is necessary for enabling binding ability of the protein [18, 19].
High affinity ligand–receptor interactions can be searched using different physico-chemical approaches [20]: isothermal titration calorimetry [21, 22], fluorescent methods [23, 24], Fourier infrared spectroscopy [25], Landsteiner’s inhibition method [26]. To determine expression of Mϕ antigens and pathways of their activation flow cytometry is also used [27]; confocal microscopy is used for visualizing cellular absorption of drug carriers [28]. Computer simulation is an approach, which is being actively developed. Molecular dynamics (MD) and artificial neural networks (NNs) make it possible to model various chemical processes, including ligand–receptor interactions. The in silico methods make it possible to study a wide range of compounds with variable structure and spatial organization, synthesis of which in laboratory is laborious, time-consuming and frequently cannot be realized.
MD allows researchers to study interaction mechanisms of receptor proteins with ligands: pathways [29-31] and kinetics of complex dissociation [32], as well as binding of ligands with receptors [33-35]. MD makes it possible to evaluate complexation parameters: free energy of interaction, contribution of hydrogen bonds, van der Waals (vdW) and E, energy of solvation and desolvation [33, 36, 37]. MD is a good approach for studying and refinement of crystal structures of proteins and their complexes, namely: simulations reveal essential ligand–receptor interactions, which are absent in the crystal [34]. MD reveals interrelation between the hydrophobicity and hydrophilicity of a ligand, its shape (elongated, T-shaped, curved), complex stability, and kinetics of the binding [38]. However, the MD approach requires significant computational power and long simulation time, which could be reasonable in the cases when it is important to detect mechanism of interaction of molecules under study. At the same time, an artificial neural network is a complementary method (or a replacement of MD) for high throughput screening of many ligands for evaluating their affinity for a receptor.
Several neural networks predicting dissociation (association) constants of ligand–receptor complexes or of inhibition constant based on the PDBbind database (SE-OnionNet [39], Pafnucy [1], Nnscore 2.0 [40]) are known. The main advantage of neural network approach in comparison with MD is a short computation time (several minutes as compared to days or weeks in the MD simulation), and also the alternative principle of NN functioning, i.e., the “comparison” of the given ligand–receptor pair with the ones known from the literature (PDBbind) in a set of parameters (19 in the present work), including types of constituent atoms, valences, hybridizations, charges. Accuracy of the affinity prediction depends on the “training” of the network, number of layers and neurons in the network, and the algorithm complexity. It should be noted that the computational methods are being actively improved that opens prospects for using MD and NNs as important tools in biochemistry.
Recently, a number of works appeared in the literature clearly demonstrating high potential of neural networks. Thus, in the work of Lahey and Rowley [41] stability of molecular conformations was predicted using NNs with accuracy comparable to the quantum chemical calculations, but with a significantly decreased computational costs of the simulation of ligand–receptor interactions (for instance, phosphodiesterase 5A with tadalafil). NNs was able to predict the receptor and ligand positions during binding, as well as the value of Gibbs energy (with good correlation with experimental data) for some biomolecules, e.g., biotin carboxylase, dehydrofolate reductase [42]. Using NNs and artificial intelligence technologies facilitated the search of potential drugs among the substances used in medicine or tested in clinical trials: faldaprevir – in hepatitis C, the immunodepressant cyclosporin, remdecevir, mefuparib, etc. These therapeutic agents can be repurposed for reducing the viral load, relieving symptoms of COVID-19, and effective treatment of viral infection [43].
However, in silico methods, including the neural network technology, only begin to be used by researchers for direct study of biosystems. Nevertheless, a significant potential of computer simulation has been demonstrated already in some works [44-46]. That is why one purpose of the present work was to demonstrate the prospects of using NNs and also of MD for investigation of ligand–receptor interactions of mono- and oligosaccharides with the CRD4 of the CD206 mannose receptor, as well as with the model lectin concanavalin A. For some ConA–ligand complexes, experimental constants have been reported in the literature, and this allowed us to validate and optimize on this basis simulation methods and to study interactions of a series of ligands with the fourth carbohydrate-binding domain (CRD4) of the mannose receptor of CD206, for which the experimental parameters were not described previously.
MATERIALS AND METHODS
Structures of complexes. Spatial structures of the ConA receptor molecules and of 15 carbohydrate ligands were reconstructed using crystallographic PDB data (table). Structures and spatial organization of the ligands 1-15 were varied: the carbohydrate residue type, the number of Man- and GlcNAc-residues in the carbohydrate (from 1 to 5), the Me-group presence in the O1-position of the carbohydrates, the glycoside bond type (α1→2, 1→3, 1→6). Four protein subunits consisting each of 237 aa, Ca2+ and Mn2+ cations in the binding sites of ligands, crystallographic water were considered. Structure of the fourth carbohydrate-binding domain of the mannose receptor of CD206 was constructed on the basis of the PDB crystallographic data (Acc. No. 7JUF). The receptor consists of 135 aa and Ca2+ cation. For Ca2+ and Mn2+ ions the unbound model 12-6-4 of Lennard–Jones potential was used. Structures of the CD206 ligands were generated and brought up to the binding site manually using a visualization tool PyMol (https://pymol.org/2/) (table).
Dissociation constants of complexes of ConA and the CRD4 domain of the mannose receptor CD206 with carbohydrate ligands
| Number | Ligand name, code of PDB complex with ConA, and corresponding Fig. number | Kd (ConA–ligand), µM | Kd (CD206 CRD4–ligand), µM | ||||
|---|---|---|---|---|---|---|---|
| molecular dynamics | literature data | neural network | molecular dynamics | literature data | neural network | ||
| 1 | α-mannopyranose [5CNA]; Fig. 5 and Fig. S5 in the Supplement | 1450 | 1100 | 360 | 3450 | – | 3700 |
| 2 | Me-mannopyranoside [5CNA]; Figs. 5, 7, and Figs. S3, S5 in the Supplement | 600 | 160 | 190 | 2900 | 2400 | 2360 |
| 3 | Me-α(1→2)-dimannopyranoside [1BXH]; Fig. 4 | 30 | 7 | 60 | 1700 | – | 20 |
| 4 | α (1→2)-dimannopyranoside [1BXH]; Fig. S4 in the Supplement | 43 | 24 | 190 | 2290 | 1280 | 1700 |
| 5 | Me-α(1→3)-dimannopyranoside [1QDO/C]; Fig. 4 | 14 | 30 | 56 | 1800 | – | 2860 |
| 6 | α (1→3)-dimannopyranoside; Fig. S4 in the Supplement | 16 | 71 | 78 | 1600 | 2290 | 1800 |
| 7 | α (1→6)-dimannopyranoside; Figs. S4, S7 in the Supplement | 35 | 75 | 145 | 2400 | 1010 | 1600 |
| 8 | Me-α(1→6)-dimannopyranoside; Fig. 4, Fig. S2 in the Supplement | 27 | 120 | 80 | 1500 | – | 1500 |
| 9 | Me-3,6-di-O-(mannopyranosyl)-α-mannopyranoside [1ONA] | 6 | 2 | 70 | 1080 | – | 2860 |
| 10 | 3,6-di-O-(mannopyranosyl)-α-mannopyranose; Fig. 2 | 16 | 3 | 40 | 780 | – | 650 |
| 11 | 3,6-di-O-(β(1→2)-N-acetylglucosamino-mannopyranosyl)-α-mannopyranose [1TEI]; Fig. S6 in the Supplement | 2 | 0,7 | 30 | 480 | – | 1000 |
| 12 | Me-α-glucopyranoside [1GIC]; Fig. S2 in the Supplement | 590 | 560 | 200 | >6000* | >6000* | >6000* |
| 13 | Me-α-galactopyranoside [1GIC]; Fig. 3, Fig. S2 in the Supplement | 70 | 500 | 370 | >6000* | >6000* | >6000* |
| 14 | Me-GlcNAc | 11 | 1350 | 150 | 2400 | 5300 | 4200 |
| 15 | Fuc-α(1→3)-GlcNAc | 3 | – | 170 | 2300 | – | 1400 |
Note. The values are calculated using computer simulation, in comparison with the literature data of isothermal calorimetry [21] and Landsteiner’s inhibition [26], as well as with data calculated from the shifts in NMR spectra [52, 53] and competitive binding [13]. T = 300 K. pH = 7. Concentration of NaCl is 1 M.
* Nonspecific interaction.
The structures were prepared using tLeaP from AmberTools20, 21 [47]: missing hydrogen atoms were added as well as Na+ ions for neutralizing total charge of the complex. The system was solvated with water molecules TIP3P [48] with the minimal distance between the cell border and the protein 10 Å. On average, the cell size with ConA tetramer was 90 × 95×90 Å3 with the domain CD206 60×65×60 Å3. Force fields Amber ff14SBonlysc, GLYCAM_06j-1 were used for describing atom interactions.
Carrying out molecular dynamics. Simulation was carried out using the molecular dynamics Amber20 package. Initially, the systems (receptor–ligand complexes) in aqueous solution were minimized using 5000 steps of the steepest descent algorithm followed by 5000 steps of the conjugated gradient algorithm. The system was heated from 0 to 300 K for 0.1 ns according to the Langevin’s model using the collision frequency of 2.0 ps−1 and under periodic boundary conditions of constant volume. Then simulation was performed for 100 ps with the constant pressure of 1 atm. Then the system was equilibrated within 100 ps and directly MD was performed (production). For each model, three independent cycles were carried out with the temperature maintained at 300 K with a Langevin thermostat (ntt = 3). In the case of ConA tetramer, MD were performed for 10 ns (cut-off 8 Å, the step of 2 fs). The fourth domain of MR of CD206 was simulated for 50-250 ns (cut-off 8 Å, 2-fs steps). Increase in the duration of modeling for the mannose receptor was caused by inaccuracy of the initial coordinates; in some cases, the step was decreased to 0.5-1.0 fs to avoid technical errors. All bonds containing hydrogen atoms were constrained by the algorithm SHAKE [49].
Analysis of trajectories and topological files of the complexes. Trajectories were analyzed using MMPBSA.py [50] and cpptraj [51]. Complexation energies were calculated based on the equilibrium (final) part of the trajectory within 3-5 ns at the salt concentration of 1.0 M for minimization of nonspecific E using the GB and PB methods.
Neural network analysis of complexes. The Pafnucy [1] neural network was chosen because of its leading position in the rating of algorithms predicting receptor–ligand affinities (CASF-2016). All spatial structures of the receptor–ligand complexes obtained after the MD were analyzed using the Pafnucy NNs. Structures averaged over 30 frames of the final part of the trajectory (ConA), as well as unique structures from the trajectory, minimized using 10,000 steps of the steepest descent algorithm followed by 10,000 steps of the conjugated gradient algorithm (CD206) were used as input files. A set of 30 complexes (15 per receptor) was prepared in the hdf format using prepare.py.
Two configurations of the Pafnucy neural network were used: (i) the initial NN, trained on the basis of PDBbind2016 [https://gitlab.com/cheminfIBB/pafnucy; http://www.pdbbind.org.cn/index.php]; (ii) the neural network based on the 1, with the training set on the basis of PDBbind2020, including 14,107 complexes in the general set, 5109 – validation, 226 – core set; it was prepared by the authors of this article using the pdbbind data.ipynb and scripts split_dataset.py, training.py. The training was performed with the default parameters, except for the number of cycles (epochs) equal to 25 (Fig. S1, Table S1 in the Supplement). The validation error decreased approximately to the fifth epoch, further the accuracy was optimized only for the training set.
NNs predict the value of Kd or Ki based on the analysis of 19 characteristics of the atoms: the atom type [B, C, N, O, P, S, Se, a halogen, or metal (nine variants)], hybridization and valence (three variants), bonds with heavy atoms or with heteroatoms, additional parameters (hydrophobicity, aromaticity, acceptor/donor properties, being a component of the cycle), partial charge and affiliation of the atom to the receptor (–1) or to the ligand (1).
Mathematical processing the data. Free energy values were calculated on the basis of three independent simulation cycles by averaging; for the ConA-tetramer, the calculations were carried out for four subunits and then averaged. The obtained data were normalized to the experimental data by the equation: ΔGbind = ΔGbind(init) k + b (kcal/mol). In the case of ConA: k = 0.1125 and b = 2.07 (R2 = 0.71) based on the method of Poisson–Boltzmann for MD; k = 2.1961 and b = –9.05 (R2 = 0.67) based on optimization of the neural network. The following coefficients were used for CRD4 of CD206: k = 0.0137 and b = 2.99 (R2 = 0.47) based on the method of Poisson–Boltzmann for MD; k = 0.3855 and b = 1.33 (R2 = 0.78) based on NN. The higher correlation of the NNs data on the ConA receptor was obtained using normalization of not the energies, but the constants: Kd = 8.24·Kd(init) + 10–5 (M).
RESULTS AND DISCUSSION
Energetic characteristics of ConA and CD206 domain complexation with carbohydrate ligands. To identify parameters of the ligands that increase affinity for the mannose receptors, interaction of the carbohydrates consisting of Man-, Gal-, Glc-, Fuc-, or GlcNAc-residues was modeled (Fig. 1, table, Tables S2 and S3 in the Supplement). Relevance of the values of constants and free energies determined in the course of modeling was validated by comparison with the literature data for ConA obtained by isothermal calorimetry [21] and the data for the MR domain of CD206 obtained from the shifts in the NMR spectra [52, 53] and by competitive binding (Fig. 1) [13]. As expected, the absolute values of the free energies did not match, however, a rather high correlation for in silico methods could be determined visually from the likeness of the free energy dependences (Fig. 1). Pearson’s correlation coefficients with the literature data were for ConA r = 0.82 and for CD206 r = 0.58 that was acceptable considering that the mannose receptor has been only poorly studied. Note that the data nearest to the experimental ones were the values obtained in the course of the neural network analysis of the receptor–ligand complexes after MD. CD206 practically cannot be produced in the form suitable for in vitro screening, thus, computer methods are promising for such systems.
Fig. 1.
Energy of complexation of ConA and of the CRD4 domain of the mannose receptor CD206 with carbohydrate ligands calculated using computer simulation, in comparison with the literature data [13, 20, 21, 26, 52, 53]. For ConA, the average values between the subunits are presented: T = 300 K, pH = 7. Concentration of NaCl is 1 M.
It should be noted that experimental data on the MR complexation have been described in the literature only for the limited number of ligands: the data obtained from NMR-shifts and competitive binding [13, 52, 53] for four out of 15 ligands considered in the present work. Computer simulation of CD206 or of its carbohydrate-binding domain was not performed earlier, except the work of Asciutto et al. [54] in which CysRD-CTLD2/3 (a part of MR) was studied (the domains, which do not play an important role in binding carbohydrates [55]). For the mannose receptor domain of CD206 (CRD4) we have calculated nine values of constants, which were not published earlier.
Role of MD in optimization of complex structures. Although structures from PDB were used as initial coordinates for nine ConA complexes and four CD206 complexes with ligands, computer simulation even of such systems makes it possible to significantly optimize spatial arrangement of the receptor and the ligand. The complex structures are experimentally determined using X-ray crystallographic analysis of the crystal [56]. However, this method has some limitations associated with the discrepancy between the conditions of the protein crystallization with the ligand and experiments on complexation, uncertainty of the hydrogen atom positions [57], and difference in the receptor structures in solution and in the crystal. The MD method makes it possible to overcome these disadvantages and reveal significant ligand–receptor interactions absent in the crystal [34]. The role of MD in optimization of the protein–ligand complex structure is demonstrated in Fig. 2 where the positions of trimannoside 10 in the complex with ConA by the X-ray crystallography are compared with those after the 50-ns modeling. During receptor binding, trimannose 10 (Fig. 2) interacts through the central Man-residue with Arg222 (three significant hydrogen bonds 1.8-2.3 Å). The left (α1→6) Man-residue is coordinated by the higher number of amino acids, including Asn14, Gly221 due to generation of the energy-rich hydrogen bonds of the atoms O4,5,6 (1.7-2.7 Å). The right (α1→3) Man-residue is approached to Thr15 by 0.3 Å and Asp. The more energetically advantageous position of the ligand was shown in the binding site with respect to the PDB complex (1ONA) in the course of simulation.
Fig. 2.
Search for optimal position of the ligand using molecular dynamics. Complexes ConA–trimannoside 10 are shown that are obtained from X-ray diffraction data (a) and after 50-ns molecular dynamics simulation (b). The green sphere is Ca2+.
ConA has motifs of the carbohydrate-binding domain structure, which are similar to those of CD206. Further, it is shown how the structural similarity is translated into the functional likeness. Mechanism of ligand binding by the fourth domain of MR of CD206 will be shown using the dimannose 8 interaction with the receptor as an example (Fig. S2 in the Supplement). In the initial state, the ligand does form any hydrogen bonds with amino acid residues. In the course of modeling, spatial arrangement of dimannose is optimized: the mannose residue α1 is approaching receptor, and binding occurs with the Glu107, Asn121, Hie127 residues (Fig. S2 in the Supplement). Concurrently, the residue α6 is rotated around the glycosidic bond producing additional interactions with MR. Note that when the receptor with the manually supplied ligand is used as an initial position, computational time should be increased as compared to the case of the initial PDB-structure (from 10-30 ns to 50-250 ns). From Fig. S2 of the Supplement it follows that 30 ns in the first case were insufficient for optimization of the complex structure. Not less than 100 ns of MD simulation were necessary.
Main regularities of binding of carbohydrate ligands with CRD4 of CD206 and the model lectin ConA. Based on the dissociation constants of the ligand–receptor complexes calculated using MD and NNs (table, Tables S2 and S3 in the Supplement) [58] and complexation mechanisms (Figs. 2-5 and Figs. S2-S8 in the Supplement) the following regularities can be revealed. According to the MD data, the lowest values of dissociation constants are observed for the complexes of receptors with biantennary ligands 9-11 and 15: Kd (ConA – (GlcNAc)2-triMan) = 2 µM, Kd (ConA – Fuc-α (1→3)-GlcNAc) = 3 µM. Similarly, the mannose receptor domain forms the most stable complexes with the ligands 9-11 with Kd 1080, 780, and 480 µM, respectively.
Fig. 5.
Effect of the O1 atom methylation on mannose binding by the fourth domain of the CD206 mannose receptor. a) α-D-mannose 1. b) Me-α-mannopyranoside 2. 200-ns molecular dynamics simulation.
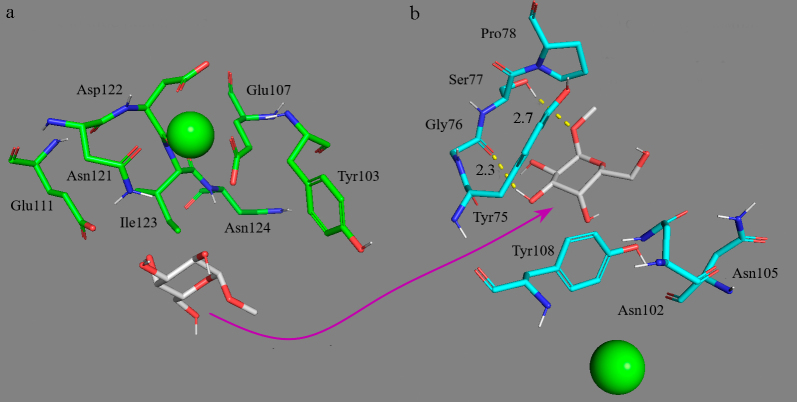
Receptor specificity to the carbohydrate residue type. According to data of the neural network analysis of the complexes, affinity of the carbohydrate residues for ConA increased in the row: (Gal≈Fuc) < (Glc≈Man) < GlcNAc, which correlated with the literature data [20, 21]. A somewhat different trend was specific for the fourth domain of MR of CD206; the affinity for ligands increased in the following row: (Glc≈Gal) < GlcNAc < (Fuc≈Man) (table). Note that the methylated derivatives of α-D-glucose 12 and galactose 13 (Fig. 3) interacted extremely weakly with MR, but associated with ConA with higher affinity (Fig. S3 in the Supplement). In the course of CD206 modeling, the ligand (12, 13) was released from the binding site and then interacted nonspecifically with the lateral amino acid residues (Fig. 3). The other ligands under study bound specifically at the carbohydrate recognition site.
Fig. 3.
Nonspecific interaction of methyl-α-D-galactopyranoside 13 (white) with the domain of the CD206 mannose receptor. a) Initial arrangement. b) Complex structure after 200-ns molecular dynamics simulation. Green sphere is Ca2+.
Affinity of receptors for ligands depending on the number of Man-residues. Carbohydrates containing only one mannopyranosyl ring (Fig. S4 in the Supplement), Man 1 and MeMan 2 (methyl-α-D-mannopyranoside) do not demonstrate high affinity for ConA, and the larger number of the terminal Man/GlcNAc-residues in the clusters are required. However, it follows from the data on calorimetric titration [21] that the affinity for ConA of the glycopeptides Man7-9, which simulate oligosaccharides of the cell wall of microorganisms, is virtually not higher than the affinity of the ligand 11 (the triMan derivative – trimannoside), i.e., there is an optimal number of carbohydrate residues involved in the binding. In other words, the model lectin ConA has the highest affinity for the conserved nucleus of trimannoside, that is, the ligand–receptor specificity limit is reached. Based on the data obtained using MD and NNs, the affinity of ligands for MR grows with increase in the number of available Man-residues in the case of CRD4, but is less pronounced. This also follows from the data obtained from the competitive binding experiments in the work of Feinberg et al. [13]: Man9 is more than the one magnitude order more specific than MeMan, whereas trimannoside is only three times more specific than MeMan. The affinity of MR for the mannose-containing ligands increases in a series starting from the ligands containing one-two residues and up to the large oligosaccharides and polymers (for instance, Man23, mannan) [15].
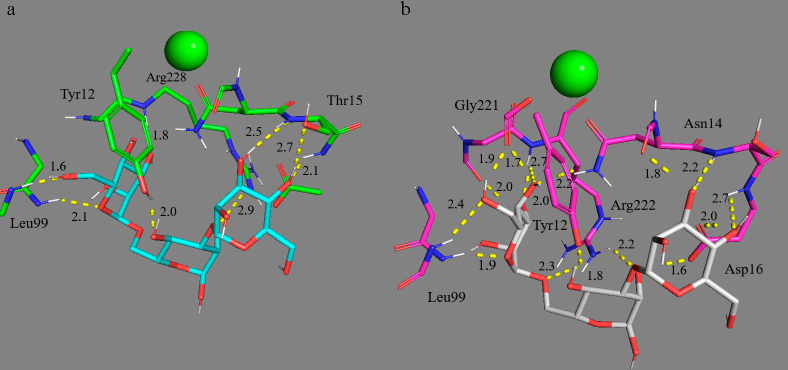
Influence of the glycoside bond type in dimannosides on the affinity to the receptor. The ConA receptor recognizes dimannosides 3-8 (Fig. 4 and Fig. S2 in the Supplement) with the affinity increasing in the row: α1→2 < α1→6 < Me-α1→6 < α1→3 << Me-α1→3 ≈ Me-α1→2, in which conventional names of dimannosides and their methylated derivatives are presented (neural network, table). Thus, the bond of Man-residues through oxygen atoms is optimal in C1 and C2/3. However, based on the complex structures, it may be concluded that in the case of α1→2 and α1→6 glycoside bond in α-D-mannopyranosyl-α-D-mannose (diMan) the effect of a fork or biantennary is achieved, i.e., binding by a larger number of atoms (Fig. 4) and involvement of two Man-residues. Common motifs in the diMan–ConA complexes are as follows: 0MA residues (terminal mannopyranosides) form hydrogen bonds with Leu99, Tyr100, Asn14, Asp208, Arg228, which are conserved in the majority of the complexes. Contribution of these interactions to free energy is as follows: Leu and Tyr – 3.95 and 2.45 kcal/mol (vdW, E, NP); Asn and Asp – 3.0 and 4.62 (E); Arg – 3.79 (P); where vdW are van der Waals and E are electrostatic interactions, P is polar solvation, and NP is nonpolar solvation. However, for the 2MA residue (Man with the α2 position for binding) there are differences in the complexes of dimannose isomers with ConA. In particular, 2MA is virtually not involved in the binding of the α1→3 isomer (Fig. 4). In the other isomers, hydrogen bonds are formed with Tyr12 (3.5 kcal/mol; E, NP), Asn14 and Thr15 (5.6 and 3.8 kcal/mol; vdW, E, NP), Asp16 (7.0 kcal/mol; E). The most energetically advantageous interactions are due to electrostatic attraction with the Asp and Asn residues. Hence, the α1→6 glycoside bond in diMan makes Man-residues accessible for the receptor and increases affinity.
Fig. 4.
Influence of the glycoside bond type on the binding of dimannose (white) by ConA (green). a) Me-α1→2-dimannopyranoside 3 – subunit A. b) Me-α1→3-dimannopyranoside 5 – subunit B. c) Me-α1→6-dimannopyranoside 8 – subunit A. Green sphere is Ca2+; 10-ns molecular dynamics simulation.
On the contrary, α1→2-dimannopyranoside became biantennary on interaction with CRD4 of CD206 (Fig. S5 in the Supplement). In this case the receptor binds the other Man-residue due to additional interaction of Lys113 (3.3 kcal/mol; vdW, E, NP) and Glu111 (4.5 kcal/mol; E). Based on the NNs data (table), the affinity of MR for dimannose 3 with α1→2 glycoside bond is virtually two orders of magnitude higher than for dimannoses 6-7 with α1→3 or α1→6.
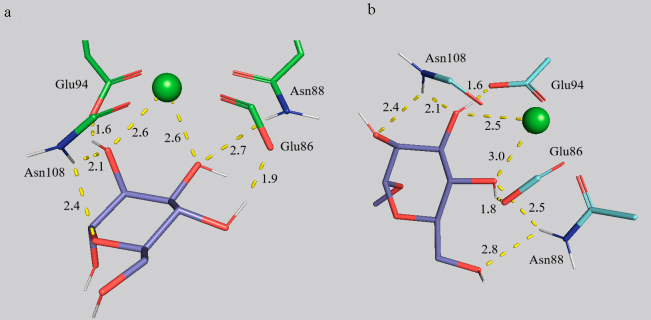
The role of CH3-group at the O1-position. Based on the MD data, methylation of OH-groups at O1-atoms of carbohydrates increases affinity for the ConA lectin (Fig. S6 in the Supplement): 2.4-fold in the case of mannose 1-2, 1.4-fold in the case of dimannose 3-4, 1.14-fold in the case of dimannose 5-6, 1.3-fold in the case of dimannose 7-8, and 2.7-fold in the case of trimannosides 9-10. A similar pattern is observed in the case of the CD206 domain (Fig. 5) for mannose and for α1→2 and α1→6 isomers of dimannose, however, methylation of the α1→3 isomer and of trimannose leads to the decrease in affinity. Thus, methyl group in the oligosaccharides prevents binding with CD206, which is in good agreement with the absence of such group in glycans of microorganisms recognizable by MR.
There is an interesting mechanism of increase in the monosaccharide affinity for MR due to introduction of a hydrophobic group and prevention of formation of hydrogen bonds with the O1-atom. The CH3-group is not directly involved in the interaction with the receptor (Fig. 5 and Fig. S6 in the Supplement), however, it reduces the possibility of interactions of the O1H-group with the receptor that leads to about 90° change in the spatial orientation of the Man-residue and, respectively, to optimization of the mannose binding by amino acid residues of CD206, including Asn108, Asn88, and Glu94; coordination by the calcium cation also changes.
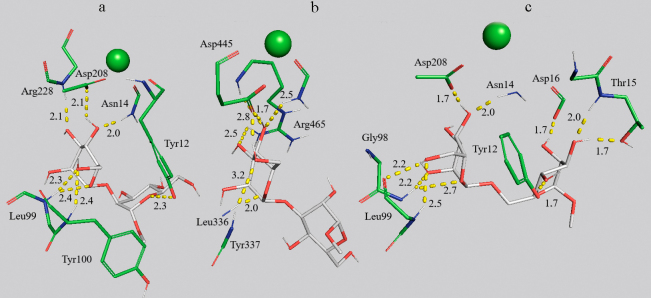
Multivalent binding of trimannosides. Trimannoside is a natural ligand of ConA, the conserved nucleus of triMan in oligosaccharides has high affinity for the receptor [20, 21]. Let us consider the binding of trimannosides 9-11 (Fig. S2 in the Supplement) with ConA: two planes of mannopyranosyl residues are perpendicular, whereas the third plane is inclined approximately at 45° angle to the central plane. In such case, the binding occurs by an “improved mechanism”: on average, 15 hydrogen bonds are formed with five-nine of them mediated additionally by water. The lectin site is enlarged: in addition to the above-mentioned residues, the following amino acid residues are involved: Asp16, Thr15, Pro13, Tyr12, Asp208. This determines the strength of the complexes with ConA.
Introduction of terminal GlcNAc-residues to triMan leads to interaction with Thr226, Glu98, Arg228, and Gly224 (Fig. S7 in the Supplement). The ligand 11 with two terminal GlcNAc residues attached through the glycoside bond β(1→2) to the trimannoside conserved nucleus, appears to be the most specific to ConA and CD206 among the presented: Kd (ConA – the ligand 11) = 2 µM; Kd (CRD4 – the ligand 11) = 480 µM.
Thermodynamic parameters of the receptor–ligand complexation. Energy decomposition. As it has been considered above, the ligand affinity for ConA and CD206 increases with increase in the number of Man- or GlcNAc-residues. Hydrogen bonds formed in the complex between the amino acid residues of the protein and the ligand are considered. The number of these bonds correlates with the interaction affinity; however, this parameter is not sufficient. It is necessary to take into account additionally vdW and E interactions, P and NP. A large number of aromatic residues (especially Tyr) in the biding sites of carbohydrates seems to promote binding due to CH–π interactions [59], for instance, in the cases of cellulose-synthase, β-galactosidase of Escherichia coli (PDB 1JZ8) [60].
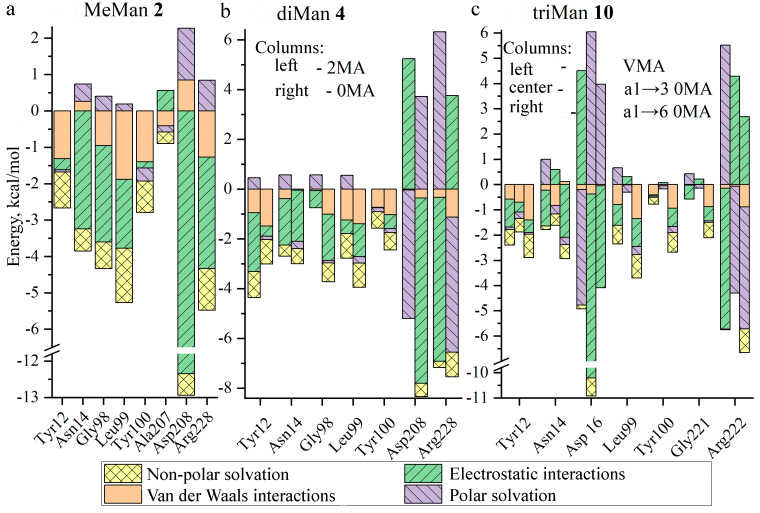
We have performed decomposition of the complexation free energy into four components indicated above for amino acid residues involved in the binding (Fig. 6).
Fig. 6.
Components of the free energy of interaction of ConA amino acid residues with the ligands MeMan 2 (a), diMan 4 (b), and MetriMan 10 (c). The values are given in kcal/mol. For the ligands 4 and 10 the decomposition is shown into the constituent Man-residues: 0MA is the terminal residue; 2MA are Man with the α2-position for binding, VMA is the central Man-residue in the trimannoside.
The largest contribution to the free energy of monosaccharide binding to ConA (Fig. 6a), is provided by electrostatic interactions (70%) of H and O atoms of the peptide bonds and the charged groups of Asp, Asn, Arg with the ligand atoms. An additional stabilization of the monosaccharide binding is due to the vdW-interactions (18%) and NP (20%). The polar solvation is an interfering factor – 8% of the energy consumption.
During the complexation the stacking-interactions (CH–π) can be realized between Tyr and the Man-residue with a contribution of 1-2 kcal/mol to the free energy. Thus, on transition from Man to diMan and triMan, each new carbohydrate residue interacts with Tyr, although with the lower thermodynamic advantage, however, the total value of the energy contribution increases from 2.3 to 4.4 kcal/mol.
As in the case of MeMan, binding of dimannose (Fig. 6b) occurs due to electrostatic interactions of the charged groups of Asp, Asn, Arg, but with lower contribution (47%), because of reduction of the total energy due to repulsion of the second residue (2MA or 0MA). Hydrophobic interactions with Tyr12, Tyr100 (including the CH-π stacking with the Man-residue planes), Leu99 become more significant.
Complexation of the biantennary trimannoside (Fig. 6c) is similar to dimannoside with regards of the energy components. In particular, binding of the carbohydrate ligands occurs essentially due to electrostatic interactions [35], which is in agreement with the observed reduced ability of ConA to bind carbohydrates at pH < 4. However, hydrophobic residues, including aromatic ones, play an important role in the increase of the affinity due to CH–π-interactions.
Displacement of water molecules. Moreover, it has been shown using GIST [61, 62] that the interaction energies of water molecules with the amino acid residues of the receptor are unfavorable, Esw = –2 kcal/(mol Å3) near to the binding site of ConA and CRD4, whereas the solvent–solvent energies are more advantageous energetically, Eww = –18 kcal/(mol·Å3). Domain orientation entropy of water decreases from 4.4 to 0.7 kcal/(mol·Å3) in the course of complexation of trimannoside 9 with the CD206 and position component increases from –139 to –102 kcal/(mol·Å3) due to redistribution of the solvent molecules. Thus, displacement of water molecules by the ligand in the course of complexation provides an additional stabilizing thermodynamic component [63, 64].
Comparison of the CD206 domain and ConA. One of purposes of the present work was to determine the limits of applicability of ConA as a model for mannose receptor. Knowledge of the similarities and differences between the receptors will make it possible to test drug delivery systems using available lectin and only after this the MRs themselves, which will simplify significantly in vitro and in vivo experiments [3, 20]. We have considered regimens of complexation, structures of binding sites, mechanisms of involvement of metal cations in the binding of carbohydrates, values of complexation energies and dissociation constants of ligand–receptor complexes, as well as the literature examples.
Similarity between the regularities of carbohydrate binding by ConA and CD206 was most convincingly confirmed by the closeness of the relative changes in the dissociation constants of the complexes (table). This makes it reasonable to use the lectin model for optimization of in vitro and in vivo experiments in order to be able to examine a larger number of ligands and testing of potential drug carriers. In particular, correlation coefficient between the free energy of complexation for the six complexes of ligands (nos. 2, 4, 6, 7, 10, 14) with CD206 and ConA described in the literature is 0.90. Rather relevant energy values were obtained in the course of modeling, moreover, high correlation between the complexes of both receptors was observed: the MD data on the CRD4 complexation correlate with the data for the neural network analysis of ConA with the coefficient r = 0.91. Thus, the observed regularities of binding of mono- and oligosaccharides have shown that ConA is a good model of the mannose receptor.
Regimens of complexation of mannose-containing ligands with receptor. ConA has a tetrameric structure, and this is what mainly differentiate it from the CD206 domain. It has been believed that all subunits of ConA interact similarly with the ligands [65], but this was called into question in the course of modeling (Table S2 in the Supplement). It may be caused by the possible interaction of the ligand with various amino acid residues and not only with the identified ones (for instance, Gly98 and Leu99 located in the binding site instead of Arg228). Such mobility of the ligands (especially of monosaccharides) is observed during the modeling within the pico- and nanosecond time scale; however, an averaged picture is observed in the in vitro experiments.
In order to explain differences in the subunits, details of the complexation mechanism should be considered. Binding of Me-Man to four subunits seems similar (Fig. S4 in the Supplement), however, in the subunits A and B there is only one hydrogen bond mediated by water, whereas in the subunit C O3 is not bound to Arg228, but there is the O2–Leu99 bond. Moreover, distances in the subunit D are mostly higher than in the other subunits, and the affinity is lower.
Differences in the mechanisms of complexation indicate existence of several regimes of binding, which are realized in the subunits A-D of ConA. The possibility of variative binding of ligands by CRD4 of CD206 has not been described in the literature, but could be likely manifested through involvement of calcium cation and definite aa in the ligand binding. It is assumed that such variability could be especially noticeable when at least several carbohydrate-binding domains (CRD4-8) are participating in the process. In the literature, a similar phenomenon has been described for the mannose-specific lectin ERGIC-53 [66] and also ConA [67]. Although all four subunits in ConA have identical amino acid composition, there are some differences in their structural organization (relative arrangement of the chains) as a result of formation of the protein quaternary structure that is responsible for the phenomena described above. Therefore, the most correct parameters can be obtained by averaging the values of the binding energies for all four subunits, because in practice all variants of binding are realized.
Comparison of structures of the CD206 domains and ConA (Fig. S8 in the Supplement). The main similarities of the structural organization of ConA and the CRD4 domain of CD206 are as follows: an approximately identical spatial arrangement of amino acids, similar amino acid composition of the binding sites of carbohydrates (two Tyr residues, Asn, Asp, Ala, Leu, Pro) that facilitates binding via energy-rich electrostatic interactions of the charged amino acids residues with additional stabilization by hydrophobic and CH–π stacking interactions; presence of Ca2+ (green sphere) is required for formation of the binding site.
Role of Ca2+ and Mn2+ cations in the binding site of the ConA and CD206 receptors (Fig. S7 in the Supplement). As it has been discussed above, presence of the metal cation in the binding site is necessary for maintaining spatial orientation of the receptor amino acid residues. In ConA, this role is played by Ca2+, which fixes the residues Asp703, Asp712, and Asp895, Asn707, Tyr705, and water (Fig. 7a). The coordinating polyhedron for calcium cation is a distorted octahedron (coordination number is 6, ionic radius is 100 pm). Moreover, positions of the amino acid residues and calcium are additionally stabilized by the Mn2+ cation, which is positioned at a distance of 4.2-4.4 Å of Ca2+. Mn2+ coordinates the residues Glu701, Asp703, and Asp712, as well two molecules of water (Fig. 7a). This facilitates formation of the high affinity binding site for the conserved nucleus of trimannoside [68-70].
Fig. 7.
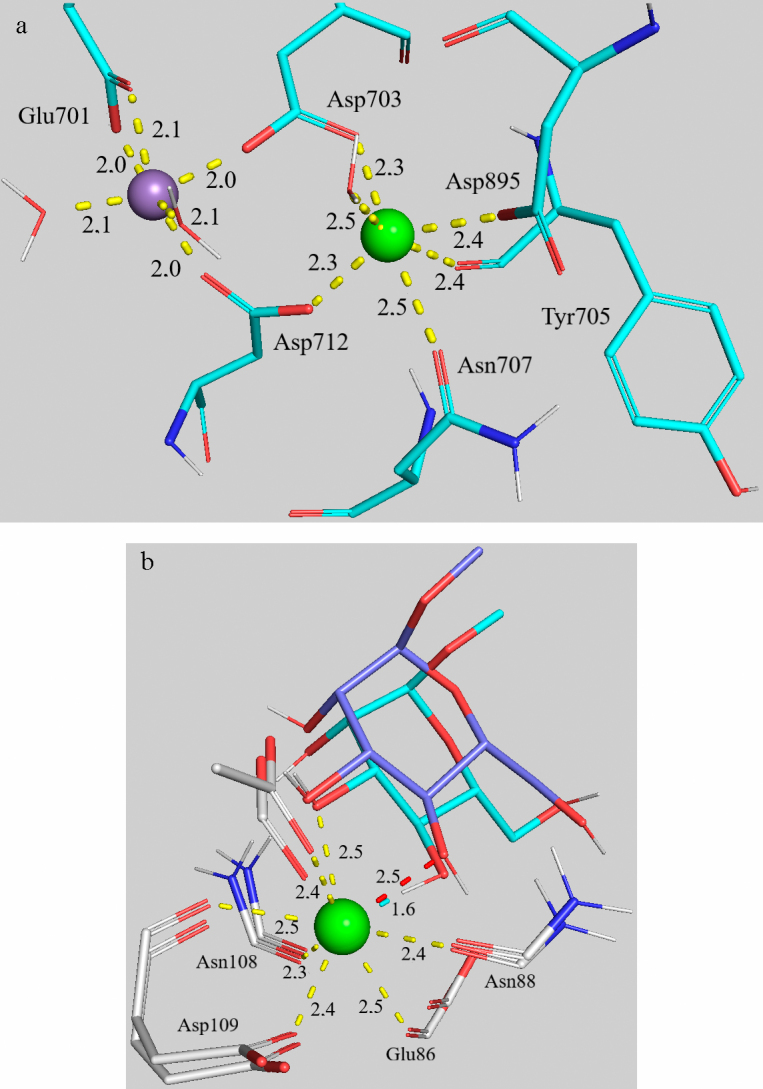
a) Coordination environment of Mn2+, Ca2+ in the binding site of ConA (subunit C) during binding trimannoside 9 (PDB Acc. No. 1ONA) according to the data of 10-ns molecular dynamics simulation. b) Coordination environment of Ca2+ in the binding site of the CD206 domain during binding methylmannoside 2 (PDB Acc. No. 7JUB). Comparison of the initial coordinates from PDB (cyan) and the structure after 100-ns molecular dynamics simulation (purple).
Specificity of the CD206 mannose receptor to Man-, Fuc-, and GlcNAc-residues in glycans is provided by the mechanism similar to the considered above for ConA. Ca2+ coordinates Asn88, Asn108, Asp109, and Glu86, but contrary to the site in ConA, in the case of CD206 it has high coordination number of 8 and ionic radius of 112 pm. Moreover, Ca2+ cation in CRD4 plays an important role in the direct binding of ligands. Interaction of methylmannoside 2 with Ca2+ is shown in Fig. 7b. Change of the calcium ion coordination by O2,3 atoms of MeMan occurred during modeling of the binding based on the initial coordinates from PDB to the average distance of 2.5 Å, which resulted in formation of the stable square antiprism (Fig. 7b).
Literature data on similarity of CRD4 and ConA. According to the literature data, CRD4 is highly similar to the mannane-binding lectin A, which, in turn, resembles ConA in the regularities of carbohydrate binding [71]. The following positive effects were observed in the in vivo and in vitro experiments using mannose-containing ligands highly specific to ConA and targeted to MR for modification of vesicles for drug delivery to macrophages [20]: absorption of the mannosylated particles by the cells [72, 73], increase in the circulation time of the drug in the blood flow and increase of its concentration in macrophages [3], biodistribution of mannosylated liposomes mainly in the lungs [74]. All these data show relevance of using ConA as a model of MR.
Present situation and prospects of using molecular dynamics and neural network analysis methods. Values of complexation energy and, respectively, of dissociation constants of receptor–ligand complexes have been calculated for 15 ligands and two receptors, ConA and CRD4 of CD206. One of them for concanavalin A and nine for the mannose receptor were not reported previously in the literature. Reliability of the obtained data is demonstrated by comparing them to the literature data. Correlation coefficients of the free energy values for ConA and CRD4 of CD206 obtained by the MD method (the mmpbsa.py analysis) are 0.68 and 0.52, respectively, that may be considered a good result taking into account the number of ligands studied and the fact that MR have not been investigated in sufficient detail.
It should be noted that the existing algorithms are far from perfect, and computer simulation seldom correlates with absolute values obtained by experimental methods. However, with development of technologies, this problem is being solved step-by-step. Neural networks are being actively improved as is obvious from results of the “CASF-2013 competitions” [75, 76]. We have chosen the Pafnucy NN because of its leading position among the algorithms for predicting the ligand–receptor affinity. However, the initial algorithm trained by the developers on the basis of PDBbind2016 displayed low accuracy when applied to the systems under consideration. Correlation coefficients of the free energy values for ConA and CRD4 of CD206 (the neural network analysis no. 1) were found to be no more than 0.50, which could be associated with inappropriate weights in the NN layers for the systems under consideration. That is why the authors of the present work prepared a training set on the basis of PDBbind2020, increasing the number of training cycles to 25 and choosing suitable coefficients (see “Materials and Methods” section, Fig. S1, and Table S1 in the Supplement). The neural network with the new parameters displayed higher prediction accuracy, which was better than the MD method: correlation coefficients of the free energy values for ConA and CRD4 of CD206 (the neural network analysis no. 2) were 0.82 and 0.8, respectively. On average, the achieved accuracy is the same as for the algorithms described in the literature [77], although, it can be increased further.
Prospects of in silico methods are wide. Improvement of NN algorithms and preparation of training sets with larger amount of relevant data on complexes will increase accuracy of the predictions as has been shown above. Using molecular dynamics with the refined force fields (amber) and increased simulation time makes it possible to determine more accurately thermodynamic values and structures of molecules, including protein–ligand complexes, under conditions close to real ones (solution, salt concentration, temperature).
Thus, the parameters of lectin–ligand interactions have been determined using molecular dynamics and artificial neural networks with consideration of model optimization. Computer methods made it possible to obtain spatial structures of ConA and CRD4 of CD206 complexes with carbohydrate ligands, majority of which were not described earlier. Moreover, the mannose receptor complexation has been studied that is very difficult to do in vitro.
CONCLUSIONS
Targeting of the drug delivery vesicles to mannose receptors of macrophages seems to be a promising strategy for increasing effectiveness of treatment of various dangerous diseases, including autoimmune, oncological, and infectious diseases. Therefore, it is necessary to create highly selective mannosylated drug carriers; optimal configuration of such agents can be elucidated using computer simulation. In the present work, computer simulation was performed of complexation of 15 carbohydrate ligands with the model tetramer ConA and the fourth domain of CD206 mannose receptor (the highest contributor to carbohydrate binding) using methods of molecular dynamics and Pafnucy artificial neural network. These ligands may be used as a targeting label on a molecule for delivery to macrophages. Artificial neural networks have been actively developing, but yet their application in biological systems is not widespread. In the present work it is shown that the neural network trained on the PDBbind2020 basis, together with the molecular dynamics simulation is an effective tool for studying mechanisms of ligand–receptor interaction. In the course of computer simulation, we have calculated dissociation constants of ligand–ConA complexes that correlate well with the literature data. Using the obtained model, complexation of the mannose receptor of CD206 with ligands was studied for the first time, moreover, we have calculated nine dissociation constants, which were not reported earlier. Similarities between ConA and the fourth domain of CD206 were shown manifested via regularities of carbohydrate binding, but some differences were also detected. The ConA lectin is highly specific to the nucleus of trimannoside and to its derivatives, whereas MR more tightly binds with branched oligosaccharides consisting of Man-residues resembling surface carbohydrates of the cell wall of microorganisms. This opens a possibility to simulate complexation of the mannose receptor of CD206 with oligo- and polymeric molecules modified by the highest affinity ligands among those considered in this work, e.g., highly mannosylated cyclodextrins and chitosans, which are promising drug carriers capable of targeting macrophages.
Electronic supplementary material
Acknowledgments
Authors are grateful sincerely to V. V. Drobot (Belozersky Institute of Physico-Chemical Biology, Faculty of Chemistry, and Research Computing Center, Lomonosov Moscow State University) for consulting and advices concerning molecular dynamics; to A. A. Vinogradov (Ph.D. Chem. Sci.) for conceptual, methodical, and stylistic proposals for improvement of the presented materials; to D. N. Zlotnikov for realizing the technical platform for performing molecular simulations and neural network analysis using the docking technique.
Abbreviations
- ConA
concanavalin A
- CRD
carbohydrate-recognizing domain
- diMan
α-D-mannopyranosyl-α-D-mannose
- E
electrostatic interactions
- Man
mannose
- MeMan
methyl-α-D-mannopyranoside
- MD
molecular dynamics
- Mϕ
macrophages
- MR
mannose receptor
- NN
neural network
- NP
nonpolar solvation
- P
polar solvation
- triMan
trimannoside
- vdW
van der Waals interactions
Ethics declarations
The authors declare no conflicts of interest. This article does not describe any research involving humans or animals as objects.
References
- 1.Stepniewska-Dziubinska M. M., Zielenkiewicz P., Siedlecki P. Development and evaluation of a deep learning model for protein–ligand binding affinity prediction. Bioinformatics. 2018;34:3666–3674. doi: 10.1093/bioinformatics/bty374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Banerjee, S., and Roy, S. (2019) Polysaccharide Installed Lipid Nanoparticles in Targeted Antituberculosis Drug Delivery Applications, in Polysaccharide Carriers for Drug Delivery, pp. 397-411, 10.1016/b978-0-08-102553-6.00014-3.
- 3.Filatova L. Y., Klyachko N. L., Kudryashova E. V. Targeted delivery of anti-tuberculosis drugs to macrophages: targeting mannose receptors. Russ. Chem. Rev. 2018;87:374–391. doi: 10.1070/rcr4740. [DOI] [Google Scholar]
- 4.Wong M. E., Jaworowski A., Hearps A. C. The HIV reservoir in monocytes and macrophages. Front. Immunol. 2019;10:1435–1450. doi: 10.3389/fimmu.2019.01435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nikitina E., Larionova I., Choinzonov E., Kzhyshkowska J. Monocytes and macrophages as viral targets and reservoirs. Int. J. Mol. Sci. 2018;19:2821–2845. doi: 10.3390/ijms19092821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tormoen G. W., Crittenden M. R., Gough M. J. Role of the immunosuppressive microenvironment in immunotherapy. Adv. Rad. Oncol. 2018;3:520–526. doi: 10.1016/j.adro.2018.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shan H., Dou W., Zhang Y., Qi M. Targeted ferritin nanoparticle encapsulating CpG oligodeoxynucleotides induces tumor-associated macrophage M2 phenotype polarization into M1 phenotype and inhibits tumor growth. Nanoscale. 2020;12:22268–22280. doi: 10.1039/d0nr04520a. [DOI] [PubMed] [Google Scholar]
- 8.Le Menn G., Neels J. Regulation of immune cell function by PPARs and the connection with metabolic and neurodegenerative diseases. Int. J. Mol. Sci. 2018;19:1575. doi: 10.3390/ijms19061575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Arora S., Dev K., Agarwal B., Das P., Syed M. A. Macrophages: Their role, activation and polarization in pulmonary diseases. Immunobiology. 2018;223:383–396. doi: 10.1016/j.imbio.2017.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lyadova I. V., Panteleev A. V. Th1 and Th17 cells in tuberculosis: Protection, pathology, and biomarkers. Med. Inflamm. 2015;2015:854507. doi: 10.1155/2015/854507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang H.-L., Zheng X.-Y., Zhu J. Th1/Th2/Th17/Treg cytokines in Guillain–Barré syndrome and experimental autoimmune neuritis. Cyt. Grow. Fact. Rev. 2013;24:443–453. doi: 10.1016/j.cytogfr.2013.05.005. [DOI] [PubMed] [Google Scholar]
- 12.Stahl P. D. The macrophage mannose receptor: Current status. Am. J. Resp. Cell Mol. Biol. 1990;2:317–318. doi: 10.1165/ajrcmb/2.4.317. [DOI] [PubMed] [Google Scholar]
- 13.Feinberg H., Jegouzo S. A. F., Lasanajak Y., Smith D. F., Drickamer K., et al. Structural analysis of carbohydrate binding by the macrophage mannose receptor CD206. J. Biol. Chem. 2021;296:100368–100385. doi: 10.1016/j.jbc.2021.100368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Feinberg H., Park-Snyder S., Kolatkar A. R., Heise C. T., Taylor M. E., et al. Structure of a C-type carbohydrate recognition domain from the macrophage mannose receptor. J. Biol. Chem. 2000;275:21539–21548. doi: 10.1074/jbc.m002366200. [DOI] [PubMed] [Google Scholar]
- 15.Taylor M. E., Drickamer K. Structural requirements for high affinity binding of complex ligands by the macrophage mannose receptor. J. Biol. Chem. 1993;268:399–404. doi: 10.1016/S0021-9258(18)54164-8. [DOI] [PubMed] [Google Scholar]
- 16.Naismith J. H., Emmerich C., Habash J., Harrop S. J., Helliwell J. R., et al. Refined structure of concanavalin A complexed with methyl α-D-mannopyranoside at 2.0 Å resolution and comparison with the saccharide-free structure. Acta Crystallogr. Sec. D Biol. Crystallogr. 1994;50:847–858. doi: 10.1107/s0907444994005287. [DOI] [PubMed] [Google Scholar]
- 17.Derewenda Z., Yariv J., Helliwell J. R., Kalb A. J., Dodson E. J., et al. The structure of the saccharide-binding site of concanavalin A. EMBO J. 1989;8:2189–2193. doi: 10.1002/j.1460-2075.1989.tb08341.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Brewer C. F., Brown R. D., Koenig S. H. Metal ion binding and conformational transitions in concanavalin A: A structure–function study. J. Biomol. Struct. Dyn. 1983;1:961–997. doi: 10.1080/07391102.1983.10507497. [DOI] [PubMed] [Google Scholar]
- 19.Kaushik S., Mohanty D., Surolia A. The role of metal ions in substrate recognition and stability of concanavalin A: A molecular dynamics study. Biophys. J. 2009;96:21–34. doi: 10.1529/biophysj.108.134601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zlotnikov I. D., Kudryashova E. V. Mannose receptors of alveolar macrophages as a target for delivery of medicines to the lungs. Russ. J. Bioorg. Chem. 2022 doi: 10.1134/S1068162022010150. [DOI] [Google Scholar]
- 21.Mandal D. K., Kishore N., Brewer C. F. Thermodynamics of lectin–carbohydrate interactions. Titration microcalorimetry measurements of the binding of N-linked carbohydrates and ovalbumin to concanavalin A. Biochemistry. 1994;33:1149–1156. doi: 10.1021/bi00171a014. [DOI] [PubMed] [Google Scholar]
- 22.Dam T. K., Roy R., Das S. K., Oscarson S., Brewer C. F. Binding of multivalent carbohydrates to concanavalin A and Dioclea grandiflora lectin. J. Biol. Chem. 2000;275:14223–14230. doi: 10.1074/jbc.275.19.14223. [DOI] [PubMed] [Google Scholar]
- 23.Landschoot A., Loontiens F. G., Bruyne C. K. Binding of manno-oligosaccharides to concanavalin A. Substitution titration with a fluorescent-indicator ligand. Eur. J. Biochem. 1980;103:307–312. doi: 10.1111/j.1432-1033.1980.tb04316.x. [DOI] [PubMed] [Google Scholar]
- 24.Zlotnikov I. D., Vanichkin D. A., Kudryashova E. V. Methods for determination of parameters of receptor–ligand interactions on the model of concanavalin A and mannosylated chitosans ‒ promising carriers for drug delivery to alveolar macrophages. Biothechnologiya. 2021;37:28–40. doi: 10.21519/0234-2758-2021-37-5-28-40. [DOI] [Google Scholar]
- 25.Le-Deygen I. M., Mamaeva P. V., Skuredina A. A., Kudryashova E. V. A spectral approach to study interaction between chitosan modified with mannose and concanavalin A for the creation of address delivery systems of antituberculosis drugs. Moscow Univ. Chem. Bull. 2020;75:213–217. doi: 10.3103/S0027131420040045. [DOI] [Google Scholar]
- 26.Goldstein, I. J., and Poretz, R. D. (1986) The Lectins Properties, Functions and Applications in Biology and Medicine, Academic Press.
- 27.Gordon S. Alternative activation of macrophages. Nat. Rev. Immunol. 2003;3:23–35. doi: 10.1038/nri978. [DOI] [PubMed] [Google Scholar]
- 28.Sharma A., Porterfield J. E., Smith E., Sharma R., Kannan S., et al. Effect of mannose targeting of hydroxyl PAMAM dendrimers on cellular and organ biodistribution in a neonatal brain injury model. J. Control. Rel. 2018;283:175–189. doi: 10.1016/j.jconrel.2018.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tran D. P., Kitao A. Dissociation process of MDM2/p53 complex investigated by parallel cascade selection molecular dynamics and Markov state model. J. Phys. Chem. B. 2019;123:2469–2478. doi: 10.1021/acs.jpcb.8b10309. [DOI] [PubMed] [Google Scholar]
- 30.Hollingsworth S. A., Nguyen B. D., Chreifi G., Arce A. P., Poulos T. L. Insights into the dynamics and dissociation mechanism of a protein redox complex using molecular dynamics. J. Chem. Inf. Model. 2017;57:2344–2350. doi: 10.1021/acs.jcim.7b00421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tran D. P., Takemura K., Kuwata K., Kitao A. Protein–ligand dissociation simulated by parallel cascade selection molecular dynamics. J. Chem. Theory Comput. 2017;14:404–417. doi: 10.1021/acs.jctc.7b00504. [DOI] [PubMed] [Google Scholar]
- 32.Mollica L., Decherchi S., Zia S. R., Gaspari R., Cavalli A., et al. Kinetics of protein-ligand unbinding via smoothed potential molecular dynamics simulations. Sci. Rep. 2015;5:11539. doi: 10.1038/srep11539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fu Y., Zhao J., Chen Z. Insights into the molecular mechanisms of protein–ligand interactions by molecular docking and molecular dynamics simulation: a case of oligopeptide binding protein. Comput. Math. Meth. Med. 2018;2018:1–12. doi: 10.1155/2018/3502514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bradbrook G. M., Gleichmann T., Harrop S. J., Habash J., Raftery J., et al. X-Ray and molecular dynamics studies of concanavalin-A glucoside and mannoside complexes relating structure to thermodynamics of binding. J. Chem. Soc. Faraday Trans. 1998;94:1603–1611. doi: 10.1039/a800429c. [DOI] [Google Scholar]
- 35.Bryce R. A., Hillier I. H., Naismith J. H. Carbohydrate–protein recognition: Molecular dynamics simulations and free energy analysis of oligosaccharide binding to concanavalin A. Biophys. J. 2001;81:1373–1388. doi: 10.1016/s0006-3495(01)75793-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Arcon J. P., Defelipe L. A., Modenutti C. P., Lopez E. D., Alvarez-Garcia D., et al. Molecular dynamics in mixed solvents reveals protein–ligand interactions, improves docking, and allows accurate binding free energy predictions. J. Chem. Inf. Model. 2017;57:846–863. doi: 10.1021/acs.jcim.6b00678. [DOI] [PubMed] [Google Scholar]
- 37.Zacharias M. Rapid protein–ligand docking using soft modes from molecular dynamics simulations to account for protein deformability: binding of FK506 to FKBP. Prot. Str. Fun. Bioinf. 2004;54:759–767. doi: 10.1002/prot.10637. [DOI] [PubMed] [Google Scholar]
- 38.Mollica L., Theret I., Antoine M., Perron-Sierra F., Charton Y., et al. Molecular dynamics simulations and kinetic measurements to estimate and predict protein–ligand residence times. J. Med. Chem. 2016;59:7167–7176. doi: 10.1021/acs.jmedchem.6b00632. [DOI] [PubMed] [Google Scholar]
- 39.Wang S., Liu D., Ding M., Du Z., Zhong Y., et al. SE-OnionNet: a convolution neural network for protein–ligand binding affinity prediction. Front. Gen. 2021;11:607824. doi: 10.3389/fgene.2020.607824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Durrant J. D., McCammon J. A. NNScore 2.0: A neural-network receptor–ligand scoring function. J. Chem. Inf. Model. 2011;51:2897–2903. doi: 10.1021/ci2003889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lahey S.-L. J., Rowley C. N. Simulating protein–ligand binding with neural network potentials. Chem. Sci. 2020;11:2362–2368. doi: 10.1039/c9sc06017k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhou Y., Wang F., Tang J., Nussinov R., Cheng F. Artificial intelligence in COVID-19 drug repurposing. Lanc. Dig. Heal. 2020;2:667–676. doi: 10.1016/s2589-7500(20)30192-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pham T.-H., Qiu Y., Zeng J., Xie L., Zhang P. A deep learning framework for high-throughput mechanism-driven phenotype compound screening and its application to COVID-19 drug repurposing. Nat. Mach. Intel. 2021;3:247–257. doi: 10.1038/s42256-020-00285-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kniga A. E., Polyakov I. V., Nemukhin A. V. In silico determination of the specificity of neoantigen-reactive T-lymphocytes. Biomed. Khimiya. 2021;67:251–258. doi: 10.18097/pbmc20216703251. [DOI] [PubMed] [Google Scholar]
- 45.Manasaryan G., Suplatov D., Pushkarev S., Drobot V., Kuimov A., et al. Bioinformatic analysis of the nicotinamide binding site in Poly(ADP-ribose) polymerase family proteins. Cancers. 2021;13:1201. doi: 10.3390/cancers13061201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Timonina D., Sharapova Y., Švedas V., Suplatov D. Bioinformatic analysis of subfamily-specific regions in 3D-structures of homologs to study functional diversity and conformational plasticity in protein superfamilies. Comput. Struct. Biotech. J. 2021;19:1302–1311. doi: 10.1016/j.csbj.2021.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Case, D. A., Aktulga, H. M., Belfon, K., Ben-Shalom, I. Y., Brozell, S. R., et al. (2021) Amber 2021: Reference Manual, University of California, San Francisco.
- 48.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- 49.Ryckaert J. P., Ciccotti G., Berendsen H. J. C. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–334. doi: 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- 50.Miller B. R., McGee T. D., Swails J. M., Homeyer N., Gohlke H., et al. MMPBSA.py: An efficient program for end-state free energy calculations. J. Chem. Theory Comput. 2012;8:3314–3321. doi: 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- 51.Roe D. R., Cheatham T. E. PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013;9:3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- 52.Hitchen P. G., Mullin N. P., Taylor M. E. Orientation of sugars bound to the principal C-type carbohydrate-recognition domain of the macrophage mannose receptor. Biochem. J. 1998;333:601–608. doi: 10.1042/bj3330601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mullin N. P., Hitchen P. G., Taylor M. E. Mechanism of Ca2+ and monosaccharide binding to a C-type carbohydrate-recognition domain of the macrophage mannose receptor. J. Biol. Chem. 1997;272:5668–5681. doi: 10.1074/jbc.272.9.5668. [DOI] [PubMed] [Google Scholar]
- 54.Asciutto E. K., Kopanchuk S., Lepland A., Simón-Gracia L., Aleman C., et al. A phage display-derived peptide binds to human CD206 and modeling reveals a new binding site in the receptor. J. Phys. Chem. B. 2019;123:1973–1982. doi: 10.1021/acs.jpcb.8b11876. [DOI] [PubMed] [Google Scholar]
- 55.Taylor M. E., Bezouska K., Drickamer K. Contribution to ligand binding by multiple carbohydrate-recognition domains in the macrophage mannose receptor. J. Biol. Chem. 1992;267:1719–1726. doi: 10.1016/S0021-9258(18)46005-X. [DOI] [PubMed] [Google Scholar]
- 56.Berman H. M., Battistuz T., Bhat T. N., Bluhm W. F., Bourne P. E., et al. The protein data bank. Acta Cryst. Sect. D Biol. Cryst. 2002;58:899–907. doi: 10.1107/s0907444902003451. [DOI] [PubMed] [Google Scholar]
- 57.Böhm, H. J., and Schneider, G. (2003) Protein–Ligand Interactions, in Methods and Principles in Medicinal Chemistry, pp. 3-20, 10.1002/3527601813.
- 58.Huang K., Luo S., Cong Y., Zhong S., Zhang J. Z. H., et al. Accurate free energy estimator: Based on MM/PBSA combined with interaction entropy for protein–ligand binding affinity. Nanoscale. 2020;12:10737–10750. doi: 10.1039/c9nr10638c. [DOI] [PubMed] [Google Scholar]
- 59.Spiwok V. CH/π interactions in carbohydrate recognition. Molecules. 2017;22:1038. doi: 10.3390/molecules22071038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Spiwok V., Lipovova P., Skalova T., Buchtelova E., Hasek J., et al. Role of CH/π interactions in substrate binding by Escherichia coli β-galactosidase. Carb. Res. 2004;339:2275–2280. doi: 10.1016/j.carres.2004.06.016. [DOI] [PubMed] [Google Scholar]
- 61.Lazaridis T. Inhomogeneous fluid approach to solvation thermodynamics. 1. Theory. J. Phys. Chem. B. 1998;102:3531–3541. doi: 10.1021/jp9723574. [DOI] [Google Scholar]
- 62.Nguyen C. N., Young T. K., Gilson M. K. Grid inhomogeneous solvation theory: hydration structure and thermodynamics of the miniature receptor cucurbit[7]uril. J. Chem. Phys. 2012;137:044101. doi: 10.1063/1.4733951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hüfner-Wulsdorf T., Klebe G. Protein–ligand complex solvation thermodynamics: Development, parameterization, and testing of GIST-based solvent functionals. J. Chem. Inf. Model. 2020;60:1409–1423. doi: 10.1021/acs.jcim.9b01109. [DOI] [PubMed] [Google Scholar]
- 64.Ramsey S., Nguyen C., Salomon-Ferrer R., Walker R. C., Gilson M. K., et al. Solvation thermodynamic mapping of molecular surfaces in AmberTools: GIST. J. Comp. Chem. 2016;37:2029–2037. doi: 10.1002/jcc.24417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Dimick S. M., Powell S. C., McMahon S. A., Moothoo D. N., Naismith J. H., et al. On the meaning of affinity: Cluster glycoside effects and concanavalin A. J. Am. Chem. Soc. 1999;121:10286–10296. doi: 10.1021/ja991729e. [DOI] [Google Scholar]
- 66.Satoh T., Suzuki K., Yamaguchi T., Kato K. Structural basis for disparate sugar-binding specificities in the homologous cargo receptors ERGIC-53 and VIP36. PLoS One. 2014;9:87963. doi: 10.1371/journal.pone.0087963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Moothoo D. N., Canan B., Field R. A., Naismith J. H. Man α1-2 Man α-OMe-concanavalin A complex reveals a balance of forces involved in carbohydrate recognition. Glycobiology. 1999;9:539–545. doi: 10.1093/glycob/9.6.539. [DOI] [PubMed] [Google Scholar]
- 68.Naismith J. H., Field R. A. Structural basis of trimannoside recognition by concanavalin A. J. Biol. Chem. 1996;271:972–976. doi: 10.1074/jbc.271.2.972. [DOI] [PubMed] [Google Scholar]
- 69.Gupta D., Dam T. K., Oscarson S., Brewer C. F. Thermodynamics of lectin–carbohydrate interactions. J. Biol. Chem. 1997;272:6388–6392. doi: 10.1074/jbc.272.10.6388. [DOI] [PubMed] [Google Scholar]
- 70.Mandal D. K., Bhattacharyya L., Koenig S. H., Brown R. D., Oscarson S., et al. Studies of the binding specificity of concanavalin A. Nature of the extended binding site for asparagine-linked carbohydrates. Biochemistry. 1994;33:1157–1162. doi: 10.1021/bi00171a015. [DOI] [PubMed] [Google Scholar]
- 71.Weis W. I., Drickamer K. Structural basis of lectin-carbohydrate recognition. Annu. Rev. Biochem. 1996;65:441–473. doi: 10.1146/annurev.bi.65.070196.002301. [DOI] [PubMed] [Google Scholar]
- 72.Ghotbi Z., Haddadi A., Hamdy S., Hung R. W., Samuel J., et al. Active targeting of dendritic cells with mannan-decorated PLGA nanoparticles. J. Drug Target. 2010;19:281–292. doi: 10.3109/1061186X.2010.499463. [DOI] [PubMed] [Google Scholar]
- 73.Chen P., Zhang X., Jia L., Prud’homme R. K., Szekely Z., et al. Optimal structural design of mannosylated nanocarriers for macrophage targeting. J. Control. Rel. 2014;194:341–349. doi: 10.1016/j.jconrel.2014.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Nimje N., Agarwal A., Saraogi G. K., Lariya N., Rai G., et al. Mannosylated nanoparticulate carriers of rifabutin for alveolar targeting. J. Drug Target. 2009;17:777–787. doi: 10.3109/10611860903115308. [DOI] [PubMed] [Google Scholar]
- 75.Li Y., Liu Z., Li J., Wang R. Comparative assessment of scoring functions on an updated benchmark: 1. Compilation of the test set. J. Chem. Inf. Model. 2014;54:1700–1716. doi: 10.1021/ci500080q. [DOI] [PubMed] [Google Scholar]
- 76.Li Y., Han L., Liu Z., Wang R. Comparative assessment of scoring functions on an updated benchmark: 2. Evaluation methods and general results. J. Chem. Inf. Model. 2014;54:1717–1736. doi: 10.1021/ci500081m. [DOI] [PubMed] [Google Scholar]
- 77.Nguyen D. D., Xiao T., Wang M., Wei G.-W. Rigidity strengthening: A mechanism for protein–ligand binding. J. Chem. Inf. Model. 2017;57:1715–1721. doi: 10.1021/acs.jcim.7b00226. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.