Schools opening and Covid-19 diffusion: Evidence from geolocalized microdata

Abstract

Are schools triggering the diffusion of the Covid-19? This question is at the core of an extensive debate about the social and long-run costs of stopping the economic activity and human capital accumulation from reducing the contagion. In principle, many confounding factors, such as climate, health system treatment, and other forms of restrictions, may impede disentangling the link between schooling and Covid-19 cases when focusing on a country or regional-level data. This work sheds light on the potential impact of school opening on the upsurge of contagion by combining a weekly panel of geocoded Covid-19 cases in Sicilian census areas with a unique set of school data. The identification of the effect takes advantage of both a spatial and time-variation in school opening, stemming from the flexibility in opening dates determined by a Regional Decree, and by the occurrence of a national referendum, which pulled a set of poll-station schools towards opening earlier or later September 24th. The analysis finds that census areas where schools opened earlier observed a significant and positive increase in the growth rate of Covid-19 cases between 2.5–3.7%. This result is consistent across several specifications, including accounting for several determinants of school opening, such as the number of temporary teachers, Covid-19 cases in August, and pupils with special needs. Finally, the analysis finds lower effects in more densely populated areas, on younger population, and on smaller class size. The results imply that school reopening generated an increase of one third in cases.

1. Introduction

Since last October, a harsh second wave of the Covid-19 pandemic has been hitting many countries’ economic, health, and educational systems. A major challenge for policymakers is to understand the role of these sectors on the diffusion process of Covid-19. With an estimated drop in GDP spanning between 14.7 and 32.9 percent in the EU and the US (e.g., Chudik et al., 2020), identifying and calibrating a set of policies that still avoid large scale shutdowns while minimizing the levels of contagion is vital.

Among the set of early actions policymakers undertook was to implement school closures since children are often considered a major source of contagion. Fig. 1 shows the time pattern of smoothed new Covid-19 cases, weighted by millions of inhabitants for 6 OECD countries, and the first day of school opening registered in each country.1 The evidence appears to be mixed: while the cases increased after mid-September occurred in all the countries, the first day of school varies sensibly, with countries that started schools earlier as Germany and others where the increase in cases and school opening was almost concomitant, such as Italy and Spain.

Fig. 1.

Covid-19 cases and school opening by countries.

However, the efficacy of school closures has been the subject of intense debate in policy and academic circles. The difficulty of reaching a consensus about the role of school on Covid-19 diffusion is multifold. First, when the pandemic hit the world in the early months of 2020, the knowledge of health professionals about the new disease was limited, and governments were unprepared to deal with a pandemic that constitutes an unprecedented shock for the world, at least in the modern era. As a result, the first phase of intervention has focused on reducing the health cost of the diffusion by implementing strict lockdowns, including shutting down the face-to-face classes without a precise estimate of the impact of these policies on Covid-19 diffusion. Second, the symptomatology of Covid-19 itself may hinder a proper identification of the virus among children, as these are more often asymptomatic and thus less likely to get tested. Third, drawing conclusions from extant studies on similar diseases may not help to find a solution. One reason is that while the literature on the role of schools on the diffusion of influenza is large, the wide availability of influenza vaccines may impede direct comparisons with the case of Covid-19, for which vaccines have just started to be available to special groups. Another reason for the inability of influenza studies to provide helpful information on SARS-type viruses like Covid-19 and common influenza is due to their differences in incubation and serial periods that determine the speed of transmission of the viruses.2

This article investigates the role of schooling in the diffusion of Covid-19 by exploiting exogenous variation in school opening dates from a quasi natural experiment using Italian microdata from Sicily. We take advantage of the spatial variation in the opening of schools due to a sudden change in regulation from the Regional Government and the occurrence of a national referendum, held on September 20th–21st. Since some schools were used as polling stations, the school opening date varied up to one month after the planned official opening date, generating granular space–time heterogeneity, which allows to identify the differential effect of school opening on the diffusion of Covid-19.

Our paper contributes to the current literature in several ways. First, our study is instrumental to the literature on the present and future social costs of closing schools. Some recent works show as these costs may be huge from the side of human capital losses. A recent macro study at country levels from Psacharopoulos et al. (2020) estimates a loss of 8% in future earnings that match a similar loss in aggregate human capital. Other studies with microdata on school data achievement (but without Covid-19 data) show similar evidence. Engzell et al. (2020) find a loss in learning equal to about 3%, measured through the final tests conducted in Dutch primary schools right after the first wave and lockdown of Covid-19. Agostinelli et al. (2020) examine the effects of school closures during the Covid-19 pandemic on children’s education by considering the interaction of schools, peers, and parents. Using the Add Health data, they find that school closures have an asymmetric, large and persistent effect on educational outcomes, leading to higher educational inequality.

Second, more directly, this work deals with the effects of school opening as a trigger of Covid-19 increases. A growing strand of literature has started to address this relationship using various approaches and levels of time and space definition. One approach is based on direct comparisons between cases within the school system with respect to the general population. On this line of work, the survey of Lewis (2020) and the work of Oster (2020) suggest low rates of contagion in US schools, contingent on students’ participation in the survey. Similarly, Buonsenso et al. (2020) study total infections in Italian schools and find that less than 2% of schools show infections on October 5th. Sebastiani and Palú (2020) find an upward trend of Italian cases a few weeks after the school openings. Another approach exploits the differences in the timing of school opening. For example, Isphording et al. (2021) find no evidence on schools as triggers of Covid-19 upsurge when looking at the time discontinuity in schools opening among German landers. For the Italian case, Lattanzio (2020) exploits the differences in school reopening among Italian regions and finds a positive relationship between earlier opening and regional variation in total Covid-19 cases.

The aforementioned approaches are likely to provide results subject to several biases. One potential source of bias are the students themselves, as these are more likely to be asymptomatic than the older population. Therefore, one may argue that the number of cases tested and detected is much lower than the remaining population.3 Students may act as triggers of contagion within their households or social network, and this may be likely to reduce the difference between treated (students) and controls (population) while increasing the overall level of contagion.

Another concern is that analyzes based on aggregated data at the regional level are unable to account for idiosyncratic elements, such as the heterogeneity in testing or healthcare management or other related factors. More precisely, the starting date at the regional level is based on a political decision, which may depend on the level of Covid-19 at the time of the decision and the number of cases in the relevant territory or among the employees. Not accounting for these factors would result in identifying spurious relationships driven by other hidden effects such as bureaucratic efficiency. Furthermore, the decision of opening schools may be delayed by school managers according to a set of local regulations, or when schools are seats of polling stations during elections in the early stage of a school year. Age groups analyzes are very likely to suffer from the young population bias due to the absence of a true counterfactual group. Unfortunately, some of these issues remain unsolved when comparing different policies at the national level, which are often unable to capture the local level volatility of their implementation.4 .

A recent literature has started to use more disaggregated county data for the US and gave evidence of the effect of schooling reopening on Covid-19 cases such as Chernozhukov et al. (2021a) that found an effect between 4 and 6% and Goldhaber et al. (2021). At the same time, this is broadly confirmed by Vlachos et al. (2021) that found an effect of 1.5% on a sample of Swedish students and teachers’ families.

Within this field, our study has two major advantages: we use low-level granularity data (census/bloc level) so that we are not subject to the above limitations regarding the use of country, region data and we exploit a variability in the opening of the schools due to the national referendum (that is not present by using county-level data).

The present work also contributes to the recent literature on Covid-19 and the educational sector by shedding light on the role of schools opening on the recent upsurge of Covid-19 cases at the local level. The analysis employs a unique panel data of Covid-19 cases geocoded at census area level for the region Sicily, consisting of blocks of about 150 inhabitants. These data are merged with granular geocoded data on school opening dates, collected from the online official documents (Circolare) and communication to parents of each of the 4,223 public schools in Sicily. The identification is based on space and time variation of school openings while controlling for unobserved time-invariant heterogeneity, time dummies, and the lagged level of Covid-19 cases in the same census area. Spatially, this work combines Covid-19 data at census area level with date of opening of the schools within 1 km, as this is the average travel distance of students up to the secondary schools.

The results suggest that census areas anticipating school opening observed a strongly significant differential positive effect on Covid-19 cases, ranging between 2.5–3.7% in the specifications for the cases of the whole population. The effect is lower for the population under 19 years, supporting the asymptomatic hypothesis of the young cohort of the population, while it is higher for the remaining cohorts. Also, the effect appears larger for areas with schools holding larger class sizes and less densely populated census areas, where schools are likely to represent the primary source of social interactions. Finally, using the estimated coefficients, the final part of the article presents a set of alternative scenarios offering the magnitude of decrease in cases if the school would not have reopened or if contacts within the schools would have contained more.

The work is organized as follows. Section 2 provides background information about the Covid-19 diffusion in Sicily and Section 3 describes the data. Section 4 specifies the econometric model, Section 5 presents the results, and Section 6 concludes.

2. Background: Covid-19 diffusion in Sicily

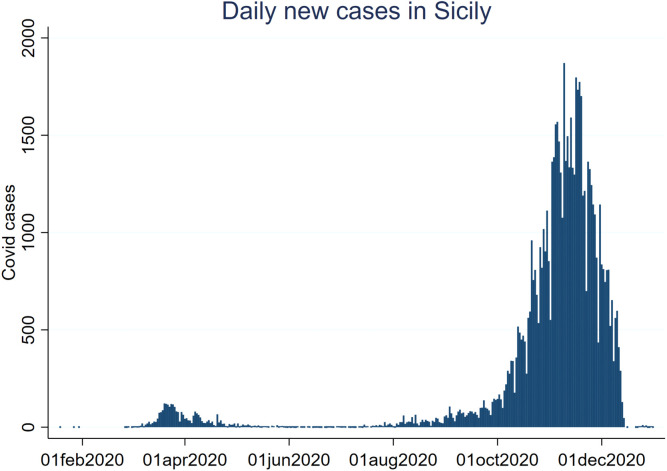
This analysis relies on data from Istituto Superiore di Sanità (ISS) (2020) collected and provided, on a daily basis, by the Sicilian Region. These contain anonymized information on daily new cases, age sex of the individual, and a dummy whether they are linked to the educational sector.5 Sicily was just marginally affected by the first Covid-19 wave of February–May 2020, with only 2,735 positive cases registered between February and May, a level much lower than the rest of Italy. From the end of September onward, the pattern of diffusion increased substantially, becoming most similar to the other most affected regions in Italy. The cases reach a peak of 1,871 new cases on November 9th, equal to about 68 percent of all the Sicilian cases during the first wave of Covid-19 (see Fig. 2). The increase observed in late September may have many explanations. On one side, national public opinion has pointed to the decrease in restrictions and enforcement of controls that occurred during summer, implemented to save the tourist season, which in Sicily represents one of the major industries. On the other side, the timing of the increase has been aligned with school opening, suggesting the salient role of school in the diffusion of COVID-19. Finally, seasonality may have determined an increase in Covid-19 cases, which as other coronaviruses proliferate in colder environments as summarized in Carlson et al. (2020).

Fig. 2.

New daily Covid-19 cases in Sicily.

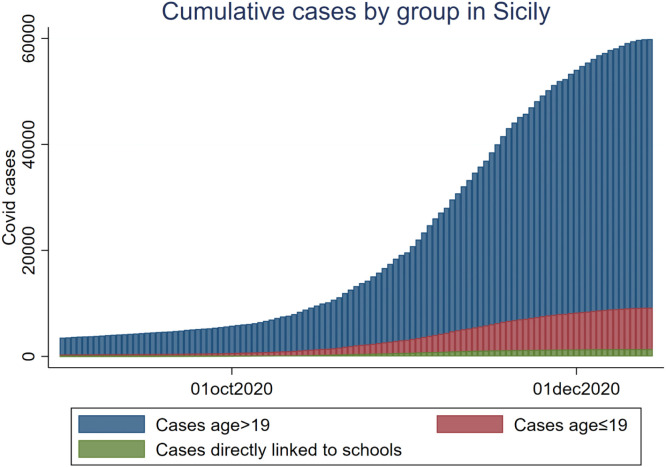
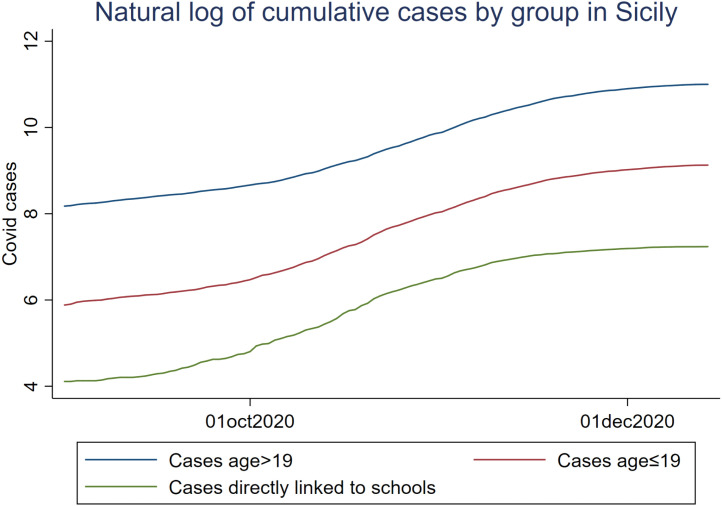
According to the data, the total cumulative cases December 14th are more than 70,000, but some consist of individuals with residence outside Sicily, such as tourists and commuters, who are excluded from geocoding. The total cases of residents on the island are about 69,107 cases, a number that is considered per capita is in line with the rest of the Southern regions and about half of the average in the Northern ones. Fig. 3 reports the cumulative cases from September 1st onwards and suggest that, out of all the resident cases, 59,899 are people aged 20 or above, while the remaining 9,208 are 19 or younger. School-related cases are 1,391, all of them from September 1st onward since this information has been collected only starting from this date. Despite the differences in the cumulative trend, the cumulative growth of cases remains quite similar across the groups, as shown by Fig. A.1 in Appendix.

Fig. 3.

Cumulative cases by group from September onwards.

Fig. A.1.

Natural log of cumulative cases by group from September onwards.

In terms of diffusion of the virus, at the regional level, the weekly Rt reproduction index slightly increases by 0.4 points from late August until early October, passing from 0.82 on August 24th–30th, up to 1.22 on September 28th–October 4th (Istituto Superiore di Sanità (ISS), 2020).6 Despite the growth of cases shows an upward trend in concomitance with the opening of the school, and this evidence needs to be taken with caution because of all the aforementioned challenges in identification. An additional confounding factor may derive from a dramatic change in testing in September, which may have determined an increase in the positive cases spotted in concomitance with school opening. As Fig. 4 shows, this does not seem to hold for the case of Sicily: while the growth rate of cases has increased sharply from September onwards, the growth rate of tests has remained constant, pointing to an increase in the share of positive found per number of tests.7

Fig. 4.

Growth rate of Covid-19 cases and testing.

This evidence indicates that keeping everything else constant, the number of cases increased after September. Also, this suggests that any result from the present analysis is robust to sudden changes in the number of tests.

3. Data

The analysis involves unique panel data at the census area level for August 1st–December 14th, obtained by merging daily Covid-19 cases in Sicily in each area with information on public school opening for the school year 2020–21. Sicily counts about 36,681 census areas, but we keep just the areas hosting at least one inhabitant, according to the 2011 official census of the National Statistical Office (ISTAT). For this reason, our unit of observations is 33,184 census areas observed for 20 weeks. Since the baseline specification includes the 4th lag of the Covid-cases, the number of time observations for each unit reduces to 16 weeks, which determines the final number of the unit by time observations, equal to 530,944. According to the 2011 National Census conducted by the Istituto Nazionale di Statistica (ISTAT) (2020a), each census area contains on average 152 and a maximum of 3,036 residents. These units have a median area of 0.13 km${}^2$ for inhabited zones, for an average population density of about 714.71 inhabitants/km${}^2$.8

3.1. Covid data

Our dependent variable is the geolocalized change in the log of weekly Covid-19 cases at the census area obtained from Istituto Superiore di Sanità (ISS) (2020), the office monitoring the Covid-19 pandemic.9 Our choice to aggregate the data at the weekly frequency follows the standard practice in the literature to account for the serial time of infection that is 7 days (e.g., Cereda et al., 2020).

In particular, selecting seven days accounts for the incubation time, which takes about five days, and the additional time to conduct the testing and receive the results. To account for the dynamic evolution of contagion at the census area level, the empirical specification will include the lag of the change in the log of the Covid-19 cases in the same census area and the second, third, and fourth lag of the level of Covid-19 cases in the census area following the recent literature on this (Chernozhukov et al., 2021a, Chernozhukov et al., 2021b). To keep the zero-valued observation, we add one before taking the log of each observation.10

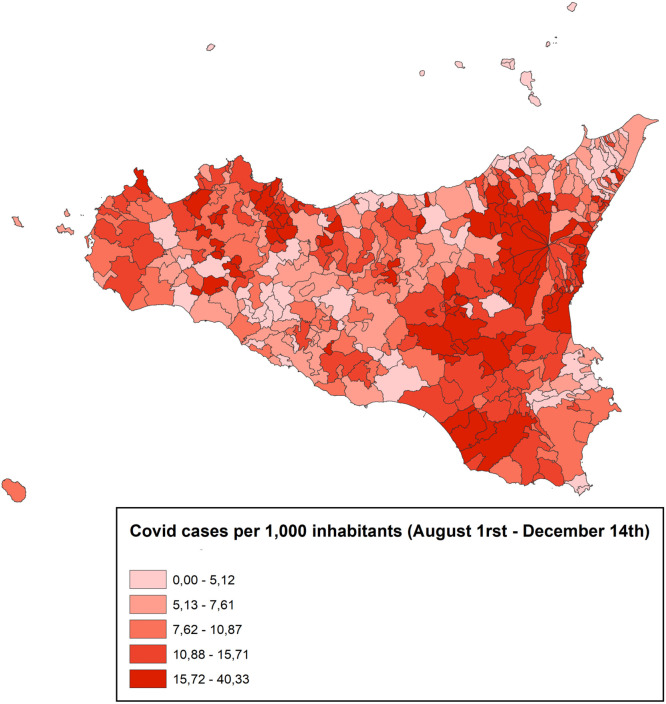
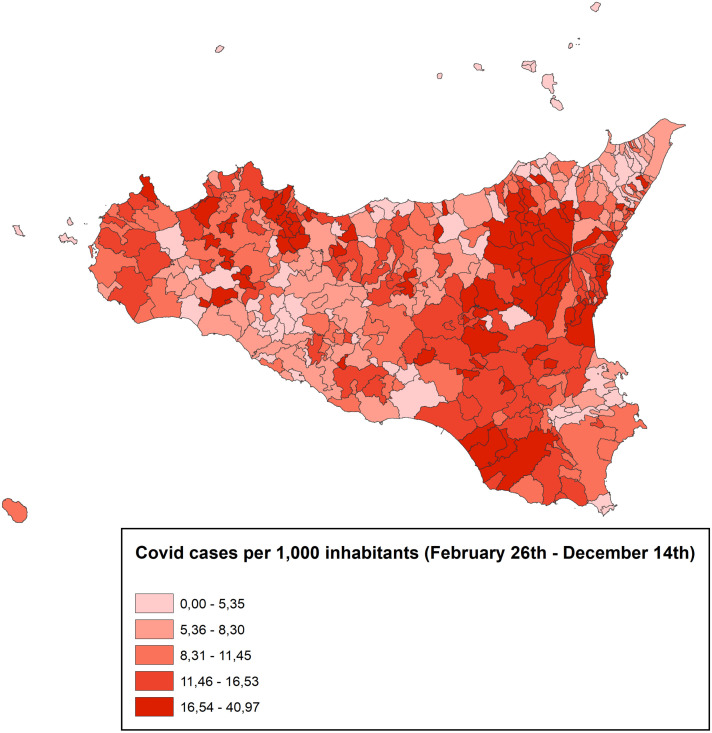
Using these population data, Fig. 5 reports the quintile map of cumulative Covid-19 cases overpopulation at the municipality level for August 1st–December 14th. While using the municipality level helps to evidence eventual spatial clusters within Sicily, in the analytical part, the unit of analysis remains the census areas, which are in a magnitude order of 1:100 with respect to municipalities. The most densely populated municipalities, including Palermo in the north-west, Catania on the east, and Siracusa in the south-east, observe the highest rate of Covid-19 cases per 1,000 inhabitants, spanning between 15.72 and 40.33 for the period under consideration.11 Fig. A.3 in the Appendix offers a disaggregated picture of the unit of analysis and the dependent variable by visualizing Covid-19 cases at the census-area level for Palermo, measured around the peak of cases.

Fig. 5.

Cumulative cases at December 14th at commune level.

Fig. A.3.

Cumulative cases by population at 2011 at October 15th: census areas of Palermo.

Weekly indicators at census areas are then merged to dates on school opening, the precise school location, which is obtained by extracting the latitude and longitude of the school official address.

3.2. Construction of the indicator on public school opening

Our key explanatory variable is the indicator of public school opening. We construct this variable using the information on the particular initial day of the 2020–21 school year for 4,223 public schools in Sicily listed both in the official school list of the Ministry of Education and in the one of the Regional Department of Education. The analysis gathered this information from all the schools’ public documents, including official communication to parents and internal directives (“Circolari”). From the end of August onwards, school managers are obliged to communicate to the public the precise date of the school reopening in September.12

The 2020–21 school opening in Sicily shows a huge degree of unforeseen variability due to a set of unexpected events linked to Covid-19 diffusion combined with a national referendum. With a first decree dated August 20th, the Regional Government of Sicily has determined that public schools, from primary onwards, could have started the school year on September 14th, with the only exception of those that were polling stations for the national referendum of September 20th–21st, which had the option to start from September 24th.13

How many polling station schools had the option to open later? Since an official regional dataset of polling station schools is not publicly available, we collected information for the four major municipalities, Palermo, Catania, Messina, and Siracusa, hosting about 26.4% of the regional population. In this subsample, the polling stations in schools are 40.3%, or 357 out of 886. A few days before the official opening, on August 31st, Sicily allowed all the public schools, including the non-polling station ones, to set up their schedule with a second decree. This decree included the possibility of opening even after September 24th (see Fig. 6, Fig. 7). Some school managers have delayed the opening time to assess the final settlements for emergencies. Other school managers, however, stuck to the original plan due to the short notice of the decree and the minimum number of school days to be conducted in a school year, which remained constant.

Fig. 6.

Schools starting dates in Sicily.

Fig. 7.

Date of first day in class.

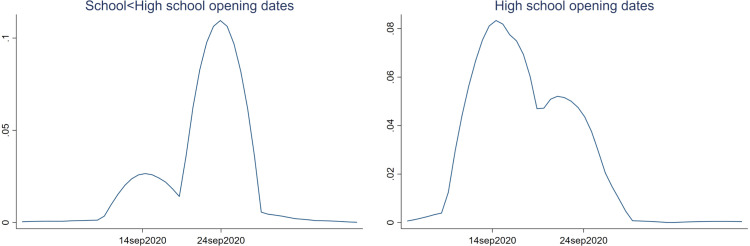
The unexpected change in regulation has determined a large variability in the school year’s starting date, with schools opening from September 1st until October 9th. Figs. 7 show the distribution of observed school opening weighted by students across all the possible ranges, suggesting that school managers’ decisions were bimodal with the modes around the original date (September 14th) and the new “poll station” date (September 24th).14

From an analytical perspective, this set of unexpected events has inadvertently generated a reasonable time discontinuity adapt to measure Covid-19 diffusion through school, larger both than the median incubation time of 4–5 days (McAloon et al., 2020) and of the serial interval time of 7.5 days (Cereda et al., 2020). The latter is defined as the time between a primary case-patient with symptom onset and a secondary case-patient with symptom onset. The time discontinuity persists when focusing on the different levels of schooling (see Fig. 8) but changes depending on the level itself. Infancy, primary and middle schools are more likely to be selected as electoral poll stations, thus following the general path of opening, with a large share of school opening around September 24th and a lower share around September 14th. Secondary schools, instead, are less likely to be poll stations and were more likely to start the school year as originally planned, on September 14th. In Palermo, the regional capital and largest city, out of 610 polling stations, only seven are located in three secondary schools and seven in hospitals. All the remaining electoral poll stations are infancy, primary, middle schools, and general institutes involving all three types of schools.15 However, since only 40.3% of public schools are seats of polling stations, the distribution of the opening dates suggests that many school managers decided to start the school year on or after September 24th, contrary to what was originally planned by the first Regional Decree. Accounting for the determinant of school opening decision becomes crucial to ensure a comparison between treated census areas, where the school year started earlier, and control areas, where the school year started later.

Fig. 8.

Date of first day in class (weighted by students) for level of schools.

An important point for the research design depends on whether students go to schools close to their residence or not. Setting the distance threshold requires a clear understanding of the school-residence linkage. The traditional rule in Italy suggests sending the children to schools in the areas neighboring the residence unless the household requires another location due to some particular situations, linked, for instance, to parents’ job. This rule holds especially for kindergarten, primary and middle schools, where the subjects are equal across all the schools. In contrast, secondary schools are different by the subject of education and thus determine much more mobility than the lower grades. According to official statistics, 79%–83% of students younger than 15, thus including all the students from the infant up to middle school, employ less than 15 min to reach school from their residence. At the same time, this percentage drops to 34 and 22% for the first and second cycle of high school (Istituto Nazionale di Statistica (ISTAT), 2020c).16 Similar evidence emerges from the literature. A survey of Alietti et al. (2011) finds that 71%–75% of students employ up to 10 min to go to school and reports that the vast majority of students attend primary school within 1 km from their house. This does not seem a peculiar Italian scenario. For Alberta’s case in Canada, Bosetti and Pyryt (2007) highlight that 83% of parents send their children to their designated school, which is very close to their residence. Schneider et al. (1997) show that similar evidence holds for NYC districts, where 60% of the students in the district are accepted into their first-choice school. Overall, this suggests that the potential confounding effect deriving from students attending schools far away from their residence should not play a major role in Covid-19 diffusion, especially for early education levels. To build our dummy indicator, a given census area is assigned to the average date of opening of the schools within 1 km of its ray, weighted by the number of students. Fig. 9 provides an example of the logic of this approach for a set of census areas and four schools in the city of Palermo. Census areas falling under the pink circle are assigned with the date of opening of the reference school. When a census area falls under more than one school, those in darker pink located between school three and school four, the resulting date will be the average date of those schools weighted by the number of students of each school. The empirical specification, then, integrates this information with a dummy activating two weeks after the weighted date of school opening in a given census area and remaining activated for the rest of the period, as typical of a Diff-in-Diff approach with time dummies and unit-level fixed effects, also included in this analysis. Most part of the schools, indeed, had a progressive reopening with first-year classes and 3 h of lessons on the day of opening, and a gradual reopening of the other classes during the next days. This means that direct effects should range between 1 and 16 days from reopening. The dummy segments the set of census areas in 26,925 units that get treatment across the time depending heterogeneously on the specific date on which school opened within their ray of 1 km, as in a Diff-in-Diff approach. Also, the data contains 9,756 cells that never get treated. Finally, the identification of the effect derives from the time discontinuity in treatment of the treated cells, accounting for the local level dynamic nature of Covid-19 pandemic evolution, both in other treated and controls cells. Being a Diff-in-Diff, the coefficient of the dummy has to be interpreted as a shift in the intercept of the model for the treated census areas.

Fig. 9.

School opening effects on census areas.

3.3. School variables and students coverage

To model the school-manager decision about the opening date of each school, we have collected a wide set of information on the school characteristics. These are obtained from the official school level data-sheet of the Ministry of Education, including average class size, number of teachers, number of non-permanent teachers, pupils with special needs.17 Some of these variables are available at a disaggregated school level, while others are only at the institute level, which is a group of more schools in the same area.

Table A.1 in the Appendix reports summary statistics for individual school level variables as class size, number of students, and pupils with special needs. These data show how secondary schools collect a relatively higher number of students due to higher education based on specific subjects. Table A.1 also reports data for the number of teachers and share of non-permanent teachers.

Table A.1.

Public school characteristics in Sicily.

School type	N. of pupils	Class size	% of pupils with special needs	Teachers	% of temporary teachers
Pre-primary
Mean	69.1	19.93	2.6%
Sd. dev.	47.26	3.97	0.027
Min	3	3	0
Max	342	39	26.7%
Primary
Mean	158.1	17.05	4.8%
Sd. dev.	119.5	3.74	0.037
Min	3	3	0
Max	798	37.5	33.8%
Middle
Mean	232.5	18.70	5.2%
Sd. dev.	172.4	3.47	0.038
Min	8	8	0
Max	978	31.3	29.4%
Secondary
Mean	360.9	20.20	3.6%
Sd. dev.	379.4	4.34	0.044
Min	5	5	0
Max	2688	40	27.5%
All levels
Mean	169.9	18.84	3.7%	103.1	0.12
Sd. dev.	207.8	4.11	0.037	33.76	0.085
Min	3	3	0	2	0
Max	2688	40	33.8%	344	0.9

This analysis focuses only on public schools because of three reasons. Firstly, public schools were more likely to change their date following the Regional Government’s change in regulation and the occurrence of the national referendum on September 20th–21st (see 2.3), also given that private schools are not used as polling stations. Second, it is impossible to access the information on private schools openings due to the lack of mandatory communications about this to the public. Third, most importantly, the public school system includes and moves the vast majority of the school population in Sicily.18 In terms of the student population, ISTAT data for 2018/19 in Table 1 highlight that the percentage of students in public Sicilian schools is about 95.3% of the total students’ population, leaving only 4.7 percent of private students out of our sample. In terms of distribution across levels of schools, the lowest share of students going to public school is found at the pre-primary level (86.2%), where the school is not mandatory, and much higher shares in all other levels, equal to 96.5%, 99.0%, and 95.3% in primary, middle and high school, respectively. Students distribution over public and private schools, as well as over different grades, appear similar also across the Sicilian provinces, as displayed in Table 1. This suggests that focusing only on public schools should not substantially bias the sample in terms of the student population and geographical representation. Table A.1 reports a set of other statistics by level and shows that the average class is slightly lower than 19 pupils (18.84), while the local unit average of employees in Sicily is 3.8 by the last census of 2011.19

Table 1.

Share of students in public schools by provinces in 2018/19.

	Pre-primary	Primary	Middle	High	Total
Sicily	86.2%	96.5%	99.0%	96.6%	95.3%
Trapani	88.2%	99.4%	100.0%	98.4%	97.3%
Palermo	79.1%	94.5%	98.4%	94.7%	92.9%
Messina	87.3%	96.5%	98.5%	97.5%	95.7%
Agrigento	87.7%	99.0%	100.0%	96.4%	96.5%
Caltanissetta	89.4%	97.2%	100.0%	98.7%	97.0%
Enna	96.1%	100.0%	100.0%	98.0%	98.7%
Catania	89.0%	95.6%	98.4%	96.4%	95.3%
Ragusa	88.1%	96.7%	100.0%	96.4%	95.8%
Siracusa	87.7%	98.2%	99.5%	97.4%	96.4%

ISTAT (2020a)

A simple comparison is useful to see why understanding the potential role of schools in Covid-19 diffusion is relevant. As both Istituto Nazionale di Statistica (ISTAT) (2020a) and Regional Department of Education data20 suggest, the public schools hosted 717,524 students for the schooling year 2019/20, a number that increases up to 823,595 when considering teachers and other staff members, equal to about 16.5 percent of the total regional population or, just to give an idea, is equivalent to more than half of total employed in the region (Istituto Nazionale di Statistica (ISTAT), 2020b). To summarize the data explanation of this section, the descriptive statistics of our final working sample that we will use in the econometric estimates are in Table 2 below. For a rough comparison with, for instance, Chernozhukov et al. (2021b), we have a much higher value of school opening because the period lies in the second wave of Covid-19 rather than in the summer season. On the other hand, we have more minors cases and growth rates because the spatial dimension of our unit is much smaller (the average size of a US county ranges from 31 km to 52k km squared, while in our case the average census area 0.13 km squared).

Table 2.

Descriptive stats for the final working sample.

	Obs.	Mean	Std. dev.
Covid-19 cases	530,944	0.122	0.604
Covid-19 within school cases	530,944	0.002	0.055
Covid-19 above 19 years old - cases	530,944	0.106	0.536
Covid-19 below or equal 19 years old - cases	530,944	0.016	0.158
Covid-19 growth rate (%)	530,944	0.076%	0.285
Covid-19 within school - growth rate (%)	530,944	−0.001	0.049
Covid-19 above 19 years old - growth rate (%)	530,944	0.066	0.268
Covid-19 below or equal 19 years old - growth rate (%)	530,944	0.013	0.123
School opening dummy	530,944	0.582	0.493
School neighbors opening dummy	530,944	0.634	0.481

4. Empirical strategy

Our empirical framework follows a Diff-in-diff (DiD) dynamic process with fixed effects for the growth rate of Covid-19 cases as in Chernozhukov et al. (2021a).

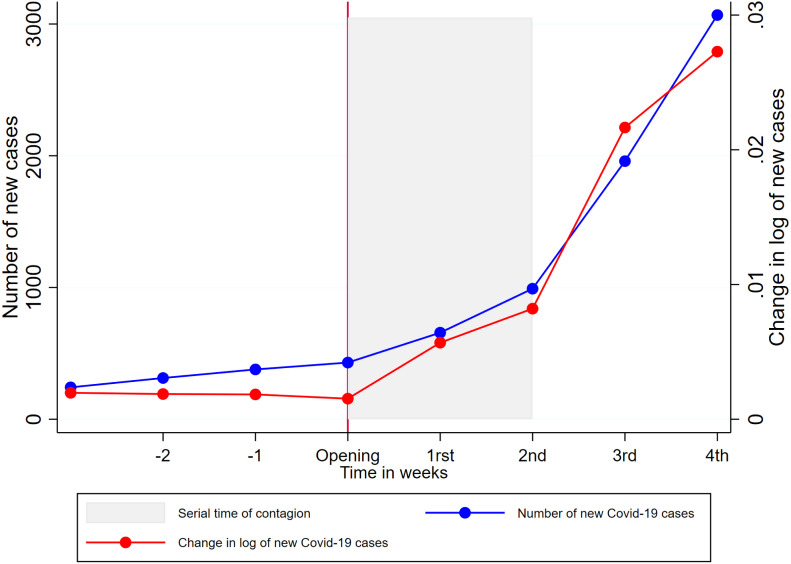
Fig. 10 provides a visualization of the staggered Diff-in-Diff application about the impact of school opening on the levels and growth rate of Covid-19 cases. The time dimension is relativized around the treatment time of each unit, and the shaded area denotes the referral time of two weeks.21 Fig. 10 suggests that once a school opens within 1 km of a census area, both the level and the growth rate of cases observe an increase, which becomes more evident after the referral time.

Fig. 10.

Pattern of Covid-19 cases after the school opening.

Similar evidence emerges when comparing the level and growth rate of Covid-19 cases for treated and control observations and highlighting the period when the wide majority of the treated census areas get the treatment (September 14th–24th). Fig. 11 suggests that, while treated and control areas show a similar path in cases before the treatment, this trend starts to diverge right after the treatment period, which is probably indicating a potentially strong role of school opening in affecting the diffusion of Covid-19 cases.22

Fig. 11.

Pattern of Covid-19 cases for areas with and without schools.

The main empirical specification of the analysis relies on the dynamic panel regression model:

$$\Delta y_{i,t}={\alpha }_i+{\rho }_1\Delta y_{i,t-1}+\sum _{j=2}^4{\beta }_j{y}_{i,t-j}+\gamma t+\lambda S_{i,t-2}+u_{i,t},i=1,2,\dots ,n,t=1,2,\dots ,T,$$ (1)

where $\Delta$$y_{i,t}$ denotes the change in log of the Covid-19 cases in a given census area $i$ at time $t$ and $y_{i,t}$ indicates the natural logarithm of Covid-19 cases for census locality $i$ at time $t$. Following Chernozhukov et al. (2021b) we include three lagged values of $y_{i,t}$ to capture lagged level effects.23 The key variable of interest is the dummy for school opening $S_{i,t-2}$ that takes the value 0 before the opening and 1 after the date on school opening. This variable enters the model with a lag of two weeks to reflect the serial time of infection and the delays in detecting the virus among children. The parameter $\lambda$ measures the causal effect of the opening of schools on the growth of Covid-19 cases. Additionally, the model includes the census areas fixed effects denoted by ${\alpha }_i$ that capture common shocks to the Covid-19 cases of all census localities $t$. $u_{i,t}$ is an error term capturing the remaining unobserved heterogeneity.

While our estimation approach can account for time-invariant unobserved heterogeneity and common shock in times, one may still argue that the school opening decision may remain an endogenous time-varying decision. Indeed, the decision of the school managers could be based on several reasons, including the percentage of Covid-19 cases in the area, the preparation time due to longer management times for some internal organizational issues, and other administrative matters. This implies that an ideal estimation should account for this endogenous decision when modeling the effect of school opening. In doing so, we hereby consider a two-stage problem, where the first stage relates to the decision on the date of opening. The dummy for school opening $S_{it,}$ is modeled by a set of inverse probability weights, obtained from a Propensity Score Matching (PSM) estimation on several indicators affecting school opening decisions for school managers.

The vector of indicators ${\mathbf{z}}_i$ includes the number of Covid-19 cases in August in the same census area, the average class size, the number of pupils with special needs, permanent and temporary teachers, the total number of schools within 1 km of ray. The algorithm employed for the matching is the five-nearest neighbor, but the result is robust to other specifications such as kernel-based matching or caliper matching. Formally, the PSM model is given by the probit model

$$e_i\stackrel{\mathrm{def}}{=}Pr({\overline{s}}_i=1|{\mathbf{z}}_i)=F\left({\mathbf{z}}_i^{\prime }\pi \right),$$ (2)

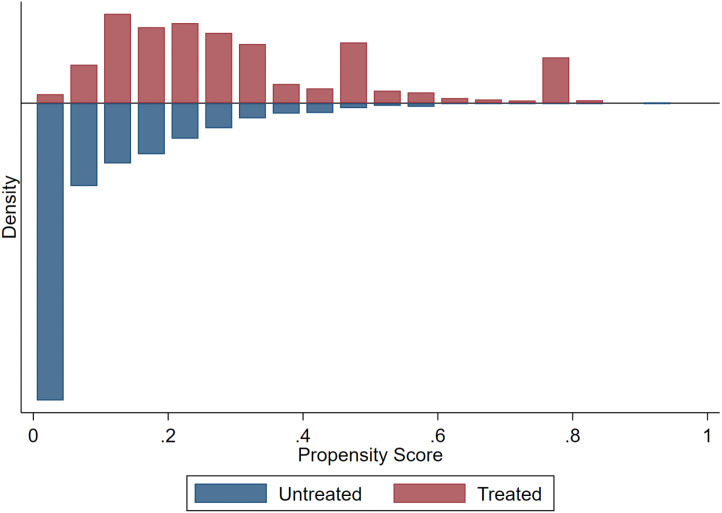
where $F\left(\cdot \right)$ is the Normal cumulative density function that models the probability of being treated on a set of determinants measured before the treatment. The treatment variable ${\overline{s}}_i$ for the PSM is a dummy activating whether the average date of school opening has been on September 14th or earlier, representing one of the two modes in Fig. 7. We then obtain the propensity ${\hat{\theta }}_i$ that we use to build the weight $1/{\hat{\theta }}_i$ for the treated units and $1/(1-{\hat{\theta }}_i$) for the control units. These weights are then incorporated in model (1) to weigh both the dependent and the explanatory variables. Effectively, our approach involves a two-step estimation, where in the first step we obtain the propensity scores via model (2) and then in the second step, to estimate a weighted version of the model (1). Table A.3 in the Appendix introduces the results from the PSM, which are consistent with our expectations, e.g., the more the Covid-19 cases in August, the lower is the probability of opening earlier the schools. As the common support region in Fig. 12 shows, for each treated census area, the PSM has found a counterfactual census area across all the score distribution. It, therefore, allows the inclusion of all the census areas in a weighted version of Eq. (1).

Table A.3.

Scores from the propensity score matching.

	Coef.	Std. err.
Covid-19 cases in August	−0.003*	(0.002)
Class size	0.094***	(0.004)
Pupils with special needs	18.173***	(0.689)
Teachers	0.001***	(0.000)
Temporary Teachers	0.321***	(0.031)
Number of Schools	−0.052***	(0.001)
Constant	−3.140***	(0.083)
Obs		36681
Pseudo $R^2$		0.27

Robust standard errors are in parentheses. Dependent variable is treatment date at 14 September. ***, **, and * denote significance at 1%, 5%, and 10%, respectively.

Fig. 12.

Common and out of support area of the Propensity Score Matching.

5. Results

Results displayed in Table 3 suggest that school opening has affected the diffusion of Covid-19 during the last months of 2020 and that the growth rate of Covid-19 cases increased significantly two weeks after school opening in the nearby areas. In terms of magnitude, the results from the unweighted baseline specification run on the entire sample suggest that the growth rate of Covid-19 cases has increased by 2.6%, everything else kept equal. This result remains consistent with the exclusion of the last month of data, involving the December observations, where probably more effects are likely to confound.24 Again, the magnitude of the coefficient suggests that school opening has likely contributed to an increase of about 2.7% in the growth rate of the local Covid-19 cases. The third column deals with the potential problem of Nickell’s bias. While the result is robust to other alternative specifications, including GMM system and difference estimation25 we show as the analytical bias computation of the de-biased fixed effect estimator of Chen et al. (2019) reports a coefficient with very similar magnitude, equal to 2.3% (with 500 replications bootstrapped standard errors). To further account for time-varying endogeneity in school opening, the baseline specification has been run with the inverse probability weights (IPW) obtained from the propensity score matching introduced above. The fourth column of Table 3 displays the estimated coefficient, which suggests an impact of about 2.5% in the growth rate of Covid-19 cases, a result that remains consistent with the unweighted baseline specification. The last two columns of Table 3 test eventual changes in the estimated impact when accounting for spatial spillovers across neighbor areas and spatial correlation. The weighted specification of column 3 is modified by adding a dummy indicator that activates, for a given census area, when at least a neighbor census area observes a school opening. This dummy, therefore, allows us to account for the indirect effect of school opening through neighbor areas.

In contrast, the direct effect of school opening remained captured by the original variable in the baseline model. The results from this further exercise suggest that the overall impact remains relatively stable. Indeed, while the sum of the coefficients is slightly higher (2.9%), the range is still well within our previous results. This seems to confirm the potential spatial spillover effects of the infection process. Finally, the last column of Table 3 accounts for the spatial correlation in infection diffusion using the Hsiang (2010) implementation of Conley (1999) clustering, consisting of an arbitrary correlation regression (Colella et al. 2020) with a threshold of 2 km.26 and Newey–West standard error correction. Again, the result remains robust, and the estimated impact increases to ＋3.7%.27

To sum up, the range of our estimated 2.5%–3.7% effect is well within the bounds of no effects as Isphording et al. (2021) and appears to be close to the window of 4%–6% as Chernozhukov et al. (2021a). Note how this effect is relatively lower than the influenza reduction effect of Ali et al. (2018) given by school closures in Hong Kong. This is an interesting comparison due to the same time window, that is, the weekly average coefficient. The size of difference (60% concerning our favorite benchmark of Table 3) may be explained by considerable heterogeneity of type of virus transmission, period, data, and use of masks.

Table 3.

Covid-19 cases and school opening.

Specification	Dependent variable: Change in ln of Covid-19 weekly cases
	Full sample	date$<$December 2020	De-biased ABC	IPW	Spatial correlated errors	Neighbors effect
	(1)	(2)	(3)	(4)	(5)	(6)
School opening (2nd lag)	0.026***	0.027***	0.023***	0.025***	0.012***	0.037***
	(0.001)	(0.001)	(0.001)	(0.001)	(0.003)	(0.003)
School opening neighboring sections					0.017***
					(0.003)
Covid-19 (ln, 2nd lag)	−0.787***	−0.759***	−0.745***	−0.786***	−0.786***	−0.558***
	(0.004)	(0.005)	(0.006)	(0.008)	(0.008)	(0.011)
Covid-19 (ln, 3rd lag)	0.010***	0.036***	0.000	0.013***	0.013***	0.086***
	(0.003)	(0.004)	(0.003)	(0.005)	(0.005)	(0.006)
Covid-19 (ln, 4th lag)	−0.020***	0.035***	−0.027***	−0.015***	−0.015***	0.046***
	(0.003)	(0.005)	(0.004)	(0.005)	(0.005)	(0.008)
Covid-19 (change ln lag)	−0.864***	−0.855***	−0.806***	−0.864***	−0.864***	−0.733***
	(0.003)	(0.004)	(0.002)	(0.006)	(0.006)	(0.008)
Time dummies	Y	Y	Y	Y	Y	Y
Census area FE	Y	Y	Y	Y	Y	Y
Spatial autocorrelation	N	N	N	N	N	Y
Propensity scores weighting	N	N	N	Y	Y	Y
Number of Census areas	33,184	33,184	33,184	33,184	33,184	33,184
Observations	530,944	464,576	530,944	530,944	530,944	790,768
R${}^2$ within	0.43	0.41	–	0.43	0.43	0.35

***, **, and * denote significance at 1%, 5%, and 10%, respectively. Standard errors are clustered at census area level in columns 1, 2, 4 and 6.

5.1. Heterogeneity analysis

How may the above effect change with the school and population characteristics? This subsection investigates this question using a set of cross-sectional variables available at the census-area level. Table 4 reports three types of results. Column 1 estimates the effect of reopening on cases linked to the within school population, involving only people directly active in schools as students, teachers, staff. While the effect is strongly significant, the point estimate is lower, and the dynamic process loses time persistency, which may be explained by two arguments. First, as already introduced above, the school population mostly involves youths, which may be more likely to be asymptomatic. Thus, the observed increase in cases is lower than the real increase. Second, schools may have been efficient in isolating classes with positive cases, a condition that may explain both the lower increase in cases and the absence of a dynamic within the school population. Matching this result with what was observed in Table 3, suggests that most of the direct contagion within the school system then develops itself in other contexts, such as within the families other social networks. In this sense, schools may act as the initial spark of a larger contagion within these networks.

Table 4.

Covid-19 cases and school opening. Heterogeneity linked to schools.

Dependent variable: Change in ln of Covid-19 weekly cases
	(1)	(2)	(3)	(4)	(5)
	Covid-19 within school	Below high school	High school	Class size$\le$median	Class size$>$median
School opening (2nd lag)	0.001***	0.024***	0.003	0.003	0.037***
	(0.000)	(0.002)	(0.002)	(0.004)	(0.002)
Covid-19 (ln, 2nd lag)	−1.096***	−0.786***	−0.785***	−0.784***	0.789***
	(0.011)	(0.008)	(0.008)	(0.012)	(0.010)
Covid-19 (ln, 3d lag)	−0.074***	−0.013***	−0.013***	−0.006	−0.017***
	(0.003)	(0.004)	(0.005)	(0.007)	(0.006)
Covid-19 (ln, 4th lag)	−0.078***	−0.015***	−0.015***	−0.027***	−0.008
	(0.003)	(0.005)	(0.005)	(0.008)	(0.006)
Covid-19 (change ln lag)	−1.038***	−0.864***	−0.864***	−0.859***	−0.869***
	(0.010)	(0.006)	(0.006)	(0.009)	(0.007)
Time dummies	Y	Y	Y	Y	Y
Census area FE	Y	Y	Y	Y	Y
Observations	530,944	530,944	530,944	185,584	345,360
R${}^2$ within	0.52	0.43	0.43	0.43	0.43
Number of Census areas	33,184	33,184	33,184	11,599	21,585

All regressions are weighted by propensity scores. ***, **, and * denote significance at 1%, 5%, and 10%, respectively. Standard errors are clustered at census area level. The dependent variable of column 1 is the natural log of Covid-19 cases occurring within the school system. The dependent variables of columns 2, 3, 4, and 5 is the natural log of Covid-19 cases.

A second essential type of heterogeneity derives from the kind of school. To study this mechanism, the analysis is conducted separately for schools lower than the high schools, including infancy, primary and middle school, and for the high school itself. As explained above, this clustering is justified by the different spatial mobility students show concerning the type of school. Columns 2 and 3 report the result obtained when activating the school opening dummy separately for these two groups. As expected, the coefficient associate with infancy, primary and middle schools is much higher and more significant than the one associated with middle schools. On average, the first one is related to an increase in the census-area case by 2.4 percent, while the second ones are linked to a much lower increase, close to 0. Again the difference in this result is strongly linked to the difference in the students’ local spatial dynamic, which are more likely to go to schools within a ray of 1 km when attending school lower than middle school. Therefore, it is possible that the high schools may have a similar effect but more spatially dispersed across the municipality’s territory, a result that is still compatible with Munday et al. (2020), which suggest that secondary schools may be more robust drivers of contagion.

Finally, columns 4 and 5 introduce the heterogeneity results across class size, conducted clustering the regression for census areas with average class size below and above the median value, equal to about 20 students. In this case, the estimated effect appears that the effect of school opening is not different from zero for schools with smaller classes. At the same time, it is equal to ＋3.7% in areas with average classes larger than the median. This is in line with recommendations of Lordan et al. (2020) and suggests that reducing the number of students per class may reduce the contagion induced by school opening.

Table 5 reports the heterogeneous analysis across the population characteristics. Columns 1 and 2 consider two new dependent variables built for the cases on the population above the school-age (older than 19) or within the school age. As expected, the impact appears higher in magnitude for individuals outside the school age, with an estimated increase in the cases growth rate equal to 2.3 percent, which is four-times larger than the effect estimated for the individuals within school age, equals only to about 0.5 percent. Similar to what was found for the within school population in Table 4, the effect of school opening on the growth rate of Covid-19 cases among the younger population appears less persistent. Finally, when pooling the dataset above and below the average population density of the census areas, the effect of school opening appears significantly stronger in less populated areas. While this result may be unexpected, a potential explanation certainly relies on the fact that, in these areas, schools act as a social collector and potentially represent a higher share of interaction concerning schools in big cities where there can expected a higher presence of more random or weak ties in denser areas as in Sato and Zenou (2015).28

Table 5.

Covid-19 cases and school opening. Heterogeneity linked to population.

	(1)	(2)	(3)	(4)
	Covid-19 cases$\le$19 yo.	Covid-19 cases$>19$ yo.	Covid-19 cases pop density$\le$mean	Covid-19 cases pop density$>$mean
School opening (2nd lag)	0.005***	0.023***	0.031***	0.001
	(0.000)	(0.001)	(0.002)	(0.003)
Covid-19 (ln, 2nd lag)	−1.011***	−0.799***	−0.765***	−0.820***
	(0.010)	(0.008)	(0.007)	(0.007)
Covid-19 (ln, 3d lag)	−0.036***	−0.010**	−0.010**	−0.012***
	(0.006)	(0.005)	(0.004)	(0.004)
Covid-19 (ln, 4th lag)	−0.046***	−0.016***	−0.022***	−0.020***
	(0.006)	(0.005)	(0.004)	(0.005)
Covid-19 (change ln lag)	−1.000***	−0.871***	−0.846***	−0.890***
	(0.006)	(0.006)	(0.005)	(0.005)
Time dummies	Y	Y	Y	Y
Census area FE	Y	Y	Y	Y
Observations	530,944	530,944	319,296	211,648
R${}^2$ within	0.50	0.44	0.42	0.45
Number of Census areas	33,184	33,184	19,956	13,228

All regressions are weighted by propensity scores. ***, **, and * denote significance at 1%, 5%, and 10%, respectively. Standard errors are clustered at census area level. The dependent variables of column 1 and 2 are the natural log of Covid-19 cases in the population above and below 19 years old, respectively. The dependent variable of column 3 and 4 is the natural log of Covid-19 cases in all the population.

5.2. Robustness

This section introduces the results of a set of exercises to test the robustness of the main results. The first test consists of switching the time of observation from the serial time, equal to 7 days, to the incubation period of 5 days (Cereda et al., 2020). Column 1 of Table 6 reports the estimated coefficient, which is slightly smaller (1.9%) in magnitude but still strongly significant, with the Covid-19 autoregressive coefficients remaining unchanged. This exercise would require changing the time lag of the dummy school lag from 2 to 3 to consider the same period of days.29

Table 6.

Robustness tests on Covid-19 cases and school opening.

	Serial Time=5 days	IHS	Cases over Population	Interaction term
	(1)	(2)	(3)	(4)
School opening (2nd lag)	0.019***	0.026***	0.024***	0.026***
	(0.001)	(0.001)	(0.001)	(0.001)
School opening (2nd lag) X 2nd lag dependent				−0.002
				(0.005)
Covid-19 (ln, 2nd lag)	−0.785***	−0.609***	−0.789***	−0.788***
	(0.005)	(0.004)	(0.005)	(0.005)
Covid-19 (ln, 3d lag)	0.057***	0.008***	0.011***	0.011***
	(0.003)	(0.002)	(0.003)	(0.003)
Covid-19 (ln, 4th lag)	0.022***	−0.016***	−0.021***	−0.020***
	(0.003)	(0.002)	(0.003)	(0.003)
Covid-19 (change ln lag)	−0.881***	−0.669***	−0.865***	−0.863***
	(0.003)	(0.003)	(0.004)	(0.005)
Time dummies	Y	Y	Y	Y
Census areas fixed effects	Y	Y	Y	Y
Observations	796,416	530,944	505,856	530,944
R${}^2$ within	0.44	0.43	0.43	0.43
Number of Census areas	33,184	33,184	31,616	33,184

All regressions are weighted by propensity scores. ***, **, and * denote significance at 1%, 5%, and 10%, respectively. Standard errors are clustered at census area level. The dependent variables are the natural log of the Covid-19 cases measured with a serial time of 5 days (column 1), the Inverse Hyperbolic Sine Transformation (IHS) of the Covid-19 cases (column 2); the share of Covid-19 cases over the census area population in 2011 (column 3); and the log of the Covid-19 cases (column 4).

A second robustness test consists of replacing the dependent variable’s natural log with the correspondent inverse hyperbolic sine transformed value (IHS), following the methodology developed by Bellemare and Wichman (2020). As column 2 reports, the estimated coefficients remain positive and significant, with a level of magnitude unchanged with consistent with respect to the benchmark of Table 3.

As the third robustness test, we run the baseline model substituting the dependent variable with the share of Covid-19 cases over the total census population. As already discussed, given that precise population estimates at the census area level are available only for 2011, calculating the share is prone to error due to migration and residence changes. According to official estimates, about 738,000 individuals have changed residence between 2011 and 2018 (Istituto Nazionale di Statistica (ISTAT), 2020d)30 in Sicily. When projecting this share to the ten years, this could have involved up to 21% of the population of the island population, which still represents a lower bound because some people moved their residence without formally communicating it to the authorities. These figures justify why using population shares would have been quite unreliable. However, testing this with the available data could remain essential to understanding whether the effect is somehow driven by population level in a given census area. As column 3 shows, the result remains consistent when adopting the share of population positive to Covid-19 as a dependent and autoregressive variable. The estimated increase in level is equal to about 2.4% and strongly significant, a result that remains totally in line with the previous ones.

As a final test, the analysis in column (4) includes the interaction between the dummy on school opening and the level of Covid-19 cases at the time of the opening of schools, to account for the dynamic role of school opening on the diffusion that may fit in a better way some explosive patterns.

This additional coefficient is not significant, and once again, results are overlapped to the benchmark specification.

5.3. Simulation of contagion over space and time

As a consequence of the above estimates, one may ask what would have been the number of Covid-19 cases if the school without school opening and spatial spillover effects. Our model allows us to simulate a set of counterfactual scenarios taking out the contribution of the school opening in a given census area and the neighboring sections. The results need to be taken with caution, as maybe full school closure would have favored different times of interaction between pupils outside school. For example, parents could have felt safer allowing their children to go out, reducing the effect of school closure.

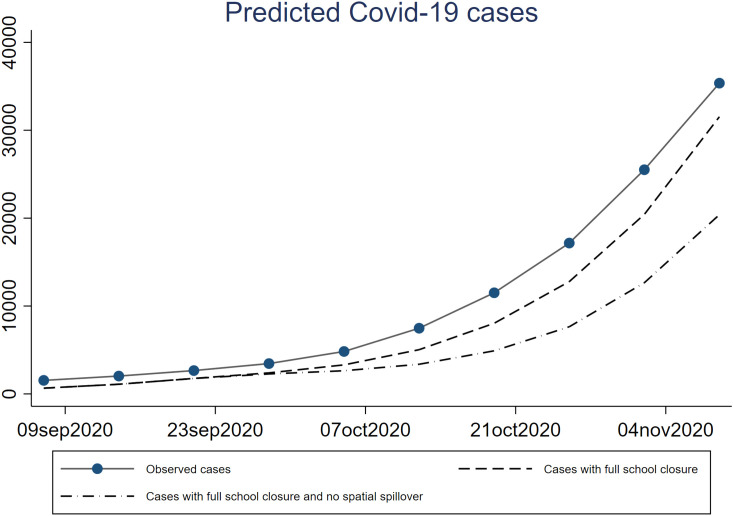
For the sake of this simulation, we use the estimated coefficients of column 4 in Table 3 and focus on a reduced time span around November 1st. As Fig. 13 suggests, the number of predicted Covid-19 cases would have shown different dynamics and lower numbers without school opening and without spatial spillovers. In particular, in the first scenario, the total number of cases would have decreased to a value between 31,538 rather than the 38,908 cases observed around the week of November 9th. In the second scenario, when taking out also the spatial spillover effect, the total number of cases would have reduced to 20,394. The magnitude of the decrease depends on whether the school closures would have entailed the absence of any other social contact of the students with their school social network or whether the reduction of contacts would have been just slightly reduced.

Fig. 13.

Cumulative Covid-19 cases and predicted cases with three school closure scenarios.

6. Conclusions

This work has employed a design based on differences in school opening time to test for the localized total effect of opening a school concerning the Covid-19 increase in the census area. The dataset includes more than 66,000 geo-localized Covid-19 cases for the Sicily region, matched with precise information on the date on which schools have opened in the surrounding area. The time discontinuity of school opening derives from a change in the regulation that occurred two weeks before the school year’s official start, together with a referendum that has delayed the opening of schools selected as seats of poll stations. These two conditions have generated a wide variation on the date of commencement. The endogeneity of school manager decisions has been modeled as a two-stage problem. Therefore, the empirical strategy has involved a propensity score model in weighting the census areas on the school-manager determinants of school opening. Thus, the selected estimating strategy consisted of a DiD estimation, able to account for the dynamic evolution of Covid-19 infection in each census area. To the best of our knowledge, this is the first work accounting for the dynamic process of Covid-19. Unlike the previous literature, which has based its estimates on regional or province data, this work is the first to rely on very granular geocoded data, measured at census area, which corresponds to about a block of 0.13 ${\mathrm{km}}^2$. This work can also investigate the impact of school opening on cases within the schools and on claims that occurred in the geographical areas where the students reside. In this sense, the estimates obtained from this exercise can be considered the global (direct and indirect) localized effects of school opening.

Results show that nearby schools observed a positive short-run localized increase of +2.5–3.7% in the Covid-19 cases after the school opening.

Finally, a set of potential mechanisms and policy options emerge from the heterogeneity tests presented in Section 5.1. First, larger class sizes are associated with a higher impact of school opening on Covid-19, while reducing the number of students per class appears to reduce infection potential. Second, even though school opening involves most of the region’s youth population, the impact on Covid-19 cases is more substantial for a population older than 19. This may reflect that many students remain asymptomatic and may spread their infection in families or social networks outside the school. Therefore, increasing the number of testing within schools is crucial to reduce the disease. Finally, the contagion appears to be higher in zones more sparsely populated, highlighting the relevance of stronger social interactions.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix. Other data specifications and results

See Fig. A.1, Fig. A.2, Fig. A.3 and Table A.1, Table A.2, Table A.3.

Fig. A.2.

Covid-19 cases by population at 2011 whole period.

Table A.2.

Rt Weekly reproduction rate for Sicily.

Reference week	Rt	Lower bound	Upper bound
August 24–30	0.82	0.53	1.16
August 31–September 6	0.96	0.66	1.32
September 21–27	1.08	0.70	1.43
September 14–20	1.2	0.77	1.75
September 21–27	1.19	0.88	1.57
September 28–October 4	1.22	0.79	1.64
October 5–11	1.23	0.88	1.69
October 12–18	1.28	0.99	1.49
October 19–25	1.42	1.21	1.61
October 26–November 1	1.4	1.15	1.69
November 2–8	1.18	1.02	1.44
November 9–15	1.13	0.95	1.26
November 16–22	1.05	0.73	1.31
November 23–29	0.84	0.62	1.16
November 30–December 6	0.72	0.59	0.88
December 7–13	0.73	0.64	0.82
December 14–20	0.8	0.71	1.01

Data availability

Data will be made available on request.