Representation of molecules for drug response prediction

Abstract

The rapid development of machine learning and deep learning algorithms in the recent decade has spurred an outburst of their applications in many research fields. In the chemistry domain, machine learning has been widely used to aid in drug screening, drug toxicity prediction, quantitative structure–activity relationship prediction, anti-cancer synergy score prediction, etc. This review is dedicated to the application of machine learning in drug response prediction. Specifically, we focus on molecular representations, which is a crucial element to the success of drug response prediction and other chemistry-related prediction tasks. We introduce three types of commonly used molecular representation methods, together with their implementation and application examples. This review will serve as a brief introduction of the broad field of molecular representations.

Introduction

The emergence of large-scale datasets in drug combination synergy or monotherapy drug sensitivity data in recent years, including the DrugComb [1], the Broad Institute Cancer Cell Line Encyclopedia [2] (CCLE) and the Genomics of Drug Sensitivity In Cancer [3] (GDSC) datasets, has made it possible to carry out machine learning research aiming at predicting drug responses, many of which have shown promising results with growing prediction accuracy [4–10]. In many application scenarios, a successful drug response prediction model generally requires appropriate representations for drug molecules and/or cell line-specific genomic profiles [11]. This review mainly focuses on the representation of drug molecules. The field of molecular representations is growing rapidly, and scientists are proposing many new ways of representations every year. Therefore, a comparison between different types of representations is crucial to understanding their applications to drug response prediction. There are general reviews about artificial intelligence and drug discovery [12–16], whereas in this review the main goal is to provide readers that have little machine learning background with a brief introduction of key ideas and differences between common molecular representation methods for drug response prediction.

A naive and intuitive way to represent a molecule is through its name. However, simply naming chemical substances has been a challenge in history. The major concern of a naming rule resides in its robustness—one substance should be mapped to a unique name, regardless of how complicated the chemical structure is. Intuitively, why cannot a well-designed naming scheme, e.g. what is taught in organic chemistry class, serve as a good molecular representation? Unfortunately, the chemical nomenclature is typically difficult to follow. Meanwhile, the chemical names themselves do not explicitly capture the structural and bonding information. Therefore, different ways of molecular presentations were developed based on simple rules as well as being able to capture useful information.

We classify the numerous molecular representations into three broad categories shown in Table 1: (i) the linear notation category, of which the data structure is a string, (ii) the molecular descriptor category, which uses hash-mapped bit string to represent the 2D structure of a molecule and (iii) the graph notation category, which uses a graph to represent the full connectivity as well as the atomic features of a molecule. Of note, there is always a trade-off between the complexity and the description power of representations. While the aim of many ongoing researchers is to achieve a representation method that is both cheap in memory and strong in description power, the reality is such a trade-off is inevitable. Therefore, the following sections will be roughly following the logic of going from simpler and weaker representations, to more complicated and powerful representations.

Table 1.

Three major categories of molecular representations

Category	Names of molecular representations
(1) Linear notations	Simplified molecular-input line-entry system (SMILES)
	International chemical IDENTIFIER (InChI)
(2) Molecular FPs	Structural keys
	Circular FPs
(3) Graph notations	Graph representations
	MPNN-based representations

Although the recent focus of the field has been majorly devoted to the complicated graph notation category, the other two types of representations have also shown great performance in many drug response prediction tasks [15, 17–19]. Therefore, it is still worth introducing the two earlier types of molecular presentations. When evaluating a molecular representation, three basic principles should be considered. First, a representation should be able to capture structural information of chemical substances, since chemical or drug properties are heavily dependent on structural information. Second, the generation rule of a representation should be reasonably simple so that a program can robustly follow it. Third, a representation should be as simple as possible in its mathematical form, so that it can be easily handled by downstream machine learning frameworks. We will follow these principles throughout this paper.

As the advances of machine learning algorithms and availability of large-scale datasets in recent years, many computational approaches emerge for predicting drug responses. Here, we briefly summarize related works in Table 2. There are mainly two types of input: (i) genomic profiles [e.g. RNA-seq, copy number variation (CNV), DNA methylation and DNA mutation] of cell lines or patient samples, and (ii) physico-chemical properties of drug molecules. In addition, auxiliary data such as protein–protein interaction networks and drug targets are sometimes considered to further extract features from raw data for machine learning models. Although we primarily focus on molecular presentations in this review, related studies that only use genomic data as inputs without drug-based features are also listed in Table 2 for references. In addition to cell line-based drug responses, we included other types of studies using PDX (studies 1 and 25), organoids (study 2) or human clinical trials (studies 4, 5, 13, 16 and 20). In these studies, the most widely used gold standard label is IC50, which is defined as the concentration of a drug treatment that achieves half of its maximal inhibitory effect. Depending on the data type, other labels were occasionally used. For example, in the study 5 in Table 2, clinical trial data of breast cancer patients were used. The patients were classified into responders and non-responders, which were determined by the rate of pathological complete response. Another example is the study 11 in Table 2, where the Connectivity Map (CMap) scores were used to determine the drug response similarity between two drugs. The CMap score was obtained by measuring gene expression changes after drug treatment.

Table 2.

Studies about drug response and synergy prediction

	Feature types	Dataset	Model	Design for model testing	Performance
study 1 [19]	Morgan FP; individual genotypes	GDSC, CTRPv2, PDX samples	Neural network	Across cell line-drug pairs	Median Spearman’s rho = 0.37
study 2 [21]	Gene expression; genomic mutation; protein interaction network	Colorectal and bladder cancer patients	Ridge regression	Across organoid	Correlation r square = 0.89/0.98
study 3 [22]	Gene expression	GDSC, CCLE, LINCS	Ensemble learning	Cross validation within dataset	MSE = 2.0–4.8
study 4 [23]	Gene expression	Three clinical datasets of cancer patients	Transfer learning	Cross validation within dataset	Mean AUC = 0.758
study 5 [24]	Gene expression	GDSC, clinical trial data	Neural network	Cross validation within dataset	The difference of predicted IC50s
study 6 [25]	gene expression; genomic mutation; CNV	GDSC, CCLE	rotation forest	cross validation within dataset	MSE = 3.14 on GDSC and 0.404 on CCLE
study 7 [26]	Gene expression; DNA methylation; genomic mutation; CNV	265 anti-cancer drugs in 961 cell lines	SVM and elastic net regression	Cross validation within dataset	Pearson’s correlation = 0.3–0.5
study 8 [27]	Gene expression	CTRPv2, LINCS	Semi-supervised autoencoder	Across cell lines	AUROC = ~0.7
study 9 [28]	Gene expression; protein targets of drugs and pathways	GDSC	Bayesian model, MTL	Within and across cell lines and drugs	Pearson’s correlation = 0.30–0.93
study 10 [29]	Structure-based drug similarity; cell line similarity	GDSC, CCLE	A heterogeneous network	Across cell lines	Pearson’s correlation = ~0.8 on CCLE and ~0.45 on GDSC
study 11 [30]	ECFPs; drug response similarity	CMap of 2.9 million compound pairs	Neural network	Across compound pairs	Pearson’s correlation = 0.518
study 12 [31]	Gene expression	GDSC	LASSO	Across tumor samples	P-values on response differences
study 13 [32]	Gene expression	The NeoALTTO clinical trial dataset	Gene expression similarity	Leave-one-out cross-validation across samples	Concordance index > 0.8
study 14 [33]	Chemoinformatic features and FPs; multiomic data	GDSC, CCLE	Logistic regression	Across drug-cell line pairs	AUROC = ~0.7 on GDSC
study 15 [34]	Cell line mutations; protein–protein interaction network	GDSC, CCLE	A link prediction approach	Leave-one-out cross-validation	AUROC = 0.8474
study 16 [35]	Gene expression	GDSC, clinical trials of two drugs	Kernelized rank learning	Cross validation within dataset	precision = 23% - 36%
study 17 [36]	Chemoinformatic features and FPs; genomic data	NCI-ALMANAC	Neural network	Cross validation within dataset	Pearson’s correlation = 0.97
study 18 [37]	Gene expression	Pan-cancer TCGA	Random forest	Across tumor samples	accuracy = 86% and AUC = 0.71
study 19 [38]	Molecular FPs; gene expression	GDSC, CCLE	Neural network	Cross validation within dataset	AUROC = 0.89 on GDSC and 0.95 on CCLE
study 20 [39]	Gene expression	Clinical trial data from TCGA	SVM	Leave-one-out cross-validation	Accuracy > 80%
study 21 [40]	Proteomic, phosphoproteomic and transcriptomic data	Multiple cancer cell lines	Multiple regression models	Across cell lines	MSE < 0.1 and Spearman’s correlation = 0.7
study 22 [10]	Molecular graphs; genomic data	GDSC	GNN	Across cell lines, drugs, and cell line-drug pairs	Pearson’s correlation = 0.9310 and RMSE = 0.0243 across pairs
study 23 [6]	Omic data; monotherapy; gene–gene interaction network	GDSC, CCLE, AZSDC	Random forest	Across drug–drug pairs	Pearson’s correlation = 0.47
study 24 [4]	Monotherapy; genomic mutation; CNV; gene expression	AZSDC	Random forest	Across drug–drug pairs	Pearson’s correlation = 0.53
study 25 [41]	Monotherapy; omic data	GDSC, COSMIC, AZSDC, PDX	Ensemble models	Across drug–drug pairs	Pearson’s correlation = 0.24 and ANOVA –log10(p) = 12.6
study 26 [42]	Chemoinformatic features, SMILES and FPs; genomic data	GDSC	Neural network	Across cell lines	Pearson’s correlation = 0.79 and RMSE = 0.97
study 27 [43]	Molecular FPs; sequence variation	GDSC, COSMIC	Neural network	Within cancer types	Coefficient of determination = 0.843 and RMSE = 1.069
study 28 [44]	SMILES; gene expression; protein–protein interaction network	GDSC	Neural network	Across cell lines, drugs, and cell line-drug pairs	Pearson’s correlation = 0.928 and RMSE = 0.887 across pairs
study 29 [45]	Gene expression; genomic mutation	CCLE, CTD2, UCSC TumorMap	Neural network	Across cell line-drug pairs	Pearson’s correlation = 0.70–0.96
study 30 [46]	SMILES and FPs; gene expression data	GDSC	Neural network	Across cell line and drugs	RMSE = 0.110 + − 0.008
study 31 [17]	Canonical SMILES; mutation state; CNV	GDSC	Neural network	Across cell line-drug pairs	Pearson’s correlation = 0.909 and RMSE = 0.027
study 32 [47]	Graph representation; genomic mutation; CNV; DNA methylation	GDSC, CCLE, TCGA	GNN	Across cell lines, drugs, and cell line-drug pairs	Pearson’s correlation = 0.923 across pairs on TCGA
study 33 [48]	Molecular FPs	NCI-ALMANAC	Neural network	Across drug–drug pairs	Pearson’s correlation = 0.95–0.98
study 34 [49]	Chemoinformatic features and FPs; gene expression	Multiple cancer cell lines	Neural network	Across drug–drug pairs	Pearson’s correlation = 0.73
study 35 [50]	Chemoinformatic features and FPs	NCI-ALMANAC	Random forest, XGBoost	Across drug–drug pairs	Pearson’s correlation = 0.43–0.86
study 36 [51]	Drug target; gene expression	AZSDC, GDSC, NCI-ALMANAC	Multitask learning	Across cell lines	Pearson’s correlation = 0.23 breast/0.36 colon/0.17 lung
study 37 [52]	Molecular FPs and SMILES; gene expression; monotherapy	Multiple drug synergy databases	Neural network	Across drug–drug pairs	AUROC = 0.9577 and MSE = 174.3
study 38 [53]	Drug similarity and protein similarity; drug target	Multiple drug synergy databases	Multitask learning	Across drug–drug pairs	AUROC = 0.8658 / 0.8715/0.8791
study 39 [54]	Drug similarity; gene expression similarity	NCI-DREAM Drug Synergy data	Logistic regression	Across drug–drug pairs	AUROC = 0.43–0.74 and Pearson’s correlation = 0.42–0.74
study 40 [55]	Drug target pathways; monotherapy	Drug Combination Database, literature	A manifold ranking algorithm	In vitro validation	Probability concordance = 0.78

CTRP, Cancer Therapeutics Response Portal; TCGA, The Cancer Genome Atlas; PDX, Patient-Derived Xenograft; AZSDC, AstraZeneca-Sanger Drug Combination Prediction DREAM Challenge; NCI, National Cancer Institute; AUROC, Area Under Receiver Operating Characteristic curve; SVM, Support Vector Machine; MSE, Mean Squared Error; RMSE, Root Mean Squared Error; ALMANAC, A Large Matrix of Anti-Neoplastic Agent Combinations.

Of note, although we provide the predictive performances of related studies in Table 2, those results are not directly comparable to each other. This is because predictive performance is closely associated with many factors, including different datasets, train-validation-test partitions, experimental designs (e.g. predictions and evaluations across drugs, cell lines or drug-cell line pairs) and evaluation metrics. Since these factors vary dramatically across studies in Table 2, we cannot directly draw conclusions that one model is better than another simply based on the score numbers. Moreover, without held-out blind testing, issues of overfitting and information leakage are often observed in machine learning studies. In recent years, data challenges emerge and provide a unique opportunity to systematically and stringently benchmark different methods [20]. In data challenges, participants used the same training data to build models and the predictive performance was evaluated using the same metric on held-out testing data without overfitting or information leakage. Nevertheless, in Table 2, we include the performances reported in literature, so that readers can have an estimation of performances of these studies. Next, we will introduce the three categories of molecular representations one by one.

Linear notations

The representations introduced in this section are referred to as linear notations for two main reasons. First, these molecular representations are in the format of a 1D string. Second, the generation rules generally follow a 1D graph traversal algorithm. While this type of graph traversal algorithm is robust and easy to follow, its output in nature carries only 1D information.

The IUPAC International Chemical Identifier [56] (InChI) and the Simplified Molecular-Input Line-Entry System [57] (SMILES) are two basic linear representations. Both representations are generated by traversing the molecular connectivity graph based on a depth-first search algorithm, which always exhausts a branch of the graph to its leaf atom and returns the 1D traversal result as a string. Two examples of the SMILES representation, namely the isopropyl 4-hydroxybenzoate molecule and the 2-methoxy ethyl formate molecule, are shown in Figure 1. The arrows in both subfigures illustrate the linear molecule traversal process that ultimately generates the SMILES representation. Since the 1D traversal result depends on the starting atom, there are multiple valid SMILES representations given a molecule and the mappings between representations and molecules are not unique. The idea of canonical SMILES has been created to avoid degeneracy and generate a unique representation for each molecule. In practice, the generation principles of canonical SMILES differ between cheminformatic toolkits, but the uniqueness of SMILES can be guaranteed within one toolkit. In contrast to SMILES, the presentation of each molecule by InChI is guaranteed to be unique. Although SMILES has the ‘bad’ degeneracy property, it turns out to be beneficial when data augmentation is needed. It has been reported that using multiple SMILES strings for the same molecule as an augmentation strategy had successfully boosted model performance [58–60].

Figure 1.

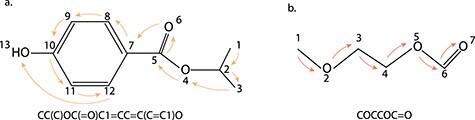
Two Examples of SMILES Representations. The SMILES representation of (A) isopropyl 4-hydroxybenzoate molecule and (B) 2-methoxy ethyl formate molecule. In both sub-figures, the atom traversal order is labeled by numbers, while the traversal operation is shown with the arrows.

These two representations, especially InChI, have been widely used for storing chemical structures. A user can easily fetch these representations for existing molecules in databases such as Drugbank [61] and Pubchem [62]. They can also be generated from many well-established software packages, including the CADD Group’s Cheminformatic Tools and User Services [63] and the InChl generating package [64]. The major advantages of SMILES and InChI have already surfaced: they are easy to generate, have trivial mathematical structures and require small storage space. However, before we present any application cases, one can easily notice an inherent disadvantage of SMILES and InChI: they are 1D in nature so that they cannot capture complicated structural information. Moreover, SMILES notation mainly focuses on molecules with bonds that can fit the 2-electron valence model and fails for molecules that lie outside of this criteria [65].

Owing to the simplicity of their form, linear notations, especially SMILES, can be efficiently used in many machine learning-based drug-related tasks [66], including drug response predictions. The earliest usage of SMILES in the drug response prediction dates back to a research on the GDSC dataset (study 30 in Table 2) [46]. A more recent study where SMILES are used as molecular descriptors in the drug response prediction domain is listed as the study 31 in Table 2.

Molecular fingerprint

Aiming at capturing more structural information, people developed molecular fingerprint (FP) methods to represent molecules. Although a molecular FP is generally in the form of a bit string, it is generated by functional group (structural key) or circular neighbor (circular FPs) mapping algorithms, which are inherent 2D algorithms and differ from a linear notation. The generation rule of molecular FPs is slightly more complicated than SMILES, yet it is still easy to implement. The most commonly used molecular FPs, including the FP2 [67], Molecular Access System (MACCS) [68] and ECFP [69] FPs, are well integrated into existing open-source cheminformatics software packages such as RDKit [70], OpenBabel [67] and CDK [71].

Before introducing specific types of molecular FPs, we will first summarize the pros and cons of these representations. The major advantage of the molecular FP is its simple mathematical structure: it is always a fixed-length bit string (often 100 to 5000 bits), regardless of the size, shape and atom types of input molecules. This characteristic makes it extremely friendly to many downstream machine learning tasks. Furthermore, to achieve better performance in drug response prediction tasks, it is often necessary to integrate multiple features from both the drugs and the genomic profiles of cell lines or patients. The simple form of molecular FP enables it to be integrated into machine learning models with other types of features. Another advantage of molecular FPs is that they are very small in size, resulting in fast model training and testing for downstream machine learning.

Although molecular figureprints are simple in their mathematical structure, they are very powerful in many applications, except for tasks that require 3D structural information such as stereochemistry. While linear notations inevitably sacrifice description power for model simplicity, molecular FPs reside at a well-balanced point. Here, we briefly introduce two major types of molecular FPs based on the generation strategies: the structural key FP and the circular FP.

Structural keys

The generation rule of the structural keys is simple: it uses a binary bit string of 0 and 1 to encode the absence and presence of functional groups. Two widely used structural keys are the MACCS Keys [68] and the Chemically Advanced Template Search [72]. The structural keys reliably encode the functional groups of a molecule. However, one major disadvantage is that they do not provide relative positions of these functional groups, leading to information losses of the local environment or the scaffold of molecules. One potential consequence is that structural keys cannot distinguish structurally unrelated but biologically similar compounds [73]. Another disadvantage is that they can only encode known functional groups, and the determination of functional groups is a difficult and subjective task.

It is worth mentioning how structural keys are involved in the drug response prediction tasks. As covered in a recent review by Güvenç et al. [74], structural keys can be used for calculating drug similarity scores together with other drug descriptors. These similarity scores were further used as features for downstream machine learning tasks [74]. The aforementioned review provides a good summary of downstream machine learning methods that accept drug similarity scores as features.

Circular FPs

Rather than describing the existence of functional groups, circular FPs aim at representing the neighborhood environment of each atom. One of the most widely used circular FPs is the Extended Connectivity FPs (ECFPs) [69]. The most popular ECFP is Morgan’s FP, which generates FPs based on Morgan’s algorithm. First, the user needs to pre-define a radius of interest. Then for each atom, this algorithm determines the neighboring sub-structures within the radius of interest and hash the results into a fixed length of bit-string. After repeating this procedure for every atom, the FP is obtained. A scheme of this process is shown in Figure 2 for the isopropyl 4-hydroxybenzoate molecule. This generation rule is simple, which has been implemented in many cheminformatics softwares.

Figure 2.

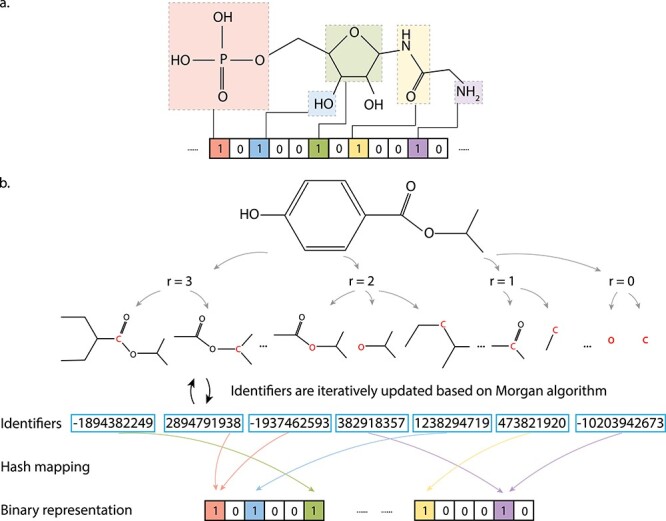
Examples of the MACCS FP and the ECFP Type FP. (A) We use the MACCS FP of the glycinamide ribonucleotide molecule as an example, where the presence of functional groups is denoted by 1 in the FP bit string, absence of functional groups is denoted by 0. (B) The FP generation process of the isopropyl 4-hydroxybenzoate molecule is shown based on an ECFP type strategy. For each non-hydrogen atom (red), an initial integer identifier is assigned to represent the local information (e.g. numbers of bonds and connecting atoms) through a hash mapping function. Then, the identifiers are iteratively updated based on the Morgan algorithm, which combines the initial identifiers with identifiers of neighboring atoms. The neighboring atoms are defined by a circular fragment, where the radius value (r = 0,1,2,3 in the figure) gradually increases to include more neighboring atoms. Finally, redundant identifiers (e.g. two circular fragments contain identical atoms and connections) are removed and a fixed length bit string is derived from the identifier list.

Compared with the structural keys, ECFP can always generate a meaningful FP representation through self-learning substructures based on the pre-defined radius of interest without prior knowledge of any functional groups. However, if we examine Figure 2 more carefully, there are cases that multi sub-structures are hash-mapped into the same bit. As a result, it is not directly interpretable, since we cannot undo the hash-map process and decipher what each 0 or 1 of the bit-string refers to. Moreover, the hash-map operation would inevitably lead to information loss due to bit collision issues. If interpretability is not a concern, ECFPs are in general very powerful, as illustrated by the Morgan’s FP used in study 1 in Table 2 [19].

Graph notations

In recent years, graph notation has become a state-of-the-art molecular representation. Compared with the simpler linear notations and FPs, the graph notation encodes more structural information [75]. As a trade-off between description power and complexity, the graph notation is complicated in many ways and machine learning methods on the graph representations by themselves have become a focus of the current study [75–77]. We therefore divide this section into two parts: we will first introduce the graph representation methods, then briefly introduce some existing graph propagation methods. For a more detailed review of the entire graph notation regime, we refer readers to a thorough review by Sun et al. [78].

The graph representation

In the graph representation of molecules, each atom is represented as a node, while bonded atoms are connected by edges. The connectivity relationship between nodes can be easily described by an N*N adjacency matrix (N being the number of atoms), usually referred to as the matrix A, where the element a_ij denotes whether or not the node i and the node j are connected. Another important matrix in the graph representation is the node feature matrix X, where each node is encoded by a set of user-defined features. The feature matrix of a molecule can take in common chemical properties of atoms, for instance, atom electronegativity, formal charge, radius, etc. If we incorporate the 3D dimensional coordinates of each atom into the node feature, then the graph notation would be capable of capturing the full 3D structural information of a molecule, which cannot be achieved by any of the previous molecular representations. Similar to the idea of node feature matrix X, one can create a matrix E to represent edge features as well, for instance, bond orders, bond types, bond length, for each chemical bond. Figure 3A is an example of the adjacency matrix A, the node feature matrix X and the edge feature matrix E of the butadiene molecule. This is the most intuitive and simple type of graph representation for molecules.

Figure 3.

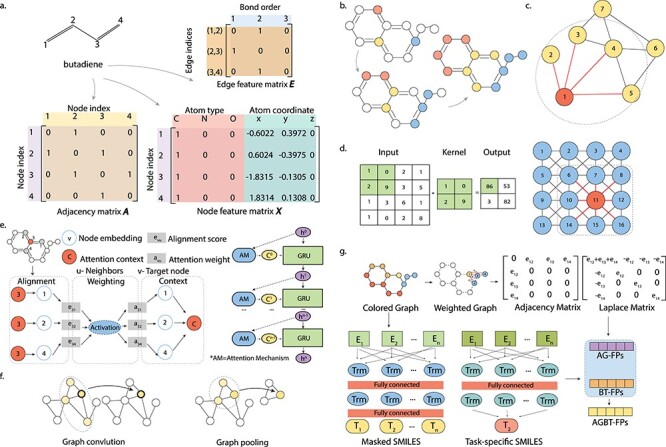
Illustration of graph representations and graph convolution. (A) Graph representation matrices, namely, the Adjacency matrix A, node feature matrix X and edge feature matrix E, of the butadiene molecule. (B) Information flows through graph convolution. (C) The graph convolution operation in a GNN architecture, the node of interest is colored in red and edges connected to the node of interest are colored in red. (D) The scheme of a convolution operation in a CNN architecture. On the left, an example 2-by-2 convolutional kernel and the corresponding input and output are shown. On the right, the node of interest is colored in red and the kernel is represented by the dashed square. (E) The scheme of the Attentive FP model. The graph attention mechanism is introduced as a trainable feature to represent both topological adjacency and intramolecular interactions between atoms with large topological distances. For each target atom and its neighboring atoms, state vectors are used to describe the local environment through node embedding. These state vectors are progressively updated to include more information from neighborhoods through the attention mechanism, where state vectors are aligned and weighted to obtain attention context vectors and gated recurrent unit layers are used to update state vectors. (F) Instead of predicting a specific property of a molecule, a GCN-based approach was proposed to predict universal properties of molecules as well as materials. (G) The scheme of the AGBT method that extracts information from weighted colored algebraic graphs of molecules. This method combines two types of molecular representations: the BT features generated from bidirectional transformers treatment on SMILES, and the AG features generated from eigenvalues of the molecular graph’s Laplacian matrix.

Application-wise, the generation of graph representations has been achieved by many existing softwares, including the RDKit [70] package and DeepChem [79], which are specifically designed for chemistry purposes, and Deep Graph Library [80], which is a more generic graph neural network (GNN) module. These softwares have documented API, a live and resourceful user community, and are well maintained. While these packages deal with the heavy lifting of generating the adjacency matrix, how to customize the node and edge features is a key factor to improve performance.

Graph-based neural networks

Once we have the graph presentations, the next question is how to feed them into machine learning models. Owing to the complexity of the mathematical structure used in graph presentations, advanced machine learning algorithms are needed, such as GNNs. In addition to chemistry, other research fields that analyze graph-like data are also interesting, including social media connectivity [81, 82] and recommendation systems [83, 84]. In recent years, various types of graph learning methods or frameworks have been developed [76, 85, 86]. We will introduce the widely used Message Passing Neural Network (MPNN) framework and Neural FP model, as well as more recent approaches including Attentive FP, a universal graph convolutional network (GCN) and algebraic graph-assisted bidirectional transformer (AGBT). We will further introduce advanced treatments of graphs. In terms of implementations, there are many well-established software packages, such as the Keras- and Tensorflow-based Spektral [87] and DeepChem [79]. Both packages have APIs with the existing machine learning and deep learning modules integrated with graph representations of popular GNN-related datasets. A user who is familiar with traditional machine learning and deep learning models is able to pick up these two packages.

Examples of GNNs and graph-based molecular presentations

Many GNN propagation rules are under the MPNN framework [86, 88]. It is a general framework for learning node embeddings or learning the whole graph representations. The MPNN framework decomposes the learning into two phases: (i) the message passing phase, during which the information is shared between nodes to update node features, and (ii) the readout phase, during which the feature vector of the whole graph is learned [86]. An example of this framework is the GCN developed by Kipf et al. [76]. In Figure 3B–D, the convolution operation in a GCN is very similar to that in a traditional convolutional neural network (CNN). While the convolution operation in a CNN collects information from the node of interest in a given-sized kernel, the convolution operation in a GCN collects the information from neighborhood nodes that are connected to the node of interest. The connectivity between nodes is encoded in the adjacency matrix, which plays a similar role as the convolution kernel in a CNN. The major difference is that in GCN, the convolution operation is actually used to update information, instead of generating a new feature map in CNN. Intuitively, multiple rounds of graph convolution operations can capture information from distal nodes [86]. We can also borrow the idea of pooling layers in CNN as readout functions for GCNs, or any MPNNs [86]. Study 22 and study 32 in Table 2 are two examples on the direct application of the GCN on popular datasets within the drug response prediction domain. Besides GCN, there are many other implementations of the MPNN framework, which have shown promising results on drug classification [85, 89–91], drug response prediction and chemistry.

In addition to the MPNN framework, other types of GNNs have been proposed recently to further improve the graph-based propagation procedure. In the Neural FP model [92], for a target node of interest within a molecular graph, the influence of its neighbor nodes decreases with the topological distance. However, the topological adjacency is not the only factor that determines node–node interactions. Nodes with large topological distance are still able to form intramolecular interactions such as hydrogen bonds. In Figure 3E, the Attentive FP model was proposed to address this issue, in which the impact of a node was learned through a graph attention mechanism [89]. Compared with previous graph-based molecular presentations, Attentive FP balances the contribution of topological adjacency as well as hidden linkage among nodes through the attention mechanism. In Figure 3F, a GCN-based approach was proposed for predicting universal properties of molecules and materials [93]. It is also the first attempt to predict the properties of 2D and porous materials by GCN. Moreover, a new method inspired by algebraic graphs has been reported recently [94]. In this AGBT framework in Figure 3G, the 3D molecular information is first encoded into a weighted colored algebraic graph. By calculating the eigenvalues of graph Laplacians, the algebraic graph features are extracted. Briefly, the first non-zero eigenvalue, Fiedler value, corresponds to the algebraic connectivity that reflects the overall connectivity and robustness of the graph. The number of zero eigenvalues corresponds to the number of connected components. Moreover, the algebraic graph is mathematically associated with the geometric graph, so that molecular descriptors can be obtained through calculating statistics (e.g. the maximum, minimum and standard deviations) of non-trivial eigenvalues of the Laplacian matrix. The computational cost of eigenvalue calculation is relatively expensive. Meanwhile, the information from unlabeled molecular data was learned and extracted as latent vectors by the bidirectional encoder of a transformer model. By fusing multiple representations from the algebraic graph, the bidirectional transformer and other machine learning algorithms, the AGBT framework improved the predictions of many molecular properties.

Advanced topics: pre-training and multi-task learning

Beyond different ways of constructing GNN architectures, there are two practical topics on GNN applications that can further boost predictive performance: pre-training and multi-task learning (MTL). The pre-training strategy [95] proves to be powerful in natural language processing [96] and computer vision [97]. Thus, it is not surprising that this idea has been brought into GNN applications in chemistry [98]. The motivation of pre-training is to solve two issues in GNN training: first, in many application scenarios, the dataset is scarce [99], which is a common issue for many chemistry datasets; second, GNNs in chemistry often run on out-of-distribution graph structures [100]. The main idea of pre-training is straightforward: a model could be first trained on a larger dataset, which does not necessarily share the same task as the actual dataset. Then, the pre-trained model will be trained, or fine-tuned, on the actual dataset. If we treat this procedure as an optimization strategy, the pre-training step leverages other datasets to help the model move toward the desired global minimum, whereas the fine-tuning step helps the model to actually arrive at that point. Of note, this strategy requires extra caution, because improper pre-training may lead to a decrease in performance [101]. Nevertheless, several studies have reported that a properly implemented pre-training strategy enhanced the performance of GNNs for both classification tasks [100] and regression tasks [102].

The second strategy is MTL, which also aims at solving the data scarcity issue similar to pre-training. The pre-training strategy prioritizes one task and treats other tasks as reference datasets, whereas MTL does not prioritize any given task and trains all tasks in parallel. The extra tasks serve as constraints during MTL, which improves both the performance and training speed [103]. A review article introduces more about MTL [103] and this strategy is reported to be successful in many classification tasks on GNNs [86, 104]. For regression tasks, an advanced kernelized MTL strategy was tested in a recent work about predicting drug response [5]. These results indicate that MTL together with GNNs are beneficial to drug-related tasks.

Summary of graph notations

As the state-of-the-art molecular representation method, graph notations are not perfect owing to the interpretable issues. The saliency map, a commonly used tool in computer vision, provides an opportunity to analyze the activation of the input graphs and rationalize the feature importance of graphs, or even produce better features [10]. Unlike the better-established molecular FP representations, the graph representation is still developing rapidly, so that selecting a proper notation, as well as a proper GNN architecture, may be very challenging. Another issue of graph notations is that they may fail to describe complicated molecules, such as coordination molecules or ionic molecules [12]. In terms of predictive performance, graph-based molecular representations are not necessarily the best solution. A recent comprehensive benchmark study shows that on average descriptor-based traditional machine learning models outperformed graph-based neural networks on 11 datasets related to drug discovery [105]. In addition, descriptor-based models require much less computational resources than neural networks. These results indicate that traditional descriptor-based methods should be considered and tested, especially given the low computational cost and competitive performance.

Conclusion and future perspectives

Throughout the review, we mainly provide application examples in the drug response prediction domain. In fact, many molecular representations and their advanced variants have shown promising performance in other tasks in the broader field of drug discovery. For instance, two variants of the linear notations, the Self-referencIng Embedded Strings (SELFIES) [106] and the SMILES Pair Encoding [107], have both shown promising performance in generation tasks on the QM9 dataset [108] and the ChEMBL25 dataset [109, 110], respectively. A novel molecular FP combining the concepts of substructure and atom-pair FP was proposed [111]. It was benchmarked on a virtual screening dataset [112] and demonstrated good performance. Although these examples are not direct applications in the drug response field, the results indicate that new representations with better descriptive powers may be beneficial for drug response prediction.

At the end of this review, one may raise a question on how to choose representation given a drug response prediction task. As we mentioned earlier, stringent comparisons such as data challenges are needed to benchmark the performance of different methods. The recent graph notation-based approaches have shown promising better results on many tasks, yet we also need to consider the trade-off among descriptive power, complexity, feasibility and computational resources. Linear notations and molecular FPs are inherently much easier to be incorporated with the genomic data in a machine learning model, which can be achieved by a simple vector concatenation.

We encourage beginners to start with a simpler molecular representation, then gradually try more advanced ones. The majority of molecular representations we introduced in this review have been maturely implemented and incorporated into existing software packages. Considering many application cases mentioned above, even simple representations, SMILES and molecular FPs, can provide an acceptable performance on the drug response prediction task. Therefore, there is no need to treat molecular representations as rocket science—it is just an easy but powerful tool to help us build better drug response prediction models.

Key Points

• This review provides a thorough survey on widely used molecular representation methods.

• For each molecular representation method, we introduce its generation mechanism.

• We present its implementation along with application examples in drug response prediction.

Xin An is a master student studying bioinformatics at the University of Michigan, Ann Arbor. She is a Research Assistant under the guidance of Dr Yuanfang Guan and is interested in computational medicine.

Xi Chen is a Postdoctoral Research Associate at the University of Michigan, Ann Arbor in Prof. Yuanfang Guan’s lab. He is dedicated to the delemetoment of novel drug descriptors and their applications in drug response predictions.

Daiyao Yi graduated from the University of Michigan with a master degree of bioengineering. She will attend the University of Florida for PhD study.

Hongyang Li is a Research Investigator at the University of Michigan, Ann Arbor. He develops machine learning models related to functional genomics, biomedical imaging and protein-small molecule interactions.

Yuanfang Guan is an Associate Professor at the University of Michigan, Ann Arbor. She has led the development of several top-performing algorithms in benchmark studies for drug response predictions.

Funding

National Institutes of Health (NIH/NIGMS R35GM133346-01) and the National Science Foundation (NSF/DBI #1452656).