Abstract
Recent outbreaks of novel infectious diseases (e.g., COVID-19, H2N3) have highlighted the threat of pathogen transmission, and vaccination offers a necessary tool to relieve illness. However, vaccine efficacy is one of the barriers to eradicating the epidemic. Intuitively, vaccine efficacy is closely related to age structures, and the distribution of vaccine efficacy usually obeys a Gaussian distribution, such as with H3N2 and influenza A and B. Based on this fact, in this paper, we study the effect of vaccine efficacy on disease spread by considering different age structures and extending the traditional susceptible-infected-recovery/vaccinator(SIR/V) model with two stages to three stages, which includes the decision-making stage, epidemic stage, and birth-death stage. Extensive numerical simulations show that our model generates a higher vaccination level compared with the case of complete vaccine efficacy because the vaccinated individuals in our model can form small and numerous clusters slower than that of complete vaccine efficacy. In addition, priority vaccination for the elderly is conducive to halting the epidemic when facing population ageing. Our work is expected to provide valuable information for decision-making and the design of more effective disease control strategies.
Keywords: Vaccination behaviors, Age structure, Birth-death process, Disease spreading, Population ageing
1. Introduction
For centuries, infectious diseases (e.g., SARS, H7N9, COVID-19, etc.) have been a serious threat to human life and health, causing great damage to people’s lives and property [1], [2], [3]. Therefore, the topic of how to prevent each disease from spreading becomes an active area. The most effective method of making the epidemic disappear is vaccination, and factors related to humans play a crucial role in preventing the epidemic and gaining scholars’ attention [4], [5].
In the field, elements of human behaviours, such as characteristics [6], [7], [8], behavioural patterns [9], [10], and age [11], [12], have proven crucial in halting epidemics. However, an epidemic can fail to be eradicated due to the vaccination dilemma [13]. The vaccination dilemma indicates that the optimal strategy for vaccination campaigns for individuals does not mean that it is optimal for the group when individuals act in their own interest with perfect information about their risk of infection. In other words, the Nash equilibrium is different between individuals and groups. Non-vaccinated individuals face two scenarios: keep healthy (free riders) or become infected from those that hitchhike unsuccessfully. Successful free riders may result in vaccination levels lower than the optimal vaccination levels required by the population, implying that a vaccination dilemma arises [14], [15]. To investigate the vaccination dilemma, evolutionary game theory [16], [17] and network theory [18], [19] offer a useful tool for studying this perplexing dilemma. Fu mentioned a two-stage model to describe voluntary vaccination campaigns by combining evolutionary game theory and epidemic processes [20]. Furthermore, different elements, such as the utility of delayed vaccination [21], a third strategy [22], different update methods [23], and different influenza diseases [24], are considered. For example, Jun Tanimoto combined two influenza disease (influenza A and B) transmission processes with two types of vaccine decision processes to study the impact of different vaccination decisions and found different vaccination levels depending on the costs of vaccines [25].
In fact, adverse events following immunization due to vaccines are ubiquitous [26], [27]. There is increasing evidence that vaccines can only provide partial immunization in the process of most propagation. According to the experimental data, vaccine efficacy is bound up with individuals’ age, and it turns out that age is related to vaccine efficacy [28], [29], [30], [31], [32]. In addition, the distribution of vaccine efficacy by age is a Gaussian distribution. That is, when the age range is between 18 and 50, the rate of vaccine efficacy is higher than those outside that range. Thus, the vaccination process according to age structure needs to be explored. When we consider the age structure in a model, it indicates that birth and death processes must be considered. In our study, the birth-death process by age structure was introduced to explore the effect of inoculation efficacy on the population. To simplify our model, we extend the two-stage model (vaccination campaign, and epidemic stage) to a three-stage model (vaccination campaign, epidemic stage, and birth-death stage) to describe our model with an expedient age structure. After experiencing vaccination, the risk of infection for vaccinated individuals is closely linked to their age. According to the research data, we build a failure rate function whose shape is the inverse Gaussian distribution to describe the relationship between vaccine failure rate and age. Moreover, individual age increases holdings, the probability of death also increases, and dead individuals are replaced by newborns. Exploring the specific phenomena in which a higher percentage of vaccination is contrasted with the absence of vaccine failure in our model relieves the vaccination dilemma to some extent. Given the limited vaccine supply, the epidemic size can be suppressed when offering vaccines preferentially to the elderly group. The findings shed new light on controlling an epidemic’s spread.
This paper is organized as follows. First, we combined the relationship between age structure and failure rate with the SIR/V dynamic model. Then, we obtained a series of results to explain the issues arising from the results. Finally, we summarize and discuss the potential patterns and implications.
2. Model
To clearly show our model, following common practice [20], we construct repeated three-stage processes in structured networks and well-mixed populations to describe the voluntary vaccination program: the decision-making stage, the epidemic stage, and the birth-death stage. The repeated three-stage process is shown in Fig. 1 . We present the model from the following groups: payoff structure, dynamic in the structured population, and dynamic in the well-mixed population.
Fig. 1.
Schematic diagram of a three-stage vaccination dynamic model. The first stage is the public vaccination campaign, which occurs prior to any infection. In this stage, each individual decides whether to be vaccinated or not. Vaccination imposes a cost to the vaccinator, . Here, we assume that the vaccine is not fully effective. In the second stage, the epidemic strain infects an initial number of individuals and then spreads according to SIR dynamics. The third stage is the birth and death change of the age structure.
2.1. Payoff structure
We must express the payoff provided at various phases when introducing human behavior on vaccination. In the first period (stage 1), each individual decides whether to vaccinate, which occurs before the beginning of the epidemic season. Different strategy options receive different payoffs, with for vaccination and no measures for 0. Here, cost is closely associated with immediate expenditure, side effects on health, and other factors. We employed the conventional susceptible-infection-recovery (SIR) model with a vaccination procedure as the disease transmission model in the second phase (stage 2). The model is the most natural fit for seasonal influenza-like illnesses, where vaccination provides imperfect immunity for one season. The population within the epidemic range is divided into four exclusive categories: susceptible (S), refers to the lack of immune capacity but not sick individuals, easy to infect after contact with the infected, infected (I), has been infected, it can spread to the susceptible; recovery (R), a person who has immunity after recovery, and vaccinator (V), indicates individuals who have been vaccinated, regardless of whether the vaccines work successfully subsequently. The process occurs along with costs. The costs are 0, , and for susceptible, infected individuals who are susceptible, and vaccinated but infected individuals. We set unless otherwise noted.
According to the payoff structure specification, individuals’ total compensation is determined by their category membership, as summarized in Table 1 . The individual’s strategy encompasses vaccination and nonvaccination, and the individual’s status is divided into illness and healthy. Vaccinated and healthy individuals have a payoff of . However, vaccinated but infected individuals have a payoff . In addition, the payoffs of successful free riders () and unsuccessful free riders () are assigned as 0 and , respectively. Let be the relative cost of vaccination.
Table 1.
Individuals’ states (in equilibrium) with their payoffs.
| Strategy/Status | Healthy | Infected |
|---|---|---|
| Vaccinated(V) | ||
| Nonvaccinated(NV) | 0 | -1 |
2.2. Dynamic in the structured-population
Here, players follow voluntary vaccination rule on the different complex networks. During the decision-making process, individuals evaluate their payoffs after an epidemic season and decide whether to mimic others’ strategies or maintain their strategies. The likelihood of imitating others’ strategies by comparing payoffs is calculated using the pairwise Fermi update function [33], [34], where an agent having the strategy with the payoff adopts the strategy of a randomly chosen neighbour having the payoff with the probability:
| (1) |
where the parameter measures the strength of selection. A smaller signifies strong selection, that is, individuals are more responsive to the payoff difference. Due to the effectiveness of the vaccine, individuals who are vaccinated but infected tend not to adopt the strategy of vaccination. Thus, we set a special parameter on the Fermi function to portray this feature. The probability that individuals imitate others is that:
| (2) |
And has form:
| (3) |
where and denote the number of vaccinated neighbors and vaccinated but infected neighbors centering on individual . Specially, when , let . Unless stated otherwise, is 0.1.
In the epidemic process, susceptible individuals can be infected by their infected neighbours with probability and infected turn to recovery with . Vaccinated individuals turn susceptible again at a rate . The data revealed that pandemics of H3N2, influenza A and B, among others, had higher vaccine failure rates among adolescents and older age groups compared to those in their prime years [30], [35]. Therefore, it is reclassified using an age-dependent Gaussian function to present the vaccine failure rate at age for each individual
| (4) |
where is age, is the central age of the Gaussian function, and is the width of the function. To better fit the true vaccine failure rate, we take [36].
In the last stage, the birth-death process happens. Note that, at the beginning of the dynamic, we endow each individual with an age , which is produced from a uniform distribution of . When performing a Monte Carlo step, the age for all individuals adds one. According to the conclusion from demography [36], individuals die with probability defined by a sigmoid distribution:
| (5) |
where and are defined to ensure that the average life expectancy is 75 years. When an individual dies, their age is reset [36].
Note that, initially, individuals vaccinate randomly. Besides, we introduce initial infected individuals into the susceptible population at each step and simulate the transmission process of infectious diseases by Gillespie algorithm program [37]. In general, the second stage terminates until no more new infected individuals arose. Unless otherwise stated, we set .
2.3. Dynamic in the well-mixed population
According to the dynamic description of the structured population, the dynamics of these compartments are given by
| (6) |
where is the average level of vaccine failure. The total population is evident: . The , , , and correspond to the proportion of susceptible, vaccinated, infected, and recovery, respectively. The initial conditions were , , and , where is the initial vaccination level.
In a classical SIR model, the basic reproduction ratio denotes the average number of secondary infections caused by a single infectious agent. When , the disease outbreaks. Conversely, it dies out. According to previous studies [20], [38], the final size of the epidemic is . However, in the SIR/V model with vaccine efficacy, the fraction of susceptible individuals is . Therefore, the basic reproduction ratio [39] and is defined as
| (7) |
| (8) |
The risk of infection in an infinite population is given as follows:
| (9) |
where is the final size of the epidemic. The vaccination rate is obtained according to Nash equilibrium theory [20]:
| (10) |
where , is the infection risk in infinite population obtained from Nash equilibrium. Augmenting the vaccine failure rate leads to an upswing in the vaccination level, and if , then is workable. The threshold is known as the ”herd immunity threshold” above which the infection will not spread in the population.
The evolution of the vaccination strategy is estimated by the following equations, derived from mean-field theory in a well-mixed population:
| (11) |
These variables can be calculated based on the final epidemic size (the proportion of each component when the SIR/V process is stable):
(i)The proportion of vaccinated and healthy is
(ii) The proportion of vaccination but infected is
(iii)The proportion of successful free-riders is
(iv) The proportion of unsuccessful free riders who are infected is .
The vaccination level and the proportion of sick individuals under equilibrium can be measured by Eq. (9) and Eq. (11), respectively. The theoretical solution can be obtained after numerical simulation.
3. Results
3.1. Results in the well-mixed population
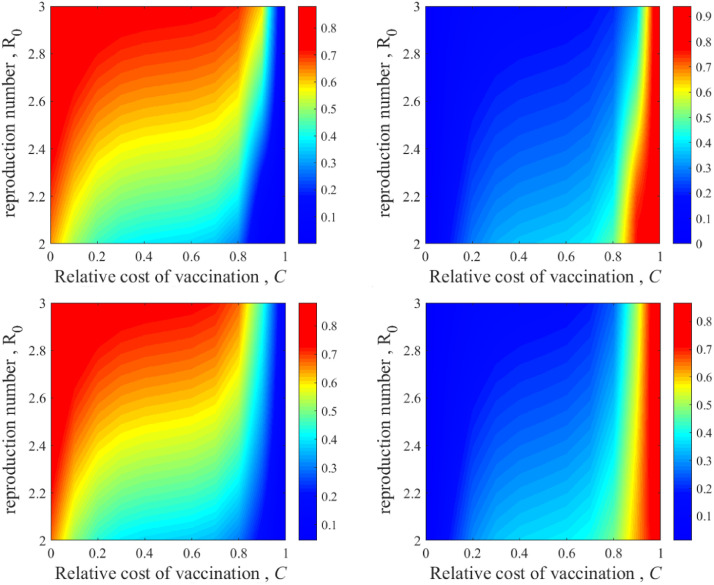
To explore the impact of age structure on vaccination campaigns, Fig. 2 portrays the vaccination level (left) and final epidemic size (right), as a function of the relative cost of vaccination and the basic reproduction ratio , from two perspectives: mean-field approximation analysis (the top of the panel) and Monte Carlo simulation (the bottom of the panel) in a well-mixed population. Comparing the results from the two methods, it is observed that qualitative agreement between simulations and theoretical predictions is obtained. However, the reason some deviations happen between the two results is the stochastic nature of disease transmission in Monte Carlo simulations and the deterministic nature of the theoretical analysis. When the relative cost is on the verge of 0, the proportion of vaccination is so high as to achieve herd immunity, meaning the disease cannot pass among humans. As grows, the vaccination level shows a progressive convergence to zero regardless of . The larger is, the greater the probability of a disease outbreak, leading individuals to tend to vaccinate even when is high.
Fig. 2.
versus phase graph with different effectiveness levels presuming mean-field (top) and multi-agent simulation (bottom) approaches (in a well-mixed population). Phase graphs of vaccination level (left) and final epidemic size (right) depending on the basic reproduction ratio and relative cost of vaccination, , respectively. The simulated and theoretical results are essentially identical. Parameters: the proportion of vaccinated seeds and the proportion of infected seeds .
3.2. Results in the lattice network
The aforementioned results are achieved with an unstructured population, and we focus on the results obtained from the structured population. In Fig. 3 , we consider three-stage dynamics on a square lattice. To facilitate observation, we set a baseline (black line) obtained by the model whose setting is complete efficacy. When is zero, herd immunity is obtained, as shown in Fig. 3(a), leading to no epidemic (see Fig. 3(b)). Additionally, the vaccination level is higher than the baseline in a majority of the range of . In particular, as a result of imperfect vaccine, making the vaccination individuals distribute in the system, thus, the vaccination level is high, resulting in a small level on the final epidemic size. However, the proportion of vaccinated individuals is so infrequent that vaccinated but infected individuals are also rare. Thus, the proportion of vaccinated but infected individuals experienced a peak in Fig. 3(c).
Fig. 3.
(Color online) Vaccination dynamics in a Lattice Network. The proportions of vaccinated (a), infected (b), and vaccination failure and infected (c) individuals are shown as a function of the relative cost of vaccination, . The intensity of selection is set to 0.1. In our simulation , , and . The black points indicate the failure rate, , for vaccination, and the red points are where there is age structure failure, obtained from our Monte Carlo simulations. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
To further elucidate the reasons for the enhancement of the vaccination level, we present a time evolution plot of the vaccination level and typical snapshots at certain steps in Fig. 4 . The top of the panel shows that the vaccination level decreases at first and stabilizes soon after. The state of the individual in the middle part of the image corresponds to the strategy of the individual in the bottom part. Typical snapshots are taken at steps 1, 3, 4, 20, and 15000. At the initial moment, 50% of the vaccinated individuals and 1% of infected individuals are randomly distributed in the network. At time step 3, the individuals’ choice of strategy begins to form small clusters, and diseased individuals begin to reproduce. Individuals choosing vaccination strategies form small and numerous clusters, and disease spread widely across the population at time step 4. Individual selection of strategies forms clusters, and the proportion of diseased individuals reaches equilibrium at time step 20. Finally, in equilibrium, the proportions of vaccinated and diseased individuals converge to 0.18 and 0.4, respectively. Vaccinated individuals successfully protected a fraction of susceptible individuals from infection.
Fig. 4.
(Color online) Proportion of vaccinated individuals as a function of time and a typical snapshot of the state configuration of a square grid subgroup at rest. The panel diagram shows the system with parameter = 0.1, the middle image is the panel diagram of the individual status, and the bottom plot is a panel diagram of the individual strategy choices. The middle image corresponds to the results at the same time step as the bottom image. Yellow denotes vaccinated individuals who did not fail, purple denotes successful free riders, and red denotes infected individuals. Blue denotes individuals who choose to be vaccinated, and green denotes individuals who choose not to be vaccinated. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Why is the vaccination rate greater in our model than that in conditions of complete efficacy? We note that individuals are randomly distributed initially, and as time goes on, vaccinated individuals cluster together accordingly. Many vaccinated individuals are surrounded by successful free riders. These vaccinated individuals are buried in unvaccinated individuals and prefer to imitate free riders who receive relatively low benefits. Thus, this behavioural clustering is generated by imitation dynamics. That is, vaccinated individuals tend to gather around vaccinated individuals, while unvaccinated individuals tend to collect around unvaccinated individuals. The aggregation of unvaccinated individuals contributes to the spread of the disease, increasing the likelihood of an outbreak. However, in the presence of vaccine failure, this clustering weakens accordingly because vaccinated individuals cluster in vaccination failure, and vaccination failure tends to cluster with unvaccinated individuals, weakening the formation rate. Moreover, vaccinated and infected individuals clustering with vaccinated individuals are more likely to be revaccinated because they receive relatively low benefits. This pattern is why the epidemic size (vaccine coverage) in our model is smaller (greater coverage) than the epidemic size (vaccine coverage) in the absence of vaccine failure. Indeed, mimicry leads to the aggregation of susceptible individuals. This pattern may exacerbate the outbreak of infectious diseases [40].
3.3. Results in the ER and SW networks
To go a step further and validate the results from the structured population, we carry the dynamic on a Erdos-Renyi random network (the top of Fig. 5 ) and a small-world network (the bottom of Fig. 5). The phenomena produced by the simulation are largely consistent across the different networks. However, the inoculation level increases more obviously in these networks, and the proportion of vaccinated but infected individuals is higher than that in the lattice network.
Fig. 5.
(Color online) Vaccination dynamics in Erdos-Renyi random networks and small-world networks. The proportions of vaccinated (a)(d), infected (b)(e), and vaccination failure and infected (c)(f) individuals are shown as a function of the relative cost of vaccination, . The intensity of selection is set to 0.1. In our simulation, , , and . The black points indicate the failure rate, , for vaccination, and the red points are where there is age structure failure, obtained from our Monte Carlo simulations. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.4. Results in the barabsialbert scale-free network
To verify the robustness of our model, in Fig. 6 , we study the effect of the relative cost of vaccination level and final epidemic size in a BarabsiAlbert scale-free network [41]. Comparing the conclusion of Fig. 5, we observe a similar trend in Fig. 6: increasing cost leads to a decrease in the proportion of vaccinators, which in turn causes an increase in final epidemic size. However, our model generates a lower vaccination level compared with the case of complete vaccine efficacy at . In addition, our model generates a higher final epidemic compared with the case of complete vaccine efficacy. Because scale-free networks have severe heterogeneity and their connectivity status among nodes has uneven distribution, the few nodes in the network called hub nodes have many connections, while most nodes have only very few connections. A few hub nodes play a dominant role in the dynamic process of scale-free networks. For another thing, from a specific point of view, the reasons for this situation are analysed through strategy and state distribution for each degree on scale-free networks.
Fig. 6.
(Color online) Vaccination dynamics in on a scale-free network. The proportions of vaccinated (a), infected (b), and vaccination failure and infected (c) individuals are shown as a function of the relative cost of vaccination, . The intensity of selection is set to 0.1. In our simulation, , , and . The black points indicate the failure rate, , for vaccination, and the red points are where there is age structure failure, obtained from our Monte Carlo simulations. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
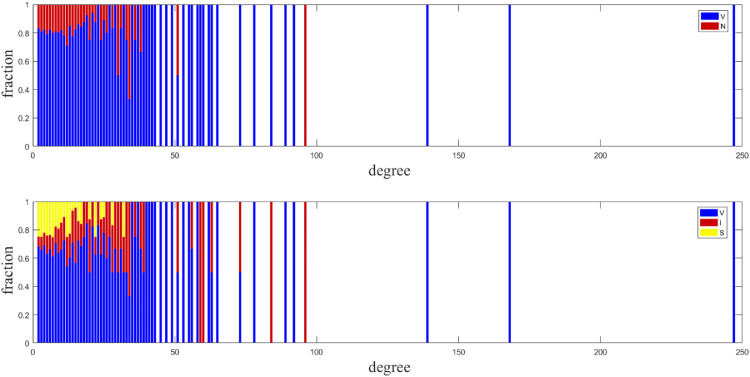
It is meaningful for us to understand why scale-free networks produce different results from other networks. We present a detailed description of the strategy and state distribution for each degree in Fig. 7 . We clearly find that hub nodes tend to be vaccinated. Hub nodes become infected more easily once they are not vaccinated or fail after vaccination. In this condition, infected hub nodes promote the spread of disease. Therefore, our model generates a higher final epidemic in the case of much higher vaccination than in the case of complete vaccine efficacy. With the cost of the vaccine set at , our model generates a lower vaccination level compared with the case of complete vaccine efficacy, which is due to hub nodes becoming infected more easily once they are not vaccinated or fail after vaccination, where fewer hub nodes are vaccinated. Nodes with small degrees tend not to be vaccinated when updating strategy in Fig. 8 . Thus, this phenomenon in Fig. 6 arises from the heterogeneity of scale-free networks and the influence of hub nodes.
Fig. 7.
Strategy and state distribution for each degree on a scale-free network. Strategy distribution: The fractions of vaccinated and nonvaccinated populations are represented by blue and red, respectively. State distribution: The fraction of the vaccinated population, infected population, and successful free riders are represented by blue, red, and yellow, respectively. The total fraction of each bar adds up to 1. Other parameters are set as , . (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 8.
Strategy and state distribution for each degree on a scale-free network. Strategy distribution: The fractions of vaccinated and nonvaccinated populations are represented by blue and red, respectively. State distribution: The fraction of the vaccinated population, infected population, and successful free riders are represented by blue, red, and yellow, respectively. The total fraction of each bar adds up to 1. Other parameters are set as and . (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.5. Results in case of priority vaccination
Facing problems in the ageing of the population, we compare the results under conditions of limited seasonal vaccine supply. To obtain the effect of priority vaccination, a new experiment is carried out. Here, crowds are divided into three zones, the youth (below 17 years), the adults (18–50 years), and the old (above 51 years), according to the effectiveness of a vaccine [42]. Given the limited seasonal vaccine supply , the vaccine is preferentially given to a certain population. That is to say, the vaccine can offer them freely. Thus, they are divided into three strategies: youth-priority strategy, adult-priority strategy, and old-priority strategy.
Fig. 9 shows the vaccination level (a) and final epidemic size (b) as a function of for different strategies. When the vaccine supply is low in a certain population, the vaccination level is the same as the vaccine supply. When is no fewer than a certain population, after the certain population is vaccinated, other populations can vaccinate on their own by paying cost . However, when the vaccine supply exceeds a certain population, the epidemic level has little distinction between adult priority and old priority strategies. In addition, the results produced by the youth-priority strategy are inferior to those produced by other strategies regardless of the indicators (vaccination level and epidemic size).
Fig. 9.
(Color online) Vaccination dynamics for controlling the proportion of age-structured vaccinations in the lattice network. The proportions of vaccinated (a) and infected (b) individuals are shown as a function of the vaccine percentage. The blue, red, and green lines represent the results of vaccination at different priority ages. In our simulation, , , , and . (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
4. Conclusion
In the two-stage model [20], individuals experience the vaccination decision period before an epidemic stage. Based on this design, we extend it to a three-stage vaccination campaign. By endowing each individual with age, the birth-death process and vaccine efficacy related to age are introduced. The results show that when vaccine efficacy is closely related to age, vaccines given preferentially to the elderly are more effective than offering others. In addition, within the framework of limited vaccine effectiveness in homogeneous networks, the vaccination level can be improved. In heterogeneous networks, due to the influence of hub nodes, the vaccination level is reduced when the relative cost of vaccine , which has also been validated by the multi-agent simulation approach. These practical limitations notwithstanding, our results emphasize the surprising value of what vaccination priority being more effective facing an aging society, with important implications for the fight against the epidemic.
In this study, the learning strategy comes from the choice of rational individuals. However, learning methods in real life are diverse and complex. The specific but realistic situation of individual vaccination decisions and disease transmission can be significantly influenced by the spatial structure connecting individuals and human characteristics. When considering the influence of tools for information dissemination, the decision-making method becomes more intricate. In the next step, a diversity of learning strategies conforming to realistic situations will be introduced to predict the spread of epidemics and provide valuable advice for human pandemic preparedness.
CRediT authorship contribution statement
Lu Yin: Conceptualization. YiKang Lu: Formal analysis. ChunPeng Du: Writing – original draft. Lei Shi: Writing – original draft.
Declaration of Competing Interest
We declare we have no competing interests.
Acknowledgement
L.S. was supported by a key project (no. 11931015) of the National Natural Science Foundation of China (NNSFC) and NNSFC project no. 11671348. Yikang Lu was supported by NNSFC project no. 32160239. Lu Yin was supported by project (no. 2021Y555) of Yunnan Provincial Education Department Science Foundation of China.
References
- 1.Xiong C., Hu S., Yang M., Luo W., Zhang L. Mobile device data reveal the dynamics in a positive relationship between human mobility and covid-19 infections. Proceedings of the National Academy of Sciences. 2020;117(44):27087–27089. doi: 10.1073/pnas.2010836117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang Z., Andrews M.A., Wu Z.-X., Wang L., Bauch C.T. Coupled disease–behavior dynamics on complex networks: a review. Phys Life Rev. 2015;15:1–29. doi: 10.1016/j.plrev.2015.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang L., Wang Z., Zhang Y., Li X. How human location-specific contact patterns impact spatial transmission between populations? Sci Rep. 2013;3(1):1–10. doi: 10.1038/srep01468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Valdano E., Ferreri L., Poletto C., Colizza V. Analytical computation of the epidemic threshold on temporal networks. Phys Rev X. 2015;5(2):021005. [Google Scholar]
- 5.Dietz K. The estimation of the basic reproduction number for infectious diseases. Stat Methods Med Res. 1993;2(1):23–41. doi: 10.1177/096228029300200103. [DOI] [PubMed] [Google Scholar]
- 6.Liu X.-T., Wu Z.-X., Zhang L. Impact of committed individuals on vaccination behavior. Physical Review E. 2012;86(5):051132. doi: 10.1103/PhysRevE.86.051132. [DOI] [PubMed] [Google Scholar]
- 7.Lu Y., Geng Y., Gan W., Shi L. Impacts of conformist on vaccination campaign in complex networks. Physica A. 2019;526:121124. [Google Scholar]
- 8.Zou R., Deng Z., Lu Y., Hu J., Han Z. Study of spreading phenomenon in network population considering heterogeneous property. Chaos, Solitons & Fractals. 2021;153:111520. [Google Scholar]
- 9.Xia S., Liu J. A computational approach to characterizing the impact of social influence on individuals vaccination decision making. PLoS ONE. 2013;8(4):e60373. doi: 10.1371/journal.pone.0060373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tanaka M., Tanimoto J. Is subsidizing vaccination with hub agent priority policy really meaningful to suppress disease spreading? J Theor Biol. 2020;486:110059. doi: 10.1016/j.jtbi.2019.110059. [DOI] [PubMed] [Google Scholar]
- 11.McLean H.Q., Thompson M.G., Sundaram M.E., Kieke B.A., Gaglani M., Murthy K., et al. Influenza vaccine effectiveness in the united states during 2012–2013: variable protection by age and virus type. J Infect Dis. 2015;211(10):1529–1540. doi: 10.1093/infdis/jiu647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Murphy J., Vallières F., Bentall R.P., Shevlin M., McBride O., Hartman T.K., et al. Psychological characteristics associated with covid-19 vaccine hesitancy and resistance in ireland and the united kingdom. Nat Commun. 2021;12(1):1–15. doi: 10.1038/s41467-020-20226-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bauch C.T., Galvani A.P., Earn D.J. Group interest versus self-interest in smallpox vaccination policy. Proceedings of the National Academy of Sciences. 2003;100(18):10564–10567. doi: 10.1073/pnas.1731324100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gittings K., Matson K.L. Establishing herd immunity against ebola through vaccination. Vaccine. 2016;34(24):2644–2647. doi: 10.1016/j.vaccine.2016.04.047. [DOI] [PubMed] [Google Scholar]
- 15.Wei Y., Lin Y., Wu B. Vaccination dilemma on an evolving social network. J Theor Biol. 2019;483:109978. doi: 10.1016/j.jtbi.2019.08.009. [DOI] [PubMed] [Google Scholar]
- 16.Huang K., Wang Z., Jusup M. Incorporating latent constraints to enhance inference of network structure. IEEE Trans Network Sci Eng. 2018;7(1):466–475. [Google Scholar]
- 17.Zhu Z., Dong Y., Lu Y., Shi L. Information exchange promotes and jeopardizes cooperation on interdependent networks. Physica A. 2021;569:125772. [Google Scholar]
- 18.Dai J., Huang K., Liu Y., Yang C., Wang Z. Global reconstruction of complex network topology via structured compressive sensing. IEEE Syst J. 2020;15(2):1959–1969. [Google Scholar]
- 19.Huang K., Wu S., Li F., Yang C., Gui W. Fault diagnosis of hydraulic systems based on deep learning model with multirate data samples. IEEE Trans Neural Netw Learn Syst. 2021:1–13. doi: 10.1109/TNNLS.2021.3083401. [DOI] [PubMed] [Google Scholar]
- 20.Fu F., Rosenbloom D.I., Wang L., Nowak M.A. Imitation dynamics of vaccination behaviour on social networks. Proceedings of the Royal Society B: Biological Sciences. 2011;278(1702):42–49. doi: 10.1098/rspb.2010.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Alvarez-Zuzek L.G., La Rocca C.E., Iglesias J.R., Braunstein L.A. Epidemic spreading in multiplex networks influenced by opinion exchanges on vaccination. PLoS ONE. 2017;12(11):e0186492. doi: 10.1371/journal.pone.0186492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pastor-Satorras R., Castellano C., Van Mieghem P., Vespignani A. Epidemic processes in complex networks. Rev Mod Phys. 2015;87(3):925. [Google Scholar]
- 23.Shi B., Qiu H., Niu W., Ren Y., Ding H., Chen D. Voluntary vaccination through self-organizing behaviors on locally-mixed social networks. Sci Rep. 2017;7(1):1–11. doi: 10.1038/s41598-017-02967-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Arinaminpathy N., Ratmann O., Koelle K., Epstein S.L., Price G.E., Viboud C., Miller M.A., Grenfell B.T. Impact of cross-protective vaccines on epidemiological and evolutionary dynamics of influenza. Proceedings of the National Academy of Sciences. 2012;109(8):3173–3177. doi: 10.1073/pnas.1113342109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Arefin M.R., Masaki T., Kabir K.A., Tanimoto J. Interplay between cost and effectiveness in influenza vaccine uptake: a vaccination game approach. Proceedings of the Royal Society A. 2019;475(2232):20190608. doi: 10.1098/rspa.2019.0608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.François G., Duclos P., Margolis H., Lavanchy D., Siegrist C.-A., Meheus A., et al. Vaccine safety controversies and the future of vaccination programs. Pediatr Infect Dis J. 2005;24(11):953–961. doi: 10.1097/01.inf.0000183853.16113.a6. [DOI] [PubMed] [Google Scholar]
- 27.de Vrieze J. Suspicions grow that nanoparticles in pfizers covid-19 vaccine trigger rare allergic reactions. Science. 2020;10 [Google Scholar]
- 28.de Montigny S., Adamson B.J., Mâsse B.R., Garrison L.P., Kublin J.G., Gilbert P.B., et al. Projected effectiveness and added value of hiv vaccination campaigns in south africa: a modeling study. Sci Rep. 2018;8(1):1–12. doi: 10.1038/s41598-018-24268-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dean N.E., Gsell P.-S., Brookmeyer R., De Gruttola V., Donnelly C.A., Halloran M.E., Jasseh M., Nason M., Riveros X., Watson C.H., et al. Design of vaccine efficacy trials during public health emergencies. Sci Transl Med. 2019;11(499) doi: 10.1126/scitranslmed.aat0360. [DOI] [PMC free article] [PubMed] [Google Scholar]; eaat0360–eaat0360
- 30.Sah P., Alfaro-Murillo J.A., Fitzpatrick M.C., Neuzil K.M., Meyers L.A., Singer B.H., Galvani A.P. Future epidemiological and economic impacts of universal influenza vaccines. Proceedings of the National Academy of Sciences. 2019;116(41):20786–20792. doi: 10.1073/pnas.1909613116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tsang T.K., Fang V.J., Ip D.K., Perera R.A., So H.C., Leung G.M., et al. Indirect protection from vaccinating children against influenza in households. Nat Commun. 2019;10(1):1–7. doi: 10.1038/s41467-018-08036-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fitzpatrick M.C., Galvani A.P. Optimizing age-specific vaccination. Science. 2021;371(6532):890–891. doi: 10.1126/science.abg2334. [DOI] [PubMed] [Google Scholar]
- 33.Blume L.E. The statistical mechanics of strategic interaction. Games Econ Behav. 1993;5(3):387–424. [Google Scholar]
- 34.Schlag K.H. Why imitate, and if so, how?: a boundedly rational approach to multi-armed bandits. J Econ Theory. 1998;78(1):130–156. [Google Scholar]
- 35.Cowling B.J., Feng S., Finelli L., Steffens A., Fowlkes A. Assessment of influenza vaccine effectiveness in a sentinel surveillance network 2010–13, united states. Vaccine. 2016;34(1):61–66. doi: 10.1016/j.vaccine.2015.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Souza P.V.S., Silva R., Bauch C., Girardi D. Cooperation in a generalized age-structured spatial game. J Theor Biol. 2020;484:109995. doi: 10.1016/j.jtbi.2019.109995. [DOI] [PubMed] [Google Scholar]
- 37.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81(25):2340–2361. [Google Scholar]
- 38.Kabir K.A., Tanimoto J. Vaccination strategies in a two-layer sir/v–ua epidemic model with costly information and buzz effect. Commun Nonlinear Sci Numer Simul. 2019;76:92–108. [Google Scholar]
- 39.Van den Driessche P., Watmough J. Mathematical epidemiology. Springer; 2008. Further notes on the basic reproduction number; pp. 159–178. [Google Scholar]
- 40.Ndeffo Mbah M.L., Liu J., Bauch C.T., Tekel Y.I., Medlock J., Meyers L.A., et al. The impact of imitation on vaccination behavior in social contact networks. PLoS Comput Biol. 2012;8(4):e1002469. doi: 10.1371/journal.pcbi.1002469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Barabási A.-L., Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 42.Singh R., Adhikari R.. Age-structured impact of social distancing on the covid-19 epidemic in india. arXiv preprint arXiv:2003120552020.