Evaluating the state of the art in missing data imputation for clinical data

Abstract

Clinical data are increasingly being mined to derive new medical knowledge with a goal of enabling greater diagnostic precision, better-personalized therapeutic regimens, improved clinical outcomes and more efficient utilization of health-care resources. However, clinical data are often only available at irregular intervals that vary between patients and type of data, with entries often being unmeasured or unknown. As a result, missing data often represent one of the major impediments to optimal knowledge derivation from clinical data. The Data Analytics Challenge on Missing data Imputation (DACMI) presented a shared clinical dataset with ground truth for evaluating and advancing the state of the art in imputing missing data for clinical time series. We extracted 13 commonly measured blood laboratory tests. To evaluate the imputation performance, we randomly removed one recorded result per laboratory test per patient admission and used them as the ground truth. DACMI is the first shared-task challenge on clinical time series imputation to our best knowledge. The challenge attracted 12 international teams spanning three continents across multiple industries and academia. The evaluation outcome suggests that competitive machine learning and statistical models (e.g. LightGBM, MICE and XGBoost) coupled with carefully engineered temporal and cross-sectional features can achieve strong imputation performance. However, care needs to be taken to prevent overblown model complexity. The challenge participating systems collectively experimented with a wide range of machine learning and probabilistic algorithms to combine temporal imputation and cross-sectional imputation, and their design principles will inform future efforts to better model clinical missing data.

Introduction

Clinical data are increasingly being mined to derive new medical knowledge in order to improve diagnostic precision, better personalize interventions and increase efficient utilization of health-care resources [1]. However, unlike experimental data that are collected per a research protocol, the primary role of clinical data is to help clinicians care for patients, so the procedures for its collection are not often systematic. Clinically appropriate data collection often does not occur on a regular schedule but rather is guided by patient condition and clinical or administrative requirements. Thus, electronic health record data are often only available at irregular intervals for selected variables that vary between patients and type of data. While the absence of recorded data may be clinically appropriate, machine learning algorithms’ performance typically suffers from biased and incomplete data. Although numerous imputation algorithms are available for imputing missing measurements [2–5], many of these only focus on a time snapshot using the cross-sectional correlation (e.g. correlation across subjects or across variables) and are not well-suited to longitudinal clinical data [6]. In fact, for clinical data, including longitudinal data, multiple imputation (MI), for example, multivariate imputation by chained equations (MICE) [2], is still a widely used standard practice for addressing the presence of missing data [7, 8]. However, clinical data will usually include a non-continuous and asynchronous time component as patients will have different symptoms and findings recorded, diagnostic studies performed and treatments provided across different time points. Thus, testing algorithm’s ability to explicitly account for the correlation across irregular time points in clinical data motivates the Data Analytics Challenge on Missing data Imputation (DACMI) challenge. Before the challenge, there were a few emerging research efforts attempting to combine cross-sectional correlation and longitudinal correlation [6, 9–11]. Aiming to draw from community research expertise to further improve the state of the art, the DACMI challenge took place from March to June 2019 with a data embargo period in the following year and is the first shared-task challenge on clinical time series imputation to our best knowledge.

Methods

Dataset generation

We developed a dataset from the public intensive care unit (ICU) database, MIMIC3 [12], and provided it as a shared-tasked dataset to develop and validate clinical data imputation algorithms. Figure 1 shows our data generation and inclusion and exclusion criteria. We extracted all admissions in MIMIC3 where each of the 13 blood laboratory tests, shown in Table 1, was recorded at least once. We selected these specific laboratory tests because they are frequently measured on ICU admissions, are quantitative and are clinically meaningful (e.g. serum creatinine in acute kidney injury identification). We further organized data by unique patient admissions. We excluded time points (the time when a lab test was performed) with more than half of the 13 laboratory tests missing. We excluded admissions without at least 10 remaining time points for each variable. This inclusion and exclusion criteria are motivated by the need to randomly mask recorded laboratory test results to create the ground truth, as detailed below. By keeping a significant number of observations both cross-sectionally and longitudinally, we can effectively limit the impact that the masking alters the clinical time series (i.e. the more observations, the less impact from masking one of them). We also refer the reader to the Discussion section for consideration of the clinical context regarding inclusion and exclusion criteria. We have released our source code for dataset creation so that future research can investigate alternative inclusion and exclusion criteria suitable for different goals. We further excluded three ICU admissions that had a constant value across all the time points for one or more laboratory tests, as exactly the same measurements repeated throughout admission indicate signs of problematic recording. Our dataset has 16 534 unique ICU admissions that contain 396 631 time points and 4 773 769 non-missing test result measurements. We randomly split the dataset into a training set and a test set, each containing half of the patient admissions.

Figure 1.

Flowchart of DACMI challenge data generation. The flowchart describes the filters applied and the number of data points taken forward at each step.

Table 1.

Characteristics of selected clinical laboratory tests

Laboratory test	Unit	Interquartile range	Native missing rate (%)	Native + Artificial missing rate (%)
Chloride	mmol/l	100–108	1.19	5.36
Potassium	mmol/l	3.7–4.4	1.31	5.48
Bicarb	mmol/l	22–28	1.40	5.57
Sodium	mmol/l	136–142	1.26	5.43
Hemotocrit	%	26.8–32.7	12.48	16.65
Hemoglobin	g/dl	8.9–11.0	15.01	19.18
MCV	fl	86–94	15.13	19.30
Platelets	k/ul	131–331	14.49	18.65
WBC count	k/ul	7.1–14.1	14.75	18.91
RDW	%	14.4–17.4	15.25	19.42
BUN	mg/dl	16–43	0.76	4.92
Creatinine	mg/dl	0.7–1.8	0.72	4.89
Glucose	mg/dl	100–148	2.67	6.84

Notes: Abbreviations: MCV, mean corpuscular volume; WBC, white blood cell

The generated dataset contains tests that were not performed for a specific patient and have no measured values, which we call natively missing data. The natively missing data do not have ground truth for evaluating the performance of an imputation algorithm. Although participating teams still imputed natively missing data, such data were not included in the evaluation of imputation algorithms. Thus, we randomly removed one recorded result per laboratory test per patient admission, which gave 13 masked results with actually measured ground truth, scattered throughout the varying time points, see Supplementary Table 1, available online at http://bib.oxfordjournals.org/, for an example of natively and artificially missing data. This masking choice to create artificially missing data is to balance the need to have enough ground truth for evaluation and to minimally alter the clinical time series. Table 1 shows that the native missing rates of tests had small differences (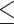5%) to the combined missing rates. Supplementary Table 2, available online at http://bib.oxfordjournals.org/, shows the sequence length and available lab tests per patient for the selected clinical laboratory tests. We further preserved the time irregularities and varying lengths of stays to reflect the real clinical scenario. We asked the challenge participants to impute both the natively missing and the artificially missing data. We only compared their imputed values for artificially missing data with corresponding ground truth when evaluating the challenge participating systems.

Challenge organization and participating teams

The challenge was part of the IEEE International Conference on Healthcare Informatics (ICHI) and leveraged the global outreach of the conference for advertisement in order to attract participating teams. We have also cross-promoted the challenge in the community forums of American Medical Informatics Association and at chapter events of American Statistical Association. The DACMI challenge took place from March to June 2019 and attracted participation from 12 teams worldwide (Table 2). They came from multiple continents, including Asia, Europe and North America. They also span across academia and multiple industries, including technology, insurance and pharmaceutical companies. The challenge workshop was held 10 June 2019, colocated with IEEE ICHI, and had a data embargo period in the following year.

Table 2.

Challenge participating system method comparison

Team (Continent Organization)	Main algorithm	Temporal and cross-sectional modeling consideration	Pre-filling
Ping An [14] (A, I)	LightGBM	Multi-directional temporal and cross-sectional features
AstraZeneca [16] (E, P)	MICE	GP estimated trend features and summary statistics to augment cross-sectional features for MICE
Vanderbilt [17] (N, U)	XGBoost	Measurements from concurrent and pre- and post-three time-stamps	Global mean, local mean, SVD and Soft-Impute
HKBU [20] (A, U)	Fusion layer to combine RNN and MLP outputs	Temporal features for RNN, cross-sectional features for MLP	Temporal decay
Padova [21] (E, U)	Weighted average of KNN and linear interpolation outputs	Temporal features for linear interpolation, cross-sectional features for KNN
TSU [22] (N, U)	Piecewise linear interpolation and non-linear extension of MICE	Temporal features for linear interpolation, cross-sectional features for non-linear extension of MICE	Linear interpolation for tests with over 0.5 correlation with time
DLUT [23] (A, U)	KNN, Soft-Impute and nuclear norm matrix factorization	No explicit modeling for temporal trends
NCSU [24] (N, U)	Matrix factorization methods	Regularization term for modeling temporal locality
Drexel [25] (N, U)	Similarity weighting	Time window based similarity to capture temporal locality
Buffalo/Virginia [26] (N, U)	Fusion gate to combine RNN outputs	Separate RNNs for temporal features of each test and for cross-sectional features
IBM [27] (N, T)	XGBoost as the ensemble method	Base models: linear model for temporal imputation; KNN, RF, MLP for cross-sectional imputation; and bi-directional GRU and LSTM for combined imputation
Iowa [28] (N, U)	Ridge regression, LASSO or gradient boosting as the ensemble method	Base models: spline basis functions for temporal imputation; RBF neural network for cross-sectional imputation; and bi-directional LSTM for combined imputation	RBF interpolation

Continent: A – Asia, N – North America, E – Europe. Organization: I – Insurance, P – Pharmaceutical, U – University, T – Technology.

Evaluation metrics

We evaluated the performance of systems using range normalized root-mean-square deviation (nRMSD). RMSD is frequently used to measure the differences between the model-predicted values and the observed values [13]. Normalizing the RMSD brings different laboratory tests to the same scales and facilitates comparison between them, and we adopted the common choice of range normalization. Let 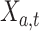denote the imputed values for laboratory test 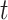of admission 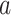, 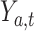represent the actual measured values of the test, 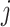index the sequences of the time series 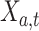and 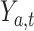. nRMSD for test 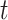is

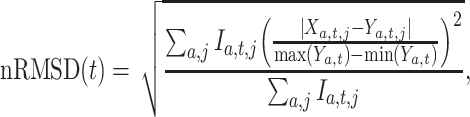where 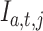is 1 if admission 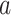, test 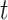at index 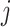is missing and 0 otherwise. Range normalization brings fluctuation of different laboratory tests to a comparable scale. For nRMSD, smaller is better.

Ethics

Ethics approval is waived since MIMIC3 is a public de-identified dataset.

Challenge participating systems

To offer a reference standard for the challenge participating systems, we provided three-dimensional MI with chained equations (3D-MICE) implementation and its data handling utilities to the challenge participating teams for quickly getting familiarized with the data. We also provided 3D-MICE results on the challenge dataset as a performance reference. MICE [2] assumes a conditional model for each variable to be imputed, with the other variables as possible predictors. MICE can rely on regression from predictors to target variables or sampling target variables from joint probability distribution with predictors. 3D-MICE combined regression-based MICE and Gaussian Process (GP) to integrate the cross-sectional and temporal imputations using heuristic weights [14].

Team Ping An [14] used LightGBM [15] to integrate both temporal and cross-sectional features. They included the following feature sets. F1 consists of the values of the other laboratory tests in the current time-stamp. F2 consists of the current time index (see examples in Supplementary Table 1 available online at http://bib.oxfordjournals.org/) and the current time-stamp. F3 consists of the durations between the current time-stamp and the time-stamps before and after. F4 consists of the values of all the 13 laboratory tests in pre and post 3 time-stamps. F5 consists of the max/min/mean values of all the laboratory tests of the current patient admission. They separately built one model for each laboratory test.

Team AstraZeneca [16] proposed a variant of 3D-MICE. They calculated local temporal features, including F1 and F4, as described above and the slope of change trend at each time-stamp estimated using GP. They additionally calculated global patient similarity features using summary statistics (min, max, percentile, mean and SD) for the laboratory tests. Instead of using heuristics to combine temporal and cross-sectional imputation, they used both local temporal features and global patient admission similarity features to augment MICE features and to let MICE’s conditional probability modeling determine how to combine it with cross-sectional imputation. When choosing the regressor for MICE, they used random forest (RF) for laboratory tests with high skewness [red cell distribution width (RDW) and blood urea nitrogen, creatinine and glucose (BUN)] and LASSO for the others.

Team Vanderbilt [17] applied XGBoost [18] and explored pre-filling strategies, including global mean, local mean, iterative Singular Value Decomposition (SVD) and Soft-Impute (iteratively replacing the missing values with those calculated from a soft-thresholded SVD [19]) that do not explicitly account for temporal features. They found that iterative SVD and Soft-Impute pre-filling are more effective than the other two. After pre-filling, they used window-size-based extraction to create features used by XGBoost, and their features are essentially F1 and F4 as described above. They normalized each laboratory test using global mean and standard deviation before imputation. They observed that pre-filling enables a faster convergence for XGBoost. They also observed that increasing the window size resulted in modest improvement in accuracy for glucose imputation and little improvement for other laboratory tests.

Team Hong Kong Baptist University (HKBU) [20] proposed Context-Aware Time Series Imputation (CATSI) to explicitly capture the patient admission condition by a global context vector to augment a bi-directional recurrent neural network (RNN). They used multilayer perceptron (MLP) to learn the model for cross-sectional imputation and used a fusion layer to integrate the temporal imputation and the cross-sectional imputation. They pre-filled the raw measurements using a trainable temporal decay method where measurements farther apart have smaller weights (multiplicative decay factors) when pre-filling the current missing value [10].

Team Padova [21] combined weighted K-Nearest Neighbors (KNN) and linear interpolation to capture the cross-sectional correlation and the temporal correlation, respectively. For KNN imputation, they used population-level Maximal Information Coefficient between laboratory tests to weight the differences between different laboratory tests when calculating the distances between patient admissions. They then computed the imputed value using the average of values of the same test from nearest neighboring patient admissions, weighted by the KNN distances. Either KNN or linear interpolation, or their weighted average, were then selected separately for each variable based on validation set performance.

Team Tennessee State University (TSU) [22] used piecewise time interpolation, a non-linear extension of MICE, and their combination to capture the non-linear trends for imputation. Their piecewise time interpolation used only temporal correlation. Their non-linear extension of MICE essentially replaces MICE’s linear regressors with non-linear gradient boosting tree regressors. Their hybrid model applies piecewise time interpolation to laboratory tests whose correlation with time is >0.5, then runs non-linear extension of MICE on all laboratory tests in the second stage.

Team Dalian University of Technology (DLUT) [23] experimented with KNN, Soft-Impute and matrix factorization using nuclear norm as loss function as imputation methods. Nuclear norm is defined as the sum of singular values of a matrix and is a continuous approximation to a matrix’s rank. Intuitively, matrix factorization using nuclear norm aims to recover a low-rank matrix from the observed subset of its entries. Their models do not explicitly use temporal correlations.

Team North Carolina State University (NCSU) [24] applied regularized matrix decomposition that seeks low-rank approximation to the observed data matrix for imputation. Their regularizations aim to reduce overfitting and preserve temporal locality (closer time-stamps imply closer measurements). They experimented with configurations where patient admissions share latent factors or have unique latent factors.

Team Drexel [25] calculated patient admission similarities based on observed data and used the similarities to weight the contribution to the imputing target from the measured values of the same variables of similar patients. They calculated time-sensitive similarity by filtering the target patient admission using a time window (consisting of F1 and F4 as previously described) around the time-stamp to be imputed, generating a target segment. They generated reference segments with the same length as the target segment, from each of the rest patient admissions, and calculated the similarity between target and reference segments.

Team Buffalo/Virginia [26] used a RNN to learn the global representations of all laboratory tests and a series of RNNs to learn laboratory test-specific patterns and to merge them through a fusion gate. They enabled both forward and backward directions of recurrence for imputation in order to improve its ability of long-term memory. They also added a regression layer on top of the recurrence layer to utilize correlation between temporal trends.

Team IBM [27] developed a stacked ensemble learner that employs six base models: linear base model for temporal imputation, KNN, RF, MLP for cross-sectional imputation, bi-directional Gated Recurrent Unit (GRU) and bi-directional Long Short-Term Memory (LSTM) for combined imputation. They then used XGBoost to combine the base models.

Team Iowa [28] used an ensemble learner with base models, including regularized regression with smoothing spline basis functions, radial basis function (RBF) kernel interpolation, RBF neural network and bi-directional LSTM using RBF interpolation for pre-filling. They experimented with ridge regression, LASSO or gradient boosting as the ensemble method.

Comparing the challenge participating systems, we note that several teams adopted the gradient boosting algorithms as primary tools for imputation [14, 17, 22]. A few teams used RNN (including LSTM and GRU) for imputation [20, 26–28]. Several teams used KNN-based approaches [21, 23, 27]. Some teams used ensemble models to combine simple models, such as linear regression and/or advanced models such as RNN [27, 28]. Matrix factorization methods (including SVD and Soft-Impute) were used by multiple teams, either as the primary imputation methods [23, 24] or during the pre-filling step [17]. Participating teams performed cross-validation for parameter tuning to avoid overfitting. We refer to the reader to Table 2 for a more convenient and detailed comparison between challenge participating systems.

Evaluation results

Table 3 shows the results of the teams. Team Ping An [14] achieved the best overall nRMSD of 0.1782, using LightGBM-based system, significantly better than other teams with non-overlapping 95% confidence intervals (CIs) (see Supplementary Table 3 available online at http://bib.oxfordjournals.org/). Team AstraZeneca [16] leveraged the probabilistic framework of MICE instead of machine learning models to optimize the combination of cross-sectional and temporal imputations, and achieved an nRMSD of 0.1862. Team Vanderbilt [17], using XGBoost, achieved an nRMSD of 0.1871, which was close to that of Team AstraZeneca with overlapping 95% CIs (Supplementary Table 3 available online at http://bib.oxfordjournals.org/). The top three teams significantly outperformed other teams and 3D-MICE by a margin with non-overlapping 95% CIs (Supplementary Table 3 available online at http://bib.oxfordjournals.org/). For example, the top team’s 95% CI [0.1774, 0.1789] is non-overlapping with 3D-MICE’s 95% CI [0.2263, 0.2282], suggesting the statistical significance of the difference. In addition, for specific lab tests, the top three systems that use machine learning or probabilistic models to integrate temporal and cross-sectional correlations significantly (non-overlapping 95% CIs) outperform 3D-MICE. Feature analysis for the top team ranked F4 as the most important feature set, followed by F2, F3 and F5 (see Challenge participating systems section for feature set definition), all being temporal and cross-sectional features. These observations suggest the benefits of properly trained machine learning or probabilistic models to learn to combine the temporal and cross-sectional imputations when compared with heuristic combination used in 3D-MICE. On the other hand, we also noticed that ensemble machine learning models [27, 28], that combined many base models used by the top performers (Table 2), in fact came last in performance. Note that many such base models (e.g. LSTM and neural networks) are themselves advanced models instead of weak models. Unlike the conventional wisdom that an ensemble of weak models leads to performance improvement, we see that an ensemble of non-weak machine learning models may actually lead to performance decline, possibly due to too complex optimization objective function as a result of too many parameters. While machine learning and probabilistic models are in principle more effective than heuristic models, care needs to be taken to prevent overblown model complexity. Although we chose to only include directly measured lab tests, there are strong correlations among some of the tests (e.g. hematocrit can be estimated as tripling the hemoglobin concentration and dropping the units). However, our previous study showed that such correlation for estimation, though strong, is not perfect [6]. Such correlations can be readily utilized by linear regression based models, but none of the systems relying on linear regressions [27, 28] placed top in the evaluation (even when only looking at hematocrit and hemoglobin). This suggests that machine learning tools used by top performers likely helped them to obtain more accurate results than calculating based on standard approaches. CATSI replaced temporal imputation-derived features with RNN component but did not perform as competitively. This is likely because the ICU clinical time series have highly variable lengths and impose challenges to the parameter sharing of RNN across admissions during imputation. Time-Aware LSTMs and variants [29] may partially address such challenges. KNN-based methods slightly outperformed 3D-MICE, suggesting limited benefits of only exploring similar patients instead of all the patients when imputing missing values for the patient of interest.

Table 3.

Challenge participating team test-set performance

Team	Overall	Chloride	Potassium	Bicarb	Sodium	Hematocrit	Hemoglobin	MCV	Platelets	WBC	RDW	BUN	Creatinine	Glucose
Ping An [14]	0.1782	0.1351	0.2255	0.1794	0.1561	0.1002	0.092	0.2289	0.158	0.1986	0.2021	0.1341	0.1827	0.244
AstraZeneca [16]	0.1862	0.1448	0.232	0.1836	0.1604	0.1003	0.0957	0.2336	0.1685	0.216	0.1978	0.1498	0.2002	0.257
Vanderbilt [17]	0.1871	0.1406	0.2284	0.1818	0.16	0.106	0.0986	0.2421	0.1597	0.2026	0.2158	0.1337	0.1856	0.2816
HKBU [20]	0.2035	0.1738	0.2431	0.2026	0.1958	0.1436	0.1349	0.2534	0.1862	0.227	0.213	0.1574	0.206	0.2602
Padova [21]	0.2092	0.1921	0.2542	0.2118	0.2085	0.1518	0.1485	0.2644	0.1794	0.2198	0.2056	0.1546	0.2135	0.2677
TSU [22]	0.2240	0.2043	0.2611	0.2118	0.2256	0.2314	0.229	0.2644	0.1794	0.2198	0.2056	0.1546	0.2135	0.2797
DLUT [23]	0.2245	0.2076	0.2566	0.2129	0.2235	0.2328	0.2317	0.261	0.1842	0.2227	0.2067	0.1616	0.2156	0.2756
3D-MICE [6]a	0.2272	0.2	0.2632	0.2314	0.2145	0.1505	0.1488	0.2713	0.2294	0.256	0.2458	0.1846	0.2338	0.2769
NCSU [24]	0.2305	0.2084	0.2533	0.2369	0.2145	0.1815	0.1811	0.2733	0.2108	0.2457	0.2417	0.2113	0.2332	0.2794
Drexel [25]	0.2488	0.2377	0.2755	0.2444	0.2534	0.2556	0.2486	0.2891	0.21	0.2562	0.2268	0.1943	0.2354	0.2888
Buffalo/Virginia [26]	0.2683	0.1685	0.2468	0.2044	0.19	0.1514	0.1516	0.4308	0.3413	0.2519	0.4102	0.2234	0.2645	0.263
IBM [27]	0.3348	0.2278	0.2517	0.2311	0.2596	0.1904	0.1756	0.4604	0.3337	0.2996	0.4768	0.3127	0.5742	0.2927
Iowa [28]	0.5666	0.3297	0.2763	0.3313	0.4034	0.6091	0.5358	0.5501	0.4898	1.4703	0.4253	0.1819	0.2346	0.2901

Notes: For each laboratory test and overall comparison, we mark the first place in bold and the last place in italic fonts.

^a 3D-MICE as reference system.

Looking more closely at the differences in the results from individual laboratory test, we note that the top performers are usually the overall top performer, with a few exceptions where Team AstraZeneca came first in RDW and Team Vanderbilt came first in BUN. On the other hand, the bottom performers for individual laboratory tests are usually the overall bottom performer, with a few exceptions where Team IBM came last in RDW, BUN, creatinine and glucose. In order to evaluate the impact when a certain subset of the data points were missing, we compare missing clinical data at the beginning (the first time-stamps, 5.6% out of total missing), in the middle, and at the end (the last time-stamps, 5.2% out of total missing) of the patient admissions in the test data. Figure 2 shows the imputation performance differences for missing data at different stages of patient admissions across all the laboratory tests for each challenge participating team. The general pattern shows significantly larger (with non-overlapping 95% CIs) imputation errors for beginning and end time-stamps than for middle time-stamps. For nine of the teams, beginning time-stamps are associated with significantly larger (with non-overlapping 95% CIs) imputation errors than end time-stamps, while for the rest three teams, end time-stamps are associated with modestly larger imputation errors than beginning time-stamps. Supplementary Figure 1 through Supplementary Figure 13, available online at http://bib.oxfordjournals.org/, show laboratory test-specific imputation performance differences for missing data at different stages of patient admissions, for each challenge participating team. Laboratory test specific patterns are in general similar to the patterns across all the laboratory tests. In rare cases (e.g. Team Iowa in hematocrit and hemoglobin), imputation errors for middle time-stamps are larger than those for end time-stamps, likely a system-specific pattern.

Figure 2.

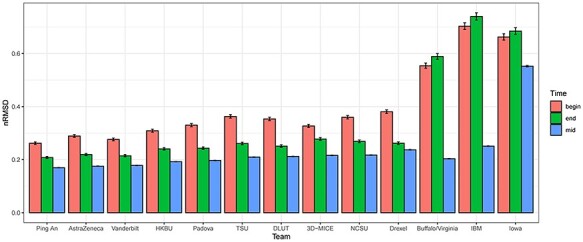
The imputation performance differences for missing data at different stages of patient admissions across all the laboratory tests for each challenge participating team. The label ‘begin’ (‘end’) corresponds to the first (last) time-stamps of the patient admissions, and the label ‘mid’ corresponds to the time-stamps between the first and the last.

Discussion

This challenge has several limitations. First, our choice of the ICU dataset MIMIC3 to derive the challenge dataset excludes non-ICU inpatients and outpatients. Practically speaking, MIMIC3 is arguably the most widely used public large clinical data by the machine learning community. Moreover, medicine has evolved into an era where hospitals progressively adopt more real-time monitoring for the patients and generate ICU-like clinical data, making today’s ICU a snapshot for tomorrow’s standard of care [30]. On the other hand, data missing rate varies for different clinical settings. For example, one typically expects higher missing rate in general inpatients than ICU patients and higher missing rate in outpatients than inpatients. Comparing results from this challenge to the original 3D-MICE study that focused on general inpatients [6], it is not surprising that higher missing rate results in less imputation accuracy, but in both settings, combining the cross-sectional correlation and longitudinal correlation results in improved accuracy from leveraging either correlation alone. Future work on outpatient imputation may further chart the missing rate landscape and illustrate where the ceiling effect of clinical data imputation might be.

Another limitation concerns artificially missing data as ground truth in performance evaluation. Although measuring natively missing data is most ideal, it is logistically impossible for retrospective dataset such as MIMIC3. To assess objectively imputation for natively missing data, one will need to collect prospectively and unbiasedly spare samples (e.g. blood samples) to produce ground truth, which is our ongoing work with an in-house patient cohort. However, we made best efforts to minimally alter the clinical time series and ensured that the native missing rates of tests had small differences (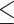5%) to the combined native and artificial missing rates. Moreover, the combined missing data make the imputation task harder than observed reality and render our performance evaluation a conservative one. On the other hand, the statistics on available lab tests per patient (Supplementary Table 2 available online at http://bib.oxfordjournals.org/) show a grouping pattern, e.g. Chem-7 panel tests (chloride, potassium, bicarb, sodium, BUN, creatinine and glucose) versus other tests. Tests from the same group tend to have similar median and interquartile range of available lab tests per patient (Supplementary Table 2 available online at http://bib.oxfordjournals.org/) although the time of missing has large variations (e.g. Supplementary Table 1 available online at http://bib.oxfordjournals.org/). This may favor algorithms that put an emphasis on leveraging cross-sectional correlations to a limited degree.

Another limitation concerns the inclusion criteria that all patients need to have at least 10 time points of contemporaneous no more than 50% missing complete blood count (CBC) and Chem-7 tests. Table 1 suggests Chem-7 tests tend to be ordered more than other tests, which is corroborated by previous case reports for ICU lab test utilization frequency [31]. This partially informed our choice of requiring a least 7 out of 13 labs to be present, as such a missing CBC component would not eliminate a time point but a missing Chem-7 component would. However, this may not always be the case. For example, a patient with ongoing bleeding may present with a low hemoglobin but normal Chem-7. This patient would likely be monitored closely for CBC (e.g. every 6 h), but less frequently for Chem-7 (e.g. once a day). The patient will undergo quick interventions to fix the bleeding. As a result, the hemoglobin may return to normal when Chem-7 is taken. In this case, our strict inclusion criteria could lead to not being able to learn how well these different imputation techniques work on more physiologically deranged values. Although the summary statistics in Table 1 and previous reports [31] suggest such cases may not be too prevalent, they may nevertheless arise with certain clinical scenarios. Thus, we have released our source code for dataset creation so that future research can investigate more relaxed inclusion criteria and its impact on the imputation system performance.

Another limitation concerns the fact that often in clinical medicine if a lab result is missing, it is because the clinical provider felt like that test result would be normal or unhelpful in diagnosing or treating the patient. As a result, these data are missing not at random, and the missing pattern contains inherent information. Evaluating the utility of such missing pattern asks for a downstream task (e.g. diagnosis or intervention) and is beyond the scope of this challenge but will be our future work. For this challenge, we applied range normalization to bring variation of different laboratory tests to a comparable scale and used nRMSD as evaluation metric. How much of the degree of improvement as measured by a standardized metric will lead to tangible clinical benefits (e.g. improved prediction on diagnosis or even intervention choice) likely depends on clinical tasks and settings and is worth systematic evaluation through communitywide effort in both the informatics and clinical communities. Complicating the issue of missing data, clinical data quality also depends on the fact that its primary role is to help clinicians care for patients. As a result, factors related to health-care operation and delivery can greatly bias and impact the data availability and quality [32]. The design principles of some of the challenge participating teams may also inform future algorithms to potentially overcome these issues. For example, extending on the global context vector idea by Team HKBU [20], one can add a time-varying bias vector to RNN and similar models in order to capture and quantify the underlying bias factors contributing to the observed data quality issues.

The DACMI challenge has generated considerable interests both across and beyond the challenge participating teams. Although the challenge has an extended embargo period for its full data release due to the pandemic, the released training part of the challenge data has been enabling development of advanced algorithms for clinical longitudinal data imputation, including Time-Aware Multi-Modal Auto-Encoder [33]. For latest progress on imputation for time series in the general domain, we refer the reader to the surveys [34, 35] that complement this article. The DACMI challenge has provided a solid foundation to evaluate and advance the state of the art in imputing missing data in clinical time series. The challenge has attracted numerous international teams spanning three continents across multiple industries and academia. Given the rapid progress in the past years, we expect that more exciting developments of clinical data imputation will continuously shape the emerging landscape and provide opportunities for researchers to contribute.

Key Points

• Most clinical datasets contain missing data and are longitudinal by nature. However, most commonly used imputation methods do not directly accommodate longitudinal, clinical time series.

• The DACMI challenge is the first shared-task challenge on clinical time series imputation to our best knowledge. We presented a shared clinical dataset with ground truth for evaluating and advancing the state of the art in imputing missing data for clinical time series.

• The challenge attracted 12 international teams spanning three continents across multiple industries and academia.

Yuan Luo is Chief AI Officer at Northwestern University Clinical and Translational Sciences Institute and Institute for Augmented Intelligence in Medicine. His research interests include machine learning, natural language processing, time series analysis, computational phenotyping and integrative genomics for precision medicine.

Funding

National Library of Medicine (R01LM013337).

Data availability

Our datasets are derived from MIMIC3 dataset https://mimic.physionet.org/, which is a large real-world ICU database. To officially gain access, the reader needs to sign MIMIC data user agreement by following the instructions specified at https://mimic.physionet.org/gettingstarted/access/. Then, by running our code at https://github.com/yuanluo/mimic_imputation, the reader can generate the dataset used in the DACMI challenge.

Code availability

The code to generate the dataset and evaluate the imputation accuracy is available at https://github.com/yuanluo/mimic_imputation.