Prediction of disease-associated nsSNPs by integrating multi-scale ResNet models with deep feature fusion

Abstract

More than 6000 human diseases have been recorded to be caused by non-synonymous single nucleotide polymorphisms (nsSNPs). Rapid and accurate prediction of pathogenic nsSNPs can improve our understanding of the principle and design of new drugs, which remains an unresolved challenge. In the present work, a new computational approach, termed MSRes-MutP, is proposed based on ResNet blocks with multi-scale kernel size to predict disease-associated nsSNPs. By feeding the serial concatenation of the extracted four types of features, the performance of MSRes-MutP does not obviously improve. To address this, a second model FFMSRes-MutP is developed, which utilizes deep feature fusion strategy and multi-scale 2D-ResNet and 1D-ResNet blocks to extract relevant two-dimensional features and physicochemical properties. FFMSRes-MutP with the concatenated features achieves a better performance than that with individual features. The performance of FFMSRes-MutP is benchmarked on five different datasets. It achieves the Matthew’s correlation coefficient (MCC) of 0.593 and 0.618 on the PredictSNP and MMP datasets, which are 0.101 and 0.210 higher than that of the existing best method PredictSNP1. When tested on the HumDiv and HumVar datasets, it achieves MCC of 0.9605 and 0.9507, and area under curve (AUC) of 0.9796 and 0.9748, which are 0.1747 and 0.2669, 0.0853 and 0.1335, respectively, higher than the existing best methods PolyPhen-2 and FATHMM (weighted). In addition, on blind test using a third-party dataset, FFMSRes-MutP performs as the second-best predictor (with MCC and AUC of 0.5215 and 0.7633, respectively), when compared with the other four predictors. Extensive benchmarking experiments demonstrate that FFMSRes-MutP achieves effective feature fusion and can be explored as a useful approach for predicting disease-associated nsSNPs. The webserver is freely available at http://csbio.njust.edu.cn/bioinf/ffmsresmutp/ for academic use.

Introduction

Genetic mutations may lead to protein structure changes, which impact protein stability and biological function [1, 2]. As reported, approximately 58% of the exonic single nucleotide polymorphisms (SNPs) in the human genome can lead to changes in protein amino acid sequences, which are called non-synonymous single nucleotide polymorphisms (nsSNPs) [2, 3]. Existing studies have shown that nearly one-third of nsSNPs are deleterious to human health and cause many diseases [4]. More than 6000 kinds of diseases, such as cystic fibrosis and Alzheimer’s disease, are caused by nsSNPs [5]. Such nsSNPs are called disease-associated mutations. To date, although some nsSNPs have little or no discernible effects on protein functions [6], there are many nsSNPs whose disease-associated effects on protein function and structure are yet to be characterized [7].

Next-generation sequencing technology has led to the rapid accumulation of a large amount of genetic mutation data for genome analysis. It is vitally important to identify disease-related mutations in a high-throughput and cost-effective manner [5]. However, it is time-consuming and laborious to apply traditional biomedical methods to determine whether nsSNPs are pathogenic. To address this, researchers have proposed computational methods [8], which are helpful to understand the pathogenesis of genetic diseases [9]. Early detection of nsSNPs also contributes to disease prediction and diagnosis at the initial stage [10].

A number of computational methods have been developed to predict nsSNPs’ impact [1], such as SVM, RF, HMM and ANN. Notably, these methods can be divided into four major groups according to feature extraction methods: (1) sequence-based or sequence-derived methods, such as SIFT [11] and FATHMM [12]; (2) methods based on structure, such as SDM [13] and APOGEE [14]; (3) combined hybrid methods, such as SNAP [15], FunSAV [16] and Polyphen-2 [17], and (4) consensus methods (built on individual prediction outputs), such as PredictSNP1 [18] and CONDEL [19]. In general, ensemble classifiers [20] and consensus methods are usually superior to individual ones [1].

In the mutation effect prediction field, some methods can predict the effect of coding mutations (such as SNPeffect 4.0 [21], PolyPhen-2 [17] and SIFT [8]) or noncoding mutations (for instance, DeepSEA [22], CpGenie [23] and SNPDelScore [24]), while others have the ability to predict the effect of both coding and noncoding mutations [1] (for example, GWAVA [25], Eigen [26] and CADD [27]). In terms of the impact of mutations on protein stability, a variety of methods (Ref. [28]), such as STRUM [2] and FoldX [29], have been developed to detect protein stability changes upon mutations. In view of mutations and clinical data, MutEx [30] has been developed to store the relationships among gene expression, somatic mutations and survival data for cancer patients, which can also evaluate mutation impact based on gene expression alteration. In addition, some methods have also been developed to predict mutations in specific proteins, such as Pred-MutHTP [31] and mCSM-membrane [32].

Despite the considerable efforts, it remains a challenging problem to precisely identify disease-causing nsSNPs from the neutral ones [5, 33]. In recent years, deep learning-based methods have been developed for mutation prediction, for instance, MVP [34] and Ref. [35]. Specifically, MVP utilized a deep residual network with only two blocks and achieved high accuracy with fewer features [34]. In Ref. [35], Kvist developed a deep ResNet network (we named this method as KVIST-Deep), which mainly utilized multiple sequence alignment (MSA) information and other predicted structural information. Many existing methods have been developed to predict the impact of SNVs on human health [36]. Nevertheless, they still have a high false prediction rate, which can be better addressed by computational approaches based on combined features [10].

In this study, some further improvements are made in the following main aspects: (1) we use four types of protein sequence- and structure-based features to characterize nsSNPs, rather than the one hot encoding commonly used in deep learning models. These four types of features include position-specific scoring matrix, predicted secondary structure, predicted relative solvent accessibility and predicted disorder (PDO), which have been found to be discriminative in previous studies [37]; (2) as reported, the functional impact of one mutation site is related to itself and several sites around it [38]. PROVEAN [39] calculated the delta score (the semi-global alignment score changes of the query protein and its variation with respect to another protein subject) for both the mutation and surrounding sites. Accordingly, we extract several residues surrounding the mutation site, termed as ‘microenvironment’, which can reflect the natural characteristics of the mutation site [32]; (3) different types of features are often concatenated serially in protein attribute prediction and then used as the input to train a prediction model. However, in many cases, such serial combination may not necessarily improve the prediction performance. Herein, we propose a new deep feature fusion strategy and adopt multi-scale 2D-ResNet and 1D-ResNet to extract two-dimensional features and physicochemical properties. This approach is termed FFMSRes-MutP and can achieve a better performance with concatenated features than models with individual features. Extensive benchmarking experiments on four datasets and blind test dataset demonstrate that FFMSRes-MutP outperforms several existing state-of-the-art nsSNP impact predictors.

Datasets and feature representation

Benchmark datasets

In the present work, we utilized four benchmark datasets, including PredictSNP [18], MMP [18], HumDiv [17] and HumVar [17], to evaluate and compare the performance of different predictors. PredictSNP and MMP were downloaded from PredictSNP1 [18]. Mutations in PredictSNP were collected from five different sources by removing those duplicate/inconsistent mutations, or those that had been utilized as the training data by eight existing tools. MMP was an integrated and non-redundant dataset, in which some overlapped mutations were removed [18]. Mutations in HumVar and HumDiv were extracted from the UniProt database and available at PolyPhen-2 [17] website, which were downloaded without any further deletion. A statistical summary of the benchmark datasets is provided in Table 1.

Table 1.

Statistical summary of the benchmark datasets

Dataset	n_positivea	n_negativeb	Total number of variants	Number of proteins#
PredictSNP	19800	24082	43882	10085
MMP	4456	7538	11994	13
HumDiv	5564	7539	13103	978
HumVar	22196	21151	43347	9679

Note: n_positive^a and n_negative^b represent the numbers of positive (i.e., disease-associated) mutations and negative (i.e., neutral) mutations; number of proteins^# denotes the number of proteins from which mutations were collected.

As listed in Table 1, PredictSNP comprises 19800 disease-associated and 24082 neutral mutations from 10085 proteins. MMP contains 4456 disease-associated and 7538 neutral mutations from only 13 proteins. HumDiv and HumVar encompass 13103 and 43347 mutations, collected from 978 and 9679 proteins, respectively.

Blind test dataset

To further assess the prediction performance of the newly developed model, blind test experiments were conducted on a third-party dataset. We downloaded non-synonymous mutations from BorodaTM [40], which comprised 29033 disease-associated and 38680 neutral mutations. Next, we deleted some proteins and mutations whose wild-type amino acids were inconsistent with those deposited in the UniProt database [41]. The transmembrane (TM) protein mutation dataset was constructed after deleting 13 disease-associated and 116 neutral mutations. The final dataset included 29020 disease-associated and 38564 neutral mutations, from 2581 and 11597 proteins, respectively.

Feature representation

For nsSNP prediction, several different types of protein sequence- and structure-based features are commonly used [1]. In addition, one-dimensional sequence information (such as position-specific scoring matrix and physicochemical properties) is also extracted as sequence-based features. Protein structure-based features are generated from 3D structure files stored in the PDB database [42]. Effective tools are applied to proteins with unknown 3D structures to predict the structural characteristics from sequence information. Five types of features utilized here are introduced below.

Position-specific scoring matrix

During biological evolution, protein sequence can be divided into conservative and non-conserved regions [11]. Generally, mutations occurring in conserved regions may affect protein stability and further affect its interaction with neighboring proteins [11]. Position-specific scoring matrix (PSSM) is one kind of such characteristic [43]. As reported, PSSM has been utilized in protein-DNA interaction [44], protein-vitamin binding [45] and nsSNP prediction [46].

Herein, PSI-BLAST [43] is applied to generate PSSM information by searching the specific database, with the iteration of 3 and e-cutoff of 1e-3., PSI-BLAST [43] first searches against the SWISS-PROT database [41] for generating MSA for each query protein. Then, PSI-BLAST calculates PSSM values for each residue and provides a feature matrix with L × 20 values. Then, we further transform the original PSSM values into the range (0, 1) by applying the following sigmoid function:

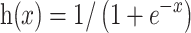(1)

where x is the original PSSM value. The transformed PSSM can be written as follows:

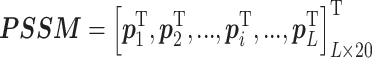(2)

where 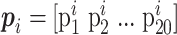denotes the i-residue value, 20 is the number of natural amino acids, and L is the sequence length of the query protein.

Predicted secondary structure (PSS)

Predicted secondary structure (PSS) has been shown as an effective feature for protein-ATP binding [47] and mutation prediction [46], which can be generated by PSIPRED [48]. The output of PSIPRED is a probability matrix with L × 3 dimensionality, in which three values for each residue indicate the probability of belonging to three secondary structure (SS) types (i.e., coil, helix and strand), shown below:

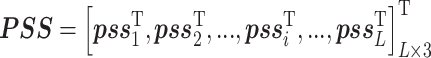(3)

where 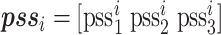denotes the probability of the residue belonging to the three SS classes and L is the length of the query protein.

Predicted relative solvent accessibility

Relative solvent accessibility (RSA) describes the relative solvent exposure status of residues in protein 3D structure. SANN [49] is applied to generate predicted relative solvent accessibility (PRSA) information, which provides a probability matrix with L × 3 dimensionality, shown below:

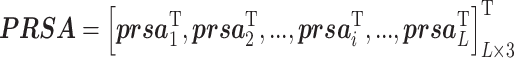(4)

where 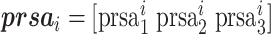indicates the probability of a residue belonging to three RSA classes (i.e., exposed, hidden and intermediate) and L is the length of the query protein.

Predicted disorder

The protein disordered region has no fixed tertiary structure. Such disordered regions are related to DNA recognition and the affinity of protein binding [50]. Herein, DISOPRED [51] is adopted to predict the disorder information, which provides a matrix with L × 1 dimensionality and can be expressed as:

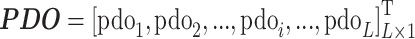(5)

where pdo_i is the disorder value of the mutation site i and L is the length of the query protein.

Physicochemical properties

Physicochemical properties of residues in a protein can affect the secondary and tertiary structure and biological function [52]. Herein, we utilized physicochemical properties with 28 values to represent mutations, which were collected from the AAindex database [53], such as isoelectric point (ZIMJ680104) and net charge (KLEP840101). Some substitution matrices were also adopted here, such as BLOSUM62 (HENS920102) [54], PHAT (NGPC000101) [55] and non-symmetric substitution matrix (SLIM) (MUET01010) [56]. Then, the MinMax method from scikit-learn [57] was used to normalize these properties. Please refer to the Supplementary Text S1 for more details about the physicochemical properties used.

Neighbor microenvironment

In nsSNP prediction, some studies utilized characteristics within 5Å around the mutation site as part of feature representation [58]. Ye and Zhao et al. extracted three residues before and after the mutation site as the mutation microenvironment [38]. Herein, we also extracted such information stored in the neighbor microenvironment of the mutation site, labeled as M_L. For PredictSNP, HumDiv and HumVar datasets, M_L was set to 59 (For the MMP dataset, M_L was set to 9 to avoid model over-fitting, because its protein number is relatively small); The extracted feature matrices for each mutation are 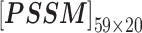, , 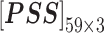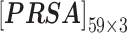and 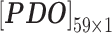(for the MMP dataset, 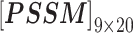, , 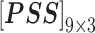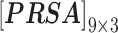and ).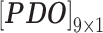

Performance evaluation methods

Independent test

Each dataset is divided into three parts, including training data (accounting for 90%), validation data (10% of the training data) and independent test data (10%). During the model training procedure, 10% of the training data was taken as the validation data to validate the model performance. The model is trained, validated and tested on three subsets correspondingly. Generally, for large datasets, the model training procedure typically requires more time and computing resources than traditional machine learning methods. Therefore, the independent test is more suitable for performance comparison of different features and diverse models.

10-fold cross-validation

For this method, a benchmark dataset is randomly divided into ten parts and the prediction procedure is repeated for ten cycles. In each cycle nine parts are used as the training data, while the rest is utilized as the test data. After this process is traversed once, the performance metrics are averaged and used as the final performance indicators.

Performance evaluation metrics

Several performance metrics are commonly used to evaluate the performance of models, including specificity (Spe), precision (Pre), false positive rate (FPR), false negative rate (FNR), negative predictive value (NPV), error rate (ER), F₁-score (F₁), Recall, sensitivity (Sen), accuracy (ACC) and Matthew’s correlation coefficient (MCC), which are defined as follows:

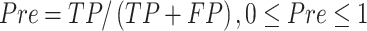(6)

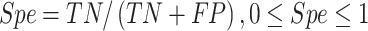(7)

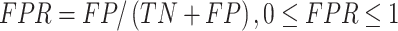(8)

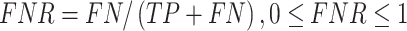(9)

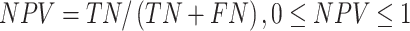(10)

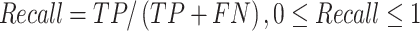(11)

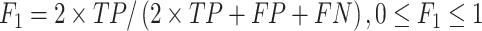(12)

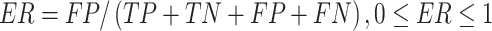(13)

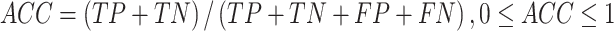(14)

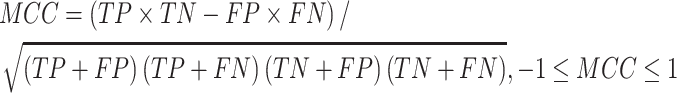(15)

where TP (true positive) and TN (true negative) are the numbers of correctly predicted disease-associated and neutral mutations, respectively; FN (false negative) is the number of disease-associated mutations incorrectly predicted as neutral ones; FP (false positive) is the number of neutral mutations incorrectly predicted as disease-associated ones.

MCC is considered to be the best performance indicator, especially when dealing with imbalanced datasets [59]. ROC (receiver operating characteristic curve) [60] is a curve plotted with TPR as ordinate and FPR as abscissa. Given different thresholds, (FPR, TPR) coordinates of each threshold are drawn in ROC. AUC is the area under ROC, with a value ranging from 0 to 1. A perfect classifier has an AUC of 1, whereas the AUC of a random classifier is 0.5 [61]. Generally, the larger AUC, MCC, Pre, Spe, NPV, F₁, Recall (equal to Sen) values and the lower FPR, FNR, ER values, the better and more accurate the model.

MSRes-MutP AND FFMSRes-MutP MODELS

Description of MSRes-MutP and FFMSRes-MutP models

In the present work, two novel deep learning models (i.e., MSRes-MutP and FFMSRes-MutP) are developed and introduced in the following subsections.

MSRes-MutP. As illustrated in Figure 1, there are three main parts of MSRes-MutP, including (1) mutation feature matrix extraction, (2) multi-scale ResNet layers and (3) fully-connected (FC) and prediction layers. Please refer to http://csbio.njust.edu.cn/bioinf/ffmsresmutp/ for more details about the MSRes-MutP model.

Figure 1.

An overall workflow of MSRes-MutP.

(1) Mutation feature matrix extraction (Figure 1A). In this part, four different types of tools were applied to generate sequence-based and structure-based characteristics and feature matrix (M_L × 27) for each mutation.

(2) Multi-scale ResNet layers. This part consists of three groups that utilize different neurons (F₁, F₂ and F₃) to extract features. Specifically, three kernel sizes (i.e., 3, 5 and 7) are set in convolution layers, followed by ‘Convolution-block’ (Figure 1B) and ‘Identity-block’ (Figure 1C).

(3) FC and prediction layers. FC layer takes the outputs of multi-scale ResNet parts, and softmax takes the obtained characteristics to generate two classification outputs. Herein, for nsSNPs, we labeled disease-associated and neutral mutations as 1 and 0, respectively.

FFMSRes-MutP. Based on MSRes-MutP, we further developed FFMSRes-MutP (Figure 2). Compared with the former, the latter has the following improvements:

Figure 2.

An overall workflow of FFMSRes-MutP. Note: (1) kernel = 3, 5 or 7 means kernel = (3, 3), (5, 5) or (7, 7) in convolution-2D layers and kernel = 3, 5 or 7 in convolution-1D layers; (2) the ‘Add’ layer calculates the sum of previous outputs of multi-scale 2D-ResNet or 1D-ResNet models; (3) neurons for the first, second and third groups are set to [128, 128, 512], [256, 256, 1024] and [512, 512, 2048], respectively.

• (1) The input feature matrix. The input of FFMSRes-MutP comprises three parts: sequence-based feature matrix with M_L × 20, structure-based feature matrix with M_L × 7, and physicochemical properties with 28 values.

• (2) Multi-scale 2D-ResNet and 1D-ResNet blocks. FFMSRes-MutP not only applies multi-scale 2D-ResNet for sequence-based (Figure 2A) and structure-based feature matrices (Figure 2B) but also adopts multi-scale 1D-ResNet for physicochemical properties (Figure 2C).

• (3) Deep feature fusion. Deep feature fusion serves to concatenate and capture more comprehensive features from different perspectives. For example, Li et al. utilized deep ResNet containing 24 residual blocks to learn the fused characteristics from three types of features for inferring protein contact-maps [62]. Herein, its detailed descriptions are documented in the ‘Deep feature fusion’ Section.

• (4) FC and prediction layers. The output of the flatten layer was passed on to four groups of FC layers with different neurons (i.e., 2048, 1024, 512 and 256) and dropout layers (0.4). Then, we fed extracted features into the softmax layer to generate two classification outputs. For more details about ‘Convolution_block_2D’, ‘Identity_block_2D’, ‘Convolution_block_1D’ and ‘Identity_block_1D’, please refer to the Supplementary Figures S1 and S2.

Deep feature fusion

As depicted in Figure 2, three kinds of features, including PSSM (M_L × 20), PSS + PRSA+PDO (M_L × 7) and physicochemical properties (1 × 28), were not directly concatenated after passing through the ‘feature extraction by fusing multi-scale ResNet models’ part. Specifically, the outputs of Figure 2A and B were concatenated, followed by three 2D-ResNet blocks and one flatten layer (Figure 2D). Then, deep feature fusion was applied during the follow-up concatenation, with details depicted in Figure 3.

Figure 3.

Details of deep feature fusion in FFMSRes-MutP.

After passing through the ‘feature extraction by fusing multi-scale ResNet models’ part, sequence-based and structure-based features were in shape (3, 3, 2048) and (3, 1, 2048) (Figure 3A) and concatenated with axis = −2. Then, feature matrix was sequentially passed through one batch-normalization (BN) layer, one Max-pooling layer, one ‘Convolutional_block_2D’ layer with [512, 512, 2048], two ‘Identity_block_layer_2D’ layers with [512, 512, 2048] and one flatten layer (Figure 3B). On the other hand, the output of the physicochemical properties’ part was in shape (4, 2048) (Figure 3A) and then flattened and concatenated with the above flatten layer. As depicted in Figure 3C, the outputs of the concatenated layer were fed into the FC and prediction layers to generate the final prediction outcome.

Multi-scale ResNet and FC layers

Convolution layers with different kernel sizes can extract more informative features than those with a single kernel size [63]. Accordingly, in MSRes-MutP and FFMSRes-MutP, the obtained feature matrices were passed through multi-scale convolution and ResNet layers. Meanwhile, ResNet blocks can preserve the original information of the initial input matrix or outputs of previous multi-scale parts.

Each multi-scale part contains one convolution layer, one BN layer, one max-pooling layer, one activation layer and one add layer. The add layer takes the sum of the previous three layers and uses ReLU as the activation function to avoid model over-fitting:

(16)

where is the output of BN and is the input of the convolution layer. Herein, BN is used to speed up the training process, while the max-pooling layer is applied to reduce the model’s parameters and computation. The FC and prediction part consists of flatten layers, four groups of FC layers and the softmax function shown below:

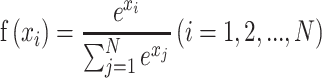(17)

where 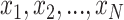are the input values of softmax and 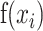denotes the probability of the nsSNP belonging to the i-th class [64].

Parameters setting for training and avoiding model over-fitting

Some parameters were set for model training and avoiding over-fitting. These included: (1) each dataset was split into three parts: training data, validation data and testing data; (2) batch size was set to 32 and learning rate was set to 0.001; (3) the SGD optimizer [65] was utilized to perform stochastic gradient descent with loss function ‘categorical-crossentropy’; (4) early-stopping strategy was applied to avoid model over-fitting. Specifically, the loss of the training and validation data was calculated after each training cycle. The training process will be terminated if the validation loss does not decrease after three more training cycles. The weights with the lowest loss value were saved and then utilized on the test data; (5) dropout (with 0.4) was adopted to avoid model over-fitting.

Results and discussions

Serial combination of different features does not improve the performance of MSRes-MutP

In this section, we implemented some experiments to assess the contribution of different features and serial combinations to the predictive performance. Specifically, we fed P (i.e., PSSM), PS (i.e., PSSM+PSS), PSP (i.e., PSSM+PSS + PRSA), SPP (i.e., PSS+ PRSA+PDO) and PSPP (i.e., PSSM+PSS+ PRSA+PDO) into MSRes-MutP. After model training and validation, MSRes-MutP was tested on the independent test data. Performance comparison results are provided in Table 2 and Figure 4. TP, TN, FN, ER, FPR and FNR values were also documented in the Supplementary Table S1 and Text S2.

Table 2.

Performance evaluation of MSRes-MutP using different features and serial combinations on the independent test datasets

Dataset	Feature	MCC	ACC	Recall/Sen	Spe	Pre	NPV	F1	AUC
PredictSNP	P	0.4831	0.7314	0.8307	0.6512	0.6579	0.8265	0.7343	0.7409
	PS	0.3979	0.6958	0.7389	0.6611	0.6378	0.7581	0.6846	0.7000
	PSP	0.4260	0.7163	0.6813	0.7446	0.6830	0.7431	0.6822	0.7130
	SPP	0.4745	0.7348	0.5125	0.9143	0.8285	0.6990	0.6333	0.7134
	PSPP	0.4345	0.7225	0.6119	0.8118	0.7242	0.7214	0.6633	0.7119
MMP	P	0.5745	0.8058	0.6818	0.8776	0.7634	0.8265	0.7203	0.7797
	PS	0.5861	0.8025	0.7841	0.8132	0.7084	0.8668	0.7443	0.7986
	PSP	0.5910	0.8075	0.7659	0.8316	0.7247	0.8599	0.7448	0.7987
	SPP	0.5691	0.8033	0.6795	0.8750	0.7589	0.8251	0.7170	0.7773
	PSPP	0.5500	0.7892	0.7318	0.8224	0.7046	0.8412	0.7179	0.7771
HumDiv	P	0.4635	0.7323	0.7469	0.72145	0.6645	0.7942	0.7033	0.7342
	PS	0.4168	0.7193	0.5619	0.8355	0.7162	0.7208	0.6298	0.6987
	PSP	0.3538	0.6903	0.4847	0.8422	0.6941	0.6887	0.5708	0.6635
	SPP	0.4301	0.6941	0.8420	0.5849	0.5997	0.8336	0.7005	0.7134
	PSPP	0.3715	0.6911	0.6571	0.7162	0.6310	0.7387	0.6438	0.6866
HumVar	P	0.5189	0.7546	0.6661	0.8451	0.8147	0.7122	0.7329	0.7556
	PS	0.3852	0.6884	0.8047	0.5693	0.6565	0.7403	0.7231	0.6870
	PSP	0.4344	0.7172	0.7153	0.7191	0.7226	0.7118	0.7189	0.7172
	SPP	0.5032	0.7488	0.6829	0.8161	0.7916	0.7156	0.7333	0.7495
	PSPP	0.4184	0.6939	0.5182	0.8735	0.8074	0.6393	0.6313	0.6959

Figure 4.

Violin plots of four performance metrics of MSRes-MutP using different features and serial combinations. Violin plot shows the kernel density estimation of the maximum, minimum, upper and lower quarter and median values. Generally, the more concentrated evaluation metrics, the minor influence of the model on evaluation metrics.

According to the results in Table 2, we have the following observations:

• (1) Using the P feature only, MSRes-MutP achieved MCC values of 0.4831, 0.4635 and 0.5189, and AUC values of 0.7409, 0.7342 and 0.7556, on PredictSNP, HumDiv and HumVar datasets, respectively.

• (2) Based on the linear concatenation of PSSM and PSS features (i.e., PS), the prediction performance of MSRes-MutP did not obviously improve. For instance, on PredictSNP, HumDiv and HumVar datasets, the MCC values of MSRes-MutP (with PS) were 0.3979, 0.4168 and 0.3852, which were 0.0852, 0.0467 and 0.1337, respectively, lower than those of MSRes-MutP trained using the P feature. Similar observations can also be made in terms of AUC values.

• (3) Compared with MSRes-MutP using P (sequence-based) and SPP (structure-based) features, not much difference was observed. For example, on the PredictSNP, MMP and HumVar datasets, ACC values of MSRes-MutP with P were 0.7314, 0.8058 and 0.7546, and ACC values of MSRes-MutP with SPP were 0.7348, 0.8033 and 0.7488, respectively. In terms of MCC and AUC, similar trends can also be seen.

• (4) Serial combination of four types of features (i.e., PSPP), the prediction performance did not improve compared with individual ones. Specifically, on PredictSNP, MMP, HumDiv and HumVar datasets, MSRes-MutP with PSPP achieved MCC values of 0.4345, 0.5500, 0.3715 and 0.4184, which were 0.0400, 0.0191, 0.0586 and 0.0848, respectively, lower than MSRes-MutP with SPP, and were 0.0486, 0.0245, 0.0920 and 0.1005, respectively, lower than MSRes-MutP with P.

We also draw violin plots of four performance metrics in Figure 4. As can be seen, the maximum, minimum, median and upper/lower quarter values of MCC, ACC and AUC were relatively concentrated on PredictSNP and MMP datasets, indicating that different features and serial combinations had a minor influence on the performance of MSRes-MutP. In contrast, values of MCC, ACC and AUC were relatively scattered on HumDiv and HumVar datasets, indicating that different features and serial combinations (i.e., P, PS, PSP, SPP and PSPP) had a distinct influence on the prediction performance of MSRes-MutP on such two datasets. Among all performance metrics, Pre had the most significant fluctuation on the four datasets.

In conclusion, serial combinations (i.e., PSSM+PSS + PRSA+PDO) could not improve MSRes-MutP’s performance expectantly. Such observations are consistent with conclusions made by Hu et al. [66] and Chen et al. [67]. The underlying reasons might be that noisy and redundant information exists between PSSM, PSS, PRSA and PDO. Through serial features combination, such information might mislead the weights of the model during the training process. Accordingly, the extracted features obtained from the deep model may have relatively poor classification ability and hence decrease model performance. Thus, we developed a second model FFMSRes-MutP.

FFMSRes-MutP with (M_L×(20 + 7)) outperforms MSRes-MutP (M_L × 27)

In this section, several experiments were implemented to compare the performance of MSRes-MutP with that of FFMSRes-MutP. The input of MSRes-MutP is the feature matrix with M_L × 27 dimensionality (i.e., PSSM+PSS + PRSA+PDO), while the input of FFMSRes-MutP comprises of two matrices: PSSM (M_L × 20) and PSS+ PRSA+PDO (M_L × 7). The experiment procedure is the same as that described in the previous section. The performance comparison results are depicted in Figures 5 and 6. As can be seen from Figure 5, FMSRes-MutP predicted more TP and TN, and fewer FP and FN, clearly outperforming MSRes-MutP on the four datasets.

Figure 5.

Confusion matrix of MSRes-MutP and FFMSRes-MutP with PSPP on the independent test datasets. In the confusion matrix, principal diagonal values represent TN and TP, while counter-diagonal values indicate FP and FN. Accordingly, the larger principal diagonal values, the more accurate the prediction models.

Figure 6.

Performance assessment of MSRes-MutP and FFMSRes-MutP with PSPP on the independent test datasets.

As shown in Figure 6, FFMSRes-MutP was also superior to MSRes-MutP in terms of other performance metrics. For instance, on the HumVar dataset, the MCC, ACC and AUC values of FFMSRes-MutP were 0.5446, 0.7716 and 0.7693, which were 0.1262, 0.0777 and 0.0734, respectively, higher than those of MSRes-MutP. Similar conclusions can also be drawn on the other three datasets.

The underlying reasons for such phenomena are discussed as follows: First, PSSM contains sequence conservation information built on MSA. Meanwhile, PSS, PRSA and PDO are predicted secondary structures, relative solvent accessibility and disorder, which mainly describe the residues’ structural information. In FFMSRes-MutP, the two types of features were passed through two multi-scale ResNet channels. As such, FFMSRes-MutP is able to train two groups of weights independently and reduce noisy and mutually exclusive factors between the two types of features. In contrast, MSRes-MutP can only train one group weight by feeding the concatenated feature matrix (i.e., PSSM+PSS + PRSA+PDO) into the multi-scale part as a whole. Second, in MSRes-MutP, the previously extracted features through multi-scale parts were directly fed into the fully connected layer. However, in FFMSRes-MutP, the previously extracted features were concatenated through the deep feature fusion. This can enable the capture of more comprehensive features from different perspectives.

Taken together, the deep feature fusion strategy is effective for predicting nsSNPs, and benchmarking results show that FFMSRes-MutP can further improve the prediction performance than MSRes-MutP.

Incorporation of physicochemical properties improves the performance of FFMSRes-MutP

In order to further enrich feature representation, physicochemical properties were added into FFMSRes-MutP. As depicted in Figure 2, the input of FFMSRes-MutP consisted of three parts: (1) PSSM (M_L × 20), (2) PSS + PRSA+PDO (M_L × 7) and (3) physicochemical properties with 28 values.

In this section, comparison experiments were conducted to examine the impact of the above features and combinations. The results are listed in Table 3. In addition, TP, TN, FP, FN, ER, FPR and FNR values of experiments are documented in the Supplementary Table S2 and Text S3.

Table 3.

Performance comparison of FFMSRes-MutP using physicochemical properties, PSPP and combinations on the independent test datasets

Dataset	Features	MCC	ACC	Recall/Sen	Spe	Pre	NPV	F1	AUC
PredictSNP	PSPP#	0.5432	0.7751	0.7149	0.8237	0.7661	0.7816	0.7396	0.7693
	1D28#	0.2493	0.6309	0.3962	0.8272	0.6573	0.6209	0.4944	0.6117
	PSPP+1D28#	0.6422	0.8230	0.7466	0.8856	0.8425	0.8100	0.7916	0.8160
MMP	PSPP#	0.5813	0.8083	0.6977	0.8724	0.7599	0.8329	0.7275	0.7850
	1D28#	0.2293	0.6600	0.3874	0.8201	0.5584	0.6951	0.4574	0.6037
	PSPP+1D28#	0.6226	0.8242	0.7190	0.8893	0.8010	0.8363	0.7577	0.8041
HumDiv	PSPP#	0.4507	0.7323	0.5797	0.8500	0.7489	0.7238	0.6535	0.7148
	1D28#	0.7885	0.8848	0.9872	0.8110	0.7901	0.9888	0.8777	0.8991
	PSPP+1D28#	0.9690	0.9847	0.9737	0.9932	0.9911	0.9800	0.9823	0.9834
HumVar	PSPP#	0.4184	0.6939	0.5182	0.8735	0.8074	0.6393	0.6313	0.6959
	1D28#	0.5245	0.7499	0.9063	0.5906	0.6929	0.8608	0.7853	0.7484
	PSPP+1D28#	0.9436	0.9713	0.9507	0.9925	0.9924	0.9517	0.9711	0.9716

Note: PSPP^# means that the input of FFMSRes-MutP contains two features matrices, PSSM (M_L × 20), PSS + PSA + PDO (M_L × 7). 1D28^# indicates that the input of FFMSRes-MutP only contains physicochemical properties. PSPP+1D28^# means that the input of FFMSRes-MutP comprises of three parts, i.e., PSSM (M_L × 20), PSS + PSA + PDO (M_L × 7) and physicochemical properties (1 × 28).

From Table 3, we can see that FFMSRes-MutP with ‘PSPP+1D28’ was superior to the corresponding models with ‘PSPP’ and ‘1D28’. For example, on the HumDiv dataset, MCC, ACC and AUC values of FFMSRes-MutP with ‘PSPP+1D28’ were 0.9690, 0.984 and 0.9834, which were 0.5183, 0.2524 and 0.2686, respectively, higher than those with ‘PSPP’, and 0.1805, 0.0999 and 0.0843 higher than those with ‘1D28’. Similar conclusions can also be drawn on the other three datasets. On the HumVar dataset, Recall/Sen, Spe, Pre, NPV, F₁ values of FFMSRes-MutP with ‘PSPP+1D28’ were 0.9507, 0.9925, 0.9924, 0.9517 and 0.9711, which were 0.0444, 0.4019, 0.2995, 0.0909 and 0.1858, respectively, higher than those with ‘1D28’, and were 0.4325, 0.1190, 0.1850, 0.3124 and 0.3398, respectively, higher than those with ‘PSPP’.

The added 28 features describe physicochemical properties of wild type and mutant amino acid at the mutation site, such as net charge (KLEP840101), isoelectric point (ZIMJ680104), etc. Therefore, such features can further enrich the feature representation of mutations. In general, the richer features the deep model’s input has the more useful classification information the model can learn. Similar to FFMSRes-MutP with M_L×(20 + 7), these 28 features pass through the third multi-scale ResNet path to train another group of model weights. When integrated with deep feature fusion again, the prediction performance of FFMSRes-MutP can be further improved by combining the physicochemical properties.

F‌FMSRes-MutP outperforms four traditional machine learning methods

In this section, experiments were further implemented to compare FFMSRes-MutP with four traditional machine learning methods, including SVM [68], KNN [69], DT [70] and RF [71]. Performance comparison results are provided in Table 4 and Figure 7. In addition, TP, TN, FP, FN, ER, FPR and FNR values are documented in the Supplementary Table S3 and Text S4.

Table 4.

Performance comparison of FFMSRes-MutP and four traditional machine learning methods on the independent test datasets

Dataset	Method	MCC	ACC	Recall/Sen	Spe	Pre	NPV	F1	AUC
PredictSNP	SVM	0.4092	0.7095	0.6125	0.7890	0.7041	0.7130	0.6551	0.7008
	RF	0.4424	0.7254	0.6085	0.8213	0.7362	0.7191	0.6663	0.7149
	DT	0.3352	0.6701	0.6464	0.6895	0.6305	0.7041	0.6384	0.6680
	KNN	0.3635	0.6851	0.4750	0.8574	0.7319	0.6658	0.5761	0.6662
	FFMSRes-MutP	0.6422	0.8230	0.7466	0.8856	0.8425	0.8100	0.7916	0.8160
MMP	SVM	0.4983	0.7692	0.5708	0.8920	0.7661	0.7704	0.6542	0.7314
	RF	0.5832	0.8067	0.6688	0.8920	0.7933	0.8130	0.7258	0.7804
	DT	0.4978	0.7642	0.6754	0.8192	0.6982	0.8029	0.6866	0.7473
	KNN	0.5786	0.8033	0.7037	0.8650	0.7636	0.8250	0.7324	0.7844
	FFMSRes-MutP	0.6226	0.8242	0.7190	0.8893	0.8010	0.8363	0.7577	0.8041
HumDiv	SVM	0.4364	0.7285	0.5781	0.8395	0.7269	0.7293	0.6440	0.7088
	RF	0.4284	0.7246	0.5530	0.8514	0.7333	0.7205	0.6305	0.7022
	DT	0.3392	0.6766	0.6248	0.7149	0.6181	0.7206	0.6214	0.6698
	KNN	0.3499	0.6880	0.5296	0.8050	0.6674	0.6985	0.5906	0.6673
	FFMSRes-MutP	0.9690	0.9847	0.9737	0.9932	0.9911	0.9800	0.9823	0.9834
HumVar	SVM	0.4351	0.7179	0.7273	0.7078	0.7276	0.7075	0.7274	0.7175
	RF	0.4488	0.7232	0.6925	0.7561	0.7529	0.6962	0.7214	0.7243
	DT	0.3579	0.6791	0.6818	0.6762	0.6932	0.6645	0.6875	0.6790
	KNN	0.3835	0.6805	0.5490	0.8216	0.7676	0.6293	0.6402	0.6853
	FFMSRes-MutP	0.9436	0.9713	0.9507	0.9925	0.9923	0.9517	0.9711	0.9716

Figure 7.

Violin plots of FFMSRes-MutP and four machine learning methods in terms of four performance metrics.

It can be seen that FFMSRes-MutP was superior to traditional machine learning models. For example, on the HumDiv dataset, MCC, ACC and AUC values of FFMSRes-MutP were 0.9690, 0.9847 and 0.9834, which were 0.5326, 0.2562 and 0.2746, respectively, higher than those of SVM. On the other three datasets, similar observations can also be made.

In terms of other performance metrics, FFMSRes-MutP also outperformed the four machine learning methods. For example, on the PredictSNP dataset, FFMSRes-MutP achieved Recall/Sen, Spe, Pre, NPV, F₁ values of 0.7466, 0.8856, 0.8425, 0.8100 and 0.7916, which were 0.1381, 0.0643, 0.1063, 0.0909 and 0.1253, respectively, higher than those of RF. Similar observations can also be made on the other three datasets.

Figure 7 displays violin plots of MCC, ACC, AUC and Pre of FFMSRes-MutP and four machine learning methods. As shown in Figure 7A and B, MCC, ACC, AUC and Pre values were relatively concentrated on the PredictSNP and MMP datasets. For example, on the PredictSNP dataset, ACC and AUC were range in (0.6701, 0.8230) and (0.6662, 0.8160). As depicted in Figure 7C and D, MCC values were quite scattered on HumDiv and HumVar datasets. Specifically, MCC values were in the range of (0.3392, 0.9690) and (0.3579, 0.9436).

As can be seen, the performance metrics values on PredictSNP and MMP datasets were relatively concentrated, while those on HumDiv and HumVar were quite scattered. One underlying reason for such phenomena may be that PredictSNP and MMP were reconstructed datasets based on several resources and without redundant mutations. In conclusion, compared with traditional machine learning models, more parameters can be trained and more nonlinear characteristics can be captured in the deep learning model. Using graphics processing unit, model training becomes faster even with large amount of parameters. Therefore, FFMSRes-MutP has a better predictive capability than machine learning methods for large-scale nsSNP prediction.

10-fold cross-validation is better for performance comparison of FFMSRes-MutP and existing predictors

For large datasets, model training typically requires more time and computing resources. In this case, the ‘independent test’ method is suitable for comparing the performance of different features and models. On ‘10-fold cross-validation’, all mutations in the dataset will be predicted and assessed. Herein, comparison experiments were implemented using these two evaluation methods. The results are shown in Figure 8 and Table 5.

Figure 8.

Confusion matrix of FFMSRes-MutP on the independent test and 10-fold cross-validation.

Table 5.

Performance assessment of FFMSRes-MutP on the independent test and 10-fold cross-validation

Dataset	Method	MCC	ACC	Recall	Spe	Pre	NPV	F1	AUC	ER	FPR	FNR
PredictSNP	Ind#	0.6422	0.8230	0.7466	0.8856	0.8425	0.8100	0.7916	0.8160	0.0629	0.1144	0.2534
	10-fold#	0.5926	0.7970	0.7856	0.8063	0.7715	0.8218	0.7772	0.7959	0.1063	0.1937	0.2144
MMP	Ind#	0.6226	0.8242	0.7190	0.8893	0.8010	0.8363	0.7577	0.8041	0.0683	0.1107	0.2810
	10-fold#	0.6176	0.8202	0.7724	0.8485	0.7510	0.8635	0.7612	0.8104	0.0952	0.1515	0.2277
HumDiv	Ind#	0.9690	0.9847	0.9737	0.9932	0.9911	0.9800	0.9823	0.9834	0.0038	0.0068	0.0263
	10-fold#	0.9605	0.9807	0.9734	0.9869	0.9822	0.9797	0.9772	0.9796	0.0075	0.0131	0.0277
HumVar	Ind#	0.9436	0.9713	0.9507	0.9925	0.9923	0.9517	0.9711	0.9716	0.0037	0.0075	0.0493
	10-fold#	0.9507	0.9748	0.9741	0.9754	0.9773	0.9745	0.9751	0.9748	0.0120	0.0246	0.0259

Note: Ind^#, Independent test; 10-fold^#, 10-fold cross-validation. The results of ‘10-fold^#’ in Table 5 are the average values of 10 cycles in 10-fold cross-validation.

From Figure 8 and Table 5, we can see that the prediction performance of the two evaluation methods had no much difference. For example, on the HumVar dataset, MCC, ACC and AUC values of FFMSRes-MutP on ‘10-fold cross-validation’ were 0.9507, 0.9748 and 0.9748, which were 0.0071, 0.0035 and 0.0032, respectively, slightly higher than the model on ‘independent test’. In addition, on the PredictSNP dataset, MCC, ACC and AUC values of FFMSRes-MutP on the ‘independent test’ were 0.6422, 0.8230 and 0.8160, which were 0.0496, 0.026 and 0.0201, respectively, higher than those on ‘10-fold cross-validation’. Similar results could also be observed in terms of Spe, Pre, F1, TN and FP values.

In contrast, ‘independent test’ means that only 10% of mutations in the dataset were predicted. While after the ‘10-fold cross-validation’ process was traversed once, all mutations were predicted. Therefore, ‘10-fold cross-validation’ is a better and fairer way to compare the performance of existing predictors.

Performance comparison of FFMSRes-MutP with several existing predictors on PredictSNP and MMP datasets

To further evaluate the predictive capability of FFMSRes-MutP, we implemented comparison experiments with several existing predictors. For PredictSNP and MMP datasets, two comparison experiments were performed to compare with single predictors in the ‘Performance comparison of FFMSRes-MutP with eight single and one consensus predictors’ section and consensus predictors in the ‘Performance comparison of FFMSRes-MutP with consensus predictors’ section.

Performance comparison of FFMSRes-MutP with eight single and one consensus predictors

In this section, we compared FFMSRes-MutP with nine predictors on the PredictSNP and MMP datasets. As described in the ‘Benchmark datasets’ section, these two datasets were reconstructed by combining diverse sources and deleting inconsistent and repeated mutations [18]. However, some predictors required special needs, and a portion of the mutation data in the above two datasets could not be predicted. Accordingly, ‘percent (%)’ is utilized to represent the percentage of the mutations predicted. Please refer to Ref. [18] for more details. Performance comparison results are provided in Table 6.

Table 6.

Performance comparison of FFMSRes-MutP, MSRes-MutP and nine existing predictors on the PredictSNP and MMP datasets

Metric	Dataset	MAPP	nsSNP Analyzer	PANTHER	PhD-SNP	PPH-1	PPH-2	SIFT	SNAP	PredictSNP1	MSRes-MutP	FFMSRes-MutP
Percent #(%)	PredictSNP	87.8	33.5	54.6	100.0	98.8	100.0	97.1	99.1	100.0	100.0	100.0
	MMP	99.8	91.5	61.9	100.0	97.7	97.7	95.4	100.0	100.0	100.0	100.0
	Overall	93.8	62.5	58.25	100.0	98.25	98.85	96.25	99.55	100.0	100.0	100.0
ACC	PredictSNP	0.711	0.632	0.642	0.746	0.682	0.701	0.723	0.670	0.747	0.716	0.797
	MMP	0.707	0.618	0.603	0.629	0.684	0.677	0.646	0.709	0.708	0.786	0.820
	Overall	0.709	0.625	0.623	0.688	0.683	0.689	0.685	0.690	0.728	0.751	0.809
MCC	PredictSNP	0.423	0.219	0.296	0.494	0.364	0.407	0.447	0.346	0.492	0.432	0.593
	MMP	0.400	0.228	0.227	0.255	0.357	0.359	0.308	0.406	0.408	0.541	0.618
	Overall	0.412	0.224	0.262	0.375	0.361	0.383	0.378	0.376	0.450	0.487	0.606
AUC	PredictSNP	0.773	0.634	0.692	0.812	0.695	0.776	0.784	0.732	0.808	0.717	0.796
	MMP	0.759	0.620	0.676	0.685	0.720	0.774	0.710	0.769	0.787	0.770	0.810
	Overall	0.766	0.627	0.684	0.745	0.708	0.775	0.747	0.751	0.798	0.744	0.803

Note: PPH-1, PolyPhen-1; PPH-2, PolyPhen-2; Percent^#: percent of the evaluated mutations by predictors. Values of percent^#, ACC, MCC and AUC of nine predictors were collected from PredictSNP1. The ‘overall’ row is the average value of two datasets. The evaluation metrics of the MSRes-MutP model on 10-fold cross-validation using the PSPP features were documented in Supplementary Tables S4 and S5.

Among the above predictors in Table 6, MAPP [72], nsSNPAnalyzer [73], PANTHER [74], PhD-SNP [75], PolyPhen-1 [76], PolyPhen-2 [17], SIFT [11] and SNAP [15] are regarded as single predictors, which mainly apply Naïve Bayes, score threshold, neural network and other machine learning algorithms. PredictSNP1 is a consensus predictor by integrating the outputs of several single predictors. Generally, consensus predictors are superior to single predictors [18]. Detailed results are discussed below.

Results on the PredictSNP dataset

• (1)Eight single predictors: ‘percent’ values ranged from 33.5 to 100% with the average of 83.86%. ACC values ranged from 0.632 to 0.746 with the average of 0.688. MCC values were in the range from 0.219 to 0.494 with the average of 0.375. AUC values were in the range from 0.634 to 0.812 with the average of 0.737.
• (2)Consensus and deep learning predictors: For PredictSNP1, ‘percent’, ACC, MCC and AUC values were 100%, 0.747, 0.492 and 0.808, which were 16.14%, 0.059, 0.118 and 0.071, respectively, higher than the corresponding average values of eight single predictors. Apparently, PredictSNP1 achieved a significant performance and was the best predictor among nine existing predictors. On the other hand, the ACC, MCC and AUC values of MSRes-MutP and FFMSRes-MutP were 0.716, 0.432, 0.717 and 0.797, 0.593, 0.796, respectively. The ACC and MCC values of PredictSNP1 were 0.031 and 0.060, respectively, higher than those of MSRes-MutP, but 0.050 and 0.101, respectively, lower than those of FFMSRes-MutP.

Results on the MMP dataset

• (1)Eight single predictors: ‘percent’ values were in the range of (61.9%, 100.0%) with the average of 93.0%. ACC values were in the range of (0.603, 0.709) with the average of 0.659. MCC values were in the range of (0.227, 0.406) with the average of 0.318. AUC values were in the range of (0.620, 0.774) with the average of 0.714.
• (2)Consensus and deep learning predictors: In the case of PredictSNP1, it achieved ‘percent’, ACC, MCC and AUC values of 100.0%, 0.708, 0.408 and 0.787, which were 7.00%, 0.049, 0.091 and 0.073, respectively, higher than the averages of eight single predictors. Again, PredictSNP1 achieved a significant performance improvement over eight single predictors on the MMP dataset. The ACC, MCC and AUC values of MSRes-MutP were 0.786, 0.541 and 0.770, respectively. In contrast, FFMSRes-MutP further increased the corresponding performance metrics values to 0.820, 0.618 and 0.810, which were 0.112, 0.21 and 0.023, respectively, higher than those of PredictSNP1.

Taken together, on the PredictSNP and MMP datasets, FFMSRes-MutP was superior to eight single predictors and also superior to the consensus predictor PredictSNP1. There are three main possible reasons: First, PredictSNP and MMP datasets were reconstructed datasets. For single predictors, they may have excellent prediction performance on their own datasets. However, when switched to PredictSNP and MMP datasets, their prediction performance may be lower. Second, PredictSNP1 is a consensus predictor, which takes six best prediction outputs of eight single predictors. Generally, consensus predictors perform better and are also more robust than single predictors. Third, deep learning models can learn more informative features and extract more non-linear relationships among different types of features than machine learning models. In particular, FFMSRes-MutP applied different convolution kernel sizes to capture such features in different ranges by leveraging the 2D-ResNet and 1D-ResNet blocks. As a result, FFMSRes-MutP outperformed traditional machine learning methods and is more suitable for large-scale nsSNP prediction.

Performance comparison of FFMSRes-MutP with consensus predictors

On the MMP dataset, we conducted comparison experiments with three consensus predictors, including CONDEL [19], Meta-SNP [77] and PredictSNP1 [18]. As the MMP dataset is relatively small, we set M_L to 9 to avoid model over-fitting. Performance comparison results are listed in Table 7.

Table 7.

Performance comparison of FFMSRes-MutP and MSRes-MutP with three consensus predictors on the MMP dataset

Metric	CONDEL	Meta-SNP	PredictSNP1	MSRes-MutP	FFMSRes-MutP
Percent#(%)	100.0	99.7	100.0	100.0	100.0
ACC	0.640	0.673	0.708	0.786	0.820
MCC	0.349	0.351	0.433	0.541	0.618
AUC	0.770	0.730	0.780	0.770	0.810

Note: Percent^#(%), ACC, MCC and AUC values of CONDEL, Meta-SNP and PredictSNP1 were collected from PredictSNP1.

As listed in Table 7, ‘percent’ values of the three consensus predictors CONDEL, Meta-SNP and PredictSNP1 were in the range of (99.7%, 100%) with the average of 99.9%. Besides, ACC, MCC and AUC were in the ranges of (0.640, 0.708), (0.349, 0.433) and (0.730, 0.780) with the average of 0.674, 0.378 and 0.760, respectively. The best-performing model was FFMSRes-MutP, which achieved the highest percent (100%), ACC (0.820), MCC (0.618) and AUC (0.810). In terms of the AUC value, the second-best predictor PredictSNP1 achieved ACC of 0.708, MCC of 0.433 and AUC of 0.780. In conclusion, FFMSRes-MutP outperformed the three consensus predictors on the MMP dataset.

Performance comparison of FFMSRes-MutP with existing predictors on the HumDiv and HumVar datasets

On the HumDiv and HumVar datasets, several experiments were implemented to compare FFMSRes-MutP with existing predictors. The results are discussed according to three parts below. In the ‘Submitting mutations to predictors’ webservers’ section, we discussed the results using the predictors’ webservers and performance calculation based on output files. In the ‘Prediction results collected from published literature’ section, we discuss prediction results collected from published literature, while in the ‘Performance comparison with the deep learning method’ section, we discuss performance comparison results with a representative deep learning method.

Submitting mutations to predictors’ webservers

We submitted mutations to the webservers of FATHMM [12], PolyPhen-2 [17] and PROVEAN [39] and then downloaded the prediction output files. Some ‘blank’ and/or ‘NA’ marks were present in these files. For instance, on the HumDiv dataset, there were 32 ‘no weights’ in FATHMM (weighted), 20 ‘blank’ in FATHMM (not weighted), 12 ‘blank’ in PROVEAN and 796 ‘NA/blank’ in SIFT. Similar situations also existed in the HumVar dataset. For more information about predictors’ outputs, please refer to the Supplementary Table S6.

In order to evaluate the prediction of each mutation in the dataset, we divided predictors’ outputs into two scenarios: (1) All mutations with no prediction results were marked as ‘error predictions’. For example, there were 5 more FN and 27 more FP in FATHMM (weighted). The corresponding results are listed in Table 8, Supplementary Table S7 and Text S5. (2) All mutations with no prediction results were marked as ‘correct predictions’. For instance, there were 5 more TP and 27 more TN in FATHMM (weighted). The corresponding values are provided in the Supplementary Figure S3, TableS8 and Text S6.

Table 8.

Performance comparison of FFMSRes-MutP, MSRes-MutP and five predictors having batch input webservers on the HumDiv and HumVar datasets

Dataset	Predictor	MCC	ACC	Recall/Sen	Spe	Pre	NPV	F1	AUC
HumDiv	PROVEAN	0.7274	0.8674	0.8176	0.9041	0.8629	0.8704	0.8396	0.8608
	SIFT	0.6675	0.8357	0.8381	0.8339	0.7883	0.8747	0.8124	0.8360
	FATHMM (weighted)	0.2374	0.5838	0.8036	0.4215	0.5062	0.7441	0.6211	0.6160
	FATHMM (not weighted)	0.5947	0.8000	0.6226	0.9309	0.8693	0.7697	0.7255	0.7007
	PolyPhen-2	0.7858	0.8948	0.8916	0.8971	0.8647	0.9181	0.8780	0.8943
	MSRes-MutP	0.4158	0.7086	0.7199	0.7003	0.6396	0.7719	0.6774	0.7098
	FFMSRes-MutP	0.9605	0.9807	0.9724	0.9869	0.9822	0.9797	0.9772	0.9796
HumVar	PROVEAN	0.6190	0.8095	0.8073	0.8119	0.8183	0.8006	0.8128	0.8096
	SIFT	0.5785	0.7887	0.8363	0.7388	0.7706	0.8113	0.8021	0.7875
	FATHMM (weighted)	0.6838	0.8403	0.8015	0.8811	0.8762	0.8088	0.8371	0.8413
	FATHMM (not weighted)	0.4747	0.7305	0.6313	0.8347	0.8003	0.6833	0.7058	0.7330
	PolyPhen-2	0.5975	0.7958	0.8786	0.7089	0.7601	0.8477	0.8150	0.7938
	MSRes-MutP	0.4357	0.7149	0.8197	0.6049	0.6851	0.7619	0.7464	0.7123
	FFMSRes-MutP	0.9507	0.9748	0.9741	0.9754	0.9773	0.9745	0.9751	0.9748

Results on the HumDiv dataset

As listed in Table 8, on the HumDiv dataset, the MCC values of five existing predictors ranged from 0.2374 to 0.7858 with the average of 0.6026. ACC ranged from 0.5838 to 0.8948 with the average of 0.7963. AUC ranged from 0.6160 to 0.8943 with the average of 0.7816. Among the five predictors, PolyPhen-2 performed best, with MCC of 0.7858, ACC of 0.8948 and AUC of 0.8943.

As can be seen, PolyPhen-2 outperformed MSRes-MutP; however, FFMSRes-MutP predicted more TP and/or TN, and fewer FP and/or FN than PolyPhen-2 and other existing predictors. Its superior performance was also reflected by MCC, ACC and AUC values. For instance, FFMSRes-MutP achieved MCC of 0.9605, ACC of 0.9807 and AUC of 0.9796, which were 0.1747, 0.0859 and 0.0853, respectively, higher than those of PolyPhen-2.

Results on the HumVar dataset

As listed in Table 8, amongst the five existing predictors, FATHMM (weighted) outperformed best with MCC of 0.6838, ACC of 0.8403 and AUC of 0.8413, respectively. We can see that FFMSRes-MutP predicted more TP and/or TN, and fewer FP and/or FN than these existing predictors. MCC, ACC and AUC values of FFMSRes-MutP were 0.9507, 0.9748 and 0.9748, which were 0.2669, 0.1345 and 0.1335, respectively, higher than those of FATHMM (weighted).

In conclusion, FFMSRes-MutP outperformed MSRes-MutP and five existing predictors on two datasets, which can be attributed to the following key reasons: First, features used: SIFT [11] mainly utilized the probabilities of amino acids in the MSA. PolyPhen-2 [17] mainly adopted the characteristics from MSA and protein 3D structure information. PROVEAN [39] used differences in the e-value from BLAST. FATHMM [12] applied amino acid probabilities in an HMM. SIFT and PROVEAN belong to sequence-based tools, while PolyPhen-2 and FATHMM are combined tools. All four methods mainly utilized protein sequence characteristics. In contrast, FFMSRes-MutP adopted three major types of features, as described in the ‘Feature representation’ section. Therefore, FFMSRes-MutP employed richer features than the above predictors. Second, machine learning techniques: SIFT [11], PROVEAN [39] and FATHMM [12] used scoring-based functions. PolyPhen-2 [17] adopted Naïve Bayes. FFMSRes-MutP leveraged the advantages of three techniques, including deep feature fusion, multi-scale convolution, and 2D-ResNet and 1D-ResNet blocks. On large-scale datasets, deep learning models can generally outperform machine learning-based models.

Prediction results collected from published literature

In nsSNP prediction, the HumDiv and HumVar datasets have also been used by other groups. SNPdryad [78] is one such method. We collected the prediction results from SNPdryad and compared them with FFMSRes-MutP.

SNPdryad [78] utilized two types of protein sequences, including orthologous sequences from Inparanoid [79] and homologous sequences from UniRef100 [80]. Accordingly, SNPdryad generated two parts of evaluation values and provided in a range as shown in Table 9. Herein, we chose the larger value to represent the performance of SNPdryad.

Table 9.

Performance comparison of SNPdryad, Mutation Taster, MSRes-MutP and FFMSRes-MutP on the HumDiv and HumVar datasets

Dataset	Predictor	AUC	ACC	MCC
HumDiv	SNPdryad	0.96–0.98	0.89–0.93	-
	Mutation Taster	0.90	-	-
	MSRes-MutP	0.7098	0.7086	0.4158
	FFMSRes-MutP	0.9796	0.9807	0.9605
HumVar	SNPdryad	0.90–0.91	0.81–0.83	-
	Mutation Taster	0.86	-	-
	MSRes-MutP	0.7123	0.7149	0.4357
	FFMSRes-MutP	0.9748	0.9748	0.9507

Note: On HumDiv and HumVar datasets, MCC values of SNPdryad and Mutation Taster and ACC value of Mutation Taster did not provide in SNPdryad.

From Table 9, we can see that FFMSRes-MutP was superior to the other two predictors and MSRes-MutP, with a more pronounced performance on the HumVar dataset. The results are discussed as follows: (1) On the HumDiv dataset: the AUC value of FFMSRes-MutP was 0.9796, which was 0.0796 higher than that of Mutation Taster. The AUC of SNPdryad was 0.0004 and slightly higher than that of FFMSRes-MutP. In terms of ACC, FFMSRes-MutP achieved ACC of 0.9807, while SNPdryad achieved ACC of 0.89–0.93. (2) On the HumVar dataset: AUC values of SNPdryad and Mutation Taster were 0.91 and 0.86, which were 0.1977 and 0.1477, respectively, higher than MSRes-MutP, but 0.0648 and 0.1148, respectively, lower than that of FFMSRes-MutP. SNPdryad achieved ACC of 0.83, while FFMSRes-MutP improved to 0.9748.

The underlying reasons are discussed below: First, SNPdryad mainly adopted physicochemical properties and characteristics from MSA [78]. In addition, SNPdryad tried random forest [81], naive Bayes [82], Bayes network [83], AdaBoost [84], SVM [85], etc. and finally chose random forest as the classifier. Mutation Taster [86] mainly used evolutionary conservation scores and Bayes classifier for making the prediction. In contrast, FFMSRes-MutP employed richer feature representations as described in the ‘Feature representation’ section. Second, FFMSRes-MutP also applied multi-scale 2D-ResNet and 1D-ResNet blocks, and deep feature fusion strategies to capture more informative characteristics and hence performed better than machine learning methods (also refer to the discussions in the ‘MSRes-MutP AND FFMSRes-MutP MODELS’ section).

Performance comparison with the deep learning method

In this section, we compare the performance of FFMSRes-MutP and MSRes-MutP with a representative deep learning model KVIST-deep [35]. In its original work, KVIST-deep was evaluated on the independent data (by 20%) of datasets, which was not provided exactly. In order to make a fair comparison, ‘10-fold cross-validation’ was performed to compare with KVIST-deep [35]. The performance comparison results are shown in Figure 9. Note that the performance values of KVIST-deep were collected from Ref. [35].

Figure 9.

Performance comparison of KVIST-deep, MSRes-MutP and FFMSRes-MutP in terms of seven performance metrics on the HumDiv and HumVar datasets.

As shown in Figure 9, FFMSRes-MutP outperformed KVIST-deep on both HumDiv and HumVar datasets. For example, on the HumDiv dataset, the ACC, MCC and AUC values of FFMSRes-MutP were 0.98, 0.96 and 0.98, which were 0.16, 0.28 and 0.02, respectively, higher than those of KVIST-deep. In terms of the Pre, NPV, Recall/Sen and Spe values, FFMSRes-MutP performed the best and clearly outperformed KVIST-deep. KVIST-deep performed the second best and outperformed MSRes-MutP. Similar conclusions can be made on the HumVar dataset. Several factors are attributed to the performance improvement of FFMSRes-MutP: First, features utilized: KVIST-deep mainly utilized the MSA information, one-hot encoding and predicted structural features based on low range MSA [35]. In contrast, FFMSRes-MutP utilized three types of structural features as described in the ‘Feature representation’ section, providing a richer feature set than KVIST-deep. Second, the intrinsic characteristics of mutation site: the characteristics of mutant and wild-type amino acids may be a critical factor for affecting the mutational outcome. Different from KVIST-deep, FFMSRes-MutP applied physicochemical properties with 28 values to enrich the representation of mutation characteristics. Third, deep feature fusion and multi-scale ResNet: KVIST-deep was built on six ResNet blocks and different kinds of features were concatenated directly. In contrast, FFMSRes-MutP adopted the deep feature fusion strategy coupled with the multi-scale ResNet blocks to enable the learning of more informative and discriminative features.

Blind test on 67,584 mutations in transmembrane proteins

FFMSRes-MutP was trained on the PredictSNP dataset and tested on the TM dataset. For existing predictors, there were some mutations that had no prediction results, similar to the situations described in the ‘Submitting mutations to predictors’ webservers’ section. For more details about existing predictors’ outputs, please refer to the Supplementary Table S9.

Herein, we evaluated the predictors’ performance by dividing their prediction results under two scenarios. First, all mutations with no prediction results were marked as ‘error predictions’. The corresponding evaluation results are documented in Table 10, Supplementary Table S10 and Text S7. Second, all mutations with no prediction results were marked as ‘correct predictions’. The performance results are provided in the Supplementary Tables S11-S12 and Text S8.

Table 10.

Performance evaluation of FFMSRes-MutP with existing predictors on the TM dataset

Predictor	ACC	Pre	Recall	F1	Spe	NPV	MCC	AUC
SIFT#	0.7298	0.6422	0.8370	0.7268	0.6491	0.8411	0.4847	0.7430
PolyPhen-2#	0.7363	0.6374	0.8953	0.7446	0.6166	0.8868	0.5180	0.7616
PROVEAN#	0.7680	0.6963	0.8155	0.7512	0.7323	0.8406	0.5423	0.7739
FATHMM#	0.7268	0.6953	0.6475	0.6706	0.7865	0.7478	0.4385	0.7170
FFMSRes-MutP	0.7602	0.6956	0.7851	0.7376	0.7414	0.8209	0.5215	0.7633

Note: PROVEAN^#, http://provean.jcvi.org; PolyPhen-2^#, http://genetics.bwh.harvard.edu/pph2; FATHMM^#, using the ‘not weighted’ and webserver address: http://fathmm.biocompute.org.uk/cancer.html.

From Table 10, we had the following observations: First, for four existing predictors, ACC ranged from 0.7268 to 0.7680, MCC from 0.4385 to 0.5423 and AUC from 0.7170 to 0.7739, with the average of 0.7402, 0.4959 and 0.7489, respectively. Second, PROVEAN performed best among the existing predictors, with ACC of 0.7680, MCC of 0.5423 and AUC of 0.7739. PolyPhen-2 was the second-best method with ACC, MCC and AUC values of 0.7363, 0.5180 and 0.7616, respectively. The three values of PROVEAN were 0.0317, 0.0243 and 0.0123, respectively, higher than those of PolyPhen-2. Third, on blind test, FFMSRes-MutP achieved ACC, MCC and AUC values of 0.7602, 0.5215 and 0.7633, which were 0.0078, 0.0208 and 0.0106, respectively, lower than PROVEAN. In terms of MCC, FFMSRes-MutP performed as the second-best method due to its advantages of integrating multi-scale ResNet models with deep feature fusion. Compared to FFMSRes-MutP, PROVEAN demonstrated its advantages in terms of the proposed delta alignment score and the top 30 clusters of closely related sequences [39]. Altogether, the results indicate that FFMSRes-MutP is also an effective approach for nsSNP prediction when tested on a third-party blind dataset.

Conclusions

In the present work, we have developed two multi-scale ResNet models, namely MSRes-MutP and FFMSRes-MutP. In MSRes-MutP, serial concatenation of several individual features did not considerably improve the prediction performance than individual features. To address this, we further proposed FFMSRes-MutP based on the deep feature fusion strategy for the concatenation of several different features. Specifically, three types of features were fed into three multi-scale ResNet paths for feature extraction. Feature matrices were concatenated through deep feature fusion layers and then flattened to make the final prediction. Extensive benchmarking experiments on four different datasets and blind test demonstrated that FFMSRes-MutP also outperformed MSRes-MutP and several state-of-the-art mutation impact predictors. We anticipate that FFMSRes-MutP will be explored as a powerful tool for facilitating community-wide efforts for annotating and prioritizing pathogenic nsSNPs from a large amount of genomic sequence data.

Key Points

• Rapid and accurate prediction of pathogenic nsSNPs plays an important role in understanding the genetics of diseases and design of new drugs for individuals.

• Building upon the protein evolutionary information, predicted secondary structure, relative solvent accessibility, disorder of the query protein and physicochemical properties of wild-type and mutant amino acids, FFMSRes-MutP is developed as a new computational framework to predict nsSNPs.

• Extensive benchmarking experiments demonstrate the superior performance of FFMSRes-MutP compared with existing mutation impact predictors.

• Three key factors can be attributed to the performance improvement of FFMSRes-MutP: First, deep feature fusion for feature combination is applied; second, 2D-ResNet and 1D-ResNet are applied to extract two-dimensional features and physicochemical properties; Third, three groups of multi-scale ResNet blocks are applied to capture the characteristics in different ranges surrounding the mutation site.

• The web server of FFMSRes-MutP (http://csbio.njust.edu.cn/bioinf/ffmsresmutp/) is publicly available for community-wide prediction of disease-associated nsSNPs.

Fang Ge received her B.S. degree from Anhui Xinhua University and M.S. degree from Anhui University. She is currently a Ph.D. candidate in the School of Computer Science and Engineering, Nanjing University of Science and Technology and a member of the Pattern Recognition and Bioinformatics Group. Her research interests include bioinformatics, pattern recognition and data mining.

Ying Zhang received her M.S. degree in control science and engineering from Yangzhou University in 2020. She is currently a Ph.D. candidate in the School of Computer Science and Engineering at Nanjing University of Science and Technology. Her research interests include bioinformatics, machine learning and pattern recognition.

Jian Xu received his Ph.D. degree from Nanjing University of Science and Technology, on the subject of data mining in 2007. He is currently a full professor in the School of Computer Science and Engineering, Nanjing University of Science and Technology. His research interests include event mining, log mining and their applications to complex system management and machine learning. He is a member of both China Computer Federation (CCF) and IEEE.

Arif Muhammad received the BS in Computer Science from University of Malakand in 2008 and Master's degree in computer science from Abdul Wali Khan University Mardan, Pakistan, in 2016. He earned his PhD degree in computer science and technology, from Nanjing University of Science and Technology, China in 2021. Currently, he is an assistant professor in the Department of Informatics and Systems, School of Science and Technology, University of Management and Technology, Johar Town, Lahore, Pakistan. His research interests include bioinformatics, pattern recognition, and machine learning.

Jiangning Song is an associate professor and group leader in the Monash Biomedicine Discovery Institute and the Department of Biochemistry and Molecular Biology, Monash University, Melbourne, Australia. He is also affiliated with the Monash Centre for Data Science, Faculty of Information Technology, Monash University. His research interests include bioinformatics, computational biomedicine, machine learning and pattern recognition.

Dong-Jun Yu received his Ph.D. degree from Nanjing University of Science and Technology in 2003. He is currently a full professor in the School of Computer Science and Engineering, Nanjing University of Science and Technology. His research interests include pattern recognition, machine learning and bioinformatics. He is a senior member of the China Computer Federation (CCF) and a senior member of the China Association of Artificial Intelligence (CAAI).

Abbreviations

PredictSNP

predict single nucleotide polymorphism;

MMP

massively mutated proteins;

PDB

protein data bank;

SVM

support vector machine;

RF

random forest;

KNN

k-nearest neighbor;

DT

decision tree;

HMM

hidden Markov model;

ANN

artificial neural network;

SIFT

sorting intolerant from tolerant;

PROVEAN

protein variation effect analyzer;

FATHMM

functional analysis through hidden Markov models;

SDM

site-directed mutate;

APOGEE

pathogenicity prediction through logistic model tree;

SNAP

screening for non-acceptable polymorphisms;

Polyphen-2

polymorphism phenotyping v2;

Condel

consensus deleteriousness score of missense mutations;

PredictSNP1.0

predict single nucleotide polymorphism v1.0;

Meta-SNP

meta single nucleotide polymorphism;

GWAVA

genome-wide annotation of variants;

CADD

combined annotation dependent depletion;

STRUM

structure-based prediction of protein stability changes upon single-point mutation;

Pred-MutHTP

prediction of mutations in human transmembrane proteins;

MVP

missense variants prediction;

ResNet

residual neural network;

MAPP

multivariate analysis of protein polymorphism.

Funding

The National Natural Science Foundation of China (62072243, 61772273 and 61872186), the Natural Science Foundation of Jiangsu (BK20201304), the Foundation of National Defense Key Laboratory of Science and Technology (JZX7Y202001SY000901), the National Health and Medical Research Council of Australia (NHMRC) (1144652, 1127948), the Australian Research Council (ARC) (LP110200333 and DP120104460), the National Institute of Allergy and Infectious Diseases of the National Institutes of Health (R01 AI111965) and a Major Inter-Disciplinary Research (IDR) project awarded by Monash University, and the Natural Science Foundation of Anhui Province of China (KJ2018A0572).