BML: a versatile web server for bipartite motif discovery

Abstract

Motif discovery and characterization are important for gene regulation analysis. The lack of intuitive and integrative web servers impedes the effective use of motifs. Most motif discovery web tools are either not designed for non-expert users or lacking optimization steps when using default settings. Here we describe bipartite motifs learning (BML), a parameter-free web server that provides a user-friendly portal for online discovery and analysis of sequence motifs, using high-throughput sequencing data as the input. BML utilizes both position weight matrix and dinucleotide weight matrix, the latter of which enables the expression of the interdependencies of neighboring bases. With input parameters concerning the motifs are given, the BML achieves significantly higher accuracy than other available tools for motif finding. When no parameters are given by non-expert users, unlike other tools, BML employs a learning method to identify motifs automatically and achieve accuracy comparable to the scenario where the parameters are set. The BML web server is freely available at http://motif.t-ridership.com/ (https://github.com/Mohammad-Vahed/BML).

Introduction

Transcription factors (TF) are essential regulatory patterns that control gene expression. Transcription factor binding sites (TFBS) are critical to a comprehension of gene expression regulations. The discovery of TFBS is one long-lasting issue in computational biology, with almost a hundred algorithms developed in the last 30 years [1–3]. It is important to identify the binding motifs for a single block of TFBS and motifs for two-block (bipartite) of TFBS separated by variable gaps. Many various types of bipartite motifs exist in both eukaryotes and prokaryotes [4]. Position weight matrices (PWMs) are generally used to identify and represent TFBSs [5]. They are based on the assumption that each nucleotide independently participates in the TFBSs of DNA sequence interaction. However, it has been long known that interactions between neighboring DNA bases affect TFBSs of DNA sequences interactions. For example, there are many interdependencies between neighboring positions of LexA and cyclic AMP receptor protein (CRP) binding sites in Escherichia coli [6]. Methods that used dinucleotide weight matrix (DWM) outperformed those based on PWM [7].

Despite the algorithmic progress, most methods are difficult for non-experts to use. To overcome this problem, several web tools are available in the public domain, including MEME [8], GLAM2 [9], Bipad [10, 11], BioProspector [12] and AMD [13]. MEME and GLAM2 were developed to predict one-block TFBS, while tools such as Bipad, BioProspector and AMD are designed for ab initio discovery of bipartite motifs for a set of DNA sequences. BioProspector is based on Gibbs sampling, and BiPad is based on the entropy minimization algorithm. Both of them use PWM and enable bipartite motif prediction with variable gaps. On the other hand, AMD predicts bipartite motifs with constant gaps by comparing the target sequences with the background sequences. Most motif discovery web tools push certain levels of burden for motif parameterization to non-expert users, such as the motif length, direction, gap range, the number of occurrences or the number of genes that include motifs. Some tools attempt to circumvent this problem by setting reasonable (yet not optimized) default parameters, however leading to sub-optimal performance.

To lessen the burden of motif parameterization for users but still deliver optimal performance, we propose using BML (short for Bipartite Motif Learning), a new parameter-free (PF) web server for motif-finding. BML is a novel ensemble learning method based on a hybrid of three-component algorithms (Gibbs sampling, minimize entropy and expectation–maximization [EM]), each aimed at a specific motifs category. BML can be used to find de-novo patterns using input RNA or DNA sequences beyond the prior knowledge of a database of known motifs. It is based on our previous dipartite method [14], which discovers the bipartite motifs by considering the interdependencies of neighboring positions in the ChIP-seq data [15]. Specifically, we have improved BML in three aspects: (1) adding a novel PF method for discovering motifs, (2) increasing the accuracy of the results for the adjusted parameter method and (3) adding the graphical result such as sequence web logo and diagram.

Materials and Methods

BML web server

We used ASP.NET, C#, Java, HTML and CSS to implement BML. The absence of nuisance parameters enabled us to implement a clean and straightforward interface for input data, which can be either DNA or RNA sequences. Upon uploading or pasting sequence data, users can choose either with parameter mode or with PF mode. Users can select the method to find motif: PWM or DWM that only require setting some parameters. In the parameter mode, users will need to provide some additional information, e.g. lengths of motifs and gaps, strand direction, option to allow degenerate sites, the number of acceptable repeats and the option of expecting motif sites (one occurrence per sequence, any number of repetition, or zero or one occurrence per site). PF mode enables the practicing biologists to obtain comparable results with those of other motif finders without the hassle of guessing or experimenting with the combination of parameters that gives the best performance. Methods supporting PF mode are described in the following sections.

Results from BML are displayed both in graphic and text formats. The best significant motifs found by BML are displayed graphically as consensus sequences on the main results page. Below is a table containing summary statistics for each motif. Additional detailed information about the motifs is listed on the bottom part as texts. It shows the entropy scores in the iterations, consensus sequences, the position weight matrix (PWM and DWM) constructed from all instances of the motifs and locations of the motif in each site (Figure 1).

Figure 1.

Snapshots of BML web-tool and outputs. (A) BML web tool takes the following inputs from users: sequencing data (in fasta or text format), DNA or RNA type, analysis method and yes/no for degenerated sites. (B) After BML finishes the motif detection, the results of each prediction are shown graphically as sequence logo and text format including the PWM diagram.

Expectation–maximization expressions

The EM algorithm is a family of algorithms for learning probability models in problems that involve a hidden state [16]. In our problem, the hidden state is where the motifs start in each training sequence. EM algorithm repeats the following two steps until convergence: ‘E’ step: Estimate the missing information using the current model parameters. ‘M’ step: Optimize the model parameters using the estimated missing information. The initial values for the motif model are done by randomly choosing the motif start point for each input sequence, then counts each nucleotide’s occurrence at different motif positions, and creates a consensus structure. The PF method implemented in BML assumes that each column in PWM or DWM can be identified as one nucleotide of the motif. In the context of motif discovery, this can be viewed as calculating the probability for the motif occurrences at a specific position in the input dataset. The M-step then evaluates the estimation by maximizing the expected value of the log-likelihood function. Below, we describe the EM algorithm mathematically.

Let us denote the observed part of the data by X, and the missing information by Z. In our case, X represents the input sequences and Z the positions of the motifs. The aim is to find the model parameters θ maximizing the log-likelihood given the observed data:

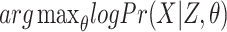(1)

The EM algorithm is used to solve this optimization problem. The log-likelihood for the observed data might be difficult to obtain directly, thus we start by considering the conditional log-likelihood for the observed data given the missing information [17–22]:

(2)

X_i is the ith sequence, and Z_i,j in the matrix Z represents the probability that the motif starts in position j in sequence i. The w is the length of the motif, c is the length of each sequence and k is the position of the motif, 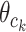represents the probability of character c in column k. We calculate the probability of a training sequence given a hypothesized starting position:

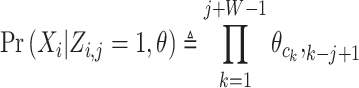(3)

To calculate the probability of a motif, BML computes the probability of motif sequence range, as well as the probability of these background sequences before and after the motif range. It is the outcome of probabilities over the w positions in the motif and the remaining background positions (Supplementary Figure S1). This time using background probabilities for all positions within sequence i:

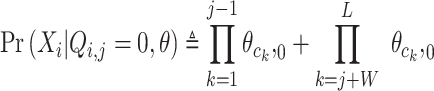(4)

Q functions as the {X, Z} background log-likelihood. The novel index variable Q_i,j is 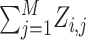, and j is motif start position.

In the E-step, the anticipated counts of all nucleotides at each position are calculated based on the parameters’ current guess. The E-step needs to assess the probability of the hidden data p(Z|X, θ), that is, 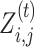for each position. Then, Bayes’ theorem is applied to specify 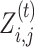in parts of Equation (6):

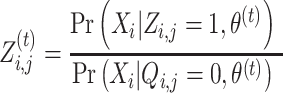(5)

For all i ∈ {1, …, N} and j ∈ {1, …, M} (N is # of sequences, M is # of nucleotides in each sequence).

In the M-step, all parameters are updated based on the values calculated in the E-step. The M-step estimating, recall 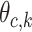represents the probability of character c in position:

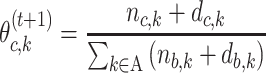(6)

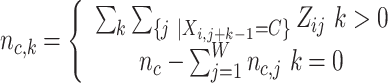For j ∈ {1, …, W}, A ∈ {A, C, G, T} for PWM and A ∈ {AA, AC, AG, AT, CA, .., TT} for DWM, 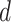is pseudo-counts (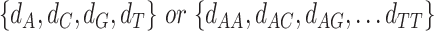), and 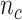is total # of c’s in data set and b is background.

BML iteratively does the E and M steps until the change in formula (Euclidean distance) falls below a threshold (default: 10⁻⁸). EM algorithm makes maximum likelihood estimation to maximize an objective function. Since the E and M steps are repeated, the EM algorithm converges to a maximum.

Objective function

The objective function minimizes Shannon’s entropy for PWM and DWM of the concatenated TFs of the left and right motifs, in Equation (7) below:

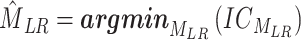(7)

where M_LR is the concatenated motif, and 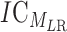is the entropy for the motif M_LR. 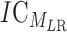is given by:

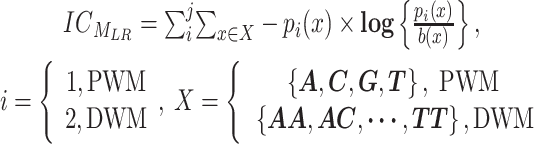(8)

where 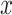is a mononucleotide in PWM, or a dinucleotide for DWM, 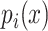and 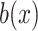are the compositions of x in the motif sites and the background sites (no motif sites), respectively. 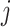is the sum of the lengths of the left and right motifs. 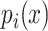and 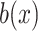are given by:

(9)

(10)

where 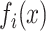is the frequency of x at position i, i.e. the mononucleotide at the position 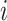for PWM (or PWM-L), or the dinucleotide at the positions 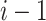, and 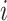for DWM (or DWM-L). β is the pseudo-count (β = 1). k is the number of the patterns, i.e. 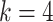for PWM (PWM-L) or 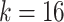for DWM (DWM-L). N is number of sequences in the input data. 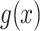is the frequency of x in the background sites. n is the total number of the background mononucleotides for PWM (PWM-L) or background dinucleotides for DWM (DWM-L), which do not harbor the motif sites.

Filtering motifs

To reduce the false positive scores and optimize motif results, we add the cut-off value on the standardized motif scores. The normalization is done as the following:

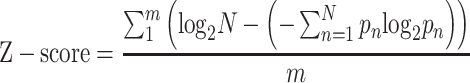(11)

where m is the number of sites in input sequences data, p_n is the detected frequency of symbol n at a special sequence position and N is the number of different symbols for the read sequence type. As a result, the maximum sequence conservation per site is log₂ 16 = 4 bits for dinucleotide (DWM) and log₂ 4 = 2 bits for mononucleotide (PWM). Only motifs with scores larger than the minimum cut-off scores (equation 12) are shown as the output ofBML.

Real datasets

Cyclic AMP receptor protein data

CRP is a prokaryotic TF that is significant in regulating genes involved in energy metabolism. It binds to 22-bp consensus motif sites in E. coli. The sequences were recovered from Regulon Database as ‘TFBSs’ (Release: 9.4 Date: 05-08-2017) [23]. Among 374 sequences of CRP-binding sites, we used 323 unique sequences for performance comparison whose lengths are 36–42 bp. The motif lengths are: 16 bp (11 sites), 17 bp (1 site), 20 bp (1 site), 22 bp (308 sites) and 23 bp (two sites).

Promoter motifs in human

We selected the motifs among 1460 motifs in human [24], where the left and right motifs (or two-block motifs) are more than 3-nt and the gap length is more than the left/right motif length, due to the limitation of BioProspector and Bipad in detecting bipartite motifs. As a result, we obtained 40 motifs. We retrieved the promoter sequences around each binding site (500 bp upstream to 500 bp downstream) as the datasets.

GLAM2 has an input size limit of 60 000 bp and did not work for 11 of the 40 datasets, namely, CCCNNNNNNAAGWT-4, GGCNNNNNKCCAR-13, GTTNMNNNNNAAC-18, GTTNNNNNKNAAC-19, MCAATNNNNNGCG-23, MYAATNNNNNNNGGC-25, TGGNNNNNNKCCAR-32, TTTNNNNNAACW-35, WGTTNNNNNAAA-38, YKACANNNNNCAGA-39, YTGGMNNNNNGCC-44 and YTGGMNNNNNNCCA-45.

Sigma factor data

We used nine datasets of bipartite motifs with variable gap lengths from the sigma factor dataset in Bacillus subtilis from DBTBS [25]. Minimum and maximum gap lengths, and left motif and right motif lengths are determined by DBTBS, with the abbreviation Motif_Left < (Min_Gap,Max_Gap] > Motif_Rigth:

-SigA (344 sequences ranging between 38 bp and 93 bp, 6< [11, 23]>6).

-SigB (64 sequences ranging between 39 bp and 64 bp, 6< [12, 18]>6).

-SigD (30 sequences ranging between 44 bp and 57 bp, 4< [12, 18]>8).

-SigE (70 sequences ranging between 41 bp and 58 bp, 7< [12, 18]>8).

-SigF (25 sequences ranging between 41 bp and 71 bp, 5< [13, 19]>10).

-SigG (55 sequences ranging between 40 bp and 76 bp, 5< [15, 20]>7).

-SigH (25 sequences ranging between 41 bp and 60 bp, 7< [9, 18]>5).

-SigK (53 sequences ranging between 38 bp and 85 bp, 4< [9, 17]>9).

-SigW (34 sequences between from 38 bp to 53 bp, 10< [13, 17]>6).

Mus musculus data

We used 10 single motif datasets of Mus Musculus from the JASPAR server [31]. The matrix ID, name and other details (‘Left Motif Length < Gap > Right Motif Length’) of all motifs were determined based on all identified binding sites described below. The 10 M. musculus motifs were determined based on all identified binding sites: MA0018.2(CREB1, 5), MA0029.1(Mecom, 14), MA0079.2(SP1, 10), MA0099.2(FOS::JUN, 7), MA0150.1(NFE2L2, 11), MA0152.1(NFATC2, 7), MA0153.1(HNF1B, 12), MA0157.1(FOXO3, 8), MA0160.1(NR4A2, 8) and MA0442.1(SOX10, 6).

Arabidopsis thaliana data

We include seven bipartite motifs datasets from the JASPAR server, determined based on all identified binding sites: MA0005.1 (AG, 6 <2 > 3), MA1165.1(HHO6, 3 <1 > 7), MA1207.1(GT-A3, 9 <1 > 7), MA1214.1(ATHB40, 14<3 > 4), MA1235.1(AIL7, 2 <1 > 8), MA1270.1(AT3G45610, 10 <2 > 7) and MA1390.1(HHO2, 5 <1 > 7).

Homo sapiens data

We include five bipartite motifs datasets from the JASPAR server, determined based on all identified binding sites: MA0119.1 (NFIC::TLX1, 5 <4 > 5), MA0256.1(ESR2, 8 <3 > 6), MA0486.1 (HSF1, 9 <2 > 4), MA0501.1(MAF::NFE2, 11 <1 > 3) and MA0513.1(SMAD2::SMAD3::SMAD4, 7 <1 > 5).

Other programs used for comparison

Five popular tools, namely MEME (ver. 5.1.1), GLAM2 (ver. 5.1.1), BioProspector (release 2), BiPad (ver. 2) and AMD, were compared with BML. For the CRP dataset, MEME was executed with the options ‘-mod oops,’ ‘-dna,’ ‘-minw 22,’ ‘-maxw 22’ and ‘-w 22’. GLAM2 was executed with the options ‘-z 100’ ‘-a 22’ ‘-b 22’ ‘-w 22’ ‘-r 1’ ‘-n 2000’ ‘-D 0.1’ ‘-E 2.0’ ‘-I 0.02’ ‘-J 1.0’. BioProspector was executed with the options ‘Width (22, 22),’ ‘Gap (0, 0),’ ‘-n 50’ and ‘-n 3’. BiPad was executed with the options ‘-l 22,’ ‘-a 0,’ ‘-r 0,’ ‘-i,’ ‘-b 0’ and ‘-y 1000’. AMD was executed with the options ‘-MI’ and ‘-T 1’. For human promoter and Sigma factor datasets, we used the same above settings for each tool but different motif size and gap ranges. AMD did not work on SigE and SigF, we used option ‘-T 2.’ For the background sequences in AMD, we used the 200 bp upstream areas of 4314 genes in E. coli K-12 (NC_000913.3) for CRP TF binding sequence data, the promoter sequences of human genes (hg17: upstream1000.fa.gz) for human promoter TF binding sequence dataset, and the 200 bp upstream areas of 4448 genes in B. subtilis 168 (NC_000964.3) for Sigma factors.

Evaluation of prediction accuracy

To evaluate the performance of each tool, we use the nucleotide-level correlation coefficient (nCC) with the same datasets and parameters [26]. The nCC is calculated as:

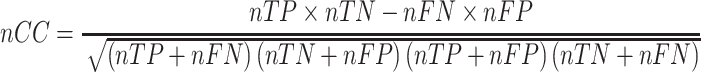(12)

where nTP is the number of nucleotides in sequences that correctly detected motifs, nFP is the number of background nucleotides incorrectly detected motifs, nTN is the number of background nucleotides correctly identify as the background, 4. nFN is the number of nucleotides with motifs but incorrectly be called as the background. The graphic illustrations of nTP, nFP, nTN and nFN are provided in Supplementary Figure S2.

Results

Summary of BML web server

We used ASP.NET, C#, Java, HTML and CSS to implement BML. In designing the web interface for BML, we aimed for the optimal user experience with as minor technical nuisance as possible, maximized the amount of output information and minimalized run-time for each task. BML takes sequence data as the input and uses two methods to find motifs: PWM and DWM. It also has two modes of motif discovery: with parameters or parameters-free (PF) mode. In the parameter mode, the users can choose the default values or decide a small set of input parameters, such as length of motifs and gaps, sequence type as DNA or RNA, forward or reverse direction, option to allow degenerate motif sites, the number of iterations to run the algorithm, and expected motif site distribution in the sequences (Figure 1A). In the PF mode, users do not need to set any parameters, instead the BML-PF methods (PWM-PF and DWM-PF) will predict the motifs based on sequence input data alone.

Results from BML are displayed both in the graphic and text format (Figure 1B). BML shows the best motif logos graphically on the main results page, with a table containing summary statistics for each motif. It also shows more detailed information about the motif in the text format underneath, such as the entropy scores over iterations, the position weight matrix (PWM and DWM) constructed from all instances of the motifs, and the starting/ending site of each motif. A typical run of BML takes between 5 s and 10 min. Runtime is dependent mostly on the size of input data and whether users provide parameter values in BML. BML-PF method is slower due to its search space over a wide number of parameters.

Benchmarking BML (with parameters) against other web tools

Using experimentally determined datasets as the testing cases, BML identified motifs with a significantly higher accuracy level than several other popular motif finding tools (with their default parameters). Below we describe the comparison results on CRP TF binding sequence data, human promoter sequence data and sigma factor data in bacteria B. subtilis 168 sequentially. We use the nCC as the metric for accuracy (see Methods).

Performance on CRP sequence dataset

We evaluated the performance of BML (BML_PWM and BML_DWM) with the five popular motif discovery tools (MEME, GLAM2, BioProspector, BiPad and AMD) by using the TF-binding sites of CRP (Figure 2A and B). We chose 323 unique sequences out of 374 sequences of CRP-binding sites as the test datasets. For testing the one-block motif, namely, the 22-bp motif, BML performs the best among all methods. BML_DWM is slightly better than BML_PWM, as expected, with a nCC of 0.944 (Figure 2A). Next, we compared the accuracy of detecting the bipartite motif on these sequences (Figure 2B). Similar to the annotation in dipartite [14], we annotate a bipartite motif as: L < d > R where L and R are the lengths of left and right motifs respectively, and d is the gap range. Among all three types of bipartite motifs 8< [6]>8, 6< [8]>8, 6< [10]>6, BML_PWM and BML_DWM are superior to BiPad and BioProspector. To evaluate the robustness of the methods, we randomly sampled 100 datasets with 100 sequences from these CRP-binding sites. Again, we obtained consistent conclusion: BML_DWM and BML_PWM slightly outperform other tested tools (Supplementary Figure S3). Taking them together, BML shows better performance at identifying the bipartite and one-block motifs.

Figure 2.

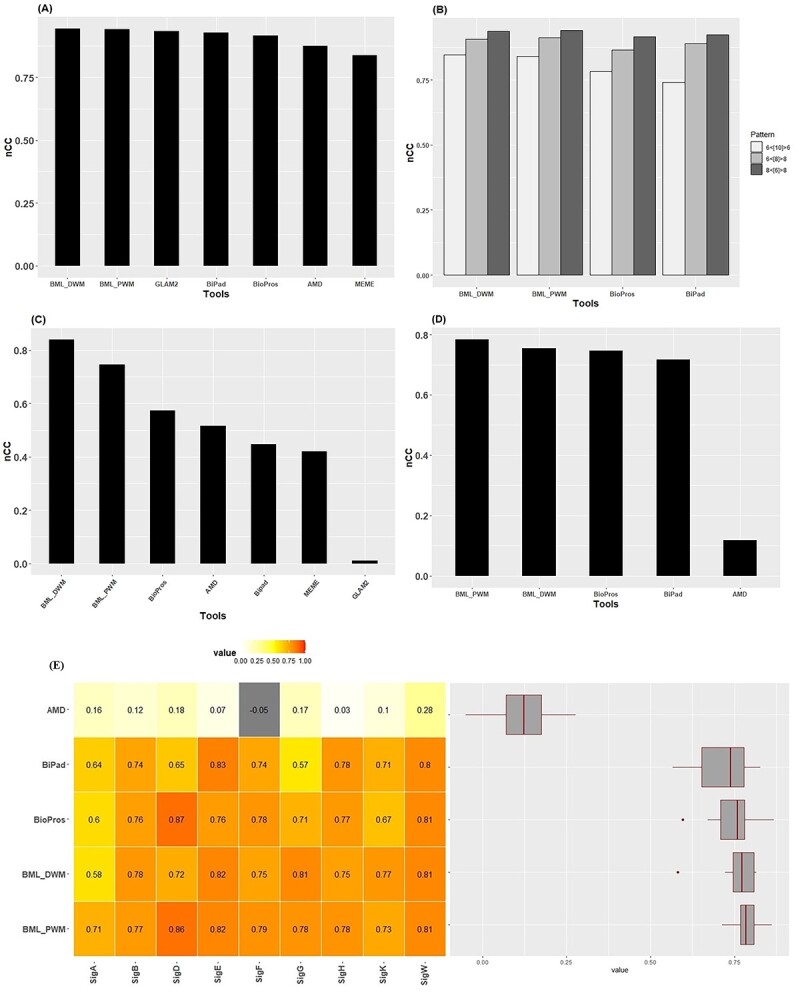
The motif detection comparison on CRP sequences, Human Promoter and sigma factor dataset in B. subtilis. (A) Average nCC results for searching the one-block motif, i.e. the 22 bp motif, in descending order on BML webserver (BML_PWM and BML_DWM modes), GLAM2, BiPad, BioProspector, AMD and MEME. (B) Average nCC results for searching the bipartite motifs, i.e. 6< [10]>6, 6< [8]>8 and 8< [6]>8, on BML_PWM, BML_DWM, BioProspector, BiPad and PWM. (C) The combined nCC values calculated using a total of 3054 sequences from 40 bipartite human motifs datasets. Note: GLAM2 can only support 29 datasets due to the limit of max input sequence length of 60 000 bp. (D) Average nCC results of all sigma (σ) factor datasets. Datasets σA, σB, σD, σE, σF, σG, σH, σK and σW consist of 344, 64, 30, 70, 25, 55, 25, 53 and 34 sequences, respectively. (E) Heat map and boxplots of the nCC values by different motif methods on all nine Sigma datasets.

Figure 3.

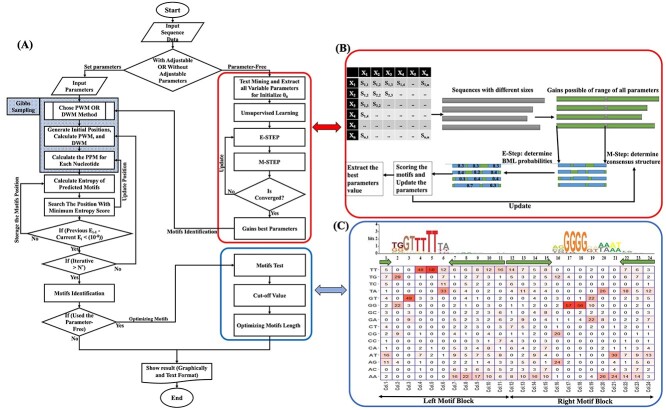
Illustration of BML algorithm. (A) The overall workflow of BML. BML uses two methods, with parameter and PF modes. It proposes bipartite motifs based on PWM or DWM iteratively. Each iteration starts from randomly generated positions until differences of the entropy are minimized. (B) Strategy of EM algorithm for BML_PF to extract the best parameter values. Initialized with the maximally acceptable motif length, in each iteration EM algorithm updates the PPM and improves the positions of the motifs by M-Step and E-Step, then updates the motif score table. (C) Normalization and filtering of motif sequences in BML_PF. In this step, dynamic programming is used to update the motif scores. The low-value motif sequences are filtered separated from the beginning and the end of the motifsbody.

Performance on human promoter sequence datasets

We evaluated the performance of bipartite motif detection by different methods on the 40 human promoter motif datasets that met our selection criteria (see Methods). Due to the input size limit of GLAM2, it only accepted 29 out of 40 datasets. BML_DWM significantly outperforms other tested tools on the human promoter datasets, with the highest nCC = 0.84 and is followed by BML_PWM with nCC = 0.74 (Figure 2C). This confirms that DWM improves the bipartite motif detection upon PWM, as the dataset does consist of dinucleotides. Other tools BioProspector, AMD, Bipad, MEME and GLAM2 have sequentially descending performance after BML methods, with nCCs of 0.57, 0.44, 0.42 and 0.01, respectively. Closer examinations show that AMD, Bipad and MEME also have larger interquartile ranges, suggesting the lack of stability in their predictions (Supplementary Figure S4).

Performance on sigma factor datasets

We next evaluated the performance of BML with other methods over bipartite motifs with variable gaps between two block motifs. For this, we used nine bipartite motifs in sigma TF in B. subtilis, from DBTBS as the testing datasets. The nine sigma factor datasets are, SigA (344 sequences), SigB (64 sequences), SigD (30 sequences), SigE (70 sequences), SigF (25 sequences), SigG (55 sequences), SigH (25 sequences), SigK (53 sequences) and SigW (34 sequences). Overall BML methods (BML_PWM and BML_DWM) perform the best, with the average nCC of 0.78 and 0.75 for BML_PWM and BML_DWM, respectively (Figure 2D and E). They also show the smallest variations among datasets (Figure 2E). AMD has significantly worse nCC values (average nCC = 0.11) than all other methods, confirming that it is not desirable at handling variable gap lengths in bipartite motifs.

One challenge in motif discovery comes from noises in some input datasets. We evaluated the performance of BML under different noise levels (10%, 25% and 50%) using the CRP dataset, as compared to MEME (Supplementary Table SS1). BML has consistently better true positive rates (TPR), with values of 0.96, 0.85 and 0.83 at 10%, 25% and 50% noise levels, as compared to 0.85, 0.77 and 0.75 for MEME; on the other hand, MEME maintains better true negative rate (TNR) at 95% in all three noise levels.

Using BML to predict bipartite motifs with the parameter-free mode

In some cases, the users do not know what best parameters should be used as the input. To handle these situations, they may use BML-PF mode (Figure 3) to find the bipartite motifs with variable gaps based on input sequences only. The BML-PF algorithm is inspired by the unsupervised approach to estimate the parameters of the probability distributions to best fit the motifs of a given dataset. It is implemented by an iterative approach of EM algorithm that cycles between two steps (Equations 5 and 6, Methods). The EM algorithm is applied quite widely in machine learning and is frequently used in unsupervised learning problems, such as density estimation and clustering without input parameters [27–30]. In our application, the first step (E-step) attempts to estimate the latent variables. The second step (M-step) attempts to optimize the parameters of the model to discover the best motifs on sequences data (Figure 3B).

Figure 4.

The performance of BML in PF mode. (A-B) The robust assessment on randomly generated subsets from SingA dataset using PF modes. 100 datasets were generated by sub-sampling of the SigA dataset, yielding 10, 20, 50, 100, 150, 200, 300 sequences in each of the 100 datasets. (A) nCCs of BML_PWM and BML_PWM_PF; (B) nCCs of BML_DWM and BML_DWM_PF. (C) Average nCC results for searching the one-block motif of CRP TF binding sequences. (D) Average nCC results for searching the one-block motif of all nine sigma factor datasets. (E) Sequence logos of Motifs discovered on SigW dataset, by BML using PWM and DWM with parameterization, or under PF mode using PWM_PF and DWM_PF.

Initialized with the maximally acceptable motif length, in each iteration EM algorithm updates the position probability matrix (PPM) and improves the positions of the motifs (Figure 3B). The sequences data along with the best-fit parameters extracted in the EM step are sent back to the Gibbs sampling for motif predictions (Figure 3A). We have observed that the EM algorithm sometimes chooses some nucleotides with low scores as a motif. To reduce the false positive scores and optimize results, we add the cut-off value on the standardized motif scores. Only motifs with scores larger than the minimum cut-off scores (Equation 11, see Methods) are shown as output (Figure 3C). As a default, BML assumes 0.5 as the minimum Z-score shown in the sequencelogo.

Comparing PF- and parameter-based modes in BML

We first demonstrate BML results in the PF mode as compared to the set-parameter mode (Figure 4), on the same CRP TF binding sequence, Human promoter sequence and Sigma factor datasets as described earlier. We first evaluated the effect of input data size on the performance of BML-PF using the sequences of SigA in B. subtilis (Figure 4A and B). By randomly sampling the sequences of SigA, we generated 100 datasets, where each dataset contains 10, 20, 50, 100, 150, 200 and 300 sequences, respectively. With increasing the size of the datasets, BML exhibits better performance on both the average values and variances of nCC scores (Figure 4A and B). BML_PWM-PF variances for the datasets with 200 and 300 sequences are relatively close to those of BML_PWM (Figure 4A). Interestingly, BML_DWM-PF has an even better performance than BML_DWM on this simulated dataset based on SigA (Figure 4B). On the other hand, the averaged results of the BML PF method (BML_PWM-PF and BML_DWM-PF) are both similar but slightly less compared to BML with adjusted parameters (BML_PWM and BML_DWM), on both CRP TF binding (Figure 4C) and on all nine sigma factor datasets (Figure 4D). Out of nine sigma factors, SigW has the highest average nCCs (Figure 1E) in both PWM (0.808) and DWM (0.811) approaches, indicating the presence of base interdependencies in the motif of SigW. We thus compared the PF and parameter modes to the real motif in SigW next (Figure 4E). BML PWM_PF and DWM_PF have nCCs of 0.752 and 0.808, respectively, very similar to the scenarios with parameters where PWM and DWM approaches have nCCs of 0.808 and 0.811, respectively. This shows the accuracy of the BML-PF method. Confirming by the logos, all four approaches largely recover the bipartite motif as determined by DBTBS, which includes 10 bp (TGAAACTTT) on the left and 6 bp (CGTATA) on the right.

Figure 5.

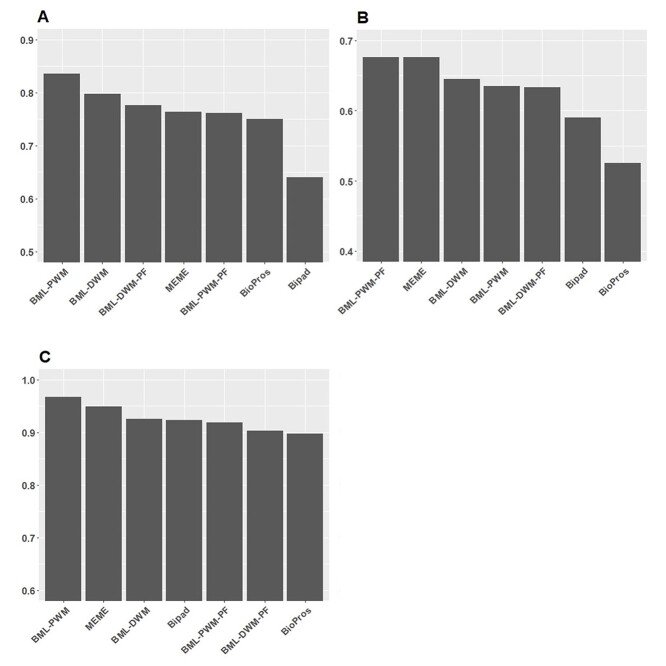
The performance comparisons among BML (with or without PF), MEME, BioPros and Bipad, in M. musculus, A. thaliana and H. sapiens. (A) Combined nCC values of detecting 10 M. musculus motifs on a total of 195 sequences. (B) Combined nCC values of detecting seven A. Thaliana motifs on a total of 6198 sequences. (C) Combined nCC values of detecting five H. Sapiens motifs using a total of 2246 sequences.

We also compared the performance of BML with MEME, Bipad and BioProspector for single block motif and bipartite motifs from three organisms: mouse, Arabidopsis and human (Figure 5). Specifically, we compared the nCCs on detecting motifs of 10 M. musculus transcription factors (Figure 5A), seven Arabidopsis thaliana transcription factors (Figure 5B) and five homo sapiens transcription factors (Figure 5C), where sequences were taken from the JASPAR server (see Methods). As shown in Figure 5A, BML_PWM is the best method for detecting given motifs in mouse in human (Figure 5A and C), and BML_PWM-PF is the equally best method (with MEME) for detecting motifs in A. thaliana (Figure 5B). Despite the data-set dependent differences, BioProspector and Bipad tend to have worse accuracy (Figure 5).

Additionally, we tested the running time among BML, MEME, BioProspector and Bipad using five different datasets generated from 50, 100, 250, 500 and 1000 randomly sampled sequences from the CRP dataset (Supplementary Figure S5). There is a clear trade-off between performance and speed. MEME and BioProspector are the fastest software among tested software, but their accuracy is worse, as shown before (Figure 2A and B). BML_PWM has comparable speed with Bipad, but BML_DWM needs a longer running time than BML_PWM due to the complexity of identifying bipartite motifs. BML PF mode also takes longer processes to detect the best parameters for motifs discovery.

Conclusion

Here we present the BML web server, a very user-friendly motif exploration method that enables both expert and non-expert biologists to identify one-block motifs and bipartite motifs. We evaluate the performance of BML on various datasets compared with other freely available tools, namely, MEME, GLAM2, BioProspector, AMD and BiPad for motif discovery. We show that BML performs significantly better than these alternatives. When naïve users are not sure about the values of the input parameters, they can use BML as a PF web server and still retrieve consistent motifs. Currently, BML implements EM algorithm and Gibbs sampling for motif predictions, we plan to test deep-learning methods for accuracy improvement in the future. BML is available for use at http://motif.t-ridership.com/ (https://github.com/Mohammad-Vahed/BML).

Key Points

• We compared computational methods for motif discovery. Most motif discovery web tools are either not designed for non-expert users or lacking optimization steps when using default settings.

• We developed a new web tool called bipartite motifs learning (BML) for bipartite motif discovery.

• BML achieved significantly better accuracies with or without parameters provided by the users, making it an ideal tool of motif discovery for both expert and non-expert users.

Mohammad Vahed is currently a postdoctoral researcher at Washington University in St. Louis, the School of Medicine. He was a visiting scholar in Dr. Lana Garmire's group. He obtained his Ph.D. in Bioinformatics from Chiba University — Chiba, Japan. His research interests include machine learning and data mining in big data and implementing new tools and web tools in bioinformatics fields.

Majid Vahed is currently a postdoctoral researcher at Shahid Beheshti University of Medical Sciences, Iran, Tehran. He obtained his Ph.D. in Physicochemical from Chiba University — Chiba, Japan. His research interests include experimental and computational studies on Alzheimer's disease and cancer.

Lana Garmire is an Associate Professor at University of Michigan. Her research interests are translational bioinformatics, including multi-modal and multi-omics data integration, single cell bioinformatics, drug reposition for precision medicine in applications including cancers and women's health.

Authors’ contribution

M.V. envisioned the project and conducted the implementation and analysis, M.V. participated in designing and coordinating the study. L.X.G. supervised the study and provided funding support. M.V. and L.X.G. wrote the manuscript. All authors have read and approved the manuscript submission.

Funding

This research was supported by grants K01ES025434 awarded by NIEHS through funds provided by the trans-NIH Big Data to Knowledge (BD2K) initiative (www.bd2k.nih.gov), R01 LM012373 and LM012907 awarded by NLM, R01 HD084633 awarded by NICHD to L.X.G.