Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2022 Jan 4;7(2):1733–1739. doi: 10.1021/acsomega.1c04564

Generation of Spin Defects by Ion Implantation in Hexagonal Boron Nitride

Nai-Jie Guo 1, Wei Liu 1,*, Zhi-Peng Li 1, Yuan-Ze Yang 1, Shang Yu 1, Yu Meng 1, Zhao-An Wang 1, Xiao-Dong Zeng 1, Fei-Fei Yan 1, Qiang Li 1, Jun-Feng Wang 1, Jin-Shi Xu 1, Yi-Tao Wang 1,*, Jian-Shun Tang 1,*, Chuan-Feng Li 1,*, Guang-Can Guo 1
PMCID: PMC8771700  PMID: 35071868

Abstract

graphic file with name ao1c04564_0005.jpg

Optically addressable spin defects in wide-band-gap semiconductors as promising systems for quantum information and sensing applications have recently attracted increased attention. Spin defects in two-dimensional materials are expected to show superiority in quantum sensing due to their atomic thickness. Here, we demonstrate that an ensemble of negatively charged boron vacancies (VB–) with good spin properties in hexagonal boron nitride (hBN) can be generated by ion implantation. We carry out optically detected magnetic resonance measurements at room temperature to characterize the spin properties of ensembles of VB defects, showing a zero-field splitting frequency of ∼3.47 GHz. We compare the photoluminescence intensity and spin properties of VB– defects generated using different implantation parameters, such as fluence, energy, and ion species. With the use of the proper parameters, we can successfully create VB defects with a high probability. Our results provide a simple and practicable method to create spin defects in hBN, which is of great significance for realizing integrated hBN-based devices.

1. Introduction

Solid-state spin defects have attracted widespread attention as promising quantum systems in recent decades1 and have numerous applications in quantum information2,3 and quantum sensing.4,5 Some prominent systems have been studied extensively, including the nitrogen vacancy (NV) center6−9 and the silicon vacancy center10,11 in diamond and the divacancy center12,13 and the silicon vacancy center14,15 in silicon carbide. Although these defects have many remarkable properties, such as a long spin coherence time at room temperature,16 there are some intrinsic limitations due to the three-dimensional nature of the materials. For example, it is difficult to prepare spin defects close to the sample surface, which affects the sensitivity of the sensor.17

Recently, the emergence of spin defects in two-dimensional materials and van der Waals crystals has provided a remedy for the limitations of three-dimensional materials. One of the outstanding materials is hexagonal boron nitride (hBN), which possesses a wide bandgap and a variety of atom-like defects, making hBN a good quantum system for single-photon emitters18−24 and spin-addressable systems23−27 at room temperature. Currently, most studies of spin defects are focused on the negatively charged boron vacancy (VB–) that consists of a missing boron atom that is replaced by an extra electron in the hBN crystal.25−35 The VB defects are photostable and exhibit good spin properties at room temperature.25 In addition, the VB– defects have a triplet ground state (S = 1) and can be initialized, manipulated, and optically read out at room temperature, showing the potential for spin-based quantum information and sensing applications.25,26

In this context, we demonstrate a new way to generate VB– defects in hBN crystals by an ion implantation process using an ion implanter. At present, VB defects can be generated by high-dose neutron irradiation,25 focused ion beam (FIB) implantation,30 femtosecond laser writing,31 and high-energy electron irradiation.32 With appropriate energy and fluence for implanted ions, we successfully created ensembles of VB– defects using an ion implanter, which exhibit good contrast in the optically detected magnetic resonance (ODMR) results. In addition, we measured the Rabi oscillations and spin–lattice relaxation time (T1) of the defects (see the Supporting Information).

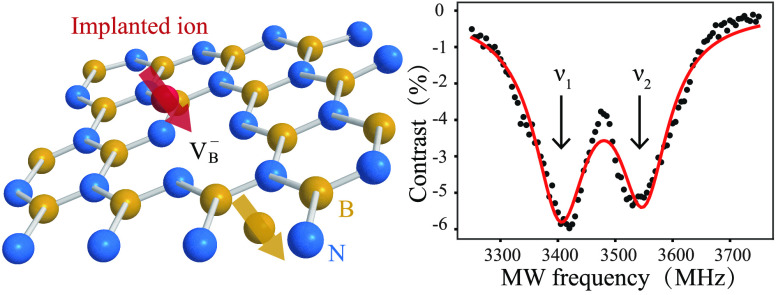
In the experiment, we used a commercially available monocrystalline hBN sample purchased from HQ Graphene with a lateral size of ∼1 mm. Monocrystalline hBN was exfoliated with tape into 10–100 nm thick flakes, which were later transferred onto a silicon substrate. The sample was then put into an ion implanter (IonImplantatation-CETC-M56100), and the hBN flakes were implanted with parallelized ion beams over a large area. Through the ion implantation process, we successfully created VB– defects. The process is schematically shown in Figure 1a. The high-energy ions break the B–N bonds in the hBN lattice and knock out boron atoms, leaving behind negatively charged vacancies. The photoluminescence (PL) and spin properties of the defects were characterized using a confocal microscope system combined with a microwave system. We used a 532 nm laser to excite the defects with a laser power of 4.7 mW, used a 0.5 N.A. objective (Olympus) to focus onto the sample, collected the fluorescence utilizing a 9 μm core-diameter fiber attached to an avalanche photodiode, and used a copper wire with a diameter of 20 μm placed close to the implanted sample as an antenna to deliver a microwave field.28,36

Figure 1.

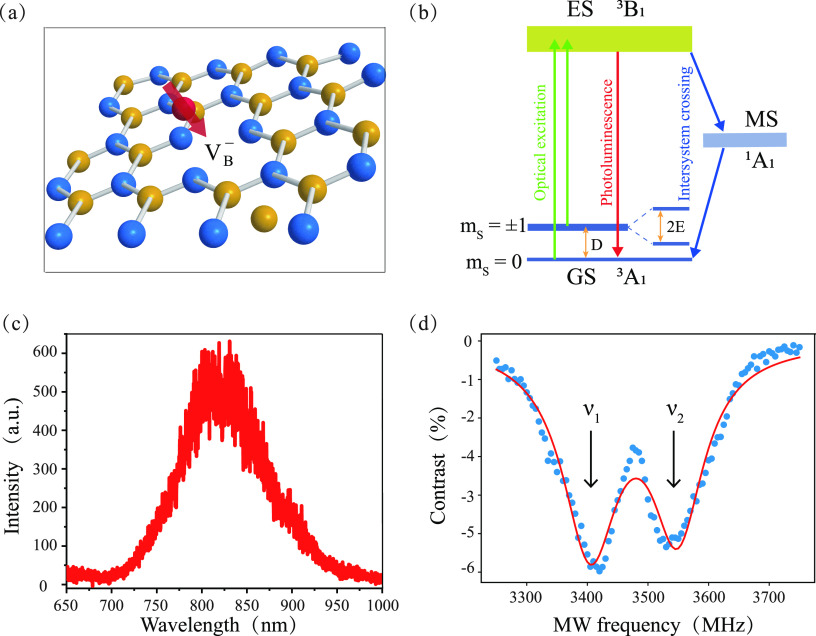
Figure 1

Open in a new tab

Generation of VB– defects in hBN by implanting nitrogen ions with an energy of 30 keV and a fluence of 1 × 1014 ions/cm2. (a) Schematic of the ion implantation process. Alternating boron (red) and nitrogen (blue) atoms form the crystalline hexagonal structure of an hBN monolayer. Implanted nitrogen (green) ions knock out boron atoms from the hBN lattice to generate VB defects. (b) Simplified VB– energy-level diagram and the transitions among the ground state (3A1), excited state (3B1), and metastable state (1A1). (c) Photoluminescence (PL) spectrum for the implanted sample at room temperature, showing an emission centered at ∼820 nm. (d) ODMR measurement of the spin defects generated by ion implantation without an external magnetic field. The red line is a fit to a two-Lorentzian function, where ν1 ∼ 3405 MHz and ν2 ∼ 3548 MHz.

2. Results and Discussion

With the setup described above, we first characterized the PL spectrum of an ensemble of defects generated by implanting nitrogen ions with an energy of 30 keV and a fluence of 1 × 1014 ions/cm2, as shown in Figure 1c. The implanted samples exhibit strong PL emission ranging from 700 to 1000 nm and a center at approximately 820 nm, which is characteristic of VB– centers and consistent with reported VB defects created by neutron irradiation, FIB, and laser writing.25,30,31 In addition, the VB– defects that we created were stable for an extended period of time at room temperature (see the Supporting Information).

To further verify that the ensemble of defects generated by ion implantation were VB– centers, we performed optically detected magnetic resonance (ODMR) measurements at room temperature. ODMR measurements were carried out by scanning the frequency of the microwave field from 3250 to 3750 MHz without an external magnetic field, and the ODMR spectrum was fitted by a two-Lorentzian function, as shown in Figure 1d. The result indicates that the fluorescence signal drops when the microwave field oscillates at ν1 ∼ 3405 MHz and ν2 ∼ 3548 MHz, which is consistent with the ODMR spectra measured for VB defects in previous works.25,28Figure 1b shows that the ms = ±1 excited state of the VB– center is more likely to return to the ms = 0 ground state through nonradiative intersystem crossing, so the VB spin will be polarized into the ms = 0 ground state under continuous laser excitation. When the microwave frequency is in resonance with the split between the ground state sublevels, electrons in the ms = 0 state will be pumped into the ms = ±1 state, leading to a decrease in the fluorescence intensity.28 The VB– center has a triplet ground state (S = 1) with a zero-field splitting (ZFS) described by the parameters D and E. The resonance frequencies ν1 and ν2 in the ODMR spectrum can be represented by 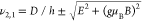Inline graphic, where h is the Planck constant, g is the Landé factor, μB is the Bohr magneton, and B is the static magnetic field.25 In the absence of external magnetic field, the ZFS parameters D and E are given by D/h = (ν1 + ν2)/2 and E/h = (ν2 – ν1)/2, respectively. In our experiment, we find D/h = 3475 ± 5 MHz and E/h = 70 ± 5 MHz. The VB defects exhibit a good ODMR contrast (up to 22%, see the Supporting Information) and a long relaxation time (up to 17 μs, see the Supporting Information) at room temperature, showing the promising spin properties for VB– defects generated by ion implantation.

Next, we studied the effect of different implantation parameters, such as implantation fluence, energy, and ion species. First, we compared the implantation effect of different fluences. We generated defects by implanting nitrogen ions with the same energy (30 keV) and increasing the fluence from 1 × 1013 to 1 × 1016 ions/cm2. Figure 2a shows a comparison of the room-temperature PL spectra for four defect samples. We find that the intensity of the PL spectra increases with the increasing fluence at low doses. When the fluence increases to 1 × 1014 ions/cm2, the PL intensity is shown to decrease slightly, which is similar to that observed for VSi defects in silicon carbide and NV and SiV centers in diamond.36−38 This decrease can be considered a saturation phenomenon for the VB– defects generated by ion implantation, which might result from the ion-induced damage of the crystal lattices that accumulates in the form of multiple vacancy defects.36−38 The ODMR spectra with the two-Lorentzian fitting at different fluences are shown in Figure 2b. The measurements were carried out without an external magnetic field at room temperature. We find that the ZFS parameter D is stable at ∼3475 MHz (see the Supporting Information), while the ZFS parameter E increases almost linearly with the fluence ranging from 1 × 1013 to 1 × 10 15 ions/cm2, as shown in Figure 2c. Nevertheless, when the fluence reaches 1 × 1016 ions/cm2, the ZFS parameter D is no longer stable and varies from 3460 to 3520 MHz, and E is no longer linear (see the Supporting Information). Furthermore, we measured the spin–lattice relaxation times T1 of the defects, as shown in Figure 2d, which were found to be negatively correlated with the implantation fluence. The dependence of E and T1 on fluence can be attributed to the increasing crystal damage with the increasing fluence. Damage due to ion implantation can give rise to local strain fields,39 which have an effect on electron spin transitions. The strain field in hBN is mainly manifested as transverse strain when the damage is not very large,40,41 and the effect of transverse strain, as stated in ref (42), is equivalent to a modification of E. The more severe the damage, the larger the transverse strain and thus the larger the transverse splitting. Meanwhile, the damage can deteriorate the spin and optical coherence properties of defects,43 which suggests that more severe damage will lead to a shorter T1.

Figure 2.

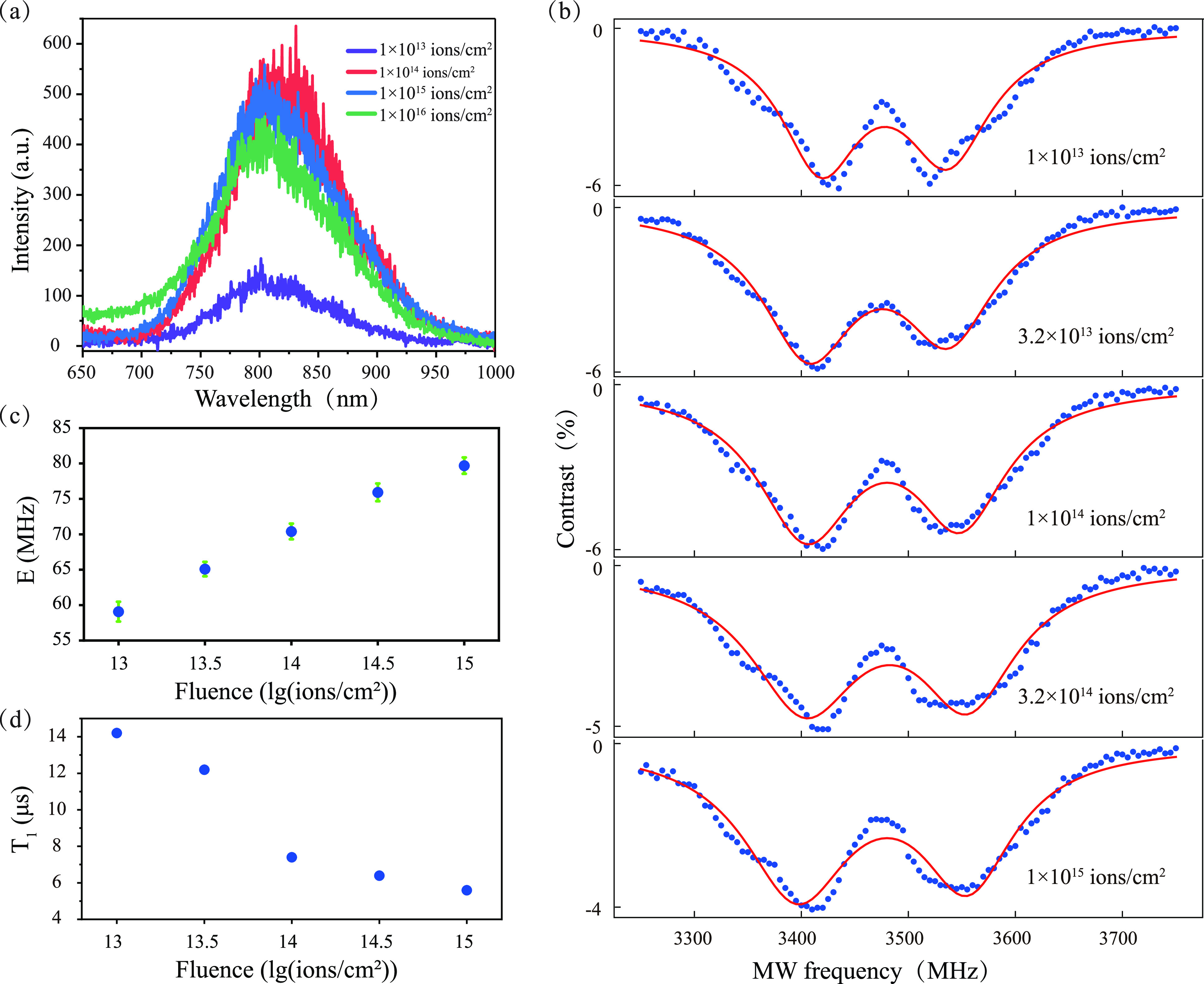
Figure 2

Open in a new tab

Effects of implantation fluence on the defects. The fluence was varied from 1 × 1013 to 1 × 1016 ions/cm2. The energy of the implanted nitrogen ions was fixed at 30 keV. (a) PL spectra at room temperature for the defects created with different fluences. (b) ODMR measurements without an external magnetic field for the defects created with different fluences. (c) The ZFS parameter E as a function of fluence from 1 × 1013 to 1 × 1015 ions/cm2. (d) The spin–lattice relaxation time T1 as a function of fluence from 1 × 1013 to 1 × 1015 ions/cm2.

Then, to compare the implantation effect of different energies, we generated defects by implanting nitrogen ions with the same fluence (1 × 1014 ions/cm2) and varying energies from 20 to 40 keV. Figure 3a shows a comparison of the PL spectra measured for these defect samples, and Figure 3b shows a comparison of the ODMR spectra measured at room temperature. We can see that different energies mainly affect the PL intensity but have almost no effect on the spin properties of the VB– defects. The PL spectrum for the VB defects generated at an energy of 30 keV displays a higher intensity than those of VB– defects generated at other energies, while the ODMR spectra of the VB defects generated at different energies display the same resonance frequency, i.e., the same ZFS parameters D and E. Additionally, we find that the spin–lattice relaxation times T1 scarcely change with the implantation energies (see the Supporting Information). Because our hBN samples are 10–100 nm thick flakes, ions can easily penetrate the flakes rather than remain in the samples, even at low energy. Although the implantation energies are different, the damage due to ion implantation with the same ion species and fluence is similar. Therefore, the implantation energy does not affect the spin properties of the defects.

Figure 3.

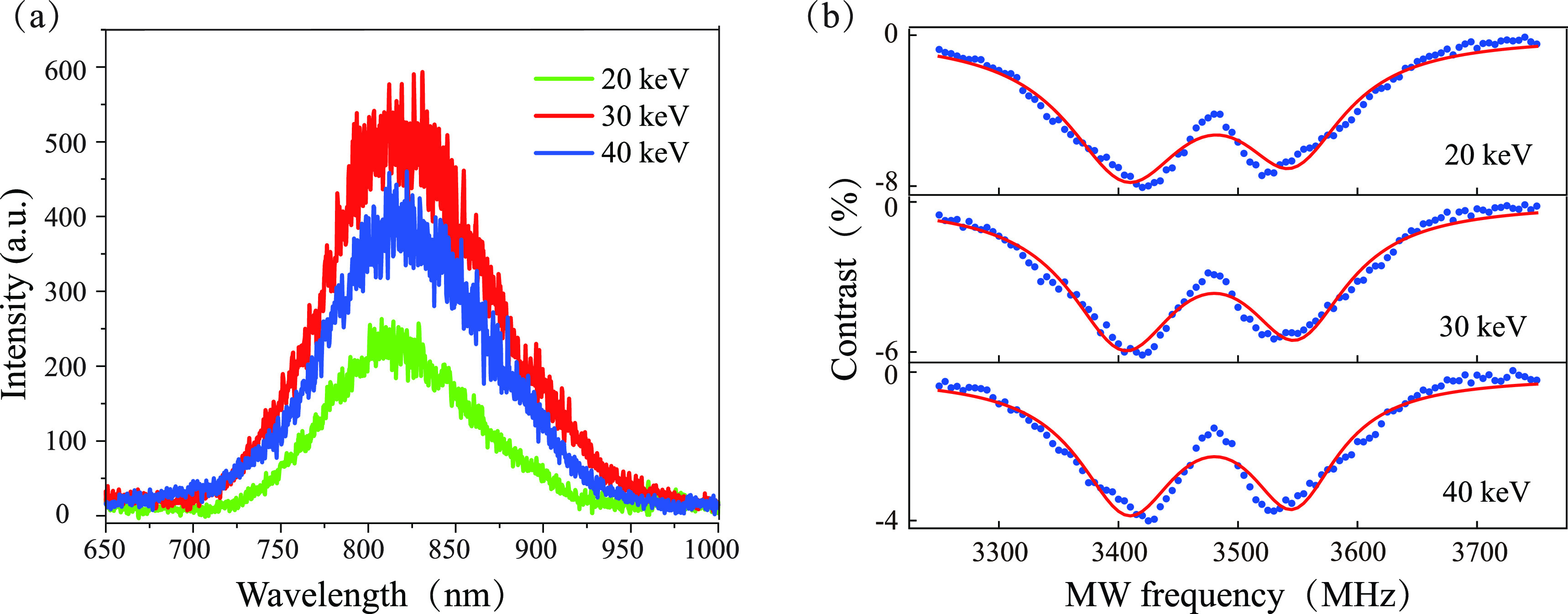
Figure 3

Open in a new tab

Effects of the energy of the implanted nitrogen ions on the defects. The energy was varied from 20 to 40 keV. The implantation fluence was fixed at 1 × 1014 ions/cm2. (a) PL spectrum at room temperature for the defects created with different energies. (b) ODMR measurements without an external magnetic field for the defects created with different energies.

Finally, to compare the implantation effect of different ion species, we generated defects by implanting nitrogen, argon, helium, and carbon ions with the same fluence (1 × 1014 ions/cm2) and energy (30 keV). We simulate the theoretical distribution of the VB– defects with a depth created by different ions using a stopping-and-range-of-ions-in-matter (SRIM) simulation, as shown in Figure 4a. The result indicates that the number of generated defects and the penetration depth are obviously different for different ions. Argon ions are more likely to create shallow defects, while helium ions can be used to create defects in thicker samples. Figure 4b shows a comparison of the PL spectra measured for these samples at room temperature, from which we can see that the sample implanted using nitrogen ions has the highest PL intensity. Figure 4c shows the ODMR spectra for the defects generated by different implantation ions, indicating that they all have spin properties. We find that when we implant different ions, the ZFS parameter D is stable at ∼3475 MHz (see the Supporting Information), while the ZFS parameter E is different, which is similar to implantation with different fluences. The difference in the ZFS parameter E is shown in Figure 4d, showing that the ZFS parameter E increases as the ion radius increases. Additionally, the spin–lattice relaxation times T1 for the defects decrease as the ion radius increases, as shown in Figure 4e. Similar to the dose-dependent relationship mentioned above, the dependence of E and T1 on the ion species can also be attributed to crystal damage. With the increasing atomic number, the damage increases due to the larger collision cross-section; thus, E increases and T1 decreases.

Figure 4.

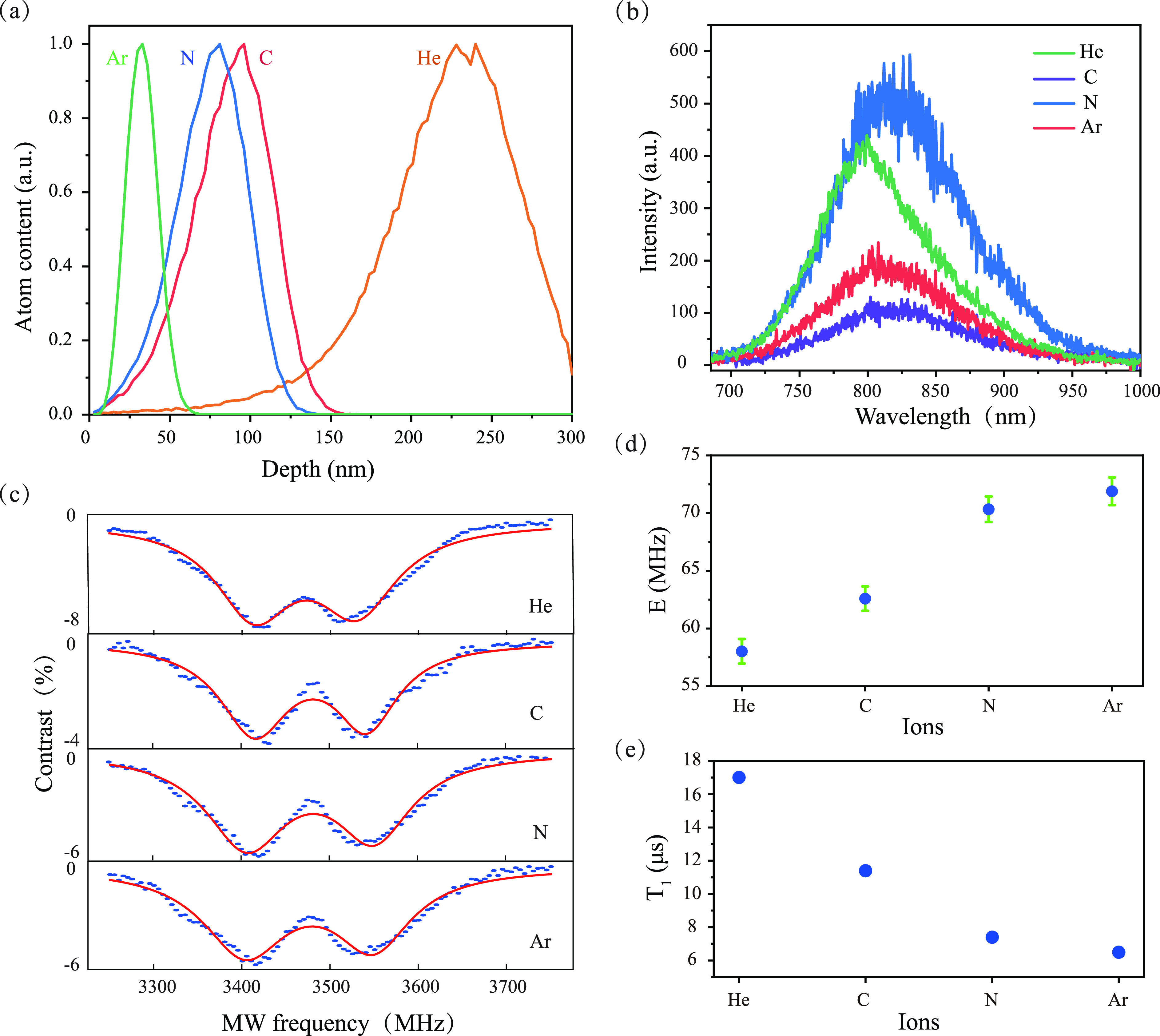
Figure 4

Open in a new tab

Effects of different implanted ion species on the defects. The implantation fluence was fixed at 1 × 1014 ions/cm2, and the energy was fixed at 30 keV. (a) SRIM simulation of the defect distribution with depth generated by implanting different ions (He, C, N, and Ar). (b) PL spectra at room temperature for the defects created with different ions. (c) ODMR measurements without an external magnetic field for the defects created with different ions. (d) The ZFS parameter E varies with different ions. (e) The spin–lattice relaxation time T1 varies with different ions.

3. Conclusions

We successfully generated optically active VB– defects by ion implantation in hBN. There are also several other ways to generate VB defects, such as the neutron irritation method, the FIB method, the laser writing method, and the electron irradiation method. All these methods have their own advantages and disadvantages. For example, the neutron irritation method is the primary way to generate VB– defects, but it needs to be carried out in a nuclear reactor, which is not very convenient and slightly expensive. Comparatively, the ion implantation method is convenient and inexpensive because the ion implanter is commercially available. The FIB method allows for the patterning of arrays of spin defects due to its controllability and good positioning. This is the advantage of this method. However, to the best of our knowledge, the ion source often used for commercial FIBs is Ga, and the use of other ion sources is rare. In contrast, the ion implanter has a variety of available ion sources (He+, C+, N+, Ar+, etc.) and, moreover, the ion implantation method can be used to create VB defects over a large scale. The laser writing method is simple and flexible, as it can be conducted in an ambient environment with no vacuum requirement. However, the required femtosecond laser pulse has a relatively large energy and is possibly destructive toward the sample. In comparison, the ion implantation method is gentle and results in little damage to the sample. In addition, the electron irradiation method makes it possible to avoid the clustering of defects, but it requires very high electron energy (2 MeV). Relatively, the ion implantation method needs only a relatively low ion energy (30 keV). Therefore, our ion implantation method will be a good supplement to all the above-mentioned methods.

Our results show that the implantation parameters, such as fluence, energy, and ion species, have clear effects on the PL intensity and spin properties of ion implantation-generated VB– defects. Therefore, we can create good ensembles of VB defects with a high probability by adjusting the fluence (1 × 1014 ions/cm2) and the energy (30 keV) of the implanted nitrogen ions. The VB– defects exhibit a good ODMR contrast at room temperature, which is important for spin-addressable systems. Furthermore, we find that the defects created by implanting helium ions with an energy of 30 keV and a fluence of 1 × 1014 ions/cm2 have the longest spin–lattice relaxation time of 17 μs at room temperature, which is comparable to that achieved for defects created by neutron irradiation.26,27 Our work provides a simple and practicable method for the controllable engineering of spin defects in hBN and paves the way for integrated quantum information and sensing applications.

Acknowledgments

This work was supported by the National Key Research and Development Program of China (no. 2017YFA0304100), the National Natural Science Foundation of China (Grants 12174370, 11822408, 12174376, 11774335, 11821404, and 11904356), the Open Research Projects of Zhejiang Lab (no. 2021MB0AB02), the Key Research Program of Frontier Sciences of the Chinese Academy of Sciences (Grant no. QYZDY-SSW-SLH003), the Fok Ying-Tong Education Foundation (no. 171007), Science Foundation of the CAS (no. ZDRW-XH-2019-1), Anhui Initiative in Quantum Information Technologies (AHY020100 and AHY060300), and the Fundamental Research Funds for the Central Universities (nos. WK2470000026, WK2030000008 and WK2470000028). This work was partially carried out at the USTC Center for Micro and Nanoscale Research and Fabrication.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c04564.

  • Additional data, PL stability, and probability of generating a VB– center (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c04564_si_001.pdf (2.3MB, pdf)

References

  1. Awschalom D. D.; Bassett L. C.; Dzurak A. S.; Hu E. L.; Petta J. R. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 2013, 339, 1174–1179. 10.1126/science.1231364. [DOI] [PubMed] [Google Scholar]
  2. Togan E.; Chu Y.; Trifonov A. S.; Jiang L.; Maze J.; Childress L.; Dutt M. V. G.; Sørensen A. S.; Hemmer P. R.; Zibrov A. S.; Lukin M. D. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 2010, 466, 730–734. 10.1038/nature09256. [DOI] [PubMed] [Google Scholar]
  3. Waldherr G.; Wang Y.; Zaiser S.; Jamali M.; Schulte-Herbrüggen T.; Abe H.; Ohshima T.; Isoya J.; Du J. F.; Neumann P.; Wrachtrup J. Quantum error correction in a solid-state hybrid spin register. Nature 2014, 506, 204–207. 10.1038/nature12919. [DOI] [PubMed] [Google Scholar]
  4. Kolkowitz S.; Jayich A. C. B.; Unterreithmeier Q. P.; Bennett S. D.; Rabl P.; Harris J. G. E.; Lukin M. D. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 2012, 335, 1603–1606. 10.1126/science.1216821. [DOI] [PubMed] [Google Scholar]
  5. Maze J. R.; Stanwix P. L.; Hodges J. S.; Hong S.; Taylor J. M.; Cappellaro P.; Jiang L.; Dutt M. V. G.; Togan E.; Zibrov A. S.; Yacoby A.; Walsworth R. L.; Lukin M. D. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. 10.1038/nature07279. [DOI] [PubMed] [Google Scholar]
  6. Gali Á. Ab initio theory of the nitrogen-vacancy center in diamond. Nanophotonics 2019, 8, 1907–1943. 10.1515/nanoph-2019-0154. [DOI] [Google Scholar]
  7. Plakhotnik T.; Doherty M. W.; Cole J. H.; Chapman R.; Manson N. B. All-optical thermometry and thermal properties of the optically detected spin resonances of the NV– center in nanodiamond. Nano Lett. 2014, 14, 4989–4996. 10.1021/nl501841d. [DOI] [PubMed] [Google Scholar]
  8. Stanwix P. L.; Pham L. M.; Maze J. R.; Le Sage D.; Yeung T. K.; Cappellaro P.; Hemmer P. R.; Yacoby A.; Lukin M. D.; Walsworth R. L. Coherence of nitrogen-vacancy electronic spin ensembles in diamond. Phys. Rev. B 2010, 82, 201201. 10.1103/PhysRevB.82.201201. [DOI] [Google Scholar]
  9. Wang J.; Zhang W.; Zhang J.; You J.; Li Y.; Guo G.; Feng F.; Song X.; Lou L.; Zhu W.; Wang G. Coherence times of precise depth controlled NV centers in diamond. Nanoscale 2016, 8, 5780–5785. 10.1039/C5NR08690F. [DOI] [PubMed] [Google Scholar]
  10. Becker J. N.; Pingault B.; Groß D.; Gündoğan M.; Kukharchyk N.; Markham M.; Edmonds A.; Atatüre M.; Bushev P.; Becher C. All-optical control of the silicon-vacancy spin in diamond at millikelvin temperatures. Phys. Rev. Lett. 2018, 120, 053603. 10.1103/PhysRevLett.120.053603. [DOI] [PubMed] [Google Scholar]
  11. Rogers L. J.; Jahnke K. D.; Metsch M. H.; Sipahigil A.; Binder J. M.; Teraji T.; Sumiya H.; Isoya J.; Lukin M. D.; Hemmer P.; Jelezko F. All-optical initialization, readout, and coherent preparation of single silicon-vacancy spins in diamond. Phys. Rev. Lett. 2014, 113, 263602. 10.1103/PhysRevLett.113.263602. [DOI] [PubMed] [Google Scholar]
  12. Li Q.; Wang J.-F.; Yan F.-F.; Zhou J.-Y.; Wang H.-F.; Liu H.; Guo L.-P.; Zhou X.; Gali A.; Liu Z.-H.; Wang Z.-Q.; Sun K.; Guo G.-P.; Tang J.-S.; Li H.; You L.-X.; Xu J.-S.; Li C.-F.; Guo G.-C. Room temperature coherent manipulation of single-spin qubits in silicon carbide with high readout contrast. National Science Review 2021, nwab122. 10.1093/nsr/nwab122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Seo H.; Falk A. L.; Klimov P. V.; Miao K. C.; Galli G.; Awschalom D. D. Quantum decoherence dynamics of divacancy spins in silicon carbibe. Nat. Commun. 2016, 7, 12935. 10.1038/ncomms12935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dong W.; Doherty M. W.; Economou S. E. Spin polarization through intersystem crossing in the silicon vacancy of silicon carbide. Phys. Rev. B 2019, 99, 184102. 10.1103/PhysRevB.99.184102. [DOI] [Google Scholar]
  15. Carter S. G.; Soykal Ö.; Dev P.; Economou S. E.; Glaser E. R. Spin coherence and echo modulation of the silicon vacancy in 4H-SiC at room temperature. Phys. Rev. B 2015, 92, 1671202. 10.1103/PhysRevB.92.161202. [DOI] [Google Scholar]
  16. Balasubramanian G.; Neumann P.; Twitchen D.; Markham M.; Kolesov R.; Mizuochi N.; Isoya J.; Achard J.; Beck J.; Tissler J.; Jacques V.; Hemmer P. R.; Jelezko F.; Wrachtrup J. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 2009, 8, 383–397. 10.1038/nmat2420. [DOI] [PubMed] [Google Scholar]
  17. Zhang W.; Zhang J.; Wang J.; Feng F.; Lin S.; Lou L.; Zhu W.; Wang G. Depth-dependent decoherence caused by surface and external spins for NV centers in diamond. Phys. Rev. B 2017, 96, 235443. 10.1103/PhysRevB.96.235443. [DOI] [Google Scholar]
  18. Xia Y.; Li Q.; Kim J.; Bao W.; Gong C.; Yang S.; Wang Y.; Zhang X. Room-temperature giant Stark effect of single photon emitter in van der Waals material. Nano Lett. 2019, 19, 7100–7105. 10.1021/acs.nanolett.9b02640. [DOI] [PubMed] [Google Scholar]
  19. Tran T. T.; Elbadawi C.; Totonjian D.; Lobo C. J.; Grosso G.; Moon H.; Englund D. R.; Ford M. J.; Aharonovich I.; Toth M. Robust multicolor single photon emission from point defects in hexagonal boron nitride. ACS Nano 2016, 10, 7331–7338. 10.1021/acsnano.6b03602. [DOI] [PubMed] [Google Scholar]
  20. Li C.; Xu Z. Q.; Mendelson N.; Kianinia M.; Toth M.; Aharonovich I. Purification of single-photon emission from hBN using post-processing treatments. Nanophotonics 2019, 8, 2049–2055. 10.1515/nanoph-2019-0099. [DOI] [Google Scholar]
  21. Camphausen R.; Marini L.; Tawfik S. A.; Tran T. T.; Ford M. J.; Palomba S. Observation of near-infrared sub-Poissonian photon emission in hexagonal boron nitride at room temperature. APL Photon. 2020, 5, 076103. 10.1063/5.0008242. [DOI] [Google Scholar]
  22. Bourrellier R.; Meuret S.; Tararan A.; Stéphan O.; Kociak M.; Tizei L. H.; Zobelli A. Bright UV single photon emission at point defects in h-BN. Nano Lett. 2016, 16, 4317–4321. 10.1021/acs.nanolett.6b01368. [DOI] [PubMed] [Google Scholar]
  23. Mendelson N.; Chugh D.; Reimers J. R.; Cheng T. S.; Gottscholl A.; Long H.; Mellor C. J.; Zettl A.; Dyakonov V.; Beton P. H.; Novikov S. V.; Jagadish C.; Tan H. H.; Ford M. J.; Toth M.; Bradac C.; Aharonovich I. Identifying carbon as the source of visible single-photon emission from hexagonal boron nitride. Nat. Mater. 2021, 20, 321–328. 10.1038/s41563-020-00850-y. [DOI] [PubMed] [Google Scholar]
  24. Stern H. L.; Jarman J.; Gu Q.; Barker S. E.; Mendelson N.; Chugh D.; Schott S.; Tan H. H.; Sirringhaus H.; Aharonovich I.; Atatüre M.. Room-temperature optically detected magnetic resonance of single defects in hexagonal boron nitride. arXiv (Condensed Matter.Mesoscale and Nanoscale Physics). March 30, 2021, 2103.16494, ver. 1. https://arxiv.org/abs/2103.16494. [DOI] [PMC free article] [PubMed]
  25. Gottscholl A.; Kianinia M.; Soltamov V.; Orlinskii S.; Mamin G.; Bradac C.; Kasper C.; Krambrock K.; Sperlich A.; Toth M.; Aharonovich I.; Dyakonov V. Initialization and read-out of intrinsic spin defects in a van der Waals crystal at room temperature. Nat. Mater. 2020, 19, 540–545. 10.1038/s41563-020-0619-6. [DOI] [PubMed] [Google Scholar]
  26. Gottscholl A.; Diez M.; Soltamov V.; Kasper C.; Sperlich A.; Kianinia M.; Bradac C.; Aharonovich I.; Dyakonov V. Room temperature coherent control of spin defects in hexagonal boron nitride. Sci. Adv. 2021, 7, abf3630. 10.1126/sciadv.abf3630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Liu W.; Li Z.-P.; Yang Y.-Z.; Yu S.; Meng Y.; Wang Z.-A.; Guo N.-J.; Yan F.-F.; Li Q.; Wang J.-F.; Xu J.-S.; Dong Y.; Chen X.-D.; Sun F.-W.; Wang Y.-T.; Tang J.-S.; Li C.-F.; Guo G.-C.. Rabi oscillation of VB– spin in hexagonal boron nitride. arXiv (Quantum Physics). January 27, 2021, 2101.11220, ver. 1. https://arxiv.org/abs/2101.11220.
  28. Liu W.; Li Z.-P.; Yang Y.-Z.; Yu S.; Meng Y.; Wang Z.-A.; Li Z.-C.; Guo N.-J.; Yan F.-F.; Li Q.; Wang J.-F.; Xu J.-S.; Wang Y.-T.; Tang J.-S.; Li C.-F.; Guo G.-C. Temperature-dependent energy-level shifts of Spin Defects in hexagonal Boron Nitride. ACS Photon. 2021, 8, 1889–1895. 10.1021/acsphotonics.1c00320. [DOI] [Google Scholar]
  29. Gottscholl A.; Diez M.; Soltamov V.; Kasper C.; Krauße D.; Sperlich A.; Kianinia M.; Bradac C.; Aharonovich I.; Dyakonov V. Spin defects in hBN as promising temperature, pressure and magnetic field quantum sensors. Nat. Commun. 2021, 12, 4480. 10.1038/s41467-021-24725-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kianinia M.; White S.; Froch J. E.; Bradac C.; Aharonovich I. Generation of spin defects in hexagonal boron nitride. ACS Photon. 2020, 7, 2147–2152. 10.1021/acsphotonics.0c00614. [DOI] [Google Scholar]
  31. Gao X.; Pandey S.; Kianinia M.; Ahn J.; Ju P.; Aharonovich I.; Shivaram N.; Li T. Femtosecond Laser Writing of Spin Defects in Hexagonal Boron Nitride. ACS Photon. 2021, 8, 994–1000. 10.1021/acsphotonics.0c01847. [DOI] [Google Scholar]
  32. Murzakhanov F. F.; Yavkin B. V.; Mamin G. V.; Orlinskii S. B.; Mumdzhi I. E.; Gracheva I. N.; Gabbasov B. F.; Smirnov A. N.; Davydov V. Y.; Soltamov V. A. Creation of Negatively Charged Boron Vacancies in Hexagonal Boron Nitride Crystal by Electron Irradiation and Mechanism of Inhomogeneous Broadening of Boron Vacancy-Related Spin Resonance Lines. Nanomaterials 2021, 11, 1373. 10.3390/nano11061373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ivády V.; Barcza G.; Thiering G.; Li S.; Hamdi H.; Chou J. P.; Legeza Ö.; Gali A. Ab initio theory of the negatively charged boron vacancy qubit in hexagonal boron nitride. npj Comput. Mater. 2020, 6, 41. 10.1038/s41524-020-0305-x. [DOI] [Google Scholar]
  34. Sajid A.; Thygesen K. S.; Reimers J. R.; Ford M. J. Edge effects on optically detected magnetic resonance of vacancy defects in hexagonal boron nitride. Commun. Phys. 2020, 3, 153. 10.1038/s42005-020-00416-z. [DOI] [Google Scholar]
  35. Abdi M.; Chou J. P.; Gali A.; Plenio M. B. Color centers in hexagonal boron nitride monolayers: a group theory and ab initio analysis. ACS Photon. 2018, 5, 1967–1976. 10.1021/acsphotonics.7b01442. [DOI] [Google Scholar]
  36. Wang J.-F.; Li Q.; Yan F.-F.; Liu H.; Guo G.-P.; Zhang W.-P.; Zhou X.; Guo L.-P.; Lin Z.-H.; Cui J.-M.; Xu X.-Y.; Xu J.-S.; Li C.-F.; Guo G.-C. On-demand generation of single silicon vacancy defects in silicon carbide. ACS Photon. 2019, 6, 1736–1743. 10.1021/acsphotonics.9b00451. [DOI] [Google Scholar]
  37. Schwartz J.; Michaelides P.; Weis C. D.; Schenkel T. In situ optimization of co-implantation and substrate temperature conditions for nitrogen-vacancy center formation in single-crystal diamonds. New J. Phys. 2011, 13, 035022. 10.1088/1367-2630/13/3/035022. [DOI] [Google Scholar]
  38. Schröder T.; Trusheim M. E.; Walsh M.; Li L.; Zheng J.; Schukraft M.; Sipahigil A.; Evans R. E.; Sukachev D. D.; Nguyen C. T.; Pacheco J. L.; Camacho R. M.; Bielejec E. S.; Lukin M. D.; Englund D. Scalable focused ion beam creation of nearly lifetime-limited single quantum emitters in diamond nanostructures. Nat. Commun. 2017, 8, 15376. 10.1038/ncomms15376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. van Dam S. B.; Walsh M.; Degen M. J.; Bersin E.; Mouradian S. L.; Galiullin A.; Ruf M.; IJspeert M.; Taminiau T. H.; Hanson R.; Englund D. R. Optical coherence of diamond nitrogen-vacancy centers formed by ion implantation and annealing. Phys. Rev. B 2019, 99, 161203. 10.1103/PhysRevB.99.161203. [DOI] [Google Scholar]
  40. Jin C.; Lin F.; Suenaga K.; Iijima S. Fabrication of a Freestanding Boron Nitride Single Layer and Its Defect Assignments. Phys. Rev. Lett. 2009, 102, 195505. 10.1103/PhysRevLett.102.195505. [DOI] [PubMed] [Google Scholar]
  41. Feng J.; Deschout H.; Caneva S.; Hofmann S.; Lončarić I.; Lazić P.; Radenovic A. Imaging of Optically Active Defects with Nanometer Resolution. Nano Lett. 2018, 18, 1739–1744. 10.1021/acs.nanolett.7b04819. [DOI] [PubMed] [Google Scholar]
  42. Teissier J.; Barfuss A.; Appel P.; Neu E.; Maletinsky P. Strain Coupling of a Nitrogen-Vacancy Center Spin to a Diamond Mechanical Oscillator. Phys. Rev. Lett. 2014, 113, 020503. 10.1103/PhysRevLett.113.020503. [DOI] [PubMed] [Google Scholar]
  43. Tetienne J. P.; De Gille R. W.; Broadway D. A.; Teraji T.; Lillie S. E.; McCoey J. M.; Dontschuk N.; Hall L. T.; Stacey A.; Simpson D. A.; Hollenberg L. C. L. Spin properties of dense near-surface ensembles of nitrogen-vacancy centers in diamond. Phys. Rev. B 2018, 97, 085402. 10.1103/PhysRevB.97.085402. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Citations

  1. Stern H. L.; Jarman J.; Gu Q.; Barker S. E.; Mendelson N.; Chugh D.; Schott S.; Tan H. H.; Sirringhaus H.; Aharonovich I.; Atatüre M.. Room-temperature optically detected magnetic resonance of single defects in hexagonal boron nitride. arXiv (Condensed Matter.Mesoscale and Nanoscale Physics). March 30, 2021, 2103.16494, ver. 1. https://arxiv.org/abs/2103.16494. [DOI] [PMC free article] [PubMed]
  2. Liu W.; Li Z.-P.; Yang Y.-Z.; Yu S.; Meng Y.; Wang Z.-A.; Guo N.-J.; Yan F.-F.; Li Q.; Wang J.-F.; Xu J.-S.; Dong Y.; Chen X.-D.; Sun F.-W.; Wang Y.-T.; Tang J.-S.; Li C.-F.; Guo G.-C.. Rabi oscillation of VB– spin in hexagonal boron nitride. arXiv (Quantum Physics). January 27, 2021, 2101.11220, ver. 1. https://arxiv.org/abs/2101.11220.

Supplementary Materials

ao1c04564_si_001.pdf (2.3MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES