Predictive statistical model of early cranial development

Abstract

Objective:

We present a data-driven method to build a spatiotemporal statistical shape model predictive of normal cranial growth from birth to the age of 2 years.

Methods:

The model was constructed using a normative cross-sectional computed tomography image dataset of 278 subjects. First, we propose a new standard representation of the calvaria using spherical maps to establish anatomical correspondences between subjects at the cranial sutures – the main areas of cranial bone expansion. Then, we model the cranial bone shape as a bilinear function of two factors: inter-subject anatomical variability and temporal growth. We estimate these factors using principal component analysis on the spatial and temporal dimensions, using a novel coarse-to-fine temporal multi-resolution approach to mitigate the lack of longitudinal images of the same patient.

Results:

Our model achieved an accuracy of 1.54 ± 1.05 mm predicting development on an independent longitudinal dataset. We also used the model to calculate the cranial volume, cephalic index and cranial bone surface changes during the first two years of age, which were in agreement with clinical observations.

Significance:

To our knowledge, this is the first data-driven and personalized predictive model of cranial bone shape development during infancy and it can serve as a baseline to study abnormal growth patterns in the population.

I. Introduction

THE calvaria is the part of the neurocranium that encloses the brain and it is formed by the two frontal, two parietal and occipital bones. Its normal growth during childhood is driven by a combination of sutural growth, bone remodeling and bone displacement [1] primarily induced by a growing brain [2]. The quantitative characterization of bone growth in the calvaria is essential to understanding the underlaying mechanisms that are responsible for the coupled development of the neurocranium and the brain: both the genetic signaling pathways and the mechanical forces that drive bone displacement and growth. However, it is not fully understood what abnormal modifications of these complex mechanisms result in pediatric cranial pathologic developments. An example of this is craniosynostosis, the premature fusion of one or more cranial sutures, which affects 1 in 2,100 live births [3]. While the causes of suture fusion have a known genetic origin for 30% of children with craniosynostosis, the reason why the remaining 70% present this condition is unknown [4].

To identify and quantify abnormal growth patterns, it is necessary to establish normative references of development. Although many works have used large medical image datasets, and especially magnetic resonance images (MR), to create normative models of the developing brain [5], [6], there has been a paucity of works focused on the equally important development of the neurocranium. One of the main reasons is that traditional MR images do not provide clear imaging of the bones and other modalities are less common in pediatric populations because of the concerns of using radiation in young children. In the current work, we create a normative model of cranial bone development in a pediatric population using a large retrospective, cross-sectional dataset of computed tomography (CT) images.

A. Normative statistical models of cranial shape

For decades, the traditional evaluation of cranial abnormalities has relied on two simple metrics: the head circumference [7] and the cephalic index [8] (the ratio between the biparietal and occipitofrontal distances). These metrics are evaluated using regressed reference values from normative populations. The intracranial volume has also been used to evaluate longitudinal cranial and brain growth when data were available [9]. However, these metrics provide very limited information about cranial shape, have high inter-observer variability and provide low discriminative power to identify cranial development disorders [10], [11].

For these reasons, different groups have created population-based statistical models of the cranial shape to improve the assessment and treatment of cranial developmental conditions. Early works [12] used age-matched population averages as references to guide the surgical treatment of craniosynostosis. Later, personalized statistical models were proposed to quantify cranial malformations from CT images [13] and 3D photography [14], and to estimate the optimal surgical plan for cranial reconstruction surgery [15]. While such methods have provided useful quantitative tools to objectify and support clinical decisions, they did not account for normal dynamic cranial shape changes that occur during childhood. In addition, previous models did not consider the complex anatomy of the calvaria formed by different bone plates because of the difficulties establishing anatomical correspondences between subjects (i.e., the calvaria was modeled as one uniform object).

In [16], a statistical model representing the normal cranial growth was presented. The authors used principal component analysis (PCA) on a series of anatomical landmarks to model the statistical variability of the skull geometry. Then, they used temporal regression to describe the temporal evolution of the PCA coefficients and generate synthetic references between birth and 3 years. However, each regression function assumed a specific temporal pattern of the average changes observed in the population and temporal predictions were not adapted to the specific anatomy of every subject.

Other studies have created models of cranial growth using simulation frameworks [17]–[19]. However, they are not data-driven or based on quantitative evidence, and their predictive accuracy using longitudinal datasets is often absent or only qualitative.

B. Spatiotemporal statistical anatomical models from medical images

Similarly to the work presented in [16], early data-driven methods to model temporal anatomical changes in the population were based on regression and succeeded in identifying average temporal changes [20]–[23]. These methods, however, did not relate the variations of the observed temporal patterns to the specific anatomy of different subjects.

Durrleman et al. [24] created spatiotemporal shape models from the temporal trajectories observed in longitudinal image sequences by decomposing the observed variations into morphological changes and temporal differences. However, the method requires longitudinal data for the analyzed subjects, which is often not feasible with clinical data. Addressing such limitation, Fishbaugh et al. [25] presented a framework to estimate a continuous deformation field in the space of diffeomorphisms using cross-sectional observations from medical images. However, their geodesic representation assumed continuous and smooth shapes and did not account for local anatomical correspondences between observations or regional subdivisions. In their later work, they also incorporated image appearance changes [6].

Others have used a learning-based approach. Hoogendoorn et al. [26] presented a method to model heart changes during the cardiac cycle. The inter-subject anatomical variability was modeled separately from the temporal changes based on the bilinear formulation introduced by Tenenbaum and Freeman [27]. The method in [26] was based on bilinear PCA and required a longitudinal dataset with aligned temporal observations between subjects.

Since large longitudinal image datasets are uncommon, especially in pediatric populations, regression-based development models have become more popular. Some works, however, have proposed hybrid approaches. Aside from [16], Kishimoto et al. [28] combined group-wise PCA and temporal interpolation to model shape changes at different temporal stages of embryo development. Saito et al. [29] used regression to estimate a time-varying average shape from cross-sectional data. Then, they optimized the calculation of the principal modes of anatomical variation to preserve their relationships through the temporal sequence. All previous methods either require a longitudinal dataset [24], [26] or were designed to infer temporal patterns from cross-sectional data based on specific assumptions or constraints about the anatomy [6], [25] or its temporal changes [16], [28], [29].

In the current work, we base on our previous methods to automatically segment and label the cranial bones from CT images. Then, we introduce a new two-dimensional (2D) standard representation of the calvaria using spherical sampling that allows establishing anatomical correspondences between subjects at the cranial sutures. Based on this standard representation, we propose a temporal multi-resolution approach to infer temporal growth patterns and we use them to solve the bilinear model equation proposed in [26], [27]. Finally, we evaluate the accuracy of our model using an independent longitudinal dataset. As shown in this paper, we also used the constructed model to create normative references of cranial bone growth in the population.

The technical contributions of our work are: (1) a fully automatic pipeline to create a cranial growth model from CT images; (2) a simplified, intuitive standard representation of the cranium that establishes local anatomical correspondences between subjects at the cranial sutures; and (3) a novel iterative approach to build a data-driven and personalized bilinear model of cranial development using only cross-sectional data. Unlike traditional temporal regression, our method avoids assumptions about temporal changes in the populations and creates predictions that are specific to every subject. Additionally, unlike most learning-based methods, it does not require longitudinal data.

II. Materials and methods

A. Data

After approval by the local internal review board at the University of Colorado Anschutz Medical Campus (protocol #20–1563) and the Children’s National Hospital (protocol #03792), retrospective head axial CT images of 278 subjects (128 female, 150 male) with age 10.19 ± 6.88 months (range 0–2 years) without cranial pathology were used as training data to create the cranial growth model. One CT image was available for each subject. Most CT images were acquired after referral for trauma and cranial pathology was discarded in all of them after clinical evaluation. Image axial resolution was 0.38 ± 0.05 mm and slice thickness 1.16 ± 0.66 mm. Images were acquired with different scanners: General Electric LightSpeed Ultra and LightSpeed Discovery 690 (General Electric, Fairfield, Conn.), and Philips Brilliance 40 and Brilliance 64 (Philips, Amsterdam, The Netherlands). The age and sex distribution of this population is shown in Fig. 1. In addition, two longitudinal images from 16 different subjects, (age at first study 7.84 ± 6.16 months, time between studies 3.78 ± 5.44 months) with the same imaging characteristics were used to evaluate the predictive accuracy of the model.

Fig. 1.

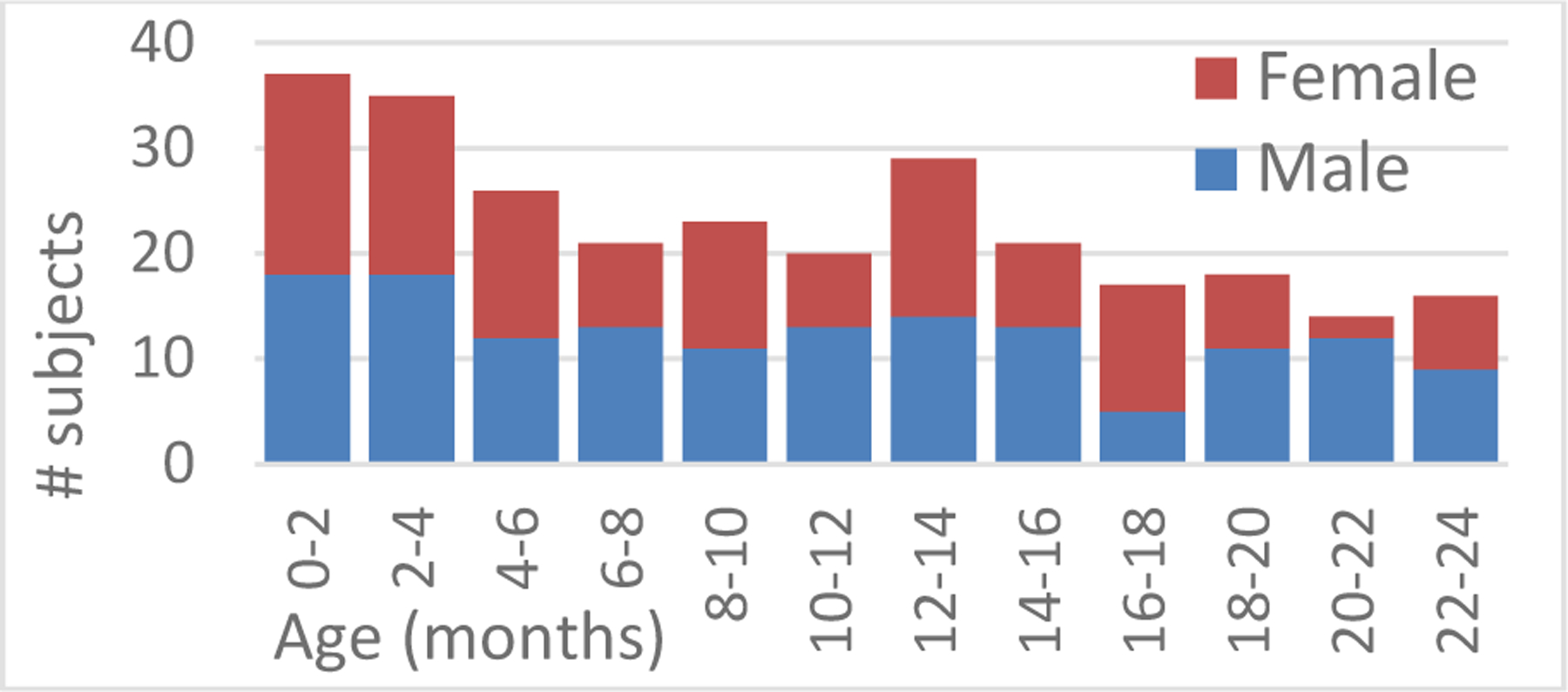
Age and sex distribution of the subjects in our training dataset.

B. Cranial bone segmentation from CT images

1). Reference template

We used our previous methods to segment and label the cranial bones at the calvaria [9], [13]–[15]. These methods are guided by the manual annotations on the CT image of a healthy reference subject that was selected as a template based on image quality and lack of any abnormalities during expert assessment. Four cranial base landmarks were manually annotated in the template at the glabella, two temporal processes of the dorsum sellae and the opisthion as represented in Fig. 2 (a), which allow separating our five bones of interest (two frontal, two parietal and occipital) from the cranial base. Each cranial bone was also manually labeled in the template, including the visible parts of the temporal bones to establish the border of the parietal bones, as shown in Fig. 2 (a).

Fig 2.

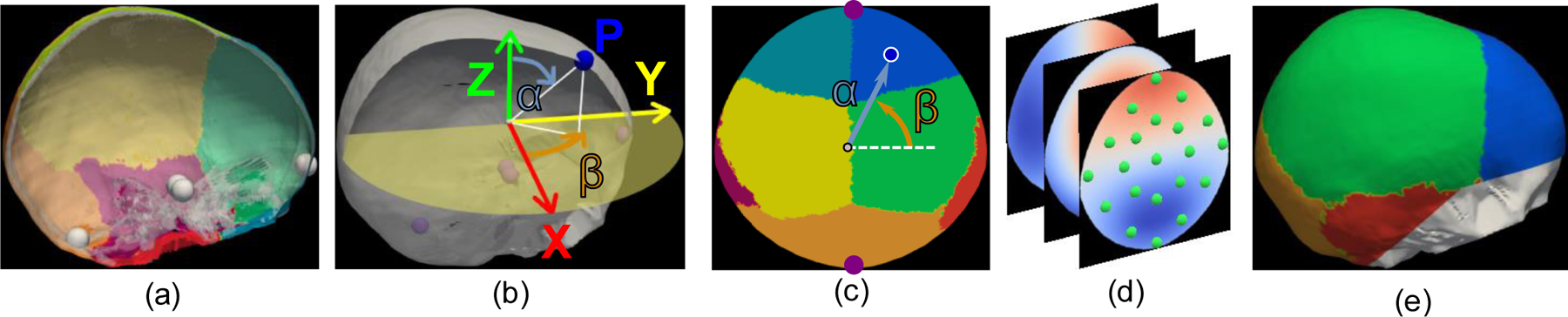
Standard representation of the calvaria. (a) Right lateral view of the cranial bones of an example subject together with the cranial base landmarks represented as white spheres. (b) Representation of the spherical sampling of the external surface of the calvaria in the Euclidean space. The X axis is aligned with the left-to-right direction, the Y axis with the posterior-to-anterior-direction and the Z axis with the inferior-to-superior direction. (c) Representation of the elevation (α) and azimuth (β) angles in the bone labeling spherical map of the subject in (a). The landmarks at the glabella (top) and opisthion (bottom) are shown as purple circles for reference. (d) Three maps of the sampled Euclidean coordinates (X, Z and Y coordinates, from back to front) of the surface of the calvaria, together with a representation of the control point defining the radial basis functions as green circles. (e) Reconstruction of the external surface of the calvaria from the spherical maps in (d) using radial basis functions. The original base of the cranium for this patient is represented in white for reference.

2). Bone segmentation and labeling

We used the adaptive thresholding algorithm presented by Dangi et al. [30] to segment the cranium from CT images. Given the binary segmentation image of the cranium of a patient, we aligned it with the reference template using affine registration to estimate the location of its cranial base landmarks, which we used to separate the calvaria from the rest of the skull, similar to [13]–[15], [30].

To label each cranial bone from the binary image of the calvaria, we used the previously presented graph-cut-based optimization method in [13], [15] guided by our reference template. This method targets the minimization of the following cost function to find the optimal bone labeling in a binary image:

$$E(l)=\gamma {\sum }_{x\in X}{D}_x\left(l_x\right)+{\sum }_{(x,y)\in K}{V}_{x,y}\left(l_x,l_y\right),$$ (1)

where γ is a weighting parameter, D_x(l_x) is the Euclidean distance between the voxel at coordinates x with label l_x and its closest voxel in the reference template with the same label, V_x,y(l_x, l_y) is the function that penalizes for neighboring voxels at coordinates x and y having different labels, and K is the set of voxels in the neighborhood of x. In this formulation, the first term guides labeling based on the location of each label in the reference template, and the second term promotes bone boundaries in areas where bone plates are separated at the sutures. All details about Eq. (1) can be found in [13].

C. Standard representation of the calvaria and dimensionality reduction

We propose a new simplified 2D representation of the calvaria. First, we centered the cranial anatomy of the reference template at the origin of coordinates. We aligned the posterior-to-anterior direction with the Y axis, the inferior-to-superior direction with the Z axis and the left-to-right direction with the X axis, as presented in Fig. 2 (b). Then, we used the cranial base landmarks calculated for all the subjects to align their crania with the oriented reference template by estimating analytically the optimal rotation and translation using singular value decomposition (SVD) [31]. Note that the scale is preserved during alignment.

We used the marching cubes algorithm [32] to create a volumetric mesh of the calvaria. Then, we sampled it in spherical coordinates using ray-casting [33] from the origin of coordinates. This created a 2D image based on the sampled elevation αϵ[0,π] and azimuth βϵ[−π,π] angles as represented in Fig. 2 (b) and (c). At each point of the 2D spherical map, we assigned the corresponding bone label as shown in Fig. 2 (c). In addition, we also matched each point in the 2D spherical map with its corresponding Euclidean coordinates from the ray intersections with the external surface of the calvaria. This created three additional maps for the X, Y and Z Euclidean coordinates, respectively, as shown in Fig. 2 (d). As the information about the Euclidean coordinates of every point in the calvaria is now contained in our 2D spherical maps, its geometry can be reconstructed from them as shown in Fig. 2 (e). Note that our model focuses only on the flat bones of the calvaria (frontal, parietal and occipital) and does not incorporate the cranial base.

To establish anatomical correspondences between subjects, we iteratively registered their bone-labeled spherical maps (Fig. 2 (c)) to the average in the population using the diffeomorphic demons registration algorithm [12]. As a result, all subjects were aligned at each cranial bone and suture.

Benefiting from the continuous and smooth anatomy of the healthy cranium, we used radial basis functions (RBF) to reduce the dimensionality of the spherical maps. Hence, the Euclidean coordinates x of each point with spherical coordinates u were represented continuously as

$$\mathit{x}(\mathit{u})={\sum }_{\forall i}{\mathit{c}}_{i}k\left(\Vert \mathit{u}-{\mathit{u}}_i\Vert {}_2\right),$$ (2)

where i represents each control point as shown in Fig. 2 (d), c_i is the coefficient vector at control point i, u_i is the spatial location of control point i in the spherical map, and k(∙) is a Gaussian kernel. Note that Eq. (2) is bijective since the external surface of the calvaria lies on a spherical manifold.

D. Statistical shape model of cranial development

Using the proposed 2D RBF, the calvaria can be represented as a continuous surface using only the c_i = {c_xi, c_yi, c_zi} coefficients at each control points i located at homologous anatomical locations in reference to the cranial sutures. In this context, modeling the statistical variability of the cranial anatomy in the population is equivalent to modeling the variability of the control point coefficients.

As formulated by Tenenbaum et al. [27] and presented by Hoogendoorn et al. [26] to create a spatiotemporal cardiac model, the vectorized observations of a changing anatomical structure of a subject s at time t can be represented as a bilinear function:

$${\mathit{y}}_{s,t}={\mathit{a}}_s\mathit{W}{\mathit{b}}_t,$$ (3)

where y_s is the observation of s after removing the average observation in the population, a_s is a coefficient vector that represents the specific anatomy of subject s, b_t is a coefficient vector that represents the temporal anatomical changes at time t and W is a matrix that represents the relationships between a_s and b_t. Given a longitudinal dataset, Eq. (3) can be written in matrix form as

$$\mathit{Y}={(\mathit{W}\mathit{A})}^{VT}\mathit{B},$$ (4)

where VT indicates the vector transpose operation as defined in [26], [34] (note the difference with respect to a matrix transposition), each column of matrix A corresponds to a subject-specific coefficient vector a_s, and each column of B corresponds to a time-specific coefficient vector b_t. In this formulation, Y is a MN × T matrix, where M is the number of subjects, T the number of temporal observations, and N the number of data points of each observation.

When a longitudinal dataset is available, the bilinear formulation presented in Eq. (4) can be solved using PCA to estimate the values of A and B iteratively via SVD [26]. However, when only sparse data of different subjects at different time instants are available, as it is the case of many medical image datasets, such formulation does not have a unique solution. Hence, finding an adequate solution would require the introduction of constraints or boundary conditions in the model. While assumptions about the statistical distribution of the cranial shape in the normative population would likely create unrealistic or biased models, we can use basic knowledge about cranial bone development. As we show next, we used the fact that cranial bone growth is temporally continuous to solve Eq. (4) and create a longitudinal development model using cross-sectional data.

Our method had to overcome two challenges: (1) the lack of observations at some ages; and (2) the lack of longitudinal observations from any subjects. To mitigate them, we propose a temporal multi-resolution approach to simulate realistic longitudinal observations for each subject based on the overall temporal patterns observed in the population. Our method is structured in three main steps: model initialization, solving the bilinear equation and refinement of the temporal resolution.

1). Model initialization

Before modeling cranial shape changes, all subject observations c_i (the values of the control points representing the cranial anatomy as defined in Section II.C) were centered on the origin of coordinates, rescaled to a uniform size, and the average shape in the population was removed from the observations as in [26]. Note that this process decouples scale from shape, which is essential to capture subtle shape changes.

To retain temporal volume changes, we regressed temporally the average scale of the data using a logarithmic function as shown in Fig. 3. (b). To model temporal shape changes, we divided the subjects into age intervals at a low temporal resolution R₀. This resolution has to be low enough so the average shape at each age interval is representative of the population average. The average observations at each temporal interval (note the difference from the average shape of the entire population that was subtracted from all observations) were stacked as columns to create matrix ${\overline{\mathit{Y}}}_0$, where the subscript refers to the temporal resolution. Similar to [26], we initialized the age coefficients B₀ via SVD of the data in ${\overline{\mathit{Y}}}_0$:

$$\text{SVD}\left({\overline{\mathit{Y}}}_0\right)={\mathit{U}}_{{\mathit{B}}_0}{\mathbf{\Sigma }}_{{\mathit{B}}_0}{\mathit{V}}_{{\mathit{B}}_0}{}^{\prime }={\mathit{U}}_{{\mathit{B}}_0}{\mathit{B}}_0,$$ (5)

where ${\mathit{U}}_{B_0}$ and ${\mathit{V}}_{B_0}$ are the left and right singular vectors of ${\overline{\mathit{Y}}}_0$, ${\mathbf{\Sigma }}_{{\mathit{B}}_0}$ its singular values and ′ is the matrix transpose operator. Note that this step is equivalent to doing PCA on matrix ${\overline{\mathit{Y}}}_0$, and B₀ represents the temporal variations of the average observations across all age intervals at resolution R₀.

Fig. 3.

(a) Cranial shape fitting error using radial basis functions. (b) Average control point scale for each subject in the cross-sectional dataset (in blue) together with the regressed scale (in orange). (c) Temporal coefficients in matrix B estimated at a resolution of 8 months (big circles) and their interpolated values used to initialize training at a resolution of 2 months (dots). Orange represents the first component, blue the second and green the third component. (d) Temporal coefficients estimated for the first three components in matrix B at different temporal resolutions. Circles correspond to a resolution of 8 months, crosses correspond to 2 months, and continuous lines represent a resolution of 5 days. (e) Predictive error evaluated in the longitudinal dataset. Red represents the results obtained with the proposed method, and black a green are the results from the traditional regression model and the PCA-based regression, respectively. The continuous and dotted lines represent the regressed average error and the range of one standard deviation, respectively. The horizontal axis in (b)-(e) represents the age in months.

After this initialization of B₀ (with columns ${\mathit{b}}_{t_0}$), we can use Eq. (3) to calculate a_sW for each subject s from its available cross sectional observation y_s,t at age t (represented by the initialized ${\mathit{b}}_{t_0}$), as ${\mathit{y}}_{s,t}{\mathit{b}}_{t_0}{}^{-1}={\mathit{a}}_s{\mathit{W}}_0$. In this case, each product a_sW₀ represents the cranial anatomy of a subject independently from its age in the model. Hence, if all products a_sW₀ are stacked as rows in a matrix K, we can estimate the age-independent anatomical variability between subjects as

$$\text{SVD}\left({\mathit{K}}^{VT}\right)={\mathit{U}}_{\mathit{A}}{\Sigma }_{\mathit{A}}{\mathit{V}}_{\mathit{A}}{}^{\prime }={\mathit{U}}_{\mathit{A}}\mathit{A},$$ (6)

where U_A and V_A are the left and right singular vectors of K^VT and Σ_A its singular values. From this initialization of both subject and age coefficients in matrices A and B₀, respectively, we calculated analytically the mixing matrix W₀ at temporal resolution R₀ using Eq. (3).

2). Solution to the bilinear equation

Once A, B₀ and W₀ were initialized, we estimated the overall changes of the cranial shape over time for each patient at the lower temporal resolution R₀ using equation (4) as ${\widehat{\mathit{Y}}}_0={\left({\mathit{W}}_0\mathit{A}\right)}^{VT}{\mathit{B}}_0$. Hoogendoorn et al [26] showed that the bilinear formulation in Eq. (4) can be solved iteratively until convergence using SVD as

$$\begin{gathered} \text{SVD}\left({\left({\widehat{\mathit{Y}}}_0{\mathit{B}}_0{}^{-1}\right)}^{VT}\right)={\mathit{U}}_{\mathit{A}}{\mathbf{\Sigma }}_{\mathit{A}}{\mathit{V}}_{\mathit{A}}{}^{\prime }={\mathit{U}}_{\mathit{A}}\mathit{A},\text{ and} \\ \text{SVD}\left({\left({\widehat{\mathit{Y}}}_0{}^{VT}{\mathit{A}}^{-1}\right)}^{VT}\right)={\mathit{U}}_{{\mathit{B}}_0}{\mathbf{\Sigma }}_{{\mathit{B}}_0}{{\mathit{V}}_{{\mathit{B}}_0}}^{\prime }={\mathit{U}}_{{\mathit{B}}_0}{\mathit{B}}_0. \end{gathered}$$ (7)

However, unlike in previous work, our data matrix ${\widehat{\mathit{Y}}}_0$ is only an initial estimation of the global longitudinal cranial shape changes in the training population at a low temporal resolution. Hence, although Eq. (7) was shown to converge to a solution [27], that solution may not be accurate. To ensure convergence to an accurate representation of the true available observations, we introduced a new step in the solution of the bilinear equation to optimize the data matrix ${\widehat{Y}}_0$. Hence, at each iteration we solve for ${\widehat{Y}}_0$, A, and B₀ as

$$\begin{gathered} {\widehat{\mathit{y}}}_{s,t}^j=\underset{{\widehat{y}}_{s,t}^{j-1}}{\underbrace{{\left({\mathit{a}}_s\mathit{W}\right)}^{VT}{\mathit{b}}_{t_s}}}+({\mathit{y}}_{s,t_s}-\underset{{\widehat{y}}_{s,t_s}^{j-1}}{\underbrace{{\left({\mathit{a}}_s\mathit{W}\right)}^{VT}{\mathit{b}}_{t_s}}})k(\Vert t-t_s\Vert ), \\ \text{SVD}\left({\left({{\widehat{\mathit{Y}}}_0}^{j^{VT}}{\mathit{A}}^{-1}\right)}^{VT}\right)={\mathit{U}}_{{\mathit{B}}_0}{\mathbf{\Sigma }}_{{\mathit{B}}_0}{{\mathit{V}}_{{\mathit{B}}_0}}^{\prime }={\mathit{U}}_{{\mathit{B}}_0}{\mathit{B}}_0,\text{ and} \\ \text{SVD}\left({\left({\widehat{\mathit{Y}}}_0{}^j{\mathit{B}}_0^{-1}\right)}^{VT}\right)={\mathit{U}}_{\mathit{A}}{\mathbf{\Sigma }}_{\mathit{A}}{\mathit{V}}_{\mathit{A}}{}^{\prime }={\mathit{U}}_{\mathit{A}}\mathit{A}, \end{gathered}$$ (8)

where j is the iteration number, ${\widehat{y}}_{s,t}^j$ represents the columns of data matrix ${\widehat{Y}}_0$ with the estimated observation of subject s at age t and iteration j, t_s is the age at which the true observation of subject s is available and $y_{s,t_s}$ is that true observation.

With this approach, we ensure that the predicted data, which are temporally continuous, equal the original training data at every iteration. Note that the temporal simulations for each subject in ${\widehat{Y}}_0$ are updated only if the cranial shape estimated at the age at which observations are available differs from the true observations; i.e., if $y_{s,t_s}-{\left(a_{s}W\right)}^{VT}{b}_{t_s}\ne 0$. The estimations of A and B₀ will gradually converge to a solution that accurately matches the true observations at temporal resolution R₀, as shown in [27] with longitudinal data. As previously also reported in [27], we always reached convergence within five iterations.

It is important to estimate the model parameters in the order expressed in Eq. (8); the temporal parameters need to be calculated before the subject-specific parameters. By doing so, we ensure that when new temporal patterns are introduced in ${\widehat{\mathit{Y}}}_0$, they are modeled by the coefficients in matrix B. Hence, the coefficients in matrix A will only explain the subject-specific anatomical features that cannot be modeled as a temporal pattern in the population.

3). Refinement of the temporal resolution

Assuming that the temporal changes of the age coefficients B₀ are continuous – as is the case with cranial development – we can increase the temporal resolution of the model using interpolation to create a new age coefficient matrix B₁ at resolution R₁. In this work, we used cubic spline interpolation [35]. Fig. 3 (c) shows an example of interpolated temporal coefficients between two different resolution levels. After estimating B₁, we repeat steps 2 and 3 to create new simulated observations ${\widehat{Y}}_1$ and model coefficients A, B₁ and W₁ at resolution R₁. This process can be repeated iteratively until achieving the desired temporal resolution. Note that, at each increment of the temporal resolution, the model coefficients in matrices A, B and W will only change if there are temporal patterns in the data matrix $\widehat{\mathit{Y}}$ that were not observed at a lower resolution.

III. Experiments and Results

In this section, we first present our experiments to select the optimal number of control points to represent the cranial shape using RBFs. Then, we build a statistical model from our cross-sectional image database and determine its accuracy predicting cranial bone growth using our longitudinal database. As a comparative framework, we quantified the performance improvements over two other methods: a traditional temporal regression and our implementation of the method described in [16]. Finally, we simulate a longitudinal dataset from the training data to create normative references of cranial bone growth in a pediatric population.

A. Selection of the number of control points

To select the optimal number of control points to represent the 2D anatomical maps using RBFs, we tested the reconstruction error for increasing numbers of subdivisions of the elevation angle (α) in our training dataset (see Fig. 2 (c) and (d)). As shown in Fig. 3 (a), the error converged at 18 subdivisions of α, which created 279 uniformly sampled control points. This provided an average reconstruction error of 1.16 ± 1.09 mm. Note that the average reconstruction error is within the range of the average voxel spacing in the original CT images (p = 0.062).

B. Predictive accuracy of the model

After representing the cranial anatomy of each subject in the training dataset using RBFs, we created a statistical model from them using an initial temporal resolution of 8 months, and increasing it progressively to 2 months, 15 days and 5 days. We did not find any changes in the estimation of our temporal coefficients if we trained our model at a temporal resolution higher than 5 days. This suggests that any changes in the normal patterns of cranial development during a period of less than five days are either negligible or cannot be captured with our dataset. Fig. 3 (d) shows the changes of the estimated temporal coefficients for the first three components (rows of matrix B) at different temporal resolutions.

We tested the accuracy of the model predicting temporal changes in our longitudinal test population. We used the observation from the first CT image of each subject together with the trained age-specific parameters b_t to estimate the subject/anatomy-specific parameters a_s using Eq. (3). Then, using the calculated a_s and the model coefficients b_t that describe the age of the patient at the second CT image, we predicted the coefficients describing the cranial shape at the time of the second study using Eq. (3). From those coefficients, we used Eq. (2) to reconstruct the cranial shape of every patient. To estimate the predictive accuracy, we compared the predicted observations at the time of the second study with the true observation. As previously explained, the scale change due to volume increase was estimated using the temporal logarithmic function shown in Fig. 3 (b).

The optimal number of components required to model inter-subject variability and temporal changes was chosen by testing all combinations of the number of components. Unlike in traditional PCA, component selection cannot be done independently during training and was addressed after the model construction based on the accuracy evaluated on the independent longitudinal dataset [26]. We selected 166 components to model inter-subject variability and 3 components to model temporal shape changes. Our model obtained a prediction error of 1.54 ± 1.05 mm, which was similar to the reconstruction error using RBFs (p = 0.211). This prediction error improved progressively from 1.86 ± 1.38, 1.58 ± 1.05 and 1.55 ± 1.05 mm obtained at the intermediate resolutions of 8 months, 2 months and 15 days, respectively. Importantly, our predictive error was significantly lower than the error achieved when compensating only for scale changes using our logarithmic regression model from Fig. 3 (b) (2.24 ± 1.97 mm, p = 0.001). This indicates the importance of considering shape changes in addition to volume. Fig. 3 (e) shows the predictive error of our model for every subject in our longitudinal dataset and its regressed value as a function of the age at the first study. Our regressed error at birth was 1.02 ± 0.28 mm and at 2 years of age was 2.07 ± 0.99 mm. Our model also had an average error of 3.09 ± 9.85% predicting volume growth, and of −0.88 ± 2.27 % predicting cephalic index changes.

C. Comparative accuracy

We compared the predictive accuracy of our model with two other different methods: a traditional temporal regression and a temporal regression of PCA coefficients as proposed in [16].

To implement a traditional regression, we fitted a smooth temporal function f(t) to each of the control point coefficients c_i in Eq. (2) that describe the cranial shape of the patients in our cross-sectional dataset, where t represents age in days. In our implementation we tested polynomial functions of degree 2, 3 and 4, sigmoid and logarithmic functions. For every patient with two longitudinal images available, we calculated the values of its coefficients ${\mathit{c}}_i{}^{t_0}$ from the cranial shape segmented from the first image acquired at age t₀ solving Eq. (2). Then, we estimated the coefficient values ${\widehat{\mathit{c}}}_i{}^{t_1}$ predicting the cranial shape at the age of acquisition of the second image t₁ as ${\widehat{\mathit{c}}}_i{}^{t_1}={\mathit{c}}_i{}^{t_0}+\left(f_i\left(t_1\right)-f_i\left(t_0\right)\right)$. We compared the cranial shapes reconstructed using Eq. (2) with the true cranial shapes from the image at age t₁, similar to our previous experiments. We achieved the best performance using a polynomial regression function of fourth degree. The average error was 4.78 ± 0.81 mm, which was significantly higher than the error with our proposed method (p < 0.001). The error for every subject in our longitudinal population is presented in Fig. 3 (e). This model also achieved errors of −1.96 ± 8.94 % (p = 0.14, compared to our proposed method) and −0.87 ± 2.62% estimating ICV and CI, respectively (p = 0.99).

We also implemented the approach presented in [16]. In summary, we first performed PCA on the control point coefficients c_i of our cross-sectional training population. These coefficients were represented as C = MZ, where Z contains the projections of the control point coefficients in the PCA space and M represents the principal components. As proposed in [16], we used the same approach than in our traditional temporal regression to fit regression functions f(t) to the PCA projections of our training population in Z. To predict the growth of every patient with available longitudinal images, we calculated the control points coefficients ${\mathit{c}}_i{}^{t_0}$ that represent the cranial shape segmented from the first image acquired at age t₀ and we projected them on the PCA space to obtain ${\mathit{Z}}_j{}^{t_0}$. Then, we estimated the PCA coefficients at the age of the second image study as ${\mathit{z}}_{\mathit{j}}{}^{t_1}={\mathit{z}}_j{}^{t_0}+(f_j\left(t_1\right)-f_j\left(t_0\right))$, and we calculated the control points coefficients at the time of the second study as ${\widehat{\mathit{C}}}^{t_1}=\mathit{M}{\mathit{Z}}^{t_1}$. We compared the cranial shapes reconstructed using Eq. (2) with the true cranial shapes obtained from the available image acquired at age t₁. Similar to our traditional regression, we achieved the best performance a polynomial regression function of fourth degree. The average error was 4.76 ± 0.81 mm, which was significantly higher than the error with our proposed method (p < 0.001). The error for every subject in our longitudinal population is presented in Fig. 3 (e). This model also achieved errors of −1.68 ± 9.00 % (p = 0.16) and −1.15 ± 2.16% (p = 0.73) estimating ICV and CI, respectively.

D. Estimation of normative population statistics

We used Eq. (4) to simulate the cranial development of each subject in our training population for whom only one image was available. First, we used our image segmentation and spherical mapping methods to create the standard anatomical maps for each subject from the CT image available. Then, we calculated the coefficients c_i that represent the cranial shape of each patient using Eq. (2). We used c_i, the trained matrix W and the learned temporal coefficients b_t to calculate the subject-specific coefficients a_s using Eq. (3). With a_s, we used the general model formulation presented in Eq. (4) to simulate the cranial shapes of each subject at all ages. Fig. 4 shows the average cranial shape changes observed during the first two years of life. We also used previous simulations to infer normative references for the clinical metrics of cranial bone growth: intra-cranial volume and cephalic index. In addition, we provided for the first time reference values for the surface change of each individual cranial bone. Results are shown in Fig. 5.

Fig. 4.

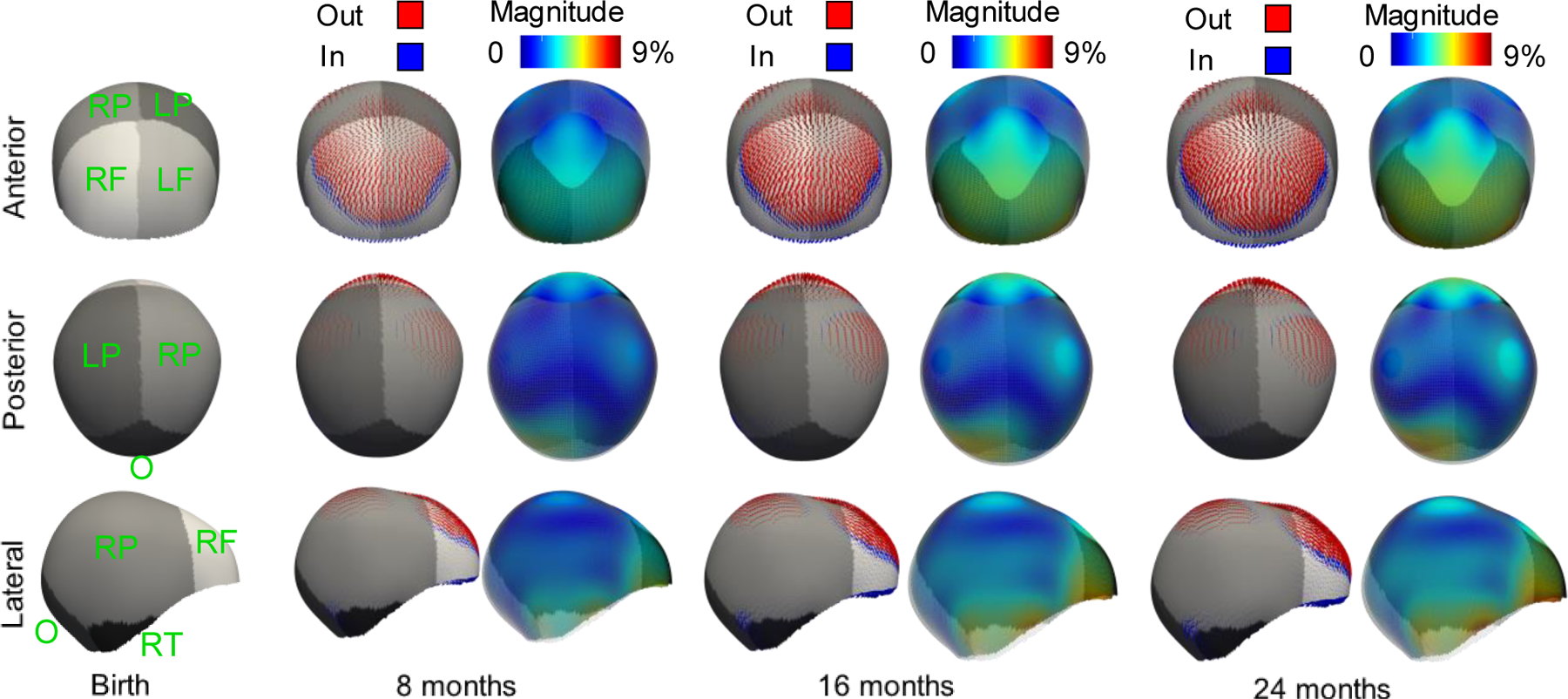
Temporal cranial shape changes with respect to the average shape at birth calculated from the age coefficients of the model (matrix B) at different ages. Different shades of gray represent different cranial bones: left (L) and right (R) frontal (F), parietal (P), temporal (T) and occipital (O) bones. At each age, the first column shows the vectors indicating the local direction of shape change. The second column shows the colorcoded magnitude of those changes. Dark blue represents areas with no change and red represents areas with maximum change. The transparent wireframe overlay in the second column represents the initial shape at birth for reference. As the scale effect is removed, the magnitudes are represented as a percentage of the average scale.

Fig. 5.

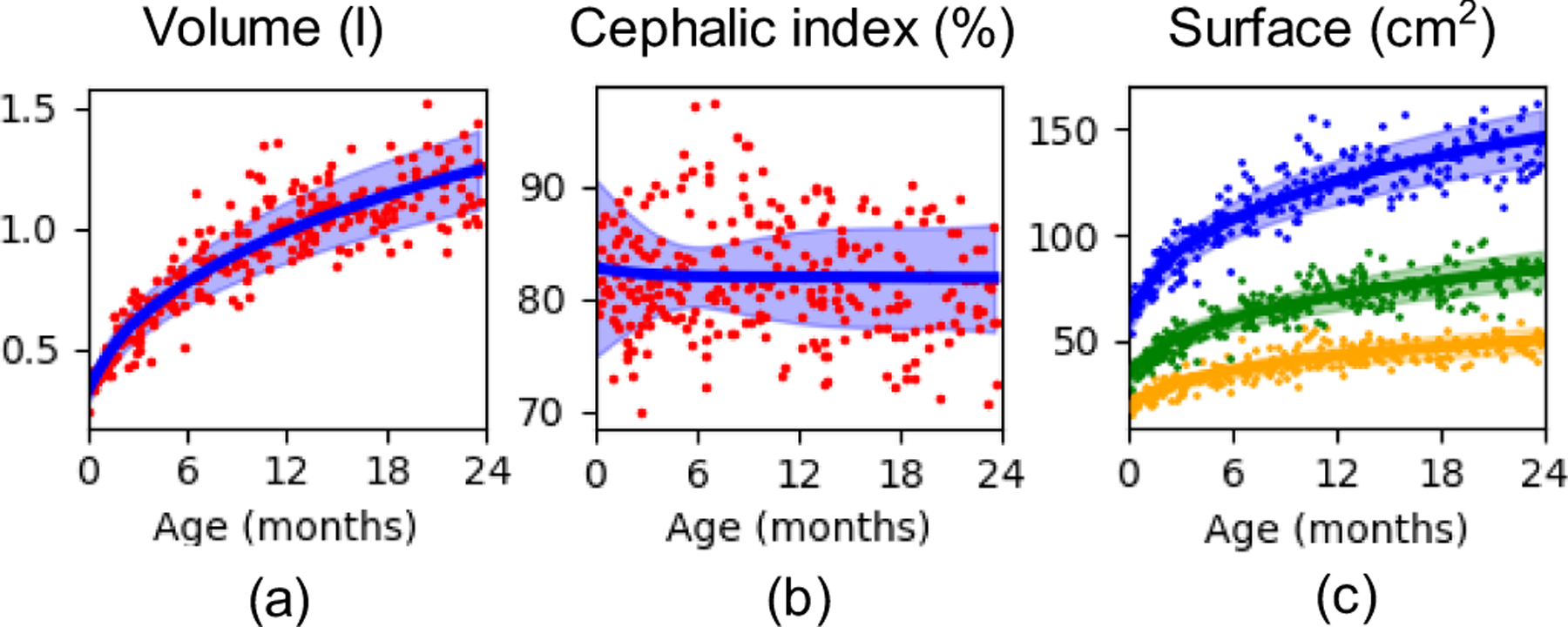
Metrics of cranial bone growth obtained for the longitudinal observations simulated using the cross-sectional dataset. (a) shows the cranial volume, (b) the cephalic index and (c) the average surface of the frontal (orange), parietal (blue) and occipital (green) bones. Dots represent the true available observations in the dataset, the continuous lines represent the average value of the simulated longitudinal dataset and the shaded areas indicate the range of one standard deviation from the average prediction.

We obtained an average volume increase from 0.32 ± 0.05 to 1.25 ± 0.16 l from birth to the age of two years, which represents an increment of 290.63 % of the cranial volume. In addition, we found a reduction in the cephalic index from 82.73 ± 7.96 to 81.82 ± 4.81 %. Finally, our results showed an increase of the surface of each frontal bone from 19.28 ± 2.77 to 50.30 ± 6.11 cm², each parietal bone from 60.13 ± 6.62 to 146.06 ± 13.52 cm² and the occipital bone from 33.24 ± 5.19 to 83.59 ± 8.71 cm². This represents an average increase of 160.89 %, 142.91 % and 151.47 % for the frontal, parietal and occipital bones, respectively.

IV. Discussion

We have presented a new method to create a spatiotemporal statistical model of cranial bone growth using only cross-sectional data. Existing computational personalized references of cranial bone growth are based on biomechanical simulations that depend on assumptions and simplifications about the physiological processes driving development [19]. Unlike those types of work, our statistical modeling approach is data-driven and based on true observations in the healthy population, does not introduce anatomical or temporal constraints and only assumes temporal continuity of development. Our model was built from a cranial dataset with local anatomical correspondences between subjects at the cranial sutures. This was achieved using a new simplified standard representation of the calvaria that we proposed. We evaluated the predictive accuracy of our statistical model using an independent longitudinal dataset of CT images and our predictive error was in the range of the reconstruction error of the cranial shapes. While normative regression models of intra-cranial volume changes during childhood have been available for decades, our work focused on the quantification of the changes in the cranial shape, as there are no data-driven models of these changes available. Importantly, the cranial shape changes predicted by our model provided a significantly improved accuracy over a regression model that only considers volume changes, which justifies the importance of modeling shape changes to quantify the normative development of the calvaria.

We compared our predictive error with two other modeling approaches, a traditional temporal regression and a combination of temporal regression with PCA [16]. Our method outperformed them predicting local growth. However, the three methods did not provide statistically different results when looking at global metrics such as intra-cranial volume or cephalic index.

We also used our model to predict the evolution of every subject in our cross-sectional database between birth and two years. This allowed estimating normative ranges for the volume of the calvaria and the cephalic index, two metrics that are clinically used to assess cranial shape. Our estimated volumes were in agreement with the observations presented in other works [9], [36]. We also observed a subtle reduction of the cephalic index in the growing infants, which matches previous reports [37]. Moreover, our method allowed, for the first time, quantifying the growth of each cranial bone in the calvaria as shown in Fig. 5 (c), which could be used as references during clinical evaluation of cranial development.

We also simulated the temporal development of the average cranial shape to provide insight about local shape changes during the first two years of life. As we can observe in Fig. 4, our model shows considerable growth around the area of the anterior fontanelle, which is located at the intersection of the frontal and parietal bones. Our data shows that this growth is divergent, drives the separation between the two frontal and parietal bones and produces a local volume increase in the fontal bone area relative to the rest of the cranium. These observations were expected as the anterior fontanelle is normally wide open at birth and slowly closes before 18 months of age. In fact, the clinical manifestations of its abnormal early closure include reduced frontal volume and an abnormal triangular shape of the head [38]. Fig. 4 also shows a slight narrowing at the laterals of the cranial base. Note that Fig. 4 represents only shape changes and this observation does not imply volume loss.

The main limitations of this study are related to data availability. Our model succeeds to show local patterns of development, but it also captures common abnormalities not associated to pathology present in our dataset. For example, positional plagiocephaly is a common and often subtle malformation present in young children. Plagiocephaly is more prevalent on the right side of the head than on the left side as it is directly related to the parents’ handedness [39]. Indeed, our normative statistical model correctly identified some flattening in the right posterior side (see posterior view in Fig. 4) and compensatory overgrowth on the left posterior side. In addition, although our average cephalic index aligns with other reports, our normative ranges show a narrowing of these ranges at about 6 months of age (see Fig. 5 (b)). This may be related the variability observed in our dataset at that age. After curation of our subjects, we did not identify a reason to exclude any of them from the current study.

Another possible limitation is related to the use of PCA to model both inter-subject and temporal variability in our model, which assumes that there is global relationship between the location and the temporal trajectories of all the points in the calvaria. Although we obtained a good performance with our model, we could explore in the future different ways to modify our formulation to incorporate other statistical modeling approaches such as factor analysis or independent component analysis.

Future work also includes the incorporation of more subjects to our database to improve robustness of the model to the presence of cranial abnormalities that are often observed in the healthy population. In addition, we plan to adapt our previous methods [13], [14] to quantify cranial malformations by considering the temporal information embedded in our new model, which will enable evaluating abnormalities from a developmental perspective. Given the coupled development of the brain and the calvaria [40], such quantification could potentially provide insight into brain pathology.

V. Conclusion

We presented a new method to construct a spatiotemporal statistical shape model of the growing cranium from birth to two years of age. This data-driven model was built from a large cross-sectional image database by avoiding anatomical and temporal assumptions. We validated the accuracy of the model to predict temporal changes using an independent longitudinal population, and we established age-specific normative ranges for metrics of cranial development, i.e., cranial volume and cephalic index. This is the first time that normative references of growth for each individual cranial bone are created. This normative model may be used as a reference to predict cranial growth and provides baseline to study cranial abnormalities from a developmental perspective. Translational applications to clinical settings remain potentially unlimited for the diagnosis and management of cerebral developmental pathophysiology.