Random survival forest model identifies novel biomarkers of event-free survival in high-risk pediatric acute lymphoblastic leukemia

Graphical abstract

Abstract

High-risk pediatric B-ALL patients experience 5-year negative event rates up to 25%. Although some biomarkers of relapse are utilized in the clinic, their ability to predict outcomes in high-risk patients is limited. Here, we propose a random survival forest (RSF) machine learning model utilizing interpretable genomic inputs to predict relapse/death in high-risk pediatric B-ALL patients. We utilized whole exome sequencing profiles from 156 patients in the TARGET-ALL study (with samples collected at presentation) further stratified into training and test cohorts (109 and 47 patients, respectively). To avoid overfitting and facilitate the interpretation of machine learning results, input genomic variables were engineered using a stepwise approach involving univariable Cox models to select variables directly associated with outcomes, genomic coordinate-based analysis to select mutational hotspots, and correlation analysis to eliminate feature co-linearity. Model training identified 7 genomic regions most predictive of relapse/death-free survival. The test cohort error rate was 12.47%, and a polygenic score based on the sum of the top 7 variables effectively stratified patients into two groups, with significant differences in time to relapse/death (log-rank P = 0.001, hazard ratio = 5.41). Our model outperformed other EFS modeling approaches including an RSF using gold-standard prognostic variables (error rate = 24.35%). Validation in 174 standard-risk patients and 3 patients who failed to respond to induction therapy confirmed that our RSF model and polygenic score were specific to high-risk disease. We propose that our feature selection/engineering approach can increase the clinical interpretability of RSF, and our polygenic score could be utilized for enhance clinical decision-making in high-risk B-ALL.

1. Introduction

In the United States, approximately 3,700 new cases of pediatric leukemia are diagnosed every year, with 80% of those cases being acute lymphoblastic leukemia [1]. Pediatric acute lymphoblastic leukemia (ALL) is the most common childhood malignancy, affecting 5 out of every 100,000 children and representing 24.9% of all childhood cancers [1]. Most pediatric ALL cases (approximately 80%) are classified as ALL of the B cell lineage (B-ALL). These patients are further subdivided into standard- and high-risk groups, where high-risk classification is defined based on the presence of one or more factors: white blood cell count (WBC) > 50,000 at diagnosis, age of onset > 10 years old, hypodiploidy at the time of diagnosis, a variety of gene fusions, or poor response to induction therapy (e.g., prednisone). This risk stratification strategy is used to guide treatment regimen selection, but despite receiving more intensive treatment, high-risk patients continue to have worse outcomes. For standard-risk patients, the 5-year negative event rate, defined as 1 - event-free survival (EFS; the time between clinical remission and first recurrence or negative event such as death) is approximately 11% [2], whereas high-risk patients can have 5-year negative event rates up to 25% [3]. Interestingly, high-risk patients exhibit heterogenous response to therapy, perhaps due to their significant genomic diversity [4], [5], [6], implying that high-risk patients may benefit from further disease subclassification at diagnosis. Thus, accurately modeling and identifying molecular markers of risk of relapse that are present at the time of diagnosis in high-risk patients would facilitate personalized therapeutic decisions that should improve outcomes in this disease [4], [5], [6].

Typically, pediatric B-ALL (including high-risk patients) is treated with a long-term regimen of combination chemotherapy that is broken into phases, including induction, consolidation, and maintenance, with the potential for further delayed intensification or reconsolidation phases [7], [8], [9]. The first phase of chemotherapy is referred to as the induction phase owing to its intent to potentially induce remission in patients and is given during a continuous hospital stay that typically lasts 28 days [7], [8]. Induction therapy usually involves a combination of microtubule disruptors (such as vincristine), anthracyclines (such as daunorubicin), metabolic inhibitors (such as asparaginase), and corticosteroids (such as prednisone), with high-risk patients receiving higher or more frequent doses [3], [7], [10]. At the end of this phase, most patients (both standard-risk and high-risk) are in clinical remission. Patients who have not clinically responded to induction chemotherapy or have evidence of high levels of minimal residual disease (MRD) are typically treated with an extended induction phase or changed to another more aggressive treatment regimen [11], [12], [13], [14]. After the induction phase, patients then transition to a consolidation phase that lasts 4–8 weeks and involves high doses of chemotherapy to eradicate any remaining cancer cells [7], [8]. Chemotherapy classes used during consolidation typically match those used during induction therapy, but the specific drugs can differ [7], [8]. Once consolidation therapy ends, patients transition to a maintenance phase that can last several years [7], [8]. During maintenance, high-risk patients can receive delayed intensification or reconsolidation phases, which typically mirror the first consolidation phase.

Chemoresistance can lead to relapse any time after induction. One of the hypothesized causes of chemoresistance is that genomic mutations responsible for or which facilitate resistance are present in some cells at the time of diagnosis and therefore could be utilized as early predictors of event-free survival (EFS). In standard-risk patients, several genomic markers that result in lower risk of relapse have been identified, including trisomies of chromosomes 4 and 10 and ETV6-RUNX1 fusions [6], [8], [15], yet there is a lack of similar markers of relapse in high-risk patients, and this represents an unmet need that motivated our investigation of genomic determinants present at the time of diagnosis in high-risk patients.

In recent years, machine learning models of prognosis and outcomes have become popular methods to identify new candidate biomarkers in cancer [16], [17], [18], [19]. Diverse machine learning methods, including support vector machines [19], [20], [21], [22], [23], [24], [25], [26], Bayesian networks [27], [28], [29], and neural networks [30], [31], [32], have used molecular and/or clinical markers to predict cancer prognosis. Because machine learning models are robust to a variety of challenges faced by traditional statistical models, they have the potential to enable more nuanced therapeutic decision-making than has been previously possible [17], [18], [33], [34], [35], [36].

One machine learning method, random forest, has shown good performance in oncology applications because it is well suited for moderately sized datasets commonly seen in clinical settings [37]. Random forests have been previously used to effectively predict outcomes for colorectal and gastric cancers using standard-of-care variables, and these models showed better results than traditional Cox proportional hazards models [38], [39]. The random forest algorithm has been extended to a variety of clinical use cases, including random survival forests, which are capable of modeling time-to-event outcomes with censored data, such as EFS in our study [40], [41], [42]. Previous oncology studies using random survival forests have shown the ability of random survival forests to effectively predict survival and identify novel panels of molecular biomarkers in hepatocellular carcinoma [43], colorectal cancer [44], and esophageal carcinoma [45], among others.

Whereas traditional random forest approaches seek to predict singular values, random survival forests predict cumulative hazard functions for each patient, which represents the cumulative probability of a patient experiencing an event over time [40]. This cumulative time-dependent probability function can naturally be used to specify the predicted survival probability of a patient over time [46]. Furthermore, random survival forests are especially relevant for modeling outcomes based on genomic data, which often includes many uninformative or weakly informative features that are ineffective for survival prediction in other modeling approaches. This is due to the variable subsampling and branch selection components of the tree-building process, which can then be translated into variable importance in the final models that directly predict time-dependent probability of outcomes [41].

We report a random survival forest modeling pipeline with a novel feature engineering approach to efficiently select input genomic features, identify specific genomic regions of interest, develop an accurate model that predicts EFS in high-risk B-ALL patients, and meaningfully interpret the effects of candidate biomarkers on survival. To achieve this goal, we used data from high-risk B-ALL patients who had bone marrow whole exome sequencing performed as a part of the TARGET-ALL study (n = 156), which was then divided into training (n = 109, or 70% of the dataset) and testing cohorts (n = 47, or 30% of the dataset). Our novel variable selection/engineering approach, which was applied to the training cohort, identified the genes most predictive of EFS and selected mutational hotspots in those genes, which maximized interpretability in the final model. These variables were used as inputs for our random survival forest model. This model identified 7 genomic regions of particular significance for predicting EFS. Furthermore, our random survival forest model outperformed several other EFS modeling approaches, including a random survival forest wherein variables were eliminated using recursive feature elimination (a commonly utilized feature reduction approach), a multivariable Cox proportional hazards model, and a random survival forest model using current gold-standard prognostic variables. Validation in clinically diverse patient cohorts confirmed that our model was specific for high-risk pediatric B-ALL.

2. Methods

2.1. Patients cohorts

The patient cohorts analyzed in this study (Table 1) were comprised of patients from the TARGET Pediatric ALL project, which is derived from patients from multiple clinical trials. The patient cohort (n = 156) used for training (n = 109) and testing (n = 47) our original random survival forest represents a subset of patients analyzed as part of the TARGET-ALL project who had high-risk disease (by COG criteria, newly diagnosed B-ALL age 1 to 9 years with initial WBC ≥ 50,000/μL or 10 to 30 years with any initial WBC) and were treated on COG protocol AALL0232 (clinical trial #: NCT00075725) [47]. Inclusion criteria for our study were availability of paired tumor-normal whole exome sequencing data in the dbGap database (project accession number phs000218.v24.p8) and complete clinical data in the TARGET-ALL data matrix [48].

Table 1.

Overview of cohorts used in this study.

Subset	Number of patients	Induction duration	Clinical trial	Purpose
High-risk B-ALL	156	4 weeks*	COG AALL0232 (NCT00075725)	Model training and testing
Training cohort	109	4 weeks*	COG AALL0232 (NCT00075725)	Model training
Testing cohort	47	4 weeks*	COG AALL0232 (NCT00075725)	Model testing
High risk B-ALL with induction failure	3	6 weeks	COG AALL0232 (NCT00075725) to rescue therapy at physician’s discretion after failure	Validation
Standard-risk B-ALL	174	4 weeks	COG AALL0331 (NCT00103285)	Validation

* Patients with MRD > 1% at day 29 could receive up to 6 weeks of induction therapy

All patients on COG protocol AALL0232 received a multi-phase regimen based on the combination of vincristine, daunorubicin, cytarabine, mercaptopurine, pegaspargase, methotrexate, and a corticosteroid, although the corticosteroid used (prednisone or dexamethasone) and methotrexate dosing schedules during maintenance phases varied. After induction therapy consisting of vincristine, daunorubicin, pegaspargase, methotrexate, and corticosteroids, patients were evaluated for MRD and clinical remission. This protocol (AALL0232) only included high-risk patients with favorable response to induction therapy. Patients with postinduction MRD > 1% and < 25% received two extra weeks of induction chemotherapy and were included in this protocol upon favorable response. According to this protocol, patients with > 25% postinduction MRD or failure to respond to induction chemotherapy were removed from the original trial. Patients who responded to induction therapy and, in addition, had < 1% MRD continued to consolidation therapy with cyclophosphamide, cytarabine, mercaptopurine, vincristine, pegaspargase, and methotrexate and then maintenance therapy with a variety of different methotrexate and corticosteroid doses. Patients received one or two delayed intensifications of vincristine, dexamethasone, doxorubicin, pegaspargase, cyclophosphamide, cytarabine, thioguanine, and methotrexate. Patients were followed for up to 10 years, with a primary endpoint of EFS. In our study, EFS was defined as in clinical trial AALL0232: the time from clinical remission, with all patients included in this trial achieving remission during induction therapy, to the time of first negative event. In most cases, this negative event was relapse, although negative events also included 7 deaths and 1 secondary myeloid neoplasm as a result of chemotherapy. Patients who did not experience any negative events after remission were considered censored at the time of last follow-up. Clinicodemographic information for the 156 high-risk B-ALL patients included in our training and test sets are shown in Table 2.

Table 2.

Clinicodemographic data for the AALL0232 cohort and training and testing subsets.

Characteristic	All AALL0232 (n = 156)	Training cohort (n = 109)	Testing cohort (n = 47)	P-value (training versus testing)
Age at diagnosis, mean (range) years	10 (1–21)	10 (1–21)	10 (1–21)	0.44
Sex, no. of patients				0.96
Male	95	67	28
Female	61	42	19
Race, no. of patients				0.21
White	117	84	33
Black	6	5	1
Asian	1	0	1
Pacific islander	4	4	0
Other/Unknown	28	16	12
Ethnicity, no. of patients				0.75
Hispanic or Latino	37	25	12
Not Hispanic or Latino	111	80	31
Unknown	8	4	4

For further validation, we analyzed two additional patient cohorts that were not included in any model training step. First, we analyzed a validation set of 3 patients with postinduction MRD > 25% to assess the efficacy of our model in patients who never responded to induction therapy. We also analyzed another set of 174 patients from the TARGET-ALL database. These patients were diagnosed with standard-risk B-ALL and treated on COG protocol AALL0331 (clinical trial #: NCT00103285), with positive response to induction (similarly to our original cohort) [2]. They received a less intense treatment regimen that generally included the same drugs as COG AALL0232, with trial arms focused on varying dose intensities during consolidation, maintenance, and delayed intensification phases. This trial had a primary endpoint of EFS. Clinicodemographic information for these validation patients are shown in Supplementary Table 1.

All patients considered in our study had diagnostic bone marrow blast percentages above 70%, with most having bone marrow blasts above 85%.

2.2. Whole exome sequencing

All sequencing data analyzed in this trial was whole exome sequencing data. The whole exome sequencing methodology for TARGET-ALL has been previously reported [49]. Briefly, libraries were prepared using robotic workstations and then hybridized to SeqCap EZ Exome 2.0 design (44 Mb, NimbleGen) probes. These captured libraries were then sequenced on Illumina HiSeq 2000 platforms using the manufacturer’s recommended protocol to generate 100-basepair paired-end reads for a total of approximately 100 million reads per sample, with a targeted coverage of 20X or greater in 95% of sequenced exons.

2.3. Bioinformatics analysis

An overview of our bioinformatics strategy is shown in Supplementary Fig. 1. Briefly, raw tumor and normal (germline control, derived from blood or normal bone marrow cells) whole exome sequencing FASTQ files generated by the TARGET-ALL project were obtained from the dbGap database (study accession number phs000218.v24.p8) and were downloaded using fasterq-dump from the SRA Tools package (ver. 2.10.8) [50]. We then used bcbio (ver. 1.1.5) [51] to align raw reads to GRCh38.p13 using bwa-mem (ver. 0.7.1) [52], which generated BAM files, and performed base quality score recalibration using GATK (ver. 4.1.2) [53] and duplicate marking using picard (ver. 2.21.1) [54]. Processed BAM files were then used for somatic variant calling using VarDict (ver. 1.6) [55], and variants were filtered using a minimum per-patient variant allele frequency (VAF) of 10%, a minimum coverage level of 20 reads, and a mean phred score > 22.5. Variants were annotated with ANNOVAR (ver. 20191024) using ENSEMBL annotations [56].

2.4. Stratified sampling for training and test cohorts

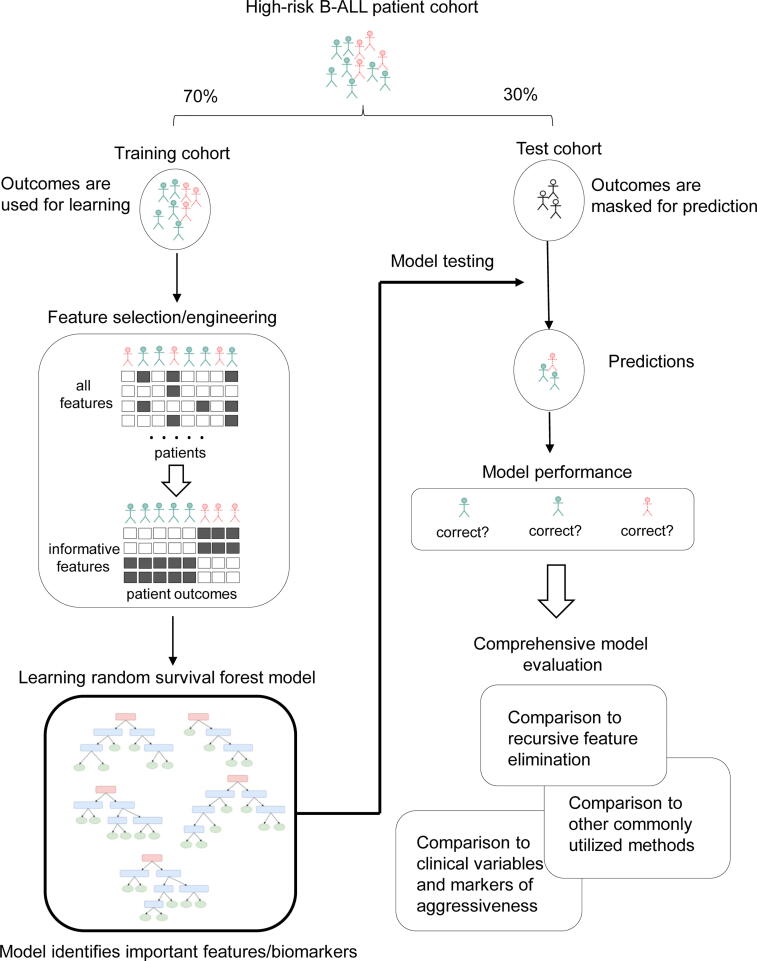
An overview schematic of our modeling strategy is presented in Fig. 1. The high-risk patient cohort was separated into training and test cohorts using stratified sampling based on National Cancer Institute (NCI) risk criteria (age and WBC count at the time of diagnosis) discretized by quartiles. The training cohort contained 109 patients (70% of the total cohort), and the testing cohort contained 47 patients (30% of the total cohort). Clinicodemographic information and P-values for significant differences are shown in Table 2.

Fig. 1.

Schematic representation of study design. Patients were split into training and test cohorts, and the training cohort was used for feature selection/engineering and training the random survival forest. The trained random survival forest was then interrogated to identify potentially informative biomarkers and used to generate test set predictions. These test set predictions were compared to several other models and variable sets applied to the same test data.

2.5. Variable selection/engineering

The initial variable set consisted of all nonsynonymous variants passing our bioinformatic filtering criteria mentioned above (69,215 variants). Any gene that contained nonsynonymous variants in>20% of patients in the training set was selected (2,543 genes). All further variable selection/engineering was performed specifically on the training cohort.

The variable selection/engineering step for our machine-learning model used a three-stage approach. In the first stage, variants in the selected genes were collapsed into gene-level variables with each variable representing the variant with the highest VAF in a given gene for a given patient. This was done to reduce the sparsity of the variant-level data to a level appropriate for downstream modeling. To obtain clinically meaningful variables, each variable was used as input for a univariable Cox proportional hazards model using EFS as the endpoint. Genes with Wald P-values ≤ 0.05 were selected as significant (n = 106 genes).

In the second stage of feature selection/engineering, the 106 genes were used as candidates for positional feature engineering. Positional feature engineering was performed by examining variant prevalence across all positions in a gene’s exons and using that prevalence to generate derived variables. For genes where > 60% of variants were located in a specific subregion of the gene, the genomic variable was “trimmed” to cover only that hotspot region. For genes where ≤ 60% but ≥ 40% of variants were located in a specific subregion, the gene was split into two variables, with one variable representing the hotspot region and another variable representing the rest of the gene. Genes with no clear hotspots for somatic mutations were defined by regions containing all exons for that gene. In the case of multiple variants in a single region or gene for a patient, the variant with the highest VAF was selected. All selected regions are listed in Supplementary Table 2 (n = 64 regions derived from 48 genes).

Finally, in the third stage of feature engineering, these selected regions were assessed for collinearity, which can negatively affect the estimation of random forest variable importance [57], [58]. Specifically, variables were subjected to pairwise correlation testing using Spearman’s ρ, and the resulting correlogram was clustered using Ward’s method. There were no statistically significant correlations, and none of the candidate variables showed correlation values above 0.5 or below −0.5, so all were retained for random forest training.

2.6. Pathway analysis

Candidate variables were analyzed for pathway membership using the STRING database (v11) [59]. Interaction settings for this STRING analysis were set to only the highest confidence interactions (STRING confidence score > 0.9) [60], with no>20 interactors in the first or second shell. Significant enrichment was defined as a false discovery rate-corrected (FDR) P-value ≤ 0.05.

2.7. Random survival forest models

Variables remaining after all three feature selection/engineering stages were used as input variables to train a random survival forest to predict EFS in B-ALL patients, using the training cohort. Random survival forests were constructed using the randomForestSRC package (ver. 2.9.3) [40], [42], [61]. Survival objects were constructed using the survival package (ver. 3.1.8) [62], with events classified as any negative event, including relapse, death, or secondary malignant neoplasm. Performance was measured using Harrell’s concordance index (C-index), with error rates defined as the value of 1-C-index [63], [64]. For all forests, the log-rank statistic was used as a splitting rule [65]. Due to the large number of variables in our dataset and the negative effects of bagging on performance estimation and tuning, all forests used sampling without replacement [66], [67].

Forest tuning parameters included: (i) the number of variables assessed at each split (i.e., “mtry”), (ii) the maximum number of samples in the terminal (leaf) nodes (i.e., “nodesize”), and (iii) the maximum number of trees (i.e., “ntrees”). The mtry and nodesize variables were optimized using a grid search approach to maximize C-index over the training cohort. Most iterations of the ntrees tuning grid search converged to stable C-index values between 2,000 and 3,000 trees, so the upper limit of 3,000 trees was selected.

After the model was built, variable importance in the final random survival forest model derived from the training cohort was assessed using (i) variable permutation; and (ii) maximal subtree analysis [68], [69]. Elbow analysis identified an inflection point in variable importance by random permutation after the 7th variable, so the top 7 variables by permutation were selected for more in-depth analysis. These variables were further analyzed using pairwise maximal subtree analysis to identify any significant interactions. Finally, the sum of the VAF values of the top 7 variables were used to generate an aggregate linear model for predicting EFS outcome.

Model performance was initially validated using the test cohort of patients. For this validation, patient outcomes were masked, and the probability of EFS over time was predicted for each patient in the test set. To evaluate how accurately the model predicted outcomes, the initial EFS information was unmasked, and model performance was estimated using C-index error rate and time-dependent ROC-AUC [70]. For clinical model applicability, a cutoff value for the aggregate top-7 variable score (or polygenic score) was defined using the rounded mean of the distribution of the score to cluster patients into high 7-variable (>0.5; n = 43) and low 7-variable (≤0.5; n = 66) sub-groups, and their survival was compared using Kaplan-Meier survival analysis, using log-rank test for significance and Cox proportional hazards for hazard ratio estimation.

For validation in other sample sets, the random survival forest and polygenic score were applied to both the induction failure and standard-risk validation cohorts, and results were assessed in the same manner as they were for the test set.

2.8. Performance comparison to other modeling strategies for EFS

To a demonstrate the advantages of our model over other common modeling strategies, we have compared performance of our model to (i) a random survival forest with recursive feature elimination and (ii) traditionally used multivariable Cox proportional hazards modeling.

First, we compared our model to a random survival forest model with a reduced variable set selected using recursive feature elimination to test its effect on model performance [57], [71]. The starting point for this approach was the same training cohort and variables that were used to generate the base random survival forest model. At each iteration of recursive feature elimination, a random survival forest was tuned and trained on our training cohort, and the variable with the lowest importance by random permutation over 10-tree blocks [72], [73] was eliminated for all subsequent iterations, and each iteration was assessed for performance on the test cohort. The recursive feature elimination procedure was continued until out-of-sample error and test set error (both assessed by C-index error rate) converged.

Second, we compared our model to a traditionally used white-box machine learning technique, a multivariable Cox proportional hazards model. We used a stepwise approach to generate the final Cox model. First, variables from the feature selection/engineering step (n = 118) were filtered to remove any variables that violated the proportional hazards assumption of the Cox model by testing the Pearson product-moment correlation between Schoenfeld residuals and EFS time (n = 7 with P-value < 0.05) [62]. Variables with correlation P-values for time dependence ≥ 0.05 (n = 111) were used as inputs for a multivariable Cox proportional hazards model. This analysis identified 29 significant variables (Wald P-value < 0.05), which were used as inputs for the final multivariable Cox model. The final Cox model identified 16 significant variables (Wald P-value < 0.05) and was used for comparison with our original random survival forest model.

2.9. Performance comparison to known markers of B-ALL risk

Finally, we sought to compare the efficacy of our original genomic random survival forest model to a random survival forest model limited to known clinical variables (e.g., WBC at diagnosis) and known markers of aggressiveness (e.g., TCF3-PBX fusion), which represent the current gold-standard for prognostic scoring in pediatric B-ALL (Table 3). These clinical and fusion variables were collected according to COG protocol AALL0232 and used as input variables to construct a new model using the same patients included in the training cohort from the original random survival forest model. This model based on clinical and fusion variables was tuned and trained using the same approach described for the original model, although this model’s performance stabilized with <1,000 trees, perhaps because the limited number of variables represented a much smaller feature space.

Table 3.

Prognostic features for the AALL0232 cohort and training and test subjects.

Characteristic	All AALL0232 (n = 156)	Training cohort (n = 109)	Testing cohort (n = 47)	P-value (training versus testing)
WBC at diagnosis, mean (range) K/µL	78.412 (0.6–463)	76.1 (0.6–374.7)	84.2 (1–463)	0.62
CNS status at diagnosis, no. of patients				0.30
CNS1	138	91	34
CNS2	27	15	11
CNS3	5	3	2
ETV-RUNX1 fusion status				0.11
Positive	32	16	13
Negative	132	88	33
Unknown	6	5	1
TCF-PBX1 fusion status				0.94
Positive	8	5	1
Negative	112	77	28
Unknown	50	27	18
BCR-ABL1 fusion status				0.23
Positive	6	6	0
Negative	163	102	47
Unknown	1	2	0
Trisomies 4/10 status				0.53
Positive	23	17	5
Negative	144	89	42
Unknown	3	3	0
MLL status				0.97
Positive	9	5	3
Negative	158	101	44
Unknown	3	3	0
Down syndrome				1
Positive	2	1	1
Negative	168	108	46

2.10. Statistical methods and software

All analyses were conducted using R version 3.6.1. Statistical significance was set at P-value ≤ 0.05. Differences between continuous clinical variables were assessed using Student’s 2-sided t-test (t.test function from base R), and differences in categorical variable frequencies were assessed using the Chi-squared test (chisq.test function from base R). Model performance evaluation and comparison was done using out-of-sample C-index error rate and test set C-index error rate.

3. Results

3.1. Training and test set selection

The high-risk B-ALL patient cohort (n = 156 patients) was split into training and test cohorts using stratified sampling based on age and WBC count at diagnosis. This resulted in a training cohort of 109 patients and a test cohort of 47 patients, and there were no statistically significant differences in clinical or histopathological variables between groups (Table 2).

EFS throughout this study was defined as in the clinical trial NCT00075725. Specifically, EFS was defined as the time from clinical remission (which occurred during induction therapy in this cohort) to first event the patient experienced, which could include relapse, death from disease, or secondary myeloid neoplasm, or to the last follow-up (Fig. 2A).

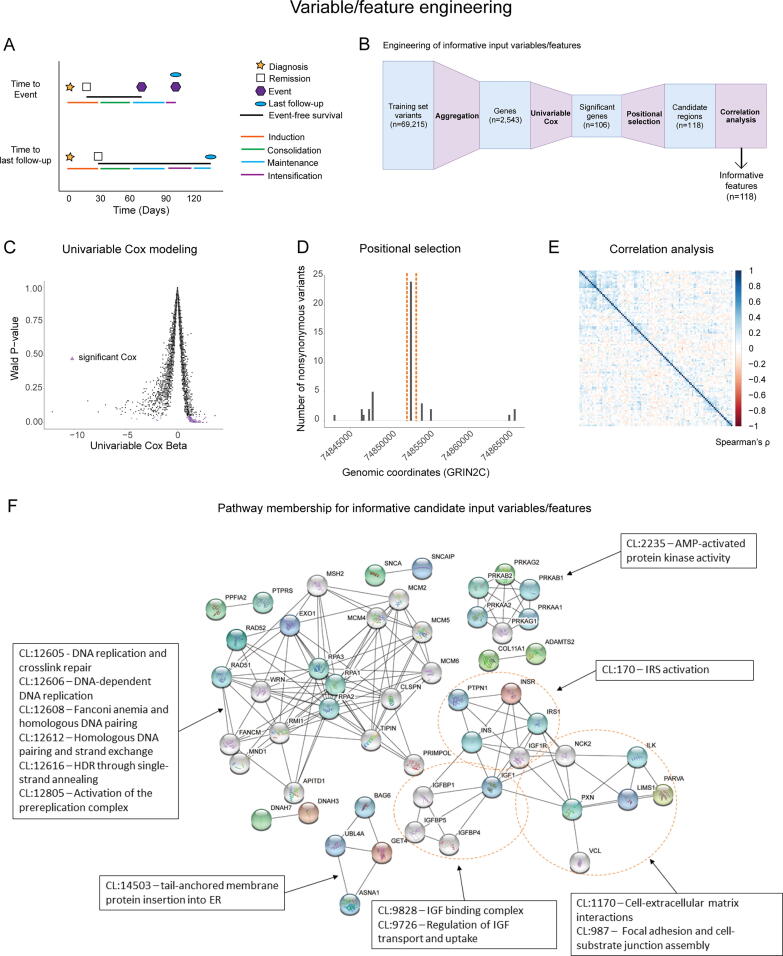
Fig. 2.

Feature selection/engineering against training cohort variants produces a reduced feature space of non-correlated variables. (A) Schematic illustrating common EFS scenarios. EFS is considered as the time from clinical remission to the time of first event or last follow-up. Events and last follow-up could occur in any treatment phase after remission. (B) Schematic illustrating the steps used for variable selection/engineering. (C) Scatter plot of univariable Cox beta values as a function of Wald P-values, where Cox estimated ability of each variable to predict EFS. Selected variables are represented by purple triangles. (D) Example of positional selection approach in the gene GRIN2C. A single hotspot region contained > 60% of all variants found in GRIN2C in this dataset, and that region was selected. (E) Correlogram showing low Spearman’s ρ values for all variables used in this study. (F) STRING cluster membership and interactions among selected variables. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2. Variable selection/engineering

Variable selection/engineering consisted of a three-stage process (Fig. 2B) with the goal of reducing the variable space, minimizing model overfitting, and enhancing prediction interpretability. We started with 69,215 non-synonymous variants identified in whole-exome sequencing data (Fig. 2B). Collapsing these variants to the gene level and filtering for frequency (see Methods) resulted in 2,543 candidate genes in the training cohort for variable selection/engineering.

In the first stage of variable selection/engineering, we applied a univariable Cox proportional hazards model to each of the 2,543 candidate variables to evaluate their ability to predict EFS. Significant Wald P-values (P-value < 0.05) derived from these univariable Cox proportional hazards models were used to reduce the variable space to 106 variables (Fig. 2C).

In the second stage, these 106 genes were converted into positional variables by truncating or splitting on specific genomic coordinates with an emphasis on identifying mutational hotspots, as defined by prevalence in the training cohort (see Methods), to increase disease specificity and reduce noise associated with random mutation, which resulted in 118 variables (Fig. 2D; Supplementary Table 2). In particular, out of 106 genes, our positional selection approach identified 33 genes where most variants were present in a small region, or hotspot, which allowed us to define one narrow genomic regions for each of those variables. Furthermore, 14 genes were split into 2 variables, and one gene (OTOA) was split into 3 variables due to 3 distinct hotspots. The remaining 58 genes did not show any evident hotspots, and in those genes, the somatic variant with the highest VAF across all exons in the gene was used as a variable. This stage of variable selection/engineering expanded our variable set from 106 genes to 118 genomic regions. These 118 variables were assessed for any co-linearity, which can negatively affect the interpretability of random forest-based models, and no significant correlations (Spearman ρ > 0.5 or < −0.5) were found (Fig. 2E), which resulted in 118 variables utilized as inputs for our machine learning pipeline.

3.3. Pathway analysis

Pathway analysis was conducted for the 106 input genes that represented the 118 final variables using the STRING database [59]. Of the 106 analyzed genes, 83 genes were characterized using Benjamini-Hochberg corrected P-values for enrichment in local STRING network clusters (Fig. 2F) [59]. Twenty-nine pathways (as represented by local network clusters in the STRING database) were significantly enriched in the data. Among these network clusters, the 5 clusters with the lowest corrected P-values were all associated with homologous DNA repair or DNA replication, and 4 other clusters out of 29 were associated with other aspects of DNA damage repair or associated diseases, such as Fanconi anemia. Among the remaining 20 interaction clusters, 4 were associated with insulin-like growth factor (IGF) signaling pathways, and 4 were associated with extracellular signaling pathways.

3.4. Model tuning and training

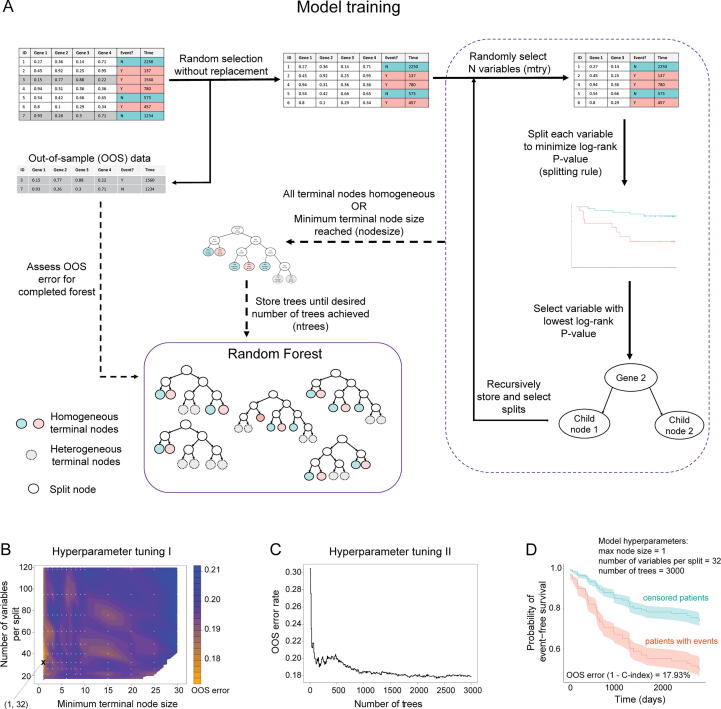
Fig. 3A shows a schematic representation of random survival forest training and the hyperparameters optimized in this study: minimum terminal leaf node size (nodesize), number of variables considered at each split (mtry), and number of trees in the forest (ntrees). Using 118 input genomic variables across the 109-patient training cohort, we tuned the hyperparameters of our random survival forest model of EFS using a grid search approach. This hyperparameter tuning identified optimal hyperparameters of a minimum terminal node size = 1 and a number of variables tested per split = 32 (Fig. 3B), and 3000 trees (Fig. 3C). We utilized these parameters to run the training step for our random survival model. This model training resulted in an out-of-sample (OOS) error rate (1-C-index) of 17.93%, with aggregate predictions for training cohort outcomes shown in Fig. 3D, indicating that our model was highly accurate.

Fig. 3.

Trained random survival forest model is highly accurate. (A) Schematic illustrating the general random survival forest algorithm as well as key hyperparameters. (B) Hyperparameter tuning grid and interpolated performance surface for minimum terminal node size and number of variables used per split. Lower values of OOS error (better) are colored in orange, and higher values are colored in blue. White dots represent each tested grid point, with the minimal training error identified by an X (node size = 1; variables per split = 32). (C) Cumulative OOS performance versus number of trees up to 3000 in the random survival forest using final nodesize and mtry parameter settings. (D) Aggregate predicted EFS and 95% confidence intervals for training cohort patients who experienced events (red) and did not (teal), with OOS error rate (1 – C-index) of 17.93%. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.5. Evaluating variable importance

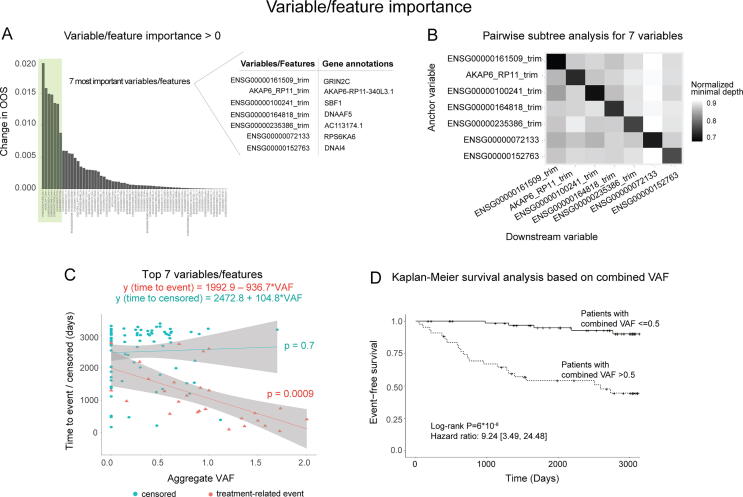
To identify variables with strong association with EFS in pediatric B-ALL, we conducted variable importance analysis on our trained random survival forest model. This analysis used variable permutation [42], [68] (see Methods) and identified 7 variables that had a significantly greater effect on OOS error than the rest of the variable set (Fig. 4A), with variable frequencies shown in Supplementary Table 3. Further investigation of these variables by pairwise maximal subtree analysis [68], [69] showed that none of these interactions approached the variable significances of each variable alone (Fig. 4B). Interestingly, out of the top 7 genes in the random survival forest, 3 genes (SBF1, DNAI4, and DNAAF5) were members of the STRING local cluster associated with the dynein complex and primary ciliary dyskinesia.

Fig. 4.

Model identifies 7 variables strongly associated with EFS. (A) Variable importance by permutation in our random survival forest model, highlighting the top 7 variables that were identified by elbow analysis. (B) Pairwise subtree analysis showing weak interactions between most of the top 7 variables. (C) Linear models of the sum of the top 7 variables (polygenic score) in our random survival forest versus patient outcomes. Event = red; no event = teal. (D) Kaplan-Meier curves of patients with polygenic score > 0.5 (n = 43) and ≤ 0.5 (n = 66). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

To enhance the clinical interpretability of our model, we further investigated the relationship between each of these top 7 variables and EFS (Supplementary Fig. 2). In most cases, the relationship between variable value and EFS there was a tendency toward an inverse relationship between variable VAF and time to negative event (Supplementary Fig. 2), which motivated us to aggregate the VAFs of the 7 variables into a single polygenic score, defined as the unweighted sum of VAFs for all top-7 variables in each patient. The resulting score showed a clear negative linear relationship (slope of the regression line β = -936.7; P-value = 0.0009) with time-to-event in patients who experienced negative events in the training cohort (Fig. 4C). Conversely, there was no significant association between the polygenic score and time to last follow-up in patients who did not experience events (slope of the regression line β = 104.8; P-value = 0.7). Finally, we sought to evaluate the clinical utility of this score in the training cohort. We divided patients into two groups based on the mean value of the polygenic score among the training cohort, with one group having a polygenic score > 0.5 (n = 43), and the other having a score ≤ 0.5 (n = 66), and subjected them to Kaplan-Meier survival analysis (log-rank P-value = 6*10^-8) and Cox proportional hazards analysis (hazard ratio: 9.24 [3.49, 24.48]), with higher score values being associated with worse outcomes (Fig. 4D).

3.6. Random survival forest: Model testing

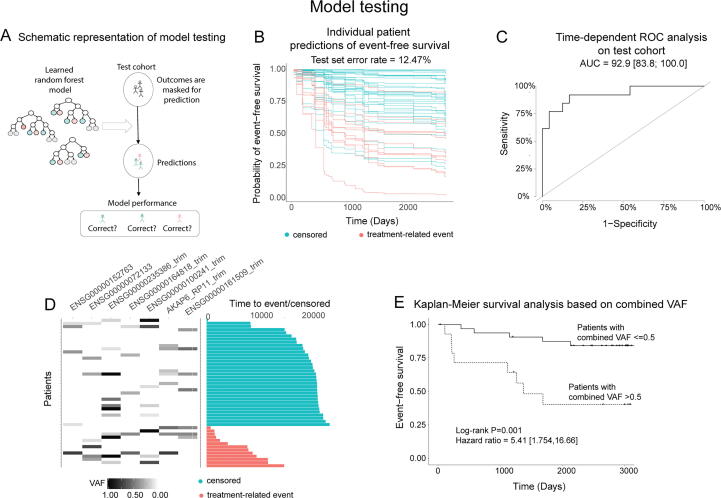
After our model was trained, the next step of our analysis was to test the model’s ability to make accurate predictions in our test cohort (n = 47; Fig. 5A). In the test cohort, our random survival forest model effectively predicted lower EFS in patients who experienced events versus those who did not, with test cohort error rate (1 - C-index) of 12.47% (Fig. 5B), and this model had a time-dependent ROC-AUC value of 92.9% with a 95% confidence interval of [83.8,100] (Fig. 5C), indicating high predictive accuracy in our model. Similar to the training cohort, patients who experienced events were more likely to have higher VAFs or multiple mutations in the top-7 genes than patients who did not experience events (Fig. 5D).

Fig. 5.

Random survival forest accurately predicts test cohort outcomes. (A) Schematic representation of model testing strategy. (B) Predicted per-patient EFS probabilities over time for each patient in the test cohort. (C) Time-dependent ROC-AUC for random survival forest test set performance. (D) Prevalence and values of top 7 variables in each test cohort patient. Patients were clustered by event status and time to event/censoring. (E) Kaplan-Meier curve for patients with top-7 variable sums>0.5 (n = 15) versus less than or equal to 0.5 (n = 32).

Furthermore, to confirm the clinical utility of our polygenic score, we assessed its efficacy in our test cohort. When we divided the test cohort into two groups based on the polygenic score, as in the training cohort above (>0.5; n = 15, and ≤ 0.5; n = 32), there was a statistically significant difference in survival outcomes between the groups (log-rank P-value = 0.001; Fig. 5E). The hazard ratio associated with this measure was 5.41, with a 95% confidence interval of [1.754,16.66]. This indicates that the polygenic score can effectively identify patients with lower and higher risk of negative events in high-risk pediatric B-ALL patients.

3.7. Comparison to other models: Recursive feature elimination and multivariable Cox proportional hazards

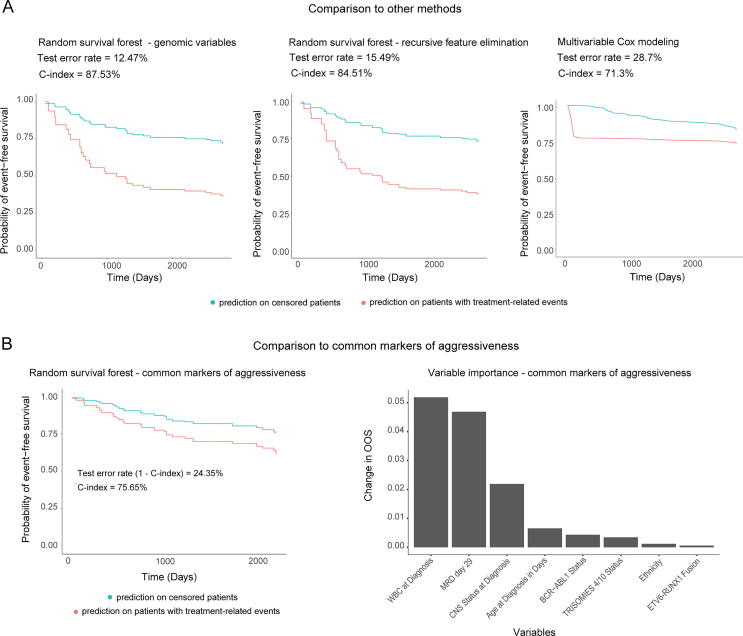
To understand the advantages of our modeling approach in comparison to other survival modeling strategies, we compared our original random survival forest model to both a random survival forest model using recursive feature elimination and a multivariable Cox proportional hazards model (Fig. 6). First, to understand the efficacy of our feature selection/engineering approach, we used a common variable selection method, recursive feature elimination, with a termination criterion of equalization between out-of-sample and test cohort error (see Methods). This approach eliminated 26 variables out of the original 118 variables, and as iterations progressed, out-of-sample error rate in the training cohort and test cohort error rates converged. The final random survival forest after recursive feature elimination used 92 genomic variables and had an out-of-sample error rate (1-C-index) in the training cohort of 15.49%. This model’s out-of-sample error rate in the training cohort (15.49%) was lower than that seen in the original random survival forest (17.93%). The test cohort error rate for the recursive feature elimination model was 15.49%, which was higher than the test cohort error rate for the original random survival forest model was 12.47% (Fig. 6A). These results imply that recursive feature elimination could potentially lead to model overfitting in the training cohort and underperformance in the test cohort, in comparison to our feature selection/engineering approach.

Fig. 6.

Original random survival forest approach with feature selection/engineering outperforms other common modeling approaches. (A) Original random survival forest EFS predictions for the test cohort versus random survival forest with recursive feature elimination and multivariable Cox proportional hazards models of EFS for the same cohort. (B) Test cohort EFS predictions for a random survival forest generated using current gold-standard prognostic variables and variable importance (assessed by variable permutation) in that model.

Second, to evaluate the performance of our random survival forest model in the context of more traditional survival modeling methods, we constructed a multivariable Cox proportional hazards model using a typical stepwise approach (see Methods). Several variables that were highly important in the random survival forest model were unsuitable for the multivariable Cox model due to significant violations of the proportional hazards assumption, which is not a requirement for random survival forests. The final multivariable Cox model consisted of 30 variables, and the training set error rate (1-C-index) of 5.7%, which is characteristic for maximum likelihood-based models such as Cox proportional hazards. However, the test cohort error rate for our multivariable Cox proportional hazards model was 28.7%, indicating that multivariable Cox underperformed when compared to our original random survival forest model (test cohort error rate = 12.47%).

3.8. Comparison to clinical variables and known markers of aggressiveness

To compare our identified variables to current gold-standard prognostic variables with respect to predicting EFS, we trained a random survival forest model based on 16 prognostic variables that represent current gold-standard variables for prognostic risk classification for pediatric B-ALL patients (Fig. 6B; Table 3). A grid search tuning strategy identified a maximum terminal node size = 8 and a number of variables to try per split = 3. The error rate converged before 1000 trees. This tuned random forest model had an out-of-sample error rate (1 - C-index) of 32.79% in the training cohort. The variable importance metrics seen in the gold-standard prognostic variable model generally recapitulate current knowledge, with WBC at diagnosis and MRD at day 29 being the most predictive variables and fusions also being important for predicting outcomes (Fig. 6B). The test cohort error rate for the random survival forest using gold-standard prognostic variables was 24.35%. The gap between test cohort performance in the original random survival forest model (error rate: 12.47%) and the gold-standard prognostic variable model implies that the identified genomic variables may provide additional information to effectively assess risk of negative events (as represented by EFS) in patients with high-risk B-ALL.

3.9. Model evaluation in B-ALL clinical subtypes

To assess the applicability of our original random survival model for B-ALL clinical subtypes, we analyzed 3 cohorts of patients: (1) high-risk patients who received 2 additional weeks of induction therapy (which were a subset of our original cohort), (2) high-risk patients who never responded to induction therapy, and (3) standard-risk patients that responded favorably to induction. High risk patients who never responded to induction therapy (group 2) and standard risk patients that responded favorably to induction (group 3) were not used for any previous training or testing step and were utilized for external model evaluation only. To understand if our model performed well in patients who received additional induction therapy, we selected a subset of patients who received 2 weeks of extended induction due to MRD > 1% at day 29 in our initial patient cohort. Our original high-risk patient cohort contained 12 of these patients, with 9 in the training cohort and 3 in the test cohort, and we specifically assessed model performance in these 3 patients. All 3 patients in the test cohort had predicted probabilities of EFS that were representative of their final outcomes, resulting in a test set error rate of 0% (Supplementary Fig. 3A), indicating that our model provides accurate predictions for this patient subset.

To assess the specificity of our model, we also evaluated its performance in two additional patient cohorts: patients who never responded to induction chemotherapy and standard-risk B-ALL patients. Although publicly available whole exome sequencing data for patients who never responded to induction therapy in pediatric ALL are relatively rare, we were able to identify 3 patients who had postinduction MRD > 25%. Among these 3 patients, there was only one variant detected in any of the 118 genomic regions used in our original random survival forest model. Because nearly all variable values were 0 for these patients, our random survival forest model had an error rate (1 – C-index) of 50% in these patients, potentially indicating a different genomic landscape for this group of patients. Another caveat of this analysis is that these patients all had precursor B-cell disease, and the discrepancies in genomics may be confounded by that fact. However, due to the small sample size, it is difficult to definitively conclude whether this lack of variants is biologically relevant or simply a result of the small sample size.

Finally, we analyzed a larger cohort of standard-risk B-ALL patients that responded favorably to induction (n = 174) and showed that our model had an error rate (1 – C-index) of 45.4% (Supplementary Fig. 3C and D). Furthermore, our 7-gene polygenic score was unable to predict survival outcome in this standard-risk cohort (log-rank P-value = 0.3; Supplementary Fig. 3E). These findings indicate that our original random survival forest model and polygenic score were both specific for high-risk B-ALL.

4. Discussion

Here we report a machine learning pipeline that produced a random survival forest model to accurately predict the EFS of patients with high-risk pediatric B-ALL and identified 7 genomic regions that are predictive of EFS (test error rate: 12.47%; time-dependent ROC-AUC: 92.9%). Furthermore, our novel feature selection/engineering strategy was able to effectively filter a starting pool of over 65,000 candidate somatic variants down to a final list of 118 genomic regions. Of the 118 variables, 7 in particular showed higher individual variable importance in our model. A polygenic score representing the sum of nonsynonymous variant allele frequencies present in these 7 genomic regions clearly identified patients at higher risk of relapse or other negative events. However, it should be noted that various arms of trial AALL0232 received slightly different treatment regimens that could affect EFS in the analyzed patients, and thus, it is challenging to directly mechanistically relate variables in this study to a specific regimen.

Innovations in this study includes a multi-stage feature selection/engineering strategy to reduce overall variable space, minimize model overfitting, and enhance prediction interpretability. First, the use of univariable Cox proportional hazards models as an initial variable selection step in our modeling pipeline represents a computationally efficient way to select genes that are specifically associated with EFS and thereby significantly reduce the size of a whole-exome variable set. We recognize that some edge cases, such as non-proportional hazards, may result in spurious inclusion of variables. However, the inclusion of these variables in the model does not affect random survival forest performance, and such variables will have low variable importance in the final model [61], [69].

The second stage of variable engineering/selection was to engineer variables based on specific genomic positions, which greatly enhanced the utility of our model by allowing us to identify specific genomic regions associated with EFS. In our study, defining variables using specific genomic coordinates rather than entire genes allowed us to leverage our model to identify several key genomic regions which can potentially affect gene function.

For example, we specifically identified variants in the C-terminal region of SBF1 as important for EFS. SBF1 has been identified as a driver of lymphoid proliferation due to its ability to bind SET domain proteins with its catalytically inactive phosphatase domain [74]. However, in this study, the most relevant region of SBF1 was not the phosphatase domain but rather a C-terminal region that contains a pleckstrin homology domain, which is a common domain responsible for membrane localization and is associated with cytoskeletal dynamics [75], and pleckstrin homology domain mutations have been previously identified as driver mutations in a large number of cancers [76], [77].

In fact, this region of SBF1 is of particular interest because of its association with the ciliary cytoskeleton. Cilia represent highly active extracellular signaling structures, and their disruption has recently been identified as a mechanism of chemotherapy resistance and progression in a variety of cancers [78], [79], [80]. Our findings in the context of this data imply that poor outcomes in high-risk pediatric B-ALL may be driven, in part, by disruptions in primary cilia function.

In addition to cilia-associated genes, the most significant variable in our model was a region of GRIN2C, an NMDA receptor that may have effects on hematopoietic differentiation by controlling calcium homeostasis in differentiating cells [81], [82]. Although the full structure and function of this gene has yet to be elucidated, we identified a narrow 50-basepair region in GRIN2C’s N-terminal extracellular domain that is significantly associated with accelerated relapse in high-risk pediatric B-ALL patients. Because GRIN2C has been associated with hematopoietic differentiation and calcium influx, the region identified in this study may be specifically associated with the gene’s behavior in hematopoietic cells or chemotherapy response.

Our top-7 variables also included other genes with known associations to chemotherapy response and outcome. With respect to ciliary function, besides SBF1, our model also identified DNAI4 and DNAAF5, both of which are dyneins associated with primary cilia. Finally, RPS6KA6 (also known as RSK4), another top-7 variable, is a known driver of oncogenesis in a variety of tumor types [83], and has been associated with chemotherapy resistance in breast cancer [84].

Validation of this study in standard-risk B-ALL revealed that both our random survival forest model and the polygenic score derived from it were specific for high-risk B-ALL. Furthermore, among a small cohort of high-risk B-ALL patients who did not respond to induction therapy, there was very little genetic overlap with our training cohort, with PCSK5 [85] being the only gene mutated in both the induction failure cohort and the training cohort. This resulted in an inability of our model to accurately predict outcomes in these patients. However, the patients in the induction failure cohort were all diagnosed with precursor B-ALL, which may also have different genomic drivers than mature B-ALL. Furthermore, the sample size in this dataset was small, so it is possible that these findings are a results of low sample size and may not be representative of induction failure patients as a whole.

Many machine learning strategies, including random survival forests, based on genomic variables are difficult to translate into clinical use because they involve significant numbers of genes and require whole-genome or whole-exome sequencing to assess [34], [86]. The level of sequencing coverage necessary for these strategies can be prohibitive in terms of both cost and accessibility [34], [35], [36]. Although our modeling strategy used whole-exome sequencing for input data, our feature selection/engineering and modeling pipeline showed significant correlations between EFS and 7 genomic regions (which defined a polygenic score) with a total size amenable to targeted sequencing. Well-validated methods exist to apply targeted sequencing panels to most human tissues stored and/or transported under a variety of conditions, and these panels are more cost-effective than whole-exome sequencing.

This study presents a machine learning pipeline that employs an innovative variable selection/engineering approach that offers enhanced interpretability over other modeling strategies. We propose that the polygenic score comprised of 7 genomic variables identified by our model could be utilized for enhanced clinical decision-making in high-risk B-ALL.

5. Financial Support

Antonina Mitrofanova is supported by Rutgers School of Health Professions Start-up funds, NIH R01LM013236-01, ACS Research Scholar grant RSG-21-023-01-TBG, and NJCCR COCR21RBG003.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: