Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2022 Jan 21.
Published in final edited form as: Hum Mov Sci. 2019 Feb 13;64:191–202. doi: 10.1016/j.humov.2019.01.008

Foot and shoe responsible for majority of soft tissue work in early stance of walking

Eric C Honert 1, Karl E Zelik 1,2,3
PMCID: PMC8777387  NIHMSID: NIHMS1762158  PMID: 30769210

Abstract

Soft tissues located throughout the human body are known to perform substantial mechanical work through wobbling and deforming, particularly following foot impacts with the ground. Yet, it is not known which specific tissues in the body are responsible for the majority of the soft tissue work. The purpose of this study was to quantify how much of the soft tissue work after foot contact was due to the foot and shoe, vs. from tissues elsewhere in the body, and how this distribution of work changed with walking speed and slope. We collected ground reaction forces and whole-body kinematics while ten subjects walked at five speeds (0.8 to 1.6 m/s) and seven different slopes (9 degrees downhill to 9 degrees uphill). Using a previously-published Energy-Accounting analysis to estimate the amount of soft tissue work, we found that the majority of the soft tissue energy absorption during early stance was due to deformation of the foot and shoe. The percentage of work did not vary significantly with speed but did vary significantly with slope: the foot and shoe were responsible for ~60–70% of the soft tissue work during level and uphill walking, and 80–90% during downhill walking.

Keywords: Energy absorption, heel pad, shoe cushioning, slope walking, distal foot power

1. Introduction

Soft tissues located throughout the human body are known to passively perform mechanical work through wobbling and deforming, particularly following foot impacts with the ground. During the initial phase of walking after foot contact both active muscles as well as passive soft tissues perform negative work (often termed Collision phase). Previous studies have estimated ~60% of the negative work done was due to the deformation of distributed soft tissues, with the remaining ~40% being work performed by muscles and tendons acting about lower-limb joints (ankle, knee, hip, Zelik & Kuo, 2010). The magnitude of work performed by soft tissues has been found to increase with walking speed, and to be higher in obese individuals relative to non-obese (Fu, Zelik, Board, Browning, & Kuo, 2015). Soft tissue work has also been estimated to contribute to other tasks, such as running (Riddick & Kuo, 2016) and jump landing (Cazzola, 2009; Zelik & Kuo, 2012).

It is not yet known which specific tissues in the body are responsible for the majority of the soft tissue work. Soft tissues capable of performing work (i.e., absorbing energy) during different activities include: intervertebral discs (Virgin, 1951), viscera (Cazzola, 2009; Minetti & Belli, 1994), adipose tissue (Fu et al., 2015), wobbling muscle mass (Pain & Challis, 2002; Schmitt & Günther, 2011), and the subcalcaneal fat pad in the foot (termed the heel pad hereafter, Aerts, Ker, De Clercq, Ilsley, & Alexander, 1995; Bennett & Ker, 1990; Ker, Bennett, Alexander, & Kester, 1989; Whittle, 1999). For practical measurement reasons, the deformation of footwear (Aerts & Clercq, 1993; Klute, Berge, & Segal, 2004; Shorten, 1993; Whittle, 1999) is often lumped in with the biological soft tissue estimates (i.e., experimental studies yield estimates of combined foot and shoe work, Zelik & Honert, 2018; Zelik, Takahashi, & Sawicki, 2015).

Recent studies suggest that the deformation of the foot and shoe may be responsible for a considerable amount of the soft tissue work during walking and running (Kelly, Cresswell, & Farris, 2018; Takahashi, Worster, & Bruening, 2017). The purpose of this study was to quantify how much of the soft tissue work after foot contact was due to the foot and shoe, versus from soft tissues elsewhere in the body, and how this distribution of work changed with walking speed and slope.

2. Methods

2.1. Summary

We collected ground reaction forces and whole-body kinematics while subjects walked at different speeds and on different slopes. We computed various estimates of mechanical power, then utilized a previously-published Energy-Accounting analysis, to estimate the amount of soft tissue work immediately following foot contact. Next we extended this prior analysis by parsing out how much of this soft tissue work was due to deformation of the foot (including the shoe) vs. work done by soft tissues elsewhere in the body.

2.2. Data Collection

Ten healthy subjects (5 male, 5 female, Age: 22±2 years, Height: 1.7±0.11 m, Weight: 68.5±13.7 kg) participated in an instrumented gait analysis study. All subjects provided written informed consent to the protocol, which was approved by the Institutional Review Board at Vanderbilt University. Each subject walked at five different speeds (0.8, 1.0, 1.2, 1.4, 1.6 m/s) on seven different slopes (0, ±3, ±6, ±9), for a total of 35 different trials, on a split-belt, force-instrumented treadmill (Bertec, Columbus, OH, USA). Seventy six retro-reflective markers were affixed to each subject (see Appendix A) in order to track upper- and lower-limb motions during walking. Ground reaction forces and marker data were collected for each trial for 30 seconds at 2000 Hz and 100 Hz, respectively. The center-of-pressure of the instrumented treadmill was accurate to less than 5 mm under static loads. The motion capture system (Vicon T40S, Oxford, UK) image error was less than 0.3 mm for all subjects and trials.

2.3. Data Analysis

Analysis was performed using Visual3D software (C-Motion, Germantown, MD, USA) and a custom MATLAB (MathWorks, Natick, MA, USA) script. Marker and force data were low-pass filtered at 10 Hz and 15 Hz, respectively, with 3rd order, dual pass, Butterworth filters. These data were used to compute different power metrics (detailed in the subsequent paragraphs). After cross-over steps (e.g., left foot on right belt) were removed, each power metric was parsed into strides based on left foot contact. Mean intra-subject power metrics were computed for each subject and trial (i.e., combination of speed and slope). Then, mean inter-subject power and work metrics were computed for each trial.

2.4. COM & Peripheral Powers

We computed Center-of-Mass (COM) power for each lower-limb using the individual-limbs method (Donelan, Kram, & Kuo, 2002) and the Peripheral power (i.e., rate of energy change, van der Kruk, van der Helm, Veeger, & Schwab, 2018; Zelik et al., 2015) of the hands, forearms, upper arms, thighs, shanks and feet with respect to the body’s COM. COM and Peripheral power terms were computed as detailed and derived in Zelik et al. (2015). The COM power reflects the time rate of change of kinetic and potential energy of the COM while the Peripheral power terms represent the time rate of change of segmental energies with respect to the COM of the body (Zelik et al., 2015). The summation of the COM and Peripheral powers from all limbs provides an estimate of whole-body power (rate of energy change), which we term here as the Total power (see Fig. 1). This summation of the COM and Peripheral powers is consistent with the rationale and interpretation described in van der Kruk et al. (2018).

Figure 1. Energy-Accounting analysis used to estimate soft tissue power contributions during early stance.

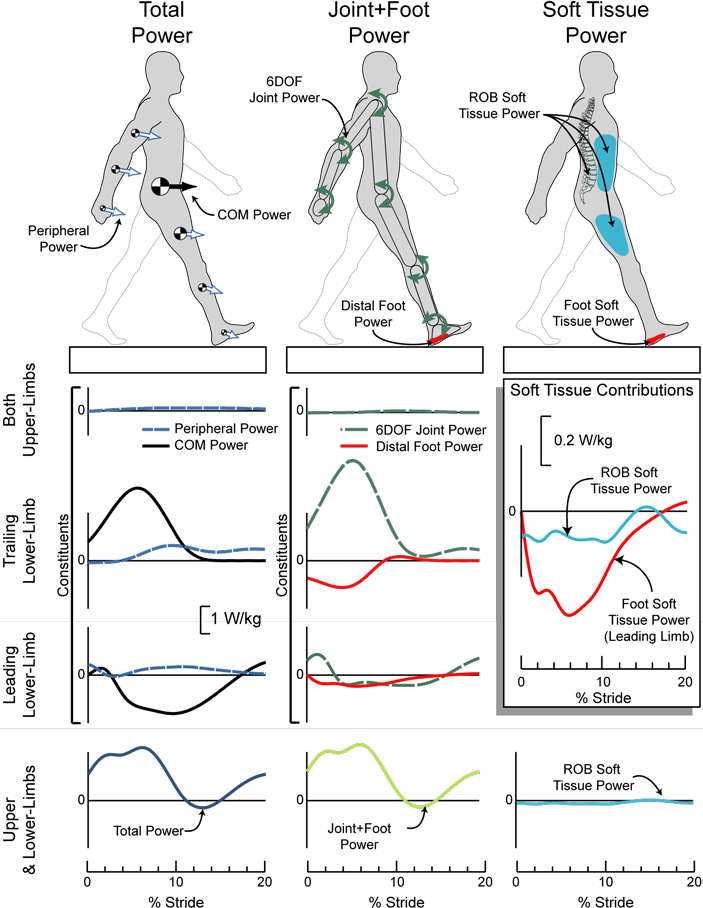
Figure 1.

Open in a new tab

The Foot Soft Tissue power is estimated by computing the leading limb Distal Foot power during Foot Absorption (~0–15% of stride), and represents power due to deformation of the foot and shoe. The ROB Soft Tissue power is computed as the difference between the Total power and the Joint+Foot power curves, and is power attributed to soft tissues elsewhere in the body. Total power is the summation of the Peripheral power of the arms (i.e., hands, forearms, upper arms) and legs (i.e., feet, shanks, thighs) and the COM power from the leading and trailing limbs; collectively signifying the rate of energy change of the whole-body. The Joint+Foot power is the summation of the upper- (i.e., wrists, elbows, shoulders) and lower-limb (ankles, knees, hips) joint powers and the Distal Foot power from the leading and trailing foot. For aesthetic simplicity, the cartoons only depict the leading limb power contributions. The results shown here are study averaged (N = 10) at 1.2 m/s on level ground.

2.5. Joint & Distal Foot Powers

Six degree-of-freedom (6DOF) joint powers for the lower-limb joints (i.e., ankles, knees, hips; Zelik et al., 2015) and upper-limb joints (i.e., wrists, elbows, shoulders; Riddick & Kuo, 2016) were estimated using rigid-body inverse dynamics calculations. Lower-limb joint powers were estimated using a bottom-up approach (starting calculations from the ground reactions forces, Robertson, Caldwell, Hamill, Kamen, & Whittlesey, 2013), whereas upper-limb joint kinetics were computed using a top-down approach (starting calculations from finger tips, Ashby, Vlietstra, Hickox, & Alderink, 2015; Cimolin et al., 2012). We did not estimate the lumbosacral joint power, which has been estimated to be very small during normal walking (Zelik & Kuo, 2010). The power due to deformation of the foot and shoe was estimated using a Distal Foot power calculation (rationale discussed below, Siegel, Kepple, & Caldwell, 1996; Takahashi & Stanhope, 2013; Zelik & Honert, 2018). Note that for brevity we use the term foot to encompass both the biological segment and the shoe surrounding it.

2.6. Foot Absorption Phase of Gait

Distal Foot power was used to define the initial phase of the gait cycle over which we computed negative work (energy absorption) summary metrics. We term this part of the gait cycle Foot Absorption and it covers roughly 0–15% of the stride cycle (Fig. 1). It is formally defined from foot contact to when the Distal Foot power curve crossed −0.05 W/kg. This non-zero threshold was necessary as the Distal Foot power does not always cross zero during early stance, but comes close. Foot Absorption is used instead of the more traditional COM Collision phase (which is often used to study level ground walking, Zelik et al., 2015) because the individual-limb COM power curve often does not exhibit negative power after foot contact during incline walking and Collision phase is thus ill-defined on these slopes (Franz, Lyddon, & Kram, 2012).

2.7. Rest-of-Body (ROB) Soft Tissue Power & Work

The power curves summarized above were then used to compute estimates of Soft Tissue power for the rest-of-body (ROB). ROB Soft Tissue power includes contributions from jiggly, wobbly and deformable tissues throughout the body (e.g., fat/muscle around the thigh, the intervertebral disks and viscera, see Fig. 1, Fu et al., 2015; Zelik & Kuo, 2010; Zelik et al., 2015), minus the foot (since this is captured by Distal Foot power, see below). Similar to prior literature (Fu et al., 2015; Zelik & Kuo, 2010; Zelik et al., 2015), the term Soft Tissue is capitalized to distinguish that these are quantitative estimates of power and work that we attribute to the deformation of non-rigid tissues/materials (based on certain assumptions, as detailed below and in: Zelik & Kuo, 2010; Zelik et al., 2015), as opposed to a colloquial discussion of (lower-case) soft tissues in the body.

The ROB Soft Tissue power was estimated using a previously-published Energy-Accounting analysis (Zelik et al., 2015), as the difference between the Total power of the body (sum of COM power from each lower limb plus Peripheral powers for all limbs and segments, Fig. 1) and Joint+Foot power (all 6DOF joint powers plus Distal Foot powers, see Fig. 1). Written out, this mechanical power balance, detailed in Zelik et al. (2015), is as follows:

Joint+Foot power+ROB Soft Tissue power=Total power

This equation is similar to the power balance presented in Aleshinsky (1986) and van der Kruk et al. (2018); however, there are a few notable differences because in our analysis of soft tissue contributions we relax the rigid-body and idealized articulating joint assumptions. For instance, relative to van der Kruk et al. (2018), we compute 6DOF joint power rather than 3DOF joint power on the left hand side of the equation, because the former is insensitive to the estimated joint center location (Zelik et al., 2015). We additionally compute the Distal Foot power, which is analogous to the environmental power term in van der Kruk et al. (2018), and we include an additional term called ROB Soft Tissue power on the left hand side of the equation to account for the relaxed rigid-body assumptions in our analysis. Finally, we compute whole-body rate of energy change (i.e., summed kinetic and gravitational power) on the right hand side of the equation in accordance with König’s theorem, similar to Kruk et al. (2018). Experimentally, this allows us to forego rigid-body assumptions in the calculation of COM power (Zelik et al. 2015). In our analysis of treadmill walking, we also assumed negligible air resistance and ground deformation (i.e., frictional power terms defined in van der Kruk et al. (2018)).

There were also a few notable differences in our methods relative to the Energy-Accounting analysis presented in Zelik et al. (2015). First, the prior study only included lower-limb joint powers (ankle, knee, hip) and the Distal Foot power. Here we extend the analysis to also include the shoulder, elbow and wrist joint powers. Second, the prior study sought to examine the positive work during the Push-off phase of gait and therefore presented an individual-limb analysis (which requires some additional assumptions, Zelik et al., 2015). Here we apply a more complete whole-body analysis (i.e., summing contributions from all upper and lower-limbs), which is beneficial because it circumvents the need for these additional assumptions. Next, ROB Soft Tissue work (in Joules) was computed by integrating under the negative portion of the ROB Soft Tissue power curve during Foot Absorption.

2.8. Foot Soft Tissue Power & Work

During Foot Absorption, we use the Distal Foot power of the leading limb as an estimate of Foot Soft Tissue power. The Distal Foot power represents the 6DOF power between the foot and the ground, meaning the translational power due to the motion of the COM of the foot relative to the ground plus the rotational power of the foot relative to the ground. In this model, the foot is modeled as a single, rigid body segment (Zelik & Honert, 2018). Note that the Distal Foot power provides a lumped (i.e., net power) estimate from both passive (e.g., subcalcaneal fat pad, midsole shoe cushioning) and active (e.g., intrinsic foot muscle) power sources; in contrast to multi-segment foot modeling approaches that are employed to further parse out various power sources within the foot (e.g., due to metatarsophalangeal joint rotation).

Next, Foot Soft Tissue work (in Joules) was computed by integrating under the negative portion of the Distal Foot power curve during Foot Absorption. We should acknowledge that our own recent work indicates that it is preferable to use Distal Calcaneus power rather than Distal Foot power (Zelik & Honert, 2018) in order to more fully capture foot dynamics. This is primarily important during mid- and late-stance (e.g., Push-off phase of gait). However, this recommendation was not known to us at the time of data collection for this current study, and thus in our current data set the markers used were insufficient to estimate Distal Calcaneus power (as it requires at least three markers on the hindfoot). Fortunately, Distal Foot power and Distal Calcaneus power appear to be very similar during early stance based on the data currently available in the literature (Zelik & Honert, 2018), thus Distal Foot power was deemed a reasonable surrogate measure here. For a full derivation of the Distal Foot power, see the appendix in Zelik & Honert, 2018.

2.9. Total Soft Tissue Work

We defined Total Soft Tissue work during Foot Absorption as the summation of the Foot Soft Tissue work and the ROB Soft Tissue work (Fig. 1).

2.10. Statistical Analysis

Statistical analyses were performed to determine the correlation of key outcome metrics with increasing speed and slope. The key outcome metrics computed during Foot Absorption were: (i) Foot Soft Tissue work, (ii) ROB Soft Tissue work, (iii) Total Soft Tissue work, and (iv) the percentage of the Total Soft Tissue work that was performed due to foot deformation (i.e., Foot Soft Tissue work divided by Total Soft Tissue work, multiplied by 100 to report as a percentage). We computed Spearman’s rank correlations with a Holm-Sidak post-hoc error correction for each outcome metric. Significance was evaluated with a family-wise α=0.05.

3. Results

The Total power of the body and the Joint+Foot power showed very strong qualitative agreement across the full range of speeds and slopes (Fig. 2). As a result, the difference between these two curves (i.e., the ROB Soft Tissue power) was relatively small across the entire gait cycle (on average < 0.7 W/kg, Fig. 2). During the Foot Absorption phase, the Foot Soft Tissue power typically exhibited greater power absorption (negative power) than the ROB Soft Tissue power (except when walking slowly uphill, Fig. 3).

Figure 2. Total power (dark blue), Joint+Foot power (light green), and ROB Soft Tissue power (light blue) for a wide range of walking speeds and slopes. Uphill is denoted with positive slopes and downhill with negative slopes.

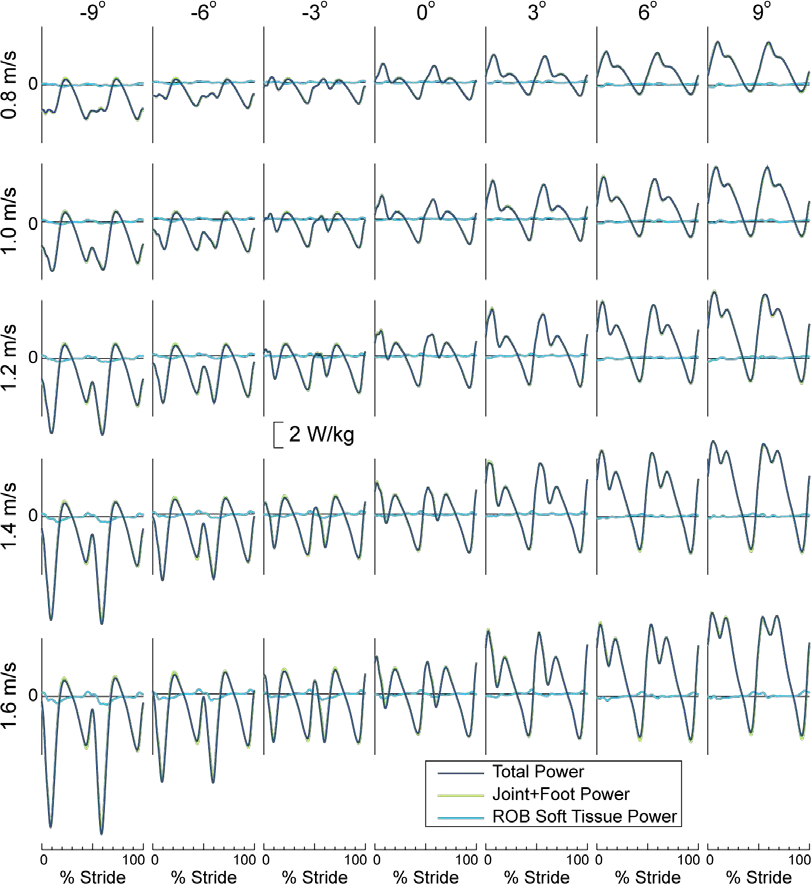
Figure 2.

Open in a new tab

The difference between the Total power and Joint+Foot power is defined as the ROB Soft Tissue power. Results shown are the inter-subject mean (N = 10).

Figure 3. Soft Tissue powers during early stance.

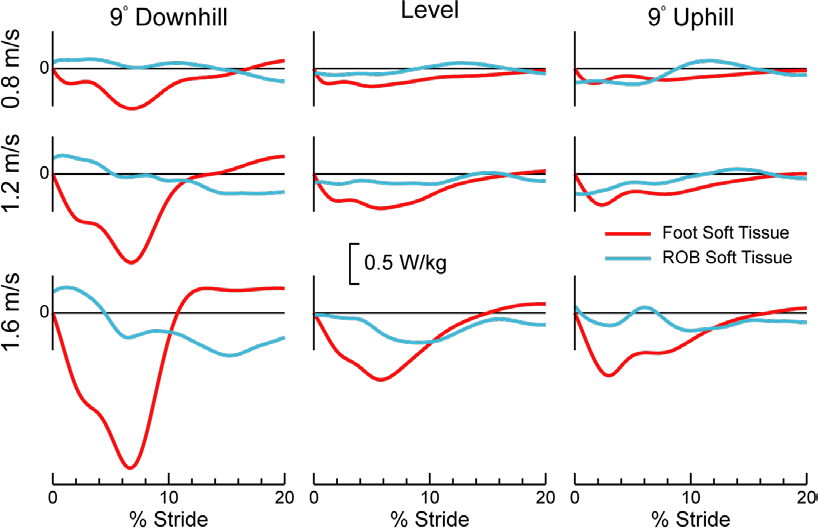
Figure 3.

Open in a new tab

The leading limb Distal Foot power provides an estimate of Foot Soft Tissue power (due to deformations within the foot and shoe). ROB (rest-of-body) Soft Tissue power is an estimate of contributions from deformable tissues elsewhere in the body (minus the foot). Results depicted are the inter-subject mean (N = 10).

Increasing gait speed (from 0.8 to 1.6 m/s) led to an increasing trend in the magnitudes of Foot Soft Tissue work and Total Soft Tissue work during the Foot Absorption phase, regardless of slope (p<0.0001, see Table 1 and 3). The ROB Soft Tissue work magnitude increased with increasing speed during downhill walking (p<0.006, see Table 2) and during one uphill slope (3 degrees, p<0.002). The percentage of Total Soft Tissue work done by the foot varied up to 19% with increasing speed, on average, but no significant trends were found as a function of speed (Table 4, Fig. 4).

Table 1. Foot Soft Tissue work (J) during Foot Absorption at different speeds and slopes.

Negative slopes indicate downhill walking. P-values indicate the significance of the trend in work with increasing speed for each slope (at the bottom of each column), and with increasing slope for each speed (at the right of each row). Asterisks indicate significant trends. All results shown are the inter-subject mean ± one standard deviation (N=10).

Slope (°)
−9 −6 −3 0 3 6 9 p-value
Speed (m/s) 0.8 −2.8±1.1 −2.6±1.0 −2.5±1.0 −2.2±0.7 −1.9±0.5 −1.8±0.4 −1.7±0.4 <0.0001*
1.0 −3.7±1.6 −3.3±1.2 −3.0±1.1 −2.6±0.7 −2.2±0.6 −2.3±0.6 −2.0±0.5 <0.0001*
1.2 −5.0±2.0 −4.2±1.6 −3.9±1.4 −3.1±1.0 −2.8±0.8 −2.8±0.8 −2.5±0.8 <0.0001*
1.4 −6.0±2.2 −5.7±1.9 −4.5±1.8 −4.2±1.0 −3.4±0.9 −3.5±0.9 −3.3±1.0 <0.0001*
1.6 −7.5±2.9 −6.6±2.3 −5.6±2.3 −4.5±1.3 −4.4±1.0 −4.3±1.1 −4.0±1.1 <0.0001*
p-value <0.0001* <0.0001* <0.0001* <0.0001* <0.0001* <0.0001* <0.0001*
Open in a new tab

Table 3. Total Soft Tissue work (J) during Foot Absorption at different speeds and slopes.

Negative slopes indicate downhill walking. P-values indicate the significance of the trend in work with increasing speed for each slope (at the bottom of each column), and with increasing slope for each speed (at the right of each row). Asterisks indicate significant trends. All results shown are the inter-subject mean ± one standard deviation (N=10).

Slope (°)
−9 −6 −3 0 3 6 9 p-value
Speed (m/s) 0.8 −3.2±1.3 −3.2±1.2 −3.1±1.4 −3.2±1.2 −2.8±0.8 −3.0±1.2 −3.6±2.2 0.4
1.0 −4.5±2.0 −3.8±1.4 −3.6±1.4 −3.8±1.3 −3.3±0.9 −3.8±1.1 −3.6±1.4 0.2
1.2 −5.8±2.2 −5.0±1.8 −4.6±2.1 −4.5±1.5 −4.5±1.8 −4.3±1.4 −4.7±1.5 0.05
1.4 −6.8±2.3 −6.6±2.0 −5.9±2.9 −5.9±1.9 −5.3±1.2 −5.2±1.4 −5.0±1.5 0.001*
1.6 −8.9±3.2 −8.5±2.5 −6.9±3.1 −6.8±2.1 −6.7±1.7 −6.9±2.0 −6.3±1.9 0.002*
p-value <0.0001* <0.0001* <0.0001* <0.0001* <0.0001* <0.0001* 0.0009*
Open in a new tab

Table 2. ROB (rest-of-body) Soft Tissue work (J) during Foot Absorption at different speeds and slopes.

Negative slopes indicate downhill walking. P-values indicate the significance of the trend in work with increasing speed for each slope (at the bottom of each column), and with increasing slope for each speed (at the right of each row). Asterisks indicate significant trends. All results shown are the inter-subject mean ± one standard deviation (N=10).

Slope (°)
−9 −6 −3 0 3 6 9 p-value
Speed (m/s) 0.8 −0.4±0.4 −0.6±0.5 −0.6±0.7 −1.0±0.9 −0.8±1.0 −1.2±1.3 −1.9±2.2 0.009
1.0 −0.8±0.8 −0.5±0.5 −0.6±0.6 −1.2±1.0 −1.0±0.9 −1.5±1.2 −1.5±1.5 0.02
1.2 −0.9±0.8 −0.7±0.7 −0.8±1.0 −1.3±1.0 −1.7±1.7 −1.5±1.0 −2.1±1.4 0.0003*
1.4 −0.9±0.5 −0.9±0.6 −1.4±1.5 −1.7±1.3 −1.9±0.9 −1.7±1.3 −1.7±1.4 0.03
1.6 −1.3±0.9 −1.9±1.2 −1.3±1.2 −2.3±1.4 −2.3±1.2 −2.6±1.6 −2.3±1.6 0.02
p-value 0.006* <0.0001* 0.0006* 0.01 0.002* 0.06 0.6
Open in a new tab

Table 4. Percentage of Total Soft Tissue work performed by the Foot at different speeds and slopes.

Negative slopes indicate downhill walking. P-values indicate the significance of the trend in work with increasing speed for each slope (at the bottom of each column), and with increasing slope for each speed (at the right of each row). Asterisks indicate significant trends. All results shown are the inter-subject mean ± one standard deviation (N=10).

Slope (°)
−9 −6 −3 0 3 6 9 p-value
Speed (m/s) 0.8 90±18% 83±13% 83±16% 70±23% 71±23% 64±24% 52±26% 0.003*
1.0 82±21% 89±9% 85±12% 69±22% 70±23% 63±23% 62±24% 0.002*
1.2 87±19% 86±12% 84±11% 71±16% 64±20% 69±17% 58±17% <0.0001*
1.4 89±14% 87±9% 77±14% 72±17% 66±13% 70±19% 71±22% 0.002*
1.6 86±9% 79±15% 81±12% 67±16% 67±14% 64±19% 68±20% 0.0006*
p-value 0.4 0.1 0.06 0.9 0.3 0.9 0.1
Open in a new tab

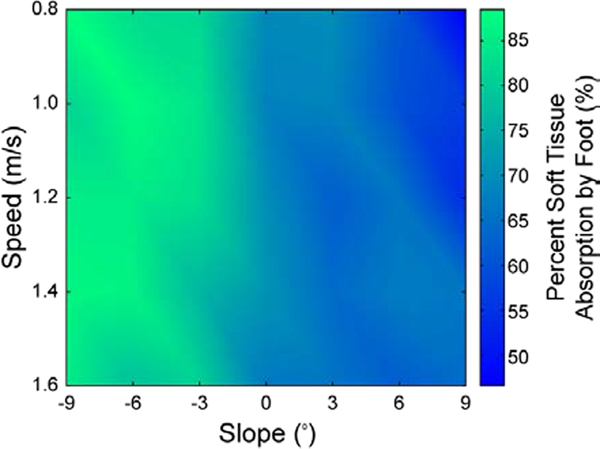
Figure 4. Percentage of Total Soft Tissue work performed by the foot across speeds and slopes.

Figure 4.

Open in a new tab

Increasing slope reduced the percentage of soft tissue energy absorption done by the foot, regardless of speed. Increasing speed has little effect on the percent soft tissue absorption performed by the foot. This heat map was created based on mean data from Table 4 for visualization purposes, using the default interpolated shading algorithm in MATLAB for aesthetic smoothing.

Increasing slope (from −9 to +9 degrees) led to a decreasing trend in the magnitude of Foot Soft Tissue work (Table 1) and in the percentage of Total Soft Tissue work done by the Foot (Fig. 4, Table 4, p<0.003), regardless of speed. The ROB Soft Tissue work (Table 2) and Total Soft Tissue work (Table 3) did not exhibit consistent trends with increasing slopes, resulting in some statistically significant and some non-significant trends at different speeds (Tables 2–3).

4. Discussion

The results indicate that deformation of the foot (which includes both biological and shoe structures in our study) is responsible for the majority of the energy absorption (negative work) done by soft tissues across a broad range of walking speeds and slopes during early stance. The foot absorbed as much as 7.5 J and contributed up to 90% of the Total Soft Tissue work after foot contact. During level and uphill walking the percentage of Soft Tissue work done by the foot was typically about 60–70%, and during downhill walking this was observed to increase to 80–90% (Table 3). The Foot Soft Tissue work increased by up to 3.5 J with decreasing slope (9 degrees uphill vs. 9 degrees downhill at 1.6 m/s, see Table 1) and increased by up to 4.7 J with increasing speed (0.8 m/s vs. 1.6 m/s at 9 degree downslope, Table 1). Kelly, Cresswell and Farris (2018) found a similar trend in running: more energy absorption by the foot at higher speeds.

The Foot Soft Tissue work observed here was in good agreement with energy absorption estimates reported in prior literature, including from impact studies, finite element models and gait analysis studies. We observed the Foot Soft Tissue absorption work to be 2.6–3.1 J for level ground walking at 1–1.2 m/s (Table 1). Impact studies with peak forces similar to walking at 1–1.2 m/s estimated foot absorption to be ~3–7 J (Aerts & Clercq, 1993; Kinoshita, Ogawa, Kuzuhara, & Ikuta, 1993). These studies estimated the foot energy absorption by fixating a person’s lower-limb, dropping an instrumented mass onto their foot (and shoe) and then measuring the force and displacement of the mass (Aerts & Clercq, 1993; Bennett & Ker, 1990; Jørgensen & Bojsen-Møller, 1989; Ker et al., 1989; Kinoshita et al., 1993). Of note, these types of impact studies may overestimate foot absorption because other soft tissues (e.g., wobbling calf muscles) may also be responsible for a portion of the energy absorbed (Pain & Challis, 2001). When just the foot and shoe were examined via finite element analysis, they were estimated to absorb ~2.5 J during locomotion, again with similar peak forces to the gait speeds mentioned above (Verdejo & Mills, 2004). In a barefoot gait analysis study, the heel pad was estimated to absorb 1.5 J at ~1.0 m/s. This was estimated by multiplying heel pad displacement (measured via radiographs) with heel forces (measured by a foot pressure sensor, Wearing, Hooper, Dubois, Smeathers, & Dietze, 2014). Another barefoot walking study estimated 3.8 J of heel pad energy absorption at 1.3 m/s, though they employed a calculation that captured the combined contribution from both the foot and the ankle (Baines, Schwab, & Soest, 2018). Overall, our estimate of Foot Soft Tissue work seems to be in reasonable agreement with the range of values reported in prior literature.

While most biomechanical studies historically focus on joint mechanics (e.g., ankle, knee, hip), the results here re-emphasize that soft tissues also provide substantial contributions to early stance gait dynamics. This is highlighted by comparing Total Soft Tissue work (Table 3) to the negative joint work from the leading limb (ankle+knee+hip) during Foot Absorption (Table 5). We observe that the Total Soft Tissue work (Table 3) greatly exceeded the joint work during the Foot Absorption phase (Table 5) in uphill walking. During level ground walking, the Total Soft Tissue work was ~150% of the magnitude of the joint work at slow speeds and ~50% of the joint work magnitude at fast speeds. During downhill walking the Total Soft Tissue work was ~20–50% of the magnitude of the joint work during Foot Absorption phase. These trends are consistent with those observed in our previous jump landing study (Zelik & Kuo, 2012), which showed that with increased Collision magnitudes there was a reduced percent contribution from soft tissues. Although it is possible for soft tissues to absorb a larger percentage of the negative work (e.g., by locking the knee into a fully extended position at foot impact, (Zelik & Kuo, 2012), this may be undesirable due to associated pain or risk of injury. Indeed, in prior barefoot impact studies, experimenters limited their testing range because impacts that required ~3.7 J of heel pad absorption instigated pain in the subjects (Kinoshita et al., 1993).

Table 5. Leading limb negative lower-limb joint (ankle+knee+hip) work performed during Foot Absorption at different speeds and slopes.

Negative slopes indicate downhill walking. All results shown are the inter-subject mean ± one standard deviation (N=10).

Slope (°)
−9 −6 −3 0 3 6 9
Speed (m/s) 0.8 −18.1±5.6 −12.1±3.1 −7.7±2.4 −2.1±1.3 −0.2±0.3 −0.1±0.1 0.0±0.0
1.0 −24.1±9.3 −17.4±4.3 −10.0±2.8 −3.2±2.0 −0.2±0.3 0.0±0.2 0.0±0.0
1.2 −32.4±12.2 −20.4±5.8 −13.6±4.1 −5.5±2.8 −0.6±0.7 −0.1±0.1 0.0±0.0
1.4 −35.4±6.7 −23.8±4.6 −16.7±4.8 −7.9±3.4 −1.5±1.7 −0.2±0.3 0.0±0.0
1.6 −41.1±11.5 −30.0±7.0 −20.7±5.5 −11.1±4.5 −2.8±2.3 −0.7±0.9 −0.1±0.1
Open in a new tab

The correspondence between Total power and Joint+Foot power – across all speeds and slopes – was frankly remarkable (Fig. 2). Despite the theoretical basis for expecting summed Joint+Foot power to match well with the Total (whole-body) power (Aleshinsky, 1986; van der Kruk et al., 2018), to our knowledge this has never actually been shown experimentally for walking. For a variety of practical and methodological reasons, prior attempts have only yielded partial agreement over certain portions of the gait cycle (e.g., Winter, 1979; Zelik et al., 2015), or when both estimates are derived from the same rigid body assumptions (Ebrahimi, 2018). Our current findings suggest benefits to applying a whole-body approach when performing Energy-Accounting analysis, which enables inclusion of upper-limb joint powers, requires fewer assumptions (e.g., related to partitioning COM and Peripheral powers between limbs, Zelik et al., 2015), and reduces the discrepancies between Total power and 6DOF Joint+Foot power (Figs. 2 and 5). Collectively, these current findings give confidence in the empirical accuracy and methodological completeness of the power estimates computed in this study.

Figure 5. Energy-Accounting analysis using a (A) individual-limb analysis and (B) whole-body analysis.

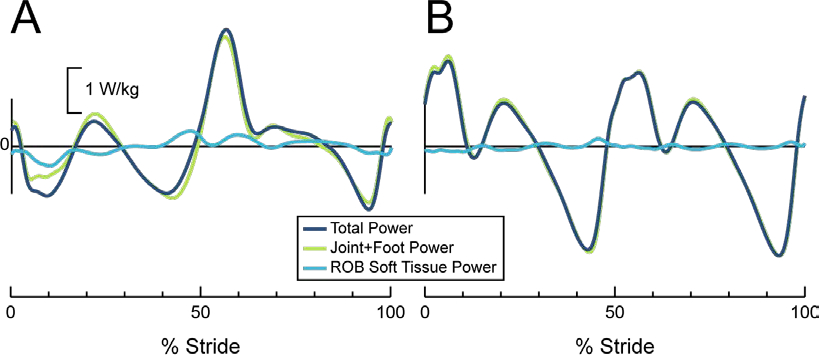
Figure 5.

Open in a new tab

The whole-body analysis (summing together all upper- and lower-limb powers) provides a more complete estimate of Total power of the body. Whereas individual-limb analysis requires some additional assumptions related to partitioning COM and Peripheral powers between limbs.

There are several limitations to acknowledge with this study. Each of the subjects wore their own shoes which can affect the Distal Foot power (Aerts & Clercq, 1993; Zelik & Honert, 2018). This study was performed on a relatively young, non-obese population. As such, the results (e.g., percentage of Total Soft Tissue work done by the foot) should not be assumed to generalize to all other ages and body types. Of note, the properties of the heel pad change with age (Hsu, Wang, Tsai, Kuo, & Tang, 1998) and the magnitude of Soft Tissue work after foot contact has previously been shown to increase in obese individuals (Fu et al., 2015). We interpret the ROB Soft Tissue power to be the net power contributions from deformable structures throughout the body (excluding the foot). However, this waveform may also be due, at least in part, to inaccuracies in model parameters (e.g., segment inertia) or imperfect measurements (e.g., ground reaction forces or moments, kinematics). Additionally, the marker and force data were filtered at different frequencies. Prior studies suggest this filtering approach may lead to transient peaks in joint moment estimates during the first ~50 ms after foot contact in high impact movements (Kristianslund, Krosshaug, & Bogert, 2012; McCaw, Gardner, Stafford, & Torry, 2013; Roewer, Ford, Myer, & Hewett, 2014) and in running (Bezodis, Salo, & Trewartha, 2013). To confirm that this effect was not skewing our results we applied the same marker and force filtering frequency (15 Hz) to our walking data in this study. We found no major effects on the key outcome metrics, trends, conclusions or interpretations. In general, when computing mechanical work and power metrics over longer periods of time (e.g., Foot Absorption was an average of 160 ms ), we have not found the use of different filtering cut-off frequencies (e.g,, 10 Hz motion vs. 15 Hz force) to substantially alter results or conclusions (Zelik & Honert, 2018; Zelik & Kuo, 2012). In our power balance we assumed rolling friction was negligible, and did not compute energy loss due to slight variations in treadmill belt speed. However, prior studies suggest this energy loss may be small; for instance Sloot et al. (2014) estimated ~0.25 J of treadmill energy loss in early stance of walking (1.3 m/s) due to variations in belt speed. Lastly, we did not compute the power contributions from the neck or spine joints. It is expected that these joints have small power contributions, as the neck and trunk (e.g., lumbosacral joint) generally undergo little rotation (Hirasaki, Moore, Raphan, & Cohen, 1999) and have relatively small moments during walking (Callaghan, Patla, & McGill, 1999).

5. Conclusion

In summary, we found that most of the Soft Tissue work that occurs after foot contact was due to deformation of the foot and shoe: ~60–70% of the Total Soft Tissue work during level and uphill walking, and 80–90% during downhill walking.

Supplementary Material

Appendix A

Acknowledgements

We gratefully acknowledge Erik Lamers for his assistance with data collection and Tristan Gilbert, Lauren Branscombe, Joshua Fleck, Ellen Turner, Eric Speer, Jacqueline Cabello, and Brendan Wilder for their assistance with data analysis.

Funding

This work was supported by funding from the National Institutes of Health (K12HD073945).

Glossary

Center-of-Mass (COM) power

The rate of work being performed on the body’s COM. This quantity is equivalent to the sum of k rate of change of the kinetic and potential energies of the COM

Distal Foot power

A 6DOF joint power modeled between a rigid-body, single-segment foot and the ground. This power accounts for translation and rotation that occurs between the foot segment and the ground, such as the compression of the heel pad

Energy-Accounting analysis

The approach where we compare summed 6DOF joint powers and Distal Foot powers to the Total power (rate of energy change) of the body. The approach provides a means of evaluating the completeness of our biomechanical measures, and estimating Soft Tissue power contributions

Foot Absorption

The phase immediately following foot contact, corresponding to roughly 0–15% of the stride cycle

Foot Soft Tissue power

Equal to the Distal Foot power during Foot Absorption

Foot Soft Tissue work

The integral under the negative portion of the Foot Soft Tissue power curve during Foot Absorption

Joint+Foot power

The summation of the 6DOF joint powers from the wrists, elbows, shoulders, hips, knees and ankles and the Distal Foot powers from each foot

Peripheral power

The translational and rotational kinetic powers (rate of energy change) of body segments relative to the whole-body COM

Rest-of-body (ROB) Soft Tissue power

The difference between the Total power and Joint+Foot power

Rest-of-Body (ROB) Soft Tissue work

The integral under the negative portion of the ROB soft tissue power curve during Foot Absorption

Six degree-of-freedom (6DOF) joint power

The rotational and translation power between two segments

Total power

The summation of the COM power from the leading and trailing limb and the Peripheral power from the hands, forearms, upper arms, thighs, shanks and feet

Total Soft Tissue work

The summation of the Foot Soft Tissue work and the ROB soft tissue work during Foot Absorption

Footnotes

Competing Interests

We have no competing interests

References

  1. Aerts P, & Clercq DD (1993). Deformation characteristics of the heel region of the shod foot during a simulated heel strike: The effect of varying midsole hardness. Journal of Sports Sciences, 11(5), 449–461. 10.1080/02640419308730011 [DOI] [PubMed] [Google Scholar]
  2. Aerts P, Ker RF, De Clercq D, Ilsley DW, & Alexander RM (1995). The mechanical properties of the human heel pad: A paradox resolved. Journal of Biomechanics, 28(11), 1299–1308. 10.1016/0021-9290(95)00009-7 [DOI] [PubMed] [Google Scholar]
  3. Aleshinsky SY (1986). An energy ‘sources’ and ‘fractions’ approach to the mechanical energy expenditure problem—II. Movement of the multi-link chain model. Journal of Biomechanics, 19(4), 295–300. 10.1016/0021-9290(86)90004-7 [DOI] [PubMed] [Google Scholar]
  4. Ashby BM, Vlietstra N, Hickox LJ, & Alderink GJ (2015). METHODS FOR FULL BODY INVERSE DYNAMICS ANALYSIS OF STANDING LONG JUMP. In 39th Annual Meeting of the American Society of Biomechanics (pp. 84–85). Columbus, OH, USA. [Google Scholar]
  5. Baines PM, Schwab AL, & Soest AJ van. (2018). Experimental estimation of energy absorption during heel strike in human barefoot walking. PLOS ONE, 13(6), e0197428. 10.1371/journal.pone.0197428 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bennett MB, & Ker RF (1990). The mechanical properties of the human subcalcaneal fat pad in compression. Journal of Anatomy, 171, 131–138. [PMC free article] [PubMed] [Google Scholar]
  7. Bezodis NE, Salo AIT, & Trewartha G (2013). Excessive fluctuations in knee joint moments during early stance in sprinting are caused by digital filtering procedures. Gait & Posture, 38(4), 653–657. 10.1016/j.gaitpost.2013.02.015 [DOI] [PubMed] [Google Scholar]
  8. Callaghan JP, Patla AE, & McGill SM (1999). Low back three-dimensional joint forces, kinematics, and kinetics during walking. Clinical Biomechanics, 14(3), 203–216. 10.1016/S0268-0033(98)00069-2 [DOI] [PubMed] [Google Scholar]
  9. Cazzola D (2009). INVESTIGATING THE METABOLIC PROFILE OF RUN-UP RACES AND THE MECHANICS OF WOBBLING VISCERAL MASS IN VERTICAL JUMPS. UNIVERSITÁ DEGLI STUDI DI MILANO, Milan, Italy. Retrieved from https://air.unimi.it/handle/2434/150073#.WtYVxC7wbIU [Google Scholar]
  10. Cimolin V, Galli M, Albertini G, Crivellini M, Romkes J, & Brunner R (2012). Quantitative analysis of upper limbs during gait: a marker set protocol. Journal of Applied Biomaterials & Functional Materials, 10(1), 49–55. 10.5301/JABFM.2012.9277 [DOI] [PubMed] [Google Scholar]
  11. Donelan JM, Kram R, & Kuo AD (2002). Simultaneous positive and negative external mechanical work in human walking. Journal of Biomechanics, 35(1), 117–124. 10.1016/S0021-9290(01)00169-5 [DOI] [PubMed] [Google Scholar]
  12. Ebrahimi A (2018). The Development and Application of a Framework for Exploring the Energetics of Gait Strategy Adaptations. University of Delaware. [Google Scholar]
  13. Franz JR, Lyddon NE, & Kram R (2012). Mechanical work performed by the individual legs during uphill and downhill walking. Journal of Biomechanics, 45(2), 257–262. 10.1016/j.jbiomech.2011.10.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fu X-Y, Zelik KE, Board WJ, Browning RC, & Kuo AD (2015). Soft Tissue Deformations Contribute to the Mechanics of Walking in Obese Adults. Medicine and Science in Sports and Exercise, 47(7), 1435–1443. 10.1249/MSS.0000000000000554 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hirasaki E, Moore ST, Raphan T, & Cohen B (1999). Effects of walking velocity on vertical head and body movements during locomotion. Experimental Brain Research, 127(2), 117–130. 10.1007/s002210050781 [DOI] [PubMed] [Google Scholar]
  16. Hsu T-C, Wang C-L, Tsai W-C, Kuo J-K, & Tang F-T (1998). Comparison of the mechanical properties of the heel pad between young and elderly adults. Archives of Physical Medicine and Rehabilitation, 79(9), 1101–1104. 10.1016/S0003-9993(98)90178-2 [DOI] [PubMed] [Google Scholar]
  17. Jørgensen U, & Bojsen-Møller F (1989). Shock Absorbency of Factors in the Shoe/Heel Interaction—With Special Focus on Role of the Heel Pad. Foot & Ankle, 9(6), 294–299. 10.1177/107110078900900607 [DOI] [PubMed] [Google Scholar]
  18. Kelly LA, Cresswell AG, & Farris DJ (2018). The energetic behaviour of the human foot across a range of running speeds. Scientific Reports, 8. 10.1038/s41598-018-28946-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ker RF, Bennett MB, Alexander RM, & Kester RC (1989). Foot Strike and the Properties of the Human Heel Pad. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine, 203(4), 191–196. 10.1243/PIME_PROC_1989_203_038_01 [DOI] [PubMed] [Google Scholar]
  20. Kinoshita H, Ogawa T, Kuzuhara K, & Ikuta K (1993). In Vivo Examination of the Dynamic Properties of the Human Heel Pad. International Journal of Sports Medicine, 14(06), 312–319. 10.1055/s-2007-1021184 [DOI] [PubMed] [Google Scholar]
  21. Klute GK, Berge JS, & Segal AD (2004). Heel-region properties of prosthetic feet and shoes. Journal of Rehabilitation Research and Development; Washington, 41(4), 535–546. [DOI] [PubMed] [Google Scholar]
  22. Kristianslund E, Krosshaug T, & van den Bogert, A. J. (2012). Effect of low pass filtering on joint moments from inverse dynamics: Implications for injury prevention. Journal of Biomechanics, 45(4), 666–671. 10.1016/j.jbiomech.2011.12.011 [DOI] [PubMed] [Google Scholar]
  23. McCaw ST, Gardner JK, Stafford LN, & Torry MR (2013). Filtering Ground Reaction Force Data Affects the Calculation and Interpretation of Joint Kinetics and Energetics During Drop Landings. Journal of Applied Biomechanics, 29(6), 804–809. 10.1123/jab.29.6.804 [DOI] [PubMed] [Google Scholar]
  24. Minetti AE, & Belli G (1994). A model for the estimation of visceral mass displacement in periodic movements. Journal of Biomechanics, 27(1), 97–101. 10.1016/0021-9290(94)90036-1 [DOI] [PubMed] [Google Scholar]
  25. Pain MTG, & Challis JH (2001). The role of the heel pad and shank soft tissue during impacts: a further resolution of a paradox. Journal of Biomechanics, 34(3), 327–333. 10.1016/S0021-9290(00)00199-8 [DOI] [PubMed] [Google Scholar]
  26. Pain MTG, & Challis JH (2002). Soft Tissue Motion during Impacts: Their Potential Contributions to Energy Dissipation. Journal of Applied Biomechanics, 18(3), 231–242. 10.1123/jab.18.3.231 [DOI] [Google Scholar]
  27. Riddick RC, & Kuo AD (2016). Soft tissues store and return mechanical energy in human running. Journal of Biomechanics, 49(3), 436–441. 10.1016/j.jbiomech.2016.01.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Robertson G, Caldwell G, Hamill J, Kamen G, & Whittlesey S (2013). Research Methods in Biomechanics (2nd ed.). Human Kinetics. [Google Scholar]
  29. Roewer BD, Ford KR, Myer GD, & Hewett TE (2014). The ‘impact’ of force filtering cut-off frequency on the peak knee abduction moment during landing: artefact or ‘artifiction’? Br J Sports Med, 48(6), 464–468. 10.1136/bjsports-2012-091398 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schmitt S, & Günther M (2011). Human leg impact: energy dissipation of wobbling masses. Archive of Applied Mechanics, 81(7), 887–897. 10.1007/s00419-010-0458-z [DOI] [Google Scholar]
  31. Shorten MR (1993). The energetics of running and running shoes. Journal of Biomechanics, 26, 41–51. 10.1016/0021-9290(93)90078-S [DOI] [PubMed] [Google Scholar]
  32. Siegel KL, Kepple TM, & Caldwell GE (1996). Improved agreement of foot segmental power and rate of energy change during gait: Inclusion of distal power terms and use of three-dimensional models. Journal of Biomechanics, 29(6), 823–827. 10.1016/0021-9290(96)83336-7 [DOI] [PubMed] [Google Scholar]
  33. Sloot LH, van der Krogt MM, & Harlaar J (2014). Energy exchange between subject and belt during treadmill walking. Journal of Biomechanics, 47(6), 1510–1513. 10.1016/j.jbiomech.2014.02.001 [DOI] [PubMed] [Google Scholar]
  34. Takahashi KZ, & Stanhope SJ (2013). Mechanical energy profiles of the combined ankle–foot system in normal gait: Insights for prosthetic designs. Gait & Posture. 10.1016/j.gaitpost.2013.04.002 [DOI] [PubMed] [Google Scholar]
  35. Takahashi KZ, Worster K, & Bruening DA (2017). Energy neutral: the human foot and ankle subsections combine to produce near zero net mechanical work during walking. Scientific Reports, 7(1), 15404. 10.1038/s41598-017-15218-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. van der Kruk E, van der Helm FCT, Veeger HEJ, & Schwab AL (2018). Power in sports: A literature review on the application, assumptions, and terminology of mechanical power in sport research. Journal of Biomechanics, 79, 1–14. 10.1016/j.jbiomech.2018.08.031 [DOI] [PubMed] [Google Scholar]
  37. Verdejo R, & Mills NJ (2004). Heel–shoe interactions and the durability of EVA foam running-shoe midsoles. Journal of Biomechanics, 37(9), 1379–1386. 10.1016/j.jbiomech.2003.12.022 [DOI] [PubMed] [Google Scholar]
  38. Virgin WJ (1951). Experimental investigations into the physical properties of the intervertebral disc. The Journal of Bone and Joint Surgery. British Volume, 33-B(4), 607–611. 10.1302/0301-620X.33B4.607 [DOI] [PubMed] [Google Scholar]
  39. Wearing SC, Hooper SL, Dubois P, Smeathers JE, & Dietze A (2014). Force–Deformation Properties of the Human Heel Pad during Barefoot Walking: Medicine & Science in Sports & Exercise, 46(8), 1588–1594. 10.1249/MSS.0000000000000281 [DOI] [PubMed] [Google Scholar]
  40. Whittle MW (1999). Generation and attenuation of transient impulsive forces beneath the foot: a review. Gait & Posture, 10(3), 264–275. 10.1016/S0966-6362(99)00041-7 [DOI] [PubMed] [Google Scholar]
  41. Winter DA (1979). A new definition of mechanical work done in human movement. Journal of Applied Physiology, 46(1), 79–83. 10.1152/jappl.1979.46.1.79 [DOI] [PubMed] [Google Scholar]
  42. Zelik KE, & Honert EC (2018). Ankle and foot power in gait analysis: Implications for science, technology and clinical assessment. Journal of Biomechanics, 0(0). 10.1016/j.jbiomech.2018.04.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zelik KE, & Kuo AD (2010). Human walking isn’t all hard work: evidence of soft tissue contributions to energy dissipation and return. The Journal of Experimental Biology, 213(24), 4257–4264. 10.1242/jeb.044297 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zelik KE, & Kuo AD (2012). Mechanical Work as an Indirect Measure of Subjective Costs Influencing Human Movement. PLOS ONE, 7(2), e31143. 10.1371/journal.pone.0031143 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zelik KE, Takahashi KZ, & Sawicki GS (2015). Six degree-of-freedom analysis of hip, knee, ankle and foot provides updated understanding of biomechanical work during human walking. The Journal of Experimental Biology, 218(6), 876–886. 10.1242/jeb.115451 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Appendix A
NIHMS1762158-supplement-Appendix_A.pdf (44.2KB, pdf)

RESOURCES