Abstract
Objective:
Photoplethysmography (PPG) waveform analysis is being increasingly investigated for continuous, non-invasive, and cuff-less blood pressure (BP) measurement. However, the efficacy of this approach and the useful features and models remain largely unclear. The objectives were to develop easy-to-understand models relating PPG waveform features to BP changes (after a cuff calibration) and to determine their value in BP measurement accuracy.
Methods:
The study data comprised finger, toe, and ear PPG waveforms, an ECG waveform, and reference manual cuff BP measurements from 32 human subjects (25% hypertensive) before and after slow breathing, mental arithmetic, cold pressor, and nitroglycerin administration. Stepwise linear regression was employed to create parsimonious models for predicting the intervention-induced BP changes from popular PPG waveform features, pulse arrival time (PAT, time delay between ECG R-wave and PPG foot), and subject demographics. Leave-one-subject-out cross validation was applied to compare the BP change prediction root-mean-squared-errors (RMSEs) of the resulting models to reference models in which PPG waveform features were excluded.
Results:
Finger b-time (PPG foot to minimum second derivative time interval) and ear “STT” (PPG amplitude divided by maximum derivative), when combined with PAT, reduced the systolic BP change prediction RMSE of reference models by 6–7% (p <0.022). Ear STT together with pulse width reduced the diastolic BP change prediction RMSE of the reference model by 13% (p=0.003).
Conclusion:
The two PPG fast upstroke time intervals can offer some added value in cuff-less BP trending. Significance: This study offers important information towards achieving non-invasive and passive BP monitoring without a cuff.
Keywords: cuff-less blood pressure, machine learning, mobile physiological monitoring, photoplethysmography (PPG), PPG waveform analysis, PPG waveform features, pulse arrival time (PAT), pulse transit time (PTT), wearables
I. Introduction
PHOTOPLETHYSMOGRAPHY (PPG) is a simple yet effective technique for measuring pulsatile blood volume changes in small arteries. Since blood volume is related to blood pressure (BP), PPG waveform analysis is believed to be a potential approach for achieving continuous, non-invasive, and cuff-less BP measurement (typically in between periodic cuff measurements). PPG waveform analysis is more convenient than the pulse transit time (PTT) approach [1], which nominally requires two sensors for measurement. Alternatively, it can be combined with PTT, which is often detected via a PPG waveform, to seamlessly improve its accuracy.
However, unlike PTT, PPG waveform analysis for BP measurement may have little theoretical basis. The Kelvin-Voigt model of viscoelasticity, which is profound in small arteries [1], provides a simple relationship between the oscillatory components of BP and PPG waveforms at the same site in the frequency-domain (ΔP(ω) and ΔV (ω)) as follows:
| (1) |
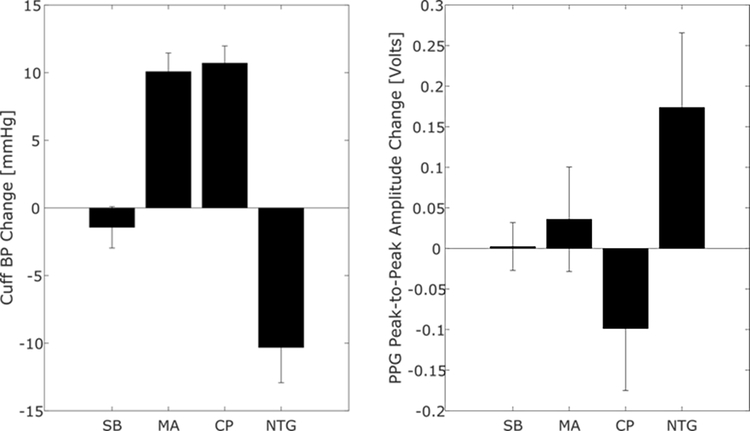
where E and η are the elastic modulus and coefficient of viscosity of the arterial wall [2]. The transfer function here is a lowpass filter with gain of 1/E and cutoff frequency of E/η. Hence, the PPG waveform is a lowpass filtered version of the BP waveform. In this way, the PPG waveform is embedded with BP information. However, the lowpass filter changes with BP variations and smooth muscle contraction, which is modulated by the brain on the time scale of seconds and can occur independently of BP changes [1]. So, for example, the PPG peak-to-peak amplitude can vary with BP or viscoelastic parameters. For this reason, as shown in Fig. 1, this PPG amplitude has little value in predicting BP changes during different physiologic interventions [3].
Fig. 1.
The peak-to-peak amplitude of the photoplethysmography (PPG) waveform does not track intervention-induced blood pressure (BP) changes [3]. SB is slow breathing; MA, mental arithmetic; CP, cold pressor; and NTG, nitroglycerin. Bars are mean±SE.
Nevertheless, PPG waveform analysis for cuff-less BP monitoring is being increasingly investigated [4]–[10] due to its unparalleled convenience and the current era of data-driven, machine learning. However, the accuracy of this approach, especially in terms of added value over demographic and other basic information or PTT, remains largely unknown. As a concrete example of the importance of such added value, suppose a BP prediction model with PPG waveform features and PTT as input yields a low BP error (say 5 mmHg) using unseen data. One may conclude that this model and the PPG waveform features therein are effective. However, suppose a “reference model” with only PTT as input yields a similar BP error (say 5.1 mmHg) on the same data. Now, it is clear that the PPG waveform features do not provide added value over PTT and are thus actually not useful at all. Hence, it is crucial to understand if a PPG waveform feature model provides added value (i.e., significantly greater BP prediction accuracy) relative to reference models that exclude PPG waveform features as input. Furthermore, the useful features and models relating the features to BP continue to be mostly unclear. Knowledge of useful features is particularly important given that a rigorous theory may be lacking. Finally, many of the studies have not invoked diverse interventions to change BP [4], [5], [8], which is crucial for assessing the more viable “cuff-calibrated, cuff-less” approach, or have used surgery or intensive care data [6], [9], which include challenging BP changes but may not be germane to interesting hypertension detection or control applications.
We investigated PPG waveform analysis in terms of tracking BP changes induced by a battery of diverse BP interventions in normotensive and hypertensive human volunteers. We specifically aimed to create readily interpretable models relating PPG waveform features to BP changes and to determine if they provided added value in BP measurement. The models that we reveal, with accompanying results herein, suggest that PPG fast upstroke time intervals can offer some added value in cuff-less measurement of BP changes.
II. Methods
We analyzed physiologic data that we previously collected from human subjects. Our overall approach was to apply stepwise linear regression to create models for predicting intervention-induced BP changes from popular PPG waveform features, PTT, and demographics and use leave-one-out cross validation to compare the BP change prediction errors of the resulting models to reference models in which PPG waveform features were excluded as input.
A. Human Physiologic Data
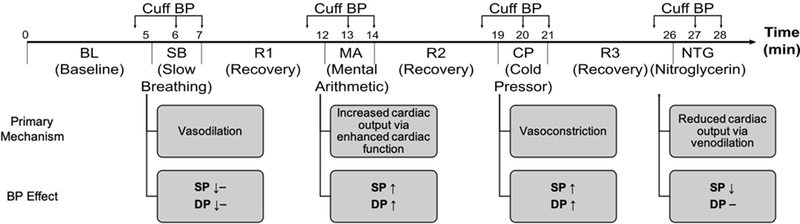
We described the human physiologic data for study in detail previously [3] and provide a summary here. We performed the procedures under IRB approval (Michigan State University LEGACY14–694F and University of Rochester Medical Center RSRB#56366, 2015-) and with written, informed consent from the subjects. We recorded finger, toe, and ear PPG waveforms, an electrocardiography (ECG) waveform, and manual cuff BP before and after slow breathing (SB); mental arithmetic (MA); a cold pressor test (CP); and, in subjects with sufficiently high BP levels (about 60% in total), sublingual nitroglycerin (NTG) administration. As shown in Fig. 2, these interventions increased or decreased systolic and diastolic BP (SP and DP) to varying extents via distinct physiologic mechanisms. As also indicated in the figure, we obtained cuff BP immediately prior to each intervention for baseline (BL) and three recovery (R1–3) measurements and usually obtained cuff BP twice during each intervention for up to eight intervention measurements. We thus had up to 12 sets of four waveforms and cuff BP measurements during up to eight distinct conditions per subject. We viewed the waveform segments within ±30 sec of each cuff BP measurement and selected a > 7 sec sub-segment for which all four waveforms were relatively free of artifact. If there were no such sub-segment, we excluded the entire measurement set from further analysis. If there were two sets of waveform sub-segments with minimal artifact for a condition, we excluded the set with the smaller BP change. We excluded entire subject records with less than five measurement sets in subjects without NTG and less than six measurement sets or six measurement sets without three or more interventions in subjects with NTG. As explained previously [3], this strict data exclusion criteria ensures a meaningful, apples-to-apples comparison of the BP prediction models. A total of 214 sets of the four clean waveform segments and reference cuff BP values from 32 subjects (see characteristics in Results) remained for analysis. We previously analyzed these data to compare conventional PTTs as markers of BP and found that the best correlation by a significant extent was between toe pulse arrival time (PAT), which is the time delay between the ECG R-wave and toe PPG trough or foot, and SP (subject average r = −0.63±0.05) [3].
Fig. 2.
A battery of challenging interventions was employed to change BP differently via distinct physiologic mechanisms according to the indicated timeline [11]–[14]. SP and DP are systolic and diastolic BP.
B. Data Analysis
We further analyzed the data to determine if incorporating PPG waveform features could improve the tracking of the intervention-induced BP changes. Our strategy for this data-driven investigation was to employ methods intended for when the number of subjects is not high.
1). Pre-Processing:
We first applied bandpass filters with cutoff frequencies of 0.5 and 6 Hz to the finger and toe PPG waveforms and 0.5 and 9 Hz to the ear PPG waveform. We selected these cutoff frequencies as follows. First, for each of the three PPG waveform, we plotted features of the waveforms after application of filters of various cutoff frequencies versus the same features of the waveforms after only light filtering. We then further considered only those cutoff frequencies that yielded datapoints largely on the identity line. We finally selected the cutoff frequencies that yielded feature histograms with fewest outliers. In this way, the chosen cutoff frequencies represented a good trade-off between removing noise and retaining features.
We detected the peaks of the PPG waveform via ECG-gating and then the waveform feet using the intersecting tangent method [1]. We subtracted the amplitude at the leading foot of each PPG waveform beat from the entire beat. We next selected consistent beats from each > 7 sec waveform segment as follows. For each beat in a segment, we computed the beat interval, peak amplitude and timing, and lagging foot amplitude. We then computed the median of each of these four features over all the beats followed by the normalized-root-mean-squared-difference between the features of each of the beats and their median values. We finally selected the five beats with the smallest normalized-root-mean-squared-differences.
2). Feature Extraction:
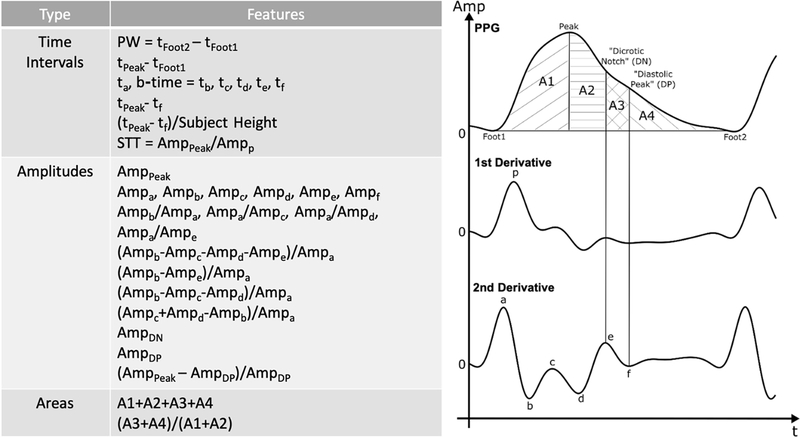
We limited the candidate PPG waveform features to popular or promising ones. Fig. 3 shows the 31 candidate features that we considered. The amplitudes, timings, and areas of the PPG waveform and its first and second derivatives are perhaps the most widely studied [15], while “slope transit time (STT)” has been shown to be inversely correlated with BP during respiratory maneuvers [16]. We also detected finger, toe, and ear PAT as the time delay between the ECG R-wave and the PPG waveform foot as another waveform feature that would also require an ECG measurement. We extracted all of these features from each of the five beats of a segment and then took the mean of the three middle values for each feature. Some features (e.g., tc, td, te, tf, AmpDN, and AmpDP) were not always detectable. If a feature were not detected, we set its value to that of the previous segment in the subject for which the feature was detected. This process was always possible in the dataset.
Fig. 3.
A total of 31 popular or promising PPG waveform features [15], [16] were considered as candidates for predicting the intervention-induced BP changes. Subject demographic information and pulse arrival time (PAT, the time delay between the R-wave of the ECG waveform and the leading foot of the PPG waveform) were also possible features.
3). Model Development:
We sought to develop linear regression models to predict the BP changes relative to the first or “baseline” cuff BP measurement of each subject. We thus subtracted the baseline cuff BP/waveform feature value from the remaining cuff BP/waveform feature values of each subject. We also normalized each waveform feature change with the baseline feature value (unless it was near zero). In addition, we allowed age, gender, height, weight, and the baseline cuff BP values as possible person features, which are static per subject. The models for mapping waveform features (w) or person features (p) to BP (XP with X = S for systolic and X = D for diastolic) via linear parameters (α) thus took on the following form:
| (2) |
where the superscripts i and j denote the ith value of the jth subject (e.g., a superscript of 1,j indicates the baseline value of the jth subject); the subscript k signifies the kth feature; m indicates the number of features (model order); and e is the model residual error. For gender, we used two features to effectively define one model intercept for males and another model intercept for females.
We selected the features and estimated the model parameters and order using forward stepwise regression with an “elbow” method. We added one feature at a time to the model, starting with zero features and ending with six features, and selected the new feature at each iteration as the one that minimized the mean square of the residual error. We conservatively chose six as the maximal model order, as 20–30 data points are typically needed to estimate one parameter and about 180 data points (see first and third paragraphs below) were available to estimate the BP change prediction model. In post hoc analysis, the results proved to be insensitive to small changes to the maximal model order. We then fitted two lines to the monotonically decreasing curve relating mean squared residual error to the model order and selected the order, and thus the final model, via the intersection of the two lines. We found that this empirical method to identify the curve elbow yielded more parsimonious models than other methods such as lasso and ridge regression.
We employed the above steps in a leave-one-out cross validation framework. We specifically estimated 32 models using data from all combinations of 31 of the subjects and left the remaining subject data for testing each model. In this way, we leveraged as much data as possible for training while also allowing testing on all subjects without using the same data for training and testing. We created separate models for the finger, toe, and ear PPG waveforms to predict the different changes in SP and DP and thus arrived at six PPG waveform feature models.
For comparison, we also created three reference models. The first model is to use the baseline cuff BP value as the predictor of the ensuing BP (i.e., no BP changes) in the subject (“baseline BP reference model”). The second model is to predict the BP changes from only the person features using the stepwise regression, elbow, and leave-one-out methods (“demographic reference model”). The third model is to predict the BP changes from only 1/PAT, which correlated slightly better than PAT to BP here, for each PPG waveform using regression and leave-one-out methods (“PAT reference model”).
4). Model Evaluation:
There were a total of M=182 BP changes between each condition and baseline of each of the N=32 subjects (i.e., 214 total measurements – 32 baseline measurements). We evaluated the 182 BP change predictions of each model against the reference cuff measurements from the 32 leave-one-out test subjects using standard correlation and Bland-Altman analyses. We computed the Bland-Altman bias and precision errors (μ and σ) via the basic sample mean and SD of the errors, as mixed effects modeling to account for the repeated measures per subject [17] hardly impacted the σ. To conveniently quantify the overall error, we used the root-mean-squared-error
We used the RMSE metric to perform statistical comparisons of two models (i.e., PPG waveform feature model versus a reference model). We applied non-parametric cluster bootstrapping to calculate confidence intervals and make the comparisons [18]. We took 10,000 random samples of the 32 subjects with replacement of the subjects (i.e., each time a subject is drawn from the cohort and then documented, it is returned to the cohort before the next subject is drawn). The number of subjects in each sample was 32, and we included all BP change errors from a subject per sample. For each sample, we computed the RMSE as described above for each model and the difference between the RMSEs of the two models for comparison (model 1 – model 2). We calculated both 95% CIs of each RMSE and X% CIs of each RMSE difference from the corresponding distribution of 10,000 values via a standard percentile bootstrap. If the upper CI for the RMSE difference were less than zero, then model 1 would be considered superior to model 2. Since we made six comparisons, we applied a Holm’s correction [19] such that a two-sided p < 0.05/(6 + 1 − k), where k is the comparison with the kth lowest p-value (i.e., X = 99.17 for k = 1), was considered statistically significant.
III. Results
A total of 214 PPG-BP measurement sets with minimal artifact from 32 subjects (50% female; 52 (17) (mean (SD)) years of age; 166 (10) cm in height; 89 (34) kg in weight; 25% with treated hypertension; 31% with smoking history; and 9% with LDL cholesterol >=190 mg/dL) formed the study data. The baseline SP and DP (mean±SE) were 121±3 and 79±2 mmHg (N=32), respectively.
Table I shows the results of the PPG waveform feature models versus reference models in leave-one-subject-out prediction of the intervention-induced BP changes relative to the subject baseline values (M=182, i.e., 214 total measurements – 32 subject baseline measurements). This table also presents those models that proved to be useful. Each of the useful models was stable across the 32 leave-one-out training sets in the sense that 97–100% of the 32 models yielded the same features, and the models displayed in the table are representative ones resulting from training on all 32 subject datasets.
TABLE I.
Root-Mean-Squared-Errors (RMSEs) of the Intervention-Induced Blood Pressure (BP) Changes Predicted By The Models Against Reference Cuff BP Measurements
| Models | RMSE (lower and upper 95% CIs) (Mean (μ) ± SD (σ)) | |
|---|---|---|
| SP (Systolic BP) | DP (Diastolic BP) | |
|
Baseline BP Reference SPi = SP1 DPi = DP1 |
10.9 (9.5 – 12.4) (3.7 ± 10.2) | 6.5 (5.6 – 7.3) (0.9 ± 6.4) |
| Demographic Reference | 10.8 (9.2 – 12.7) (0.5 ± 10.8) | 6.6 (5.7 – 7.5) (0.0 ± 6.6) |
|
Finger PAT Reference
|
10.1 (8.6 – 11.8) (2.8 ± 9.7) | 6.3 (5.5 – 7.1) (0.6 ± 6.3) |
|
Ear PAT Reference
|
10.2 (8.6 – 11.9) (1.7 ± 10.1) | 6.5 (5.6 – 7.4) (0.6 ± 6.5) |
|
Toe PAT Reference
|
9.1 (7.6 – 10.9) (2.1 ± 8.9) | 6.2 (5.3 – 7.1) (0.4 ± 6.2) |
|
Finger PPG Waveform Feature
|
9.5 (7.9 – 11.5)*† (2.3 ± 9.3) | 7.0 (6.1 – 7.7) (0.5 ± 7.0) |
|
Ear PPG Waveform Feature DPi = 30.6 (STTi) − 40.4(PWi) + DP1 |
9.5 (7.8 – 11.4)*† (0.7 ± 9.5) | 5.7 (5.0 – 6.3)* (0.2 ± 5.7) |
|
Toe PPG Waveform Feature
|
9.1 (7.6 – 10.9)* (2.1 ± 8.9) | 6.5 (5.6 – 7.4) (0.2 ± 6.5) |
denotes statistical significance (p < 0.05 with Holm’s correction for multiple comparison) versus baseline BP reference model (which predicts BP during the interventions simply via the baseline cuff BP measurement) and
denotes statistical significance versus corresponding pulse arrival time (PAT) reference model (which predicts the BP changes via 1/PAT alone). The demographic reference model (which predicts the BP changes via subject age, height, weight gender, and baseline cuff BP) did not offer value and was not compared. The models are shown only if they provided added value over reference models. Each feature (1/PAT, b-time, STT, and PW as defined in Fig. 3) actually represents the current feature minus the baseline feature divided by the baseline feature as shown in Fig. 4.
The baseline BP reference model, which simply employs the baseline cuff BP of each subject to predict the ensuing BP, yielded RMSEs of 10.9 mmHg for SP and 6.5 mmHg for DP. While these error levels are near or within the regulatory limits of 5 and 8 mmHg bias and precision errors [20], the BP change prediction models must yield lower errors to offer any value. The demographic reference model, which includes subject age, gender, height, weight, and the baseline cuff SP and DP as candidate features, provided no such value. The PAT reference models, which include the time delay as the sole feature, were helpful in predicting changes in SP but not DP. As shown previously [3], toe PAT was clearly the best in tracking the SP changes.
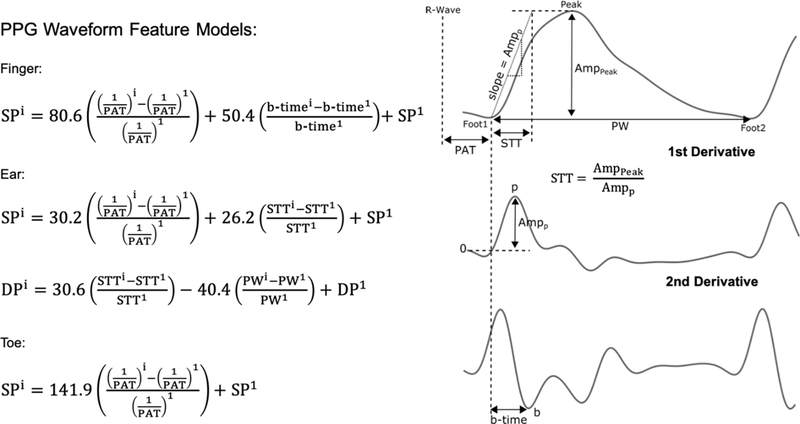
Three of the six PPG waveform feature models afforded added value over the reference models. The finger and ear PPG waveform feature models for predicting SP changes included 1/PAT as the primary feature and the b-time (time to the minimum second derivative of the PPG waveform) or STT (amplitude divided by the maximum derivative of the PPG waveform) as a secondary feature, all with positive regression parameters. These models yielded RMSEs of 9.5 mmHg (p < 0.022 versus baseline BP and finger and ear PAT reference models). The ear PPG waveform feature model for predicting DP changes included STT as the primary feature with positive regression parameter and PW (pulse width) as a secondary feature with negative regression parameter. This model produced an RMSE of 5.7 mmHg (p = 0.003 versus baseline BP reference model). Note that the toe PPG waveform feature model for predicting SP changes included only 1/PAT as input. However, this model yielded an RMSE of 9.1 mmHg (p = 0.004 versus baseline BP reference model). Fig. 4 presents in full detail the four PPG waveform feature models that showed added value in predicting BP changes.
Fig. 4.
The PPG waveform feature models that provided added value in predicting BP changes. The b-time and STT, which are PPG fast upstroke time intervals (see Fig. 3 for definitions), reduced the BP change root-mean-squared-error (RMSE) relative to reference models not including PPG waveform features as input by about 10% (see Table I). The superscript i is the ith measurement; i=1, baseline measurement for cuff calibration.
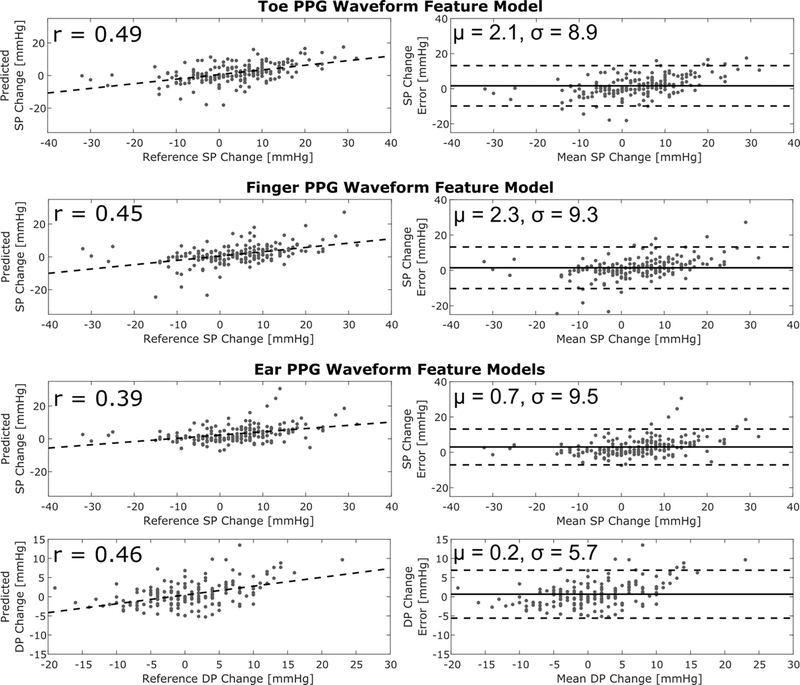
Fig. 5 shows correlation and Bland-Altman plots of the BP change predictions of the four useful PPG waveform feature models versus the reference cuff BP measurements (M=182). These results allow visualization of the key numerical results in Table I and indicate that the correlation coefficients between the predicted and reference BP changes were 0.39–0.49.
Fig. 5.
Correlation and Bland-Altman plots of BP changes predicted by the PPG waveform feature models that offered added value (see Table I) versus the reference cuff BP measurements. M = 182 measurements from N = 32 subjects. The dashed line in the correlation plots is the best-fit line; r, correlation coefficient; μ and σ bias and precision errors.
In sum, the b-time and STT, which are time intervals of the fast upstroke, of ear and finger but not toe PPG waveforms were the only useful features in tracking changes in BP. For SP, these PPG fast upstroke time intervals were helpful in conjunction with PAT but not as standalone features. For DP, STT of the ear PPG waveform was useful by itself. The PPG fast upstroke time intervals were positively rather than negatively related to the BP changes. They reduced the BP change RMSEs of the reference models by 6–13%.
IV. Discussion
PPG waveform analysis is being increasingly investigated for continuous, non-invasive, and cuff-less BP monitoring [4]–[10]. However, this data-driven approach is not well understood in terms of both efficacy and useful features and models. In this study, we sought to develop easy-to-understand models relating PPG waveform features to BP changes (after a single cuff calibration) and to determine conclusively whether they provide added value or not in BP measurement accuracy compared to reference models that exclude PPG waveform features as input.
We analyzed finger, toe, and ear PPG waveforms along with ECG waveforms and reference manual cuff BP measurements from 32 normotensive and hypertensive volunteers during a battery of challenging interventions that changed SP and DP differently (see Figs. 1 and 2). These data thus allowed us to create six PPG waveform feature models for predicting intervention-induced BP changes corresponding to the three PPG waveforms and two BP levels.
We chose analysis tools to create models that are readily interpretable and effective when the subject number is not high. More specifically, we limited the candidate features to popular or promising PPG waveform features (see Fig. 3) plus subject demographic information and PAT (time delay between ECG R-wave and PPG foot); applied stepwise linear regression for forward selection of the features and estimation of the model parameters; used a parsimonious elbow method for determining the number of features; and employed leave-one-subject-out cross validation to leverage the data as much as possible for independent training and testing. We also verified our approach in terms of robustness to user-selected variables and overfitting relative to other tools.
We assessed the BP changes relative to the subject baseline BP predicted by the PPG waveform feature models against the reference cuff BP measurements using standard Bland-Altman and correlation analysis. Crucially, to ascertain added value, we compared the BP change RMSEs of these models to reference models without PPG waveform features as input (e.g., demographic or PAT models). We performed these comparisons statistically via cluster bootstrapping while reducing the significance level for multiple comparisons.
Four PPG waveform feature models showed added value in predicting BP changes (see Fig. 4). These models were stable across the 32 leave-one-out training datasets. Note that the toe PPG waveform feature model included only PAT as input. The other three models each included a PPG waveform feature and reduced the RMSE of the reference models by about 10% (see Table I). The correlations between the predicted BP changes of the four models and the reference measurements were about 0.4–0.5 (see Fig. 5).
Hence, almost all of the 31 candidate features for study were of no value in tracking the BP changes despite their popularity [15]. In fact, a number of these features were often not well detected or detectable at all (e.g., tc, td, te, tf, AmpDN, and AmpDP), which surely reduced their utility. This limitation of the considered features has been noted before [15], [21]. Only the b-time (tb) and STT, which were generally well defined and reflect the fast upstroke time interval of the PPG waveform, showed value in BP measurement.
However, the PPG fast upstroke time intervals were positively related to the BP changes. This finding opposes conventional thinking that an increase in cardiac contractility or preload (via, e.g., exercise) would increase BP while reducing the PPG upstroke interval to create a negative relationship. STT was also introduced as a single-site measurement of PTT and shown to be positively related to PTT and thus inversely related to BP [16]. The positive relationship that we found may be due to small artery viscoelasticity. As we previously found [22], when BP increases, the cutoff frequency of the viscoelastic lowpass filter may decrease such that the PPG upstroke time interval increases (see Eq. (1) in Introduction). This viscoelastic mechanism could be most important over a range of BP interventions, especially for fast upstroke time intervals in which the lowpass filtering effect would be more pronounced. Note that, even if the PPG fast upstroke time interval decreases during exercise, the models in Fig. 4 may still correctly predict BP increases via the other feature in these models.
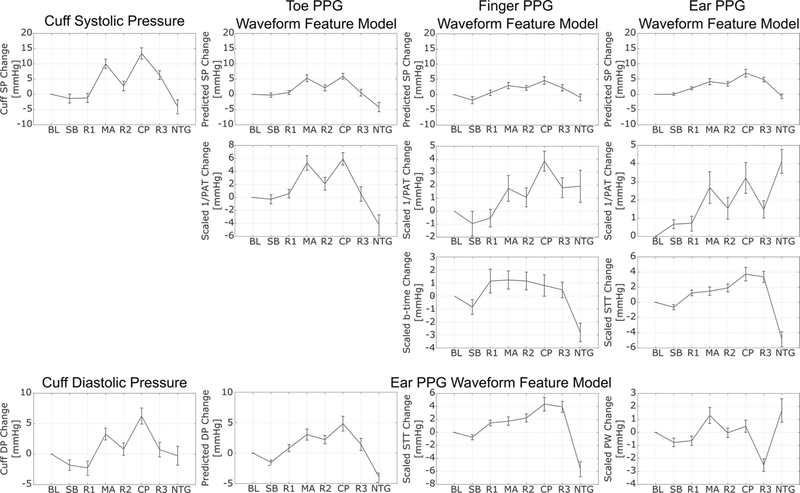
In fact, a PPG fast upstroke time interval was only of added value in predicting changes in SP when combined with PAT. Fig. 6 shows the subject average trends of the reference SP and DP changes and of each feature, scaled by its associated model parameter, in each of the four models over the interventions. The so-calibrated finger and ear 1/PAT trends appear to track the SP trend well except for the nitroglycerin (NTG) intervention, and the calibrated PPG fast upstroke time interval seems to be of most value for this intervention without significantly compromising the other interventions. The steep decline in the PPG fast upstroke time interval after NTG may be due to the reduction in SP as well as smooth muscle relaxation, which could both conceivably increase the viscoelastic lowpass filter cutoff frequency. However, PPG waveform features alone did add value in predicting changes in DP. The calibrated PW (pulse width) appears to help STT in tracking of the DP trend during a few interventions including mental arithmetic (MA) and NTG, which both increased the heart rate. For SP or DP, Fig. 6 along with Fig. 4 indicate that STT, which again stands for “slope transit time”, is not negatively related to BP in general and may thus benefit from a name change.
Fig. 6.
Subject average trends of reference cuff BP changes and predicted BP changes with the models shown in Fig. 5 over the interventions shown in Fig. 2. Each feature in each model is also shown after scaling by its model parameter to yield the component of BP in units of mmHg predicted by that feature. These trends help explain how the PPG fast upstroke time intervals add value to BP measurement accuracy. Values are mean±SE.
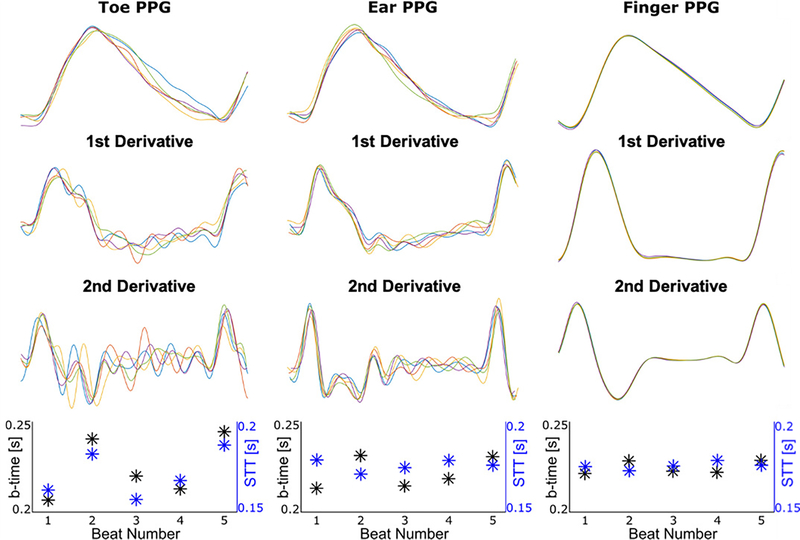
However, the PPG fast upstroke time interval is not always of added value and the precise definition matters. Fig. 7 illustrates typical toe, ear, and finger PPG waveform beats over a segment and their first and second derivatives. The toe PPG waveform tended to be noisier than the other two PPG waveforms, so the fast upstroke time intervals were more variable and thus not selected for the toe PPG waveform feature model. The ear PPG waveform tended to have a wider peak region such that the b-time was more variable than STT, and the latter feature was selected for the ear PPG waveform feature model. Both the b-time and STT were relatively consistent for the finger PPG waveform, but the b-time happened to provide more value. Hence, PPG waveform analysis for tracking BP changes depends importantly on the measurement site. While back-of-the-wrist PPG waveforms are popular due to their convenience in watch form factors [5], these waveforms are notoriously poor in quality. It is thus difficult to imagine that they could have yielded more or as useful features for tracking BP changes in this study.
Fig. 7.
Example of toe, ear, and finger PPG waveform beats from an intervention indicating the typical extent of variability of the fast upstroke time intervals. This example helps explain why measurement site and precise definition of the fast upstroke time interval made a difference.
It is worth reiterating that static person features such as age and gender were also considered but did not appear in the final models (see Fig. 4). While BP depends on age and gender [23], we studied the more realistic prediction of BP changes after a cuff calibration rather than prediction of absolute BP. Hence, demographic information may have been less important here.
In this laboratory investigation, the PPG sensor contact pressure (the external pressure applied by the sensor on the skin) was likely maintained throughout the BP changes. However, in practice, PPG sensor contact pressure can vary with, for example, replacement of a fingertip on a smartphone PPG sensor for on-demand measurement or putting a smartwatch with PPG sensor on the wrist each day for continuous measurement. We previously showed that the maximum change in finger PAT over a physiologic range of finger PPG sensor contact pressures (30–80 mmHg) was 22±2 ms despite no change in BP in 17 healthy subjects [22]. We applied the finger PPG waveform feature model developed in this study (see Fig. 4) to the data collected in our previous study [22] to gain some quantitative understanding of the impact of PPG sensor contact pressure variations on PPG waveform analysis for BP measurement. We found that the maximum change in SP predicted by the finger PPG waveform feature model over the physiologic contact pressure range was 12.0±1.7 mmHg. For comparison, the maximum predicted SP change of the finger PAT reference model built in this study (see Table I) was 7.2±0.7 mmHg. Hence, as expected, PPG waveform analysis is significantly more impacted by PPG sensor contact pressure variations than PAT (67% here). Since the regulatory bias and precision error limits are again 5 and 8 mmHg [20], these additional findings underscore the importance of controlling for PPG sensor contact pressure when applying PPG waveform analysis for BP tracking in practice.
A strength of this study is the use of challenging interventions to change BP in subjects relevant to hypertension applications. At the same time, these interventions, especially NTG, are not simple to employ and limited the number of subjects for study. As a result, we had to confine our analysis tools and could not explore more exhaustive candidate feature sets and nonlinear models. Including more features and nonlinear combinations of features would result in overfitting here and thus false alarms in the selected features. While we also could not investigate calibration-free prediction of BP from PPG waveforms, this approach is far less viable based on first principles. Another limitation of this study is that we did not record the mean component of the PPG waveforms. Normalizing the oscillatory component by the mean component could improve the value of features involving the PPG amplitude (but not PPG time intervals) by mitigating the variability in environmental conditions (which were largely controlled in this study) or skin pigmentation. However, such normalization would likely not have helped improve the PPG peak-to-peak amplitude in tracking the BP changes here (see Fig. 1). A third limitation is that the pre-filtering of the PPG waveforms could have adversely impacted the utility of the derivative-based features studied herein. However, such filtering was necessary, as differentiation amplifies noise, and our filter selection process was good enough to yield a couple of useful features from the first and second derivatives.
V. Conclusion
We have explicitly presented easy-to-understand models to relate PPG waveform features to intervention-induced BP changes in human subjects and have clearly shown that they can afford some added value in BP measurement accuracy over reference models that exclude PPG waveform features as input. Future investigations should test the generalizability of these PPG waveform feature models, especially the PPG fast upstroke intervals therein, as well as create extensive and relevant training datasets to more fully explore the value of PPG waveform analysis in cuff-less BP measurement.
Acknowledgments
This work was supported in part by the National Institute of Biomedical Imaging and Bioengineering, National Institutes of Health, under Grant U01EB018818.
Contributor Information
Keerthana Natarajan, Department of Electrical and Computer Engineering, Michigan State University, East Lansing, MI 48823 USA.
Robert C. Block, Department of Public Health Sciences, School of Medicine and Dentistry, University of Rochester, Rochester, NY 14642, USA
Mohammad Yavarimanesh, Department of Electrical and Computer Engineering, Michigan State University, East Lansing, MI 48823 USA.
Anand Chandrasekhar, Department of Electrical and Computer Engineering, Michigan State University, East Lansing, MI 48823 USA. He is now with the Microsystems Technology Laboratories, Massachusetts Institute of Technology, Cambridge, MA 02142 USA..
Lalit K. Mestha, Palo Alto Research Center East (a Xerox Company), Webster, NY 14580, USA. He is now with the Department of Electrical Engineering, University of Texas, Arlington, TX 78712, USA..
Omer T. Inan, School of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA..
Jin-Oh Hahn, Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA.
Ramakrishna Mukkamala, Department of Electrical and Computer Engineering, Michigan State University, East Lansing, MI 48823, USA..
References
- [1].Mukkamala R, Hahn J-O, Inan OT, Mestha LK, Kim C-S, Toreyin H, and Kyal S, “Toward ubiquitous blood pressure monitoring via pulse transit time: Theory and practice,” IEEE Transactions on Biomedical Engineering, vol. 62, pp. 1879–1901, 6 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Flugge W, “Viscoelastic models,” in¨ Viscoelasticity, pp. 4–33, Springer Berlin Heidelberg, 1975. [Google Scholar]
- [3].Block RC, Yavarimanesh M, Natarajan K, Carek AM, Mousavi A, Chandrasekhar A, Kim C-S, Zhu J, Schifitto G, Mestha LK, Inan OT, Hahn J-O, and Mukkamala R, “Conventional pulse transit times as markers of blood pressure changes in humans,” Scientific Reports, vol. 10, pp. 1–9, 10 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Xing X, Ma Z, Zhang M, Zhou Y, Dong W, and Song M, “An unobtrusive and calibration-free blood pressure estimation method using photoplethysmography and biometrics,” Scientific Reports, vol. 9, pp. 1–8, 6 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Nachman D, Gepner Y, Goldstein N, Kabakov E, Ishay AB, Littman R, Azmon Y, Jaffe E, and Eisenkraft A, “Comparing blood pressure measurements between a photoplethysmography-based and a standard cuff-based manometry device,” Scientific Reports, vol. 10, pp. 1–9, 9 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Ruiz-Rodríguez JC, Ruiz-Sanmartín A, Ribas V, Caballero J, García-Roche A, Riera J, Nuvials X, de Nadal M, de Sola-Morales O, and Serra J, “Innovative continuous non-invasive cuffless blood pressure monitoring based on photoplethysmography technology,” Intensive Care Medicine, vol. 39, pp. 1618–1625, 6 2013. [DOI] [PubMed] [Google Scholar]
- [7].Radha M, Groot KD, Rajani N, Wong CCP, Kobold N, Vos V, Fonseca P, Mastellos N, Wark PA, and Velthoven N, “Estimating blood pressure trends and the nocturnal dip from photoplethysmography,” Physiological Measurement, vol. 40, 2 2019. [DOI] [PubMed] [Google Scholar]
- [8].Xing X, Ma Z, Zhang M, Gao X, Li Y, Song M, and Dong W-F, “Robust blood pressure estimation from finger photoplethysmography using age-dependent linear models,” Physiological Measurement, vol. 41, 3 2020. [DOI] [PubMed] [Google Scholar]
- [9].Kachuee M, Kiani MM, Mohammadzade H, and Shabany M, “Cuffless blood pressure estimation algorithms for continuous health-care monitoring,” IEEE Transactions on Biomedical Engineering, vol. 64, pp. 859–869, 6 2016. [DOI] [PubMed] [Google Scholar]
- [10].Watanabe N, Bando YK, Kawachi T, Yamakita H, Futatsuyama K, Honda Y, Yasui H, Nishimura K, Kamihara T, Okumura T, Ishii H, Kondo T, and Murohara T, “Development and validation of a novel cuff-less blood pressure monitoring device,” JACC: Basic to Translational Science, vol. 2, pp. 631–642, 12 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Abrams J, “Hemodynamic effects of nitroglycerin and long-acting nitrates,” American Heart Journal, vol. 110, pp. 217–224, 7 1985. [PubMed] [Google Scholar]
- [12].Joseph CN, Porta C, Casucci G, Casiraghi N, Maffeis M, Rossi M, and Bernardi L, “Slow breathing improves arterial baroreflex sensitivity and decreases blood pressure in essential hypertension,” Hypertension, vol. 46, pp. 714–718, 8 2005. [DOI] [PubMed] [Google Scholar]
- [13].Al’Absi M, Bongard S, Buchanan T, Pincomb GA, Licinio J, and Lovallo WR, “Cardiovascular and neuroendocrine adjustment to public speaking and mental arithmetic stressors,” Psychophysiology, vol. 34, pp. 266–275, 7 1996. [DOI] [PubMed] [Google Scholar]
- [14].Jr EAH and Brown GE, “The cold pressor test for measuring the reactibility of the blood pressure: Data concerning 571 normal and hypertensive subjects,” American Heart Journal, vol. 11, pp. 1–9, 1 1936. [Google Scholar]
- [15].Elgendi M, “On the analysis of fingertip photoplethysmogram signals,” Current Cardiology Reviews, vol. 8, pp. 14–25, 2 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Addison PS, “Slope transit time (stt): A pulse transit time proxy requiring only a single signal fiducial point,” IEEE Transactions on Biomedical Engineering, vol. 63, pp. 2441–2444, 2 2016. [DOI] [PubMed] [Google Scholar]
- [17].Bland JM and Altman DG, “Agreement between methods of measurement with multiple observations per individual,” Journal of Biopharmaceutical Statistics, vol. 17, pp. 571–582, 7 2007. [DOI] [PubMed] [Google Scholar]
- [18].Efron B and Tibshirani R, “The bootstrap estimate of standard error,” in An introduction to the bootstrap, pp. 45–59, Chapman & Hall, 1993. [Google Scholar]
- [19].Holm S, “A simple sequentially rejective multiple test procedure,” Scandinavian Journal of Statistics, vol. 6, pp. 65–70, 12 1977. [Google Scholar]
- [20].“ISO 81060–2:2018: Non-invasive sphygmomanometers part 2: Clinical investigation of intermittent automated measurement type,” 2018.
- [21].Fujita D and Suzuki A, “Evaluation of the possible use of ppg waveform features measured at low sampling rate,” IEEE Access, vol. 7, pp. 58361–58367, 5 2019. [Google Scholar]
- [22].Chandrasekhar A, Yavarimanesh M, Natarajan K, Hahn J-O, and Mukkamala R, “Ppg sensor contact pressure should be taken into account for cuff-less blood pressure measurement,” IEEE Transactions on Biomedical Engineering, vol. 67, pp. 3134–3140, 11 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Mukkamala R and Hahn J-O, “Toward ubiquitous blood pressure monitoring via pulse transit time: Predictions on maximum calibration period and acceptable error limits,” IEEE Transactions on Biomedical Engineering, vol. 65, pp. 1410–1420, 6 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]