Utilizing a Language Model to Improve Online Dynamic Data Collection in P300 Spellers

Abstract

P300 spellers provide a means of communication for individuals with severe physical limitations, especially those with locked-in syndrome, such as amyotrophic lateral sclerosis (ALS). However, P300 speller use is still limited by relatively low communication rates due to the multiple data measurements that are required to improve the signal-to-noise ratio of event-related potentials for increased accuracy. Therefore, the amount of data collection has competing effects on accuracy and spelling speed. Adaptively varying the amount of data collection prior to character selection has been shown to improve spelling accuracy and speed. The goal of this study was to optimize a previously developed dynamic stopping algorithm that uses a Bayesian approach to control data collection by incorporating a priori knowledge via a language model. Participants (n = 17) completed online spelling tasks using the dynamic stopping algorithm, with and without a language model. The addition of the language model resulted in improved participant performance from a mean theoretical bit rate of 46.12 bits/min at 88.89% accuracy to 54.42 bits/min (p < 0.0065) at 90.36% accuracy.

I. Introduction

THE primary motivation for brain-computer interfaces (BCI) is to provide communication and/or control abilities to patients whose severe physical limitations may limit or preclude their use of most commercially available assistive devices, such as patients with locked-in syndrome e.g. due to amyotrophic lateral sclerosis [1]. BCIs enable the neurological pathways of the user to be bypassed when transmitting different types of electrophysiological signals to interpret the user’s intent and execute commands; although some studies have shown that some voluntary control, like eye gaze, enhances user performance [2], [3]. ERP-based BCI spellers translate in real time time-locked event-related potentials (ERP) that occur in electroencephalography (EEG) data into commands for a spelling or word processing program. P300-based BCIs rely predominantly on eliciting a P300 signal after the presentation of rare stimuli within the context of an oddball paradigm [4], [5], as well as other ERPs that can enhance performance [6], [7]. The P300 speller operates by processing the user’s EEG data after character subsets of a speller grid are flashed on a screen; the illumination of a target character (i.e. the character that the user intends to spell) elicits a P300 [8]. Classification techniques are used to distinguish between target and non-target EEG responses, [9], [10], to determine the character that the user intends to spell and the character with the largest combined classifier response after data collection is selected as the user’s intended choice. In recent studies, P300 spellers have been shown to be a viable communication tool in patients with ALS [11]-[14].

The P300 speller’s use is primarily limited by relatively low communication rates due to the long character selection time as character selection is made after averaging over multiple EEG measurements to increase signal-to-noise ratio and improve accuracy [15]. Most conventional ERP-based BCI spellers average data over a fixed number of trials for all users, with the number of trials set prior to online operation. However, the amount of data collection prior to character selection has competing effects on accuracy and spelling speed: decreasing it improves spelling speed while increasing it improves accuracy. Some approaches have optimized the amount of data collected prior to character selection for each user [13]. Alternatively, adaptively determining the optimal amount of data collection prior to each character selection can improve accuracy and communication speed [16], [17]. Most approaches vary the number of sequences from one character to the next based on a threshold [18]-[22]. Although these approaches showed promising results, some either relied on the past performance of participants or used parameters obtained by averaging training data across a participant pool. Since P300 signals exhibit cyclical and inter-subject variability [23] and are also affected by attention drift, fatigue or mood [24], [25], methods that rely solely on the quality of the data currently being collected are hypothesized to provide the best performance.

Throckmorton et al. demonstrated a statistically significant improvement in accuracy and communication rate using a Bayesian approach to dynamically control data collection when compared to static data collection [26]. In their algorithm, a probability distribution was maintained over characters and each classified response score was integrated into the model via a Bayesian update. Once the probability of a character being the target character attained a preset threshold value, the algorithm stopped data collection and selected the most probable character as the target character. The dynamic stopping algorithm had the advantage of being efficient in using subject-independent parameters for flash-to-flash evaluations of the user’s EEG data to adaptively vary the amount of data collection based on the quality of the data. While the algorithm provided statistically significant improvements, it was hypothesized that performance might be further improved if prior knowledge of the probability of each character was incorporated into the algorithm using a language model.

Statistical language models have been proposed to enhance P300 spellers as language is governed by a set of structural rules, such as phonetics, syntax, semantics or word order, that dictate the composition of clauses, phrases and words [27]. Language models are used in many applications such as speech recognition, machine translation, spelling correction, text retrieval or text entry. For example, predictive spelling maximizes user output by potentially reducing the number of keystrokes by predicting the completion of a word a user intends to type based on spelling history.

Utilizing a priori knowledge of the user’s language is thus beneficial as language models have shown promising results in improving the online performance of P300 spellers [28], [29]. Ryan et al. developed a P300 speller used in conjunction with a predictive spelling program where numbered word options were displayed beside the P300 speller grid and updated based on the user spelling history [28]. The user could select one of those options if desired by focusing on its corresponding number in the P300 speller grid. Although a significant decrease in task completion time was observed with predictive spelling compared to non-predictive spelling, the accuracy using predictive spelling was negatively affected. This decrease in accuracy was hypothesized to be due to the increased task difficulty and cognitive load in selecting the numbered predictive word options that adversely affected P300 amplitudes. Kaufmann et al. integrated the predicted word options directly into the speller grid as a new column [29]. A significant decrease in task completion time was observed when using their predictive word completion option compared to conventional character-by-character selection. However, they did not observe a decrease in accuracy as task difficulty and workload was minimized because the predictive text was selected in a comparable manner to single character selection.

Speier et al. performed offline simulations comparing P300 speller performance using static, dynamic and natural language processing (NLP) methods to control data collection [30]. The dynamic method was similar to the Throckmorton et al. approach of initializing character probabilities with uniform prior and updating these probabilities via Bayesian inference until a threshold was reached. The NLP incorporated a language model to initialize letter probabilities. However, doing an offline analysis enabled them to optimize parameters for each subject post-hoc, an approach that is not possible in an online study. In addition, their trigram model did not account for possible non-alphabet character choices in a P300 speller grid, e.g. numeric characters, keyboard commands, punctuation marks etc., such as those shown in Fig. 1.

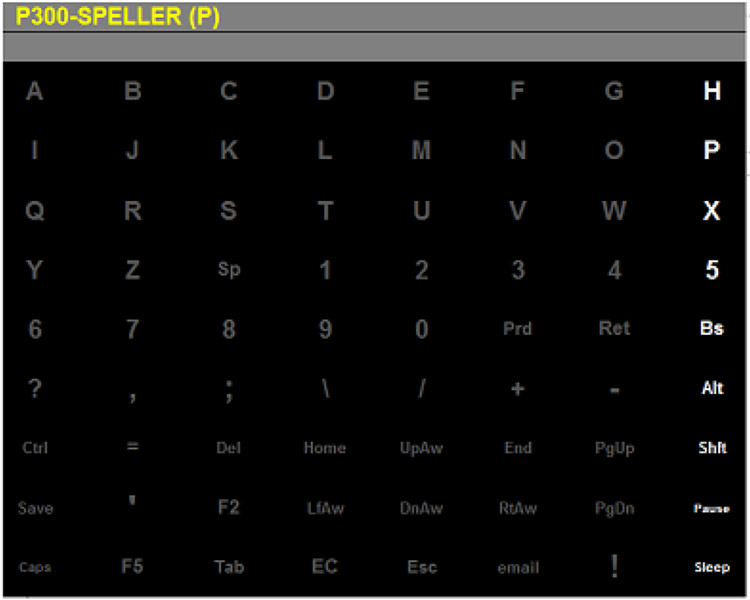
Fig. 1.

Screen display used for the P300 speller in this study. The word to be spelled is displayed in the top left, with the current target character in parentheses. Rows and columns are flashed in random order prior to character selection. If feedback is desired, the selected choice is displayed below the intended target after character selection has been made.

Given the potential benefit of language models that have been implemented in the literature, we propose optimizing the Throckmorton et al. dynamic stopping criterion by integrating a language model to improve online P300 speller performance. The Throckmorton et al. algorithm has the advantage that the initialization procedure for character probabilities provides a mechanism for inclusion of language-based knowledge without affecting the general function of the interface, thus avoiding potential issues associated with increased cognitive load. The language model used in this study sets the initial character probabilities based on whether the previous character selection was alphabetic or non-alphabetic. The added predictability was hypothesized to reduce the number of flashes prior to character selection thereby potentially improving spelling speed. In this study, we compare the online performances of participants using the dynamic stopping criterion with and without the language model.

II. Methods

A. Participants

Seventeen healthy participants were recruited from the student and work population at Duke University (10 males and 7 females), and gave informed consent prior to participating in this study. The Duke University Institutional Board Review approved the study. Participants were numbered in the order they were recruited.

B. Equipment

The open source BCI2000 software package was used for stimulus presentation and data collection [31], with additional functionality added to implement dynamic stopping and dynamic stopping with language model algorithms [26]. EEG responses were measured using 32-channel electrode caps (Electro-Cap International, Inc.) connected to a computer via two 16-channel biosignal amplifiers (Guger Tec g.USBamp).

C. Signal Acquisition

Data collected from electrodes Fz, Cz, P3, Pz, P4, PO7, Po8, and oz, which have been shown to optimize performance in P300 spellers, were used for classification [9], [32]. (While only a subset of electrodes was used for signal processing and classification, data from 32 channels were recorded to have a more comprehensive potential map of the whole scalp to use for offline algorithm development). The left and right mastoids were used for ground and reference electrodes, respectively. The EEG signals were digitized at 256 samples/s and filtered between 0.5Hz - 30Hz. From the third participant, a considerable degree of 60Hz noise started to be visually observed in some participant waveforms where we recorded high electrode impedance values; high impedance values are a common cause of residual mains interference [33]. While we typically record with impedance values ≤10 kΩ, sometimes those values could not be achieved. Subsequently, a notch filter was used to minimize the electrical noise in those participants.

D. P300 Speller Paradigm

The row-column paradigm in BCI2000 was used to flash character subsets on a screen [8]. Participants were presented with a 9×8 grid of characters on a computer screen, (see Fig. 1). A sequence consists of flashing all rows and columns i.e. 1 sequence = 9 rows + 8 column flashes = 17 flashes. Word or number tokens to be spelled were shown on the top left of the matrix, with the intended characters to spell displayed in parentheses at the end of the word. The task consisted of locating the specified character in parentheses in the grid matrix, focusing on this character and mentally counting the number of times it was flashed on the screen. The flash duration was 62.5 ms and was followed by an interstimulus interval of 62.5 ms prior to the next flash. After a target character was selected, an interval of 3.5 seconds occurred prior to selection of the next character.

Participants completed the study in a single session, which consisted of six training and six online test runs for both dynamic stopping algorithms. Each run consisted of six-character tokens: 5 word tokens and 1 number token. The tokens were randomly selected, with the word tokens drawn at random from a subset of the available words in the English Lexicon project [34]. The word set consisted of 400 six-character words with the highest frequency of occurrence in written communication as measured by the Hyperspace Analogue to Language (HAL) corpus frequency [35].

E. Classification

The training runs consisted of the participants copy spelling the tokens with no feedback provided. Data collected for each character was obtained from flashing 10 sequences per character, corresponding to a total of 6120 row/column flashes. Feature extraction and P300 classifier training were done using MATLAB software (MathWorks Inc.). Features extracted from the EEG data from the training session were used to train a Stepwise Linear Discriminant Analysis (SWLDA) classifier [36] to obtain feature weights that were used in the dynamic stopping and dynamic stopping with language model algorithms. Using the SWLDA classifier calculated from the training run data, participants were tested using both dynamic stopping algorithms by performing copy-spelling tasks with feedback and no error correction. The tasks were counterbalanced across participants to avoid biasing the results by algorithm order. The odd-numbered participants tested in the order dynamic stopping followed by dynamic stopping with the language model, while the even-numbered participants tested in the reverse order.

Features extracted from the training EEG data were used to train a single classifier that was used in all six testing runs (see Krusienski et al. (2008) for details [32]). Following each flash, 800 ms of data was extracted from the raw EEG signal from each of the 8 channels and decimated to a rate of approximately 20 averaged time samples/s by averaging 13 time samples to generate one feature point (as a result, the last 10 time samples were discarded). The features were concatenated across the channels of interest to generate a 1×120 observation feature vector, f, (120 features/flash = 15 features/channel*flash × 8 channels), with a corresponding truth label assigned based on whether the target character was or was not present in the flash. With 6120 flashes generated during training, there were 720 target and 5400 non-target responses per participant. A training set for each participant consisted of a 6120×120 matrix of observation features vectors and a 6120×1 vector of corresponding truth labels. The features and corresponding truth labels were used to generate features weights for a classifier using SWLDA. SWLDA weights each feature by its ability to discriminate between non-target and target responses.

F. Dynamic Stopping Criterion (DS)

The dynamic stopping algorithm consists of an offline and online portion and is described in Throckmorton et al. [26]. In the offline phase, EEG data obtained during the training phase were grouped into target and non-target responses. The weight vector, w (1 × 120), obtained from training the SWLDA classifier were used to calculate classifier response scores, x, from feature vectors obtained from the training data, where x = wf^⊤. Kernel density estimation was used to smooth the histograms of the grouped scores to generate likelihood probability density functions (pdfs) of the non-target and target responses, p(x∣H₀) and p(x∣H₁), respectively.

In the online testing phase of the dynamic stopping algorithm without a language model, character probabilities were initialized from a uniform distribution i.e. $\frac{1}{N}$, where N is the number of choices in the grid. With each new flash of a subset of characters, S_i, the classifier response score, x_i, was calculated and used to estimate the character non-target and target likelihoods from the likelihood pdfs. The character posterior probabilities were updated with these likelihood values using Bayesian inference:

$$P(C_n\mid x_i,{\mathit{X}}_{i-1},S_i)=\frac{P(C_n\mid {\mathit{X}}_{i-1})\times p(x_i\mid C_n,S_i)}{{\sum }_{n=1}^{N}P(C_n\mid {\mathit{X}}_{i-1})\times p(x_i\mid C_n,S_i)}$$ (1)

where P(C_n∣x_i, X_i−1, S_i) is the posterior probability of character C_n being the target, given the current classifier score, x_i, all the previously observed classifier responses, X_i−1 = [x₁, … , x_i−1], and the current subset of flashed characters, S_i; P(C_n∣X_i−1) is the prior probability of character C_n being the target, given all the previously observed classifier responses, X_i−1; p(x_i∣C_n, S_i) is the likelihood of the current classifier response, x_i, given that the character was or was not present in the current subset of flashed characters, S_i; and the denominator normalizes the probabilities over all the character probabilities. The likelihood, p(x_i∣C_n, S_i), was set according to:

$$p(x_i\mid C_n,S_i)=\{\begin{array}{cc}p(x_i\mid H_0),\hfill & C_n\notin S_i\hfill \\ p(x_i\mid H_1),\hfill & C_n\in S_i\hfill \end{array}\phantom{\}}$$ (2)

If a character probability exceeded the threshold probability of 0.9, it was selected as the target character. A maximum limit of 10 sequences was imposed and if the threshold probability was not reached, the character with the maximum probability was selected as the target. For the next character, the character probabilities were re-initialized to $\frac{1}{N}$ and the above process to update the probabilities was repeated.

G. Dynamic Stopping Criterion with Language Model (DSLM)

In DSLM, the initialization probability of a character depended on the previously spelled character, implemented via a letter bigram model. An n-gram language model assigns a probability to a sequence of tokens, ${\mathit{c}}_1^k=c_1,c_2,\dots ,c_k$, (c_i can denote letters in a word or words in a sentence; i denotes the position of the token in the sequence), using the chain rule of probability:

$$P({\mathit{c}}_1^k)=\prod _{i=1}^{k}P(c_i\mid {\mathit{c}}_1^{i-1})\approx \prod _{i=1}^{k}P\left(c_i\mid {\mathit{c}}_{i-(n-1)}^{i-1}\right)$$ (3)

where $P({\mathit{c}}_1^k)$ denotes the probability of a sequence of tokens; ${\prod }_{i=1}^{k}P(c_i\mid {\mathit{c}}_1^{i-1})$ denotes the chain rule probability decomposition; $P\left(c_i\mid {\mathit{c}}_{i-(n-1)}^{i-1}\right)$ denotes the model approximation that reflects the Markov assumption that only the most recent n − 1 tokens are relevant in determining the conditional probability of the next token [27]. With the letter bigram model, i.e. n = 2, the conditional probability of the letter c_i given letter c_i−1 can be estimated by maximum likelihood estimation using a relative frequency count:

$$P(c_i\mid c_{i-1})=\frac{f(c_{i-1},c_i)}{f(c_{i-1})}$$ (4)

where f(c_i−1, c_i) and f(c_i−1) are counts of the number of times that c_i−1 was followed by c_i, and that c_i−1 appears in a given body of text, respectively.

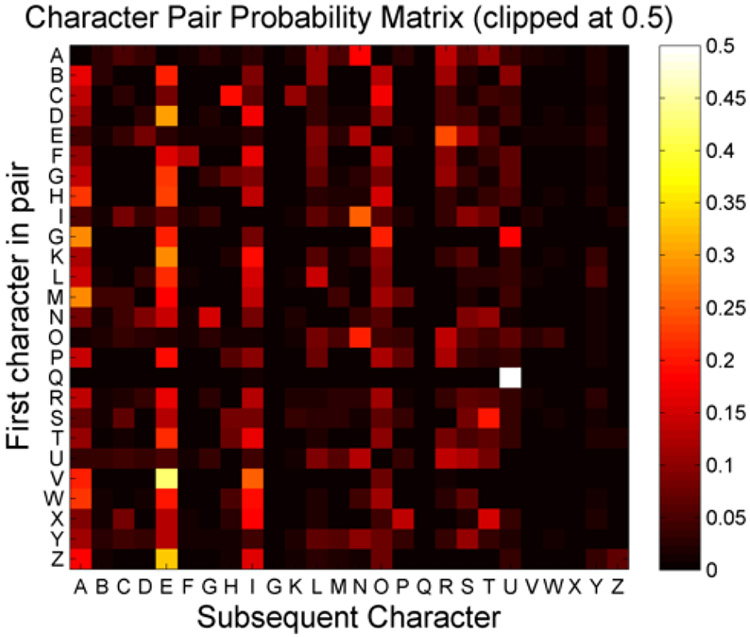
A character pair probability matrix, Fig. 2, was generated from the Carnegie Mellon University online dictionary [37]. The element in the i^th row and j^th column of the matrix denotes the conditional probability, $P({\mathcal{A}}_j\mid {\mathcal{A}}_i)$, that the next spelled letter is j^th letter of the alphabet, ${\mathcal{A}}_j$, given the most recently spelled letter is i^th letter, ${\mathcal{A}}_i$. For example, if the preceding letter is a Q, the likelihood of the subsequent character being a U is very high, hence the character pair probability is much higher for P(U∣Q) compared to P(T∣Q) or P(A∣Q). For the first character of a word, the character initialization probabilities were assigned from a uniform distribution. For subsequent character selection, the initialization probabilities were based on whether the previous character was alphabetic or non-alphabetic, with the uniform distribution used if it was non-alphabetic. If the previous character was alphabetic, the initialization probabilities of non-alphabet characters (NAC, e.g. !, Space, 4, see Fig. 1) were assigned a probability of $\frac{1}{N}$, where N is the total number of character choices in the speller grid. For alphabet characters, the initialization probabilities were originally calculated according to:

$$P(C_n\mid {\mathit{X}}_0)=P(C_n\mid {\mathcal{A}}_{t-1})\left(1-\sum _{NAC}\frac{1}{N}\right)$$ (5)

where P(C_n∣X₀) denotes the initialization estimate of the character’s probability of being the target; $P(C_n\mid {\mathcal{A}}_{t-1})$ denotes the conditional probability that the next letter is C_n, given the previously spelled letter is ${\mathcal{A}}_{t-1}$; and $\left(1-{\sum }_{NAC}\frac{1}{N}\right)$ is the sum of the non-alphabet probabilities, which is subtracted from 1 to normalize the probabilities.

Fig. 2.

Character Pair Probability matrix generated from Carnegie Mellon University online dictionary. The element in the i^th row and j^th column in the matrix denotes the probability, $P({\mathcal{A}}_j\mid {\mathcal{A}}_i)$, that the next spelled letter is the j^th letter in the alphabet, given the most recently spelled letter is i^th letter. Probability values were clipped at 0.5 to enhance visualization.

However, there is the possibility of a misspelled character due to the initialization probabilities. For example, misspelling a Q would result in most of the initial character probabilities to be set to zero for the subsequent character. If the correct character’s initial probability is set to zero, it is unlikely that it would be successfully selected. In order to mitigate this potential issue, the initialization probability of the alphabet characters is set to a weighted sum of the bigram model probability and a uniform distribution according to:

$$P(C_n\mid {\mathit{X}}_0)=\alpha P(C_n\mid {\mathcal{A}}_{t-1})\left(1-\sum _{NAC}\frac{1}{N}\right)+(1-\alpha )\frac{1}{N}$$ (6)

where α denotes the weight of the bigram model probability and 1 − α denotes the weight of the uniform distribution. Offline simulations were conducted to assess the potential advantage/disadvantage of different weights for the bigram model. Target and non-target likelihoods were generated from the data collected in [26] and random draws from these distributions were used to simulate subject responses to flashes. The weight of the bigram model was systematically varied between 0 and 1 in steps of 0.1, where 0 would indicate no bigram model and 1 would indicate only the bigram model was used. Based on the simulations, a bigram weight of 0.9 was shown to have no negative influence on accuracy or spelling speed and was selected for this study.

The character probabilities are updated via the Bayesian technique according to (1) and (2) until character selection when the threshold probability was reached. Once a character was selected, the character probabilities are re-initialized using (6) and the above process to update the probabilities was repeated.

H. Performance Measures

For each participant, the words spelled by the P300 speller and the number of flashes used to spell each character were recorded. The performance metrics used to compare both algorithms include accuracy, task completion time and bit rate. Accuracy is the percent of characters (out of 36) correctly spelled by the user. The task completion time (TCT) is the time the participant used in the spelling task in the testing run, including the time pauses between character selections. The maximum possible completion time, including pauses between character selection times, was 14 minutes, 47.5 seconds due to a sequence limit of 10.

Bit rate is a communication measure that takes into account the accuracy, number of possible target choices and task completion time [38], and was calculated according to:

$$B={\log }_{2}N+P{\log }_{2}P+(1-P){\log }_2\left(\frac{1-P}{N-1}\right)$$ (7)

$$BitRate=B\left(\frac{36}{TCT}\right)$$ (8)

where B is the number of transmitted bits/ character selection, N is the number of possible character selections in the speller grid; P is the participant accuracy and $\frac{36}{TCT}$ represents the average number of selections transmitted per minute, based on the participant task completion time.

Theoretical bit rate differs from bit rate by excluding the time pauses (3.5 seconds) between character selections, so it represents the upper bound of the user’s possible communication rate. Time pauses between character selections vary across research studies as the values are often adjusted for user comfort. Theoretical bit rate may provide a more consistent measure of performance.

Statistical significance was tested using the Wilcoxon signed-ranked test, since it could not be guaranteed that the participant population was normally distributed.

III. Results

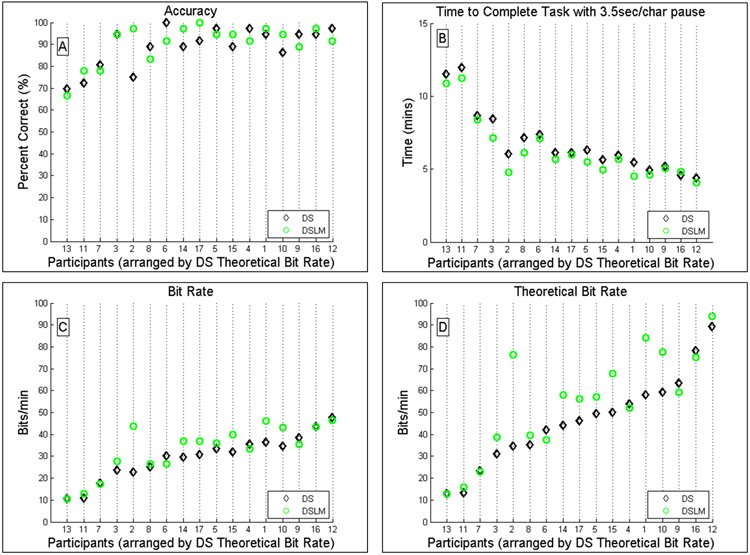
The addition of the language model to the dynamic stopping criterion was hypothesized to improve P300 speller performance. Fig. 3(A-D) compares the accuracy, task completion time, bit rate and theoretical bit rate, respectively, achieved using the dynamic stopping algorithm with and without the language model. The average performance results are summarized in Table 1 and participant-specific results are shown in Table II.

Fig. 3.

Comparison of performance measures between DS and DSLM in terms of (A) Accuracy, (B) Task Completion Time, (C) Bit Rate and (D) Theoretical Bit Rate. The accuracy is the percentage of the 36 characters that the participant correctly spelled. The maximum possible completion time, including pauses between character selection times, was 14 minutes, 47.5 seconds due to a sequence limit of 10. Bit rate is a communication rate that takes into account accuracy, task completion time and the number of possible character choices. Theoretical bit rate excludes the 3.5-second pauses between character selections.

TABLE I.

Results Summary Comparing DS and DSLM

PERFORMANCE MEASURE	DS	DSLM	p-value
Time to complete task (mins)	6.8 ± 2.21	6.27 ± 2.11	< 0.02426
Accuracy (%)	88.89 ± 9.32	90.36 ± 9.32	< 0.00025
Bit Rate (bits/min)	29.55 ± 10.23	33.15 ± 11.29	< 0.0221
Theoretical Bit Rate (bits/min)	46.12 ± 20.63	54.42 ± 23.78	< 0.0065

TABLE II.

Participant performance comparing Dynamic Stopping (DS) and Dynamic Stopping with Language Model (DSLM)

	DS					DSLM
Participant	ACC (%)	TCT (mins)	BR (bits/min)	TBR (bits/min)	PBR (bits/min)	ACC (%)	TCT (mins)	BR (bits/min)	TBR (bits/min)	PBR (bits/min)
1	94.44	5.46	36.37	58.08	36.14	97.22	4.53	46.23	84.17	46.32
2	75.00	6.03	22.82	34.52	18.43	97.22	4.79	43.75	76.31	43.84
3	94.44	8.44	23.54	31.05	23.39	94.44	7.15	27.77	38.86	27.60
4	97.22	5.92	35.35	53.95	35.42	91.67	5.66	33.34	52.13	32.69
5	97.22	6.28	33.33	49.39	33.40	94.44	5.52	36.00	57.14	35.78
6	100.00	7.35	30.23	41.86	30.23	91.67	7.08	26.65	37.44	26.13
7	80.56	8.64	17.76	23.26	15.71	77.78	8.37	17.37	22.97	14.74
8	88.89	7.13	25.17	35.28	24.24	83.33	6.12	26.45	39.69	24.20
9	94.44	5.17	38.41	63.45	38.17	88.89	5.07	35.36	59.18	34.05
10	86.11	4.91	34.68	59.33	32.64	94.44	4.60	43.15	77.53	42.88
11	72.22	11.97	10.85	13.09	8.25	77.78	11.22	12.96	15.84	11.00
12	97.22	4.39	47.72	89.25	47.81	91.67	4.05	46.56	93.80	45.66
13	69.44	11.52	10.63	12.92	7.50	66.67	10.88	10.59	13.04	6.81
14	88.89	6.10	29.40	44.18	28.31	97.22	5.66	37.02	57.93	37.09
15	88.89	5.62	31.92	50.12	30.74	94.44	4.97	39.97	67.83	39.72
16	94.44	4.58	43.35	78.17	43.08	97.22	4.83	43.36	75.11	43.44
17	91.67	6.13	30.82	46.23	30.22	100.00	6.00	37.05	56.17	37.05

ACC refers to percent accuracy. TCT refers to task completion time. BR, TBR and PBR refer to bit rate, theoretical bit rate and practical bit rate, respectively.

In Fig. 3, participants are sorted based on their Ds theoretical bit rate. Odd-numbered participants were tested with Ds first, then DsLM while even-numbered participants were tested first with DsLM, then with Ds. No order effects were observed for the four performance metrics plotted. From Fig. 3(A), participant accuracy was similar across both conditions. In general, the proportion of correct characters spelled per number of flashes was similar under both conditions. No significant difference was observed between the accuracies of DS (mean = 88.89%, SD = 9.32%) and DSLM (mean = 90.36%, SD = 8.95%), p < 0.2426. However, all but one participant completed the spelling task in less time, as shown in Fig. 3(B) under DSLM (mean = 6.27 minutes, SD = 2.11 minutes), compared to DS (mean = 6.80 minutes, SD = 2.21 minutes), p < 0.00025.

The consistent reduction in task completion time resulted in a significant increase in communication rates, Fig. 3(C-D). A significant increase in both bit rate and theoretical bit rate was observed under DSLM (mean = 33.15 bits/min, SD = 11.29 bits/min; mean = 54.42 bits/min, SD = 23.78 bits/min, respectively), respectively, compared to DS (mean = 29.55 bits/min, SD = 10.23 bits/min, p < 0.0221; mean = 46.12 bits/min, SD = 20.63 bits/min, p < 0.0065). As calculated, the bit rate and theoretical bit rate may overestimate the actual user’s communication rate, as spelling errors were not corrected by the user. The spelling task was designed with no error correction to test the robustness of including the error factor in the language model. However, practical bit rate, a communication rate that includes correcting for errors and the time pause between character selection, can also be considered and was calculated according to [13]. The average practical bit rate is significantly higher for DSLM (mean = 32.29 bits/min, SD = 12.24 bits/min), compared to DS (mean = 28.45 bits/min, SD = 11.17 bits/min, p < 0.0379) for this data collection.

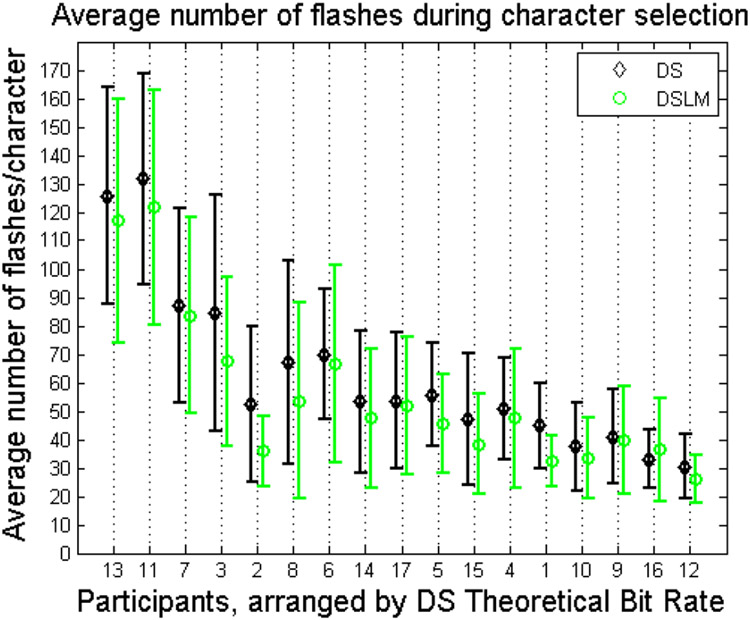
The data was further analyzed to determine the difference in the number of flashes between DS and DSLM. Fig. 4 shows a plot of the average number of flashes used to spell a character under both algorithms, with the error bars representing the standard deviation. The number of flashes used to spell each character varied across characters for each participant, with the mean number of flashes/character decreasing with increased communication rate. However, it can be observed that the average number of flashes decreased when using DSLM (mean = 55.53 flashes, SD = 28.11 flashes) compared to DS (mean = 62.70 flashes, SD = 29.47 flashes, p < 0.00025), resulting in the observed significant reduction in task completion time.

Fig. 4.

Average number of flashes to spell a character using DS and DSLM algorithms for each participant. The error bars represent the standard deviation. The maximum number of flashes possible to spell each character was 170 flashes due to a sequence limit of 10.

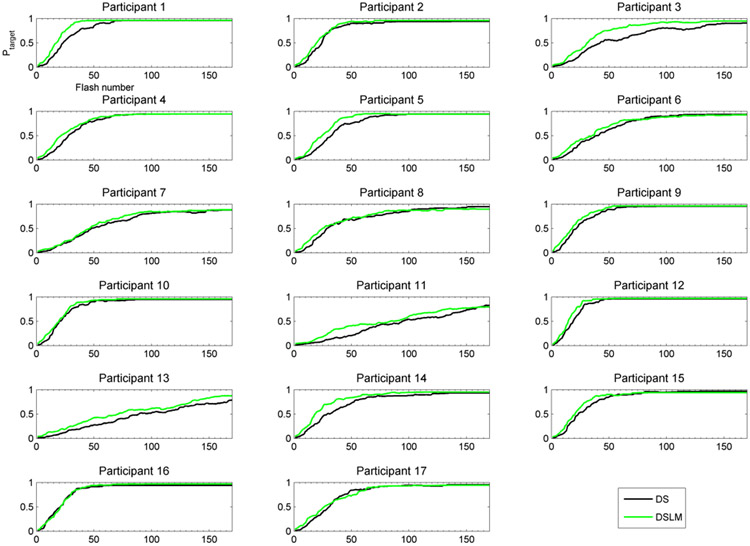
The impact of using a language model in the Bayesian update process to set the character initializations was further analyzed. In offline simulations, each participant’s SWLDA classifier, target and non-target pdfs developed in the training phase, and respective algorithm EEG data collected in the testing phase were used to determine the flash-to-flash progression of the selected target probabilities for each character selection under DS and DSLM. The results were averaged across the characters, excluding the first character in each word since the character initialization probability was uniform in both algorithms. In order to keep the number of averaged points constant across the number of flashes, flash-to-flash progressions that ended with less than 170 flashes due to dynamic stopping were padded with the final probability. In Fig. 5, the progression of the average target probability with respect to the flash number is shown for each participant. The offset between DS and DSLM is not constant as might be expected if the impact of adding the language model was to merely increase the initial target probability. Instead, the rate at which the target probability reaches threshold increases in some cases (e.g. participant 1). These results suggest that the impact of the language model is to not only start the target at a higher initial probability, but also enable the updating process to discard non-targets more quickly.

Fig. 5.

Offline calculations of the average selected target probability flash-to-flash progression during character selection under DS and DSLM (excluding the first character of each token).

IV. Discussion

The primary goal of this study was to determine if the Throckmorton et al. dynamic stopping algorithm could be improved by incorporating a priori knowledge via a language model. A significant improvement in accuracy was not expected, as the threshold limit for both algorithms was the same, 0.9, resulting in the average accuracy of about 90% observed across both algorithms. The added predictability of the language model reduced the number of flashes required to reach the decision threshold, hence a significant reduction in task completion time was observed in all but one participant. By reducing the task completion time while maintaining similar accuracy on average, a significant increase in communication rates was achieved.

While an improvement in communication rates was observed, mostly mid-performing participants derived an appreciable benefit in the bit rate or theoretical bit rate from the inclusion of the language model. The high performing participants are already performing close to the upper limit of communication rate and so it is difficult to improve on their already high performance. The lower performing participants used a much higher number of flashes and though they observed a reduction in their task completion time, it was not enough to observe a noticeable improvement in communication rate. Nonetheless, the high number of flashes leaves room for reducing the task completion time to improve their communication rates.

Similar to Throckmorton et al., the list of words were randomly chosen from the English Lexicon project, which are words that are typically used in communication, so the words should not result in a heavy cognitive load to the P300 speller user due to rare usage. However, an additional consideration when using the language model is the possibility that character pair combinations with low initialization probabilities might adversely impact the algorithm performance, e.g. the pair ‘in’ in single has a relatively high probability compared to ‘af’ in afraid. Since each participant was tested with a randomly selected set of words, it might be hypothesized that the performance of some participants would be adversely affected by the words selected for them.

In order to determine the impact of randomly selecting words per participant, offline analyses were performed prior to this study and the potential bias in two performance metrics, accuracy or task completion time, was assessed. Using the Throckmorton et al. data, participant target/nontarget likelihood distributions were generated and dynamic stopping with the language model was simulated on words by initializing character probabilities, performing random draws of scores from participant likelihood distributions and updating character probabilities until the threshold for character selection was met. A comparison was done on two types of word sets: randomly selected words for each participant and identical words for all participants. It was hypothesized that if word selection were to have an impact, then the variance for accuracy and time to completion would be much higher for random word selection. However, variances for the two metrics were similar for both methods of word selection. while these conclusions were drawn with respect to the above simulations, based on an additional literature review, it has not been shown that word complexity affects speller performance. The advantage of using random words is that the results from this study are not tied to a specific selection of relevant words, thereby avoiding the issue of whether similar performance could be achieved for other word selections.

By incorporating the language model in the background within the algorithm, this approach avoided negatively influencing accuracy due to increased cognitive load and task difficulty. In Ryan et al., even though a significant decrease in task completion time was observed in the predictive speller, the increased task difficulty in selecting the numbered predicted options negatively affected accuracy [28]. Our dynamic stopping algorithm can be modified to accommodate the approach used in Kaufmann et al. where the predictive word options were displayed as a new column in the speller grid [29], with the modification of basing initialization priors of the new word options on a higher order n-gram model.

The ability of dynamic stopping algorithms to significantly outperform static stopping algorithms, both in terms of accuracy and communication rate, has been well demonstrated in general, [16], [18]-[21] and [17], as well as specifically for this algorithm, in Throckmorton et al. [26]. In comparison with other dynamic approaches, Throckmorton et al. demonstrated comparable [21] to improved performance with other dynamic stopping approaches used in the offline comparison study by Schreuder et al. (2011) [16]. One outcome of [16] was that the dynamic stopping approaches worked well for good performing participants and worse for low-performing participants, and this outcome was also observed in the updated comparison study, Schreuder et al. (2013) [17]. Throckmorton et al. demonstrated their approach was beneficial to low-performing (less than 60% accuracy in static data collection) as well as high performing participants. Thus, it can be inferred that the significant improvement in communication rate observed with the addition of the language model would add to the significant improvements of a dynamic stopping system when compared to a static stopping system.

The approach in this study is similar to that used by Speier et al., comparing static, dynamic and natural language processing (NLp) methods to control data collection [30]. They assumed Gaussian likelihood distributions (verified via Kolmogorov-Smirnov tests) for the target and non-target classifier scores and used a trigram model obtained from the Brown corpus. Their analysis was performed offline on training data using SWLDA weights obtained from nine-fold cross-validation. offline data analysis enabled them to vary the threshold probability in the dynamic data collection in order to optimize bit rates for each subject. Statistical significance was not tested between the dynamic stopping method and the NLP method; however, mean accuracy improved from 89.6% correct to 93.3% correct and bit rate improved from 27.7 bits/min to 33.2 bits/min, respectively. The online results presented in this study are similar to these results despite the lack of a priori knowledge of the optimal parameters. Further, the independence of training and testing datasets and real-time closed-loop user responses did not have a negative impact. These results indicate the robustness of a language model, as implemented here, to provide an improvement in communication rate for P300 spellers.

Our algorithm can be improved by further advancing the language model. The Carnegie Mellon corpus was used to train the language model and this large vocabulary of words might not be applicable to a particular user. A user-specific body of text can be used to provide even more language context. A higher order n-gram model based on all the user’s spelling history can be used as it utilizes more information in assigning initialization probabilities. For example, if a user has already spelled LIST, the initialization probabilities of grid character C_n will be based on all the previous character selections, instead of a bigram model, P(C_n∣T), or trigram model, P(C_n∣ST). With the added predictability of a higher order n-gram model, we hypothesize there will be a further reduction in the number of flashes required to reach the decision threshold. This is because the number of possible letters to complete a word begins to narrow down as the user spells and so a higher order model will tend to bias the initialization probabilities towards these possible letters. As noted earlier, participants did not correct for spelling errors with the backspace command as the error factor was introduced to account for possible misspellings. The algorithm can be improved by incorporating spelling correction with feedback on user errors, e.g. [39], obtained via error-related potentials which occur due to the user being aware of, or perceiving an error [40].

The dynamic stopping with language model algorithm was evaluated in healthy individuals. Mak et al. note that P300-based BCI literature have predominantly been in young and healthy adults, with limited reported results in patients with disabilities who represent the target P300 speller population [41]. The utility of the algorithm will need to be validated in disabled individuals, as results from the healthy participants do not necessarily generalize to those with disabilities who exhibit differences due to the causes and/or progression of their disabilities. Recent P300 speller studies have demonstrated accuracy levels as high as 70-100% [11]-[14]. In comparison to healthy individuals, patients with disabilities typically operate the system with a 6×6 matrix at slower flash rates and require more sequences per character selection (Townsend et al. and Sellers et al. used a 9×8 matrix in ALS patients). Although Townsend et al. optimized the number of sequences for character selection in ALS patients, the range of sequences was not reported. If the trend of the results in Throckmorton et al. and our study holds true for the disabled population, this will hopefully result in a more practical and efficient P300 speller system for daily use in severely disabled patients, thereby improving their quality of life.

V. Conclusion

Enhancing accuracy, spelling speed and communication rates results in more practical and efficient daily use of BCI-based spellers in patients with severe disabilities. This study contributes to research by demonstrating a significant improvement in online P300 task completion time and communication rates using dynamic data collection with a language model. The language model developed in this study accounts for spelling non-alphabet and alphabet characters and possible misspellings of characters.

Biography

Boyla O. Mainsah received a combined B.S. and M.E. in biomedical engineering from Worcester Polytechnic Institute, Worcester MA, USA in 2008, and an M.S. in electrical and computer engineering from Duke University, Durham, NC, USA in 2014.

She was previously at the Divisional Quality Assurance department at Covidien in New Haven, CT. She is currently pursuing a Ph.D. in electrical and computer engineering at Duke University, Durham, NC 27708, researching non-invasive brain-computer interfaces and machine learning.

Ms. Mainsah is also a member of the Society for Neuroscience.

Kenneth A. Colwell (M’11) was born in New Haven, CT, in 1987 and raised in Portland, OR. He earned a B.S. in engineering physics from Cornell University, Ithaca, NY, USA in 2009, and a M.S. in electrical and computer engineering from Duke University, Durham, NC, USA in 2012.

He has worked as a research and development intern at the electron microscopy firm FEI Company, and at the National Ignition Facility at Lawrence Livermore National Laboratory in Livermore, CA. Currently he is a Ph.D. student in electrical and computer engineering at Duke University in Durham, NC, researching non-invasive brain-computer interfaces and machine learning.

Mr. Colwell is also a member of the Society for Neuroscience and the American Statistical Association.

Leslie M. Collins (M’96-SM’01) was born in Raleigh, NC. She received the B.S.E.E. degree from the University of Kentucky, Lexington, and the M.S.E.E. and Ph.D. degrees in electrical engineering from the University of Michigan, Ann Arbor.

She was a Senior Engineer with the Westinghouse Research and Development Center, Pittsburgh, PA, from 1986 to 1990. In 1995, she became an Assistant Professor in the Department of Electrical and Computer Engineering (ECE), Duke University, Durham, NC, and became an Associate Professor in ECE in 2002 and has been a Professor in the ECE Department since 2007. Her current research interests include incorporating physics-based models into statistical signal processing algorithms, and she is pursuing applications in subsurface sensing, brain computer interfaces as well as enhancing speech understanding by hearing impaired individuals.

Dr. Collins is a member of the Tau Beta Pi, Eta Kappa Nu, and Sigma Xi honor societies.

Chandra S. Throckmorton earned a BS in electrical engineering from the University of Texas at Arlington, Arlington, Texas, USA in 1995 and her MS and Ph.D. in signal processing from the electrical engineering department of Duke University, Durham, NC, USA in 1998 and 2001 respectively.

She served as Post-doctoral Research Associate for two years at Duke University. She was promoted to Research Scientist in 2004 and Senior Research Scientist in 2008. Her research focuses on improving systems through the application of signal processing techniques, pattern recognition, and machine learning. She is currently involved in developing improvements for cochlear implants, brain-computer interfaces, and EEG-based seizure prediction systems.

Dr. Throckmorton is a member of the Society for Neuroscience, the Association for Research in Otolaryngology, the Acoustical Society of America and the American Auditory Society.