Keywords: coordinate system, implicit adaptation, mirror reversal, motor learning, sensorimotor adaptation
Abstract
Learning in visuomotor adaptation tasks is the result of both explicit and implicit processes. Explicit processes, operationalized as reaiming an intended movement to a new goal, account for a significant proportion of learning. However, implicit processes, operationalized as error-dependent learning that gives rise to aftereffects, appear to be highly constrained. The limitations of implicit learning are highlighted in the mirror-reversal task, where implicit corrections act in opposition to performance. This is surprising given the mirror-reversal task has been viewed as emblematic of implicit learning. One potential issue not being considered in these studies is that both explicit and implicit processes were allowed to operate concurrently, which may interact, potentially in opposition. Therefore, we sought to further characterize implicit learning in a mirror-reversal task with a clamp design to isolate implicit learning from explicit strategies. We confirmed that implicit adaptation is in the wrong direction for mirror reversal and operates as if the perturbation were a rotation and only showed a moderate attenuation after 3 days of training. This result raised the question of whether implicit adaptation blindly operates as though perturbations were a rotation. In a separate experiment, which directly compared a mirror reversal and a rotation, we found that implicit adaptation operates in a proper coordinate system for different perturbations: adaptation to a mirror reversal and rotational perturbation is more consistent with Cartesian and polar coordinate systems, respectively. It remains an open question why implicit process would be flexible to the coordinate system of a perturbation but continue to be directed inappropriately.
NEW & NOTEWORTHY Recent studies have found that implicit learning may operate inappropriately in some motor tasks, requiring explicit strategies to improve performance. However, this inappropriate adaptation could be attributable to competitive interactions between explicit and implicit processes. After isolating implicit processes, we found that implicit adaptation remained in the wrong direction for a mirror reversal, acting as if it were a rotation. Interestingly, however, the implicit system is sensitive to a particular coordinate system, treating mirror reversal and rotation differently.
INTRODUCTION
Since the seminal findings of bilateral hippocampal lesion patient H.M., there has been a tendency to view motor learning as the result of an implicit process (1–3). However, in recent years, it has become clear that motor learning can result from a number of different learning processes (4–8). As such, there has been considerable interest in isolating implicit learning from these other processes to better characterize its operation (9–13). One of the most surprising findings from these efforts to study implicit learning, in the context of a visuomotor adaptation task, is that it appears to have a very limited dynamic range: The adaptive response is relatively insensitive to the magnitude of the perturbation (11, 14, 15), only corrects for errors in one direction (16), operates automatically regardless of task goals (11, 12), saturates at a value far below complete learning (14, 17), and may even reduce its contribution with extended training (18).
These findings present a significant challenge to current theories of sensorimotor adaptation, which center around the idea of an internal forward model (19–22). Indeed, it has been suggested that the implicit adaptation process observed in visuomotor adaptation tasks may not reflect the operation of an internal forward model and, perhaps, it should be considered the outcome of a different computational process (17, 18, 21, 23–25). In fact, it is the mirror-reversal task used with Patient H.M. that underscores the limitations of this implicit process. Upon experiencing a mirror reversal, feedback corrections appear to be in the wrong direction and this response only gently decreases with extended training (26–28). Likewise, the adaptive response is similarly in the wrong direction, creating trial-by-trial instabilities in performance (21) and only becomes suppressed with days of training (17). Thus, it appears that, at least initially, implicit motor adaptation shows a highly stereotyped response that is incompatible with the operation of a forward model (21).
Although it might be tempting to reach this conclusion based on the recent findings in the mirror-reversal task, it should be noted that in these previous studies learning may be contaminated by other processes, such as explicit reaiming strategies. Recent studies have found that explicit strategies warp the generalization of implicit learning (29, 30), task performance errors interact with implicit adaptation processes (12, 13), and how explicit and implicit processes are measured may influence the observed pattern of results (31). Although it seems unlikely that the operation of other learning processes, or the way in which they are assayed, could dramatically alter the underlying operation of the implicit adaptation process, such as reversing the direction of corrective or adaptive response, it still remains worthwhile to attempt to isolate it.
The task-irrelevant visual-error clamp task has recently been developed with the hopes of isolating implicit adaptation from other sources of potential contamination (11). Here, in a center-out visuomotor-rotation task, the angular direction of cursor feedback is fixed regardless of hand direction. Participants have control only over the radial direction of the movement and are instructed to ignore cursor feedback entirely. Despite the task irrelevance of the feedback, movements gradually begin drifting in the direction opposite of the cursor, most often without awareness of the participants.
Although these initial studies applied a rotational perturbation to the cursor, the perturbation can equally arise from a mirror reversal, thus, presenting the opportunity to study implicit adaptation in a mirror-reversal task in relative isolation from other processes. If implicit adaptation is as stereotyped and rigid, as described by other studies, then we anticipate that implicit adaptation to a mirror reversal would act as though the perturbation was generated by a rotation. Here, we employed this mirror-reversal clamped-feedback task to better characterize implicit adaptation over the course of three consecutive days of training. Regardless of the participants’ reach direction, cursor feedback was clamped in the opposite direction to the target across the mid-sagittal axis (i.e., x-axis) of the workspace. Participants were informed that the movement of the cursor was not under their control, so they should ignore it and try their best to place their hand under the presented target. Similar to previous reports of implicit adaptation under a mirror reversal, we found that implicit adaptation was in the inappropriate direction and only gently decreased across sessions. What’s more, the observed pattern of adaptation was consistent with what would be expected in a dual-adaptation paradigm where participants adapted to opposing rotation in the left and right workspace (32, 33).
The finding that adaptation to a mirror reversal is homologous to a rotation raises the question: does implicit adaptation truly operate as though visual errors arise from a rotational perturbation? That is, does adaptation operate in a polar-like coordinate system? This question has been asked before by Hudson and Landy (34) in a paradigm where the perturbations were either drawn from a polar or Cartesian-based coordinate system. They found that the adaptive response was flexible, counteracting perturbations generated from either coordinate system. Thus, we sought to revisit this question contrasting adaptive responses to mirror-reversal and rotational perturbation using a paradigm that assays both implicit and explicit learning (15, 35) in experiment 2. If implicit adaptation blindly operates as if the visual perturbation were a rotation, both mirror-reversal and rotational perturbation will be adapted in a polar system, whereas if the implicit system has some degree of sensitivity to the nature of the perturbation, then the mirror-reversal perturbation will be adapted in a more Cartesian-based system compared with rotational perturbation. Although we again found that the direction of implicit adaptation to a mirror reversal was similar to a rotation, the pattern of the adaptive response appeared to be appropriate for the coordinate system.
MATERIALS AND METHODS
Participants
Fourteen young adults (6 women, age: 20.5 ± 0.5 yr) were recruited for experiment 1. One participant withdrew midway through the study, resulting in 13 participants for analysis. Twenty-four participants (13 women, age: 23.2 ± 4.3 yr) were recruited for experiment 2, with 12 participants in each condition. All participants were right handed, verified by the Edinburgh handedness test (36) and reported normal or corrected-to-normal visual acuity. All participants provided informed, written consent before participation. The study protocol was reviewed and approved by the Princeton University’s Institutional Review Board. All participants received course credit or financial compensation for their participation.
Power Analysis
The sample sizes of both experiments were determined by our previous 5-day mirror-reversal task (17), where the magnitude of implicit adaptation reached the peak at the end of the first day and gradually decreased over the course of the next 4 days of training. Based on these findings, in experiment 1, it is reasonable to hypothesize that the adaptation in the early phase of the training under the clamped mirror also decreases after multiple days of training. To determine a necessary sample size to detect a reliable decrease in adaptation, we compared the mean of implicit adaptation at the end of day 1 with the end (32 trials) of day 2, day 3, day 4, and day 5 from our previous 5-day mirror task study (17). Effect sizes of d = 0.99, 1.08, 1.08, 1.53 were found for day 2, day 3, day 4, day 5 compared with day 1, respectively. A paired t test using a two-tailed α of 0.05 and power of 0.8 suggested that a sample size of 17, 14, 14, and 7 participants was needed, respectively. Considering the constraints in participant recruitment, we decided to perform a 3-day experiment with 14 participants for experiment 1, which was chosen as a balanced compromise in terms of length of the experiment, power, and typical sample sizes in visuomotor adaptation experiments.
The sample size of experiment 2 was determined by how many participants would be needed to detect significant adaptation following a single day of training. In our previous study (17), we found an effect size of d = 1.4 for the mean of implicit adaptation at the end of 1 day of training. A paired t test using a two-tailed α of 0.05 and power of 0.8 suggested that a sample size of only seven participants was needed. As this estimate appeared small, we decided to recruit 12 participants for each task, which is a typical sample size in visuomotor adaptation experiments and matched that used in our previous study.
Apparatus
Participants performed a center-out reaching task, making horizontal movements with their right hand. Movements were recorded by a digitizing tablet (Wacom Co., Kazo, Japan), which recorded the motion of a digitizing pen held in the hand. Stimuli were displayed on a 60 Hz, 17-in. touch-sensitive monitor (Planar Systems, Hillsboro, OR), which was mounted horizontally above the tablet and, thus, obscured view of the limb. The task was controlled by custom software coded in MATLAB (The MathWorks, Natick, MA), using Psychtoolbox extensions (37, 38) and run on a Dell OptiPlex 7040 computer (Dell, Round Rock, TX) with Windows 7 operating system (Microsoft Co., Redmond, WA).
Procedure
Experiment 1.
Experiment 1 aimed to test whether the implicit system’s adaptive response to a mirror-reversal perturbation is in the wrong direction even when it is isolated from explicit strategies. Each trial began with participants holding their right hand in the center of the workspace for 500 ms. After this delay, a green target (0.25 cm radius) appeared 7 cm from the start location. The target could appear at 1 of 12 locations (±30°, ±60°, ±75°, ±105°, ±120°, ±150°; see Fig. 1A). Participants were instructed to move as quickly as possible to slice through the target in one smooth movement and then return back to the center. During the outbound portion of the reach, a small circular cursor (0.15 cm radius) was displayed. Depending on the phase of the experiment, the cursor either represented the location of the hand or clamped feedback (see the next paragraph). In addition, a neutral “click” sounded to indicate that the participant’s hand exceeded 7 cm. If the movement time from the start to 7 cm exceeded 800 ms, then a computer-generated voice sounded “Too Slow” following the “click” (<1% of trials, which were excluded from further analysis). During the return portion of the reach, the small circular cursor was replaced by a white ring that was centered on the start location and with a radius that matched the distance of the participants’ hand to the start location. This form of feedback was used to help guide participants back to the start location by providing only radial but not directional information.
Figure 1.
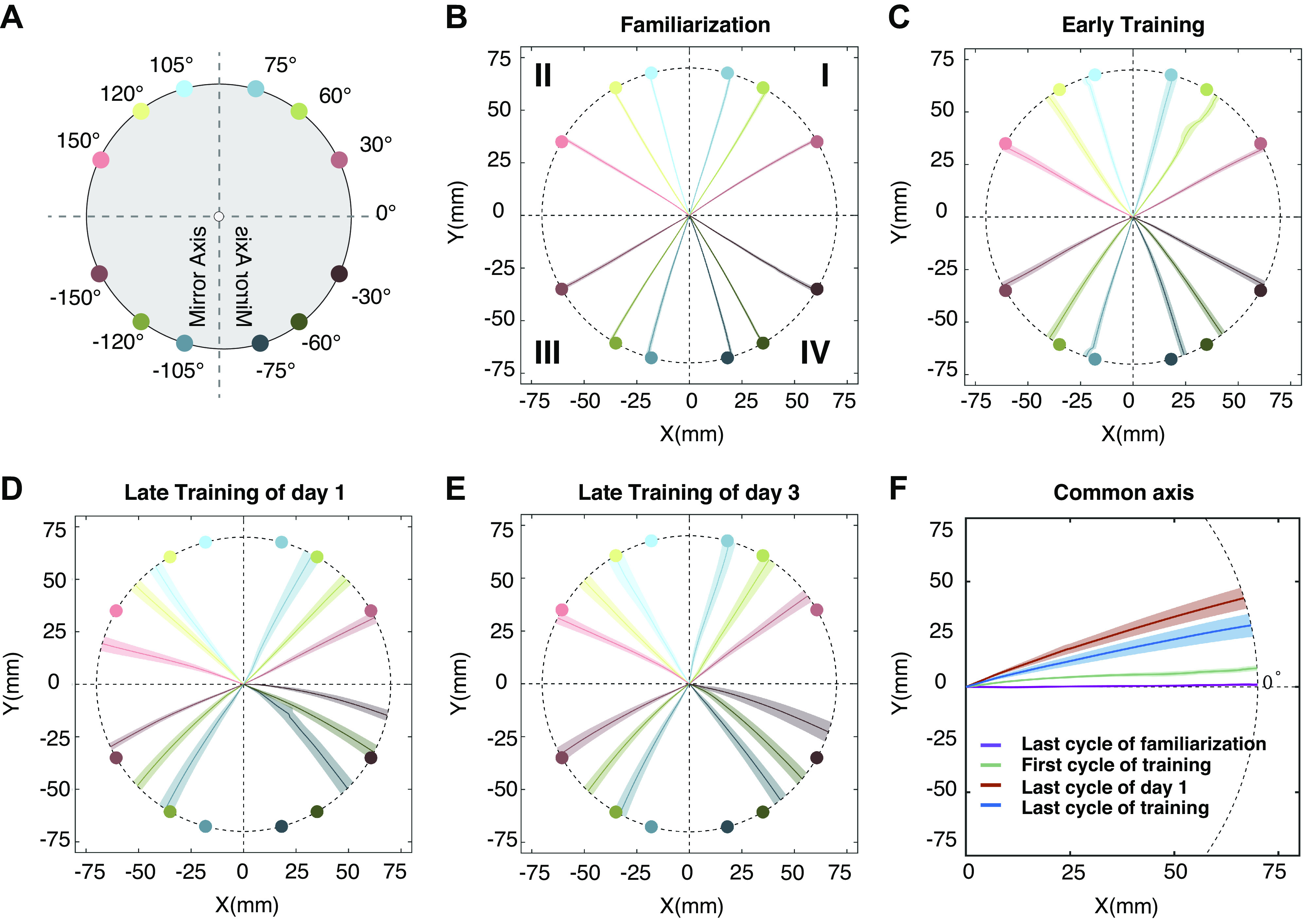
Target locations and moving trajectories of experiment 1. A: the locations of 12 targets: ±30°, ±60°, ±75°, ±105°, ±120°, ±150°. Mirror reversal was applied along the y-axis and centered on the starting location. Targets are color coded by the size of error between clamped feedback and target location: red: 120°, green: 60°, and blue: 30°. Different darkness levels indicate four quadrants. B: moving trajectory of the last cycle in the familiarization phase. Each trajectory is averaged over 13 participants and colored according to the target it aims. The shaded area represents standard error. Same below. C: moving trajectory of the first circle in the clamped phase of day 1. D: moving trajectory of the last circle in the clamped phase of day 1. E: moving trajectory of the last circle in the clamped phase of day 3. F: averaged moving trajectories of B–E. All 12 targets in one circle are flipped and rotated into a common axis at 0° (see MATERIALS AND METHODS) and averaged.
Participants received either veridical feedback or clamped feedback in different phases of experiment 1. On veridical feedback trials, the cursor accurately showed the location of the hand. For visual-error clamp feedback trials, the feedback followed a trajectory that was fixed along a specific heading angle (11, 39). This fixed heading angle was determined as the mirror-reversed direction of the target angle across the vertical axis (midsagittal axis). For example, when the participant reached for the 30° target, the cursor would be clamped at 150°. The radial location of the cursor was based on the radial extent of the participant’s hand (up to 7 cm amplitude) but was independent of the angular location of the hand.
Experiment 1 consisted of separate 1-h sessions spread across 3 days of participation. Participants performed each session approximately at the same time each day. On the first day of the experiment, participants experienced a familiarization phase consisting of 60 trials with veridical, online feedback. Following the familiarization phase, the experimenter then paused the task to explain the visual-error clamped feedback. Participants were informed that they could no longer control the direction of the cursor movement in the following sessions of the experiment. They were instructed to ignore the cursor and continue to reach directly to the visual location of the target. Participants then practiced completing 12 trials, one to each target location, with the clamped feedback. The experimenter then paused the experiment again to ensure that the participants understood the instructions and confirmed that they understood that they could not, and should not, attempt to control the direction of the cursor. Following this practice phase, participants completed another 996 trials with clamped feedback (clamp phase). On the second day of the experiment, participants completed another 1,008 trials of clamped feedback, which was present on the very first trial. On the third day of the experiment, participants completed 1,500 trials of clamped feedback and ended the experiment with a “washout” of 60 trials without any feedback. Before the washout, participants were instructed that the cursor would be hidden and they should continue reaching for the target. In sum, participants completed 3,636 trials in total and note, they were instructed to aim at the visual target directly in all phases of the experiment.
Experiment 2.
Experiment 2 was designed to directly compare the degree of implicit adaptation and its respective coordinate system for a rotation and mirror reversal within the same targets. Each trial began with participants holding their right hand in the center of the workspace for 500 ms. After the delay, a circular orange target (0.25 cm radius) appeared 7 cm from the start location. The target could appear at one of four locations (45°, 135°, −135°, and −45°). The order of the targets was pseudorandomized, such that each of the four targets was visited once before being repeated. Aiming report paradigm was applied in experiment 2 to separate the implicit and explicit components during the training. To begin the trial, participants indicated their intended reaching position by tapping at any position on the screen with their left hand (15, 35). Once an aim was recorded, the target turned from orange to green, and participants were allowed to begin their reaching movement with the right hand. If a participant attempted to begin moving their right hand before an aiming location was registered, the message “Remember to report aim” was displayed and the trial restarted. Participants were instructed to move quickly and, different from experiment 1, they are instructed to stop either on the target or the aim position depending on task phases. If the location of the cursor overlapped with the target (<2 mm of deviation), the participant heard a pleasant “ding”; otherwise, an unpleasant “buzz” was sounded. The feedback “Too Slow” was given if the reaching time exceeded 1,200 ms. After participants stopped moving their right hand (speed <1.3 mm/s), a small circular cursor (0.15 cm radius) appeared to provide feedback for 500 ms. During the perturbation phase, two groups of participants experienced either a mirror reversal or a visual rotation. In mirror reversal, the end point feedback was reversed over the y-axis. In rotation, the end point feedback was rotated 90° to the clockwise direction to match the size of the perturbation in the mirror-reversal task. To avoid priming participants with a certain coordinate system, no visual guidance was used to help participants get back to the center of the workspace. Instead, a small sticker was attached to the tablet surface to provide a tactile cue of the start location. The next trial began once the subject reached the start location.
The experiment began with 16 trials with online feedback to get participants accustomed to the task. Then, an 80-trial familiarization phase with veridical end point feedback helped participants learn the distance between targets and start location. After that, a baseline phase was composed of 32 trials without feedback to determine whether any subject held strong biomechanical biases that would not be averaged out by the target set. Participants were not asked to report their aim during the familiarization phases and baseline phase, as it was assumed that they would always be aiming at the target. A pause was included after the baseline phase so that the experimenter could explain the aiming procedure to the participants. Following these instructions, participants completed 32 trials with veridical feedback to familiarize themselves with the touch screen and aiming procedure. A perturbation phase of 400 trials with either mirror-reversal or visual-rotation feedback followed this familiarization. The experiment ended with a no-feedback and no-aiming report washout phase with 32 trials, where participants were instructed to abandon any strategy they used and to aim directly to the target.
Data Analysis
All initial data analyses were conducted in MATLAB, with the exception that repeated-measures ANOVAs were conducted in SPSS (IBM, 2011). The Greenhouse–Geisser correction was used for ANOVAs when data violated the homoscedasticity assumptions. Multiple comparisons were Bonferroni corrected. In experiment 1, task performance was assessed by calculating the angular difference between the target and the initial heading angle of the hand. In experiment 1, the initial heading angle of the hand was calculated as the angle between the first and last sample of the hand position between 1 and 3 cm radially from the start location. In experiment 2, trajectories of the right hand were recorded by the digitizing tablet, whereas the intended aiming location was recorded by the location tapped by the participant with their left hand on the touch screen monitor. The first data point collected after the movement’s speed was lower than 1.3 mm/s was registered as the terminal right-hand reach location.
Our previous study employing a mirror reversal found that the direction of the implicit component of motor adaptation was not in a direction consistent with counteracting a mirror reversal but instead in a direction consistent with countering a rotation (17). As such, this requires a relatively unintuitive transformation of the data to get it to a common axis. Figure 1D presents the raw hand trajectory of the last 10 trials toward each target at the end of the first-day training. It is clear from this figure that to transform the data to a common axis, the movements in quadrants II–IV need to be transformed as follows: II) the x-locations of the second quadrant movements (experiment 1: targets 105°, 120°, 150°; experiment 2: target 135°) were multiplied by −1 to flip the y-axis, III) both x- and y-locations of the third quadrant movements (experiment 1: targets −105°, −120°, −150°; experiment 2: target −135°) were multiplied by −1, and IV) the y-locations of the fourth quadrant movements (experiment 1: targets −30°, −60°, −75°; experiment 2: target −45°) were multiplied by −1. After this, the flipped trajectories were rotated to a common axis, as though the intended target was always located at 0°, despite being oriented at different target directions. With these transformations, a positive angle indicates movements of the hand in a counterclockwise direction relative to the target. Similarly, to make the solutions to perturbations of the rotation task to be positive in experiment 2, hand and aiming locations of targets in I, II, and IV were rotated for 180°, 90°, and 270° clockwise, respectively, to match the target in quadrant III.
To minimize the influence of target order differences between subjects and the potential biomechanical biases associated with specific target directions, trials were averaged into bins of 12 trials (1 cycle) in experiment 1 and 8 trials (2 cycles) in experiment 2. In addition, the averaged hand angle of the last 36 trials in the clamp phases was calculated for each day, respectively, to assess the adaptation of training of each day. The hand angles in the clamp phase and washout were corrected by subtracting with the mean of the baseline phase.
Model Simulation
To predict the time courses of the Cartesian-based correction model and the Polar-based correction model in experiment 2, we used a modified version of the two-state model (40). Here, we modeled explicit reaiming as the fast process (Pf) and implicit adaptation as the slow process (Ps) over the course of 624 trials (14). Besides, we assumed that explicit reaiming is updated based on target error, whereas implicit adaptation is updated based on the aim-to-cursor distance (14; Eqs. 1 and 2):
| (1) |
| (2) |
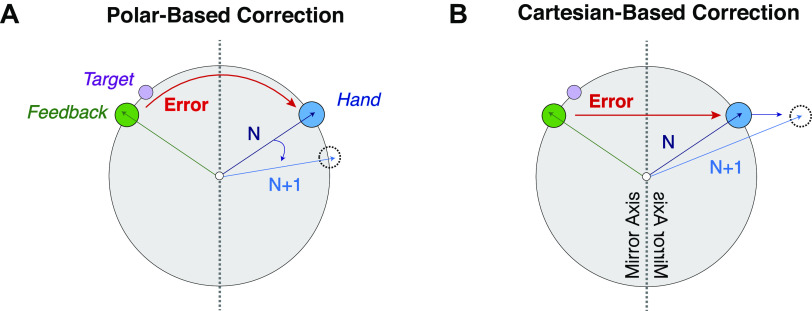
where Ef is the error between the target and the cursor locations, whereas Es is the error between explicit reaiming (Pf) and the cursor location. In the Polar-based correction model (see Fig. 3, left), the errors (Ef, Es) are supposed to be coded in the θ-dimension, thus the correction (Pf, Ps) is also performed in the θ-dimension. Everything remained zero in the ρ-dimension:
| (3) |
| (4) |
| (5) |
Figure 3.
Illustration of correction and target locations in experiment 2. Appropriate correction of implicit adaptation for polar (A) and Cartesian (B) coordinate. In the Polar-based correction, error was only perceived in the θ-dimension. In the Cartesian-based correction, error was only perceived in x-dimension.
In the Cartesian-based correction model (see Fig. 3, right), Pf, Ps, Ef, and Es were all coded in x-dimension and everything remained zero in the y-dimension:
| (6) |
| (7) |
| (8) |
As our primary interest focused on implicit adaptation during the training, rather than how the participants solved the perturbation with explicit strategies, the models assumed that the explicit system can solve the mirror task as in the study by Wilterson and Taylor (17). That is, the participants could figure out the solution to explicit reaiming (Xf) after observing perturbation for one trial. In the following trials, explicit reaiming (Xf) was updated, according to the equations mentioned above. The values for ɑf, βf, ɑs, and βs were determined by hand tuning these parameters to the simple rotation case (ɑf = 1, βf = 0.0005, ɑs = 0.99, and βs = 0.003). The same parameters were used for the two models. Note, both models assumed the slow process (Xs) updates to compensate mirror reversal as if it were visuomotor rotation. The simulated data were processed with the same procedure as the behavioral data to make the figures comparable. Note, for simplicity, we opted to present both the model simulations and the behavioral analyses in the Cartesian coordinate system (instead of polar) because if learning in the mirror-reversal task is sensitive to the coordinate system, then the majority of learning would be confined to the x-dimension (see Fig. 4).
Figure 4.
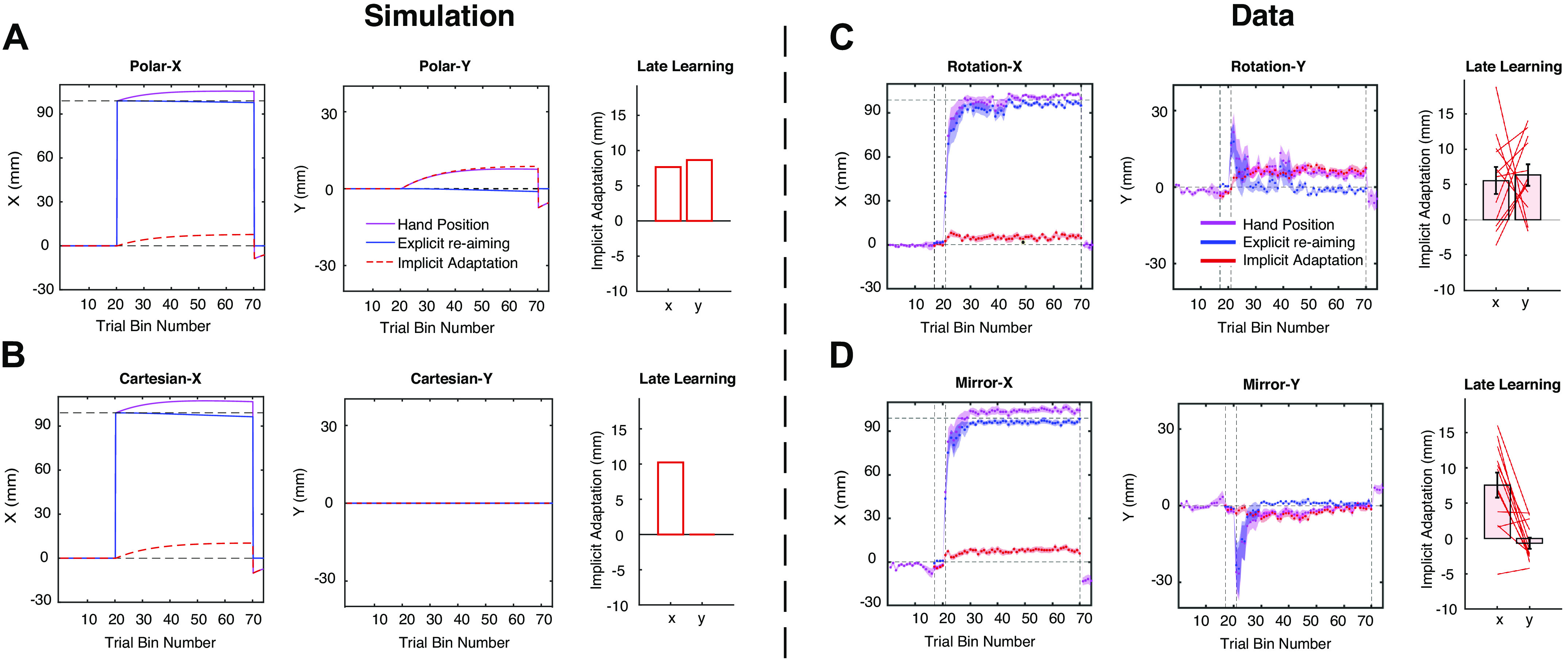
Time courses of model predictions and behavioral results in experiment 2. Simulations of the Polar-based correction model (A) and the Cartesian-based correction model (B). Left and middle: time courses presented by the changes in x- and y-dimensions, respectively. Right: the x- and y-values of implicit adaptation at the end of the perturbation phase. Participants’ performance in the rotation task (C) and the mirror task (D). Left and middle: The time course for hand location (purple), cognitive strategy/explicit reaiming (blue), and implicit adaptation (red). The vertical dashed lines represent the onset of aiming report, then the onset of the visual perturbation, then the end of visual perturbation. The horizontal dashed lines represent the value of 0 and 99.0 mm, respectively, which were the perfect solutions of visual perturbation in y- and x-dimensions, respectively. The shaded areas represent standard error. Right: the x- and y-values of implicit adaptation at the end of the perturbation phase. Each line represents a participant. Error bar represents standard error.
RESULTS
Previous studies of adaptation under mirror-reversed feedback have found that feedback corrections and adaptation are in a direction that is counterproductive to overcoming the mirror perturbation. Instead, the responses appear to be more consistent with an adaptation system that treats the perturbation as though it was a rotation. However, as training progresses, the inappropriate response is gradually decreased. Here, we set out to study this behavior in more detail by isolating implicit adaptation over the course of 3 days of training under clamped mirror feedback.
Experiment 1 (Clamped Mirror Task)
The direction of adaptation.
Before the introduction of the clamped-mirror feedback, participants practiced reaching to the targets with veridical feedback. Their reaches were fairly accurate in reaching toward the target (0.94 ± 0.74°, means ± standard deviation, same below, Fig. 1B). Following this familiarization phase, cursor feedback was mirror reversed and clamped, where the mirror reversal was applied along the y-axis and centered on the starting location and the angle of the cursor feedback was fixed.
Initially, participants’ reaching movements were directed toward the target, but with training their reaches deviated from the target (Fig. 1, C and D). For targets in all four quadrants, the heading angle of reaching movements biased considerably away from the mirror axis at the end of the first day (Fig. 1D) and this bias was still present at the end of the third day of training (Fig. 1E). Specifically, the heading angle drifted clockwise in quadrant I and quadrant III and drifted counterclockwise in quadrant II and quadrant IV. When considering the target location in the workspace relative to the mirror axis, this pattern of results suggests that implicit adaptation is acting to in a direction more consistent with adaptation to a visuomotor rotation rather than a mirror reversal, as we have observed previously (17, 21). Indeed, when we transformed the data to a common axis (see materials and methods), it is clear that implicit adaptation is acting as if to counter a visuomotor rotation (Fig. 1F).
Figure 1F also reveals that the amount of adaptation on the final day of training is less than that observed at the end of the first day. With the data now on a common axis, it is evident that the amount of implicit adaptation peaked at the end of the first day (15.8 ± 6.3°) and only gently decreased over the remaining 2 days of training (Fig. 2A); by the end of day 2, adaptation was 13.6 ± 6.9° and by the end of day 3 was 10.8 ± 7.1°. This decrease was confirmed by submitting these data to a one-way, repeated measures ANOVA with the factor of day ANOVA: F2,24 = 8.32, P = 0.002, = 0.41 (Fig. 2B). Although there is a significant decrease over the course of 3 days, the decrease is quite modest averaging only 2°–3° each day. In the post hoc comparisons, only day 1 and day 3 showed a significant difference (P = 0.02). However, it appears as though the reduction occurs between days rather than within a day. To test this possibility, we performed a separate linear regression on the time series of hand angles for each day of training to determine whether there was a significant slope to the time course. As expected, we found a positive slope in day 1 (0.077 ± 0.068°/trial, t12 = 4.08, P = 0.002), and almost a zero slope in day 2 (0.0007 ± 0.0406°/trial, t12 = 0.06, P = 0.95) and day 3 (−0.007 ± 0.027°/trial, t12 = −0.90, P = 0.39), indicating almost no decrease within a day.
Figure 2.
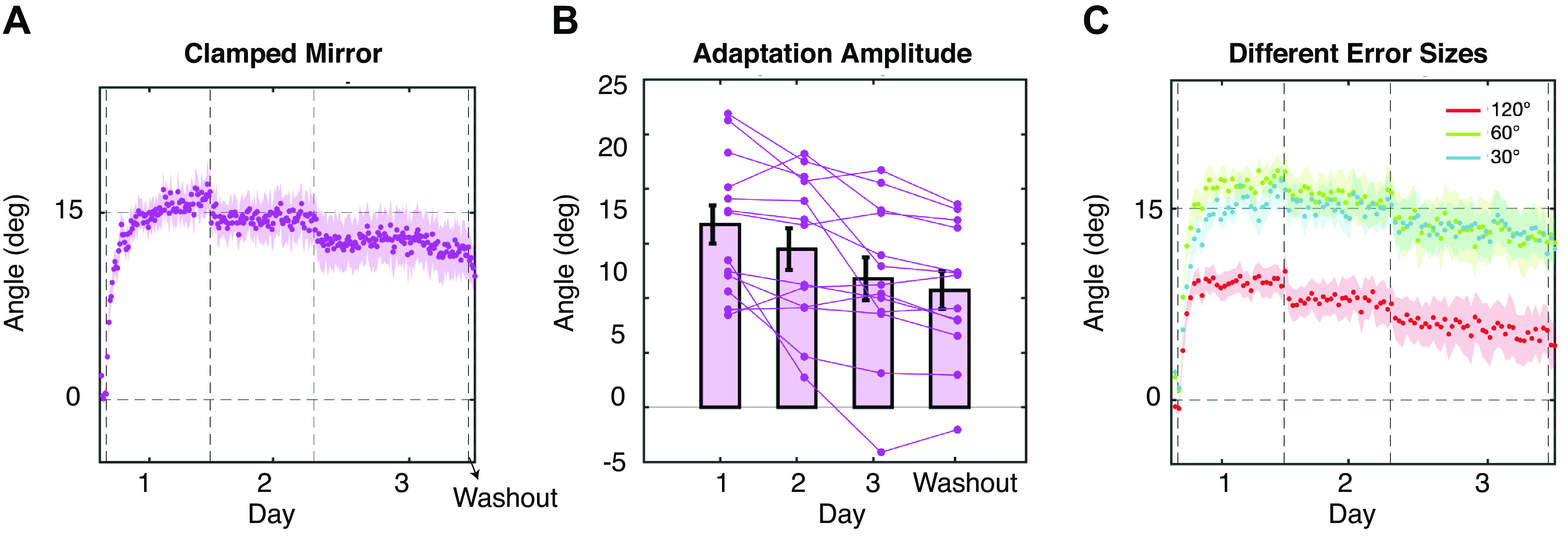
Time course of the adaptation in experiment 1. A: time course of the hand angle over 12 targets across 3 days. Each dot is an average of 12 trials (1 cycle). The vertical dashed lines represent first the onset of the mirror-clamp perturbation, then day breaks, then the start of washout. The shaded area represents standard error. Same below. B: amplitude of adaptation after each day of training. The error bars indicate mean and standard error. C: time courses of the hand angle for three different error sizes. Each dot is the average of 12 trials (3 cycles).
Although we observed a reduction in the amount of implicit adaptation over the course of 3 days of training, it remains an open question as to whether the adaptive response of the implicit system would become appropriate for a mirror reversal or simply be suppressed. Note, if the adaptation was in the mirror direction, i.e., the adaptation worked to bring the cursor to the target following the rule of a mirror, the hand would have drifted in the direction of the cursor. The cursor was in the counterclockwise direction to the targets in quadrant I (the clamped feedback for them was in quadrant II), so the hand angle would be negative instead of positive. Nevertheless, after the 3 days of training, only one participant showed a slight negative hand angle at the end of day 3, whereas all the other participants’ hand angles remained positive throughout the whole training period (Fig. 2B).
In the washout phase with no visual feedback, implicit adaptation was still present (9.8 ± 6.2°), which was slightly smaller than the end of the training session (t12 = 2.46, P = 0.03). Notably, before the washout phase, we needed to pause the program to give participant instruction, which resulted in a longer intertrial interval (11.3 ± 3.8 s) than the normal intertrial interval in the training phase (1.2 ± 0.1 s). This may be one reason why adaptation in washout is smaller than at the end of training.
Influence of error size.
The finding that implicit adaptation under a mirror reversal resembles that observed under a visuomotor rotation and that previous studies have revealed that the extent of generalization of a rotation is narrow, then we should expect that each target direction is learned relatively independently. Furthermore, if the mirror-reversal task is acted upon by the implicit system as a rotational perturbation, then each target would technically have a different degree of rotation. For example, reaches to the 30° target (quadrant I) results in errors near the 150° target (quadrant II), which could be viewed as a 120° rotation. Likewise, reaches to the 75° target (quadrant I) results in errors at 105° (quadrant II), which could be viewed as a 30° rotation. Morehead et al. (11) found that in a rotation-based visual-error clamp, adaptation declines as the size of the rotation increases (adaptation decreased at a point between 95° and 135°). Thus, if implicit adaptation treats mirror-reversal perturbations as a rotational error, then we would expect more adaptation for targets resulting in smaller errors (<95°–135°). Indeed, when we separate the learning curves by targets resulting in similar errors, the adaptation for different error sizes showed a significant difference after the first day of training (F2,24 = 27.2, P < 0.001, = 0.28). Post hoc pairwise comparisons showed that the adaptation to targets of 120° errors (targets ±30, ±150; 9.9 ± 3.3°) was significantly smaller than the adaptation to targets of 60° errors (targets ±60, ±120; 16.3 ± 4.9°, P < 0.001) or the adaptation to targets of 30° errors (targets ±60 and ±120; 15.6 ± 5.4°, P = 0.002). No difference was found between the adaption to 60° errors and the adaptation to 30° errors (P = 0.504), consistent with Morehead and colleagues (11).
Experiment 2 (Adaptation to a Rotation vs. Mirror Reversal)
The findings from experiment 1 suggest that implicit adaptation, even under a mirror reversal, acts as though the error arises from a rotational perturbation: The implicit system adapted in a direction opposite to the visual error and the magnitude of adaptation was target dependent, which is consistent with a rotational-based error signal. This raises the question: does the implicit system truly operate in a rotational manner, such as being transformed into a polar-like coordinate system, or does it simply act to bring visual feedback toward the intended reach direction, such as an equal and an opposite corrective behavior, which would be more similar to a Cartesian-based system? Note, we do not necessarily think that adaptation actually operates in such a well-defined coordinate system but may be more consistent with a particular coordinate system. In fact, Hudson and Landy (34) asked this question in a clever visuomotor adaptation task that sought to dissociate these two coordinate systems. Interestingly, they found that participants appropriately adapted to perturbations generated from either coordinate system.
At face value, our current results appear to be at odds with the findings from Hudson and Landy (34), as implicit adaptation appeared to treat the mirror reversal as a rotation. However, their study was likely conducted before the distinction between explicit and implicit learning processes was firmly established. As such, it could be the case that the flexibility to the particular coordinate system observed in their study could partially be the result of explicit reaiming strategies, which may not have been considered at the time. Explicit reaiming strategies have been shown to be quite flexible to the details of the perturbation (16, 35, 41). Although the nature of their perturbations would seem unlikely to afford a large contribution from explicit reaiming, it still remains an open question. Experiment 1 was ill-equipped to shed light on this issue because it used a center-out task design with shooting movements that always passed the target location (7 cm), which prevents the potential coordinate system underlying adaptation to be observed.
Here, we sought to revisit this question by using a modified version of the visual-error clamp method in which participants were required to stop on the target without visual feedback. Once the movement terminated, clamped mirror-reversal end point feedback was provided. To dissociate explicit and implicit learning, participants were asked to report their intended reaching location (reaiming) using a touch screen monitor before starting the movement. As such, this method would allow us to observe both the x- and y-positions of the hand to observe whether learning was more consistent with a rotational correction (e.g., more polar-like coordinates; Fig. 3A) or with an equal and opposite correction (e.g., more Cartesian-like coordinates; Fig. 3B).
The coordinate system of adaptation.
Both groups of participants were able to hit the target precisely in the familiarization phase (rotation: X, −0.7 ± 3.7 mm; Y, −1.4 ± 2.7 mm; mirror: X, −1.9 ± 2.7 mm; Y, −0.3 ± 1.9 mm). Although some weak biases were generated in the x-axis during the no-feedback baseline phase in the mirror perturbation group (−5.8 ± 8.2 mm), this bias was quickly washed out when the veridical end point feedback came back at the beginning of the aiming report (−1.9 ± 5.0 mm). After the participants became familiar with the aiming-report procedure, the perturbation was introduced (mirror reversal or 90° rotation). In both tasks, participants appeared to solve the perturbations relatively quickly. The hand angle is close to the perfect solution for each perturbation at the end of training (Table 1, row 1). In both tasks, this compensation was carried out in a quite explicit way, as participants could aim precisely at the perfect solutions to the perturbations without any systematic bias at the group level (Table 1, row 2). Although explicit strategy itself is almost sufficient to meet with the task command, the hand positions still deviated away from the aiming positions, indicating the involvement of implicit adaptation (Table 1, row 3).
Table 1.
The hand location, aiming location, and implicit adaptation at the end of the mirror-reversal or rotation perturbation in experiment 2
| Rotation-X | Rotation-Y | Mirror-X | Mirror-Y | |
|---|---|---|---|---|
| Hand | 102.8 (3.2) | 4.93 (4.3) | 104.6 (7.7) | 0.40 (2.2) |
| Aim | 97.2 (4.5)n.s. | −1.42 (2.2)n.s. | 96.3 (6.0)n.s. | 0.94 (1.8)n.s. |
| Implicit | 5.6 (6.6)* | 6.35 (5.3)* | 8.3 (6.0)* | −0.54 (2.8)n.s. |
Values are means (SD) (in mm). The values of aiming locations are compared with the perfect solutions (99.0 mm for x and 0 mm for y) by simple t tests. The values of implicit adaptation were compared with 0; *P < 0.05; n.s., P > 0.05.
Importantly, the Polar-based correction model and the Cartesian-based correction model predicted different time courses of learning for explicit and implicit processes in the perturbation phase. In the Polar-based correction model, implicit adaptation gradually increased in both x- and y-dimensions (Fig. 4A) and reached a considerable amplitude at the end of the perturbation phase. However, the Cartesian-based correction model predicted that implicit adaptation would only appear in the x-dimension, whereas adaptation in the y-dimension would remain zero (Fig. 4B). Interestingly, we found that implicit adaptation in the rotation and mirror tasks are different. Implicit adaptation in the rotation task was aligned to the prediction of the Polar-based correction model (Fig. 4C). Participants showed considerable implicit adaptation in both x and y-dimensions under the rotation (X: 5.57 ± 6.61 mm, t11 = 2.92, P = 0.014; Y: 6.35 ± 5.26 mm, t11 = 4.18, P = 0.002). On the contrast, implicit adaptation in the mirror task was similar to the prediction of the Cartesian-based correction model (Fig. 4D), where adaptation only appeared in x-dimension (8.27 ± 5.96 mm, t11 = 4.81, P = 0.0005). A slight negative implicit adaptation was found in the y-dimension at the beginning of the mirror task, but it dropped back to zero late into the perturbation (−0.54 ± 2.77 mm, t11 = −0.67, P = 0.515). Similar to experiment 1, this adaptation in the mirror task was in the “wrong” direction for mirror reversal, which increased the error instead of compensating for it. When comparing between two tasks, implicit adaptation in x and y-dimensions was roughly equal in the rotation task (t11 = 0.267, P = 0.794), whereas they showed a large difference in the mirror task (t11 = 3.95, P = 0.002). These results indicated that the implicit learning system applied different coordinate systems under different visual perturbations.
To illustrate the adaptation in a more straight-forward way, we presented the aiming location and hand location in the late training of mirror reversal and visual rotation, respectively (Fig. 5). We get clearly different patterns between the two tasks. In the rotation task, aiming location and hand location fall on a ring with a radius of target distance (Fig. 5A), whereas in the mirror task, the aim and the hand had a large divergence in the x-dimension but little difference in y-dimension (Fig. 5B). Thus, when plotting the two tasks together, it is clear that the implicit adaptation in the rotation task is more consistent with a polar system, and implicit adaptation in the mirror task is more consistent with a Cartesian system (Fig. 5C). Moreover, in the mirror task, the hand overshoot in the x-dimension relative to the aim, indicating that implicit adaptation to mirror reversal is still in the inappropriate direction.
Figure 5.
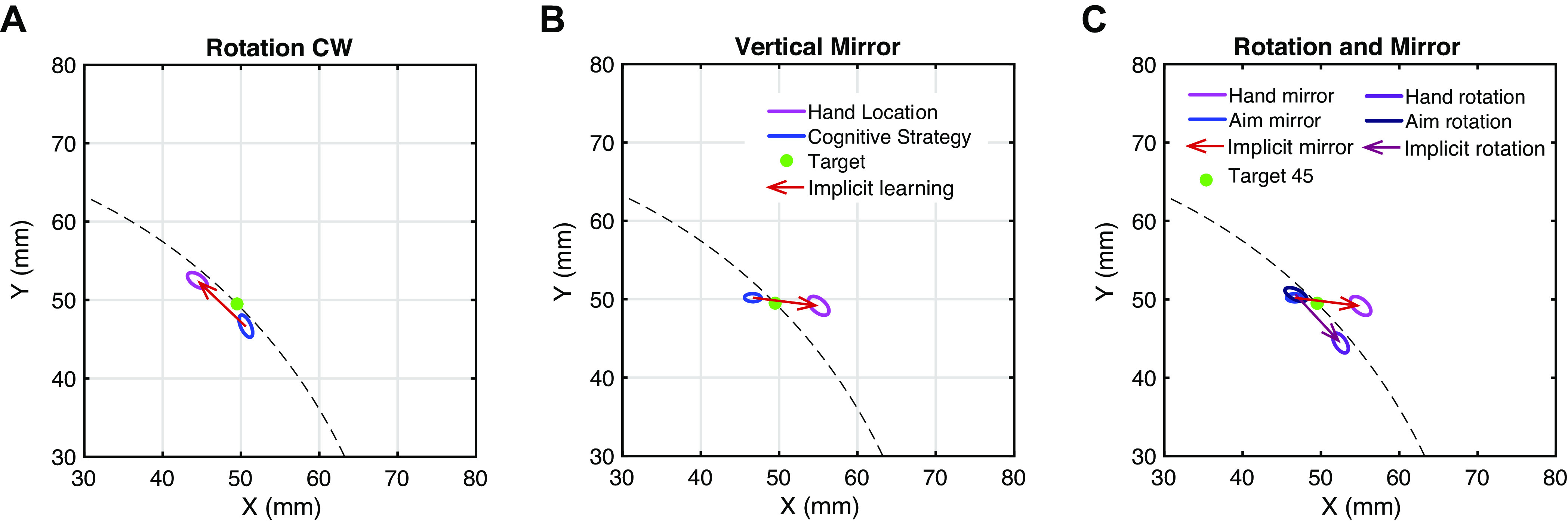
Hand location and aiming location at the end of rotation task and mirror task. A: covariance ellipses of hand (purple) and aiming location (blue) for 95% CI at the end of the rotation. The data of 12 participants were averaged trial by trial. Hand location and aiming location of all targets are aligned as if the target were in quadrant IV (target −45°, unshown). The covariance of the last 40 trials in the perturbation phase was calculated to plot the covariance ellipses. Green spot indicates the target location in quadrant I. B: covariance ellipses of hand location and aiming location at the end of the vertical mirror. Hand location and aiming location are aligned as if the target were in quadrant II (target 135°, unshown). C: comparison between the rotation and mirror reversal. To make them comparable, the rotation was plotted as if it were a counterclockwise rotation. Hand and aim positions in A are mirror reversed according to the y-axis and are then rotated for 90° to the counterclockwise direction. Hand and aim positions in mirror reversal remain the same as B.
Aftereffect.
In both tasks, no significant aftereffect was found in the washout. In the rotation task, there was almost nothing left in both the x- (−0.07 ± 6.42 mm, t10 = 0.039, P = 0.97) and y-dimension (−2.81 ± 6.80 mm, t10 = 1.38, P = 0.20) in the washout. In the mirror task, hand location slightly went negative in the x-dimension (−6.97 ± 7.17 mm, t10 = 3.36, P = 0.06). As a correct reaiming location in training is the same location as another target on the opposite side of the mirror axis, the new aiming location in washout (i.e., directly at the target) is at the same location as that for the opposite target in training. Therefore, the negative aftereffect in the x-dimension was aligned with the positive implicit adaptation in the training. Again, very little was found in the y-dimension (4.61 ± 5.15 mm, t10 = 3.10, P = 0.10) in the mirror task. One reason for the weak aftereffect might be we only presented the feedback at the movement end, which has proved to induce less adaptation compared with presenting the feedback during the whole movement (42).
DISCUSSION
In the current study, we examined the direction and the coordinate system of implicit adaptation under a mirror-reversal perturbation. In the first experiment, we isolated the implicit learning process with clamp-mirror perturbation and confirmed that implicit adaptation is in the wrong direction for the mirror reversal, in which the adaptation could only increase the error instead of compensating for it. Interestingly, this adaptation was somehow suppressed over the course of the 3 days of training. In the second experiment, we examined whether the implicit system was sensitive to the difference in coordinate systems between the rotation and mirror perturbations. This was accomplished by using an aiming report procedure that allowed us to separate implicit and explicit components during the learning. We found that the implicit learning system appeared to be consistent with the coordinate system of the particular perturbation, but puzzlingly continued to adapt in the wrong direction for a mirror reversal.
Adaptation to Mirror Reversal Is in the Right Coordinate System but Wrong Direction
Both our experiments aligned with several previous studies that have found that the implicit system learns the mirror reversal in the wrong direction (17, 21, 26–28). Hadjiosif et al. (21) have suggested that this pattern of adaptation in the mirror reversal is inconsistent with the internal forward model framework for sensorimotor adaptation (19, 20, 22). Here, the forward model supposes that the implicit learning system works to minimize the sensory-prediction error (SPE), that is, the error between the aim position and the feedback. To reduce an SPE in a mirror reversal, the participant’s hand should adapt closer to the mirror axis, which would bring the cursor and hand to get close to each other. However, the hand appears to adapt in the direction of the rotation and, thus, increases the error in a mirror-reversal task (17, 21). This raised concerns to the internal forward model framework and suggests that other computational frameworks may be needed to explain the implicit learning process. Remarkably, even though the implicit component failed to work under mirror reversal, participants actually performed well in the mirror task in experiment 2 by applying reaiming strategies. Consistent with previous studies (17), our result suggested that learning under mirror reversal is at least initially made possible through explicit reaiming strategies.
Besides the direction of adaptation, the degree of implicit adaptation to different targets in the mirror reversal were consistent with adaptation to different sizes of rotations (11, 32, 33). The strong similarity between the performance in mirror and rotation tasks raises the question of whether the implicit system could only process the perturbation as a rotation. However, in a two-dimensional reaching task, in which participants need to control both movement angle and radius, we found that implicit adaptation under a mirror reversal was very different from that under a 90° rotation in terms of the coordinate system. This result is consistent with the study by Hudson and Landy (34), where participants were exposed to perturbations that altered over trials following a sinewave pattern. Perturbations of different frequencies were either applied to the two axes in the polar system (ρ, θ) or the Cartesian system (X, Y), respectively. They found that participants could correct for the errors regardless of the coordinate system. However, it remains unknown how the implicit and explicit systems contribute to this result. Our findings suggest that both implicit and explicit learning systems appear to be sensitive to the coordinate system of the perturbation.
We note that, unlike mirror reversal, which is somewhat artificial and unlikely to be encountered in everyday life, errors in different coordinate systems may be more common in motor learning. For example, controlling a steering wheel or a bicycle handle asks for manipulation in the polar system, whereas a computer mouse may need motor planning in the Cartesian system. However, what information signals the appropriate coordinate system remains to be determined. For every single target in experiment 2, there was 90° of separation between targets, which is generally outside the range of generalization (43–45). This limitation in the breadth of generalization would suggest that the coordinate system would have to be determined individually at each target location.
There is the possibility that the global pattern of errors could signal the coordinate system of the errors; however, evidence for metalearning processes such as this is scant. Although incidental contextual cues have been shown to affect learning and change the pattern of generalization (42), it most likely operates on explicit reaiming. We made sure to remove these visual cues, such as the arrangement of the targets or requiring shooting movements in experiment 2. However, explicit strategies might still operate in different coordinate systems for mirror and for rotation, as they ask for different mental manipulations. Different explicit strategies might generate errors in different coordinate systems, which then influences the selection of the coordinate system for implicit adaptation. Another possibility is the consistency of the error signals, which has been shown to reduce the sensitivity of implicit adaptation (15, 46, 47). In the mirror-reversal task, the sign of the error changes across the workspace, whereas in the rotation task it remains consistent. Again, however, it is unclear whether the memory for errors (48) operates globally and could serve as a cue to signal a particular coordinate system.
Suppression of the Implicit Adaptation
One interesting result in experiment 1 is that the adaptation in the wrong direction is suppressed significantly during the 3-day training. We also observed suppression of implicit adaptation in our previous 5-day contingent mirror task (17). One explanation for this suppression is that the implicit system changed its error-correction policy during the extended training. When exposed to the mirror reversal, a transformation matrix for a rotation was initially applied, which caused the unsuitable adaptation, but after days of training, the implicit system may gradually change the error derivative (21, 49) or create a more appropriate transformation matrix for a mirror reversal. However, even after days of training, the accumulated adaptation is still in the wrong direction, and to our knowledge, no research has observed an adaptation to the correct direction under mirror reversal. This poses the question of whether the implicit system figure can eventually correct for a mirror reversal or just becomes suppressed.
Attenuation of implicit adaptation does not appear to be specific to the mirror-reversal task. Previous studies also found attenuation of the implicit system in some rotation tasks (18). Our previous 5-day rotation task (17) showed a tendency of attenuation in explicit adaptation in the extended training. Moreover, a recent study indicated that implicit adaptation would be attenuated in the re-exposure of the visual perturbation compared with the original adaptation (18, 50). What’s more, another study manipulated the variation of the perturbation in a rotation task suggesting that the error sensitivity of the implicit system seems to be suppressed when continuously exposed to the error signal of different directions (47, 51). Although the error signal is clamped to each target in our experiment 1, the error direction is opposite in terms of clockwise or counterclockwise for targets on the two sides of the mirror axis. Thus, exposure to inconsistent error directions might contribute to the attenuation of implicit adaptation in our result.
The Utility of the Implicit System in the Sensorimotor Learning
The incorrect adaptation direction for mirror reversal and the suppression of the adaptation across days raise the question regarding the utility of implicit adaptation in motor learning. As the mirror task was indeed the experiment that defined implicit learning (1), it is strange that recent studies showed that implicit adaptation could not overcome the mirror reversal. A plausible account is that another implicit learning system, e.g., reinforcement learning system, might be critical in motor learning instead of the so-called “implicit adaptation” defined here. The “implicit adaptation” referred to in our analysis was initially defined and proved to be useful in the visuomotor rotation task (8, 10). However, as accumulated evidence showed the limitations of this implicit adaptation (11, 12, 15, 39, 41, 52), its utility might be restricted to several specific tasks but unable to fulfill complex task demands, e.g., mirror reversal. In those complex situations, this implicit system might be suppressed, and other implicit learning systems somehow help explore and select a proper policy.
Conclusions
Our study confirmed that implicit adaptation operates in the wrong direction under mirror reversal perturbation. This adaptation was attenuated in the extended training across 3 days. Although in the wrong direction, the implicit system does appear sensitive to a particular coordinate system. These findings are consistent with previous reports challenging the flexibility of this implicit adaptation process (11, 17, 21, 41).
DATA AVAILABILITY
The data that support the findings of this study and code for the task and for data analyses are available from the corresponding author upon request.
GRANTS
This work was supported by National Institute of Neurological Disorders and Stroke Grant R01 NS-084948 (to J. A. Taylor).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
T.W. and J.A.T. conceived and designed research; T.W. performed experiments; T.W. analyzed data; T.W. and J.A.T. interpreted results of experiments; T.W. prepared figures; T.W. and J.A.T. drafted manuscript; T.W. and J.A.T. edited and revised manuscript; T.W. and J.A.T. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Eugene Poh and Sarah A. Wilterson for helpful discussions and Chandra Greenberg for helping with data collection.
REFERENCES
- 1.Cohen NJ, Squire LR. Preserved learning and retention of pattern-analyzing skill in amnesia: dissociation of knowing how and knowing that. Science 210: 207–210, 1980. doi: 10.1126/science.7414331. [DOI] [PubMed] [Google Scholar]
- 2.Corkin S. Acquisition of motor skill after bilateral medial temporal-lobe excision. Neuropsychologia 6: 255–265, 1968. doi: 10.1016/0028-3932(68)90024-9. [DOI] [Google Scholar]
- 3.Squire LR. Memory systems of the brain: a brief history and current perspective. Neurobiol Learn Mem 82: 171–177, 2004. doi: 10.1016/j.nlm.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 4.Heuer H, Hegele M. Adaptation to visuomotor rotations in younger and older adults. Psychol Aging 23: 190–202, 2008. doi: 10.1037/0882-7974.23.1.190. [DOI] [PubMed] [Google Scholar]
- 5.Hegele M, Heuer H. Implicit and explicit components of dual adaptation to visuomotor rotations. Conscious Cogn 19: 906–917, 2010. doi: 10.1016/j.concog.2010.05.005. [DOI] [PubMed] [Google Scholar]
- 6.Izawa J, Shadmehr R. Learning from sensory and reward prediction errors during motor adaptation. PLoS Comput Biol 7: e1002012, 2011. doi: 10.1371/journal.pcbi.1002012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Verstynen T, Sabes PN. How each movement changes the next: an experimental and theoretical study of fast adaptive priors in reaching. J Neurosci 31: 10050–10059, 2011. doi: 10.1523/JNEUROSCI.6525-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Taylor JA, Krakauer JW, Ivry RB. Explicit and implicit contributions to learning in a sensorimotor adaptation task. J Neurosci 34: 3023–3032, 2014. doi: 10.1523/JNEUROSCI.3619-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci 26: 3642–3645, 2006. doi: 10.1523/JNEUROSCI.5317-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Taylor JA, Ivry RB. Flexible cognitive strategies during motor learning. PLoS Comput Biol 7: e1001096, 2011. doi: 10.1371/journal.pcbi.1001096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Morehead JR, Taylor JA, Parvin DE, Ivry RB. Characteristics of implicit sensorimotor adaptation revealed by task-irrelevant clamped feedback. J Cogn Neurosci 29: 1061–1074, 2017. doi: 10.1162/jocn_a_01108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim HE, Morehead JR, Parvin DE, Moazzezi R, Ivry RB. Invariant errors reveal limitations in motor correction rather than constraints on error sensitivity. Commun Biol 1: 19, 2018. doi: 10.1038/s42003-018-0021-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Leow L, Marinovic W, Rugy A, Carroll TJ. Task errors contribute to implicit aftereffects in sensorimotor adaptation. Eur J Neurosci 48: 3397–3409, 2018. doi: 10.1111/ejn.14213. [DOI] [PubMed] [Google Scholar]
- 14.McDougle SD, Bond KM, Taylor JA. Explicit and implicit processes constitute the fast and slow processes of sensorimotor learning. J Neurosci 35: 9568–9579, 2015. doi: 10.1523/JNEUROSCI.5061-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hutter SA, Taylor JA. Relative sensitivity of explicit reaiming and implicit motor adaptation. J Neurophysiol 120: 2640–2648, 2018. doi: 10.1152/jn.00283.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Butcher PA, Taylor JA. Decomposition of a sensory prediction error signal for visuomotor adaptation. J Exp Psychol Hum Percept Perform 44: 176–194, 2018. doi: 10.1037/xhp0000440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wilterson SA, Taylor JA. Implicit visuomotor adaptation remains limited after several days of training. eNeuro 8: ENEURO.0312-20.2021, 2021. doi: 10.1523/ENEURO.0312-20.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Avraham G, Morehead JR, Kim HE, Ivry RB. Reexposure to a sensorimotor perturbation produces opposite effects on explicit and implicit learning processes. PLOS Biol 19: e3001147, 2021. doi: 10.1371/journal.pbio.3001147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Krakauer JW, Shadmehr R. Consolidation of motor memory. Trends Neurosci 29: 58–64, 2006. doi: 10.1016/j.tins.2005.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shadmehr R, Smith MA, Krakauer JW. Error correction, sensory prediction, and adaptation in motor control. Annu Rev Neurosci 33: 89–108, 2010. doi: 10.1146/annurev-neuro-060909-153135. [DOI] [PubMed] [Google Scholar]
- 21.Hadjiosif AM, Krakauer JW, Haith AM. Did we get sensorimotor adaptation wrong? Implicit adaptation as direct policy updating rather than forward-model-based learning. J Neurosci 41: 2747–2761, 2021. doi: 10.1523/JNEUROSCI.2125-20.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jordan MI, Rumelhart DE. Forward models: supervised learning with a distal teacher. Cogn Sci 16: 307–354, 1992. doi: 10.1207/s15516709cog1603_1. [DOI] [Google Scholar]
- 23.Wolpert DM, Ghahramani Z, Flanagan JR. Perspectives and problems in motor learning. Trends Cogn Sci 5: 487–494, 2001. doi: 10.1016/S1364-6613(00)01773-3. [DOI] [PubMed] [Google Scholar]
- 24.Abdelghani MN, Lillicrap TP, Tweed DB. Sensitivity derivatives for flexible sensorimotor learning. Neural Comput 20: 2085–2111, 2008. doi: 10.1162/neco.2008.04-07-507. [DOI] [PubMed] [Google Scholar]
- 25.Krakauer JW, Hadjiosif AM, Xu J, Wong AL, Haith AM. Motor learning. Compr Physiol 9: 613–663, 2019. [Erratum in Compr Physiol 9: 1279]. doi: 10.1002/cphy.c170043. [DOI] [PubMed] [Google Scholar]
- 26.Gritsenko V, Yakovenko S, Kalaska JF. Integration of predictive feedforward and sensory feedback signals for online control of visually guided movement. J Neurophysiol 102: 914–930, 2009. doi: 10.1152/jn.91324.2008. [DOI] [PubMed] [Google Scholar]
- 27.Telgen S, Parvin D, Diedrichsen J. Mirror reversal and visual rotation are learned and consolidated via separate mechanisms: recalibrating or learning de novo. J Neurosci 34: 13768–13779, 2014. doi: 10.1523/JNEUROSCI.5306-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kasuga S, Telgen S, Ushiba J, Nozaki D, Diedrichsen J. Learning feedback and feedforward control in a mirror-reversed visual environment. J Neurophysiol 114: 2187–2193, 2015. doi: 10.1152/jn.00096.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Day KA, Roemmich RT, Taylor JA, Bastian AJ. Visuomotor learning generalizes around the intended movement. eNeuro 3: ENEURO.0005-16.2016, 2016. doi: 10.1523/ENEURO.0005-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McDougle SD, Bond KM, Taylor JA. Implications of plan-based generalization in sensorimotor adaptation. J Neurophysiol 118: 383–393, 2017. doi: 10.1152/jn.00974.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Maresch J, Werner S, Donchin O. Methods matter: your measures of explicit and implicit processes in visuomotor adaptation affect your results. Eur J Neurosci 53: 504–518, 2021. doi: 10.1111/ejn.14945. [DOI] [PubMed] [Google Scholar]
- 32.Schween R, Hegele M. Feedback delay attenuates implicit but facilitates explicit adjustments to a visuomotor rotation. Neurobiol Learn Mem 140: 124–133, 2017. doi: 10.1016/j.nlm.2017.02.015. [DOI] [PubMed] [Google Scholar]
- 33.Schween R, Taylor JA, Hegele M. Plan-based generalization shapes local implicit adaptation to opposing visuomotor transformations. J Neurophysiol 120: 2775–2787, 2018. doi: 10.1152/jn.00451.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hudson TE, Landy MS. Sinusoidal error perturbation reveals multiple coordinate systems for sensory motor adaptation. Vision Res 119: 82–98, 2016. doi: 10.1016/j.visres.2015.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bond KM, Taylor JA. Structural Learning in a Visuomotor Adaptation Task Is Explicitly Accessible. eNeuro 4: ENEURO.0122-17.2017, 2017.doi: 10.1523/ENEURO.0122-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9: 97–113, 1971. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- 37.Kleiner M, Brainard D, Pelli D, Ingling A, Murray R, Broussard C. What’s new in psychtoolbox-3. Perception 36: 1–16, 2007. doi: 10.1068/v070821. [DOI] [Google Scholar]
- 38.Brainard DH. The psychophysics toolbox. Spat Vis 10: 433–436, 1997. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- 39.Shmuelof L, Krakauer JW, Mazzoni P. How is a motor skill learned? Change and invariance at the levels of task success and trajectory control. J Neurophysiol 108: 578–594, 2012. doi: 10.1152/jn.00856.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol 4: e179, 2006. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bond KM, Taylor JA. Flexible explicit but rigid implicit learning in a visuomotor adaptation task. J Neurophysiol 113: 3836–3849, 2015. doi: 10.1152/jn.00009.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Taylor JA, Hieber LL, Ivry RB. Feedback-dependent generalization. J Neurophysiol 109: 202–215, 2013. doi: 10.1152/jn.00247.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Brayanov JB, Press DZ, Smith MA. Motor memory is encoded as a gain-field combination of intrinsic and extrinsic action representations. J Neurosci 32: 14951–14965, 2012. doi: 10.1523/JNEUROSCI.1928-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Krakauer JW, Pine ZM, Ghilardi M-F, Ghez C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J Neurosci 20: 8916–8924, 2000. doi: 10.1523/JNEUROSCI.20-23-08916.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhou W, Fitzgerald J, Colucci-Chang K, Murthy KG, Joiner WM. The temporal stability of visuomotor adaptation generalization. J Neurophysiol 118: 2435–2447, 2017. doi: 10.1152/jn.00822.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gonzalez Castro LN, Hadjiosif AM, Hemphill MA, Smith MA. Environmental consistency determines the rate of motor adaptation. Curr Biol 24: 1050–1061, 2014. doi: 10.1016/j.cub.2014.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Albert ST, Jang J, Sheahan HR, Teunissen L, Vandevoorde K, Herzfeld DJ, Shadmehr R. An implicit memory of errors limits human sensorimotor adaptation. Nat Hum Behav 1: 1–15, 2021. doi: 10.1038/s41562-020-01036-x. [DOI] [PubMed] [Google Scholar]
- 48.Herzfeld DJ, Vaswani PA, Marko MK, Shadmehr R. A memory of errors in sensorimotor learning. Science 345: 1349–1353, 2014. doi: 10.1126/science.1253138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lillicrap TP, Moreno-Briseño P, Diaz R, Tweed DB, Troje NF, Fernandez-Ruiz J. Adapting to inversion of the visual field: a new twist on an old problem. Exp Brain Res 228: 327–339, 2013. doi: 10.1007/s00221-013-3565-6. [DOI] [PubMed] [Google Scholar]
- 50.Leow L-A, Marinovic W, de Rugy A, Carroll TJ. Task errors drive memories that improve sensorimotor adaptation. J Neurosci 40: 3075–3088, 2020. doi: 10.1523/JNEUROSCI.1506-19.2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fernandes HL, Stevenson IH, Kording KP. Generalization of stochastic visuomotor rotations. PLoS One 7: e43016, 2012. doi: 10.1371/journal.pone.0043016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Schaefer SY, Shelly IL, Thoroughman KA. Beside the point: motor adaptation without feedback-based error correction in task-irrelevant conditions. J Neurophysiol 107: 1247–1256, 2012. doi: 10.1152/jn.00273.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study and code for the task and for data analyses are available from the corresponding author upon request.