Boundary Element Fast Multipole Method for Modeling Electrical Brain Stimulation with Voltage and Current Electrodes

Abstract

Objective:

To formulate, validate, and apply an alternative to the finite element method (FEM) high-resolution modeling technique for electrical brain stimulation – the boundary element fast multipole method (BEM-FMM). To include practical electrode models for both surface and embedded electrodes.

Approach:

Integral equations of the boundary element method in terms of surface charge density are combined with a general-purpose fast multipole method and are expanded for voltage, shunt, current, and floating electrodes. The solution of coupled and properly weighted/preconditioned integral equations is accompanied by enforcing global conservation laws: charge conservation law and Kirchhoff’s current law.

Main results:

A sub-percent accuracy is reported as compared to the analytical solutions and simple validation geometries. Comparison to FEM considering realistic head models resulted in relative differences of the electric field magnitude in the range of 3–6% or less. Quantities that contain higher order spatial derivatives, such as the activating function, are determined with a higher accuracy and a faster speed as compared to the FEM. The method can be easily combined with existing head modeling pipelines such as headreco or mri2mesh.

Significance:

The BEM-FMM does not rely on a volumetric mesh and is therefore particularly suitable for modeling some mesoscale problems with submillimeter (and possibly finer) resolution with high accuracy at moderate computational cost. Utilizing Helmholtz reciprocity principle makes it possible to expand the method to a solution of EEG forward problems with a very large number of cortical dipoles.

1. Introduction

Brain stimulation therapies are important and effective treatments for people with depression (a fourfold US surge in 2020 [1]) and other mental disorders. Along with critical applications related to the senior population, depression has been the leading cause of disability in the US among young people ages 15 to 44 [2],[3]. 50–60% of people with depression who have failed to receive benefit from medications experience a clinically meaningful response with brain stimulation. About one-third of them experience a full remission [3]. Over the past fifteen years, the number of brain stimulation devices to undergo the FDA approval processes has grown exponentially in number and has shown significant sustained interest [4]. This behavior has been true for the most challenging implanted invasive devices: those targeting Parkinsonian symptoms and tremors [4]. Other demanding clinical applications include presurgical mapping in epileptic patients and accurate motor mapping prior to brain tumor surgery (cf. [5]-[7]), as well as brain-computer interfaces (cf. [8]-[13]). Major electric brain stimulation modalities to date are:

• Transcranial electrical stimulation (TES) – including transcranial direct current stimulation (tDCS) and transcranial alternating current stimulation (tACS) – a low-cost portable application technique with applied currents usually less than 1–2 mA. Its uses include therapy for chronic conditions, mostly depressive disorders, electroanesthesia, or better sleep and memory consolidations [15]-[19].

• Cortical stimulation (CS) and intracortical microstimulation (ICMS) – invasive yet precise versions of TES with smaller injected currents. Small implanted electrodes may target/activate selected populations or nuclei of neurons and have applications in brain and motor mapping pertinent to epilepsy [20],[21], neuro-oncology [22],[23], vision [24],[25] as well as in brain/machine and brain/computer interfaces [26]-[28].

• Deep brain stimulation (DBS) – an invasive technique with a permanently implanted neurostimulator targeting deep parts of the brain such as the subthalamic nucleus and forebrain bundle to reduce symptoms of treatment-resistant depression and Parkinson’s disease [29]-[31]. The success of subthalamic deep brain stimulation for Parkinson’s disease is highly dependent on knowledge of the anatomical extent of the electric field surrounding the active electrode contact [32],[33].

The (intra) cortical stimulation is often combined with direct recordings using subdural or intraparenchymal depth electrodes. A modern high-resolution intracranial recording technique – intracranial electroencephalography or iEEG – is blossoming in various fields of human neuroscience [34],[35].

The finite-element method (FEM) is a simple, powerful, and versatile numerical technique, which is naturally applicable to modeling anisotropic biological tissues. For this reason, the finite element method is widely and successfully used to solve the corresponding bioelectric field problem for different electrode configurations using anatomical isotropic and anisotropic head models. The leading open-source fast TES FEM modeling software is SimNIBS (cf. [36],[37]). For a realistic MRI-derived head mesh with surface mesh density of 0.5 nodes per mm² and an average edge length of 2 mm, the SimNIBS 3.0 FEM requires about 30 sec for assembling and solving a TES FEM system on an ordinary laptop [37]. The whole simulation time including preprocessing and postprocessing is slightly less than 70 seconds [37]. Another open-source FEM simulation package for TES problems is ROAST [38]. Both packages are not yet meant to model embedded electrodes. On the other hand, an open-source SciRun FEM simulation package [39] is frequently used for the solution of DBS problems with embedded electrodes – cf., for example, [40],[41],[42],[43]. Commercial packages such as Ansys Maxwell FEM software and COMSOL are also widely employed, mostly for the solution of common geometries for DBS electrodes [32],[44],[45],[46] where the resulting high-resolution fields are then coupled with axonal activation models. Different FEM packages such as SimNIBS and COMSOL may be also combined together [47].

At the same time, the finite-element method is less frequently used for the solution of some coupled problems with challenging geometries. One could mention, for example, a microarray embedded into an MRI-derived head model. Tetrahedral meshing alone between macroscopic brain compartments and microscopic array details may be somewhat challenging. Another relevant problem is related to tightly coupled brain compartments such as brain membranes, which are currently not included in any of the FEM solvers. Next, an FEM-based solution in terms of the electric potential has also some difficulties when evaluating a neuron activating function – the directional derivative of the electric field – in space. This step requires a double differentiation of the numerical solution; such a differentiation magnifies a numerical error.

In this study, we formulate, validate, and demonstrate possible applications of an alternative numerical approach to model electric brain stimulation. This is the boundary element fast multipole method or BEM-FMM, which is formulated in terms of the induced surface charge density on interfaces. The approach possesses numerically unconstrained field resolution in space including regions close to fine anatomical structures or miniature electrodes. This resolution is not limited by the size of the underlying tetrahedral mesh. Therefore, it might potentially be capable of modeling mesoscale problems with different mesh resolutions at macroscopic (major brain compartments) and microscopic (submillimeter and finer) scales, respectively. On the other hand, macroscopic medium anisotropy is not straightforwardly included into the BEM algorithm. In the past, the BEM-FMM approach was formulated for transcranial magnetic stimulation (TMS) [48]-[50] and EEG/MEG recording problems [51].

Modeling of electrical stimulation requires substantial modifications and extensions of the algorithm intended to (i) more accurately resolve electric fields varying by up to two orders of magnitude through the intracranial volume, (ii) construct adequate models of voltage and current electrodes and, (iii) properly implement global conservation laws.

The study is organized as follows. Section 2 provides a higher-level description of the methodological details of the algorithm. A more formal step-by-step method description is separately given in Appendix A. Section 3 presents four validation examples including two analytical problems as well as FMM-based computing an activating function for a simple DBS geometry. Another validation example is given in Appendix B. Section 4 presents two application examples with multicompartment head/body models pertinent to DBS and ICMS, respectively. Section 5 discusses the results. It also discusses one trivial yet efficient extension of the BEM-FMM method to a homogeneous anisotropic medium. Section 6 concludes the study.

2. Materials and Methods

2.1. Charge-based simulation approach

Once an electromagnetic stimulus generated by electrodes is applied, induced charge density will reside on electrode surfaces themselves as well as on tissue conductivity interface(s) with an abrupt conductivity change. This induced surface charge density completely determines the quasi-electrostatic solution: electric potential, electric field, and its directional derivatives anywhere in the biological conducting medium; no other parameters are necessary. All three electric quantities obey Coulomb’s law with the field derivatives found as a gradient of the potential of a double layer [52]. Note that no division into primary and secondary fields is necessary here, in contrast to TMS and EEG/MEG modeling. An integral equation for surface charge density on the conductivity interfaces (Fredholm integral equation of the second kind) still remains the same, but with the excitation term equal to zero everywhere except electrode surfaces. The corresponding detailed derivation is provided in Appendix A.

The BEM surface charge formulation for quasistatic problems is not new. It was known yet to Barnard et al [53] and then repeatedly discussed and investigated by Rahmouni et al (cf. [54]) as an adjoint double layer formulation. Van Bladel ([55], Ch. 6), calls this formulation a “Phillips type” of integral equation and cites previous relevant work related to magnetostatics and magnetic surface charges [56],[57],[58]. In [59], this formulation was sequentially applied to electrostatics of metals and dielectrics, DC conduction problems, and magnetostatic problems. However, in neither of these studies the charge-based formulation was used in conjunction with the fast multipole method where its application becomes natural.

2.2. Electrode configurations under study

Fig. 1 schematically illustrates possible electrode configurations under study. They may include (i) imprinted TES surface electrodes, (ii) embedded ICMS electrode arrays of different configurations (planar or laminar), and (iii) embedded DBS electrodes.

Fig. 1.

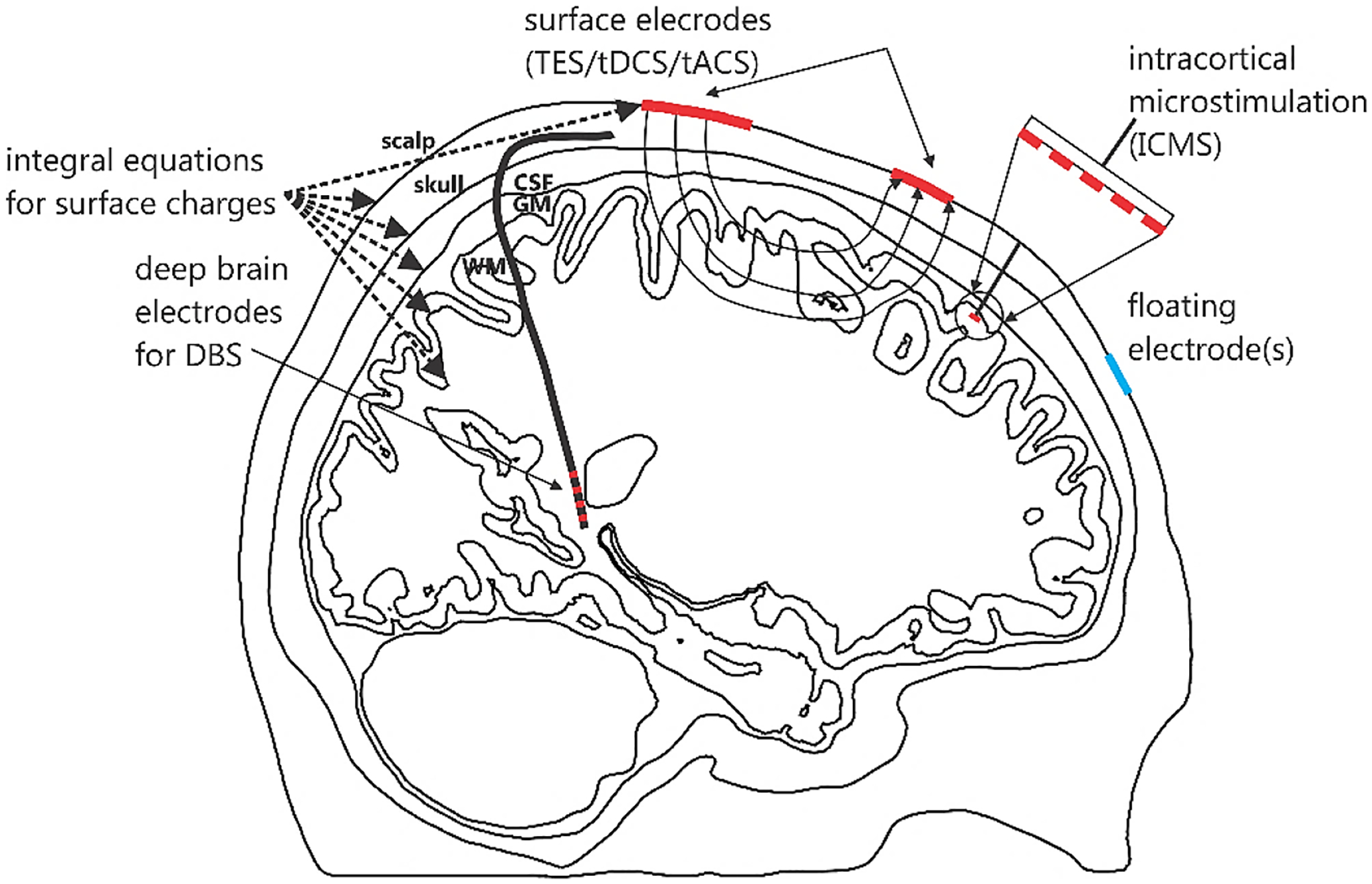
Different electrode types modeled by BEM-FMM: (i) imprinted TES surface electrodes, (ii) embedded ICMS electrode arrays of (planar or laminar), and (iii) embedded DBS electrodes.

Previously, BEM-FMM was formulated for simpler excitations by a prescribed external volumetric field (e.g., a primary coil field of TMS [48]-[50] or a primary field of internal EEG/MEG dipolar sources [51]). For the present case, the integral equations of the BEM-FMM algorithm have to be modified for different physical electrode types.

For the BEM approach, there is not much difference between surface electrodes or embedded electrodes with reference to Fig. 1. However, the electrical excitations and material types – the physics of the electrodes – may vary widely. Depending on an electric circuit (a voltage amplifier or a current amplifier) connected to the metal (with a very large conductivity) electrodes, we can distinguish between voltage or shunt (with a predefined net constant current [60]) electrodes, respectively. Both voltage and shunt electrodes may refer to TES surface electrodes, ICMS embedded electrode arrays, and DBS embedded electrodes. In either case, the voltage over the electrode surface remains constant. However, for shunt electrodes [60], the primary constant voltage-based solution must be further normalized to assure a required net current (cf., for example, [46]). Due to problem linearity, this step is rather trivial. Often, the shunt electrodes are also called current electrodes.

On the other hand, for sponge electrodes, the voltage over a reference electrode surface is not necessarily constant but the current density is constant or has a predefined profile. True current electrodes (with a predefined strictly uniform current distribution over the entire electrode surface and a non-uniform voltage distribution) may approximate contact sponges [61] or used as a tool for reciprocity analyses [62],[63]. Difference electrochemical impedance conditions [60] may be enforced on the electrode surface by combining voltage and current electrode models.

Floating electrodes are the electrodes which are disconnected from an electric circuit (have zero net inflowing or outflowing current). For floating metal electrodes, the voltage is still constant over the electrode surface, but it remains a priori unknown.

Appendix A reports modeling approaches for voltage, shunt, current, and floating electrodes described above. Two formulations are required: a Fredholm integral equation of the first kind for most common voltage and shunt electrodes, and a Fredholm integral equation of the second kind for current and floating electrodes.

2.3. Simulation method and its major features

Coupled integral equations for electrodes and conductivity interfaces are discretized on triangular surface facets with zeroth-order pulse basis functions which support a constant charge distribution over the facet. The standard Galerkin method is then applied, with the second integration over every facet. A simple diagonal electrode preconditioner or a full left electrode preconditioner are precomputed and used for the for the most common voltage and shunt electrodes while current and floating electrodes do not need a preconditioner. Details are given in Appendix A. The resulting system of linear equations is solved iteratively using the generalized minimum residual method (GMRES) [65] and its flexible version [66]. GMRES was found to converge better than the bi-conjugate gradients method and its variations. Since except the electrode surfaces, the Fredholm equation of the second kind is solved, with a strong diagonal dominance, the relative residual error approaches the relative solution error. The number of iterations typically does not exceed 20–40.

The matrix-vector product of the iterative solution is equivalent to finding weighted electric field at multiple observation (or target) points due to multiple point charges (sources) located at the source points. This is the classic problem of the fast multipole method where the sources are located at the centers of triangular facets. The general-purpose FMM [67] and its most recent software implementation [68] are therefore applied to compute the matrix-vector product of the iterative solution. The accuracy of the corresponding FMM (the number of levels) is unlimited; it is conventionally estimated for arbitrary volumetric charge distributions. However, for surface-based charge distributions, a better relative accuracy is observed than for the arbitrary volumetric distributions. Therefore, the relative FMM precision levels of 10⁻¹ to 10⁻³ were found to be adequate when compared to the most accurate analytical or numerical solution.

Electrostatic near-field interactions between the neighbor uniformly charged facets in the form of double surface integrals are directly pre-calculated [69],[70] and stored in a sparse near-field BEM matrix using analytical integration for the inner integral and a Gaussian quadrature of 10^th degree of accuracy [71] for the outer integrals at the preprocessing stage. The corresponding matrix-vector product is added to the FMM result and the inaccurate center-point neighbor integrals are simultaneously subtracted. The number of geometrical (based on Euclidian distance) neighbors may vary, but a relatively reasonable number (4–16) was found to be adequate. The double self-integrals for the electric field are no longer set to zero; they are computed as an average of the topological neighbors.

For tightly spaced interfaces – intracranial compartments or embedded devices– there is a dilemma between precomputing and storing more neighbor integrals or, conversely, putting more integration points over (all or selected) triangular facets themselves. The first approach is generally faster, but it requires large preprocessing times and extensive storage. The second approach is equivalent to internal triangle subdivision while keeping the original mesh topology the same. It is trivially handled by the FMM engine using barycentric or Gaussian triangle subdivisions (barycentric or Gaussian cubatures on triangles [71]). We attempt to achieve a balance between the two approaches depending on the problem under study. In any way, the average triangle size for two tightly spaced interfaces is chosen smaller than the separation between the interfaces (cf. Appendix A).

Two global conservation laws are employed as described in Appendix A. They are a net charge conservation law for current and floating electrodes and a net current conservation law (Kirchhoff’s law) for voltage and shunt electrodes. Both conservation laws are enforced in a “weak” form i.e., by additively combining them with every equation of the iterative solution.

Most of the simulations reported below have been performed on Windows multicore workstations with the clock speed of 2.1–2.4 GHz (MATLAB 2020b).

2.4. Error estimates for vector electric fields at multiple observation points

While the errors for the scalar fields e.g., for electric potential, φ(r_k) k = 1:K, distributed in space are customary given by an L₂ or Euclidian norm ‖·‖, the situation complicates for the vector fields. Consider two different vector electric fields: a reference or “exact” field E(r_k) and a test field E′(r_k), both defined at multiple observation points r_k, k = 1, … , K in the three-dimensional space. Then, several meaningful definitions of the error norm, ‖E(r) − E′(r)‖, are possible. The standard definition (which is, for example, a default choice of MATLAB) is a 2-norm denoted by the same symbol, ‖E(r) − E′(r)‖, which is a maximum singular value of the matrix {E(r_k) − E′(r_k)} on the size 3 × K. This definition is less intuitive. Second possible definition is a Frobenius norm, which is obtained by squaring the magnitudes of the individual field differences at the observation points,

$${\Vert \mathit{E}\left(\mathit{r}\right)-{\mathit{E}}^{\prime }\left(\mathit{r}\right)\Vert }_F=\sqrt{\sum _{k=1}^K{\Vert \mathit{E}\left({\mathit{r}}_k\right)-{\mathit{E}}^{\prime }\left({\mathit{r}}_k\right)\Vert }^2}=\sqrt{\sum _{k=1}^K\sum _{n=1}^3{(E_{nk}-E_{nk}^{\prime })}^2}$$ (1)

Another applicable definition is an L₂₁ norm [72], which does not square the magnitudes of the individual field differences at the observation points,

$${\Vert \mathit{E}\left(\mathit{r}\right)-{\mathit{E}}^{\prime }\left(\mathit{r}\right)\Vert }_{21}=\sum _{k=1}^K\Vert \mathit{E}\left({\mathit{r}}_k\right)-{\mathit{E}}^{\prime }\left({\mathit{r}}_k\right)\Vert =\sum _{k=1}^K\sqrt{\sum _{n=1}^3{(E_{nk}-E_{nk}^{\prime })}^2}$$ (2)

This error definition might be considered somewhat more robust since the error for each data point in space is not squared. It is used in robust data analysis. Eq. (2) is more sensitive to the errors in smaller field values than Eq. (1). For electrical stimulation, smaller fields may be important. Both 2 norm and L₂₁ norm will be used and specified in every case to estimate the vector field error(s) in the subsequent study. Based on the definition from Eq. (2) or any other norm definition, a relative vector field error, ε, with respect to the reference field has the form

$$\epsilon =\frac{\Vert \mathit{E}\left(\mathit{r}\right)-{\mathit{E}}^{\prime }\left(\mathit{r}\right)\Vert }{\Vert \mathit{E}\left(\mathit{r}\right)\Vert }$$ (3)

Based on the norm definition from Eq. (2) or any other norm definition, we will also employ a relative difference error measure or RDM [73] in the following form:

$$RDM=0.5\times \Vert \frac{\mathit{E}\left(\mathit{r}\right)}{\Vert \mathit{E}\left(\mathit{r}\right)\Vert }-\frac{{\mathit{E}}^{\prime }\left(\mathit{r}\right)}{\Vert {\mathit{E}}^{\prime }\left(\mathit{r}\right)\Vert }\Vert$$ (4)

2.5. Code availability

Codes for validation examples given in the following section and in Appendix B are available online. The most recent up to date code version along with short documentation can be found in [74]. Examples for MRI derived head models can be found in [75]. The BEM-FMM codes are written in MATLAB under Windows and could be executed on any Windows machine. They run as is and do not require extra dependencies, compilations, or downloads. Validation codes could be directly extended to a multicompartment head model. A multicore computer is strongly recommended for an efficient FMM execution. It is also recommended to have no less than 8–16 Gbytes of RAM. For Linux machines with different architectures, an individual compilation of the FMM library [68] is required.

3. Results – Validation Examples

In the following, we investigated the performance and accuracy of the BEM-FMM approach for several examples which validated the method implementation against two analytical and two numerical reference solutions obtained with FEM, respectively. An additional validation example is given in Appendix B. Codes for the validation examples are available online [74].

3.1. Example 1. Comparison with a one-dimensional analytical solution

The problem geometry is shown in Fig. 2a. It includes a sandwiched brick with sixteen 1 mm thick layers having interleaving static conductivities of 0.5 S/m (medium 1) and 0.2 S/m (medium 2), respectively. The brick has the dimensions of 30×30×16 mm. The media are isotropic, with the same values of the dielectric constant. Two electrodes (± 10 V, chosen as infinitely thin plates for the BEM-FMM solution) cover the top and the bottom of the brick. The goal is to obtain the BEM-FMM numerical solution and compare it with the analytical reference solution. The analytical solution inside (but not outside) the brick implies strictly one-dimensional piece-wise constant z-directed current density and electric field distributions, and a linear electric potential distribution which satisfy all the necessary boundary conditions and Laplace equation. The electric current density is constant inside the volume, while the electric field is piecewise constant. Using the corresponding lumped-circuit model, one has for the current density and the electric field,

$$I_{\mathit{\text{total}}}=0.3214\text{\hspace{0.17em}A},J_z=357.143\frac{A}{m^2},E_{z1}=714.286\frac{V}{m},E_{z2}=1785.714\frac{V}{m}$$ (5)

The observation grid is composed of the centers of cubic voxels inside the grid. Two voxel sizes are considered: 0.5×0.5×0.5 mm (0.12 M voxels in total) and 0.2 mm (1.8 M voxels in total), respectively. The relative error in the vector electric field, ε, follows Eq. (3) with the exact field given by Eq. (5). The RDM error follows Eq. (4). The L₂₁ norm given by Eq. (2) is used.

Fig. 2.

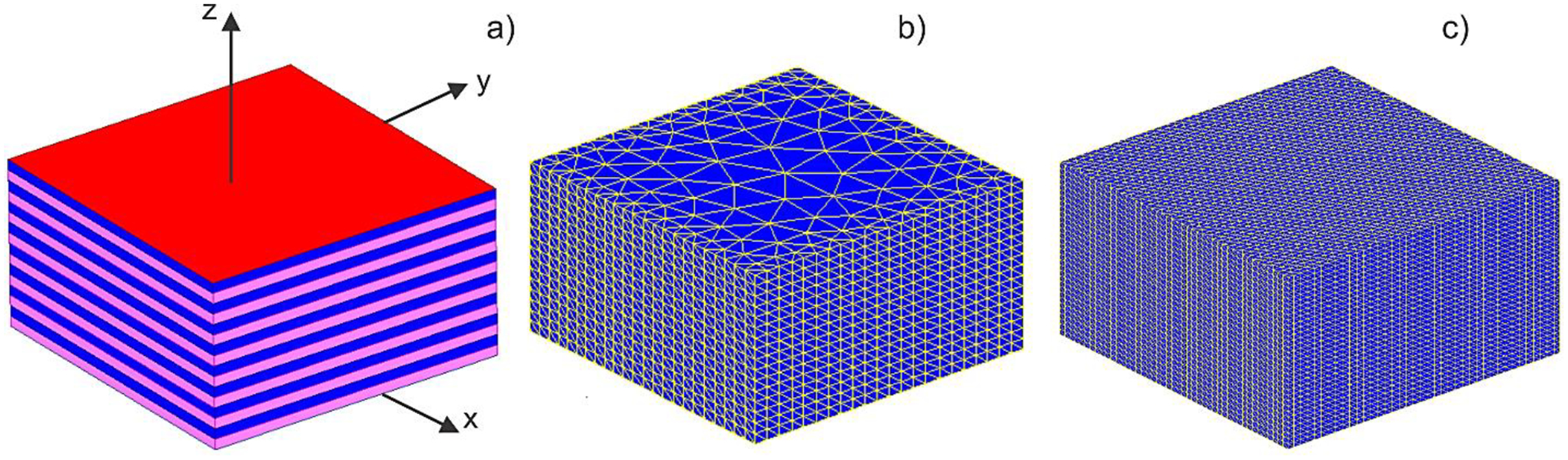
a) – Problem geometry under study. The top electrode (+10 V) is marked in red. Coarse b) and fine c) surface meshes used for the solution are shown. The inner facets separating every conducting layer are not shown.

The BEM-FMM solution uses 20 adaptive passes, precise analytical expressions for sixty four neighbor surface integrals, relative FMM precision of 10⁻², and the full left preconditioner (Eq. (13b) of Appendix A) at the electrode surfaces. The core BEM-FMM core solution (without pre- and postprocessing) runs in approximately 2–7 sec on a multicore 2.1 GHz Windows workstation (MATLAB 2020b) depending on the surface mesh size. Two surface meshes are considered: an extruded coarse transversally unstructured mesh with 7,693 facets and an extruded fully structured mesh with 69,593 facets, respectively, as shown in Figs. 2b,c. Table 1 reports the relative field error values between the exact vector electric field observed at the center of each voxel and the BEM-FMM iterative solution as well the computational run times for both meshes. The error is somewhat larger in the second case due to smaller distances of the observation points from the electrodes and the brick walls.

Table 1.

Relative error values from Eqs. (3) and (4) computed at the center of each voxel for two different BEM-FMM meshes. Voxels are used for error calculations only. All simulations have been performed on a Windows multicore workstation with Intel 6148 CPUs at 2.4 GHz (MATLAB 2020b).

Voxel size	ε: mesh with 7,693 facets	ε: mesh with 69,593 facets	RDM: mesh with 7,693 facets	RDM: mesh with 69,593 facets	Solution time: mesh with 7,693 facets	Solution time: mesh with 69,593 facets
0.5 mm (0.11 M voxels)	1.92%	0.73%	0.86%	0.36%	2 sec	7 sec
0.2 mm (1.8 M voxels)	2.07%	0.84%	0.93%	0.41%	2 sec	7 sec

Surface field recovery times just inside/outside any surface are less than 0.5 sec. Volumetric field recovery times at the voxel centers are significantly longer. For the BEM-FMM mesh with 69,593 facets, they are 42 sec (0.5 mm voxel size) and 392 sec (0.2 mm voxel size), respectively.

A sub-percent vector field accuracy can be obtained for both voxel grids with the BEM-FMM meshes of ~50,000 triangular facets or greater on a 2.1 GHz machine. The present solution offers a way to carefully investigate the effect of different numerical parameters on the resulting accuracy. In particular, fine tuning (e.g., reducing the number of iterations) as appropriate substantially reduces the execution times in Table 1.

Note that a typical FEM solution with first-order basis functions - Lagrangian P1 elements – employs a linear approximation of the electric potential and a piecewise constant approximation of the electric field. The electric field has a constant value within each element and is discontinuous across element boundaries. Therefore, the FEM solution would be exact when the one-dimensional problem of Fig. 1 is solved just inside, for any tessellation of the inner volume. Any distortion of the one-dimensional geometry will result in a nontrivial solution.

3.2. Example 2. Comparison with analytical EEG solution for a multilayer sphere using Helmholtz reciprocity principle

The quasistatic reciprocity (duality) principle or theorem [62],[63] makes it possible to interrelate a TES problem with surface electrodes and a forward EEG problem with embedded dipolar point current sources [76], [77]. For EEG analyses, the corresponding powerful analytical solutions for a multilayered sphere are well known and are readily available – cf. [78], [79] – they will be utilized in what follows.

Consider a pair of arbitrarily located small TES surface voltage electrodes with a differential voltage v. The first electrode sources net current I while the second (reference) electrode sinks the same current I. An auxiliary dipolar point current source embedded at any point r with a vector dipole moment Q(r) [A·m] will generate the same differential voltage v at the electrodes if the following reciprocity relation is satisfied [62],[63]:

$$-\mathit{E}\left(\mathit{r}\right)·\mathit{Q}\left(\mathit{r}\right)=vI$$ (6)

where E(r) is the electric field generated at r by TES electrodes with the voltage v and the net current I. Strictly speaking, Eq. (6) is only valid for point electrodes. However, reasonably small on-skin voltage electrodes with a local mesh refinement of the electrode surface and its immediate vicinity will already provide an excellent approximation for the boundary element method as it will be seen later.

The application of Eq. (6) to multiple dipoles is based on problem linearity. Consider an n-th dipole. Given its moment Q_n and the location of interest r_n, v_n is found from the EEG analytical solution [78],[79] at step 1. At step 2, a generic TES numerical solution with a fixed electrode voltage of, say, ±1 V is executed. As a result, the total electrode current I_fixed and the field E_fixed (r) at any point r_n of interest are computed. TES electrode currents and TES field are linearly dependent. Therefore, Eq. (6) could be cast in the following form:

$$-{\mathit{E}}_{\mathit{\text{fixed}}}\left({\mathit{r}}_n\right)·{\mathit{Q}}_n=v_n{I}_{\mathit{\text{fixed}}}$$ (7)

Two error measures are now possible. The relative error between exact v_n found at step 1 and v_n found from Eq. (7) is the EEG numerical error. It occurs when the forward EEG problem is solved with the help of the reciprocal TES solution which could be beneficial for a very large (literally infinite) number of EEG dipoles.

On the other hand, an error between the directly computed E_fixed (r_n) · Q_n and the same expression but found from Eq. (7) using the exact (analytical) value of v_n is a field error of the TES solution itself. The result additionally depends on a presumably small error in the net electrode current I_fixed. However, since I_fixed is the same for all observation points and for all field components to be tested, it cancels out in the RDM error definition given by Eq. (4) which will output the RDM error for the field only. Furthermore, I_fixed can be pre-computed using a most accurate numerical solution and then considered as an exact value. This method is used for the estimation of the relative field error, ε, in the present study. Thus, the reciprocity principle makes it possible to estimate both the relative error and the RDM error for any TES field component in any domain of interest.

A standard EEG/MEG example is a four-compartment spherical geometry shown in Fig. 3a with the spherical radii of 92 (skin), 86 (skull), 80 (cerebrospinal fluid or CSF), and 78 (brain) mm, and conductivities chosen as 0.43, 0.01, 1.79, and 0.33 S/m – cf. [80],[81],[82],[37].

Fig. 3.

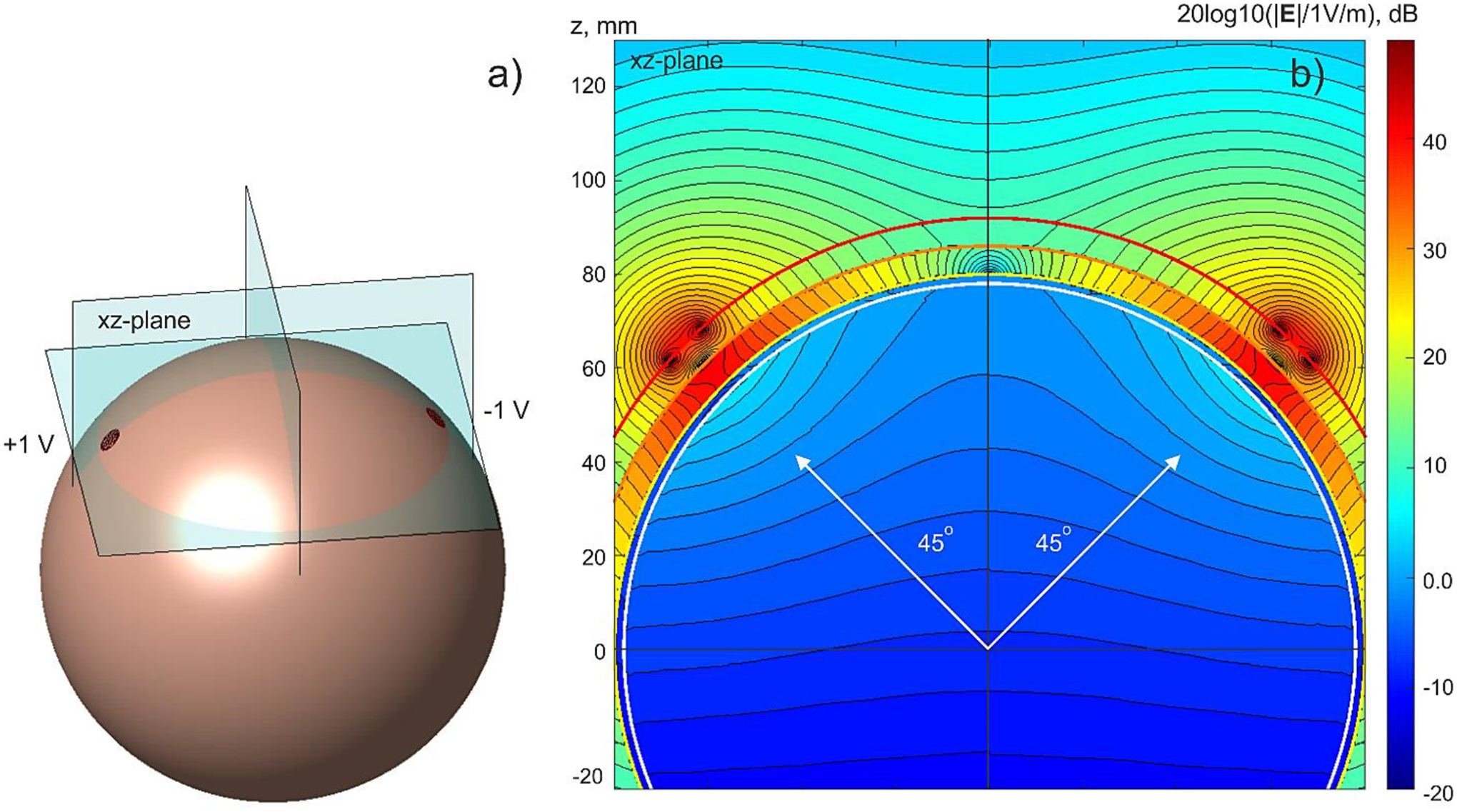
a) – TES problem geometry with imprinted voltage electrodes (± 1 V). Only outer (skin) spherical shell is shown. Every sphere has 47,492 facets; average edge length of the skin shell is 2.3 mm. b) – Total electric field (magnitude) distribution in the xz-plane using a logarithmic scale. Blocking effect of the low-conducting skull shell (0.01 S/m) is clearly visible.

Two TES electrodes with the diameter of 6.9 mm each (three times average edge length) are imprinted in the same azimuthal plane and at a 45 deg elevation angle – cf. Fig. 3a. The field within the brain shell is evaluated. This is a numerically challenging problem since the field there is by a factor of ~200 less than the field in the immediate vicinity of the electrodes – cf. Fig. 3b.

Table 2 gives relative and RDM tangential- and normal-field error values computed from Eq. (7) with the help of either tangential or radial auxiliary dipoles nearly uniformly distributed at 1 mm below the innermost shell. Every spherical shell has 47,492 facets. The BEM-FMM solution uses 35 (for lower skull conductivity) and 25 (for higher skull conductivity) iterations, precise analytical expressions for 16 topological neighbor surface integrals, relative FMM precision of 10⁻², and the full left preconditioner (Eq. (13b) of Appendix A) at the electrode surfaces. Additionally, two closest innermost surfaces in Fig. 3b are internally subdivided in proportion 1:4 to make sure that their average edge lengths are smaller than the separation distance. The terminal relative residual reaches 10⁻⁴ – 10⁻⁵ in every case.

Table 2.

Relative tangential- and normal-field error values computed from Eq. (7) with the help of auxiliary dipoles nearly uniformly distributed at 1 mm below the innermost shell in Fig. 3b. Every shell of the model has 47,492 facets. Preprocessing (to be done only once) time is ~40 sec. Solution run times with 35 iterations are ~40 sec. Field restoration time via FMM at 855,232 dipole positions is ~8 sec. Simulations have been performed on a Windows multicore workstation with Intel 6148 CPUs at 2.4 GHz (MATLAB 2020b). Last row gives the error of the Ansys FEM for one value of skull conductivity.

Skull cond., S/m	Testing tangential field with 855,232 auxiliary horizontal dipoles located 1 mm below the innermost shell		Testing vertical field with 855,232 auxiliary vertical dipoles located 1 mm below the innermost shell
	ε from Eq. (3) using 2 norm	RDM from Eq. (4) using 2 norm	ε from Eq. (3) using 2 norm	RDM from Eq. (4) using 2 norm
0.005	1.40%	0.37%	1.50%	0.48%
0.01	0.85%	0.23%	0.93%	0.29%
0.02	0.69%	0.21%	0.77%	0.26%
FEM software Ansys Maxwell Electronics Desktop 2020 R2
0.01	26.7%/10.0%	2.08%	27.3%/9.35%	2.17%

Conductivity of the field-blocking skull shell is varied in Table 2 in order to highlight its effect on the solution accuracy. It should be noted that the numerical EEG error in the surface electric potential from Eq. (7) exactly coincides with the values given in Table 2. This result is to be expected due to reciprocity.

The last row of Table 2 also reports the corresponding error of the FEM software Ansys Maxwell. The same shell meshes were used there (imported as *.stl files) and the same electrodes have been imprinted. Both methods are executed on the same workstation. The Ansys FEM solution (parallelized with 8 cores) requires 1 h 23 min to run. It uses 5 adaptive passes; the final mesh has 1.8 M tetrahedra. This Ansys project is made available online too [74].

Note that there are two numbers for the relative 2 norm error in the last row of Table 2. The first number is the authentic Ansys FEM result obtained when using the electrode current of 2.634 mA in Eq. (7). This value of the total current was computed from the FEM solution itself, by integrating the current density over the electrode surface. The second number is the same result but obtained when using the total electrode current found from the BEM-FMM solution, again after integration over the electrode surface. The BEM-FMM solution yields quite a different and apparently much more accurate value of 3.906 mA. Both values correspond to the ± 1 V voltage electrodes.

3.3. Example 3. Comparison with FEM for the field derivative along a path which is proportional to an activating function

A sample DBS-related problem geometry is considered next as shown in Fig. 4a. A cylindrical electrode body of 2 mm in diameter is modeled as a non-conducting lead with 4 full rings of perfectly conducting electrodes (with a vertical dimension of 1.5 mm and spacing of 2 mm each) embedded into a homogeneous isotropic medium of infinite extent. The exact conductivity value does not matter in this particular case; the auxiliary value of 0.1 S/m has been used.

Fig. 4.

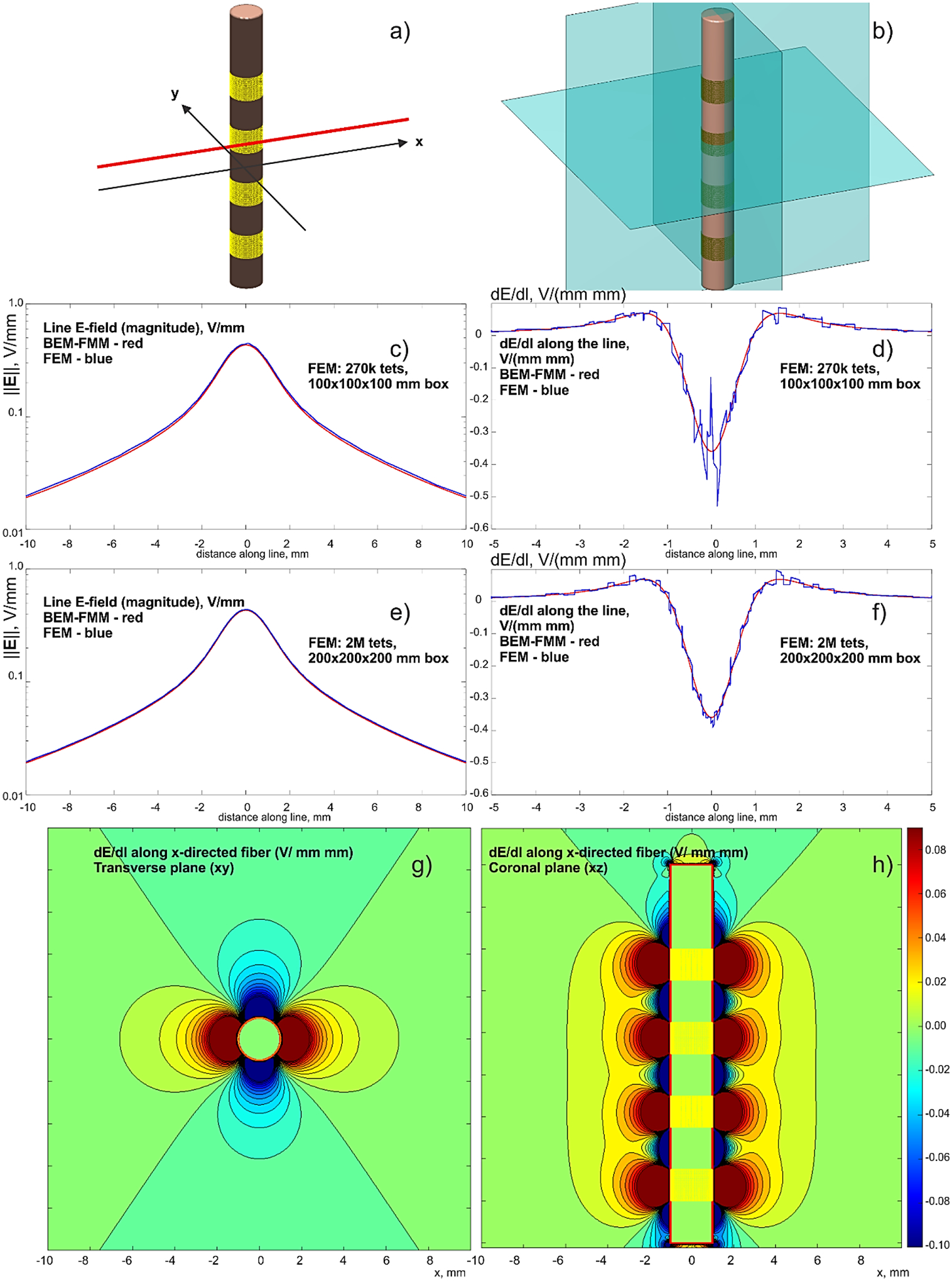
a,b) – Problem geometry with the observation planes. The insulating lead is 18 mm long. Four ring electrodes are driven with –1 V each. c,d) – Comparison with a lower-resolution FEM solution; e,f) – the same results for a finer FEM solution with a larger enclosing box. BEM-FMM solution is red; FEM solution is blue. g,h) – dE/dl for the x-directed fiber in two observation planes – BEM-FMM solution.

Using the FMM method of Appendix A, the field itself and the derivative of the field’s tangential component (proportion to an activating function) along a path are both computed. The path is a straight observation line shown in Fig. 4a. This observation line is separated from the electrode by 0.2 mm. The BEM-FMM solution uses 26,000 facets and 16 neighbor integrals. It executes in under 2 sec with the relative residual error of 10⁻⁶.

The concurrent FEM solution (FEM software Ansys^® Maxwell Electronics Desktop 2020 R2 with adaptive mesh refinement) uses an enclosing box of 100×100×100 or 200×200×200 mm and 0.27 M or 2 M tetrahedra, respectively. It executes in 17 and 24 min, respectively, using the same computer. Comparison results are given in Figs. 4c–h. Along with the corresponding BEM-FMM project, the Ansys FEM project is also made available online [74].

In Fig. 4, all four ring electrodes are driven with –1 V each to better highlight the solution behavior. The reference electrode (IPG) is at infinity. Figs. 4c,d show a comparison with the lower-resolution FEM solution for the electric field magnitude along the line and dE/dl along the line, respectively. For FEM, dE/dl is found by a direct differentiation of the numerical E-field solution. The corresponding results for the finer (and slower) FEM solution are given in Figs. 4e,f.

Finally, Figs. 4g,h show volumetric plots of dE/dl for the x-directed fiber in two observation planes obtained from the BEM-FMM solution (Appendix A, Eq. (23)). The spatial resolution (which is numerically unconstrained for BEM-FMM) of these plots has been chosen as 33 μm.

3.4. Example 4. Comparison with FEM for realistic head model – test of current electrodes

A validation example pertinent to TES is adopted from [83] and subsequently revised. Two circular TES electrodes with a fronto–medial placement and with a diameters of 30 mm each are imprinted onto the skin surface of subject #110411 of the Connectome database [84] as shown in Fig. 5a. Surface meshes have been obtained with the SimNIBS 2.1 pipeline [36] using the mri2mesh segmentation software; tissue properties – DC conductivity values – are adopted from [85]. The composite model has 0.86 M facets. The model of current electrodes (with a uniform current distribution and total current of 1 mA) is now used (Appendix A, Eqs. (10) and (11)).

Fig. 5.

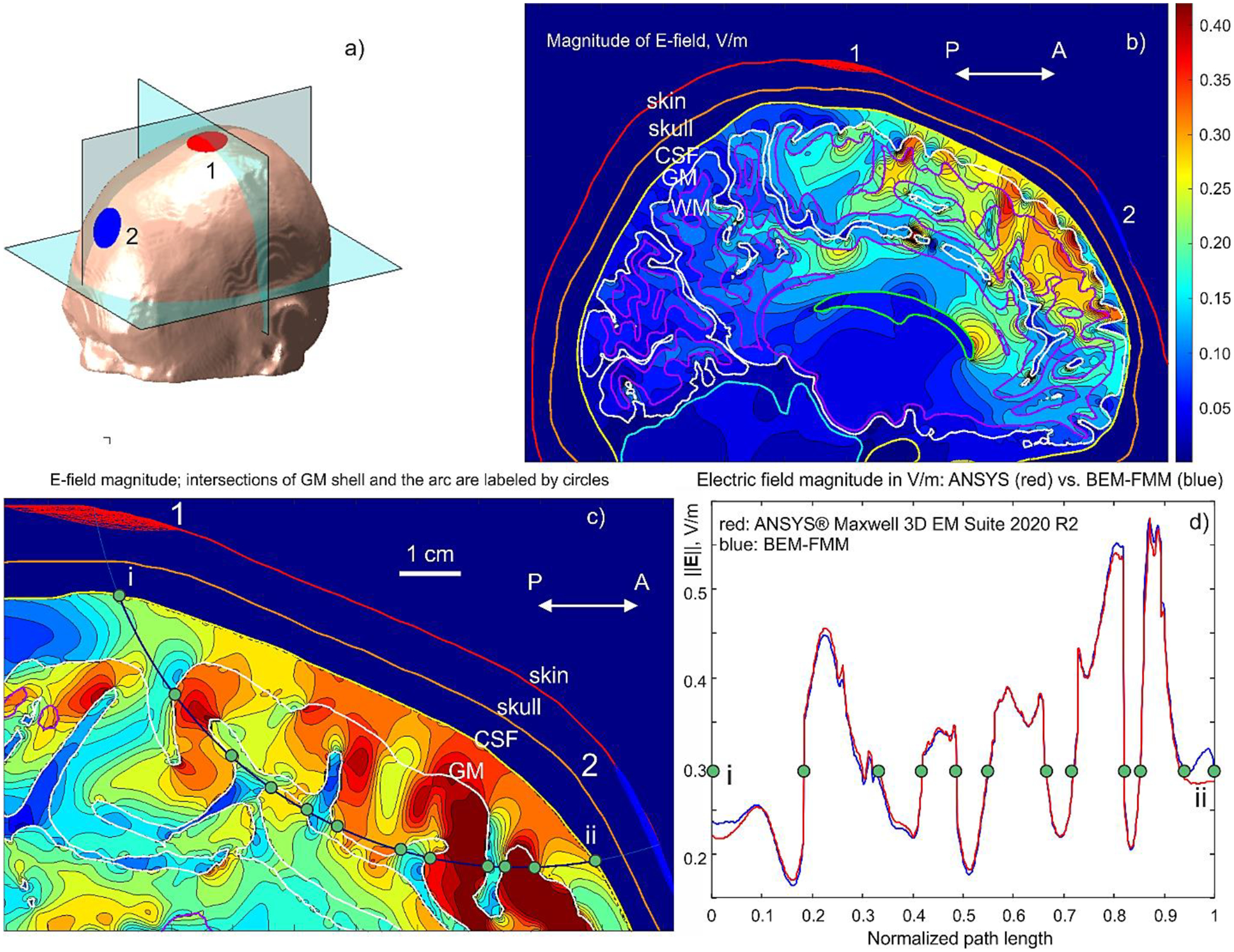
a) – Conformal electrodes with a fronto–medial placement for Connectome subject #110411; b) – Electric field magnitude in the intracranial volume in the sagittal plane; c) – Electric field magnitude in a plane containing an arc connecting electrode centers. Tissue intersections (CSF and GM) are shown by green dots. d) – Comparison of electric field magnitude along the arc connecting electrode centers with Ansys Maxwell FEM software. The same green dots – tissue interfaces – as in c) are depicted. Conductivity values are (S/m): scalp – 0.333 (avg.); skull – 0.0203; CSF – 2.0; GM – 0.106; WM – 0.065.

A numerical solution is again compared to FEM using Ansys^® Maxwell Electronics Desktop 2020 R2 but with voltage electrodes generating the same current (shunt electrodes). Fig. 5b shows the resulting electric field distribution (field magnitude) in the intracranial volume using BEM-FMM with eight neighbor integrals. Fig. 5c displays an arc connecting the electrode centers. Fig. 4d compares the electric field magnitude for both methods computed along the arc connecting the electrode centers. The FEM curve is shown in red, while the BEM-FMM curve is blue.

Next, Table 3 compares both simulations. For BEM-FMM, the required RAM did not exceed 6 Gbytes for the iterative solution while the FEM solution required 8 Gbytes for three adaptive passes and nearly 30 Gbytes of RAM for 6 adaptive passes. Its power loss error is ~0.2%.

Table 3.

Comparative performance of two modeling methods for a realistic (isotropic) head model. The FEM run times are for Intel Xeon E5–2698 v4 CPU (2.20 GHz) workstation with 256 Gbytes of RAM. The BEM-FMM run times are given for Intel Xeon E5–2683 v4 CPU (2.1 GHz) based workstation. The relative error in the field magnitude (based on 2 norm) is given for intracranial tissues (CSF, gray/white matter) only.

Ansys FEM	Ansys sol. time (8 cores)	BEM-FMM sol. Time	Intracranial rel. field magn. error for an arc in Fig. 4c	Intracranial rel. field magn. error in the entire coronal plane
4.8 M tets, 3 adapt. passes	2 h 29 m	~60 sec (rel. residual of 10−3)	3.1%	6.31%
6.9 M tets, 4 adapt. passes	6 h 23 m		3.0%	6.15%
9.0 M tets, 5 adapt. passes	8 h 43 m		2.9%	6.06%

4. Results – Application Examples

In the following, we investigated the performance of BEM-FMM for two application examples: one for a more realistic DBS scenario and another – for an epidural ICMS array embedded into a multicompartment high-resolution head model. Both examples require fine (submillimeter or better) resolution close to the electrodes.

4.1. DBS electrodes in a multicompartment model: Potential, field, and dE/dl distributions

A multi-compartment head-body model with a fully implanted DBS device (including IPG – internal pulse generator) and DBS electrodes (Fig. 6a) was constructed based on a realistic device configuration extracted from CT images of a patient at Northwestern University, Chicago IL (Figs. 6b,c).

Fig. 6.

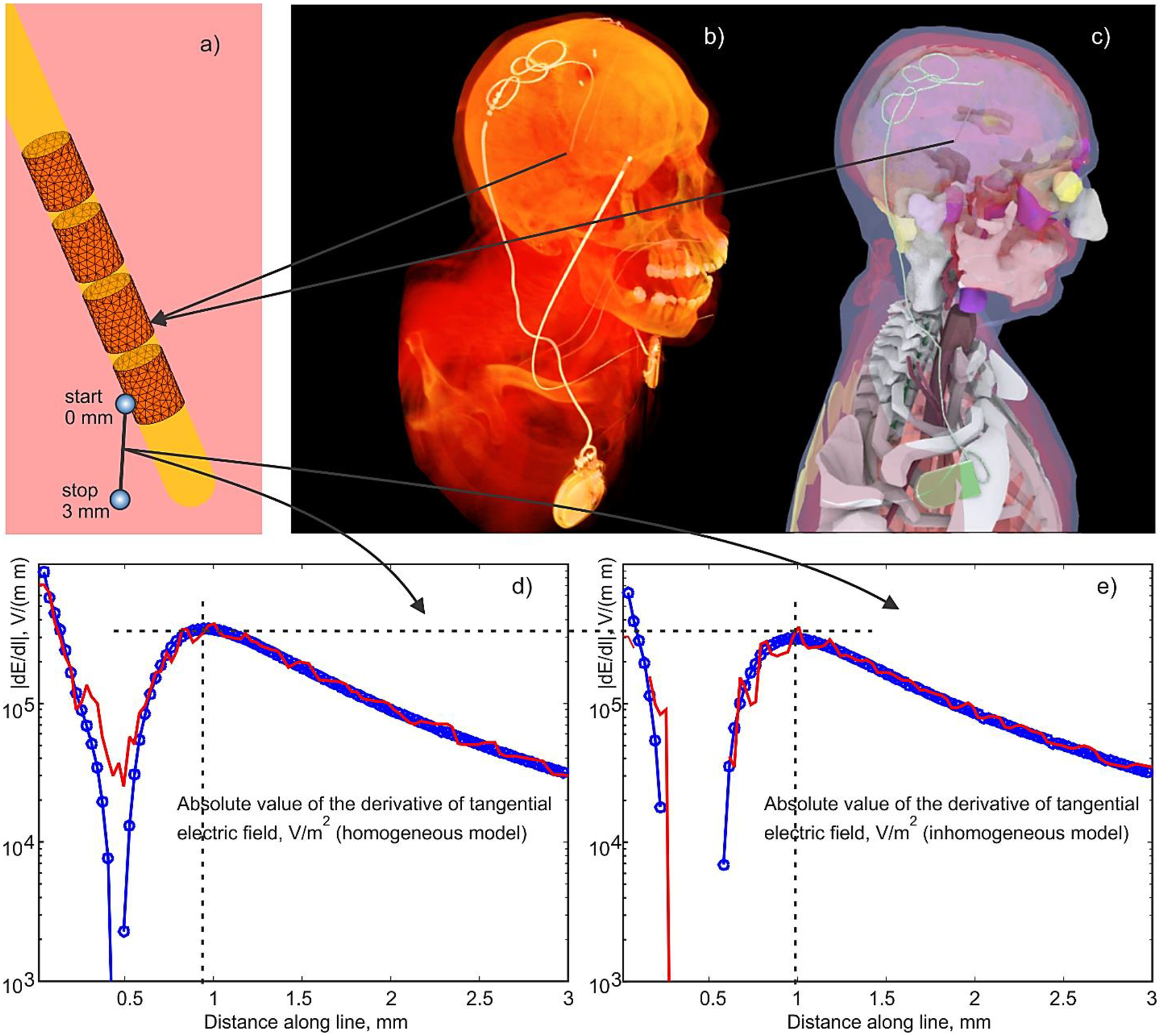
a) – BEM-FMM Electrode mesh assembly around insulating urethane lead. Active electrode is assigned –1 V vs IPG (held at zero voltage), and no specific voltage is assigned to other electrodes (floating condition). b) –CT of insulating lead/IPG with the electrodes; the second electrode relates to another device. c,d) – IPG Device with the lead and electrodes embedded into the CAD model; d,e) – magnitude of the derivative of the tangential electric field, dE/dl (the second derivative of the electric potential), along a small fraction of the polyline with the length of 3 mm shown in Fig. 6a which starts in the middle of the active electrode held at –1 V for homogeneous (d) and inhomogeneous (e) head/torso model, respectively. Ansys Maxwell FEM solution is marked red; BEM-FMM solution is marked blue.

A head model was further combined with a torso of another subject having multiple tissue objects to additionally model the fields close to the IPG when necessary. The device trajectory was manually segmented, and a 3D model of the implant was constructed and registered to a heterogeneous human body model consisting of 77 individual head/upper torso compartments. The DBS electrode is a Medtronic 3389 electrode (Medtronic^® Inc, Minneapolis, MN, USA) implanted into the thalamus volume. The resulting surface-based CAD model was imported into FEM software Ansys^® Maxwell 3D Electromagnetics Suite 2019 R1 and assigned the corresponding DC conductivity values adopted from [85]. The identical model was used in the BEM-FMM algorithm.

Fig. 6a shows the BEM-FMM electrode mesh assembly around the insulating urethane lead (assigned zero conductivity). Every electrode is assigned an independent voltage vs IPG (which is held at zero volts), or no specific voltage is assigned to some electrodes (the floating condition, Appendix A, Section A4.4). For better visibility, the non-conducting lead in Fig. 6a is shown transparent. However, only the BEM formulation on the external problem is solved; nothing is solved inside electrode body (Appendix A).

Fig. 6b shows an original CT image of the IPG device with embedded lead and electrode assembly. Fig. 6c shows the resulting multi-tissue human model with the registered lead and electrodes.

Figs. 6d,e show a variable part of the activating function, i.e. the magnitude of the derivative of the tangential electric field, dE/dl (the second derivative of the electric potential [87]-[93]), along a small straight external observation line with the length of 3 mm shown in Fig. 6a. The line itself starts just outside the active electrode (#1) held at –1 V for both homogeneous (d) and inhomogeneous (e) head/torso models, respectively. It has an incidence angle of 30°degrees with respect to the surface of electrode #1. All other electrodes are floating. The Ansys Maxwell FEM solution is marked in red and the BEM-FMM solution is marked in blue in both plots. We emphasize that the entire observation line in Fig. 6a is external to the lead; a lacuna seen in Figs. 6d,e occurs in the external space, at the distance of approximately 0.5 mm away from the electrode.

The ANSYS Maxwell FEM solution with 7 adaptive passes executes in approximately 1 h 36 min using a PowerEdge R815 4 AMD Opteron 6378/32 cores 2.4 GHz Windows S 2016 workstation using the high-performance parallel computing (HPC) option of ANSYS. The BEM-FMM solution with 50 iterations, sixteen neighbor integrals, and a relative residual of 10⁻⁶ executes in approximately 2.2 min using an Intel Xeon E5–2683 v4 CPU/48 cores 2.1 GHz Windows S 2016 workstation and MATLAB^® 2020b platform. This relatively large execution time (the model has only 0.4 M facets) is due to (i) a larger number of iterations needed and; (ii) a larger number of neighbor analytical integrals (128) needed in the solution. Such a number is found to be important because the model has facets of very different sizes.

Close to the electrode surface in Fig. 6a, the tangential electric fields along the line are very similar to each other for both numerical solutions. However, the tangential-field derivatives, which are proportional to the activating function of an axonal fiber [87]-[93], are not. The BEM-FMM solution in Figs. 6d,e is much smoother as compared to the FEM solution.

For a longer polyline that starts exactly as shown in Fig. 6a and then eventually terminates at the IPG, i.e. connects the center of the active electrode and the IPG, the least-squares error for the electric potential between the two solutions is 2.3%. The least-squares error in the tangential component of the electric field along the polyline is 2.0% despite the fact that both solutions change abruptly when passing through the tissue interfaces. Overall, both solutions for the electric potentials and the electric fields are hardly distinguishable visually. Similar results have been obtained for the homogeneous model.

4.2. Epidural planar ICMS array

A planar rectangular epidural ICMS array on the size of 5×5×0.5 mm with 100 circular electrodes (each with radius of 167 μm) was embedded into the head model of a 27 year old healthy female above the M1_HAND area of the left hemisphere. The surface meshes were generated with T1 and T2 images (Siemens Skyra fit 3 T, Max Planck Inst., Leipzig) using the “headreco” pipeline from SimNIBS 3.1 and extra refined. The default SimNIBS conductivity values have been used. Additionally, a dura (combined with arachnoid) mater shell was constructed with a thickness of 1.21 mm and a conductivity of 0.1 S/m by expanding the CSF shell and reducing the overall skull thickness accordingly. Fig. 7 shows the topology of the surface mesh superimposed onto T1 NIfTI data of the subject in the sagittal plane along with the synthetic dura shell. Fig. 8a shows the array electrode assembly and dimensions.

Fig. 7.

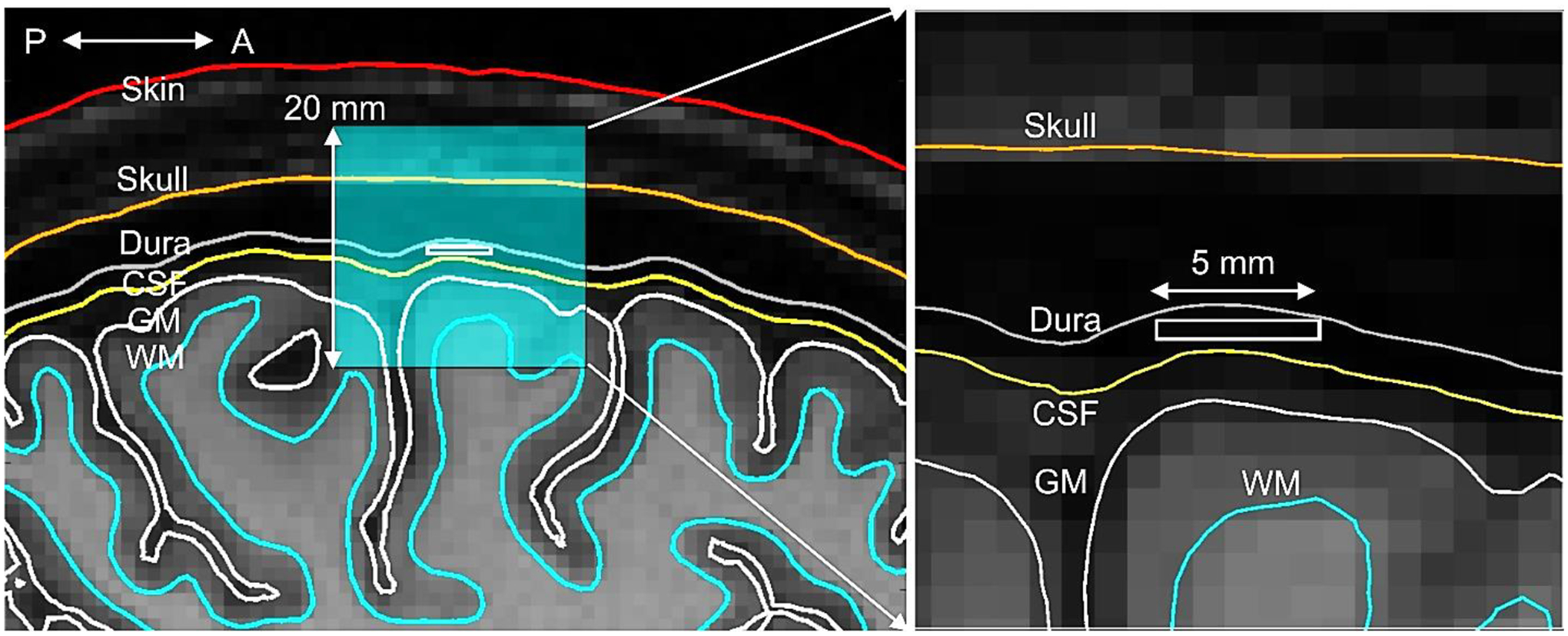
Topology of the surface mesh (sagittal plane) along with the synthetic dura shell superimposed onto T1 NIfTI data of the subject and the cross-section of the embedded array. The array cross-section is given by a white rectangle. Fig. 7b shows a zoomed in topology of the region of interest.

Fig. 8.

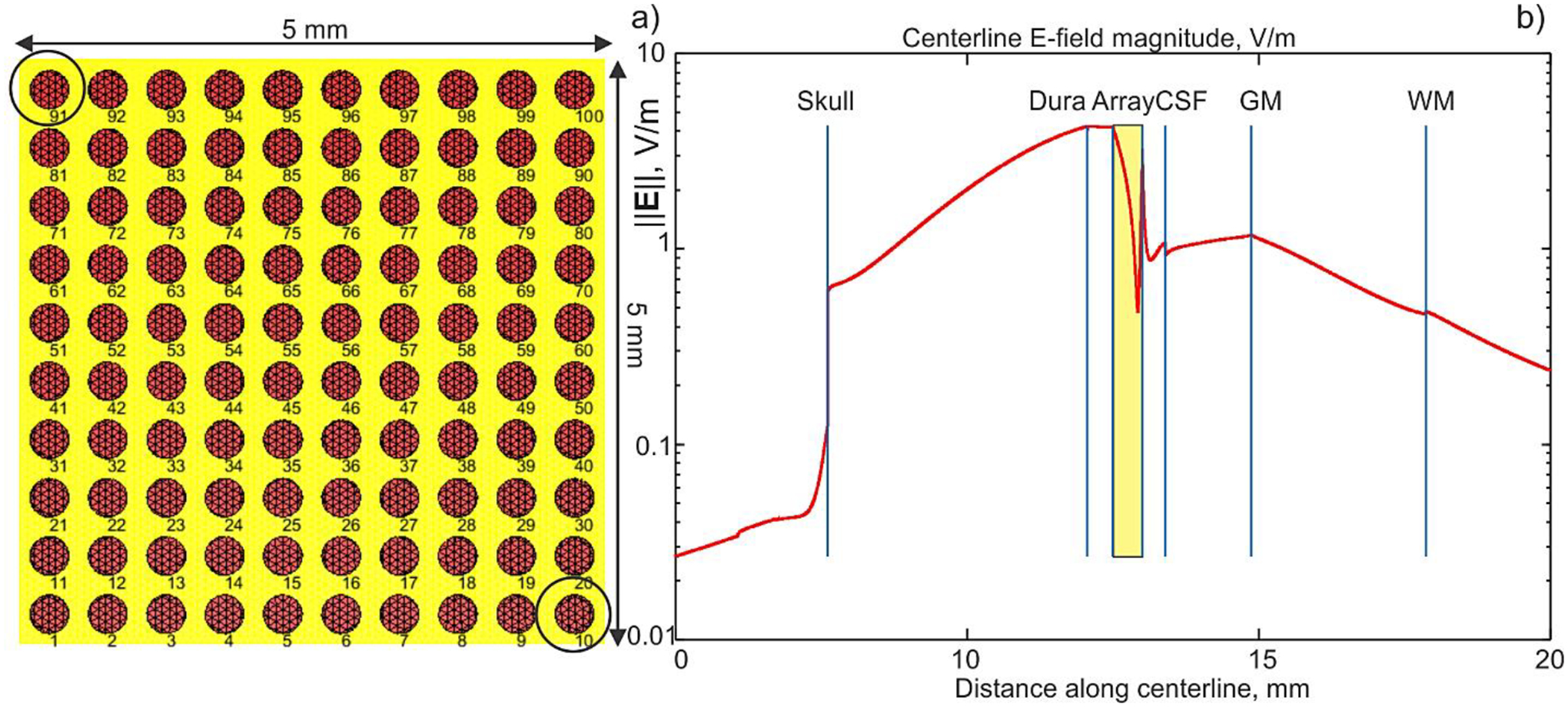
a) – Planar ICMS array assembly. Electrode radius is 167 μm. The insulating case is yellow. The array thickness is 0.5 mm. b) – Magnitude of the total electric field along array centerline which crosses different tissues. Array cross-section is marked by yellow rectangle. The array is targeting the M1_HAND area of the left hemisphere. Conductivity values in S/m are: scalp – 0.465 (avg.); skull – 0.01; Dura mater – 0.1; CSF – 1.654; GM – 0.275; WM – 0.126.

The array case in Fig. 8a is made insulating. The electrodes are driven as follows. Electrode #91 is assigned +1 V, electrode #10 is assigned – 1 V, and all other electrodes are assigned zero volts. After appropriate mesh refinement and adding the dura mater, the total number of faces in the full head model with the embedded array approached 2.6 M. The solution time of the BEM-FMM with four neighbor integrals was approximately 200 secs for 20 iterations and the relative residual of 10⁻³ on a 2.1 GHz Windows workstation (MATLAB 2020b); the required RAM did not exceed 11 Gbytes.

Fig. 8b shows the computed magnitude of the electric field along array centerline which crosses different tissues. Note the logarithmic scale of the plot. Array cross-section is marked by yellow rectangle. The array is targeting the M1_HAND area (Ω-shaped in the figure) of the left hemisphere. Simulation results reveal that, for the given array position and assembly, relatively small values of the electric field in the cortical volume will be generated. These values still approach ~1 V/m, despite the small array size. The distance between the array and the white matter shell is 8 mm. The same array could be used for iEEG recordings.

To examine the spatial array field distribution into the depth, Fig. 9 demonstrates magnitude distributions of the total electric field obtained just inside the following interfaces from Fig. 7a: CSF (Fig. 9a), gray matter or GM (Fig. 9b), a mid-surface between GM and WM (Fig. 9c), not shown in Fig. 7a, and white matter or WM (Fig. 9d). The initial focality is well preserved just inside the CSF interface where the electric field is also very high.

Fig. 9.

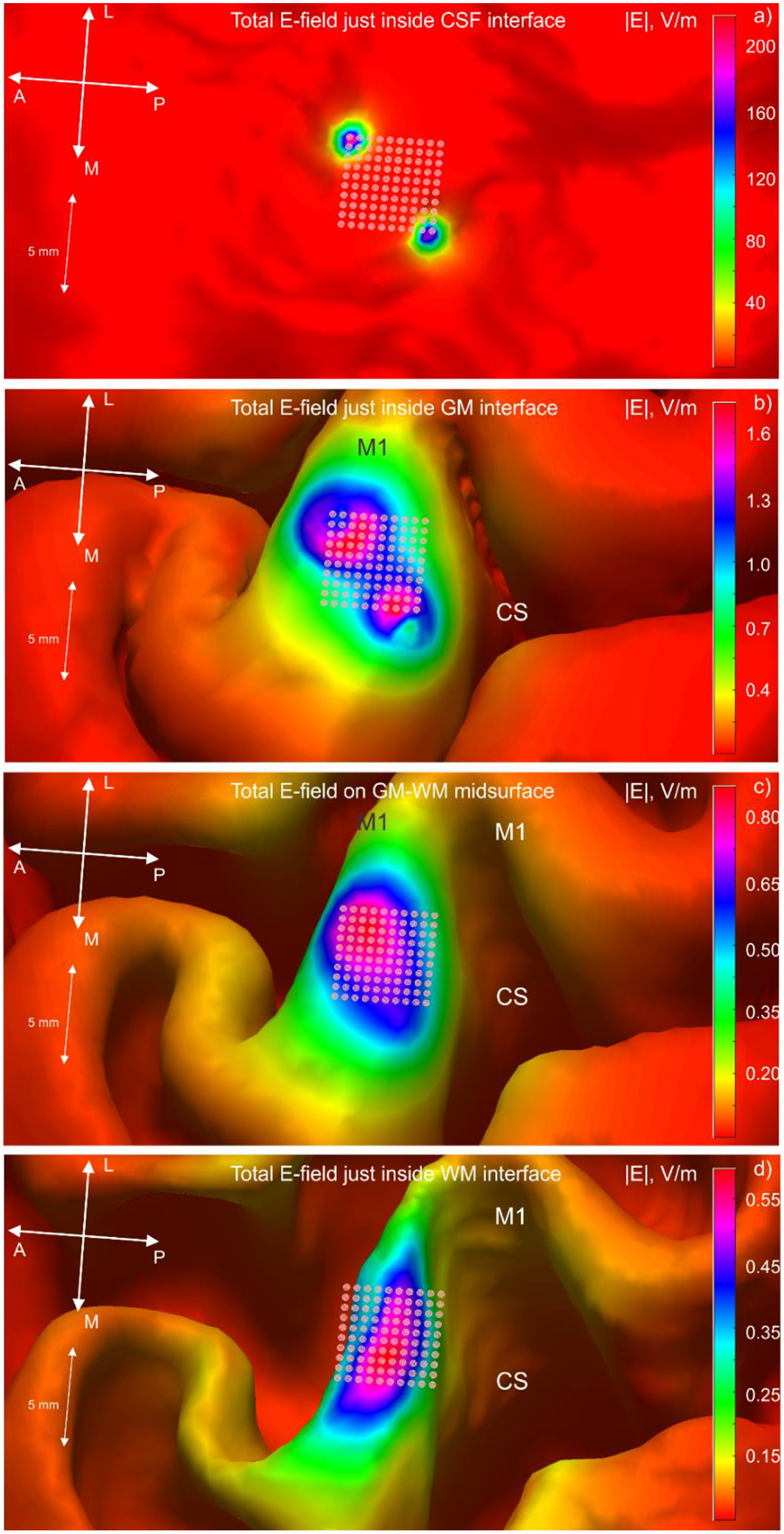
Magnitude distributions of the total electric field of the array just inside CSF interface (Fig. 9a), GM (Fig. 9b), mid-surface between GM and WM (Fig. 9c), and WM (Fig. 9d).

However, the array focality significantly deteriorates just inside the GM interface in Fig. 9b. There, the field also decreases by almost two orders of magnitude. Even a thin CSF volume thus blocks the bulk of the electric field of the embedded array. In the present case, the CSF effect may resemble the well-known blocking effect of the skull for TES.

When moving deeper, the focal spot in Fig. 9 approaches the array size at the mid-surface between gray and white matter, and continues to behave similarly just below the white matter interface. Other electrode excitation patterns leaded to similar results.

5. Discussion

5.1. Some general remarks

The examples presented in this study demonstrate that the BEM-FMM approach, whose background is described in detail in Appendix A, may be a viable tool for modeling electric brain stimulation with macro- and microelectrodes. In particular, it may potentially be beneficial for

1. Modeling TES problems for MRI-derived head models (Section 3.4) with a high tissue heterogeneity. For example, Ref. [94] specifically underscores a critical value of tissue heterogeneity for DBS simulations. This conclusion is partially based on a numerical study with a detailed FDA MIDA head model of 0.5 mm isotropic resolution [95] reduced to 12 compartments. On the other hand, BEM-FMM described here can perform accurate simulations for the same but complete MIDA model with 116 separate (yet isotropic) compartments in approximately 30 min as it was recently shown in [96],[97].

2. Modeling embedded ICMS arrays and other similar devices using a coupled meso- or multi-scale head-device model (Section 4.2) with a numerically unconstrained field resolution.

3. Accurate modeling of the activating function for embedded DBS electrodes and similar devices in a homogeneous (Section 3.3) medium and in realistic (Section 4.1) human models, with a numerically unconstrained spatial resolution. BEM-FMM offers the possibility to calculate field derivatives more accurately and faster than FEM as shown in Fig. 4, 6, and 10. A basic example for a homogeneous anisotropic medium that replicates the results for the DBS probe from Fig. 4 is discussed later in this section (Fig. 10). Authors are not aware of any similar result created with FEM.

4. Modeling EEG forward problems with a very large number of elementary dipoles (corresponding to a high cortical resolution) via the Helmholtz reciprocity principle (Section 3.3) and with a sufficiently high accuracy. This task likely requires a separate dedicated study.

Fig. 10.

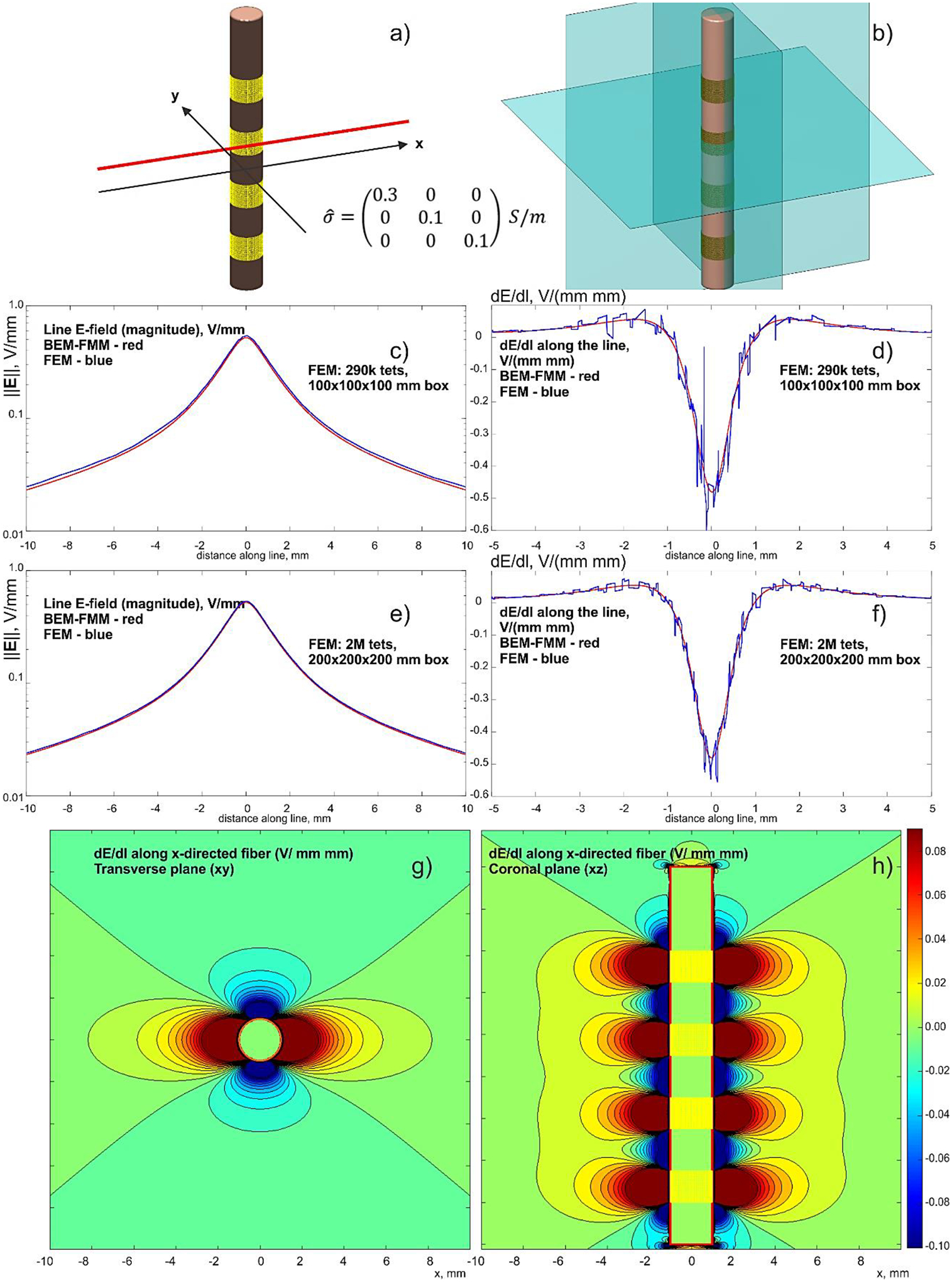
a,b) – Problem geometry with the observation planes. The insulating lead is 18 mm long. Four ring electrodes are driven with –1 V each. c,d) – Comparison with a lower-resolution FEM solution; e,f) – the same results for a finer FEM solution with a larger enclosing box. BEM-FMM solution is red; FEM solution is blue. g,h) – dE/dl for the x-directed fiber in two observation planes – BEM-FMM solution.

While the concepts of the voltage, shunt, and floating electrodes are common, the model of the true current electrodes (Appendix A) is rarely used and not implemented in any software packages known to the authors. On the other hand, it may be useful for the surface electrodes with sponges. Another immediate application is related to bioelectrodes with an impedance boundary condition [60], which involves both the voltage and the current density. This boundary condition is due to an electrochemical effect that takes place at the contact interface between the electrode and the biological medium [60].

5.2. Speed and memory consumptions

The BEM-FMM execution times are ~ 3 sec per iteration for a realistic head model with 0.86 M facets and ~10 sec per iteration for an accurate model with 2.55 M facets using a 2.1 GHz workstation. Thus, the simulation time scales nearly linearly with increasing mesh size for the surface-based model. In consequence, we observed that the memory requirements of the BEM-FMM may be twofold or even sixfold less than for the FEM (Section 3.4) when the same problem is solved. It should be noted that the differences between BEM-FMM and FEM are not solely originating from inaccuracies of the BEM-FMM. They also result from the approximate nature of the FEM model due to too coarse discretizations as it is shown by Gomez et al. 2020 [101] in the framework of TMS. In this case, the FEM solution should not be interpreted as a reference solution. Rather, it is a comparative solution.

While the memory requirements of the BEM-FMM are more advantageous, the FMM algorithm used in this study requires a heavy parallelization. All results reported above have been obtained on the workstations with 40 and 48 cores, respectively. Our experience indicates that the number of cores is much more critical than the amount of RAM. The low RAM requirement and the good scalability in terms of CPU cores opens the possibility of an efficient GPU implementation which may reduce the computing time significantly.

The BEM-FMM computational speeds reported in this study are slower than those for TMS modeling [50] due to inclusion of a larger number of neighbor potential integrals and due to the fact that a typical electrode-based solution requires around 20–40 iterations to resolve the field singularities at the electrodes reasonably well. It is well known that both the surface charge density and the electric field are singular at the electrode rims [55].

5.3. Numerical accuracy as compared to analytical results

The multi-sphere validation example with imprinted electrodes from Section 3.2 summarized in Table 2 is perhaps most interesting from the numerical and/or testing point of view. The quasistatic reciprocity theorem [62],[63],[76],[77] applied in this study allows us to test the TES numerical solutions against the well-known and powerful EEG (and MEG) analytical results for the challenging geometries. The accuracy of the comparison results given in Table 2 is remarkable despite the finite electrode size (strictly speaking, a point electrodes are required for the reciprocity). These results are rather general; they were obtained without using tailored improvements such as solution error subtraction for a degenerate case of a zero-conductivity skull shell [99],[73]. The error for a very low skull conductivity in Table 2 indeed increases but it could likely be tolerated in the range of realistic tissue conductivity values.

The modern and powerful FEM EEG/MEG modeling software DUNEuro ([100], see also [81],[82]) may reach a comparable accuracy for the given problem. There are ways to further reduce the numerical error of the BEM-FMM solution too. One can apply the well-known approach such as solution error subtraction for the fully non-conducting skull [99],[73], reduce electrode size, increase the number of accurate neighbor integrals, etc.

However, the reported sub-percent numerical accuracy may already be good enough. Other physical error sources (conductivity, segmentation, and electrode impedance uncertainties) will certainly more substantially contribute to the final modeling solution.

5.4. Open problems pertinent to numerical accuracy of BEM-FMM

There is a dilemma between precomputing and storing more neighbor potential integrals or, conversely, putting more integration points over (all or selected) triangular facets themselves and then employing the power of the FMM. The first approach seems to be faster, but it requires larger preprocessing times and extensive storage. The second approach is equivalent to internal triangle subdivision while keeping the original mesh topology the same. It is trivially handled by the FMM engine using barycentric or Gaussian triangle subdivisions into smaller triangles. Moreover, the triangular mesh does not have to be manifold for the pulse basis functions defined on individual triangles. We attempt to achieve a balance between the two approaches. The average triangle size for two tightly spaced interfaces should likely be chosen smaller than the separation between the interfaces (cf. Appendix A). Otherwise, a prohibitively large number of the precomputed potential integrals might be necessary.

In every case, the accuracy and convergence of the BEM-FMM solver strongly depend on the proper inclusion of potential integrals. They must always be present, for at least immediate neighboring facets. One can distinguish between neighbor facets belonging to the same interface or neighbor facets on the tightly coupled interfaces. A proper selection of the number of neighbors should be done carefully in this case and in the case when the objects with very different surface mesh sizes (as in the ICMS array example) are modeled, in the vicinity of each other. This procedure is not automated. An adaptive mesh refinement at the electrodes and elsewhere is another highly desired step.

5.5. On inclusion of tissue anisotropy

The present modeling approach does not include tissue anisotropy into consideration. In terms of the method of volume integral equation (cf. for example, [103],[104]) and the charge-based approach, the anisotropy results in appearance of some volumetric dipolar charge density distributed in the entire anisotropic volume. To support this charge density, a tetrahedral mesh could be used, either in a region of interest or in the entire volume. Then, a proper coupling could be made between the surface and volume integral equations as suggested in Ref. [103], and both equations can be solved simultaneously. If the tetrahedral mesh is used in the entire volume, the advantages of the BEM (and BEM-FMM) approach could become questionable. A very interesting approach by introducing a spatial distribution of one-dimensional “brain fibers” instead of the tetrahedral mesh has been discussed in [104].

The effect of anisotropy is particularly important for DBS, especially in a small volume close to the electrodes themselves [98]. A simple anisotropic BEM-FMM solution is possible in this case that is described below and illustrated in Fig. 10. It is assumed that the anisotropic conductivity tensor is (locally) constant and that the medium is (locally) homogeneous. The solution is based on an almost trivial co-ordinate transform discussed yet by Smythe [105] that makes the Laplace equation isotropic by normalizing each Cartesian coordinate by the square root of the corresponding conductivity. Similar transform can be applied to locally spherical models.

The example of Section 3.3 is considered again but the homogeneous medium surrounding the electrode body is now anisotropic with the conductivity tensor given by

$$\widehat{\sigma }=\left(\begin{array}{ccc}0.3& 0& 0\\ 0& 0.1& 0\\ 0& 0& 0.1\end{array}\right)S/m$$ (8)

i.e. with the predominantly x-directed axonal fiber. A BEM-FMM solution again executes in under 2 sec while a concurrent FEM solution (Ansys^® Maxwell ED 2020 R2) requires up to 30 min to achieve a sufficient solution accuracy. The comparison results are given in Fig. 10 that follows.

This figure is an exact replica of Fig. 4, but with the anisotropic conductivity tensor. The same scales have been used in both cases. Figs. 10c,d show comparison with the lower-resolution FEM solution for the electric field magnitude along the line and dE/dl along the line, respectively. For FEM, dE/dl is found by direct differentiation of the numerical solution. The corresponding results for the finer FEM solution (~ 30 min execution time) are given in Figs. 10e,f. Figs. 10g,h show dE/dl for the x-directed fiber in two observation planes obtained with the help of the BEM-FMM solution. The spatial resolution has been chosen as 33 μm.

As compared to Fig. 4, the distribution of dE/dl substantially “stretches” in the x-direction dure to anisotropy. The corresponding stretching factor can be estimated analytically as $\sqrt{3}\approx 1.7$. Compared to Fig. 4, the FEM solution indicates more noisiness in the activating function while the BEM-FMM solution does not.

Another point of concern is that the linear Lagrangian P1 FEM approach used in this study for comparison purposes does not lead to current preserving solutions and therefore may lead to inaccuracies, especially in the modeling of embedded electrodes. Other FEM approaches [81],[82] might lead to more accurate results than the used FEM approach.

The method suggested and discussed in this section could probably be useful for efficient approximation of deep brain stimulation and the induced electric fields in the immediate vicinity of DBS electrodes or for approximation of electric fields close to microarrays. For example, it could replace isotropic FEM computations with commercial software COMSOL used in clinically oriented modern DBS modeling software [46] by providing a much higher speed, better accuracy and resolution of the activating function, and by additionally including any required local tissue anisotropy in a simple way.

6. Conclusions

In this study, the boundary element fast multipole method (BEM-FMM) was formulated as an alternative to the finite element method (FEM) for modeling electrode-induced fields in the brain. The suggested method implementation is based on two properly coupled integral equations: one for tissue interfaces and another for the electrodes. It supports voltage, shunt, floating, and current electrodes.

Comparison with the analytical solutions and with the commercial FEM software demonstrated higher accuracy of the BEM-FMM algorithm for various models, both in the vicinity of the electrodes as well as in the entire tissue volume. The method can be easily combined with existing head modeling pipelines such as headreco or mri2mesh by using the segmented and meshed surfaces. The simulation time is similar to fast TES FEM solvers such as SimNIBS and exceeds the speed of the commercial solvers (Ansys Maxwell and COMSOL) by approximately two orders of magnitude.

Two application examples demonstrated the advantage of the BEM-FMM, namely its potential applicability to model multiscale problems with submillimeter (and finer if necessary) resolution.